Multiple Imputation for Missing Edge Data: A Predictive Evaluation Method with Application to Add Health

Abstract

Recent developments have made model-based imputation of network data feasible in principle, but the extant literature provides few practical examples of its use. In this paper we consider 14 schools from the widely used In-School Survey of Add Health (Harris et al., 2009), applying an ERGM-based estimation and simulation approach to impute the network missing data for each school. Add Health's complex study design leads to multiple types of missingness, and we introduce practical techniques for handing each. We also develop a cross-validation based method – Held-Out Predictive Evaluation (HOPE) – for assessing this approach. Our results suggest that ERGM-based imputation of edge variables is a viable approach to the analysis of complex studies such as Add Health, provided that care is used in understanding and accounting for the study design.

1. Introduction

Missing edge variable data – i.e. edge variables in an observed network whose states are unknown – has long been recognized to be a serious problem for social network analysis (Burt 1987). Network analytic concepts and measures are generally defined with respect to a completely observed graph (Wasserman and Faust, 1994) and the non-extensive nature of many network properties makes them difficult or impossible to estimate by e.g. simply averaging observed local network information. While ad-hoc methods such as treating missing edges as absent, dropping vertices with missing edge information, etc. have been employed, these can produce misleading or incorrect estimates (see Ghani et al., 1998; Huisman and Snijders, 2003; Kossinets, 2006; Huisman and Steglich, 2008; Huisman, 2009; Almquist, 2012); methods for handling missingness from one source by integrating measurements from other sources (e.g. Butts, 2003) can work well, but require data unavailable to most network researchers. Unfortunately, missingness is sometimes impossible to avoid, or arises from flaws in study design that are unrecognized until after data collection. Given the importance and scope of this problem, finding practical and principled ways to deal with it has been an important priority in network research.

A significant development in this regard has been the emergence of techniques for fitting exponential family random graph models (ERGMs) in the presence of missing data. The core insight (introduced by Handcock in 2002) is that the latent missing data framework developed by Rubin (1976) in a non-network context can also be applied to edge variables: given a parametric model, and appropriate assumptions regarding the nature of missingness, one can derive the likelihood of the observed data as a marginalization of the complete-data likelihood over the possible states of the missing variables (in some cases weighted by a factor related to the probability of the observed pattern of missingness). Techniques for performing maximum likelihood estimation (MLE) under these conditions (and theory regarding the nature of the assumptions required) have been developed by Robins et al. (2004) and Handcock and Gile (2010), with recent Bayesian extensions by Koskinen et al. (2010, 2013).

The current state of the art may be briefly summarized as follows. First, it is usually assumed that the pattern of missingness is ignorable (i.e., that any unknown parameters governing the observation process are distinct from those being estimated, and the probability of the pattern of missingness depends only on the values of the observed data and/or covariates). Ignorability can in some cases be relaxed (albeit not without altering the likelihood calculation), but is satisfied exactly or approximately for many real-world designs [see, e.g., Handcock and Gile (2010) for a discussion]. Second, a model is posited for the graph as a whole (here, a parametric model in ERGM form). Finally, the likelihood for a given parameter vector is then calculated by marginalizing the ERGM likelihood for the full network over all possible complete networks that are compatible with the observed data. This observed data likelihood is then employed for purposes of inference.

Although the emphasis of these techniques is on ERGM inference, it is clear that they also provide an approach to the more general problem of network imputation: given an adjacency matrix Y with realization y of which portion y^obs is observed and y^mis is missing, y^mis can be modeled via conditional prediction from an ERGM fit to y^obs. Specifically, let θ′ be an estimate (e.g., an MLE) for the parameter vector of an ERGM with sufficient statistic t given data y^obs. Then we generate draws Y^mis ∼ ERGM(θ′|y^obs), where ERGM(θ′|z) denotes the ERGM distribution with statistic t and parameter θ conditional on z (i.e., with the elements of Y contained in z held fixed). Such draws may be taken using standard Markov chain Monte Carlo (MCMC) methods (see Snijders, 2002; Snijders et al., 2006; Wasserman and Robins, 2005), and indeed simulations of this sort are used as part of the latent missing data estimation process described above. Draws from Y^mis can then be used to estimate various features of y^mis (the true missing data) or y=y^obs∪y^mis (the true state of the graph).

While the basic logic of ERGM-based network imputation is straightforward, there are to date few published use cases (to our knowledge, e.g., Handcock and Gile, 2010; Koskinen et al., 2010, 2013). Likewise, the existing literature gives little guidance on assessing the quality of network imputation (an important practical consideration in everyday use). In this paper, we attempt to rectify this latter deficit by introducing a simple cross-validation based method – what we term Held-Out Predictive Evaluation (HOPE) – to assess the accuracy of imputed draws from an observed-data ERGM.

We apply the ERGM-based network imputation method to model the missingness and error inherent in the Add Health data set (Harris et al., 2009). This provides for a useful demonstration given that this is a widely used study in the literature, and that it has a high level of missingness making it a very complex and challenging case. The Add Health case is also useful for demonstrating the use of multiple sources of information (particularly, marginal constraints on degree and group-specific mixing) in aiding estimation (something not explored in most published work to date). For our study, we use the friendship networks from 14 schools in the saturated sample of Add Health. As we are using a real-world data set (rather than simulated data), our focus is on technique illustration rather than method evaluation per se; however, as we will demonstrate, one feature of our approach is that it provides some basis for evaluation on available data. As we show, ERGM-based imputation can produce reasonable results in a real-world setting (although careful attention must be paid to the complexities of one's study design).

As a complement to the above-mentioned methods of imputation, we introduce a simple strategy we call Held-Out Predictive Evaluation (HOPE) for evaluating the quality of imputation in real-world settings. As discussed below, HOPE involves holding out a stratified sample of edge variables from the graph prior to model estimation and imputation, and using the predictive accuracy of the model on the imputed data as an indicator of imputation quality. It is worth emphasizing that the HOPE method sets a relatively high bar for accuracy, compared to common methods of assessing the latent missing data imputation framework developed by Rubin (1976) outside of the network context. In that context, the typical approach for assessing the quality of imputation is to assess how well the estimated parameters for the imputed data compare to the true parameters. Thus, the question posed is whether the imputed data are able to accurately capture the proper coefficients for a specific model. By contrast, HOPE directly assesses the ability of an imputation model to correctly identify present and absent edges in the (unknown) true network. This tough but general standard is useful when imputation is being performed without knowledge of what analyses will need to be subsequently conducted on the resulting graph (e.g., when the imputed draws will be shared with other researchers, or at the early stages of a multi-stage investigation), and/or when the same imputed draws will be used for several different purposes (rendering any single model-based evaluation problematic). HOPE may also be useful as an easily interpretable adjunct to other quality measures, and can serve as the basis for a wider range of predictive evaluation measures employing specific graph properties.¹

2. Data source, multiple types of network data missingness, and treatments

2.1 Data source

Our data comes from the first wave of the National Longitudinal Study of Adolescent to Adult Health (Add Health), a longitudinal study of a stratified sample of US schools from 7th to 12th grades (see Harris et al., 2009). (A “school” in this case consists of a high school, in some cases united with a “feeder” school whose students ultimately attend it. We use the singular “school” to refer to such high school/feeder school pairs.) All participants were invited to take the In-School Survey (n = 90,118) during 1994 and 1995. A random sample of 20,745 students selected from the In-School Survey respondents completed a wave 1 In-Home Survey, which was administered between April and December, 1995. Approximately one year later, participants who had not yet graduated from high school were asked to take a Wave 2 In-Home Survey (n = 14,738) between April and December, 1996. Information on social and demographic characteristics (i.e., gender and grade) of the respondents, attending classes and grades, extracurricular activities (i.e., club and sport-team participation), education and occupation of parents, household structure, risk behaviors including tobacco and alcohol use, expectations for the future, self-esteem, and health status were collected. Each student was also asked to nominate up to five best female friends and five best male friends.² In this paper we focus on the saturated sample of 4,431 students collected from 14 out of 132 participating schools.³ As shown in table 1, the roster size of our 14 schools range from 30 to 2,104.

Table 1. Descriptive statistics for the 14 schools.

School ID	Roster size	No outgoing edge missingness		Partial outgoing edge missingness		Complete outgoing edge missingness
		Cases	Percentage	Cases	Percentage	Cases	Percentage
002	85	78	92%	0	0%	7	8%
003	178	131	74%	1	1%	46	26%
007	181	155	86%	8	4%	18	10%
008	133	106	80%	5	4%	22	17%
028	193	132	68%	1	1%	60	31%
058	1024	782	76%	23	2%	219	21%
077	2104	1544	73%	56	3%	504	24%
081	135	115	85%	0	0%	20	15%
088	102	64	63%	15	15%	23	23%
106	95	82	86%	3	3%	10	11%
115	30	26	87%	3	10%	1	3%
126	60	50	83%	0	0%	10	17%
194	47	44	94%	1	2%	2	4%
369	64	62	97%	0	0%	2	3%

2.2 Multiple types of network data missingness

As described above, missingness in a study like Add Health can arise for many reasons. Setting aside the by-design censoring of responses by gender, and focusing entirely on relations within each school, we may summarize the overall level of missingness in the Add Health wave 1 network data by the frequency of three basic patterns (summarized in Table 1):

1. No outgoing edge missingness: The respondent completed the In-School Survey, and we know how many female and male friend(s) he or she nominated and who they were. Essentially, this respondent has provided complete network information. As shown in Table 1, the lowest proportion of respondents having no outgoing edge missingness is 63%, from school 088.

2. Partial outgoing edge missingness⁴: In some cases, respondents completed the survey but had alters who could not be validly and uniquely identified. One way this could arise was by a respondent entering an invalid code; this was either recognized to refer to no student (and marked invalid), or referred to a student whose gender did not match (i.e. a female or male ID in the male or female friend list). This is properly an example of informant inaccuracy, but one that leaves us uncertain as to the identity of the alter in question (and hence manifests as missing data). Examination of the rank placement (friend list ordering, from 1 to 5) of misplaced nominees suggests that these are non-systematic (random) errors, thus we consider them as missing edges (i.e., we assume that the gender is correct but the nominee ID is wrong). As shown in Table 1, this situation is found in 10 out of 14 schools. The number of misplaced ID(s) ranges from 1 to 56. None of our respondents is found to have two or more nominees in the wrong-gender friend list. A second way in which partial edge missingness could arise was by a respondent reporting that a particular edge was in fact a romantic partner. In these circumstances, the Add Health administrators coded these edges anonymously for privacy reasons. We code these as missing (i.e., we know that an edge exists to someone of the appropriate gender, but not the identity of the alter).

3. Complete outgoing edge missingness (missing actors)⁵: Some respondents of the 14 schools are found to take the wave 1 In-Home Survey and/or the wave 2 In-Home Survey but never took the In-School Survey. Those respondents were included in the Add Health survey roster from the very beginning – despite missing (e.g. due to a sick day) the actual In-School Survey assessment. Using constant covariate data from later waves, we are able to recover personal information on respondents' gender and grade. As shown in Table 1, the proportion of missing actors ranges from 3% to 31%.

Overall, Table 1 shows that the degree of missingness in the Add Health data is quite high. Even leaving aside censoring, a large fraction of respondents in many schools either did not provide nominations (e.g., were absent) or provided nominations that could not be uniquely matched to individual alters. This raises significant difficulties for analyses requiring detailed network structure (or even simple properties such as in-degree). Nevertheless, there are principled means of accounting for missingness, to which we now turn.

2.3 Treatment of network data missingness

For each saturated school, friendship networks are generated according to directed binary relational choices. This choice structure can be represented by an adjacency matrix Y of dimension n by n, where n is the number of respondents in the school. If a respondent i nominated another respondent j as a friend, we code the edge variable as “1” (edge presence) otherwise it is coded as “0” (edge absence). Our matrix represents a directed network in which nomination choices are not necessarily reciprocated. For example, i can nominate j as a friend but j can choose to not nominate i as a friend (i.e., Y_i,j ≠ Y_j,i). Therefore the elements above and below the main diagonal of the sociomatrix may not be symmetric. The relationships of respondents to themselves, i.e., the main diagonal elements of the sociomatrix, are undefined.

Because this network was measured in such a way as to make degree constraints inherent to the elicitation process, we further treat our graph as degree constrained; specifically, the out-degree of each vertex with respect to the set of vertices within each gender is constrained to be not greater than five. This can be understood as defining missingness relative to the fully observed data – i.e., the data set that would have been observed if all respondents had completed the questionnaire as asked, in a way that validly identified all alters – rather than to the underlying social network. Although it is tempting to attempt inference to the latter, this requires additional assumptions regarding the effect of the censoring point on respondent behavior, as well as informant accuracy more generally (Butts, 2003). Lacking a firm basis for such assumptions, we here restrict ourselves to the problem of imputing the answers that would potentially have been obtained had there been no limitations due to off-roster nomination, non-response, and the like.

Given the above, we proceed by considering different sources of information available regarding nominated alters, and accounting for as much of this as possible within a combination of observed data and conditioning constraints on the unobserved edge variables. As a first step, we note that for respondents with no missing outgoing edges, their rows in the adjacency matrix are fully specified; both their outgoing nominations (edges, or 1s) and potential alters not nominated (nulls, or 0s) are uniquely defined, and can be treated as fixed.

Second, for respondents with invalid or censored nominations (e.g., due to gender mismatch, off-roster nomination, or romantic tie) in a given gender category, we regard their row entries for potential alters of the specified gender (and, if applicable, off-roster status) other than those validly named to be uncertain (i.e., missing, or NAs). E.g., if respondent i has an invalid alter named in his or her female list, all elements in row i associated with females who were not validly named as alters are treated as NAs. Validly named alters are treated as 1s (since we are certain that the ego in question named them). In the event that respondent i instead named an off-roster (but otherwise valid) alter in a his or her female list, only entries pertaining to off-roster females would be treated as NAs (since only this group is in question). In all cases, we record the number of incompletely identified alters named, by gender and roster status (where known). This information is used by our model when inferring where to place missing edges (as discussed below).

Finally, for respondents who did not respond to the survey, we treat their entire row of the adjacency matrix as missing (NAs). Note that such respondents may or may not be uniquely identified as alters by other egos (depending on roster status), and hence may have non-NA elements in their respective adjacency matrix columns.

The result of this process is an incomplete adjacency matrix whose i,j entries are: 0 if it is known that student i did not nominate student j; 1 if it is known that student i did nominate student j; and NA if it is not known whether student i “did nominate” (or, in some cases, “would have nominated”) student j as a friend. We have also, for each student, the minimum and maximum number of nominations from him or her to: the set of all male students; the set of all female students; the set of all male off-roster students; and the set of all female off-roster students. [These counts are inferred from the invalid and/or off-roster entries in each respondent's male and female nominee lists, and (for non-respondents) from the global male/female out-degree constraint.] The edge variables that are coded as NAs are the portion of the adjacency matrix that the ERGM model will impute during the simulation portion of the process, subject to the group-specific out-degree constraints described above.

3. ERGM estimation and simulation process

By a combination of inference and simulation, we may employ model-based procedures to estimate uncertain edge states associated with missing data. Here, we pursue this within an ERGM-based framework.

A random graph model in ERGM form can be expressed as

$$\text{Pr}(Y=y|\theta ,X)={\mathrm{I}}_{\mathcal{Y}}(y)exp({\theta }^{T}t(y,X))/[{\sum }_{y\prime \in \mathcal{Y}}exp({\theta }^{T}t(y\prime ,X))]$$ (1)

where Y is the (random) adjacency matrix with state y, t is a vector of real-valued sufficient statistics, θ is a real-valued vector of parameters, X is a covariate set, and I_𝒴 is an indicator for membership in the support (𝒴). In the case of missing data, we follow Handcock and Gile (2010) in constructing the observed data likelihood for the above model as

$$\text{Pr}(Y^{\mathit{\text{obs}}}=y^{\mathit{\text{obs}}}|\theta ,X)=[{\sum }_{y^{\mathit{\text{mis}}}\in {\mathcal{Y}}^{\text{mis}}({\mathrm{y}}^{\text{obs}})}exp({\theta }^{T}t(y^{\mathit{\text{mis}}}\cup y^{\mathit{\text{obs}}},X))]/[{\sum }_{y\prime \in \mathcal{Y}}exp({\theta }^{T}t(y\prime ,X))]$$ (2)

where y^obs is the non-missing portion of y, and 𝒴^mis(y^obs) is the set of all “completions” of the observed data (i.e., assignments of 1s and 0s to the NA portions of y) that satisfy the known minimum and maximum group-specific out-degree constraints. This is a valid likelihood (i.e., it correctly describes the probability of the observed data marginalizing across the unobserved data) under relatively general conditions, as described in detail by Handcock and Gile (2010). We employ this approach in the analyses that follow.

Maximum likelihood inference for θ within the above framework requires a complex MCMC-based algorithm; we employ the implementation of this method in the ergm (version 3.2.4) package (Hunter et al., 2008) of the statnet (Handcock et al., 2008; Goodreau et al., 2008) software suite. Support constraints were enforced via the attribute-specific degree bounding functionality also implemented within the package; as indicated above, this implies that we are modeling our observed data with respect to the set of all networks that could have been obtained by the Add Health design, given the numbers of students, covariates, and inherent features of the design (e.g., censoring). This approach is appropriate for imputing unobserved values given the administered questionnaire, our primary goal.

To impute the unobserved elements in our respective nomination networks, we must first model each network. Using the above approach, we estimate a series of five progressively inclusive specifications of ERG models for each of the 14 schools. Model 1 contains only the edge count statistic (i.e., a homogeneous Bernoulli digraph with support constraints). Model 2 adds a mutuality/reciprocity effect. Model 3 further adds effects for the absolute difference in school grades (de facto age) and node mixing by gender. Model 4 further adds homophily effects for those in the same class(es), the same club(s), and the same sport-team(s). Finally, model 5 includes a geometrically weighted edgewise shared partner term (gwesp)⁶ fixed at its optimal value (δ_opt)⁷ The models constrain maximum out-degree for each gender at five female and five male friends, with additional constraints as noted above for off-roster students as needed.

Assessing when an ERGM model has reached satisfactory convergence is an ongoing area of study, and we employ several different criteria that represent the current state of the art. First, the ergm package (Hunter et al., 2008) incorporates several internal convergence checks based on the adequacy of the importance sampling approximation used to obtain final estimates. Second, we assess whether convergence had occurred by using a heuristic proposed by Snijders (2002), calculated as $t_k=\frac{{ź}_{\theta }-z_{\mathit{\text{obs}}}}{{\mathit{\text{SD}}}_{\theta }}$, where ź_θ is the sample average of parameter values from m simulating graphs, z_obs is the observed parameter values, and SD_θ is the sample standard deviation of parameter values from m simulating graphs. Third, we employ a stricter overall maximum convergence ratio criterion that is suggested in the RSiena (R-based Simulation Investigation for Empirical Network Analysis) literature (see Ripley et al., 2015, page 57), calculated as ${\mathit{\text{tconv}}}_{\mathit{max}}=\sqrt{({\overline{z}}_{\theta }-z_{\mathit{\text{obs}}})\prime {\sum }^{-1}({\overline{z}}_{\theta }-z_{\mathit{\text{obs}}})}$. Values less than 0.25 are preferred.

For the twelve small schools, the models employed here converge within 2,000 iterations with the criteria of |t_k| ≤ 0.1 and tconv_max≤ 0.25 satisfied. In the two large schools, 058 and 077, many more iterations are needed (e.g., between 20,000 and 200,000), and the t-ratios for parameters rarely meet the threshold of 0.3 that Snijders (2002) describes as “fair” model fit.⁸ The other convergence criteria, however, are satisfied, and the models show no other signs of poor behavior; as we are unable to obtain further improvement through longer model runs, we retain these as the best available models for purposes of the present study.

After estimating the model parameters, we employ conditional ERGM simulation to impute missing edge states. In this case, missing edge variables (NAs) are imputed based on the model estimated with the observed data, with observed edges (1s) and nulls (0s) unaltered and all degree constraints based on the observed data enforced. Thus, rows corresponding to individuals with no missing out-edge information are retained precisely as they are in the observed data. For those with partially observed out-edge information, observed cells of y^obs are retained, while NA cells are simulated (based on the model) subject to the constraint that the known minimum/maximum numbers of ties from each individual to males and/or females on and/or off-roster are preserved. For those with no outgoing edge information, the simulation exploits information contained in the observed ties, the model parameters, and the base degree constraints (no more than five male and female nominations, respectively).

4. Held-Out Predictive Evaluation (HOPE) and its application to Add Health

How do we assess how well our imputation scheme is working? Although we cannot know the true values of y^mis, we can potentially assess the quality of our imputation procedure by designating some of our observed edge variables as missing (thus holding them out), re-estimating the model, and comparing the imputed edge states under the new model with the held out data. We refer to this approach as Held-Out Predictive Evaluation (HOPE).

The HOPE procedure is performed as follows. 1) We select some specified number, k, of observed edges (1s) and nulls (0s) from y^obs and replace them with NAs to produce a modified y^obsH. 2) Using the selected ERGM family, we estimate θ^H|y^obsH. 3) We simulate D multiple draws from Y^misH|θ^H,y^obsH. The number of draws (D) can be determined by the researcher.⁹ 4) Using the simulated draws, we estimate the predictive accuracy of the imputation procedure via the mean fraction of held-out 1s and 0s (jointly or respectively) that are correctly imputed. The estimates produced by HOPE provide evidence of the extent to which the imputation procedure is able (or unable) to reconstruct missing edge states within the graph. They can in this respect be viewed as a form of model adequacy check (albeit a fairly stringent one, since accuracy is assessed on a per-edge basis).

Given that missingness in Add Health arises through both incomplete information from a given respondent and complete non-response, we explore both cases directly. We begin with the case of partial missingness, and then proceed to non-response.

4.1 Situation 1: Partial edge missingness only

Situation 1 is the case in which there are partial missing edges. We generate this form of missing data, perform our imputation approach, and assess the results. First, 25 present edges (1s) and 25 absent edges (0s) observed during the In-School Survey are randomly selected and replaced as missing edges (NAs). Then we use five progressively inclusive specifications of ERG models to simulate those missing edges 10 times. We then compute the percentage of accurately reproduced present edges and absent edges for each individual school.

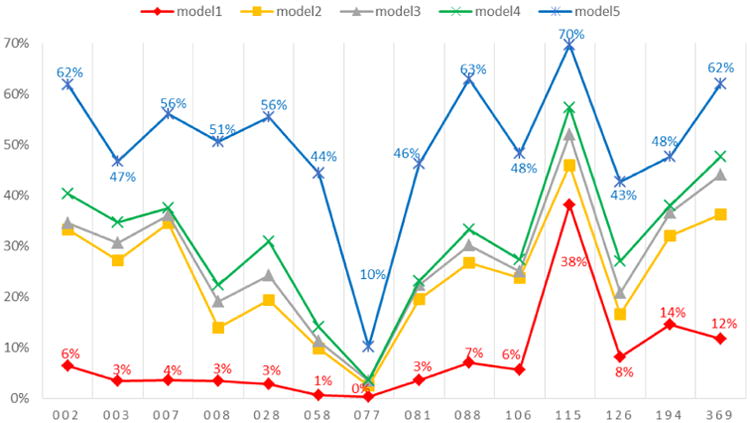
We first examine the accuracy of reproducing present edges (1s). As illustrated in Figure 1, there is considerable variance in the quality of the predictions across these models: the edge effect in model 1 provides a baseline for the ERGM simulation. The mutuality/reciprocity effect added in model 2 greatly increases the accuracy for most schools over the baseline model. Although model 3 (adding grade and gender effects) and model 4 (adding a homophily effect for classes, clubs, and sport-teams) do not provide noticeable improvement, the introduction of the gwesp term in model 5 improves the accuracy considerably. Thus, model 5 does the best job, with accuracy ranging from 10% in school 077 (the largest school) to 70% in school 115 (the smallest school).

Figure 1. Accuracy of reproducing present edges (1s) through ERGM for each school.

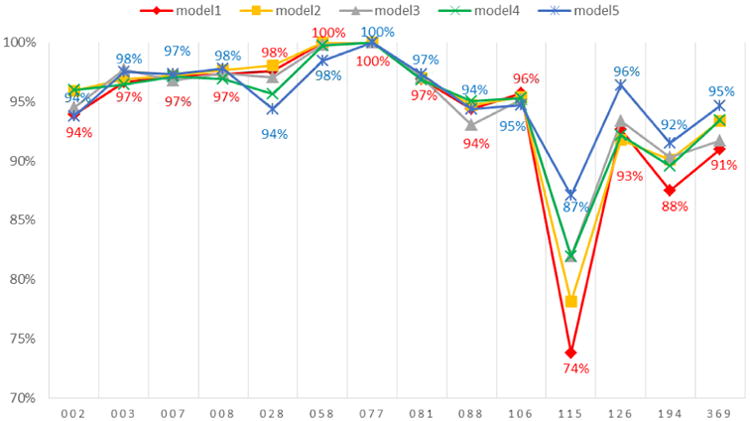
Turning to the accuracy of reproducing absent edges (0s), we see in Figure 2 that the model does quite well across all schools, with match rates typically greater than 90 percent. Even the baseline model's accuracy in reproducing absent edges is much higher than that of reproducing present edges (1s), which is unsurprising given the sparseness of the networks. Adding additional parameters sequentially from model 1 to model 5 does not substantially improve the predictions. Only School 115 seems to be exceptionally poor; given the very small size of the associated network (30 respondents), this may be because we are removing a relatively high proportion of the observed ties. Nonetheless, even in this school, model 5 is accurately reproducing 87% of the absent edges.

Figure 2. Accuracy of reproducing absent edges (0s) through ERGM for each school.

We next calculate the overall accuracy of the prediction as the percentage of ties accurately predicted (both present and absent edges). As shown in Table 2, the overall HOPE accuracy based on model 5 ranges from 55% in school 077 to 79% in school 088. The average accuracy across these schools is 73%. Note that these percentages are considerably higher than randomly assigning edges (i.e., 50 percent), even for the largest school 077.

Table 2. The predictive accuracy of model 5 for each school.

School	Predictive accuracy			School	Predictive accuracy
	1s	0s	overall		1s	0s	overall
002	62%	94%	78%	081	46%	97%	72%
003	47%	98%	72%	088	63%	94%	79%
007	56%	97%	77%	106	48%	95%	72%
008	51%	98%	74%	115	70%	87%	78%
028	56%	94%	75%	126	43%	96%	70%
058	44%	98%	71%	194	48%	92%	70%
077	10%	100%	55%	369	62%	95%	78%

In ancillary analyses, we modify the above analyses in two ways. First, instead of simulating the missing edges 10 times, we increase the replication count to 50 times. Second, we increased the number of present or absent edges set to missing from 25 to 100 each. In these subsidiary analyses, the accuracy of reproducing the edges remained approximately the same.

As a side note, given the differences in predictive accuracy across the 14 schools we briefly explore the question of whether we could explain these differences. This is accomplished by taking the results from model 5 – our best model for edge imputation – and estimating linear regression models in which the outcome variables are 1) the percentage correct observed edges (1s), and 2) the percentage correct absent edges (0s). As shown in Table 3, roster size alone explains 68% of variation in the predictive accuracy of present edges (1s), while network density alone explains 80% of variation in the predictive accuracy of nulls (0s).

Table 3. Linear regression analysis of predictive accuracy on network size and density.

	Accuracy (%) of present edges (1s)		Accuracy (%) of nulls (0s)
	Model 1 beta(s.e.)	Model 2 beta(s.e.)	Model 3 beta(s.e.)	Model 4 beta(s.e.)
Roster size	-0.02*** (0.00)	-0.02** (0.00)		0.00 (0.00)
Network density		48.97 (38.07)	-45.41*** (6.62)	-40.81*** (6.65)
Constant	56.81*** (2.57)	53.34*** (3.68)	97.96*** (0.56)	97.28*** (0.64)
R2	0.68	0.72	0.80	0.84
N	14	14	14	14

Notes:

^*two-sided p < 0.05;

^**two-sided p < 0.01;

^***two-sided p < 0.001.

The correlation coefficient between roster size and network density is -0.39.

4.2 Situation 2: Complete as well as partial edge missingness

In situation 2 we generate both partial and complete missing edges, and then perform imputations and assess the results. In this situation we again randomly set 25 present edges (1s) and 25 absent edges (0s) to missing as we did in situation 1. However, we also gradually add missing actors (from 0% to 30%) by randomly selecting respondents with no edge missingness and replacing all their out-going ties as missing edges (NAs). We then use model 5 – our best model for edge imputation in situation 1 – to reproduce the missing edges.

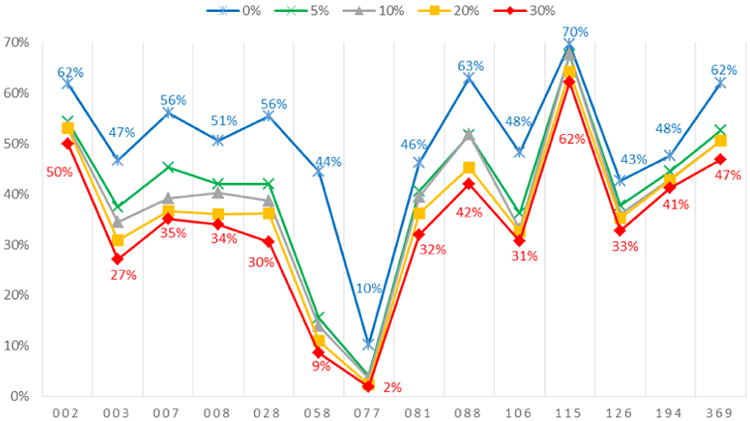
The accuracy of reproducing present edges (1s) across these various levels of complete missingness is displayed in Figure 3. As expected, increasing numbers of missing actors decrease the accuracy of reproducing present edges. The top line in this figure matches the top line in Figure 2, and displays the case with no complete missingness (only partial edge missingness). For example, school 002 has 62% accuracy when there is no complete missingness, but this slides to 54% with 5% complete missingness, 54% with 10% complete missingness, and then to 53% and 50% when complete missingness rises to 20 or 30 percent, respectively. Notably, for the smallest school 115, even in this most stringent scenario in which 30% of the observations have complete missingness the accuracy for reproducing present edges is still as high as 62%. For the two largest schools 058 and 077, as the proportion of missing actors increases the accuracy for reproducing present edges falls even further. Thus, in general the ERGM-based estimation and simulation approach works better in reproducing present edges for small schools (with their relatively denser networks, i.e., with a network density of about 66 out of 1,000 on average) than for large schools (with sparse networks, i.e., with a network density of about 5 out of 1,000 for school 058 and about 1 out of 1,000 for school 077).

Figure 3. Accuracy of reproducing present edges (1s) with additional missing actors.

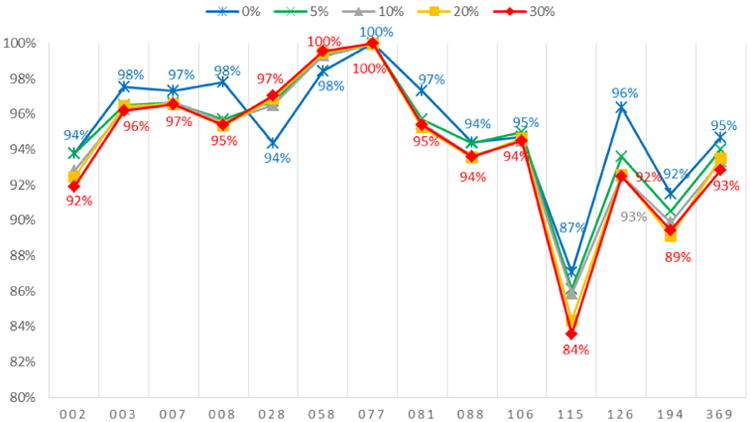
We next assess the impact of higher levels of complete missingness on the accuracy of reproducing absent edges, and as demonstrated in Figure 4 there are quite small degradations in accuracy. For most schools, the accuracy of reproducing absent edges remains above 90% even with as much as 30% complete missingness. The one minor exception is school 115 with the smallest roster size, but even here accuracy of reproducing absent ties only decreases from 87% to 84% when moving from 0% to 30% complete missingness.

Figure 4. Accuracy of reproducing absent edges (0s) with additional missing actors.

Finally, we computed the overall accuracy for reproducing both present and absent edges for each of these complete missingness scenarios. As shown in Table 4, increasing the proportion of missing actors decreases the overall accuracy, as expected. In the most stringent scenario with 30% respondents having complete missingness, the overall accuracy ranges from 51 percent (the largest school 077) to 73 percent (the smallest school 115). Across all 14 schools the overall accuracy decreases from 73 percent to 64 percent on average between no complete missingness to 30 percent complete missingness.

Table 4. The overall accuracy with different levels of missing actors for each school.

Mssing actors	0%	5%	10%	20%	30%
School ID
002	78%	74%	74%	73%	71%
003	72%	67%	65%	64%	62%
007	77%	71%	68%	67%	66%
008	74%	69%	68%	66%	65%
028	75%	68%	69%	67%	64%
058	71%	57%	57%	55%	54%
077	55%	52%	52%	51%	51%
081	72%	67%	68%	66%	64%
088	79%	73%	73%	69%	68%
106	72%	66%	64%	64%	63%
115	78%	77%	75%	76%	73%
126	70%	65%	65%	64%	63%
194	70%	67%	66%	66%	65%
369	78%	72%	73%	72%	70%
Average	73%	67%	67%	66%	64%

Before concluding, we note that the predictive accuracy of existing edges (1s) was typically lowest for the larger schools, especially the largest school 077. There are several possible explanations for this. The most obvious is the fact that the difficulty of edge imputation necessarily increases with decreasing density. Specifically, for a network of density d, it follows immediately from Bayes's Theorem¹⁰ that the conditional likelihood ratio for the presence of an arbitrary edge (versus its absence) must be greater than (1-d)/d in order to obtain a predicted tie probability greater than 0.5. Thus, if a randomly chosen ego is tied to e.g. 1 in 1000 potential alters, then a 1000 to 1 conditional likelihood ratio is needed in order to reach even odds of a given ego/alter tie being present. This is a substantial amount of information, which in practice must come from a combination of covariate and edge dependence effects in the ERGM employed for imputation. While accurate edge imputation in large, sparse graphs is possible, increasingly informative models are required as density declines; otherwise, accuracy for the imputation of edges will fall with density. This base rate effect is a fundamental property of any classification task, and is not specific to ERGMs (or, indeed, to network data per se).

An alternative reason for poorer performance with large graphs could in principle be lower-quality parameter estimates. Given that current software implementations of ERGMs require MCMC simulations to perform parameter estimation, fitting to large networks poses the challenge of running the underlying Markov chain algorithm sufficiently long to reach effective convergence. As noted above, we employ a variety of checks to assess convergence in the present case; while we do not regard it as likely, it is in principle possible that the models used here for the large schools suffered from lower-quality estimation, and that improved fitting techniques applied to the same data could yield better results. However, it is worth highlighting that when we employ more stringent criteria than those conventionally used by the (statnet) ERGM imputation in the smaller schools studied here, our predictive ability as assessed by the HOPE approach typically only improve 1 or 2%. In experimenting with alternative diagnostics and estimation parameters, we do not find predictive performance to be very sensitive to the approach taken; nevertheless, we note that the robustness of tasks such as imputation to choice of convergence criteria is a potentially fruitful target for further study. We also observe that predictive techniques such as HOPE provide a more direct approach to the evaluation of model performance than is readily available for assessing e.g. parameter estimates or standard errors.

5. Conclusion

The existence of missing data is a challenge for network researchers. We have addressed this issue here by using an ERGM estimation and simulation approach to impute network missing data. We distinguished between partial missingness (individual missing edges) and complete missingness (missing actors, and all their out-going edge information), and introduced practical treatments in each situation. We demonstrated the approach using data from 14 schools in the In-School Survey of Add Health. We also developed a validation method to assess this approach – the Held-Out Predictive Evaluation (HOPE) strategy. Our results using HOPE indicated that the ERGM approach does a satisfactory job of imputing data in the presence of network missingness for this commonly used dataset. Compared to the traditional approach of treating missing edges as null or simply truncating all the missing actors from network data, the ERGM estimation and simulation approach can serve as a better alternative.

We emphasize that this was a demonstration of ERGM-based network imputation using a specific dataset. Our goal was not to assess the imputation technique in a situation in which the true network is known (i.e., a Monte Carlo simulation) but rather to demonstrate how it works on a specific network dataset with considerable missing data challenges. Although the results were quite promising for the approach, there were nonetheless differences in the predictive ability across the 14 networks in the study. For this set of networks, we found that network size and density explained most of the difference in the ability of the ERGM framework to reproduce present or absent edges across networks. Although we are cautious in extrapolating this insight more generally, we do feel it is an important point to consider as the technique is further developed.

In closing, we point out that the ERGM estimation and simulation approach could also be a useful supplement for longitudinal network analysis. For example, the RSiena model (Snijders et al., 2010b; Snijders, 2011) utilizes advanced methods in the MLE option which make it possible to deal with missing network data in later waves (see Huisman and Snijders, 2003; Huisman and Steglich, 2008; Snijders et al., 2010a), but for missing edges in the first wave it simply drops them or treats them as absent (see Ripley et al., 2015, page 32). As Hipp et al. (2015) found, either of these approaches can yield biased estimates in RSiena models. Our cross-sectional imputation method can be used as a more principled way to bridge this gap.

Highlights.

• We use an ERGM-based imputation approach to handle complex network data missingness

• We employ multiple criteria to check the ERG model convergence

• We develop a Held-Out Predictive Evaluation (HOPE) strategy to assess this approach

• We provide possible explanations for differences in recovery rates across schools

• Results suggest this approach has advantages in dealing with missing data challenge

Appendix: R script for ERGM estimation and simulation (tested on ergm 3.2.4)

R script for ERGM estimation

• model1 <- ergm(net∼edges,constraints=∼bd(attribs=sexattr,maxout=maxout))

• model2 <- ergm(net∼edges+mutual,constraints=∼bd(attribs=sexattr,maxout=maxout))

• model3 <- ergm(net∼edges+mutual +absdiffcat(‘grade’)+nodemix(‘female’,base=1), constraints=∼bd(attribs=sexattr,maxout=maxout))

• model4 <- ergm(net∼edges+mutual +absdiffcat(‘grade’)+nodemix(‘female’,base=1) +nodematch(class)+nodematch(clubs)+nodematch(sports), constraints=∼bd(attribs=sexattr,maxout=maxout))

• model5 <- ergm(net∼edges+mutual+absdiffcat(‘grade’)+nodemix(‘female’,base=1) +nodematch(class)+nodematch(clubs)+nodematch(sports) +gwesp(δ_opt,fixed=T), constraints=∼bd(attribs=sexattr,maxout=maxout))

Application of convergence criterions (Model 5 as an example)

sf <- model5$sample-model5$sample.obs

t.k <- abs(apply(sf,2,mean))/apply(model5$sample,2,sd)

tconv.max <- sqrt(t(apply(sf,2,mean) %*% solve(as.matrix(cov(sf))) %*% apply(sf,2,mean)))

while (max(t.k)>0.1 | tconv.max>0.25) {

  par <- coef(model5)

  model5 <- ergm(net∼edges+mutual+absdiffcat(‘grade’)+nodemix(‘female’,base=1)

              +nodematch(class)+nodematch(clubs)+nodematch(sports)

              +gwesp(δopt,fixed=T),

              constraints=∼bd(attribs=sexattr,maxout=maxout),

              control=control.ergm(init=par,MCMLE.maxit=20000))

  sf <- model5$sample-model5$sample.obs

  t.k <- abs(apply(sf,2,mean)/apply(model5$sample,2,sd))

  tconv.max <- sqrt(t(apply(sf,2,mean) %*% solve(as.matrix(cov(sf))) %*% apply(sf,2,mean)))

}

R script for ERGM simulation (Model 5 as an example)

net.fit<-model5

net.sim5<-simulate(net.fit,

              constraints=∼observed+bd(attribs=sexattr,minout=minout,maxout=maxout),

              nsim=250)

For more details about ERGM estimation and simulation terms and options, please see the online tutorial for ERGM version 3.2.4 by Handcock et al. (2015) at http://cran.r-project.org/web/packages/ergm/ergm.pdf.