Gene regulation network inference with joint sparse Gaussian graphical models

Abstract

Revealing biological networks is one key objective in systems biology. With microarrays, researchers now routinely measure expression profiles at the genome level under various conditions, and, such data may be utilized to statistically infer gene regulation networks. Gaussian graphical models (GGMs) have proven useful for this purpose by modeling the Markovian dependence among genes. However, a single GGM may not be adequate to describe the potentially differing networks across various conditions, and hence it is more natural to infer multiple GGMs from such data. In the present study, we propose a class of nonconvex penalty functions aiming at the estimation of multiple GGMs with a flexible joint sparsity constraint. We illustrate the property of our proposed nonconvex penalty functions by simulation study. We then apply the method to a gene expression data set from the GenCord Project, and show that our method can identify prominent pathways across different conditions.

1 Introduction

Recent advances in high-throughput technology make it possible to simultaneously measure tens of thousands of molecular components. Researchers now routinely collect expression profiles at the genome level under various conditions and infer gene regulation networks by analyzing these datasets with various statistical methods such as Bayesian networks, relevance networks, and Gaussian graphical models (GGMs). Among these methods, we focus on the GGMs, because they have proven among the best in inferring conditional dependence (Markov dependence) networks (Werhli et al., 2006; Soranzo et al., 2007).

When the datasets from multiple conditions are available, it is important to improve the power of the study by modeling all the data so as to effectively accommodate characteristics of the datasets. One characteristic that we incorporate in our approach is joint sparsity, which describes the fact that the number of regulations in a biological network is far less than that of a fully connected network, and this sparsity is preserved across multiple conditions. For example, the regulations curated in the KEGG pathway database have tree structures and the established connections among genes only represent a very small fraction of all possible connections.

The joint sparsity principle has been utilized in other multiple GGM approaches with various penalty functions. Chiquet et al. (2009) proposed to use a group lasso penalty, but their approach does not allow the network structure change across conditions. Later, Guo et al. (2011) proposed a group bridge penalization, and it indeed produces network structures that vary across conditions. Hence, the group bridge penalization is preferred in case of estimating multiple gene regulation networks with datasets from multiple tissues/conditions. More recently, Danaher et al. (2012) proposed a joint graphical lasso approach, where they used various ℓ₁ regularization methods for promoting graph similarities. The formulation is convex and can be useful for very high-dimensional problems.

Among these previous approaches, we find that Guo et al. (2011)’s approach can be extended to a wider class of penalty functions, which consists of nonconvex functions. In fact, our proposed class of noncovex penalty functions gives a flexibility in controlling the level of joint sparsity by the choice of the penalty function. Since the level of joint sparsity among multiple biological networks might be much higher (or lower) than what is specified in Guo et al. (2011)’s approach, the broader class of penalty functions in our approach can gain power by putting more (or less) weights on the common network structures.

The rest of this article is organized as follows: In Section 2, we provide a detailed description of our joint estimation procedure with nonconvex penalty functions and show how the level of joint sparsity can be controlled through these penalty functions. We also present the consistency and sparsistency results of the estimate in this section. In Section 3, we show the performance of the methods under various scenarios via simulation, and then in Section 4, we apply our approach to the microarray dataset from the GenCord project (Dimas et al., 2009), which reveals prominent pathways across different cell types in umbilical cords. A brief conclusion follows in Section 5.

2 Estimation of multiple Gaussian graphical models with joint sparsity

In this section, we first review GGMs briefly and then formulate multiple GGMs with joint sparsity that is achieved by using a nonconvex penalty function.

2.1 Brief review of GGMs

A graphical model encodes conditional independence relationships among multiple random variables, X₁, …, X_p, by using a graph = (Γ, E), where Γ is an index set for vertices and E is a subset of Γ × Γ for edges. Under the graphical model, a pair of random variables X_i and X _j are conditionally independent given all the rest if and only if there is no edge between vertices i and j on the graph. Inferring conditional relationships among random variables is not a simple task, because it involves investigation of the joint density factorization. However, if X = (X₁, …, X_p)′ is assumed to follow a multivariate normal distribution N(0, Ω⁻¹), where Ω is the inverse covariance matrix and u′ denote the transpose of a vector u, such conditional independence relationships can be directly read from the zero elements of Ω (Lauritzen, 1996). Thus, ω_i,j = 0 if and only if X_i and X_j are conditionally independent given all the other variables, where ω_i,j is the (i, j)th element of Ω. Because of this property, the network inference problem is considered as a sparse precision matrix estimation problem under GGMs. The sparse GGM estimation has been extensively studied recently including Meinshausen and Buhlmann (2006); Yuan and Lin (2007); Peng et al. (2009); Lam and Fan (2009); and Guo et al. (2011).

There are non-likelihood-based approaches including graphical Dantzig selector (Yuan, 2010) and CLIME (Cai et al., 2011). The graphical Dantzig selector improves the pseudo likelihood approach of Meinshausen and Buhlmann (2006). CLIME tries to minimize |Ω⁻¹ − S|_∞ instead of the negative log likelihood, where S is the sample covariance matrix and |A|_∞ is a matrix max norm for a matrix A. It has been shown that both approaches perform well computationally as well as asymptotically. It is possible that one can apply a joint sparsity constraint under various loss functions. However, we do not pursue these approaches in this manuscript, since we are interested in improving the regularization in order to achieve flexible joint sparsity.

2.2 Nonconvex penalty functions for joint sparsity

We consider multiple GGMs across T conditions. Specifically, we assume that a p dimensional random vector X^t,i ~ N_p(0,(Ω^t)⁻¹) independently, for i = 1, …, n_t and t = 1, …, T. The negative log likelihood can be written as

$$L({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)=\sum _{t=1}^T\frac{n_t}{2}(\text{tr}({\mathbf{S}}^t{\mathbf{\Omega }}^t)-logdet({\mathbf{\Omega }}^t)),$$

where S^t and Ω^t are sample covariance and precision matrices for the tth condition and tr(A) and det(A) denote trace and determinant of a matrix A, respectively.

Motivated by the property that the number of edges in a biological network is far less than that of a fully connected network (e.g. a pathway from KEGG database is often represented as a tree which has p − 1 edges for p nodes) and that the sparse structure tends to be preserved across multiple conditions, we attempt to improve the accuracy of GGM estimation by employing joint sparsity regularization. Such regularization is achieved by introducing sparsity into the precision matrix through nonconvex penalty functions. The penalized negative log likelihood (PL) is defined as follows:

$${PL}_i({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)=L({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)+\lambda \sum _{j\ne j^{\prime }}{f}_i\left(\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid \right),$$ (1)

where ${\omega }_{j,j^{\prime }}^t$ is the (j, j′)th element of Ω^t and f_i is a nonconvex penalty function. We consider the following three nonconvex penalty functions:

1. f₁(x) = |x|^1−ν for 0 < ν < 1

2. $f_2(x)=(log(\mid x\mid )-log\epsilon +1)I(\mid x\mid >\epsilon )+\frac{\mid x\mid }{\epsilon }I(\mid x\mid \le \epsilon )$

3. f₃(x) = (−|x|^1−ν + νε^1−ν) I(|x| > ε) − (1 − ν)|x|ε^−ν I(|x| ≤ ε) for ν > 1.

Here, ε is a small positive constant. The f₁ penalty function has been used in group bridge estimation in a regression context (Huang et al., 2009). The f₂ penalty function is a truncated log function, and f₃ is a truncated inverse polynomial in which truncation occurs when |x| ≤ ε to avoid infinity. We remark that the log penalty function has been used by others including Sweetkind-Singer (2004) and Mazumder et al. (2011) in different contexts.

The joint estimation of multiple GGMs by using a nonconvex penalty function is not new, as Guo et al. (2011) used the penalty function of $\sqrt{x}$ for the purpose. They showed that the use of $\sqrt{x}$ function is equivalent to the hierarchical penalization of common and condition-specific regularization. In their work, the common structure was introduced to represent an edge set that is the union of all individual edge sets, and it was denoted as a p × p matrix Θ. They specifically set θ_j,j′ to be proportional to $\sqrt{{\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid }$, where θ_j,j′ is the (j, j′)th element of Θ. We found that the joint sparsity regularization can be achieved similarly with functions other than the square root function, which is shown in the following Proposition 1.

Proposition 1

If ${\{{\widehat{\mathbf{\Omega }}}^t\}}_{t=1}^T$ is a local minimizer of ${PL}_i({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)$, there exists Θ̂ such that ( ${\{{\widehat{\mathbf{\Omega }}}^t\}}_{t=1}^T$, Θ̂) is a local minimizer of

$${\stackrel{\sim }{PL}}_i({\{{\mathbf{\Omega }}^t\}}_{t=1}^T,\mathrm{\Theta })\mathit{subject}to{\theta }_{j,j^{\prime }}\ge 0,\mathit{for}1\le j,j^{\prime }\le p,$$ (2)

where ${\stackrel{\sim }{PL}}_i({\{{\mathbf{\Omega }}^t\}}_{t=1}^T,\mathrm{\Theta })$ is defined as follows:

$${\stackrel{\sim }{PL}}_i({\{{\mathbf{\Omega }}^t\}}_{t=1}^T,\mathrm{\Theta })=L({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)+\tau \left(\sum _{j\ne j^{\prime }}{g}_i({\theta }_{j,j^{\prime }})\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^r\mid +\sum _{j\ne j^{\prime }}{\theta }_{j,j^{\prime }}\right),$$

1. $g_1(x)=x^{\frac{-\nu }{1-\nu }}$; and λ = τν^−ν(1−ν)^ν−1

2. $g_2(x)=\{\begin{array}{cc}\frac{exp(1-x)}{\epsilon }& x>1\\ \frac{1}{\epsilon }& 0\le x\le 1\end{array}$; and λ = τ

3. $g_3(x)=\{\begin{array}{cc}\frac{\nu -1}{\nu }{\left(\nu {\epsilon }^{1-\nu }-x\right)}^{\frac{\nu }{\nu -1}}& x>(\nu -1){\epsilon }^{1-\nu }\\ \frac{\nu -1}{(\nu ){\epsilon }^{\nu }}& 0\le x\le (\nu -1){\epsilon }^{1-\nu }\end{array}$; and $\lambda =\frac{\tau }{\nu }$.

Here, τ > 0 is a tuning parameter for $\stackrel{\sim }{PL}$.

Conversely, if ( ${\{{\widehat{\mathbf{\Omega }}}^t\}}_{t=1}^T$,Θ̂) is a local minimizer of (2), ${\{{\widehat{\mathbf{\Omega }}}^t\}}_{t=1}^T$ is a local minimizer of ${PL}_i({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)$.

The proof is given in Appendix. In the proposition, θ̂_j,j′(≥ 0) is interpreted as a common structure, and defined by the minimizer of the objective function (2). Hence, each nonconvex function yields a different form of θ̂_j,j′. In fact, θ̂_j,j′ is proportional to ${({\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid )}^{1-\nu },log({\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid )$, and $\left(\frac{\nu }{{\epsilon }^{\nu -1}}-\frac{1}{{({\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid )}^{\nu -1}}\right)$, for functions f₁, f₂, and f₃, respectively, when ${\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid >\epsilon$. These are increasing functions with respect to ${\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid$ with varying curvatures.

From the proposition, one can find that our proposed approach regularizes the common and condition-specific structures hierarchically with two characteristics. First, the common edge selection is guided by the choice of nonconvex function. As discussed in the previous paragraph, θ̂_j,j′ is differently defined depending on the type of the nonconvex function, where f₃ enforces the joint sparsity most strongly, followed by f₂ and f₁. Second, condition-specific edge selection is guided by the weight function g_i(θ̂_j,j′). Since g_i is a monotone decreasing function with respect to θ̂_j,j′, an edge with a small common structure is penalized more heavily than an edge with a large common structure. Thus, the proposition shows that our approach achieves the joint regularization via the use of a nonconvex penalty function and has flexibility of controlling the balance between common and condition-specific edge selection via the choice of the nonconvex function.

2.3 Algorithm

In this subsection, we describe an algorithm that uses the local linear approximation to find a solution of (1). It has been shown that the minimizer of (1) with the $\sqrt{x}$ penalty function can be found by the local linear approximation (Zou and Li, 2008), which was also used in Guo et al. (2011). The penalty function can be approximated as $f_i({\mathrm{\sum }}_{j\ne j^{\prime }}\mid {\omega }_{j,j^{\prime }}^t\mid )\approx f_i({\mathrm{\sum }}_{j\ne j^{\prime }}\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid )+{\mathrm{\sum }}_{j\ne j^{\prime }}{f}_i^{\prime }({\mathrm{\sum }}_{j\ne j^{\prime }}\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid )(\mid {\omega }_{j,j^{\prime }}^t\mid -\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid )$. By extracting terms related to the ${\omega }_{j,j^{\prime }}^t$, we get the computational algorithm as follows:

1. Initialize Ω̂^t for all 1 ≤ t ≤ T.

2. Update Ω̂^t for all 1 ≤ t ≤ T by solving

   $${\text{argmin}}_{{\mathbf{\Omega }}^t}\frac{n_t}{2}(\text{tr}({\mathbf{S}}^t{\mathbf{\Omega }}^t)-log\{det({\mathbf{\Omega }}^t)\})+\stackrel{\sim }{\lambda }\sum _{j\ne j^{\prime }}\frac{\mid {\omega }_{j,j^{\prime }}^t\mid }{{({\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid )}^{\nu }},$$

   using a glasso, where ${\widehat{\omega }}_{j,j^{\prime }}^t$, is the estimate from the previous iteration and ν > 0, λ̃ = λ for f₂ and λ̃ = |1 − ν| for f₁ and f₃.

3. Repeat step 2 until convergence is achieved.

In the algorithm, ν is the same as the one used in (1) for penalty functions f₁ and f₃, and ν is set to be 1 for penalty function f₂. Specifically, the penalty function f₁, also known as a bridge penalty, considers 0 < ν < 1; the penalty function f₂ corresponds to ν = 1; and the penalty function f₃ corresponds ν > 1. Thus, these three penalty functions comprise the continuum of the iteratively reweighted graphical lasso with ν > 0.

Our algorithm only guarantees to yield a local solution, and thus the choice of the initial value is important to get an appropriate estimate. When n ≥ p, one can use (S^t + δI)⁻¹ as an initial estimate, where δ ≥ 0 is chosen to be a small constant to avoid singularity. However, when n < p, this form of the initial estimate does not perform well. In this case, one can use the solution of separate GGM approaches with an ℓ₁ regularization, because in high-dimensional estimation, a reasonable estimate can be obtained by using a sparsity regularization.

The tuning parameter, λ, can be selected by minimizing the approximation of Bayesian information criterion (aBIC) as in Yuan and Lin (2007). The aBIC is defined by

$$\text{aBIC}(\lambda )=\sum _{t=1}^T\left\{-logdet({\widehat{\mathbf{\Omega }}}^t(\lambda ))+\text{tr}({\mathbf{S}}^t{\mathbf{\Omega }}^t(\lambda ))+\frac{log(n_t)}{n_t}d{f}_t\right\},$$

where ${\{{\widehat{\mathbf{\Omega }}}^t(\lambda )\}}_{t=1}^T$ are the minimizer of (1) with a tuning parameter λ, and $\text{card}\{(j,j^{\prime }):j\le j^{\prime },{\widehat{\omega }}_{j,j^{\prime }}^t(\lambda )\ne 0\}$ with card representing the cardinality of a finite set. We remark that d f_t is a heuristic degrees of freedom and hence the proposed aBIC is an approximation of the original BIC criterion.

2.4 Consistency and Sparsistency

In this subsection, we show that the estimate from the formulation (1) above achieves consistency and sparsistency. The sparsistency, however, is limited in that it only finds a group structure, rather than individual structures.

Denote ${\mathbf{E}}_t=\{(j,j^{\prime }):j\ne j^{\prime },{\mathbf{\Omega }}_{0,j,j^{\prime }}^t\ne 0\}$ to be the set of indices of all nonzero off-diagonal elements in ${\mathbf{\Omega }}_0^t$, E = E₁ ∪ … ∪ E_T, q_t = |E_t| and q_t = |E_t|, where ${\mathbf{\Omega }}_0^t$ is a true precision matrix.

We assume the following regularity conditions as in Guo et al. (2011):

1. There exist constants ξ₁ and ξ₂ such that for all p ≥ 1 and 1 ≤ t ≤ T,

   $$0<{\xi }_1<{\varphi }_{\mathit{min}}({\mathbf{\Omega }}_0^t)\le {\varphi }_{\mathit{max}}({\mathbf{\Omega }}_0^t)<{\xi }_2<\infty ,$$

   where ϕ_min(A) and ϕ_max(A) represent the minimal and maximal eigenvalues of a matrix A.

2. There exists a constant ξ₃ > 0 such that

   $$\underset{1\le t\le T}{min}\underset{(j,j^{\prime })\in {\mathbf{E}}_t}{min}\mid {\mathbf{\Omega }}_{0,j,j^{\prime }}^t\mid \ge {\xi }_3.$$

Theorem 1

Under regularity conditions 1 and 2, when $\frac{(p+q)(logp)}{n}=o(1)$ and ${\mathrm{\Lambda }}_1\sqrt{\frac{logp}{n}}\le \lambda \le {\mathrm{\Lambda }}_2\sqrt{(1+p/q)\frac{logp}{n}}$, there exists a local minimizer of the objective function (1), such that ${\displaystyle \sum _{t=1}^T}{\Vert {\widehat{\mathbf{\Omega }}}^t-{\mathbf{\Omega }}_0^t\Vert }_F=O_p\left(\sqrt{\frac{(p+q)logp}{n}}\right)$.

Here ||A||_F represents the Frobenius norm of a matrix A.

Theorem 2

Under all of the assumptions in Theorem 1, and the assumptions of ${\mathrm{\sum }}_{t=1}^T{\Vert {\widehat{\mathbf{\Omega }}}^t-{\mathbf{\Omega }}_0^t\Vert }^2=O_p({\eta }_n)$, where η_n → 0 and $\sqrt{\frac{logp}{n}}+\sqrt{{\eta }_n}=O(\lambda )$, the local minimizer of the objective function (1) satisfies that (a) ${\widehat{\omega }}_{j,j^{\prime }}^t=0$ for all 1 ≤ t ≤ T for any (j, j′) ∈ E^c and (b) ${\widehat{\omega }}_{j,j^{\prime }}^t\ne 0$ for some 1 ≤ t ≤ T for any (j, j′) ∈ E with probability tending to 1. Here ||A|| represents the operator norm of a matrix A.

From Theorem 2, we find that the sparsistency holds only at the group level, meaning that it is able to declare edges that do not appear in any condition, but that the sparsistency is not guaranteed to hold at the condition-specific level. In order to achieve sparsistency at the condition-specific level, a separate GGM estimation with a nonconvex penalty function for each condition should be used. We further find that consistency and sparsistency can be achieved simultaneously in very limited scenarios, which was discussed in Guo et al. (2011). It is because λ needs to be bounded both below and above for the consistency, but λ needs to be bounded below only for the sparsistency. These bounds can be matched, when $\sqrt{\frac{logp}{n}}+\sqrt{{\eta }_n}=O\left(\sqrt{\frac{(1+p/q)logp}{n}}\right)$. Due to the norm relationship of a p × p matrix $\mathbf{A}({\Vert \mathbf{A}\Vert }_F/\sqrt{p}\le \Vert \mathbf{A}\Vert \le {\Vert \mathbf{A}\Vert }_F)$, we have that η_n = O((p+q) log p/n) in the worst case scenario and η_n = O((1+q/p) log p/n) in the best case scenario. Hence, q should be O(1) in the worst case and q can be O(p) in the best case. If Theorem 1 is improved to show the operator norm consistency, the inconvenient consistency condition of Theorem 2 can be removed.

3 Simulation Study

3.1 Performance as function of tuning parameter

An incidence matrix with a scale-free network structure is generated using the Barabasi-Albert algorithm (Barabasi and Albert, 1999). We start from six edges, and add one edge at each step. We first generate shared edges and then, for each condition, we add randomly selected 0.1M edges as condition-specific edges, where M is the total number of edges in the shared structure. The total number of nodes in a graph, p, is set to be 500, and we consider 5 conditions (T = 5). Further, we set the sample size for each condition (n_t) to be 150.

We generate precision matrices by setting the nonzero elements to values that are sampled from Unif([−1, −0.5] ∪ [0.5, 1]). We then set the diagonal elements to (1.5 Σ_j≠i |ω_i,j|). In this way, the resulting Ω^t may not be positive definite, and thus we repeat this precision matrix generation process until Ω^t becomes a positive definite matrix. Due to the scale-free structure, some diagonal elements are much larger than the others. We thus adjust the precision matrices as in Danaher et al. (2012) by replacing the nonzero elements of Ω^t with those of Ω̃^t, where Ω̃^t = (D^t−1/2Σ̃^tD^t−1/2)−1; Σ̃ = 0.6Ω^t−1 + 0.4D^t; and D^t is the diagonal matrix whose (i, i)th elements is the (i, i)th element of Ω^t−1. Finally, the p dimensional random vectors are simulated from N(0, Ω^t−1). All of the simulation results are based on 100 replicates.

We use ν = 0.5 for f₁; ν = 1 for f₂; and ν = 2 for f₃ penalty function. We compare the performance of our proposed nonconvex penalty approaches to that of a single global GGM and that of multiple GGMs separately, as well as that of Danaher et al. (2012)’s GGL approach. For the GGL approach, we reparametrize the tuning parameters as in the simulation study of Danaher et al. (2012), where ${\omega }_1={\lambda }_1+\frac{1}{\sqrt{2}}{\lambda }_2$ and ${\omega }_2=\frac{1}{\sqrt{2}}{\lambda }_2/({\lambda }_1+\frac{1}{\sqrt{2}}{\lambda }_2)$. Throughout the simulation study, we set ε = 1.0 × 10⁻⁶, and thr = 0.1 for glasso algorithm in our approach. The initial estimate of Ω^t was obtained by applying glasso algorithm with $\lambda =\frac{1}{T{p}^2}{\mathrm{\sum }}_t{\mathrm{\sum }}_i{\mathrm{\sum }}_j\mid {\mathbf{S}}_{ij}^t\mid$, separately.

When we estimate a single global GGM and multiple separate GGMs, we consider the following objective functions PL_G and PL_S, respectively:

$$\begin{array}{l}{PL}_G(\mathbf{\Omega })={\mathrm{\sum }}_{t=1}^T\left(\frac{n_t}{2}\text{tr}({\mathbf{S}}^t\mathbf{\Omega })-logdet(\mathbf{\Omega })\right)+\lambda {\mathrm{\sum }}_{j\ne j^{\prime }}{f}_2\left(\mid {\omega }_{j,j^{\prime }}\mid \right)\\ {PL}_S({\mathbf{\Omega }}^t)=\frac{n_t}{2}(\text{tr}({\mathbf{S}}^t{\mathbf{\Omega }}^t)-logdet({\mathbf{\Omega }}^t))+\lambda {\mathrm{\sum }}_{j\ne j^{\prime }}{f}_2\left(\mid {\omega }_{j,j^{\prime }}^t\mid \right),\end{array}$$

for t = 1, …, T. The nonconvex penalty function is used for promoting model selection consistency.

A part of criteria to compare the methods are as follows:

• C1
  # of falsely declared edges at λ:

  $$\sum _{t=1}^T\text{card}\{(i,j):i>j,{\omega }_{i,j}^t=0\text{and}{\widehat{\omega }}^t{(\lambda )}_{i,j}\ne 0\},$$

  where, card(A) for a set A represents the cardinality of the set A.

• C2
  # of correctly declared edges at λ:

  $$\sum _{t=1}^T\text{card}\{(i,j):i>j,{\omega }_{i,j}^t\ne 0\text{and}{\widehat{\omega }}^t{(\lambda )}_{i,j}\ne 0\}.$$
• C3
  # of falsely declared edges in a combined graph at λ:

  $$\text{card}\{(i,j):i>j;{\omega }_{i,j}^t=0\text{for}\text{all}t=1,\dots ,T;\text{and}{\widehat{\omega }}^t{(\lambda )}_{i,j}\ne 0\text{for}\text{some}t,1\le t\le T\}.$$
• C4
  # of correctly declared edges in a combined graph at λ:

  $$\text{card}\{(i,j):i>j;{\omega }_{i,j}^t\ne 0\text{for}\text{some}t,1\le t\le T;\text{and}{\widehat{\omega }}^t{(\lambda )}_{i,j}\ne 0\text{for}\text{some}1\le t\le T\}.$$
• C5
  Relative squared distance (RSD) at λ:

  $$\frac{1}{T}\sum _{t=1}^T{\Vert {\mathbf{\Omega }}^t-{\widehat{\mathbf{\Omega }}}^t(\lambda )\Vert }_F^2/{\Vert {\mathbf{\Omega }}^t\Vert }_F^2.$$

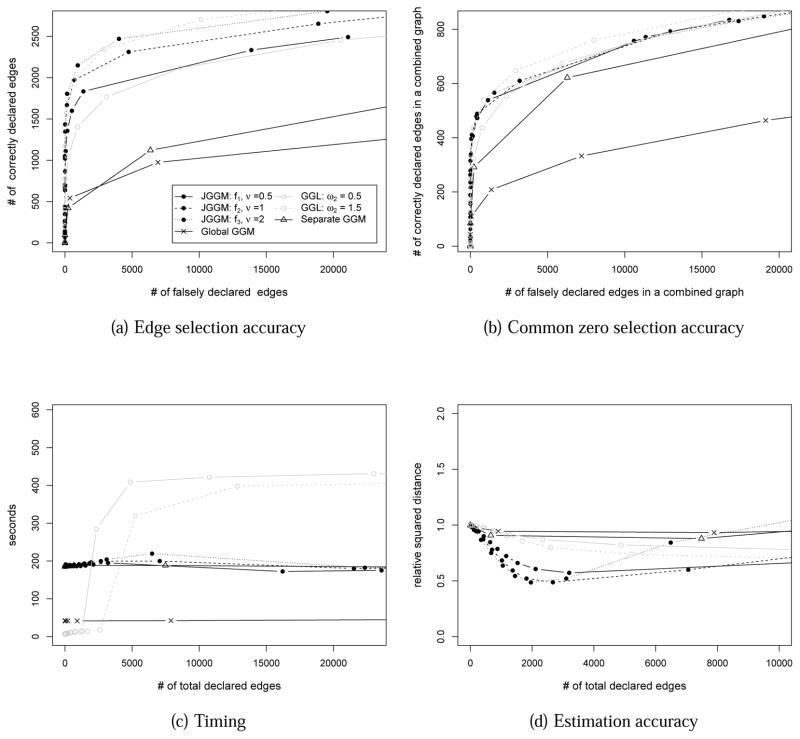
The simulation study shows that our proposed method performs similarly to the GGL in terms of edge selection accuracy (Figure 1 (a)). Our approach and GGL perform better than the approach of finding a single global GGM or separate multiple GGMs. This trend stays the same, when all methods are compared in terms of finding non-edges across all conditions (common zeros) (Figure 1 (b)). When the methods are compared in terms of timing (Figure 1(c)), our approach starts to show benefit when the estimated graphs become dense. In this simulation, the total number of possible edges was 623,750, and the true number of edges was 8090. When the estimated graph size is greater than 5590, which is a reasonable range of the estimated graph size, our approach is faster than GGL. Finally, when the relative squared distances are compared (Figure 1 (d)), our approach shows the best performance. As shown in subsection 2.4, our approach has consistency in both estimation and model selection, which is reflected in this result. The simulation study suggests that our proposed approach performs very well in terms of model selection, timing, and estimation.

Figure 1.

Performance comparison on simulated data of n_t = 150, p = 500 and T = 5. The performances of joint sparsity GGMs (JGGM) with f₁, ν = 0.5; f₂, ν = 1; and f₃, ν = 2 are compared to the performances of the single global GGM approach and the separate GGM approaches, as well as group graphical lasso (GGL) (Danaher et al., 2012) with ω₂ = 0.5 and ω₂ = 1. (a): The number of correctly declared edges is plotted against the number of falsely declared edges. (b): The number of correctly declared edges in a combined graph is plotted against the number of falsely declared edges in a combined graph. (c): Running time (in seconds) is plotted against the number of total declared edges. (d): The relative squared distance (RSD) of the estimated models from the true models is plotted.

Additionally, the simulation study shows that the use of the extended class of nonconvex function gives the flexibility of controlling the balance of common and condition specific edges. In current scenario, the f₃, ν = 2 penalty function performs the best by enforcing common structures.

3.2 Performance as a function of n, p and T

In this subsection, we compare three different nonconvex functions (f₁, ν = 0.5; f₂, ν = 1; f₃, ν = 2) under various settings of n, p and T. The datasets are simulated as in the previous subsection 3.1, and the results are based on 100 replicates.

The tuning parameter λ is chosen by using the aBIC criterion. Table 3 shows that when the number of condition is large (T = 5), the f₃, ν = 2 penalty function performs the best. When T = 2, the f₂, ν = 1 penalty performs the best in any combination of n and p. Across all simulations, the f₂, ν = 1 penalty function performs better than the f₁, ν = 0.5 penalty function.

Table 3.

Performance as a function of n, p and T. Means (standard deviations) over 100 replicates are shown for five criteria defined in Section 3.1. The tuning parameter λ was selected by using aBIC criterion.

Setting			Tuning parameter		Comparison criteria
p	nt	T	Penalty type	log10 2 λ/nt	Criterion C1	Criterion C2	Criterion C3	Criterion C4	Criterion C5
500	150	5	f1, ν = 0.5	−1.0	173.98 (20.58)	1355.98 (52.67)	155.88 (16.92)	406.22 (15.79)	0.66 (0.01)
500	150	5	f2, ν = 1	−1.4	699.42 (47.57)	1970.92 (60.20)	439.58 (26.00)	488.00 (15.13)	0.49 (0.01)
500	150	5	f3, ν = 2	−1.9	404.38 (44.84)	1981.66 (67.37)	168.32 (16.62)	437.74 (15.77)	0.48 (0.01)
500	150	2	f1, ν = 0.5	−1.1	313.90 (26.22)	393.72 (25.70)	299.38 (24.33)	257.20 (16.58)	0.78 (0.02)
500	150	2	f2, ν = 1	−1.5	343.98 (30.90)	448.36 (28.54)	293.58 (24.61)	264.82 (17.02)	0.72 (0.02)
500	150	2	f3, ν = 2	−2.3	659.60 (181.48)	527.50 (33.94)	476.40 (156.66)	291.80 (20.66)	0.85 (0.04)
1000	150	2	f1, ν = 0.5	−0.8	132.76 (17.06)	383.10 (24.56)	131.78 (16.84)	285.26 (16.42)	0.91 (0.01)
1000	150	2	f2, ν = 1	−1.2	527.52 (35.33)	625.80 (29.85)	502.08 (33.42)	408.60 (19.34)	0.81 (0.01)
1000	150	2	f3, ν = 2	−2.2	4195.08 (97.95)	1079.98 (39.09)	3648.30 (82.54)	642.00 (25.28)	0.97 (0.02)
1000	500	2	f1, ν = 0.5	−1.5	1774.14 (65.72)	2481.38 (32.03)	1674.50 (60.00)	1445.36 (20.29)	0.29 (0.01)
1000	500	2	f2, ν = 1	−2.0	1301.30 (60.64)	2519.94 (34.97)	1072.66 (46.47)	1417.20 (21.53)	0.24 (0.01)
1000	500	2	f3, ν = 2	−3.0	1920.64 (74.52)	2611.12 (35.09)	1273.74 (47.60)	1434.72 (20.99)	0.26 (0.01)

3.3 Discussion on penalty function selection

One can select an appropriate type of penalty function by adopting a tuning criterion. This requires two-way tuning for the regularization parameter λ and the type of nonconvex function (equivalently, the choice of ν), which has been adopted in the adaptive lasso (Zou, 2006). However, it is quite challenging to find an optimal tuning parameter in high-dimensional problems with low sample sizes, which often occur in many genomic data analyses. Based on our simulation studies, we find that imposing a stronger level of sparsity generally improves the performance under this setting with more benefit of using f₂ over f₁ than that of using f₃ over f₂. We thus recommend to use the f₂ penalty function, when it is challenging to use the two-way tuning in case of high-dimensional and low sample size problems.

4 Real data analysis

We apply the proposed joint estimation of multiple GGMs with a nonconvex penalty function to a gene expression dataset. It has been suggested that gene regulations differ among conditions due to differential use of the regulatory elements of genes, and understanding this differential regulation is an interesting scientific problem. One such study was done by Dimas et al. (2009), in which gene expressions were measured from three cell types, primary fibroblasts, Epstein-Barr virus (EBV)-immortalized B-cells, and T-cells of 85 individuals participating in the GenCord project. We remark that these three cell types were extracted from umbilical cords, where the fibroblasts were obtained by culturing finely cut cord tissue, and B-cells from cord blood with EBV-immortalization; and T-cells from cord blood with PHA stimulation (Dimas et al., 2009).

Since each individual contributed the three cell types, and thus the three sets of datasets are not independent to each other. This aspect is not properly addressed in the current analysis, which is our future work. However, the possible similarity of graphs due to the dependence can be reflected with the joint sparsity regularization. The dataset contains mRNA levels that are quantified with 48,804 probes with the Illumina WG-6 v3 expression array. We convert the probe level data to the gene level data by taking the average of the probes mapped to a gene. We then take the log transformation to make the data more normally distributed, and then use a total of 17,945 autosomal RefSeq genes’ expression for inferring network of genes.

Due to the limitation of the sample size (n₁ = n₂ = n₃ = 85), we partition genes into smaller groups by using pathway information. We extract the information of 528 pathways from the KEGG database. Among these, we separately analyze 277 pathways that contain at least 3 and at most 29 genes in our dataset. We apply our approach with the f₂, ν = 1 penalty function and select 2λ̃/n_t from a total of 300 possible values equally spaced in log₁₀ scale between 10⁻⁵ and 1. When the ratio of the largest to the smallest eigen value of S^t is smaller than or equal to 1000, we use (S^t)⁻¹ as the initial estimate. Otherwise, we use (S^t + δI_p)⁻¹ as the initial estimate, where $\delta =max(\frac{1}{1000}{\Vert {\mathbf{S}}^t\Vert }^2,\frac{1}{10p^2}{\mathrm{\sum }}_{i,j}\mid {\mathbf{S}}_{i,j}^t\mid )$. This choice was made in order to reflect the differing size and signal strength of the networks.

In our analysis, we extracted edge information from the database, and treated this as a true network structure. We considered this true structure as a collection of condition-specific edges without the condition information, because the database is curated by collecting the parts of gene regulations over various conditions. If an approach can preserve the tissue-specificity, it would capture the true edges more accurately than the approaches that capture only the common ones.

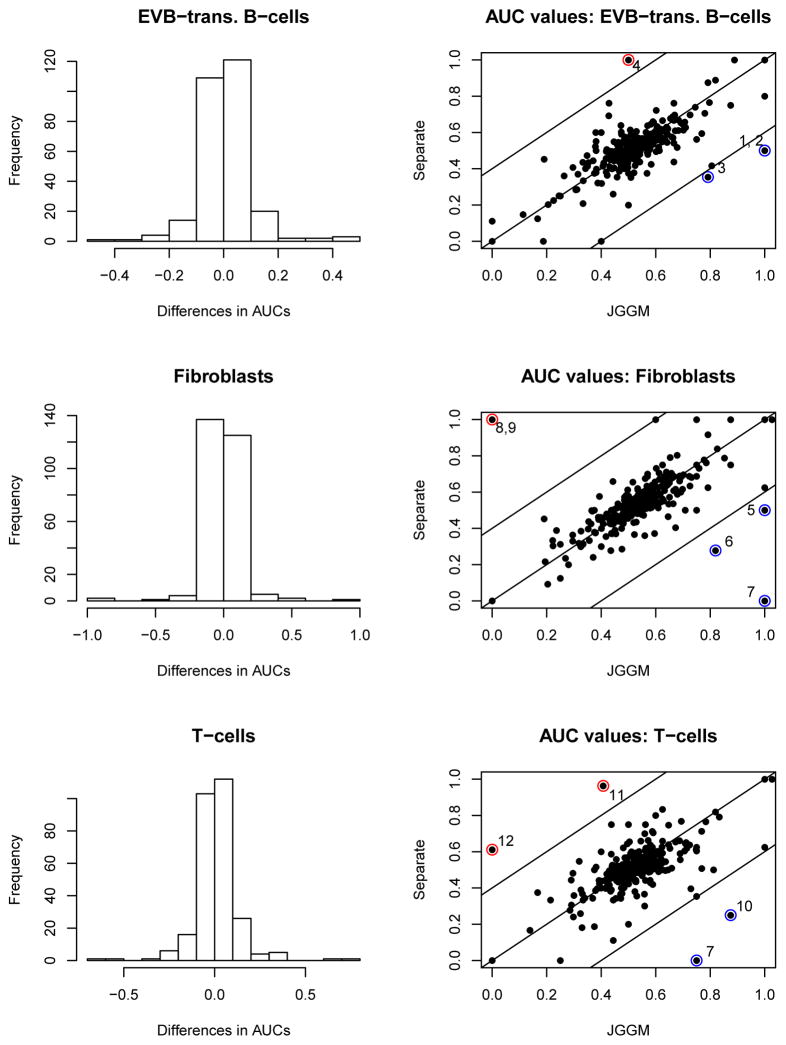
Rather than handpicking one of the 277 pathways for the presentation, we summarize our results using the true network structure. We compute the area under the curve (AUC) of each receiver operating curve (ROC) for each pathway. The AUC is used in order to avoid tuning parameter selection. Therefore, we evaluate three AUC values for each pathway corresponding to the three cell types. We then sort the pathways based on their AUC values, and list the pathways that have AUC values larger than 0.8 in Table 1. We compared our approach to the global and the separate approaches. The detailed comparison of the JGGM and the separate approaches is in Supplementary Materials. The pathways that have AUC values of 1 tend to have small graphs. However, even for these small graphs, the other methods do not always have the AUC values of 1, suggesting that the AUCs of 1 are not just automatic results from the nature of tiny graphs.

Table 1.

The selected pathways by using the JGGM approach. For the JGGM and the separate GGM approaches, three AUC values corresponding to three cell types were evaluated for each pathway. For each cell type, the pathways that have AUC values from JGGM higher than 0.8 are listed and the corresponding AUC values from global and separate approaches are shown for comparison. The number of genes and the number of edges from the KEGG database are presented.

EBV-transformed B cells
Pathway name	AUC			# genes	# edges
	JGGM	Global	Separate
Basic Mechanisms of SUMOylation pathway	1.00	1.00	0.80	4	5
Basic mechanism of action of PPARa, PPARb(d) and PPARg and effects on gene expression pathway	1.00	1.00	0.50	3	2
Dendritic cells in regulating TH1 and TH2 Development pathway	1.00	0.75	1.00	4	2
IL 18 Signaling Pathway pathway	1.00	1.00	1.00	3	1
Acetylcholine Synthesis	1.00	0.63	1.00	4	2
Beta Oxidation of Unsaturated Fatty Acids	1.00	0.00	1.00	3	2
Cytokines and Inflammatory Response	1.00	1.00	0.50	3	2
Steroid Biosynthesis	1.00	0.00	1.00	3	2
hsa00830 (Retinol metabolism)	0.89	0.56	1.00	4	3
Cytokine Network pathway	0.88	1.00	0.75	4	2
Embryonic Stem Cell	0.82	0.79	0.89	6	3
Free Radical Induced Apoptosis pathway	0.81	0.74	0.42	6	6
Primary Fibroblasts
Basic Mechanisms of SUMOylation pathway	1.00	1.00	0.80	4	5
Basic mechanism of action of PPARa, PPARb(d) and PPARg and effects on gene expression pathway	1.00	1.00	1.00	3	2
Dendritic cells in regulating TH1 and TH2 Development pathway	1.00	0.75	0.63	4	2
IL 18 Signaling Pathway pathway	1.00	1.00	0.50	3	1
Cytokines and Inflammatory Response	1.00	1.00	1.00	3	2
Steroid Biosynthesis	1.00	0.00	0.00	3	2
hsa00750 (Vitamin B6 metabolism)	1.00	0.60	1.00	4	5
Cytokine Network pathway	0.88	1.00	0.75	4	2
Acetylcholine Synthesis	0.88	0.63	1.00	4	2
hsa05010 (Alzheimer’s disease)	0.85	0.58	0.79	8	6
Th1 Th2 Differentiation pathway	0.83	0.53	0.84	18	11
Embryonic Stem Cell	0.82	0.79	0.28	6	3
Primary T-cells
Basic Mechanisms of SUMOylation pathway	1.00	1.00	1.00	4	5
Basic mechanism of action of PPARa, PPARb(d) and PPARg and effects on gene expression pathway	1.00	1.00	1.00	3	2
Dendritic cells in regulating TH1 and TH2 Development pathway	1.00	0.75	0.63	4	2
IL 18 Signaling Pathway pathway	1.00	1.00	1.00	3	1
Beta Oxidation of Unsaturated Fatty Acids	1.00	0.00	1.00	3	2
Cytokines and Inflammatory Response	1.00	1.00	1.00	3	2
Cytokine Network pathway	0.88	1.00	0.25	4	2
Cycling of Ran in nucleocytoplasmic pathway	0.83	0.71	0.79	5	6
Embryonic Stem Cell	0.82	0.79	0.82	6	3
Acetylcholine Synthesis	0.81	0.63	0.50	4	2

Our results show that the identified pathways from these three distinct cell types are very similar to each other. Notably, the identified pathways are mostly relevant to immune responses, where the role of PPARgamma in immune response regulation via dendritic cell control and lipid metabolism was demonstrated in the literature (Szatmari et al., 2007; Wieser et al., 2008). Considering that the fibroblast cells are quite different from the other cells, this result might need some more validation. The possible explanation could be the fact that these cells were all taken from the umbilical cords. Also, a similar conclusion was reached by Flutre et al. (2013), when they analyzed the same dataset for finding expression quantitative loci (eQTL). They found that most of genetical genomic controls are not cell-type specific, suggesting that these three cell types might function similarly in the umbilical cords.

There are few pathways that were selected in a specific cell type; retinol metabolism pathway appears in the top list only in EBV-transformed B-cells, where it is known that retinol is essential for growth of activated human B-cells (Buck et al., 1990); Alzheimer’s disease pathway appears only in the fibroblasts cells; and Cycling of Ran in nucleocytoplasmic pathway appears only in the activated T-cells, where Ras gene is an oncogene that is related to abnormal cell proliferation (Xia et al., 2008).

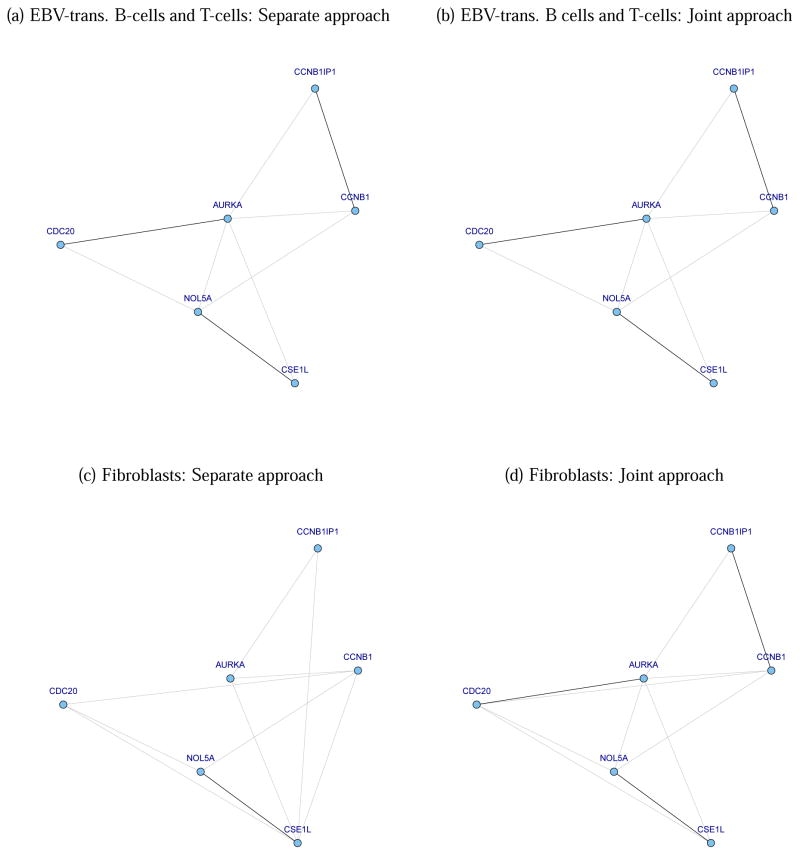
Figure 2 shows the estimated GGMs with genes consisting of an embryonic stem cell pathway. We set 2λ̃/n_t to be 2.4477×10⁻⁴ for the separate approach and 1.8738×10⁻⁵ for our joint analysis by using the aBIC criterion. We can confirm that a joint approach is able to produce different graphs for the three different cells. The graphs of the EBV-transformed B-cells and the T-cells are the same, but the graph of fibroblasts contains few more edges, which is consistent with the fact that the B-cells and T-cells are more close to each other than to the fibroblasts cells.

Figure 2.

The estimated GGMs for Embryonic Stem Cell pathway

Edges from the separate approach and joint approach (f₂, ν = 1) are depicted with gray lines, and the edges that match with the KEGG database are colored with black. The graphs of the EBV-transformed B-cells and T-cells are the same in both separate and joint approaches, but that of the fibroblasts has few more edges, which is consistent with the fact that the B-cells and T-cells are more similar to each other.

5 Conclusion

With the advancement of biological network annotations and network theory developments, researchers now attempt to use network information to decipher biological processes. Although useful, the network annotation itself is not complete, and much can be learned through inferring a network structure from multiple sources of data. In this paper, we propose to infer GGMs from gene expression data with a nonconvex penalty function for joint sparsity in order to effectively estimate multiple network structures.

We have shown the consistency and sparsistency of the proposed approach and have found that the sparsistency holds only for group-level selection. Nonetheless, this limitation is not critical because the sample size is often not large enough to invoke such theoretical results in a real application. Our simulation study showed that the proposed nonconvex function performs well by capitalizing the shared sparsity across different conditions.

We have applied the proposed approach to analyze a gene expression dataset from the GenCord project. We utilized the KEGG pathway information to facilitate our analysis and interpretation. We found that the pathways related to immune responses were pronounced in our study of umbilical cord tissues. We remark that the conclusion is based only on AUC values that do not account for associated random errors, and finding a measure that leads to a proper graph enrichment study will be our future work.

Although we suggested that the proposed nonconvex objective function can be optimized via an iteratively reweighted adaptive lasso algorithm, we did not prove that this solution is a global one. This is a general problem in most regularization approaches that use nonconvex penalty functions, and we leave it as an important problem for future research. Our future work further includes characterizing uncertainties in inferred network structures. We could use the bootstrap approach, but we would like to find the approximate variance of our proposed estimator for computational efficiency.

Figure 3.

The histograms of the differences in AUC values (JGGM - Separate) and the scatter plots of the AUC values are presented. 150, 134 and 149 pathways (out of 277) show higher AUC values with the JGGM approach for B-cells, fibroblasts and T-cells, respectively. The pathways with the AUC difference greater than 0.4 are marked and the names are given in Table 2.

Table 2.

The names of pathways that show the differences of AUC values greater than 0.4.

1	Basic mechanism of action of PPARa, PPARb(d) and PPARg and effects on gene expression pathway
2	Cytokines and Inflammatory Response
3	hsa04940 (Type I diabetes mellitus)
4	Degradation of the RAR and RXR by the proteasome pathway
5	IL 18 Signaling Pathway pathway
6	Embryonic Stem Cell
7	Steroid Biosynthesis
8	Oxidative reactions of the pentose phosphate pathway pathway
9	hsa00471(D-Glutamine and D-glutamate metabolism)
10	Cytokine Network pathway
11	Inhibition of Huntington’s disease neurodegeneration by histone deacetylase inhibitors pathway
12	Rho-Selective Guanine Exchange Factor AKAP13 Mediates Stress Fiber Formation pathway

Appendix

Proof of Proposition 1

Proof 1

The proof for the f₁ penalty function is provided in Huang et al. (2009).

We start to prove the proposition for the case of the f₂ penalty function. When ${\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid >\epsilon$, one can find that the solution of the derivative equation, $\frac{\partial }{\partial {\theta }_{j,j^{\prime }}}\stackrel{\sim }{PL}({\{{\mathbf{\Omega }}^t\}}_{t=1}^T,\mathrm{\Theta })=0$, is ${\theta }_{j,j^{\prime }}=1-log(\epsilon )+log({\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid )$. Hence, ${\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid >\epsilon$ is equivalent to θ̂_j,j′ >1. Pluggin this into $\stackrel{\sim }{PL}({\{{\mathbf{\Omega }}^t\}}_{t=1}^T,\mathrm{\Theta })$ yields a profiled penalized likelihood of $\stackrel{\sim }{\mathit{pPL}}({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)=L({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)+\tau {\mathrm{\sum }}_{j\ne j^{\prime }}(log({\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid )-log\epsilon +1)$. By taking λ = τ, one can find that $\stackrel{\sim }{\mathit{pPL}}({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)=PL({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)$.

When ${\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid \le \epsilon$, the penalty form of $PL({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)$ becomes $\frac{1}{\epsilon }{\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid$. This is equivalent to not assuming a common structure, which can be achieved by setting g(θ̂_j,j′) to be a constant function $\frac{1}{\epsilon }$ when 0 ≤ θ̂_j,j′ ≤ 1.

We then prove the proposition for the case of the f₃ penalty function by using the same principle. We find that the solution ${\theta }_{j,j^{\prime }}=\nu {\epsilon }^{1-\nu }-{({\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }})}^{1-\nu }$. Hence, ${\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid >\epsilon$ is equivalent to θ̂_j,j′ > (ν−1)ε^1−ν. This yields a profiled likelihood of $\stackrel{\sim }{\mathit{pPL}}({\{{\mathbf{\Omega }}^t\}}_{t=1}^T,)=L({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)+\frac{\tau }{\nu }{\mathrm{\sum }}_{j\ne j^{\prime }}(\nu {\epsilon }^{1-\nu }-{\mathrm{\sum }}_{t=1}^T{\mid {\omega }_{j,j^{\prime }}\mid }^{1-\nu })=PL({\{{\mathbf{\Omega }}^t\}}_{t=1}^T)$ by taking $\lambda =\frac{\tau }{\nu }$.

Lemma 1

If either x or y is greater than τ(> 0), then |x^α − y^α|τ^1−α ≤ |x − y|, for 0 < α < 1.

Proof 2

Without loss of generality, we can assume that x ≥ y.

When x > τ > y,

$$\begin{array}{l}(x^{\alpha }-y^{\alpha }){\tau }^{1-\alpha }\le x-y^{\alpha }{\tau }^{1-\alpha }\\ \le x-y.\end{array}$$

When x > y > τ,

$$x^{\alpha }-y^{\alpha }\le \frac{1}{y^{1-\alpha }}(x,y)\le \frac{1}{{\tau }^{1-\alpha }}(x-y).$$

Proof of Theorem 1

Proof 3

Theorem 1 can be proved with a slight extension to the proof of Guo et al. (2011), which is similar to the proof of Theorem 1 of Rothman et al. (2008).

Denote the objective function 1 as Q(Ω), where $\mathbf{\Omega }={\{{\mathbf{\Omega }}^t\}}_{t=1}^T$ and we write the true precision matrices as ${\mathbf{\Omega }}_0=\{{\mathbf{\Omega }}_0^t\}$. We would like to show Q(Ω) has the local minimum near Ω₀.

Specifically, we would like to show that P(Q̃(Δ) = Q(Ω₀ + Δ) − Q(Ω₀) > 0) converges to 1, when Δ ∈ ∂ 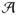, where $\partial \mathcal{A}=\{\mathrm{\Delta }:{\mathrm{\sum }}_{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F=M{r}_n\}$, and ${\mathrm{\Delta }}^t={\widehat{\mathbf{\Omega }}}^t-{\mathbf{\Omega }}_0^t$, and M is a positive constant and $r_n=\sqrt{\frac{(p+q)logp}{n}}$.

We will use the following notation: for a matrix M = [m_j,j′]_p×p, |M|₁ = Σ_j,j′|m_j,j′|, M⁺ is a diagonal matrix with the same diagonal as M, M⁻ = M − M⁺, and M_S is M with all elements outside an index set S replaced by zeros. Also, vec(M) for the vectorized form of M, and ⊗ for the Kronecker product of two matrices.

As in Guo et al. (2011), Q̃ is the sum of the following components:

$$\begin{array}{l}{I}_1=\sum _{t=1}^T\mathit{trace}(({\mathbf{S}}^t-{\mathbf{\sum }}_0^t){\mathrm{\Delta }}^k)\\ I_2=\sum _{t=1}^T{{\stackrel{\sim }{\mathrm{\Delta }}}^t}^{\prime }{\int }_0^1(1-v){({\mathbf{\Omega }}_0^t+v{\mathrm{\Delta }}^t)}^{-1}\otimes {({\mathbf{\Omega }}_0^t+v{\mathrm{\Delta }}^t)}^{-1}dv{\stackrel{\sim }{\mathrm{\Delta }}}^t\\ I_3=\lambda \sum _{(j,j^{\prime })\in {\mathbf{E}}^c}{f}_i(\sum _{t=1}^T(\mid {\delta }_{j,j^{\prime }}^t\mid ))\\ I_4=\lambda \sum _{(j,j^{\prime })\in \mathbf{E}}(f_i(\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid )-f_i(\sum _{t=1}^T\mid {{\omega }_0}_{j,j^{\prime }}^t\mid ))\end{array}$$

The bound for the likelihood part can be found in Guo et al. (2011), where

$$\begin{array}{l}\mid I_1\mid \le C_1\sqrt{\frac{logp}{n}}\sum _{t=1}^T{\mid {\mathrm{\Delta }}^{t-}\mid }_1+C_2\sqrt{\frac{\mathit{p}logp}{n}}\sum _{t=1}^R{\Vert {\mathrm{\Delta }}^{t+}\Vert }_F,\\ I_2\ge \frac{1}{4{\xi }_2^2}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F^2,\end{array}$$

for some constants C₁ and C₂ with probability tending to 1.

When (p + q)(log p)/n is small,

$$I_3\ge \lambda \sum _{t=1}^T{\mid {\mathrm{\Delta }}_{{\mathbf{E}}^c}^{t-}\mid }_1,$$

due to the concavity of the penalty functions.

Also,

$$I_4\le \lambda \sum _{j\ne j:(j,j^{\prime })\in \mathbf{E}}\left|f_i(\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid )-f_i(\sum _{t=1}^T{{\omega }_0}_{j,j^{\prime }}^t)\right|.$$

For the f₁ function, by using Lemma 1,

$$\begin{array}{l}{I}_4\le \frac{\lambda }{{\xi }_3^{\nu }}\sum _{j\ne j^{\prime }:(j,j^{\prime })\in \mathbf{E}}\mid \sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid -\sum _{t=1}^T\mid {{\omega }_0}_{j,j^{\prime }}^t\mid \mid \\ \le \frac{\lambda }{{\xi }_3^{\nu }}\sum _{t=1}^T\sum _{j\ne j^{\prime }:(j,j^{\prime })\in \mathbf{E}}\mid {\omega }_{j,j^{\prime }}^t-{{\omega }_0}_{j,j^{\prime }}^t\mid \\ \le \frac{\lambda }{{\xi }_3^{\nu }}\sqrt{q}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F\\ \le \frac{{\mathrm{\Lambda }}_2}{{\xi }_3^{\nu }}\sqrt{\frac{(p+q)logp}{n}}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F.\end{array}$$

For the functions f₂ and f₃,

$$\begin{array}{l}\mid I_4\mid \le \lambda \sum _{j\ne j^{\prime }:(j,j^{\prime })\in \mathbf{E}}\mid f_i(\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid )-f_i(\sum _{t=1}^T\mid {{\omega }_0}_{j,j^{\prime }}^t\mid )\mid \\ \le \lambda \sum _{j\ne j^{\prime }:(j,j^{\prime })\in \mathbf{E}}{f}_i^{\prime }({\xi }_3-\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F)\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t-{{\omega }_0}_{j,j^{\prime }}^t\mid \\ \le \lambda \sum _{j\ne j^{\prime }:(j,j^{\prime })\in \mathbf{E}}{f}^{\prime }({\xi }_3/2)\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t-{{\omega }_0}_{j,j^{\prime }}^t\mid \mathit{for}\mathit{sufficiently}\mathit{small}{r}_n,\\ \le \lambda \sum _{j\ne j^{\prime }(j,j^{\prime })\in \mathbf{E}}\frac{\nu -1}{{({\xi }_3/2)}^{\nu }}\sum _{t=1}^T\mid {\omega }_{j,j^{\prime }}^t-{{\omega }_0}_{j,j^{\prime }}^t\mid \\ \le \frac{(\nu -1)\lambda }{{({\xi }_3/2)}^{\nu }}\sqrt{q}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F\\ \le \frac{(\nu -1){\mathrm{\Lambda }}_2}{{({\xi }_3/2)}^{\nu }}\sqrt{\frac{(p+q)logp}{n}}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F,\end{array}$$

where ν ≥ 1 and $f_i^{\prime }(a)$ denotes $\frac{\partial f_i(x)}{\partial x}\mid x=a$

The second inequality comes from the application of the mean value theorem and the fact that f′ is decreasing function as well as $\mid {{\omega }_0}_{j,j^{\prime }}^t\mid >{\xi }_3$.

Combining all the results,

$$\begin{array}{l}\stackrel{\sim }{Q}(\mathrm{\Delta })\ge -\mid I_1\mid +I_2+I_3-\mid I_4\mid \\ \ge -C_1\sqrt{\frac{logp}{n}}\sum _{t=1}^T({\mid {\mathrm{\Delta }}_{\mathbf{E}}^{t-}\mid }_1+{\mid {\mathrm{\Delta }}_{{\mathbf{E}}^c}^{t-}\mid }_1)-C_2\sqrt{\frac{\mathit{p}logp}{n}}{\Vert {\mathrm{\Delta }}^{t+}\Vert }_F+\frac{1}{4{\xi }_2^2}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F^2+{\mathrm{\Lambda }}_1\sqrt{\frac{logp}{n}}\sum _{t=1}^T{\mid {\mathrm{\Delta }}_{{\mathbf{E}}^c}^{t-}\mid }_1-\frac{{\mathrm{\Lambda }}_2}{g({\xi }_3)}\sqrt{\frac{(p+q)logp}{n}}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F\\ \ge ({\mathrm{\Lambda }}_1-C_1)\sqrt{\frac{logp}{n}}\sum _{t=1}^T{\mid {\mathrm{\Delta }}_{{\mathbf{E}}^c}^{t-}\mid }_1-(C_1+C_2)\sqrt{\frac{(p+q)logp}{n}}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F+\frac{1}{4{\xi }_2^2}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F^2-\frac{{\mathrm{\Lambda }}_2}{g({\xi }_3)}\sqrt{\frac{(p+q)logp}{n}}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F\\ \ge \frac{1}{4{\xi }_2^{2}T}{(\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F)}^2-(C_1+C_2)\sqrt{\frac{(p+q)logp}{n}}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F-\frac{{\mathrm{\Lambda }}_2}{g({\xi }_3)}\sqrt{\frac{(p+q)(logp)}{n}}\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F\mathit{for}{\mathrm{\Lambda }}_1>C_1\\ ={(\sum _{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F)}^2\left(\frac{1}{4T{\xi }_2^2}-\frac{C_1+C_2+\mathrm{\Lambda }/g({\xi }_3)}{{\mathrm{\sum }}_{t=1}^T{\Vert {\mathrm{\Delta }}^t\Vert }_F/\sqrt{\frac{(p+q)(logp)}{n}}}\right),\end{array}$$

where g(ξ) = ξ^ν for f₁ penalty function, and g(ξ) = (ν−1)(ξ/2)^−ν for f₂ and f₃ penalty functions.

Thus, for sufficiently large M, we have Q̃(Δ) > 0 for any Δ ∈ ∂ .

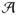Proof of Theorem 2

Proof 4

Define E_n = E_n,1 ∪ … ∪ E_n,T, where ${\mathbf{E}}_{n,t}=\{(j,j^{\prime }):j\ne j^{\prime },{\widehat{\omega }}_{j,j^{\prime }}^t\ne 0\}$.

We first show that P(E ⊆ E_n) converges to 1. $P(\mathbf{E}\subseteq {\mathbf{E}}_n)=P(\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid >0\mathit{for}\mathit{some}t\in 1,\dots ,T\mathit{for}\mathit{all}(j,j^{\prime })\in \mathbf{E})$. Since ${\mathrm{\sum }}_{t=1}^T{\Vert {\widehat{\mathbf{\Omega }}}_{j,j^{\prime }}^t-{\mathbf{\Omega }}_{0,j,j^{\prime }}^t\Vert }_F=O_p(\sqrt{\frac{(p+q)logp}{n}})$ by Theorem 1, one can see that $P(\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid >0\mathit{for}\mathit{some}t\in 1,\dots ,T\mathit{for}\mathit{all}(j,j^{\prime })\in \mathbf{E})\to P(\mid {\omega }_{0,j,j^{\prime }}^t\mid >0\mathit{for}\mathit{some}t\in 1,\dots ,T\mathit{for}\mathit{all}(j,j^{\prime })\in \mathbf{E})$ which should be 1 due to the fact that $\mid {\omega }_{0,j,j^{\prime }}^t\mid >{\xi }_3>0$ for some t for all (j, j′) ∈ E.

In order to show that P(E_n ∈ E) converges to 1, we will show $P({\mathbf{E}}^c\subseteq {\mathbf{E}}_n^c)$ converges to 1. For this, we need to show that for any (j, j) ∈ E^c, the derivative $\frac{\partial Q}{\partial {\omega }_{j,j^{\prime }}^t}$ has the same sign as ${\widehat{\omega }}_{j,j^{\prime }}^t$ for all 1 ≤ t ≤ T with probability tending to 1.

We first discuss the f₁ penalty function. The derivative of the objective function can be written as

$$\frac{\partial Q}{\partial {\omega }_{j,j^{\prime }}^t}=W_1(t,j,j^{\prime })+W_2\mathit{sign}({\omega }_{j,j^{\prime }}^t),$$

where $W_1(t,j,j^{\prime })={\mathbf{S}}_{j,j^{\prime }}^t-{\mathbf{\sum }}_{j,j^{\prime }}^t$ and $W_2=\lambda (1-\nu ){({\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid )}^{-\nu }$, where 0 < ν 1.

Arguing as in Theorem 2 of Lam and Fan (2009), one can show that ${max}_{t,j,j^{\prime }}{W}_1(t,j,j^{\prime })=O_p({(\frac{logp}{n})}^{1/2}+{\eta }_n^{1/2})$.

For (j, j′) ∈ E^c, ${\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid =O_p({\eta }_n)$ and ${\eta }_n^{-\nu }$ goes to ∞, and ${(\frac{logp}{n})}^{1/2}+{\eta }_n^{1/2}=O(\lambda )$, W₂ dominates max_(t,j,j′) W₁(t,j,j′).

For the functions f₂ and f₃, $W_2=\frac{\lambda }{max(({\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid ),\epsilon )}$ and $W_2=\frac{\lambda (\nu -1)}{max({({\mathrm{\sum }}_{t=1}^T\mid {\omega }_{j,j^{\prime }}^t\mid )}^{\nu },{\epsilon }^{\nu })}$, respectively, and ν > 1.

For (j, j′) ∈ E^c, ${\mathrm{\sum }}_{t=1}^T\mid {\widehat{\omega }}_{j,j^{\prime }}^t\mid =O_p({\eta }_n)$. Then, $W_2=O_p(\lambda min({\eta }_n^{-\nu },{\epsilon }^{-\nu }))$, ν ≥ 1 and W₂ dominates max_t,j,j′ W₁(t, j, j′), by taking sufficiently small ε.