Intuition, deliberation, and the evolution of cooperation

Significance

The role of intuition versus deliberation in human cooperation has received widespread attention from experimentalists across the behavioral sciences in recent years. Yet a formal theoretical framework for addressing this question has been absent. Here, we introduce an evolutionary game-theoretic model of dual-process agents playing prisoner’s dilemma games. We find that, across many types of environments, evolution only ever favors agents who (i) always intuitively defect, or (ii) are intuitively predisposed to cooperate but who, when deliberating, switch to defection if it is in their self-interest to do so. Our model offers a clear explanation for why we should expect deliberation to promote selfishness rather than cooperation and unifies apparently contradictory empirical results regarding intuition and cooperation.

Abstract

Humans often cooperate with strangers, despite the costs involved. A long tradition of theoretical modeling has sought ultimate evolutionary explanations for this seemingly altruistic behavior. More recently, an entirely separate body of experimental work has begun to investigate cooperation’s proximate cognitive underpinnings using a dual-process framework: Is deliberative self-control necessary to reign in selfish impulses, or does self-interested deliberation restrain an intuitive desire to cooperate? Integrating these ultimate and proximate approaches, we introduce dual-process cognition into a formal game-theoretic model of the evolution of cooperation. Agents play prisoner’s dilemma games, some of which are one-shot and others of which involve reciprocity. They can either respond by using a generalized intuition, which is not sensitive to whether the game is one-shot or reciprocal, or pay a (stochastically varying) cost to deliberate and tailor their strategy to the type of game they are facing. We find that, depending on the level of reciprocity and assortment, selection favors one of two strategies: intuitive defectors who never deliberate, or dual-process agents who intuitively cooperate but sometimes use deliberation to defect in one-shot games. Critically, selection never favors agents who use deliberation to override selfish impulses: Deliberation only serves to undermine cooperation with strangers. Thus, by introducing a formal theoretical framework for exploring cooperation through a dual-process lens, we provide a clear answer regarding the role of deliberation in cooperation based on evolutionary modeling, help to organize a growing body of sometimes-conflicting empirical results, and shed light on the nature of human cognition and social decision making.

Cooperation, where people pay costs to benefit others, is a defining feature of human social interaction. However, our willingness to cooperate is puzzling because of the individual costs that cooperation entails. Explaining how the “selfish” process of evolution could have given rise to seemingly altruistic cooperation has been a major focus of research across the natural and social sciences for decades. Using the tools of evolutionary game theory, great progress has been made in identifying mechanisms by which selection can favor cooperative strategies, providing ultimate explanations for the widespread cooperation observed in human societies (1).

In recent years, the proximate cognitive mechanisms underpinning human cooperation have also begun to receive widespread attention. For example, a wide range of experimental evidence suggests that emotion and intuition play a key role in motivating cooperation (2–5). The dual-process perspective on decision making (6–8) offers a powerful framework for integrating these observations. In the dual-process framework, decisions are conceptualized as arising from competition between two types of cognitive processes: (i) automatic, intuitive processes that are relatively effortless but inflexible; and (ii) controlled, deliberative processes that are relatively effortful but flexible. In many situations, intuitive and deliberative processes can favor different decisions, leading to inner conflict: Rather than being of a single mind, people are torn between competing desires.

Despite the widespread attention that dual-process theories have received in the psychological and economic sciences (including incorporation into formal decision making models; refs. 9–11); the existence of related discussion in the theoretical biology literature regarding error management (12–14), tradeoffs between fixed and flexible behaviors (15–18), and cultural evolution and norm internalization (2, 19, 20); and a long interdisciplinary tradition of arguments suggesting that strategies developed in repeated interactions spill over to influence behavior in one-shot anonymous settings (21–25), the dual-process framework has been almost entirely absent from formal models of the evolution of cooperation. Traditional evolutionary game theory models of cooperation focus on behavior, rather than the cognition that underlies behavior. Therefore, these models do not shed light on when selection may favor the use of intuition versus deliberation, or which specific intuitive and deliberative responses will be favored by selection.

In this paper, we build a bridge between ultimate and proximate levels of analysis to address these questions, introducing an evolutionary game-theoretic model of cooperation that allows for dual-process agents. These agents interact in a varied social environment, where interactions differ in the extent to which current actions carry future consequences. To capture the tradeoff between flexibility and effort that is central to many dual-process theories, we allow our agents to either (i) use an intuitive response that is not sensitive to the type of interaction currently faced; or (ii) pay a cost to deliberate, tailoring their action to the details of the current interaction.

We then use this framework to explore the consequences of reciprocity and assortment (26, 27), two of the most widely studied mechanisms for the evolution of cooperation. We ask when (and to what extent) agents evolve to pay the cost of deliberation; when evolution favors intuitive responses that are selfish versus cooperative; and whether deliberation serves to increase or decrease social welfare. In doing so, we provide a formal theoretical framework to guide the emerging body of empirical work exploring prosociality from a dual-process perspective, and provide insight into the cognitive underpinnings of human cooperation.

Model

There are two key dimensions on which our model differs from typical models of the evolution of cooperation: (i) in each generation, agents play more than one type of game; and (ii) agents need not have a single fixed strategy, but can engage in costly deliberation to tailor their response to the type of game they are facing.

With respect to multiple game types, our agents face both one-shot anonymous prisoner’s dilemma (PD) games (which occur with probability 1−p) and PDs where reciprocal consequences exist (which occur with probability p). In the one-shot PDs, agents can cooperate by paying a cost c to give a benefit b to their partner, or defect by doing nothing. In the games with reciprocal consequences, we capture the core of reciprocity [be it via repeated interactions, reputation effects, or sanctions (1)] by modifying the off-diagonal elements of the PD payoff structure: When exploitation occurs, such that one player defects while the other cooperates, the benefit to the defector is reduced (due to, e.g., lost future cooperation, damaged reputation, or material punishment), as is the cost to the cooperator (due to, e.g., switching to defection, improved reputation, or material rewards). As a result, the social dilemma of the PD is transformed into a coordination game: It becomes payoff-maximizing to cooperate if one’s partner also cooperates. For simplicity, we focus on the limiting case where when one player cooperates and the other defects, both receive zero payoffs. Because this simplified payoff structure is analogous to the average payoff per round of an infinitely repeated PD between “tit-for-tat” and “always defect,” for expositional purposes, we refer to games with reciprocal consequences as “repeated games.” Critically, however, our results do not rely on this simplifying assumption, or on the use of repeated games more generally (mitigating potential concerns about alternative repeated game strategy sets; ref. 28). Rather, they hold whenever agents face any of a broad class of cooperative coordination games with probability p; see SI Appendix, Section 6 for details. Similarly, the social dilemma that occurs with probability 1−p need not be a one-shot PD—equivalent results would be obtained by using any game where cooperation always earns less than noncooperation.

We also consider the other main force that has been argued to underlie the evolution of human cooperation: assortment (29). An agent plays against another agent having the same strategy as herself with probability a and plays with an agent selected at random from the population with probability 1−a. Thus, a captures the extent to which agents of similar types are more likely than chance to interact. This assortment could arise from relatedness, spatial or networked interactions, or group selection (1).

With respect to multiple strategies within a single agent, our model allows agents to use two forms of decision making: intuition or deliberation (see Fig. 1 for a visual depiction of an agent’s decision process; and SI Appendix, Section 1 for further details). Among the various dimensions upon which these modes of cognitive processing differ (6), we focus on the fact that intuitive responses are quick and relatively effortless (and thus less costly), but also less sensitive to situational and strategic details than deliberative responses. For simplicity, we focus on the limiting case where intuition is totally inflexible and deliberation is perfectly flexible/accurate. When agents decide intuitively, they cooperate with some fixed probability S_i, regardless of whether the game is one-shot or repeated. Deliberating, conversely, allows agents to potentially override this intuitive response and tailor their strategy to the type of game they are facing. When deliberating, agents cooperate with probability S₁ if the game they are facing is one-shot, and cooperate with probability S_r if it is repeated.

Fig. 1.

Agents play PD games that are either one-shot or involve reciprocity, and either use a generalized intuitive strategy that does not depend on game type, or engage in costly deliberation and tailor their strategy based on game type. The strategy space for the agents in our model, which consists of four variables T, S_i, S₁, and S_r, is visualized here along with the sequence of events within each interaction between two agents (both agents face the same decision, so for illustrative simplicity only one agent’s decision process is shown). First, the agent’s cost of deliberation for this interaction d* is sampled uniformly from the interval [0, d]. The agent’s deliberation threshold T then determines which mode of cognitive processing is applied. If d* > T, it is too costly to deliberate in this interaction and she makes her cooperation decision based on her generalized intuitive response S_i; intuition cannot differentiate between game types, and so regardless of whether the game is one-shot (probability 1−p) or repeated (probability p), she plays the cooperative strategy with probability S_i. If d* ≤ T, however, deliberation is not too costly, so she pays the cost d* and uses deliberation to tailor her play to the type of game she is facing: If the game is one-shot, she plays the cooperative strategy with probability S₁, and if the game is repeated, she plays the cooperative strategy with probability S_r. For example, when deliberating, an agent could decide to defect in a one-shot game (S₁ = 0) but cooperate in a repeated game (S_r = 1). In contrast, when using intuition, this agent must either cooperate in both contexts (S_i = 1) or defect in both contexts (S_i = 0).

The flexibility of deliberation, however, comes at a cost (30, 31). This cost can take several forms. First, deliberation is typically slower than intuition, and this greater time investment can be costly. For example, sometimes decisions must be made quickly lest you miss out on the opportunity to act. Second, deliberation is more cognitively demanding than intuition: Reasoning your way to an optimal solution takes cognitive effort. Furthermore, because intuitions are typically low-level cognitive processes that are triggered automatically and reflexively (7, 8), cognitive resources may also be required to inhibit intuitive responses when deliberation reveals that they are suboptimal. These cognitive demands associated with deliberation can impose fitness costs by reducing the agent’s ability to devote cognitive resources to other important tasks unrelated to the cooperation decision. The fitness costs associated with this need to redirect cognitive resources are particularly large when agents are under cognitive load or are fatigued.

Thus, deliberation is costly, but the size of that cost varies from decision to decision (between 0 and some maximum value d). For simplicity, in each interaction, we independently sample a cost of deliberation d* for each agent from a uniform distribution over [0, d].

In addition to evolving different intuitive and deliberative responses, we allow natural selection to act on the extent to which agents rely on intuition versus deliberation. Specifically, each agent’s strategy specifies a deliberation cost threshold T, such that they deliberate in interactions where the deliberation cost is sufficiently small, d* ≤ T, but act intuitively when deliberation is sufficiently costly, d* > T. Thus, in any given interaction, an agent with threshold T deliberates with probability T/d and uses intuition with probability 1−T/d. The higher an agent’s value of T, the more that agent tends to deliberate.

In sum, an agent’s strategy is defined by four variables: her (i) probability of intuitively cooperating S_i, (ii) probability of cooperating when she deliberates and faces a one-shot game S₁, (iii) probability of cooperating when she deliberates and faces a repeated game S_r, and (iv) maximum acceptable cost of deliberation T. For example, consider an agent with S_i = 1, S_r = 1, S₁ = 0, and T = 0.5 engaging in a one-shot game. If she received a randomly sampled deliberation cost of d* = 0.7, she would play her intuitive choice S_i, and cooperate. Alternatively, if she received a lower randomly sampled deliberation cost of d* = 0.3, she would play her deliberative strategy for one-shot games S₁ and defect (and incur the deliberation cost of 0.3).

Within this framework, we consider the stochastic evolutionary dynamics of a population of finite size N evolving via the Moran process. This dynamic can describe either genetic evolution where fitter agents produce more offspring, or social learning where people preferentially copy the strategies of successful others. In each generation, an individual is randomly picked to change its strategy (“die”), and another individual is picked proportional to fitness to be imitated (“reproduce”). (Fitness is defined as e^wπ, where w is the “intensity of selection” and π is the agent’s expected payoff from interacting with the other agents in the population.) With probability u, experimentation (“mutation”) occurs, and instead a random strategy is chosen. For our main analyses, we perform exact numerical calculations in the limit of low mutation using a discretized strategy set (SI Appendix, Section 4); we obtain equivalent results by using agent-based simulations with higher mutation and a continuous strategy space (SI Appendix, Section 5 and Fig. S3). Code implementing the model in MATLAB is available at https://gist.github.com/adambear91/c9b3c02a7b9240e288cc.

Results

What strategies, then, does evolution favor in our model? We begin by varying the extent of reciprocity p in the absence of assortment (a = 0) (Fig. 2A). When most interactions are one-shot (p is small), selection favors agents who intuitively defect, S_i = 0, and who rarely deliberate, T∼0. (Because the deliberative choices of these agents, S_r and S₁, are seldom used, their values have little effect on fitness, and drift pulls their average values toward neutrality, 0.5; nonetheless, deliberation always favors cooperation over defection in repeated games, S_r > 0.5, and defection over cooperation in one-shot games, S₁ < 0.5.)

Fig. 2.

Reciprocity leads evolution to favor dual-process agents who intuitively cooperate but use deliberation to defect in one-shot games. (A) Shown are the average values of each strategy variable in the steady-state distribution of the evolutionary process, as a function of the probability of repeated games p. When most interactions are one-shot (p is small), agents intuitively defect (S_i = 0) and rarely deliberate (T∼0) (as a result, the deliberative cooperation strategies for one-shot games S₁ and repeated games S_r are rarely used, and so their values are dominated by neutral drift and sit near 0.5). Conversely, when the probability of repeated games (i.e., the extent of reciprocity) is sufficiently high (p > 0.3 for these parameters), agents evolve to be intuitively cooperative (S_i = 1) and to pay substantial costs to deliberate (T >> 0); and when these agents deliberate, they cooperate in repeated games (S_r = 1) and defect in one-shot games (S₁ = 0). As the probability of repeated games p increases beyond this point, these intuitive and deliberative responses do not change, but agents become less willing to deliberate (T decreases). Evolutionary calculations use N = 50, b = 4, c = 1, d = 1, w = 6, and a = 0; see SI Appendix, Fig. S2 for calculations using other parameter values. (B) To better understand the dynamics in A, we perform Nash equilibrium calculations. There are two possible equilibria, which are described here: (i) the ID strategy, which never deliberates (T = 0) and always intuitively defects (S_i = 0; S₁ and S_r are undefined because deliberation is never used); and (ii) the DC strategy, which intuitively cooperates (S_i = 1) and is willing to pay a maximum cost of T = c(1−p) to deliberate, in which case it cooperates in repeated games (S_r = 1) and switches to defection in one-shot games (S₁ = 0). (C) Evolutionary calculations using only these two strategies successfully reproduce the results of the full strategy space in A. Thus, these two strategies are sufficient to characterize the dynamics of the system: We find that the population shifts from entirely ID to entirely DC once p becomes large enough for DC to risk-dominate ID (see SI Appendix for calculation details). (D) As a result, cooperation in repeated games goes to ceiling as soon as p passes this threshold, whereas cooperation in one-shot games slowly increases with p.

Once p increases beyond some critical threshold, we observe the simultaneous emergence of both (i) intuitive cooperation, S_i = 1; and (ii) the use of deliberation, T >> 0, to implement the “rational” behaviors of cooperating in repeated games, S_r = 1, but defecting in one-shot games, S₁ = 0. Thus, when faced with a repeated game, these agents’ intuition and deliberation agree upon cooperating. When faced with a one-shot game, however, the agents experience internal conflict: Intuition prescribes cooperation, but deliberation overrules this cooperative impulse in favor of defection.

As p increases further, agents’ intuitive and deliberative responses do not change, but their propensity to engage in deliberation steadily declines. Once p becomes sufficiently close to 1, agents are again relying almost entirely on intuition—albeit, now, a cooperative intuition (unlike when p was small).

What explains this pattern of results? A Nash equilibrium analysis provides clear insight (see SI Appendix, Section 2 for technical details). There are at most two equilibria (Fig. 2B). The intuitive defector (ID) strategy profile, which is always an equilibrium, has defection as its intuitive response, S_i = 0, and never deliberates, T = 0. The second possibility, which is only an equilibrium when repeated games are sufficiently likely (p > c/b), is the dual-process cooperator (DC) strategy profile. DC players intuitively cooperate, S_i = 1, and deliberate when the cost of deliberation is not greater than T = c(1−p). On the occasions that DC players deliberate, they cooperate if the game is repeated, S_r = 1, and defect if the game is one-shot, S₁ = 0. In other words, DC players use deliberation to override their cooperative intuitions when they find themselves in a one-shot game, and instead defect.

Together, these two Nash equilibria reproduce the pattern observed in the evolutionary dynamics (Fig. 2C). The transition from ID to DC occurs precisely at the point where DC risk-dominates ID (i.e., where DC earns more than ID in a population where both strategies are equally likely, which is known to predict evolutionary success; see SI Appendix, Section 3 for details), after which point mean T = c(1−p) (declining linearly in p). Furthermore, after this point, increasing the probability of games being repeated p has no effect on cooperation in repeated games (which is at ceiling), but instead increases cooperation in one-shot games (Fig. 2D): Across a wide range of parameters, cooperation in repeated games is high, and cooperation in one-shot games is lower but substantially greater than zero [as is typical of human behavior (1)].

Why is T = c(1−p) the maximum cost for which DC will deliberate? Deliberation allows DC to avoid cooperating (and, thus, avoid incurring a cost c) in the fraction (1−p) of interactions that are one-shot; in the fraction p of interactions that are repeated, there is no benefit to deliberating, because DC’s intuitive and deliberative responses agree on cooperating. Therefore, c(1−p) is DC’s expected payoff gain from deliberating, and so deliberation is disadvantageous when it is more costly than c(1−p). This condition emphasizes the fact that deliberation’s only function for DC agents is to restrain the impulse to cooperate in one-shot games. Intuition, conversely, functions as a “repeated game” social heuristic (24, 25), prescribing the cooperative strategy that is typically advantageous (given the sufficiently high prevalence of repeated games).

Critically, we do not observe an equilibrium that intuitively defects but uses deliberation to cooperate in repeated games. This strategy is not an equilibrium because of a coordination problem: It is only beneficial to override a defecting intuition to cooperate in a repeated game when your partner also plays a cooperative strategy. Thus, ID’s expected payoff from deliberating when playing a repeated game with an ID partner is discounted by the extent to which their partner fails to deliberate (and so the partner defects, even though the game is repeated). As a result, IDs maximize their payoff by deliberating less than their partners, leading to an unraveling of deliberation: Any nonzero deliberation threshold is not Nash, because there is an incentive to deviate by deliberating less than your partner. (This is not true for the intuitively cooperative strategy DC deliberating in one-shot games, because in one-shot games it is always beneficial to switch to defection, no matter what the other agent does.)

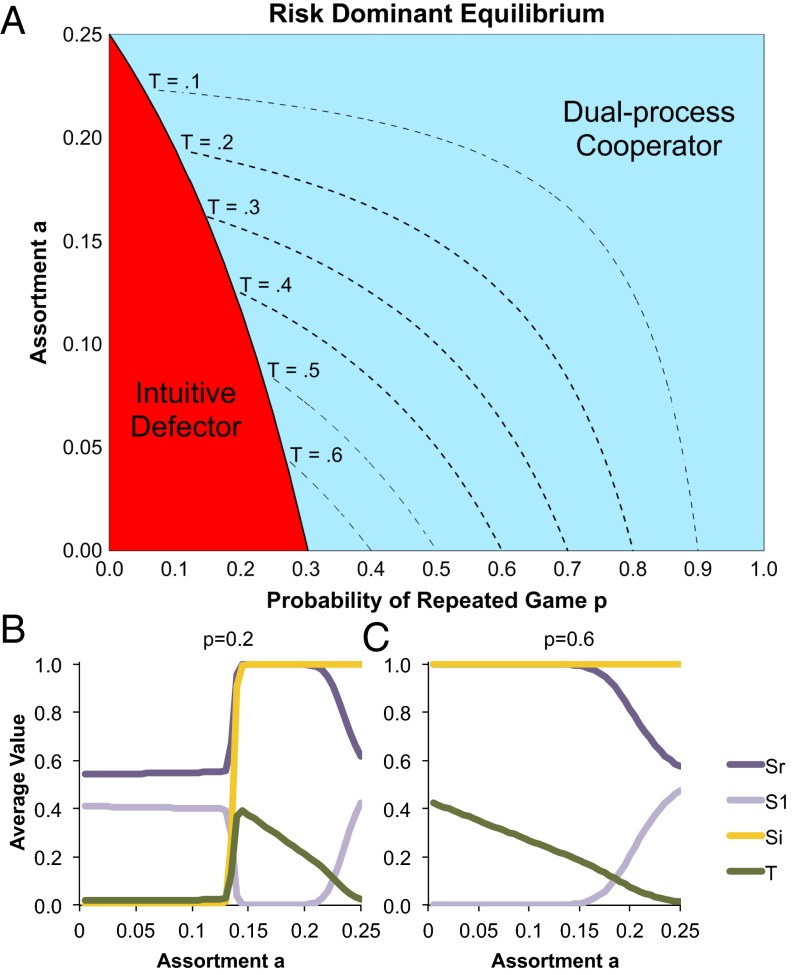
Finally, we investigate the effect of assortment in our model. Nash equilibrium analysis again shows that ID and DC are the only equilibria, with DC’s deliberation threshold now being T = (c−ba)(1−p). Increasing a acts in a similar way to increasing p, allowing DC to be favored over ID and, subsequently, reducing T (Fig. 3A). Consistent with this analysis, evolutionary calculations show an interaction between a and p. When repeated games are rare (small p), increasing a allows intuitive cooperation to succeed and initially increases T (as DC begins to outperform ID); as a increases further, however, T decreases (Fig. 3B). When repeated games are common (large p), conversely, DC is dominant even without assortment; therefore, increasing a always decreases T (Fig. 3C). These analyses show that our results are robust to assumptions about the evolutionary history of humans: Regardless of whether most interactions involved reciprocity with little assortment, or most interactions were one-shot but assorted, selection favors the same intuitively cooperative dual-process strategy (and never a strategy that uses deliberation to cooperate by overruling intuitive defection).

Fig. 3.

Assortment also favors the evolution of dual process cooperators. (A) Nash equilibrium calculations with assortment (a > 0) again find that ID and DC are the only possible equilibria. The risk-dominant strategy is shown as a function of the probability of repeated games p and the level of assortment a (risk-dominance indicates which strategy will be favored by selection; see SI Appendix, Fig. S1 for corresponding evolutionary calculations). DC is favored so long as either p or a are sufficiently large. Thus, regardless of whether evolution occurs in a world where reciprocity is powerful and assortment is weak, or where reciprocity is weak and assortment is strong, selection favors intuitive cooperation combined with deliberative defection in one-shot games. Also shown are isoclines for T within the region where DC is favored. Here, increasing either a or p decreases T. Thus, we find an interaction with reciprocity when considering how assortment affects cognitive style: when p is low, assortment initially increases deliberation, but when p is high, assortment monotonically decreases deliberation. This interaction is visualized by showing the average values of each strategy variable in the steady-state distribution of the evolutionary process as a function of assortment a, for p = 0.2 (B) and p = 0.6 (C). Evolutionary calculations use N = 50, b = 4, c = 1, d = 1, and w = 6.

Discussion

By integrating dual-process cognition into a game-theoretic model of the evolution of cooperation based on reciprocity and assortment, we provide a formal theoretical framework for considering the question of whether prosociality is intuitive or whether it requires self-control. We find that evolution never favors strategies for which deliberation increases cooperation. Instead, when deliberation occurs, it always works to undermine cooperation in one-shot interactions. Intuition, conversely, acts as a social heuristic (24, 25), implementing the behavior that is typically advantageous (cooperation, unless p and a are both sufficiently small, because the cost of missing out on reciprocal cooperation outweighs the cost of needlessly cooperating in one-shot games (14). Thus, our model helps to explain why people cooperate even in one-shot anonymous settings, but less frequently than they do in repeated interactions. Furthermore, we offer an explanation for why cooperation in such situations is typically “conditional” rather than “unconditional” (32) (i.e., why people will cooperate in one-shot games, but only if they expect their partner to also cooperate): when one-shot cooperation evolves in our model, it occurs via an intuitive response that treats social dilemmas as if they were coordination games.

Our model also makes numerous clear, testable predictions about human cognition. First, in one-shot anonymous interactions, promoting intuition (increasing the cost of deliberation d*) should, on average, increase cooperation relative to promoting deliberation (reducing d*). This prediction holds even in laboratory experiments where participants are explicitly told that the game they are playing is one-shot, for at least two reasons. First, deliberation is required to translate this explicit knowledge about game length into a strategic understanding that cooperative intuitions should be overridden (many participants mistakenly believe that it is in their self-interest to cooperate even when they are told the game is one-shot, as shown for example in refs. 33 and 34). Second, further cognitive effort may be required to inhibit the intuitive response because it is triggered automatically. In line with this prediction, data from numerous research groups show that experimentally inducing participants to decide more intuitively using time pressure (4, 24, 33), cognitive load (35–37), conceptual inductions (3, 4, 38), or variation in payment delays (11, 39) can increase prosociality in one-shot economic games.

Furthermore, our model predicts substantial heterogeneity across individuals in this effect. People who developed their strategies in social settings with little future consequence for bad behavior (small p) and low levels of assortment (small a) are predicted to intuitively defect (S_i = 0), and to engage in little deliberation, regardless of the cost (T = 0). Thus, experimentally manipulating the cost of deliberation should not affect these participants’ cooperation. Consistent with this prediction, time constraint manipulations were found to have little effect on participants with untrustworthy daily-life interaction partners (34) or participants from a country with low levels of interpersonal trust and cooperation (40). Furthermore, our model predicts that when p and/or a becomes sufficiently large, T also approaches 0 (albeit with a cooperative intuition, S_i = 1). Therefore, people who developed their strategies in contexts that were extremely favorable to cooperation should also be relatively unaffected by cognitive process manipulations. This prediction may help to explain why some one-shot game studies find no effect of manipulating intuition (41). Further support for the predicted link between extent of future consequences and intuitive one-shot cooperation comes from laboratory evidence for “habits of virtue,” where repeated game play spills over into subsequent one-shot interactions, but only among participants who rely on heuristics (25). These various experience-related results emphasize that our model operates in the domain of cultural evolution and social learning (1, 19, 20), in addition to (or instead of) genetic evolution.

Our model also predicts variation in the effect of intuition versus deliberation across contexts: Whereas deliberating undermines cooperation in one-shot games, it is predicted to have no effect in repeated games. The DC strategy’s cooperative intuition is supported (and, therefore, unaffected) by deliberation in repeated games; and the ID strategy defects under all circumstances, and so is unaffected by deliberation. Consistent with this prediction, manipulating intuition had little effect on cooperation in a repeated four-player PD (42) or a modified public goods game where cooperating was individually payoff-maximizing (34).

Although our model predicts that manipulating the use of intuition versus deliberation will have the aforementioned effects, it conversely predicts that there will likely not be a consistent correlation between one-shot cooperation and an individual’s willingness to deliberate T (i.e., their “cognitive style”): Highly intuitive (low T) individuals can either be intuitive defectors or intuitive cooperators. In line with this prediction, little consistent association has been found between an individual’s cognitive style and their overall willingness to cooperate in one-shot games (4, 43, 44). Furthermore, individual differences in reaction times, which are often interpreted as a proxy for intuitiveness (although see refs. 45 and 46 for an alternative interpretation based on decision conflict), have been associated with both increased (4, 47–49) and decreased (50, 51) cooperation. Our model therefore helps to explain the otherwise-puzzling difference in experimental results between cognitive process manipulations and reaction time correlations. Our model also makes the further prediction, untested as far as we know, that a consistent correlation between cognitive style and cooperation should emerge in samples that are restricted to individuals who developed their strategies under conditions where p and/or r were sufficiently large.

The model we have presented here is, in the game-theoretic tradition, highly stylized and focused on limiting cases for tractability. In particular, we assume (i) that agents engage in only two different types of games, rather than, for example, sampling PD game lengths (or coordination game payoffs) from a distribution; (ii) that deliberation is perfectly accurate in assessing the type of game being played, whereas intuition is totally insensitive to game type; and (iii) that the cost of deliberation is sampled from a uniform distribution on the interval [0, d], rather than a more realistic distribution of costs. Future work should extend the framework we introduce here to explore the effects of relaxing these assumptions and incorporate other nuances of dual-process cognition that were not included in this first model. For example, intuitive thinking might be made observable, such that agents could condition on the cognitive style of their partners (as in recent work on “cooperation without looking”; ref. 52). Or, feedback between the population state and the environment (i.e., the model parameters) could be incorporated, as has been done in recent models of the evolution of dual-process agents in the context of intertemporal choice (17, 18).

Future work should also use the framework introduced here to explore the evolution of cognition in domains beyond cooperation. For example, our framework could easily be extended to describe the internalization of a variety of social norms unrelated to cooperation, such as rituals or taboos. Consider any situation in which following the norm is individually costly, but becomes payoff-maximizing when interacting with others who also follow the norm (e.g., because they would sanction norm violations). Our model’s logic suggests that selection can favor a strategy that (i) intuitively follows the norm, but (ii) uses deliberation to violate the norm in settings where there is little threat of sanctions (e.g., because one’s behavior is unobservable), so long as the overall probability of being sanctioned and/or the severity of the sanctions are sufficiently high.

Our framework could also be extended to explain rejections in the ultimatum game (UG). In this game, Player 1 proposes how a monetary stake should be divided between herself and Player 2. Player 2 can then either accept, or reject such that both players receive nothing. Behavioral experiments suggest that in the one-shot anonymous UG, intuition supports rejecting unfair offers, whereas deliberation leads to increased acceptance (53–55) (although neurobiological evidence is somewhat more mixed; refs. 56 and 57). Such a pattern of intuitive rejection is easily explained by our framework, because rejecting unfair offers is advantageous in repeated games, but costly in one-shot games. Thus, the same logic that leads to selection favoring intuitive cooperation and deliberative defection in our model’s one-shot PDs can lead selection to favor intuitive rejection and deliberative acceptance in one-shot UGs.

In sum, we have integrated dual-process theories of cognition from the behavioral sciences with formal game-theoretic models of the evolution of cooperation. Our model shows how it can be adaptive for humans to think both “fast and slow” and provides an explanation for why people sometimes (but not always) cooperate in one-shot anonymous interactions. In doing so, we provide a formal demonstration of how spillovers from settings where cooperation can be payoff-maximizing (e.g., repeated interactions) lead to cooperation in social dilemmas where cooperation is never in one’s self-interest (21–25, 58). Although many have suggested that it takes cold, deliberative reasoning to get people to engage in this kind of prosocial behavior, our evolutionary model finds precisely the opposite. It is not reflective thought that allows people to forego their selfish impulses, but rather reflective thought that undermines the impulse to cooperate.