SpringSaLaD: A Spatial, Particle-Based Biochemical Simulation Platform with Excluded Volume

Abstract

We introduce Springs, Sites, and Langevin Dynamics (SpringSaLaD), a comprehensive software platform for spatial, stochastic, particle-based modeling of biochemical systems. SpringSaLaD models biomolecules in a coarse-grained manner as a group of linked spherical sites with excluded volume. This mesoscopic approach bridges the gap between highly detailed molecular dynamics simulations and the various methods used to study network kinetics and diffusion at the cellular level. SpringSaLaD is a standalone tool that supports model building, simulation, visualization, and data analysis, all through a user-friendly graphical user interface that should make it more accessible than tools built into more comprehensive molecular dynamics infrastructures. Importantly, for bimolecular reactions we derive an exact expression relating the macroscopic on-rate to the various microscopic parameters with the inclusion of excluded volume; this makes SpringSaLaD more accurate than other tools, which rely on approximate relationships between these parameters.

Introduction

Computational modeling has become indispensable for elucidating the properties of complex biochemical networks. In a traditional modeling approach the modeler defines the various chemical species of interest and the reaction kinetics between them, which defines a closed network of reactions that can be simulated in a number of ways. If the copy number of the individual species is low, the kinetics should be simulated by solving the chemical master equation for the stochastic population probabilities. If the number of molecules is large enough and the system is well mixed, then deterministic simulations can be performed by numerically solving ordinary differential equations (ODEs). Copasi (copasi.org) is a popular example of a simulator for ODEs and stochastic network models (1). Spatial dynamics within an explicit geometry can be modeled by adding diffusion terms to the reaction equations and solving the resulting partial differential equations. MCell (mcell.org (2)) and Smoldyn (smoldyn.org (3)) are popular software platforms for modeling discrete Brownian motion and stochastic reactions. Virtual Cell (vcell.org) is a comprehensive software environment for modeling and simulating reaction networks and membrane transport either stochastically or deterministically, with the option of accounting for diffusion in realistic cellular geometries (4, 5). But there are two problems with these commonly used tools for computational systems biology: they cannot readily handle models with combinatorial complexity, and, for spatial models, they do not accurately model the excluded volume and spatial extent of interacting molecules or clusters.

A combinatorially complex system makes it difficult or impossible for the modeler to specify a reaction network without additional computational tools. For example, a receptor with 10 phosphorylation sites can exist in 2¹⁰ = 1028 states, with an even larger number of reactions needed to describe the transitions between these states. In general, the size of the reaction network grows exponentially with the number of potential protein modifications or binding sites, and this phenomenon is termed “combinatorial complexity”. Tools such as BioNetGen (6, 7) automatically generate reaction networks from a small number of defined rules, but the exponential increase in network size ultimately limits the practical simulation of such large networks. In a recent study (8), we estimated that it would take a 2.54 GHz Intel Xeon processor 290 years to generate the reaction network for simple model of the synaptic kinase CaMKII. Even if network generation completed in a reasonable amount of time, we would not have the computational resources required to simulate such a large system of differential equations or store the results of such calculations.

Some particle-based methods circumvent the problems of combinatorial complexity by avoiding the process of enumerating all species and reactions (9, 10, 11, 12). Instead, these methods (also known as agent-based or network-free simulators) use reaction rules to probabilistically spawn the states of individual molecules during the simulation, and therefore only need to consider the potential reactions for species (i.e., states) that are actually present in the system. These methods are implemented in several openly accessible software tools (11, 13, 14).

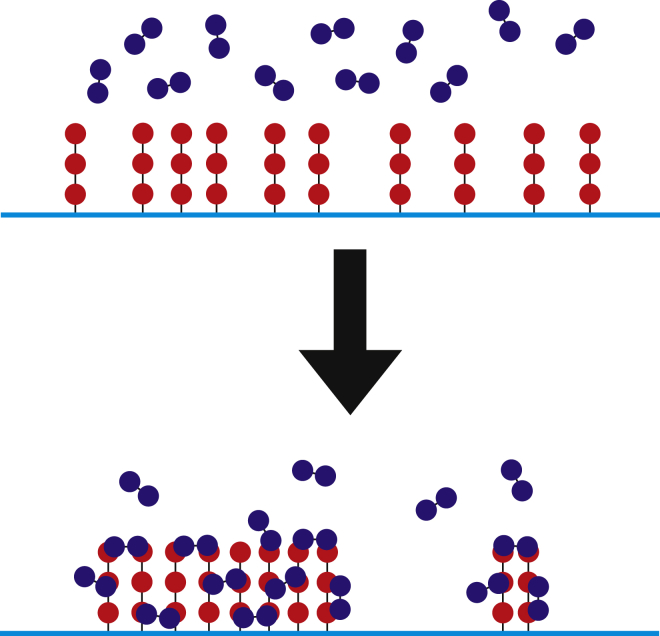
A major limitation of most spatial simulators is that they treat all molecules, even large multicomponent complexes, as point particles. Various approaches exist to model the effects of excluded volume, such as adding density-dependent terms in reaction-diffusion equations (15, 16) or by defining a reaction that moves nearby particles apart (as implemented in Smoldyn), but in general such methods are unable to model important properties that depend on the spatial extent and composition of the complex, such as the effects of spatial orientation and the reduced diffusion of larger complexes. One biologically important example of such a system is ligand-induced membrane receptor clustering, as illustrated in Fig. 1, which shows a system of trivalent receptors clustered by interacting with bivalent ligands. Such interactions lead to the formation of molecular clusters that increase local concentration of biomolecules, potentially triggering signaling events. We have included such complexes in a class of biophysical structures called pleomorphic ensembles (PEs) (12, 17, 18), because these complexes are often plastic, with dynamic and variable composition. Accurate modeling of PEs requires tools that account for their extended spatial structure and excluded volume, as these properties underlie essential features of PEs, such as reduced access to open binding sites on the interior of the cluster or rebinding of newly dissociated monomers. Furthermore, because the sizes and compositions of pleomorphic ensembles are open-ended (i.e., sampling an infinite number of states), a particle-based algorithm is required. For these reasons, pleomorphic ensembles cannot be modeled by computational tools such as MCELL, Smoldyn, or Virtual Cell.

Figure 1.

Receptor clustering example. Ligand-induced clustering of membrane receptors is one example of a system with combinatorial complexity where spatial organization and excluded volume can strongly modify system dynamics and equilibrium organization. Bivalent ligands are shown in blue, trivalent receptors are shown in red, and the cyan line represents the membrane. To see this figure in color, go online.

In principle, PEs could be modeled with molecular dynamics (MD) simulations, but the large sizes of these systems, which consist of tens to hundreds of proteins, make such simulations computationally impractical. These systems are best modeled using a mesoscopic, coarse-grained approach, where individual proteins are modeled as a single site or a collection of linked sites. In recent years a number of programs have become available for such mesoscopic modeling, most notably SRSim (19) and ReaDDyMM (20, 21). However, these and other programs of this class require a level of computational expertise that makes them inaccessible to the typical biologist. Moreover, all available programs implement bimolecular reactions by relating macroscopic on-rates to the microscopic parameters using formulae that are only approximate in the presence of excluded volume, or which were derived assuming well-mixed conditions that are invalid for the typical systems studied.

Here we introduce a standalone modeling and simulation package, SpringSaLaD, which implements spatial, particle-based models with excluded volume and accurate biochemical reactions, including the treatment of allostery. Notably, we derive and implement an exact formula to relate bimolecular macroscopic on-rates to the various microscopic parameters. The platform offers a simple but powerful user interface and allows for the simulation of receptor clustering and other multistate pleomorphic ensembles. It will run in a reasonable time on any modern personal computer (hours to a few days, depending on the number of molecules simulated). The software is written in Java and is freely available as a standalone .jar file for Windows, Mac, or Linux at www.ccam.uchc.edu/resources/ccam_software.html#SpringSaLaD. The simulation code is bundled as an independent .jar file, and may be used on the command line to, for example, run hundreds of simultaneous simulations on a Linux cluster. A User’s Guide and Tutorial are included in the downloadable zip file, and are also available in the Supporting Material. Source code is freely available on Github at pjmichalski/SpringSaLaD (GUI components) and pjmichalski/LangevinNoVis01 (simulation components).

Materials and Methods

Please see the Supporting Material.

Results

Molecule description

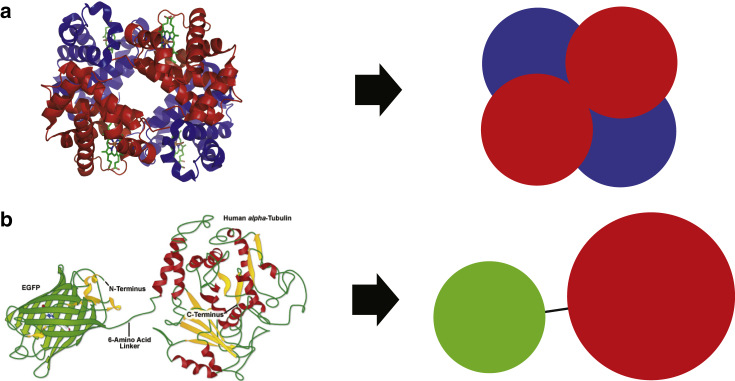
Springs, Sites, and Langevin Dynamics (SpringSaLaD) describes the molecules in the system as a set of distinct spherical sites connected by links, which are modeled with stiff springs. The sites may represent different domains within the macromolecule, and may be selected as binding sites for potential reactions with other binding sites. Many biological molecules of interest can be described in such a manner, and two of these are shown in Fig. 2: the hemoglobin tetramer and a GFP-tagged α-tubulin. Models that seek to describe finer details, such as the motion of individual amino acids, are more appropriately simulated with MD, while models with less detail will run faster with simulators that assume molecules to be infinitesimal points.

Figure 2.

Examples of coarse-grained models. Two examples of proteins that can be readily decomposed into nanometer-sized domains appropriate for coarse-grained modeling with SpringSaLaD. (a) The hemoglobin tetramer can be coarse-grained into four independent biochemical sites. (b) Any globular GFP-tagged protein can be represented as two connected sites. Here we show GFP-tagged α-tubulin. The images on the left are modified from the original images available at (a) http://zeiss-campus.magnet.fsu.edu/articles/probes/fpintroduction.html, and (b) http://upload.wikimedia.org/wikipedia/commons/3/3d/1GZX_Haemoglobin.png. To see this figure in color, go online.

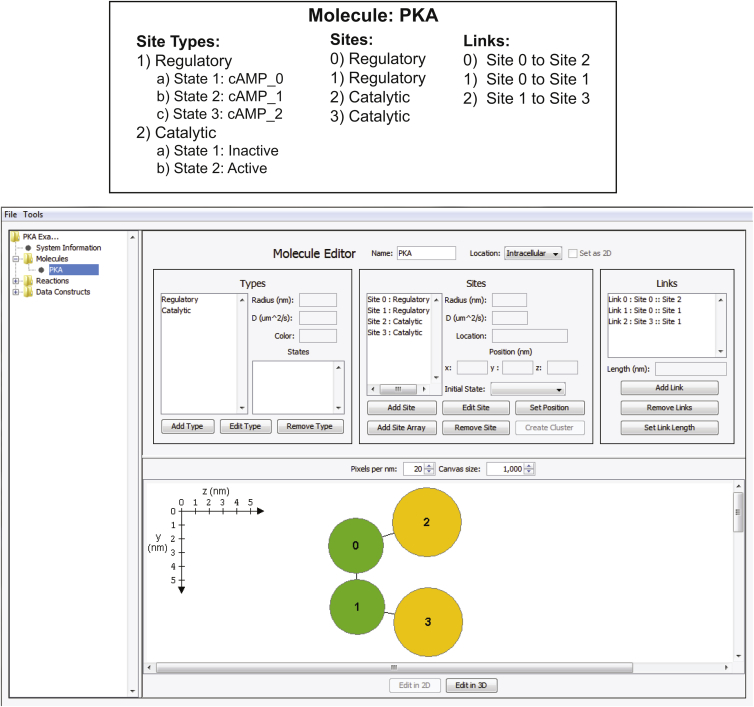
We will use a model of protein kinase A (PKA) to illustrate the three steps involved in molecule construction. These steps and the GUI for molecule construction are shown in Fig. 3. Firstly, we define the types of sites in the molecule. For example, PKA contains two types of sites: regulatory and catalytic domains. Each type can have associated with it an arbitrary number of internal states with their own associated set of biochemical reactions (reactions are described below). For example, the regulatory domain could have three states describing the number of bound cAMP molecules (0, 1, or 2), and the catalytic domain could have an inactive and active state reflecting its kinase activity. Each type also has an associated physical size, diffusion constant, and color (for visualization purposes).

Figure 3.

PKA model. (Top) A description of PKA in terms of SpringSaLaD model components. PKA is composed of two regulatory sites and two catalytic sites. The state of a regulatory site is defined by the number of bound cAMP molecules, while the catalytic subunit can be in either an inactive or an active state. (Bottom) The SpringSaLaD molecule editor GUI, as used to construct the PKA molecule described on the top. To see this figure in color, go online.

Secondly, sites are added to the molecule, and each site is assigned one of the previously defined types. To construct PKA we would add four sites, assigning two of them to be regulatory domains and two to be catalytic domains. Physically, sites are modeled as impenetrable spheres to accurately capture excluded volume effects.

Thirdly, links are added to connect the sites to each other. Each site can be linked to an arbitrary number of other sites in either two or three dimensions. The only requirement is that sites cannot overlap. Links are stiff and thus define an intersite distance, but are free to rotate around the sites. For example, a triangular molecule with three sites will not maintain its geometry in the simulation with only two links, but will if a third bond is added to enforce a distance between the two outer sites. Links are only used to control the distance between sites and do not occupy physical space, and both sites and other links are free to pass through a link. Excluded volume is only enforced by sites.

To specify membrane-bound molecules, a special anchor designation is assigned to a site, which restricts it to two-dimensional diffusion within the membrane; the anchor site can then be linked to sites that diffuse in the adjacent volume, effectively restricting those sites to be part of a membrane-bound molecule.

SpringSaLaD provides several convenience methods for constructing large linear polymers, and other convenience methods for constructing large arrays of linked receptors. Molecules must be defined as intracellular, extracellular, or membrane-bound. These and other details can be found in the User’s Guide and Tutorial, which are available in the Supporting Material.

Geometry

SpringSaLaD currently only supports a rectangular geometry with reflecting boundary conditions. The rectangular geometry is partitioned into an extracellular space, a planar membrane, and an intracellular space. The size of the membrane and the depths of the intra- and extracellular spaces are user-defined. Future versions of SpringSaLaD will support a wider variety of geometries.

Particle motion: diffusion and constraints due to binding

Particle motion is influenced by two classes of forces: random forces that lead to diffusional motion, and interparticle forces that impose the constraints from intra- and intermolecular bonds. These forces are incorporated in the overdamped Langevin equation (22),

$$\zeta \stackrel{\rightharpoonup }{v}={\stackrel{\rightharpoonup }{F}}_{\text{rand}}+{\stackrel{\rightharpoonup }{F}}_{\text{bonds}},$$ (1)

where ζ is the coefficient of viscous friction, $\stackrel{\rightharpoonup }{v}$ is the particle velocity, and ${\stackrel{\rightharpoonup }{F}}_{\text{rand}}$ and ${\stackrel{\rightharpoonup }{F}}_{\text{bonds}}$ represent the random forces and the total force of bonds. The random forces are guaranteed to recapitulate the desired diffusion, provided they are chosen from normal distribution with variance

$${\langle \stackrel{\rightharpoonup }{F}}_{\text{rand}}\left(t\right)·{\stackrel{\rightharpoonup }{F}}_{\text{rand}}\left(t^{\prime }\right)\rangle =2n_{d}D{\zeta }^2\delta \left(t-t^{\prime }\right),$$ (2)

where D is the desired diffusion coefficient, $n_d$ is the dimension of the system (here $n_d=3$), and the delta-function simply states that the random force is uncorrelated in time. The bonds are modeled as stiff springs,

$${\stackrel{\rightharpoonup }{F}}_{\text{bonds}}=\sum _i{k}_i\left(r_i-r_{0,i}\right){\hat{r}}_i,$$ (3)

where the sum runs over all bonds, $k_i$ is a spring constant, ${\hat{r}}_i$ is the unit vector pointing from the particle to the neighbor with which it shares a bond, $r_i$ is the current interparticle distance, and $r_{0,i}$ is the equilibrium bond distance. The exact value of the spring constant is not important, provided the spring is stiff enough to keep sites near the expected distances but not so stiff that accurate motion requires unreasonably small time steps. In practice, only the ratio $k/\zeta$ is required, and in SpringSaLaD this ratio is the same for all bonds and links, namely, $k/\zeta ={10}^8{\text{s}}^{-1}$; this allows us to use time steps of ∼1–100 ns for biologically relevant diffusion constants.

Reactions

Zeroth-order

SpringSaLaD supports particle creation reactions, which may be used to buffer the concentration of a species. Given a macroscopic creation rate, $k_{\text{create}}$, with units μM/s, a single molecule is added to the system at each time step with probability $k_{\text{create}}Vdt$, where V is either the intra- or extracellular volume depending on the location of the molecule. A molecule is added by testing random positions in the system until a position is found that does not overlap with other particles. Note that this mechanism will fail in extremely dense systems. In such a system a simple, constant-rate zeroth order reaction is not consistent with physical constraints, and is not an appropriate modeling construct.

First-order

SpringSaLaD supports three general types of first-order reactions, all of which are described by a reaction rate, r, with units s⁻¹, and which occur at each time step with probability rdt. These are:

• 1)Bond dissociation reactions: when a dissociation reaction occurs, the bond is simply removed from the system.
• 2)Internal state transitions: these describe the transitions between the internal states of each site, as defined by the type of that site. The probability of these transitions can depend on the identities of binding partners or the states of other sites in the same molecule. The former dependency would be used, for example, to prevent a transition from an unphosphorylated to a phosphorylated state unless the site is bound to a kinase. The latter dependency can be used to model allosteric interactions.
• 3)Decay reactions: these are used to remove molecules from the system.

Second-order

SpringSaLaD supports binding reactions between two sites. A bond is modeled by the creation of a new link between the reacting sites. The link is modeled identically to the links that hold molecules together, except it has an associated off-rate controlling molecular dissociation. Particle-based simulations often use the Smoluchowski approach (23) to model bimolecular reactions, but such an approach is incompatible with excluded volume. Instead, we modified the approach described in Erban and Chapman (24) to account for excluded volume. Each site is associated with two radii: the physical radius, ${\rho }_i$ (i = 1,2), which is defined in molecule construction and enforces excluded volume, and a slightly larger reaction radius, $R_i$. Two reactive sites undergo a binding reaction with probability $\lambda dt$ per time step when their reaction radii overlap. The reaction rate λ is related to the macroscopic on-rate, $k_{\text{on}}$, with units of $\mu {\text{M}}^{-1}{\text{s}}^{-1}$, through

$$k_{\text{on}}=\frac{4\pi RD\varphi }{1-\frac{R}{a}\varphi },$$ (4)

where

$$\varphi =1-\left(\frac{r_0}{R}\right)\frac{r_0\text{sinh}\left(\frac{R-\rho }{r_0}\right)+\rho \cosh \left(\frac{R-\rho }{r_0}\right)}{\rho \text{sinh}\left(\frac{R-\rho }{r_0}\right)+r_0\cosh \left(\frac{R-\rho }{r_0}\right)}$$ (5)

and $r_0=\sqrt{D/\lambda }$, $D=D_1+D_2$, $\rho ={\rho }_1+{\rho }_2$, $R=R_1+R_2$, and a is the dissociation radius.

The derivation of this equation and additional discussion of bimolecular reactions can be found in the Supporting Material.

Data analysis

SpringSaLaD comes packaged with an interactive three-dimensional viewer to visualize simulation results. The viewer is implemented in Java3D and provides methods for saving images and generating movies in a variety of formats. (Currently, the viewer will only work on Windows and Linux machines. The viewer is disabled on Macs because of an incompatibility between Java3D and the latest versions of Java on Macs.) Two example videos (Movies S1 and S2) that show clustering in the Nck-nephrin-Nwasp system are available in the Supporting Material. The program keeps track of a variety of observables, such as the number and types of bound particles or the number of sites in a particular state, and automatically displays this data in a convenient tabular format. Stochastic simulations require many runs to compute average properties. SpringSaLaD provides the option to launch runs in sequence or in parallel, depending on the user’s computational resources, and automatically computes averages and standard deviations of the observables in the data tables. Instructions for the viewer and data analysis are provided in the User’s Guide and Tutorial.

Algorithm implementation verification

We constructed simple models of analytically tractable systems to verify the accuracy and implementation of all simulation algorithms. These included various tests of diffusion and all implemented reactions. As an example, we modeled a system consisting of a single species undergoing a creation and decay reaction. In this case SpringSaLaD reproduces the full population distribution predicted by the time-dependent solution to the chemical master equation. In the Supporting Material, we provide a discussion of all the tests, the models used, and the simulation results.

Discussion

The software presented here fills an important gap in the spectrum of publicly available biochemical simulation platforms, allowing the simulation of systems that exhibit combinatorial complexity, are too large for MD simulations, and are influenced by spatial effects. Many important biological systems fall into this category, such as chromatin dynamics in the confines of a crowded nucleus, signaling in the dense and diverse postsynaptic density of dendritic spines, signaling in the narrow foot processes of kidney podocytes, and the large variety of structures, such as receptor clusters, cell adhesion complexes, or mRNA granules, which we have described as PE (17). The primary conceptual requirement is that molecules must be described in a coarse-grained manner as a linked collection of biochemically distinct sites, with radii of a few nanometers. Modeling at a finer scale requires MD simulations, while coarser models can be simulated more efficiently with other methods. The description in terms of linked sites automatically captures emergent properties of a dynamic system, such as the reduced diffusion coefficient of larger clusters because of the disordered individual motions of its components.

There are three significant but unavoidable drawbacks to our approach. Firstly, there is the increased computational cost associated with tracking the hundreds of individual sites. The simulation runs time scales linearly in the number of particles (for a fixed concentration), which puts practical limits on the number of molecules in the system. Secondly, the simulation must use time steps of 10 ns to accurately enforce excluded volume and prevent overextending the springs holding sites together. This is orders-of-magnitude smaller than the 100 μs time steps typical in Smoldyn and the 1 ms to 1 s time steps common in ODE or partial differential equation simulations. On the other hand, it is many orders-of-magnitude larger than the femtosecond time steps used in MD simulations. We find that simulations following up to 1000 particles over the course of 1–10 s will run in 1–5 days. We have several improvements planned, such as a port to C++ and parallelization of individual simulations, which will allow simulation of larger systems.

Thirdly, there is the practical difficulty in relating some microscopic parameters required in the model to macroscopic parameters measured in the lab. For example, SpringSaLaD requires the user to define a diffusion constant for each site in a molecule, whereas the experimentally accessible parameter is the diffusion coefficient of the molecule as a whole. In some cases, such as linear polymers or spherical globules, the two parameters can be related, but for an arbitrary geometry there is no exact formula to relate the macroscopic and microscopic diffusion coefficients, and the modeler may have to try several microscopic values to find one that is appropriate. A similar difficulty arises when defining the on-rate of a bimolecular reaction. If the reactive site is buried in a relatively inaccessible pocket of a large molecule, then the true microscopic on-rate may be many orders-of-magnitude larger than the macroscopic value. Again, no exact relation exists for an arbitrary geometry, and a parameter scan may be required to find a suitable value. These limitations are not unique to SpringSaLaD, but are faced in any coarse-grained modeling approach.

To our knowledge, the one truly new feature described here is the Smoluchowski-like algorithm used to model bimolecular interactions with excluded volume. Although Eq. 4 is derived with standard methods, we are not aware of its previous publication, and it is not used in any other biochemical simulation platform. SpringSaLaD packages these methods together with standard treatments of first-order reactions, allosteric state transitions, and Langevin dynamics within a convenient, user-friendly interface, which will make these methods available to a broader community of biochemical modelers. In the next year we plan to integrate SpringSaLaD with the Virtual Cell modeling and simulation platform (4, 5, 25, 26), where it will be offered as an additional tool to complement the wide variety of modeling methods supported by VCell.

Author Contributions

P.J.M. and L.M.L. conceived the project; P.J.M. wrote the software code and validated the algorithms; L.M.L. tested the software; and L.M.L. and P.J.M. wrote the article.

Editor: Stanislav Shvartsman.