Partial Correlation-Based Retinotopically Organized Resting-State Functional Connectivity Within and Between Areas of the Visual Cortex Reflects More Than Cortical Distance

Abstract

Numerous studies have demonstrated functional magnetic resonance imaging (fMRI)-based resting-state functional connectivity (RSFC) between cortical areas. Recent evidence suggests that synchronous fluctuations in blood oxygenation level-dependent fMRI reflect functional organization at a scale finer than that of visual areas. In this study, we investigated whether RSFCs within and between lower visual areas are retinotopically organized and whether retinotopically organized RSFC merely reflects cortical distance. Subjects underwent retinotopic mapping and separately resting-state fMRI. Visual areas V1, V2, and V3, were subdivided into regions of interest (ROIs) according to quadrants and visual field eccentricity. Functional connectivity (FC) was computed based on Pearson's linear correlation (correlation), and Pearson's linear partial correlation (correlation between two time courses after the time courses from all other regions in the network are regressed out). Within a quadrant, within visual areas, all correlation and nearly all partial correlation FC measures showed statistical significance. Consistently in V1, V2, and to a lesser extent in V3, correlation decreased with increasing eccentricity separation. Consistent with previously reported monkey anatomical connectivity, correlation/partial correlation values between regions from adjacent areas (V1-V2 and V2-V3) were higher than those between nonadjacent areas (V1-V3). Within a quadrant, partial correlation showed consistent significance between regions from two different areas with the same or adjacent eccentricities. Pairs of ROIs with similar eccentricity showed higher correlation/partial correlation than pairs distant in eccentricity. Between dorsal and ventral quadrants, partial correlation between common and adjacent eccentricity regions within a visual area showed statistical significance; this extended to more distant eccentricity regions in V1. Within and between quadrants, correlation decreased approximately linearly with increasing distances separating the tested ROIs. Partial correlation showed a more complex dependence on cortical distance: it decreased exponentially with increasing distance within a quadrant, but was best fit by a quadratic function between quadrants. We conclude that RSFCs within and between lower visual areas are retinotopically organized. Correlation-based FC is nonselectively high across lower visual areas, even between regions that do not share direct anatomical connections. The mechanisms likely involve network effects caused by the dense anatomical connectivity within this network and projections from higher visual areas. FC based on partial correlation, which minimizes network effects, follows expectations based on direct anatomical connections in the monkey visual cortex better than correlation. Last, partial correlation-based retinotopically organized RSFC reflects more than cortical distance effects.

Introduction

Since Hubel and Wiesel's seminal work (1962), the functional architecture of the visual cortex has been one of the most rigorously studied themes in the field of neuroscience. This theme covers a wide range of subjects, including the functional properties of visual brain areas such as retinotopic organization and functional specificity. The majority of fine-scaled findings about the functional architecture of the cortex have been achieved using traditional invasive techniques such as electrophysiological recordings (e.g., Hubel and Wiesel, 1962) and optical imaging (e.g., Bonhoeffer and Grinvald, 1991; Shmuel and Grinvald, 2000). Another subject of interest is the thalamocortical and corticocortical connections. Traditionally, this subject has been studied by anatomical tract tracing (e.g., Felleman and Van Essen, 1991). More recently, functional connectivity (FC) analysis based on functional magnetic resonance imaging (fMRI) allows studying the connectivity of the visual cortex noninvasively, thus it is readily usable on human subjects.

FC refers to the temporal correlation between spatially remote neurophysiological events (Friston et al., 1993). FC analyses can be pursued during subject stimulation, task performance, or rest. It can be applied to data obtained with any modality of measurement over time, such as positron emission tomography, blood oxygenation level-dependent (BOLD) fMRI, electroencephalography, and magnetoencephalography. FC analyses based on BOLD signal are particularly promising because they can offer high spatial resolution and high spatial specificity relative to where the corresponding changes in neurophysiological signals take place compared with all other noninvasive imaging modalities (Shmuel et al., 2007). In general, FCs based on spontaneous signal fluctuations introduces no confounds to consider due to coactivation of areas in response to a particular stimulus. In addition, this approach offers convenience in paradigm. Another advantage of this method is that it can elucidate brain connectivity at a large-scale system level, for example, revealing coherent systems of executive control, language or pain (Smith et al., 2009). This allows identifying the locations of the systems within the brain in order to pursue analyses within a system or between systems. This is complementary to FC analyses at the meso scale, that is, at the scale of local circuits measured by neurophysiology. Resting-state FC analyses can potentially further understanding of neuroanatomical models (Fox and Raichle, 2007; Wang et al., 2013).

To date, only a few studies have applied fMRI-based resting-state FC (RSFC) analysis at a spatial scale finer than that of a cortical area in the visual cortex. Vincent and colleagues (2007) demonstrated preliminary results on retinotopically organized RSFC between areas V1 and MT of the anesthetized monkey. Heinzle and colleagues (2011) and Arcaro and colleagues (2015) have demonstrated that the FC between spontaneous fMRI fluctuations recorded in two visual areas depends on their retinotopic coordinates. Raemaekers and colleagues (2014) and Arcaro and colleagues (2015) have recently considered FC within human visual areas V1, V2, and V3, and indicated that the small-scale connectivity information was superimposed on the FC of larger scale networks reflected in the same data.

One criticism of resting-state FC analysis using BOLD fMRI data is that the connectivity observed is largely a reflection of distance effects between regions. There have been several studies that focused on large-scale networks and have demonstrated a tendency of FC to be greatest with close proximity of the regions involved (e.g., Katsuki et al., 2014; Liang et al., 2013; Liao et al., 2013). This phenomenon is usually attributed to the abundant presence of anatomical connections at a local scale, as postulated by the small-world theory of connectivity in the brain (Kaiser and Hilgetag, 2004). This theory of connectivity has been widely supported with evidence, such as in the macaque brain (Sepulcre et al., 2010). However, in these large-scale networks, long-range highly functionally connected regions have been identified, indicating that FC analyses can indeed capture information that is more meaningful than a reflection of distance (Liao et al., 2013). We strive to elucidate that within smaller local networks that are densely connected through anatomical connections such as the visual cortex, there is also meaningful information contained in the FC networks beyond distance.

Using BOLD fMRI resting-state FC, we assess the functional connections within and between visual areas of the human occipital cortex, putting an emphasis on how FC depends on retinotopic eccentricity and cortical distance. We evaluate FC using two measures: correlation (Corr) and partial correlation (Pcorr). We have chosen to pursue analyses through these two measures due to their simplicity, the fact that they are widely used in FC analyses, and given that they have been shown to be relatively successful in this type of analysis compared with other common models (Dawson et al., 2013; Smith et al., 2011). Corr is indeed very widely used. However, in small local networks, we expect the observed correlations to be high for nearly all connections due to contribution to synchronization from nodes that are not directly connected. Because of this, we include Pcorr, which is potentially better equipped to deal with local networks given that time courses from all regions of interest (ROIs) in the network are regressed out before assessing the Corr between two regions.

We hypothesize that (1) RSFC within and between lower visual areas is retinotopically organized; (2) the relatively dense anatomical connectivity and projections from higher visual areas cause network effects that increase Corr-based FC across lower visual areas, even between regions that do not share a direct anatomical connection; (3) FC measured by Pcorr (that reduces network effects) roughly follows expectations based on the direct anatomical connectivity in the monkey visual cortex; and 4) if network effects are minimized, retinotopically organized RSFC reflects more than cortical distance effects.

To test our hypotheses, we look separately at the connectivity within the dorsal and ventral quadrants of the visual cortex in a hemisphere, and between these quadrants, due to the largely symmetric nature of their visual field representation. This separation of within quadrant versus between quadrants also presents a logical separation of generally closer range connections along the cortex (within a quadrant) and longer range connections (between quadrants). In addition, the symmetrical arrangement of the visual areas between quadrants creates a distribution of distances within an area that are short (e.g., V1), long (e.g., V3), or intermediate (e.g., V2). We expect higher FC measures within a visual area, even when computing FC between quadrants. For example, we expect relatively high FC measures between regions representing similar eccentricities in V2 and residing in the dorsal and ventral quadrants, respectively, or similarly, regions representing similar eccentricities in V3 and residing in these different quadrants. This creates a scenario in which distant regions residing in different quadrants show relatively high FC compared with ROI pairs that are closer (such as a pair of ROIs, respectively, in V1 and V2, one residing in the dorsal quadrant and the other in the ventral quadrant, and representing distant eccentricities). This arrangement of visual areas allowed us to test our fourth hypothesis, namely that within the network of retinotopic visual areas, FC measures do no solely reflect distance.

Materials and Methods

Six normally sighted subjects participated in this study after giving written consent in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki). Each subject was scanned in two sessions: one to obtain high-resolution anatomical images and fMRI for retinotopy and the other to obtain high-resolution anatomical images and fMRI in the resting state.

Resting-state fMRI

Data were acquired on a 3T Magnetom TIM Trio scanner (Siemens, Erlangen, Germany). A phased-array head coil was used, with 32 channels employed for resting-state scans. Echo-planar imaging was used to measure BOLD changes in image intensity. Resting-state fMRI was obtained in 8 runs of 8.5 min (68 min of data in total) from each of the subjects. Note the very long data acquisition for each subject compared with more common resting-state run lengths. This long duration ensures a high signal-to-noise ratio and convergence of RSFC (Birn et al., 2013; Dawson et al., 2013). To check for sleep, we communicated with the subjects at the end of each scan and they were all immediately responsive. Each run consisted of 256 contiguous echo planar imaging (EPI) whole-brain functional volumes (repetition time [TR] = 2000 msec; echo time [TE] = 30 msec; flip angle = 90°; 30 slices; matrix =112 × 112; field of view [FOV] = 224 mm; acquisition voxel size = 2 × 2 × 2.2 mm).

Resting-state runs were preprocessed using FSL's FEAT software package (Jenkinson et al., 2012). This deletes the first three volumes, performs motion correction, high-pass filtering (0.01 Hz), slice-time correction, and registration to the T1-weighted (MPRAGE) anatomical volume from the retinotopy session (see section on Retinotopic mapping and ROIs for FC analyses). In terms of denoising, a cerebrospinal fluid (CSF) mask and white matter (WM) mask were created by segmenting the resting-state anatomical image using FSL's FAST software package (Zhang et al., 2001). The masks were then eroded by one voxel, thresholded (80% tissue type probability), and registered to the preprocessed functional image. The average time courses of the CSF and WM masks were obtained and the two time courses were regressed out of the functional image time series.

Retinotopic mapping and ROIs for FC analyses

This study applied new analyses to data from one of our recently published articles (Dawson et al., 2013). Detailed descriptions of methods pertaining to the retinotopy data acquisition and preprocessing can be found therein.

Retinotopic mapping was pursued with axial-oblique slices (TR = 2000 msec; TE = 30 msec; flip angle = 90°; 28 slices; matrix = 128 × 128; FOV = 263 mm; acquisition voxel size = 2.05 × 2.05 × 3 mm). Retinotopy runs were motion corrected and slice-time corrected using Freesurfer (http://surfer.nmr.mgh.harvard.edu/).

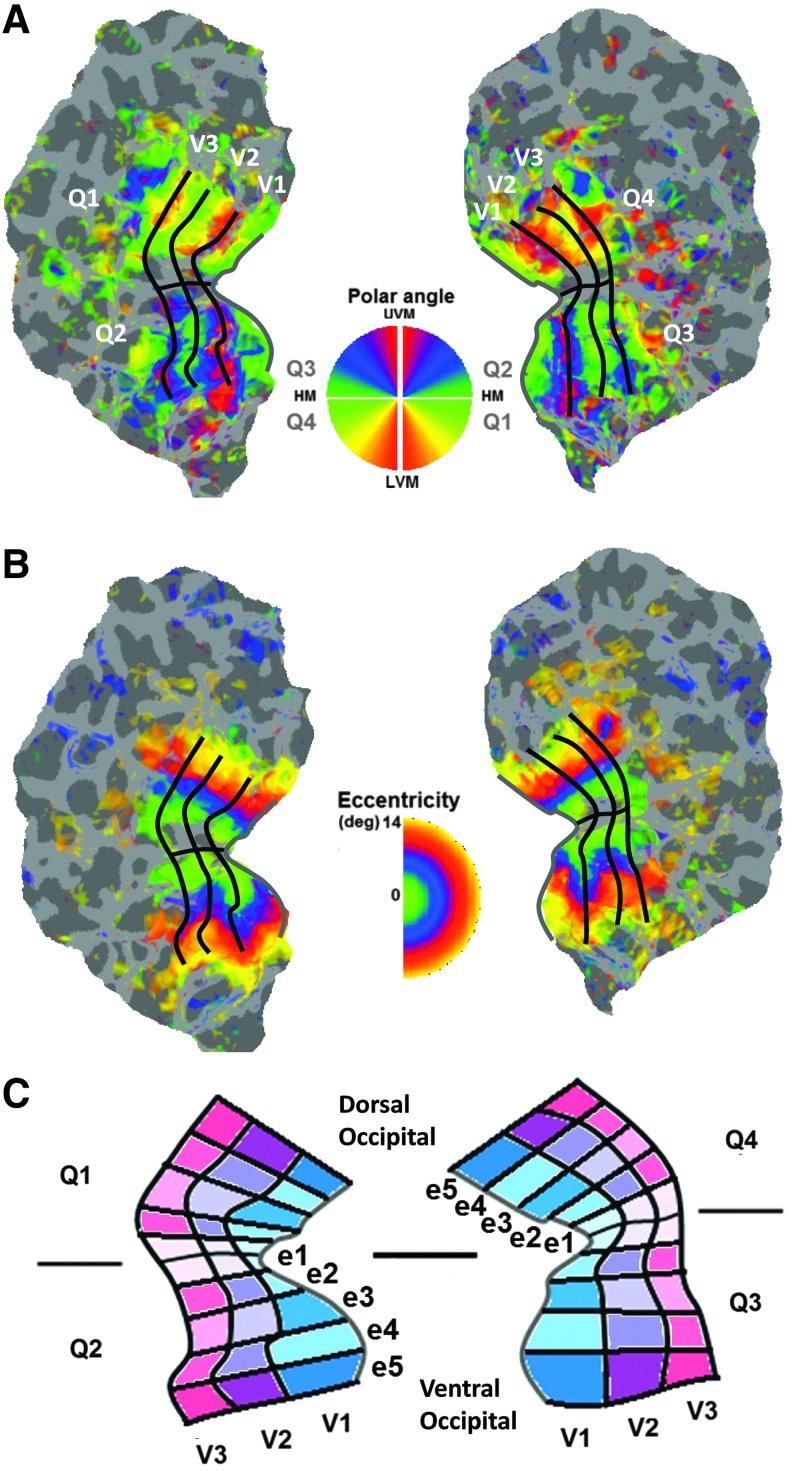
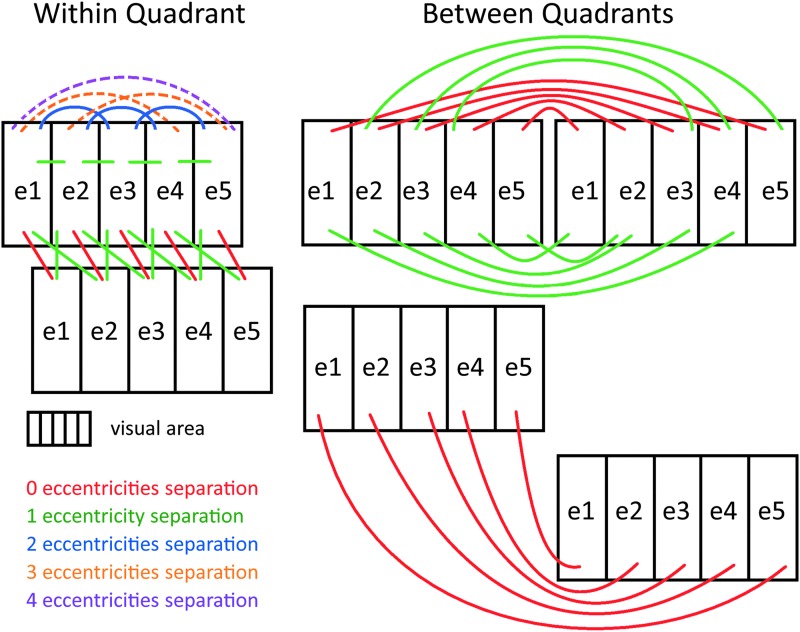
Figure 1 presents the methodology related to the definition of ROIs and the network under investigation. We evaluated a local visual network defined within a hemisphere, which is subdivided into ventral and dorsal sections. Data were obtained from the two hemispheres of each subject, thus from four quadrants of the visual cortex (cortical regions, which respond to stimuli in the four quadrants of the visual field). To achieve this, we measured the subject-specific retinotopic response evoked by rotating wedge and expanding/contracting ring stimuli. Phase-encoding analysis was pursued to define visual areas V1, V2, and V3. The area-specific ROIs were defined with a gap between visual areas V1, V2, and V3, by means of selecting voxels with the polar angle within ±35° of the oblique meridian in each quadrant of the visual field. This left a 20° gap in polar angle between the midpoint polar angle of each included voxel and that of the closest possible voxel in another visual area across the interareal border. This gap minimized the possibility of mixing signals with origin in two different visual areas, which can be detrimental to estimation of FC (Smith et al., 2011).

FIG. 1.

Retinotopy and ROI definition. Data presented are from one subject. Visual areas, V1, V2, and V3, were defined by examining the reversal of direction of increasing polar angle phases perpendicular to the isoeccentricity lines. Next, each hemisphere was divided into dorsal and ventral sections corresponding to quadrants of visual cortex. (A) We see the functional response to a stimulus changing in terms of polar angle, and (B) we see the response to a stimulus changing in terms of eccentricity. HM, horizontal meridian; LVM, lower vertical meridian; UVM, upper vertical meridian. (C) Voxels from each visual area in a quadrant were further classified into five eccentricity bins: e1 (central), e2, e3, e4, and e5 (peripheral), with the boundaries 0.5° to 1.7°, 1.7° to 4.1°, 4.1° to 7.1°, 7.1° to 10.4°, and 10.4° to 14°, respectively. ROI, region of interest. Color images available online at www.liebertpub.com/brain

The visual areas in each quadrant were further subdivided into five eccentricity regions of approximately equal size based on the numbers of their voxels. The eccentricity boundaries for the quadrant-based ROIs were 0.5° to 1.7°, 1.7° to 4.1°, 4.1° to 7.1°, 7.1° to 10.4°, and 10.4° to 14°. This definition of ROIs allows us to observe fine spatial specificity of FC measures within our network.

FC analyses

The resting-state fMRI time series were averaged over all voxels in each ROI to pursue ROI-based FC. RSFC measures were obtained for each run by computing the Corr and Pcorr coefficients between the time courses of each pair of ROIs. In this case, Corr refers to Pearson's linear correlation and Pcorr refers to Pearson's linear correlation between time course residuals from two ROIs, which have the time courses from all other ROIs in the network regressed out. Since in the current study we were interested in the FC within the small network of retinotopic visual areas, we neither regressed out the global average signal (Carbonell et al., 2011) nor corrected for its impact (Carbonell et al., 2014). Analyses were based on a network configuration of 60 ROIs (2 hemispheres × 2 quadrants within a hemisphere × 3 visual areas × 5 eccentricity-defined ROIs). Using the FC measures obtained from this network, we analyzed (1) within-quadrant FC, with the results from four quadrants (dorsal and ventral quadrants from each hemisphere) analyzed separately and their respective results combined statistically, and (2) between-quadrant within-hemisphere FC, with the results from the two hemispheres analyzed separately and their respective results combined statistically.

Statistics

FC was quantified within our network of 60 nodes by computing matrices (each with 60 × 60 entries) of Corr and Pcorr coefficients for each of the eight data sets available from each subject (resulting in eight coefficients per subject for each ROI pair). To examine statistical significance, coefficients were tested against zero and separately against a time-shuffled surrogate distribution (Supplementary Figs. S1–S4; Supplementary Data are available online at www.liebertpub.com/brain) and a Fourier surrogate distribution (Supplementary Figs. S5–S8). Time-shuffled surrogate data were generated by computing the Corr/Pcorr between ROI time courses shuffled in time. Shuffling was pursued based on the indices of the eight scans, while keeping the time course from each scan unchanged; we computed FC measures for the maximal possible number of permutations: ([8 × 8] − 8)/2 = 28. Thus, for each subject, 28 surrogate coefficients were computed for each ROI pair. To create the Fourier surrogate, we extracted the amplitude and phase values from the Fourier transform of the original time series, shuffled the original phases, assigned these newly shuffled phase values to the amplitudes of the original Fourier transforms, and then computed the inverse Fourier transform. The results obtained when comparing FC measures with zero (Figs. 4–8) and with the surrogate data (Supplementary Figs. S1–S8) were consistent.

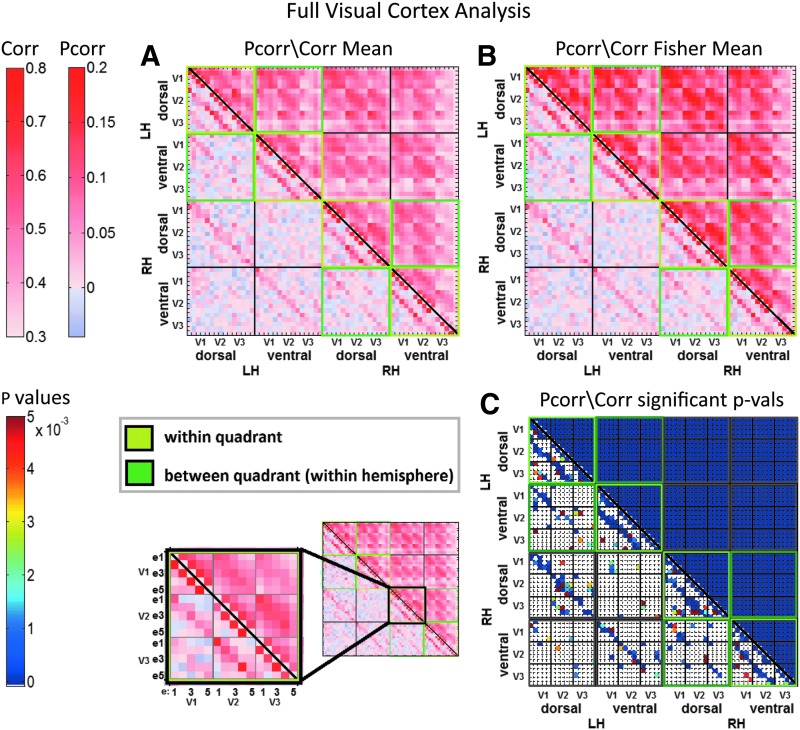
FIG. 4.

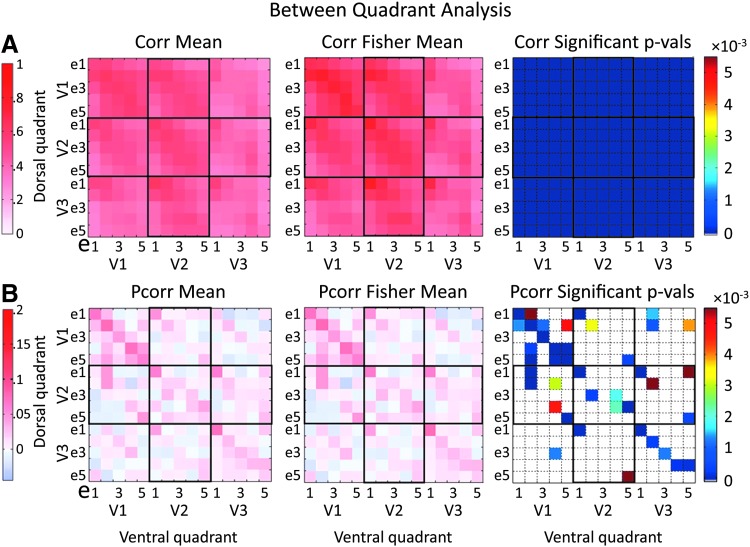
Mean Pcorr/Corr, Fisher coefficients, and p-values associated with functional connections of the full visual cortex network (all four quadrants analyzed together). In each matrix, Pcorr coefficients/p-values are presented in the lower left triangle and Corr coefficients/p-values are in the upper right triangle. (A) Mean Pcorr/Corr coefficients across all subjects (6) and runs per subjects (8) (6 × 8). (B) Mean Fisher coefficients across all subjects and runs. (C) p-Values of statistically significant Pcorr/Corr associated with the functional connections in the full visual cortex network. The five defined eccentricity regions are labeled as e1, e2, e3, e4, and e5. Significance is thresholded at 0.05, with false discovery rate correction. Connections that did not show statistical significance are presented in white. LH, left hemisphere; RH, right hemisphere. Color images available online at www.liebertpub.com/brain

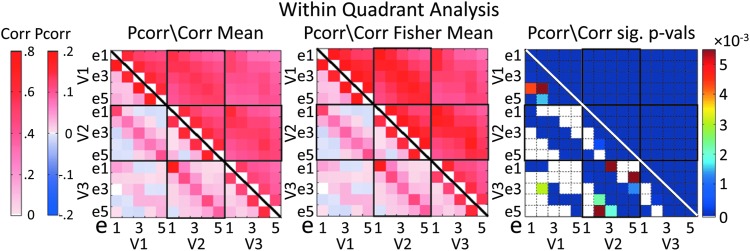
FIG. 5.

Mean functional connectivity (FC) measures within a quadrant, computed across all subjects, runs per subject, and the four quadrants. Mean Pcorr and Corr connectivity measures are reflected below and above the diagonal, respectively. White connections (far right matrix) did not show statistical significance. Presentation is as in Figure 4. Color images available online at www.liebertpub.com/brain

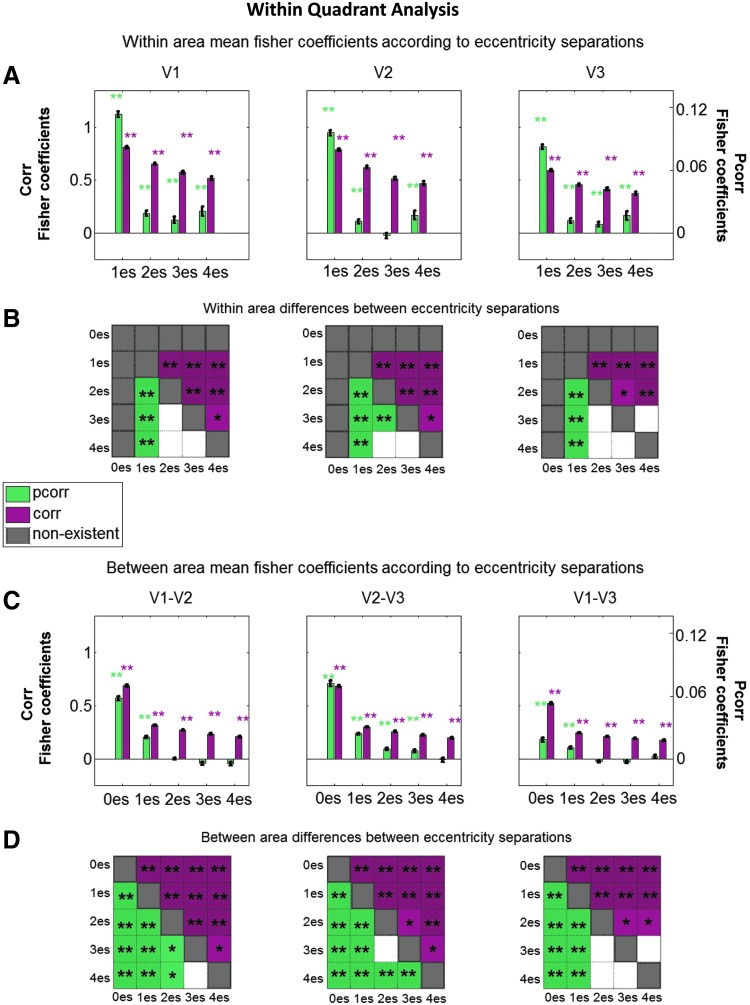
FIG. 6.

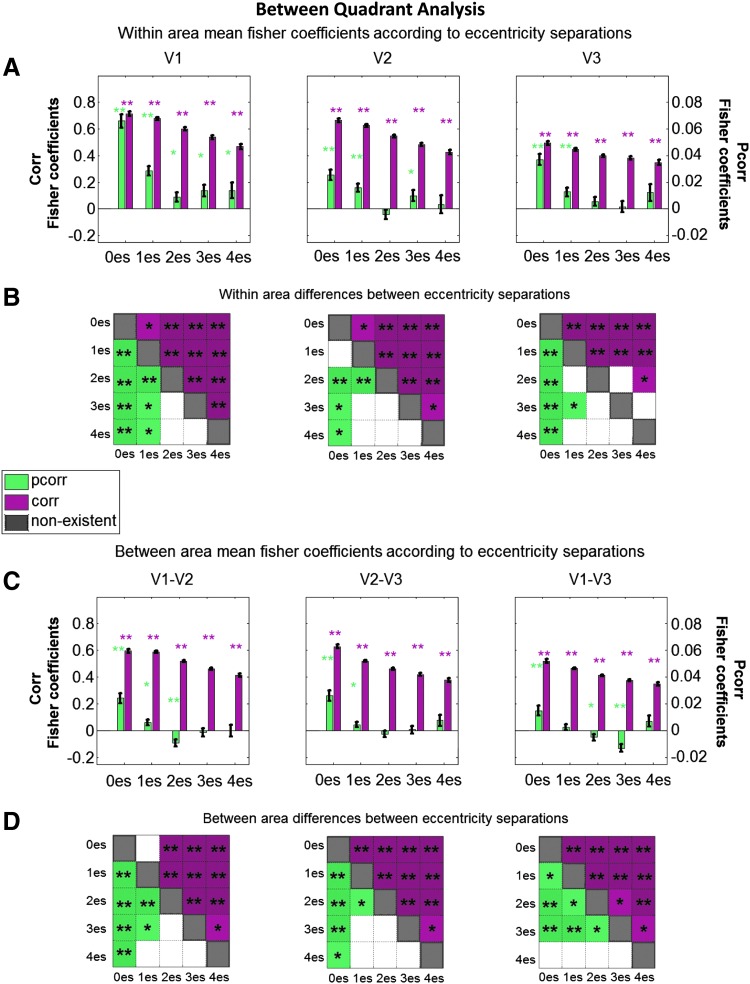
Mean FC measures for connections grouped according to eccentricity separations within a quadrant. (A, C) Across all plots, green and purple bars represent the mean Fisher-transformed Pcorr and Corr, respectively, computed across all subjects, runs, and quadrants. Error bars reflect the standard error of the mean across measurements. (A) Within-visual area Fisher coefficients for different eccentricity separations. Plots in C show the between-area Fisher coefficients of different eccentricity separations. A zero eccentricity separation (0es) indicates regions with the same eccentricity; a separation of one eccentricity (1es) means the regions' eccentricities were adjacent, and a separation of two eccentricities (2es) means there was a gap between the two regions' eccentricities, etc., (see the Materials and Methods section for further details). Individual connections are shown to be significant with an asterisk directly above the bar. (B, D) Differences between eccentricity separation bins are shown to be significant with an asterisk within the colored squares of the matrices. Green and purple squares represent Pcorr and Corr, respectively. White squares represent differences that were not significant. Gray squares represent differences not testable (nonexistent) in this analysis. For (A–D), statistical significance was assessed using alpha values of 0.05 (*) and 0.001 (**), following repeated-measures statistical analyses. Color images available online at www.liebertpub.com/brain

FIG. 7.

Mean FC measures associated with functional connections between ROIs residing in different quadrants within a hemisphere. The mean connectivity measures were computed across all subjects, runs, and the two quadrant pairs. (A, B) Reflect Corr and Pcorr connectivity measures, respectively. White entries (far right matrices) represent connections that did not show statistical significance. The format of presentation is as in Figure 4. Color images available online at www.liebertpub.com/brain

FIG. 8.

Mean FC measures for connections grouped according to eccentricity separations between quadrants within a hemisphere. (A, C) Across all plots, green and purple bars represent the mean Fisher-transformed Pcorr and Corr, respectively, computed across all subjects, runs, and hemispheres. Error bars reflect the standard error of the mean across measurements. Green and purple entries in (B, D) represent significant differences in Pcorr and Corr eccentricity bin separations (es), respectively. For (A–D), statistical significance was assessed using alpha values of 0.05 (*) and 0.001 (**), following repeated-measures statistical analyses. Presentation is as in Figure 6. Color images available online at www.liebertpub.com/brain

Fisher's z transform was applied to individual Corr/Pcorr coefficients (r) before use in statistical tests by calculating as follows:

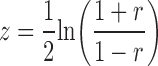The Fisher-transformed coefficients were then submitted to a mixed-effects, repeated-measures General Linear Model (GLM) obtained from the SurfStat MATLAB toolbox (www.math.mcgill.ca/keith/surfstat/#mixed). Within a quadrant, 32 ([8 functional runs of data] × [4 quadrants]) Fisher-transformed Corr and Pcorr coefficients were computed for all pairs of ROIs for each subject and were treated as separate data acquired for the given subject. For the within-hemisphere, between-quadrant statistical tests, we had 16 ([8 functional runs of data] × [2 pairs of quadrants]) sets of Fisher-transformed Corr and Pcorr coefficients for all pairs of ROIs for each subject.

A t statistic, degrees of freedom, and p-value for the contrast of interest, namely the contrast between the Corr/Pcorr coefficients and zero, were generated by the GLM analysis for each pair of ROIs. Using an alpha of 0.05, p-values were assessed for significance after applying the false discovery rate (FDR) correction (Benjamini and Hochberg, 1995). In all FC figures, we present statistical results for both Corr and Pcorr results. Considering the FDR correction, the adjusted alpha values for the two tests (within quadrant and between quadrants) were 10⁻¹⁶ and 10⁻¹⁶ for Corr and 0.0086 and 0.0163 for Pcorr, respectively.

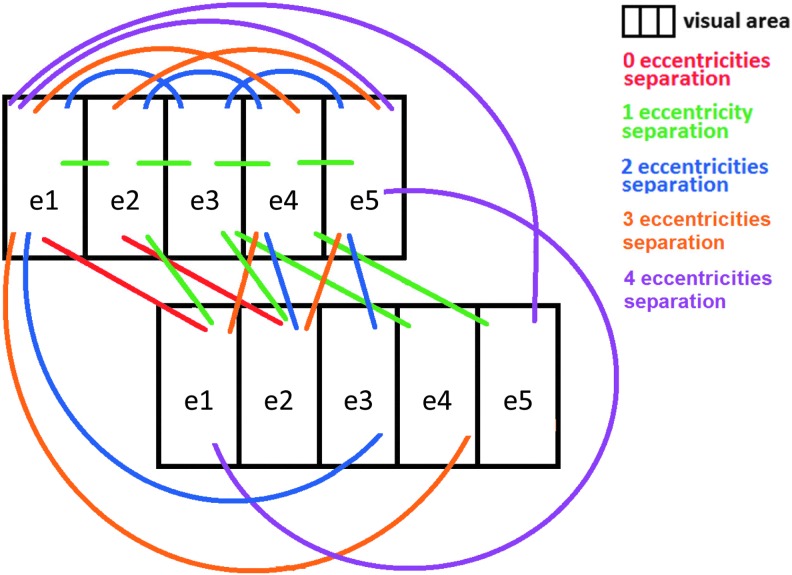
In both the within- and between-quadrant analyses, we statistically compared Corr/Pcorr values as a function of eccentricity bin difference (Figs. 6 and 8). This analysis was performed according to the number of eccentricity regions separating the two ROIs being correlated (see Fig. 2 for a schematic showing these connections). With five eccentricity regions, we could have 0 (if the ROIs are in different visual areas), 1, 2, 3, or 4 eccentricity bin separations between ROIs (we denote these eccentricity bin separations as 0es, 1es, 2es, 3es, and 4es, respectively, es signifying eccentricity separation). A 0es indicates that the two ROIs whose connectivity is being evaluated share the same eccentricity bin, that is, they are both e1, both e2, or both e3, etc. A 1es indicates that the ROIs are adjacent in eccentricity, that is, e1 and e2 or e2 and e3, etc. A 2es indicates that the ROIs are separated by a gap the width of one eccentricity region, that is, e1 and e3, e2 and e4, or e3 and e5. A 3es indicates that the ROIs are separated by a gap the width of two eccentricity regions, that is, e1 and e4, or e2 and e5. Finally, a 4e separation means a connection between the most central and most peripheral regions, that is, e1 and e5. Within a visual area, there are zero 0es connections within a quadrant and five 0es connections between quadrants, four 1es connections, three 2es connections, two 3es connections, and one 4es connection. Between visual areas, there are five 0es connections, eight 1es connections, six 2es connections, four 3es connections, and two 4es connections. These analyses were also done using the repeated-measures GLM, although p-values were not adjusted for multiple comparisons here as only a few comparisons were made.

FIG. 2.

Schematic of separations between ROIs within and between visual areas. For statistical testing, ROIs were grouped according to the number of eccentricity regions separating them. Note that these are a few representative connections. For the total number of connections of each type, see the Materials and Methods section. Color images available online at www.liebertpub.com/brain

Cortical distance calculations

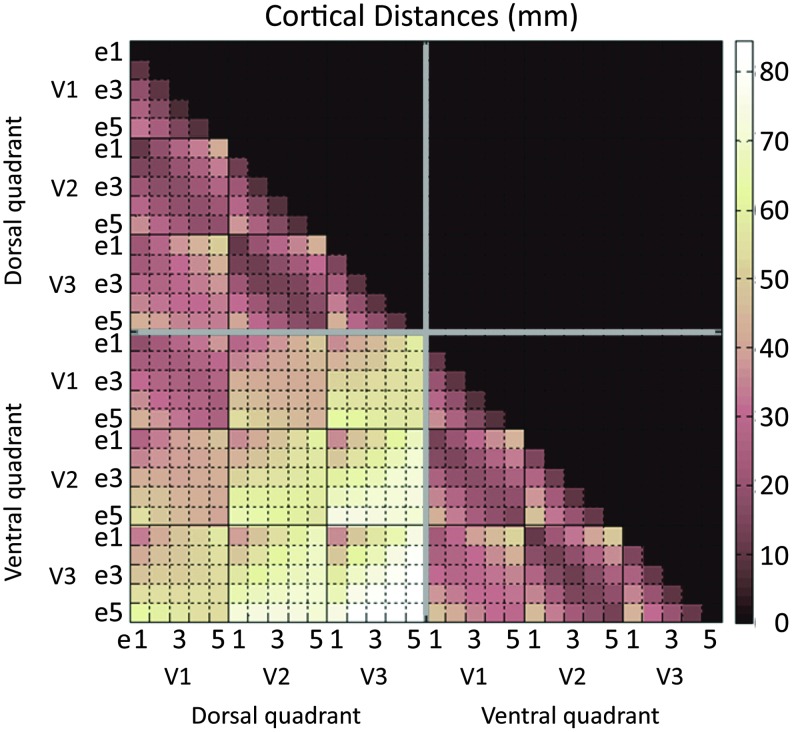
Cortical distance was estimated using Freesurfer's mris_pmake function along the smoothened surface of the cortex. For each subject, central voxels within each ROI were estimated, and then cortical distances between these centroids were computed. Distances were computed for all ROI combinations within the hemisphere, these being within and between quadrants. Figure 3 presents the cortical distances averaged across hemispheres and subjects.

FIG. 3.

Distances along the surface of the cortex between pairs of ROIs. Distances were computed within a hemisphere using the quadrant division of ROIs such that there are two full quadrants considered per hemisphere, one dorsal and one ventral. The matrix presents mean distances computed across all five subjects and their two hemispheres. The defined eccentricity regions are labeled as e1, e2, e3, e4, and e5. Color images available online at www.liebertpub.com/brain

The relationship between the Corr/Pcorr coefficients and the cortical distance between ROIs was examined with first- and second-order regressions, as well as an exponential fit. These functions were fit to the mean of the Corr/Pcorr values and cortical distances across subjects and hemispheres. The linear, quadratic, and exponential trend lines were computed using Matlab's fit function. Goodness of fit of the models was evaluated using a Bayesian Information Criterion (BIC) measure:

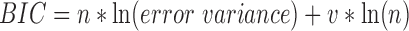where n is the number of data points, v is the degrees of freedom of the model, and the error variance is as follows:

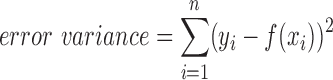where y_i is the mean Corr/Pcorr for a given cortical distance, x_i, and f(x_i) is the model prediction at that cortical distance.

This definition of the BIC assumes that the model errors are independent and normally distributed and that the derivative of the log likelihood with respect to the true variance is zero. When comparing several models, the model with the lowest BIC is expected to best represent the data (Priestley, 1981).

To quantify the confidence one can have in the model selected based on the BIC values, we computed the Bayes factor (Sotero et al., 2009):

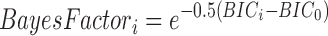where the subscript i represents the different models and the subscript 0 represents the reference model, here selected as the model with the lowest BIC. The Bayes factor allows us to compute the percentage confidence we can have in the fact that the model with the lowest BIC fits better than the other models:

Results

Below we present the results from grouped quadrant analyses. First, for within-quadrant analyses, we consider all four quadrants as separate data sets for a given subject. Next, for between-quadrant analyses, we consider pairs of quadrants from the same hemisphere as separate data sets for a given subject. For the results of the full visual cortex analysis, see Figure 4.

Retinotopic organization of FC: within-quadrant analysis

FC within and between areas in the human visual cortex, including V1, V2, and V3, was measured by calculating the Corr and, separately, Pcorr coefficients between BOLD fMRI time courses acquired in the resting state. Each area was divided into four quadrants (regions responding to stimuli in the quadrants of the visual field). To observe the retinotopic organization of FC in these early visual areas, voxels were classified into five retinotopic ROIs based on the retinotopic phase encoding in eccentricity (see the Materials and Methods section for details).

FC within an area

In the within-quadrant results (Fig. 5), the Corr/Pcorr values between two nearby regions in eccentricity were typically larger than those between more distant regions. This pattern of retinotopic organization of FC based on eccentricity is consistently observed throughout the three visual areas and in both Corr and Pcorr analyses. Pcorr values between regions adjacent within a visual area and those along the diagonal between adjacent visual areas stand out as being among the strongest.

To determine which pairs of regions take part in the resting-state functional network, Fisher-transformed Corr and Pcorr coefficients (in separate tests) were input to a repeated-measures GLM; these values tested against zero. Figure 5 (right) shows the results of statistical testing of the within-quadrant connections, with an alpha of 0.05, corrected for multiple comparisons using the FDR correction to 10⁻¹⁶ for Corr and 0.0086 for Pcorr. All Corr connections within a quadrant were significantly different from zero. Most within-area Pcorr connections showed statistical significance, and all connections between same eccentricity regions between visual areas showed statistical significance. Between adjacent visual areas, all connections reaching to regions with adjacent eccentricities were also significant. Thus, Pcorr-based FC between visual areas reflected retinotopic organization.

To quantify the effect of retinotopic distance on the Corr/Pcorr measures, we pursued repeated-measures GLM statistical testing while grouping ROI pairs, which were separated by the same number of eccentricity regions. Within visual areas (Fig. 6A), all Corr-based connection strengths were different than zero (all p < 10⁻¹⁶). There was a statistically significant effect of decreasing Corr values with increasing eccentricity separation in V1, V2, and V3 as demonstrated in Figure 6B through differences in eccentricity separations (Fig. 6B, above diagonal; Table 1 presents the corresponding p-values). In Pcorr-based functional connections, nearly all eccentricity separations were found to have a strength that was significantly different than zero as well (with the exception of V2 3es; see p-values in Table 1). There was a statistically significant effect of decreasing Pcorr measures with increasing eccentricity separation, although the drop-off is more abrupt than in correlation: all adjacent eccentricity connections were found to be significantly different from the connections between nonadjacent ROIs (Fig. 6B, below diagonal; Table 1).

Table 1.

Within-Quadrant Significant p-Values in Eccentricity Bin Analyses (Associated with Fig. 6)

Within-quadrant significant p-values
	Partial correlation			Correlation
Visual areas	Eccentricity bin coeffs > zero	Eccentricity bin differences		Eccentricity bin coeffs > zero	Eccentricity bin differences
V1-V1	1es p < 10−16	1es > 2es p < 10−16		All p < 10−16	1es > 2es p < 10−16	2es > 3es p = 1.4 × 10−6
	2es p = 1.0 × 10−14	1es > 3es p < 10−16			1es > 3es p < 10−16	2es > 4es p = 1.8 × 10−10
	3es p = 1.7 × 10−5	1es > 4es p < 10−16			1es > 4es p < 10−16	3es > 4es p = 0.0059
	4es p = 4.1 × 10−7
V2-V2	1es p < 10−16	1es > 2es p < 10−16	2es > 3es p = 3.4 × 10−5	All p < 10−16	1es > 2es p < 10−16	2es > 3es p = 1.3 × 10−10
	2es p = 2.9 × 10−7	1es > 3es p < 10−16			1es > 3es p < 10−16	2es > 4es p = 5.5 × 10−13
	4es p = 1.9 × 10−5	1es > 4es p < 10−16			1es > 4es p < 10−16	3es > 4es p = 0.0273
V3-V3	1es p < 10−16	1es > 2es p < 10−16		All p < 10−16	1es > 2es p < 10−16	2es > 3es p = 0.0135
	2es p = 1.4 × 10−8	1es > 3es p < 10−16			1es > 3es p < 10−16	2es > 4es p = 1.6 × 10−4
	3es p = 5.8 × 10−4	1es > 4es p < 10−16			1es > 4es p < 10−16
	4es p = 3.1 × 10−5
V1-V2	0es p < 10−16	0es > 1es p < 10−16	1es > 2es p < 10−16	All p < 10−16	0es > 1es p < 10−16	1es > 2es p = 6.0 × 10−6
	1es p < 10−16	0es > 2es p < 10−16	1es > 3es p < 10−16		0es > 2es p < 10−16	1es > 3es p = 2.2 × 10−13
		0es > 3es p < 10−16	1es > 4es p < 10−16		0es > 3es p < 10−16	1es > 4es p = 1.3 × 10−13
		0es > 4es p < 10−16	2es > 3es p = 0.0081		0es > 4es p < 10−16	2es > 3es p = 4.4 × 10−4
			2es > 4es p = 0.0242			2es > 4es p = 1.3 × 10−6
						3es > 4es p = 0.0310
V2-V3	0es p < 10−16	0es > 1es p < 10−16	1es > 2es p < 10−16	All p < 10−16	0es > 1es p < 10−16	1es > 2es p = 8.0 × 10−6
	1es p < 10−16	0es > 2es p < 10−16	1es > 3es p < 10−16		0es > 2es p < 10−16	1es > 3es p = 4.9 × 10−12
	2es p < 10−16	0es > 3es p < 10−16	1es > 4es p < 10−16		0es > 3es p < 10−16	1es > 4es p = 5.3 × 10−13
	3es p = 4.4 × 10−9	0es > 4es p < 10−16	2es > 4es p = 9.9 × 10−7		0es > 4es p < 10−16	2es > 3es p = 0.0018
			3es > 4es p = 1.2 × 10−4			2es > 4es p = 3.0 × 10−6
						3es > 4es p = 0.0221
V1-V3	0es p < 10−16	0es > 1es p = 9.3 × 10−5	1es > 2es p < 10−16	All p < 10−16	0es > 1es p < 10−16	1es > 2es p = 9.0 × 10−5
	1es p < 10−16	0es > 2es p < 10−16	1es > 3es p = 2.2 × 10−16		0es > 2es p < 10−16	1es > 3es p = 5.3 × 10−8
		0es > 3es p < 10−16	1es > 4es p = 1.2 × 10−4		0es > 3es p < 10−16	1es > 4es p = 1.8 × 10−8
		0es > 4es p = 4.1 × 10−10	0es > 4es p < 10−16			2es > 3es p = 0.0377
						2es > 4es p = 7.4 × 10−4

The first column indicates the visual areas involved, including within-area measures (first three rows) and between-area measures (next three rows). The second column presents the results of testing for statistical significance of Pcorr measures as a function of eccentricity bin difference. The third column presents the results of testing for differences in Pcorr values with increasing eccentricity separation. The fourth and fifth columns present results for Corr measures.

FC between areas

Retinotopic organization of FC was also observed between visual areas upon examination of the Corr and Pcorr connectivity matrices (Fig. 5, first two matrices). Retinotopically close pairs of ROIs from different visual areas show higher Corr/Pcor values than distant pairs of ROIs. For example, common eccentricity regions tend to be connected with the highest Corr/Pcorr values, particularly between V1 and V2, and V2 and V3.

While assessing the strength of connection between two ROIs, we found that Pcorr between adjacent visual areas (V1-V2 and V2-V3) significantly differed from zero for all common eccentricity connections (all p < 10⁻¹⁶) and all but one adjacent eccentricity connections (all p < 4 × 10⁻⁵ (Fig. 5, right). V1 and V3 had 4 of 5 same eccentricity region significant Pcorr as well as a few adjacent eccentricity connections, although not all. These findings suggested that the functional connections between adjacent visual areas (V1-V2 and V2-V3) are stronger than those between nonadjacent areas (V1-V3). Corr/Pcorr values between regions from adjacent visual areas were indeed significantly higher than Corr/Pcorr values from V1-V3 connections (p < 10⁻¹⁶ for Corr and Pcorr; two-tailed paired t-test).

In evaluating the range of Corr/Pcorr along the eccentricity dimension between visual areas, we turn our attention to Figure 6C. The between area eccentricity bin separation plots show consistent significance of correlations for all eccentricity separations (significantly different from zero; p-values, all p < 10⁻¹⁶ are presented in Table 1). There were significant differences between the magnitudes of the coefficients for all the different eccentricity bin separations (except for 3es compared with 4es between V1 and V3): the Corr coefficients decreased with increasing eccentricity separation (Fig. 6D, above diagonal; Table 1).

The between area plots for the Pcorr analysis show consistent significance with 0es and 1es (significantly different from zero; Figure 6C; p-values presented in Table 1). Connections with 2es and 3es between adjacent visual areas, V2 and V3, showed statistical significance too. In all cases, connections between ROIs separated by four eccentricity bins did not show statistically significant Pcorr. We observed a statistically significant effect of decreasing Pcorr coefficients as the eccentricity separation increased, particularly in adjacent visual areas (Fig. 6D, below diagonal; Table 1). These results lead us to conclude that Pcorr-based FC between visual areas is largely limited to identical and adjacent eccentricity regions, whereas Corr measures are not.

See Figure 8 for a summary of the connections identified within a quadrant based on the Pcorr eccentricity bin separation analyses.

Retinotopic organization of FC: between-quadrant within-hemisphere analysis

FC within an area

Figure 7A and B shows the Corr and Pcorr coefficients for within-hemisphere between-quadrant connectivity. The Corr analysis (Fig. 7A) shows that e1-e1 connections and, to a lesser extent, connections between other retinotopically close regions within a visual area (close to the diagonal) stand out with higher correlations. Pcorr matrices (Fig. 7B) also reflect stronger e1-e1 connections, although less noticeably so than Corr. They also show relatively high Pcorr between other regions of the same eccentricity (e2-e2, e3-e3) within a visual area (along the diagonal).

Figure 7A and B (far right matrices) shows the results of between-quadrant statistical tests against zero, with an alpha of 0.05, FDR corrected to 10⁻¹⁶ for Corr and 0.0163 for Pcorr. All Corr-based functional connectivities (Fig. 7A, far right) were significantly different from zero. The Pcorr statistical analysis (Fig. 7B, far right) shows that 11 of 15 connections along the diagonal, representing connections between regions of same eccentricity belonging to the same visual area, have partial correlations significantly greater than zero. In addition, several within-area adjacent eccentricity region connections show statistically significant Pcorr, particularly in V1. V1 also shows three other significant connections: dorsal e4–ventral e2, dorsal e5–ventral e2, and dorsal e2–ventral e5. From this, we concluded that the range of Pcorr-based connectivity within a visual area between dorsal and ventral quadrants of a hemisphere is at most to the adjacent eccentricity region in V2 and V3, unlike within the quadrant, where some nonadjacent eccentricity regions were significantly different than zero as well.

Within-area correlations were statistically significant for all eccentricity separations for V1, V2, and V3 (Fig. 8A; all p-values for between-quadrant eccentricity bin analyses are presented in Table 2). To test the effect of the retinotopic distance within a visual area between quadrants of a hemisphere, we analyzed the difference between the various eccentricity bin Fisher-transformed correlations. There were significant differences between nearly all eccentricity bin separations in V1, V2, and V3; the only separations that did not show a statistically significant difference were 2es and 3es, and 3es and 4es in V3 (Fig. 8B; Table 2). We concluded that between quadrants, but within a visual area, Corr coefficients differ in a similar manner to within a quadrant such that there is a notable decreasing effect in coefficients with increasing retinotopic distance.

Table 2.

Between-Quadrant Significant p-Values in Eccentricity Bin Analyses (Associated with Fig. 8)

Between-quadrant significant p-values
	Partial correlation			Correlation
Visual areas	Eccentricity bin coeffs > zero	Eccentricity bin differences		Eccentricity bin coeffs > zero	Eccentricity bin differences
V1-V1	0es p < 10−16	0es > 1es p = 2.0 × 10−10	1es > 2es p = 9.1 × 10−5	All p < 10−16	0es > 1es p = 0.0297	1es > 2es p = 3.0 × 10−7
	1es p < 10−16	0es > 2es p < 10−16	1es > 3es p = 0.0096		0es > 2es p = 2.8 × 10−11	1es > 3es p < 10−16
	2es p = 0.0141	0es > 3es p = 8.6 × 10−14	1es > 4es p = 0.0451		0es > 3es p < 10−16	1es > 4es p < 10−16
	3es p = 0.0026	0es > 4es p = 5.0 × 10−9			0es > 4es p < 10−16	2es > 3es p = 1.7 × 10−4
	4es p = 0.0175					2es > 4es p = 2.2 × 10−10
						3es > 4es p = 8.3 × 10−4
V2-V2	0es p = 4.2 × 10−10	0es > 2es p = 1.6 × 10−8	1es > 2es p = 7.0 × 10−6	All p < 10−16	0es > 1es p = 0.0067	1es > 2es p = 2.7 × 10−9
	1es p = 6.2 × 10−8	0es > 3es p = 0.0073			0es > 2es p = 3.4 × 10−14	1es > 3es p < 10−16
	3es p = 0.0145	0es > 4es p = 0.0041			0es > 3es p < 10−16	1es > 4es p < 10−16
					0es > 4es p < 10−16	2es > 3es p = 2.6 × 10−5
						2es > 4es p = 7.3 × 10−10
						3es > 4es p = 0.0052
V3-V3	0es p < 10−16	0es > 1es p = 1.1 × 10−6	1es > 3es p = 0.0371	All p < 10−16	0es > 1es p = 9.8 × 10−4	1es > 2es p = 8.7 × 10−5
	1es p = 4.6 × 10−5	0es > 2es p = 6.9 × 10−10			0es > 2es p = 3.3 × 10−10	1es > 3es p = 4.1 × 10−6
		0es > 3es p = 9.7 × 10−10			0es > 3es p = 8.5 × 10−11	1es > 4es p = 3.5 × 10−7
		0es > 4es p = 7.6 × 10−4			0es > 4es p = 9.9 × 10−10	2es > 4es p = 0.0059
V1-V2	0es p = 6.2 × 10−10	0es > 1es p = 4.0 × 10−5	1es > 2es p = 3.0 × 10−6	All p < 10−16	0es > 2es p = 3.6 × 10−8	1es > 2es p = 8.8 × 10−12
	1es p = 0.0047	0es > 2es p = 1.4 × 10−13	1es > 3es p = 0.0476		0es > 3es p < 10−16	1es > 3es p < 10−16
	2es p = 1.7 × 10−4	0es > 3es p = 1.9 × 10−7			0es > 4es p < 10−16	1es > 4es p < 10−16
	(2es negative Pcorr)	0es > 4es p = 2.6 × 10−5				2es > 3es p = 4.2 × 10−7
						2es > 4es p = 7.3 × 10−13
						3es > 4es p = 0.0012
V2-V3	0es p = 1.1 × 10−10	0es > 1es p = 4.9 × 10−7	1es > 2es p = 0.0241	All p < 10−16	0es > 1es p = 4.4 × 10−16	1es > 2es p = 9.9 × 10−10
	1es p = 0.0242	0es > 2es p = 2.0 × 10−10			0es > 2es p < 10−16	1es > 3es p < 10−16
		0es > 3es p = 1.8 × 10−7			0es > 3es p < 10−16	1es > 4es p < 10−16
		0es > 4es p = 0.0016			0es > 4es p < 10−16	2es > 3es p = 1.2 × 10−4
						2es > 4es p = 1.9 × 10−9
						3es > 4es p = 0.0023
V1-V3	0es p = 6.0 × 10−5	0es > 1es p = 0.0042	1es > 2es p = 0.0178	All p < 10−16	0es > 1es p = 8.5 × 10−5	1es > 2es p = 6.8 × 10−8
	2es p = 0.0365	0es > 2es p = 5.8 × 10−6	1es > 3es p = 1.7 × 10−5		0es > 2es p = 1.3 × 10−14	1es > 3es p = 1.8 × 10−15
	3es p = 8.2 × 10−6	0es > 3es p = 3.7 × 10−9	2es > 3es p = 0.0325		0es > 3es p < 10−16	1es > 4es p = 8.9 × 10−16
	(for 2es and 3es, negative Pcorr)				0es > 4es p < 10−16	2es > 3es p = 0.0011
						2es > 4es p = 4.6 × 10−6
						3es > 4es p = 0.0364

The format of presentation is similar to that used for Table 1.

Within-area Pcorr values were statistically significant between common eccentricity regions (0es) and regions adjacent in eccentricity (1es) for V1, V2, and V3 (Fig. 8A). In addition, Pcorr between more distant eccentricity regions within V1 (2es, 3es, and 4es) showed statistical significance. To test the effect of retinotopic distance within a visual area between quadrants of a hemisphere, we analyzed the difference between the various eccentricity bin Fisher-transformed partial correlations. In all visual areas, same eccentricity partial correlations were significantly higher than those with eccentricity bin separations (Fig. 8B; Table 2). A similar effect was observed for differences between adjacent eccentricity and higher eccentricity bin separations consistently in V1, as well as for 1es and 2es in V2, and 1es and 3es in V3. We concluded that as retinotopic distance increases within visual areas V1, V2, and V3, across dorsal and ventral quadrants, there is an effect of decreasing resting-state Pcorr values and most notably so in V1.

FC between areas

Between visual areas and between quadrants of a hemisphere, the e1-e1 connections stand out with higher coefficients, particularly in the Corr coefficients (Fig. 7A). As with the within-quadrant analyses, connections between V1 and V3 have somewhat lower coefficients than between V1 and V2 and between V2 and V3. In a two-tailed paired t-test of correlations, the connections between adjacent visual areas, that is, V1 and V2 together with V2 and V3, were found to have significantly higher correlations than V1-V3 connections (p < 10⁻¹⁶). Partial correlations were also significantly different in this between-quadrant test (p = 0.0120).

Between visual areas, all Corr values showed statistically significant differences relative to zero in both the analysis between individual ROIs (Fig. 7A, far right matrix) and in the eccentricity bin analyses (Fig. 8C). This being said, Corr was able to differentiate between all eccentricity bin separations in all pairs of visual areas, except V1-V2 0es and 1es (Fig. 8D, above diagonal; Table 2).

The findings for Pcorr are quite different than those of Corr between visual areas, between quadrants. Partial correlations that showed statistical significance relative to zero were mainly those of the same eccentricity connections between adjacent visual areas (Fig. 7B, far right). V1-V2, V2-V3, and V1-V3 0es connections showed significant Pcorr (Fig. 8C; Table 2). In adjacent visual areas, V1-V2 and V2-V3, the 1es connections were also found to be significantly greater than zero. Some negative partial correlations were found to be significant between V1-V2 (2es) and V1-V3 (2es, 3es). As was observed within visual areas, between visual areas the Pcorr values in the 0es bin were found to be significantly different than those in the other eccentricity separations (except V1-V3 0es and 4es) (Fig. 8D). There are also several differences between 1es connections and those with greater separations (all visual area combinations). This means that connections between regions with the same or similar eccentricity are particularly strong in all between-quadrant connections, with those differing in eccentricity showing significantly smaller Pcorr values.

Cortical distance analyses

Given the observed relationship between retinotopic distance and Corr/Pcorr and the relationship between retinotopy and distance along the cortex, we undertook an analysis comparing distances between ROI centroids along the cortex and Corr/Pcorr connectivity measures between those ROIs. We have continued with the separation of within-quadrant and between-quadrant connections given that we saw different connectivity profiles in these subsets of connections. With differing trends in correlations/partial correlations, it stands to reason that the relationship of cortical distance to the correlations/partial correlations may also differ.

Figure 3 shows the mean computed cortical distances within a hemisphere. The mean is across all subjects and hemispheres. The analysis showed shorter distances for connections between regions from the same quadrant, with the same eccentricity, and from adjacent visual areas (for example, within-quadrant adjacent visual area distances between e1-e1: ∼11–13 mm, mean = 11.9 mm, standard deviation (STD) = 0.96 mm; e3-e3: ∼13–18 mm, mean = 15.7 mm, STD = 2.6 mm; e5-e5: ∼15–19 mm, mean = 16.2 mm, STD = 1.9 mm). Between quadrants, the shortest connections are between e1 and e1, with e2-e2, e3-e3, e4-e4, and e5-e5 being progressively more distant. In addition, distances between V1 ROIs belonging to the dorsal and ventral quadrants (between-quadrant connections) were relatively short (<42 mm). These observations follow expectations from the cortical organization of V1, V2, and V3 (Fig. 1).

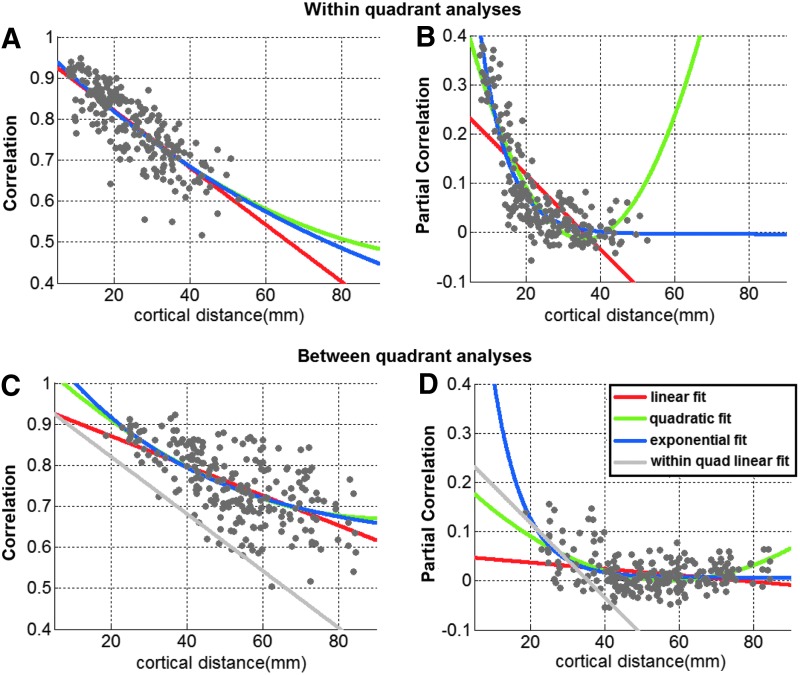
Figure 9 presents plots of the mean Corr (Fig. 9A) and Pcorr (Fig. 9B) coefficients versus mean cortical distance between ROI pairs within a quadrant, the figure reflecting dorsal and ventral results together in the same plot. There is a clear trend in the within-quadrant scatter plots of data, with decreasing coefficients for greater distances. The linear and quadratic regressions, as well as the exponential fit, were computed for each plot and are included in the figure for reference. The linear function seems to fit best the Corr values versus distance (Bayes factor confidence of 84.7% and 85.7% for linear fit being better than quadratic and exponential, respectively, Table 3). The exponential function fits best to the Pcorr values versus distance (∼100% confidence for exponential function better than both linear and quadratic, Table 3).

FIG. 9.

Mean Corr/Pcorr coefficients versus cortical distance plots for within- and between-quadrant connections. Within-quadrant coefficients are presented on the top row (A, B) and between-quadrants coefficients are on the bottom row (C, D). The mean coefficients and distances were computed across subjects and hemispheres. Color images available online at www.liebertpub.com/brain

Table 3.

Goodness of Fit of the Linear, Quadratic, and Exponential Fits to Correlation/Partial Correlation Versus Cortical Distance Plot

	p-Value of correlation between coefficients and distance	BIC of linear fit to mean	BIC of quadratic fit to mean	BIC of exponential fit to mean	% confidence that the model with the best BIC is better than the other models: 100% × (1-Bayes factor)
Corr
Within quadrant	4.28E−49	−1228.52	−1224.77	−1224.63	84.68 Lin > quad	85.69 Lin > exp
Between quadrants	5.05E−24	−1187.35	−1188.31	−1188.43	41.76 Exp > lin	5.85 Exp > quad
Pcorr
Within quadrant	9.33E−36	−1086.76	−1218.09	−1261.53	100 Exp > lin	99.99999996 Exp > quad
Between quadrants	9.37E−05	−1487.55	−1534.07	−1526.42	99.999999992 Quad > lin	97.81 Quad > exp

All columns quantify the data plotted in Figure 9. For each connection, we computed the mean cortical distance across hemispheres and mean correlation/partial correlation coefficient across runs, hemispheres, and subjects. Thus, for within a quadrant, we considered 210 connections: two sets (dorsal and ventral) of 105 coefficients each (number of within-quadrant connections), and for between quadrants, there are 225 coefficients (number of between-quadrant connections). The first column presents the p-value of testing the statistical significance of correlation between functional connectivity measures and cortical distances. Goodness of fit (columns 2–4) was evaluated using the BIC. A smaller BIC (more negative) implies a better fit relative to the other models. Bold values indicate the best BIC. To test differences between measures of goodness of fit, a Bayes factor was computed. We present the percent confidence that one model is better than the others tested (columns 5–6). Bold font indicate a strong confidence that one model is a better choice than the others.

BIC, Bayesian Information Criterion.

If RSFC within a network with dense connections depends on cortical distance alone, we should expect a similar approximately linear trend between Corr and cortical distance between quadrants too. We therefore pursued similar analysis of the mean Corr (Fig. 9C) and Pcorr (Fig. 9D) coefficients versus mean cortical distance between ROI pairs between quadrants of a hemisphere. The exponential fit, linear, and quadratic regression results are plotted, as well as the mean linear trend (in gray) from the within-quadrant analysis for easy comparison. While the Corr plot once again looks mostly linear, where Pcorr is concerned, following the initial drop in connectivity with increased distance, there seems to be an increase in connectivity measures when distances are greater than ∼55 mm.

To investigate if the increase in Pcorr for distances longer than ∼55 mm was statistically significant, we compared the Pcorr values of the most distant connections and mid-range connections between quadrants. To this end, we pursued a two-tailed t-test between the Fisher-transformed mean partial correlations for the 10 most distant connections (largest average distances across all subjects and hemispheres: distances of 79–85 mm) and 10 connections with distances starting at 54 mm (54–55 mm). The mean Pcorr for the distant connections was found to be significantly greater than that for the mid-range distance connections (p < 10⁻³, two-tail t-test).

To evaluate whether the trends in the distributions of Corr/Pcorr versus cortical distance were different for within and between quadrants, we quantified the goodness of fit of the linear, quadratic, and exponential regressions (Fig. 9). The first data column of Table 3 shows that both the within-quadrant and between-quadrant Corr coefficients were significantly correlated with distance along cortex (p∼E⁻⁴⁹ and p∼E⁻²⁴, respectively). Pcorr showed statistically significant correlation with distance, too for both within (p∼E⁻³⁶) and between (p∼0.0001) quadrants. The slopes of the linear fits within and between quadrants were found to be significantly different for Pcorr (p = 10⁻¹¹), with steeper slopes within a quadrant than between quadrants.

To compare the goodness of fits of the three regressions in the four conditions (Corr/Pcorr, within/between quadrant), we computed the BIC of each regression, and then we computed the Bayes factor, which allows us to determine the confidence we can have that the model with the lowest BIC is better than the other models (see the Materials and Methods section; values in Table 3). We found that for Corr, the linear fit is the best within a quadrant (∼85% confidence). Although the exponential fit was best between quadrants, the associated level of confidence was low (under 42% for exponential fit better than linear; under 6% for exponential better than quadratic). For Pcorr, the confidences observed were very strong, and we observed a difference between the within-quadrant and between-quadrant cases. Within a quadrant, the exponential fit was the best fit (∼100% confidence, it is better than both linear and quadratic, Table 3). Between quadrants, the quadratic was the best fit (∼100% and 97.8%, it is better than linear and exponential, respectively, Table 3). These results suggest that the relationship between Pcorr and distance along the cortex was not identical within and between quadrants.

Discussion

There are two types of connections, which we investigated: (1) within-visual area connections and (2) between-visual area connections. Both of these connections were evaluated within the quadrant and between quadrants of the same hemisphere. We look separately at the connectivity within the dorsal and ventral quadrants of the visual cortex in a hemisphere, and between these quadrants, due to the largely symmetric nature of their visual field representation. This separation of within-quadrant versus between-quadrant analyses also presents a logical separation of generally closer range connections along the cortex (within a quadrant) and longer range connections (between quadrants). In addition, the symmetrical arrangement of the visual areas between quadrants creates a distribution of distances within an area that are short (e.g., V1), long (e.g., V3), or intermediate (e.g., V2). This wide distribution of distances has allowed us to demonstrate a complex relationship between FC measures and distance.

Within-visual area connections

Within a quadrant, within visual areas, all Corr and Pcorr FC measures showed statistical significance (Figs. 6A and 10). Across visual areas, Corr (all visual areas) and Pcorr (all visual areas, 1es > all other es) values decreased with increasing eccentricity separation, demonstrating the dependence of RSFC on retinotopic eccentricity (Fig. 6B).

FIG. 10.

Summary figure of the statistically significant connections from the eccentricity bin analyses for partial correlation. Connections which seem like they may be anomalous were omitted. Dashed lines represent weaker connections. The panel to the left shows connections within quadrant: within area (upper scheme), and between areas (upper and lower schemes combined). The panel to the right shows connections between quadrants: within area (upper scheme), and between areas (upper and lower schemes combined). Color images available online at www.liebertpub.com/brain

We went into these analyses with some expectations based on the well-studied organization and anatomical connectivity of the primate visual cortex. Horizontal connections, namely direct neuronal linkages within a visual area, have been shown to be generally quite short in the macaque monkey visual cortex, the longest being of less than 2.5 mm in V1 and 5 mm in V2 in the macaque brain (Amir et al., 1993; Markov et al., 2011). In humans, these connections may be up to twice as long (up to ∼5 mm in V1 and ∼10 mm in V2, respectively). This estimation is based on the fact that the cycle of ocular dominance columns in humans is approximately double that in the monkey (Adams et al., 2007). Assuming that this scaling factor applies to other features of the organization, the length of horizontal connections in humans should be approximately double their length in monkeys. Now, to put this into the context of our study across different eccentricity regions within a quadrant of the visual cortex, visual areas in a quadrant have a length of around 4.5–6 cm on the cortex (Tootell et al., 1998). Therefore, our five eccentricity regions within the visual quadrant would have an average length of around 9–12 mm. This scale of distances along the cortex was confirmed in our distance analysis between central voxels of ROIs, where pairs of adjacent ROIs from within a visual area of a single quadrant were separated by an average distance of 10.6 mm (STD = 2.3 mm). Pairs of ROIs separated by a gap (one of the five eccentricity regions) (i.e., 2es as depicted in Fig. 2), also from within a visual area of a single quadrant, were separated by an average distance of 20.4 mm (STD = 3.9 mm). Between the most central and the most peripheral regions (4es), within-visual area ROIs, the distance is of mean = 40.1 mm (STD = 5.7 mm). Notice that both the mean distances for 2es and 4es connections are much longer than the maximum of 5 and 10 mm expected from monosynaptic horizontal connections in V1 and V2, respectively. In spite of the long distances associated with 2es and 4es connections in V1 and V2, these connections are found to be statistically significant.

Anatomical projections in V1 with origin in the LGN and to a lesser extent from monosynaptic horizontal connections in V1 can drive action potential responses in the neurons they project to. However, these two types of connections show high retinotopic specificity. For example, the connections from the LGN to V1 (Salin and Bullier, 1995) and monosynaptic horizontal connections within V1 (Angelucci et al., 2002) are by far more visuotopic than the connections from V3 to V1 (Angelucci et al., 2002). Therefore, given that within areas V1 and V2, within a quadrant, we observe significant correlations/partial correlations between regions separated by ∼20 mm (2es) and ∼40 mm (4es), we expect that the underlying mechanisms of fMRI-based FC measures are not limited to input from the LGN or to direct, monosynaptic neuronal linkages through horizontal connections. Alternative or additional mechanisms may include feedback from higher visual areas (Angelucci et al., 2002; Salin and Bullier, 1995; Shmuel et al., 2005) or from the pulvinar (de Zwart et al., 2013; Liu et al., 2012). We therefore hypothesize that the long-range correlation-based FC within visual areas V1, V2, and V3, is the result of polysynaptic connections involving local connectivity, higher visual areas, and the pulvinar. Indeed, feedback from higher visual areas reaches regions beyond those targeted by monosynaptic horizontal connections (Angelucci et al., 2002; Salin and Bullier, 1995). Similarly, the input from the pulvinar to retinotopic visual areas can drive responses, and neuronal responses in the pulvinar show wide tuning to stimulus position in the visual space. For correlation-based FC in this very local-scale network, these two types of inputs will vary gradually with distance. We can therefore expect the FC correlation coefficients to reflect nearly all nodes being functionally connected, with a gradual decrease in correlation values with increasing distance. Indeed, correlation-based FC decreases with increasing distance in an approximate linear manner (Fig. 9).

Given the regression of time courses from all nodes in the network when using Pcorr, we expect that these polysynaptic functional connections should be largely removed. The reason for this expectation is that there will be additional regions between or near the two regions whose FC is computed, which will receive similar polysynaptically transmitted signals. Signals based on propagation along polysynaptic horizontal connections will have to traverse the distance between the two ROIs in question, thus leaving traces that can be regressed out by Pcorr. Retinotopically broad feedback signals from higher visual areas or the pulvinar will make their impression on additional ROIs near the two ROIs in question, thus making it possible to regress them out. Indeed, Pcorr values were significantly lower than Corr values. Moreover, Pcorr-based FC is more specific to regions with similar eccentricities than Corr-based FC (Figs. 5–8) and it does not change linearly with increasing distance (Fig. 9).

Note that the longest horizontal connections expected in V1 (2.5 mm × 2 = 5 mm) are much shorter than in V2 (5 mm × 2 = 10 mm). Comparatively, horizontal connections within V2 and within V4 are known to be more spread out than horizontal connections in V1 (Amir et al., 1993). Given the relatively narrow horizontal connections expected in V1, one could expect that the range of FC within V1 would be relatively small. Remarkably, we see the opposite when comparing within-area connections in V1 with those in V2 and V3; across all tests, V1 is not only among the most abundantly (functionally) connected visual areas, with high correlations in particular, but also with partial correlations. These findings are consistent with previous studies that combined fMRI simultaneously with intracortical neurophysiological recordings (Schölvinck et al., 2010; Shmuel and Leopold, 2008). These studies demonstrated wide regions in V1 whose spontaneous fMRI signals correlated with time series of gamma band-limited amplitude recorded by one electrode (one cortical site) in V1.

Within and between quadrants, V1 is found to have significantly higher correlations and partial correlations than V2 (within: Corr p = 4.2 × 10⁻¹¹, Pcorr p = 1.4 × 10⁻¹⁰; between: Corr p = 2.9 × 10⁻⁴, Pcorr p = 2.2 × 10⁻⁷) and V3 (within: Corr p = 10⁻¹⁶, Pcorr p = 1.3 × 10⁻⁷; between: Corr p = 10⁻¹⁶, Pcorr p = 7.7 × 10⁻¹¹). This evidence further emphasizes that Corr/Pcorr-based FC involves mechanisms beyond monosynaptic horizontal connections, probably involving feedback from higher visual areas or the thalamus.

Between-visual area connections

Within a quadrant, between visual areas, Corr values showed statistical significance for all eccentricity separations (Fig. 6C). Pcorr showed consistent significance between regions with the same eccentricity and adjacent eccentricities and, in addition, between V2 and V3 with 2es and 3es (Figs. 6C and 10). Pairs of ROIs with similar eccentricity showed higher Corr/Pcorr than pairs of ROIs distant in eccentricity, demonstrating that RSFC between lower visual areas is retinotopically organized (Fig. 6D).

The main expectation we had of between-visual area within-quadrant connections was that there would be a bias toward stronger connectivity between ROIs of similar eccentricities (Heinzle et al., 2011). In fact, Heinzle and colleagues (2011) identified that the maximum eccentricity range of significant connections between visual areas V1 and V3, was around pi/3 rad in phase values or 2.1° ([(pi/3 rad)/(2 pi rad)] = [2.1°/12.5°]; 12.5° was the maximal eccentricity they mapped). In terms of eccentricity degrees, the boundaries around the ROIs that we used were 0.5° to 1.7°, 4.1°to 7.1°, and 10.4° to 14°. With a maximum potential range of around 2.1°, we should expect statistically significant FC limited to ROIs of same or possibly adjacent eccentricity. Indeed, between V1 and V3, the only statistically significant Pcorr values were obtained for ROIs of same eccentricity and adjacent eccentricities. Thus, our within-quadrant Pcorr analysis, which is comparable with the Corr-based weights and permutation test analysis pursued by Heinzle and colleagues, agrees with that expectation. In this study, we expand on Heinzle and colleagues' results by quantifying the functional connections between V1 and V2 and V2 and V3. V1-V2, V2-V3, and V1-V3 show a common eccentricity region as well as adjacent eccentricity region Pcorr-based connectivity. V2-V3 shows, in addition, more distant connectivity (up to 3es).

A recent study by Haak and colleagues (2013) shows that connective field maps based on visual stimulation are retinotopically organized, similar to the retinotopic organization we show here in the resting state. They accomplished this by computing the stimulus-based connective field maps between regions in area V1 and sites in areas V2-hV4. They then demonstrate that the eccentricity and polar angle maps for visual areas derived with conventional receptive field mapping are spatially correlated with connectivity maps computed using the time courses of voxels in these areas. These results are in line with our findings of retinotopically organized FC of lower visual areas in the resting state.

When considering the effect of retinotopic distance along the eccentricity dimension on FC in the human visual cortex, one factor to consider is the population receptive field sizes (pRFs) in each of the visual areas. Dumoulin and Wandell (2008) and Harvey and Dumoulin (2011) demonstrated that pRFs become progressively larger as we move from V1 to V2 and further to V3. In addition, within each visual area, the pRFs become larger as we move from central to more peripheral eccentricities. This trend of increasing pRFs with eccentricity is strongest in V3 and weakest in V1 and has been supported by evidence in human and monkey studies (Amano et al., 2009; Haak et al., 2013; Hubel and Wiesel, 1974; Kay et al., 2008; Smith et al., 2001; Van Essen et al., 1984; Winawer et al., 2010). V2 and V3 are expected to have broader pRFs relative to V1, thus leading us to expect significant FC across a wider range of eccentricity regions between these areas. This is confirmed in Figure 5 (right) and Figure 6C, where we see significant partial correlations between regions in V2 and V3 separated by two or three of the five eccentricity regions. In contrast, between V1 and V2 or V1 and V3, the most we see is significance with a separation of one of five eccentricity regions.

Within a quadrant, between visual areas, Corr/Pcorr values between regions from adjacent visual areas (V1-V2 and V2-V3) were higher than those between nonadjacent areas (V1-V3). These results are in agreement with the anatomical connectivity in the monkey visual cortex. Markov and colleagues (2011) show that in the macaque visual cortex, the output from V1 to V2 is at least an order of magnitude higher than the communication between any other areas. More generally, the direct monosynaptic connectivity between cortical areas decreases as the distance between the areas increases (Ercsey-Ravasz et al., 2013). Thus, within quadrant V1-V3 Pcorr statistically significant functional connections are limited to same eccentricity regions because (1) they are weaker and/or (2) the regression of the time courses of V2 nodes regresses out a large part of the contributions between V1 and V3 because they are expected to be similar.

Considerations of cortical distance

Within a quadrant, Corr and Pcorr showed a strong effect of decreasing coefficients for greater distances (an approximately linear effect for Corr; a strong exponential effect for Pcorr). Between quadrants, the linear effect was still no worse than quadratic or exponential trends for modeling Corr as a function of cortical distance. However, for Pcorr, the optimal fit was no longer exponential; in particular, coefficients first decreased and then increased with increasing distance, with the minimum of the quadratic trend line appearing at ∼55 mm. The BIC Bayes factor showed high confidence that the quadratic fit was better than the linear and exponential fits for Pcorr as a function of cortical distance (Fig. 9; Table 3). These results demonstrate that the relationship between Pcorr-based FC measures and distance along the cortex is different within and between quadrants.

One could suspect that the retinotopic effect in correlations/partial correlations observed between within-quadrant ROIs is determined largely by cortical distance and not necessarily by retinotopic differentiation. There are several reasons for this expectation. First, the cortical distance between ROIs within a quadrant and within an area is a continuous function of retinotopic distance. This is the essence of retinotopic mapping: cortical distance depends on retinotopic distance within a quadrant in a continuous manner (as shown by Sereno et al. (1995), DeYoe et al. (1996), Engel et al. (1997), Duncan and Boynton (2003), Larsson and Heeger (2006), Wandell et al. (2007), and others). In addition, the majority of anatomical connections impinging on any cortical neuron are of local origin with distances at the mm scale (Braitenberg and Shuez, 1998). This creates an effect of locally dense connectivity that drops with distance. Last, since lower visual areas are densely intra- and interconnected, one may expect network effects to play a significant role, creating not only network-scale but also region-scale synchronized fluctuating signals. Therefore, dependence of FC measures on distance in a small, densely connected network could reflect a combination of the underlying anatomical connections and network effects. Consistent with these expectations, the scatter plots in Figure 9 demonstrate that within a quadrant there is an inverse relationship between Corr and cortical distance (see also statistical results from Table 3).

Note that for Corr within a quadrant, not only the quadratic fit's BIC value was not smaller than that of the linear fit (Table 3) but also qualitatively we can observe in the plots that the minimum of the quadratic curve is outside of the range of the data. Thus, the fact that for Corr the quadratic fit Bayes factor does not differ with high percentage confidence from that of the linear fit should not be interpreted as evidence against linearity. A similar phenomenon can be observed for Corr between quadrants: although the BIC for the exponential fit is smallest in this case, it is not significantly better than the linear fit. For both within a quadrant and between quadrants, the only effect that is really observed is the approximately linear decreasing of coefficients with increasing cortical distance. We conclude that the FC Corr measures found within a quadrant and between quadrants vary approximately linearly with cortical distance.

These observations, which show a strong relationship between Corr and distance, raise concerns that RSFC within a small, densely connected network does not carry any information on the anatomical connectivity structure of the network. Given these concerns, we sought evidence indicating that FC measures reflect more than cortical distance alone. We verified that there exist regions within the small network we analyzed, which are quite separated in terms of cortical distance and yet maintain a Pcorr significantly different from zero, demonstrating that the effect which we extract in such a Pcorr analysis is not simply a reflection of the effect of proximity of regions. In our between-quadrant analysis where we have measured the mean cortical distance between ROIs, some examples of partial correlations that are contrary to the effects of cortical distance include V3-e4 to V3-e5 (∼84 mm) and V3-e4 to V3-e4 (∼83 mm), which are relatively distant and are statistically significant when compared with zero (p = 10⁻⁵ and p = 1.2 × 10⁻⁴, respectively), while closer connections between V1 and V3 between quadrants (∼35–60 mm) do not show statistically significant Pcorr.

Several additional findings show differences between the relationship of Pcorr FC and cortical distance within and between quadrants. First, between quadrants, there is an initial decrease in coefficients with increasing cortical distance, as observed within a quadrant, followed by a minimum coefficient (occurring around ∼55 mm cortical distance between ROIs), and then finally an increase in coefficients with greater distance. Indeed, the 10 most distant ROI pairs have significantly greater between-quadrant Pcorr strengths than the 10 mid-range distanced ROI pairs starting at 54 mm. Quantitatively, a true (with minimum within the range of the data points) quadratic fit is better than the simpler linear fit (∼100% confidence) and exponential fit (97.8% confidence, Table 3) for between-quadrant Pcorr versus distance analyses (yet, this is not the case within a quadrant where exponential is the clear best fit: 99+% confidence). Last, there is a significant difference between within- and between-quadrant slopes of linear fits and quadratic curvatures for Pcorr. Taken together, these findings demonstrate that within the small, densely connected network of lower visual areas, there is no simple mapping between FC based on Pcorr and cortical distance.

The reason for the difference in trends in the plots for within-quadrant and between-quadrant FC versus cortical distance can be analyzed by tracking which connections populate the critical parts of the scatter plots of Pcorr against cortical distance. Since Pcorr-based FC within a visual area is high even when computing FC between quadrants, regions in V3 residing in the dorsal and ventral quadrants can be expected to show relatively high Pcorr at the tail end of the Pcorr versus distance curve. This creates a scenario in which relatively distant regions residing in different quadrants show relatively high FC compared with ROIs that are closer (such as regions in V1 and V2 residing in the dorsal and ventral quadrants, respectively, and representing distant eccentricities). Indeed, upon examining the cortical distances observed for within- and between-quadrant connections, the majority (51.6%) of the between-quadrant connections are longer than the longest within-quadrant connection (52.7 mm). Within a quadrant, it is only connections with three or four eccentricity region separations that are longer than 39 mm, with most (18/21) of these connections connecting ROIs in different visual areas and showing no statistically significant Pcorr. In the Pcorr versus distance plots between quadrants, we see a minimum at around 55 mm. The most distant connections either connect regions within V3 or regions in V2 and V3, thus either connecting regions within an area or between areas adjacent in the hierarchy of visual areas, with the majority of these connections showing or approaching statistically significant Pcorr.

Correlation versus partial correlation

Pcorr is becoming increasingly used in connectivity analyses due to its greater ability to weed out false positives in the search for direct connections over simple Corr (Calabro and Vaina, 2012; Dawson et al., 2013; Pandit et al., 2013; Smith et al., 2011). Pcorr uses a linear regression to regress out fluctuations from other network nodes during the analysis of connectivity between two nodes and, in this way, is able to ensure that predicted connections are more representative of direct linkages. In our analyses, this was vital to obtaining utilizable results given that Corr predicted all connections as significantly connected in all quadrant-based analyses (within and between quadrants). These kinds of results can be expected when the network of study is densely connected, with network effects of indirect connections potentially accounting for significant correlations. What we wish to portray is that Pcorr identifies direct connections better than Corr, as evidenced by the fact that it can identify some direct connections we know to exist in the monkey (same eccentricity regions between visual areas), while not identifying some we know to not be directly connected from the monkey (regions with a large eccentricity difference that reside in two different visual areas).

Raemaekers and colleagues (2014) found that in their Corr analysis, small-scale connectivity was nearly completely obscured by large-scale network effects unless the effects of larger networks (the first several Independent Component Analysis components) were removed, which could be interpreted as a global-type signal affecting the network of interest. With the use of Pcorr instead of Corr, we are able to reflect synchrony between nodes with reduced contributions from other network nodes, even with the global signal intact in the data. Pcorr regresses out time courses of all other nodes in the network from the two nodes between which connectivity is being assessed to eliminate contributions from indirect connections from its network prediction. This in effect also removes any global signal that is observable within the network's nodes. Therefore, statistically significant Pcorr suggests the potential existence of a direct, monosynaptic anatomical connection within the network. This being said, Pcorr coefficients can reflect common input from outside of the network to those two ROIs only.

Conclusions

We report our findings on FC within and between visual areas V1, V2, and V3 at a scale finer than that of cortical areas. Within-quadrant Corr and Pcorr are found to be significant for all connections within a visual area. Corr, and to a lesser extent Pcorr, spanning beyond nearby eccentricities within a visual area demonstrates that FC reaches further than direct horizontal connections. Consistently in V1 and V2, and somewhat less so in V3, Corr and Pcorr values decrease with increasing eccentricity separation. Between-visual area within-quadrant Pcorr spans to same eccentricity regions and to adjacent eccentricity regions, with connections between V2 and V3 reaching even further. Pairs of ROIs with similar eccentricity in two different areas show higher Corr/Pcorr than pairs of ROIs distant in eccentricity (see Fig. 10 for a summary of within-quadrant Pcorr connectivity). Significant differences were found between the Corr/Pcorr for adjacent visual areas, V1-V2 and V2-V3, and between more distant areas V1-V3. The relationship between Corr FC and cortical distance separating the tested ROIs was approximately linear. Pcorr showed a more complex relationship to distance, with exponential and quadratic curves fitting best for within and between quadrants, respectively.

We conclude that resting-state functional connectivities within and between lower visual areas are retinotopically organized. Furthermore, Pcorr FC follows expectations based on the anatomical connectivity in the monkey visual cortex better than Corr does. Last, partial correlation-based retinotopically organized RSFC reflects more than cortical distance effects.

Acknowledgments

The authors thank Roberto Sotero and Sepide Movaghati for their comments on an earlier version of the manuscript and Ilana Leppert and Bruce Pike for support with MRI physics. This work was supported by an NIH grant, R01 EY015219, awarded to J.M. and grants from the Human Frontier Science Program (RGY0080/2008) and the Natural Sciences and Engineering Research Council of Canada (RGPIN 375457-09 and RGPIN 2015-05103) awarded to A.S.

Data Sharing

Please check http://www.bic.mni.mcgill.ca/∼amirs for information on how to download the data we collected for this article.

Author Disclosure Statement

No competing financial interests exist.