Identification of Homogeneous and Heterogeneous Variables in Pooled Cohort Studies

Summary

Pooled analyses integrate data from multiple studies and achieve a larger sample size for enhanced statistical power. When heterogeneity exists in variables’ effects on the outcome across studies, the simple pooling strategy fails to present a fair and complete picture of the effects of heterogeneous variables. Thus, it is important to investigate the homogeneous and heterogeneous structure of variables in pooled studies. In this paper, we consider the pooled cohort studies with time-to-event outcomes and propose a penalized Cox partial likelihood approach with adaptively weighted composite penalties on variables’ homogeneous and heterogeneous effects. We show that our method can characterize the variables as having heterogeneous, homogeneous, or null effects, and estimate non-zero effects. The results are readily extended to high-dimensional applications where the number of parameters is larger than the sample size. The proposed selection and estimation procedure can be implemented using the iterative shooting algorithm. We conduct extensive numerical studies to evaluate the performance of our proposed method and demonstrate it using a pooled analysis of gene expression in patients with ovarian cancer.

1. Introduction

Pooled studies can achieve a large sample size and facilitate investigations on rare diseases, rare exposures, and topics not easily addressed in a single study. For example, Ganzfried et al. (2013) made a concerted effort to create a curated database consisting of clinical and microarray gene expression data on 2970 ovarian cancer patients from 23 studies using 11 gene expression measurement platforms. This pooled database empowers researchers to investigate the prognostic effect of genetic biomarkers on ovarian cancer survival in a uniform and consistent fashion. But as seen in this and many other pooled studies, inter-study heterogeneity in the association between the biomarkers and the outcome often exists and its source includes differences in study populations, sampling methods, disease ascertainments, and measurement methods. Although harmonizing the data can alleviate this issue (Ganzfried et al., 2013), heterogeneity often is inherent in pooled studies. In some studies, heterogeneity itself is important for understanding disease disparity and progression at different phases (Moreno et al., 1996). Therefore, the analysis of pooled studies needs to properly account for heterogeneity to yield meaningful results.

To estimate covariate effects in pooled studies, the two-step procedure is commonly used, in which study-specific effects are first estimated using individual study data and then combined using a fixed-effects model (Hedges and Olkin, 1985) or a random-effects model (DerSimonian and Laird, 1986). However, the two-step procedure has difficulty in handling multiple variables. If heterogeneity exists in variables’ effects across studies we want to distinguish the variables with heterogeneous effects versus those without, as the effect of a homogeneous predictor should be modeled using a common parameter across studies to reduce model complexity and improve efficiency, while heterogeneous effects should be modeled by distinct parameters for different studies to build accurate models. Methods for discovering heterogeneity in variable’s effects include examining its interactions with the study-membership indicator variables or the heterogeneity statistics such as Cochran’s Q and I², but these often have low power especially when the number of studies is small and the number of predictors is large (Hedges and Olkin, 1985).

In this paper, we consider the heterogeneity issue in pooled studies with time-to-event endpoint, and formulate the problem in the framework of group variable selection. Specifically, we treat a variable’s effects across studies as a group and aim to classify the variables into three categories according to their effects: homogeneous, heterogeneous, and null. Group penalty regularized methods have been proposed to select variables with pre-specified group structure (Kim et al., 2012; Ma et al., 2007), and the composite absolute penalties (CAP) of Zhao et al. (2009) could accommodate complex group structures. Recently, Liu et al. (2013) investigated the use of adaptive CAP regularized partial likelihood estimation in the context of pooled nested case-control studies with heterogeneity. These methods, however, cannot delineate variables into the desirable categories.

Inspired by some recent developments in structure identification in the partially linear model (Zhang et al., 2011) and the time-varying Cox model (Yan and Huang, 2012), we employ the adaptively weighted L₁ and L₁/L₂ penalties on variables’ average effects and heterogeneous effects respectively, and propose a penalized partial likelihood approach to characterize the variables’ heterogeneity and simultaneously estimate variables’ effects. We establish asymptotic results for the proposed estimator when the number of parameters is fixed and also when it diverges with the sample size. The rest of the article is organized as follows. We introduce the composite L₁ + L₁/L₂ penalty regularized partial likelihood approach and the computation algorithm in Section 2. We also establish the theoretical properties of our proposed estimator, with the proofs provided in the Web Appendix. Section 3 contains numerical simulations and real study applications in the pooled ovarian cancer study. Section 4 gives concluding remarks.

2. Regularized Method for Identifying Homogeneous and Heterogeneity Variables

2.1 Penalized partial likelihood function

We consider a pooled study consisting of K sub-studies, with n_k subjects in study k and ${\sum }_{k=1}^K{n}_k=n$. Let $T_{ki}^{*}$ and C_ki be the failure time and censoring time for the ith subject in study k. Define the observed event time $T_{ki}=\text{min}(T_{ki}^{*},C_{ki})$, and the occurrence indicator of the failure event ${\delta }_{ki}=I(T_{ki}^{*}<C_{ki})$. We assume a Cox proportional hazards model for $T_{ki}^{*}$:

$${\lambda }_k\{t|Z_{ki}\}={\lambda }_{0k}(t)\text{ exp}\{{\beta }_k^{\prime }{Z}_{ki}\},k=1,\dots ,K,$$ (1)

where λ_0k(·) is the baseline hazard function, and β_k = (β_k1, …, β_kp)′ is a p × 1 vector characterizing the effects of covariates Z in study k. For the pooled study data under model (1), the log partial likelihood is expressed as

$$\ell ({\beta }_1,\dots ,{\beta }_K)=\sum _{k=1}^K\sum _{i=1}^{n_k}{\delta }_{ki}[{\beta }_k^{\prime }{Z}_{ki}-\text{log}\{\sum _{j=1}^{n_k}I(T_{kj}>=T_{ki})\text{ exp}({\beta }_k^{\prime }{Z}_{kj})\}].$$

To separate out homogeneous and heterogeneous effects, we reformulate model (1) into

$${\lambda }_k\{t|Z_{ki}\}={\lambda }_{0k}(t)\text{ exp}(\mu \prime Z_{ki}+({\beta }_k-\mu )\prime Z_{ki}\}\triangleq {\lambda }_{0k}(t)\text{ exp}\{\mu \prime Z_{ki}+{\alpha }_{k·}^{\prime }{Z}_{ki}\},$$

where μ = (μ₁, …, μ_p)′ denotes the average effects and α_k· = (α_k1, …, α_kp)′ denotes the deviance of effects in study k from the average effects μ. To accommodate the constraint that, for each covariate l, l = 1, …, p, ${\sum }_{k=1}^K{\alpha }_{kl}=0$, we denote α_l = (α_2l, …, α_Kl)′ and work with $\theta =(\mu \prime ,{\alpha }_1^{\prime },\dots ,{\alpha }_p^{\prime })\prime$. We classify p predictors into three mutually exclusive categories: (1) homogeneous effects if μ_l ≠ 0 and the Euclidean norm of α_l: ‖α_l‖ = 0; (2) heterogeneous effects if ‖α_l‖ ≠ 0; (3) null effects if μ_l = 0 and ‖α_l‖ = 0. To estimate this homogeneous and heterogeneous structure, we propose the following composite penalty regularized partial likelihood estimator

$$\hat{\theta }=\text{arg min }{Q}_n(\theta )=\text{arg min}\{-\ell (\theta )+{\lambda }_{1n}\sum _{l=1}^p{\omega }_{0l}|{\mu }_l|+{\lambda }_{2n}\sum _{l=1}^p{\omega }_{1l}\Vert {\alpha }_l\Vert \},$$ (2)

where ω_0l and ω_1l are data-dependent weights and here chosen as ω_0l = 1/|μ̃_l|, ω_1l = 1/‖α̃_l‖, where (μ̃_l, α̃_l) are some initial root-n consistent estimators.

2.2 Computation algorithm

We use the iterative shooting algorithm (Fu, 1998; Zhang and Lu, 2007) to minimize Q_n(θ) in (2). Let G = −∂ℓ/∂θ, H = −∂²ℓ/∂θ∂θ′, and X′X be the Cholesky decomposition of H. By defining a pseudo response vector Y = (X′)⁻¹{Hθ − G}, we can approximate −ℓ(θ) by a quadratic form $\frac{1}{2}(Y-X\theta )\prime (Y-X\theta )$. Furthermore, we consider the L₁ norm as a special case of the Euclidean norm with one element and rewrite the composite penalty terms in (2) as an adaptive group lasso problem with 2p groups

$$\frac{1}{2}(Y-X\theta )\prime (Y-X\theta )+\sum _{g=1}^{2p}{\lambda }_g\Vert {\theta }_g\Vert ,$$ (3)

where θ_g = μ_g and λ_g = λ_1nω_0g for g = 1, …, p and θ_g = α_g and λ_g = λ_2nω_1g for g = (p+1), …, 2p.

By the Karush–Kuhn–Tucker condition, Yuan and Lin (2006) showed that the necessary and sufficient condition for θ to be a solution of (3) is

$$-X_g^{\prime }(Y-X\theta )+{\lambda }_g{\theta }_g/\Vert {\theta }_g\Vert =0,{\theta }_g\ne 0;$$ (4)

$$\Vert -X_g^{\prime }(Y-X\theta )\Vert \le {\lambda }_g,{\theta }_g=0.$$ (5)

Note that the condition (4) is equivalent to

$$S_g=(X_g^{\prime }{X}_g+{\lambda }_g{\theta }_g/\Vert {\theta }_g\Vert I_{d_g}){\theta }_g,$$ (6)

where $S_g=X_g^{\prime }(Y-X{\theta }_{-g})$, with ${\theta }_{-g}=({\theta }_1^{\prime },\dots ,{\theta }_{g-1}^{\prime },0,{\theta }_{g+1}^{\prime },{\theta }_{2p}^{\prime })\prime$, I_dg is the identity matrix of dimension d_g, and d_g is the number of parameters in group g. Thus, our shooting algorithm is:

1. Initialize with θ⁽⁰⁾.

2. For each g = 1, …, 2p, if θ_g = 0, then it stays at 0. Otherwise, update θ_g with

   $${\theta }_g=\{\begin{array}{cc}{(X_g^{\prime }{X}_g+{\lambda }_g/\Vert {\theta }_g\Vert )}^{-1}{S}_g,\hfill & \text{if}\Vert S_g\Vert >{\lambda }_g;\hfill \\ 0,\hfill & \text{if}\Vert S_g\Vert \le {\lambda }_g.\hfill \end{array}$$

3. Update θ with the new θ_g, and repeat until convergence.

We choose the tuning parameters λ_1n and λ_2n over a two-dimensional grid by minimizing the Bayesian information criterion (BIC),

$$\mathrm{B}\mathrm{I}\mathrm{C}(\hat{\theta })=-\ell (\hat{\theta })+\text{log}(n)\times df,$$

where $\hat{\theta }=({\hat{\mu }}_l^{\prime },{\hat{\alpha }}_l^{\prime })\prime$ is a minimizer of (2) under λ_1n and λ_2n, and the degree of freedom (d f) is defined following Yuan and Lin (2006), $df={\sum }_{l=1}^{p}I(|{\hat{\mu }}_l|>0)+{\sum }_{l=1}^{p}I(\Vert {\hat{\alpha }}_l\Vert >0)+(K-2){\sum }_{l=l}^p\Vert {\hat{\alpha }}_l\Vert /\Vert {\tilde{\alpha }}_l\Vert$. The BIC-based tuning parameter selection corresponds to maximizing the posterior probability of selecting the true model and has been shown to be consistent for model selection in various settings (Wang et al., 2007; Zhang et al., 2010). Our simulation experiences also support the use of the BIC-based selection method.

Following Fan and Li (2001), we estimate the covariance of θ̃ by

$$\widehat{\text{COV}}(\hat{\theta })={\left\{{(H+\mathrm{\Sigma })}^{-1}H{(H+\mathrm{\Sigma })}^{-1}\right\}|}_{\hat{\theta }},$$ (7)

where Σ = diag{λ_g/‖θ_g‖I_dg }_{g=1, …, 2p}.

2.3 Theoretical properties

Denote the true parameters by ${\theta }_n^{*}$, where we use the general notation with the subscript n to allow the number of parameters (p_n) to go to infinity as the sample size n increases. Let q_n = Kp_n be the total number of parameters. Define 𝒜_1n = {l : μ_l ≠ 0, l = 1, …, p_n}, 𝒜_2n = {l : ‖α_l‖ ≠ 0, l = 1, …, p_n}, and 𝒜_n = 𝒜_1n ∪ 𝒜_2n. The total number of parameters corresponding to 𝒜_n is s_n = |𝒜_1n| + (K − 1) × |𝒜_2n|. Under the regularity conditions specified in Web Appendix, the following asymptotic properties hold.

Theorem 1 (Estimation Consistency)

If ${\lambda }_{1n}/\sqrt{n}\to 0,{\lambda }_{2n}/\sqrt{n}\to 0$, and $q_n^4/n\to 0$, then $\Vert {\hat{\theta }}_n-{\theta }_n^{*}\Vert =O_p\{{(n/q_n)}^{-1/2}\}$.

Theorem 2 (Selection Consistency)

If λ_1n/q_n → ∞ and λ_2n/q_n → ∞, then $P({\hat{\theta }}_{{𝒜}_n^c}=0)\to 1$.

Because the dimension of θ̂_𝒜n may diverge as sample size goes to infinity, for asymptotic normality property below, we consider its arbitrary linear combination B_nθ̂_𝒜n, where B_n is an arbitrary m × s_n matrix with a finite m and $B_n{B}_n^{\prime }\to G$ and G is positive-definite.

Theorem 3 (Asymptotic Normality)

If ${\lambda }_{1n}/\sqrt{n/g_n}\to 0,{\lambda }_{2n}/\sqrt{n/g_n}\to 0$, λ_1n/q_n → ∞, λ_2n/q_n → ∞, and $q_n^4/n\to 0$, then

$$\sqrt{n}{B}_n{I}_{{𝒜}_n}^{1/2}({\hat{\theta }}_{{𝒜}_n}-{\theta }_{{𝒜}_n}^{*}){\to }_{d}N(0,G),$$

where I_𝒜n is the Fisher information matrix corresponding to ${\theta }_{{𝒜}_n}^{*}$.

Therefore, as the sample size goes to infinity, the proposed estimator θ̂_n in (2) can perform as well as the correct model when that correct model is known in advance. Proofs are given in Web Appendix.

3. Numerical Studies

3.1 Simulations

We conducted simulations to evaluate the performance of our method under practical settings and compared it with four methods including the maximum likelihood estimation (MLE) method, the two-step method (two-step) with the random-effects model (DerSimonian and Laird, 1986), and the penalized partial likelihood methods with adaptive group Lasso (agLASSO) penalty (Yuan and Lin, 2006; Kim et al., 2012) and adaptive composite absolute (aCAP) penalty (Zhao et al., 2009; Liu et al., 2013). For the MLE method, we obtained the study-specific effects and checked whether the average effect and the heterogeneous effects of each variable were significantly different from 0. In the two-step method, we used Cochran’s Q-test to examine the heterogeneity. The agLASSO method imposed a weighted L₂ penalty on the group of coefficients consisting of each variable’s effects across studies. The aCAP approach imposed a weighted composite penalty as ${\lambda }_{1n}{\sum }_{l=1}^p{\omega }_{0l}\Vert ({\mu }_l,{\alpha }_l)\Vert +{\lambda }_{2n}{\sum }_{l=1}^p{\omega }_{1l}\Vert {\alpha }_l\Vert$.

3.1.1 Example 1: fixed number of covariates

We first considered a pooled study with 3 sub-studies of size N = 150 or 300, and generated 11 covariates from a multivariate normal distribution with mean 0 and covariance cov(z_i, z_j) = 0.5^|i−j|. The survival times were generated using the Cox proportional hazards model (1) with the Weibull distribution (shape= 10, scale = 1) determining the baseline hazard. The true θ* was specified as follows:

$${\theta }^{*}=\left(\begin{array}{c}\hfill \mu \hfill \\ \hfill {\alpha }_{2·}^{\prime }\hfill \\ \hfill {\alpha }_{3·}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ccccccccccc}\hfill Z_1\hfill & \hfill Z_2\hfill & \hfill Z_3\hfill & \hfill Z_4\hfill & \hfill Z_5\hfill & \hfill Z_6\hfill & \hfill Z_7\hfill & \hfill Z_8\hfill & \hfill Z_9\hfill & \hfill Z_{10}\hfill & \hfill Z_{11}\hfill \\ \hfill 0.6\hfill & \hfill 0.4\hfill & \hfill 0.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.6\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -0.4\hfill & \hfill -0.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -0.4\hfill & \hfill 0.4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -0.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).$$

Thus, covariates Z₁ and Z₇ had homogenous effects, Z₂, Z₃, and Z₈ had heterogeneous effects, and the rest were null variables. Censoring times were generated from the uniform distributions [0, 1.28] or [0, 1.77] to yield event rates around 25% or 45%.

Tables 1 – 4 report the simulation results. Table 1 reports the average numbers of correctly and incorrectly selected homogeneous and heterogeneous variables over 200 simulations. We use the square root of mean square errors (E‖θ̂ − θ*‖²)^1/2 (rMSE) to measure the estimation error. Our method performs very well for identifying the correct structure in all scenarios and outperforms all other methods in terms of having the smallest rMSE. Its overall performance improves with increasing sample size. When the sample size increases to 300, with an event rate of 45%, the average number of correctly identified homogeneous variables by the proposed method is 1.96, and the average number of correctly identified heterogeneous variables is 3. The agLASSO method is only capable of identifying the non-zero group of coefficients, and cannot differentiate homogenous from non-homogenous effects. The random-effects model gives a large estimation error as the method cannot estimate the study-specific effects for each variable.

Table 1.

Simulation results on variable selection and root mean square errors in Example 1.

		25% event rate					45% event rate
		Homo	Homo	Hetero	Hetero		Homo	Homo	Hetero	Hetero
N	Method	Corr (2)	Incorr (0)	Corr (3)	Incorr (0)	rMSE	Corr (2)	Incorr (0)	Corr (3)	Incorr (0)	rMSE
150	our method	1.9	0.69	2.37	0.31	0.83	1.93	0.3	2.84	0.26	0.57
	agLASSO	0	0	2.63	2.25	0.87	0	0	2.93	2.21	0.62
	aCAP	1.76	0.55	1.96	0.35	0.98	1.76	0.44	2.41	0.35	0.79
	two-step	1.78	0.60	2.41	0.74	1.39	1.84	0.41	2.89	0.61	1.30
	MLE	1.67	0.68	2.63	1.24	1.42	1.72	0.43	2.94	1.02	0.93
300	our method	1.94	0.14	2.95	0.27	0.48	1.96	0.06	3.00	0.16	0.35
	agLASSO	0	0	2.98	2.16	0.54	0	0	3	2.14	0.40
	aCAP	1.77	0.28	2.55	0.3	0.70	1.84	0.29	2.57	0.21	0.64
	two-step	1.85	0.25	2.97	0.57	1.27	1.87	0.31	3	0.51	1.25
	MLE	1.75	0.30	3	0.87	0.79	1.80	0.35	3.00	0.89	0.55

Homo/Hetero Corr: average numbers of correct homogeneous/heterogeneous effects; Homo/Hetero Incorr: average numbers of incorrect homogeneous/heterogeneous effects; rMSE: root mean square errors.

Table 4.

Simulation results on variable selection and root mean square errors in Example 2 with cohort size of 200 and 40% event rate.

		Homo	Homo	Hetero	Hetero
ρ	p	Corr (8)	Incorr (0)	Corr (10)	Incorr (0)	rMSE
0.5	250	6.92	0.96	9.81	1.58	1.86
	450	6.87	1.03	9.75	1.56	1.90
0.75	250	6.52	0.38	9.61	2.02	2.02
	450	6.31	0.41	9.62	2.31	2.05

Homo/Hetero Corr: average numbers of correct homogeneous/heterogeneous effects; Homo/Hetero Incorr: average numbers of incorrect homogeneous/heterogeneous effects; rMSE: root mean square errors

Table 2 presents the detection frequencies of each variable’s average and heterogeneous effects under the scenario with 45% event rate and N = 300 in each study. Our method identifies all variables’ structure with good accuracy. The agLASSO method cannot differentiate between the average effect and heterogeneous effects, and always selects the variable as long as it has at least one non-zero effect, e.g. Z₁ and Z₇. The aCAP also shows a reasonable performance except for variable Z₈, which has zero mean effect but non-zero heterogeneous effects. The two-step method fails to identify the non-zero average effect of variable Z₂, because Z₂ has a small average effect size, and the heterogeneity of the effects of Z₂ is captured with a large variance estimated by the random-effects model. Because of the collinearity between variables, the MLE method does not perform well for variables with null effects. Similar results are observed in other scenarios.

Table 2.

Simulation results on the frequency of identifying nonzero mean effect and heterogeneous effects for each variable in Example 1 with cohort size of 300 and 45% event rate.

		Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9	Z10	Z11
		200 0	200 200	200 200	0 0	0 0	0 0	200 0	0 200	0 0	0 0	0 0
Method	Structure
our method	μ ≠ 0	200	200	200	2	3	2	200	1	1	0	4
	α ≠ 0	2	200	200	3	5	3	6	200	2	7	3
agLASSO	μ ≠ 0	200	200	200	1	9	5	200	200	4	6	3
	α ≠ 0	200	200	200	1	9	5	200	200	4	6	3
aCAP	μ ≠ 0	200	199	200	15	18	11	200	114	10	8	6
	α ≠ 0	9	199	200	2	4	1	24	114	1	1	1
two-step	μ ≠ 0	200	0	119	14	16	7	200	0	5	13	7
	α ≠ 0	7	200	200	14	15	14	20	200	8	13	11
MLE	μ ≠ 0	200	200	200	15	21	11	200	10	8	15	14
	α ≠ 0	19	200	200	27	25	18	22	200	15	25	25

Table 3 presents the estimated standard errors for covariates Z₁, Z₂, and Z₈ based on the sandwich formula (7), and compares them with the sample standard deviations calculated from 200 iterations. The empirical variance estimates and asymptotic estimates show some discrepancies in these finite-sample settings, but the overall performance improves with the sample size.

Table 3.

Simulation results on the estimated standard error and sample standard deviation (in the parenthesis) of estimators for selected variables in Example 1 with cohort size of 300 and 45% event rate.

		variable 1	variable 2			variable 8
N	Method	μ1	μ2	α22	α32	α28	α38
150	our method	0.083(0.109)	0.086(0.131)	0.099(0.135)	0.099(0.130)	0.088(0.140)	0.084(0.124)
	agLASSO	0.073(0.119)	0.090(0.118)	0.122(0.139)	0.122(0.146)	0.078(0.144)	0.077(0.130)
	aCAP	0.082(0.121)	0.093(0.114)	0.093(0.115)	0.093(0.105)	0.090(0.138)	0.088(0.122)
	MLE	0.107(0.126)	0.124(0.144)	0.165(0.199)	0.165(0.191)	0.161(0.187)	0.161(0.162)
300	our method	0.059(0.068)	0.063(0.077)	0.077(0.082)	0.077(0.086)	0.068(0.088)	0.065(0.083)
	agLASSO	0.056(0.072)	0.067(0.072)	0.090(0.083)	0.090(0.086)	0.065(0.099)	0.064(0.095)
	aCAP	0.058(0.069)	0.067(0.079)	0.073(0.072)	0.073(0.072)	0.065(0.093)	0.064(0.083)
	MLE	0.068(0.072)	0.079(0.080)	0.106(0.104)	0.106(0.101)	0.103(0.105)	0.103(0.103)

3.1.2 Example 2: diverging number of covariates p > N

We still considered pooling 3 studies, with each study size of N = 200. The number of covariates was set to be p = 250 or 450, and the covariate vector was generated from the multivariate normal distribution with mean 0 and covariance cov(z_i, z_j) = ρ^|i−j|, ρ = 0.5 or 0.75. The survival times were generated from the Cox proportional hazards model with a constant baseline hazard function λ₀(t) = 0.1 and the true coefficients θ* were specified as follows:

$${\theta }^{*}=\left(\begin{array}{c}\hfill \mu \hfill \\ \hfill {\alpha }_{2·}\hfill \\ \hfill {\alpha }_{3·}\hfill \end{array}\right)=\left(\begin{array}{cccc}\hfill Z_{1,\cdots ,8}\hfill & \hfill Z_{9,\cdots ,13}\hfill & \hfill Z_{14,\cdots ,18}\hfill & \hfill Z_{19,\cdots ,p}\hfill \\ \hfill 1.5·{\mathbf{1}}_8\hfill & \hfill 1·{\mathbf{1}}_5\hfill & \hfill 0.5·{\mathbf{1}}_5\hfill & \hfill {\mathbf{0}}_{p-18}\hfill \\ \hfill {\mathbf{0}}_8\hfill & \hfill 1·{\mathbf{1}}_5\hfill & \hfill -0.5·{\mathbf{1}}_5\hfill & \hfill {\mathbf{0}}_{p-18}\hfill \\ \hfill {\mathbf{0}}_8\hfill & \hfill -1·{\mathbf{1}}_5\hfill & \hfill 0.5·{\mathbf{1}}_5\hfill & \hfill {\mathbf{0}}_{p-18}\hfill \end{array}\right),$$

where a_m denotes a m-vector of a’s. Therefore, covariates Z₁ to Z₈ had homogeneous effects, Z₉ to Z₁₈ had heterogeneous effects, and the rest were null variables. Censoring times were generated from the uniform distribution U(0, 2) to yield the event rate around 40% in each cohort. Table 4 reports the average numbers of correctly and incorrectly selected homogeneous and heterogeneous variables by our method and the rMSE over 200 replicates. Our results show that the proposed method achieves good accuracy in identifying the homogeneous and heterogeneous effects and maintains low error rates when the number of covariates is greater than the sample size.

3.2 Pooled ovarian cancer study

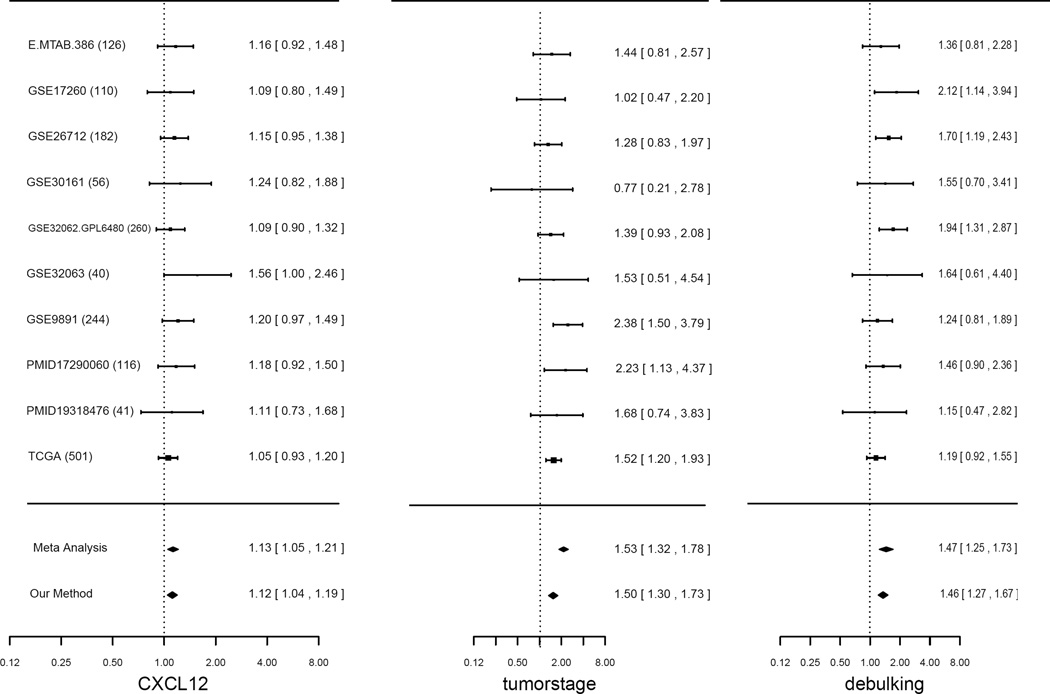
Using the pooled data from 1676 patients from 10 studies, which had complete information on tumor stage and debulking surgery, Ganzfried et al. (2013) found that the expression level of chemokine CXCL12 was associated with patient survival, which was not detected in individual studies due to insufficient power. We first examined whether the three variables CXCL12, tumor stage and debulking were homogeneous across studies, and applied our method and the meta-analysis method with random-effects model respectively. Both methods identified all three variables as homogeneous variables and yielded similar results on effect estimation. Figure 1 shows the forest plot of hazard ratios (HRs) of the variables.

Figure 1.

Forest plot of the hazard ratio estimates of variables CXCL12, tumorstage, debulking from the pooled ovarian cancer study with 10 sub-studies. The study names are listed at the left and study sizes are given in the parentheses. Three vertical dash lines are reference lines of the hazard ratio being 1.

To further study the association between other genetic variables and survival, we examined 21 candidate genes related to breast and ovarian cancer according to the reports from the National Cancer Institute (http://www.cancer.gov/cancer topics/pdq/genetics/breast-and-ovarian/HealthProfessional), which are CXCL12, CXCR4, RAD51C, RAD51, BABAM1, MLH1, MSH2, MSH6, TP53, HOXD1, CHEK2, HOXD3, CASP8, IRS1, TIPARP, PLEKHM1, BNC2, SKAP1, CERS6, BRCA1, and BRCA2. We also included three clinical variables: tumor stage, debulking, and age at initial pathologic diagnosis. The pooled analysis was conducted in 1053 patients from 4 studies in the database, with study size over 100 and complete information on the genetic and clinical variables. Table 5 reports the estimated coefficients by our method and the meta-analysis. The proposed method identified no heterogeneous variables, supporting the quality of data curation by Ganzfried et al. (2013).We found that clinical variables age, tumor stage, and debulking still remained as important risk factors associated with ovarian cancer, and identified important genetic biomarkers including BNC2, BRCA2, CASP8, CXCL12, CXCR4, HOXD1, and IRS1 (Goode et al., 2010; Welcsh and King, 2001; Ding et al., 2012; Kajiyama et al., 2008; Ma et al., 2011). The meta-analysis method also identified 6 out of these 10 variables as important factors with no heterogeneity, with the remaining 4 variables being non-significant, which resembled our findings in the simulation study that the meta-analysis can be of low power for small average effects. The remaining 14 variables were classified as null variables by our method, 11 of which were concluded the same by the meta-analysis method.

Table 5.

Estimates of the log hazard ratios of genetic and clinical variables in the pooled ovarian cancer study.

Variable	Our method	Two-step
age	0.022(0.004)	0.026(0.006)*
tumor stage	0.455(0.085)	0.536(0.100)*
debulking	0.248(0.071)	0.297(0.157)
BNC2	0.076(0.030)	0.145(0.058)*
BRCA2	0.140(0.036)	0.183(0.049)*
CASP8	−0.061(0.030)	−0.138(0.074)
CXCL12	0.042(0.026)	0.089(0.055)
CXCR4	−0.098(0.034)	−0.118(0.051)*
HOXD1	−0.011(0.015)	−0.111(0.137)
IRS1	0.072(0.029)	0.158(0.057)
BABAM1	0(−)	−0.075(0.131) +
BRCA1	0(−)	0.024(0.054)
CERS6	0(−)	−0.014(0.100)
CHEK2	0(−)	−0.023(0.102)
HOXD3	0(−)	0.072(0.072)
MSH2	0(−)	0.126(0.083)
MSH6	0(−)	−0.159(0.072)*
MLH1	0(−)	−0.018(0.051)
PLEKHM1	0(−)	0.034(0.055)
RAD51	0(−)	0.108(0.067)
RAD51C	0(−)	0.017(0.099)+
SKAP1	0(−)	0.020(0.052)
TIPARP	0(−)	0.017(0.086)
TP53	0(−)	−0.014(0.058)

^*denotes nonzero average effects;

⁺denotes nonzero heterogeneous effects with random-effects model; Standard errors are reported in the parentheses.

4. Discussion

In this article, we address the question of identifying variables’ homogeneous and heterogeneous effects on a time-to-event outcome in pooled studies using a group variable selection approach based on penalized regression. The proposed method requires that each study has the same predictors in the pooled studies. We establish the theoretical properties and show good numerical performances of the proposed method. In practice, to better estimate the variables’ effects, we could refit the data using the variables and their homogeneous/heterogeneous structure identified by our method, or we could randomly partition the data into two parts, one part of which is to detect heterogeneity and the other part for estimating effects. Also note that the proposed method can be easily extended to linear models and generalized linear models.

When the number of covariates diverges with the sample size, we establish the convergence rate of $p_n^4/n\to 0$ following Cai et al. (2005). More recently, Huang et al. (2013) established the oracle inequalities in the p_n ≫ n sparse Cox model setting, which may potentially be applicable to our context and needs further investigation.

For tuning parameter selection, it is well known that the generalized cross validation (GCV) and AIC-based methods may select irrelevant predictors with a non-vanishing probability as n → ∞ (Wang et al., 2007). The BIC-based selection of tuning parameters to select models is consistent for model selection in various settings (Wang et al., 2007; Zhang et al., 2010). The log partial likelihood of the Cox proportional hazards model can be quadratically approximated so that the optimization is conducted in a similar fashion to the least-square setting, which supports the use of BIC for our proposed method. The cross-validation score approximating the Kullback-Leibler divergence can also be used to select the tuning parameter (Du et al., 2010), but needs further investigation when both n and p tend to infinity.