Abstract
In this chapter, we describe how to create mathematical models of synaptic transmission and integration. We start with a brief synopsis of the experimental evidence underlying our current understanding of synaptic transmission. We then describe synaptic transmission at a particular glutamatergic synapse in the mammalian cerebellum, the mossy fiber to granule cell synapse, since data from this well-characterized synapse can provide a benchmark comparison for how well synaptic properties are captured by different mathematical models. This chapter is structured by first presenting the simplest mathematical description of an average synaptic conductance waveform and then introducing methods for incorporating more complex synaptic properties such as nonlinear voltage dependence of ionotropic receptors, short-term plasticity, and stochastic fluctuations. We restrict our focus to excitatory synaptic transmission, but most of the modeling approaches discussed here can be equally applied to inhibitory synapses. Our data-driven approach will be of interest to those wishing to model synaptic transmission and network behavior in health and disease.
1. INTRODUCTION
1.1. A brief history of synaptic transmission
Some of the first intracellular voltage recordings from the neuromuscular junction (NMJ) revealed the presence of spontaneous miniature end plate potentials with fast rise and slower decay kinetics.1 The similarity of these “mini” events to the smallest events evoked by nerve stimulation, together with the discrete nature of the fluctuations in the amplitude of the end plate potentials,2 lead to the hypothesis that transmitter was released probabilistically in discrete all-or-none units called “quanta,”3 units that were subsequently shown to be vesicles containing neurotransmitter. The quantum hypothesis is an elegantly simple yet extremely powerful statistical model of transmitter release: the average number of quanta released at a synapse per stimulus (quantal content, m) is simply the product of the total number of quanta available for release (NT) and their release probability (P):
| (13.1) |
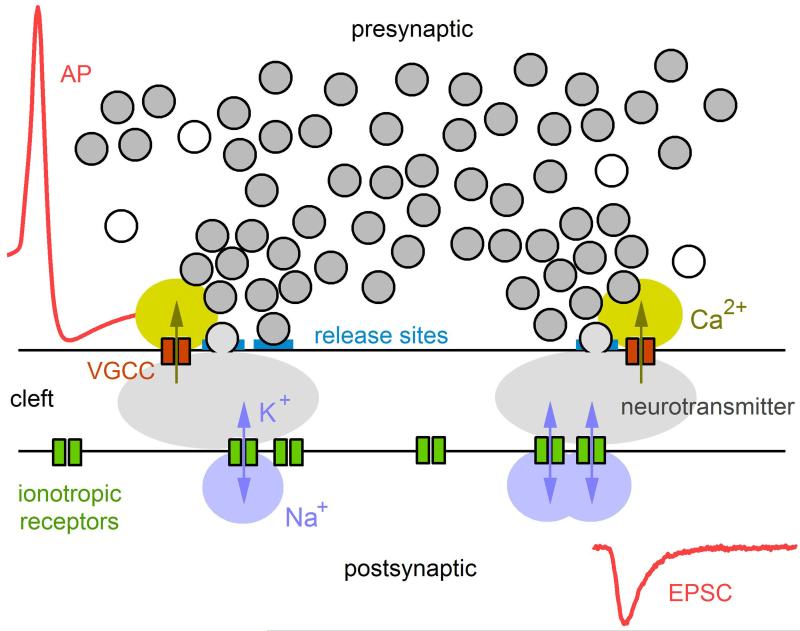
Quantitative comparison of the predictions of the quantum hypothesis against experimental measurements confirmed the hypothesis,3 albeit under nonphysiological conditions of low release probabilities. Subsequent electron micrograph studies revealed presynaptic vesicles clustered at active zones,4–7 providing compelling morphological equivalents for the quanta and their specialized release sites. Other work around the same time revealed the dynamic nature of synaptic transmission at the NMJ, providing the first concepts for activity-dependent short-term changes in synaptic strength.8,9 Further work by Katz and colleagues lead to the concept of Ca2+-dependent vesicular release and the refinement of ideas regarding the activation of post-synaptic receptors.3 Together, this early body of work on the NMJ provided the basis for our current understanding of the intricate signaling cascade underlying synaptic transmission. The basic mechanisms underlying synaptic transmission are summarized in Fig. 13.1: an action potential, propagating down the axon of the presynaptic neuron, invades synaptic terminals. The brief depolarization of the terminals causes voltage-gated Ca2+ channels (VGCCs) to open, leading to Ca2+ influx and a transient increase in the intracellular Ca2+ concentration ([Ca]i) in the vicinity of the VGCCs. For those vesicles docked at a release site near one or more VGCCs, the local increase in [Ca]i triggers the vesicles to fuse with the terminal membrane and release their content of neurotransmitter into the synaptic cleft. The released neurotransmitter diffuses across the narrow synaptic cleft and binds to post-synaptic ionotropic receptors, transiently increasing their open probability. The resulting flow of Na+ and K+ through the receptors’ ion channels results in an excitatory postsynaptic potential (EPSP) or excitatory postsynaptic current (EPSC) depending on whether the intracellular recording is made under a current- or voltage-clamp configuration.
Figure 13.1. Cartoon illustrating the basic sequence of events underlying synaptic transmission.
The sequence starts with an action potential (AP) invading a presynaptic terminal, leading to the opening of voltage-gated Ca2+ channels (VGCCs), some of which are located near vesicle release sites within one or more active zones. For those release sites containing a readily releasable vesicle, the local rise in [Ca2+]i causes the fusion of the vesicle with the terminal’s membrane, resulting in the release of neurotransmitter packed inside the vesicle. The neurotransmitter diffuses across the synaptic cleft to reach the postsynaptic membrane where it binds to ionotropic receptors, causing the channels to open and pass Na+ and K+. The permeation of these ions through the ionotropic receptors leads to a local injection of current, known as the EPSC. The EPSC often contains fast and slow components due to the fast activation of receptors immediately opposite to the vesicle release site and the slower activation of receptors further away (i.e., extrasynaptic). Kinetics of the EPSC will also depend on the receptor’s affinity for the neurotransmitter and the receptor’s gating properties, which may include blocked and desensitization states.
Some 20 years after the early work on the NMJ, development of the patch-clamp method increased the signal-to-noise ratio of electrophysiological recordings by several orders of magnitude over traditional sharp-electrode recordings.10 The patch-clamp method not only confirmed the existence of individual ion channels but also enabled resolution of significantly smaller EPSCs, thereby paving the way for studies of synaptic transmission in the central nervous system (CNS). Although these studies revealed the basic mechanisms underlying synaptic transmission are largely similar at the NMJ and in the brain (Fig. 13.1), there are a number of key differences. For example, whereas synaptic transmission in the NMJ is mediated by the release of 100–1000 vesicles2 at highly elongated active zones,11 synaptic transmission between neurons in the brain is typically mediated by the release of just a few vesicles at a handful of small active zones.12,13 The number of postsynaptic receptors is also quite different: vesicle release activates thousands of postsynaptic receptors in the NMJ14 but only a few (~10–100) at central excitatory synapses.15,16 These differences in scale link directly to synaptic function: the large potentials generated at the NMJ ensure a reliable relay of motor command signals from presynaptic neuron to postsynaptic muscle. In contrast, the much smaller potentials generated by central synapses require spatiotemporal summation in order to trigger action potentials.
Another important distinction between the NMJ and central synapses is the difference in neurotransmitter (acetylcholine at the NMJ vs. glutamate, GABA, glycine, etc., in the CNS) and the diversity in postsynaptic receptors and their function. Here we focus on excitatory central synapses, where two major classes of ionotropic glutamate receptors, AMPA and NMDA receptors (AMPARs and NMDARs), are colocalized.17,18 These two receptor types have different gating kinetics and current–voltage relations and therefore play distinct roles in synaptic transmission. The majority of AMPARs, for example, have relatively fast kinetics and a linear (ohmic) current–voltage relation, often expressed as:
| (13.2) |
where V is the membrane potential and EAMPAR is the reversal potential of the AMPAR conductance (GAMPAR), which is typically 0 mV. Both of these properties, i.e., fast kinetics and a linear current–voltage relation, make AMPARs well suited for mediating temporally precise signaling and setting synaptic weight. NMDARs, in contrast, have slower kinetics and a nonlinear current–voltage relation, the latter caused by Mg2+ block at hyperpolarized potentials.19 These properties make NMDARs well suited for coincidence detection and plasticity, since presynaptic glutamate release and postsynaptic depolarization are required for NMDAR activation.20 Certain subtypes of NMDARs, however, show a weaker Mg2+ block (i.e., those containing the GluN2C and GluN2D subunits) and therefore create substantial synaptic current at hyperpolarized potentials.21,22 These types of NMDARs are thought to enhance synaptic transmission by enabling temporal integration of low-frequency inputs.22 Of course, numerous other differences exist between the NMJ and central synapses, including those pertaining to stochasticity- and time-dependent plasticity. These are discussed further in the next section where we introduce the MF-to-GC synapse, our synapse of choice for providing accurate data for the synaptic models presented in this chapter.
1.2. The cerebellar MF–GC synapse as an experimental model system
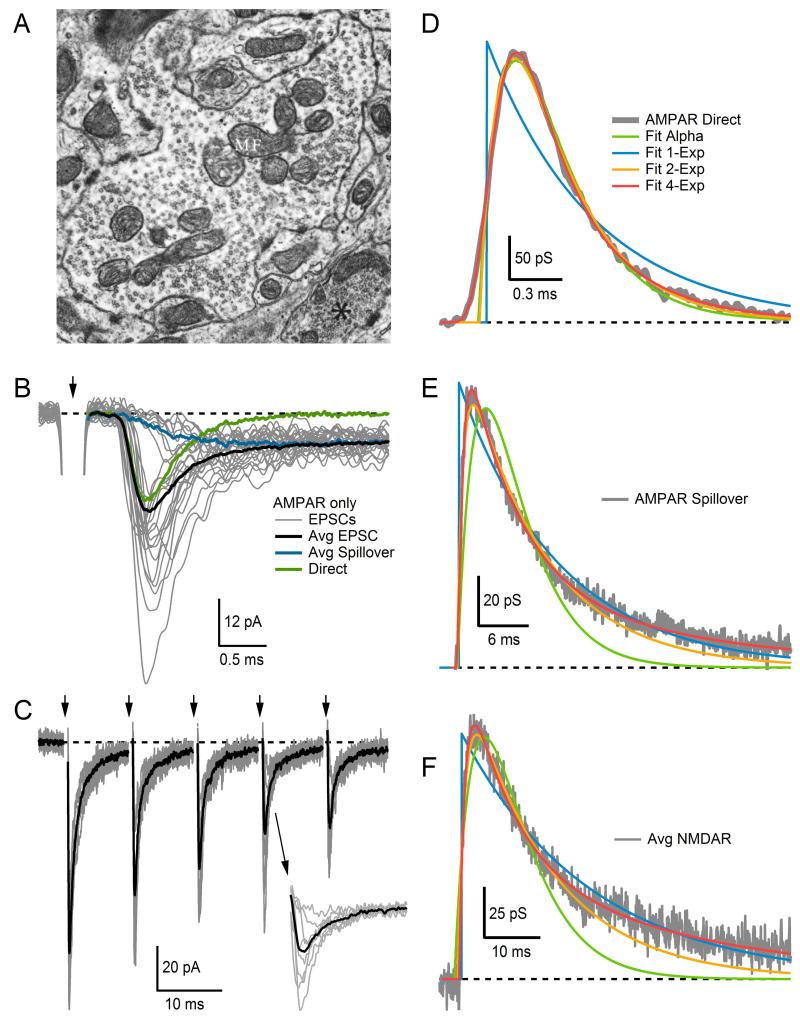
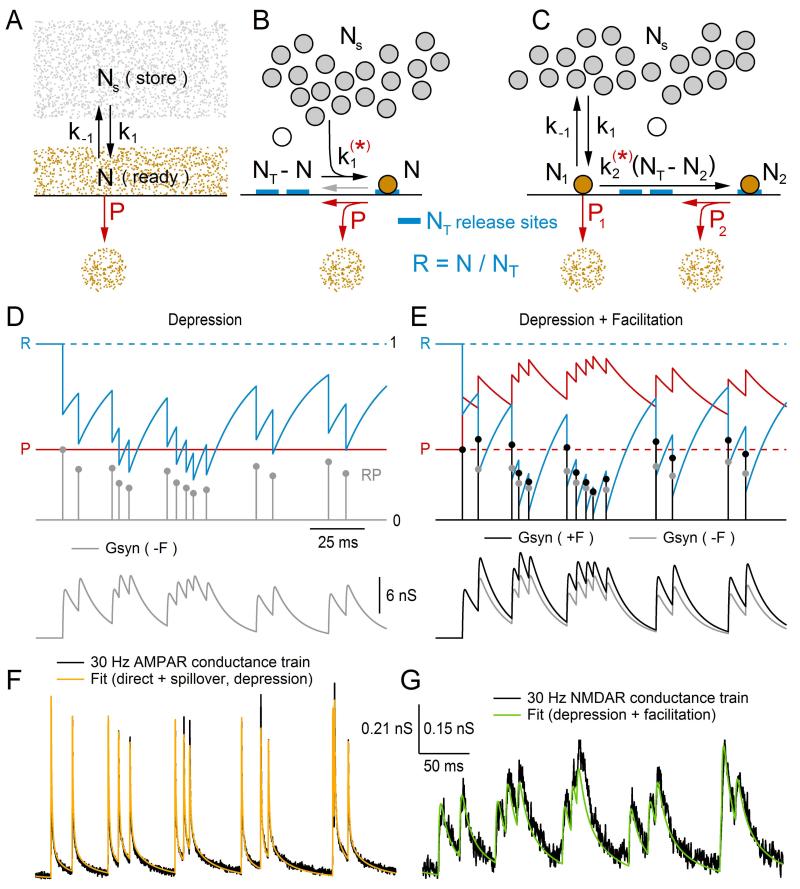
The input layer of the cerebellum receives sensory and motor signals via MFs23 which form large en passant synapses, each of which contacts several GCs (Fig. 13.2A). Although GCs are the smallest neuron in the vertebrate brain, they account for more than half of all neurons. Each GC receives excitatory synaptic input from 2 to 7 MFs, and each synaptic connection consists of a handful of active zones.27,28 The small number of synaptic inputs, along with a small soma and electrically compact morphology, makes GCs particularly suitable for studying synaptic transmission.15,18 In Fig. 13.2B, we show representative examples of EPSCs recorded at a single MF–GC synaptic connection under resting basal conditions (gray traces). Here, fluctuations in the peak amplitude of the EPSCs highlight the stochastic behavior of synaptic transmission introduced above. Analysis of such fluctuations using multiple-probability fluctuation analysis (MPFA), a technique based on a multinomial statistical model, has provided estimates for NT, P and the postsynaptic response to a quantum of transmitter (Q), for single MF–GC connections. MPFA indicates that at low frequencies synaptic transmission is meditated by 5–10 readily releasable vesicles (or, equivalently the number of functional release sites NT), with each vesicle or site having a vesicular release probability (P) of ~0.5.26,29 Experiments with rapidly equilibrating AMPAR antagonists suggest that release is predominantly univesicular at this synapse (one vesicle released per synaptic contact), an interpretation that is supported by the finding that at some weak MF–GC connections a maximum of only one vesicle is released even when P is increased to high levels.15,26
Figure 13.2. Synaptic transmission at the cerebellar MF–GC synapse.
(A) Electron micrograph of a cerebellar MF terminal filled with thousands of synaptic vesicles and a few large mitochondria. Synaptic contacts with GC dendrites appear along the contours of the MF membrane at several locations, evident by the wider and darker appearance of the membrane due to clustering of proteins within the presynaptic active zone and postsynaptic density. (B) Superimposed AMPAR-mediated EPSCs (gray) recorded from a single MF–GC connection, showing considerable variability in amplitude and time course from trial to trial. On some trials, failure of direct release revealed a spillover current with slow rise time. Such trials were separated using the rise time criteria of Ref. 24. The average direct-release component (green) was computed by subtracting the average spillover current (blue) from the average total EPSC (black). Arrow denotes time of extracellular MF stimulation, which occurred at a slow frequency of 2 Hz; most of the stimulus artifact has been blanked for display purposes. (C) Superimposed AMPAR-mediated EPSCs (gray) recorded from a single MF–GC connection and their average (black). The MF was stimulated at 100 Hz with an external electrode (arrows at top). Successive EPSCs show clear signs of depression. Inset shows EPSC responses to fourth stimulus on expanded timescale, showing the variation in peak amplitude. Stimulus artifacts have been blanked. (D) Average direct-release AMPAR conductance waveform (gray) fit with Gsyn(t) defined by the following functions: alpha (Eq. 13.5), one-exponential (Eq. 13.4), two-exponential (Eq. 13.6), multiexponential (4-Exp, Eq. 13.7). Most functions gave a good fit except the one-exponential function (blue). The conductance waveform was computed from the average current waveform in (B) via Eq. (13.3). (E) Same as (D) but for the average spillover component in (B). Most functions gave a good fit except the alpha function (green). (F) Same as (D) but for an average NMDAR-mediated conductance waveform computed from four different MF–GC connections. Again, most functions gave a good fit except the alpha function (green). Dashed lines denote 0. (A) Image from Palay and Chan-Palay25 with permission. (B) Data from Sargent et al.26 with permission.
Synaptic responses to low-frequency presynaptic stimuli (e.g., those in Fig. 13.2B) provide useful information about NT, P, and Q under resting conditions. To explore how these quantal synaptic parameters change in an activity-dependent manner, however, paired-pulse stimulation protocols or high-frequency trains of stimuli are required. Figure 13.2C shows an example of the latter, where responses of a single MF–GC connection to the same 100 Hz train of stimuli are superimposed (gray traces). Here, fluctuations in the peak amplitude of the EPSCs can still be seen (see inset), but successive peaks between stimuli also show clear signs of depression. The average of all responses (black trace) reveals the depression more clearly. Although by eye, signs of facilitation are not apparent in Fig. 13.2C, facilitation at this synapse most likely exists. We know this since lowering P at this synapse, by lowering the extracellular Ca2+ concentration, has revealed the presence of both depression and facilitation; however, because depression predominates under normal conditions, facilitation is not always apparent.29 As described in detail later in this chapter, mathematical models have been developed to simulate synaptic depression and facilitation. If used appropriately, these models can provide useful insights into the underlying mechanisms of synaptic transmission. Such models have revealed, for example, a rapid rate of vesicle reloading at the MF–GC synapse (k1=60–80 ms−1) as well as a large pool of vesicles that can be recruited rapidly at each release site (~30029–31). These findings offer an explanation as to how the MF–GC synapse can sustain high-frequency signaling for prolonged periods of time.
The MF–GC synapse forms part of a glomerular-type synapse, which also occur in the thalamus and dorsal spinocerebellar tract. While the purpose of the glomerulus has not been determined definitively, experimental evidence from the MF–GC synapse indicates this glial-ensheathed structure promotes transmitter spillover between excitatory synaptic connections24,32 and between excitatory and inhibitory synaptic connections.33 AMPAR–mediated EPSCs recorded from a MF–GC connection, therefore, exhibit both a fast “direct” component arising from quantal release at the MF–GC connection under investigation (Fig. 13.2B, green trace) and a slower component mediated by glutamate spillover from neighboring MF–GC connections (blue trace). While direct quantal release is estimated to activate about 50% of postsynaptic AMPARs at the peak of the EPSC,34 spillover is estimated to activate a significantly smaller fraction. However, because spillover produces a prolonged presence of glutamate in the synaptic cleft, activation of AMPARs by spillover can contribute as much as 50% of the AMPAR-mediated charge delivered to GCs.24
Glutamate spillover also activates NMDARs, but mostly at mature MF–GC synapses when the NMDARs occupy a perisynaptic location.35 At a more mature time of development, MF–GC synapses also exhibit a weak Mg2+ block due to the expression of GluN2C and/or GluN2D subunits.22,36,37 The weak Mg2+ block allows NMDARs to pass a significant amount of charge at subthreshold potentials, thereby creating a spillover current comparable in size to the AMPAR-mediated spillover current. Using several of the modeling techniques discussed in this chapter, we were able to show the summed contribution from both AMPAR and NMDAR spillover currents enables GCs to integrate over comparatively long periods of time, thereby enabling transmission of low-frequency MF signals through the input layer of the cerebellum.22
In the following sections, we describe how to capture the various properties of synaptic transmission recorded at the MF–GC synapse in mathematical forms that can be used in computer simulations. We start with the most basic features of the synapse, the postsynaptic conductance waveform, and the resulting postsynaptic current, and add biological detail from there. However, several aspects of synaptic transmission are beyond the scope of this chapter. These include long-term plasticity (i.e., Hebbian learning) and presynaptic Ca2+ dynamics. Mathematical models of these synaptic processes can be found elsewhere.38–42
2. CONSTRUCTING SYNAPTIC CONDUCTANCE WAVEFORMS FROM VOLTAGE-CLAMP RECORDINGS
The time course of a synaptic conductance, denoted Gsyn(t), can be computed from the synaptic current, Isyn(t), measured at a particular holding potential (Vhold) using the whole-cell voltage-clamp technique. If the synapse under investigation is electrotonically close to the somatic patch pipette, as is the case with the MF–GC synapse, then adequate voltage clamp can be achieved and the measured Isyn(t) will have relatively small distortions due to poor space clamp. On the other hand, if the synapse under investigation is electrotonically distant to the somatic patch pipette, for example, at the tip of a spine several hundred micrometers from the soma, then significant errors due to poor space clamp will distort nearly all aspects of Isyn(t), including its amplitude, kinetics, and reversal potential.43 To overcome this problem, a technique using voltage jumps can be used to extract the decay time course under conditions of poor space clamp, or dendritic patching can be used to reduce the electrotonic distance between the synapse and recording site.44
When measuring Isyn(t) under voltage clamp, individual current components (e.g., the AMPAR and NMDAR current components, IAMPAR and INMDAR) can be cleanly separated using selective antagonists (e.g., APV or NBQX), and the reversal potential of the currents (e.g., EAMPAR and ENMDAR) can be established by measuring the current–voltage relation and correcting for the liquid junction potential of the recording pipette. The synaptic current component can then be converted to conductance using the following variant of Eq. (13.2):
| (13.3) |
where Esyn denotes the reversal potential of the synaptic conductance under investigation. The next step is to find a reasonable mathematical expression for Gsyn(t). The simplest way to do this is to first remove stochastic fluctuations in the amplitude and timing of Gsyn(t) by averaging many EPSCs recorded under low-frequency conditions (e.g., see Fig. 13.2B) and then fit one of the waveforms described below (Eqs. 13.4–13.7) to the averaged EPSC. Later in the chapter, we discuss methods for incorporating stochastic fluctuations into the mathematical representation of Gsyn(t).
Exponential functions are typically used to represent Gsyn(t). If computational overhead is a major consideration, for example in large-scale network modeling, single-exponential functions can be used since they are described by only two parameters, the peak conductance gpeak and a single decay time constant τd:
| (13.4) |
where t′ = t – tj. Here, the arrival of the presynaptic action potential at t = tj leads to an instantaneous jump in Gsyn(t) from 0 to gpeak, after which Gsyn(t) decays back to zero (note, here and below Gsyn(t) = 0 for t < tj; for consistency, a notation similar to that of Ref. 41 has been used). This mathematical description of Gsyn(t) may be sufficient if the decay time is much larger than the rise time. However, if the precise timing of individual synaptic inputs is important, as in the case of an auditory neuron performing synaptic coincidence detection, then a realistic description of the rise time should be included in Gsyn(t). In this case, the simplest description is to use the alpha function, which has an exponential-like rise time course:
| (13.5) |
where t′ is defined as in Eq. (13.4). The convenience of the alpha function is that it only contains two parameters, gpeak and τ, which directly set the peak value and the time of the peak. However, the alpha function only fits waveforms with a rise time constant (τr) and τd of similar magnitude, which is not usually the case for synaptic conductances. When τr and τd are of different magnitude, then a double-exponential function is more appropriate for capturing the conductance waveform:
| (13.6) |
Here, the constant anorm is a scale factor that normalizes the expression in square brackets so that the peak of Gsyn(t) equals gpeak (see Ref. 41 for an analytical expression of anorm). Still, Eq. (13.6) may not be suitable for some conductance waveforms. Synaptic AMPAR conductance waveforms, for example, typically exhibit a sigmoidal rise time course, which can usually be neglected, but there are certain instances when it is important to accurately capture this component.26,32 In this case, a multiexponential function with an mxh formalism can be used to fit the conductance waveform45:
| (13.7) |
Here, the first expression in square brackets describes the rise time course, which, when raised to a power x > 1, exhibits sigmoidal activation. The second expression in square brackets describes the decay time course and includes three exponentials for flexibility, one or two of which can be removed if unnecessary. This function is flexible in fitting synaptic current or conductance waveforms and has produced good fits to the time course of miniature EPSCs recorded in cultured hippocampal neurons45 and AMPAR and NMDAR currents recorded from cerebellar GCs.24,32,46 With nine free parameters, however, Eq. (13.7) is not only computationally expensive but also has the potential to cause problems when used in curve-fitting algorithms. We have found the best technique for fitting Eq. (13.7) to EPSCs is to begin with x fixed at 1 (no sigmoidal activation) and one or two decay components fixed to zero (d2=0 and/or d3=0). If the initial fits under these simplified assumptions are inadequate, then one by one the fixed parameters can be allowed to vary to improve the fit. The scale factor anorm can be calculated by computing the product of the expressions in square brackets at high temporal resolution and setting anorm equal to the peak of the resulting waveform.
To illustrate how well the different mathematical functions capture synaptic conductance waveforms in practice, we fit Eqs. (13.4)–(13.7) to the average direct-release AMPAR conductance component of the MF–GC synapse (computed from currents in Fig. 13.2B) and plotted the fits together in Fig. 13.2D. The single-exponential function (Eq. 13.4) fit neither the rise nor decay time course. The two-exponential function (Eq. 13.6) fit well, except for the initial onset period, which lacked a sigmoidal rise time course. The alpha function (Eq. 13.5) fit both the rise and decay time course well since τr and τd of the direct-release component are of similar magnitude. The multiexponential function (Eq. 13.7) showed the best overall fit. The same comparison was computed for the average spillover AMPAR conductance component (Fig. 13.2E). This time only the multiexponential function provided a good fit to both the rise and decay time course. The two-exponential function also fit well except for a small underestimate of the decay time course; an additional exponential decay component would improve this fit. The one-exponential function provided a suitable fit to the decay time course but not the rise time course. The alpha function fit neither the rise or decay time course. Finally, the same comparison was made for an average NMDAR conductance waveform computed from four MF–GC connections (Fig. 13.2F). These results were similar to those of the spillover AMPAR conductance. Hence, as the results in Fig. 13.2D–F highlight, Eqs. (13.4)–(13.7) can reproduce a Gsyn(t) with different rise and decay time courses. These differences may or may not be consequential depending on the computer simulation at hand. In most instances, it is always preferable to choose the simplest level of description, but it is also important to verify the simplification does not significantly alter the outcome or conclusions of the study.
As a general guide, the direct AMPAR current typically has a rise time course of 0.2 ms and a decay time course between 0.3 and 2.0 ms at physiological temperatures, depending on the AMPAR subunit composition at the synapse type under investigation.18,47,48 The spillover AMPAR current typically has a rise time course of 0.6 ms and decay time course of 6.0 ms, measured at the MF–GC synapse.24 The NMDAR current has the slowest kinetics, with a rise time course of ~10 ms and a decay time course anywhere between 30 and 70 ms, but can even be longer than 500 ms depending on the NMDAR subunit composition.49,50
3. EMPIRICAL MODELS OF VOLTAGE-DEPENDENT MG2+ BLOCK OF THE NMDA RECEPTOR
The voltage dependence of the synaptic AMPAR component can usually be modeled with the simple linear current–voltage relation described in Eq. (13.2). In contrast, the synaptic NMDAR component exhibits strong voltage dependence due to Mg2+ binding inside the receptor’s ion channel.19 The block is strongest near the neuronal resting potential and becomes weaker as the membrane potential becomes more depolarized. This unique characteristic of NMDARs allows them to behave like logical AND gates: the receptors conduct current only when they are in the glutamate-bound state AND when the postsynaptic neuron is depolarized. It is this AND-gate property combined with their high Ca2+ permeability that enables NMDARs to play such a pivotal role in long-term plasticity, learning and memory.20,51–53 Here, we consider how to model the electrophysiological AND-gate properties of synaptic NMDARs.
As mentioned in the previous section, the time course of the NMDAR component can be captured with a multiexponential function. The key additional step required for modeling the NMDAR component is the nonlinear voltage-dependent scaling of the conductance waveform, here referred to as φ(V), which is the fraction of the NMDAR conductance that is unblocked. This scaling can be easily incorporated into a current–voltage relation as follows:
| (13.8) |
Typically, a Boltzmann function is used to describe φ(V), which takes on values from 0 at the most hyperpolarized potentials (all blocked) to 1 at the most depolarized potentials (all unblocked), and is commonly written as:
| (13.9) |
where V0.5 is the potential at which half the NMDAR channels are blocked and k is the slope factor that determines the steepness of the voltage dependence around V0.5. While the Boltzmann function is simple and easy to use, its free parameters V0.5 and k do not directly relate to any physical aspect of the Mg2+ blocking mechanism. The two-state Woodhull formalism,54 in contrast, is derived from a kinetic model of extracellular Mg2+ block, in which case its free parameters have more of a physical meaning. In this two-state kinetic model, an ion channel is blocked when an ion species, in this case extracellular Mg2+, is bound to a binding site somewhere inside the channel, or open when the ion species is unbound (Fig. 13.3A). If the rate of binding and unbinding of the ion species is denoted by k1 and k−1, respectively, then φ(V) will equal:
| (13.10) |
where
Here, K1 and K−1 are constants, δ is the fraction of the membrane voltage that Mg2+ experiences at the blocking site, z is the valence of the blocking ion (here, +2), F is the Faraday constant, R is the gas constant and T is the absolute temperature. Dividing through terms, Eq. (13.10) can be expressed in a more familiar notation that includes a dissociation constant (Kd):
| (13.11) |
where Kd0 is the dissociation constant at 0 mV and equals K−1/K1. This equation, like the Boltzmann function (Eq. 13.9), has two free parameters, Kd0 and δ. However, unlike the Boltzmann function, both parameters now directly relate to the Mg2+ blocking mechanism: Kd0 quantifies the strength or affinity of Mg2+ binding and δ quantifies the location of the Mg2+ binding site within the channel. On the other hand, Eqs. (13.9) and (13.11) are formally equivalent since their free parameters are directly convertible via the following relations: k = (δϕ)−1 and V0.5 = δϕ·ln([Mg2+]o/Kd0). Under physiological [Mg2+]o, Eq. (13.11) is also equivalent to a more complicated three-state channel model with an open, closed, and blocked state.55
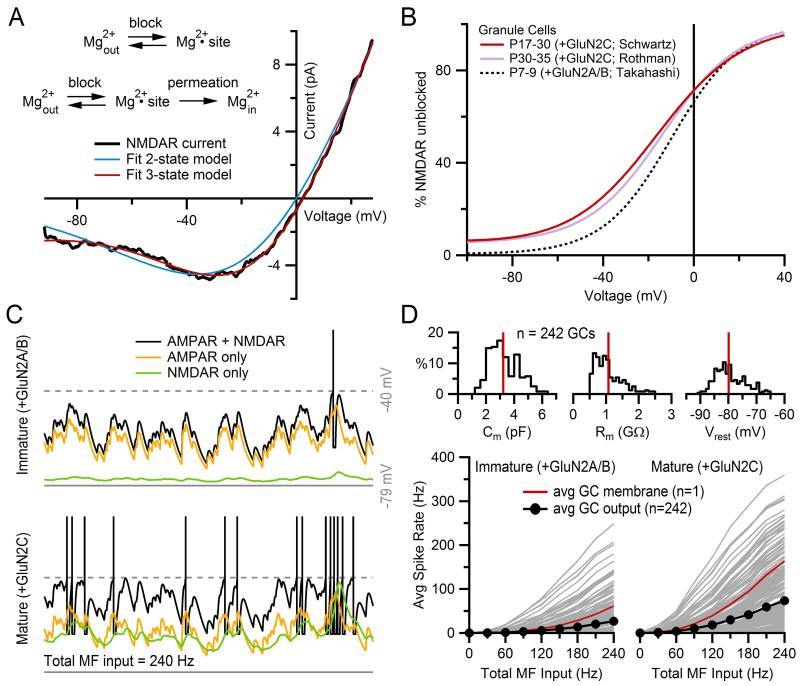
Figure 13.3. Weak Mg2+ block in GluN2C-containing NMDARs.
(A) Current–voltage relation of an NMDAR current from a mature GC (black) fit to Eq. (13.8) (ENMDAR = 0 mV) where φ(V) was defined by either a two-state kinetic model (blue; Eq. 13.11) or a three-state kinetic model that includes Mg2+ permeation (red; Eq. 13.12). The latter kinetic model produced the better fit. Kinetic models are shown at top. (B) Percent of unblocked NMDARs, φ(V), from the three-state kinetic model fit in (A) (red), compared to φ(V) derived from fits to the same model for another data set of mature GCs (purple; data from Ref. 46) and immature GCs (black; data from Ref. 50). At nearly all potentials, NMDARs from mature GCs show weaker Mg2+ block than those from immature GCs. This difference is presumably due to the developmental maturation switch in GCs from GluN2A/B-containing receptors to GluN2C-containing receptors, discussed in text. (C) IAF simulations (Eq. 13.20) of a GC with immature (top, +GluN2A/B) and mature (bottom, +GluN2C) NMDARs, using φ(V) functions in (B) (black and red, respectively), demonstrating the enhanced depolarization and spiking under mature NMDAR conditions. Identical simulations were repeated with GNMDAR = 0 (yellow) and GAMPAR = 0 (green) to compare the contribution of AMPARs and NMDARs to depolarizing the membrane. GAMPAR consisted of a simulated direct and spillover component, both with depression, as described in Fig. 13.5F. GNMDAR was simulated with both depression and facilitation, as described in Fig. 13.5G. The peak value of the GNMDAR waveform equaled that of the GAMPAR waveform, giving an amplitude ratio of unity, which is in the physiological range for GCs. The total synaptic current consisted of the sum of four independent Isyn, each representing a different MF input. Spike times for each MF input were generated for a constant mean rate of 60 Hz (Eq. 13.16), producing a total MF input of 240 Hz. Total Isyn also contained the following tonic GABA-receptor current not discussed in this chapter: IGABAR = 0.438(V + 75). IAF membrane parameters matched the average values computed from a population of 242 GCs: Cm = 3.0 pF, Rm = 0.92 GΩ, Vrest = −80 mV. Action potential parameters were: Vthresh = −40 mV (gray dashed line), Vpeak = 32 mV, Vreset = −63 mV, τAR = 2 ms. Action potentials were truncated to −15 mV for display purposes. (D) Average output spike rate of the IAF GC model as shown in (C) as a function of total MF input rate for immature (bottom left) and mature (bottom right) NMDARs, again demonstrating the enhanced spiking caused by GluN2C subunits. A total of 242 simulations were computed using Cm, Rm, Vrest values derived from a data base of 242 real GCs (top distributions, red lines denote average population values), with the average output spike rate plotted as black circles. Red line denotes one GC simulation whose Cm, Rm, Vrest matched the average population values shown at top, which are the same parameters used in (C). Note, the output spike rate of this “average GC” simulation is twice as large as the average of all 242 GC simulations due to the nonlinear behavior of the IAF model. Data in this figure is from Schwartz et al.22 with permission.
While the simple Boltzmann function and the equivalent two-state Woodhull formalism are often used to describe φ(V), the two functions have not always proved adequate in describing experimental data. Single-channel recordings of NMDAR currents, for example, have indicated there are actually two binding sites for Mg2+: one that binds external Mg2+ and one that binds internal Mg2+.56–60 Moreover, there are indications Mg2+ permeates through the NMDAR channel.19,57 Hence, more complicated expressions of φ(V) have been adopted. The three-state Woodhull formalism depicted in Fig. 13.3A, for example, has been used to describe Mg2+ block.57,59 This model includes Mg2+ permeation through the NMDAR channel, described by k2, which is assumed to be nonreversible (k−2 = 0), in which case φ(V) equals:
| (13.12) |
This equation reduces to Eq. (13.11) but with Kd as follows:
| (13.13) |
Here, separate δ have been used for each k (δ1, δ−1, δ2) to conform to the more general notation of Kupper and colleagues. If the original Woodhull assumptions are used (δ1 = δ−1 = δ and δ2 = 1 – δ), then Eq. (13.13) reduces to:
| (13.14) |
which has three free parameters: δ, Kd0, and Kp0. In previous work, we found this latter expression of φ(V) (Eqs. 13.12 and 13.13) gives a better empirical fit to the Mg2+ block of NMDARs at the MF–GC synapse than the two-state Woodhull formalism (Fig. 13.3A; Ref. 22). At this synapse, the Mg2+ block of NMDARs is incomplete at potentials near the resting potential of mature GCs (Fig. 13.3B), presumably due to the presence of GluN2C subunits.21,36,37 Using simple models as described in this chapter, we were able to show the incomplete Mg2+ block at subthreshold potentials boosts the efficacy of low-frequency MF inputs by increasing the total charge delivered by NMDARs, consequently increasing the output spike rate (Fig. 13.3C and D). Hence, these modeling results suggested the incomplete Mg2+ block of NMDARs plays an important role in enhancing low-frequency rate-coded signaling at the MF–GC synapse.
Characterization of the Mg2+ block of NMDARs is still ongoing. Besides the potential existence of two binding sites, and Mg2+ permeation, it has been shown that Mg2+ block is greatly affected by permeant monovalent cations.60,61 This latter finding has the potential to resolve a longstanding paradox referred to as the “crossing of δ’s,” where the two internal and external Mg2+ binding site locations (i.e., their δ’s), estimated using the Woodhull formalisms described above, puzzlingly cross each other within the NMDAR.61 Other details of Mg2+ block have been added by studies investigating the response of NMDARs to long steps of glutamate application.62,63 These studies have revealed multiple blocked and desensitization states, and slow Mg2+ unblock due to inherent voltage-dependent gating, all of which are best described by more complicated kinetic-scheme models. Hence, given the added complexities from these more recent studies, it is all the more apparent that the often-used equations for φ(V) described above are really only useful for providing empirical representations of the blocking action of Mg2+ (i.e., for setting the correct current–voltage relation described in Eq. 13.8), rather than characterizing the biophysical mechanisms of the Mg2+ block. In this case, parameters for φ(V) are best chosen to give a realistic overall current–voltage relation of the particular NMDAR under investigation. Because the voltage dependence of NMDARs is known to vary with age, temperature, subunit composition and expression (i.e., native vs. recombinant receptors), care must be taken when selecting these parameters. Ideally, one should select parameters from studies of NMDARs in the neuron of interest, at the appropriate age and temperature.
4. CONSTRUCTION OF PRESYNAPTIC SPIKE TRAINS WITH REFRACTORINESS AND PSEUDO-RANDOM TIMING
To simulate the temporal patterns of activation that a synapse is likely to experience in vivo, it is necessary to construct trains of discrete events that can be used to activate model synaptic conductance events, Gsyn(t), as described in Eqs. (13.4)–(13.7), at specific times (i.e., tj). These trains can then be used to mimic the timing of presynaptic action potentials as they reach the synaptic terminals. Real presynaptic spike trains can exhibit a wide range of statistics. The statistical properties of the spike trains reflect the manner in which information is encoded. Often, sensory information conveyed by axons entering the CNS is encoded as firing rate, and the interval between spikes has a Poisson-like distribution.64–66 Other types of sensory input may signal discrete sensory events as bursts of action potentials.67 In sensory cortex, information is typically represented as a sparse code and the firing rate of individual neurons is low on average (<1 Hz 68). The inter-spike interval of cortical neurons can exhibit a higher variance than expected for a Poisson process where the variance equals the mean. Here, we describe how to generate spike trains with specific statistics; however, another approach would be to use spike times measured directly from single-cell in vivo recordings.
To compute an arbitrary train of random spike times tj (j = 1, 2, 3, …) with instantaneous rate λ(t), a series of interspike intervals (Δtj) can be generated from a series of random numbers (uj) uniformly distributed over the interval (0, 1] by solving for Δtj in the following equation69,70:
| (13.15) |
where σ is the integration variable. The right-hand side of this equation represents the cumulative distribution function of finding a spike after tj−1, in which case λ(t) is the probability density function. Since λ(t) can be any arbitrary function of time, Eq. (13.15) is extremely flexible in generating any number of random spike trains. Here, we outline a few examples.
First, we consider the simplest case of generating a random spike train with constant instantaneous rate: λ(t) = λ0. In this case, Eq. (13.15) reduces to:
| (13.16) |
Plugging a series of random numbers uj into Eq. (13.16) results in a series of Δtj with exponential distribution (i.e., Poisson) and mean 1/λ0. Since the solution contains no memory of the previous spike time (i.e., there are no terms containing tj−1), Δtj can be computed independently and then converted to a final tj series.
Next, we consider the case of generating a random spike train with an exponential instantaneous rate of decay: λ(t) = λ0 exp(−t/τ). In this case, Eq. (13.15) reduces to:
| (13.17) |
Unlike Eq. (13.16), this solution contains memory of the previous spike in the term λ(t = tj−1), in which case values for Δtj and tj must be computed in consecutive order.
One problem with Eqs. (13.16) and (13.17) is that they do not take into account the spike refractoriness of a neuron, which can be on the order of 1–2 ms at physiological temperatures. A solution to this problem is to reject any Δtj that are less than the absolute refractory period (τAR) or evaluate the integral in Eq. (13.15) from tj−1 + τAR to tj−1 + Δtj. However, both procedures will increase the average of Δtj in which case the final instantaneous rate of the tj series will not match λ(t). To produce a tj series with instantaneous rate matching λ(t), one can correct λ(t) for refractoriness via the following equation71:
| (13.18) |
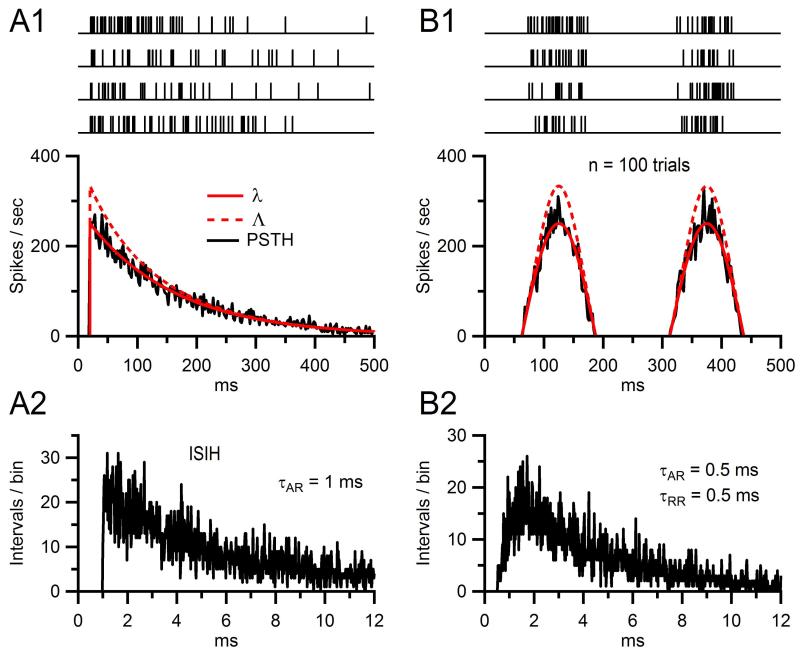
where λ(t)−1 > τAR, which should be the case if both λ(t) and τAR are derived from experimental data. As a simple example, if we consider the case of a constant instantaneous rate, where λ(t) = λ0 = 0.25 kHz and τAR = 1 ms, then Λ(t) = 0.333 kHz. Another simple example is shown in Fig. 13.4A1, where 200 spike trains (four shown at top) were computed for λ(t) that exhibits an exponentially decaying time course (bottom, solid red line) and τAR = 1 ms. Λ(t), the corrected rate function used to compute the spike trains, is plotted as the dashed red line, which only shows significant deviation from λ(t) at rates above 100 Hz. Computing the peri-stimulus time histogram (PSTH, noisy black line) from the 200 spike trains confirmed the instantaneous rate of the trains matched that of λ(t), and computing the interspike interval histogram (ISIH; Fig. 13.4A2) confirmed the spike intervals had an exponential distribution with τAR = 1 ms.
Figure 13.4. Simulated spike trains with refractoriness and pseudorandom timing.
(A1) Trains of spike event times (top) computed for an instantaneous rate function λ(t) with exponential decay time constant of 150 ms (bottom, solid red line) and absolute refractory period (τAR) of 1 ms. To compute the trains, a refractory-corrected rate function Λ(t) (dashed red line) was first derived from Eq. (13.18) and then used in the integral of Eq. (13.15) to compute the spike intervals in sequence. The PSTH (black, 2-ms bins) computed from 200 such trains closely matches λ(t). (A2) Interspike interval histogram (ISIH) computed from the same 200 trains in (A1), showing the 1 ms absolute refractory period. The overall exponential decay of the ISIH is a hallmark sign of a random Poisson process. (B1) and (B2) Same as (A1) and (A2) except λ(t) was a half-wave rectified sinusoid with 250 ms period, and refractoriness was both absolute and relative: τAR = 0.5 ms and τRR = 0.5 ms. Intervals were computed via Eq. (13.19).
A more complicated scenario arises when τAR is followed by a relative refractory period (τRR). In this case, one will need to multiply the instantaneous rate by a probability density function for refractoriness, H(t), similar to a hazard function, which takes on values between 0 and 1. A simple H(t) would be one that starts at 0 and rises exponentially to 1, in which case a tj series could be computed via the following:
| (13.19) |
where t′ = t – tj−1 – τAR. Examples of 200 spike trains computed via Eq. (13.19) are shown in Fig. 13.4B1 (top), where λ(t) was a half-wave rectified sinusoid (solid red line), τAR = 0.5 ms and τRR = 0.5 ms. Also shown is H(t) (dashed red line) which again only shows significant deviation from λ(t) at rates above 100 Hz. Computing the PSTH of the 200 spike trains again confirmed the instantaneous rate matched that of λ(t), and computing the ISIH confirmed the spike intervals had an exponential distribution with τAR = 0.5 ms and τRR = 0.5 ms (Fig. 13.4B2).
The above solutions for a simple λ(t) described in Eqs. (13.16) and (13.17) were relatively easy to compute since Eq. (13.15) could be solved analytically. If an analytical solution is not possible, however, then Eq. (13.15) (or Eq. 13.19) must be obtained numerically with suitably small time step dσ. Ideally, this can be achieved using an integration routine with built-in mechanism to halt integration based on evaluation of an arbitrary equality. If the integration routine does not have such a built-in halt mechanism, then integration will have to proceed past t = tj−1 + Δtj, perhaps to a predefined simulation end time, and Δtj computed via a search routine that evaluates the equality defined in Eq. (13.15). To improve computational efficiency, an iterative routine can be written which computes the integration over small chunks of time, and the search routine implemented after each integration step. The length of the consecutive integration windows could be related to Λ(t = tj−1), such as 3/Λ.
5. SYNAPTIC INTEGRATION IN A SIMPLE CONDUCTANCE-BASED INTEGRATE-AND-FIRE NEURON
Once we have built a train of presynaptic spike times (tj) and synapses with realistic conductance waveforms (GAMPAR and GNMDAR) and current–voltage relations (IAMPAR and INMDAR), we are well on our way to simulating synaptic integration in a simple point neuron like the GC, which is essentially a single RC circuit with a battery. The simplest neuronal integrator is the integrate-and-fire (IAF) model.72 Most modern versions of the IAF model act as a leaky integrator with a voltage threshold and reset mechanism to simulate an action potential.73,74 The equation describing the subthreshold voltage of such a model is as follows:
| (13.20) |
where Cm, Rm, and Vrest are the membrane capacitance, resistance, and resting potential, and Isyn(V,t) is the sum of all synaptic current components, such as IAMPAR and INMDAR (e.g., Eqs. 13.2 and 13.8) which are usually both voltage and time dependent. Spikes are generated the moment integration of Eq. (13.20) results in a V greater than a predefined threshold value (Vthresh). At this time, integration is halted and V is set to the peak value of an action potential (Vpeak) for one integration time step. V is then set to a reset potential (Vreset) for a period of time defined by an absolute refractory period (τAR) after which integration of Eq. (13.20) is resumed. To produce realistic spiking behavior, the parameters can be tuned to match the particular neuron under investigation. Vthresh, Vpeak, and Vreset, for example, can be set to the average onset inflection point, peak value, and minimum after-hyperpolarization of experimentally recorded action potentials. τAR can be set to the minimum interspike interval observed during periods of high spike activity, and further tuned using input–output curves (e.g., matching plots of spike rate vs. current injection for experimental and simulated data). Due to the complexity of Isyn(V,t), the solution of Eq. (13.20) will most likely require numerical integration. The integration can be implemented in a similar manner as that described for λ(t) above, using a built-in integration routine to solve Eq. (13.20) over small chunks of time, and searching for V the moment it exceeds Vthresh, or using an integration routine with built-in mechanism to halt integration once V exceeds Vthresh. Usually, all of the above procedures can be implemented using few lines of code.
Due to their electrically compact morphology and simple subthreshold integration properties, GCs are particularly well suited for modeling with an IAF modeling approach.22,46 Example simulations of an IAF model tuned to match the firing properties of an average GC can be found in Fig. 13.3C. Here, the model was driven by Isyn(V,t) that contained either a mixture of IAMPAR and INMDAR or the two currents in isolation. To simulate the convergence of four MF inputs, four different trains of Isyn(V,t) with independent spike timing were computed and summed together before integration of Eq. (13.20). Because repetitive stimulation of the MF–GC synapse at short time intervals often results in depression and/or facilitation of IAMPAR and INMDAR, plasticity models of the two currents were included in the simulations. These plasticity models are described in detail in the next section.
One consideration often overlooked in simulations of synaptic integration is the variability in Cm, Rm, and Vrest. We have found, for example, that the natural variability of these parameters in GCs can produce dramatically different output spike rates for a given synaptic input rate, as shown in Fig. 13.3D (gray curves). Moreover, due to the nonlinear nature of spike generation, using average values of Cm, Rm, and Vrest in a simulation (red) does not replicate the average output behavior of the total population (black): the spike rate of the “average GC” simulation in Fig. 13.3D is twice the average population spike rate. Hence, control simulations that include variation in Cm, Rm, and Vrest should be considered when simulating synaptic integration.
If the neuron under investigation has extended dendrites that are not electrically compact, then a multicompartmental model may be required. In this case, Eq. (13.20) can be used to describe the change in voltage within the various compartments where synapses are located, with an additional term on the right-hand side of the equation denoting the flow of current between individual compartments. Spike generation is then computed as described above but occurs only in the compartment designated as the soma. Also, an additional current due to spike generation can be added to the soma. Further details about multicompartment IAF modeling can be found in Gerstner and Kistler.38 More often than not, however, multicompartmental models are simulated with Hodgkin-Huxley-style Na+ and K+ conductances to generate realistic action potentials.75 Popular simulation packages developed to solve these more complex multicompartmental models with Hodgkin-Huxley-style conductances include NEURON and GENESIS, which are discussed further below.
6. SHORT-TERM SYNAPTIC DEPRESSION AND FACILITATION
So far, we have only considered the simulation of fixed amplitude synaptic conductances recorded under basal conditions. At synapses with a relatively high release probability, repetitive stimulation at short time intervals often results in depression of the postsynaptic response (see, e.g., Fig. 13.2C). This kind of synaptic depression was first described by Eccles et al.8 for endplate potentials at the NMJ and has since been described for synapses in the CNS. Because recovery from synaptic depression takes a relatively short time, on the order of tens of milliseconds to seconds, it is referred to as short-term depression, distinguishing it from the longer-lasting forms of depression, including long-term depression that is believed to play a central role in learning and memory. Here, we refer to short-term depression as simply depression or synaptic depression.
Since the discovery of synaptic depression, numerous studies have sought to determine its underlying mechanisms and potential roles in neural signaling (for review, see Refs. 76,77). Often these studies have employed mathematical models to test and verify their hypotheses. The first model of presynaptic depression was described by Liley and North in 1953, before the discovery of synaptic vesicles. At the time, depression was thought to reflect a depletion of a finite pool of freely diffusing neurotransmitter available for release, and recovery from depression was thought to reflect a replenishment of the depleted pool, via synthesis from a freely diffusing chemical precursor. This explanation fit well with the observation that increasing the initial release of neurotransmitter produced a larger degree of depression, and the recovery from depression followed an exponential time course. Liley and North formalized this hypothesis by a simple mathematical treatment of synaptic transmission at the NMJ, known as a “depletion model,” whereby a size-limited pool of readily releasable neurotransmitter (N) is in equilibrium with a large store of precursor (Ns) with forward and backward rate constants k1 and k−1 (Fig. 13.5A). In response to stimulation of the nerve, say at time tj, a fraction (P) of N is released into the synaptic cleft, disturbing the equilibrium with Ns. The change of N with respect to time after the stimulus can then be described by the following differential equation:
| (13.21) |
If Ns is relatively large, one can assume Ns is constant and Eq. (13.21) has the following solution:
| (13.22) |
where N∞ = Nsk1/k−1 and τr = 1/k−1. Here, N∞ is the steady-state value of N, τr is the recovery time constant, and Nj+ε is the value of N immediately after transmitter release at time tj. This solution means that, after a sudden depletion of N due to a stimulus, N will exponentially increase from Nj+ε to N∞ with time constant τr. By comparing their experimental data to predictions of their mathematical model, Liley and North were able to estimate the steady-state value of P was 0.45, as well as reveal subtle signs of potentiation during a short train of stimuli, a conditioning tetanus, which they speculated was due to a brief period of temporarily raised P. At the time, such facilitation had long been reported8 and was thought to be due to an increase in size of the nerve action potential, or an increase in the extra-cellular K+ concentration. Today, facilitation is thought to be largely due to a rise in the intracellular Ca2+ concentration ([Ca2+]i) as described further below.
Figure 13.5. Modeling short-term depression and facilitation.
(A) Original depletion model of Liley and North9 describing release of freely diffusing transmitter (N). N is in equilibrium with a large store of precursor molecules (Ns), governed by forward and backward rate constants k1 and k−1. The arrival of an action potential causes a rise in [Ca2+]i, triggering a fraction (P) of N to be released (NP) into the synaptic cleft (red), disrupting the balance between N and Ns. N recovers back to its steady-state value (N∞) with an exponential time course (τr), where N∞ and τr are set by k1 and/or k−1. (B) A modern version of the depletion model with a large store of synaptic vesicles (Ns, gray circles) and a fixed number of vesicle release sites (NT, blue), where N now represents the number of vesicles docked at a release site and are therefore readily releasable (orange circle). The arrival of an action potential now triggers a certain fraction of the readily releasable vesicles to be released (NP), freeing release sites. The number of free release sites at any given time is equal to NT – N. Variations of this model include a k1 that is dependent on residual [Ca2+]i (red star), in which case [Ca2+]i is explicitly simulated, and the inclusion of a backwards rate constant k−1 (gray arrow) representing the undocking of a vesicle, that is, the return of N to Ns. (C) A more recent version of the depletion model, similar to that in (B), has two pools of readily releasable vesicles (N1 and N2) with low- and high-release probabilities, respectively (P1 and P2). The difference in probabilities is related to the distance vesicles in pools N1 and N2 are from VGCCs, where vesicles in pool N2 are more distant. Here, the model includes a maturation process where N2 emerges from N1 at a rate set by k2, but some models have N2 emerging from Ns in parallel with N1. In some models, k2 is dependent on residual [Ca2+]i (red star), in which case [Ca2+]i is explicitly simulated. Only the second pool has a fixed number of vesicle release sites (NT2). (D) Synaptic model with depression implemented using RP recursive algorithm described in Eqs. (13.28)–(13.32) (τr = 20 ms; R = N/NT). The time evolution of R and P are shown at top (blue and red), where P∞ = 0.4. Since there is no facilitation (ΔP = 0), P is constant. At the arrival of an action potential at tj, the fraction of vesicles released (Re) is computed: Re = RP (gray circles). Re is then used to scale a synaptic conductance waveform Gsyn(t = tj) (Eq. 13.30) and also subtracted from R (Eq. 13.31). The time evolution of the sum of all Gsyn(t = tj) is shown at the bottom (gray). (E) The same simulation in (D), except the synaptic model includes facilitation (ΔP = 0.5, τf = 30 ms). For comparison, Re and the sum of all Gsyn(t = tj) are plotted in black (+F) along with their values in (D) (−F, gray). (F) Fit of a synaptic model with depression (yellow) to a 30 Hz MF–GC AMPAR conductance train (black). The fit consisted of the sum of two separate components, the direct and spillover components, where each component had its own depression parameters. Parameters for the fit can be found in Schwartz et al.22 (G) Same as (F) but for a corresponding 30 Hz MF–GC NMDAR conductance train. This time the fit (green) consisted of a single component that had depression and facilitation. Scale bars are for (F) and (G), with two different y-scale values denoted on the left and right, respectively. Data in (F) and (G) is from Schwartz et al.22 with permission.
Subsequent to Liley and North’s study, Betz78 modified the depletion model to account for vesicular release. More recently, Heinemann et al.79 added to the depletion model a pulsatile increase in [Ca2+]i leading to a steep increase in P from a near zero value. While the latter addition made the depletion model more realistic, it introduced the added complication of simulating the time dependence of [Ca2+]i. The added complication proved useful, however, in that Heinemann and colleagues were able to explore the consequences of adding a Ca2+-dependent step to the process of vesicle replenishment (i.e., k1), as supported by experimental evidence at the time. One such consequence was an increase in the number of readily releasable vesicles during a spike-plateau Ca2+ transient, thereby enhancing secretion during subsequent stimuli. More recent experimental evidence supports such a link between increased levels of [Ca2+]i and enhanced vesicle replenishment (k1).80–84
As noted by Heinemann et al.79, k−1 was introduced into their model in order to limit the steady-state value of readily releasable vesicles (N∞). An alternative approach to limit N∞, they noted, would be to allow a finite number of vesicle release sites at the membrane (NT), and let N denote the number of release sites filled with a vesicle, or equivalently the number of readily releasable vesicles (Fig. 13.5B). In this case, the number of empty release sites will equal NT – N, and the rate at which the empty release sites are filled will equal k1(NT – N). Hence, Eq. (13.21) can be rewritten as:
| (13.23) |
This equation has the same solution defined in Eq. (13.22) except N∞ = NT and τr = 1/k1. Because NT now directly defines N∞, k−1 is no longer necessary. Although the backward reaction defined by k−1 may very well exist, its rate is usually presumed small and neglected. In most depletion models, however, it is customary to express Eq. (13.23) with respect to the fraction of release sites filled with a vesicle (i.e., N/NT), also known as site occupancy, which is assumed to be unity under resting conditions (i.e., low stimulus frequencies). To be consistent with these other models, therefore, we define a fractional “resource” variable R = N/NT. Substituting terms, Eq. (13.23) becomes:
| (13.24) |
which has the following solution based on Eq. (13.22):
| (13.25) |
where τr = 1/k1. This is the expression one often sees in depletion models (e.g., Ref. 85); however, sometimes R is denoted as D,86 x,87 n,88 or as the ratio N/NT.80
To simulate vesicle release, many depletion models treat the process of spike generation, Ca2+ channel gating and vesicle release as instantaneous events (Fig. 13.5B, red P). To do this, one first computes the fraction of the resource of vesicles released (Re) at the time of a stimulus: Re = RP. Next, Re is used to compute the amplitude of the postsynaptic response, for example: gpeak = QNTRe (see Eqs. 13.4–13.7), where Q is the peak quantal conductance. Finally, Re is subtracted from R (R → R – Re) increasing the number of empty release sites. A few variations in this release algorithm are worth noting. First, in some models, the latter decrement in R is expressed with respect to a depression scale factor (D). However, the result is the same since D can be expressed as D = 1 – P, in which case, R → RD = R(1 – P) = R – Re. Second, in some models, a synaptic delay is added to the postsynaptic response. However, if the same delay is added to each response, then the result is the same with only an added time shift. Third, in some models, the release sites become inactive after a vesicle is released.87 This requires the addition of an inactive state, after release and before the empty state. Transition from the inactive state to the empty state (i.e., recovery from inactivation) is then determined by an extra time constant. Hence, in this three-state model, the recovery of N will have a double-exponential time course. Because of the added complexity, differential equations of the three-state model will most likely have to be solved using numerical methods. Finally, in the more detailed models that simulate [Ca2+]i, such as the Heinemann model discussed above, the stimulus (i.e., action potential) will often cause an instantaneous increase in [Ca2+]i followed by a slower decay. Since P is a nonlinear function of [Ca2+]i, it may remain elevated above zero for some time following an action potential, causing a delayed component of vesicular release. This scenario therefore requires the added complication of calculating release continuously as a function of [Ca2+]i, which may have to be solved via numerical methods.
More recent studies investigating vesicle release in the calyx of Held42 and cerebellar MF30 have reported success in replicating experimental data using a depletion model with two pools of releasable vesicles (N1 and N2), one with a low release probability (P1, reluctantly releasable), the other with a high release probability (P2, readily releasable; Fig. 13.5C). In this two-pool model, the size of N1 is not limited by a fixed number of release sites, but rather is limited by the forward and backward rate constants k1 and k−1. The size of N2, on the other hand, is limited by a finite number of release sites (NT2). As depicted in Fig. 13.5C, N2 emerges from N1 via a maturation process that is Ca2+ independent (i.e., k2). However, Trommershäuser and colleagues modeled N2 emerging from Ns in parallel with N1, where k2 was Ca2+ dependent. The success of both models in replicating experimental data may indicate true differences in the synapse types under investigation, or may indicate a need for more experimental data to constrain this type of model. To simulate two different release probabilities, P1 and P2 are defined according to a biophysical model that places the vesicles of pools N1 and N2 at different distances from VGCCs (Ref. 42; see also Ref. 89). The result is individual [Ca2+]i expressions for each pool of vesicles, which adds to the complexity of this type of depletion model.
As noted above, Liley and North9 observed signs of facilitation at the NMJ which they attributed to a brief period of temporarily raised P after stimulation of the presynaptic terminal. Today, there is considerable evidence the raised P is due to an accumulation of residual Ca2+ in the synaptic terminal following an action potential (for review, see Ref. 77). Although facilitation may well be a universal characteristic of all chemical synapses, it has not always been readily apparent at some synapse types, for example, the climbing fiber synapse.80 The lack of observable facilitation at some synapse types is thought to be due to a presence of strong depression that dominates over facilitation (due to a higher release probability), or the presence of intracellular Ca2+ buffers that significantly speed the decay of residual [Ca2+]i, or some molecular difference in the vesicle release machinery. The lack of observable facilitation at some synapse types has meant facilitation has not always been included in depletion models. However, for those depletion models that have included facilitation, the typical implementation of facilitation has been to instantaneously increase P after the arrival of an action potential and let P decay back to its steady-state value. In this case, the change of P with respect to time after an action potential can be described by the following differential equation:
| (13.26) |
which has the following solution:
| (13.27) |
where P∞ is the steady-state value of P (the probability of release during resting conditions, sometimes referred to as P0), τf is the time constant for recovery from facilitation, and Pj+ε is the value of P immediately after an action potential at time tj. More complicated models that simulate Ca2+ dynamics will equate P as a function of [Ca2+]i.
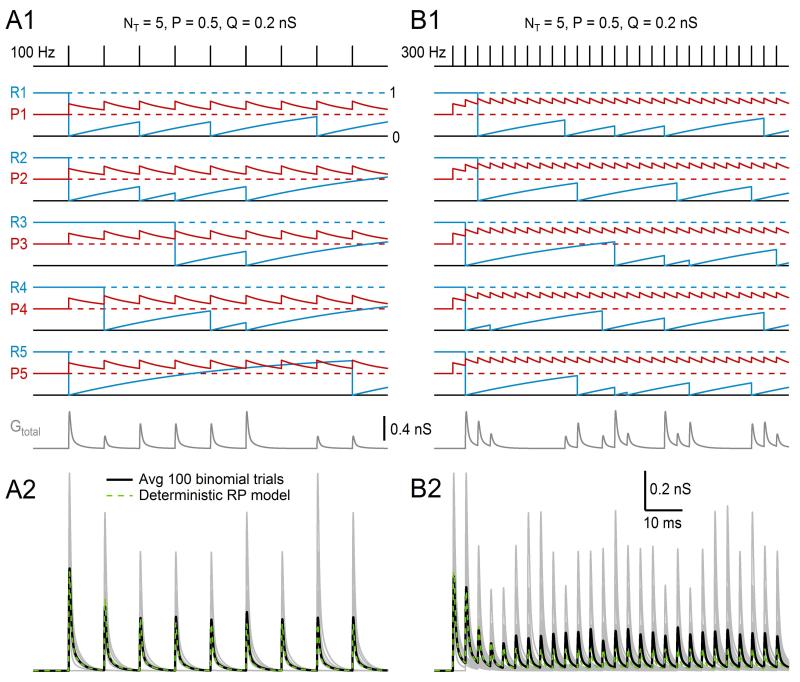
If the differential equations that describe synaptic plasticity have exact analytical solutions, then a simple recursive algorithm can be used to compute a solution for a given spike tj series. As a simple example, if the change in R and P after tj are described in Eqs. (13.25) and (13.27), then a solution can be obtained by executing the following three steps at each spike time tj (j = 1, 2, 3, …). In step 1, values for R and P at the arrival of a spike at tj are computed via the following equations derived from Eqs. (13.25) and (13.27):
| (13.28) |
| (13.29) |
where j denotes the current spike, j – 1 is the previous spike, and Δtj is the inter-spike time (Δtj = tj – tj−1). Since both R and P change instantaneously at tj, it is necessary to distinguish their values immediately before and after a spike. Here, this is accomplished with the notation −ε and +ε, respectively. Note that for the first spike (j = 1) Pj−ε = P∞. In step 2, values for R and P derived from step 1 are used to compute the amplitude of the postsynaptic response at tj:
| (13.30) |
gpeak can then be used in Eqs. (13.4)–(13.7). In step 3, values for R and P immediately after the arrival of a spike are computed:
| (13.31) |
| (13.32) |
where ΔP is a facilitation factor with values between 0 and 1. Varela et al.86 use a slightly different approach to step 3 that disconnects the usage dependency of N from P:
| (13.33) |
| (13.34) |
where ΔR and ΔP are their depression (D) and facilitation (F) factors. Equation (13.34) is similar to Eq. (13.32) in spirit; however, Pj+ε in Eq. (13.34) has the potential to grow without bound at high spike rates, in which case gpeak in Eq. (13.30) can become larger than Q·NT, the maximum amplitude possible for NT release sites. Pj+ε in Eq. (13.32), on the other hand, is limited to going no higher than 1, and therefore gpeak no higher than Q·NT.
An example of a Gsyn(t) train computed with the above RP recursive algorithm is shown in Fig. 13.5D (bottom, gray), along with the time evolution of R (top, blue), P (red), and RP (gray circles). In this example, there is no facilitation (ΔP = 0) so P is constant. To show the effects of facilitation, the same Gsyn(t) train is shown in Fig. 13.5E now with facilitation (bottom, black; ΔP = 0.5, τf = 30 ms). Comparison of Gsyn(t) with and without facilitation (black vs. gray) shows the enhancement of gpeak due to facilitation. However, the comparison also shows the signs of facilitation in this example are subtle and might not be readily apparent by visual inspection of the Gsyn(t) train.
A more realistic example of a Gsyn(t) train computed with the above RP recursive algorithm is shown in Fig. 13.5F. Here, parameters for R and P were optimized to fit a 30 Hz GAMPAR train computed from recordings from four GCs (black). Because GAMPAR of GCs contains a direct and spillover component (Fig. 13.2B), the fit (yellow) consisted of two separate components simultaneously summed together. Furthermore, because a good fit could be achieved without facilitation, only depression of the two components was considered. A similar fit to a 30 Hz GNMDAR train computed from recordings from the same four GCs is shown in Fig. 13.5G. This time a good fit (green) was achieved using one component that had both depression and facilitation.
There is one caveat, however, about the fits in Fig. 13.5F: studies have shown most of the depression of the AMPAR conductance at the MF–GC synapse at 100 Hz is not due to the depletion of presynaptic readily releasable vesicles, but to the desensitization of postsynaptic AMPARs.29,34 Hence, while the depletion model has accurately captured the overall mean behavior of the MF–GC synapse, it has done so by lumping presynaptic and postsynaptic sources of depression. This could be the case for the fit to GNMDAR as well. The technique of fitting a depletion model to the data is still valid, however, since the intended goal of the fits was to create realistic conductance waveforms that could be used in a simple IAF model, as reported elsewhere.22 An alternative approach would be to simulate each source of depression and facilitation as independent scale factors, which are then used to compute gpeak in Eq. (13.30). Whether to lump the various sources of plasticity into single components or to split them apart into individual components ultimately depends on the purpose of the plasticity model. If the aim of the plasticity model is to generate mean synaptic conductance trains for driving a neural network, or for injecting into the cell body a real neuron via dynamic clamp, then the simple lumping approach can be taken. On the other hand, if the aim of the plasticity model is to reproduce the mean and variance of the synaptic trains (see below), or gain insight into and construct hypotheses about one or more of the various components of synaptic transmission, then a “splitting” approach is perhaps better. The splitting approach will, of course, require extra experimental data to constrain the various parameters of the independent components. A more detailed description on how to model the various components of synaptic depression and facilitation independently can be found in a recent review by Hennig.88 This review also describes other sources of synaptic plasticity not discussed here, including sources of slow modulation of P, temporal enhancement of vesicle replenishment and the longer-lasting forms of synaptic plasticity, augmentation and post-tetanic potentiation. LTP at the MF–GC synapse has also been modeled in detail elsewhere.90
7. SIMULATING TRIAL-TO-TRIAL STOCHASTICITY
Up until now, the synaptic models we have presented are deterministic. However, as mentioned in Section 1, synapses exhibit considerable variability in their trial-to-trial response (see, e.g., Fig. 13.2B) due to the probabilistic nature of the mechanisms underlying synaptic transmission, from the release of quanta to the binding and opening of postsynaptic ionotropic receptors (Fig. 13.1). Here, we discuss the simulation of three sources of stochastic variation that account for the bulk of the variance exhibited by EPSCs recorded at central synapses: variation in the number of vesicles released, variation in the amplitude of the postsynaptic quantal response, and variation in the timing of vesicular release.
The main source of synaptic variation arises from the stochastic nature of vesicular release at an active zone, a process that lead Katz3 to the quantum hypothesis. Since the nomenclature of quantal release can be confusing, it is useful to define terms. Here, we use the term “release sites” to mean functional release sites (i.e., NT). This is equivalent to the maximum number of vesicles that can be released by a single action potential under resting conditions when all release sites are occupied. Synapses may have one or more than one release site per anatomical synaptic contact or active zone. Multi-vesicular release refers to the situation where multiple vesicles are released per active zone.91 A Poisson model is typically used to describe stochastic quantal release at the NMJ under conditions of low-release probability.2 This model works well since the number of release sites is large at this synapse. In contrast, a simple binomial model is typically used to describe stochastic quantal release at central synapses,92 which have relatively few release sites with intermediate release probabilities. The simple binomial model assumes the vesicular release probability P and the amplitude of the postsynaptic response to a single quantum (quantal peak amplitude, Q) are uniform across release sites. Under these assumptions, and the proviso that release is perfectly synchronous, the mean (μ), variance (σ2) and frequency (f) of the postsynaptic response can be expressed as:
| (13.35) |
| (13.36) |
| (13.37) |
where k denotes the number of quanta released from a maximum of NT release sites. The parabolic σ2–μ relation described in Eq. (13.36) has proved particularly useful as it defines how the variance of the EPSC changes with P. MPFA, or variance mean analysis, uses a related multinomial model that includes nonuniform release probability and quantal variability to estimate Q, P, and NT from synaptic responses recorded at different P. This approach is discussed in detail elsewhere.29,93,94
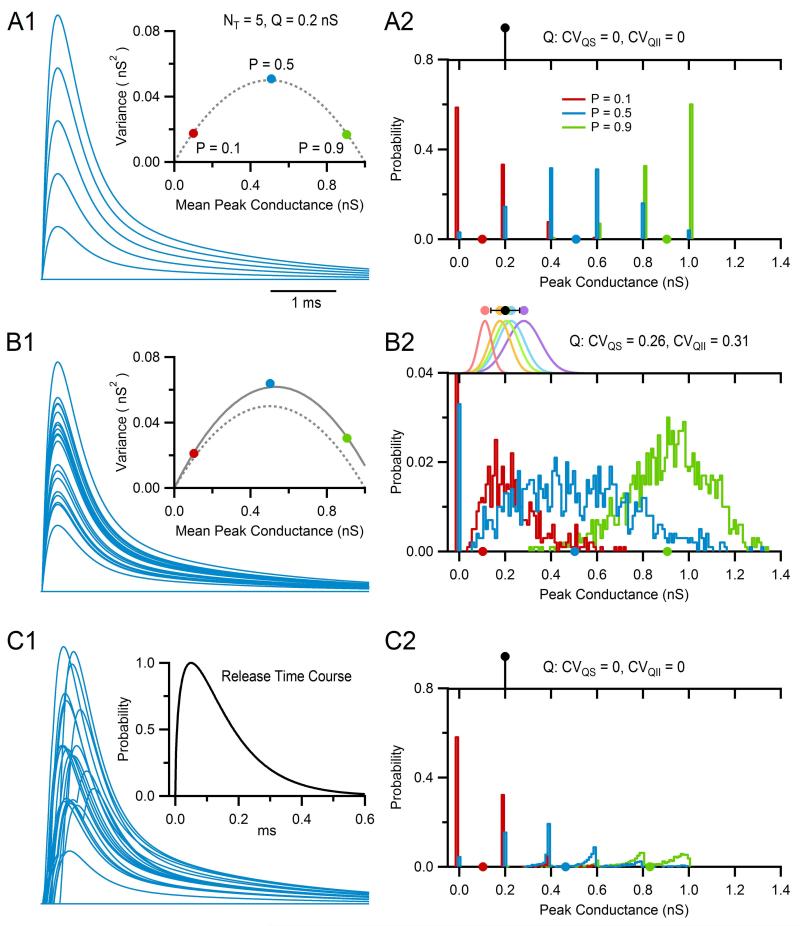
This statistical framework makes simulation of a simple binomial synapse with NT independent release sites, each with release probability P and quantal size Q, relatively straightforward. For the simulations presented in this section, Q pertains to the peak amplitude of the quantal excitatory postsynaptic conductance but could also pertain to the peak amplitude of the EPSC or EPSP. On arrival of an action potential at time tj, a random number is drawn from the interval [0, 1] for each release site. If the random number is greater than P, then release at the site is considered a failure and the site is ignored; otherwise release is considered a success and a synaptic conductance waveform with amplitude Q is generated for that site (e.g., Eqs. 13.4–13.7, gpeak = Q). After computing the release at each site, the synaptic conductances at each site are summed together giving Gtotal(t), which is used as the conductance waveform at tj. On the arrival of the next action potential, the above steps are repeated. Figure 13.6A1 shows results of such simulation (blue traces, superimposed at each tj) where values for NT, P, and Q matched those of an average GC (NT = 5, P = 0.5, Q = 0.2 nS) and stimulation was at low enough frequency that there was no residual conductance from previous events. The synaptic conductance waveform was a direct GAMPAR, similar to that in Fig. 13.2D (red trace), and the number of trials (i.e., action potentials) was 1000, 20 of which are displayed. As expected for a binomial process with NT = 5, peak values of Gtotal(t) consisted of six different combinations of Q, including 0 for the case of failures at all sites. Furthermore, the mean, variance, and frequency of the peak amplitudes (Fig. 13.6A1 and A2) matched the expected values of a random variable with binomial distribution computed via Eqs. (13.35)–(13.37). When the same synapse was simulated with a low-release probability (P = 0.1, red), most action potentials resulted in failure of release (Fig. 13.6A2). Hence, μ and σ2 of the peak values of Gtotal(t) were both low (Fig. 13.6A1). In contrast, when the release probability was high (P = 0.9, green) most action potentials resulted in release at 4 or 5 sites (Fig. 13.6A2), resulting in high μ but low σ2 (Fig. 13.6A1). A final comparison of μ and σ2 across P values showed μ and σ2 matched the parabolic relation predicted in Eq. (13.36) (Fig. 13.6A1), the hallmark sign of a simple binomial model.
Figure 13.6. Simulating trial-to-trial variability using a binomial model with quantal variability and asynchronous release.
(A1) Simulations from a binomial model of a typical MF–GC connection with five release sites (NT) each with 0.5 release probability (P) and 0.2 nS peak conductance response (Q). Q was used to scale a GAMPAR waveform with only a direct component. A total of 1000 trials were computed, 20 of which are displayed (blue). Inset shows σ2–μ relation computed from the peak amplitudes of all 1000 trials (blue circle), matching the theoretical expected value computed from Eq. (13.36) (dashed line). Repeating the simulations using a low P (0.1, red) and high P (0.9, green) confirmed the parabolic σ2–μ relation of the binomial model. (A2) Frequency distribution (bottom, blue) of the 1000 peak amplitudes computed in (A1), which closely matched the expected distribution computed via Eq. (13.37) (not shown). Circles on x-axis denote μ. Distributions for low and high P are also shown (red and green). Top graph shows Q which lacked variation. (B1) Same as (A1) except Q included intrasynaptic variation (CVQS = 0.26) and intersynaptic variation (CVQII = 0.31), creating a larger combination of peak amplitudes and therefore larger variance. Inset shows theoretical σ2–μ relation with (solid line) and without (dashed line) variation in Q, the former computed using Eq. 11 of Silver.94 (B2) Same as (A2) but for the simulations in (B1). Top graph shows the distribution of the average Q at each site i (i.e., Qi, colored circles) with μ ± σ = 0.20 ± 0.62 nS (black circle), as defined by CVQII. Gaussian curves show distribution of Q at each site, defined by Qi and CVQS. (C1) Same as (A1) except a delay, or release time (trelease), was added to each quantal release event. Values for trelease were randomly sampled from the release time course shown in the inset, which is typical for a single release site at a MF–GC connection. (C2) Same as (A2) but for the simulations in (C1). Peaks were measured over the entire simulation window.
The second main source of synaptic variability arises from variation in the quantal size Q. This can arise from trial-to-trial variation in Q at a single release site (intrasite or Type I variance) or from differences in the mean Q between release sites (intersite or Type II variance). Sources of intrasite quantal variability include variation in the amount of transmitter released per vesicle and the stochastic gating of postsynaptic receptor channels. Sources of intersite variability, on the other hand, include variation in the cleft geometry, number of postsynaptic receptors and electrotonic distance to the soma (for somatically recorded responses). Whereas the variance arising from intrasite quantal variation increases linearly with release probability, the variance arising from intersite quantal variance shows a parabolic relation as a function of release probability, since its origins are combinatorial. Both intrasite and intersite quantal variability are often expressed as coefficients of variation, CVQS and CVQII, respectively, where CV = σ/μ, using the notation of Silver94 for consistency. For GCs, CVQS was estimated to be 0.26 and CVQII to be 0.31.26 Incorporating these two sources of quantal variance into a synaptic model is again relatively straightforward. First, an average Q for each release site i, denoted Qi, is computed by drawing a random value from a Gaussian distribution with μ and σ defined by CVQII, where μ equals the desired final average peak synaptic conductance and σ = μ·CVQII. For simulations with a small NT, however, the small number of samples from the Gaussian distribution may produce a CVQII and/or μ that are relatively distant from their intended values. To avoid this problem, one can repeat the sampling of Qi until both CVQII and μ fall within a predefined tolerance range, such as 1% of their intended values. The binomial simulation for NT and P can then be executed as described in the previous paragraph, except for the additional step of adding intrasite variability to Q at the arrival of each action potential. To do this, a value for Q is randomly drawn from a Gaussian distribution with μ and σ defined by CVQS, where μ now equals Qi and σ = Qi·CVQS. Figure 13.6B1 shows the effects of adding intrasite and intersite quantal variance to the binomial model simulations in Fig. 13.6A1 (CVQS = 0.26 and CVQII = 0.31). In this case, the peak amplitude of Gtotal(t) showed a significant increase in variation (Fig. 13.6B1), resulting in a smearing of the peak-amplitude frequency distribution (Fig. 13.6B2). Hence, as these results demonstrate, a nonuniform Q tends to obscure the underlying binomial process, especially under circumstances when a single value of P is investigated. Only by varying P does the underlying binomial process become apparent in the σ2–μ relation and frequency distribution of peak values (i.e., red vs. blue vs. green data points).
The third source of synaptic variation arises from the asynchronous release of synaptic vesicles, which can be considered another source of intrasite variation, or Type I variance, unless release sites are far apart and axon conduction introduces significant delays between sites. Asynchronous release is usually quantified by a function known as the release time course (RTC), computed by measuring the latency of individual quantal events in postsynaptic recordings at low-release probability,95 or computed by deconvolution methods.26 A detailed discussion on how to estimate the RTC for synapses either with a few release sites or with many release sites is given by Minneci and colleagues.95 In GCs, the RTC for a single site has a gamma-like distribution that rises abruptly from 0 and peaks near 0.1 ms,26 similar to that shown in Fig. 13.6C1. With such a RTC distribution at hand, simulating asynchronous vesicular release only requires the following two steps. First, a release time (trelease) is randomly drawn from the RTC distribution for each release site at the arrival of an action potential at tj. Second, each site’s trelease is added to tj when computing the quantal waveform (e.g., t′ = t – tj – trelease in Eqs. 13.4–13.7) thereby creating asynchronous release. Figure 13.6C1 shows such a simulation using the RTC of a GC, where the delay in quantal release is evident in the smearing of peaks. Here, in order to show the sole effects of asynchronous release, there was no variation in Q. Computing the frequency of peak amplitudes, where peaks are computed over the entire simulation window, shows asynchronous release has no effect on release events composed of less than two quanta, as expected. However, for release events composed of two or more quanta, asynchronous release causes a reduction in peak amplitudes, that is, a smearing of peak amplitudes toward smaller values, where the smearing effect is more pronounced for those events composed of the largest number of quanta (Fig. 13.6C2). On the other hand, if the peak amplitude is computed by averaging over a fixed time window centered on the mean peak EPSC, as for MPFA, a slightly different effect is observed. In this case, variability is also observed at those release events composed of a single quantum, since the peak of these events may fall outside the measurement window.94
Deviation from the variance predicted from binomial models of vesicular release can also arise from nonuniformities in release probability P. Dispersion in the release probability across release sites, which can also be quantified by the coefficient of variation (CVP), tends to reduce the variance of the synaptic response. Since this source of variation has the largest impact at high-release probabilities, its incorporation into a binomial model may not be necessary when simulating synapses with low P. If one wishes to include variability in the release probability, however, methods for doing so can be found elsewhere.94,95
Finally, we consider the simulation of a binomial synapse with short-term depression and facilitation, similar to that described previously.96 The most flexible way to simulate such a synapse is to treat each release site independently, as this will allow one to add variability to the quantal size Q and vesicle release time. For simplicity, we here assume the differential equations that describe depression and facilitation have exact analytical solutions, in which case the RP recursive algorithm described in Eqs. (13.28)–(13.32) can be used to simulate release at each release site. However, since each site is now simulated independently, R represents the probability a release site contains a vesicle, rather than the fraction of filled release sites. Addition of binomial release then requires the following two modifications of the RP recursive algorithm. First, step 2 described in Eq. (13.30) is modified as follows: a random number is drawn from the interval [0, 1]; if the random number is greater than Rj−ε·Pj−ε (i.e., the value R times P at the arrival time of the action potential), then release at the site is considered a failure and the site is ignored; otherwise release is considered a success and a synaptic conductance waveform with amplitude Q is added to Gtotal(t). Second, step 3 described in Eq. (13.31) is modified so that the decrement in R only occurs in the event of vesicle release (the increment in P described in Eq. (13.32) is always implemented since facilitation is assumed to be linked to the arrival of the action potential, here assumed to always occur at the time of the stimulus); furthermore, in the event of vesicle release, R is now decremented to zero (i.e., Rj+ε = 0). Figure 13.7A1 shows results of such a simulation for a synapse with five release sites, each with P = 0.5 and Q = 0.2 nS. To demonstrate the effects of depression and facilitation at moderate levels, the synapse was driven with a 100 Hz train of action potentials. Here, the binomial nature of vesicle release can be seen in the time course of R at each release site (blue traces), and Gtotal(t) computed from the sum of all quanta released at each site (gray trace). The time course of P, on the other hand, is not binomial but shows an incremental increase at the arrival of each action potential. Figure 13.7A2 shows the average of 100 such simulations (black trace), which closely matches the same simulation computed for a deterministic synapse (green trace). Figure 13.7B1 and B2 shows the same analysis for a 300 Hz train of action potentials to demonstrate the effect of a larger level of synaptic depression and facilitation. Note that the simulations in Fig. 13.7 include no variability in Q or the vesicle release times. To add variability to Q, one only needs to compute a nonuniform Q for each release site as described above, using CVQS and CVQII. One can also add variability to the vesicle release times by simulating asynchronous release at each release site using a RTC function as described above.
Figure 13.7. A binomial model with short-term depression and facilitation.
(A1) Simulation of a binomial synapse with NT = 5, P = 0.5, and Q = 0.2 nS using the RP recursive algorithm described in Eqs. (13.28)–(13.32) (τr = 50 ms, ΔP = 0.5, τf = 12 ms). The stimulus was a 100 Hz train of action potentials (top). Bottom graphs show time evolution of R (blue) and P (red) for each release sight during the train. Note, action potentials always caused facilitation, but only caused depression when there was success of vesicle release. At each release site, vesicle release was a success if a random number drawn from [0, 1] was less than the product RP. Gray trace (bottom) shows the sum of resulting quantal waveforms from all five sites. The quantal waveform was a GAMPAR waveform with only a direct component, the same used in Fig. 13.6. (A2) Conductance trains of the same simulation in (A1) for 100 trials (gray). Black trace shows average of the 100 trials, which closely matches the time course of the same simulation computed for a deterministic RP model (green dashed line). (B1 and B2) Same as (A1) and (A2) but for a 300 Hz train of action potentials.
8. GOING MICROSCOPIC
The models discussed in this chapter are intended to capture the basic macroscopic features of synaptic transmission, mainly the time and voltage dependence of the transfer of charge into the postsynaptic neuron. These types of models are useful for investigating signal processing at the cellular and network level but are generally not as useful for investigating the mechanism underlying signal transmission at a microscopic level. Hence, other modeling approaches are usually adopted when studying microscopic aspects of synaptic transmission. These approaches typically use partial differential equations to describe one or more aspect of the system under investigation, which might include the diffusion of ions, buffers, and vesicles, reactions between these entities, and conformational changes of protein structures (i.e., state transitions). The equations that describe the biological system under investigation are then solved numerically. Early examples of simulating presynaptic Ca2+ dynamics, including Ca2+ influx, diffusion, buffering, and extrusion in three dimensions, include the studies of Fogelson and Zucker97 and Roberts.98 More recent studies attempt to simulate the mechanisms underlying Ca2+-secretion coupling.39,99 Finite-difference methods have also been used to simulate glutamate dynamics within the synaptic cleft, including glutamate release and diffusion in three dimensions.32,34 A Monte Carlo approach can also be used100; in this case, a simulator such as MCell should be considered (http://www.mcell.cnl.salk.edu/). On the postsynaptic side, kinetics of ionotropic receptors such as AMPARs and NMDARs can be described by Markov models with multiple states, including open, closed, blocked, and desensitized states.32,34,63,91 Solutions to Markov models can be computed via transition matrixes, or stochastically (see Ref. 41).
9. SIMULATORS AND STANDARDIZED MODEL DESCRIPTIONS
A number of options exist for creating computer simulations of the synaptic models presented in this chapter. Generic simulation and analysis packages like MATLAB (http://uk.mathworks.com/products/matlab/) and Igor Pro (http://www.wavemetrics.com) are commonly used for simulating relatively simple models. These packages have the advantage that the user is completely in control of the model structure and can perform analysis in the same scripting language as that used in the model description. However, these packages are less useful when the models become so complex that the user’s scripts start to reproduce the functionality of freely available neuronal simulation packages. The more complex scripts can also be difficult for others to understand and adapt for their own needs.
Packages like NEURON101 and GENESIS102 have been used for many years to simulate neural systems from single cells to complex neuronal networks, with inbuilt features to assist in the development of multicompartmental neurons, membrane conductances, synapse models, and spiking networks. These packages, along with a recent reimplementation of GENESIS called MOOSE (http://moose.ncbs.res.in/), are freely available, well documented, and supported by user communities. They are particularly useful for physiological data-driven simulations, for example, investigating the effects of synaptic integration in complex neuronal morphologies.46 They also have a number of inbuilt synaptic model types which users can incorporate into their own custom models, particularly in NEURON using its NMODL language. A number of published models using these simulation packages are available online at ModelDB (http://senselab.med.yale.edu/modeldb/). NEST (http://www.nest-initiative.org) and Brian (http://www.briansimulator.org) are two other popular simulation packages which focus more on spiking neural networks. While the synapse models of these packages are more phenomenological than biophysical, they have been used in several investigations into the effects of synaptic properties on network function. While it is useful having multiple simulators to build synaptic and network models, a disadvantage is that the simulators often have different languages for specifying the models, making exchange of models between investigators difficult. NeuroML (http://www.NeuroML.org; Ref. 103) is an initiative to define a simulator-independent language to define cell, ion channel, synapse, and network models and to facilitate exchange of these models. A range of synapse model types are supported, including single- and double-exponential synapses, voltage-dependent synaptic conductances, short-term plasticity, and spike-timing-dependent plasticity. NeuroML v2.0 adds greater support for users to extend the markup language and define their own synapse models in a simulator-independent manner. The Open Source Brain repository (http://www.opensourcebrain.org) is a recent initiative to encourage collaborative development of a range of models in computational neuroscience. Moreover, making the models available in NeuroML ensures transparency, accessibility and cross-simulator portability.
10. SUMMARY
In this chapter, we discussed how mathematical models can capture various aspects of synaptic transmission. At their most basic level, the models are simple empirical descriptions of the average conductance waveform and current–voltage relation of postsynaptic receptors. Above this basic level, the models can be extended to capture more and more of the behavior of real synapses, including stochasticity and short-term plasticity. Throughout the chapter, we examined how well the different models replicate the experimental behavior of the cerebellar MF–GC synapse, an extensively characterized excitatory central synapse. The techniques we used can equally be applied to other excitatory and inhibitory synapses in the CNS. In our data-driven approach, we hoped to have highlighted a few key principles about modeling synaptic transmission, and modeling neurons in general. These include considering the balance between accurately replicating the biological processes under investigation and simplifying model descriptions to reduce variables and computational overhead. We urge modelers to obtain and directly compare their models to raw data (e.g., EPSCs and current–voltage relations) from the system under investigation wherever possible. This is important for ensuring the system being modeled is operating within physiologically relevant regimes. A data-driven approach also enables higher dimensional synaptic, neuronal, and network models to be effectively constrained and the effects of natural variability of presynaptic and postsynaptic elements to be explored.
ACKNOWLEDGEMENTS
We thank Bóris Marin, Eugenio Piasini, Arnd Roth, and Stefan Hallermann for their comments on the manuscript, and Padraig Gleeson for his contribution to the section on simulator packages. This work was funded by the Wellcome Trust (086699) and ERC. R. A. S. holds a Wellcome Trust Principal Research Fellowship (095667) and an ERC Advanced Grant (294667).
REFERENCES
- 1.Fatt P, Katz B. Spontaneous subthreshold activity at motor nerve endings. J Physiol. 1952;117(1):109–128. [PMC free article] [PubMed] [Google Scholar]
- 2.del Castillo J, Katz B. Quantal components of the end-plate potential. J Physiol. 1954;124(3):560–573. doi: 10.1113/jphysiol.1954.sp005129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Katz B. The Release of Neural Transmitter Substances. Liverpool University Press; Liverpool: 1969. [Google Scholar]
- 4.Couteaux R, Pécot-Dechavassine M. Synaptic vesicles and pouches at the level of “active zones” of the neuromuscular junction. C R Acad Sci Hebd Seances Acad Sci D. 1970;271(25):2346–2349. [PubMed] [Google Scholar]
- 5.De Robertis ED, Bennett HS. Some features of the submicroscopic morphology of synapses in frog and earthworm. J Biophys Biochem Cytol. 1955;1(1):47–58. doi: 10.1083/jcb.1.1.47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Palade GE, Palay SL. Electron microscope observations of interneuronal and neuromuscular synapses. Anat Rec. 1954;118:335–336. [Google Scholar]
- 7.Palay SL. Synapses in the central nervous system. J Biophys Biochem Cytol. 1956;2:193–202. doi: 10.1083/jcb.2.4.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Eccles JC, Katz B, Kuffler SW. Nature of the ‘end-plate potential’ in curarized muscle. J Neurophysiol. 1941;5:362–387. [Google Scholar]
- 9.Liley AW, North KA. An electrical investigation of effects of repetitive stimulation on mammalian neuromuscular junction. J Neurophysiol. 1953;16(5):509–527. doi: 10.1152/jn.1953.16.5.509. [DOI] [PubMed] [Google Scholar]
- 10.Neher E, Sakmann B, Steinbach JH. The extracellular patch clamp: a method for resolving currents through individual open channels in biological membranes. Pflugers Arch. 1978;375(2):219–228. doi: 10.1007/BF00584247. [DOI] [PubMed] [Google Scholar]
- 11.Harlow ML, Ress D, Stoschek A, Marshall RM, McMahan UJ. The architecture of active zone material at the frog’s neuromuscular junction. Nature. 2001;409(6819):479–484. doi: 10.1038/35054000. [DOI] [PubMed] [Google Scholar]
- 12.Biró AA, Holderith NB, Nusser Z. Quantal size is independent of the release probability at hippocampal excitatory synapses. J Neurosci. 2005;25(1):223–232. doi: 10.1523/JNEUROSCI.3688-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Silver RA, Lübke J, Sakmann B, Feldmeyer D. High-probability uniquantal transmission at excitatory synapses in barrel cortex. Science. 2003;302(5652):1981–1984. doi: 10.1126/science.1087160. [DOI] [PubMed] [Google Scholar]
- 14.Salpeter MM, Loring RH. Nicotinic acetylcholine receptors in vertebrate muscle: properties, distribution and neural control. Prog Neurobiol. 1985;25(4):297–325. doi: 10.1016/0301-0082(85)90018-8. [DOI] [PubMed] [Google Scholar]
- 15.Silver RA, Cull-Candy SG, Takahashi T. Non-NMDA glutamate receptor occupancy and open probability at a rat cerebellar synapse with single and multiple release sites. J Physiol. 1996;494(Pt. 1):231–250. doi: 10.1113/jphysiol.1996.sp021487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Traynelis SF, Silver RA, Cull-Candy SG. Estimated conductance of glutamate receptor channels activated during EPSCs at the cerebellar mossy fiber-granule cell synapse. Neuron. 1993;11(2):279–289. doi: 10.1016/0896-6273(93)90184-s. [DOI] [PubMed] [Google Scholar]
- 17.Bekkers JM, Stevens CF. NMDA and non-NMDA receptors are co-localized at individual excitatory synapses in cultured rat hippocampus. Nature. 1989;341(6239):230–233. doi: 10.1038/341230a0. [DOI] [PubMed] [Google Scholar]
- 18.Silver RA, Traynelis SF, Cull-Candy SG. Rapid-time-course miniature and evoked excitatory currents at cerebellar synapses in situ. Nature. 1992;355(6356):163–166. doi: 10.1038/355163a0. [DOI] [PubMed] [Google Scholar]
- 19.Ascher P, Nowak L. The role of divalent cations in the N-methyl-D-aspartate responses of mouse central neurones in culture. J Physiol. 1988;399:247–266. doi: 10.1113/jphysiol.1988.sp017078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bliss TV, Collingridge GL. A synaptic model of memory: long-term potentiation in the hippocampus. Nature. 1993;361(6407):31–39. doi: 10.1038/361031a0. [DOI] [PubMed] [Google Scholar]
- 21.Monyer H, Burnashev N, Laurie DJ, Sakmann B, Seeburg PH. Developmental and regional expression in the rat brain and functional properties of four NMDA receptors. Neuron. 1994;12(3):529–540. doi: 10.1016/0896-6273(94)90210-0. [DOI] [PubMed] [Google Scholar]
- 22.Schwartz EJ, Rothman JS, Dugué GP, Diana M, Rousseau C, Silver RA, Dieudonné S. NMDA receptors with incomplete Mg2+ block enable low-frequency transmission through the cerebellar cortex. J Neurosci. 2012;32(20):6878–6893. doi: 10.1523/JNEUROSCI.5736-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eccles JC, Ito M, Szentagothai J. The Cerebellum as a Neuronal Machine. Springer; New York: 1967. [Google Scholar]
- 24.DiGregorio DA, Nusser Z, Silver RA. Spillover of glutamate onto synaptic AMPA receptors enhances fast transmission at a cerebellar synapse. Neuron. 2002;35(3):521–533. doi: 10.1016/s0896-6273(02)00787-0. [DOI] [PubMed] [Google Scholar]
- 25.Palay SL, Chan-Palay V. Cerebellar Cortex: Cortex and Organization. Springer-Verlag; Berlin: 1974. [Google Scholar]
- 26.Sargent PB, Saviane C, Nielsen TA, DiGregorio DA, Silver RA. Rapid vesicular release, quantal variability, and spillover contribute to the precision and reliability of transmission at a glomerular synapse. J Neurosci. 2005;25(36):8173–8187. doi: 10.1523/JNEUROSCI.2051-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cathala L, Holderith NB, Nusser Z, DiGregorio DA, Cull-Candy SG. Changes in synaptic structure underlie the developmental speeding of AMPA receptor-mediated EPSCs. Nat Neurosci. 2005;8(10):1310–1318. doi: 10.1038/nn1534. [DOI] [PubMed] [Google Scholar]
- 28.Jakab RL, Hamori J. Quantitative morphology and synaptology of cerebellar glomeruli in the rat. Anat Embryol (Berl) 1988;179(1):81–88. doi: 10.1007/BF00305102. [DOI] [PubMed] [Google Scholar]
- 29.Saviane C, Silver RA. Fast vesicle reloading and a large pool sustain high bandwidth transmission at a central synapse. Nature. 2006;439(7079):983–987. doi: 10.1038/nature04509. [DOI] [PubMed] [Google Scholar]
- 30.Hallermann S, Fejtova A, Schmidt H, Weyhersmüller A, Silver RA, Gundelfinger ED, Eilers J. Bassoon speeds vesicle reloading at a central excitatory synapse. Neuron. 2010;68(4):710–723. doi: 10.1016/j.neuron.2010.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hallermann S, Silver RA. Sustaining rapid vesicular release at active zones: potential roles for vesicle tethering. Trends Neurosci. 2013;36(3):185–194. doi: 10.1016/j.tins.2012.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nielsen TA, DiGregorio DA, Silver RA. Modulation of glutamate mobility reveals the mechanism underlying slow-rising AMPAR EPSCs and the diffusion coefficient in the synaptic cleft. Neuron. 2004;42(5):757–771. doi: 10.1016/j.neuron.2004.04.003. [DOI] [PubMed] [Google Scholar]
- 33.Mitchell SJ, Silver RA. GABA spillover from single inhibitory axons suppresses low-frequency excitatory transmission at the cerebellar glomerulus. J Neurosci. 2000;20(23):8651–8658. doi: 10.1523/JNEUROSCI.20-23-08651.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.DiGregorio DA, Rothman JS, Nielsen TA, Silver RA. Desensitization properties of AMPA receptors at the cerebellar mossy fiber granule cell synapse. J Neurosci. 2007;27(31):8344–8357. doi: 10.1523/JNEUROSCI.2399-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cathala L, Brickley S, Cull-Candy SG, Farrant M. Maturation of EPSCs and intrinsic membrane properties enhances precision at a cerebellar synapse. J Neurosci. 2003;23(14):6074–6085. doi: 10.1523/JNEUROSCI.23-14-06074.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cathala L, Misra C, Cull-Candy SG. Developmental profile of the changing properties of NMDA receptors at cerebellar mossy fiber-granule cell synapses. J Neurosci. 2000;20(16):5899–5905. doi: 10.1523/JNEUROSCI.20-16-05899.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Farrant M, Feldmeyer D, Takahashi T, Cull-Candy SG. NMDA-receptor channel diversity in the developing cerebellum. Nature. 1994;368(6469):335–339. doi: 10.1038/368335a0. [DOI] [PubMed] [Google Scholar]
- 38.Gerstner W, Kistler WM. Spiking Neuron Models. Single Neurons, Populations, Plasticity. Cambridge University Press; Cambridge, UK: 2002. [Google Scholar]
- 39.Meinrenken CJ, Borst JG, Sakmann B. Calcium secretion coupling at calyx of held governed by nonuniform channel-vesicle topography. J Neurosci. 2002;22(5):1648–1667. doi: 10.1523/JNEUROSCI.22-05-01648.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pan B, Zucker RS. A general model of synaptic transmission and short-term plasticity. Neuron. 2009;62(4):539–554. doi: 10.1016/j.neuron.2009.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Roth A, van Rossum MCW. Modeling synapses. In: De Schutter E, editor. Computational Modeling Methods for Neuroscientists. The MIT Press; Cambridge, Massachusetts: 2009. [Google Scholar]
- 42.Trommershäuser J, Schneggenburger R, Zippelius A. Neher E. Heterogeneous presynaptic release probabilities: functional relevance for short-term plasticity. Biophys J. 2003;84(3):1563–1579. doi: 10.1016/S0006-3495(03)74967-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Williams SR, Mitchell SJ. Direct measurement of somatic voltage clamp errors in central neurons. Nat Neurosci. 2008;11(7):790–798. doi: 10.1038/nn.2137. [DOI] [PubMed] [Google Scholar]
- 44.Häusser M, Roth A. Estimating the time course of the excitatory synaptic conductance in neocortical pyramidal cells using a novel voltage jump method. J Neurosci. 1997;17(20):7606–7625. doi: 10.1523/JNEUROSCI.17-20-07606.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bekkers JM, Stevens CF. Cable properties of cultured hippocampal neurons determined from sucrose-evoked miniature EPSCs. J Neurophysiol. 1996;75(3):1250–1255. doi: 10.1152/jn.1996.75.3.1250. [DOI] [PubMed] [Google Scholar]
- 46.Rothman JS, Cathala L, Steuber V, Silver RA. Synaptic depression enables neuronal gain control. Nature. 2009;457(7232):1015–1018. doi: 10.1038/nature07604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jonas P, Spruston N. Mechanisms shaping glutamate-mediated excitatory postsynaptic currents in the CNS. Curr Opin Neurobiol. 1994;4(3):366–372. doi: 10.1016/0959-4388(94)90098-1. [DOI] [PubMed] [Google Scholar]
- 48.Silver RA, Colquhoun D, Cull-Candy SG, Edmonds B. Deactivation and desensitization of non-NMDA receptors in patches and the time course of EPSCs in rat cerebellar granule cells. J Physiol. 1996;493(Pt. 1):167–173. doi: 10.1113/jphysiol.1996.sp021372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Feldmeyer D, Cull-Candy S. Functional consequences of changes in NMDA receptor subunit expression during development. J Neurocytol. 1996;25(12):857–867. doi: 10.1007/BF02284847. [DOI] [PubMed] [Google Scholar]
- 50.Takahashi T, Feldmeyer D, Suzuki N, Onodera K, Cull-Candy SG, Sakimura K, Mishina M. Functional correlation of NMDA receptor epsilon subunits expression with the properties of single-channel and synaptic currents in the developing cerebellum. J Neurosci. 1996;16(14):4376–4382. doi: 10.1523/JNEUROSCI.16-14-04376.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Nevian T, Sakmann B. Spine Ca2+ signaling in spike-timing-dependent plasticity. J Neurosci. 2006;26:11001–11013. doi: 10.1523/JNEUROSCI.1749-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Shouval HZ, Bear MF, Cooper LN. A unified model of NMDA receptor-dependent bidirectional synaptic plasticity. Proc Natl Acad Sci USA. 2002;99(16):10831–10836. doi: 10.1073/pnas.152343099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang XJ. Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory. J Neurosci. 1999;19(21):9587–9603. doi: 10.1523/JNEUROSCI.19-21-09587.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Woodhull AM. Ionic blockage of sodium channels in nerve. J Gen Physiol. 1973;61(6):687–708. doi: 10.1085/jgp.61.6.687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Jahr CE, Stevens CF. Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci. 1990;10(9):3178–3182. doi: 10.1523/JNEUROSCI.10-09-03178.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Johnson JW, Ascher P. Voltage-dependent block by intracellular Mg2+ of N-methyl-D-aspartate-activated channels. Biophys J. 1990;57(5):1085–1090. doi: 10.1016/S0006-3495(90)82626-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kupper J, Ascher P, Neyton J. Internal Mg2+ block of recombinant NMDA channels mutated within the selectivity filter and expressed in Xenopus oocytes. J Physiol. 1998;507(Pt. 1):1–12. doi: 10.1111/j.1469-7793.1998.001bu.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Li-Smerin Y, Johnson JW. Kinetics of the block by intracellular Mg2+ of the NMDA-activated channel in cultured rat neurons. J Physiol. 1996;491(Pt. 1):121–135. doi: 10.1113/jphysiol.1996.sp021201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wollmuth LP, Kuner T, Sakmann B. Adjacent asparagines in the NR2-subunit of the NMDA receptor channel control the voltage-dependent block by extracellular Mg2+ J Physiol. 1998;506(1):13–32. doi: 10.1111/j.1469-7793.1998.013bx.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yang YC, Lee CH, Kuo CC. Ionic flow enhances low-affinity binding: a revised mechanistic view into Mg2+ block of NMDA receptors. J Physiol. 2010;588(Pt. 4):633–650. doi: 10.1113/jphysiol.2009.178913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Antonov SM, Johnson JW. Permeant ion regulation of N-methyl-D-aspartate receptor channel block by Mg2+ Proc Natl Acad Sci USA. 1999;96(25):14571–14576. doi: 10.1073/pnas.96.25.14571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Clarke RJ, Glasgow NG, Johnson JW. Mechanistic and structural determinants of NMDA receptor voltage-dependent gating and slow Mg2+ unblock. J Neurosci. 2013;33(9):4140–4150. doi: 10.1523/JNEUROSCI.3712-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kampa BM, Clements J, Jonas P, Stuart GJ. Kinetics of Mg2+ unblock of NMDA receptors: implications for spike-timing dependent synaptic plasticity. J Physiol. 2004;556(Pt. 2):337–345. doi: 10.1113/jphysiol.2003.058842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Adrian ED, Zotterman Y. The impulses produced by sensory nerve-endings. Part II. The response of a single end-organ. J Physiol. 1926;61(2):151–171. doi: 10.1113/jphysiol.1926.sp002281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Goldberg JM, Adrian HO, Smith FD. Response of neurons of the superior olivary complex of the cat to acoustic stimuli of long duration. J Neurophysiol. 1964;27:706–749. doi: 10.1152/jn.1964.27.4.706. [DOI] [PubMed] [Google Scholar]
- 66.Rieke F, Warland D, de Ruyter van Steveninck R, Bialek W. Spikes: Exploring the Neural Code. The MIT Press; Cambridge, Massachusetts: 1999. [Google Scholar]
- 67.Rancz EA, Ishikawa T, Duguid I, Chadderton P, Mahon S, Häusser M. High-fidelity transmission of sensory information by single cerebellar mossy fibre boutons. Nature. 2007;450(7173):1245–1248. doi: 10.1038/nature05995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Margrie TW, Brecht M, Sakmann B. In vivo, low-resistance, whole-cell recordings from neurons in the anaesthetized and awake mammalian brain. Pflugers Arch. 2002;444(4):491–498. doi: 10.1007/s00424-002-0831-z. [DOI] [PubMed] [Google Scholar]
- 69.Johnson DH, Tsuchitani C, Linebarger DA, Johnson MJ. Application of a point process model to responses of cat lateral superior olive units to ipsilateral tones. Hear Res. 1986;21(2):135–159. doi: 10.1016/0378-5955(86)90035-3. [DOI] [PubMed] [Google Scholar]
- 70.Rothman JS, Young ED, Manis PB. Convergence of auditory nerve fibers onto bushy cells in the ventral cochlear nucleus: implications of a computational model. J Neurophysiol. 1993;70(6):2562–2583. doi: 10.1152/jn.1993.70.6.2562. [DOI] [PubMed] [Google Scholar]
- 71.Young ED, Barta PE. Rate responses of auditory nerve fibers to tones in noise near masked threshold. J Acoust Soc Am. 1986;79(2):426–442. doi: 10.1121/1.393530. [DOI] [PubMed] [Google Scholar]
- 72.Lapicque L. Recherches quantitatives sur l’excitation électrique des nerfs traitée comme une polarisation. J Physiol Pathol Gen. 1907;9:620–635. [Google Scholar]
- 73.Knight BW. Dynamics of encoding in a population of neurons. J Gen Physiol. 1972;59(6):734–766. doi: 10.1085/jgp.59.6.734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Stein RB. A theoretical analysis of neuronal variability. Biophys J. 1965;5(2):173–194. doi: 10.1016/s0006-3495(65)86709-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Abbott LF, Regehr WG. Synaptic computation. Nature. 2004;431:796–803. doi: 10.1038/nature03010. [DOI] [PubMed] [Google Scholar]
- 77.Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rev Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]
- 78.Betz WJ. Depression of transmitter release at the neuromuscular junction of the frog. J Physiol. 1970;206(3):629–644. doi: 10.1113/jphysiol.1970.sp009034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Heinemann C, von Rüden L, Chow RH, Neher E. A two-step model of secretion control in neuroendocrine cells. Pflugers Arch. 1993;424(2):105–112. doi: 10.1007/BF00374600. [DOI] [PubMed] [Google Scholar]
- 80.Dittman JS, Regehr WG. Calcium dependence and recovery kinetics of presynaptic depression at the climbing fiber to Purkinje cell synapse. J Neurosci. 1998;18(16):6147–6162. doi: 10.1523/JNEUROSCI.18-16-06147.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Lipstein N, Sakaba T, Cooper BH, Lin K, Strenzke N, Ashery U, Rhee JS, Taschenberger H, Neher E, Brose N. Dynamic control of synaptic vesicle replenishment and short-term plasticity by Ca2+-calmodulin-Munc13-1 signaling. Neuron. 2013;79(1):82–96. doi: 10.1016/j.neuron.2013.05.011. [DOI] [PubMed] [Google Scholar]
- 82.Sakaba T, Neher E. Calmodulin mediates rapid recruitment of fast-releasing synaptic vesicles at a calyx-type synapse. Neuron. 2001;32(6):1119–1131. doi: 10.1016/s0896-6273(01)00543-8. [DOI] [PubMed] [Google Scholar]
- 83.Stevens CF, Wesseling JF. Activity-dependent modulation of the rate at which synaptic vesicles become available to undergo exocytosis. Neuron. 1998;21(2):415–424. doi: 10.1016/s0896-6273(00)80550-4. [DOI] [PubMed] [Google Scholar]
- 84.Wang LY, Kaczmarek LK. High-frequency firing helps replenish the readily releasable pool of synaptic vesicles. Nature. 1998;394(6691):384–388. doi: 10.1038/28645. [DOI] [PubMed] [Google Scholar]
- 85.Fuhrmann G, Segev I, Markram M, Tsodyks H. Coding of temporal information by activity-dependent synapses. J Neurophysiol. 2002;87(1):140–148. doi: 10.1152/jn.00258.2001. [DOI] [PubMed] [Google Scholar]
- 86.Varela JA, Sen K, Gibson J, Fost J, Abbott LF, Nelson SB. A quantitative description of short-term plasticity at excitatory synapses in layer 2/3 of rat primary visual cortex. J Neurosci. 1997;17(20):7926–7940. doi: 10.1523/JNEUROSCI.17-20-07926.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Tsodyks M, Pawelzik K, Markram H. Neural networks with dynamic synapses. Neural Comput. 1998;10:821–835. doi: 10.1162/089976698300017502. [DOI] [PubMed] [Google Scholar]
- 88.Hennig MH. Theoretical models of synaptic short term plasticity. Front Comput Neurosci. 2013;7:45. doi: 10.3389/fncom.2013.00045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Wu LG, Borst JG. The reduced release probability of releasable vesicles during recovery from short-term synaptic depression. Neuron. 1999;23(4):821–832. doi: 10.1016/s0896-6273(01)80039-8. [DOI] [PubMed] [Google Scholar]
- 90.Nieus T, Sola E, Mapelli J, Saftenku E, Rossi P, D’Angelo E. LTP regulates burst initiation and frequency at mossy fiber-granule cell synapses of rat cerebellum: experimental observations and theoretical predictions. J Neurophysiol. 2006;95(2):686–699. doi: 10.1152/jn.00696.2005. [DOI] [PubMed] [Google Scholar]
- 91.Wadiche JI, Jahr CE. Multivesicular release at climbing fiber-Purkinje cell synapses. Neuron. 2001;32(2):301–313. doi: 10.1016/s0896-6273(01)00488-3. [DOI] [PubMed] [Google Scholar]
- 92.Kuno M. Quantal components of excitatory synaptic potentials in spinal motoneurons. J Physiol. 1964;175(1):81–99. doi: 10.1113/jphysiol.1964.sp007504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Clements JD, Silver RA. Unveiling synaptic plasticity: a new graphical and analytical approach. Trends Neurosci. 2000;23(3):105–113. doi: 10.1016/s0166-2236(99)01520-9. [DOI] [PubMed] [Google Scholar]
- 94.Silver RA. Estimation of nonuniform quantal parameters with multiple-probability fluctuation analysis: theory, application and limitations. J Neurosci Methods. 2003;130(2):127–141. doi: 10.1016/j.jneumeth.2003.09.030. [DOI] [PubMed] [Google Scholar]
- 95.Minneci F, Kanichay RT, Silver RA. Estimation of the time course of neurotransmitter release at central synapses from the first latency of postsynaptic currents. J Neurosci Methods. 2012;205(1):49–64. doi: 10.1016/j.jneumeth.2011.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Maass W, Zador AM. Dynamic stochastic synapses as computational units. Neural Comput. 1999;11(4):903–917. doi: 10.1162/089976699300016494. [DOI] [PubMed] [Google Scholar]
- 97.Fogelson AL, Zucker RS. Presynaptic calcium diffusion from various arrays of single channels. Implications for transmitter release and synaptic facilitation. Biophys J. 1985;48(6):1003–1017. doi: 10.1016/S0006-3495(85)83863-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Roberts WM. Localization of calcium signals by a mobile calcium buffer in frog saccular hair cells. J Neurosci. 1994;14(5 Pt. 2):3246–3262. doi: 10.1523/JNEUROSCI.14-05-03246.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Bucurenciu I, Kulik A, Schwaller B, Frotscher M, Jonas P. Nanodomain coupling between Ca2+ channels and Ca2+ sensors promotes fast and efficient transmitter release at a cortical GABAergic synapse. Neuron. 2008;57(4):536–545. doi: 10.1016/j.neuron.2007.12.026. [DOI] [PubMed] [Google Scholar]
- 100.Franks KM, Stevens CF, Sejnowski TJ. Independent sources of quantal variability at single glutamatergic synapses. J Neurosci. 2003;23(8):3186–3195. doi: 10.1523/JNEUROSCI.23-08-03186.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Carnevale NT, Hines ML. The NEURON Book. Cambridge University Press; Cambridge, UK: 2006. [Google Scholar]
- 102.Bower JM, Beeman D. The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation SYstem. Springer-Verlag; New York: 1998. [Google Scholar]
- 103.Gleeson P, Steuber V, Silver RA. neuroConstruct: a tool for modeling networks of neurons in 3D space. Neuron. 2007;54(2):219–235. doi: 10.1016/j.neuron.2007.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]