Abstract
Motivation: Cancer progression and development are initiated by aberrations in various molecular networks through coordinated changes across multiple genes and pathways. It is important to understand how these networks change under different stress conditions and/or patient-specific groups to infer differential patterns of activation and inhibition. Existing methods are limited to correlation networks that are independently estimated from separate group-specific data and without due consideration of relationships that are conserved across multiple groups.
Method: We propose a pathway-based differential network analysis in genomics (DINGO) model for estimating group-specific networks and making inference on the differential networks. DINGO jointly estimates the group-specific conditional dependencies by decomposing them into global and group-specific components. The delineation of these components allows for a more refined picture of the major driver and passenger events in the elucidation of cancer progression and development.
Results: Simulation studies demonstrate that DINGO provides more accurate group-specific conditional dependencies than achieved by using separate estimation approaches. We apply DINGO to key signaling pathways in glioblastoma to build differential networks for long-term survivors and short-term survivors in The Cancer Genome Atlas. The hub genes found by mRNA expression, DNA copy number, methylation and microRNA expression reveal several important roles in glioblastoma progression.
Availability and implementation: R Package at: odin.mdacc.tmc.edu/∼vbaladan.
Contact: veera@mdanderson.org
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Complex biological processes, such as the development and progression of cancer, often involve the interaction of genomic and epigenetic factors with environmental factors (Cao et al., 2011; Schadt, 2009). Research has shown that genes can promote or inhibit tumor development within coordinating modules such as functional or cell signaling pathways (Boehm and Hahn, 2011). These genes and their corresponding pathways form networks that regulate various cellular functions. Thus, the construction and exploration of the topology of such networks and their constituents is of great interest for developing and understanding the biological mechanisms behind disease development and progression.
It is well-established that sub-networks within functional regulatory networks of genes and their products undergo changes in response to different conditions, such as cellular DNA damage or environmental stress. (Bandyopadhyay et al., 2010; Califano, 2011; Luscombe et al., 2004). Analytic approaches for evaluating the regulation of such networks have sought to determine how specific genes and pathways operate in the promotion or inhibition of human disease (Goeman and Bühlmann, 2007; Khatri et al., 2012; Mitrea et al., 2013; Rhinn et al., 2013; Tarca et al., 2009; Tavazoie et al., 1999; Taylor et al., 2009). For example, a hub gene within a regulatory network is a gene that acts to influence the activity of a large number of genes or transcription factors (Flintoft, 2004). Thus, it is of interest to analyze the activity or expression of a hub gene during different stages of disease. While differential gene expression analysis evaluates the changes in the expression of the hub gene under different conditions or states, the incorporation of a network structure extends the differential gene expression analysis to differential network analysis (de la Fuente, 2010), which is one of the primary aims of this article.
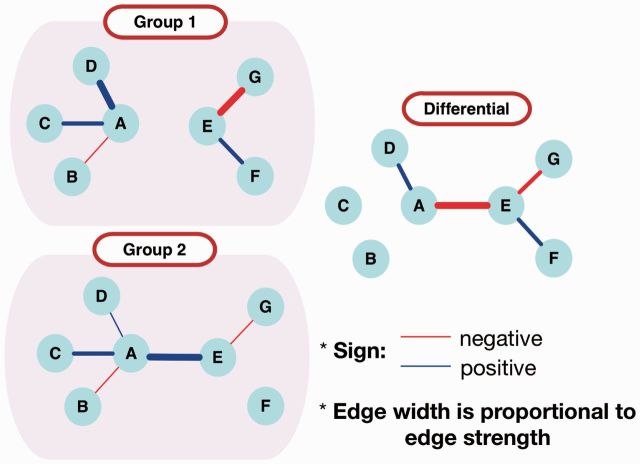
Figure 1 displays an example of the differential network analysis of data from two groups (e.g. of patients) that represent two different disease states. Each letter (vertex) represents a gene or any of its products (e.g. expression, methylation, copy number or transcription factor), and each line (edge) represents the co-expression in the network. In the group-specific networks (left panels), the edge colors and widths represent the signs and strengths of co-expression quantities. A differential network between group 1 and group 2 (right panel) is constructed by edge-wise subtraction of the co-expression quantities in the group-specific networks. In the differential network, the edge colors represent the signs of the differences and the edge widths are proportional to the strengths of the differences. This approach to network analysis allows us to discover some less obvious network relations that are not identified in the group-specific networks. At the same time, it will allow us to discard the relations that do not differentiate one disease state of interest from another (e.g. group 1 from group 2 in Fig. 1) (Ideker and Krogan, 2012; Mitra et al., 2013).
Fig. 1.
Graphical representation of the group-specific and differential networks. The differential network is constructed by the edge-wise subtraction of the strengths between the two group-specific networks
Most of the methods for differential network analysis rely on different correlation-based metrics to measure the strength of association between pairs of vertices in a network. Broadly, there are three main approaches for comparing group-specific networks in differential network analysis. The first approach obtains sparse group-specific networks and compares the network topologies, such as degrees of vertices or modularities between groups (Reverter et al., 2006; Zhang et al., 2009). The second approach handles weighted group-specific networks and uses some functions of the edge-specific weight differences as the edge weights to construct differential networks (Hudson et al., 2009; Liu et al., 2010; Rhinn et al., 2013; Tesson et al., 2010). Instead of relying on edge-wise co-expression differences, the last approach focuses more on finding gene sets and identifying which correlation patterns differ between groups. This approach formulates summary measures that represent co-expressions within a set of genes and compares the quantities between groups (Rahmatallah et al., 2014; Watson, 2006).
Although the above approaches have been useful in addressing important biological questions, the existing methods for analyzing differential networks are limited to correlation networks (i.e. two genes at a time). Also, the group-specific correlations are estimated separately using observations within each group. In this article, we obtain more refined, undirected relations than those based on correlation networks by estimating conditional dependencies between two genes after removing the effects of all other genes. This results in the construction of an undirected graph of conditional dependencies that is sparser than a correlation network (Markowetz and Spang, 2007). More importantly, the separate estimations are performed without due consideration of the global relationships that are preserved for all groups, i.e. are invariant to group specifications. For example, in our motivating example, we consider gene regulatory networks constructed using different modalities of genomic data (mRNA expression, DNA copy number, methylation status and microRNA expression). We are interested in determining how the network connectivity changes for patients with glioblastoma who experience different survival times, long-term and short-term survival times. Our hypothesis is that some conditional dependencies are shared across the groups and can be thought of as ‘passenger’ events and other conditional dependencies are unique to the groups and thus can be ‘driver’ events that change with cancer progression. The delineation of these components allows for a more refined picture of the major events (driver and/or passenger) in the elucidation of cancer progression and development.
To this end, we propose a differential network analysis in genomics (DINGO) framework, wherein we decompose the conditional dependencies among the genes/variables into a global component and a ‘local’ group-specific component and jointly estimate the group-specific conditional dependencies after adjusting for the global conditional dependencies. With the DINGO model, the dimension of the parameters is greatly reduced compared with that in separate estimations. In addition, we provide techniques for conducting rigorous statistical inference on the differential networks based on bootstrap procedures for assessing the differences in the group-specific conditional dependencies.
This article is organized as follows. In Section 2, we introduce the DINGO model and the estimation approach for calculating the group-specific networks and bootstrap thresholding to determine the significant differential edges. In Section 3, we apply our method to data obtained from The Cancer Genome Atlas (TCGA) glioblastoma study. We estimate differential networks for genes in glioblastoma cell signaling pathways, comparing data from long-term survivors (LTSs) and short-term survivors (STSs) using data from multiple platforms. In Section 4, we evaluate the DINGO method and compare it with other estimation approaches via simulations under different settings. We provide a summary and discussion in Section 5. In the Supplementary Materials, we present the technical details, additional results from the application of DINGO to TCGA glioblastoma data and additional simulation results.
2 DINGO model
We develop an approach called differential network analysis in genomics (DINGO) to infer differential patterns of network activation between patient-specific groups. Suppose we observe gene-level activity (such as mRNA, methylation or copy number) for p genes (denoted by ) measured over a patient. Furthermore, we have group-level information regarding whether a given patient belongs (generically) to group 1 or 2 (denoted by x = 0 or 1). Our aim is to construct a p-dimensional group-specific network, , that represents the relationship among the p genes belonging to a pathway and that has the following two components:
A ’global’ component, representing the relations that are common to both groups.
A ‘local’ group-specific component, , that represents the differential unique relations in each group depending on the value of x.
This decomposition serves a bi-fold objective. First, it explicitly allows for the delineation of specific network components that are conserved as well as changed across the groups, which allows for refined interpretations of differential networks. Second, as we show hereafter, it admits a natural dimension reduction technique that allows it to scale to moderate-to-large networks. Our model construction as detailed in Section 2.1 is in a general setting that includes multiple covariates and multi-categorical covariates (more than two groups) or continuous covariates. For ease of exposition, our illustrative examples focus on the case where we observe two-group membership data. In Section 2.2, the estimation methods are described under this setting and a differential network between the two groups is constructed by an inference procedure on the differences of the dependencies between the two groups. Supplementary Table S8 lists the notations that describes the various types of structure and provides definitions of all the model constructs.
2.1 Model construction
We denote the p genes by a p-dimensional vector . The conditional dependencies among p genes constitute an undirected graph, modeled via a Gaussian graphical model (GGM) for a set of vertices and a set of edges , such that any edge between and belongs to E if and only if genes a and b are conditionally dependent, given all other genes, . We assume that where is a positive definite precision matrix of and if and only if (Lauritzen, 1996). In this article, we call the precision matrix a GGM of the p genes. Suppose additionally we observe a vector of covariates . Our goal is to provide a model and estimation method for the conditional GGM of given .
Global component,
The global component represents the relations among p genes when there are no covariate effects. For example, using the example of the glioblastoma dataset, the global gene expression network describes the co-expression patterns for patients with glioblastoma, regardless of their survival times. To estimate the local group-specific component, the global component is adjusted before the covariate is introduced in the model.
We introduce a global network model,
where a p × p coefficient matrix specifies global relations among variables in V, is a vector following where is the ‘local’ GGM, the elements of which specify relations among genes in V after taking out the effects of the global relations. The local GGM can be expressed as a function of the GGM of and the global component, .
Local group-specific component,
For the local group-specific component, we model the local GGM with the covariate vector . For a residual vector , we introduce the inverse of the local GGM (covariance of ), as a function of ,
where is a p × q coefficient matrix, which is the main construction of interest and , with , is a p × p diagonal matrix whose elements, , represent variances for pure noise in . The covariance function is positive definite for all values of . This model decomposes to a rank 1 p × p matrix that depends on covariates and variances of pure noise. By constraining to be a diagonal matrix, the elements in are conditionally independent given the values of covariates . In essence, we represent the residual vector by a latent factor model with covariates (Tipping and Bishop, 1999). The covariance regression model (Hoff and Niu, 2012) decomposes the covariance matrix into two components: a covariance explained by the covariates and the global covariance. Because the model of Hoff and Niu (2012) is based on the covariance matrix of , the non-zero off-diagonal elements of represent the global relations, which are independent of .
For a square matrix, is defined by the trace. The group-specific precision matrix function, , with a covariate vector , is
| (1) |
where (Miller, 1981). This is the precision regression model as opposed to the covariance regression model. With a focus on precision matrix modeling in the DINGO model, we decompose the residual precision matrix into a full rank diagonal matrix that is independent of and a rank 1 matrix that determines the off-diagonal intensities of the precision matrices depending on . The precision regression modeling greatly reduces the number of parameters to be used in estimating the group-specific networks. When we observe two-group membership data, DINGO involves 2p parameters for and p parameters for , while a separate estimation needs parameters. When the number of groups increases, DINGO needs p additional parameters, while a separate estimation needs additional parameters. We exploit this fact in our computations involving multiple molecular networks in Section 3.
Concisely stated, the conditional GGM of given is obtained by the convolution,
| (2) |
where is the global component and is the local group-specific component related to , which is specified by parameters and in the precision regression model (1).
2.2 Joint estimation
In this section, we provide an overview and illustration of our approach in the context of TCGA glioblastoma data described in detail in Section 3. We consider how the gene networks in the cell signaling pathways differ between LTSs and STSs. The conditional GGM of given provides group-specific GGMs for LTSs and STSs. Based on the group-specific GGMs, we build a differential network between LTSs and STSs. In this section, the estimation method for the group-specific GGMs and the differential network are described under the two-group setting. A more detailed description of the technical aspects of our DINGO model and estimation, along with a simplified example and R code, are provided in Supplementary Sections S1 and S6, respectively.
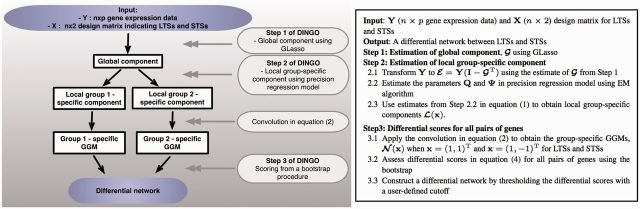
Suppose that we have n patients. We denote the n × p data matrix as , where represents the ith row of and includes expressions of p genes for the patient i. Each row is independently and identically following a p-dimensional multivariate normal distribution with a positive definite precision matrix (GGM) for all . The (q = 2) design matrix includes group information for LTSs and STSs with an intercept term. We assume that for i in the LTSs and for i in the STSs. Using gene-level data () and the design matrix indicating LTSs and STSs (), the detailed DINGO algorithm and its workflow are displayed in Figure 2. As an output, the DINGO algorithm provides differential scores for all links among the p genes.
Fig. 2.
DINGO workflow (left panel) and the detailed algorithm for estimation and inference (right panel)
2.2.1 Step 1 (estimation of global component, )
The global component is obtained by the GGM . The log likelihood of is proportional to where is the sample covariance matrix. When is positive definite and is the maximum likelihood estimate (MLE) of . Because the MLE assumes no zero restriction on the elements of N, it is a saturated model estimation (Lauritzen, 1996). This approach fails when p > n and requires n to be much larger than p. Many methods for determining the penalized MLE of have been proposed (Banerjee et al., 2008; Fan et al., 2009; Friedman et al., 2008; Rothman et al., 2008; Yuan and Lin, 2007). One of the most widely used methods is the graphical Lasso (GLasso) method (Friedman et al., 2008), which maximizes the following penalized log likelihood:
| (3) |
where η is a tuning parameter. As the tuning parameter η increases, more zero values in are induced. From the estimate of , all elements of are estimated by using for all and for all (Lauritzen, 1996). The sparse estimation of GGM provides a sparse estimate of the global component , in that there exist zero off-diagonal elements in . We use the Bayesian information criterion (BIC) to select the tuning parameter (Yuan and Lin, 2007).
2.2.2 Step 2 (estimation of local group-specific component, )
Suppose the global component is known. For the n × p data matrix , we transform the data matrix to , which is the residual data matrix after taking out the effects of global relations in . We assume each column of is standardized to have a mean of 0 and a standard deviation of 1. for and in model (1) determine the dependencies in the LTSs and STSs, respectively. The EM algorithm (Hoff and Niu, 2012) provides estimates of and . Applying the estimates of and to the precision regression model in Equation (1) provides the local group-specific component . The explicit expressions of the elements of are displayed in Supplementary Section S1.2.
2.2.3 Step 3 (differential scores for group-specific edges)
Through the above steps, we obtain estimates of the global component and the local group-specific components . The application of the estimates of and to the convolution operator in Equation (2) provides the group-specific GGMs, when and for LTSs and STSs, respectively. We then construct a differential network by thresholding a scaled difference in the conditional dependencies between two groups for each edge (a pair of vertices). The corresponding sets of partial correlations for the LTSs and STSs are denoted by and , respectively. For an edge between genes a and b, we hypothesize that two conditional dependencies corresponding to a pair of genes a and b are the same: . We construct a differential score as
| (4) |
where and are Fisher’s Z transformation of the estimates of and , respectively, and is the bootstrap estimate of the standard error obtained from Supplementary Section S1.4. The differential scores for all a < b can then be used to determine the edges in the differential network. The presence or absence of edges in the differential networks is determined by the differential scores in Equation (4): an edge (a, b) is present in a differential network if with k is a cutoff. The default k is 2 since it can be treated as a Wald-type statistic using a bootstrap estimate of the standard error. We classify the edges with into two types, conserved or differential edges according to signs in the dependencies between the LTSs and STSs, as defined below.
Conserved edges: an edge between genes a and b is defined as conserved if the dependencies between genes a and b have the same directions (i.e. positive or negative dependencies) for both groups, implying similar behavior. We define ‘conserved’ signs if ( and ) or ( and ).
Differential edges: an edge is differential if the dependencies have different directions (i.e. positive (negative) dependency in a group and negative (positive) dependency in another group). This is evaluated as ( and ) or ( and ).
For edges in a differential network, we display three components: (i) the differential strength, (width); (ii) the sign of the scores (color) and (iii) directional change, whether it is differential or conserved (type).
3 TCGA glioblastoma application
3.1 Dataset
Glioblastoma multiforme (GBM) is the most common primary brain tumor of adults. The median survival time of patients diagnosed with GBM is approximately 1 year, which places GBM among the most lethal of all cancers (McLendon et al., 2008; Mischel and Cloughesy, 2003). TCGA glioblastoma study includes 233 patients, along with their matched transcriptomic (mRNA), genomic (DNA copy number), epigenomic (methylation) and microRNA data. In this article, we take a pathway-based approach. We have focused our attention on specific pathways associated with GBM biology to investigate how the interactions between genes in a given pathway are activated and inhibited in the two sub-groups of patients: LTSs and STSs. This allows for more refined biological interpretations, especially for practitioners who tend to think in terms of pathway-based disruptions involved with disease progression for potential downstream clinical use. We present our analysis of genes that overlap with the three critical signaling pathways: RTK/PI3K, p53 and Rb signaling pathways that are involved in cell migration, survival and apoptosis (Furnari et al., 2007). The genes involved in those pathways are obtained from http://cbio.mskcc.org/cancergenomics/gbm/pathways and listed in Supplementary Section S2.2. In Supplementary Section S2.3, we describe a more comprehensive analysis involving multiple pathways from three established pathway databases: KEGG, BIOCARTA and REACTOME. It is our hypothesis that a better understanding of the interactions between the molecular data for these core pathways will provide new insights into the progression of GBM (Verhaak et al., 2010).
To define our patient groups, we partitioned the patients into two groups on the basis of their survival times, taking the top 45% (83 patients, surviving > 407 days) as LTSs and the bottom 45% (73 patients, surviving < 341 days) as STSs using an extreme discordant phenotype design (Nebert, 2000). Detailed information on this partitioning is described in Supplementary Section S2.1. We analyzed four different platforms to identify differential networks with respect to the LTSs and STSs. We downloaded data from TCGA portal for analysis, which included mRNA, DNA copy number, methylation and microRNA data generated from the Affymetrix HT Human Genome U133 Array Plate Set, Agilent Human Genome CGH Microarray 244A, Illumina Infinium Human DNA Methylation 27 and Agilent 8 × 15 K Human miRNA-specific microarrays, respectively. For DNA copy number and methylation data, we took the first principal components for several sites that correspond to a gene in the GBM pathways. For microRNA data, we took only human microRNAs. The number of vertices (p) consisted of 49 genes for mRNA, 51 for copy number, 50 for methylation and 470 for microRNA. A more detailed description of the datasets and pre-processing steps is provided in Supplementary Section S2.2.
3.2 DINGO application
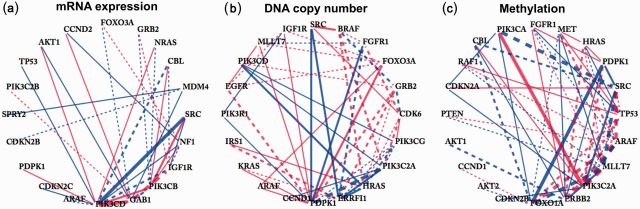
Applying our DINGO method, we obtain differential scores for all pairs of genes. The resulting differential networks with from mRNA expression, DNA copy number and methylation are displayed in Figure 3. The differential network for microRNA expression is displayed in Supplementary Figure S15 for . The corresponding list of hub genes that have degrees greater than 4 in the differential networks is presented in Table 1.
Fig. 3.
Differential networks between LTSs and STSs of glioblastoma estimated from three platforms: (a) mRNA expression; (b) DNA copy number and (c) methylation. The vertices are ordered by degrees (number of connections). The blue (red) edges indicate a positive (negative) score. The solid (dashed) lines represent conserved (differential) signs in the dependencies between the LTSs and STSs. The thickness of the edges corresponds to the strength of the associations, with stronger scores having greater thickness
Table 1.
List (degree of connectivity) of hubs detected by differential networks
| Networks | Hubs (degree of connectivity) |
|---|---|
| mRNA expression | PIK3CD (12), GAB1 (8), PIK3CB (7), IGF1R (6), NF1 (5) |
| DNA copy number | PDPK1 (13), ERRFI1 (8), HRAS (8), PIK3C2A (7), CDK6 (6), GRB2 (6), PIK3CG (6), BRAF (5), FGFR1 (5), FOXO3A (5) |
| methylation | FOXO1A (10), ERBB2 (10), ARAF (9), MLLT7 (9), PIK3C2A (9), SRC (8), TP53 (8), HRAS (6), MET (6), PDPK1 (6), FGFR1 (5) |
| microRNA expression | hsa-miR-103 (30), hsa-miR-107 (22), hsa-miR-608 (19), hsa-miR-623 (9), hsa-miR-526c (7), hsa-miR-188 (6), hsa-miR-30e-3p (5), hsa-miR-575 (5), hsa-miR-622 (5), hsa-miR-648 (5), hsa-miR-652 (5) |
3.2.1 Biological interpretations
The MYC oncogene, which contributes to cancer cell metabolism, encodes a transcription factor, c-Myc (Dang et al., 2009). The factor c-Myc has a central role in regulating the proliferation and survival of glioblastoma stem cells (Wang et al., 2008). For the indirect effects of the c-Myc gene, our data did not explicitly include the c-Myc gene; rather we found that most of the hub genes detected using our methods had c-Myc connections [Fig. 7F in Masui et al. (2013)]. PDPK1 had the highest degree in the network from DNA copy number data. Velpula et al. (2013) established PDPK1 as a key driver and candidate therapeutic target in GBM. Moreover, their study indicated that PDPK1 may promote EGFR activation, which results in malignant progression in GBM: we found an edge between PDPK1 and EGFR (Fig. 3b). EGFR activates PI3K and mTORC2 genes (Masui et al., 2013; McLendon et al., 2008). PI3K genes (PIK3CD, PIK3CB, PIK3C2A and PIK3CG) are present in all the differential networks from mRNA expression, DNA copy number and methylation. PIK3CA and PIK3C2A, which are PI3K genes, had strong differential relation in the methylation network (Fig. 3c). The PI3K pathway is frequently dysregulated in GBM and a promising therapeutic target for the disease (Wen et al., 2012). Both PI3K and mTORC2, which are regulated by EGFR, independently inhibit FOXO activity, which is associated with c-Myc levels (Masui et al., 2013). The network from methylation data shows that the FOXO1A gene had the highest degree (Fig. 3c and Table 1). The gene had connection to MLLT7 (FOXO) and PIK3CA (PI3K). The regulatory networks that include mTORC2, FOXO and c-Myc are highly intercorrelated with shorter survival of GBM patients (Masui et al., 2013). For assessing the direct effects of the c-Myc gene, the comprehensive analysis of pathways in KEGG, BIOCARTA and REACTOME (Supplementary Section S2.3) included the MYC gene, and the differential networks for neighbors of the MYC gene are shown in Supplementary Figure S3. Table 1 shows that hsa-miR-103 and hsa-miR-107 have the highest degrees. CDK5 is overexpressed and plays an important role in glioblastoma (Liu et al., 2008). The hubs, hsa-miR-103 and hsa-miR-107, regulate CDK5R1, which is a specific activator of CDK5 (Moncini et al., 2011).
3.2.2 Role of hub genes
We evaluated the effects of these hub genes on GBM progression. We took the top hub genes and assessed their direct effects on the patient survival times. We fitted univariate Cox-proportional hazards models for survival times with the hub genes as covariates/predictors. We found that FOXO3A (through DNA copy number changes), ERBB2 and MLLT7 (through methylation changes) and microRNA hsa-miR-623 were significantly associated with survival times (p-value < 0.05). Additional comparisons of the estimated group-specific and differential networks with other methods in the literature are described in Supplementary Section S4.
4 Simulation studies
To evaluate the accuracy and operating characteristics of the DINGO model, we conducted several simulation studies. In Case I of our simulation study, we generated the data by setting the parameters in the DINGO model (such as and ). In Case II (Supplementary Section S3.2), the group-specific data are generated from two separate GGMs. In this section, we display the results of Case I. We compared the performance of our method with those of a variety of separate estimation methods. As a basic method for estimating the precision matrix, we chose maximum likelihood estimation (MLE), which offers desirable statistical properties. However, it is invalid when the sample size is less than the number of variables. For high-dimensional settings (n < p), we use GLasso because the L1 penalized MLE performs well in detecting hub genes regardless of the dimension of the data (Allen et al., 2012). We assumed a sample size of 150 (n), with 75 samples in each of the two groups. In each of the datasets corresponding to the groups, we applied MLE and GLasso and compared their performance with the estimation from DINGO. For the fixed sample size, we considered two simulation settings, n > p and n < p.
Simulation setting, n > p
We simulate datasets that reflect the mRNA expression data studied in the application data example in Section 3, which includes 49 genes in the pathways (p = 49). The global component, , is determined by the GBM pathways used in Section 3. We consider the four different simulation settings described in Supplementary Section S3.1 according to the effect sizes and noise level specified by the diagonal elements of .
Simulation setting, n < p
With 100 and 500, we determine the structure of by generating a scale-free network using the Barabasi–Albert algorithm (Barabási and Albert, 1999). The scale-free networks are likely to be organized into hub genes with many edges. A hub gene within a regulatory network is a gene that acts to influence the activity of a large number of genes or transcription factors (Flintoft, 2004). We specified and as the high effect, high noise setting (A4) in Supplementary Section S3.1.
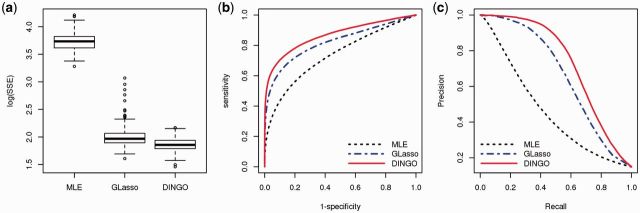
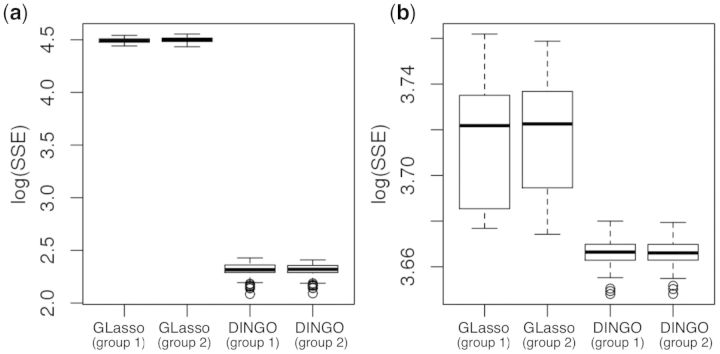
For each replication, we generate the true group-specific conditional dependencies and the data, and we base the results on 100 replications. We examine the sum of squared error (SSE), the receiver operating characteristic (ROC) curves and the precision recall (PR) curves, which are defined in Supplementary Section S3.1. Figure 4 displays the boxplots of (SSE), ROC curves and PR curves for the MLE, GLasso and DINGO methods under the setting, n > p and (A4). We combined the (SSE) from both groups in a boxplot for each method and the ROC and PR curves are averaged over 100 replications and groups. Our method provides more accurate estimates of the conditional dependencies than the MLE and GLasso methods (Fig. 4a). The ROC curve and the PR curve for our method uniformly dominate those for the MLE and GLasso methods (Fig. 4b and c). Supplementary Figures S11–S14 separately display the results for n > p settings from both groups. When the effect size is high and the noise level is low, we observe that the GLasso method performs better than the DINGO method for the group 2 network because the simulation data for the two groups are well separated (Supplementary Fig. S13). We compare GLasso and DINGO for the setting when p > n. Figure 5a and b displays boxplots of (SSE) from 100 replications for 100 and 500. For p = 100, GLasso uses 75 samples for the separate estimation, while DINGO uses all 150 observations for our joint estimation. Thus, the performances of GLasso and DINGO differed most for p = 100. When 500, DINGO provided more accurate estimates than GLasso. Overall, DINGO performed better than MLE and GLasso when the noise level was high compared to the effect size, and DINGO consistently performed better than GLasso as p increased.
Fig. 4.
Simulation results for the high effect size and noise scenario (n > p) from 100 simulation datasets. (a) Boxplots of (SSE); (b) ROC curves and (c) PR curves
Fig. 5.
Boxplots of (SSE) of n < p setting: (a) p = 100 and (b) p = 500
5 Discussion
We propose a joint modeling approach, DINGO, for estimating differential networks in various genomic data in the presence of group information. DINGO estimates separate conditional dependencies for each group and allows for global dependencies; thus, it borrows strength more efficiently between groups. We applied our DINGO method to TCGA glioblastoma data from four platforms, mRNA expression, DNA copy number, methylation and microRNA expression and we found hub genes based on the differential networks, many of which were in the regulatory network related to the c-Myc gene that contributes to the regulation of GBM proliferation and shorter survival times in GBM patients.
While pathways used in our analysis (Section 3) have been implicated in GBM in prior studies, the exact nature of the pathway components has not been studied with respect to differential patterns of activation/inactivation related to the patient prognostic groups. Our re-analysis focuses on the exact pathway breakages using data from multiple platforms, which sheds a completely different light on the various biological processes involved in GBM progression. The established pathways include up to 600 genes (Supplementary Fig. S17). For 50 and 600 genes, Steps 1 and 2 of DINGO take around 20 s and 57 min, respectively, which makes it feasible to conduct pathway-based differential network analysis. A more detailed discussion of the computation time is provided in Supplementary Section S7.
Although our DINGO method was applied to a two-group setting, the model can be generalized to incorporate multiple categories (such as multiple stages of disease and multiple subtypes) as well as continuous covariates (such as age and time). For three groups with an intercept term, we can apply and for group 1, group 2 and group 3, respectively, in the Equation (1). We can also add age as a continuous covariate by defining the covariate vectors for i in LTSs and for i in STSs. This would require additional generalizations of our estimation and computational algorithms; tasks that we leave for future consideration.
6 Software
The R package and the manual for DINGO are available at http://odin.mdacc.tmc.edu/∼vbaladan/Veera_Home_Page/Software.html.
Supplementary Material
Acknowledgements
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
Funding
This work was supported in part by the MD Anderson Cancer Center Prostate Cancer SPORE (P50 CA140388) and the Texas 4000 Endowed Distinguished Professorship (to K.-A.D.), by NIH grant R01 CA160736 (to V.B.), by the Cancer Center Support Grant (CCSG) from the NIH/NCI (P30 CA016672) (to K.-A.D. and V.B.) and by MD Anderson internal research funds (to M.J.H.).
Conflict of Interest: none declared.
References
- Allen J.D., et al. (2012) Comparing statistical methods for constructing large scale gene networks. PLoS One, 7, e29348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandyopadhyay S., et al. (2010) Rewiring of genetic networks in response to DNA damage. Science, 330, 1385–1389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee O., et al. (2008) Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data. J. Machine Learning Res., 9, 485–516. [Google Scholar]
- Barabási A.-L., Albert R. (1999) Emergence of scaling in random networks. Science, 286, 509–512. [DOI] [PubMed] [Google Scholar]
- Boehm J.S., Hahn W.C. (2011) Towards systematic functional characterization of cancer genomes. Nat. Rev. Genet., 12, 487–498. [DOI] [PubMed] [Google Scholar]
- Califano A. (2011) Rewiring makes the difference. Mol. Syst. Biol., 7, 463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Y., et al. (2011) Cancer research: past, present and future. Nat. Rev. Cancer, 11, 749–754. [DOI] [PubMed] [Google Scholar]
- Dang C.V., et al. (2009) MYC-induced cancer cell energy metabolism and therapeutic opportunities. Clin. Cancer Res., 15, 6479–6483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de la Fuente A. (2010) From differential expression to differential networking—identification of dysfunctional regulatory networks in diseases. Trends Genet., 26, 326–333. [DOI] [PubMed] [Google Scholar]
- Fan J., et al. (2009) Network exploration via the adaptive lasso and scad penalties. Ann. Appl. Stat., 3, 521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flintoft L. (2004) Rewiring the network. Nat. Rev. Genet., 5, 808–808. [Google Scholar]
- Friedman J., et al. (2008) Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9, 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furnari F.B., et al. (2007) Malignant astrocytic glioma: genetics, biology, and paths to treatment. Genes Dev., 21, 2683–2710. [DOI] [PubMed] [Google Scholar]
- Goeman J.J., Bühlmann P. (2007) Analyzing gene expression data in terms of gene sets: methodological issues. Bioinformatics, 23, 980–987. [DOI] [PubMed] [Google Scholar]
- Hoff P.D., Niu X. (2012) A covariance regression model. Stat. Sin., 22, 729–753. [Google Scholar]
- Hudson N.J., et al. (2009) A differential wiring analysis of expression data correctly identifies the gene containing the causal mutation. PLoS Comput. Biol., 5, e1000382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideker T., Krogan N.J. (2012) Differential network biology. Mol. Syst. Biol., 8, 565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khatri P., et al. (2012) Ten years of pathway analysis: current approaches and outstanding challenges. PLoS Comput. Biol., 8, e1002375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauritzen S.L. (1996) Graphical Models. Oxford University Press, USA. [Google Scholar]
- Liu B.-H., et al. (2010) DCGL: an R package for identifying differentially coexpressed genes and links from gene expression microarray data. Bioinformatics, 26, 2637–2638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu R., et al. (2008) Cdk5-mediated regulation of the PIKE-A-Akt pathway and glioblastoma cell invasion. Proc. Natl. Acad. Sci. USA, 105, 7570–7575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luscombe N.M., et al. (2004) Genomic analysis of regulatory network dynamics reveals large topological changes. Nature, 431, 308–312. [DOI] [PubMed] [Google Scholar]
- Markowetz F., Spang R. (2007) Inferring cellular networks—a review. BMC Bioinformatics, 8, S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masui K., et al. (2013) mTOR complex 2 controls glycolytic metabolism in glioblastoma through FoxO acetylation and upregulation of c-Myc. Cell Metab., 18, 726–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLendon R., et al. (2008) Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature, 455, 1061–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller K.S. (1981) On the inverse of the sum of matrices. Math. Mag., 54, 67–72. [Google Scholar]
- Mischel P.S., Cloughesy T.F. (2003) Targeted molecular therapy of GBM. Brain Pathol., 13, 52–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra K., et al. (2013) Integrative approaches for finding modular structure in biological networks. Nat. Rev. Genet., 14, 719–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitrea C., et al. (2013) Methods and approaches in the topology-based analysis of biological pathways. Front. Physiol., 4, 278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moncini S., et al. (2011) The role of miR-103 and miR-107 in regulation of CDK5R1 expression and in cellular migration. PLoS One, 6, e20038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nebert D.W. (2000) Extreme discordant phenotype methodology: an intuitive approach to clinical pharmacogenetics. Eur. J. Pharmacol., 410, 107–120. [DOI] [PubMed] [Google Scholar]
- Rahmatallah Y., et al. (2014) Gene sets net correlations analysis (GSNCA): a multivariate differential coexpression test for gene sets. Bioinformatics, 30, 360–368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reverter A., et al. (2006) Simultaneous identification of differential gene expression and connectivity in inflammation, adipogenesis and cancer. Bioinformatics, 22, 2396–2404. [DOI] [PubMed] [Google Scholar]
- Rhinn H., et al. (2013) Integrative genomics identifies APOE ε4 effectors in Alzheimer’s disease. Nature, 500, 45–50. [DOI] [PubMed] [Google Scholar]
- Rothman A.J., et al. (2008) Sparse permutation invariant covariance estimation. Electron. J. Stat., 2, 494–515. [Google Scholar]
- Schadt E.E. (2009) Molecular networks as sensors and drivers of common human diseases. Nature, 461, 218–223. [DOI] [PubMed] [Google Scholar]
- Tarca A.L., et al. (2009) A novel signaling pathway impact analysis. Bioinformatics, 25, 75–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavazoie S., et al. (1999) Systematic determination of genetic network architecture. Nat. Genet., 22, 281–285. [DOI] [PubMed] [Google Scholar]
- Taylor I.W., et al. (2009) Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat. Biotechnol., 27, 199–204. [DOI] [PubMed] [Google Scholar]
- Tesson B.M., et al. (2010) Diffcoex: a simple and sensitive method to find differentially coexpressed gene modules. BMC Bioinformatics, 11, 497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tipping M.E., Bishop C.M. (1999) Probabilistic principal component analysis. J. R. Stat. Soc. B (Stat. Methodol.), 61, 611–622. [Google Scholar]
- Velpula K.K., et al. (2013) Combined targeting of PDK1 and EGFR triggers regression of glioblastoma by reversing the Warburg effect. Cancer Res., 73, 7277–7289. [DOI] [PubMed] [Google Scholar]
- Verhaak R.G., et al. (2010) Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell, 17, 98–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., et al. (2008) c-Myc is required for maintenance of glioma cancer stem cells. PLoS One, 3, e3769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson M. (2006) CoXpress: differential co-expression in gene expression data. BMC Bioinformatics, 7, 509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen P.Y., et al. (2012) Current clinical development of PI3K pathway inhibitors in glioblastoma. Neuro Oncol., 14, 819–829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M., Lin Y. (2007) Model selection and estimation in the Gaussian graphical model. Biometrika, 94, 19–35. [Google Scholar]
- Zhang B., et al. (2009) Differential dependency network analysis to identify condition-specific topological changes in biological networks. Bioinformatics, 25, 526–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.