Study of force-induced melting of dsDNA as a function of length and conformation

Abstract

We measure the constant force required to melt double-stranded DNA (ds) as a function of length for lengths from 12 to 100,000 base pairs, where the force is applied to the 3’3’ or 5’5’ ends of the dsDNA. Molecules with 32 base pairs or less melt before overstretching. For these short molecules, the melting force is independent of the ends to which the force is applied and the shear force as a function of length is well described by de Gennes theory with a de Gennes length of less than 10 bp. Molecules with lengths of 500 base pairs or more overstretch before melting. For these long molecules, the melting force depends on the ends to which the force is applied. The melting force as a function of length increases even when the length exceeds 1000 bp, where the length dependence is inconsistent with de Gennes theory. Finally, we expand de Gennes melting theory to 3’5’ pulling and compare the predictions with experimental results.

1. Introduction

Double-stranded DNA (dsDNA) exists in a variety of different conformations in vivo, even in the absence of force. Many research groups have demonstrated that if a force of approximately 65 pN is applied to the ends of a long dsDNA, the molecule will increase in length [1–10]. At forces above 67 pN, the length/base pair is approximately 1.7 times the length/base pair in B-DNA [1–10]. This force induced length change is commonly referred to as the overstretching transition. It is studied partly because of its relevance to biology: when dsDNA is bound to RecA and its eukaryotic analogs, the length of the bound dsDNA is about 1.5 times the B-form length [11]. The increase in length that is induced by RecA binding is believed to play an important role in promoting strand exchange [12–14]. The suggestion that overstretching reduces Watson-Crick pairing is supported by experiments that have shown that when RecA is bound to dsDNA the pairing of one strand of the dsDNA to its matching strand of ssDNA that is free in solution, is enhanced [14].

The force induced increase in dsDNA length has been studied theoretically as well as experimentally. Several overstretched dsDNA conformations have been proposed [15, 16]. In these conformations, Watson-Crick pairing is maintained in the overstretched state, and the overstretching is the result of a continuous rotation of bond angles in dsDNA [15, 16] where the exact structure depends on the ends to which the force is applied [15]. It has also been suggested that the base pairs melt when dsDNA is overstretched, resulting in two parallel strands of ssDNA, where the melting force will be independent of the ends to which the force is applied [17, 18]. We note that the measured mechanical properties of the overstretched state are not the same as those for two parallel strands of ssDNA [19–21].

Recent experimental results provide support for some of the proposed structures of overstretched dsDNA since the melting force depends on the ends to which the force is applied if the molecules overstretch before they melt [21, 22]. Those experimental results have also shown that the melting force for overstretched DNA is larger than the melting force for B-form DNA [21–23] where the latter does not depend on the ends to which the force is applied [23]. These results would at first appear to contradict the suggestion that the base pairs in overstretched DNA are more weakly bound than the base pairs in B-DNA; however, de Gennes proposed a model of the melting of dsDNA that suggests that the melting force for a molecule could increase even if the binding between individual bases decreases [24].

In de Gennes model, the finite stiffness of the phosphate backbones results in a redistribution of stress between the two ssDNA strands that compose a single dsDNA molecule. This theory predicts that the rupture force for a molecule can be approximated by the product of the number of bases over which the force extends and the force required to separate one base pair. For short molecules, the rupture force extends over all of the bases in the molecule, so the model predicts that it will increase linearly with the number of bases in the molecule. For long molecules, the model predicts that the rupture force will be confined to a small number of bases near the ends of the molecule, where the number of bases over which the rupture force extends is equal to the de Gennes length, χ⁻¹. For long molecules the rupture force is independent of length and given by 2 f₁ (χ⁻¹+1), where f₁ is the rupture force/bp. Thus, even if the binding energy/bp is weaker in overstretched dsDNA than in B-form dsDNA, the rupture force for overstretched dsDNA may be larger than the asymptotic value for B-form dsDNA if the ratio for the de Gennes length of the overstretched molecule to the de Gennes length of B-form dsDNA is sufficiently large.

A recent more detailed theoretical study has considered the force induced melting of dsDNA pulled from the 3’3’ or 5’5’ ends, where the model includes stacking interactions and sequence heterogeneity [25]. The main predictions for the melting force are in good agreement with those from de Gennes simpler model, though including stacking had the important effect of removing unphysical soft modes while sequence heterogeneity caused different regions of the molecule to melt at different forces.

The crystallographic results suggest that when dsDNA is bound to RecA, only one of the phosphate backbones is under tension [26]. In both 3’3’ and 5’5’ pulling, force is directly applied to each of the backbones as shown in figures 1(b), (c), (e), and (f) ; however, when dsDNA is pulled from the 3’5’ ends, force is only directly applied to one of the backbones, as shown in figures 1(d) and (g). Thus, if one is interested in the binding between bases in dsDNA bound to RecA, it may be useful to study the force induced melting of dsDNA overstretched from the 3’5’ends. De Gennes did not consider this case, but in this work we will present an extension of de Gennes theory that can describe the force induced melting of dsDNA pulled from the 3’5’ ends.

Figure 1.

Schematic of different pulling techniques showing changes in base pair tilt and separation. (a) B-form dsDNA with no force applied to the ends; (b) overstretching by pulling from 3’3’ ends resulting in base pair tilt in the direction opposite to B-form; (c) overstretching by pulling from 5’5’ ends; (d) dsDNA overstretched from the 3’5’ ends where the force is exerted on each of the base pairs but there is no force exerted on the central base pair; (e) pulling from 3’3’ ends, (f) pulling from 5’5’ ends, and (g) pulling from 3’5’ ends, the length of the molecule in these three cases is longer than the assumed de Gennes length and the force required to shear the molecule does not increase with molecule length because the force impacts only the base pairs at the ends of the molecule and remains equally distributed regardless of the number of base pairs between the ends and the middle. Changes are exaggerated for clarity. For all constructs the number of base pairs ranges from n = −L/2 to n = L/2, where L equals the length of the molecule.

1.1. Review of de Gennes theory for 3’3’ and 5’5’ pulling

De Gennes considered the force induced melting of dsDNA pulled from the 3’3’ or 5’5’ ends, as illustrated in figure 1. The energy for each of the bonds was modeled as a harmonic oscillator, where the potential between base pairs is identical for all base pairs and characterized by a spring constant R, and the potential between phosphates is identical for all phosphates and characterized by a spring constant Q. De Gennes labeled the two backbone strands u and v, and the position of the nth phosphate on each of the backbones is described using u_n and v_n, where n runs from –L/2 to L/2 with L equal to the length of the molecule, as shown in figure 1. Given these assumptions, the total energy is given by:

$$H=\sum _{-L/2}^{\infty }\frac{1}{2}Q{(u_{n+1}-u_n)}^2+\sum _{-\infty }^{L/2}\frac{1}{2}Q{(v_{n+1}-v_n)}^2+\sum _{-L/2}^{L/2}\frac{1}{2}R{(u_n-v_n)}^2$$ (1)

De Gennes defined a constant, the de Gennes length, that depends on the ratio of the two spring constants: ${\chi }^{-1}=\sqrt{\frac{Q}{2R}}$, which is the characteristic length over which the rupture force is distributed in long molecules pulled from either their 3’3’ or 5’5’ ends. The difference in displacement between the two base pairs at the same position on opposite strands is given by:

$$u_n-v_n={\delta }_o\text{cosh}(\chi n)$$ (2)

Thus, when the length of the molecule is much less than the de Gennes length, the displacement between all of the base pairs is constant and given by δo, as shown schematically in figures 1(b) and (c). In the limit where the length of the molecule is much longer than the de Gennes length, the displacement will vary significantly as a function of the distance between the base pairs and the ends of the molecule, as shown schematically in figure 1(e) and (f).

In de Gennes model, dsDNA melts when the force on the base pairs at the ends of the molecule exceeds f₁, the force required to unzip a base pair. De Gennes ignored helicity, so the predicted melting forces for 3’3’ and 5’5’ pulling are the same. In both cases, for a sequence of length L the melting force, F, is given by:

$$F_{3\text{'}3\text{'}}=F_{5\text{'}5\text{'}}=2f_1\left\{{\chi }^{-1}\text{ tanh}\right(\chi \frac{L}{2})+1\}$$ (3)

where f₁ is the force required to separate a single base pair and assumed to be the same for all bases. The predicted normalized melting force as a function of the sequence length L is shown in figure 2(a), where each curve is normalized by dividing by 2 f₁ χ⁻¹. Each separate curve corresponds to a different de Gennes length. The first curve to the left corresponds to a de Gennes length of 5 bases, which is approximately the de Gennes length of B-form DNA. The subsequent curves from left to right correspond to de Gennes lengths of 50, 500, 5000, 50,000, and 500,000 bases.

Figure 2.

Predicted shear force as a function of length where length is shown on a log scale for various de Gennes lengths. From left to right the de Gennes lengths are 5, 50, 500, 5000, 50000, and 500000 bp, respectively. (a) Predictions for de Gennes theory, which are the same for 3’3’ and 5’5’ pulling since the theory ignores helicity. (b) Predicted shear force for 3’5’ as a function of length on a log scale. (c) Curves from (a) and (b) on the same graph where the dotted lines correspond to the predictions for 3’5’ pulling. All predicted forces are normalized as explained in the text.

1.2. Extension of de Gennes theory to 3’5’ pulling

The force equations for the displacement of the individual bases are the same for 3’3’ and 5’5’ pulling. Given that the coordinate system is chosen to be zero at the center of the molecule when dsDNA is pulled from the 3’3’ or 5’5’ ends, the extension of the base pairs as a function of n is symmetric, whereas for the 3’5’ case the solution is anti-symmetric and given by

$$u_n-v_n={\delta }_o\text{ sinh }(\chi n)$$ (4)

where δ_o is a constant independent of n. This solution implies that molecules with an odd number of bases have no force on the base pair at the center of the molecule, independent of the length of the molecule or the force applied to the ends of the molecule. For short molecules with high forces applied to the ends, the variation in force as a function of base pair number can be very large as illustrated in figure 1(d). In contrast, for short molecules pulled from the 3’3’ or 5’5’ ends, the force on all of the base pairs is the same as illustrated in figures 1(b) and (c). This large variation in force as a function of length for 3’5’ pulling implies that short molecules pulled from the 3’5’ ends may have overstretched conformations that are not uniform along the length of the molecules. In contrast, the same short molecules pulled from the 3’3’ or 5’5’ pulling ends would have the same tension on all of the base pairs, so the overstretched conformations would be uniform along their length.

For molecules with lengths that are much longer than the de Gennes length, the theory presented above implies that the force on the base pairs near the ends of the molecules is the same for 3’3’, 5’5’, and 3’5’ pulling, where the base pairs in the center of the molecule are under no force, though the backbone in the same region is under tension as illustrated in figure 1(e), (f), and (g). Thus, the finite stiffness of the backbone results in shear stress on the base pairs near the ends of the molecule, even when the molecule is pulled from the 3’5’ ends. In contrast, if the backbones were infinitely stiff, all base pairs in molecules pulled from the 3’3’ or 5’5’ ends would experience the same shear stress, whereas there would be no shear stress in molecules pulled from the 3’5’ ends. Given that the molecules melt when the shear force on the base pairs at the ends of the molecule is equal to the melting force, f₁, for a single base pair, molecules pulled from the 3’5’ ends would never melt if the backbone were infinitely stiff.

A dsDNA molecule of length L pulled from the 3’5’ ends will begin to melt when the applied force is given by:

$$F_{3\text{'}5\text{'}}=2f_1\left\{{\chi }^{-1}\text{coth}\right(\chi \frac{L}{2})+1\}$$ (5)

The predicted force calculated using equation (5) as a function of the ratio of the length of the molecule to the de Gennes length for 3’5’ pulling is shown in figure 2(b). Molecules with de Gennes lengths of 5, 50, 500, 5000, 50,000, and 500,000 bases are shown from left to right where each curve is normalized by dividing the force by 2 f₁ χ⁻¹.

Note that the force to initiate melting decreases with increasing length, and that the force approaches an asymptotic limit as the number of bases increases. This result may at first seem counterintuitive: one would imagine that longer molecules with more bases would be more stable against melting; however, for 3’5’ pulling this is not the case. The prediction makes sense if one notes that for 3’5’ pulling the melting is caused by the lattice mismatch between the ssDNA under tension and the ssDNA that is not under tension. Thus, for a given force the lattice mismatch will increase with increasing length; therefore, the force required to melt dsDNA in 3’5’ pulling decreases as a function of length. In the limit where the length of the molecule is much longer than the de Gennes length, molecules pulled from the 3’5’, 3’3’ or 5’5’ ends all begin to melt at the same force as shown in figure 2(c).

1.3. Force induced melting at a non-zero temperature

Earlier work that studied the force induced melting of dsDNA pulled from the 3’3’ and 5’5’ ends included thermal effects by allowing the number of bound bases in the dsDNA to be smaller than the number of bases in the molecule [23]. The difference is given by L_open= L-L_bound, where L_open/2 represents the average number of bases that are open at each end of the molecule. In this simple treatment equation (1) becomes:

$$F_{3\text{'}3\text{'}}=F_{5\text{'}5\text{'}}=2f_1\left\{{\chi }^{-1}\text{ tanh }\right(\chi (L-L_{\mathit{\text{open}}})/2)+1\}$$ (6)

The predictions of this equation are in good agreement with the experimentally measured melting forces. Of course in reality the number of open bases fluctuates with time and bases open up inside the molecule as well as at the ends of the molecule [27]. A more sophisticated treatment may be required to include thermal effects for the case where a molecule is pulled from the 3’5’ ends, but it is clear that small numbers of bound bases will thermally melt even in the absence of any force applied to the 3’5’.

2. Materials and methods

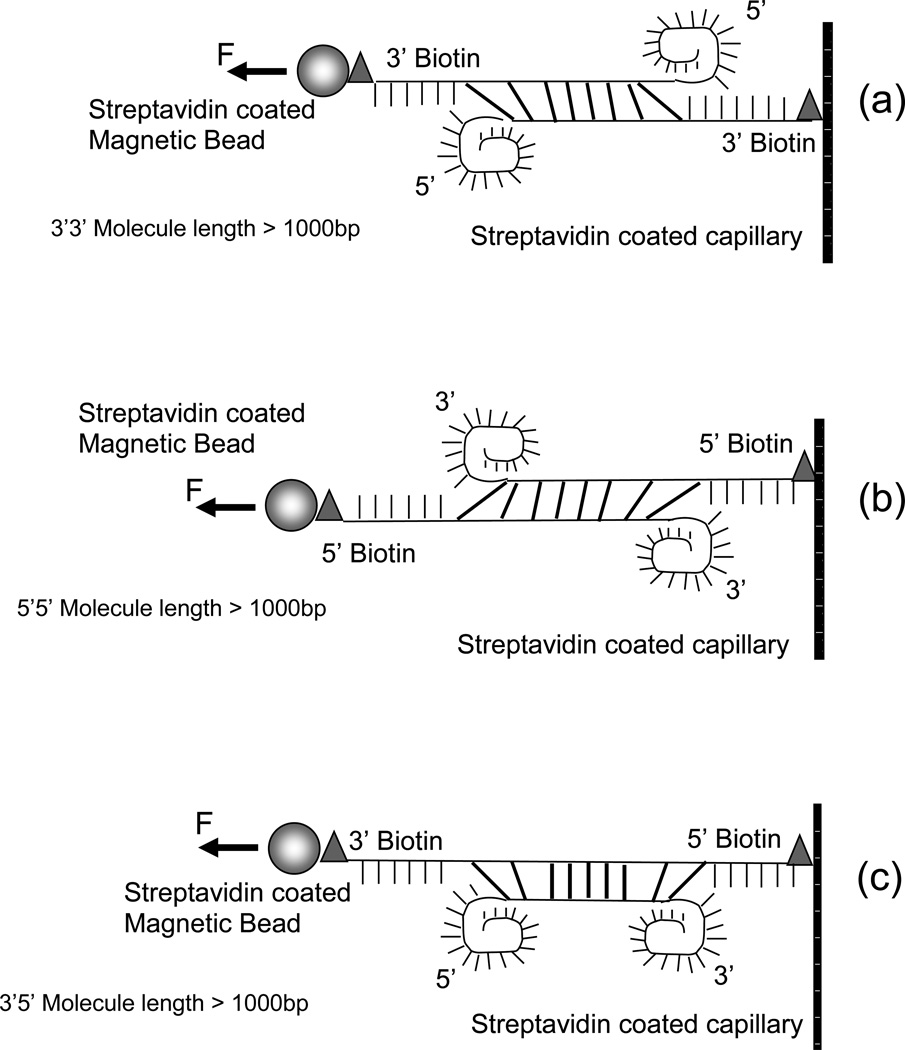
Molecular constructs were prepared for 3’3’, 5’5’, and 3’5’ force-induced melting as represented in figure 3. In order to prepare constructs containing a short double stranded fragment (12 – 50 bp) attached to a dsDNA linker (lambda phage, 48502 bp), a first oligonucleotide is attached to the linker dsDNA molecule and further hybridrized to two more oligonucleotides yielding a three base pair gap separating the fragment to be melted from the linker. The linker DNA binds to an antidigoxigenin coated capillary via its digoxigenin labeled end. The double stranded fragment to be melted is biotinylated and binds to a 4.5 μm streptavidin-coated magnetic bead (Dynabeads). These constructs are shown in figures 3(a) and 3(b). The sequences used are 50% GC and chosen to minimize improper annealing. For example, a misannealed 28 bp sequence can only have a maximum of 7 matched bases, which should not be stable at room temperature.

Figure 3.

Schematic representation for all dsDNA constructs with different lengths and pulling techniques. (a) 3’3’ construct with less than or equal to 1000 bp attached to a lambda phage linker; (b) 5’5’ construct with less than or equal to 1000 bp attached to a lambda phage linker; (c) 3’3’ pulling for molecules longer than 1000 bp; (d) 5’5’ pulling for molecules longer than 1000 bp; (e) 3’5’ pulling for molecules longer than 1000 bp.

Fragments between 100 and 1000 bp are all subregions of lambda which is a natural dsDNA sequence with substantial sequence heterogeneity and the property that one end of the molecule is more AT rich than the other. Thus, the molecules whose melting we observe may have both different lengths and different sequences. Constructs for melting of 100, 200, 500, and 1000 bp fragments were prepared following several steps. Initially PCR fragments containing approximately 100, 200, 500, and 1000 bp were obtained by typical PCR procedures. Briefly, the fragments were amplified using Pfu Ultra II fusion (Stratagene, Carlsbad, Ca) in a thermocycler using 1 ng lambda DNA (NEB, Beverly, MA), 1 X buffer, 1 mM MgCl₂, 0.5 µM dNTPs, 1 Unit Pfu Ultra II fusion in a total of 50 µl. The cycling protocol was 5 min at 95°C, 30 cycles of 30 sec at 95°C, 30 sec at 55°C, and 3 minutes at 72°C, and final extension for 15 min at 72°C. The oligonucleotides used as primers were designed so that a stretch of 20 bases would hybridize to lambda phage at positions 21498 (forward) and 21557 (reverse), 21777 (forward) and 21959 (reverse), 21498 (forward) and 21959 (reverse), and 20741 (forward) and 22709 (reverse) for each 100, 200, 500, and 1000 bp fragments, respectively. In addition the primers contained a stretch of 12 bases with restriction sites for NheI and Acc65I for 3’ melting, and restriction sites for BmtI and KpnI for 5’ melting constructs. Following the PCR preparation, the fragments were separated via gel electrophoresis on a 1X TBE 1% agarose gel and further purified using a Nucleospin kit (Machery and Nagel, Bethlehem, PA). Each fragment was double digested with the corresponding pair of restriction enzymes and modified at each end with a 3’ biotin oligonucleotide and a linker oligonucleotide at the opposite end for 3’ melting whereas a 5’ biotin oligonucleotide and a different linker oligonucleotide were used for 5’ melting constructs. The ligations were performed at 16°C overnight using E.coli T4 ligase. The modified fragments were finally ligated to a lambda phage molecule (linker) containing digoxigenin label at the 3’ distal end using thermostable DNA Ligase (Ampligase, Epicentre, Madison, WI) at 45°C for two hours.

For molecules longer than 1000 bp we used biotin labels on both ends of lambda DNA and streptavidin modified surfaces on both the magnetic beads and the capillaries. This technique does allow the binding of both ends of the DNA molecules to the same surface, which decreases the yield of tethered beads in the experiments. The constructs were obtained by cutting and isolating specific fragments run on an agarose gel and final modification of the ends with biotinylated oligonucleotides.

All the melting experiments are done at room temperature in PBS buffer (pH 7.4, 10 mM phosphate, 137 mM NaCl, 2.3 mM KCl).

We use magnetic tweezers to probe the melting force of different constructs by applying a constant force to each construct and measuring the fraction of DNA molecules that separate at that force. The spread in magnetization of the beads leads to a standard deviation of approximately 5% in the force measurements. Magnetic tweezers allow us to apply a constant force in parallel. In order to determine the melting force, the constant force is increased incrementally by a force interval ΔF after which a constant force is applied for ΔT seconds. We measure only the molecules that melt during the time interval ΔT where the force is constant. The measured melting force for each molecule is the force on the bead at the magnet position where the bead is released from the surface. At least 50 individual molecules are measured for each sequence length and pulling technique in order to determine the most probable melting force. The data is fit to a Gaussian distribution and the reported melting force and error are the mean and standard deviation of the best-fit, respectively.

3. Experimental results

3.1. Determination of melting forces using bead loss

For sequences with lengths of 1000 bp or less that are melted by pulling from the 3’3’ or 5’5’ ends, we determined the melting force by measuring the number of beads that detached from the surface as a function of the force applied to the bead. The number of beads that detach as a function of force is plotted as histograms with 5 pN bins, such as those shown in figure 4. The melting force is then determined by fitting the histograms to a Gaussian. In general, the histograms are not symmetric because some bead losses at low forces are not due to melting of molecules of the correct length, but rather due to detachment of beads that were non-specifically bound. In addition, some beads may survive at forces above the melting force if the molecule was bound non-specifically to some portion of the lambda tether rather than to the short double-stranded fragment that is separated from the lambda tether by the three-base gap. Figure 4 shows the 5 pN bin histograms for force-induced melting of a 24 bp fragment attached to a full lambda dsDNA linker as well as of full lambda phage molecules. The dashed lines show Gaussian fits to the distributions. Note that 65 pN, is the overstretching force for 3’5’ pulling. Figures 4(a) and (b) show the histograms for pulling from the 5’5’ and 3’3’ ends of 24 bp fragments plus linker, respectively. The match between the results for the two pulling techniques is excellent, showing that the force induced melting of the 24 bp sequences is the same for both 3’3’ and 5’5’ pulling. This result is true for all molecules with lengths of 32 base pairs or less. All of these molecules melt at a force that is less than the overstretching force, which is consistent with the idea that they melt in B-form. The narrow peaks in the force distributions have widths approximately equal to the spread due to the variation in bead magnetization, so the actual distributions may be quite narrow.

Figure 4.

Histograms for bead loss measured for 24 bp fragments attached to a lambda linker and full lambda phage constructs. The histograms represent the number of beads that unbind at a given force range with 5 pN force intervals where the dotted lines show Gaussian fits. (a) 24 bp fragment and 5’5’ pulling, F_c= 51.8 and σ = 4.5; (b) 24 bp frament and 3’3’ pulling, F_c= 51.9 and σ =3.5; (c) control for 3’5’ bead loss (black line) in addition to (a) and (b) histograms; (d) 5’5’ pulling of lambda dsDNA, F_c= 118.2 and σ =7.5; (e) 3’3’pulling of lambda dsDNA, F_c= 132.4 and σ =5.6; (f) 5’5’ pulling of 500 bp fragment, F_c= 76.4 and σ =5.

Magnetic beads that detach from the surface because the binding at their ends failed contribute noise to the melting data. To determine this contribution, we measured the unbinding of magnetic beads bound to the surface by molecules pulled from their 3’5’ ends. Even if these molecules melt, the bead will not detach; therefore, bead detachment corresponds to failed binding at the ends or failed ligation. The resulting histogram is shown in figure 4(c) (black line), which is a fairly uniform distribution at forces between 50 and 100 pN, and a distribution that decreases with decreasing force below 50 pN. This low force tail probably corresponds to molecules that were non-specifically bound. The 3’3’ and 5’5’ data have additional low force points that probably correspond to imperfect constructs.

Figures 4(d) and (e) show the histograms for full lambda dsDNA where 4(d) shows the results for 5’5’ pulling and 4(e) shows the results for 3’3’ pulling where only the data for molecules that overstretch is shown. These molecules were bound to the surface by multiple biotin labels at both ends, so the binding survives at much higher forces than the single biotin-single digoxygenin system used for the data shown in figures 4(a-c). The figures show that the melting force for 5’5’ pulling is significantly less than the force for 3’3’ pulling. This result is perfectly consistent with the results shown in figures 4(a) and 4(b), since figures 4(d) and 4(e) correspond to molecules that overstretch before they melt and the overstretched conformation depends on the ends to which the force is applied, whereas figures 4(a) and 4(b) represent molecules that melt in B-form where the conformation is not sensitive to the ends to which the force is applied. We note that the widths of the force distributions for the overstretched molecules are broader than the width due to the variation in bead magnetization.

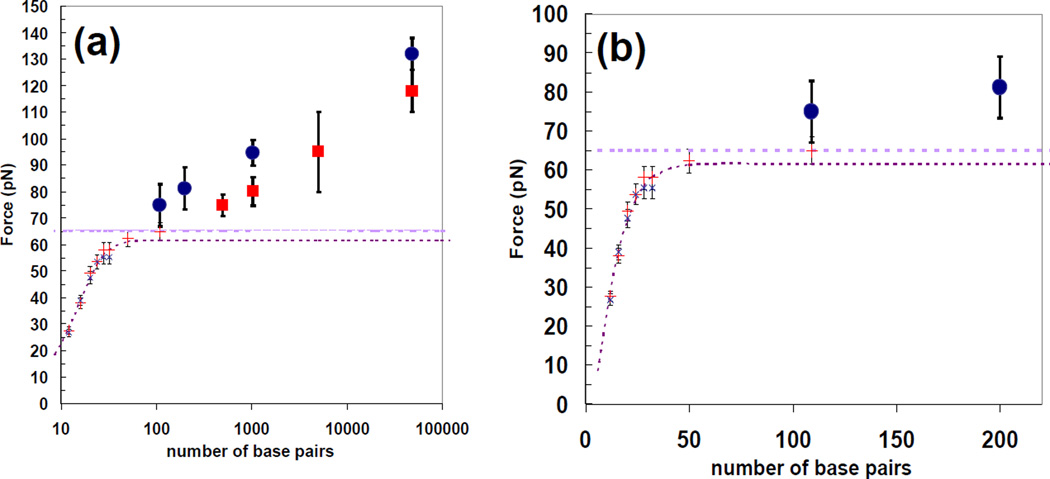
The melting forces as a function of length calculated using the bead loss technique described above are shown in figure 5, where figure 5(a) has a logarithmic x axis and figure 5(b) has a linear x axis. The dashed lines show the overstretching force for 3’5’ pulling.

Figure 5.

Melting force as a function of the number of bases in the molecule where the squares correspond to 5’5’ pulling and the circles correspond to 3’3’ pulling. The + and×symbols represent points where the molecule shears before it overstretches for 5’5’ and 3’3’ pulling, respectively. Solid symbols represent molecules that completely overstretch before they shear. (a) Data obtained from bead-loss experiments for molecules between 6 bp and 97 kb (x-axis shown in log scale); (b) data measured for molecules between 6 and 200 bp is shown. The dashed lines indicate the overstretching force and the dotted curves are fits using equation (6).

3.2. Molecules with lengths of 32 bp or less

All of these short molecules melt at a force that is significantly below the overstretching transition. The melting force for the molecules increases with length, but the increase saturates with increasing length. The dotted lines in figure 5(a) and (b) show the fit of equation (6) to the data for molecules with lengths less than 100 bp. The fit corresponds to f_1Bnorm= 3.5, L_openB = 5.6, de Gennes Length = 7.8. The agreement between equation (6) and the experimental data is quite good. Similar results are obtained when the 50 bp point is not included in the fit. The results for lengths less than 100 bp and the fits have been published previously [23]. Figure 5(b) shows the same information for lengths less than 200 bp.

The melting forces for 3’3’ and 5’5’ pulling are the same for molecules in this length range. This result is reasonable since previous results have shown that the overstretching force is independent of molecule length or pulling rate [28]; therefore, the short molecules that melt at a force below the overstretching transition must melt in the B-form state independent of the ends to which the force is applied. It is not clear whether these molecules are at or near force equilibrium when they melt.

3.3. Molecules with lengths from 50 to 1000 bp

For molecules in this range, the interpretation of the experimental results is more complex because for some molecules the difference between the melting force and the overstretching force is not significantly larger than σ_over, the width of the overstretching transition; therefore, we could not determine from the melting force alone whether or not the molecule fully overstretched before it melted. Variations in the bead magnetization result in a distribution of forces on individual molecules that increase the uncertainty in the force measurement by 3–4 pN. If we could directly monitor the extension of the short dsDNA fragments at the ends of the lambda tethers (constructs), we could determine whether they completely overstretched before they melted, but we are unable to directly monitor the extension of the short fragments.

For 100 bp fragments pulled from the 3’3’ ends, approximately half of the constructs melt at the overstretching force; however, approximately half melt at a force in excess of 70 pN. No construct melted at a force between 66 and 72 pN. This result suggests that overstretching increases the stability of the molecule against force induced melting. Similar results hold for 200 bp molecules pulled from the 3’3’ ends except that no molecule melts at a force between 66 and 78 pN. For 1000 bp molecules pulled from the 3’3 ends the number of molecules that melt during overstretching is comparable to those observed for the 3’5’ controls, suggesting that it is the result of non-specific binding.

For 100 bp molecules pulled from the 5’5’ ends, the number of molecules that melt at a force at or above the overstretching transition is significantly less than the number for the controls suggesting that all of the molecules melted before they overstretched. For 200 bp molecules pulled from the 5’5’ ends, the number of molecules with a melting force that is clearly above the overstretching transition does not exceed the number for the controls, and most molecules melt in the force range characteristic of the overstretching transition. For 500 bp molecules pulled from the 5’5’ ends shown in figure 4(f), the number of molecules that melt before overstretching is similar to the controls, and no significant bead loss is observed until the applied force exceeds 72 pN, which is significantly above the overstretching transition. For 1000 bp molecules pulled from the 5’5’ ends, all of the molecules overstretch before they melt and no significant bead unbinding is observed until the force exceeds 75 pN.

These results for the melting of molecules with lengths from 100 to 1000 bp suggest that overstretching increases the melting force stability of short molecules by approximately 5 pN. The data also suggests that molecules of a given length in this range, pulled from the 3’3’ ends overstretch at a lower force than molecules pulled from the 5’5’ ends; however, molecules of a given length melt at a higher force when pulled from the 3’3’ ends.

3.4. Molecules with lengths above 1000 bp

All of these molecules melt at a force that is significantly above the overstretching transition, so since previous results have shown that the overstretching force is independent of molecule length or pulling rate [28] these molecules must undergo force-induced melting in the overstretched state. In this length range, the melting force for 3’3’ pulling is significantly higher than the melting force for 5’5’ pulling, which is consistent with earlier results that showed that more force was required to melt a complete lambda phage molecule when it was pulled from the 3’3’ ends than when it was pulled from the 5’5’ ends [21].

For molecules with lengths of 5000 bp or longer, we were able to directly monitor the extension of the molecule as it melted. An example is shown in figure 6(a), where the black curve corresponds to a molecule with 20,000 bp pulled from the 3’3’ ends. The length increase at 65 pN corresponds to the overstretching transition. The dashed line in the figure corresponds to the force, F_start [21, 29] at which the overstretched state shows a significant change in the slope of the extension vs. force curve. Once these long molecules have overstretched, the extension at a given constant force remains stable for several minutes as long as the applied force is below F_start. Thus, there is direct experimental evidence that the molecules have fully made the transition to the overstretched state before they melt and the state that melts represents the equilibrium state at that force, at least for time scales of several minutes.

Figure 6.

(a) Extension as a function of force for a 20 kb molecule pulled from the 3’3’ ends where the gray line shows the corresponding curve for ssDNA. The vertical dotted line indicates F_start, the force above the overstretching transition at which there is a marked change in the slope of the curve. (b) Melting force as a function of the number of bases for 5’5’ pulling (squares), 3’3’ pulling (circles), and 3’5’ pulling (triangles) measured with both techniques: bead loss and F_start. The measured F_start values are represented with the hollow squares, circles, and triangles for 5’5’, 3’3’, and 3’5’ pulling, respectively. The + and × symbols represent points shown in figure 4(a) where the molecule shears before it overstretches. Solid squares and circles represent the molecules that completely overstretch before they shear also shown in figure 4(b).

The measured extension vs. force curves for molecules that overstretch can be fit to the following equation:

$${\mathrm{B}}_{\text{fraction}}[\mathrm{F}]=1/(1+\text{Exp}[(\mathrm{F}-{\mathrm{F}}_{\text{over}})/{\mathrm{\sigma }}_{\text{over}}]$$ (7)

where B_fraction is the fraction of the molecule that remains in the B-form state, F_over is the overstretching force, and σ_over is the width. Fits to the measured curves yield σ_over~ 1 ± 0.5 pN.

3.5. Determination of melting forces using F_start

If a molecule is bound by its 3’5’ ends, force induced melting results in an ssDNA molecule bound between a magnetic bead and the capillary surface rather than an unbound bead. Thus, measurements of bead unbinding do not provide information about the force induced melting of 3’5’ structures; however, earlier work has shown that single molecule measurements of force induced melting can be used to determine the melting force for dsDNA pulled from the 3’5’ ends since the extension vs. force properties for the bound ssDNA that results from force induced melting differ significantly from the properties for dsDNA [21].

In this section we will use single molecule extension vs. force curves to examine the force induced melting of long molecules pulled from the 3’3’, 5’5’, and 3’5’ ends. In this technique, the melting transition is characterized by F_start, the force at which the extension vs. force curve for the overstretched state undergoes a change in slope as shown in figure 6(a). In order for an extension vs. force curve to display a clear change in slope, the DNA must have remained bound to both the magnetic bead and the capillary surface. Thus, unlike measurements of the melting force that depend on bead loss, measurements that depend on F_start are independent of any failure of the biotin/streptavidin bonds. Similar curves were obtained for all sequence lengths in excess of 1000 bp and for all three pulling techniques. For shorter sequences, the spatial resolution of the imaging in our apparatus does not allow us to determine F_start. By definition, the F_start value for a given molecule will always be lower than the melting force for that molecule, where earlier work suggested that for complete lambda dsDNA molecules F_start is approximately 10 pN below the melting force [21].

At forces below F_start, overstretched molecules do not show any significant change in length during the dwell time at each constant force even if the force applied to the molecule is left constant for several minutes. Thus the extensions represent equilibrium extensions, at least for several minute times scales. At forces above F_start, the extension does change during the dwell time; however, the 1-second dwell time is sufficient for the extension to approach an asymptotic value at the end of the dwell time.

The result shown in figure 6(a) is not in agreement with de Gennes theory that predicts that molecules pulled from the 3’3’ or 5’5’ ends should melt catastrophically once the melting force for the molecule is reached. This difference may be the result of sequence heterogeneity since it is known that binding energy between base pairs is sequence dependent. The extension of de Gennes theory to 3’5’ predicts that structures pulled from the 3’5’ ends will require enormous force to fully melt at zero temperature; however, it is known that pulling from the 3’5’ ends completely melts dsDNA leaving a bound ssDNA strand [21,29] where the melting force for 3’5’ pulling is approximately the same as for 3’3’ pulling [21]. This discrepancy is not trivially attributable to sequence heterogeneity. In fact, the force range over which 3’3’, 5’5’, and 3’5’ molecules melt is very similar, though the range for 5’5’ might be slightly narrower. Further theoretical work will be required to determine whether the inclusion of finite temperature will be sufficient to resolve this discrepancy or whether additional factors such as conformational variations along the length of the molecule must also be included.

Figure 6(b) shows the F_start values as a function of length, as well as the melting forces that were determined by the bead loss technique. The open squares and open circles indicate the F_start values for molecules pulled from 5’5’ and 3’3’ ends, respectively, whereas the open triangles correspond to the F_start values for 3’5’ pulling. Since F_start represents the force at which a molecule begins to melt, one would expect that the F_start values for a given molecule length would be lower than the melting force values. The F_start for 3’5’ and 3’3’ pulling are very similar whereas for 5’5’ pulling F_start is lower.

3.6. Probing for pulling dependent variations in the overstretching force: using the relationship between the melting force for molecules with lengths from 50 to 1000 bp and the force at which the lambda dsDNA tether overstretches

Though we are unable to directly monitor the extension of these short molecules and determine whether the extension is at equilibrium with the force or whether they have overstretched before they melted, we can monitor the lengths of the tethers attached to the short fragments being melted. Given that the overstretching force is independent of pulling rate and length [28], one might assume that the measurements of the overstretching of the tether could be used to determine whether the short dsDNA fragment attached to the tether overstretched; however, the force on the tethers is applied to different ends than the force on the short dsDNA fragment as shown in figure 3. In particular, for short dsDNA fragments pulled from the 3’3’ ends, the tethers are pulled from the 3’5’ ends and for short dsDNA fragments pulled from the 5’5’ ends, the tethers are pulled from the 3’3’ ends.

If the overstretching force were independent of the ends to which the force is applied, this difference would not matter. Earlier results had shown some slight difference in overstretching force, but the difference did not exceed the error in the measurement [21]. Additional direct measurements of the overstretching force give 64 ± 1 pN, 65 ± 1.3 pN, and 66 ± 0.3 pN for 3’3’, 3’5’, and 5’5’ pulling respectively. Again, these measurements do not show a significant difference in overstretching force.

Given that both the tether and the tail are under tension due to the same magnetic bead, variations in bead magnetization will not affect the relative measurement of the overstretching force for the tail and the tether. If, as the data discussed above suggests, overstretching results in an increase in melting force from approximately 65 to 70 pN and the separation between the overstretching forces for the three molecules is less than 2 pN, then one can use measurements of the melting force and tether extension to determine whether the tether overstretches at a higher or lower force than the fragment.

What we observe is that for 100 bp fragments pulled from the 5’5’ ends, all of the molecules melt before the 3’3’ tether overstretches. For 200 bp fragments pulled from the 5’5’ ends, the tether overstretches before the fragment melts and the melting force for the fragment is equal to the overstretching force for the tether. For 500 bp fragments pulled from the 5’5’ ends, the 5’5’ tail probably overstretches before it melts since the melting force jumps above 70 pN and no molecules are observed to melt at lower forces. These results are consistent with molecules pulled from the 5’5’ ends overstretching approximately 2 pN above the overstretching force for 3’3’ pulling.

For 3’3’ fragments with 3’5’ tethers, 100 and 200 bp fragments have tethers that complete approximately 75 % of their overstretching transition though the 3’3’ fragments fully complete the transition. This suggests that the overstretching force for 3’3’ pulling is approximately 0.25 to 0.5 pN below the overstretching force for 3’5’ pulling.

3.7. Using free energy calculations

It has long been known that there is an association between the measured extension vs. force curves and the free energies of dsDNA molecules. In what follows we will show that the measured difference in melting forces for the overstretched states created by the different pulling techniques shown in figure 7 requires that the overstretching forces for the states also be different. In addition, the free energy calculations show that the required differences are consistent with the direct measurements of the overstretching forces as well as the indirect measurements based on a comparison of the overstretching forces for the short dsDNA fragments and the overstretching force for the lambda dsDNA tethers attached to the fragments.

Figure 7.

Partial melting of (a) 3’3’, (b) 5’5’, and (c) 3’5’. Both 3’3’ and 5’5’ have some tension in the center of the dsDNA molecule, one ssDNA end under tension at each end and one ssDNA portion that is not under tension at each other end. Similarly 3’5’ melts from the ends where one ssDNA stays under tension at both ends and the opposite single strand is not under tension at either end with some tension in the middle where dsDNA is still present.

Earlier work has calculated some properties of the overstretched state using the extension vs. force curves [19, 30]. In this work, we will use the general expression for the free energy of stretched dsDNA that was derived by Lubensky et al (2002) to determine the free energy difference between stretched dsDNA and stretched ssDNA since it is the difference between the two states that is relevant for melting, not simply the change in the free energy of the dsDNA itself.

If one assumes that at zero external force, the free energy of a stretched dsDNA molecule is zero, then the free energy of a dsDNA molecule stretched by a constant force F is given by:

$$g(F)=\underset{0}{\overset{F}{\int }}x(F\text{'})dF\text{'}$$ (8)

where x(F’) represents the equilibrium extension at a force F’ [31]. For 3’5’ pulling, melting dsDNA is equivalent to converting one dsDNA under tension to one ssDNA under tension and one ssDNA under no tension. As the dsDNA partially melts in from the ends, each end of the partially melted molecule consists of one ssDNA strand under tension and one ssDNA strand not under tension, as shown in figure 7(c). Similarly, for partially melted molecules pulled from the 3’3’ and 5’5’ ends, each end of the molecule consists of one ssDNA strand under tension and one ssDNA strand not under tension, as shown in figures 7(a) and (b). Thus, in all three cases, the melting transition for partially melted molecules occurs between one dsDNA under tension and one ssDNA strand under tension accompanied by a second ssDNA strand that is not under tension. Thus, the free energy calculation done above for 3’5’ pulling also applies to 3’3’ and 5’5’ pulling until the last step in the melting transition for 3’3’ and 5’5’ pulling where neither ssDNA is under tension because the 3’3’ or 5’5’ molecules have completely melted.

If the theory above is correct, then the difference in area between the extension vs. force curve for a 3’5’ dsDNA construct that is stretched until it melts and the extension vs. force curve for the ssDNA molecule that remains bound after melting should be equal to the free energy difference between paired and unpaired dsDNA. We have performed the calculation for the measured curves and find that the total free energy difference is approximately 3.2 kT/bp, which is in good agreement with the 2.8 kT/bp average energy for lambda phage dsDNA [32].

This same theory then argues that the integrals under the curves for 3’3’ and 5’5’ for fully melted DNA should be the same since the Watson-Crick pairing of unstressed DNA is independent of the pulling technique; however, this is not possible if both constructs have the same extension vs. force curves at forces below F_start, a force range in which 3’3’ and 5’5’ pulling have very similar extension vs. force curves.

This apparent difficulty can be resolved if there is a difference in the overstretching force, where the overstretching force for 3’3’ pulling is slightly lower than the overstretching force for 5’5’ pulling. The 3’3’ curve overstretches first, so the free energy difference between the dsDNA and ssDNA is smaller for 3’3’ than for 5’5’. The 5’5’ curve begins to melt at a lower force. Above F_start for 5’5’ pulling, the 5’5’ curve is closer to the ssDNA curve than the 3’3’. We have calculated the free energy differences for several measured curves for 3’3’ and 5’5’ melting of lambda dsDNA molecules, where we allowed the 5’5’ overstretching force to be a free parameter. The curves vary slightly, but if the overstretching force for 5’5’ pulling is 1–3 pN higher than the overstretching force for 3’3’ pulling, then the total free energy difference between the two curves is zero, as required since it must be equal to the Watson-Crick binding at zero force. Thus, though the difference between the overstretching transitions for the two constructs is very slight, it is sufficient to compensate for the difference in free energy that results from the lower melting force associated with the molecule pulled from the 5’5’ ends. This theory also suggests that the melting force difference between the 3’3’ and 5’5’ states should increase with decreasing molecule length, which is consistent with the results shown in figure 5.

For short molecules that shear before they overstretch we cannot measure the extension vs. force curves and we do not know whether the molecules are at or near equilibrium when they shear. Thus, we cannot use the technique above to calculate the total free energy difference for one force cycle that converts dsDNA to ssDNA by force induced melting, and then returns the ssDNA to low force; however, the narrowness of the melting force distributions suggests that the short molecules may fail catastrophically in accord with de Gennes theory.

4. Conclusions

We have measured the melting force as a function of length for dsDNA molecules pulled from the 3’3’, 5’5’ and 3’5’ ends. For molecules that melt before they overstretch, the melting force is the same for both 3’3’ and 5’5’ pulling which is consistent with the molecules melting in B-form. In addition, for these molecules the shear force as a function of length is well described by de Gennes theory. In molecules that melt before they overstretch, the shear force extends to fewer than 10 bp at the ends of the molecule, so increasing the length of the molecule does not substantially increase the shear force. For molecules that overstretch before they melt, the melting force depends on the pulling technique where molecules of a given length have a higher melting force if they are pulled from the 3’3’ ends than if they are pulled from the 5’5’ ends. For molecules overstretched from the 3’3’ or 5’5’ ends, the melting force as a function of length increases for lengths exceeding 1000 bp, where the increase in force with length is not consistent with de Gennes theory or with more detailed calculations that include sequence heterogeneity and constant base pair stacking [25]. For molecules that overstretch before they shear, the shear force is distributed along the entire length of the molecule, rather than confined to short regions near the ends. If overstretching decreases the stacking energy and the associated spring constant for the base pairs, then one would expect the length over which the force is distributed to increase when the molecule is overstretched, consistent with the observations presented here. Further investigation will be required to determine the effect of overstretching on f₁ and the spring constants for the base pair binding and backbone interactions.

Earlier work had shown that the length dependence of the melting force is consistent with de Gennes theory, and the results shown here suggest that the melting transition has a very narrow force range. In contrast, for molecules with lengths of 10,000 bp or longer the melting transition occurs over a range of forces where partially melted molecules can remain stable. Overall, the data suggests that for 3’3’ and 5’5’ pulling the melting force for the overstretched states increases logarithmically with length; however, the uncertainty in the high force values is sufficient that it is possible that the force saturates at 10,000 bp. There is no evidence that the melting force for 3’5’ pulling decreases with length, and though melting forces are higher than those for 5’5’ pulling they are comparable to those for 3’3’ pulling.

One would expect a mismatch between theory and the experiment if the de Gennes length and/or f₁ depend upon either applied force or length or if a variation in the angle of one base pair strongly changed the energy of neighboring base pairs due to a disruption in stacking. Recent work has shown that including an additional effective spring constant due to stacking interactions does not qualitatively change the results of the original simple de Gennes treatment [25]; however, it is possible that though the stacking interactions have only a weak effect for molecules that shear in B-form, stacking interactions for overstretched molecules may be sufficiently important to result in qualitative changes in the predicted melting force.

In the shear measurements, longer molecules shear at higher forces; therefore effects inherent to length may be confused by effects that result merely from applied force. Data from earlier work suggests that length or the molecule itself can be important even at forces just above the overstretching transition since the shear force in full lambda dsDNA was shown to extend over the complete 48,502 length of the molecule even when the applied force was only 70 pN [21]. The possibility that the structure of the molecule depends on its length as well as on the applied force is not unreasonable since the redistribution of the shear force among the bases along the molecule may depend on the length over which the redistribution can occur precisely because the stacking energy of a base pair is influenced by the conformation of the neighboring bases. An earlier theoretical work described a domino effect where the change in coordinates of one base pair can change the stability of its neighbors [33].

The results presented here and in earlier work support the suggestion that for overstretched molecules the change in the characteristic length over which the shear force is distributed depends more strongly on the length of the molecule than on the value of the applied force since complete lambda dsDNA molecules with more than 48,000 base pairs have a shear force that extends throughout the molecule even when the applied force is well below the melting force for the molecule [21], but the melting force increase between molecules with 100 and 100,000 bp is less than a factor of 2. In contrast, if the de Gennes length of overstretched dsDNA was independent of molecule length and was approximately 100,000 bp, then the melting force should have increased by a factor of more than 100. This result is consistent with the force applied at the ends of the molecule being redistributed throughout the entire length of the overstretched molecule in a manner that minimizes the total energy. This redistribution of tension results in a de Gennes length that is always of the order of the length of the molecule. In contrast, at applied forces where the molecules remain in B-form the stacking may not be strongly affected by the applied force resulting in a de Gennes length that depends only on the B-form structure and is independent of the length of the molecule. In contrast, at applied forces where the molecules remain in B-form the stacking may not be strongly affected by the applied force. Finally, the idea that in overstretched molecules the force applied at the ends is redistributed along the entire length of the molecule for all molecule lengths is also consistent with the well known highly collective nature of the overstretching transition: if the force between the base pairs varied strongly along the molecule, then the ends of the molecule would overstretch at a much lower force than the base pairs at the center of the molecule; however, the width of the overstretching transition is less than 5% of the overstretching force, suggesting that the forces on the base pairs are nearly uniform not only for molecules pulled from the 3’3’ and 5’5’ ends but also for molecules pulled from the 3’5’ ends and from both ends of both backbones simultaneously since all have very similar overstretching properties.

The idea that it is energetically expensive for different base pairs to experience different shear forces also has implications for the applicability of extending de Gennes theory to molecules pulled form the 3’5’ ends. The extension of de Gennes theory to 3’5’ pulling predicts that there will always be a very large variation in shear force as a function of position. This is inconsistent with the discussion above that suggests that the shear force and conformation of the base pairs in the overstretched state show little variation as a function of position. Thus, it may be useful to extend de Gennes theory to include the large energetic cost of a position dependent variation in stacking energy.

Free energy considerations require that if melting is an equilibrium process, then the measured difference in the melting force for the overstretched conformations requires that the overstretching force for the 3’3’ state be lower than the overstretching force for the 5’5’ state by between 1 and 3 pN. This result is also consistent with comparisons between the overstretching forces for short fragments stretched from the 3’3’ and 5’5’ ends and the overstretching forces for the longer tethers that are directly attached to each short fragment. The comparison of the forces suggests that the overstretching force for 3’3’ pulling is approximately 2 pN below the overstretching force for 5’5’ pulling and 0–1 pN below the overstretching force for 3’5’ pulling. Finally, direct measurements of the overstretching forces for the different lambda dsDNA constructs yield overstretching forces of 64 ± 1, 65 ± 1.3, and 66 ± 0.3 pN for 3’3’, 3’5’, and 5’5’ pulling, respectively. These differences in overstretching forces are not in agreement with the theoretical predictions for short homogeneous molecules [34]; however, it may be consistent with the predictions for long heterogeneous molecules.

In sum, the results reported in this work strongly support the contention that the conformations of dsDNA molecules overstretched from the 3’3’ ends differ from the conformation of dsDNA molecules overstretched from the 5’5’ ends, where the difference arises as a result of overstretching. In addition, the results show that overstretching and melting are distinct processes, though there is a range of molecule lengths between 50 and 500 bp where, melting and overstretching may occur simultaneously if a constant force is applied to the ends of the molecules.

Given that the binding of dsDNA to the RecA protein increases the length/bp for the bound dsDNA, it is worth considering how the measurements of extended dsDNA reported in this paper may reflect on the functioning of RecA given that it has been suggested that the extension of the dsDNA plays a vital role in promoting strand exchange by weakening the Watson-Crick binding between the base pairs. Free energy calculations show that overstretching does indeed reduce the free energy difference between stretched dsDNA and stretched ssDNA, with the exact difference depending on whether the force on the ssDNA is distributed over both of the phosphate backbones or over only one of the backbones. The exact tension distribution in dsDNA bound to RecA is unknown; therefore, one cannot trivially use extension vs. force measurements for naked dsDNA to calculate the free energy differences for different DNA conformations bound in RecA; however, it is interesting to note that the 80-base pair region that is included in the RecA filament during strand exchange falls near the boundary between the number of base pairs that shears before they overstretch and the number that overstretches before they shear.