Applying Multivariate Discrete Distributions to Genetically Informative Count Data

Abstract

We present a novel method of conducting biometric analysis of twin data when the phenotypes are integer-valued counts, which often show an L-shaped distribution. Monte Carlo simulation is used to compare five likelihood-based approaches to modeling: our multivariate discrete method, when its distributional assumptions are correct, when they are incorrect, and three other methods in common use. With data simulated from a skewed discrete distribution, recovery of twin correlations and proportions of additive genetic and common environment variance was generally poor for the Normal, Lognormal and Ordinal models, but good for the two discrete models. Sex-separate applications to substance-use data from twins in the Minnesota Twin Family Study showed superior performance of two discrete models. The new methods are implemented using R and OpenMx and are freely available.

The present work is an inquiry into a neglected methodological problem in human quantitative genetics: how to specialize the biometrical analysis-of-variance for phenotypes that are integer-valued counts of some phenomenon. Such phenotypes include: the number of instances that a particular life event occurred in an individual’s personal history; the number of trials eliciting a particular response in a laboratory paradigm; and the number of times an individual emitted a particular behavior while observed by the investigator (e.g., a child’s word pronunciation errors while reading aloud from text). Since the class of all count variables is quite broad, we state here that the probability distributions we will discuss are most appropriate for phenotypes that are ratio-scale counts, and have the following three characteristics. First, the occurrences being counted should be exchangeable, that is, the order in which they happen should not matter. Second, the variable should not have a strict upper ceiling (or if it does, the ceiling is high enough to be irrelevant in practice). Third, the variable should not be expected theoretically to have a multimodal distribution (at least after conditioning on covariates). Two examples we mentioned previously, life-event occurrences and word-pronunciation errors, might be plausibly assumed to possess these three properties. But again, our motivation for narrowing the scope in this manner is technical rather than substantive. Variables that are, say, multimodal would be better modeled using different distributions—a potential subject for another paper.

Most routinely-used methods for variance-component estimation and inference assume a normal distribution, but data based on counts are often poorly approximated by normality. The normal distribution is continuous, but counts are discrete, and might only take on a small number of values in a given sample. The normal distribution is symmetric and takes values across the whole real line, but counts cannot be negative, and in some domains (e.g., substance use or psychopathology) can be very positively skewed, often with the mode at zero. Occasionally, though, the normal approximation for count data is appreciably improved by analyzing the residuals from a linear regression with one or more predictor variables.

One strategy commonly used with positively skewed data is to log-transform the variable, with some constant added to scores if any are non-positive, and proceed with routine normal-theory methods. While this may or may not improve the normal approximation for the data, it will not smooth out the “choppiness” of a discrete distribution. Non-normal variables can also be ordinalized into several ordered categories, and analyzed as though they reflect some underlying multivariate-normal continuum. Ordinalization typically requires the investigator to decide how many categories to use, and which raw-score interval will be mapped to each category—decisions that are usually somewhat arbitrary. However, with count variables, ordinalization is defensible if the variable takes on relatively few unique values in the dataset, so that each unique raw score can be mapped to a category. Ordinal analysis is also a natural choice if counts happen to be collected in small intervals to begin with (e.g., “How many days last month did you use cannabis? 0–4, 5–9, 10–15 [etc.].”).

Genetically informative data often come from twin/sibling pairs, or parent-child trios, and sometimes from nuclear families or extended pedigrees. Furthermore, it is often more interesting and/or more informative to study multiple phenotypes at once, or the same phenotype at different timepoints. Thus, such data are often multivariate. We are concerned with applying parametric, multivariate discrete distributions to biometric modeling, primarily in the context of the classical twin study. To further keep the paper within a manageable scope, we will only consider multivariate discrete distributions constructed from univariate discrete distributions via “latent-variate reduction” (described below).

The simplest univariate distribution possessing our desired characteristics is the one-parameter Poisson distribution. The simplicity of the Poisson distribution makes it useful for expository purposes, so we review details concerning it in Supplementary Appendix A (Online Resource 1). However, we do not discuss Poisson models in the main text because there are two departures from Poisson distribution that are common in individual-difference variables, especially in domains of psychopathology and substance use. These are zero-inflation and overdispersion, which may co-occur in a given sample of data.

Zero-inflation (relative to the Poisson) occurs when the proportion of zeroes in a sample exceeds what would be expected from a Poisson distribution having the same mean. Discrete distributions that specially model the probability of a zero count do exist (Johnson et al., 2005; Atkins & Gallop, 2007), but it is a limitation of the present work that we do not apply them here. We return to the matter of zero-inflation in the Discussion.

A distribution is “overdispersed” (relative to the Poisson) if its variance exceeds its mean. The mean and variance of a Poisson probability distribution are necessarily equal, which is infrequently the case for many variables of interest to behavior geneticists. Importantly, if the true data-generating model is overdispersed, then Poisson-based estimates of variance components cannot be unbiased, even asymptotically. We instead focus on two distributions that allow for such overdispersion: the negative binomial and the Lagrangian Poisson (LGP). Our use of these two distributions is motivated by practical rather than theoretical reasons: both are appropriate for skewed, overdispersed data, and both have multivariate generalizations. We do not mean to imply that either is necessarily the true distribution for any particular phenotype in that the phenotypic data arose from an associated stochastic process. Instead, we use them because they potentially provide better approximation to the true distributions of some count phenotypes than other models would.

Thus, the present work will chiefly be concerned with discrete distributions that allow for overdispersion (but offer no special treatment for zero-inflation). Bivariate forms of such distributions will be applied to analyses of single phenotypes observed in twin pairs, in order to obtain maximum-likelihood estimates of biometric variance components. We now first consider the univariate forms the negative binomial and Lagrangian Poisson.

The Univariate Negative Binomial Distribution

The negative-binomial is a two-parameter distribution the variance of which always exceeds its mean, making it applicable to variables exhibiting overdispersion. If a random variable (RV) X follows a negative binomial distribution, then symbolically, X ~ NB(v, 𝓅), with probability mass function (PMF)

$$p_X(x)=\left(\begin{array}{c}v+x-1\\ v-1\end{array}\right){\mathcal{p}}^v{\mathcal{q}}^x=\frac{\mathrm{\Gamma }(v+x)}{\mathrm{\Gamma }(x+1)\mathrm{\Gamma }(v)}{\mathcal{p}}^v{\mathcal{q}}^x$$ (1)

for x = 0, 1, 2, … (zero otherwise), 0 < 𝓅 < 1, 𝓆 = 1 − 𝓅, and v > 0. We will define a negative-binomial RV with v = 0 as one with unit mass on the event X = 0. The negative binomial has an “addition rule” (or more formally, a “convolution property”) —a fact that will prove important further below. This addition rule means that, if X₁, …, X_n are independent negative-binomial RVs, with X_i ~ NB(v_i, 𝓅), for i = 1, …, n, then $Y={\sum }_{i=1}^n{X}_i$ is also a negative-binomial random variable, with $Y~\text{NB}({\sum }_{i=1}^n{v}_i,\mathcal{p})$. We review further details concerning the negative binomial in Supplementary Appendix A (Online Resource 1), and refer the reader to such references as Forbes, Evans, Hastings, & Peacock (2011), Johnson, Kemp, & Kotz (2005), and Cameron & Trivedi (1986).

The Univariate Lagrangian Poisson Distribution

Compared to the Poisson and negative binomial, the versatile Lagrangian Poisson (LGP) distribution is relatively obscure. In this section, we briefly review material that may be found in Consul & Famoye (2006), Consul (1989), and Johnson et al. (2005).

The Lagrangian Poisson belongs to the broad class of Lagrangian distributions (Consul & Famoye, 2006), which are so named because their probability-generating functions (PGFs) are recursive functions expressible in terms of a Lagrange power-series expansion. If X ~ LGP(θ, λ), then

$$\begin{array}{l}{p}_X(x)=\frac{\theta {(\theta +\lambda x)}^{x-1}exp(-\theta -\lambda x)}{x!},\text{for}x=0,1,2\dots \\ =0,\text{for}x>m\text{if}\lambda <0\end{array}$$ (2)

where θ > 0, m = −θ/λ rounded down to the next smallest integer if λ < 0, and max(−1, −θ/m) ≤ λ ≤ 1. So, when λ (the dispersion parameter) is less than zero, there is a finite upper limit m on the distribution’s support. When λ < 0, the point masses do not sum across the support to exactly 1. Consul & Famoye (2006) say that as long as m ≥ 4, the resulting error is trivial; we say that, for computational purposes, it will usually not be too burdensome to obtain the normalizing constant numerically, with which the PMF can be adjusted so that it describes a proper probability distribution. Note that when λ = 0, the Lagrangian Poisson reduces to the ordinary Poisson. For purposes of latent-variate reduction (discussed below), we will define a Lagrangian Poisson with index parameter θ = 0 as one having unit mass on the event X = 0.

The distribution’s mean and variance are:

$$\mathrm{E}(X)=\frac{\theta }{(1-\lambda )}$$ (3)

$$var(X)=\frac{\theta }{{(1-\lambda )}^3}$$ (4)

Thus, it can be seen that the Lagrangian Poisson will be overdispersed if λ > 0, equidispersed (mean and variance equal) if λ = 0, and underdispersed (variance less than mean) if λ < 0. As λ increases, the upper tail becomes progressively heavier. When λ equals its upper limit of 1, the distribution is in a sense so heavy-tailed that, as suggested by Eq. (3), none of its moments exists. Importantly, Johnson et al. (2005) point out that when λ < 0, Eqs. (3) and (4) are only approximately accurate.

The Lagrangian Poisson also has an addition rule that is very similar to that of the negative binomial. Suppose X₁, …, X_n are independent Lagrangian-Poisson RVs, with X_i ~ LGP(θ_i, λ), for i =1, …, n. Then, $Y={\sum }_{i=1}^n{X}_i$ is also a Lagrangian-Poisson random variable, $Y~\text{LGP}({\sum }_{i=1}^n{\theta }_i,\lambda )$. We remark that this property does not necessarily hold when λ < 0. For example, suppose independent X₁ and X₂ are both distributed as LGP(3, −0.5). The addition rule would give the distribution of Y = X₁ + X₂ as LGP(6, −0.5), but this is an impossibility. The distribution LGP(6, −0.5) places nonzero probability (approximately 8.9 × 10⁻¹¹) on event Y = 11, but in fact Y cannot exceed 10, since neither X₁ nor X₂ can exceed 3/0.5 rounded to the next smallest integer, 5.

Latent-Variate Reduction: Bivariate LGP and Bivariate Negative Binomial Distributions

The bivariate distributions we discuss are constructed by what we will generally call “latent-variate reduction.” In the bivariate case, this is known in the literature as “trivariate reduction” because it models the two observable variables in terms of three independent latent variables (e.g., Kocherlakota & Kocherlakota, 1992). In Supplementary Appendix B (Online Resource 1), we derive the bivariate Poisson distribution (Teicher, 1954; Holgate, 1964), which involves fewer parameters and therefore provides a slightly simpler illustration of latent-variate reduction than that presented below. Latent-variate reduction may be extended to construct multivariate discrete distributions of arbitrary dimension. As an example, we describe the trivariate Poisson distribution in Supplementary Appendix C (Online Resource 1).

In trivariate reduction, two observable random variables Y₁ and Y₂ are each modeled as the sum of two latent variables. Common to both sums is one latent variable, X₀, whereas latent variables X₁ and X₂ are unique to the definitions of Y₁ and Y₂, respectively. Thus, Y₁ = X₀ + X₁, Y₂ = X₀ + X₂, and the variance of X₀ is the covariance of Y₁ and Y₂. By construction, X₀, X₁, and X₂ are independent of one another, which permits the derivation of the joint PMF of Y₁ and Y₂ in the manner we now describe.

The bivariate Lagrangian Poisson distribution is constructed via trivariate reduction as follows (Famoye & Consul, 1995). Consider three independent (latent) RVs X₀, X₁, and X₂, where

$$\begin{array}{l}{X}_0~\text{LGP}({\theta }_0,{\lambda }_0)\\ X_1~\text{LGP}({\theta }_1,{\lambda }_1)\\ X_2~\text{LGP}({\theta }_2,{\lambda }_2)\end{array}$$ (5)

Now, define (observable) RVs Y₁ and Y₂, where

$$\begin{array}{l}{Y}_1=X_0+X_1\\ Y_2=X_0+X_2\end{array}$$ (6)

Then, Y₁ and Y₂ jointly follow a bivariate Lagrangian Poisson distribution, with cov(Y₁, Y₂) = θ₀/(1 − λ₀)³. If θ₀ = 0, then cov(Y₁, Y₂) = 0, and Y₁ and Y₂ are in fact independent. However, it is not necessarily true that Y₁ or Y₂ are marginally distributed as univariate Lagrangian Poisson, which result follows for Y₁ only if λ₀ = λ₁, and for Y₂ only if λ₀ = λ₂. When λ₀ = λ₁ = λ₂ = 0, the distribution reduces to the ordinary bivariate Poisson.

Since the latent variables X₀, X₁, and X₂ are independent, their joint PMF is:

$$\begin{array}{l}{p}_{\mathbf{X}}(x_0,x_1,x_2)=p_{X0}(x_0)·p_{X1}(x_1)·p_{X2}(x_2)\\ =p_{X0}(x_0)·p_{X1}(y_1-x_0)·p_{X2}(y_2-x_0)\end{array}$$ (7)

Logically, x₀ cannot exceed the smaller of the pair (y₁, y₂). The distribution of Y₁ and Y₂, after marginalizing out X₀, is therefore given by the PMF:

$$p_{\mathbf{y}}(y_1,y_2)={\theta }_1{\theta }_2{\theta }_{0}exp(-{\theta }_1-{\theta }_2-{\theta }_0-y_1{\lambda }_1-y_2{\lambda }_2)\sum _{x_0=0}^{min(y_1,y_2)}Q$$ (8)

where

$$Q=\frac{{[{\theta }_1+(y_1-x_0){\lambda }_1]}^{y_1-x_0-1}}{(y_1-x_0)!}·\frac{{[{\theta }_2+(y_2-x_0){\lambda }_2]}^{y_2-x_0-1}}{(y_2-x_0)!}·\frac{{({\theta }_0+x_0{\lambda }_0)}^{x_0-1}exp(x_0[{\lambda }_1+{\lambda }_2-{\lambda }_0])}{x_0!}$$ (9)

The bivariate negative binomial distribution¹ can likewise be constructed through trivariate reduction, with independent latent variables:

$$\begin{array}{l}{X}_0~\text{NB}(v_0,{\mathcal{p}}_0)\\ X_1~\text{NB}(v_1,{\mathcal{p}}_1)\\ X_2~\text{NB}(v_2,{\mathcal{p}}_2)\end{array}$$

The observable variables Y₁ = X₀ + X₁ and Y₂ = X₀ + X₂ will not necessarily be marginally distributed as negative binomial, which would require the equalities 𝓅₀ = 𝓅₁ and 𝓅₀ = 𝓅₂, respectively. The bivariate distribution has PMF:

$$p_{\mathbf{y}}(y_1,y_2)=\frac{{\mathcal{p}}_0^{v_0}{\mathcal{p}}_1^{v_1}{\mathcal{p}}_2^{v_2}{\mathcal{q}}_1^{y_1}{\mathcal{q}}_2^{y_2}}{\mathrm{\Gamma }(v_0)\mathrm{\Gamma }(v_1)\mathrm{\Gamma }(v_2)}\sum _{x_0=0}^{min(y_1,y_2)}Q$$ (10)

where

$$Q=\frac{\mathrm{\Gamma }(v_0+x_0)\mathrm{\Gamma }(v_1+y_1-x_0)\mathrm{\Gamma }(v_2+y_2-x_0)}{\mathrm{\Gamma }(x_0+1)\mathrm{\Gamma }(y_1-x_0+1)\mathrm{\Gamma }({\mathrm{y}}_2-x_0+1)}{\left(\frac{{\mathcal{q}}_0}{{\mathcal{q}}_1{\mathcal{q}}_2}\right)}^{x_0}$$ (11)

Monophenotype Twin Modeling

The bivariate distributions described above can only model independence or positive correlation, and not negative correlation. While this is a limitation for the general application of these distributions, it is not a serious shortcoming if Y₁ and Y₂ represent data of an intraclass nature, and cov(Y₁, Y₂) thus represents a component of common variance. A natural such example is if Y₁ and Y₂ represent scores on a count phenotype respectively for “twin #1” and “twin #2” in a pair. We will here describe our application of the bivariate Lagrangian Poisson and bivariate negative binomial distributions to twin modeling in the simplest case, the monophenotype² ACE model in a classical twin study. In Online Resource 1, we present application of the multivariate Poisson to twin modeling in the monophenotype case (Supplementary Appendix B, which includes a path diagram) and the diphenotype and triphenotype cases (Supplementary Appendix D).

The bivariate Lagrangian Poisson and negative binomial distributions each have a total of six parameters. However, for the purpose of monophenotype twin modeling, only four unique parameters need be estimated. To ensure that the marginal phenotypic distribution is the same for MZ and DZ twins, the three latent variables X₀, X₁, and X₂ must have the same value of λ or 𝓅, for both MZ and DZ twins. Without some such constraint, it is possible for the model-predicted MZ and DZ phenotypic distributions to have the same mean and variance, but be different distributions (reflected, for instance, by their different higher-order moments—see example in Supplementary Appendix E, Online Resource 1).

With the Lagrangian Poisson, for MZ twins:

$$\begin{array}{l}{X}_0~\text{LGP}({\theta }_A+{\theta }_C,\lambda )\\ X_1,X_2~\text{LGP}({\theta }_E,\lambda )\end{array}$$ (12)

and therefore,

$$\begin{array}{l}{Y}_1,Y_2~\text{LGP}({\theta }_A+{\theta }_C+{\theta }_E,\lambda )\\ cov(Y_1,Y_2)=\frac{{\theta }_A+{\theta }_C}{{(1-\lambda )}^3}\end{array}$$ (13)

For DZ twins,

$$\begin{array}{l}{X}_0~\text{LGP}(0.5{\theta }_A+{\theta }_C,\lambda )\\ X_1,X_2~\text{LGP}(0.5{\theta }_A+{\theta }_E,\lambda )\end{array}$$ (14)

and therefore,

$$\begin{array}{l}{Y}_1,Y_2~\text{LGP}({\theta }_A+{\theta }_C+{\theta }_E,\lambda )\\ cov(Y_1,Y_2)=\frac{0.5{\theta }_A+{\theta }_C}{{(1-\lambda )}^3}\end{array}$$ (15)

Here, θ_A, θ_C, and θ_E are “theta components,” each proportional to a corresponding variance component. For example, the additive-genetic variance V_A = θ_A(1 − λ)⁻³.

With the negative binomial, the specification is very similar. For MZ twins,

$$\begin{array}{l}{X}_0~\text{NB}(v_A+v_C,\mathcal{p})\\ X_1,X_2~\text{NB}(v_E,\mathcal{p})\end{array}$$ (16)

and therefore,

$$\begin{array}{l}{Y}_1,Y_2~\text{NB}(v_A+v_C+v_E,\mathcal{p})\\ cov(Y_1,Y_2)=\frac{(v_A+v_C)\mathcal{q}}{{\mathcal{p}}^2}\end{array}$$ (17)

For DZ twins,

$$\begin{array}{l}{X}_0~\text{NB}(0.5v_A+v_C,\mathcal{p})\\ X_1{X}_2~\text{NB}(0.5v_A+v_E,\mathcal{p})\end{array}$$ (18)

and therefore,

$$\begin{array}{l}{Y}_1,Y_2~\text{NB}(v_A+v_C+v_E,\mathcal{p})\\ cov(Y_1,Y_2)=\frac{(0.5v_A+v_C)\mathcal{q}}{{\mathcal{p}}^2}\end{array}$$ (19)

We again remark that these bivariate negative binomial and LGP twin models are motivated chiefly by pragmatism rather than any compelling theoretical rationale. Our objective is to apply bivariate distributions suitable for overdispersed count variables to twin analysis, in order to obtain maximum-likelihood estimates of biometric variance components. The negative binomial and LGP distributions are generated from particular stochastic processes, which may or may not describe how data on a specific phenotype arise. For instance, in alcohol consumption data, the negative binomial would arise if people’s latent “tendency to drink” followed a gamma distribution in the population, and conditional on some tendency to drink, the number of drinks a person has each day followed a Poisson distribution. While not obviously wrong, to our knowledge this proposition is supported by neither empirical data nor strong prior theory. Furthermore, it is not obvious how one might derive our twin models from theory of polygenic inheritance, since the summation of many small, additive allelic effects over a large number of loci will, under broad conditions, lead to an approximately normally distributed total effect³ (Lehmann, 1999). However, as shown by its derivation from the quasi-binomial I distribution (Consul & Famoye, 2006), the LGP is a limiting distribution for the sum of a large n umber of small and weakly correlated binary increaser effects. It may therefore be useful in development of discrete-data twin models with stronger theoretical justification—a topic for future research.

Simulation

In the preceding we have reviewed two bivariate discrete distributions with positively skewed, overdispersed marginals, which are likely unfamiliar to the majority of behavior geneticists. We have further introduced a novel application of these distributions to biometrical analysis-of-variance using monophenotype twin data. That is, we have introduced new candidates for the true generating distribution of data collected on twins, tailored specifically to integer-valued phenotypes. What value might this novel method have to the twin researcher, relative to widely used, more-familiar methods? In particular, if a phenotype arose from a multivariate discrete distribution, how “wrong” would conventional analyses of such data be? This question motivated a Monte Carlo simulation to compare (i) our model, when the distributional assumption is correct; (ii) our model, when the distributional assumption is incorrect; and (iii) three commonly used models. We compare these five models with respect to the properties of their point estimates, the Type I error rates of their hypothesis tests, and their performance under cross-validation in new data.

Simulation Design

We conducted the simulation in the R statistical computing environment, version 2.15.2 (R Core Team, 2013). Model-fitting was carried out in the R package OpenMx, version 1.3.2 (Boker et al., 2011). We developed our own code (Kirkpatrick, 2014; also see Online Resource 2) for computing likelihoods from the bivariate negative-binomial and Lagrangian Poisson distributions. We likewise developed R functions for generating pseudo-random numbers from the univariate Lagrangian Poisson distribution, based on Consul & Famoye (2006, chapter 16), from which random draws from the bivariate Lagrangian Poisson are easily generated.

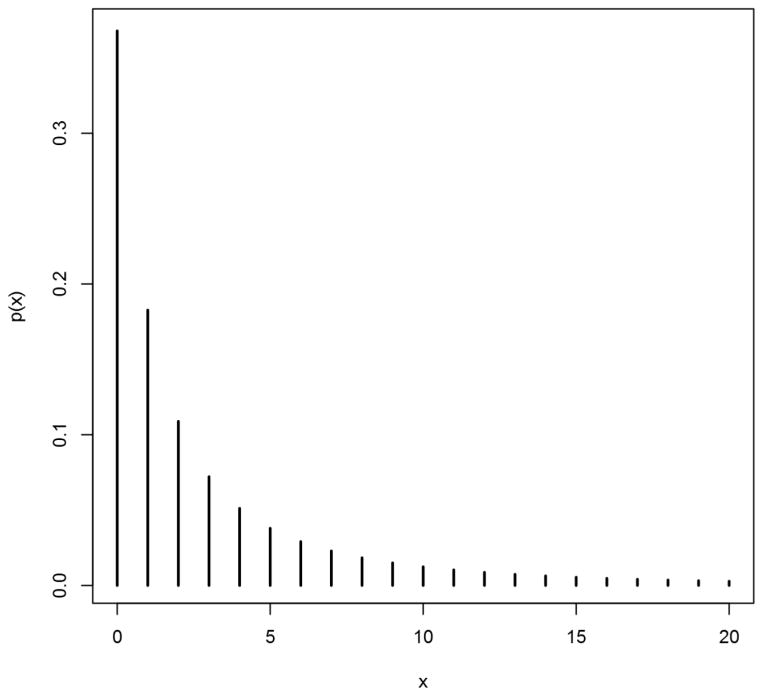
The true data-generating distribution was bivariate Lagrangian Poisson with λ = 0.7 for all three latent variables. For MZ twins, θ₀ = 0.65 and θ₁ = θ₂ = 0.35; for DZ twins, θ₀ = θ₁ = θ₂ = 0.5. Thus, the phenotype was marginally distributed as LGP(1, 0.7), which is depicted in Figure 1. The parameters of interest are the phenotypic mean and variance, the twin covariances and correlations, and the biometric variance components. These values are presented in Table I, for the raw-scale distribution as well as for two transformations thereof (described below).

Figure 1. Marginal phenotypic distribution for simulation.

Figure graphs the Lagrangian Poisson PMF, for parameters θ = 1 and λ = 0.7. for x = 0 thru 20.

Table I.

Parameters of interest in Monte Carlo simulation.

Parameter	Raw	Log-scale	Ordinalized
Mean	3.33	0.94	0
Phenotypic Variance	37.04	0.88	1
MZ Covariance	24.07	0.55	0.70
DZ Covariance	18.52	0.42	0.54
MZ Correlation	0.65	0.63	0.70
DZ Correlation	0.5	0.48	0.54
Additive-Genetic Variance	11.11	0.27	0.33
Shared-Environmental Variance	12.96	0.29	0.38
Nonshared-Environmental Variance	12.96	0.33	0.29
Heritability	0.30	0.30	0.33
Shared-Environmentality	0.35	0.33	0.38

notes: MZ = monozygotic twin, DZ = dizygotic twin. Raw parameters describe the data-generating bivariate Lagrangian Poisson distributions. Log-scale parameters describe the data-generating distributions after applying a log(y + 1) transformation to the variables. Ordinalized parameters describe the data-generating distributions after they have been ordinalized to a five-point scale. To identify the ordinal model, the mean and variance must be fixed to 0 and 1, respectively. As a result, some parameters of the ordinalized distribution are redundant with one another.

The Monte Carlo experiment had three sample-size conditions: 200, 1000, or 5000 twin pairs. Simulated samples comprised equal numbers of MZ and DZ pairs. We generated 10,000 simulated datasets in each sample-size condition. Five bivariate probability models were fitted to each dataset: normal, lognormal, ordinal, Lagrangian Poisson, and negative binomial. The normal model simply estimated parameters by maximum likelihood using the built-in bivariate-normal distribution in OpenMx, whereas we supplied purpose-built R objective likelihood functions to OpenMx for the bivariate Lagrangian Poisson and negative binomial distributions, parameterized in terms of raw variance components and their dispersion parameter (λ or 𝓅). The remaining two, the lognormal and ordinal, require some explanation.

Lognormal model

One common way of adjusting for positive skew in a variable y is to add a constant to raise all of its values above zero, then to take its natural log, and finally to analyze the data as if normally distributed. With count variables, this is equivalent to applying the lognormal distribution (Forbes et al., 2011, chapter 29) to y + 1. The lognormal distribution describes a RV the natural logarithm of which is normally distributed. Its parameters are the mean and variance of the log-transformed variable, and its probability density function (PDF) is easily derived from the normal PDF via change-of-variable. For our purposes, we required a bivariate lognormal PDF (Balakrishnan & Lai, 2009) that incorporates the upward shift by 1, which can be shown to be

$$f_{\mathbf{y}}(y_1,y_2)=\frac{{\mid \mathbf{\sum }\mid }^{-0.5}}{2\pi (y_1+1)(y_2+1)}exp(0.5{\mathbf{d}}^T{\mathbf{\sum }}^{-1}\mathbf{d})$$ (20)

where d^T = [log(y₁ + 1) − μ_y1, log(y₂ + 1) − μ_y2], μ_y1 and μ_y2 are the respective log-scale means of Y₁ and Y₂, and Σ is their log-scale covariance matrix. For details concerning this distribution, see Supplementary Appendix F (Online Resource 1).

The expectations and covariance matrix of the log(y+1)-transformed bivariate Lagrangian Poisson are not analytically tractable, but are straightforward to calculate numerically. We wrote an R function (Kirkpatrick, 2014) to calculate these quantities for the true distribution of our simulation. They are presented in Table I.

Ordinal model

The 0.2, 0.4, 0.6, and 0.8 quantiles of the LGP(1,0.7) distribution are 0, 1, 2, and 5, respectively. In each iteration of the simulation, the phenotype was recoded as an ordinal variable with categories corresponding to x=0, x=1, x=2, x=(3,4,5), and x>5. We decided to use “known” cutpoints of 0, 1, 2, and 5 in every iteration to simulate real-life instances in which reasonable cutpoints can be decided independently of data, on rational subject-matter considerations. The parameters of the ordinalized bivariate distribution are the thresholds on the standard-normal distribution corresponding to the cutpoints between adjacent categories, and the polychoric correlations for MZ and DZ twins. The thresholds are easily obtainable by converting the exact lower-tail probabilities of 0, 1, 2, and 5 in the LGP(1, 0.7) distribution to standard-normal quantiles. The ordinalized distribution can be described by a 5 × 5 table of categories, and the probabilities for each cell in the table can be calculated from the bivariate Lagrangian Poisson PMF. From these tables, the polychoric correlations can be computed. These polychoric correlations, and the standardized latent-distribution variance components they imply, are presented in Table I.

Dependent Measures

The dependent measures of our Monte Carlo experiment fall into three broad categories: (i) those concerning the properties of different models’ point estimates, (ii) Type I error rates of different models’ hypothesis tests, and (iii) models’ cross-validation performance. In addition, at each iteration we stored the results of basic “quality-control” checks on each model’s numerical results.

Point estimate properties

We assessed the bias, variance, and mean squared error (MSE, equal to variance plus squared bias) of models’ point estimates. We allowed estimates of the additive-genetic and shared-environmental variance components to be negative, even though many investigators might regard such nonsensical estimates as inadmissible for subject-matter reasons. We did so to prevent boundary conditions from interfering with likelihood-ratio tests’ Type I error rates (e.g., Wu & Neale, 2012).

Type I error rates

At each iteration, we conducted likelihood-ratio tests (LRTs) of null hypotheses that each parameter of interest is equal to its true value. LRTs could be conducted for all 11 parameters listed in Table I, by fitting a new model in OpenMx in which the parameter was held fixed at its true value, and comparing the change in deviance (−2 times the log-likelihood) relative to the full model. Under the null hypothesis and in the absence of model misspecification, this change in deviance is distributed as chi-squared on 1 degree-of-freedom.

Cross-validation performance

We evaluated cross-validation performance for all models except the ordinal, which is such a different model from the rest that legitimate comparison would be difficult. The loss function we used was model deviance (−2 times the log-likelihood). The 10,000 iterations for each sample-size condition were split into ten parallel jobs of 1,000 iterations each. Within each job, for each iteration i, i >1, each model was fitted to the simulated dataset of i (the current iteration) with its parameters fixed to their estimated values from iteration i − 1 (the previous iteration). The resulting model deviance represented the loss—the degree of “misfit” for that model—when “plugging in” parameter estimates from a separate, independent sample of the same size.

We also saved each model’s deviance when all parameters were free to be estimated from the current iteration’s sample. Because the normal, lognormal, negative binomial, and LGP all have the same number of free parameters, comparing these deviances is equivalent to comparing values of Akaike’s Information Criterion (AIC). In large samples, AIC is expected to prefer the model in the candidate set that best approximates (in the sense of Kullback & Leibler, 1951) the true model, or equivalently, the model that is expected to best cross-validate in independent samples when loss is based on a log-likelihood function (Hastie, Tibshirani, & Friedman, 2009).

Because we are applying both discrete and continuous models in this simulation, we must ensure that the likelihoods (and therefore the deviances) from both types of model are comparable. Every likelihood function was computed as a normalized “density” function (PDF or PMF, as the case may be), that is, we did not drop any normalizing constants. But even with this precaution, there remains the problem that a discrete distribution’s likelihood is the probability of an event, whereas a continuous distribution’s likelihood is a value from a PDF, and may be greater than 1. Therefore, for the purpose of calculating deviance loss, we “coarsened” the likelihoods of the normal and lognormal models as suggested by Warton (2005). Roughly, the idea is that a distribution’s density function, evaluated at some data value y, expresses the rate of change in the distribution’s cumulative distribution function (CDF) over an interval centered on y and of “atomic” width. For discrete distributions of integer-valued RVs, the unit interval is of atomic width; for continuous RVs, the atomic width is infinitesimal. Thus, for the densities to be comparable, the continuous density must be coarsened to the same atomic width as the discrete. If F(·) is the bivariate-normal CDF and y^T = [y₁, y₂] is a pair of phenotype scores from one twin pair, then the coarsened density for our normal model, given the previous sample’s MLEs θ̂_i−1, is

$$f(\mathbf{y}\mid {\widehat{\mathbf{\theta }}}_{i-1})=F(\mathbf{y}+0.5\mid {\widehat{\mathbf{\theta }}}_{i-1})-F(\mathbf{y}-0.5\mid {\widehat{\mathbf{\theta }}}_{i-1})$$ (21)

and for our lognormal model,

$$f(\mathbf{y}\mid {\widehat{\mathbf{\theta }}}_{i-1})=F(log[\mathbf{y}+1.5]\mid {\widehat{\mathbf{\theta }}}_{i-1})-F(log[\mathbf{y}+0.5]\mid {\widehat{\mathbf{\theta }}}_{i-1})$$ (22)

The coarsened log-likelihood of the model is obtained by summing the logs of the coarsened densities across twin pairs.

We used the R package mvtnorm, version 0.9 (Genz & Bretz, 2009) to calculate the coarsened densities from the bivariate normal CDF. Due to numerical imprecision, the function sometimes returns extremely small probabilities as values with a negative sign, which is problematic because the logarithm of those probabilities is required. We therefore wrote a wrapper function that coerced these negative “probabilities” to 2 × 10⁻¹⁶.

Quality control

Under the following four circumstances, we discarded all of a model’s results from a given iteration: (1) if numerical optimization failed completely (premature termination); (2) if the optimizer exceeded its maximum iterations; (3) if the optimizer’s solution did not meet first order conditions for a minimum of the objective function; or (4) if the Hessian matrix evaluated at the solution was non-positive-definite. We also discarded the result of a parameter’s LRT if any of the first three optimization problems occurred while fitting the null model for that parameter.

Results

For the sake of brevity, we focus chiefly on results for the 1,000-twin-pair condition, since that condition represents a realistic but not-too-small sample size. The raw simulation data are publicly available: Online Resource 2 contains an R script that loads the raw simulation data (quality-control checks, point estimates, LRT statistics, etc.) over the web to produce data visualizations and descriptive statistics.

On the whole, bias in point estimates was generally small, except for variance components as estimated from the negative-binomial model. As might be expected, the true model (LGP) exhibited best cross-validation performance and yielded Type I error rates at the nominal level. The negative-binomial model performed second-best with regard to cross-validation. Type I error inflation from models other than the true LGP ranged from negligible to severe, depending upon the model and parameter in question.

Quality control

Table II reports the total number of iterations in which each model reached acceptable convergence criteria in the 1000-twin-pair condition. Across sample-size conditions, the lognormal model suffered zero convergence failures, whereas the ordinal model suffered the most (perhaps due to imprecision in the numerical integration required to compute its likelihood). Overall, convergence failures were most common in the smallest sample-size condition. Hereinafter, results are computed after dropping models’ results from iterations in which they did not acceptably converge.

Table II.

Acceptable convergence frequency and cross-validation loss for N_pairs = 1000 condition.

	Normal	Lognormal	Ordinal	LGP	NegBin
# Iterations Converged	10,000	10,000	9398	9963	9944
Mean (SD) Loss	12,459.9 (291.2)	8899.3 (153.6)	--	8158.2 (146.4)	8194.1 (147.1)

notes: LGP = Lagrangian Poisson, NegBin = negative binomial. Convergence was considered acceptable unless any of the following occurred: premature termination of the optimizer, optimizer reaching its maximum number of iterations, solution not meeting first-order or second-order conditions for a minimum. Cross-validation loss is −2 times the log-likelihood of the model when all of its parameters are fixed to their estimates from the previous iteration of the simulation; smaller loss indicates better model performance. Regarding convergence frequency, a generalized estimating equations analysis using all three sample-size conditions indicated that all pairwise comparisons of models’ marginal convergence proportions were statistically significant (smallest χ²(1df) = 10.68). Regarding cross-validation loss, linear mixed-effects regression using all three sample-size conditions indicated a significant interaction of sample size with model χ²(3df) = 671,331).

Point estimates

Point estimates’ proportional bias (bias divided by true parameter value) were generally small in the 1000-twin-pair condition: most proportional biases were smaller than 2%. One of the ordinal model’s thresholds was downwardly biased by about 5%. Substantial bias was only evident for the negative-binomial model’s estimates of the variance components, and therefore, also of the twin covariances and the total phenotypic variance; these quantities were all downwardly biased by 24% to 26% percent. Table III reports the proportional mean squared errors (pMSE, which is the mean squared error divided by the square of the true parameter value) of models’ point estimates in the 1000-twin-pair condition. Because bias was small for most estimates (other than those aforementioned from the negative-binomial model), most of these pMSEs chiefly reflect sampling variance.

Table III.

Proportional mean squared error of estimation for each parameter, from each model, with N_pairs = 1000

Parameter	Normal	Lognormal	Ordinal	LGP	NegBin
Mean	0.0026	0.0007	--	0.0024	0.0024
Phenotypic Variance	0.0267	0.0014	--	0.0169	0.0683
MZ Covariance	0.0624	0.0062	--	0.0185	0.0710
DZ Covariance	0.0936	0.0115	--	0.0214	0.0707
MZ Correlation	0.0220	0.0040	0.0025	0.0012	0.0012
DZ Correlation	0.0441	0.0088	0.0128	0.0033	0.0032
Additive-Genetic Variance	0.9931	0.1554	--	0.0733	0.1071
Shared-Environmental Variance	0.5316	0.0939	--	0.0506	0.0831
Nonshared-Environmental Variance	0.0868	0.0113	--	0.0205	0.0670
Heritability	0.9045	0.1548	0.1883	0.0577	0.0561
Shared-Environmentality	0.4363	0.0903	0.1138	0.0305	0.0294

notes: Proportional mean squared error is the ratio of the mean squared error of the estimator to the square of the true parameter value. Table presents data from the simulation condition in which samples consisted of 1000 twin pairs. Because of constraints necessary to identify the ordinal model, some of its parameters are not freely estimated or are redundant with other parameters. Generalized estimating equations analyses were conducted for each parameter. The pMSE for the MZ correlation did not significantly differ between the negative binomial and LGP models, but all other pairwise comparisons were statistically significant (smallest χ²(1df) = 11.55).

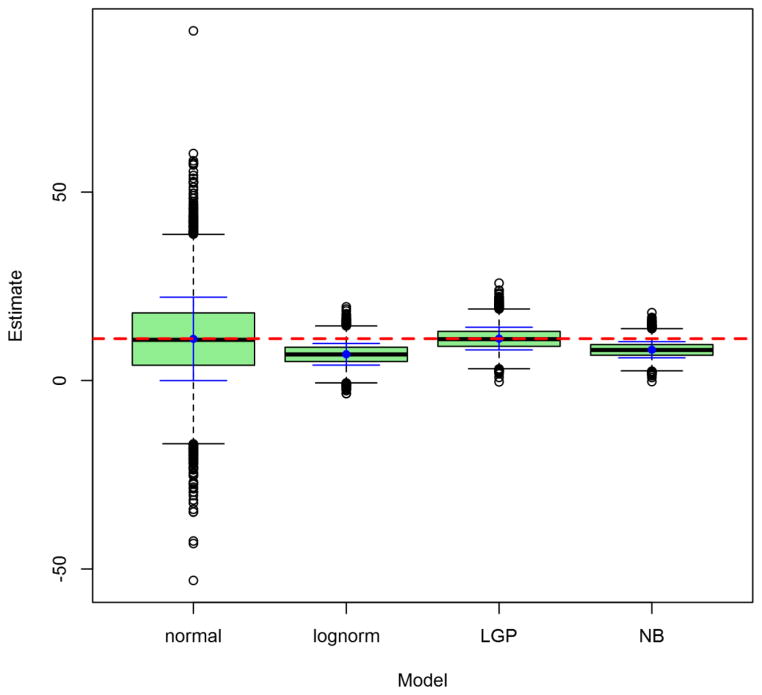
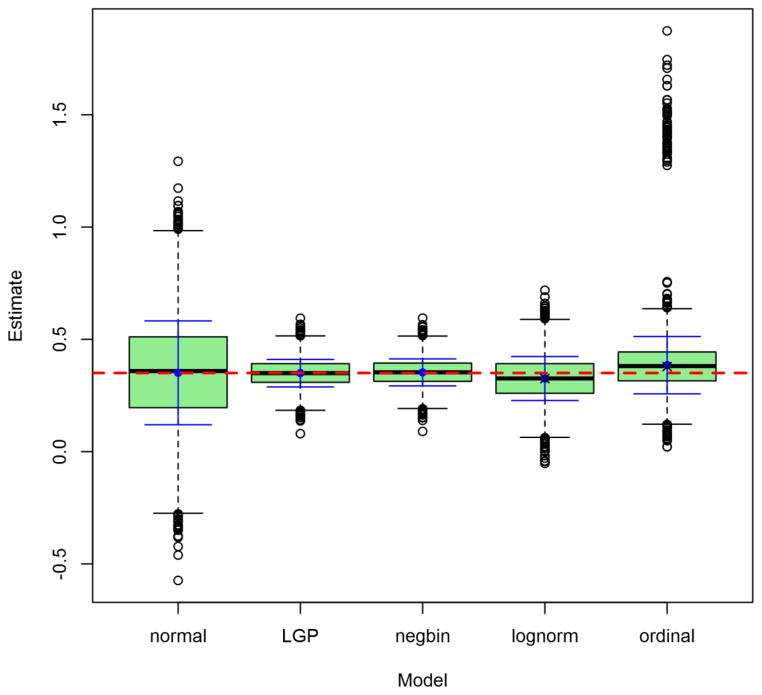
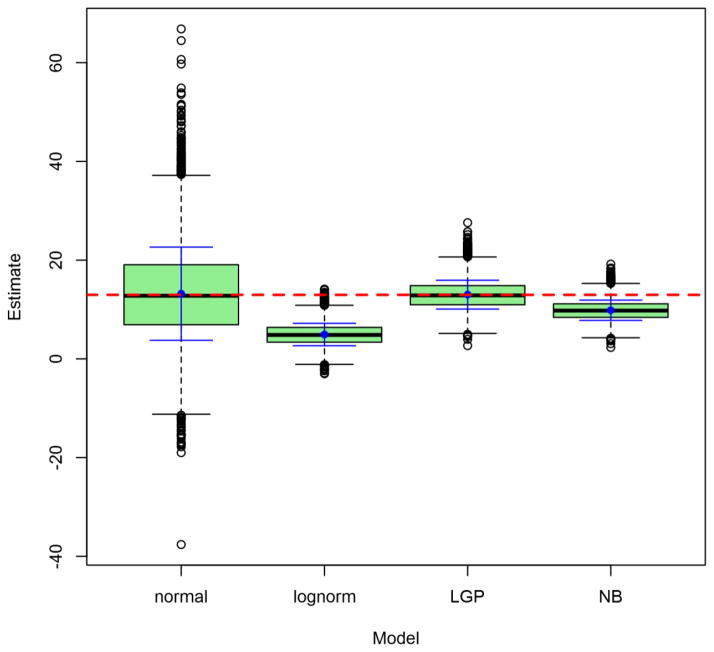
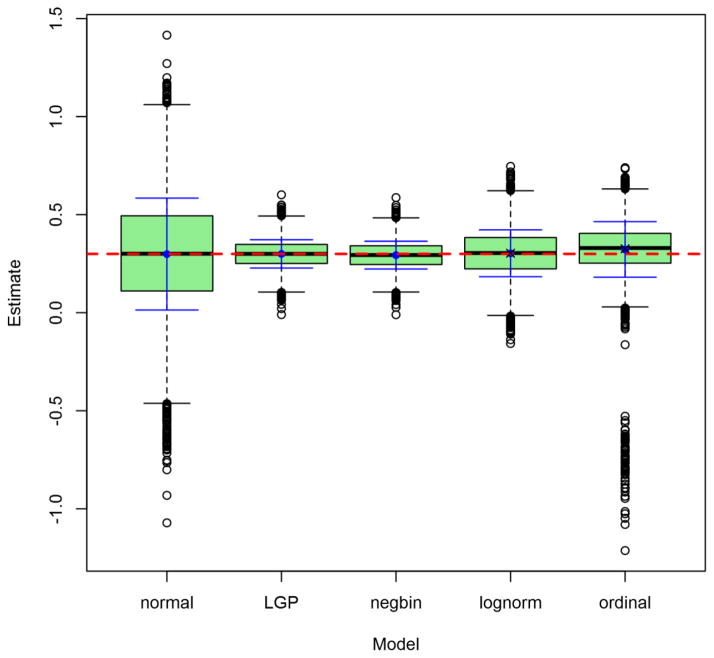
Figures 2 through 5 depict the sampling distributions of estimates for the parameters of greatest interest in the classical twin study: the additive-genetic and shared-environmental variances, and their standardized counterparts. For the raw variance components, the normal model and the LGP model both produced nearly unbiased estimates, but the normal model’s estimates were considerably greater in variance. In contrast, the negative-binomial model’s estimates had even smaller variance than did the true LGP’s, but were downwardly biased. Concerning the variance proportions, all five models’ estimates were approximately unbiased (with those from the lognormal and ordinal models approximately unbiased for the true values of the log-transformed and ordinalized distributions, respectively). Poor-quality point estimates were most common from the normal and ordinal models. The normal-model estimates had greatest variance, followed by those of the lognormal and ordinal models, followed lastly by those from the discrete models. Notably, the negative-binomial’s bias for the raw variance components did not carry over to the standardized variance proportions.

Figure 2. Observed distributions of estimated additive-genetic variance, for N_pairs = 1000.

Depicted results are from the 1000-twin-pair condition of the simulation. Labels on the x-axis identify the model: LGP = Lagrangian Poisson, negbin = negative binomial. For the lognormal model, raw-scale parameter estimates are presented. Graph depicts conventional box-and-whisker plots for each model, with additional solid whiskers superimposed over them to mark the mean (filled dot) ± 1SD of the sampling distribution. Horizontal dashed line marks true raw parameter value.

Figure 5. Observed distributions of estimated shared-environmentality, for N_pairs = 1000.

Depicted results are from the 1000-twin-pair condition of the simulation. Labels on the x-axis identify the model: LGP = Lagrangian Poisson, negbin = negative binomial. Graph depicts conventional box-and-whisker plots for each model, with additional solid whiskers superimposed over them to mark the mean (filled dot) ± 1SD. Horizontal dashed line marks true raw parameter value. X’s mark true parameter values post-transformation (log(y + 1) or ordinalizing, as the case may be).

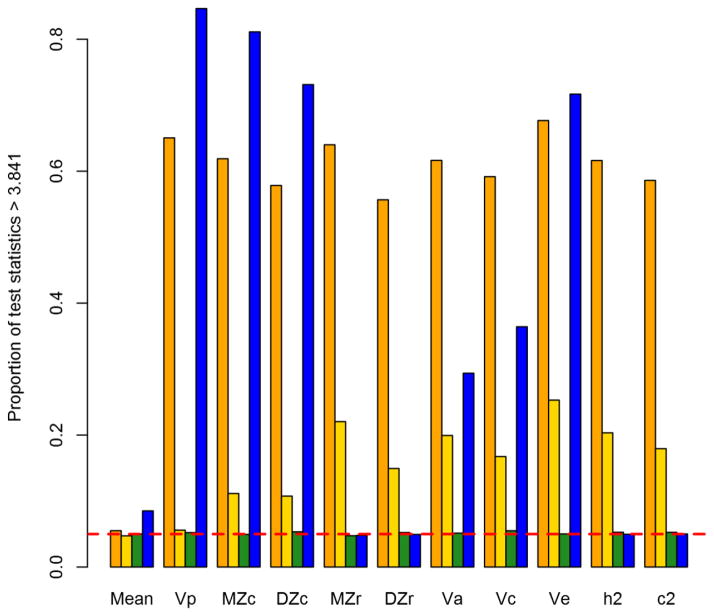
Type I error

Figure 6 depicts the Type I error rates of the normal, lognormal, LGP, and negative-binomial models at N_pairs = 1000. Encouragingly, the Type I error rates for the LGP at this sample size were all very close to the nominal level of 0.05, which is evidence for the validity of our program code, and indicates that the asymptotic properties of the likelihood-ratio test hold for the LGP at reasonable sample sizes. The results for the normal model are consistent with the supposed large-sample robustness of normal-theory inference about the mean. But, tests for all other parameters showed substantial Type I error inflation, exceeding the nominal level by more than an order of magnitude. Type I error inflation was less pronounced for the lognormal model, and in fact was very close to the nominal level for the marginal moments—the phenotypic mean and total variance. The inflation was only evident for those parameters identified by the twin model, and was at most 5 times the nominal rate (0.2530 for unshared-environmental variance). Most interesting of all is the negative binomial, which yielded unbiased hypothesis tests for the standardized parameters (variance proportions and twin correlations), but staggeringly biased tests for the raw variance components and functions thereof (the twin covariances and total variance).

Figure 6. Likelihood-ratio test Type I error rates, by parameter and model, for N_pairs = 1000.

From left to right, bars correspond to normal, lognormal, Lagrangian Poisson, and negative binomial models. Results for lognormal model are for its log-scale, not raw-scale, parameters. Horizontal dashed line marks nominal Type I error rate of 0.05. Vp = phenotypic variance, MZc = monozygotic-twin covariance, DZc = dizygotic-twin covariance, MZr = monozygotic-twin correlation, DZr = dizygotic-twin correlation, Va = additive-genetic variance, Vc = shared-environmental variance, Ve = nonshared environmental variance, h2 = narrow-sense heritability, c2 = shared-environmentality.

Cross-validation performance

Table II presents deviance loss by model for the N_pairs = 1000 condition. Not surprisingly, the true model (LGP) had the smallest deviance loss in most iterations of the simulation: 85.35% of iterations when N_pairs = 200, 99.37% when N_pairs = 1000, and 100% when N_pairs = 5000. A more interesting question would be, which model other than the true performed best under cross-validation? When the LGP model was eliminated from consideration, the negative binomial model was clearly the winner: 96.45% of iterations when N_pairs = 200, 99.44% when N_pairs = 1000, and 100% when N_pairs = 5000. The normal model almost always had the largest deviance loss (99.78% of iterations overall).

Discussion

This Monte Carlo experiment compared the performance of two discrete models, two continuous models, and an ordinal model when the data were generated from a skewed, bivariate discrete distribution. First, the simulation showed that one fares poorly indeed if one ignores the non-normality of the data and applies the “default” bivariate normal model. The normal model’s point estimates had large variances, and it performed worst under cross-validation. Finally, hypothesis tests from the normal model were aggressively biased for every parameter except the mean, with Type I error rates exceeding 10 times the nominal level.

The bivariate lognormal model is effectively the bivariate normal model with log-transformed data. One of its disadvantages is that its parameters are on the log scale, and not on the raw scale of the original count data. Indeed, the transformation serves to change even the true values of standardized parameters (variance proportions and twin correlations). Despite this distortion, the transformation appears to have some benefits. The lognormal had smaller pMSE for its estimates of the standardized parameters, relative to the normal. Its Type I error inflation was also smaller compared to the normal, but still at least twice the nominal rate for most parameters. It is possible to obtain model-expected raw-scale parameters from the lognormal’s log-scale parameters (see Supplementary Appendix E, Online Resource 1). These raw-scale estimates of the mean and total variance were downwardly biased, by 10% and 39%, respectively.

Aside from log-transforming the data, another common strategy for dealing with non-normal data is to ordinalize them. It is often not practical to have one ordered category for each unique score value in the dataset, so several score values must then be mapped to the same ordered category, which has several disadvantages. First, it coarsens the data and “throws away information.” Additionally, the number of categories to have, and the location of the cutpoints separating them, are usually arbitrary decisions (at least to some extent). If the original data are frequency counts, the practice of ordinalization becomes even more objectionable: why would one want to trade a ratio-scale variable for an ordinal one? We admit that there might sometimes be subject-matter reasons supporting a particular ordinalizing transformation, which we have tried to capture in our simulation by always using the same cutpoints to separate categories across iterations. We considered placing the cutpoints based on the empirical quantiles of each sample, but were concerned that doing so would create too many ordinal-model convergence failures in the small sample-size condition.

Even so, the ordinal model was the least numerically tractable model to fit, and produced the most convergence failures of any model. The MSEs of its point estimates were similar to those of the lognormal. In the 1000-twin-pair condition, the ordinal had less biased test statistics than the normal or lognormal model did, producing Type I errors only at about twice the nominal rate. We conclude that one would fare relatively well when ordinalizing skewed bivariate count data, provided that one’s choice of categories and cutpoints can be justified. Naturally, though, if the count variable takes only a small number of unique values in the dataset, one can create an ordinal category for every observed value—certainly a justifiable choice of categories.

The negative-binomial was the only other discrete model we fitted besides the true LGP. When the LGP was excluded from consideration, the negative binomial performed best under cross-validation, and its average deviance loss was only slightly greater than that of the LGP. Most interestingly, the negative-binomial’s point estimates and hypothesis tests were nearly identical to the LGP’s for standardized parameters, but severely biased for the raw variance components and related quantities (twin covariance and total variance). This occurs because, evidently, the univariate negative-binomial distribution that best approximates the true marginal LGP distribution simply has a smaller variance. The goodness of the approximation can be quantified with Kullback-Leibler divergence (Kullback & Leibler, 1951), which represents the amount of information lost when one distribution is approximated by another. We numerically obtained the negative-binomial parameter values that minimize Kullback-Leibler divergence from the true marginal LGP(1, 0.7) model, and found that the best approximating negative-binomial distribution has a variance of 28.3, which is not dissimilar from the mean estimate of total variance at N_pairs = 5000, which was 27.8.

One obvious practical implication of this simulation is that if one is interested in variance components, non-normality should not be ignored, and must be addressed somehow. Transformations such as the logarithmic may improve the normal approximation in some respects, but as shown in Figure 7, they do not guarantee that parametric inferences will be correct. Our simulation suggests that ordinalizing the data might also be a reasonable strategy, but we suspect our results for the ordinal model are overly optimistic for how well it would function in practice, since the data were always ordinalized using “known” quantiles of the true distribution. Finally, the negative binomial model showed that one skewed discrete distribution can be used to approximate another, but bias in variance-component estimates might need to be addressed somehow. We would suggest considering more than two discrete models if possible, selecting whichever has the smallest AIC, and then obtaining jackknife estimates of bias. Alternatively, one could estimate bias from the differences between discrete-model estimates and normal-model estimates, averaged across a large number of nonparametric bootstrap iterations. Of course, this bias is only a concern if the unstandardized variances are of interest. In many biometrical analyses, only the standardized (proportional) contributions of heredity and environment are of interest, and our simulation has shown that a discrete model can estimate the standardized parameters with negligible bias even if it cannot do so for the unstandardized parameters.

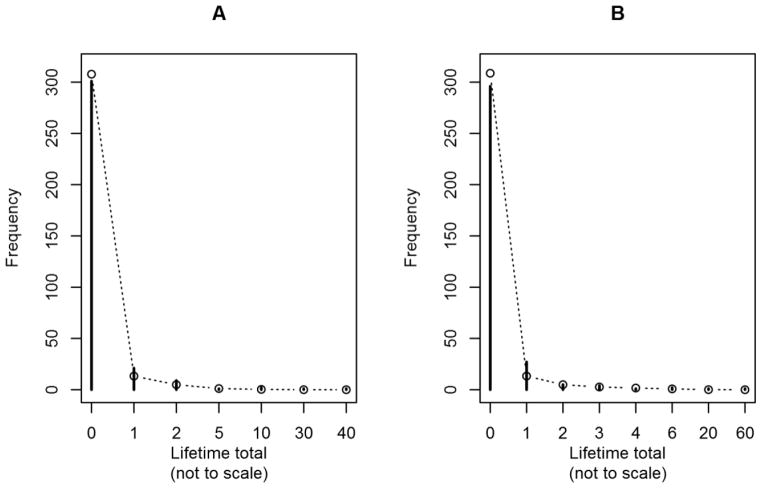
Figure 7. Observed and model-expected phenotypic distribution for 17-year-old female twins “A” and “B” in Dataset #2 (MTFS).

Solid pins represent observed frequencies; open circles represent expected frequencies per the best-performing model, conditional on female sex, and assuming that all members of 17-year-old age cohort are exactly 17.0 years old. Twins in a given pair are arbitrarily distinguished as “A” and “B.” Phenotype is self-reported lifetime number of times getting into “trouble” due to using alcohol or drugs. Note that x-axis is not drawn to scale, due to extreme outliers in this cohort.

This simulation has several limitations that reduce the potential generalizability of its conclusions. The most notable limitation is that data were generated from only one distribution (bivariate LGP), and only under one set of parameter values. Obviously, results could be quite different if the data-generating distribution were (say) a very differently shaped bivariate LGP, or a bivariate negative binomial, or something else altogether. Likewise, the data were also transformed only two different ways: logarithmic transformation, and ordinalization with cutpoints at the true 0.2, 0.4, 0.6, and 0.8 quantiles. In particular, our results from the ordinal model could have differed if we had used empirical estimates of the quantiles, or used quantiles not “equally spaced” in terms of cumulative probability, or had created one ordered category for each unique score. Finally, the simulation is not informative about the consequences of fitting a bivariate discrete distribution to data when a bivariate discrete distribution is in fact not the true model—a consequence of only using one data-generating distribution. We hope that future Monte Carlo simulations, with more-complicated experimental designs, will expand upon the present work and address these shortcomings.

Real-Data Application: Substance Use in Twins

We demonstrate the methods described above with an application to real data, collected from a life-events interview in a substance-abuse study of adolescent twins born in Minnesota. We compared the merit of four models with sample-size adjusted AIC: normal, lognormal, LGP, and negative binomial. We further evaluated the models’ merit using five-fold cross-validation, using deviance loss (as in the simulation) and a quadratic loss metric (explained below). For both AIC and deviance loss, we used the “coarsened likelihood” described above with the normal and lognormal models.

The five-fold cross-validation proceeded as follows. The full sample was randomly divided into five subsamples, of as equal size as possible, and as alike as possible in composition with regard to sex, zygosity, and proportion of incomplete twin pairs. Each subsample was left out as a validation sample once, and the models under consideration were fitted to the other four subsamples, pooled together into a calibration sample. Then, the models were applied to the validation subsample, with parameters fixed to their values as estimated from the calibration sample.

Dataset: the Minnesota Twin Family Study

The Minnesota Twin Family Study (“MTFS”; Iacono, Carlson, Taylor, Elkins, & McGue, 1999; Iacono & McGue, 2002; Keyes et al., 2009) is a longitudinal study of adolescent, same-sex twin pairs, born in the State of Minnesota, and their parents. The sample contains two age cohorts, the 11-year-old and 17-year-old cohorts, named for the target age of the twins at their intake visit to the laboratory. The data we use here come from an interview administered to twins during this intake visit, which concerned significant life events in their personal history (e.g., “has your family ever moved to a new house or apartment?”). The interview is structured so that if a participant reports that s/he has experienced a particular event, one of the follow-up questions is how many times that event has occurred. The interview question of interest here is, “have you ever gotten into trouble because of your use of alcohol or drugs?” The phenotype in this analysis is the self-reported number of times the participant experienced this life event (those answering “no” to the stem question are considered to have experienced it zero times).

We make several preliminary observations concerning this phenotype. First, the stem question is subject to interpretation—what, specifically, does it mean to have “gotten into trouble because of your use of alcohol or drugs?” Second, because responses are lifetime counts of occurrences, one would anticipate a higher mean response in the older compared to the younger. Third, of the 3,670 twins (from 1,842 pairs) in the dataset, 11 gave responses in the double digits (max = 60), all of which are multiples of 10. This is likely due to “digit preference,” and suggests that participants reporting large numbers of occurrences do not recall an exact number. Therefore, error variance may positively correlate with response. Fourth, the empirical distribution has heavy pile-up at zero, which constituted 96% of responses. This phenotype would seem to be a natural candidate for a twin models that use a zero-inflated discrete distribution, especially since the many zeroes are likely to represent a blend of those adolescents who do not use drugs and those who do but have never gotten into trouble for it. On the other hand, a count distribution can have a large frequency of zeroes simply due to having a mean close to zero (Warton, 2005), in which case special treatment of zero counts would be unnecessary. According to Warton, the decision to apply a zero-inflated distribution to a dataset should be based upon model-selection considerations, and not presumed a priori merely because most of the datapoints are zeroes. However, as we describe further in the Discussion, the matter of applying multivariate, zero-inflated discrete distributions to twin data is more complicated than one might guess. We consequently lacked a zero-inflated twin model to apply to the dataset at hand and compare to non-zero-inflated models.

We chose to graph the phenotypic frequency distribution for females from the 17-year-old cohort, amongst whom the most pronounced outliers occurred, in Figure 7. Figure 7 also depicts the expected frequency distribution from the eventual best-performing model, the Lagrangian Poisson. This best-performing model appears to fit the data reasonably well, even though it does not use a zero-inflated distribution. However, we acknowledge that we have not conducted any simulations investigating the consequences of failing to explicitly model zero-inflation when seemingly appropriate to do so.

Analyses

We inspected twin covariances and correlations by zygosity and sex. The male-twin statistics were consistent with an ACE decomposition (0.5r_MZ < r_DZ < r_MZ). The female-twin results clearly indicated an ADE decomposition (0.25r_MZ < r_DZ < 0.5r_MZ).

Sex differences in the distribution of substance-abuse phenotypes are commonplace, so we fit separate models by sex. Aside from sex, it is also generally advisable to correct for age in twin analyses (McGue & Bouchard, 1984). Because MTFS twins in a given pair visited the laboratory on the same day together, both twins in a pair were the same age at assessment. We corrected for age in our LGP and negative binomial models as follows. Conditional on z, the observed age for a given twin pair, the phenotype has mean exp(β₀ + β₁z) and variance proportional to the mean. For instance, under the LGP model, the conditional variance would be exp(β₀ + β₂z) · (1 − λ)⁻², and the conditional distribution would be LGP([1 − λ]exp[β₀ + β₁z], λ). The standardized variance components—a², c², and e², such that a² + c² + e² = 1—are not conditioned on age, and dictate how the conditional variance is divided between the common term X₀ and the unique terms X₁ and X₂. For instance, in an MZ pair, X₀ would have conditional variance equal to (a² + c²) · exp(β₀ + β₁z) · (1 − λ)⁻², leaving X₁ and X₂ with conditional variance e² · exp(β₀ + β₁z) · (1 − λ)⁻². A more complete treatment of fixed-effects regression in the context of our discrete twin models is the topic of a forthcoming paper.

It was evident from our simulation that a model may approximate the true distribution well in a Kullback-Leibler divergence sense, but poorly estimate certain features of the true distribution, such as its variance. We therefore devised a quadratic cross-validation metric to assess how well a model predicts both the phenotypic mean and the twin variance-covariance structure, given age, sex, and zygosity⁴. Let y_i denote the pair of phenotype scores for twin pair i, ŷ_i the pair of model-predicted phenotype scores for twin pair i, and V̂_i the model-predicted covariance matrix for twin pair i. Define ${\widehat{\mathbf{M}}}_i={\widehat{\mathbf{V}}}_i+{\widehat{\mathbf{y}}}_i{\widehat{\mathbf{y}}}_i^T$. Thus, M̂_i is the model’s prediction of the raw second moment—that is, E(YY^T), conditional on age, sex, and zygosity—and is a 2 × 2 matrix. Our quadratic loss metric is

$$L_2=\sum _{i=1}^n\text{tr}\left[({\mathbf{y}}_i{\mathbf{y}}_i^T-{\widehat{\mathbf{M}}}_i){({\mathbf{y}}_i{\mathbf{y}}_i^T-{\widehat{\mathbf{M}}}_i)}^T\right]=\sum _{i=1}^n{\Vert {\mathbf{y}}_i{\mathbf{y}}_i^T-{\widehat{\mathbf{M}}}_i\Vert }^2$$ (23)

where n is the number of twin pairs in the validation subsample and ||·|| denotes Frobenius norm. If twin pair i is incomplete, let y_i denote the phenotype score for the non-missing twin, ŷ_i the corresponding predicted score, and v̂_i the predicted variance. Pair i’s contribution to the above sum would then instead be ${[y_i^2-({\widehat{v}}_i+{\widehat{y}}_i^2)]}^2$.

Results

Table IV presents model-performance results for this dataset. The clear winner is LGP, which had the smallest AIC and the smallest average loss by both cross-validation metrics. Likewise, the negative binomial performed second best overall. From the standpoint of quadratic loss, the normal outperformed the lognormal, but the lognormal had smaller AIC and deviance loss than the normal.

Table IV.

Model performance results from MTFS dataset

Model	AIC	Deviance Loss Rank	Quadratic Loss Rank
Normal	12,759.36	4	3
Lognormal	3886.57	3	4
LGP	1620.20	1	1
NegBin	1646.82	2	2

notes: AIC = Akaike’s Information Criterion, LGP = Lagrangian Poisson, NegBin = negative binomial. Roman numerals I, II, and III refer to different methods of incorporating fixed-effects regression into the model. Deviance loss and quadratic loss were averages from five-fold cross-validation. They are presented here ranked from smallest (1) to largest (4). Deviance loss is −2 times the model’s log-likelihood when all of its parameters are fixed at estimates from the calibration data. Quadratic loss is a squared error of prediction metric (details in text).

We will here present interval estimates in the format point estimate [95% CI]. The substantive conclusions would be the same based on the normal model and the two discrete models: none of the familial variance proportions differs significantly from zero. In contrast, the lognormal model indicates, for males, significant narrow-sense heritability (0.325 [0.110, 0.397]) but non-significant shared-environmentality (on the order of 10⁻¹²). For females, the lognormal estimate of narrow-sense heritability was small (also on the order of 10⁻¹²) but the lognormal model indicated a significant dominance coefficient (0.327 [0.254, 0.396]). Notably, a commonly used transformation, log(y + 1), can strikingly change the conclusions one would draw about variance proportions. However, these three models agree that the phenotypic mean, as expected, significantly increased with age in both sexes (normal χ²(2df) = 70.17, p = 5.79 × 10⁻¹⁶; lognormal χ²(2df) = 165.25, p = 1.30 × 10⁻³⁶; LGP χ²(2df) = 236.00, p = 5.66 × 10⁻⁵¹). We are inclined to trust the conclusions implied by the best overall model, LGP: variance in this phenotype is almost entirely due to the nonshared environment.

Discussion and Conclusions

We have described a novel method for analyzing twin data where the phenotype is a count variable. The method applies bivariate discrete distributions constructed via latent-variate reduction, a technique of constructing multivariate discrete distributions from independent, univariate discrete latent variables. We further described the Lagrangian Poisson, a versatile distribution that can be used with our method, but which is relatively obscure in the behavioral sciences. We conducted a Monte Carlo experiment that compares the properties of: (1) our method when its distributional assumption is correct (i.e., using LGP); (2) our method when its distributional assumption is not correct (i.e., using negative binomial); and (3) conventional methods (none of which had correct distributional assumptions). As might be expected, when our method models the true distribution of the data, its point estimates have smallest mean squared error, and its LRTs have the nominal Type I error rate at reasonable sample sizes. Furthermore, when our method fits a wrong distribution to data, or when more conventional methods are used, the LRTs can have pronounced inflation in their Type I error rate. Our simulation also showed that if the true distribution is a bivariate, positively skewed discrete distribution, an incorrect though similar distribution can approximate it better than more-conventional alternatives. Nonetheless, this goodness-of-approximation does not preclude possible severe bias in variance estimates.

We have applied our method to a real dataset. We fit normal and lognormal models in addition to our bivariate LGP and negative-binomial models, and compared model performance under five-fold cross-validation. One of our performance metrics assessed how well the previously calibrated model described the validation subsample’s data, based on model deviance (in theory, this metric should tend to agree with models’ full-sample AIC). The other metric was a quadratic loss (squared error) that reflected the accuracy of the model-predicted mean and variance. Both metrics identified the LGP as the most preferred model, with the negative binomial as runner-up. This suggests that discrete data will often be better approximated by discrete rather than continuous models. That the normal model had largest deviance loss likely reflects how inapposite it is for skewed, leptokurtic data. The lognormal model had the largest quadratic loss. It may be that the accuracy of the lognormal model’s raw-scale moment estimates, when computed from MLEs of the log-scale parameters, depends critically on the true distribution actually being lognormal.

We acknowledge that the present paper is subject to a number of limitations and caveats, some of which can motivate further investigation. As stated previously, the general problem of correcting for “nuisance” covariates in the context of our discrete twin models is the topic of another paper. Also, we were somewhat frustrated by the lack of a cross-validation metric by which an ordinal model could be compared to others. Some variation on deviance loss calculated with “coarsened” likelihood might be appropriate, but would need to be carefully thought out. In any event, our simulation would have painted an overly optimistic picture of the ordinal model’s quality of approximation in new data, since every iteration used the same cutpoints between categories, based on “known” quantiles of the true distribution.

The present work is also limited by a lack of zero-inflated distributions. Although “many zeroes does not [necessarily] mean zero inflation” (title of Warton, 2005), models that provide special treatment for counts of zero would have justification in our dataset, since they would help distinguish initiation of drug use from frequency of drug use. Li et al. (1999) have provided an exposition of zero-inflated multivariate discrete distributions. Using their construction, a bivariate distribution having zero-inflated (say) Poisson marginals would be a mixture of the following four bivariate distributions: one with unit probability on the origin, one where the first marginal is almost surely zero and the second is Poisson, one where the first marginal is Poisson and the second is almost surely zero, and one which is bivariate Poisson. We judged this approach to be too cumbersome to consider in this report. One possibility we considered was to construct a zero-inflated bivariate distribution via latent-variate reduction, where latent variables X₀, X₁, and X₂ follow some univariate zero-inflated distribution. However, we found no simple way of ensuring that the marginal phenotypic distribution remain the same for MZ and DZ twins under this approach. Twin models using zero-inflated mixture distributions remain a topic for further research.

By applying the negative binomial and Lagrangian Poisson distributions to real data, we do not mean to imply that no other distribution would be appropriate for the phenotype, or even that a compelling theoretical rationale exists for applying those two distributions to the data. We utilized the negative binomial and Lagrangian Poisson distributions in our method because they are two-parameter distributions that can handle overdispersion, and, at first blush, are reasonable for the kinds of phenotypes on which we chose to focus. As we stated in our introduction, we attempted to keep the present paper within a manageable scope by considering only those phenotypes which represent counts of exchangeable events without a strict upper limit, and which could reasonably be expected to be unimodal. Future simulation studies could consider a wider set of distributions for use with latent-variate reduction, perhaps including those with more than two parameters or applicable to different kinds of phenotype. For instance, certain “stopped sum” distributions can have multiple modes (Johnson et al., 2005; Barton, 1957), and might be suitable for multimodal data.

This paper only considered multivariate discrete distributions constructed via latent-variate reduction. Latent-variate reduction has the advantages of being easy to understand, easy to simulate with random-number generation, naturally amenable to the analysis-of-variance, and (given certain restrictions on parameters) of having marginal distributions of simple form. We have already mentioned one of its disadvantages: it can only model positive association or independence, not negative association. This limitation proved no difficulty in the monophenotype twin models with which we were concerned, but it could pose difficulty for polyphenotype applications if some phenotypes are negatively correlated. A more severe limitation of latent-variate reduction is that its number of parameters scales rapidly with dimensionality. Likewise, the computational cost of evaluating its PMF scales both with dimensionality and with the smallest element of the observed vector y.

We note that there are other ways of constructing multivariate discrete distributions, which could be considered in future studies. Of course, there are multivariate distributions that arise from categorical sampling, such as the well-known multinomial (see Johnson et al., 1997), but they seem unlikely to have widespread applicability to behavioral phenotypes or to biometrically informative data. A more interesting possibility is to construct multivariate discrete distributions using copulas. Applied examples include Lee (1999) and Nikoloulopoulos & Karlis (2009). Very briefly defined, copulas are functions that can couple two (or possibly more) arbitrary univariate marginal distributions into a joint CDF. The usual theory of copulas (Nelsen, 2006; Genest & Favre, 2007) assumes that the marginals are absolutely continuous; see Genest & Nešlehová (2007) for a discussion of the theoretical implications of discrete marginals. Multivariate discrete distributions can also be constructed from PGFs based on the multivariable Lagrange expansion of Good (1960); see Chapters 14 and 15 of Consul & Famoye (2006). Bivariate discrete distributions can be constructed from the product of marginal PMFs times a multiplicative factor (Lakshminarayana, Pandit, & Rao, 1999; Kocherlakota & Kocherlakota, 2001; Famoye, 2010). This approach allows for negative correlation, though we are not aware of a generalization to more than two dimensions. Finally, dependence among observations on a discrete phenotype can be modeled with generalized linear mixed-effects regression. All of these approaches could be studied and compared to latent-variate reduction in future methodological research.

Figure 3. Observed distributions of estimated shared-environmental variance, for N_pairs = 1000.

Depicted results are from the 1000-twin-pair condition of the simulation. Labels on the x-axis identify the model: LGP = Lagrangian Poisson, negbin = negative binomial. For the lognormal model, raw-scale parameter estimates are presented. Graph depicts conventional box-and-whisker plots for each model, with additional solid whiskers superimposed over them to mark the mean (filled dot) ± 1SD of the sampling distribution. Horizontal dashed line marks true raw parameter value.

Figure 4. Observed sampling distributions of estimated heritability, for N_pairs = 1000.

Depicted results are from the 1000-twin-pair condition of the simulation. Labels on the x-axis identify the model: LGP = Lagrangian Poisson, negbin = negative binomial. Graph depicts conventional box-and-whisker plots for each model, with additional solid whiskers superimposed over them to mark the mean (filled dot) ± 1SD. Horizontal dashed line marks true raw parameter value. X’s mark true parameter values post-transformation (log(y + 1) or ordinalizing, as the case may be).