Ion transport in complex layered graphene-based membranes with tuneable interlayer spacing

A combination of experiments and simulations unveils unusual nanoconfined ion transport in layered graphene membranes.

Abstract

Investigation of the transport properties of ions confined in nanoporous carbon is generally difficult because of the stochastic nature and distribution of multiscale complex and imperfect pore structures within the bulk material. We demonstrate a combined approach of experiment and simulation to describe the structure of complex layered graphene-based membranes, which allows their use as a unique porous platform to gain unprecedented insights into nanoconfined transport phenomena across the entire sub–10-nm scales. By correlation of experimental results with simulation of concentration-driven ion diffusion through the cascading layered graphene structure with sub–10-nm tuneable interlayer spacing, we are able to construct a robust, representative structural model that allows the establishment of a quantitative relationship among the nanoconfined ion transport properties in relation to the complex nanoporous structure of the layered membrane. This correlation reveals the remarkable effect of the structural imperfections of the membranes on ion transport and particularly the scaling behaviors of both diffusive and electrokinetic ion transport in graphene-based cascading nanochannels as a function of channel size from 10 nm down to subnanometer. Our analysis shows that the range of ion transport effects previously observed in simple one-dimensional nanofluidic systems will translate themselves into bulk, complex nanoslit porous systems in a very different manner, and the complex cascading porous circuities can enable new transport phenomena that are unattainable in simple fluidic systems.

INTRODUCTION

The transport of ionic species in bulk porous solids, such as porous carbon, is a fundamental physicochemical process that is widely involved in many real-world applications such as molecular adsorption/separation, water purification, electrochemical capacitive energy storage, and catalyst and fuel cells (1–8). The behavior of ion transport confined in nanopores and nanochannels can be very different from that in bulk (9–12). A myriad of unexpected and exciting nanoscale transport phenomena have been reported, with some of the most striking being (but not limited to) ultrafast and highly selective ion permeation and an anomalous increase in capacitance in subnanometer pores (13–15). Fundamental understandings of such nanoconfined transport phenomena are traditionally based on simple, well-defined fluidic systems because it is relatively straightforward to establish robust structure-property relationships in these circumstances (11). However, in practical technologies, it is important to be able to establish a quantitative relationship of bulk materials properties with respect to nanoporous materials structures. This is difficult and inadequately explored because of the often complex, random pore characteristics and stochastic emergence of structural defects, which inevitably occur during materials assembly and processing. Direct measurement of the ion transport in porous carbon, usually in a powder form on the macroscopic level, is difficult. The complex transport path through these materials, even for recently synthesized, highly ordered porous carbon (16), depends not only on the pore structure inside a particle but also on the interparticle gaps and voids, which are often randomly distributed and far from well-defined. Interpretation of experiment results based on an oversimplified theoretical model may lead to unpredictable and sometimes inconsistent structure-property relationships, particularly for bulk, porous material systems. The discrepancies of ion transport behavior in carbon nanotubes, for instance, the slip condition of their inner surfaces, and the enhancement of electrophoretic ion mobilities measured through a single carbon nanotube versus that through a carbon nanotube membrane (effectively an assembly of multiple vertically aligned, substrate-supported nanotubes) remain unresolved (17–19). Structural imperfections such as defects, alignment, and random distribution of pore sizes are usually found in most bulk porous carbon materials used in practice and add to the complexity of describing their structures. This has severely complicated the quantitative bridging of transport phenomena observed at nanoscale with corresponding macroscopic material properties.

At the nanoscale, ion transport in porous carbon essentially involves transport phenomena in graphene-enclosed nanopores or nanochannels. Despite the simple two-dimensional (2D) structure and chemistry of graphene, the difficulty in describing its assembled structure, especially the porous structure, still remains. This issue is widely encountered in recently emerging graphene-based bulk materials, even for the simplest self-assembled membranes composed only of multiple graphene-based nanosheets interlocked face-to-face in a self-similar, layered porous architecture (20) (an example is shown in the upper inset in Fig. 1A). The complexity arises from materials synthesis and assembly and resides across multiple length scales. Current methods for mass production of graphene by exfoliation of graphite allow little control over the shape and the distribution of the lateral size of the produced graphene (21). Such graphene materials have also proved to have a microscopically corrugated molecular texture (22, 23), and there is a considerable amount of defects/holes in the sheet plane that cannot be restored (24, 25). Moreover, when assembled into a bulk membrane material, individual nanosheets cannot be combined into a structure without creating gap areas between the edges of the sheets (26). Although the porous structure of such a layered membrane can be conceptually considered as a simple array of cascading nanoslits (Fig. 1B), as it is generally treated in recent literature (27, 28), quantification of the nanoslit structure requires at least three statistical variables, namely, the height of nanoslits, the lateral size of individual nanosheets, and the gap distance between the ends of the sheets. These geometric variables are difficult to precisely determine with conventional imaging techniques used for well-defined, single nanochannel systems. Although a range of interesting and promising nanofluidic phenomena such as high selectivity and ultrafast permeation of ionic species through these membrane materials have been recently reported (29, 30), the existence of these structural complexities adds an uncertainty to the establishment of a robust quantitative relationship between the macroscopic permeation properties of these bulk graphene-based membranes and their complex porous structure at the nanoscale.

Fig. 1. LGG membranes with tuneable interlayer spacing.

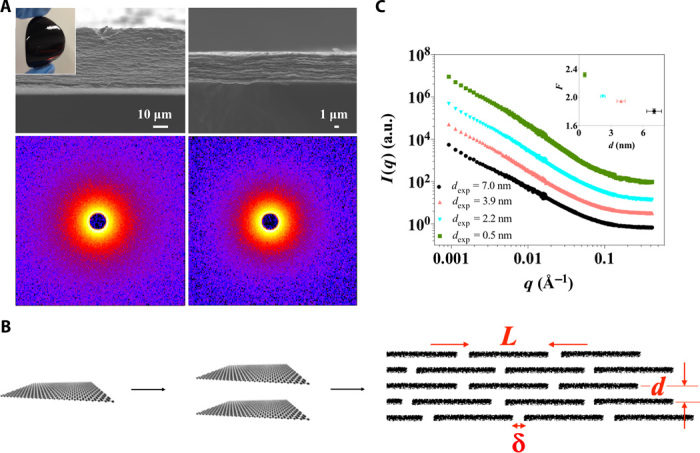
(A) Top: Scanning electron microscopy images of the cross-section of the LGG membranes with d_exp compressed to 3.2 nm (left) and 0.5 nm (right), respectively. Bottom: Isotropic SANS patterns of the compressed gel membranes with d_exp of 3.9 nm (left) and 0.5 nm (right), respectively. The inset at the upper left corner is a photograph of the LGG membrane. (B) A schematic showing the formation of an array of cascading nanoslits through parallel stacking multiple graphene nanosheets. L, d, and δ are the key geometrical variables of the proposed structural model for describing the porous structure of the LGG membrane. (C) Reduced 1D SANS data offset from the absolute intensity scale. The upper inset on the right shows the slope F from the linear regressions in the q range from 0.001 to 0.01 Å⁻¹ as a function of d_exp.

Advances in graphene chemistry, particularly in the supramolecular chemistry of graphene materials such as graphene oxide and chemically converted graphene (CCG), have provided new ways to assemble bulk carbon materials in a bottom-up manner and thus manipulate the porous structure on the molecular level (31, 32). We have recently assembled such a layered graphene gel (LGG) membrane with the entire bulk membrane structure forming through multiple CCG nanosheets stacked into a self-similar, layered configuration. The membrane is mechanically robust, allowing for direct measurement of ion transport with ease (33). As a result of microcorrugation and repulsive solvation/electrostatic forces, the individual sheets in the membrane remain largely separated, with an average interlayer spacing (the distance between the centers of the carbon atoms of neighboring layers) of about 10 nm. We demonstrated that the gel membrane can be compressed in the thickness direction in a controlled manner by capillary pressure, allowing the average interlayer spacing to be continuously adjusted in a range from about 10 nm to subnanometer (34). It is known that tuneable materials systems offer distinct advantages over their fix-dimensioned counterparts because they allow comparable analyses and comprehensible structure-property relationships to be established (35). Here, using the LGG membranes as a structure-tuneable materials platform of porous carbon, we systemically study, with experiment and simulation, how ion transport through these membranes is affected by varying the average interlayer spacing. Such a comparative study has led to the establishment of a robust, representative structure model that can capture the key features of the imperfect, cascading nanoslits embedded in the LGG membranes. The establishment of this structural model enables the understanding of ion transport properties of the bulk nanoporous graphene membranes to be achieved in a quantitative manner and thus reveals new insights into the ion transport phenomena confined in a graphene-enclosed nanochannel, where sizes vary in the region of below 10 nm.

RESULTS

Synthesis and characterization of the LGG membranes

LGG membranes (Fig. 1A) with various average interlayer spacings are prepared following the previously reported “capillary compression” method (34) (the detailed materials preparation procedure is shown in Supplementary Materials Sections I and II and fig. S1). Because CCG is microscopically corrugated, it has proven difficult to use the normal x-ray diffraction analysis to determine the interlayer spacing of CCG in the layered membrane (36, 37). Hence, we experimentally estimate the interlayer spacing (d_exp) directly from the layered membrane thickness and discuss the estimation error in Supplementary Materials Section III. The use of such an estimation to quantify the porous slit channel structure inside the membrane is based on the assumption that the individual CCG sheets remain separated in the membrane throughout the tuning procedure of capillary compression. The validity of this assumption is crucial. Graphene is prone to restack into graphite because of the strong van der Waals attraction, particularly when they are placed close together (38). If this was to happen in the LGG membranes during compression, the porous channel structure could be substantially changed as a result of the collapse of accessible nanospace between the nanosheets. Accordingly, we carry out small-angle neutron scattering (SANS) analysis to probe whether substantial graphitic aggregates form in the as-compressed membranes. Figure 1A (bottom) and fig. S2 show the SANS patterns, which are isotropic for all the compressed membranes with the smallest d_exp of 0.5 nm. This suggests an in-plane random arrangement of CCG nanosheets, consistent with previous reports on the CCG assembly behaviors at the liquid-solid interface (39). The reduced 1D SANS curves are shown in Fig. 1C. The comparable features for all the membranes across the q range from 0.4 to 0.001 Å⁻¹ indicate the absence of a distinctively defined, structural order that may form as the LGG membranes are subjected to the capillary compression procedure. Linear regression of all the curves in the range from 0.001 to 0.01 Å⁻¹ gives rise to slope F of around 2 nm (inset in Fig. 1C), which is consistent with 2D platelets as the dominant scattering elements (40). The deviation from ideal Porod behavior (shown by an F of 4) across the entire q range from 0.001 to 0.4 Å⁻¹ indicates the rough nature of the layered structure and the absence of smooth, restacked graphitic particles across a wide range of length scales. From this, we conclude that the nanospace between individual sheets does not fully collapse and that the porous network of the cascading nanoslits enclosed in the gel membranes remains largely continuous. This is likely due to the fluidic nature of the intersheet-trapped liquids, even under the situation where the membrane is substantially compressed over 20 times less than its original volume (34).

A representative structural model for the defective cascading nanoslits in LGG membranes

To establish a quantitative understanding of the ion permeation properties of the bulk graphene membrane with respect to the transport phenomena in graphene-enclosed channels at nanoscale, the complex porous structure of the LGG membrane needs to be defined. We use the representative elementary volume of an array of cascading nanoslits (Fig. 1B) to describe the fluidic contours contained in the LGG membranes. Such a methodology of describing complex structures by simplified and statistically representative elements has been widely practiced in the field of complex, multiscale materials and has allowed comprehensible structure-property relationships to be established (35). We first hypothesized in the representative element that the structure of the LGG membranes made of corrugated and defective CCG with various shapes and sheet sizes can be represented by a simplified cascading nanoslit model composed of flat, defect-free, and uniform graphene sheets. Hence, three key representative variables are used to constrain the structural model, namely, the height of nanoslits (d), the lateral size of individual nanosheets (L), and the gap distance between the ends of the sheets (δ). The height of nanochannels, d, which represents the average interlayer spacing of the corresponding LGG membrane, can be directly determined by experiment as d_exp. Considering the presence of in-plane structural defects within the individual CCG sheets and the imperfect stacking of CCG sheets, we initially assign L and δ as variables and determine their values by correlating the simulation with the experimental results. To allow direct correlation between simulation and experiment, the apparent ion diffusivity through the membrane obtained through both experiment (D_m,exp) and simulation (D_m,sim) is normalized to the diffusivity in bulk solutions (D_bulk). The most representative values of L and δ are determined by fitting the normalized ion diffusivity obtained by simulation of ion diffusion through the structural model based on established nanofluidic theories (denoted as D_sim/D_bulk) into that of the LGG membranes obtained from a standard time-lag diffusion experiment (D_exp/D_bulk). The fitting between D_sim/D_bulk and D_exp/D_bulk is carried out over eight different values of d_exp.

The data set of D_m,exp as a function of d_exp is experimentally obtained with the time-lag permeation technique using the experimental setup as illustrated in Fig. 2A (41). The strong freestanding, flexible LGG membranes allow direct measurement of ionic current, eliminating the interference from supporting substrates or any mechanical support, which are usually needed for strengthening nanostructured thin membranes (42). The membranes are thoroughly rinsed with deionized water before separating the feed and permeate compartments, which are filled with 0.5 M KCl and water, respectively. The ion permeation is continuously monitored until a steady state is reached, which is seen by a linear dependence of ions permeated against elapsed time (Fig. 2B and fig. S3A). The membrane continuity and reproducibility of experiments are checked by investigating the characteristics of the steady-state diffusion (figs. S3B and S4). Given a constant mass loading (1 mg/cm²) of CCG in each membrane, the permeation rate, which is extracted from the steady-state region of the time-lag permeation curve, is seen to decrease more than 20 times from 1.7 to 7.8 × 10⁻² mol hour⁻¹ m⁻² (nearly impermeable) as d_exp is reduced from 11 to 0.5 nm. The strong influence of d_exp on D_m,exp can be observed, and the almost linear dependence of permeation rate against d_exp suggests that the interlayer spacing is indeed the dominant structural index that changes with compression and affects ion permeability through these LGG membranes.

Fig. 2. Ion permeation through the cascading nanoslits embedded in the LGG membranes.

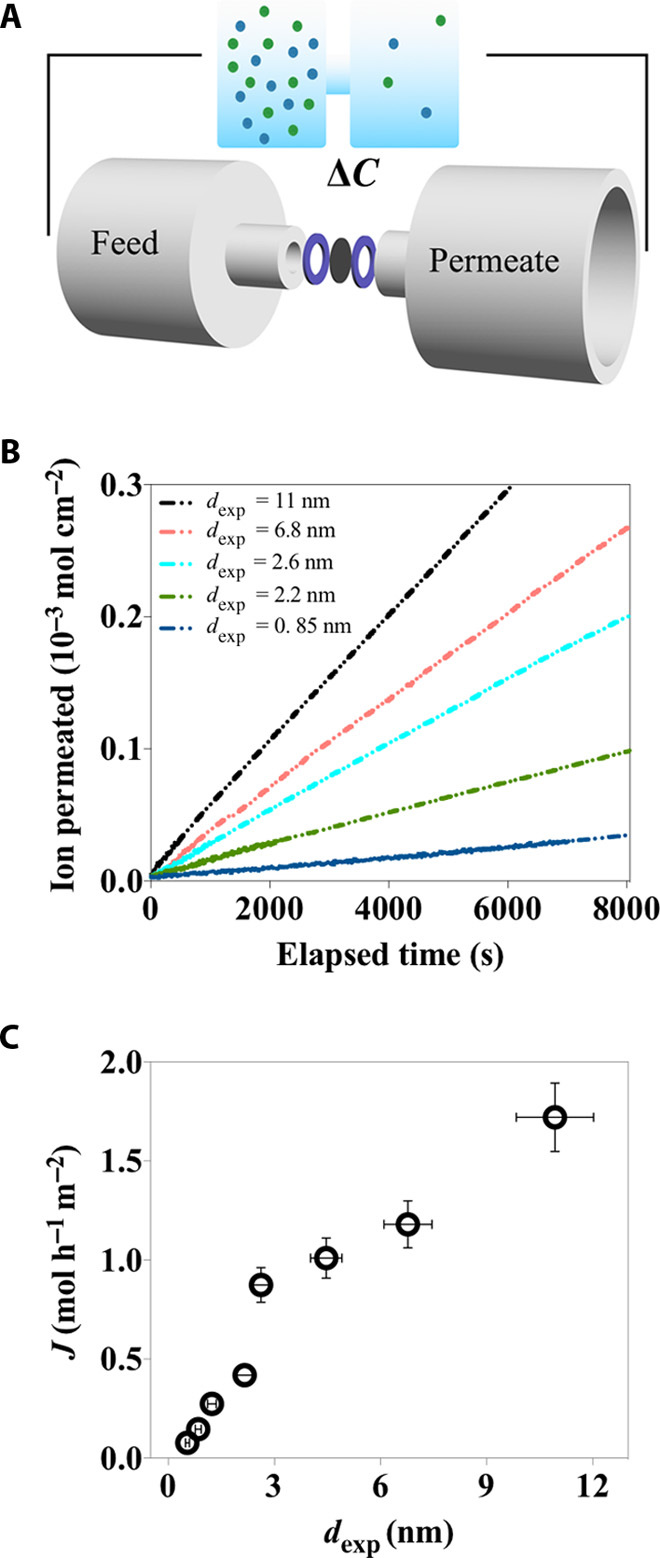
(A) A schematic of the experimental setup. (B) The concentration-driven ion permeation through the LGG membranes with d_exp varied from 11 to 0.85 nm. (C) Dependence of ion permeation rate on d_exp.

We carry out continuum simulation of ion diffusion through the layered, cascading nanoslit model as proposed (Fig. 1B) and investigate the dependence of ion permeation properties on all the structural parameters including L, d, and δ (simulation details are documented in Supplementary Materials Section VI). A 3D database of the apparent diffusion coefficient, D_m,sim (d, L, δ), through the membrane model can be obtained with simulation with d = d_exp and variables L and δ of a wide range (fig. S5). Hence, we are able to map out a range of scenarios of ion transport through this cascading, nanoslit system. As shown in Fig. 3, all three variables have a strong influence on the permeability of the nanoslit array. In particular, a strong dependence of D_m,sim on L (Fig. 3E) can be seen by an increase of more than four orders of magnitude in D_m,sim (d = 1 nm, δ = 2 nm) when L is varied from 10 to 1000 nm. The competing role between L and δ on D_m,sim, especially when they are comparable in value, results in a zone that strongly deviates from the rest of surface contour (Fig. 3F) where D_m,sim sharply increases. Such an abrupt increase in D_m,sim becomes more pronounced as d is reduced. This shows that the permeation properties of the cascading nanoslit system can be highly sensitive to the cohort of L and δ, particularly when d is small. Appropriate determination of L and δ is thus crucial for capturing the key structural features of the cascading nanoslit system and correlating ion transport properties of the bulk LGG membranes with their porous nanochannel structure.

Fig. 3. 3D data space showing the dependence of log(D_bulk/D_m,sim) as a function of L, δ, and d.

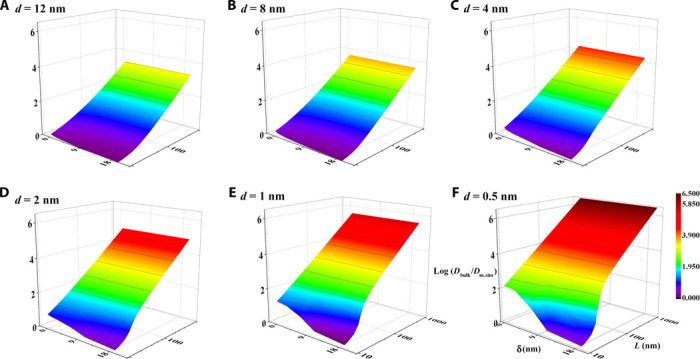
The ranges of the variables L, δ, and d are set as to 8 to 1000, 0.5 to 12, and 1 to 20 nm, respectively. The competing role of L and δ, specifically the increase in L and the decrease in δ, enhance the barrier properties of the LGG membrane as reflected by an increase in log(D_bulk/D_m,sim). When the variables L and δ are close in value, D_m,sim experiences a sharp increase, and such an increase is more pronounced as d is reduced.

Because continuum theory has been proven robust when applied to the description of nanoscale transport phenomena at a level of confinement larger than ~1 nm (9) and the interlayer spacing is the dominant structural variable changed in the LGG membrane samples during the capillary compression procedure, it is thus expected that there would be a unique set of values of L and δ that allow a high level of consistency between D_m,sim (L, δ) and D_m,exp as d_exp is varied from 11 to ~1 nm. This is under the condition that the key features of the complex, cascading transport pathways through the LGG membranes, can be well represented by the proposed representative structural element. Indeed, using reverse Monte Carlo modeling, we find that the fitting values of L and δ rapidly converge (inset in Fig.4 and fig. S6), and the most representative values of L and δ (L = 55 nm and δ = 2 nm as summarized in table S1) can be located. D_m,sim based on this geometry has values very close to D_m,exp as d_exp varies across the entire range from 10 to ~1 nm, and it can be seen that in Fig. 4 (black circles), the consistency between simulation and experiment extends to size scales of d_exp smaller than 1 nm.

Fig. 4. Comparison between experiment and simulation of the scaling behavior of ion diffusion as a function of interlayer spacing through the layered membrane.

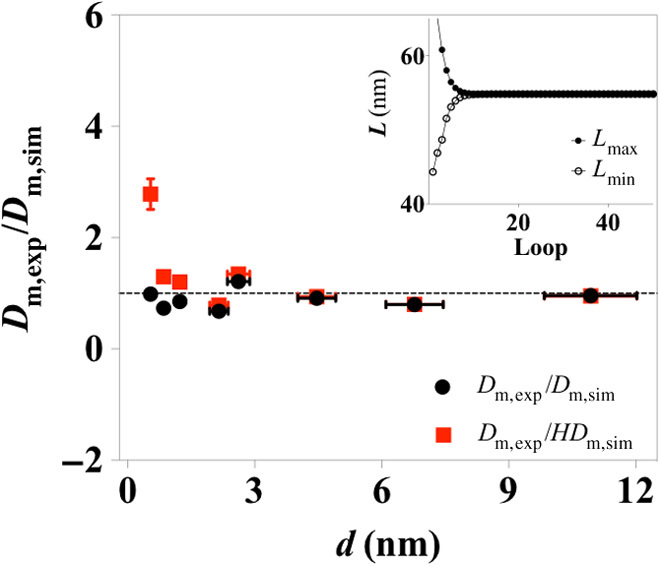
Similar comparison is made between experiment and simulation after a hindrance factor H is introduced in the simulation and is shown as red triangles. The inset shows the determination of the geometrical variables L through a reverse Monte Carlo method. The minimization was performed between D_m,exp (d) and D_m,sim (d, L, δ). The variable L rapidly converges after 10 iterations.

To allow maximum physical significance of the structural variables, we derive the values of L and δ from the model at its simplest form. Possible nanofluidic effects caused by strong fluid-wall interactions such as surface charge, surface slippage, and spatial confinement, which have been well documented in the literature, are not considered (10). To prove the robustness of the as-determined structural geometry, we have then evaluated the influences of the effects of spatial confinement and surface charge on the ion diffusion across the model of cascading nanoslits. Given that significantly enhanced liquid flow can also be expected when confined between atomically smooth surfaces like graphene (due to a possibly large slip length) (43, 44), when ion diffusion across the membrane reaches a steady state (which is the state being investigated in our experiments), the net water flux is zero; the influence from such enhanced liquid flow on apparent membrane diffusivity can be neglected. Spatial confinement effects arisen from strong particle-wall hydrodynamic interactions and steric restrictions in nanoconfined space can lead to hindered diffusion, as reflected by a decrease in solute diffusivity (45). Theoretical expressions have been developed and shown success in accounting for the decrease in ion diffusion coefficient at confinement of around 0.9 nm (19). We introduce such an effect, as hindrance factor H obtained from Dechadilok and Deen’s model (45), in our simulations. Nevertheless, our results show that other than when d_exp has a very small value of 0.5 nm, D_m,exp/HD_m,sim still gives values very close to 1 across the d_exp range from ~1 nm and above (red squares in Fig. 4). Moreover, a detailed investigation on the influence of surface charge (figs. S7 and S8) shows that the variance of as-affected D_m,sim is quite small, being ~2% (see the summary in table S2) when a surface charge of −2.3 mC/m² [comparable to that of CCG in neutral aqueous solutions (46)] is imposed on the structural model. Together, the good agreement between experiment and simulation suggests that the as-derived geometry of the cascading nanoslit model captures the key features of the complex, porous nanostructure of the LGG membranes.

Insight into the effect of structural imperfections on ion transport

Compared to the recent approach of modeling the porous structure of graphene membrane materials where the lateral size, L, of individual graphene-based nanosheets is commonly determined by visualizing them under a microscope (28, 47), we here take a different approach in which L is first assigned as a variable considering the imperfectly layered structure of the membrane. Our correlation analysis of the diffusion data obtained from the experiment and simulation gives the variable L a value of ~ 50 nm. This value is much smaller than the average size generally observed using nanoimaging techniques, in our case using atomic force microscopy, as shown in fig. S9. Because L is a key geometrical parameter that determines the tortuous transport pathways through the layered membrane, our results indicate that the determination of L plays a major role in appropriate modeling of the complex fluidic channel network and the resultant estimation of diffusion coefficient in these graphene-based membrane materials. As a demonstration, in the case of the LGG membrane with a d_exp of 11 nm, the diffusion coefficient in this membrane should not be very different from that measured in bulk because the system is sufficiently large and the influence from the channel wall can be largely neglected (48). Indeed, Fig. 4 shows that D_m,exp (d = 11) has a value nearly identical to D_m,sim (d =11) on the basis of the as-derived structural model, in which L is around 50 nm. However, if the value assigned to the variable L equalled to ~1 μm, as seen under atomic force microscopy, the diffusion coefficient of KCl in the graphene-enclosed slits conceptualized at nanoscale in the layered membrane would be 0.011 cm²/s, some unjustifiably 500 times higher than predicted by continuum theory simulation. The diffusion coefficient in the graphene-enclosed nanochannels can even be estimated several thousand times higher than that in bulk solutions, in cases where d is reduced to ~1 nm. Such a reduced value of L accounts for the statistical structural deviation between a real, bulk membrane sample and a perception of an assembly of multiple nanosheets based simply on the geometry observed at the nanoscale. Effectively, this deviation is the combined result of a broad distribution of the lateral size and shape of the nanosheets, corrugated molecular texture, and the presence of intrinsic in-plane pores.

Sub–10-nm slit-size–dependent electrokinetic ion transport in LGG membranes

The establishment of the representative structural element of cascading nanoslits has enabled us to understand the permeation properties of the bulk LGG membranes from the accumulative perspective of the transport phenomena in such an array of parallel-stacked, graphene-enclosed nanoslits. To demonstrate this, we carry out continuum simulation of electrokinetic ion transport through the cascading nanoslits based on the as-derived structural geometries and predict the membrane conductivity as a function of d and various ionic concentrations (fig. S10). To validate the prediction, we experimentally measured the conductance characteristics of the LGG membranes (fig. S11), and the comparison between experiment and theoretical prediction is shown as a ratio of κ_m,exp/κ_m,sim in Fig. 5 (black circles). κ_m,exp/κ_m,sim gives values very close to 1 in situations where d_exp is sufficiently large (larger than ~5 nm) and regardless of the variance in concentration. The agreement between experiment and simulation shows success, in that the electrokinetic ion transport properties through the bulk membrane can be described as an accumulation of the electrokinetic ion transport through an array of graphene-enclosed cascading nanoslits. In this term, it proves again that the as-derived structural element indeed captures the key features of the porous, cascading nanochannel network contained in the LGG membrane.

Fig. 5. Scaling behaviors of the electrokinetic ion transport as a function of channel size across the range of sub–10 nm and of varied ionic concentrations.

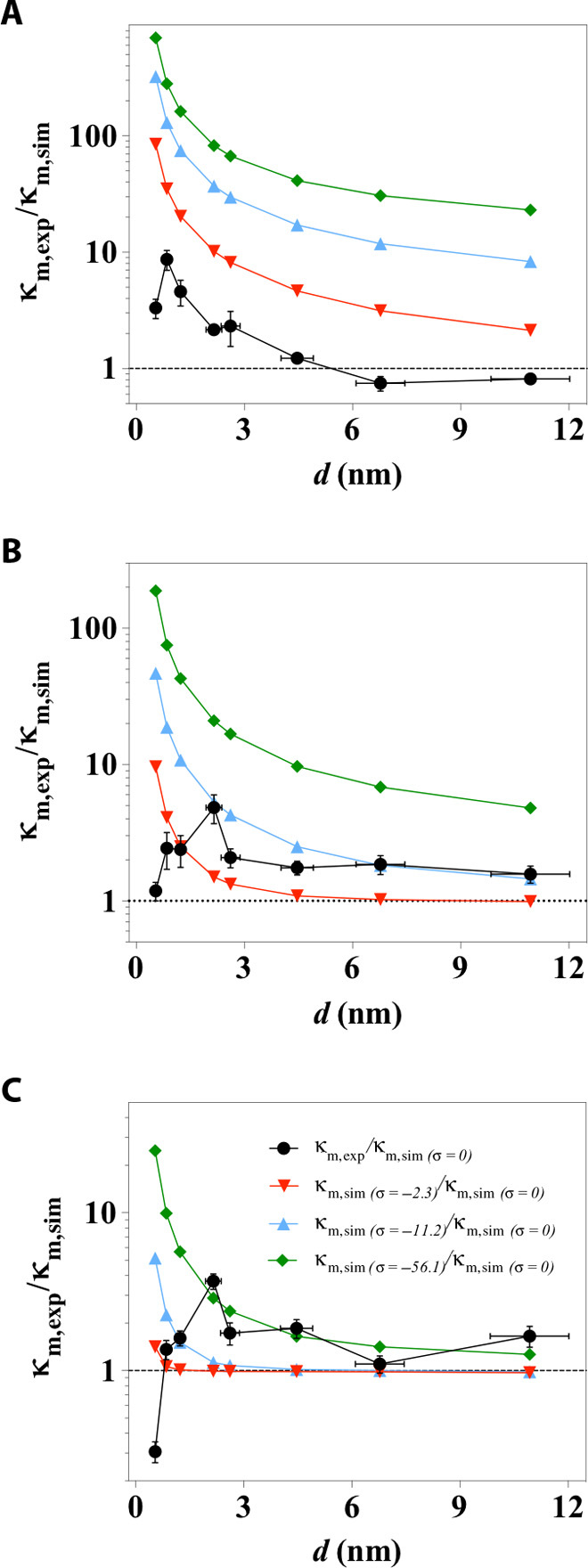
(A to C) Black symbols show the comparison between experimentally measured and simulated channel conductivity, denoted as κ_m,exp/κ_m,sim made in electrolyte concentrations of (A) 1 mM, (B) 10 mM, and (C) 100 mM KCl. κ_m,sim was calculated with zero surface charge, also denoted as κ_{m,sim (σ = 0)} for comparison with the conditions of various surface charge. The colored scatter plots are the theoretical predictions of the scaling behaviors when a surface charge of σ = −2.3 mC/m² (red triangles), σ = −11.2 mC/m² (blue triangles), or σ = −56.1 mC/m² (green diamonds) was imposed in the cascading nanoslits model.

We find that the scaling behavior of ion conductivity in the nanoslits as a function of d measured through experiment starts to deviate significantly from that predicted through simulation as the size of nanoslits becomes smaller than ~3 nm. This scaling profile of electrokinetic ion transport in the nanoslits (Fig. 5) is quite different from that of diffusive ion transport (Fig. 4), which is directly related to each other by the Einstein relation in bulk solutions. The value of κ_m,exp becomes increasingly greater than κ_m,sim, with an increase of more than an order of magnitude when d_exp is 0.85 nm and measured in 1 mM KCl. The value of κ_m,exp reaches a maximum as the channel size is further reduced, and as the concentration is increased from 1 to 100 mM, the channel conductivity enhancement becomes less pronounced, with its maxima shifting to larger d_exp from 0.85 to 2.2 nm.

Such a nonlinear increase in channel conductivity as the channel size decreases from ~10 to ~2 nm and its dependence on ionic concentration can be partially accounted for by the surface-charge–governed transport mechanism (49). Previous research has shown that, at low ionic concentrations, the nanochannel conductance is governed by surface charge, is dominated by the contribution from counterions, and becomes independent of the bulk concentration outside the nanochannels (11). To probe the surface charge status of CCG in the membranes, we carry out ion selectivity measurements using a technique established in electrophysiology and recently used to determine selective transport through membranes in the presence of leakage and multiple transport pathways (50). Our results show that the layered graphene-based membranes are mildly cation selective, with a reversal potential of 20 to 30 mV (fig. S12). This reveals that the CCG sheets are indeed negatively charged in the LGG membranes. Our simulations of the channel concentration as a result of this negative surface charge offer additional insights into the characteristics of such a nonlinear increase in channel conductivity. The simulation results show that even when a small surface charge density (σ = −2.3 mC/m²) is imposed on the slit walls, the ionic concentration of cations in the nanochannel increases by at least 2.5 times than that of anions as d approaches 2 nm (fig. S13). The elevated ionic strength is closely associated with the increase in channel conductance. The trend of the nonlinear enhancement of nanochannel conductivity observed in experiment can be reproduced with a simulation of electrokinetic ion transport in the proposed structural model, under the condition where a nonzero surface charge is imposed (color plots in Fig. 5 and fig. S14). However, given a fixed amount of surface charge (for example, σ = −11.2 mC/m²), the magnitude of the conductivity enhancement decreases more rapidly than is experimentally observed as concentration increases (see Fig. 5, blue triangles, as an example). This can be attributed to the concentration-dependent surface charge status of the CCG materials. Such a dynamic surface charge status of nanochannel walls has also been reported for conventional silicon-based materials used for fabricating nanofluidic devices (15).

DISCUSSION

Ion transport confined in nanochannels smaller than 10 nm is of fundamental importance in understanding many biological activities and a range of technological problems related to energy, separation, and diagnostics (51, 52). Because of the technical difficulties in continuously tuning the size of existing nanofluidic systems from 10 nm to subnanometer, profiling the ion transport behavior across the whole size range has not been possible (53, 54). Our approach of using layered graphene-based membrane as a structure-tuneable materials platform and a comparative analysis with experiment and simulation reveal unusual scaling behavior of electrokinetic ion transport in nanoslits, for sizes varying across the entire range of sub–10 nm. Under a confinement level of ~2 nm and above, which is the current limit of nanomachined channels of Si-based materials, the scaling behaviors of electrokinetic ion transport in nanoslits revealed with the LGG membrane platform are consistent with those previously reported in terms of both the magnitude and trend of channel conductivity enhancement as a function of channel height when measured in 1 mM KCl (15). Because the scaling law of ion transport as a function of channel sizes below 2 nm was previously unknown, our results offer the first statistical insights into the behavior at these extremely small length scales. We find that the enhancement of nanoslit conductivity starts to drop as d is approaching ~2 nm for concentrations higher than 10 mM, and as the concentration is increased from 1 to 100 mM, the channel conductivity enhancement becomes less pronounced, with its maxima shifting to larger d_exp from 0.85 to 2.2 nm. Given that the size of hydrated ions is in the order of a few angstroms (K⁺, ~0.3 nm; Cl⁻, ~0.3 nm), this phenomenon cannot be simply attributed to the effect of distortion of the hydration shell, which is commonly suggested for simple, straight nanochannel systems, such as carbon nanotubes (55). Moreover, with the increase in concentration, the unusual shift of channel conductivity enhancement also cannot be simply explained with the consideration of possible influences from surface charge or electroosmotic flow induced by a possibly large slippage on the smooth graphene surface (“Effect of electroosmotic current” in Supplementary Materials Section VII). These findings, which have not been observed in traditional 1D nanochannels, may be related to the cascading nanoarchitecture of the layered graphene-based nanoslits. The interfering nature between d and δ, particularly when they have comparable values (in this work, ~2 nm), could have a profound effect on the ion transport mechanism through the LGG membranes. Given that the striking difference between the scaling profile of ion transport driven by concentration gradient (Fig. 4) and electric field (Fig. 5) as a function of channel size at sub–10 nm is clear, the observed unusual scaling profiles highlights a region of length scales below 2 nm where complex, cascading nanofluidic circuities may lead to novel nanoconfined ion transport phenomenon.

In conclusion, we have demonstrated a combined approach of experiment and simulation to describe the complex structure of layered graphene-based membranes in a quantitative manner and the use of the model obtained to gain new insights into nanoconfined transport phenomena in cascading porous structures. By comparatively analyzing the results from both experiment and simulation, we are able to establish a robust, quantitative relationship between the macroscopic permeation properties of the graphene-based membranes and their complex nanoporous structures. This method yields unprecedented statistical insights into the effect of structural imperfections on nanoconfined ion transport and particularly the scaling behaviors of the diffusive and electrokinetic ion transport in graphene-enclosed nanochannels as a function of channel size across the entire length scales below 10 nm. Our analysis has revealed that many of the nanofluidic effects observed in well-defined, 1D fluidic systems reflect themselves in the cascading nanofluidic circuities in a very different manner. Whereas we did not see many effects from the surface-slippage–enhanced ionic flow in cases of both concentration-driven and electric field–driven ion transport, the dominant contribution from surface-charge–governed ion transport can be appreciably recognized in the electrical conductance properties of the bulk graphene-based membrane materials. Furthermore, our results show new transport phenomena in cascading nanoslits that have not been seen in simple, straight nanochannels, which not only points out the importance of bridging established nanofluidic understandings with the many complex porous systems used in practice but also indicates ample room for exploiting designable cascading nanofluidic circuities to achieve novel materials properties. Given that bulk porous carbon materials are widely used in molecular adsorption/separation and electrochemical energy storage and conversion devices, we envisage that the structural model and the ion transport scaling law reported in this work will make the graphene-based layered membrane a useful nanoionic platform for the future establishment of in-depth and robust quantitative structure-property relationships for a range of real-world applications, beyond the scope and length scale of existing porous materials.

MATERIALS AND METHODS

LGG membranes were assembled through direct flow filtration of a controlled amount of CCG colloids, prepared following the method we previously developed (33). The areal mass loading of CCG in each membrane was 1 mg/cm², and the average interlayer spacing was ~10 nm. Tuning the average interlayer spacing of CCG sheets in the membranes was achieved through a capillary compression procedure (34). Briefly, the water content inside the as-assembled hydrogel membranes was first exchanged with a ratio-controlled volatile/nonvolatile miscible solution (in this case, water/sulfuric acid mixture). The volatile liquid inside the gel membranes was then selectively removed through vacuum evaporation. The removal of the volatile part of the miscible solution exerted capillary compression between the graphene sheets in the membrane, leading to uniform shrinkage of membrane thickness and thereby decreasing the interlayer spacing. Because the nonvolatile part of the miscible solution in the gel membrane remained, the average interlayer spacing could be readily tuned from ~10 to ~0.5 nm by adjusting the ratio of volatile/nonvolatile solutions. Ion permeation experiments including both concentration-driven and electric-field–driven transport was carried out using a device built with a homemade membrane clamp attached to two symmetrical reservoirs (the feed and permeate reservoirs) on each side. The diameter of the membrane exposure area was 4.9 mm. Concentration-driven ion diffusion was monitored through the solution conductance change in the permeate reservoir. Membrane conductivity was obtained by analyzing the I-V curves. Classical continuum simulations were performed using the COMSOL Multiphysics package for both concentration-driven and electric-field–driven ion transport through the layered graphene-based membrane to comparatively analyze its microstructure and permeation properties. Detailed materials synthesis and characterization and ion transport experiments and simulations are documented in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/2/e1501272/DC1

Section I. Fabrication of the LGG membranes

Section II. Tuning the average interlayer spacing through the capillary compression method

Section III. Determination of the average interlayer spacing from membrane thickness

Section IV. Small-angle neutron scattering of the compressed LGG membranes

Section V. Time-lag diffusion and electrokinetic ion transport experiments

Section VI. Continuum modeling of concentration-driven ion diffusion through the cascading nanoslits contained in the LGG membranes

Section VII. Continuum modeling of electrokinetic ion transport through the cascading nanoslits contained in the LGG membranes

Fig. S1. A schematic showing the fabrication of the LGG membranes and tuning of the interlayer spacing.

Fig. S2. Isotropic SANS patterns of the compressed LGG membranes.

Fig. S3. Concentration-driven ion transport through the LGG membranes.

Fig. S4. Effect of circulation rate on ion permeation through the LGG membranes.

Fig. S5. The continuum simulation model for steady-state diffusion across charge-neutral cascading nanoslits.

Fig. S6. Determination of the geometrical variables L and δ through a reverse Monte Carlo method.

Fig. S7. The continuum simulation model for steady-state diffusion across negatively charged cascading nanoslits.

Fig. S8. Concentration and electric potential distribution profiles of the steady-state KCl diffusion across negatively charged cascading nanoslits.

Fig. S9. An AFM image of CCG on mica substrates.

Fig. S10. Continuum simulations of the electrokinetic ion flow across negatively charged cascading nanoslits.

Fig. S11. Representative I-V curves of the electrokinetic ion transport measurements.

Fig. S12. Typical I-V curves for the establishment of membrane selectivity.

Fig. S13. The increase in channel concentration as a result of channel surface charge.

Fig. S14. Scaling behaviors of the electrokinetic ion transport as a function of channel size across the range of sub–10 nm and of varied ionic concentrations.

Fig. S15. The continuum simulation model for electroosmotic current across the negatively charged cascading nanoslits.

Table S1. Geometries of the cascading nanoslits model.

Table S2. Effect of surface charge status on ion diffusion coefficient across the cascading nanoslits.

References (56–72)