Abstract
During the last several years, the focus of research on resting-state functional magnetic resonance imaging (fMRI) has shifted from the analysis of functional connectivity averaged over the duration of scanning sessions to the analysis of changes of functional connectivity within sessions. Although several studies have reported the presence of dynamic functional connectivity (dFC), statistical assessment of the results is not always carried out in a sound way and, in some studies, is even omitted. In this study, we explain why appropriate statistical tests are needed to detect dFC, we describe how they can be carried out and how to assess the performance of dFC measures, and we illustrate the methodology using spontaneous blood-oxygen level-dependent (BOLD) fMRI recordings of macaque monkeys under general anesthesia and in human subjects under resting-state conditions. We mainly focus on sliding-window correlations since these are most widely used in assessing dFC, but also consider a recently proposed non-linear measure. The simulations and methodology, however, are general and can be applied to any measure. The results are twofold. First, through simulations, we show that in typical resting-state sessions of 10 min, it is almost impossible to detect dFC using sliding-window correlations. This prediction is validated by both the macaque and the human data: in none of the individual recording sessions was evidence for dFC found. Second, detection power can be considerably increased by session- or subject-averaging of the measures. In doing so, we found that most of the functional connections are in fact dynamic. With this study, we hope to raise awareness of the statistical pitfalls in the assessment of dFC and how they can be avoided by using appropriate statistical methods.
Keywords: Resting state, Functional MRI, Dynamic functional connectivity, Surrogate data
Highlights
-
•
Not widely recognized is the need for proper statistical testing to assess dynamic functional connectivity in resting-state fMRI.
-
•
This study describes how to test and how not to test for dynamic functional connectivity.
-
•
Large-scale dynamic functional networks are found in macaque monkeys under anesthesia.
-
•
Dynamic functional networks comprise both cortical and sub-cortical regions.
Introduction
Resting-state blood-oxygen level-dependent (BOLD) functional magnetic resonance imaging (fMRI) studies have traditionally investigated patterns of functional connectivity (FC) that are static within the scanning period. More recently, attention shifted towards temporal fluctuations in FC within sessions. The latter is referred to as dynamic functional connectivity (dFC), as opposed to the former, which is referred to as static functional connectivity (sFC). The progress made in the study of dFC has recently been reviewed in Hutchison et al. (2013a). The most common and straightforward way to investigate dFC is using windowed FC, which consists of calculating a given FC measure, for example, the Pearson correlation coefficient or phase-locking factor (Pereda et al., 2005), over consecutive windowed segments of the data. This gives a time series of FC values, which can subsequently be used to assess fluctuations in FC within sessions (Chang and Glover, 2010, Hutchison et al., 2013b, Handwerker et al., 2012, Keilholz et al., 2013, Tagliazucchi et al., 2012, Jones et al., 2012, Allen et al., 2012, Zalesky et al., 2014, Barttfeld et al., 2015). Although such an analysis seems straightforward, there are two pitfalls that have not always been recognized in previous studies.
The first pitfall is to identify an observed value of a test statistic with its true underlying value. This means that the mere presence of fluctuations in an observed FC time series is taken as evidence for the presence of dFC. The pitfall is that of overlooking the fact that the observed FC values are estimates of the true (and unobservable) values, and hence, are subject to statistical uncertainty. As an analogue, consider repeated measurements of a physical quantity, say the speed of an approaching car, by using a laser gun. While the car is approaching, multiple measurements are made, which, due to the imperfections in the instrument and ambient noise, produces a time series of fluctuating values. Although the fluctuations are real, they are due to noise, and do not necessarily reflect fluctuations in the car’s speed, which could be constant. In the same way, observed FC values can be viewed as measurements of a quantity, namely, the true (and unobservable) FC. In classical statistical terms, one needs to distinguish between the sample FC, which is an estimator of the population FC.
Thus, to decide whether fluctuations in an observed FC time series are due to statistical uncertainty or reflect true changes in population FC, an appropriate statistical test has to be carried out. This is typically done by calculating a test statistic (also called a measure, index, or biomarker) that characterizes the fluctuations in the FC time series and subsequently test if the observed value of the test statistic falls outside the test statistics’ null distribution, that is, its distribution if the correlations would be static. Several test statistics have been proposed to test for the presence of dFC, including the variance of the FC time series (Sakoglu et al., 2010), test statistics based on the FC time series’ Fourier-transform (Handwerker et al., 2012), and non-linear test statistics (Zalesky et al., 2014), among others (Chang and Glover, 2010, Keilholz et al., 2013). Crucially, the null hypothesis under which the distribution of the test statistic is constructed should correspond to the FC being static. This might seem trivial, but the construction of such a distribution is far from trivial and this forms the second pitfall in assessing dFC, which is the use of an inappropriate null-hypothesis.
Since the null distribution cannot be derived mathematically for most dFC measures, it needs to be approximated from the data at hand. Ideally, such surrogate data is constructed such that they share all statistical properties with the observed data, except that they lack the property one wants to test for, in this case, dFC (Schreiber and Schmitz, 2000, Pereda et al., 2005). In the literature on dFC, several methods have been proposed to approximate null distributions for dFC. For example, by randomly shuffling the Fourier phases of the BOLD time series (Handwerker et al., 2012, Leonardi et al., 2013) or by randomly selecting BOLD time series from different scanning sessions (Keilholz et al., 2013). The pitfall here is that these two approaches destroy the sFC in the data and hence correspond to a different null hypothesis, namely, that of the FC being static and equal to zero. Additionally, a priori it is unclear how this affects the results of the subsequent statistical testing. A more appropriate way of constructing surrogate data is to fit a time series model to the data and to approximate the null distribution by bootstrapping from the model residuals, as done, for example, in Chang and Glover (2010) and Zalesky et al. (2014). Yet another way, which might be easier to use in practice, is to shuffle the Fourier phases in such a way so that the sFC is preserved (Prichard, 1994). As far as we know, this method has only been applied in Allen et al. (2012). In this study, we focus on the Fourier-based surrogate method.
Material and methods
Statistical assessment of dynamic FC
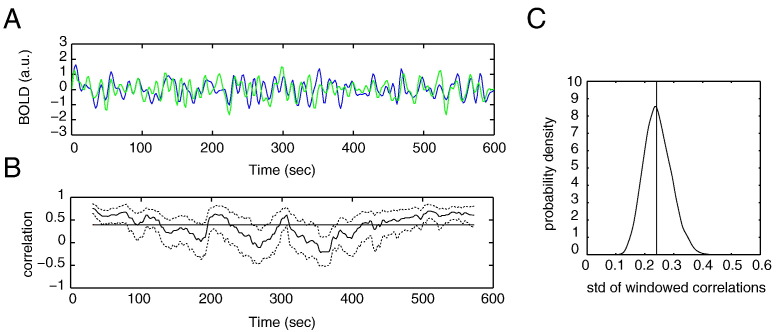
Suppose we have recorded resting-state BOLD-fMRI time series from two voxels or regions-of-interest (ROIs) like those displayed in Fig. 1A and we want to decide if the functional connectivity between the two time series is dynamic, that is, if it changes over the duration of the scan. Although the concept of functional connectivity (FC) is wide and includes any kind of statistical relationship between time series (Pereda et al., 2005, Friston, 2011), we focus on the (Pearson) correlation coefficient, which is the most widely used FC measure in resting-state fMRI research (Sakoglu et al., 2010, Chang and Glover, 2010, Hutchison et al., 2013b, Handwerker et al., 2012; Keilholz et al., 2013, Tagliazucchi et al., 2012, Jones et al., 2012, Thompson et al., 2013, Zalesky et al., 2014). The most straightforward way to proceed is to calculate correlation coefficients on overlapping segments of the time series. This results in a time series of correlation values as shown in Fig. 1B. Note that the windowed correlations have different values for different windows. In particular, we observe both negative and positive correlations, the latter are referred to as “hypersynchrony states” in Hutchison et al. (2013b). Although in some studies, the observed fluctuations in FC are taken as evidence for the presence of dynamic FC (dFC), most studies agree that a statistical test is needed to draw this conclusion. Indeed, an appropriate statistical test for dFC answers the question if the observed fluctuations in the correlation time series can be distinguished from those that would be observed if the correlation were static, that is, independent of time.
Fig. 1.
Statistical testing for dynamic FC. A, Simulation of two simultaneously recorded fMRI time series from two different voxels or ROIs. B, Time series of Pearson correlations obtained by calculating the correlation coefficients on successive 60 s segments of the fMRI time series (maximal overlap). The correlation values are plotted as a function of the window-centers. The dotted lines denote the 95% confidence intervals of the correlation values obtained by repeatedly permuting the windowed fMRI time series. The horizontal line denotes the average correlation between the fMRI time series. C, Probability density of the standard deviation of the correlation time series under the null hypothesis. The observed value was 0.24 and is marked by the vertical line.
One way to answer this question is to construct confidence intervals around the values in the correlation time series, as done, for example, in Kang et al. (2011) and Hutchison et al. (2013b). If the data is a white-noise Gaussian process, the confidence intervals can even be calculated analytically. Otherwise, they can be approximated by resampling of the windowed time series, a technique referred to as bootstrapping. The confidence intervals in Fig. 1B (dotted lines) were obtained by such a bootstrap procedure. More specifically, for each window, we selected (with replacement) unpaired sample-pairs to build a bootstrapped copy of the windowed data and calculated its sample Pearson correlation coefficient. By repeating this many times, an approximation of the null distribution is constructed, from which the confidence intervals can be calculated. Note that there are several windows for which the confidence interval does not contain the average correlation value, that is, the correlation coefficient calculated from the entire time series, denoted by the red line. In Kang et al. (2011), it has been proposed to measure the extent of dFC by the fraction of windows whose confidence interval does not contain the static correlation value. By itself, however, a non-zero fraction does not imply the presence of dFC. For this to decide, we need to return to the question what the value of a measure, in this case the above fraction, would have been if the correlation was static. We stress that this question needs to be addressed for any measure that is used to detect dFC, whether this be the correlation time series’ variance (Sakoglu et al., 2010) or some non-linear measure (Zalesky et al., 2014).
This question can be formalized in a statistical hypothesis test in which the null hypothesis corresponds to the correlation being static and the alternative hypothesis corresponds to the correlation being dynamic. The question of what the value of a given measure would have been if the correlations in the data were static then amounts to determining the measures’ distribution under the null hypothesis and calculating the probability that the observed value of the measure is drawn from this distribution. Since for most measures, the null distribution is unknown, appropriately randomized data is used, as done, for example, in Chang and Glover (2010) and Zalesky et al. (2014). The randomized data are known as surrogate data and are fundamental in the analysis of non-linear and non-stationary time series (Schreiber and Schmitz, 2000, Pereda et al., 2005). As an illustration, Fig. 1C shows the null distribution of the standard deviation of the correlation time series computed from the fMRI time series in Fig. 1A. The observed variance is indicated by the vertical line. Thus, under the null hypothesis, the measure would be a random drawing from this distribution. Since the observed value is not contained in the 2.5% percentiles of the distribution, the null hypothesis cannot be rejected, and therefore, there is no evidence for the presence of dFC. In this example, this conclusion is correct, since the time series were constructed to have a static correlation.
Simulated BOLD-fMRI data
To measure the ability of a test statistic to detect dFC in resting-state BOLD-fMRI data, we use simulated data. This allows us to control the FC (dynamic) time-series, which, in practice, is not directly observable and to investigate how the performance of the test statistic depends on the dynamics of the correlations such as their strength and timescale. To construct simulated fMRI time series, consider zero-mean Gaussian stochastic processes X = (X1, ⋯, XN) and Y = (Y1, ⋯, YN) with variances σX2 and σY2, respectively, and let ρn be the population (Pearson) correlation coefficient between Xn and Yn:
| (1) |
where denotes expectation value. Note that ρn is allowed to depend on time n, that is, to be dynamic. We moreover assume Xn and Xm to be independent for n ≠ m and similarly for Yn and Ym. This means that X and Y do not have autocorrelations, which typically is the case for pre-processed BOLD-fMRI data.
We now specify the dynamics of the correlation time series. It will be convenient to parameterize the dynamics such that their parameters correspond to observable properties, which can then be systematically varied to assess the performance of a given test statistic. Furthermore, we want the correlation time series to be stochastic and not time-locked to (the beginning of) the scanning session, which reflects the ongoing nature of resting-state BOLD fluctuations. Also, the correlation values need to be restricted to the interval [− 1, 1]. To meet the last requirement, we model ρn as a non-linearly transformed variable sn:
| (2) |
where the constant denotes the average correlation between X and Y. The time series s = (s1, ⋯, sN) is obtained by sampling from a continuous variable s(t) with sampling period TR = 2. The variable s(t) is modeled by the following stochastic differential equation:
| (3) |
which describes a harmonic oscillator with intrinsic (angular) frequency ω, damping δ, that is driven by white noise ξt with variance σ2. By choosing s(t) in this way, we assure that it is a stochastic variable that is not time-locked to the (beginning of the) scanning session.
Since the parameter vector (δ, ω, σ) is not directly observable from the simulated time series st, we fix δ and use the parameter vector (τ, η) with τ, η > 0, where
| (4) |
and
| (5) |
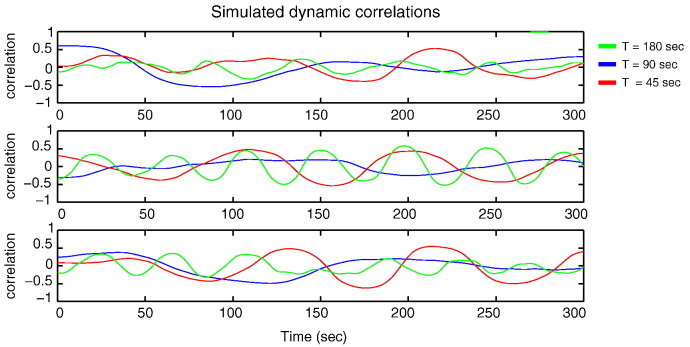
The parameters τ and η are directly related to the observable dynamics of s(t) because the autocovariance function of s(t) can be expressed in terms of δ, τ, and η (see Supplementary File 1). In particular, the (stationary) variance of s(t) equals η2 and its characteristic timescale is τ. Fig. 2 shows three simulated correlation time series, each with three dominant timescales.
Fig. 2.
Simulated correlation time series. Panels A, B, and C display independent realizations of simulated correlation time series. The colors correspond to different dominant timescales: τ = 180 s (blue), τ = 90 s (red), and τ = 45 s (green). In all cases, the average correlation was set to zero () and the strength of dFC was set to 0.5 (η = 0.5). The observation time is 300 s and the correlation time series are down-sampled to 0.5 Hz (TR = 2 s).The three panels correspond to different realizations of the model.
Correlation time series
This study focuses on the performance of test statistics that are derived from windowed correlations. For simultaneously recorded time series x = (x1, ⋯, xN) and y = (y1, ⋯, yN), the (Pearson) sample correlation coefficient is defined as
| (6) |
where and denote the sample means of x and y, respectively. It takes values in the interval [− 1, 1] and measures the strength of the linear relationship between x and y. If x and y are realizations of stationary stochastic processes X = (X1, ⋯, XN) and Y = (Y1, ⋯, YN), which means that their expectations, variances, and (population) correlation coefficient ρn between Xn and Yn does not depend on n, is an asymptotically unbiased estimator of ρ. In this case, we refer to the correlation between X and Y as being static. If ρn depends on n, we refer to the correlation between X and Y as being dynamic. In this document, we refer to ρ = (ρ1, ⋯, ρN) as the (population) correlation time series.
A straightforward estimator of the correlation time series is obtained by calculating the sample correlation coefficient from successive windowed segments of x and y. In its simplest form, the sliding-window estimator of ρk with window-length K is obtained by calculating on the windowed time series (xk − h, yk − h), ⋯, xk + h, yk + h), where h = (K − 1)/2 is the center of the window. Subsequently, k is repeatedly shifted over M samples, yielding the sample correlation time series , where L is the largest integer such that L ≤ (N − K)/M. This time series thus depends on two parameters: the window-length K and the stepsize M. In the next section, we describe two test statistics that are both based on the correlation time series: a widely used linear measure and a recently proposed non-linear measure.
Null hypothesis and test statistics
Having specified a model for the dynamics of the correlation time series, we can specify the problem of detecting dFC in formal terms. Specifically, the absence of dFC corresponds to the null hypothesis
| (7) |
and the presence of dFC corresponds to the alternative hypothesis
| (8) |
Remember that in our model, η2 is the variance of the correlation time series. Thus, within the context of this model, detecting dFC from measurements x and y corresponds to rejecting H0. Although this might seem trivial, assessment of dFC in practice is far from trivial and, as discussed above, remains to be a source of confusion in the scientific discussion on resting-state fMRI dynamics.
In this study, we focus on two test statistics and their ability to detect dFC. The first is the most widely used test statistic in resting-state fMRI studies and is also the most straightforward. It is the standard deviation, or equivalently, the variance of the sample correlation series and we will denote it by κ:
| (9) |
where is the estimated correlation time series, and denotes the sample mean of . The second test statistic, which we will denote by ζ, has been proposed recently (Zalesky et al., 2014) and is defined as follows. Let m be the median of and let n1, ⋯, nJ be the samples for which crosses m. Thus, makes J − 1 consecutive excursions from m. The length In and height Hn of the j-th excursion are defined as In = nj + 1 − nj and . The test statistic is now defined as
| (10) |
where α and β control the relative weighting of the lengths and heights of the excursions. Following Zalesky et al. (2014), we set α = 0.9 and β = 1. We note that the estimated correlation time series used in the computation of ζ differs from the one defined in the previous section in that the windows are multiplied by a weighting factor (see Zalesky et al. (2014) for the exact definition).
Detection probabilities
A model of the dynamics of FC like the one described above allows an assessment of the ability of an arbitrary test statistic T to detect the presence of dFC. Suppose that we have simulated two fMRI time series of length N, a repetition time TR, and certain fixed value of the model parameter . Remember that, within the above described model, the null hypothesis corresponds to H0 : η = 0 and the alternative hypothesis to H1 : η > 0. If we now were to perform a statistical test using the test statistic, what would be the probability of rejecting? If FC is static, the probability of rejecting H0 is given by 100α%, where α is referred to as the size of the test and is typically chosen as α = 0.05. Thus, the probability of incorrectly rejecting H0, that is, of making a Type I error, is equivalent to 5%. For a given value of the model parameter θ, we denote the probability of rejecting H0 by πT(θ). This probability is given by
| (11) |
In this formula, the function fT(−|θ) denotes the probability density of T, given θ, and ξα denotes the 100(1 − α) % percentile of fT(−|θ) under H0, that is, given . The function πT is referred to as the power function of T, because it measured the power of T to reject H0, and we approximate it using Monte Carlo simulations (see Supplementary File 2 for more details).
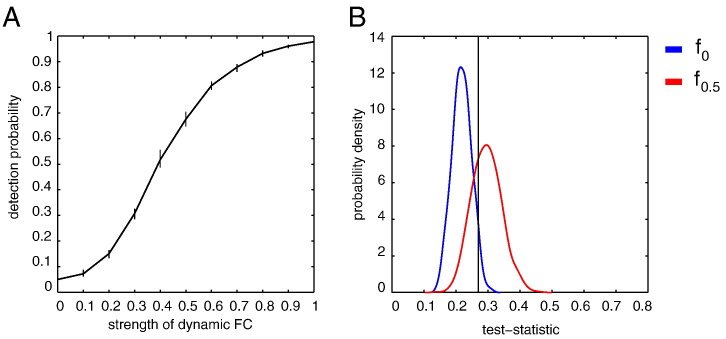
To illustrate the use of the power function, we simulated two fMRI time series x and y of length N = 301, a repetition time of TR = 2, and θ = (0, 120, 0.5). Thus, the average correlation is zero (), and the correlation is dynamic with strength η = 0.5 and characteristic timescale τ = 120 s. Remember that η denotes the standard deviation of the true fluctuations in correlation values. Suppose now that we use the standard deviation of the sample correlation time series as a measure for dFC, that is, we take T = σρ and take a window-length of K = 20 samples with maximal overlap (M = 1). What, then, is the probability of actually detecting dFC in the simulated time series? Fig. 3B shows the probability density fT(−|(0, 120, 0)) of T under H0 (blue line). Its 95th percentile is indicated by the horizontal line and equals ξα = 0.27 (α = 0.05). The probability density of fT(−|(0, 120, 0.5)), given η = 0.5, is shown in red. According to the definition of πT, the probability of detecting that the correlation between x and y is dynamic is obtained by integrating fT(−|(0, 120, 0.5)) from ξα to ∞, which gives πT ≈ 0.69. In this particular case, therefore, the probability of detecting dFC is about 70%. So if we were to scan 20 subjects, each for 10 min and with a TR of 2 s, we expect to detect dFC in 14 out of the 20 subjects. Fig. 3A shows the power function for true dFC between η = 0 and η = 1. For example, if, in reality, η = 0.1, that is, there is weak dFC, our chances of detecting it are less than 10%.
Fig. 3.
Detection probabilities. A, Densities of κ under H0 (blue) and for η = 0.5 (red). The position of the vertical line corresponds to the 95% percentile of κ under H0. It is the critical value for κ and equals κ* = 0.2702. The probability of detecting that η > 0 equals the area under the red density upwards from the κ* and equals π = 0.6914. Parameters were chosen as Ns = 301, η = 0 (blue density) and η = 0.5 (red density), K = 20 samples, τ = 120 s, Ndata = 1000. B, Detection probability πκ as a function of the strength of dFC η, obtained using 10 × 103 Monte Carlo samples. The black curve was obtained through Monte Carlo simulations and the error bars denote their minimum and maximum values for each value of η.
The construction of surrogate data
Suppose we have calculated the value of a test statistic T from two simultaneously recorded BOLD time series and obtained a value T*. How can we decide if the observed value is statistically significant? Answering this question means performing a hypothesis test in which the null and alternative hypotheses, H0 and H1, respectively, correspond to the absence and presence of dFC, respectively. In general, this is done by calculating the percentile of T* in the distribution of T under H0. If T* falls within the 5% highest values (and assuming we perform a one-sided test) we reject H0 and conclude that H1 is true, that is, we conclude that the correlations are dynamic. The probability that we are incorrect (Type I error) is then 5%.
Unfortunately, the null distribution of most test statistics is unknown so that we have to approximate it using the data at hand. More specifically, the null distribution is approximated by generating a large number of appropriately randomized copies of the data, so-called surrogate copies, and the value of the test statistic is then calculated for each of these (Schreiber and Schmitz, 2000, Pereda et al., 2005). By choosing the randomization appropriately, each surrogate copy is constructed under H0, so that the resulting distribution is indeed an approximation of the unknown null distribution of T. Ideally, a surrogate copy has the same statistical properties of the observed data, except that it lacks the property we want to test for, which in the case, is dFC. There exist two general kinds of surrogate data. The first is referred to as constrained and is constructed directly from the observed data. The second is referred to as typical and is constructed by fitting the data to a model and subsequently using the model to generate surrogate data (Schreiber and Schmitz, 2000).
The constrained randomization that is appropriate in the context of dynamic FC was first introduced in Prichard (1994). Although it can be applied to multivariate data, in this study, we only use the bivariate case. Thus, let x1, ⋯, xN and y1, ⋯, yN be simultaneously recorded BOLD signals. The method takes the discrete Fourier transformations X1, ⋯, XN and Y1, ⋯, YN, of x and y, respectively, and multiplies each with a random phase: and , where ϕ1, ⋯, ϕN is a vector of independent stochastic variables that are uniformly distributed in the interval [0, 2π]. Crucially, both X and Y are multiplied by the same phases ϕ1, ⋯, ϕN so as to preserve the (static) correlation structure. Subsequently, the inverse discrete Fourier transformation is applied to and Ỹ1, ⋯, ỸN to yield randomized copies of x and and ỹ of y.
Recordings and pre-processing
Functional MRI data were collected from three healthy male monkeys (Macaca mulatta) as described in detail previously (Logothetis et al., 2012). All experimental procedures were approved by the local authorities (Regierungsprasidium, Tubingen, Germany) and were in full compliance with the guidelines of the European Community (EUVD 86/609/EEC) for the care and use of laboratory animals. The experiments were conducted under general anesthesia maintained with remifentanil (0.5–2 g/kg/min) in combination with a fast-acting paralytic (mivacurium chloride, 5–7 mg/kg/h). Remifentanil is an ultrafast acting μ − opioid receptor agonist, and as such, has no significant effect on neurovascular activity, in particular in brain regions beyond the pain matrix (Wise, 2002, Pattinson et al., 2007). It is furthermore known to only mildly affect the magnitude and time course of neural and vascular responses (Logothetis et al., 1999, Logothetis et al., 2001, Goense and Logothetis, 2008). The physiological state of the animal was monitored continuously and maintained tightly within normal limits. Acidosis was prevented by the administration of lactated Ringer’s solution with 2.5% glucose, infused at 10 ml/kg/h.
We made measurements in a vertical 4.7 T scanner with a 40 cm diameter bore (BioSpec 47/40v, Bruker BioSpin, Ettlingen, Germany). A customized quadrature volume radiofrequency coil was used for imaging of deep brain structures. Typically, 22 axial slices were acquired, covering the entire brain. BOLD activity from these slices was acquired at a temporal resolution of 2 s with two-shot gradient-echo EPI images (repetition time = 1000 ms, echo time = 20 ms, bandwidth = 150 kHz, flip angle = 60 degrees, FOV = 96 × 96 mm, 2 mm slice thickness). T2-weighted RARE images with the same FOV were obtained using a matrix of 256 × 256, rare factor 8, effective TE of 60 ms, TR of 5000 ms, BW 42 kHz, and 4 averages. The anatomical images were later morphed to match the EPI images.
In order to avoid different image intensities in the functional scans, each voxel was normalized by dividing by the mean value of all voxels having enough intensity and multiplied by a user value of 1000.
The T1-weighted image was segmented into gray matter, white matter, and cerebrospinal fluid compartments and registered to the MNI Macaque Atlas (http://www.bic.mni.mcgill.ca/ServicesAtlases/Macaque) using a 12-parameter affine transformation. Pre-processing of the fMRI data consisted of brain extraction (employing a mask combining gray matter, white matter, and cerebrospinal fluid images), motion correction, co-registration to the T1-weighted image, and spatial alignment to the macaque MNI template using the previously calculated 12-parameter affine transformation. After registration to MNI space, we performed regression of head motion parameters and of white matter and cerebrospinal fluid signals, as well as low pass-filtering with a cutoff frequency at 0.05 Hz using a Chebychev type II filter and local averaging to obtain time series for each voxel of MNI Macaque space. Subsequently, the time series were grouped into 436 regions-of-interest (ROIs) according to the Paxinos 2008 parcellation. All pre-processing steps were carried out in Matlab using custom-written code and functions from the Statistical Parameteric Mapping toolbox version 8 (see http://www.fil.ion.ucl.ac.uk/spm).
We also analyzed resting-state BOLD-MRI data collected in 24 human participants, which were also used in a number of our previous studies (Deco et al., 2013, Mantini et al., 2013, Deco et al., 2014, Ponce-Alvarez et al., 2015). Human volunteers were informed about the experimental procedures and signed a written informed consent. The study design was approved by the Ethics Committee of Chieti University (Italy). MR data acquisition was performed with a 3 T MR Philips Achieva scanner. Participants were instructed to continuously fixate a point with no visual stimuli present in the background and not to move during the scanning. The functional images were obtained using T2*-weighted echo-planar images (EPI) with BOLD contrast using SENSE imaging. EPIs comprised 32 axial slices acquired in ascending order and covering the entire brain (32 slices, 230 × 230 in-plane matrix, TR/TE = 2000/35, flip angle = 90°, voxel size = 2.875 × 2.875 × 3.5 mm3). For each human subject, two consecutive scanning runs of 10 min were performed. Furthermore, a 3D high-resolution T1-weighted image, to be used for anatomical reference, was collected by means of an MP-RAGE sequence (TR/TE = 8.1/3.7, voxel size = 0.938 × 0.938 × 1 mm3). The pre-processing of human fMRI data was analogous to the one described above for macaque fMRI data, with the only exception being that we spatially registered the functional images to the MNI-ICBM Human Atlas (http://www.bic.mni.mcgill.ca/ServicesAtlases/ICBM152NLin2009) instead of the MNI Macaque Atlas. Furthermore, the brain parcellation used to obtain ROI time series by local averaging was the one proposed by Hagmann and was composed of 66 regions (Hagmann et al., 2008).
Dynamic FC analysis
We applied the methods of detecting dFC described in earlier sections to both the macaque and the human BOLD-fMRI data. As mentioned before, we had fMRI recordings for 25 sessions each from 3 macaque subjects and for 2 sessions each from 24 human participants. The recording duration was 5 min with a sampling period of 2 s for every session. The macaque data was parcellated into 436 ROIs while human data was parcellated into 66 ROIs.
For every session, we obtained both the linear and non-linear test statistics using two approaches. In the first approach, we obtained the correlation time series for each ROI pair using a window-length of two minutes and a step size of two seconds and then calculated the test statistics for each ROI pair. We then generated, for each session, 250 phase-randomized surrogate time series for each ROI such that the stationary correlation between every ROI pair was preserved within every set of surrogates. Next, we calculated, for every ROI pair, values of both test statistics for each of the corresponding 250 surrogates. Finally, we pooled the values of all ROI pairs together in order to obtain a p-value for the observed value of the test statistic. We also averaged the observed and the surrogate test statistic values across sessions and obtained the corresponding p-values.
In the second approach, we calculated ROI-averaged test statistics to increase the statistical power. Thus, we obtained, for each session, the correlation time series for each ROI pair using a window-length of two minutes and a step-size of one minute, calculated both statistics for each pair and then for every ROI averaged its values of each test statistic across all other ROIs. Thus, instead of the 94,830 and 2145 values of each test statistic for the macaque and human data, respectively, we now had only 436 and 66 values to compare against a surrogate distribution. Therefore, in the second approach, we generated 10,000 surrogate datasets for macaque subjects and 1500 surrogates for the human participants, each of which preserved the stationary correlation between every ROI pair and calculated the surrogate distribution of values of both linear and non-linear statistics and obtained the corresponding p-values. We repeated the procedure by averaging the observed and surrogate test statistic values across sessions and obtained the corresponding p-values.
Results
Dependence on correlation timescale
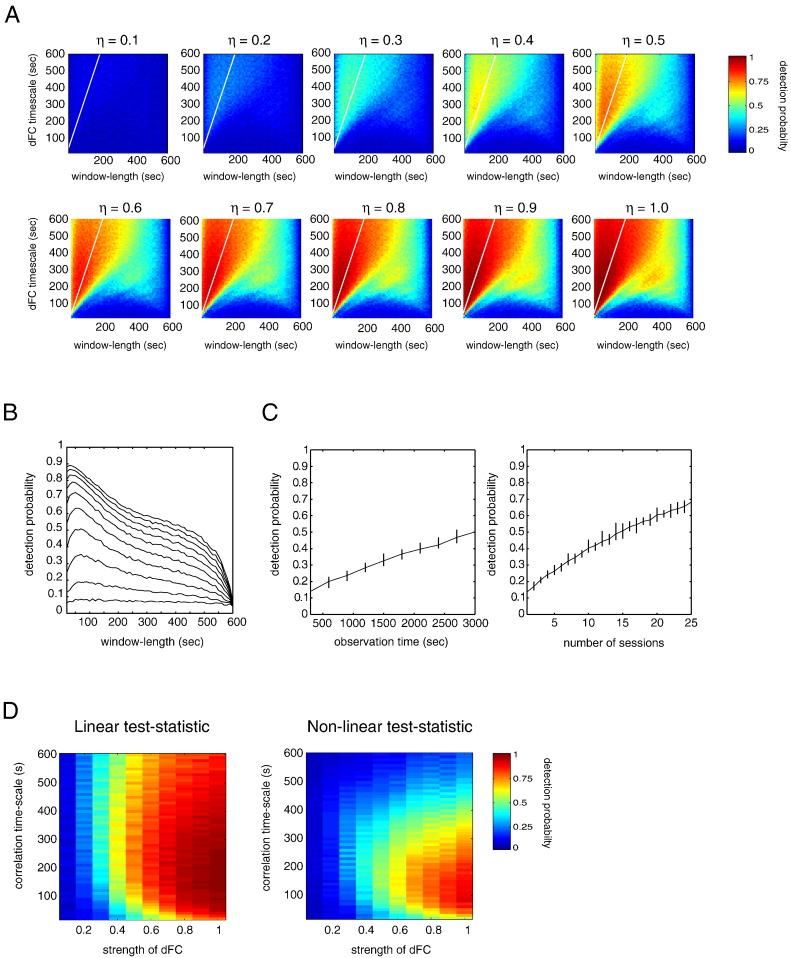
To assess how the detection power of the linear test statistic κ depends on the dynamics and strength of the (population) correlation signal ρt, we calculated the detection probability πκ for different values of the correlation timescale τ and the strength of dFC η. The remaining parameters were held fixed at values , TR = 2 s, N = 300 samples, and M = 1. We let τ range from 20 to 600 s in steps of 10 s and η between 0.1 and 1 in steps of 0.1. We let the window-length K vary over the same range as τ.
Fig. 4A shows color-coded plots of the probabilities πκ((τ, η, K)) as a function of τ and η. The different plots correspond to the values of η displayed above each figure. The plots have several interesting features. First, while the (absolute) probabilities increase with increasing η, the relative probabilities remain roughly constant. For example, choosing K < τ always yields a better chance of detecting dFC than choosing K > τ, irrespective of the strength of dFC. Second, if τ is small, say τ < 30 s, then dFC can never be detected, since no matter how strong, the chance of detection πκ ≈ α (which was set to 0.05). Third, the choice of K that yields the highest probability of detecting dFC, denoted by Kopt, is roughly given by one-third of the characteristic timescale of the correlation time series:
| (12) |
Fig. 4.
Detection probabilities of windowed correlations. A, Color-coded probabilities of detecting dFC as a function of window-length K and correlation timescale τ. The ten figures correspond to different values of η (the strength of dFC) as indicated above the figures. We let η range from 0.1 to 1 in steps of 0.1. The straight white lines are identical in each figure and denote the line (K, 3K). It is added to illustrate a rule-of-thumb for choosing that is satisfied by optimal window-length. Roughly, it equals one-third of the correlation timescale. B, Detection probabilities averaged over all correlation timescales and plotted as function of the length of the sliding-window. The ten curves correspond to the ten values of η (higher curves correspond to higher values of η). C, Detection probabilities as a function of observation time, that is, the duration of the scanning session (left) and as a function of the number of sessions (right). In all cases, the model parameters were set to and the sliding-window parameters to (K, M) = (30, 1). Furthermore, in calculating the detection probabilities in the right-hand side of the figure, the observation time was set to T = 300 s. The error bars in both figures denote the minimum and maximum probabilities from 10 simulations. D, Shown are the detection probabilities for the linear (left) and non-linear (right) test statistics. The probabilities were calculated as a function of the correlation timescale, which ranged from 20 to 600 s in steps of 1 s and strength of dFC, which ranged from 0.1 to 1 in steps of 0.1. The window-length was set to one-third of the correlation timescale and the windows were slid through the simulated fMRI time series one sample at a time. The average correlation was set to and repetition time was set to TR = 2 s.
The plots also show, however, that the fluctuations in the correlation time series are slow (large τ), Kopt < τ/3, so this choice of K should be regarded as a rule-of-thumb only. It can be understood though, since on the one hand, to reduce the variance of the test statistic, K should be as large as possible. On the other hand, an upper-boundary for K is given by τ in the same way as the Nyquist frequency gives the upper-bound for the observable frequencies in a time series, given the sampling frequency. Needless to say, the rule ≈ τ/3 only has theoretical significance, since in practice, the timescale of fluctuations in the correlation coefficient between (resting state) BOLD-fMRI time series is unknown.
By averaging the test statistic over all timescales, however, something can still be said. In Fig. 4B, we have plotted a set of detection probability curves. They denote the probabilities averaged over all correlation timescales and plotted against the window-length. The ten curves correspond to the ten values of the strength of dFC and higher-located curves correspond to higher values of η. They show that, more or less independent of the strength of dFC, in the absence of knowledge about the true correlation timescale, the optimal window-length is about 50 s. Interestingly, windows of this length are quite common in experimental studies (Chang and Glover, 2010, Hutchison et al., 2013b, Handwerker et al., 2012, Keilholz et al., 2013, Tagliazucchi et al., 2012, Jones et al., 2012, Allen et al., 2012, Zalesky et al., 2014, Barttfeld et al., 2015).
Dependence on scanning duration and number of sessions
To asses how the detection probability depends on the duration of the scanning session, we calculated it as a function of the number of samples N, which we varied between 150 and 1500 in steps of 150. With a TR of 2 s, the scanning duration is thus varied from 5 to 50 min in steps of 5 min. The model parameters were set to and the sliding-window parameters to (K, M) = (30, 1).
The results are shown in Fig. 4C (left). The figure shows that the probability of detecting dFC increases approximately linearly as a function of the scanning duration. As an example, the probability of detection dFC in a resting-state session of 5 min is about 15% and increases to about 50% for a 50-min session.
Since long scanning sessions are impractical, at least in awake human subjects, an alternative way to increase the detection probability is to measure BOLD fluctuations during multiple sessions and subsequently to average the test statistic over the sessions. To asses how the detection probability depends on the number of sessions, we calculated the detection probabilities as a function of the number of sessions (each of 5 min), which ranged from 1 to 25. For each number of sessions, the test statistics were averaged over the sessions. The results are shown in Fig. 4C (right). The figure shows that the detection probability increases approximately linearly with the number of sessions. In particular, note that between 1 and 10 sessions (which correspond to a total observation time of 300 s and 3000 s, respectively), the curves in both figure panels roughly correspond. In fact, the observed differences are entirely due to the fact that we have approximated the theoretical detection probabilities. We note that instead of sessions, test statistics can be averaged over subjects as well. In Section Application to human resting-state BOLD-fMRI, we will see that this indeed increases the probability of detecting dFC.
These observations can be understood theoretically by considering a simple case in which the distribution of the linear test statistic κ can be calculated analytically. Let’s assume that κ is calculated using non-overlapping windows (M = K) and that the population correlation time series ρt is constant within each window, say ρt = ρn, within the n-th window, and pn is normally distributed with variance η2. Although this form of the correlation time series is not a special case of our dynamical model for dFC, η2 has the same interpretation, namely, it is the variance of the population correlation time series. Under these assumptions, and if K and N are large and N is much larger than K, the expectation and variance of κ are approximately given by
| (13) |
and
| (14) |
(see Supplementary File 3). Now, let’s fix K and consider what happens when N increases. The first formula states that the expectation of κ2 approximately equals η2, that is, the strength of dFC. The second formula shows that the variance of κ2 converges to zero. This means that, irrespective of K, the overlap between the densities of κ2 under H0 : η = 0 and under H1 : η > 0 converges to zero. This implies that the detection probability πκ converges to 1. In this example, the presence of dFC, can thus always be detected, provided that the observation time is long enough. The second formula also shows however, that if dFC is small (η2 ≈ 0), a larger number of samples is required to detect it.
Linear versus non-linear measures
In the previous sections, we found that the probability of detecting dFC in single scanning sessions with a typical duration of 10 min is rather low (about 15%). This low probability could be due to the fact that the used test statistic is rather insensitive to changes in FC. Alternatively, the cause could lie in the correlation time series itself, namely in the large uncertainty (variance) of the sample correlation coefficient. This would imply that the sensitivity of any test statistic that is derived from the correlation time series is low. To make a case for the latter, we compared the detection probabilities of the (linear) test statistic κ with a recently proposed non-linear test statistic ζ, which we will denote by ξ (see Section Null hypothesis and test statistics for the definition). What is important here is that both test statistics are derived from the correlation time series, because this will enable us to identify the cause of the observed insensitivity.
In the following simulations, we set the observation time to 10 min and varied the correlation timescale τ between 20 and 600 s in steps of 10 s. The strength of dFC, as measured by η, was varied between 0.1 and 1 in steps of 0.1. The window-length for calculating the correlation time series was set to one-third of the correlation timescale, since this window-length was found to be optimal (see Section Dependence on correlation timescale). The windows were slid through the simulated fMRI time series with one sample at a time (M = 1). Furthermore, the average correlation between the simulated fMRI time series was set to zero () and TR = 2 s.
The resulting detection probabilities for both test statistics are shown in Fig. 4D. We make two observations. First, the linear test statistic yields high detection probabilities for lower dFC strengths than the non-linear test statistic does. Second, while the linear test statistic is relatively insensitive to the timescale in the correlation time series, high detection probabilities of the non-linear test statistic are confined to short correlation timescales. The cause for the latter is that the non-linear test statistic is comprised of the product of the widths and heights of the excursions in the correlation time series, of which there might be only one or two if the correlation timescale is large.
In any case, since the non-linear test statistic doesn’t do a better job in the detection of dFC, we suspect that the problem lies in the correlation time series itself, rather than in the test statistics derived from it. This conclusion is in line with the findings reported in Lindquist et al. (2014).
Effect of low pass-filtering
Pre-processing of resting-state BOLD-fMRI time series often includes low pass-filtering to remove artifacts and to select frequencies of interest. Such filtering, however, can distort the correlation time series, either directly or by introducing autocorrelations in the BOLD time series themselves. To provide insight into the relative strengths of these two effects, we express the population correlation time series of the low pass-filtered time series, denoted by ρtfilt, in terms of ρt and the normalized impulse response ht of the filter. In Supplementary File 4, we derive that
| (15) |
where ⊗ denotes the convolution operator. This formula says that if a BOLD time series is filtered by a filter with (normalized) impulse response h(t), that is, convolved with h(t), the correlation time series is filtered with impulse response h2(t). In the frequency domain, this equation takes the form
| (16) |
where Pfilt and H denote the Fourier transforms of ρfilt and h, respectively, and ω denotes (angular) frequency. Note that for a zero-phase filter, say with frequency response H0, it holds that
| (17) |
so that H is real and hence causes no distortions in the phase-spectrum of ρ.
Since the frequency response H ⊗ H has a cutoff frequency that is similar to H, we expect that if 1/τ < fc, then ρfilt(t) ≈ ρ(t). That is, we expect that if the dominant period in the (population) correlation time series ρ is smaller than the cutoff frequency fc of a zero-phase low pass-filter (with steep roll-off), then the (population) correlation time series of the filtered time series is not distorted by the filtering. When 1/τ > fc, the filtering will attenuate the fluctuations in ρ.
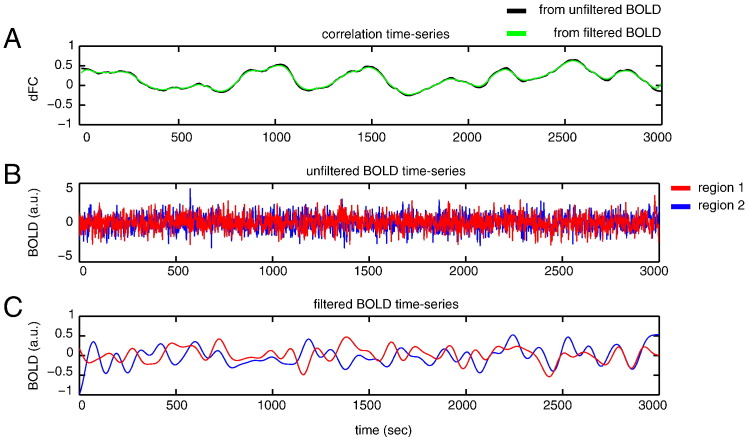
To illustrate this, we go back to the simulations described in the first paragraph of this section in which we simulated BOLD time series with η = 0.5 and low pass-filtered them with cutoff frequency fc = 0.05 Hz. Fig. 5A shows the population correlation time series (black trace) and its filtered version (green trace), as calculated from the above equation. Clearly, the filtering does not affect the correlation time series. Figs. 5B and C show the raw and filtered BOLD time series themselves. The autocorrelations that are visible in the filtered time series are caused by the low pass-filtering and decrease the detection probability of dFC.
Fig. 5.
Effect of low pass-filtering. A, Example of population correlation signal (black trace, Nsampl = 1501, η = 0.5, τ = 600), together with its filtered version (green trace) as calculated from the equations in the text and a cutoff frequency fc = 0.05 Hz). B, Simulated BOLD-fMRI time series with population correlation signal as in the top. C, The same time series but low pass-filtered with a cutoff frequency of fc Hz.
Thus, for cutoff frequencies that are typically used to filter fMR time series (0.05 < fc), fluctuations in dFC are most likely not affected. That is to say, fluctuations that can be detected by sliding-window techniques, since fluctuations with a timescale of 20 s or shorter will be attenuated when fc is as low as 0.05 Hz. We conclude that the decrease in detection power of the sliding-window estimator κ upon low pass-filtering fMRI time series is entirely due to the fact that low pass-filtering creates autocorrelations in the time series. It is worthy to note that high-pass filtering, when carried out with an appropriate cutoff frequency relative to the window-length, can minimize spurious fluctuations in the sample correlation time series (Leonardi et al., 2014).
Application to macaque BOLD-fMRI under general anesthesia
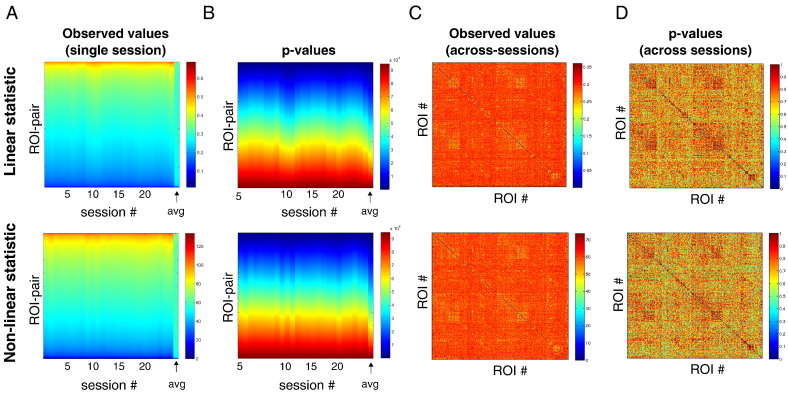
First we calculated the values of the linear and non-linear test statistic for each ROI pair (see Section Dynamic FC analysis). Fig. 6A shows the values of the linear (top) and non-linear (bottom) test statistic for all ROI pairs, for each individual session, as well as averaged across sessions (final column). For each session, the ROIs are arranged according to ascending order of the corresponding (Bonferroni corrected) p-values shown in Fig. 6B. Note that the variability in the test statistic values across pairs in each individual session is larger than when they are averaged across sessions (A, top and bottom panels). At the same time, there are more ROI pairs with lower p-values in the averaged case in comparison with any individual session. Importantly, note that the distribution of session-averaged p-values is shifted to smaller values when the test statistics are averaged across sessions. This indicates that session averaging increases statistical power, as predicted from the simulations in Section Dependence on scanning duration and number of sessions. Despite increased statistical power, however, none of the session-averaged p-values crossed the 5% significance threshold. The less conservative false discovery rate (FDR) correction for multiple testing also did not yield statistically significant dynamic FC of any ROI pair, whether in any individual session or averaged across sessions (see Figs. 6C and D). This observation extended to subjects 2 and 3 (see Fig. 1, Fig. 2, respectively).
Fig. 6.
Pairwise dynamic functional correlations in macaque monkeys under general anesthesia. A, Test statistic values for all 94830 ROI pairs, obtained individually for each of the 25 sessions and averaged across all sessions (final column). B, p-values corresponding to test statistic values in A, corrected for multiple comparisons using the Bonferroni correction. Uncorrected p-values were obtained by comparing the observed values of the test statistics with those obtained from 250 pairs of surrogate time series. In panels A and B, ROI pairs are arranged in ascending order of (Bonferroni corrected) p-values. This is done for each individual session as well as for the average. C, Values of the test statistics between every ROI pair, averaged across all 25 sessions. D, p-values corresponding to the session-averaged test statistic values in C, corrected for multiple comparisons using false discovery rate.
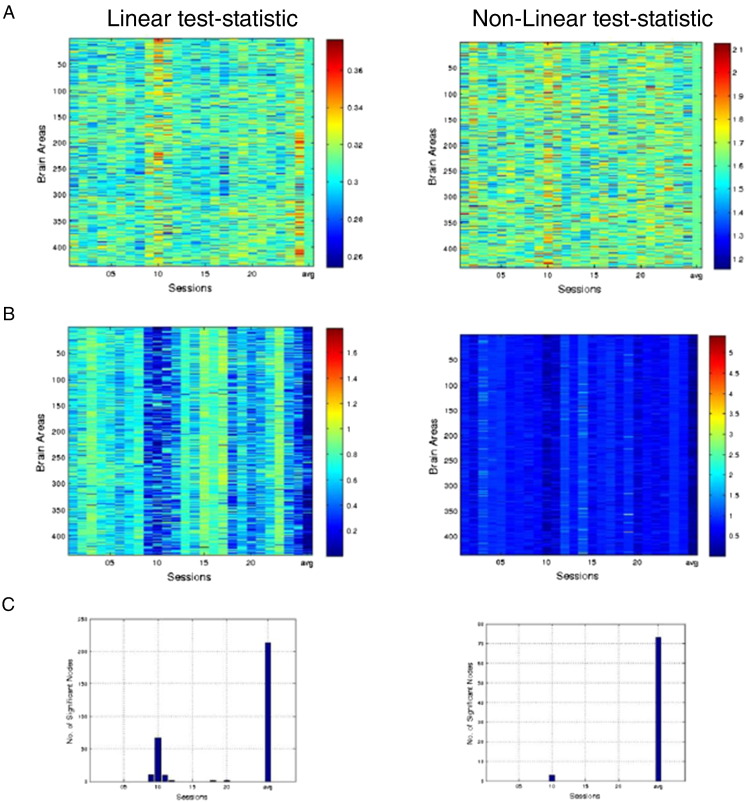
To increase statistical power, we averaged the test statistic values over ROIs (see Section Dynamic FC analysis). Fig. 7A shows these ROI-averaged values for the linear (left panel) and non-linear (right panel) test statistics and Fig. 7B shows the corresponding FDR-corrected p-values. Fig. 7C shows the number of significant dynamic connections, both for the individual sessions as well as for the session-averaged (and ROI-averaged) test statistic values. A number of remarks are in place here. First, while the fraction of significantly dynamic connections is nearly zero for both the linear and the non-linear test statistics, a much larger fraction of the connection is significantly dynamic when averaging across sessions. This observation extends to subjects 2 and 3 as well (see Supplementary Fig. 3). This is entirely in line with our simulation results in Section Dependence on scanning duration and number of sessions, which predicted an increase in statistical power when averaging over sessions. Specifically, for the linear test statistic, there were 213 ROIs (109 in the left hemisphere and 104 in the right hemisphere) with significant dynamic connections. For the non-linear test statistic, there were 73 ROIs (38 in the left hemisphere and 35 in the right hemisphere). This too is in line with our simulations (see Section Dependence on scanning duration and number of sessions), which predicted the linear test statistic to be more sensitive to dynamic FC than the non-linear test statistic.
Fig. 7.
ROI-averaged dynamic functional correlations in macaque monkeys under general anesthesia. A, ROI-averaged values of the linear (left panel) and non-linear (right panel) test statistic for each of the 436 ROIs and for each of the 25 recording sessions, as well as averaged across sessions (final columns). The correlation time series of every ROI pair in each session was obtained using a window-length of 2 min and a step size of 1 min. B, p-values corresponding to test statistic values in A, corrected for multiple comparisons using false discovery rate. Uncorrected p-values were obtained by comparing the observed values of the test statistics with those from 10,000 phase-randomized surrogate time series (Section The construction of surrogate data). C, Number of ROIs with statistically significant (at 95% confidence level) test statistic values calculated for each individual session as well as averaged across sessions.
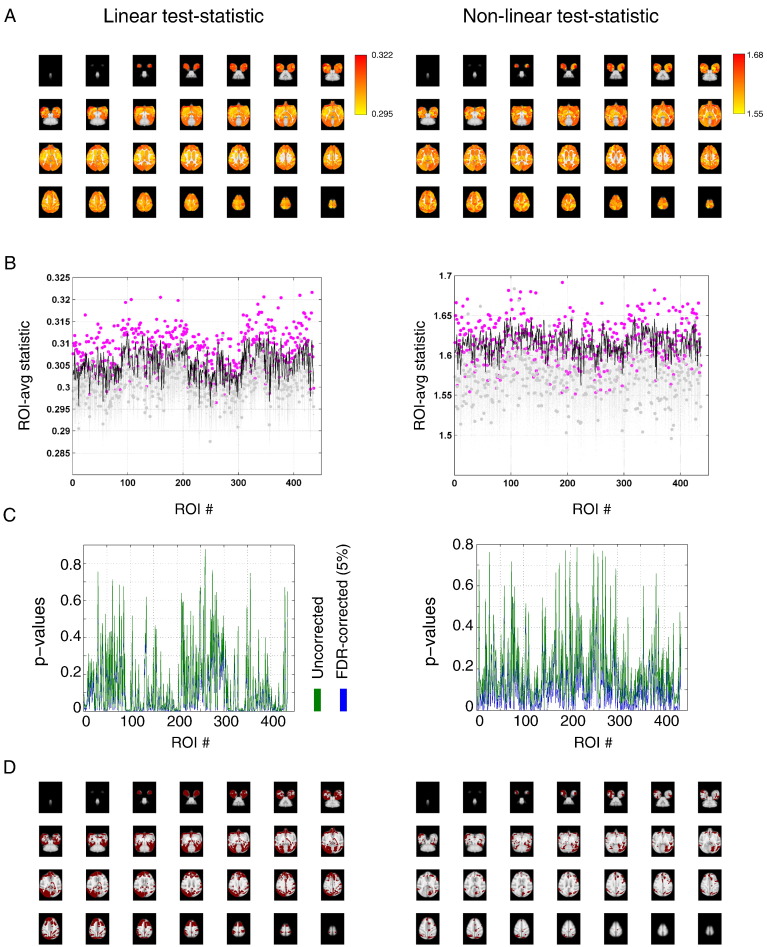
Fig. 8A shows the topography of session-averaged values of the linear (left panel) and non-linear (right panel) test statistic. Interestingly, the values are distributed rather symmetrically across the hemispheres, especially for the linear statistic, which is also the case for subjects 2 and 3 (see Supplementary Fig. 4). Fig. 8B shows the observed values (magenta), together with the 10,000 values obtained from the surrogate data (gray). The black line corresponds to the 95% confidence level. Fig. 8C shows the corresponding uncorrected and FDR-corrected p-values. Fig. 8D, the ROIs with significant dynamic FC are shown in red. Again, note the rather symmetric distribution across hemispheres in the case of the linear statistic (see Supplementary Fig. 4 for the results from subjects 2 and 3). Another interesting observation is that out of the 213 significant ROIs in case of the linear statistic, a substantial number (86) is sub-cortical. The cerebellum, in particular, seems to possess high dynamic connectivity. Furthermore, in case of the linear statistic, seven out of the nine cortical ROIs belonging to the default mode network (DMN) in macaque monkeys (Mantini et al., 2011) were dynamic. Specifically, these ROIs were areas 24 and 32 in the left anterior cingulate cortex, areas 9 and 46d in the left dorsolateral prefrontal cortex, area 8b in the arcuate sulcus, area 23 in the posterior cingulate cortex, parietal area, caudal part of temporal parietooccipital area, and medial part 17 of the parietal area. Moreover, almost all areas belonging to the hippocampal-entorhinal cortical region (CA1, CA2, CA3, CA4, para and prosubiculum and caudal, olfactory, rostral and intermediate part of the entorhinal cortex) demonstrated significant dynamic correlations on average with all other areas.
Fig. 8.
Session-averaged dynamic functional correlations in macaque monkeys under general anesthesia. A, ROI-averaged values of the linear (left panel) and non-linear (right panel) test statistic displayed color-coded on horizontal slices of the macaque MNI template. B, Values of the linear (left panel) and non-linear (right panel) test statistic observed in the data (magenta) and those from 10,000 phase-randomized surrogate time series (gray). The black lines denote the 95%-percentile of the surrogate distribution for each ROI. C, nn-values for the linear (left panel) and non-linear (right panel) test statistic, uncorrected (blue) and corrected (green) for multiple comparisons using false discovery rate. D, Topographic maps showing the spatial distribution of the ROIs displaying statistically significant values ROI-averaged dynamic correlations (in red) using the linear (left panel) and non-linear (right panel) test statistic.
Application to human resting-state BOLD-fMRI
Next, we sought to identify dynamic functional connectivity during the resting-state in human participants. Thus, at first, we calculated the linear and non-linear test statistic for each of the 2145 ROI pairs during each of the 2 sessions of 24 human participants. Supplementary Fig. 5A shows the values of the linear (top) and non-linear (bottom) test statistic for all ROI pairs, for each session of individual participant, as well as averaged across sessions from all participants (final column). Similar to the case of macaque subjects, there was lower variability in the test statistic values across pairs (A) and higher number of ROI pairs with lower p-values (B) in the averaged case in comparison with individual sessions. Thus, this analysis also confirms the prediction from the simulations in Section Dependence on scanning duration and number of sessions that session-averaging increases statistical power. However, none of the session-averaged p-values, corrected for multiple comparisons using FDR, crossed the 5% significance threshold, in line with our findings in the macaque data.
We then averaged the test statistic values over ROIs as in the case of macaque subjects. Supplementary Fig. 6A shows these ROI-averaged values for the linear (left panel) and non-linear (right panel) test statistics and Supplementary Fig. 6B shows the corresponding FDR-corrected p-values. Supplementary Fig. 6C shows the number of ROIs with significant values of ROI-averaged test statistics, both for each session of individual participants as well as averaged across sessions from all participants. We found that, for individual sessions, very few ROIs displayed significant dynamic FC averaged across all other ROIs irrespective of whether linear or non-linear statistic was considered. This number increased substantially when the test statistics were averaged across all sessions of all participants, as predicted by our simulations (see Section Dependence on scanning duration and number of sessions). Of particular interest—and in line with our observations on the macaque data as well as with the simulations performed in Section Dependence on scanning duration and number of sessions—all ROIs were found to be significantly dynamic when using the linear test statistic, while only about 30% was found to be dynamic when using the non-linear test statistic (see Supplementary Fig. 6C).
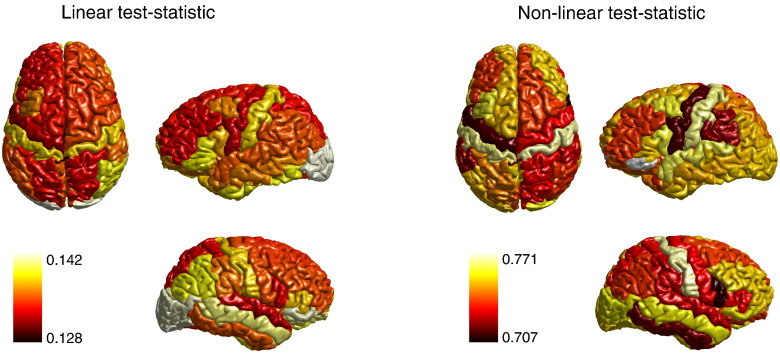
Fig. 9 shows the topographies of the values of the ROI-averaged linear and non-linear test statistics. A feature worth pointing out is their symmetry across hemispheres: the (Pearson) correlation between the values in the left and right hemispheres was 0.79 and 0.48, in case of the linear and the non-linear test statistic, respectively. These observations are in line with tests done on the macaque data.
Fig. 9.
Average dynamic functional correlations in human resting-state BOLD-fMRI. The figure shows the topographic distribution of the session- and ROI-averaged values of the linear (left panel) and non-linear (right panel) test statistic.
Discussion
The first goal of this study is to demonstrate the importance of performing proper statistical tests in the analysis of dFC in resting-state BOLD-fMRI data and to describe how such tests can be carried out by using appropriate surrogate data (Prichard, 1994, Schreiber and Schmitz, 2000). We note that such tests apply to electrophysiological (EEG/MEG) and task-related data as well. We have tried to explain why the mere presence of fluctuations in sliding-window correlation time series cannot directly be taken as evidence for the presence of dFC. The second goal is to stress the importance of selecting an appropriate null hypothesis, which is implicitly done by the way the data are randomized to produce surrogates (Handwerker et al., 2012, Keilholz et al., 2013, Leonardi et al., 2013). The last goal is to assess the performance of sliding-window based test statistics in detecting dFC in resting-state BOLD-fMRI data. Our main conclusion is that in single resting-state scanning sessions, detection probabilities are low, irrespective of the used test statistic being linear or non-linear. Indeed, the problem lies with the sliding-window technique itself. Through simulations, we have also shown, however, that detection probabilities can be increased by averaging over multiple sessions. Our findings on spontaneous BOLD fluctuations in anesthetized macaque underscore these conclusions.
Specifically, we sought to identify dFC in every pair of brain regions in 25 sessions of BOLD-fMRI data from three macaque monkeys under general anesthesia (Logothetis et al., 2012) using both a linear and a non-linear test statistic. Importantly, we found no evidence for pairwise dFC whether in individual recording sessions or by averaging the test statistic values across sessions. However, reducing the number of multiple comparisons by calculating ROI-averaged test statistics, we found strong evidence for a distributed dFC network, but only after averaging the test statistic values over sessions. The identified network was symmetric across hemispheres and included several cortical as well as sub-cortical areas. In particular, almost all regions belonging to the hippocampus and the entorhinal cortex were part of this network. This finding goes along well with the fact that in this dataset, Logothetis et al. recorded sharp-wave ripple events in the hippocampal region during each recording session (Logothetis et al., 2012). They observed that many cortical as well as sub-cortical regions displayed transient activations and de-activations, respectively, in response to these events. Therefore, these events and the responses could have contributed to the observed transient connectivities with cortical regions.
We also looked for dynamic FC in 48 sessions from 24 human participants and, similar to the case of macaque subjects, we did not find any statistically significant evidence for pairwise dFC whether in single sessions or by averaging across sessions. However, calculation of ROI-averaged test statistics yielded evidence for non-stationarity for several regions, when we averaged across all 48 sessions. While the non-linear test statistic yielded significant values for about a third of the total number of regions, the linear test statistic yield significance for all. This could be a result of the large number of sessions used for averaging as our simulations also show that the detection power increases with the number of sessions used for averaging. The values of both statistics displayed symmetry across hemispheres.
This study is limited in several ways. First, the simulated BOLD-fMRI data were constructed using a specific model for the dynamics of functional correlations. Specifically, we have assumed that the correlation time series behave as noise-driven damped harmonic oscillations. Indeed, other models have been used to simulate the dynamics of the correlation time series such as vector autoregressive (VAR) models (Cribben et al., 2012, Monti et al., 2014), deterministic oscillations (Leonardi et al., 2014, Lindquist et al., 2014), and transients (Kang et al., 2011, Lindquist et al., 2014). To a certain extent, these choices are arbitrary, since the underlying correlation dynamics are unknown. Apart from some basic requirements such as that the correlation signal is not time-locked to the beginning of the simulation, the choice depends on the question at hand. For example, in the current study, we were interested in the dependence of detection probability on the strength and timescale of the dynamic correlations. Second, we have restricted ourselves to studying the performance of two test statistics, while many more test statistics have been used in earlier studies (Sakoglu et al., 2010, Chang and Glover, 2010, Hutchison et al., 2013b, Handwerker et al., 2012, Keilholz et al., 2013, Tagliazucchi et al., 2012, Jones et al., 2012, Thompson et al., 2013, Zalesky et al., 2014), which could turn out to perform better in detecting dFC. Based on our results, we predict that the performance of all test statistics based on sliding-window correlations perform more or less similar. Rather, it is the estimated correlation time series itself that is responsible for poor detectability, as noted earlier by Lindquist et al. (2014).
A shortcoming of the surrogate data advocated in this study (Prichard, 1994) from which the constrained surrogate data as used in Chang and Glover (2010) and Zalesky et al. (2014) also suffers, is that the null-hypothesis under which the surrogates are generated is more specific than the null-hypothesis in which we are interested, namely, that of the absence of dFC. More specifically, the surrogate null-hypothesis is equivalent with the data being stationary. Although this implies the absence of dFC, the latter does not imply stationarity of the data. So when dFC is detected using either one of the two kinds of surrogate data, the only conclusion we can draw is that the data is non-stationary. This is a rather serious obstacle in the detection of dFC which is further complicated by the possibility that dFC influences the dynamics of the individual BOLD-fMRI time series so that the dynamics of the correlation time series and those of the individual BOLD-fMRI time series are entangled. Another possibility is that the signal-to-noise ratio of the BOLD-fMRI processes changes during the scanning period, which will impact the observed correlation values, although the true correlation might as well be static (Hutchison et al., 2013a). We thus see that the detection of dynamic FC is far from trivial. A possible way out is explored in Lindquist et al. (2014), and consists of fitting a parametric model to the data that takes into account possible non-stationarities and changing variances in the individual time series.
Several studies have reported correlations between fluctuations in BOLD-fMRI and measures derived from electrophysiological recordings as well as behavioral measures (Tagliazucchi et al., 2012, Di and Biswal, 2015, Di and Biswal, 2013, Chang et al., 2013, Thompson et al., 2013). For example, in Tagliazucchi et al. (2012), fluctuations in functional connectivity were found to be correlated with EEG power in different frequency bands. As another example, in Di and Biswal (2015), it was found that fluctuations in functional connectivity within several resting-state networks correlated with the level of activity of the respective networks. The presence of such correlations by itself however, cannot be taken as evidence that the functional correlations themselves are dynamic, and the same applies to studies that report differences in dFC between conditions (Sakoglu et al., 2010). What makes these studies interesting, in our opinion, is that they suggest that the coordination between BOLD-fMRI time series covaries with electrophysiological processes, thereby extending studies that investigate electrophysiological correlates, for example, EEG alpha power (Laufs et al., 2003, Moosmann et al., 2003, Gonçalves et al., 2006), of individual BOLD-fMRI time series. Thus, we do not claim that observed fluctuations in sample dFC test statistics are uninteresting or uninformative because the above cited studies clearly demonstrated that they are. What we do claim, however, is that without proper statistical testing, such fluctuations cannot be interpreted as dynamic FC because dynamic FC has a specific statistical meaning. This leads one to the important question whether a description of resting-state BOLD-fMRI data in terms of (time dependent) FC is the most natural or meaningful one. We come back to this question after clarifying the nature of a description of the data in terms of statistical moments.
An important issue which might lead to confusion and should therefore be addressed carefully, is the following: Suppose we have at our disposal a powerful statistical method which, when applied to a particular dataset, is unable to reject the null hypothesis of static FC. How is this consistent with the highly dynamic nature of neural interactions? Indeed, at rest, the dynamics of neural networks is extremely complex, non-linear, and dynamic (Destexhe et al., 2003, Destexhe and Contreras, 2006). To reconcile the two, we point out that a statistical description of the data by itself does not claim anything about the dynamical nature of the underlying system. Rather, statistical descriptions are often adopted in the absence of explicit deterministic descriptions and therefore often reflect a lack of knowledge of the internal workings of the system. The crucial point now is that only within a statistical description of the data, the notion of stationarity (or the lack thereof) has meaning since it is an inherently statistical concept (it means that the transition probability densities of a stochastic process are time-independent). In fact, it is the complexity and large number of degrees of freedom itself that allow us to adopt a statistical description of the systems’ dynamics in the first place. Thus, in our study, we do not claim that the absence of dFC implies stationarity of the system itself, since this notion has no meaning outside a statistical framework. The point of our study is this: if one adopts a statistical description of the data and asks if the FC is dynamic, one needs to answer it with the appropriate statistics tools. In the next paragraph, we argue that a purely statistical description of resting-state BOLD-fMRI data might not be the most informative one though.
A provoking question raised by our study is if dynamic functional connectivity is the most natural way to conceptualize the organization of resting-state BOLD fluctuations. This view reflects the assumption that these fluctuations comprise a series of transiently correlated activation patterns. Would it not be more natural to view them as a series of instantaneous patterns of which dFC is a derivative? Such co-activation patterns could be the building blocks of spontaneous BOLD activity and dFC a reflection of these. Such a viewpoint is taken, for example, in Majeed et al. (2011) and Liu and Duyn (2013) (see Hutchison et al., 2013a for a review). There is experimental evidence that supports this view. In Logothetis et al. (2012), the authors simultaneously recorded BOLD-fMRI and hippocampal local field potentials in macaques and used the recorded hippocampal ripples as triggers to average the BOLD time series. Their main finding was that hippocampal ripples induce distributed BOLD responses, with positive responses in neocortex and negative responses in sub-cortical structures. Another example is given in Hasson et al. (2004), in which subjects viewed a movie during fMRI acquisition. By averaging the BOLD signals over selective movie frames, they found specific co-activation patterns corresponding to faces, buildings, etc. Such observations suggest co-activation patterns to be the hemodynamic correlates of neural and cognitive events.
The following are the supplementary data related to this article.
Acknowledgments
No. 295129 by the Spanish Research Project SAF2010-16085, the CONSOLIDER-INGENIO 2010 Program CSD2007-00012, and the FP7-ICT BrainScales. The authors declare no competing financial interests. DM holds a Sir Henry Dale Fellowship jointly funded by the Wellcome Trust and the Royal Society (101253/Z/13/Z).
References
- Allen E.A., Damaraju E., Plis S.M., Erhardt E.B., Eichele T., Calhoun V.D. Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex. 2014;24(3):663–676. doi: 10.1093/cercor/bhs352. (March) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barttfeld P., Uhrig L., Sitt J.D., Sigman M., Jarraya B., Dehaene S. Signature of consciousness in the dynamics of resting-state brain activity. Proc. Natl. Acad. Sci. 2015;112(3):887–892. doi: 10.1073/pnas.1418031112. (January) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C., Glover G.H. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. NeuroImage. 2010;50(1):81–98. doi: 10.1016/j.neuroimage.2009.12.011. (March) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang Catie, Liu Zhongming, Chen Michael C., Liu Xiao, Duyn Jeff H. EEG correlates of time-varying BOLD functional connectivity. NeuroImage. 2013;72:227–236. doi: 10.1016/j.neuroimage.2013.01.049. (May) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cribben I., Haraldsdottir R., Atlas L.Y., Wager T.D., Lindquist M.S. Dynamic connectivity regression: determining state-related changes in brain connectivity. NeuroImage. 2012;61(4):907–920. doi: 10.1016/j.neuroimage.2012.03.070. (July) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G., Ponce-Alvarez A., Mantini D., Romani G., Hagmann P., Corbetta M. Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. J. Neurosci. 2013;33(27):11239–11252. doi: 10.1523/JNEUROSCI.1091-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G., Ponce-Alvarez A., Hagmann P., Romani G., Mantini D., Corbetta M. How local excitation-inhibition ratio impacts the whole brain dynamics. J. Neurosci. 2014;34(23):7886–7898. doi: 10.1523/JNEUROSCI.5068-13.2014. (June) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A., Contreras D. Neuronal computations with stochastic network states. Science. 2006;314(5796):85–90. doi: 10.1126/science.1127241. (October) [DOI] [PubMed] [Google Scholar]
- Destexhe A., Rudolph M., Paré D. The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 2003;4(9):739–751. doi: 10.1038/nrn1198. (September) [DOI] [PubMed] [Google Scholar]
- Di X., Biswal B.B. Modulatory interactions of resting-state brain functional connectivity. PLoS One. 2013;8(8) doi: 10.1371/journal.pone.0071163. (January) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di X., Biswal B.B. Dynamic brain functional connectivity modulated by resting-state networks. Brain Struct. Funct. 2015;220:37–46. doi: 10.1007/s00429-013-0634-3. (September) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K.J. Functional and effective connectivity: a review. Brain Connect. 2011;1(1):13–36. doi: 10.1089/brain.2011.0008. (January) [DOI] [PubMed] [Google Scholar]
- Goense J.B.M., Logothetis N.K. Neurophysiology of the BOLD fMRI signal in awake monkeys. Curr. Biol. 2008;18(9):631–640. doi: 10.1016/j.cub.2008.03.054. (May) [DOI] [PubMed] [Google Scholar]
- Gonçalves S.I., De Munck J.C., Pouwels P.J.W., Schoonhoven R., Kuijer J.P.A., Maurits N.M., Hoogduin J.M., Van Someren E.J.W., Heethaar R.M., Lopes Da Silva F.H. Correlating the alpha rhythm to BOLD using simultaneous EEG/fMRI: inter-subject variability. NeuroImage. 2006;30(1):203–213. doi: 10.1016/j.neuroimage.2005.09.062. (March) [DOI] [PubMed] [Google Scholar]
- Hagmann P., Cammoun L., Gigandet X., Meuli R., Honey C.J., Wedeen Van J., Sporns O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008;6(7):e159. doi: 10.1371/journal.pbio.0060159. (July) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handwerker D.A., Roopchansingh V., Gonzalez-Castillo J., Bandettini P.A. Periodic changes in fMRI connectivity. NeuroImage. 2012;63(3):1712–1719. doi: 10.1016/j.neuroimage.2012.06.078. (November) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson U., Nir Y., Levy I., Fuhrmann G., Malach R. Intersubject synchronization of cortical activity during natural vision. Science. 2004;303:1634–1640. doi: 10.1126/science.1089506. [DOI] [PubMed] [Google Scholar]
- Hutchison R.M., Womelsdorf T., Allen E.A., Bandettini P.A., Calhoun V.D., Corbetta M., Della Penna S., Duyn J.H., Glover G.H., Gonzalez-Castillo J., Handwerker D.A., Keilholz S., Kiviniemi V., Leopold D.A., de Pasquale F., Sporns O., Walter M., Chang C. Dynamic functional connectivity: promise, issues, and interpretations. NeuroImage. 2013;80:360–378. doi: 10.1016/j.neuroimage.2013.05.079. (October) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison R.M., Womelsdorf T., Gati J.S., Everling S., Menon R.S. Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Hum. Brain Mapp. 2013;34(9):2154–2177. doi: 10.1002/hbm.22058. (September) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones D.T., Vemuri P., Murphy M.C., Gunter J.L., Senjem M.L., Machulda M.M., Przybelski S.A., Gregg B.E., Kantarci K., Knopman D.S., Boeve B.F., Petersen R.C., Jack C.R. Non-stationarity in the “resting brain’s” modular architecture. PLoS One. 2012;7(6) doi: 10.1371/journal.pone.0039731. January. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang J., Wang L., Yan C., Wang J., Liang X., He Y. Characterizing dynamic functional connectivity in the resting brain using variable parameter regression and Kalman filtering approaches. NeuroImage. 2011;56(3):1222–1234. doi: 10.1016/j.neuroimage.2011.03.033. (June) [DOI] [PubMed] [Google Scholar]
- Keilholz S., Magnuson M.E., Pan W.-.J., Willis M., Thompson G. Dynamic properties of functional connectivity in the rodent. Brain Connect. 2013;3(1):31–40. doi: 10.1089/brain.2012.0115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laufs H., Kleinschmidt A., Beyerle A., Eger E., Salek-Haddadi A., Preibisch C., Krakow K. EEG-correlated fMRI of human alpha activity. NeuroImage. 2003;19:1463–1476. doi: 10.1016/s1053-8119(03)00286-6. (August) [DOI] [PubMed] [Google Scholar]
- Leonardi N., Richiardi J., Gschwind M., Simioni S., Annoni J.-M., Schluep M., Vuilleumier P., Van De Ville D. Principal components of functional connectivity: a new approach to study dynamic brain connectivity during rest. NeuroImage. 2013;83:937–950. doi: 10.1016/j.neuroimage.2013.07.019. (December) [DOI] [PubMed] [Google Scholar]
- Leonardi N., Van De Ville D., Leonardi N., Van De Ville D. On spurious and real fluctuations of dynamic functional connectivity during rest. NeuroImage. 2014:1–7. doi: 10.1016/j.neuroimage.2014.09.007. (September) [DOI] [PubMed] [Google Scholar]
- Lindquist M.A., Xu Y., Nebel M.B., Caffo B.S. Evaluating dynamic bivariate correlations in resting-state fMRI: a comparison study and a new approach. NeuroImage. 2014;101:531–546. doi: 10.1016/j.neuroimage.2014.06.052. (November) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X., Duyn J.H. Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proc. Natl. Acad. Sci. U. S. A. 2013;110(11):4392–4397. doi: 10.1073/pnas.1216856110. (March) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis N.K., Guggenberger H., Peled S., Pauls J. Functional imaging of the monkey brain. Nature. 1999;2(6):555–562. doi: 10.1038/9210. [DOI] [PubMed] [Google Scholar]
- Logothetis N.K., Pauls J., Augath M., Trinath T., Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412(12):150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- Logothetis N.K., Eschenko O., Murayama Y., Augath M., Steudel T., Evrard H.C., Besserve M., Oeltermann A. Hippocampal-cortical interaction during periods of subcortical silence. Nature. 2012;491(7425):547–553. doi: 10.1038/nature11618. (November) [DOI] [PubMed] [Google Scholar]
- Majeed W., Magnuson M., Hasenkamp W., Schwarb H., Schumacher E.H., Barsalou L., Keilholz S.D. Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans. NeuroImage. 2011;54(2):1140–1150. doi: 10.1016/j.neuroimage.2010.08.030. (January) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantini D., Gerits A., Nelissen K., Durand J.-B., Joly O., Simone L., Sawamura H., Wardak C., Orban G.A., Buckner R.L., Vanduffel W. Default mode of brain function in monkeys. J. Neurosci. 2011;31(36):12954–12962. doi: 10.1523/JNEUROSCI.2318-11.2011. (September) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantini D., Corbetta M., Romani G.L., Orban G.A., Vanduffel W. Evolutionarily novel functional networks in the human brain? J. Neurosci. 2013;33(8):3259–3275. doi: 10.1523/JNEUROSCI.4392-12.2013. (February) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monti R.P., Hellyer P., Sharp D., Leech R., Anagnostopoulos C., Montana G. Estimating time-varying brain connectivity networks from functional MRI time series. NeuroImage. 2014;103:427–443. doi: 10.1016/j.neuroimage.2014.07.033. (December) [DOI] [PubMed] [Google Scholar]
- Moosmann M., Ritter P., Krastel I., Brink A., Thees S., Blankenburg F., Taskin B., Obrig H., Villringer A. Correlates of alpha rhythm in functional magnetic resonance imaging and near infrared spectroscopy. NeuroImage. 2003;20(1):145–158. doi: 10.1016/s1053-8119(03)00344-6. (September) [DOI] [PubMed] [Google Scholar]
- Pattinson K.T.S., Rogers R., Mayhew S.D., Tracey I., Wise R.G. Pharmacological FMRI: measuring opioid effects on the BOLD response to hypercapnia. J. Cereb. Blood Flow Metab. 2007;27(2):414–423. doi: 10.1038/sj.jcbfm.9600347. (February) [DOI] [PubMed] [Google Scholar]
- Pereda E., Quian R., Bhattacharya J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 2005;77:1–37. doi: 10.1016/j.pneurobio.2005.10.003. [DOI] [PubMed] [Google Scholar]
- Ponce-Alvarez A., Deco G., Hagmann P., Romani G.L., Mantini D., Corbetta M. Resting-state temporal synchronization networks emerge from connectivity topology and heterogeneity. PLoS Comput. Biol. 2015;11(2):e1004100. doi: 10.1371/journal.pcbi.1004100. February. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prichard D. Generating surrogate data for time series with several simultaneously measured variables. Phys. Rev. Lett. 1994;73(7):951–954. doi: 10.1103/PhysRevLett.73.951. [DOI] [PubMed] [Google Scholar]
- Sakoglu U., Pearlson G.D., Kiehl K.A., Wang Y.M., Michael A.M., Calhoun V.D. A method for evaluating dynamic functional network connectivity and task-modulation: application to schizophrenia. Magn. Reson. Mater. Phys. 2010;23:351–366. doi: 10.1007/s10334-010-0197-8. (December) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber T., Schmitz A. Surrogate time series. Phys. D Nonlinear Phenom. 2000;142:346–382. [Google Scholar]
- Tagliazucchi E., von Wegner F., Morzelewski A., Brodbeck V., Laufs H. Dynamic BOLD functional dynamic in humans and its electrophysiological correlates. Front. Hum. Neurosci. 2012;6(December):339. doi: 10.3389/fnhum.2012.00339. (January) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson G.J., Magnuson M.E., Merritt M.D., Schwarb H., Pan W.-J., McKinley A., Tripp L.D., Schumacher E.H., Keilholz S.D. Short-time windows of correlation between large-scale functional brain networks predict vigilance intraindividually and interindividually. Hum. Brain Mapp. 2013;34(12):3280–3298. doi: 10.1002/hbm.22140. (December) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise R. Combining fMRI with a pharmacokinetic model to determine which brain areas activated by painful stimulation are specifically modulated by remifentanil. NeuroImage. 2002;16(4):999–1014. doi: 10.1006/nimg.2002.1146. (August) [DOI] [PubMed] [Google Scholar]
- Zalesky Andrew, Fornito Alex, Cocchi Luca, Gollo Leonardo L., Breakspear Michael. Time-resolved resting-state brain networks. Proc. Natl. Acad. Sci. U. S. A. 2014;111(28):10341–10346. doi: 10.1073/pnas.1400181111. (June) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.