Role of stag beetle jaw bending and torsion in grip on rivals

Abstract

In aggressive battles, the extremely large male stag beetle jaws have to withstand strongly elevated bite forces. We found several adaptations of the male Cyclommatus metallifer jaw morphology for enhanced robustness that conspecific females lack. As a result, males improve their grip on opponents and they maintain their safety factor (5.2–7.2) at the same level as that of females (6.8), despite their strongly elevated bite muscle force (3.9 times stronger). Males have a higher second moment of area and torsion constant than females, owing to an enhanced cross-sectional area and shape. These parameters also increase faster with increasing bending moment towards the jaw base in males than in females. Male jaws are more bending resistant against the bite reaction force than against perpendicular forces (which remain lower in battles). Because of the triangular cross section of the male jaw base, it twists more easily than it bends. This torsional flexibility creates a safety system against overload that, at the same time, secures a firm grip on rivals. We found no structural mechanical function of the large teeth halfway along the male jaws. Therefore, it appears that the main purpose of these teeth is a further improvement of grip on rivals.

1. Introduction

In many animals, males compete with each other over mating rights with ornaments or armaments. Male ornaments are used to convince females of male qualities, and weapons function in male–male battles. Male stag beetles fight each other fiercely over mating rights. While female stag beetles have small, inconspicuous jaws, males develop extremely elongated jaws and strong bite muscles for these battles [1]. Owing to their large bite muscles, males have an exceptionally high bite force (3.9 times stronger than that of females), which may put them at risk of breaking their own jaws [1–3]. When males bite, their bended jaws visibly deform [2], which causes loading (tension, compression, bending and torsion) of the jaw exoskeleton. Next to a risk of mechanical failure (i.e. breaking) of the jaws, such deformations may cause a male to lose grip on its rival.

The bending resistance of a structure is partly determined by its second moment of area (I), which depends on the cross-sectional area and shape. Hence, jaw damage can be prevented by making the exoskeleton thicker. However, the jaws must not become too thick, because their mass is constrained by the cost of running and flying [4,5]. Owing to this trade-off between robustness (which we define here as the ability to resist deformations and to prevent failure) and mass minimization, the tips of the male jaws are so delicate that the beetles have to modulate their bite muscle force to avoid breaking them [2]. A second way to improve the resistance of a structure against bending is adapting its cross-sectional shape. This does not require additional material (and hence mass), but a drawback may be that the resistance against other deformations can decrease. For example, an oval shape is more resistant against bending about its short axis, but less resistant against bending about its long axis, compared with a circular shape with the same area [6]. As a consequence, rhinoceros horns that mainly undergo bending in one direction during fights have evolved an elliptical cross section, whereas horns that are bent in an unpredictable direction are circular [7].

The cross-sectional area and shape also govern the structural resistance against torsion. Depending on the application point, a force can cause a torque on an object, which creates torsion of the object around its longitudinal axis. For example, trees twist in the wind owing to asymmetries in their crown. As a result, their leaves move downwind and cluster, which reduces the drag on the tree [8]. To benefit from the same mechanism, daffodils and sedges have a cross-sectional shape (respectively elliptical and triangular) that twists easily, but is very bending resistant. As a result, daffodils prevent damaging their flowers owing to reduced drag, and sedges avoid self-pollination [8–10]. Also for stag beetles, the functional consequences of torsion are probably different from those of bending: if its jaw shaft bends too much, a male has no firm grip on its rival anymore, yet twisting may affect a strong hold to a much lesser extent.

We investigate how the resistance against bending and torsion varies along the male jaw. Because the jaw tips are so delicate that stag beetles have to reduce their muscle force for tip biting [2], other jaw regions may be specialized for forceful biting. We hypothesize that the reaction force of biting causes less jaw bending than forces in other directions. Further, we examine if and how adaptations for bending resistance affect the torsion resistance, and how this, in turn, affects the jaw grip on rivals in battles. We also compare the bending and torsion resistance between males and females, because female jaws are probably not structurally adapted to withstand high forces [1]. Our goal is to examine whether males invest more in the structural robustness of their jaws than females, and to explore how their weaponry is adapted for their battle conducts. Further, the fluctuation of the different robustness parameters along the jaw shows how the males can use their jaws and what the associated risks are.

2. Material and methods

2.1. Laboratory animals and micro-computed tomography scans

Adult male and female Cyclommatus metallifer individuals were obtained from a commercial dealer (Kingdom of Beetle, Taiwan). This Indonesian species is eager to fight and has male jaws that grow to be as long as the rest of their body [11,12]. The experimental animals were individually housed in plastic containers (39 × 28 × 14 cm), with moist moss to provide humidity and shelter. We provided food (beetle jelly) ad libitum. We euthanized the specimens using carbon dioxide and micro-computed tomography (CT) scanned their heads [13]. The male head was scanned with a Skyscan 1172 micro-CT scanner (voxel size: 4.1 µm; Bruker micro-CT, Kontich, Belgium). We downsized the voxel size to 8.2 µm to facilitate manipulations. The female head was scanned by the Centre for X-ray Tomography of Ghent University (voxel size: 13 µm). We oriented the micro-CT slices normal to the lever arm of biting, and with the X-axis and Y-axis perpendicular and parallel to the bite force, respectively (figures 1b and 2). We will call forces parallel to the X-axis ‘dorsal/ventral’ forces.

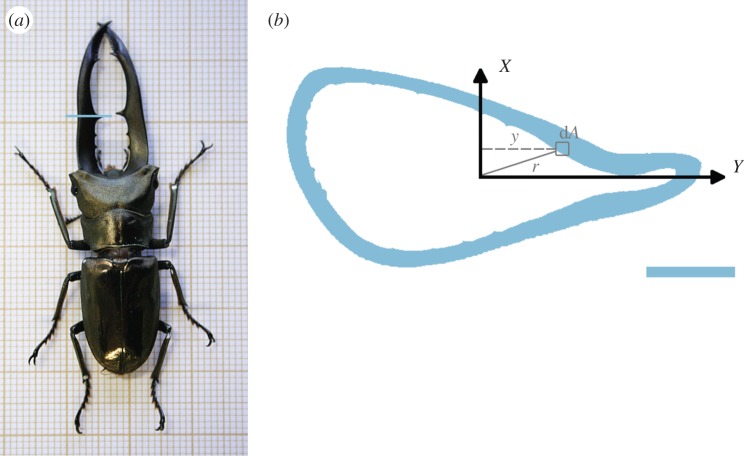
Figure 1.

(a) Picture of male Cyclommatus metallifer stag beetle. (b) Cross section through the jaw exoskeleton at the large tooth (the location is indicated in a). The resistance of this slice against bending about the X-axis (I_y) depends on the distance y to the X-axis of all partial areas dA (see also equation (2.1)). Its resistance against torsion depends on the distance r to the neutral axis of all partial areas dA (see also equation (2.2)). The scale bar indicates 1 mm. (Online version in colour.)

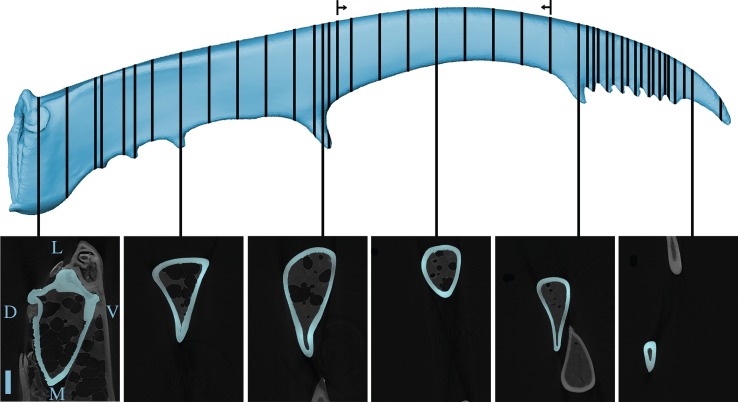
Figure 2.

Top: dorsal view of a stag beetle jaw, with lines on the location of the slices through the male jaw for which I_x, I_y and J were calculated. The arrows show the range of slices that were used to calculate the local buckling moment. Bottom: example of six micro-CT slices on which the cross section of the exoskeleton was determined (depicted in blue). The dorsal (D), ventral (V), lateral (outer jaw side, L) and medial (inner jaw side, M) side of the jaw are shown on the first slice. The scale bar indicates 1 mm. (Online version in colour.)

2.2. Bending and torsion constants

When an object bends, its material stretches at one side, whereas it compresses at the other side. The closer a material is located to the centre of area of the object, the less it deforms. Material exactly at the centre of area (the centroid) does not deform at all, and forms the neutral axis of the object. The bending resistance (or flexural rigidity) of an object is EI, with E the elastic modulus (Young's modulus) of the material and I its second moment of area. I is determined by both the amount of material, and the distance of the material from the neutral axis. Indeed, material further from the neutral axis has to be compressed or stretched more and will therefore offer more resistance. Further, the restoring forces that this material provides have a larger moment because they apply further from the neutral axis [8,14]. The general formula of I for bending about the X-axis with the origin in the centre of area is (figure 1b)

2.1

where y is the perpendicular distance of the infinitesimal element of area dA from the X-axis.

The polar moment of area T is the analogue of I for torsion (twisting): objects with more material further from the neutral axis are more resistant against twisting (figure 1):

2.2

where r is the distance of the infinitesimal element of area dA from the neutral axis. However, in a structure with a non-circular cross section, plane sections do not remain in a plane after twisting (they warp). Therefore, the torsion resistance is quantified numerically, and is called the torsion constant J.

We determined I_x, I_y and J for 24 slices through the male and female jaws, positioned at equal distances between the base and the tip of the jaw (respectively, 1.1 mm and 0.1 mm for the male and the female jaw). For the male jaw, 18 additional slices were chosen manually to ensure a good representation of the entire jaw shape (i.e. at and between the teeth and serrations; figure 2). In Amira, a three-dimensional image processing software program (Amira v. 5.4.4; 64-bit version, FEI, Hillsboro, OR), we selected the pixels that belong to the exoskeleton, with a combination of thresholding based on grey-scale values and manual corrections. With the ‘edge’ function in Matlab (Matlab R2014a, 64-bit version, Natick, MA), we subsequently found the coordinates of the edges of the exoskeleton on each slice. We exported these coordinates to ShapeDesigner (MechaTools Technologies, Quebec, Canada) and subtracted the polygon of the inner exoskeletal edge from the polygon of the outer exoskeletal edge to create the ‘hole’ inside the jaw. Next, we created a triangulated mesh between both edges of the exoskeleton, and we used this to calculate the centre of area, I_x, I_y and J for each slice. Further, we also calculated the area of the exoskeleton in each slice.

I_y determines the bending resistance against the reaction force of ‘pure’ biting (Y-direction, tangent to the turning circle of the jaw tip; figure 1b). I_x is the bending resistance against dorsal/ventral forces (X-direction; figure 1b). The shape factors of I and J are provided by dividing these deformation constants by the square of the cross-sectional area. In this way, identical cross-sectional shapes of different sizes will result in the same shape factor (S_Ix, S_Iy and S_J).

2.3. Critical local buckling load

When a long, thin-walled column is bent, it tends to ovalize. This decreases the second moment of area, which can result in a sudden inwards collapse of the walls. This type of buckling (local buckling) occurs for example when a drinking straw is bent [14]. We calculated the critical local buckling load to exclude the possibility that the male stag beetle jaw would fail by local buckling before the critical bending load is reached. The moment required for local buckling of a thin-walled column is

2.3

where R is the outer radius of the cylinder, t its wall thickness, E the Young modulus (5.1 GPa [2]) and ν the Poisson ratio (0.3 [2]). c is a constant that depends on the material, and usually is about 1 [14]. Obviously, the male jaw is not a perfect column, and hence this formula can only give a rough estimation of the moment that would cause its walls to ovalize and buckle locally. Therefore, we used equation (2.3) only for the slices of the distal part of the jaw, which has an ellipse-shaped cross section (figure 2). In Gimp (Gimp v. 2.6, free software, www.gimp.org), we measured the average wall thickness (of the dorsal, ventral, lateral and medial sides) and the average outer radius (in dorsoventral and mediolateral direction) of each cross section. It is reasonable to assume that if local buckling would occur, it would happen to this distal part of the jaw. The jaw base has a triangular cross-sectional shape which is a lot more bending resistant. Hence, much higher forces would probably be required for local buckling of the jaw base.

2.4. Failure strength experiments

The safety factor of the male jaws was reported by Goyens et al. [2]. To determine the safety factor of the female jaws, we conducted failure experiments. The base of five female jaws (of three individuals) was fixed in epoxy resin, and the jaw tip was loaded until it broke. The applied load was measured by a force transducer (isometric Kistler force transducer type 9203, Winterthur, Switzerland). The signal was subsequently amplified (Kistler charge amplifier type 5058A, Winterthur, Switzerland), and the maximal value was recorded.

3. Results

3.1. Bending and torsion resistance

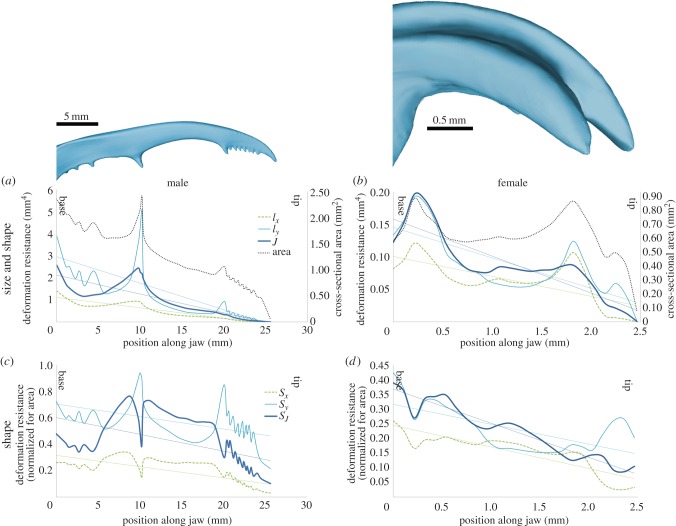
I_x, I_y and J fluctuate along the jaw because of a combination of the effects of the cross-sectional area and the shape of the jaw (figure 3a,b). For males, I_y is higher than I_x over the entire length of the jaw (figure 3a). Hence, their jaws are more robust against bite forces (Y-direction) than dorsal/ventral forces (X-direction). This effect is less pronounced in females (figure 3b). The bending moment, induced by forces at the jaw tip, increases towards the jaw base, because the moment arm decreases. In both sexes, I_x, I_y and J increase with increasing bending moment, but I_y has a higher slope than J and I_x in males only (figure 3a,b and table 1).

Figure 3.

Deformation resistance and cross-sectional area along the jaw of males (a,c) and females (b,d). A linear fit is shown for each parameter. In (a,b), three deformation parameters are compared: resistance against bending caused by biting (I_y), resistance against bending caused by dorsal/ventral forces (I_x) and resistance against torsion (J). In (c,d), the dimensionless shape factors of the deformation resistance parameters are shown. (Online version in colour.)

Table 1.

p-values of ANCOVAs of deformation resistance, with sex as a fixed factor and ‘location along the jaw’ as covariate. Results are given for absolute deformation resistance (I_x, I_y or J) and for the shape factor of the deformation resistance (S_Ix, S_Iy and S_J). Significant p-values are italicized (significance level: 0.05).

	sex	pIx,Iy,J	pslope	pinteraction
shape and area	♂	<0.001	<0.001	<0.001
	♀	0.023	<0.001	0.052
shape	♂	<0.001	<0.001	0.43
	♀	<0.001	<0.001	0.0075

3.2. Shape factor of bending and torsion resistance

By normalizing I_x, I_y and J for the influence of the cross-sectional area, we can interpret the effect of the cross-sectional shape separately. Overall, the shape of the male jaws is clearly more specialized to resist bite forces and torsion than the female jaws: S_Iy and S_J are, respectively, 2.5 and 1.9 times higher in males than in females (averaged over the entire jaw length), whereas S_Ix is only 1.3 times higher in males. Further, over the entire length of the male jaw, its jaw shape resists torsion and bending caused by bite forces more than bending caused by dorsal/ventral forces (S_Iy and S_J > S_Ix; figure 3c and table 1). In both males and females, jaw parts that undergo larger deflecting forces have a better shape (larger S_Ix, S_Iy and S_J near the jaw base; figure 3c,d and table 1). The triangular cross section at the male jaw base elevates I_y (figure 2). Yet, such a triangular cross-sectional shape is far from optimal for torsion resistance (figure 3c), but this is partly compensated by an increased cross-sectional area (compare J and S_J in figure 3a,c). At the distal half of the male jaw (between the large tooth and the serrations at the tip), the jaw has an elliptical cross-sectional shape, which improves the resistance against torsion (figures 2 and 3c). At its medial side, the male jaw has several teeth, all of which increase the resistance against bending when biting. This is particularly prominent for the largest ‘tooth’ on the jaw, located approximately halfway along the jaw. This large tooth also drastically increases the torsion resistance (figure 3a). This high torsion resistance is completely owing to the increased area in the large tooth, because the cross-sectional shape of the tooth is disadvantageous for the torsion resistance (figure 3c).

3.3. Effect of cross-sectional area on deformation resistance

Male jaws have a monotone positive relationship between cross-sectional area and the cross-sectional shape parameters S_Ix, S_Iy and S_J, which is absent in females (figure 4 and table 2). Hence, in those jaw parts where males invest in a higher area, they also adapted the cross-sectional shape to further increase bending and torsion resistance. However, figure 4 also shows that for highest areas (A > 1.6 mm²), S_Iy keeps increasing to the detriment of S_Ix and S_J.

Figure 4.

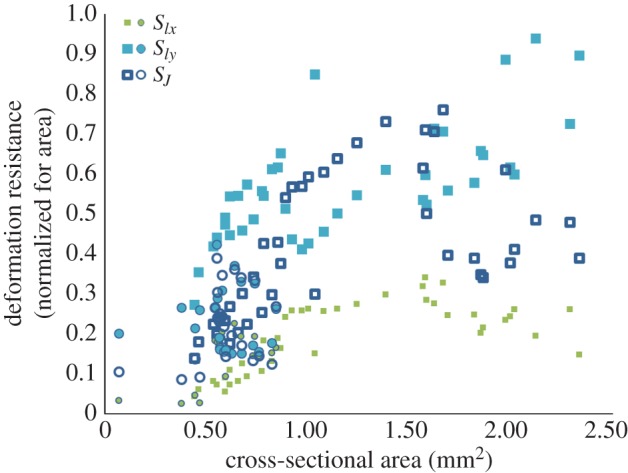
Relationship between the cross-sectional area and the shape factor of the deformation resistance against torsion (S_J) and bending by biting and dorsal/ventral forces (S_Iy and S_Ix). The results are shown for the male (squares) and female jaw (circles). (Online version in colour.)

Table 2.

Results of the Spearman rank correlation tests between the cross-sectional area and the shape factor of the deformation resistance parameters (S_Ix, S_Iy and S_J). The correlation coefficient ρ and the p-value are given for males and females separately. A significant p-value (italicized) indicates a monotone positive correlation.

		ρ	p-value
♂	SIx	0.73	<0.001
	SIy	0.74	<0.001
	SJ	0.67	<0.001
♀	SIx	0.16	0.45
	SIy	−0.23	0.27
	SJ	0.18	0.41

3.4. Local buckling resistance

In the distal jaw part, the moment that would cause local buckling gradually decreases from 0.35 Nm (near the large tooth halfway the jaw) to 0.18 Nm (near the serrations at the jaw tip; figure 5). These moments correspond to forces at the jaw tip of from 23 to 27 N, respectively. The lowest critical force is found halfway along the measured jaw part (17 N; figure 5). All critical forces largely exceed the forces that are generated by the jaws (1.2 N) and that are necessary to break the jaw by bending (6.1 N [2]). Hence, the male jaws will not fail because of local buckling.

Figure 5.

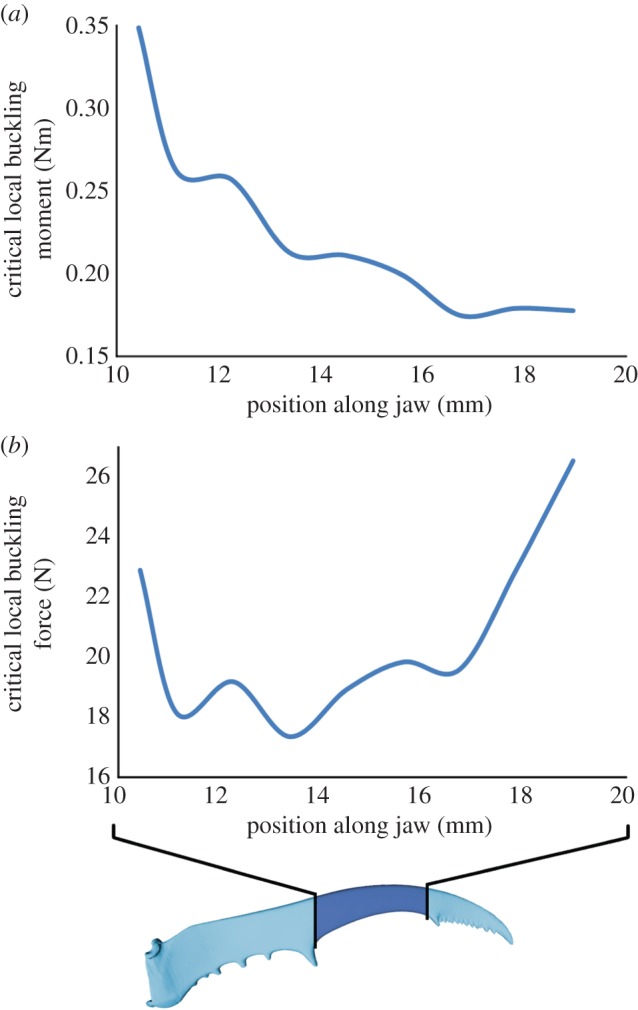
Moment (a) and force (b) that are required for local buckling. (Online version in colour.)

3.5. Male and female safety factors

The safety factor of the male jaws is 5.2 for tip biting and 7.2 for biting at the large tooth halfway along the male jaws [2]. Our failure experiments indicate that a force of 4.6 ± 1.3 N is required to break the female jaws by pushing their tips. This corresponds to an average safety factor of 6.8.

4. Discussion

4.1. Intersexual differences

Because male stag beetles bite forcefully in their pugnacious male–male battles, we expected that their jaws may be adapted to withstand high forces. Females, on the other hand, do not bite forcefully [1]. Because the male and female morphologies are very similar in stag beetle species without sexual dimorphism, female jaws can be used as a representation of a hypothetical male jaw that is not adapted to withstand high forces [5,15,16]. Hence, to test for male jaw adaptations, we compared the resistance against bending, torsion and buckling between male and female jaws. We found several male adaptations that females lack (figure 3). The male jaw robustness is increased in two ways: male jaws have a larger cross-sectional area, and also their cross-sectional shape resists deformations (bending and torsion) better. As a result, males manage to retain their safety factor at approximately the same level as that of female jaws, despite their strongly increased bite muscle force. The safety factors that we measured (5.2–7.2) are comparable to other measurements of male C. metallifer stag beetle jaws (2.05–12.7) and to those of rhinoceros beetle horns (6.5) [17,18].

The enhanced male jaw robustness comes at a cost, because the enlarged male jaw area demands material investment and the additional mass increases the energy cost of running and flying [4,5,19,20]. On the other hand, a strong cross-sectional shape has no intrinsic cost. Yet, females do not exploit this option. Hence, it seems that females, as premised, experience no (or only a limited) selection pressure for robust jaws. Females do dig in rotten wood for oviposition; however, this decaying material is probably soft enough not to require high bite forces, nor robust jaws [21–23]. Instead, the female jaw shape may be adapted for cutting, as suggested by their scissor-like appearance [5].

4.2. Adaptations for male biting

The bending resistance of the male jaws is clearly a specific adaptation to withstand their extreme bite force [1]. First, their bending resistance is a lot higher against the reaction force of ‘pure’ biting (I_y) than against dorsal/ventral forces (I_x, figure 3a). Further, the shape of the jaw parts with the largest investment in area is also most bending resistant against biting (at the cost of resistance against other force directions, figure 4). Finally, the bending resistance against biting increases the fastest with increasing bending moment (from the jaw tip to the base, figure 3a).

4.3. Increasing bending moment towards male jaw base

When biting at the jaw tips, the bending moment that the jaws experience increases from the tip to the base. This explains the need for the increase of the bending resistance in both directions (I_x, I_y) towards the jaw base (in males and females, figure 3a,b). The same was observed for the horn of Spanish ibexes, although this may also originate from their habit to clash primarily against the basal sections of their horns [24]. Also in Trypoxylus dichotomus rhinoceros beetles, the bending resistance increases towards the horn base, compared with the middle of the horn. However, it remains unexplained why their bending resistance also increases towards the tip of the horn [25]. The high cross-sectional area at the male stag beetle jaw base is partly responsible for the high bending and torsion resistance at that location (figure 3a). The triangular shape further increases the bending resistance (figure 3c), and hence secures a firm grip on the opponent. However, a triangular cross-sectional shape drastically decreases the torsion resistance at the jaw base (figure 3c). This is functional for the male grip by providing a safety system against overload, rather than being a cost of the high bending resistance.

4.4. Torsional safety system against overload to maintain grip

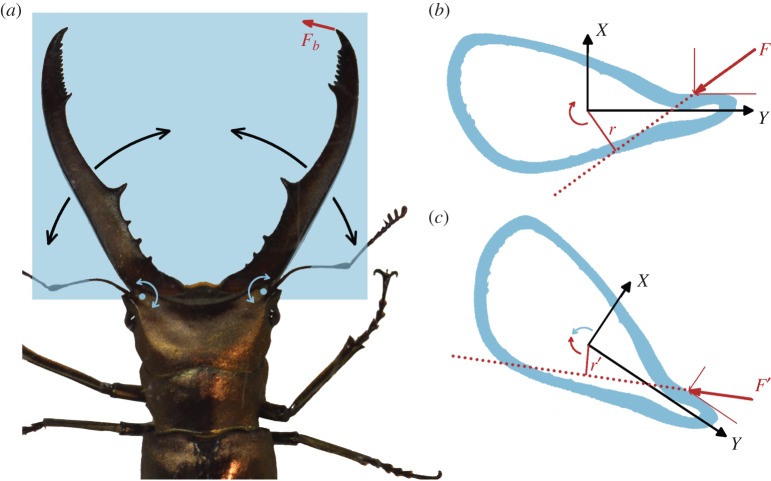
The stag beetle jaws, like those of other beetles, are a one-degree of freedom rotational system, containing a bite muscle that rotates the jaw about a single hinge axis [1,26,27]. Hence, it has a single operational plane, with the bite force vector tangent to the turning circle of the bite point (figure 6a). A naive optimization would be to use all cuticular material to resist bending in this plane (i.e. a very flat cross section). Yet, in this situation, the slightest deviation of the bite force vector out of this operational plane (owing to the shape and texture of the contact surface [3]) would cause failure. In the violent and unpredictable stag beetle battles, such deviations are common [3,12]. Male stag beetles avoid failure in two ways. First, the jaw is resistant against bending in other force directions as well (figure 3a), although this is limited by the investment it requires in jaw material and mass. Second, the low torsion resistance at the jaw base may provide a safety system against overload while retaining grip on the rival (figures 6b,c and 7). The lower the torsion resistance, the more the jaw will twist when a torque is applied (for a rough estimation of the resulting twist, see electronic supplementary material). Owing to the torsional material deformations, an internal moment is generated that will finally balance the applied torque. As a result of the deformation, however, the torque is reduced, meaning that the remaining force components are reduced and have changed orientation (figure 6b,c). As a result, less bending will occur. This is advantageous for the male stag beetles: when their jaws bend, they lose grip on their rival, which is not (or at least less) the case when twisting. The safety system is well positioned at the jaw base, where the bending moment is largest.

Figure 6.

Torsional safety system against overload in the male stag beetle jaw. (a) Photo of a male stag beetle and the operation plane of its jaws. The jaw hinges are indicated by blue dots. Black curved arrows show how the jaws can rotate. The bite force vector F_b is directed tangent to the turning circle of the jaw tip. (b) Transverse cross section through one of the jaws. The force F causes a negative (clockwise) moment (|F| . |r|) on the jaw. (c) Because of its torsional flexibility, the jaw twists owing to this moment, until the internal moment balances the remaining external moment (|F'| . |r'|). (Online version in colour.)

Figure 7.

Picture of fighting male stag beetles. The jaws of the lifted male are twisted around the jaw base of the male on the ground. (Online version in colour.)

4.5. Role of the large tooth halfway along the jaws

Male C. metallifer stag beetles have a very conspicuous tooth halfway along their jaws (figure 1a). This large ‘tooth’ has a very high bending resistance because of its high cross-sectional area, and owing to its shape. In general, the available material is most efficiently used if the bending resistance increases continuously with the bending moment [14]. Because the bending moment increases linearly from the jaw tip to the base, a local peak in bending resistance at the tooth is not useful from this mechanical point of view. Hence, we cannot mechanically explain the role of the large tooth on the male jaw. The large tooth, as well as the other smaller teeth, probably primarily serve to improve the grip on the rival. Owing to these teeth, male stag beetles prevent their opponents from slipping away, towards the jaw tips. A firm grip is not only indispensable to dislodge and lift rivals successfully [12]. The capacity to retain a competitor near the jaw base also enables males to pinch them forcefully, because their bite force is higher at the jaw base owing to a shorter output lever arm [1].

5. Conclusion

We found several adaptations of the male stag beetle jaw for failure prevention and to increase its grip on rivals. Male jaws have an enhanced bending and torsion resistance. These are due both to an increased cross-sectional area (at the cost of material and locomotion energy) and to an enhanced cross-sectional shape. The jaw is especially adapted to withstand deformations owing to the force direction of biting. Compared with females, the bending and torsion resistances are not only elevated, but the bending resistance for the force direction of biting also increases considerably faster with increasing bending moment towards the jaw base. At this jaw base, a firm hold on the opponent is further secured, because the bending resistance exceeds the torsion resistance. The teeth on the male jaws do not enhance the overall structural rigidity. Instead, they probably mainly serve to improve grip on rivals, comparable to the serrations on nutcrackers.

Ethics

Our experiments were approved by the ethical committee of the University of Antwerp (approval no. 2011-63) and conducted to conform with the legal requirements.

Data accessibility

The dataset has been uploaded to the Dryad Digital Repository (doi:10.5061/dryad.32535).

Authors' contributions

J.G. executed the micro-CT scans, determined local buckling resistance and measured the bending and torsion constants. J.G., J.D., M.P. and P.A. analysed and interpreted the findings and revised the article.

Competing interests

We declare we have no competing interests.

Funding

This study was supported by a BOF grant (IDBOFUA 2011-445-a) of the Research Council of the University of Antwerp. The SkyScan1172 high-resolution micro-CT scanner, located at the VUB facilities, was funded by the Hercules Foundation (grant no. UABR/11/004). The micro-CT reconstructions of the jaw were provided by the Centre for X-Ray Tomography, Ghent University.