Physical limits on bacterial navigation in dynamic environments

Abstract

Many chemotactic bacteria inhabit environments in which chemicals appear as localized pulses and evolve by processes such as diffusion and mixing. We show that, in such environments, physical limits on the accuracy of temporal gradient sensing govern when and where bacteria can accurately measure the cues they use to navigate. Chemical pulses are surrounded by a predictable dynamic region, outside which bacterial cells cannot resolve gradients above noise. The outer boundary of this region initially expands in proportion to the square root of time before rapidly contracting. Our analysis also reveals how chemokinesis—the increase in swimming speed many bacteria exhibit when absolute chemical concentration exceeds a threshold—may serve to enhance chemotactic accuracy and sensitivity when the chemical landscape is dynamic. More generally, our framework provides a rigorous method for partitioning bacteria into populations that are ‘near’ and ‘far’ from chemical hotspots in complex, rapidly evolving environments such as those that dominate aquatic ecosystems.

1. Introduction

In natural environments such as oceans and lakes, bacteria and other microbes navigate chemical landscapes that can change dramatically over the time scales relevant to their motility [1]. Such environments differ in fundamental ways from the static chemical gradients typically considered in studies of microbial chemotaxis (e.g. [2,3]). From the perspective of microbes, chemical cues in nature often appear as localized pulses with short duration [4,5]. For example, oil droplets from spills and natural seeps, organic matter exuded by lysed phytoplankton or excreted by other organisms, and marine particles are common sources of short-lived, micro-scale (approx. 10–1000 µm) chemical pulses [4]. Motile bacteria respond to such cues by swimming up the gradients that are generated when pulses diffuse (e.g. [5–8]). When a pulse appears, for example through the lysis of a phytoplankton cell, the distribution of chemoattractants (often, dissolved organic matter) changes rapidly over both space and time [9]. Because background conditions are highly dilute, bacteria experience the early stages of a spreading pulse as a noisy chemical gradient with low absolute concentration. In marine environments, ephemeral, micro-scale pulses of dissolved chemicals provide a substantial and perhaps dominant fraction of the resources used by heterotrophic bacteria [4,9,10]. The advantage that chemotaxis confers on cells in such dynamic environments [1,11,12] may help explain why chemotactic responses to transient nutrient sources are so common among marine bacteria [5,6,8,10].

Although chemotaxis appears to be an important driver of bacterial competition [1], evolution [11,12] and nutrient cycling [4,9], the details of bacterial chemotaxis behaviour are poorly characterized for all but a few well-studied species of bacteria. An important shared feature of bacterial chemotaxis systems, however, is that the measurements of chemical concentration that underpin chemotaxis behaviour are subject to considerable noise [13,14]. In particular, stochasticity in the times at which individual molecules of chemoattractant arrive at the bacterium's surface sets an upper bound on the precision with which the cell can measure changes in concentration [15,16]. Here, we demonstrate how this physical limit on the precision of temporal gradient sensing constrains when and where bacteria can respond to chemical pulses. Using this approach, we develop a general theory to predict the fundamental length and time scales over which chemotactic bacteria can respond to chemical pulses. Because it requires few assumptions about the underlying mechanisms responsible for chemotactic behaviour, the theory can be applied to the diverse assemblages of bacteria that occur in natural marine and freshwater environments.

We first discuss gradient estimation by a cell in a dynamic chemoattractant field. We then derive theoretical bounds on the regions of the environment in which bacteria can respond to gradients and characterize the spatio-temporal evolution of these regions as a function of physical and biological parameters. Finally, we show that changes in swimming speed in response to measurements of absolute concentration—a bacterial behaviour known as chemokinesis [10,17]—can greatly enhance a cell's ability to measure gradients in a dynamic chemoattractant field.

2. Model development

2.1. Signal and noise in temporal gradient sensing

Unlike large eukaryotic cells, which can directly measure spatial gradients in chemical concentration [18], many chemotactic bacteria navigate by measuring temporal changes in concentration as they swim [19,20]. They use these measurements to detect concentration gradients and to navigate towards more favourable conditions (towards resources, away from noxious substances). Regardless of the biochemical and behavioural mechanisms a cell uses to navigate, gradient-based navigation can only be as precise as a cell's estimate of the gradient itself; downstream transduction will, in general, only add noise [16]. One can, therefore, establish performance bounds within which real bacterial cells must operate by considering physical limits on the accuracy and precision of gradient sensing by an idealized cell. We begin by considering gradient detection by such a cell: the perfectly absorbing sphere originally described by Berg & Purcell [15]. This cell swims through a dynamic chemoattractant landscape, absorbing all molecules that reach its surface (figure 1a). In reality, bacteria absorb some ligands they use for chemotaxis, whereas others are bound only temporarily. However, absorbing ligand always leads to more accurate measurement of both absolute concentration and changes in concentration over time because molecules cannot be re-bound once they have been absorbed [13,18]. We therefore assume molecules are absorbed yielding an upper limit on measurement accuracy [18].

Figure 1.

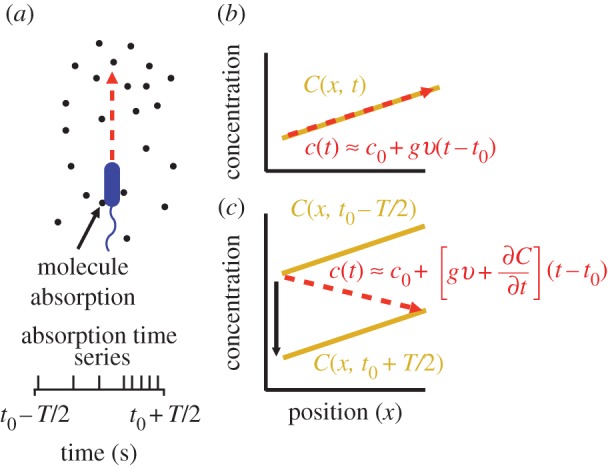
Measurement of ramp rate c₁ by an idealized cell. (a) During a time interval of length T, a cell travels from a region of low concentration to a region of higher concentration, absorbing chemoattractant molecules at times {t_i} (spikes in absorption time series). (b) In a static concentration field C(x), c₁ is equal to concentration slope g (slope of solid orange line) multiplied by swimming speed v. (c) In a dynamic concentration field C(x, t), 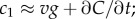g is confounded with temporal changes in concentration (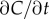) and the cell may perceive a decreasing concentration (red dashed line) although the true concentration slope is positive. (Online version in colour.)

Like the well-studied enteric bacterium Escherichia coli, marine bacteria perform chemotaxis by altering the length of relatively straight ‘runs’, which are interspersed with random re-orientation events (‘tumbles’ for E. coli [21], ‘flicks’ for marine bacteria [22,23]). As a cell swims, receptors on the cell's surface bind chemoattractant molecules and a signal from the receptors is transduced through a biochemical network to one or more flagellar motors, which control the speed and direction of the flagellar rotations that drive locomotion. Changes in receptor occupancy alter the probability that the direction of flagellar rotation will reverse, leading to a re-orientation [24], and the outcome of this is that bacteria extend runs when they perceive an increasing concentration of chemoattractant. A requirement for chemotaxis, therefore, is that the cell is capable of detecting meaningful changes in mean concentration [14] over some measurement interval of length T. This task is complicated by significant stochastic variation in the times at which molecules arrive at the cell's surface. The length of the measurement interval T is bounded above by the characteristic time scale of stochastic re-orientations (e.g. rotational diffusion, active re-orientation [15]), which for cells in the size range of E. coli and many marine bacteria ranges from hundreds of milliseconds [5] to several seconds [25]. A cell has little to gain by using the history of molecule encounters that extends beyond this time scale because rotational diffusion and active stochastic reorientation (e.g. tumbles, flicks) cause random changes in the cell's trajectory, decorrelating the cell's orientation and rendering old information useless to the cell for determining whether it is currently travelling up or down a chemoattractant gradient (this issue is discussed in detail in [15]). We therefore assume that the measurement time scale T is shorter than the time scale of stochastic reorientation and neglect processes such as rotational diffusion. For such short T, the chemoattractant concentration along the swimming cell's path, c(t), can be linearized to 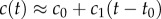over the time interval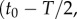 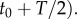The cell experiences this concentration as a noisy time series of encounters with chemoattractant molecules (figure 1a), from which it must estimate the concentration ramp rate, c₁, to determine whether concentration is increasing or decreasing.

Using maximum likelihood, one can show that the optimal way for a perfectly absorbing sphere of radius a to estimate c₁ (concentration × time⁻¹) using a sequence of molecule absorptions is, to leading order [13]:

where 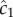is the cell's estimate of the ramp rate, n is the number of molecules absorbed over the measurement interval, D is the diffusivity of the chemoattractant and t_i is the absorption time of the ith molecule. Importantly, 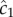has typical measurement variance no less than:

2.1

where c₀ is the true background concentration in the vicinity of the cell at time t₀, and the variance of 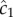does not depend on the true ramp rate c₁ as long as 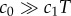(electronic supplementary material; see also [13, eqn (S44)]). This formulation assumes that a cell can ‘count’ many molecules in a typical observation window, which amounts to assuming that the time scale on which receptors bind chemoattractant molecules is fast relative to the length of the observation window, T. Receptor binding kinetics are typically very fast (millisecond time scales, e.g. [24,26]), so this assumption will generally hold unless T is extremely short. To summarize, measurements of concentration involve three time scales that are relevant to our model formulation, which are naturally separated in chemotactic bacteria [24]: (1) the time scale of absorptions, which is typically short (approx. 1 ms [24]), (2) the measurement window T, which is of intermediate length, and (3) the time scale of active re-orientations, which must be longer than T if the bacterium is to perform chemotaxis [15].

Variance in the ramp rate estimate (equation (2.1)) is solely due to stochastic arrivals of chemoattractant molecules and does not include additional sources of noise resulting, for example, from noise in the biochemical network responsible for ramp rate estimation [16,27]. Equation (2.1) thus provides a lower bound on uncertainty about the true ramp rate and a constraint within which real cells must operate, regardless of the precise biochemical mechanism through which they implement ramp rate estimation. Below we use equation (2.1) to define the regions of space where it is possible for cells to use measurements of concentration to climb chemoattractant gradients. Outside these regions, cells may attempt to perform chemotaxis; however, we will show that, for several ecologically relevant types of pulses, the signal-to-noise ratio (SNR) of a cell's estimate of the concentration slope decays sharply (like a Gaussian) far from the origin of a chemoattractant pulse. This strong decrease in the SNR with increasing distance implies that chemotactic cells far from the origin of a pulse will be responding primarily to noise and will not exhibit biased motion.

2.2. Gradient estimation in a time-varying environment

For a cell swimming at speed v, the instantaneous local slope of the concentration profile along the cell's path, which we will refer to as the concentration slope g, is given by 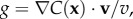where v is the cell's velocity. The concentration slope is the quantity that is useful for climbing gradients, for example, by providing a signal for cells to lengthen runs in run-and-tumble chemotaxis [21]; however, a cell the size of a bacterium (approx. 1 µm) cannot measure g directly [13]. It must instead infer g from its estimate of the ramp rate 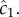In a time-invariant concentration field c₁ = gv, and the maximum-likelihood estimator of g is proportional to the ramp rate estimator: 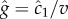(figure 1b; electronic supplementary material).

In a time-varying environment, the concentration that a swimming cell experiences, 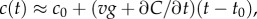is influenced by local temporal changes in concentration, 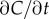(figure 1c); the ramp rate is given by 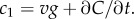In this case, the time series of molecule absorptions does not contain the information needed to estimate both g and 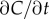, and any estimator the cell uses to measure the concentration slope g will be biased (electronic supplementary material). For example, estimating g as 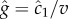means that 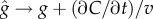in the limit of many molecule absorptions. Correcting this bias would require that the cell has an independent estimate of 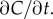In the absence of such an estimate, the cell can reduce bias by travelling faster, but not by increasing the length of its measurement window T (electronic supplementary material). This highlights an important connection between swimming speed and measurement accuracy that we explore in more detail below. Bias in the concentration slope estimate becomes important far from the origin of a pulse, where cells can perceive an increasing concentration even if they are travelling down the concentration gradient, and near the origin, where cells can perceive a falling concentration even if they are travelling up a gradient (figure 1c).

2.3. Conditions for chemotaxis and responses to chemical pulses

If a cell is to use measurements of ramp rate to climb a concentration gradient, two conditions must be met. First, the cell must be in a region of the environment where typical values of the perceived ramp rate exceed noise: i.e. the SNR of the ramp rate estimator, 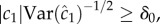where δ₀ is a constant threshold on the SNR (electronic supplementary material). Second, the ramp rate 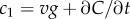and the concentration slope g must have the same sign. Applying equation (2.1) and rearranging, these conditions are:

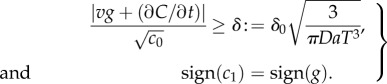2.2

For a chemoattractant field with concentration C(x, t), conditions (2.2) define the regions where cells can reliably determine the sign of the concentration slope, a requirement for gradient-based navigation.

Using conditions (2.2), we explore how bacteria perceive three types of pulses that occur in natural environments: pulses that arise from surfaces, pulses that arise as thin chemical filaments and pulses created by small point releases. Localized point pulses are created by many natural sources, including the lysis of small cells and excretions by larger organisms [4,5]. Thin chemical filaments and sheets occur when turbulence stirs dissolved chemicals. The distribution of chemicals is stretched and folded into sheets and filaments at length scales down to the Batchelor scale [4]. Mixing below the Batchelor scale is dominated by diffusion. This length scale is 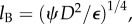where ψ is kinematic viscosity and is the turbulent dissipation rate. As changes, l_B changes slowly, implying that small point pulses and filaments or sheets spread primarily by diffusion across a broad range of flows. Across a range of realistic levels of turbulence (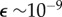 to 10⁻⁶ W kg⁻¹ [28]) the average shear rate is of order 10⁻³ to 1 s⁻¹. Except for the highest values in this range, these shear rates are typically too low to cause significant re-orientation of bacteria as they swim [29]. We therefore focus on the regime in which the effects of flow on bacterial re-orientation can be neglected for the length scales considered here.

To illustrate the utility of our theory, we consider how bacteria respond to chemical point pulses, filaments and sheets. These canonical geometries can be viewed as basic components of more complex chemical landscapes at larger scales (e.g. the types of landscapes considered in [1]). Extending our results to alternative geometries follows from straightforward calculations. At time t = 0, a single pulse appears with planar (N = 1, sheet), cylindrical (N = 2, filament) or spherical (N = 3, point pulse) symmetry. The size of the pulse is M (molecules per unit area of sheet [N = 1], per unit filament length [N = 2] or per individual point pulse [N = 3]). The three-dimensional chemoattractant field C is governed by 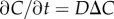and the concentration is:

2.3

where D (µm² s⁻¹) is diffusivity, r (µm) is the distance from the surface (N = 1), filament axis (N = 2) or centre of the point source (N = 3). A cell moving in this chemoattractant field with velocity v (µm s⁻¹) will experience a typical rate of change in concentration of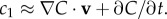

For chemoattractant pulses with concentration described by equation (2.3) (figure 2a, solid orange curve), the SNR (figure 2a, unimodal solid green curve) divides the domain surrounding a pulse into three regions. Far from the pulse, the concentration gradient is shallow and the absolute concentration is low: cells cannot accurately measure changes in concentration because they encounter few molecules during a typical observation window (figure 2b(iii)). At an intermediate distance from the pulse origin, the gradient is largest in magnitude and cells encounter many molecules during a typical observation window: the SNR is greatest in this region (figure 2b(ii)). Near the pulse origin the gradient is again shallow and variance in the concentration slope estimate is substantial (figure 2b(i)). Moreover, in this region, concentration changes rapidly over time and the concentration slope and ramp rate may differ in sign (i.e. bias in the concentration slope estimate is large, figure 2b(i),c).

Figure 2.

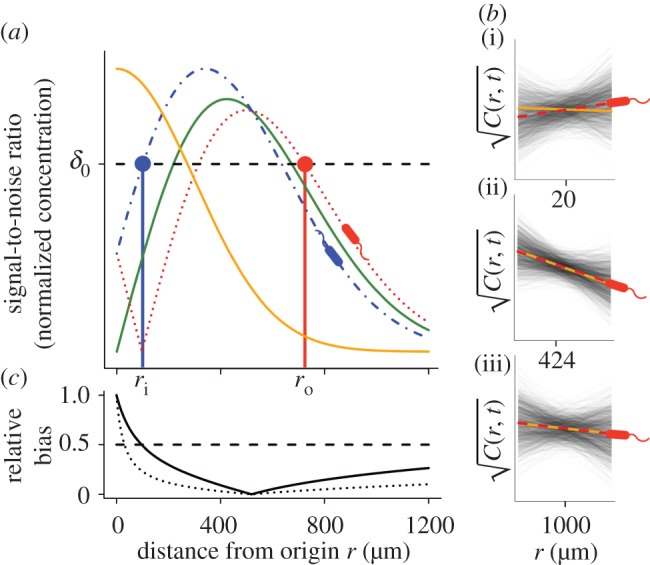
Gradient estimation in a dynamic environment. (a) Solid orange curve shows the true concentration profile at t = t₀. Solid green unimodal curve shows the SNR of 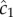a cell would experience if this concentration profile were static. Dotted red curve shows the SNR for a cell swimming directly towards the origin of the pulse. Dash-dot blue curve shows the SNR for a cell swimming directly away from the origin of the pulse. Concentration and SNR normalized to a maximum value of one. (b) Square root of concentration 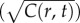at t = t₀ (solid orange line) and individual estimates of this concentration 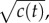semi-transparent grey; mean of estimates shown by dashed red line) made by a cell swimming towards the pulse origin. Each individual estimate is computed by calculating 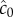and 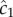(see the electronic supplementary material for equations) from a time series of random Poisson molecule arrivals [30] with an arrival rate given by the true instantaneous concentration at the bacterium's position C(x, t). (c) Relative bias of concentration slope estimate 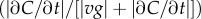measured by slow (solid curve; v = 30 µm s⁻¹) and fast swimming cells (dotted curve; v = 96 µm s⁻¹). In all panels, the concentration is governed by equation (2.3) with N = 3, M = 10¹¹ molecules, v = 30 µm s⁻¹, a = 1 µm, T = 0.1 s, t₀ = 45 s and δ₀ = 1. Pulse sizes in all figures correspond roughly to the quantity of free amino acids released from a lysed phytoplankton cell of approximately 10 µm in diameter [5]. (Online version in colour.)

3. Results

Cells far from a chemoattractant pulse cannot resolve true changes in concentration above noise (figure 2a, SNR drops below threshold δ₀ for large distance). The distance beyond which 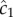becomes dominated by noise is given implicitly by

3.1

where the term in brackets is the magnitude of the true ramp rate c₁ that a cell at distance r with local concentration slope g(r, t) experiences. Because the chemoattractant field is changing, the magnitude of the ramp rate a cell measures will depend on its direction of travel. Far from the pulse, a cell travelling directly inward (figure 2a, red dotted curve) will experience a greater SNR than a cell travelling outward (figure 2a, blue dot-dash curve). Beyond the inflection point in the concentration profile, the r.h.s. of equation (3.1) is maximized for cells travelling directly up the concentration gradient (i.e. towards the pulse centre; figure 2a, red dotted curve). When the SNR threshold, δ₀, is of order one or smaller, the outer boundary beyond which cells cannot reliably perceive changes in concentration is given implicitly by equation (3.1) with 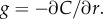We refer to the largest distance that satisfies this equation as the outer boundary of sensitivity, r_o (figure 2a, red point). At distances r > r_o, perceived changes in concentration are dominated by noise, regardless of a cell's direction of travel.

Bacteria use gradients to navigate towards regions of high attractant concentration, but also to maintain position near local maxima [12]. In order to do this, a cell travelling down the concentration gradient must experience a decreasing concentration, which provides the signal the cell uses to modify swimming behaviour [23]. Near the origin, the SNR is maximized for a cell that is travelling directly down the concentration gradient (figure 2a, blue dash-dot curve). For t greater than a critical time, t_s, there is an inner boundary at a distance r_i from the origin of the pulse (figure 2a, blue point), within which the SNR drops below threshold. For t > t_s, the location of this inner boundary is given implicitly by equation (3.1) with 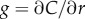(electronic supplementary material).

The boundaries r_o and r_i define a dynamic region (figure 3, blue annular region in inset), outside of which bacteria cannot reliably respond to chemoattractant gradients because either the ramp rate is too noisy to resolve or the ramp rate and the concentration slope have different signs (i.e. conditions (2.2) are violated). Figure 3 shows the dynamics of r_o and r_i for bacteria swimming at three different speeds. For all swimming speeds, the outer boundary r_o initially expands before rapidly contracting (figure 3, red dash, dot and dash-dot curves). The time dependence of this boundary can be obtained by substituting equation (2.3) into equation (3.1), solving for r_o, and expanding the resulting product-log solution (electronic supplementary material):

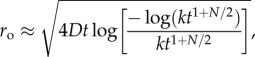3.2

where 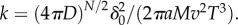Swimming speeds of motile bacteria typically range from 30 µm s⁻¹ to over 100 µm s⁻¹ [10]. For many relevant chemoattractants, D ∼ 10³ µm² s⁻¹, and the number of molecules released in a pulse, M, is generally large; for example, a point pulse created by the lysis of even a small phytoplankton cell (a common source of nutrients for marine bacteria) contains upwards of 10¹¹ free amino acid molecules [5]. This means that 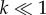such that the logarithmic term in equation (4.2) varies slowly with time for early times, and leading-order behaviour is initially governed by 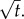Pulse size, M, occurs only inside the logarithmic terms in equation (4.2), indicating that r_o scales weakly with pulse size. For example, doubling the size of a small point pulse (N = 3) increases the volume of water in which gradients are perceived by only 50% (assuming M increases from 10¹¹ to 2 × 10¹¹ molecules, δ₀ = 1, and v = 66 µm s⁻¹). Figure 4 shows the dynamics of r_o for surface, filament and point pulses. Equation (3.2) agrees well with the exact solution for r_o obtained by solving equation (3.1) numerically (figure 4, compare solid and dashed curves).

Figure 3.

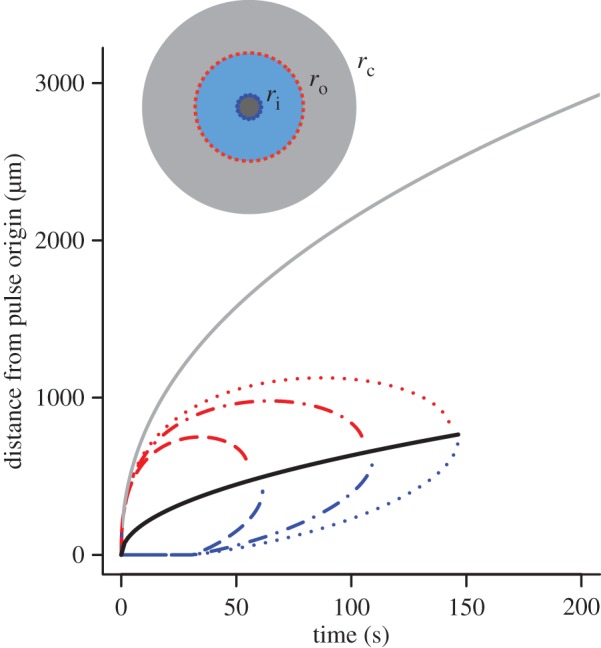
Inner (blue) and outer (red) boundaries of the region in which cells reliably perceive gradients. Dashed line shows v = 30 µm s⁻¹, maximum swimming speeds of E. coli [10]; dashed-dotted line shows v = 66 µm s⁻¹, typical cruising speed of Vibrio coralliilyticus; dotted line shows v = 96 µm s⁻¹, maximum speed of V. coralliilyticus after initiating chemokinesis [17]. Other parameters as in figure 2. Solid grey curve is the outer boundary, r_c, of the region within which cells can resolve absolute concentration. Solid black curve is 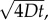the radius at which the SNR is maximized for a static profile (green curve in figure 2). Inset shows relative sizes of the region where cells can detect gradients (r_i < r < r_o, blue region), and the region where cells can resolve absolute concentration (r < r_c, grey region inward) at t = 90 s (v = 66 µm s⁻¹). (Online version in colour.)

Figure 4.

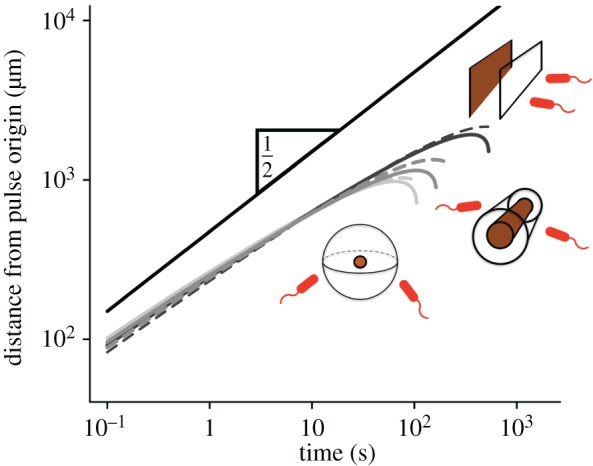
Scaling of the outer boundary of sensitivity r_o for pulses emitted from surfaces (light grey), filaments (grey) and point sources (black). Solid curves are numerical solutions to equation (3.1). Dashed curves are given by equation (3.2). The solid black line is proportional to 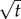. Solid curves are truncated when the SNR falls below δ₀. Dashed curves are truncated at t* (equation (3.3)). M is scaled so that pulses with different geometries have the same concentration profile at t = 10 s (M = 8.0 × 10⁵ molecules per µm² surface for surface source; M = 2.8 × 10⁸ molecules per µm length for line source; M = 10¹¹ molecules for point source); v = 66 µm s⁻¹; other parameters as in figure 2. (Online version in colour.)

Eventually the inner and outer boundaries of sensitivity intersect (figure 3), and cells can no longer reliably glean navigational information from the chemoattractant field. We refer to the time at which this occurs as t*. Finding the time when the SNR falls below threshold δ₀ everywhere shows that

3.3

where 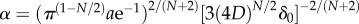and the approximation assumes 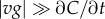at the point in space where the SNR is maximized (electronic supplementary material). This relation illustrates the relative contribution of measurement time T and speed v to the time scale of perceptible changes in concentration, t*. Moreover, equation (3.3) shows that t* is proportional to M^{2/(N + 2)}; the scaling of t* with pulse size is sublinear for all pulse geometries, meaning that doubling the size of a pulse always less than doubles the time over which it can be perceived.

The locations of inner and outer boundaries (figure 3) are governed, in part, by swimming speed. Many bacteria alter swimming speed in response to stimuli, and a natural question, therefore, is whether a cell could adjust its speed adaptively to achieve high sensitivity to chemical gradients. Some species exhibit a behaviour known as chemokinesis: cells swim at a speed that depends on the local concentration of chemoattractant, often swimming at a high speed when absolute concentration is high, and a low speed when concentration is low [10,17]. In the presence of a resolvable gradient, the interpretation of chemokinesis is straightforward: cells can climb the gradient faster if they swim at a higher speed (at the expense of a higher energetic cost of motility). However, chemokinesis may also have a second role. The SNR of the ramp rate is smaller than the SNR of the absolute concentration, c₀, implying that cells may be able to accurately detect whether absolute concentration has crossed a threshold before they can resolve changes in concentration over time. The mean rate of arrival of molecules to the surface of a sphere of radius a is 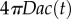[15]. Poisson molecule arrivals imply that the SNR of absolute concentration c₀ is 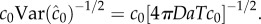Using this ratio, we define a third boundary, r_c, beyond which the SNR of 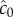falls below the threshold, δ₀:

3.4

where 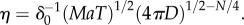This boundary has the same leading-order behaviour in time as r_o, but extends well beyond r_o (figure 3, outer solid grey curve); for example, assuming r_o is at its maximum value (figure 3), the volume within which cells can accurately measure absolute concentration in the water surrounding a small point pulse (N = 3) is six times larger than the volume in which cells can resolve changes in concentration (assuming M = 10¹¹ molecules [5], δ₀ = 1, v = 66 µm s⁻¹). Note that we use the same threshold (δ₀) on the SNR of 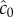and 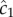for the purpose of comparison but thresholds on these ratios need not be equal.

By increasing their swimming speeds when concentration exceeds a threshold, cells can increase their sensitivity to changes in concentration (first condition (2.2); figure 3) and reduce bias in estimation of the concentration slope (figure 2c). The effect of increasing swimming speed is to expand the region of space over which the cell can resolve gradients, r_i < r < r_o, and to extend the time t* beyond which gradients become too noisy for the cell to measure (figure 3, compare curves for different swimming speeds; figure 5).

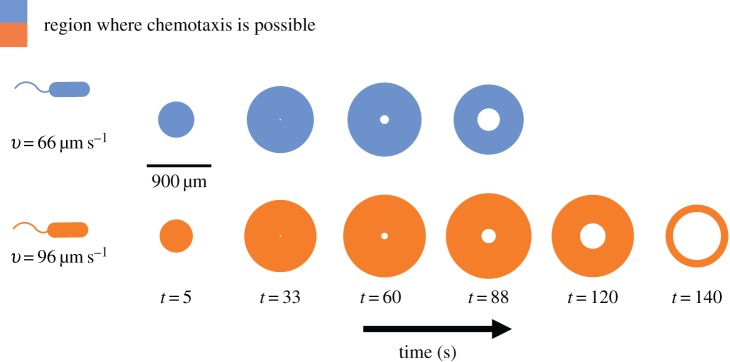
Figure 5.

Effect of swimming speed on the time evolution of the region where chemotaxis is possible. Coloured regions show a two-dimensional cross-section of the region in which cells can resolve chemoattractant gradients (i.e. conditions (2.2) are satisfied). Blue regions are those experienced by a cell travelling at a cruising speed typical of the bacterium V. coralliilyticus (approx. 66 mms⁻¹). Orange regions are those experienced by a V. coralliilyticus cell travelling at a high speed after initiating chemokinesis (approx. 96 µm s⁻¹) [17]. Other parameters as in figure 2. Note the blind spot that forms at the centre of the region as the inner boundary of sensitivity, r_i, expands. (Online version in colour.)

The effects of changes in speed may be substantial. For example, the coral pathogen Vibrio coralliilyticus increases its speed by as much as 45% when chemoattractant concentration is high [17]. The temporal evolution of a chemoattractant pulse appears very different to a bacterium swimming at 66 µm s⁻¹ (typical cruising speed of V. coralliilyticus and other Vibrio spp.; figure 5, blue regions) than it does to a bacterium travelling at speeds closer to 100 µm s⁻¹ (swimming speeds of chemokinetic V. coralliilyticus [10,17]; figure 5, orange regions).

4. Discussion

Bacteria must cope with considerable noise and estimation bias when navigating dynamic chemical landscapes. The advantage conferred by an early response to chemical pulses suggests that there may be selection for high accuracy and sensitivity in the chemotaxis response [1,4]. Our framework provides a means of studying how the basic components of bacterial navigation strategies (swimming speed, measurement time) and physical parameters (e.g. chemoattractant diffusivity, pulse size) influence when and where bacteria can perform chemotaxis. Expressions for the outer boundary of sensitivity, r_o (equation (3.2)), and the time after which gradients created by a pulse are no longer perceptible, t* (equation (3.3)), may prove particularly useful as they constrain the length and time scales over which bacteria can perceive individual chemical pulses. The relationship between the size of the pulse, pulse geometry, and the length and time scales over which the pulse is perceptible provides a basis for modelling more realistic environments where many pulses appear with characteristic sizes, geometries and temporal statistics. For example, an empirical estimate of a typical inter-pulse interval in, say, a marine environment [4] can be compared with t* to determine whether the environment is highly granular or relatively homogeneous from the perspective of bacteria. For the canonical pulse geometries considered here (equation (2.3)), the SNR of the concentration ramp rate decays sharply far from the origin of a pulse (figure 2a). In particular, substituting equation (2.3) into the expression for the SNR of 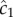(r.h.s. of equation (3.1)) shows that the SNR decays like a Gaussian for large r ( 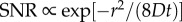for large r). This sharp transition in the SNR means that, near the outer boundary of sensitivity, there is a stark division between cells that have access to useful chemotactic information (r < r_o) and cells that do not (r > r_o). Using r_o to partition bacterial cells into subpopulations that are near and far from chemical pulses could greatly simplify models of bacterial competition and population dynamics in complex environments [1].

Our theory makes a number of predictions that could be tested with chemotaxis experiments. First, the theory predicts that, for times t < t*, the mean orientation of bacterial swimming trajectories outside the region r_i < r < r_o should be unbiased. Because the conditions considered in this work correspond to an upper bound on sensory accuracy, the region within which cells exhibit biased motion may be a sub-region of r_i < r < r_o. A second prediction is that, for times greater than t*, bacteria should not exhibit biased motion anywhere in the environment because each cell's estimate of the gradient will be dominated by noise, regardless of where it is located relative to the origin of the pulse. Again, because of the assumptions used to derive t*, the observed time at which the average directional bias of a bacterial population drops to zero may be shorter than t*.

One of the implications of our model for temporal gradient sensing is that sensory acuity is intimately linked to swimming speed (equation (3.1), figure 5). Because swimming at high speed is costly [1,15], bacteria are likely to benefit by changing speed in an adaptive way, cruising at low speed in the absence of a chemical signal and speeding up when concentration exceeds a threshold. The connection between speed and measurement accuracy may explain the counterintuitive observation that some species of marine bacteria swim at high speeds even near local maxima in chemoattractant concentration [10]; bias in the concentration slope estimate is high near local maxima (figure 2b,c). A cell cannot decrease bias by lengthening measurement time, but it can reduce bias by swimming faster, suggesting that bacteria may use chemokinesis to enhance chemotactic accuracy near the blind spot that forms at the centre of spreading chemical pulses (figure 5, t = 120, 140 s; electronic supplementary material). More generally, our framework suggests that bacteria can improve chemotactic performance by using chemokinesis and chemotaxis in concert. The hypothesis that bacteria initiate chemokinesis in response to absolute concentration to enhance sensitivity to gradients could be investigated by independently varying the concentration gradient and absolute concentration of a chemoattractant, for example using a microfluidic device [31].

Our framework uses fundamental limits on the accuracy of chemical sensing [13,16] to determine when and where chemotaxis is feasible, and provides a tool for modelling bacterial behaviour in more realistic dynamic environments. Importantly, it is agnostic to the details of bacterial movement patterns and chemosensory machinery and can therefore provide general principles that apply to the broad range of bacterial species in real ecological communities that navigate using temporal gradient sensing.

Authors' contributions

A.M.H., D.R.B., F.C., R.S. and S.A.L. conceived the study. A.M.H., D.R.B. and F.C. performed analyses. A.M.H., D.R.B., F.C., R.S. and S.A.L. wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by Army Research Office grant nos. W911NG-11-1-0385 and W911NF-14-1-0431 to S.A.L., a James S. McDonnell Foundation Fellowship to A.M.H., a Swiss National Science Foundation postdoctoral fellowship to F.C., a Human Frontier Science Program Cross-Disciplinary fellowship to D.R.B. and a Gordon and Betty Moore Marine Microbial Initiative Investigator Award (GBMF3783) to R.S.