Abstract
In this paper, we introduce a new type of tree-based method, reinforcement learning trees (RLT), which exhibits significantly improved performance over traditional methods such as random forests (Breiman, 2001) under high-dimensional settings. The innovations are three-fold. First, the new method implements reinforcement learning at each selection of a splitting variable during the tree construction processes. By splitting on the variable that brings the greatest future improvement in later splits, rather than choosing the one with largest marginal effect from the immediate split, the constructed tree utilizes the available samples in a more efficient way. Moreover, such an approach enables linear combination cuts at little extra computational cost. Second, we propose a variable muting procedure that progressively eliminates noise variables during the construction of each individual tree. The muting procedure also takes advantage of reinforcement learning and prevents noise variables from being considered in the search for splitting rules, so that towards terminal nodes, where the sample size is small, the splitting rules are still constructed from only strong variables. Last, we investigate asymptotic properties of the proposed method under basic assumptions and discuss rationale in general settings.
Keywords: Reinforcement Learning, Trees, Random Forests, Consistency, Error Bound
1. INTRODUCTION
In high-dimensional settings, the concept of sparsity—that there is a relatively small set of variables which completely convey the true signal—is both intuitive and useful. Many methods have been proposed to identify this set of true signal variables. Penalized estimation for linear models (Tibshirani, 1996) and its variations are among the most popular methods for this purpose. Machine learning tools such as tree-based approaches (Breiman et al., 1984; Breiman, 1996, 2001) have also drawn much attention in the literature due to their flexible non-parametric structure and the capacity for handling high-dimensional data. However, there is little attention on sparsity for tree-based methods, both theoretically and practically. In this paper, we propose to use reinforcement learning in combination with a variable muting strategy to pursue nonparametric signals in a sparse setting by forcing a certain level of sparsity in the constructed trees. Before giving details of the proposed method, we briefly review previous work to lay the needed foundation.
A series of works including (Breiman, 1996; Amit and Geman, 1997; Dietterich, 2000; Breiman, 2000) led to the introduction of random forests (Breiman, 2001), a state-of-the-art machine learning tool. A Random forest is essentially an ensemble unpruned classification and regression tree model (CART, Breiman et al. (1984)) with random feature selection. Many versions of random forests have been proposed since, such as perfect random forests by Cutler and Zhao (2001), which have exactly one observation in each terminal node; extremely randomized trees (ET) by Geurts et al. (2006), which use random cut points rather than searching for the best cut point; and Bayesian additive regression trees (BART) by Chipman et al. (2010), which integrate tree-based methods into a Bayesian framework. Ishwaran et al. (2008) and Zhu and Kosorok (2012) further extend random forests to right censored survival data.
The asymptotic behavior of random forests has also drawn significant interest. Lin and Jeon (2006) established the connection between random forests and nearest neighborhood estimation. Biau et al. (2008) proved consistency for a variety of types of random forests, including purely random forests (PRF). However, they also provide an example which demonstrates inconsistency of trees under certain greedy construction rules. One important fact to point out is that consistency and convergence rates for random forests (including but not limited to the original version proposed by Breiman (2001)) rely heavily on the particular implemented splitting rule. For example, purely random forests, where splitting rules are random and independent from training samples, provide a much more friendly framework for analysis. However, such a model is extremely inefficient because most of the splits are likely to select noise variables, especially when the underlying model is sparse. Up to now, there appears to be no tree-based method possessing both established theoretical validity and excellent practical performance.
As the most popular tree-based method, random forests (Breiman, 2001) shows great potential in cancer studies (Lunetta et al., 2004; Bureau et al., 2005; Díaz-Uriarte and De Andres, 2006) where a large number of variables (genes or SNPs) are present and complex genetic diseases may not be captured by parametric models. However, some studies also show unsatisfactory performance of random forests (Statnikov et al., 2008) compared to other machine learning tools. One of the drawbacks of random forests in the large p small n problem is caused by random feature selection, which is the most important “random” component of random forests and the driving force behind the improvement from a bagging predictor (Breiman, 1996). Consider the aforementioned high-dimensional sparse setting, where we have p variables, among which there are p1 ≪ p strong variables that carry the signal and p2 = p − p1 noise variables. Using only a small number of randomly sampled features would provide little opportunity to consider a strong variable as the splitting rule and would also lead to bias in the variable importance measures (Strobl et al., 2007), while using a large number of predictors causes overfitting towards terminal nodes where the sample size is small and prevents the effect of strong variables from being fully explored.
Due to these reasons, a solution is much needed to improve the performance of random forests in high-dimensional sparse settings. Intuitively, in a high-dimensional setup, a tree-based model with good performance should split only on the p1 strong variables, where p1 follows our previous notation. Biau (2012) establishes consistency of a special type of purely random forest model where strong variables have a larger probability of selection as a splitting variable. This model essentially forces all or most splits to concentrate on only the strong variables. Biau (2012) also shows that if this probability can be properly chosen, the convergence rate of the model should only depend on p1. However, behind this celebrated result, two key components require careful further investigation. First, the probability of using a strong variable to split at an internal node depends on the within-node data (or an independent set of within-node samples as suggested in Biau (2012)). With rapidly reducing sample sizes toward terminal nodes, this probability, even with an independent set of samples, is unlikely to behave well for the entire tree. This fact can be seen in one of the simulation studies in Biau (2012) where the sample size is small (less than 25): the probability of using a strong variable as the splitting rule can be very low. Second, the marginal comparisons of splitting variables, especially in high-dimensional settings, can potentially fail to identify strong variables. For example, the checker-board structure in Kim and Loh (2001) and Biau et al. (2008) is a model having little or no marginal effect but having a strong joint effect.
In this paper, we introduce a new strategy—reinforcement learning—into the tree-based model framework. For a comprehensive review of reinforcement learning within the artificial intelligence field in computer science and statistical learning, we refer to Sutton and Barto (1998). An important characteristic of reinforcement learning is the “lookahead” notion which benefits the long-term performance rather than short-term performance. The main features we will employ in the proposed method are: first, to choose variable(s) for each split which will bring the largest return from future branching splits rather than only focusing on the immediate consequences of the split via marginal effects. Such a splitting mechanism can break any hidden structure and avoid inconsistency by forcing splits on strong variables even if they do not show any marginal effect; second, progressively muting noise variables as we go deeper down a tree so that even as the sample size decreases rapidly towards a terminal node, the strong variable(s) can still be properly identified from the reduced space; third, the proposed method enables linear combination splitting rules at very little extra computational cost. The linear combination split constructed from the strong variables gains efficiency when there is a local linear structure and helps preserve randomness under this somewhat greedy approach to splitting variable selection.
One consequence of the new approach, which we call reinforcement learning trees (RLT), is that it forces the splits to concentrate only on the p1 strong variables at the early stage of the tree construction while also reducing the number of candidate variables gradually towards terminal nodes. This results in a more sparse tree structure (see Section 5 for further discussion of this property) in the sense that the splitting rule search process focuses on a much smaller set of variables than a traditional tree-based model, especially towards terminal nodes. We shall show that, under certain assumptions, the convergence rate of the proposed method does not depend on p, but instead, it depends on the size of a much smaller set of variables that contains all the p1 strong variables. This is a valuable result in its own right, especially in contrast to alternative greedy tree construction approaches whose statistical properties are largely unknown.
The paper is organized as follows. Section 2 gives details of the methodology for the proposed approach. Theoretical results and accompanying interpretations are given in Section 3. Details of the proofs will be deferred to the appendix. In Sections 4 we compare RLT with popular statistical learning tools using simulation studies and real data examples. Section 5 contains some discussion and rationale for both the method and its asymptotic behavior.
2. PROPOSED METHOD
2.1 Statistical model
We consider a regression or classification problem from which we observe a sample of i.i.d. training observations
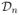 = {(X1, Y1), (X2, Y2), …, (Xn, Yn)}, where each
denotes a set of p variables from a feature space
= {(X1, Y1), (X2, Y2), …, (Xn, Yn)}, where each
denotes a set of p variables from a feature space
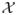 . For the regression problem, Y is a real valued outcome with E(Y2) < ∞; and for the classification problem, Y is a binary outcome that takes values of 0 or 1. To facilitate later arguments, we use
. For the regression problem, Y is a real valued outcome with E(Y2) < ∞; and for the classification problem, Y is a binary outcome that takes values of 0 or 1. To facilitate later arguments, we use
 to denote the set {1, 2, …, p}. We also assume that the expected value E(Y|X) is completely determined by a set of p1 < p variables. As discussed in the previous section, we refer to these p1 variable as “strong variables”, and refer to the remaining p2 = p − p1 variables as “noise variables”. For the sake of organizing the discussion, we assume without loss of generality, that the strong variables are the first p1 variables, which means E(Y|X) = E(Y|X(1), X(2), …, X(p1)). The goal is to consistently estimate the function f(x) = E(Y|X = x) and derive asymptotic properties for the estimator.
to denote the set {1, 2, …, p}. We also assume that the expected value E(Y|X) is completely determined by a set of p1 < p variables. As discussed in the previous section, we refer to these p1 variable as “strong variables”, and refer to the remaining p2 = p − p1 variables as “noise variables”. For the sake of organizing the discussion, we assume without loss of generality, that the strong variables are the first p1 variables, which means E(Y|X) = E(Y|X(1), X(2), …, X(p1)). The goal is to consistently estimate the function f(x) = E(Y|X = x) and derive asymptotic properties for the estimator.
2.2 Motivation
In short, the proposed reinforcement learning trees (RLT) model is a traditional random forests model with a special type of splitting variable selection and noise variable muting. These features are made available by implementing a reinforcement learning mechanism at each internal node. Let us first consider a checkerboard example which demonstrates the impact of reinforcement learning: Assume that X ~ uni f[0, 1]p, and E(Y|X) = I{I(X(1)0.5)=I(X(2)>0.5)}, so that p1 = 2 and p2 = p−2. The difficulty in estimating this structure with conventional random forests is that neither of the two strong variables show marginal effects. The immediate reward, i.e. reduction in prediction errors, from splitting on these two variables is asymptotically identical to the reward obtained by splitting on any of the noise variables. Hence, when p is relatively large, it unlikely that either X(1) or X(2) would be chosen as the splitting variable. However, if we know in advance that splitting on either X(1) or X(2) would yield significant rewards down the road for later splits, we could confidently force a split on either variable regardless of the immediate rewards.
To identify the most important variable at any internal node, we fit a pilot model (which is embedded at each internal node, and thus will be called an embedded model throughout the paper) and evaluate the potential contribution of each variable. Then we proceed to split the node using the identified most important variable(s). When doing this recursively for each daughter node, we can focus the splits on the variables which will very likely lead to a tree yielding the smallest prediction error in the long run. The concept of this “embedded model” can be broad enough so that any model fitted to the internal node data can be called an embedded model. Even the marginal search, although with poor performance in the above example, can be viewed as an over-simplified embedded model. However, it is of interest to use a flexible, yet fast embedded model so that the evaluation of each variable is accurate.
Two problems arise when we greedily select the splitting variable. First, since the sample size shrinks as we move towards a terminal node, it becomes increasingly difficult to identify the important variables regardless of what embedded model we are using. Second, the extreme concentration on the strong variables could lead to highly correlated trees even when bootstrapping is employed. Hence we propose a variable muting procedure to counter the first drawback and use linear combination splits to introduce extra randomness. Details and rationale for these two procedures will be given in their corresponding sections below.
In the following sections, we first give a higher level algorithm outlining the main features of the RLT method (Section 2.3) and then specify the definition of each component: the embedded model (Section 2.4), variable importance (Sections 2.5), variable muting (Section 2.6), and linear combination split (Section 2.7).
2.3 Reinforcement learning trees
RLT construction follows the general framework for an ensemble of binary trees. The key ingredient of RLT is the selection of splitting variables (using the embedded model), eliminating noise variables (variable muting) and constructing daughter nodes (using, for example, a linear combination split). Table 1 summarizes the RLT algorithm. The definition of the variable importance measure is given in Section 2.5, and the definition of the muted set is given in Section 2.6.
Table 1.
Algorithm for reinforcement learning trees
|
2.4 Embedded model
At an internal node A, an embedded model
is a model fitted to the internal node data DA = {(Xi, Yi) : Xi ∈ A}. The embedded model provides information on the variable importance measures
for each variable j so that the split variable can be chosen. At the root node, where the set of muted variables
, all variables in the set
 = {1, 2, …, p} are considered in the embedded model. However, as we move further down the tree, some variables will be muted so that
, and then the embedded model will be fit using only the non-muted variables, i.e., the variables {
}.
= {1, 2, …, p} are considered in the embedded model. However, as we move further down the tree, some variables will be muted so that
, and then the embedded model will be fit using only the non-muted variables, i.e., the variables {
}.
In practice, we use a slight modification of extremely randomized trees (Geurts et al. (2006)) as the embedded model by fitting each tree with a bootstrapped sample. Extremely randomized trees can achieve a similar performance to random forests at a reduced computational cost due to the random splitting value generation. Noting that the embedded model will be called many times during an RLT fitting, a fast approach has a great advantage. However, any other learning method can be an alternative, such as random forests or purely random forests.
2.5 Variable importance
Since the purpose of fitting the embedded random forests is to determine the most important variable, we need to properly define a variable importance measure VIA(j) for each variable j ∈
 at an internal node A and use the embedded model to calculate the estimate
. The variable importance defined in Breiman (2001) seems to be a natural choice here since we use a tree-based method as the embedded model. We give the formal definition of the variable importance measure in the following. In Section 3 and in the Appendix, we will carefully investigate the properties of VIA and the asymptotic properties of its estimate
.
at an internal node A and use the embedded model to calculate the estimate
. The variable importance defined in Breiman (2001) seems to be a natural choice here since we use a tree-based method as the embedded model. We give the formal definition of the variable importance measure in the following. In Section 3 and in the Appendix, we will carefully investigate the properties of VIA and the asymptotic properties of its estimate
.
Definition 2.1
At any internal node A, denoting X̃(j) as an independent copy generated from the marginal distribution of X(j) within A, the variable importance of the j-th variable within A, namely VIA(j), is defined by:
where E[·|A] is a conditional expectation defined by E[g(Y, X)|A] = E[g(Y, X)|I(X ∈ A)], for any function g.
Following the procedure in Breiman (2001) to calculate for each fitted embedded tree, we randomly permute the values of variable j in the out-of-bag data (the within-node observations which are not sampled by bootstrapping when fitting the embedded tree model) to mimic the independent and identical copy X̃(j), drop these permuted observations down the fitted tree, and then calculate the resulting mean squared error (MSE) increase. Intuitively, when j is a strong variable, randomly permuting the values of X(j) will result in a large , while randomly permuting the values of a noise variable should result in little or no increase in MSE, so should be small. Hence calculated from the embedded model can identify the variable with greatest need-to-be-split in the sense that it explains the most variation in the outcome variable Y in the current node (see Section 3). Also note that any strong variable j should have nonzero VI regardless of its marginal effect as long as f changes, as a function of the remaining p−1 arguments on some nonzero subspace, over its jth argument. For example, consider the checkerboard example we provided in Section 2.2. The VI for both strong variables are 2/3 although there is no marginal effect. Another important property that we observe is that for all the variables in the muted set , which will be introduced in the next section, since they are not involved in the embedded model , randomly permuting their values will not increase MSE. Hence, for , we must have . Table 2 gives details on how to assess the variable importance measure based on the embedded extremely randomized trees estimator .
Table 2.
Variable Importance
|
Remark 2.2
In practice, the embedded model is estimated using a small number of observations (within node data), which may give an inaccurate model fitting. However, the prediction accuracy of an embedded model is not the major concern here since we only need the ranks of variable importance measures to be reliable, i.e., variables with large VI are ranked at the top by the embedded model. Moreover, as the within node sample size gets even smaller when approaching terminal nodes, the variable muting procedure we introduce below helps to constrain the splits within the set of strong variables.
2.6 Variable muting
As we discussed previously, with sample size reducing rapidly towards a terminal node during the tree construction, searching for a strong variable becomes increasingly difficult. The lack of signal from strong variables (since they are mostly explained by previous splits) can eventually cause the splitting variable selection to behave completely randomly, and then the constructed model is similar to purely random forests. Hence, the muting procedure we introduce here is to prevent some noise variables from being considered as the splitting variable. We call this set of variables the muted set. At each given internal node, we force pd variables into the muted set, and we remove them from consideration as splitting variable at any branch of the given internal node. On the other hand, to prevent strong variables from being removed from the model, we have a set of variables that we always keep in the model, which we call the protected set. When a variable is used as a splitting rule, it is included in the protected set, hence will be considered in all subsequent nodes. We also set a minimal number p0 of variables beyond which we won’t remove any further variables from consideration at any node. Note that both the muted set and protected set will be updated for each daughter nodes after a split is done. We first take a look at the muting procedure at the root node, then generalize the procedure to any internal node.
At the root node
Assume that after selecting the splitting variable at the root node A, the two resulting daughter nodes are AL and AR. Then we sort the variable importance measures
calculated from the embedded model
and find the pd-th smallest value within the variable set
 denoted by
and the p0-th largest value denoted by
. Then we define:
denoted by
and the p0-th largest value denoted by
. Then we define:
The muted set for the two daughter nodes: , i.e. the set of variables with the smallest pd variable importance measures.
The protected set , i.e., the set of variables with largest p0 variable importance measures. Note that the variables in the protected set will not be muted in any of the subsequent internal nodes.
At internal nodes
After the muted set and protected set have been initialized at the root split, we update the two sets in subsequent splits. Suppose at an internal node A, the muted set is , the protected set is and the two daughter nodes are AL and AR. We first update the protected set for the two daughter nodes by adding the splitting variable(s) into the set:
Note that when a single variable split is used, the splitting variable is simply , and when a linear combination split is used, multiple variables could be involved.
To update the muted set, after sorting the variable importance measures , we find the pd-th smallest value within the restricted variable set , which value is denoted . Then we define the muted set for the two daughter nodes as
Remark 2.3
The muting rate pd is an important tuning parameter in RLT, as it controls the “sparsity” towards terminal nodes. pd dose not need to be a fixed number. It can vary depending on , which is the number of nonmuted variables at each internal node. In Section 4 we will evaluate different choices for pd such as 0 (no muting), (moderate muting, which is suitable for most situations), and (very aggressive muting). Moreover, in practice, pd can be adjusted according to the sample size n and dimension p. In our R package “RLT”, several ad-hoc choice of pd are available.
Remark 2.4
The splitting rules at the top levels of a tree are all constructed using the strong variables, hence these variables will be protected. This property will be demonstrated in the theoretical result. Ideally, after a finite number of splits, all strong variables are protected, all noise variables are muted, and the remaining splits should concentrate on the strong variables. But this may not be the case asymptotically when extremely complicated interactions are involved. Hence choosing a proper p0 ≥ p1 to cover all strong variables at early splits is theoretically meaningful. However, in practice, tuning p0 is unnecessary. We found that even setting p0 = 0 achieves good performance when the model is sparse.
2.7 Splitting a node
We introduce a linear combination split in this section. Note that when only one variable is involved, a linear combination splitting rule reduces to the traditional split used in other tree-based methods. Using a linear combination of several variables to construct a splitting rule was considered in Breiman (2001) and Lin and Jeon (2006). However, exhaustively searching for a good linear combination of variables is computationally intensive especially under the high-dimensional sparse setting, hence the idea never achieved much popularity.
The proposed embedded model and variable importance measure at each internal node provides a convenient formulation for a linear combination split. By using variables with large , the splitting rule is likely to involve strong variables. However, we do not exhaustively search for the loadings in the combination. This introduces an extra level of randomness within the set of strong variables duo to the complex neighborhood structure of each target point (see Lin and Jeon (2006) regarding the potential neighborhood). In our proposed procedure, two parameters are used to control the complexity of a linear combination split:
k: The maximum number of variables considered in the linear combination. Note that when k = 1, this simplifies to the usual one variable split.
α: The minimal variable importance, taking values in (0, 1), of each variable in this linear combination in terms of the percentage of maximum at the current node. For example, if α = 0.5 and at the current node, then any variable with less than 0.5 will not be considered for the linear combination.
We first create a linear combination of the form Xβ̂ > 0, where β̂ is a coefficient vector with dimension p × 1. Then we project each observation onto this axis to provide a scalar ranking for splitting. Define β̂j(A) for each j ∈ {1, …p} at node A as follows:
where is Pearson’s correlation coefficient between X(j) and Y within node A, is the kth largest variable importance estimate at node A. The components in the above definition ensure that the variables involve in the linear combination are the top k variables with positive importance measure, and are above the α threshold in terms of the maximum variable importance at the current node.
We then calculate Xiβ̂(A) for each observation Xi in the current node. This is precisely the scalar projection of each observation onto the vector β̂(A). The splitting point can be generated by searching for the best (as in random forests) or by comparing multiple random splits (as in extremely randomized trees). Biau et al. (2008) showed that an exhaustive search for the splitting point could cause inconsistency of a tree-based model, hence we generate one or multiple random splitting points (1 is the default number) and choose the best among them. Moreover, the splitting points are generated from quantiles of the observed samples to avoid redundant splits.
Remark 2.5
The construction of a linear combination requires specification of both k and α. We consider k as the decisive tuning parameter, while α is used to prevent extra noise variables from entering the linear combination when k is set too large. However, when α is set to its extreme value 1, it is essentially setting k = 1. In our simulation studies, we found that α only affects large k values, and setting α = 0.25 achieves good performance.
3. THEORETICAL RESULTS
In this section, we develop large sample theory for the proposed RLT model. We show that under basic assumptions, the proposed RLT is consistent, with convergence rate depending only on the number of strong variables, p1, if the tuning parameters are optimally chosen. We only focus on a simplified version of RLT with a single variable split (RLT1) and a fixed muting number parameter pd in the regression setting. Moreover, we assume that the number of variables p is fixed with p1 strong variables, and the number p0 of protected variables is chosen to be larger than p1. We assume, for technical convenience, that the covariates X are generated uniformly from the feature space
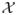 = [0, 1]p, which was also used in Lin and Jeon (2006) and Biau (2012). Although the independence assumption seems restrictive, the consequent theoretical results serve as a starting point for understanding the “greedy” tree method, whose theoretical results are largely unknown. A possible approach to address correlated variables is discussed in Section 5. Note that under the uniform distribution assumption, any internal node can now be viewed as a hypercube in the feature space
= [0, 1]p, which was also used in Lin and Jeon (2006) and Biau (2012). Although the independence assumption seems restrictive, the consequent theoretical results serve as a starting point for understanding the “greedy” tree method, whose theoretical results are largely unknown. A possible approach to address correlated variables is discussed in Section 5. Note that under the uniform distribution assumption, any internal node can now be viewed as a hypercube in the feature space
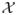 , i.e., any internal node A ⊆ [0, 1]p has the form
, i.e., any internal node A ⊆ [0, 1]p has the form
| (1) |
Throughout the rest of this paper, we will use the terms “internal node” and “hypercube” inter-changeably provided that the context is clear.
The main results are Theorem 3.6 which bounds below the probability of using strong variables as the splitting rule, and Theorem 3.7 which establishes consistency and derives an error bound for RLT1. Several key assumptions are given below for the underlying true function f and the embedded model.
Assumption 3.1
There exist a set of strong variables
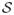 = (1, …, p1) such that f(X) = E[Y |X] = E[Y |X(j), j ∈
= (1, …, p1) such that f(X) = E[Y |X] = E[Y |X(j), j ∈
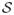 ] and
for j ∈
] and
for j ∈
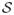 . The set of noise variables is then
. The set of noise variables is then
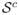 = (p1 + 1, …, p). The true function f is Lipschitz continuous with Lipschitz constant cf.
= (p1 + 1, …, p). The true function f is Lipschitz continuous with Lipschitz constant cf.
The assumption
for j ∈
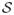 guarantees that with probability 1, a target point {(X(1), …,X(p))} is a point where all strong variables carry a signal. It is satisfied for most parametric models, such as linear, additive, single index and multiple index models, hence is not restrictive. Since our embedded model only fits the “local” (within node) data, this assumption is needed to correctly identify the strong variables at an internal node. Further, we need to precisely define how “strong” a strong variable is. Definition 2.1 of the variable importance measure suggests that V IA(j) relies on the true underlying function f restricted to a hypercube A. To avoid explicitly defining the true function f, we give the following lower bound on the variable importance, followed by a remark that makes the connection between this definition and the true functional form of f.
guarantees that with probability 1, a target point {(X(1), …,X(p))} is a point where all strong variables carry a signal. It is satisfied for most parametric models, such as linear, additive, single index and multiple index models, hence is not restrictive. Since our embedded model only fits the “local” (within node) data, this assumption is needed to correctly identify the strong variables at an internal node. Further, we need to precisely define how “strong” a strong variable is. Definition 2.1 of the variable importance measure suggests that V IA(j) relies on the true underlying function f restricted to a hypercube A. To avoid explicitly defining the true function f, we give the following lower bound on the variable importance, followed by a remark that makes the connection between this definition and the true functional form of f.
Assumption 3.2
Let hypercube A be defined in the form of Equation (1). If for any strong variable j, the interval length of all other strong variables at A is at least δ, i.e., , then there exist positive valued monotone functions ψ1(·) and ψ2(·), such that the variable importance of this strong variable j can be bounded below by
| (2) |
where V IA(j) is as defined in Definition 2.1.
Remark 3.3
This assumption can be understood in the following way. It basically requires that the surface of f cannot be extremely flat, which helps to guarantee that at any internal node A with nonzero measure, a strong variable can be identified. However, this does not require a lower bound on |∂f/∂X(j)|, which is a much stronger assumption. Further, the two functions ψ1(·) and ψ2(·) help separate (locally at A) the effects of variable j and all other strong variables. We make two observations here to show that if f is a polynomial function, the condition is satisfied: (1) If f is a linear function, then the variable importance of j is independent of the interval length (or value) of other strong variables. Then ψ1(δ) ≡ σ2 and satisfy the criteria, where σ2 is the variance of the random error (see Assumption 3.5). (2) When f is a polynomial function with interactions up to a power of k ≥ 2, the variable importance of j is entangled with the within node value of other strong variables. However, for small values of δ and bj − aj (or equivalently, for a small hypercube A), and satisfy the criteria.
Another assumption is on the embedded model. Although we use extremely randomized trees as the embedded model in practice, we do not rule out the possibility of using other kinds of embedded models. Hence we make the following assumption for the embedded model, which is at least satisfied for purely random forests:
Assumption 3.4
The embedded model f̂* fitted at any internal node A with internal sample size nA is uniformly consistent with an error bound: there exists a fixed constant 0 < K < ∞ such that for any δ > 0,
, where 0 < η(p) ≤ 1 is a function of the dimension p, and the conditional probability on A means that the expectation is taken within the internal node A. Note that it is reasonable to assume that η(p) is a non-increasing function of p since larger dimensions should result in poorer fitting. Furthermore, the embedded model f̂* lies in a class of functions
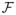 with finite entropy integral under the L2(P) norm (van der Vaart and Wellner, 1996).
with finite entropy integral under the L2(P) norm (van der Vaart and Wellner, 1996).
Finally, we assume the moment condition on the random error terms εi.
Assumption 3.5
With f(X) being the true underlying function, the observed values are Yi = f(Xi) + εi, where εis are i.i.d. with mean 0 and variance σ2. Moreover, the following Bernstein condition on the moments of ε is satisfied:
| (3) |
for some constant 1 ≤ K < ∞.
Now we present two key results, Theorem 3.6 and Theorem 3.7, followed by a sketch of the proof for each. Details of the proofs are given in the Appendix and the supplementary file. Theorem 3.6 analyzes the asymptotic behavior of the variable importance measure and establishes the probability for selecting the true strong variables and muting the noise variables. Theorem 3.7 bounds the total variation by the variable importance measures at each terminal node and shows consistency and an error bound for RLT1. For simplicity, we only consider the case where one RLT1 tree is fitted to the entire dataset, i.e, M = 1 and the bootstrap ratio is 100%. For the embedded model, we fit only one tree using half of the within node data and calculate the variable importance using the other half. To ensure the minimum node sample size, the splitting point c is chosen uniformly between the q-th and (1 − q)-th quintile with respect to the internal node interval length of each variable, where q ∈ (0, 0.5]. The smaller q is, the more diversity it induces. When q = 0.5, this degenerates into a model where each internal node is always split into two equally sized daughter nodes.
Theorem 3.6
For any internal node A ∈
 with sample size nA, where
with sample size nA, where
 is the set of all internal nodes in the constructed RLT, define ĵA to be the selected splitting variable at A and let pA denote the number of non-muted variables at A. Then, under Assumptions 3.1, 3.2, 3.4, and 3.5, we have,
is the set of all internal nodes in the constructed RLT, define ĵA to be the selected splitting variable at A and let pA denote the number of non-muted variables at A. Then, under Assumptions 3.1, 3.2, 3.4, and 3.5, we have,
-
, i.e., with probability close to 1, we always select a strong variable as the splitting variable.
, i.e., for any internal node in the constructed RLT model, the true variable importance measure for the selected splitting variable is at least half of the true maximum variable importance with probability close to 1.
The protected set contains all strong variables, i.e., .
Note that in the above three results, ψ1(·), ψ2(·), and the constants Ck and Kk, k = 1,…, 3, do not depend on pA or the particular choice of A.
The proof of Theorem 3.6 is provided in the supplementary file. There are three major components involved in the probabilities of Theorem 3.6: node sample size nA; local signal strength ; and local embedded model error rate . The proof is in fact very intuitive. We first show the consistency and convergence rate of the variable importance measure , which is related to the local embedded model error rate. Then with the lower bound on the true local variable importance (Assumption 3.2), we establish result (a), the probability of choosing a strong variable as the splitting rule. Result (b) follows via the same logic by looking at the the variable importance of the chosen splitting variable. Result (c) utilizes the facts that the variable importance measure of a strong variable is larger than that of a noise variable and that we choose p0 larger than p1.
The probabilities in Theorem 3.6 rely on the fact that the node sample size nA is large enough to make . As we discussed earlier in Remark 3.3, the functions ψ1(·) and ψ2(·) can be chosen as power functions when f is a polynomial. Hence, for any specific function f and embedded model, we precisely know ψ1(·), ψ2(·), and η(·). We can then separate all the internal nodes in a fitted RLT tree into three groups with different levels of sample sizes by defining nγ* and nγ in the following, and analyze the different groups separately:
Set
 : Internal nodes with sample size larger than nγ*, where γ* ∈ (0, 1) is chosen such that ψ1(nγ*−1) · ψ2(nγ*−1) · nγ*η(p) → ∞.
: Internal nodes with sample size larger than nγ*, where γ* ∈ (0, 1) is chosen such that ψ1(nγ*−1) · ψ2(nγ*−1) · nγ*η(p) → ∞.Set
 : Internal nodes with sample size smaller than nγ*, but larger than nγ, where γ ∈ (0, 1) is chosen such that ψ1(nγ−1) · ψ2(nγ−1) · nγη(p0) → ∞. Note the change from η(p) to η(p0) and the fact that γ is supposed to be smaller than γ*.
: Internal nodes with sample size smaller than nγ*, but larger than nγ, where γ ∈ (0, 1) is chosen such that ψ1(nγ−1) · ψ2(nγ−1) · nγη(p0) → ∞. Note the change from η(p) to η(p0) and the fact that γ is supposed to be smaller than γ*.Set
 : Internal nodes with sample size smaller than nγ.
: Internal nodes with sample size smaller than nγ.
We shall show in Theorem 3.7 that during the tree splits of
 , the noise variables are muted and the remaining protected p0 variables contain all the strong variables. During the tree splits of
, the noise variables are muted and the remaining protected p0 variables contain all the strong variables. During the tree splits of
 ∪
∪
 , all the splitting variables are within the set of strong variables. The proof does not depend on the particular function f or embedded model. The set
, all the splitting variables are within the set of strong variables. The proof does not depend on the particular function f or embedded model. The set
 is then less interesting since the sample size is too small and the remaining splits (up through the terminal nodes) are likely to behave like random choices. However, we know that there are only p0 variables for any node in
is then less interesting since the sample size is too small and the remaining splits (up through the terminal nodes) are likely to behave like random choices. However, we know that there are only p0 variables for any node in
 , and these p0 variables contain all the strong variables. To facilitate our argument here, we use a toy example (provided in the Appendix) to demonstrate the probability of selecting a strong variable as the splitting rule under different n, p, and levels of model complexity. This again confirms that splits at the top levels of a tree have larger impact.
, and these p0 variables contain all the strong variables. To facilitate our argument here, we use a toy example (provided in the Appendix) to demonstrate the probability of selecting a strong variable as the splitting rule under different n, p, and levels of model complexity. This again confirms that splits at the top levels of a tree have larger impact.
To better understand the proposed RLT method, we focus on the set
 ∪
∪
 in Theorem 3.7, where the reinforcement learning is having the greatest effect, and show a convergence result for this setting. Note that this part of the fitted tree has node sample size larger than nγ, thus forcing the minimal node sample size to be nγ. However, nγ is by no means a tuning parameter, and a tree should continue to split until the pre-defined nmin is reached. We will discuss the behavior of the set
in Theorem 3.7, where the reinforcement learning is having the greatest effect, and show a convergence result for this setting. Note that this part of the fitted tree has node sample size larger than nγ, thus forcing the minimal node sample size to be nγ. However, nγ is by no means a tuning parameter, and a tree should continue to split until the pre-defined nmin is reached. We will discuss the behavior of the set
 after the theorem.
after the theorem.
Theorem 3.7
Under Assumptions 3.1, 3.2, 3.4, and 3.5, with probability close to 1,
where r is a constant such that r > 1 and 2(1 − q)2r/q2 ≤ 1, γ defines the minimum node sample size nγ, q is the lower quintile to generate a random splitting point, and p1 is the number of strong variables.
At first glance, the rate seems slow, however, this is to compensate for the fact that we do not want to make strong assumptions on the functional form of f. The rate is essentially the convergence rate of the worst node of the entire tree (if using nmin = nγ), where some strong variables receive few splits. Since we allow arbitrary interactions in f, the signal in the worst node can be extremely weak. Apparently, with stronger assumptions on f, the rate can be greatly improved. However, the key point here is that the convergence rate does not depend on the original number of variables p since all the splits (in
 ∈
∈
 ) are constructed using strong variables. We also note that the rate does not depend on the number of protected variables p0 for the same reason. Unfortunately, this second statement is not true if we consider the entire fitted tree, which further splits the nodes in
) are constructed using strong variables. We also note that the rate does not depend on the number of protected variables p0 for the same reason. Unfortunately, this second statement is not true if we consider the entire fitted tree, which further splits the nodes in
 into smaller hypercubes that belong to
into smaller hypercubes that belong to
 . For the scope of this paper, we do not investigate further the asymptotic behavior of
. For the scope of this paper, we do not investigate further the asymptotic behavior of
 , which leads to the true convergence rate. This is because the nodes in
, which leads to the true convergence rate. This is because the nodes in
 will not be affected by reinforcement learning and the splits are more likely to behave like random choices. However, we want to make a couple of observations here to further justify the superior performance of RLT:
will not be affected by reinforcement learning and the splits are more likely to behave like random choices. However, we want to make a couple of observations here to further justify the superior performance of RLT:
The convergence rate of RLT depends at worst on the number p0. If nmin = nγ, then Theorem 3.7 gives the convergence rate of RLT1, which only depends on p1. However, in practice, nmin should be a much smaller number, which leads to further splits among the remaining p0 variables.
Without variable muting, convergence of a tree-based model should depend on p for small values of nmin. We can view the traditional marginal search in a tree-based model (such as random forests) as a simplified version of reinforcement learning which only evaluates the marginal variable importance. In that case, there still exists a threshold of node sample size such that for smaller nodes, the splitting rule behaves like a random choice. Although choosing a large nmin could limit this effect, variable muting, on the other hand, provides a convenient way to control the splits near terminal nodes.
4. NUMERICAL STUDIES
4.1 Competing methods and parameter settings
We compare our method with several major competitors, including the linear model with lasso, as implemented in the R package “glmnet” (Friedman et al. 2008); random forests (Breiman 2001), as implemented in the R package “randomforest”; gradient Boosting (Friedman 2001), as implemented in the R package “gbm”; Bayesian Additive Regression Trees (Chipman et al. 2008), as implemented in the R package “BayesTree”; Extremely randomized trees (Geurts et al. 2006), as implemented in the R package “extraTrees”. The proposed method is implemented using the R package “RLT” which is currently available at the first author’s personal webpage. We also include two interesting versions of random forests (RF-log(p) and ), and a naive version of the RLT method (RLT-naive). These three methods implement a simplified variable muting mechanism in a certain way. The two random forests adaptations, as their names suggest, first fit the RF model, select a set of log(p) (or ) most important variables, and then refit using only these variables. The RLT-naive method compares marginal signals for all variables at each split based on variance/misclassification reduction of multiple random splitting points. Then variables with low marginal signals, as opposed to global signals in RLT, are muted.
The details for all tuning parameter settings are given in the following Table 3. Noting that machine learning tools are always sensitive to tuning parameters, for all competing methods, we report the prediction error of the best tuning in each setting. For the proposed RLT model, we report the average test error for each of the 9 tunings. Note that this will benefit the competing methods and can only be done in a simulation study where the true model generator is known. However, by doing this, we eliminate as much as possible the impact of tuning for the competing methods. The reported prediction errors for competing methods thus fairly represents the best possible performance for them.
Table 3.
Tuning parameter settings
| Lasso | 10-fold cross-validation is used with α = 1 for the lasso penalty. We use lambda:min and lambda:1se for λ. | |
| Boosting | A total number of 1000 trees are fit. Testing error is calculated for every 20 trees. n:minobsinnode = 2, n1/3, 10. learning rate shrinkage = 0.001, 0.01, 0.1, interaction:depth = 1, 3, 5. | |
| BART | A total of 18 settings: ntrees = 50 or 200; Sigma prior: (3, 0.90), (3, 0.99), (10, 0.75); μ prior: 2, 3, 5. | |
| RF | A total of 36 settings: ntrees = 500, 1000; , p/3, p; nodesize = 2, n1/3. Bootstrap sample ratio = 1, 0.8, 2/3. | |
|
|
Select the top important variables from each RF model and refit with the same settings as RF (with mtry recalculated accordingly). | |
| RF-log(p) | Similar as , however with top log(p) variables selected. | |
| ET | ntrees = 500, 1000; , p/3, p; nodesize = 2, n1/3; numRandomCuts = 1, 5. | |
| RLT-naive | ntrees = 1000; nodesize = 2, n1/3; muting rate = 0%, 50%, 80%. Bootstrap sample ratio = 1, 0.8, 2/3. number of random splits = 10 or all possible splits. | |
| RLT | M = 100 trees with nmin = n1/3 are fit to each RLT model. We consider a total of 9 settings: k = 1, 2, 5, with no muting (pd = 0), moderate muting ( ), and aggressive muting ( ) as discussed in Remark 2.3. We set the number of protected variables p0 = log(p) to be on par with RF-log(p). Note that when pd = 0, all variables are considered at each internal node, hence no protection is needed. This is on par with RF. |
Remark 4.1
The purpose of reporting the test error for all RLT tunings is to compare and analyze the effect of the three different components: splitting variable selection, linear combination splitting and variable muting. Hence only the parameters involved in these components are tuned in our simulation study. Some other key parameters such as ntrees and nmin are not tuned for RLT in this simulation study since they are common to all tree-based methods. These parameters are irrelevant to the proposed new mechanism, and we want to eliminate their impact on our comparisons within RLT. In practice, we recommend that these parameters are always tuned as is done for other treebased methods.
4.2 Simulation scenarios
We create four simulation scenarios that represent different aspects which usually arise in machine learning. Such aspects include, training sample size, correlation between variables, and non-linear structure. For each scenario, we further consider three settings of the dimension p = 200, 500, 1000. We generate 1000 independent test samples to calculate the prediction mean squared error (MSE) or misclassification error. Each simulation is repeated 200 times, and the averaged prediction error (mean squared error or classification error) is presented in the way that we described previously. The simulation settings are as follows: Scenario 1: Classification with independent covariances. N = 100, . Let , where Φ denotes a normal c.d.f. Draw Yi independently from Bernoulli(μi). Scenario 2: Non-linear model with independent covariances. N = 100, . , where (·)+ represents the positive part. Scenario 3: Checkerboard-like model with Strong correlation. N = 300, , where Σi,j = 0.9|i−j|. . Scenario 4: Linear model. N = 200, . We set Σi,j = 0.5|i−j| + 0.2 · I(i≠j), and . For Scenario 2 – 4, we assume that εi are i.i.d. N(0, 1).
4.3 Simulation results
Tables 4, 5, and 6 summarize testing sample prediction error and corresponding standard error for each simulation setting. The best RLT method and competing method are bolded, with the best overall method underlined. There is clear evidence that the proposed RLT model outperforms existing methods under these settings. The proposed splitting variable selection, linear combination split, and variable muting procedure all work individually and also work in combination. In general, the results show preference towards RLT methods with aggressive muting and linear combination splits using 2 variables. Although the method falls behind the Lasso under the linear model setting (scenarios 4), which is expected, it outperforms all tree-based methods. RLT shows greater advantages for capturing the non-linear effects in scenarios 1, 2 and 3. In these scenarios across all different settings of p, the best RLT method reduces the prediction error by 31.9% – 41.5%, 23.7% – 36.4% and 16.7% – 28.8%, respectively, from the best competing method. To further understand each of the three components in RLT, we analyze them separately.
Table 4.
Classification/prediction error (SD), p = 200
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||
|---|---|---|---|---|---|---|
| RF | 21.3% (3.5%) | 8.35 (1.28) | 8.66 (0.55) | 5.93 (0.61) | ||
|
|
19.8% (3.6%) | 6.50 (1.30) | 6.97 (0.88) | 4.35 (0.47) | ||
| RF-log(p) | 15.2% (3.3%) | 4.55 (1.23) | 7.75 (1.74) | 3.23 (0.33) | ||
| ET | 18.3% (4.2%) | 4.61 (1.26) | 8.26 (0.60) | 4.57 (0.51) | ||
| BART | 25.7% (2.8%) | 8.00 (1.13) | 8.13 (0.83) | 2.63 (0.30) | ||
| Lasso | 26.5% (2.6%) | 9.99 (1.02) | 8.96 (0.50) | 1.12 (0.07) | ||
| Boosting | 21.3% (2.8%) | 8.47 (0.97) | 8.60 (0.53) | 2.85 (0.35) | ||
| RLT-naive | 19.0% (4.3%) | 4.65 (1.51) | 7.77 (0.69) | 4.59 (0.54) | ||
|
| ||||||
| RLT
|
||||||
| Muting | Linear combination | |||||
|
|
||||||
| None | 1 | 14.8% (4.0%) | 4.09 (1.00) | 5.43 (0.75) | 4.36 (0.52) | |
| 2 | 16.5% (4.3%) | 4.93 (1.27) | 5.71 (0.65) | 2.88 (0.44) | ||
| 5 | 18.9% (4.2%) | 5.52 (1.43) | 5.85 (0.62) | 2.80 (0.44) | ||
| Moderate | 1 | 11.8% (3.4%) | 3.20 (0.84) | 4.80 (0.74) | 3.27 (0.39) | |
| 2 | 12.2% (3.6%) | 3.43 (0.96) | 4.85 (0.71) | 2.13 (0.30) | ||
| 5 | 14.2% (4.0%) | 3.90 (1.18) | 4.89 (0.69) | 2.03 (0.30) | ||
| Aggressive | 1 | 10.3% (3.2%) | 2.79 (0.71) | 4.87 (0.81) | 3.23 (0.39) | |
| 2 | 9.8% (3.1%) | 2.66 (0.76) | 4.90 (0.80) | 1.84 (0.23) | ||
| 5 | 11.1% (3.4%) | 2.95 (0.94) | 4.74 (0.82) | 1.71 (0.22) | ||
For each scenario, the best two methods within each panel are bolded. The overall best method is underlined.
Table 5.
Classification/prediction error (SD), p = 500
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||
|---|---|---|---|---|---|---|
| RF | 23.5% (3.4%) | 9.44 (1.37) | 9.13 (0.59) | 6.74 (0.77) | ||
|
|
22.0% (3.6%) | 7.88 (1.44) | 8.02 (0.81) | 5.08 (0.60) | ||
| RF-log(p) | 18.5% (4.2%) | 5.34 (1.69) | 8.65 (1.48) | 3.57 (0.43) | ||
| ET | 20.9% (4.0%) | 5.92 (1.61) | 8.98 (0.60) | 5.16 (0.65) | ||
| BART | 28.0% (5.6%) | 8.95 (1.20) | 9.15 (0.59) | 3.26 (0.43) | ||
| Lasso | 27.0% (3.9%) | 10.16 (1.04) | 9.10 (0.59) | 1.14 (0.08) | ||
| Boosting | 23.7% (3.6%) | 9.23 (1.10) | 9.05 (0.59) | 3.13 (0.38) | ||
| RLT-naive | 21.7% (4.0%) | 6.00 (1.86) | 8.71 (0.71) | 5.24 (0.64) | ||
|
| ||||||
| RLT
|
||||||
| Muting | Linear combination | |||||
|
|
||||||
| No | 1 | 17.8% (4.0%) | 4.93 (1.20) | 6.96 (0.98) | 4.89 (0.62) | |
| 2 | 20.3% (4.0%) | 6.09 (1.40) | 7.09 (0.85) | 3.35 (0.52) | ||
| 5 | 22.6% (3.9%) | 6.88 (1.53) | 7.25 (0.83) | 3.27 (0.52) | ||
| Moderate | 1 | 14.9% (3.9%) | 3.88 (1.11) | 6.43 (1.08) | 3.69 (0.47) | |
| 2 | 16.5% (4.3%) | 4.53 (1.32) | 6.47 (0.98) | 2.48 (0.36) | ||
| 5 | 18.6% (4.0%) | 5.26 (1.51) | 6.54 (0.96) | 2.40 (0.36) | ||
| Aggressive | 1 | 12.8% (3.8%) | 3.39 (1.04) | 6.13 (1.09) | 3.35 (0.44) | |
| 2 | 13.5% (4.1%) | 3.45 (1.16) | 6.14 (1.06) | 2.01 (0.25) | ||
| 5 | 14.8% (4.0%) | 4.09 (1.41) | 6.11 (1.05) | 1.89 (0.24) | ||
For each scenario, the best two methods within each panel are bolded. The overall best method is underlined.
Table 6.
Classification/prediction error (SD), p = 1000
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||
|---|---|---|---|---|---|---|
| RF | 24.1% (2.7%) | 10.01 (1.32) | 9.13 (0.52) | 7.09 (0.65) | ||
|
|
22.7% (3.0%) | 8.71 (1.38) | 8.48 (0.85) | 5.42 (0.55) | ||
| RF-log(p) | 19.3% (3.7%) | 5.89 (2.40) | 8.93 (1.37) | 3.50 (0.35) | ||
| ET | 21.6% (4.0%) | 6.60 (1.65) | 9.09 (0.51) | 5.38 (0.51) | ||
| BART | 30.0% (6.2%) | 9.88 (1.30) | 9.14 (0.54) | 3.77 (0.52) | ||
| Lasso | 26.6% (3.6%) | 10.27 (1.19) | 9.07 (0.58) | 1.15 (0.09) | ||
| Boosting | 24.8% (3.1%) | 9.78 (1.16) | 9.05 (0.54) | 3.22 (0.37) | ||
| RLT-naive | 22.4% (2.5%) | 6.70 (1.90) | 9.01 (0.64) | 5.39 (0.58) | ||
|
| ||||||
| RLT
|
||||||
| Muting | Linear combination | |||||
|
|
||||||
| No | 1 | 18.8% (4.4%) | 5.64 (1.51) | 7.81 (1.07) | 5.08 (0.60) | |
| 2 | 21.0% (4.0%) | 6.97 (1.58) | 7.84 (0.87) | 3.47 (0.52) | ||
| 5 | 23.6% (3.4%) | 7.66 (1.57) | 8.01 (0.89) | 3.39 (0.52) | ||
| Moderate | 1 | 16.0% (5.0%) | 4.50 (1.47) | 7.48 (1.26) | 3.81 (0.45) | |
| 2 | 17.5% (4.5%) | 5.45 (1.68) | 7.48 (1.06) | 2.60 (0.39) | ||
| 5 | 20.4% (4.0%) | 6.26 (1.73) | 7.60 (0.98) | 2.49 (0.39) | ||
| Aggressive | 1 | 13.7% (4.9%) | 4.01 (1.38) | 7.20 (1.22) | 3.36 (0.42) | |
| 2 | 14.2% (5.1%) | 4.24 (1.55) | 7.07 (1.16) | 2.03 (0.29) | ||
| 5 | 16.1% (4.8%) | 5.05 (1.73) | 7.09 (1.05) | 1.91 (0.29) | ||
For each scenario, the best two methods within each panel are bolded. The overall best method is underlined.
Variable muting is the most effective component of RLT and this can be seen by comparing different muting rates of RLT. Across all scenarios and settings, aggressive muting versions of RLT outperform non-muting versions if not combined with linear combination. When we restrict the comparison between no muting and aggressive muting within RLT1, the improvement ranges from 10.3% to 31.8% when p = 200, ranges from 11.8% to 31.4% when p = 500, and ranges from 7.8% to 33.8% when p = 1000. Comparing the three random forest methods also reflects the benefits of limiting the splits to the strong variables. However, both and RF-log(p) can be a “hit-or-miss” approach, especially when there are strong correlations between covariates (this is observed in scenario 3 where RF-log(p) performs worse than and has large standard error). RLT, on the other hand, achieves a similar purpose in a robust way by adaptively choosing the protected variables for different nodes and different trees.
The embedded model is the foundation for our splitting variable selection, variable muting, and linear combination split. We first look at the solo effect of using the embedded model to select the splitting variable. This can be seem by comparing non-muting RLT1 with RF and ET, where the prediction error is reduced by up to 50.1% (vs. RF in Scenario 2) and 34.2% (vs. ET in Scenario 3) when p = 200. However, this solo effect reduces slightly as p increases. This is because the embedded model (a random forest model) becomes less accurate and the variable importance measure less trustworthy, especially when approaching the terminal nodes. Hence the embedded model works best when equipped with the variable muting mechanism, which can be seen by comparing aggressive RLT1 with RLT-naive, which is a model with variable muting, but not the embedded model. The performance difference of these two demonstrates the benefit of searching for global effects (RLT) and marginal effects (RLT-naive), while both perform variable muting. The improvement ranges from 29.6% to 45.9% for p = 200, ranges from 29.6% to 43.2% for p = 500, and ranges from 20.8% to 40.1% for p = 1000.
The improvement obtained from linear combination splits is also profound, especially in linear models (scenario 4). When the underlying model is linear, utilizing linear combination splits can yield huge improvements over RLT1 regardless of whether muting is implemented. The MSE reduction obtained by going from RLT1 to RLT5 is at least 33.3% under no muting and at least 43.2% under aggressive muting. The reason is that under such a structure, linear combination splits cut the feature space more efficiently. These results also demonstrate the effect of variable muting. However, this may not always be beneficial when the linear combination is not concentrated on strong variables. One cause of this is the lack of muting. Small sample size and a weak signal near terminal nodes create extra noise in the linear combination if a large number of variables need to be considered in the embedded model. The non-muting version of RLT in scenarios 1 and 2 are typical examples of this. However, as we mentioned before, the linear combination split also creates a more complex neighborhood structure within the set of strong variables when muting is implemented. Hence, RLT2 with aggressive muting can be considered the overall best method regardless of the presence of linear structure.
Our separate analysis of α in the Appendix shows that large linear combinations are likely to be affected by this tuning parameter, especially RLT5. This is because many of the noise variables are forced to enter the linear combination (such as in Scenarios 1 and 2) and to be protected. However, for RLT2, the performance is very stable, with or without muting. Also note that α does not affect RLT1 in any circumstances. In general, it is reasonable to use α = 0.25 as the default choice (implemented in the “RLT” package). And we shall use this value in the data analysis section.
4.4 Data analysis example
We analyze 10 datasets (Boston housing, parkinson, sonar, white wine, red wine, parkinson-Oxford, ozone, concrete, breast cancer, and auto MPG) from the UC Irvine Machine Learning Repository (http://archive.ics.uci.edu/ml/), a complete list of all datasets and their background information is provided in the Appendix. These datasets represent a wide range of research questions with the major purpose of either classification or regression with a single outcome variable. In this data analysis, we want to evaluate the performance of all previously mentioned methods and provide an overall comparison.
For each dataset, we standardized all continuous variables to have mean 0 and variance 1. We then randomly sample 150 observations without replacement as the training data, and use the remaining observations as a testing sample to compute the misclassification rate or mean squared error. We also add an extra set of covariates to increase the total number of covariates p to 500. Each of these extra covariates is created by combining a randomly sampled original covariate and a randomly generated noise, with a signal-to-noise ratio 1 to 2. Note that each of these extra covariates contain a small amount of signal hence they still preserve predictive values. We keep the same parameter settings as given in Table 3 for all competing methods. For RLT, considering the smaller sample size, the tuning parameter nmin is included with values 2 or n1/3.
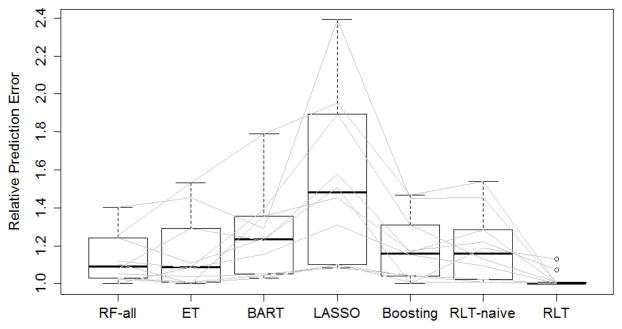
To compare results across all datasets, we plot the relative prediction errors in Figure 4.4. The relative prediction errors are calculated by comparing the performances of each method (misclassification error or mean squared error) with the best performance within the analysis of each dataset, and the best performance is always scaled to 1. RLT performs the best in 7 Out of the 10 datasets. The two largest improvement of RLT can be seen in the concrete and parkinson-Oxford datasets, where the performance of the second best methods are 29% (BART) and 25% (RF-log(p)) worse respectively. For the three datasets where RLT does not perform the best (Boston housing, sonar, and breast cancer), it remains among the top three methods with relative performance 1.01, 1.13, and 1.07 respectively. Further details of the analysis results are provided in the Appendix.
4.5 Numerical study conclusion and computational cost
In this numerical study section, we compared the performance of the proposed RLT method with several popular learning tools. Under both simulated scenarios and some benchmark machine learning Datasets, the results favor RLT methods. There is a significant improvement over competing methods in most situations, however, the results vary some depending on the choice of tuning parameters. RLT methods with moderate to aggressive muting generally perform the best and most stably across different settings, and incorporating linear combination splits seems almost always beneficial.
The proposed RLT model requires significantly larger computational cost. In a worst case scenario, RLT will fit as many as n1−γ, 0 < γ < 1 embedded models if we require the terminal sample size to be at least nγ. Hence the speed of the embedded model is crucial to the overall computational cost of RLT. In our current R package “RLT”, the default setting for an embedded model is extremely randomized trees with 100 trees and 85% resampling rate (sampled from the within-node data). Parallel computing with openMP is implemented to further improve the performance. The average computation times for Scenario 1 under different settings of n and p are summarized in Table 7. For RF and BART, the default setting is used. All simulations are done on a 4 core (8 threads) i7-4770 CPU.
Table 7.
CPU time (in seconds)
| n | 100 | 100 | 100 | 200 | 200 | 200 |
|---|---|---|---|---|---|---|
| p | 200 | 500 | 1000 | 200 | 500 | 1000 |
| RF | 0.3 | 0.8 | 5.2 | 0.6 | 1.7 | 7.8 |
| BART | 7.3 | 10.2 | 13.1 | 9.2 | 13.6 | 16.6 |
| RLT, no muting, k = 1 | 6.9 | 16.0 | 31.6 | 18.5 | 43.5 | 93.3 |
| RLT, no muting, k = 5 | 7.0 | 16.2 | 31.7 | 18.6 | 43.8 | 97.1 |
| RLT, aggressive muting, k = 1 | 2.7 | 5.8 | 10.8 | 6.6 | 14.3 | 28.6 |
| RLT, aggressive muting, k = 5 | 2.8 | 5.9 | 10.9 | 6.7 | 14.5 | 29.1 |
5. DISCUSSION
We proposed reinforcement learning trees in this paper. By fitting an embedded random forest model at each internal node, and calculating the variable importance measures, we can increase the chance of selecting the most important variables to cut and thus utilize the available training samples in an efficient way. This shares the same view as the “look-ahead” procedures in the machine learning literature (Murthy and Salzberg, 1995). The variable muting procedure further concentrates the splits on the strong variables at deep nodes in the tree where the node sample size is small. The proposed linear combination splitting strategy extends the use of variable importance measures and creates splitting rules based on a linear combination of variables. However the linear combination is not exclusively searched (Murthy et al., 1994), hence no further computational burden is introduced. All of these procedures take advantage of Reinforcement Learning and yield significant improvement over existing methods especially when the dimension is high and the true model structure is sparse. There are several remaining issues we want to discuss in this section.
The number of trees M in RLT does not need to be very large to achieve good performance. In all simulations, we used M = 100. In fact, the first several splits of the trees are likely to be constructed using the same variables, which makes them highly correlated (if we use k = 1). However, using linear combination splits (k > 1) introduces a significant amount of randomness into the fitted trees since the coefficients of the linear combinations vary according to the embedded model. In practice, the embedded model is estimated using a small number of observations, however, the prediction accuracy of an embedded model is not the major concern here since we only need the ranks of variable importance measures to be reliable, i.e., variables with large V I are ranked at the top by the embedded model. This allows many alternative methods to be used as the embedded model as long as they provide reliable variable rankings, however, exploring them is beyond the scope of this paper. For the muting parameter pd, we considered only three values and the performance is satisfactory. However, ideally the muting parameter pd can account for the different combinations of n and p. In our “RLT” package, an ad-hoc formula is proposed: for moderate muting, and 1 − (log(p)/p)1/log2(n/40) for aggressive muting. The choice is motivated by the simulation results in Biau (2012), which shows that when n = 25 and p = 20, the search for a splitting rule behaves almost like a random pick. However, our toy example in the Appendix shows that this may depend heavily on the underlying data generator. While our aggressive muting procedure achieves satisfactory performance, optimal tuning may require further experiments. We found that tuning the number of the protected variables p0 is less important in our simulations, and in practice, setting a slightly larger k value achieves the same purpose as p0. We suggested to use nm in = n1/3 based on our theoretical developments. However, in practice, tuning this parameter is always encouraged. When p is extremely large, the number of trees in the embedded model should be increased accordingly to ensure reliable variable importance measure estimation. The “RLT” package provides tunings for the embedded model. A summary of all tuning parameters in the current version of “RLT” is provided in the supplementary file.
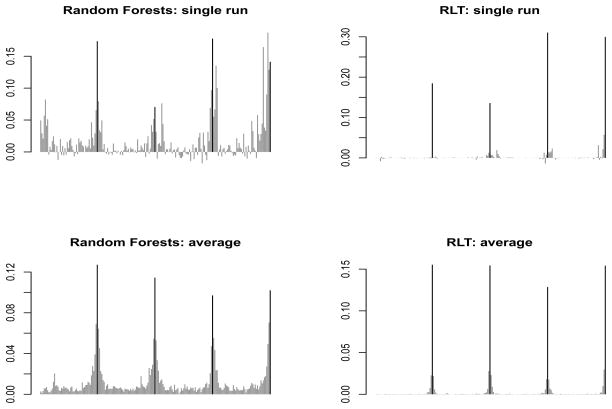
As we discussed in the introduction, a desirable property of RLT is the “sparsity” of the fitted model, although this is not directly equated with “sparsity” as used in the penalization literature. Figure 2 demonstrates this property of RLT as compared to a random forests model. We take Scenario 3 in the simulation section as our demonstration setting. The upper panel compares the variable importance measures of a single run, and the lower panel compares the averaged variable importance measures over 100 runs. In an RLT model, noise variables have very little involvement (with V I = 0) in tree construction. This is due to the fact that most of them are muted during early splits, engendering the “sparsity”. The average plot shows a similar pattern while RLT has a much larger separation between the strong and the noise variables compared to Random forests. On the other hand, random forests tend to have spikes at noise variables. This also shows that RLT is potentially a better non-parametric variable selection tool under the sparsity assumption. However, this sparsity comes at the expense of sacrificing some correlated variables, as shown in the plots. The chance of selecting the highly correlated variables (located at the neighborhood of 50, 100, 150 and 200) is reduced. In situations where correlated variables are also of interest, special techniques may be needed.
Figure 2.
Comparing variable importance of Random Forests and RLT
Black: Strong variables; Gray: Noise variables.
P = 200, strong variables are located at 50, 100, 150 and 200.
Our theoretical results analyze tree-based methods from a new perspective, and the framework can be applied to many tree-based models, including many “greedy” versions. We showed that a tree splitting process involves different phases. In the early phase (corresponding to
 ∪
∪
 in Section 3), when the sample size is large, the search for splitting rules has good theoretical properties, while in the later phase, the search for splitting variables is likely to be essentially random. This causes the convergence rates for most tree-based methods to depend on p if nmin is not large enough. Variable muting is a convenient way to solve this problem.
in Section 3), when the sample size is large, the search for splitting rules has good theoretical properties, while in the later phase, the search for splitting variables is likely to be essentially random. This causes the convergence rates for most tree-based methods to depend on p if nmin is not large enough. Variable muting is a convenient way to solve this problem.
There are several other key issues that require further investigation. First, we assume independent covariates, which is a very strong assumption. In general, correlated covariates pose a great challenge for non-parametric model fitting and variable selection properties theoretically. To the best of our knowledge, there is no developed theoretical framework for greedy tree-based methods under this setting. One of the possible solutions is to borrow the irrepresentable condition (Zhao and Yu, 2006) concept into our theoretical framework. The irrepresentable condition, given that the true model is indeed sparse, essentially prevents correlated variables from fully explaining the effect of a strong variable. Hence a strong variable will still have a large importance measure with high probability. This part of the work is currently under investigation but is beyond the scope of this paper. Second, splitting rules using linear combinations of variables results in non-hypercube shaped internal nodes, which introduces more complexity into the fitted trees. Moreover, the linear combinations involve correlated variables which adds yet further complications. Third, it is not clear how ensembles of trees further improve the performance of RLT in large samples. However, due to the feature selection approach in RLT, there is a possible connection with adaptive nearest neighborhood methods and adaptive kernel smoothers (Breiman, 2000). These and other related issues are currently under investigation.
Supplementary Material
Figure 1.
Relative prediction errors on 10 machine learning datasets
The relative performance in 10 machine learning datasets: (Boston housing, parkinson, sonar, white wine, red wine, parkinson-Oxford, ozone, concrete, breast cancer, and auto MPG). For each dataset, a random training sample of size 150 is used. RF-all represents the best performance among RF, , and RF-log p. Each gray line links the performance of the same dataset.
Acknowledgments
The authors thank the editors and reviewers for their careful review and thoughtful suggestions which led to a significantly improved paper. The authors were funded in part by grant CA142538 from the National Cancer Institute.
6. APPENDIX
Proof of Theorem 3.7
We prove this theorem in two steps. First, we show that for the entire constructed tree, with an exponential rate, only strong variables are used as splitting variables. Second, we derive consistency and error bounds by bounding the total variation using the terminal node size variable importance which converges to zero.
Step 1
In this step, we show that for the entire tree, only strong variables are used as the splitting variable, and furthermore, the variable importance measure for the splitting variable is at least half of the maximum variable importance at each split. First, it is easy to verify that, both a) and b) in Theorem 3.6 can be satisfied simultaneously with probability bounded below by
| (4) |
Define
 as the set of all internal nodes. Recall that ψ1(δ) and ψ2(bj − aj) can be approximated by δζ1 and (bj − aj)ζ2, respectively. Thus we can always find a γ* < 1 such that when nA > nγ*,
. We define two groups of internal nodes
as the set of all internal nodes. Recall that ψ1(δ) and ψ2(bj − aj) can be approximated by δζ1 and (bj − aj)ζ2, respectively. Thus we can always find a γ* < 1 such that when nA > nγ*,
. We define two groups of internal nodes
 = {Ai, s.t. Ai ∈
= {Ai, s.t. Ai ∈
 , nAi ≥ nγ*} and
, nAi ≥ nγ*} and
 = {Ai, s.t. Ai ∈
= {Ai, s.t. Ai ∈
 , nAi < nγ*}, where nAi is the sample size at node Ai. Then we bound the probability:
, nAi < nγ*}, where nAi is the sample size at node Ai. Then we bound the probability:
| (5) |
For all internal nodes in
 , the number of nonmuted variables is less than or equal to p. Hence, by the monotonicity of η(·) in Assumption 3.4 and Equation (4), the first term in Equation 5 can be bounded above by
, the number of nonmuted variables is less than or equal to p. Hence, by the monotonicity of η(·) in Assumption 3.4 and Equation (4), the first term in Equation 5 can be bounded above by
| (6) |
Note that in
 , the node sample size is less than nγ*. Since we choose the splitting point uniformly between the q-th and (1 − q)-th quintile, to reach a node in
, the node sample size is less than nγ*. Since we choose the splitting point uniformly between the q-th and (1 − q)-th quintile, to reach a node in
 , we need to go through a minimum of −γ* logq(n) splits. Noticing that this number goes to infinity, and that we mute pd variables after each split, all variables except the ones in the protected set should be muted in
, we need to go through a minimum of −γ* logq(n) splits. Noticing that this number goes to infinity, and that we mute pd variables after each split, all variables except the ones in the protected set should be muted in
 . Hence, the second term in Equation (5) can be bounded above by
. Hence, the second term in Equation (5) can be bounded above by
| (7) |
Noting that
 ∪
∪
 =
=
 , and that they contain at most n1 −
γ elements, and combining Equations (6) and (7), we obtain:
, and that they contain at most n1 −
γ elements, and combining Equations (6) and (7), we obtain:
which goes to zero at an exponential rate. Thus the desired result in this step is established.
Step 2
Now we start by decomposing the total variation and bounding it by the variable importance:
| (8) |
where f̄At is the conditional mean of f within terminal node At, and where t indexes the terminal node. Noting that each terminal node At in f̂ contains nAt ≥ nγ observations, and that the value of f̄ at each terminal node is the average of the Y s, it must therefore have an exponential tail. Hence the first term in Equation (8) can be bounded by:
| (9) |
The second sum in Equation (8) can be further expanded as
| (10) |
The Cauchy-Schwartz inequality now implies that
| (11) |
For each given At, due to the independence of Z and X, the expectation in every summand can be decomposed as
| (12) |
Note that the variables with the labels p1 + 1, …, p are in the set
 of noise variables. Changing the values of these components will not change the value of f. Hence the last term in the expectation of (12) is equal to
of noise variables. Changing the values of these components will not change the value of f. Hence the last term in the expectation of (12) is equal to
Again, since all the components of X and Z are independent, the jth term in the expectation of (12) corresponds to the variable importance of the jth variable. Thus we have:
| (13) |
It remains to show that as n → ∞. Using Lemma 2.1 in the supplementary file, we have maxj V IAt(j) = O(n−C1) = O (n−2rγlogq(1−q)/(rp1)p1+1), where r is a constant satisfying r > 1 and 2(1 − q)2r/q2 ≤ 1. Hence combining equations (8), (9) and (13), we have
| (14) |
Due to the monotonicity of the contribution from C1, this rate is also monotone decreasing in p1. Noticing that C3 does not depend on p, the convergence rate depends only on the choice of γ, q, and the number of strong variables p1. This concludes the proof.
References
- Amit Y, Geman D. Shape quantization and recognition with randomized trees. Neural Computing. 1997;9(7):1545–1588. [Google Scholar]
- Biau G. Analysis of a random forests model. Journal of Machine Learning Research. 2012;13:1063–1095. [Google Scholar]
- Biau G, Devroye L, Lugosi G. Consistency of random forests and other averaging classifiers. Journal of Machine Learning Research. 2008;9:2015–2033. [Google Scholar]
- Breiman L. Bagging Predictors. Machine Learning. 1996;24:123–140. [Google Scholar]
- Breiman L. Technical Report 577. Department of Statistics, University of California; Berkeley: 2000. Some infinity theory for predictor ensembles. [Google Scholar]
- Breiman L. Random Forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- Breiman L, Friedman J, Olshen R, Stone C. Classification and Regression Trees. Pacific Grove, California: Wadsworth International Group; 1984. [Google Scholar]
- Bureau A, Dupuis J, Falls K, Lunetta KL, Hayward B, Keith TP, Van Eerdewegh P. Identifying SNPs predictive of phenotype using random forests. Genetic epidemiology. 2005;28(2):171–182. doi: 10.1002/gepi.20041. [DOI] [PubMed] [Google Scholar]
- Chipman HA, George EI, McCulloch RE. BART: Bayesian Additive Regression Trees. Ann Appl Stat. 2010;4(1):266–298. [Google Scholar]
- Cutler A, Zhao G. PERT-perfect random tree ensembles. Computing Science and Statistics. 2001;33:490–497. [Google Scholar]
- Díaz-Uriarte R, De Andres SA. Gene selection and classification of microarray data using random forest. BMC bioinformatics. 2006;7(1):3. doi: 10.1186/1471-2105-7-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietterich T. An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting and Randomization. Machine Learning. 2000;40:139–157. [Google Scholar]
- Geurts P, Ernst D, Wehenkel L. Extremely Randomized Trees. Machine Learning. 2006;63(1):3–42. [Google Scholar]
- Ishwaran H, Kogalur UB, Blackstone EH, Lauer MS. Random survival forests. The Annals of Applied Statistics. 2008:841–860. [Google Scholar]
- Kim H, Loh W-Y. Classification trees with unbiased multiway splits. Journal of the American Statistical Association. 2001;96(454) [Google Scholar]
- Lin Y, Jeon Y. Random forests and adaptive nearest neighbors. Journal of the American Statistical Association. 2006;101:578–590. [Google Scholar]
- Lunetta KL, Hayward LB, Segal J, Van Eerdewegh P. Screening large-scale association study data: exploiting interactions using random forests. BMC genetics. 2004;5(1):32. doi: 10.1186/1471-2156-5-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy KVS, Salzberg SL. PhD thesis. Citeseer: 1995. On growing better decision trees from data. [Google Scholar]
- Murthy SK, Kasif S, Salzberg S. A system for induction of oblique decision trees. 1994 arXiv preprint cs/9408103. [Google Scholar]
- Statnikov A, Wang L, Aliferis CF. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC bioinformatics. 2008;9(1):319. doi: 10.1186/1471-2105-9-319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strobl C, Boulesteix A-L, Zeileis A, Hothorn T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC bioinformatics. 2007;8(1):25. doi: 10.1186/1471-2105-8-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 1996:267–288. [Google Scholar]
- van der Vaart A, Wellner J. Weak Convergence and Empirical Processes: With Applications to Statistics. New York: Springer; 1996. [Google Scholar]
- Zhao P, Yu B. On model selection consistency of Lasso. The Journal of Machine Learning Research. 2006;7:2541–2563. [Google Scholar]
- Zhu R, Kosorok MR. Recursively imputed survival trees. Journal of the American Statistical Association. 2012;107(497):331–340. doi: 10.1080/01621459.2011.637468. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



 for the two daughter nodes by adding the variables with the lowest variable importance measures at the current node. Details are given in Section 2.6.
for the two daughter nodes by adding the variables with the lowest variable importance measures at the current node. Details are given in Section 2.6.