The Many Flavors of Model‐Based Meta‐Analysis: Part I—Introduction and Landmark Data

Abstract

Meta‐analysis is an increasingly important aspect of drug development as companies look to benchmark their own compounds with the competition. There is scope to carry out a wide range of analyses addressing key research questions from preclinical through to postregistration. This set of tutorials will take the reader through key model‐based meta‐analysis (MBMA) methods with this first installment providing a general introduction before concentrating on classical and Bayesian methods for landmark data.

Understanding the key safety and efficacy attributes of other compounds, either on the market or in the pipeline, is of critical importance for companies developing new drugs. There is a need for new compounds to differentiate from current standard of care (SOC) treatments and it is generally no longer desirable or acceptable to produce “me too” drugs.

Clearly, when a company needs to show improvement over an SOC, it is vitally important to fully understand the safety and efficacy characteristics of that SOC in comparison to placebo (or other comparator). The best way to do this is to carry out a meta‐analysis to quantify these characteristics as accurately as possible. A meta‐analysis uses statistical methods to pool and analyze data across multiple studies.

Ideally any meta‐analysis approach should be geared toward specific research questions, and the types of questions will be discussed in more detail in the next section. Meta‐analysis can be used to answer a wide variety of questions and there are a range of methods that can be applied. Different disciplines (e.g., pharmacometrics and statistics) might use different but equally valid approaches to answer the same question using techniques that are common to their field.

The term “model‐based meta‐analysis” (MBMA) has tended to sit in the clinical pharmacology world where pharmacologic models, such as E_max, are applied to meta‐data.1 Here, the desire is to use all available relevant information, such as time‐course and dose information that fits in with the learning (rather than just confirming) approach to drug development.2 Mould3 gives an overview of how MBMA is an important tool for quantitative decision‐making and there is an increasing pool of published examples.4, 5, 6 However, MBMA is not exclusive to the clinical pharmacology area, as many meta‐analyses involve models and this tutorial uses the term in this wider context where MBMA forms part of model‐based drug development and pharmacostatistical models are applied to safety and efficacy data across all phases of drug development for informed decision‐making.7, 8

Meta‐analysis methodology continues to advance and evolve. Sutton and Higgins9 provide a useful overview of recent developments as of 2008 and, since then, areas such as network meta‐analysis (NMA) have grown exponentially.9, 10

The purpose in this set of articles is to illustrate the various models and techniques used both within and outside the clinical pharmacology world to hopefully provide a wider picture. Code and datasets will allow the reader to replicate the results presented.

Typically, meta‐analysis is the quantitative synthesis of a systematic review; a thorough review of the available data/literature using explicit and reproducible steps. This involves defining the research questions, specifying the participants, interventions, comparators, outcomes, and studies, developing the search criteria and sources, study selection, data collection, and assessment of bias.11 There is increasing literature and guidance on the process and quality of systematic review (e.g., Cochrane handbook, Grades of Recommendation, Assessment, Development and Evaluation (GRADE), and Preferred Reporting Items for Systematic Reviews and Meta‐Analyses) and, although crucial to the quality of the resulting meta‐analysis, this set of articles will assume that all data are correct and appropriate.12, 13, 14, 15

The Preferred Reporting Items for Systematic Reviews and Meta‐Analyses statement consists of a 27‐item checklist and a four‐phase flow diagram. The checklist includes items deemed essential for transparent reporting of a systematic review or meta‐analysis across seven sections: title, abstract, introduction, methods, results, discussion, and funding. There are several specialized extensions to the guidelines, including one which is tailored to the specific requirements of reporting systematic reviews and meta‐analysis of individual patient data and another developed specifically to improve the reporting of NMA.16, 17 It is strongly recommended that these guidelines are followed when reporting the results of a formal meta‐analysis. However, the focus of this set of articles was methodology and any results presented are examples to illustrate this methodology rather than a formal report.

This first article serves as an introduction to MBMA and then focuses mainly on the analysis of landmark data. The next (second) section discusses the types of questions that can be addressed with MBMA. The next (third) section describes the key methodologies for landmark data. The next (fourth) section gives an overview of some of the software that can be used to conduct meta‐analysis. The next (fifth) section presents two landmark examples, one a traditional pair‐wise meta‐analysis and the other a dose response model, along with corresponding models and results. The next (sixth) section provides some closing discussion and the next (seventh) section briefly describes some of the methodologies that will be covered in future tutorials.

In the Supplementary Materials, R, NONMEM, and OpenBUGS code are provided and the datasets used will be available from the journal website to allow users to reproduce the results.18, 19, 20

WHY META‐ANALYSES ARE CONDUCTED

The motivation behind doing a meta‐analysis can vary a great deal depending on which research questions are being asked. This section will outline some key uses of meta‐analysis in clinical drug development.

Identifying a disease level desired profile

Typically, a product concept will be developed for a disease area using customer insights from payers, prescribers, and regulatory bodies, with a goal of identifying key features of a drug together with target values. MBMA may be used to speculate how a new drug is expected to compare to the current SOC and the emerging competition, both positively and negatively. This aids a drug development strategy driven by valuable differentiation and creates a strong foundation for decision‐making as data become available.

Learning and hypothesis generating

A great deal of published meta‐analyses focus on specific endpoints, such as change from baseline at a time‐point (e.g., end of study) or an adverse event incidence rate and might look to see whether a treatment is significantly better than a placebo or a comparator. However, there is a great amount of learning that can be gained from meta‐analyses that lends itself to estimation rather than formal hypothesis testing. For example, there may be a need to understand the time‐course of a comparator and/or placebo response to assess onset of action and/or maintenance of effect. After readout of a short phase 2 study, the clinical team may want to predict the likely response at later time‐points for a phase 2b study. Correlation between end points may be useful if a drug project is changing its primary end point of interest, although this topic is not without its issues.21, 22 Studies in a specific indication may have changed over time with regard to placebo response, background therapy, or treatment comparator. Differing design or population characteristics may inform variation in placebo response. Information on all these aspects may be available in the literature or other internal drug programs.

Generating target values for decision‐making

Decision criteria are increasingly being used to help quick and efficient decision‐making after study readout. These decision criteria are commonly based on the performance characteristics of the current SOC or other advanced pipeline drugs. One such decision criteria might be that on readout of a proof of concept study, the primary end point achieves a minimum target value that comes from a meta‐analysis of a key comparator. The target value could be the point estimate itself from the meta‐analysis or a scalar of it (e.g., target is 50% greater than SOC).

Comparative effectiveness

In general, comparative effectiveness research is the direct comparison of two or more existing health care interventions to determine which works best for which patients and which poses the greatest benefits and harms. NMA, incorporating mixed treatment comparisons and indirect treatment comparisons, provides quantitative information for evidence‐based decision‐making in the absence of randomized controlled trials involving direct comparisons of all the treatments of interest within the studies.23 Mixed treatment comparisons combines both direct and indirect evidence for particular pairwise comparisons, thus synthesizing more evidence than traditional pairwise meta‐analysis.

NMA allows simultaneous comparison of multiple treatment options that have been compared in randomized controlled trials forming a connected network of treatment comparisons, and provides a framework for model comparison and assessment of evidence consistency and is typically performed on summary level data during late‐stage development in order to compare relative performance of multiple (>2) drugs, for a single end point, at a single time point for a specific treatment regime of interest.

An NMA provides two measures of comparative effectiveness for a specific outcome: the relative treatment effect for all pairwise comparisons and a ranking of the treatments.

Other forms of MBMA can also be used for comparative effectiveness in the absence of direct comparisons of all the treatments of interest.

Putting a study result into context

After a study reads out, it is useful to plot the new data alongside the relevant historical data to assess, for example, how the placebo response compares to the older data, to highlight other similarities and differences, and to investigate possible explanations for these differences.

Simulating new studies based on internal patient level data and external SOC data

It may be planned to include the SOC treatment in a future study to go head‐to‐head with the experimental drug. In order to understand the operating characteristics of this future study, a model combining the previous internal patient level data and the summary level comparator data may be used to simulate different study designs. This simulation work can help to quantify the probability of a new drug being superior to the SOC to inform the design of the study and to construct meaningful quantitative go/no go criteria for the drug program based on prior assumptions with which to compare the actual study results. The challenges of such modeling include the combining of aggregate data and individual patient data, and possibly making an indirect comparison between two compounds that have never been compared head‐to‐head.24

LANDMARK META‐ANALYSIS METHODOLOGIES

A landmark meta‐analysis is defined here as the analysis of a response at a single timepoint (e.g., pain response at week 12) across multiple studies rather than modeling multiple timepoints (longitudinal meta‐analysis). Primary and secondary end points in clinical trials are usually of this nature.

Sources of variation

To estimate mean drug effects, there are at least three sources of variation to consider:

1. Sampling error, the error caused by observing a sample instead of the whole population.

2. Study‐level characteristics, where patient differences or study differences are qualitative or quantitative effect modifiers.

3. Between‐study variation, the remaining, unexplained, variability in treatment effects across studies. Note, when pooling within‐trial contrasts, the main effect of trial has been eliminated and so this “between‐study variability” reflects the treatment‐by‐study interaction.25

Statistical models

There are two general types of statistical model for meta‐analysis which are fixed effects and random effects, as described below.26

Fixed effects

In fixed effect models (Figure 1), this tutorial uses the definition that each study provides an estimate for the same underlying mean effect (θ). There is no between‐study variation in treatment effect (after possibly accounting for covariates). The studies only differ in how well the study sample estimates θ. Each of the red dots in Figure 1 represents a study result with the assumption that the underlying true effect is identical and any observed deviation from that true effect is due to sampling error, as described above.

Figure 1.

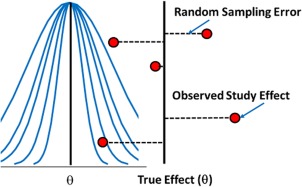
Illustration of fixed effects assumption.

It should be noted that the fixed effect method is valid without assuming a common underlying effect size.27 However, for simplicity of understanding, this article uses the definition that does assume homogeneity across trials.

Random effects

In random effects models (Figure 2), each study is associated with a different, but related, underlying parameter (θ_i) distributed around a mean effect (θ). In Figure 2, each of the red dots represents observed study results (Y_i) that are assumed to belong to a common distribution. After accounting for covariates, there is still some unexplained between‐study variability in addition to sampling error. Alternatively, there may not be any measured covariates that explain this between‐study variability in response that creates more uncertainty going forward with new studies.

Figure 2.

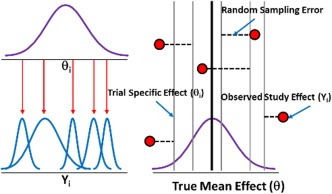
Illustration of random effects assumption.

Assessment of heterogeneity

Because meta‐analyses typically pool studies that are diverse clinically and methodologically, it is unlikely that a common effect exists. This is due to differences in studies, such as patient inclusion criteria, background treatment, dosing regimens, or study quality. If a common effect cannot be assumed, then heterogeneity is believed to be present.

There are a variety of methods to assess heterogeneity. Higgins et al.28 provide an overview and assessment of several methods, including the Q statistic, I², H², R, and the value of τ². They concluded that I² and H² are useful and so these are described below together with the Q statistic, which is used to derive both methods.

Q statistic

The classical measure of heterogeneity is Cochran's Q:

$$Q={\displaystyle \sum _{i=1}^r{W}_i}{\left({\widehat{\theta }}_i-{\widehat{\theta }}_{FE}\right)}^2, \text{where} \text{weight} W_i=\frac{1}{s_i^2},$$

s_i is the within study standard error of ${\widehat{\theta }}_i$, ${\widehat{\theta }}_i$ is the observed treatment difference for the i^th study, and ${\widehat{\theta }}_{FE}$ is the fixed effect estimate for the r studies. Q follows approximately a χ² distribution with r−1 degrees of freedom (df). A problem with the Q statistic is that it has poor power when there are small numbers of trials in the meta‐analysis and is overpowered when there are many studies.28, 29 This means that Q statistic values cannot routinely be compared across meta‐analyses.

I² statistic

I² is a commonly used measure of the degree of inconsistency across studies and is a percentage of total variance that is due to heterogeneity rather than to chance. It is calculated as:

$$I^2=100\%\times \frac{\left(Q-df\right)}{Q}$$

Like Q, I² has major flaws. Rücker et al.30 showed that, as within study precision increases, for constant between study variability (τ²), I² increases toward 100%. Given the potentially different study sizes and precision within and across meta‐analyses, this statistic may be of little use as a comparison between them.

H² statistic

H² is the relative excess in Q compared to the expected value of Q (when there is no heterogeneity). Hence, H² = Q/(r−1). Unlike Q, H² does not depend on the number of studies in the meta‐analysis. A value of one would indicate no heterogeneity. There are several methods for producing intervals for H² where the lower bound can be compared to one to evaluate whether there is meaningful heterogeneity.31

Between‐study variance (τ²)

τ² represents the between‐study variance based on a random effects analysis that provides a measure of the extent of heterogeneity but not a measure of impact. It is specific to a particular treatment measure and cannot be compared across meta‐analyses.

Prediction interval

The presence of significant heterogeneity creates uncertainty for future studies that might be conducted. A prediction interval for the true effect (θ_i) in a theoretical new study will demonstrate the consequence of heterogeneity as it incorporates both the precision of the estimate and the between‐study variability.32 Unlike a confidence interval, prediction intervals are about future expected data and in drug development that is usually an important consideration, rather than just quantifying the precision of treatment effects of different compounds. For the two examples in the fifth section, prediction intervals will be presented alongside the fixed effects and random effects estimates. As Higgins et al.32 describe, an approximate 100(1−α)% prediction interval for a new study can be written as:

$$\widehat{\mu }\pm t_{r-2}^{\alpha }\sqrt{\{{\widehat{\tau }}^2+S\widehat{E}{(\widehat{\mu })}^2\}}$$

Where there are r studies, $\widehat{\mu }$ is the random effects estimate of the response of interest, $S\widehat{E}(\widehat{\mu })$ is the corresponding standard error, and ${\widehat{\tau }}^2$ is the estimated between‐study variance. Note that with the Bayesian approach there is uncertainty in the between‐study variance estimate, as well as the effect estimate.

It is recommended that the prediction interval along with an estimate of τ and corresponding confidence interval are presented and assessed. Although cautious in advocating their use, code to produce Q, I², and H² with corresponding confidence intervals is provided in the Supplementary Materials.31

Meta‐regression

Some of the between‐study variability may be explained by covariates that have been recorded across the study publications. These covariates can be formally fitted as part of a model (meta‐regression) to assess their influence. There are challenges with having covariates that are at the mean level though, in that there may be little difference across studies in those mean covariate values if populations are similar. Patient level data will typically be more informative for understanding the effect of covariates on response. Not all studies may report the covariate of interest, further complicating the analysis. It is important not to interpret summary level meta‐regression effects as subject‐level effects, as typically covariate effects are characterized at the group level. This is analogous to ecological analysis in which all individuals (e.g., defined geographically) are assigned an average valuation for a covariate (e.g., proportion of men). Aggregation bias, or ecological fallacy, is the difference between the association at the individual and group level.33

Dose‐response models

Dose‐response is a key part of MBMA. In describing dose‐response relationships, it may be important to know, for example, the maximal drug effect, whether the effect is dose‐dependent or whether there is a lower dose to give a similar effect. There are any number of possible models that could be used for dose‐response in this descriptive sense and the choice of model depends on the range of doses studied, whether to include placebo effects and other features seen in the data, such as curvature.

The most commonly used model for dose‐response is E_max, a nonlinear function of dose closely related to the logistic curve.

$$\text{ Response}={\text{E}}_0+\frac{{\text{E}}_{\max }\times {\text{Dose}}^{\text{λ}}}{{\text{ED50}}^{\text{λ}}+{\text{Dose}}^{\text{λ}}}$$

The three main parameters are E₀ (placebo effect), E_max (maximal change over placebo), and ED₅₀ (dose to give 50% of the maximal effect). The sigmoidal E_max model, adds a fourth, Hill, parameter, $\lambda$, which describes the “steepness” of the S‐shape of the dose‐response relationship.

Other models commonly used for dose‐response relationships include exponential, linear, log‐linear, quadratic, and logistic.34

PUBLICATION BIAS

A major concern in any meta‐analysis is that not all studies may have been published and that there may be a systematic reason for this, such as only “positive” results being reported. There are a variety of tools, both qualitative and quantitative, available to assess this. A recommended first step is to produce a funnel plot that typically plots a treatment difference (or other measurement of treatment effect) vs. a function of sample size, such as the standard error or variance of the treatment difference. In the absence of publication bias, the plot should show a symmetric funnel. An asymmetric funnel plot does not necessarily mean that there is publication bias as there are several reasons why a funnel plot may not seem symmetric, including random chance and differences between the studies in terms of, for example, study designs and populations. As will be seen in the first example, when there are small numbers of studies in the meta‐analysis, it will be hard to see symmetry or asymmetry clearly. There are also quantitative techniques that attempt to formally assess the asymmetry, such as the Begg and Mazumdar35 rank correlation method and Egger et al.36 meta‐regression. These methods will be applied to the first example dataset in the next (fifth) section using the R package “Metafor.” There are several other statistical methods to assess publication bias, but we touch only on the ones already described.37

SOFTWARE

There are many software packages that can carry out meta‐analysis (STATA and Review Manager [RevMan] being just two examples).38, 39 For the traditional meta‐analysis, the authors focus on R (using the “metaphor” package with version 3.0.2 of R) and OpenBUGS (version 3.2.3 run from R).40 For the dose response example, NONMEM (version 7.2) will be used and compared with OpenBUGS.19

Within the R package “metaphor” are various meta‐analysis related functions, including “forest,” which produces forest plots and “RMA,” which can carry out fixed‐effect and random‐effects meta‐analysis and can also incorporate covariates for meta‐regression. These meta‐analysis results can be easily incorporated into the forest plot as can Bayesian estimates from OpenBUGS, which is an advantage of doing both the classical and Bayesian analyses in R.

NONMEM is commonly used for pharmacokinetic/pharmacodynamic modeling as it is well suited to fitting non‐linear mixed‐effects models and dealing with different types of pharmacokinetic models. It has also been used for MBMA, particularly for dose response and/or time‐course modeling.

Use of R, OpenBUGS, and NONMEM will be demonstrated in the Supplementary Materials with comprehensive annotations to explain the code.

EXAMPLES

Example 1: Western Ontario and McMaster Universities pain in osteoarthritis

In order to understand the efficacy characteristics of naproxen in osteoarthritis pain of the knee or hip, internal reports and external literature were searched to find placebo‐controlled studies. Only double blind, placebo‐controlled, randomized, parallel group studies were considered, in which both naproxen 500 mg (given twice a day) and placebo were treatment arms. The end point of interest was the Western Ontario and McMaster Universities (WOMAC) pain score, which consists of five pain‐related questions each of which takes a discrete value from 0 (no pain) to 4 (maximum pain).41 For each subject, the scores from these five questions are added together to give a total score between 0 (no pain) and 20 (maximum pain). This end point tends to be the primary end point in osteoarthritis pain trials and is typically treated as a continuous random variable. The week two arithmetic means were chosen to be analyzed in the meta‐analysis. Supplementary Materials Table S1 presents the difference in mean change from baseline in WOMAC pain between naproxen and placebo, with its corresponding standard error. For “flare” trials, subjects were washed out of their pain medications and were required to have a predefined increase in pain (flare) to be eligible for randomization.

Research questions

There were two specific research questions for this example. As described above, a target value was required for a two‐week proof of concept study in osteoarthritis pain for a compound with a new mechanism. As this new compound was not being directly compared to SOC in the proof of concept study, a target value was required based on the SOC vs. placebo.

The second question was whether a flare design should be used and whether the treatment effect is different between flare and non‐flare trials. This deals with inclusion criteria to select a study population, as described above in the second section.

Forest plots

Prior to any formal analysis, it is recommended to plot the data. A common approach is to present the data on forest plots.42 This is a useful way to compare treatment effects across studies, get an initial impression of any heterogeneity, and to identify any outliers. Using the Metafor package in R, there is a function “forest” that produces these plots easily. Code to produce a simple forest plot is presented in the Supplementary Materials. As we will see in subsequent sections, analysis summaries can easily be added at the bottom of this plot whether from a classical or Bayesian approach.

Models for WOMAC pain

Here, three models are described; a fixed effects model, a random effects model, and a meta‐regression model fitting “flare (yes/no)” as a binary covariate. For the classical approach, these models were fitted in R using the RMA function within the Metafor package. For the Bayesian approach, R2OpenBUGS was used. Fully annotated code used to fit these models is provided in the Supplementary Materials.

In this example, standard errors were available for all studies. When standard deviations/errors are missing, then an analyst should look to impute a value where possible. Wiebe et al.43 gave an overview of approaches available to impute missing variance measures and Stevens44 presented an example of imputing missing variances using WinBUGS.

Model descriptions

Fixed effects model

For the simple fixed effects model, suppose there are r independent studies, each comparing the treatment group with the control group.

$\theta$ denotes the true measure of treatment effect (treatment vs. control) and ${\widehat{\theta }}_i$ its estimate from the i^th study.

Then the general fixed effects model is ${\widehat{\theta }}_i=\theta +{\epsilon }_i$ with $\mathrm{E}\left({\epsilon }_{\mathrm{i}}\right)=0 \text{and} \text{Var}\left({\epsilon }_{\mathrm{i}}\right)={\xi }_i^2$.

Usually, we treat ${\xi }_i^2$ as known and equal to the estimated variance of ${\widehat{\theta }}_i$. Thus, ${\widehat{\theta }}_i\sim N\left(\theta ,s_i^2\right)$ where $s_i^2$ is the estimated variance of ${\widehat{\theta }}_i$ and assumed known and the maximum likelihood estimate for $\theta$ is:

$${\widehat{\theta }}_{\text{FE}}=\frac{{\displaystyle {\sum }_{i=1}^r{W}_i{\widehat{\theta }}_i}}{{\displaystyle {\sum }_{i=1}^r{W}_i}} \text{with} W_i=\frac{1}{s_i^2} \text{and} \text{Var}\left({\widehat{\theta }}_{\text{FE}}\right)={\left({\displaystyle {\sum }_{i=1}^r{W}_i}\right)}^{-1}$$

Random effects model

For a random effects analysis, the model becomes ${\widehat{\theta }}_i={\theta }_i+{\epsilon }_i$ where θ_i∼N(δ,τ²), $\mathrm{E}\left({\epsilon }_{\mathrm{i}}\right)=0 \text{and} \text{Var}\left({\epsilon }_{\mathrm{i}}\right)={\xi }_i^2$, as above. Note that τ² is the between‐study variance of θ_i. The maximum likelihood estimate for θ is shown below. Note that the weights (W_i) now incorporate the between‐study variability (τ²) and if this is very large compared to the within‐study variability, the studies will be weighted more equally.

$${\widehat{\theta }}_{\text{RE}}=\frac{{\displaystyle {\sum }_{i=1}^r{W}_i{\widehat{\theta }}_i}}{{\displaystyle {\sum }_{i=1}^r{W}_i}} \text{with} W_i=\frac{1}{s_i^2+{\tau }^2} \text{and} \text{Var}\left({\widehat{\theta }}_{\text{RE}}\right)={\left({\displaystyle {\sum }_{i=1}^r{W}_i}\right)}^{-1}$$

Meta‐regression model

The meta‐regression random effects model is ${\widehat{\theta }}_i={\theta }_i+{\theta }_{FL}*F_i+{\epsilon }_i$ where F_i is 0 for non‐flare and 1 for flare with θ_FL being the parameter to be estimated representing additional effect due to flare studies. θ_i has a similar distribution to the random effects model above where θ_i ∼N(δ, τ²). The flare effect could also be included in a fixed effects meta‐regression model.

Bayesian considerations for WOMAC pain models

Fixed effects model

As described above, the fixed effects model is ${\widehat{\theta }}_i=\theta +{\epsilon }_i$ and the within study variances assumed to be known, we only need to estimate θ. In a Bayesian setting, a prior distribution for θ is required. In this case, all our knowledge of the naproxen treatment difference from placebo comes from the data and, hence, an uninformative normally distributed prior centered around no drug effect was used with a large variance (∼N(0,10000)).

Random effects model

As above described, the random effects model is ${\widehat{\theta }}_i={\theta }_i+{\epsilon }_i$ where ${\theta }_i\sim N(\delta ,{\tau }^2)$ and the within study variances are assumed to be known. In addition to δ, the between‐study standard deviation (τ) is also estimated. In a Bayesian setting, prior distributions for δ and τ are required. As before, a noninformative prior was used for δ (∼N[0,10000]). Choosing prior distributions for the between‐study standard deviation has received much attention in recent years and when dealing with a small number of studies can be problematic.31, 45, 46, 47 Gelman48 discussed this issue and proposed several potential priors, including uniform and half normal distributed priors. In these examples, we used a uniform distribution but the code for a half‐normal distribution is also provided in the Supplementary Materials. Although, in this particular case, a noninformative prior was used for τ, if there had been a previous meta‐analysis for a similar mechanism drug (e.g., diclofenac, which, like naproxen, is a nonsteroidal anti‐inflammatory drug), then an informative prior may have been appropriate.

Meta‐regression

Here, flare design (yes/no) is being fitted as a categorical covariate and the random effects model is ${\widehat{\theta }}_i={\theta }_i+{\theta }_{FL}*F_i+{\epsilon }_i$ where F_i is 1 for flare designs and 0 otherwise and θ_FL is the covariate parameter to be estimated. A noninformative, normally distributed prior, centered around 0 was chosen for θ_FL (∼N(0,10000)). The other parameters are as defined for the random effects model.

Alternative modeling approach

Instead of pooling a set of treatment differences as above, another approach could be to model the treatment arms in terms of having a placebo response for each of the i studies (μ_i) and then a parameter representing the additional effect of naproxen (δ_i, which is N(d, τ²) under a random effects framework) such that $Y_{ij}={\mu }_i+{\delta }_i+{\epsilon }_{ij}$ where Y_ij is the WOMAC pain change from baseline and ε_ij is the residual (∼N(0, ${\mathrm{s}}_{\text{ij}}^2$/n)). This type of modeling approach is thoroughly described by the second National Institute for Health and Care Excellence evidence synthesis technical support document.49

In the above model, the trial‐specific placebo responses are not given any structural form and it is common for μ_i to be described as a “nuisance” parameter, something that is required in the model but is of little interest. However, it is not unusual to model the placebo response and investigate covariates that may influence it. Rightly or wrongly, there is a perception that high placebo responses “eat up” the treatment effects and so there is a desire to understand which population and/or study characteristics lead to high placebo responses and design studies to minimize this response. This placebo response is often described as a “baseline” treatment effect, which may be confusing to those who think of “baseline” as a pre‐first dose measurement in a clinical trial (e.g., baseline heart rate).

WOMAC PAIN RESULTS

Figure 3 presents a forest plot with additional estimates appended for the fixed effects estimate, random effects estimate, and the prediction interval. Bayesian and classical estimates are presented for comparison. The prediction intervals relate to the “true” underlying treatment effect rather than for the observed data. Given that the priors used in the Bayesian analysis are noninformative, it is not surprising that the two approaches give similar results. The random effects interval and prediction interval are slightly wider for the Bayesian analyses, which reflects the additional uncertainty in the between‐study variance (τ²). For both approaches, the prediction interval is noticeably wider than the interval for the random effects estimate, as such, there is increased uncertainty how naproxen might perform vs. placebo in a future trial and it may be desirable to include naproxen as a positive control in a future proof of concept study. In terms of setting target values, it could simply be set to the estimate from the analysis (−1.0 improvement over placebo) or if the target is to be better than naproxen, then the value might be set to, for example 50% greater than the naproxen effect vs. placebo (−1.5). There are many other ways that teams might define target values, but the meta‐analysis estimates will normally play a key role.

Figure 3.

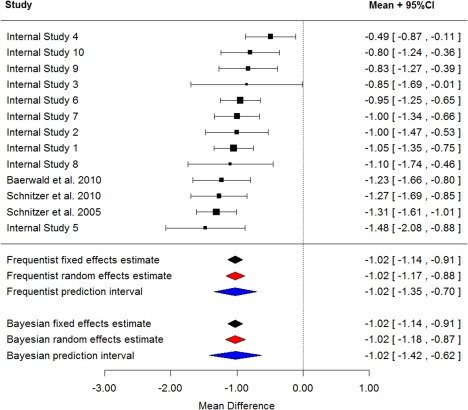
Difference in mean WOMAC pain for naproxen‐placebo at week two with model estimates.

From the meta‐regression model, flare did not seem to be a significant covariate. For the frequentist approach, the parameter estimate was −0.14 (95% confidence interval −0.47, 0.18) and for the Bayesian approach was −0.13 (95% credible interval −0.47, 0.24).

Figure 4 presents a funnel plot to examine publication bias, which shows no obvious asymmetry. Application of the Begg and Mazumdar35 rank correlation method results in a P value of 0.95 and Egger's test resulted in a P value of 0.99, suggesting that there is no evidence of funnel plot asymmetry. It is worth noting that in all the included trials, naproxen was a positive control rather than the experimental drug so one could postulate that the presence of publication bias might result in underestimation of the naproxen effect. To complicate things further, this could also apply to the placebo group response, such that the treatment difference between naproxen is less biased or not biased. Given that most of the trials (10 of 13) were internal unpublished trials, it would be hard to truly assess publication bias here and this example is simply to illustrate some common methods and how to do them in R.

Figure 4.

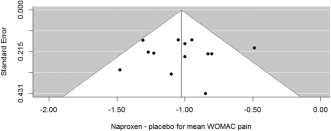
Funnel plot for WOMAC pain treatment difference.

EXAMPLE 2: PARESTHESIA RATES WITH TOPIRAMATE IN MIGRAINE PROPHYLAXIS TRIALS

Topiramate is an anti‐convulsant drug, which is used across several diseases including epilepsy, obesity, and migraine prophylaxis. A total of six placebo‐controlled studies with topiramate for episodic migraine prophylaxis were included in a dose response meta‐analysis. The paresthesia rates, across trial and dose, are presented in Supplementary Materials Table 2.

Research questions

As described above, this is an example of a learning exercise to better understand the safety and efficacy characteristics of topiramate. Driven by a need to create a product profile for a new compound, this was part of a larger piece of work looking at the therapeutic index for topiramate and what would be a similar or better therapeutic index for a new compound.50 In brief, a therapeutic index is the window between the dose that gives sufficient effect and the dose that causes toxicity. Mandema et al.51 provide an illustration of a dose response meta‐analysis to compare therapeutic indexes.

Dose response plot

Figure 5 presents the observed paresthesia rate by dose across the six episodic migraine prophylaxis studies in which placebo is included as dose = 0. There is evidence of increasing paresthesia incidence as the topiramate dose increases with bigger relative increases between placebo and 100 mg than between 100 mg and 200 mg. Based on this plot, an E_max model was chosen to characterize the dose‐response relationship. The plot also reveals variability across the trials with, for example in the placebo groups, a range of paresthesia rates from ∼4–27%.

Figure 5.

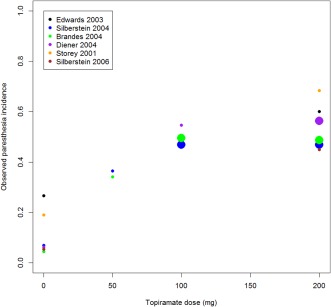
Dose vs. paraesthesia incidence across six episodic migraine prophylaxis trials.

Models for binary data

Model descriptions

Common examples of binary response date are efficacy responders (e.g., did a subject achieve at least a 60% reduction from baseline in pain) and adverse events. These data are normally summarized as a proportion (or risk) and it is these proportions that we aim to analyze at the summary data level as a dose‐response model. There are a variety of methods for analyzing proportions, including risk differences, odds ratios, and relative risk.52

In this article, we will focus on analyzing the data with a binomial model as follows. Let the observed number of subjects with paresthesia in the i^th study and j^th dose group be defined as Y_ij with N_ij being the total number of subjects at risk. Then Y_ij∼Binomial(N_ij, p_ij). It is p_ij that is modelled in logit space such that:

$$Logit(p_{ij})=E{0}_i+\frac{E_{\max }*dos{e}_{ij}}{E{D}_{50}+dos{e}_{ij}}$$

Where E0_i is the log odds of paresthesia on placebo for study i and assumed to be normally distributed with mean E₀ and variance τ². This could also be written as E_0i= E0+η_i where η_i∼N(0, τ²). This seems to be a reasonable approach given the observed trial‐to‐trial variability observed in Figure 5, although there may be covariates that explain some of this variability. Note here that the model includes a between‐study variance term on the overall function, rather than the on‐treatment effect (topiramate vs. placebo; the E_max part of the model) in contrast to the first WOMAC pain example in which treatment differences (naproxen – placebo) were modelled.

As a comparison to the dose response MBMA, a traditional meta‐analysis (using Metafor only) was carried out across the six trials for the topiramate 200 mg dose vs. placebo.

As stated above, NONMEM was used for the frequentist dose‐response model and OpenBUGS was used for the Bayesian approach.

Bayesian considerations for paresthesia data

For the dose‐response model, noninformative priors were used for E₀, E_max, ED₅₀, and τ. E₀ and E_max were given normally distributed priors (∼N[0,1.0E‐6] for E₀ and N[0,1.0E‐5] for E_max), ED₅₀ a uniform prior (U[0.0001, 1,000]) and for τ, a uniform distribution (U[0,10]) was used. Note that here, the prior for ED₅₀, lies between a value just above 0 up to a value five times that of the maximum observed dose (200 mg). For parameters such as ED₅₀ and variances (or standard deviations), it is recommended to always consider carefully the distributional form and to carry out sensitivity analyses.

Paresthesia dose‐response results

An E_max dose‐response model gave a good fit to the data across the six trials. An observed vs. predicted plot in the Supplementary Materials, generally shows good agreement. The placebo response for the two small trials (Supplementary Materials) was higher than the remaining larger trials (the two apparent outliers on the left hand side of the plot) but given their small sample sizes, they are less influential than they would be with large numbers of subjects.

Table 1 presents the parameter estimates from the frequentist and Bayesian approaches that demonstrate similar estimates between the two with the exception of τ, which is estimated as 0.17 in the frequentist results and 0.38 using the Bayesian approach.

Table 1.

Parameter estimates from the paresthesia dose response models

Parameter	Frequentist approach (95% confidence interval)	Bayesian approach (95% credible interval)
E0	−2.56 (−3.03, −2.09)	−2.51 (−3.06, −1.90)
Emax	2.91 (2.56, 3.26)	2.95 (2.50, 3.44)
ED50, mg	17.5 (11.64, 23.36)	18.18 (6.08, 36.46)
τ	0.17 (0.04, 0.30)	0.38 (0.05, 1.28)

Figure 6 presents a prediction plot, for doses 0 to 200 mg of topiramate, based on the Bayesian modeling approach together with the observed data (size of circle proportional to sample size such that bigger circles are larger studies). The black line represents the posterior mean, and the green area represents the prediction interval without accounting for between‐study variability. The blue region represents a prediction interval that does account for the heterogeneity. The additional uncertainty by incorporating between‐study variability is clear.

Figure 6.

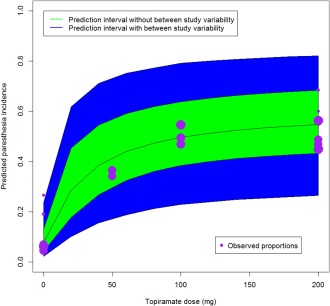
Dose response prediction plot based on Bayesian MBMA.

Figure 7 presents a forest plot where topiramate 200 mg is compared to placebo across six trials and the resulting traditional landmark random effect estimate is compared to the MBMA estimate and the two approaches yield comparable results; the Bayesian MBMA estimate is slightly higher and the corresponding 95% interval slightly smaller. The frequentist approach with NONMEM results in a more noticeably precise estimate.

Figure 7.

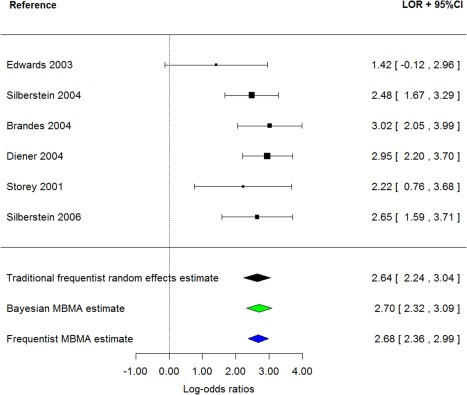
Forest plot of log odds ratios for paresthesia (topiramate 200 mg vs. placebo).

CLOSING REMARKS

The two examples are designed to be illustrative in terms of methods and implementation of those methods in R, OpenBUGS, and NONMEM. They are not designed to be exhaustive and, as alluded to above for both examples, further work would be required to understand the observed heterogeneity. Failure to do so will result in much uncertainty when running future trials.

It is strongly recommended that the starting point for these types of analyses is a random effects model as it is rare that all the underlying design, end points, and populations are effectively the same across all trials. Some between‐study variability might be explained with covariates, but the limitations of these are discussed above. Presenting random‐effects estimates and corresponding confidence intervals is not sufficient and prediction intervals should be presented to demonstrate the consequence of the estimated between‐study variability when designing future trials.

If there are only a small number of studies (e.g., <5) then the between‐study variance (τ²) is likely to be poorly estimated. In this case, it may be preferable to simply present the results from the individual trials in a forest plot but without a pooled estimate. An alternative could be, in a Bayesian setting, to use a prior for τ based on an existing meta‐analysis of a similar end point or same end point for a similar compound.53

The RMA function is well suited to simple meta‐analyses of a single timepoint, as illustrated in this tutorial, but is of limited use once more flexible model specifications, such as in the more advanced MBMA example.

Nonlinear models can be useful to describe dose‐response relationships, if this forms part of an important research question or to make inferences for a dose not present in many trials. NONMEM and OpenBUGS are both well suited to fitting such models, as are other available packages.54 In order to choose a suitable model, an exploratory plot should be produced to examine the shape of the dose response. The amount of data available on dose response will vary from compound to compound and depends on whether dose ranging studies (like those performed in phase 2b) are published.

Landmark analyses, such as the first example, are quick and straightforward to carry out but do not always use the totality of the data, which may have useful information about time course, onset of action, and maintenance of effect. Ultimately, MBMA should be used to answer the research question(s) whether that be by simple or more involved methods.

FUTURE TUTORIALS

This article is planned to be the first in a series and below is a list of proposed future tutorials:

• Longitudinal meta‐analysis.

• Combining patient and summary level data.

• Application of MBMA for clinical trial simulation.

• Multivariate meta‐analysis.

• NMA.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information