Abstract
Combining electroencephalogram (EEG) recording and functional magnetic resonance imaging (fMRI) offers the potential for imaging brain activity with high spatial and temporal resolution. This potential remains limited by the significant ballistocardiogram (BCG) artifacts induced in the EEG by cardiac pulsation-related head movement within the magnetic field. We model the BCG artifact using a harmonic basis, pose the artifact removal problem as a local harmonic regression analysis, and develop an efficient maximum likelihood algorithm to estimate and remove BCG artifacts. Our analysis paradigm accounts for time-frequency overlap between the BCG artifacts and neurophysiologic EEG signals, and tracks the spatiotemporal variations in both the artifact and the signal. We evaluate performance on: simulated oscillatory and evoked responses constructed with realistic artifacts; actual anesthesia-induced oscillatory recordings; and actual visual evoked potential recordings. In each case, the local harmonic regression analysis effectively removes the BCG artifacts, and recovers the neurophysiologic EEG signals. We further show that our algorithm outperforms commonly used reference-based and component analysis techniques, particularly in low SNR conditions, the presence of significant time-frequency overlap between the artifact and the signal, and/or large spatiotemporal variations in the BCG. Because our algorithm does not require reference signals and has low computational complexity, it offers a practical tool for removing BCG artifacts from EEG data recorded in combination with fMRI.
Keywords: EEG-fMRI, Ballistocardiogram, Pulse Artifact, Artifact removal, Regression, Functional neuroimaging
1. Introduction
Combined recording of electroencephalogram (EEG) and functional MRI (fMRI) (Goldman et al., 2000; Ives et al., 1993) is increasingly relevant in functional neuroimaging as it provides complementary measures of neuronal dynamics. Specifically, EEG-fMRI combines the high temporal and spatial resolution of EEG and fMRI, while enabling links between real-time EEG signatures and fMRI-based regional dynamics (Krakow et al., 1999; Lemieux et al., 2001). As such, EEG-fMRI has application in a wide variety of cognitive or clinical neuroscience studies – including those pertaining to evoked responses (Bonmassar et al., 2001; Debener et al., 2005), epileptic spikes (Iannetti et al., 2002; Schomer et al., 2000) and oscillatory rhythms (Goldman et al., 2002; Laufs et al., 2003). However, full realization of these applications continues to be limited by MR-environment related ballistocardiogram (BCG) artifacts corrupting EEG recorded in the scanner.
Ballistocardiogram artifacts are induced in the EEG by cardiac pulsation-related motion of the head and electrodes in the static magnetic field (Allen et al., 1998; Debener et al., 2008; Huang-Hellinger et al., 1995; Mullinger et al., 2013). Typically, large BCG artifacts (150 – 200 µV) overlap and obscure underlying neurophysiologic EEG activity (5 – 100 µV) in both time and frequency domains – particularly for 0 – 20 Hz bands (Allen et al., 1998). As a result, EEG recorded in the MRI scanner lacks (a) sensitivity for low amplitude neurophysiologic signals over ongoing artifact, and (b) specificity as it is easy to mistake BCG background for periodic brain rhythms, evoked responses or ictal discharges (Bonmassar et al., 2002). These problems limit reliable analysis of EEG acquired in the scanner. Moreover, BCG artifacts scale with static field strength (Debener et al., 2008; Mullinger et al., 2013), posing increasing challenges given the emerging preference for high-field MRI techniques. Thus, effective BCG artifact removal is crucial for EEG-fMRI applications, but is often difficult because of three concurrent challenges - (a) low SNR, (b) time-frequency overlap between artifact and signal, (c) spatial inhomogeneities and unpredictable time variations due to drifts in heart rate, blood pressure and pulsatile head motion. Two main types of techniques are used for BCG artifact removal, as reviewed below.
Reference-based methods specify templates for the BCG based on reference signals, and use these templates to estimate and remove BCG artifacts. Electrocardiogram (ECG)-based subtraction techniques assume the BCG occurs only in fixed phases of the cardiac cycle, use ECG peaks to determine intervals when the BCG occurs, and average contaminated EEG segments across a few such intervals to estimate the BCG wave-form (Allen et al., 1998; Ellingson et al., 2004; Goldman et al., 2000; Sijbers et al., 2000). While these methods are practical and widely used, they do not account for normal variations in timing, shape and amplitude of the BCG, resulting in out-of phase artifact subtraction, systematic errors and large residuals (Bonmassar et al., 2002; Musso et al., 2011; Niazy et al., 2005). Sometimes, these residuals are reduced using beamformers that build on the distinct spatial topography of the BCG (Brookes et al., 2008), but do not account time variations in the BCG. Motion-based subtraction techniques record head motion, assume that the BCG artifact is a function of head motion, and employ adaptive filtering techniques to estimate this function (Bonmassar et al., 2002). While this technique is rooted in physical features driving the BCG, it relies on a linear relation between the motion signals and the BCG. Reference-layer artifact subtraction uses a specialized recording system with an insulating layer to isolate reference channels electrically from the scalp, measure primarily artifactual reference signals and subtract out the BCG (Chowdhury et al., 2014; Mullinger et al., 2013). While this technique suppresses artifacts significantly, the reference signals are not identical to the BCG (Mullinger et al., 2013; Xia et al., 2014). Moreover, all these methods require specialized sensors or hardware, and robust recording of reference signals within the challenging MR-environment.
Component analysis or subspace separation techniques derive orthogonal or independent components that represent the BCG-corrupted measurement, designate some of these components as artifactual, and selectively remove the designated elements. These techniques use temporal principal component analysis or PCA (Niazy et al., 2005), independent component analysis or ICA (Mantini et al., 2007; Nakamura et al., 2006; Srivastava et al., 2005), or wavelet transforms (Kim et al., 2004; Wan et al., 2006). In particular, PCA-based Optimal Basis Sets (OBS) (Niazy et al., 2005) is widely used, and sometimes augmented with ICA to reduce residual artifacts (Debener et al., 2007; Vanderperren et al., 2010). While these methods have shown good performance in a number of studies, the substantial amplitude, time and frequency overlap between BCG artifacts and neurophysiologic EEG signals can compromise their inbuilt mutual orthogonality or separability assumptions. As a result, which or how many basis components comprise “BCG artifact” vs. “EEG signal” can become subjective or case-specific, and reduce effectiveness of separation (Debener et al., 2007; Grouiller et al., 2007; Nakamura et al., 2006). Further, the time-varying nature of the BCG artifact limits applicability of the stationarity assumptions in ICA (Debener et al., 2008, 2007; Laufs et al., 2008). Finally, as OBS uses the ECG reference signal to designate artifact-corrupted intervals, and uses data from these intervals for PCA, aforementioned difficulties in defining BCG intervals based on the cardiac cycle persist.
Thus, despite several advancements, prevailing challenges necessitate approaches that can overcome large, overlapping and time-varying BCG artifacts to recover underlying neurophysiologic EEG signals – without requiring high-quality reference signals or pre-specified orthogonality or separability criteria (Garreffa et al., 2004; Grouiller et al., 2007).
Here, we present a statistical model-based, reference-free BCG removal algorithm to overcome these challenges. First, we specify a mathematical basis for the BCG that is informed by the natural physiologic and physical structure and dynamics of these artifacts. Next, we model the BCG as a parametric function of this basis, and define the problem within a classical time series framework. Then, we develop efficient likelihood-based regression techniques to estimate model parameters that explain the data, and in turn, estimate and remove the BCG artifacts. We demonstrate effectiveness of our technique on challenging simulated and measured oscillatory and evoked test cases. Finally, we benchmark performance in relation to existing methods, and discuss reasons for improved performance of our model-based approach. Portions of this work have been presented in (Krishnaswamy et al., 2013).
2. Methods
2.1. Model Motivation
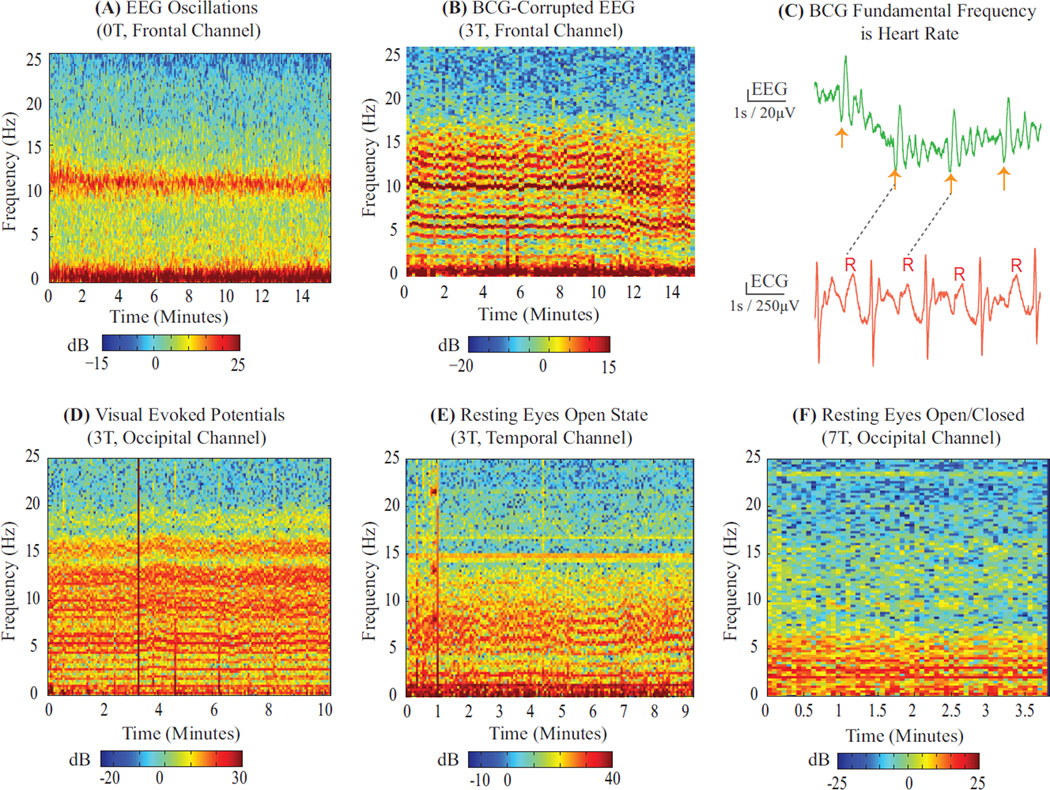
We note that the BCG artifact is driven by highly structured physiologic and physical phenomena – namely cardiac pulsation related head motion. Therefore, we assessed whether the BCG has a structured mathematical form. We examined spectrograms of EEG recorded outside vs. inside the MRI scanner under similar conditions (Fig. 1A–B). The spectrogram of EEG recorded outside the scanner clearly shows oscillatory rhythms, however, inside the scanner these rhythms are obscured by comb-like harmonic streaks. As the underlying neurophysiologic state is similar in both cases, the dominant harmonics inside the scanner must correspond to the BCG artifact. Next, we inspected EEG recorded in the scanner in the time domain, and found that the BCG harmonics manifest as high amplitude comb-like pulsatile occurrences exhibiting the same periodicity as the heartbeat (Fig. 1C). Thus, the BCG must comprise harmonics of the heart rate. Finally, we inspected a variety of EEG datasets recorded on different subjects in different experimental paradigms (oscillations and evoked studies, interleaved and continuous fMRI), scanners (3T, 7T), electrode configurations (unipolar, bipolar) and locations (frontal, occipital, temporal), and found that the harmonic feature generalizes across conditions (Fig. 1B,D–F). Thus, the comb-like harmonic structure must correspond to fundamental physiologic and physical features of the BCG artifact. Overall, this analysis suggests a natural harmonic basis for specifying the BCG artifact.
Figure 1. BCG is Harmonic in Heart Rate.
EEG spectrograms recorded (A) outside and (B) inside 3 T MRI scanner on 2 unconscious subjects under similar levels of propofol anesthesia. (A) Characteristic slow (0–1 Hz) and alpha (8–12 Hz) oscillations are seen in the spectrogram. (A vs B) BCG artifacts manifest as harmonic streaks in spectrogram, making it difficult to discern neurophysiologic oscillations. (C) Time series of BCG-corrupted EEG data aligned with simultaneous ECG recording at 3 T. Successive high amplitude BCG combs (orange arrows) have same periodicity as heartbeat (R-R intervals). (D–F) Example spectra of BCG artifacts recorded on different subjects with different study paradigms (D vs. E, F: evoked vs. spontaneous states), acquisition protocols (D,F vs. E: static field vs. continuous fMRI after removing gradient artifacts), scanners (D,E vs. F: 3 T vs. 7 T) electrode configurations (D, E vs. F: unipolar vs. bipolar) and electrode locations (E vs. D, F: temporal vs. occipital). Harmonic structure in the BCG is independent of experimental conditions - therefore reflective of underlying physiologic and physical structure. All spectra are computed using multitaper estimation with the fine (0.3 Hz) spectral resolution needed to discern harmonics separated by ~ 1 Hz heart rates. Gross broadband motion artifacts appear as vertical lines in spectrograms. Data collection procedures for Panel A and F are in (Purdon et al., 2013) and (Purdon, 2005); Panels B, C and D are in § 2.5.2, § 2.5.3 and § 2.5.1. Panel E is a resting continuous fMRI scan with acquisition system of § 2.5.3.
Closer inspection reveals that the time and spatial variations in the artifact can also be viewed within the context of a harmonic structure. First, although the BCG has varying shape, intensity and period within and across cardiac cycles (e.g., in Fig. 1C, and 10 – 14 minute section in Fig. 1B), the comb-like pulsatile or harmonic structure is preserved through time. Second, although BCG artifacts vary in shape across the head (Allen et al., 1998; Bonmassar et al., 2002), the harmonic structure is preserved across electrode locations (Fig. 1B,D–F). Thus, specifying the BCG as a parametric function of a harmonic basis allows us to account for spatiotemporal variations in the BCG with variations in the parameters.
Based on this analysis, we parametrically model the BCG artifact as a harmonic series and also parametrically specify the temporal structure of interest in the neurophysiologic EEG signal. The models provide templates for artifact and signal, and allow objective separation based on the character of the data. We detail the model in the following section.
2.2. Model
BCG-corrupted EEG data recorded in the MRI scanner comprise a multidimensional time series obtained with an array of electrodes across the head. We consider the data series measured at each electrode independently. At any given electrode, the measured data series comprises successive non-overlapping time segments. For a time segment comprising T time points t1, t2,…tT, we denote the measured data series as a T × 1 vector y = [y1, y2,…, yT]′. Then, we model y as a sum of harmonic BCG artifact s and clean neurophysiologic EEG signal v:
| (1) |
where s = [s1, s2,…, sT]′ and v = [v1, v2,…, vT]′.
The BCG artifact st can be modeled as a harmonic series:
| (2) |
where order R denotes the number of harmonics, [μo, μ1] define a linear detrend term, [Ar, Br] together define amplitude and phase of the rth harmonic, and ω specifies the fundamental frequency. Based on Fig. 1C, ω is set by the heart rate. Rewriting Eqn. 2 in matrix form, we have:
| (3) |
| (4) |
where Z(ω) and β = [μo, μ1, A1, B1, A2,…, BR]′ denote the harmonic basis and coefficients respectively.
The clean neurophysiologic EEG signal vt can be modeled to represent temporal features under study. A large variety of temporal or spectral EEG features can be represented with autoregressive (AR) processes. For example, pseudo-oscillatory features in spontaneous rhythms and background EEG in evoked responses have inherent AR structure. The AR form for vt is:
| (5) |
| (6) |
where order P denotes the number of AR terms, α = [a1, a2,…, aP]′ denotes the AR coefficients, and the εt denote independent identically distributed (i.e., white) Gaussian random variables. This model form is general and does not bias to predetermined periodicities or frequency bands. Rewriting Eqn. 5–Eqn. 6 in matrix form, we have:
| (7) |
where QT×T denotes the AR covariance matrix that is a function of the AR model parameters α and σ2.
The composite model collating Eqn. 1, Eqn. 4, and Eqn. 7 can be written compactly as:
| (8) |
The harmonic and autoregressive models reflect the empirically observed time, frequency and amplitude overlap between artifact and signal respectively. However, the harmonic BCG term has a discrete line spectrum while the AR clean EEG term has a continuous smooth spectrum. Thus, the overall forms possess distinct dynamical features to decouple artifact from signal. With this model, the problem of removing the BCG artifact and recovering the clean EEG signal becomes one of estimating s and v, or equivalently, one of estimating parameters u = [ω, β, α, σ2] that best explain the measured data y.
2.3. Algorithm
This parameter estimation problem has three defining features. First, it is akin to a spectral estimation problem with a customized harmonic basis instead of frequencies spanning a continuum from 0 to Fs/2. Second, it requires high frequency resolution to separate consecutive harmonics (~ 1 Hz apart), while retaining the underlying AR process. Third, it requires high temporal resolution to account for time variations in model parameters defining the BCG artifact and neurophysiologic EEG signal (Fig. 1). Thus, the estimation algorithm must concomitantly offer customized basis separation and high time-frequency resolution.
Given these specifications, time series regression techniques are more suitable than Fourier domain techniques. In particular, we note that this is a case of harmonic regression in the setting of an additive colored process (Eqn. 8). Maximum likelihood techniques are suitable for such harmonic regression problems (Ansley and Wecker, 1983; Brown and Schmid, 1994; Brown et al., 2004; Malik et al., 2011). Further, these techniques can be easily adapted for the case of time varying parameters by exploiting the established local likelihood estimation framework (Tibshirani and Hastie, 1987). Like in spectral estimation, local likelihood estimation assumes quasi-stationarity of parameters within a short time window, and applies maximum likelihood criteria on short windows of data to estimate the local model parameters. Thus, we develop a local likelihood algorithm to estimate parameters of our model.
For a measured data segment yT×1 defined by local model parameters u = [ω, β, α, σ2], the local log likelihood is:
| (9) |
where Q−1 is the inverse AR covariance and ST is the weighted mean square error, (y – Z(ω)β)′ Q−1 (y – Z(ω)β). Minimizing − log L gives the optimal parameter estimates (denoted with hats) for this data segment:
| (10) |
For the BCG removal problem, this minimization is (a) nonlinear as the precise instantaneous heart rate ω is unknown (Eqn. 3–Eqn. 4), and (b) high-dimensional as the BCG comprises a large number of harmonics (Fig. 1). But, existing solutions for this minimization require either (a) linearity arising from a known ω (Malik et al., 2011), or (b) Newton’s procedures (Brown and Schmid, 1994; Brown et al., 2004) that become computationally intractable for more than 3–4 harmonics and AR terms.
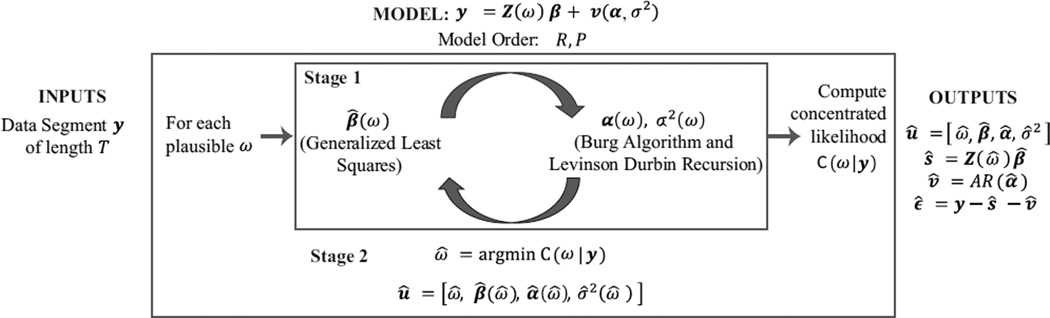
We devise an algorithm to address the challenges of a nonlinear and high-dimensional harmonic regression (Fig. 2). We simplify Eqn. 10 into a sequence of two tractable minimizations:
| (11) |
First, we solve the inner minimization in Eqn. 11 for a given ω. This gives parameter estimates û(ω) = [β̂ (ω), α̂ (ω), σ̂2(ω)] and the concentrated likelihood C(ω|y):
| (12) |
In practice, û(ω) and C(ω|y) can be obtained by adapting a cyclic descent scheme that iteratively updates the AR parameters with the harmonic estimate, and vice versa (Corradi, 1979; Malik et al., 2011). Second, we solve the outer minimization in Eqn. 11 by optimizing C(ω|y) across a range of plausible ω values:
| (13) |
Together, these two stages estimate parameters, û = [ω̂, β̂(ω̂), α̂(ω̂), σ̂2(ω̂)], for Eqn. 10. These parameters are used to determine the BCG artifact ŝ and clean EEG signal v̂.
Figure 2. Algorithm to Estimate Model Parameters and BCG Artifacts.
A parametric model of order (R, P) relates input BCG-corrupted data y with output estimates of BCG artifacts (ŝ) and clean EEG signals (v̂). Given data y, model parameters are estimated with a two-stage local likelihood algorithm. Stage 1 is a cyclic descent that iteratively estimates harmonic amplitudes and AR parameters for a given fundamental frequency ω. These estimates, denoted [β̂(ω), α̂ (ω),σ̂2(ω)], are used to compute a concentrated likelihood C(ω|y). Stage 2 is an optimization of C(ω|y) across plausible ω values. This yields the optimal estimate for fundamental frequency ω̂, and in turn, for other parameters [β̂(ω̂), α̂(ω̂),σ̂2(ω̂)]. These parameters are then used to compute the BCG (ŝ) and clean EEG (v̂) time series.
2.4. Implementation
The algorithm is implemented in MATLAB (Mathworks, Natick, MA), as summarized in step-wise form below.
Initialization:
Set inverse AR covariance estimate Q̂−1(ω) to identity IT×T.
Use the subject’s typical heart rate h to set range of plausible fundamental frequency values as [min(40, 0.5h), max(1.5h, 150)] beats/minute.
Stage 1 - Cyclic Descent Iteration:
For each plausible value of ω:
Use multitaper spectrum of measured data to derive prior covariance matrix W(ω) for the β parameter (§ Appendix A). This informs β estimation with background AR power.
Estimate harmonic amplitudes via generalized least squares on Eqn. 8: β̂ (ω) = [Z′ (ω)Q̂−1(ω)Z(ω) + W−1(ω)]−1 Z′ (ω)Q̂−1(ω) y.
Compute weighted mean square error ŜT (ω) (Eqn. 9), and AR series estimate v̂(ω) = y – Z(ω)β̂(ω).
Estimate AR parameters α̂ (ω) and σ̂2(ω) defining v̂ (ω) using the Burg algorithm.
Update inverse AR covariance estimate Q̂−1(ω) using the Levinson-Durbin Recursion on AR time series v̂(ω) and AR parameters α̂ (ω) and σ̂2(ω) (§ Appendix B).
Repeat iterations 1–5 until subsequent σ̂2(ω) values converge to within 0.01%. Set û(ω) = [β̂ (ω), α̂ (ω), σ̂2(ω)], compute C(ω|y) using Eqn. 12 and quit iteration.
Output parameter estimates û(ω) and concentrated likelihood C(ω|y).
Stage 2 - Frequency Optimization: Optimize C(ω|y) across a range of plausible ω values (Eqn. 13) to obtain ω̂. Output final optimal parameter estimates û = [ω̂, β̂(ω̂), α̂ (ω̂), σ̂2(ω̂)].
Inputs for analysis are in § 2.6.1and § Appendix C.2. Our nested minimization is efficient and performs in real-time. For a 5 second data segment, the complete estimation procedure clocks < 4.5 seconds on an 8-core Intel Xeon™ workstation. This speed is achieved by downsampling data in stage 1; running stage 1 in parallel for different values of ω; and deriving an efficient block form for the rate limiting stage 1 step 4 (§ Appendix B). We make our implementation available under an academic non-commercial use license via the MGH Martinos Software Resource located at http://www.nmr.mgh.harvard.edu/research/software. Finally, the highly structured nature of this problem and the dominant harmonics enable optimality and convergence guarantees (§ Appendix D). We now validate the method on simulated and experimental test cases.
2.5. Data Acquisition
2.5.1. Artifacts for Simulation Tests
We recorded resting state EEG data in a Siemens Trio 3 T scanner (Erlangen, Germany) on 2 healthy volunteers. Subjects were asked to lay awake and motionless, with eyes open, for 5 minutes. EEG and ECG data were acquired in the static field at 957 Hz using an MR-compatible low noise, high dynamic range 24-bit acquisition system (Purdon et al., 2008). EEG electrodes made of Ag/Ag-Cl were placed in adjacent bipolar pairs at 8 locations across the central coronal plane. These recordings measure BCG artifacts against typical background EEG activity, and were added to simulated signals to construct simulated test cases with realistic artifacts. This study was approved by the Partners Human Research Committee at Massachusetts General Hospital, and subjects provided written informed consent.
2.5.2. Propofol Anesthesia-Induced Oscillations
We recorded EEG oscillations in an interleaved EEG-fMRI study conducted at 3 T (Siemens Trio scanner, Erlangen, Germany) during propofol general anesthesia in 50–60 y/o volunteers who were healthy post-tracheostomy (Purdon et al., 2008, 2009). Propofol dose was increased progressively to induce and maintain unconsciousness. EEG data and piezoelectric motion sensor recordings (Bonmassar et al., 2002) were acquired continuously at 950 Hz using an MR-compatible acquisition system. EEG electrodes were made of Ag/Cl, housed in plastic (Gereonics, Solana Beach, CA), and bonded to “Fiber-Ohm” carbon fiber wires (7 ohms/inch resistance to avoid RF heating during MRI (Angelone and Bonmassar, 2004; Angelone et al., 2006); Marktek, Chesterfield, MI). EEG electrodes were placed in adjacent bipolar pairs at 24 locations across the head in the International 10/20 configuration. Effective TR for fMRI acquisition was 9 seconds. Each fMRI volume was acquired in 1 second. The cryopump was turned off. The pulse was measured every 5 minutes. This study was approved by the Partners Human Research Committee at Massachusetts General Hospital, and subjects provided written informed consent.
2.5.3. Visual Evoked Response Potentials
We recorded evoked EEG potentials outside and inside a head-only Siemens Allegra 3 T scanner (Erlangen, Germany) on 2 healthy volunteers. A visual evoked response paradigm comprising 1150 trials of a vertical upper and lower checkerboard wedge stimulus was used. EEG and ECG data were acquired continuously at 250 Hz using an MR-compatible acquisition system (Electrical Geodesics, Inc., Eugene, OR). EEG electrodes were vertex-referenced and placed at 256 locations across the head. fMRI data were not recorded, thus the EEG is free of gradient artifacts. The cryopump was turned off. This study was approved by the Human Subjects Institutional Review Boards of Electrical Geodesics, Inc. and the University of Oregon, and subjects provided written informed consent.
2.6. Data Analysis
2.6.1. Inputs for Analysis
Measured data series input into the algorithm are filtered to remove power line noise. For concurrently recorded EEG-fMRI, gradient artifacts can be removed with standard methods before analysis (Allen et al., 2000; Niazy et al., 2005). For interleaved EEG-fMRI recordings, the data acquisition format makes EEG windows free of gradient artifacts readily available for analysis. Analysis of data from each electrode location proceeds independently and in parallel. All analyses use the EEG referencing scheme native to the data collection. Visualizations also follow the same scheme unless otherwise noted.
Two sets of inputs are required for analysis of a recording: (a) harmonic and autoregressive model orders (R, P), and (b) length of the moving window T. First, we select model orders using standard statistical information criteria – to be large enough to explain the data, yet small enough to avoid unnecessary model complexity (§ Appendix C.1). This tradeoff is typically achieved with orders R < 20, P < 10. Second, we select the moving window interval like in spectral analysis – to be long enough for good frequency resolution, yet short enough to have the time resolution to track drifts in BCG parameters (§ Appendix C.2). This tradeoff is typically achieved with T = 2 – 6 seconds. Model orders (R, P) are reported with results. All tests use window length T = 3 seconds.
2.6.2. Parameter Estimation
We divide preprocessed recordings into consecutive time windows (indexed as k = 1, 2,…K), each of length T. For the kth window comprising time points tk, tk+1,…, tk+T−1, we denote the measurement vector as yk, and the local parameters as . For each window k, we apply maximum likelihood on yk to obtain one set of model parameter estimates ûk. To analyze the entire recording, we move data windows along in non-overlapping fashion. As heart rate and neurophysiologic EEG evolve smoothly between consecutive windows, the estimated fundamental frequency and inverse AR covariance for one window can be used to initialize the range of plausible frequencies and inverse AR covariance estimates for the next window.
Using the parameter estimates û, we compute time series estimates of the BCG artifacts ŝ, clean EEG signals v̂, and residual noise ε̂. We perform standard goodness of fit assessments on the residual noise series ε̂. First, we compare the normalized cumulative periodograms (NCPs) of the residual noise series and an ideal white noise series. If the residual noise NCP is within 95% whiteness bounds around the ideal white noise NCP, then the Kolmogorov-Smirnov goodness of fit criteria indicate insignificant temporal correlation. Second, we use quantile-quantile plots to confirm Gaussianity of the residuals.
2.6.3. Comparisons with Existing Algorithms
We benchmark performance of harmonic regression (HR) to three commonly used reference-based and/or component analysis techniques: (a) ECG-based average artifact subtraction or AAS (Allen et al., 1998), (b) ECG-based optimal basis separation or OBS (Niazy et al., 2005), and (c) motion-based adaptive filtering (Bonmassar et al., 2002). The ECG-based AAS and OBS algorithms are implemented within the FMRIB plug-in (Iannetti et al., 2005; Niazy et al., 2005) for EEGLAB (Delorme and Makeig, 2004), provided by the University of Oxford Centre for Functional MRI of the Brain (FMRIB). We used AAS and OBS with the default mean subtraction and 4 principal components settings respectively. The motion-based adaptive filter is augmented with an expectation-maximization algorithm for model parameter estimation (Purdon, 2005). For interleaved recordings, we performed adaptive filtering using intermittent observations within a missing data framework.
3. Results
First, we show that (a) the algorithm estimates the parameters accurately, and (b) the model explains the data. Next, we illustrate performance on simulated oscillatory and evoked responses corrupted with realistic BCG artifacts (§ 2.5.1). As these tests have known signals, we present three quantitative assessments of signal recovery: (a) root mean square error (RMSE) between cleaned and simulated signals, (b) SNR improvement after artifact removal for oscillations, and (c) standard deviation across epochs for evoked responses. Finally, we demonstrate qualitative recovery of actual propofol anesthesia-induced frontal multi-band oscillations (§ 2.5.2) and visual evoked responses (§ 2.5.3) from EEG recorded in the scanner. In all four cases, we report the proportion of residual artifacts, i.e., percentage of power in harmonics of ω̂ remaining after artifact removal, and benchmark performance to commonly used BCG removal methods. In each case, we present figures for a representative subject.
3.1. Accuracy of Parameter Estimates and Goodness of Fit
We applied harmonic regression (R = 16, P = 8) on the propofol EEG recordings (§ 2.5.2) to obtain estimates of model parameters û = [ω̂, β̂, α̂, σ̂2]. Then, we computed time series estimates of the model components, namely: BCG artifacts ŝ, clean neurophysiologic EEG signals v̂, and residual noise ε̂.
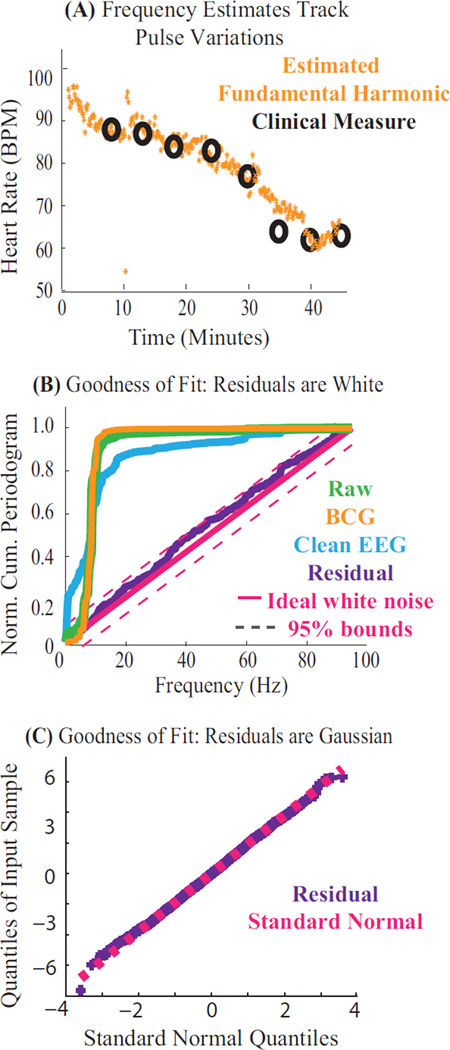
Fig. 3A shows the estimated fundamental frequency ω̂ overlaying clinically measured heart rates over time. The estimates accurately track physiological heart rates as they change with time and drug dose. While direct comparison of other parameter estimates β̂, α̂ and σ̂2 with ground truth measures is not possible, theoretical work (Corradi, 1979) suggests that accurate estimates of ω̂ lead to accurate estimates of β̂, α̂ and σ̂2.
Figure 3. Parameter Estimates are Accurate and Model Explains the Data.
Results from harmonic regression applied to EEG recorded at 3 T. (A) Estimated fundamental frequency ω̂ over a period of drug-induced changes in heart rate. The algorithm yields accurate, high resolution estimates of the fundamental frequency (orange), that match pulse oximeter measurements (black). (B–C) Goodness of fit results on residuals ε̂ (purple), shown for a typical 3 second data segment. (B) Normalized cumulative periodograms (NCP) showing spectral structure for each model component: NCP of 0.2 at 10 Hz indicates 20% of the power lies below 10 Hz. The residual series is within 95% whiteness bounds (magenta). (C) Quantile-Quantile plot of residual series confirms modeled Gaussianity.
Fig. 3B–C show that the model fits the data. First, Fig. 3B presents the normalized cumulative periodogram (NCP) of each model component. The raw data series (green, y) contains significant power below 20 Hz. The estimated BCG harmonics (orange, ŝ) explain a majority of the raw data spectral structure. However, the AR term (cyan, v̂) is necessary to explain all the systematic low-frequency variance in the data. The residual noise (purple, ε̂) lies within 95% whiteness bounds of an ideal white noise series (magenta). Second, Fig. 3C shows that the residuals are Gaussian. Together, these results demonstrate goodness of fit to the modeled white Gaussian residual structure (Eqn. 6), and confirm that the joint harmonic-AR model sufficiently explains spectral structure in the data.
3.2. Recovery of Simulated Oscillations
We generated BCG-corrupted EEG oscillations by adding simulated ON/OFF 3 – 4 Hz oscillatory signals to resting state BCG artifact recordings (§ 2.5.1). Specifically, oscillatory signals followed a periodic 17 second ON/17 second OFF pattern, and were generated by adding 3 Hz, 3.5 Hz, and 4 Hz sinusoids, each with 3 – 10 µV amplitude. ON periods contain BCG-corrupted oscillatory signals, while OFF periods are purely artifactual. We removed artifacts and recovered simulated signals with harmonic regression (R = 18, P = 6) and ECG-based methods. We computed the proportion of residual artifacts (while discounting harmonic power within simulated signals); in-band SNR i.e., ratio of average ‘signal’ power (ON minus OFF periods) to average ‘artifact’ power (OFF periods) in the signal band before and after artifact removal (Purdon, 2005); and RMSE relative to simulated signals (ON periods).
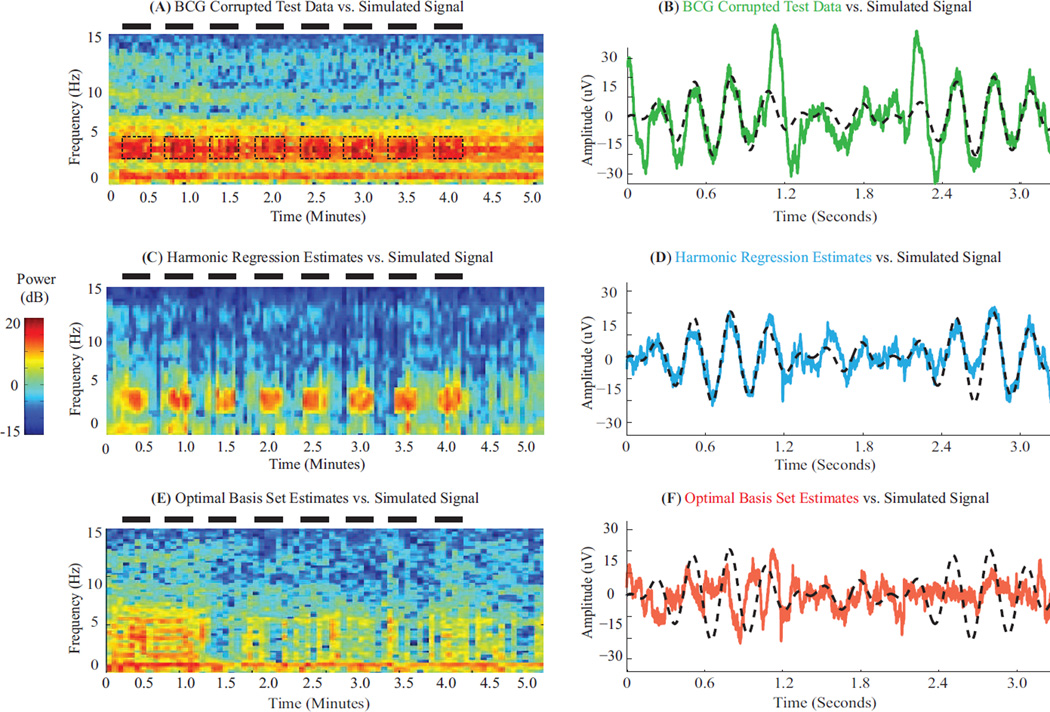
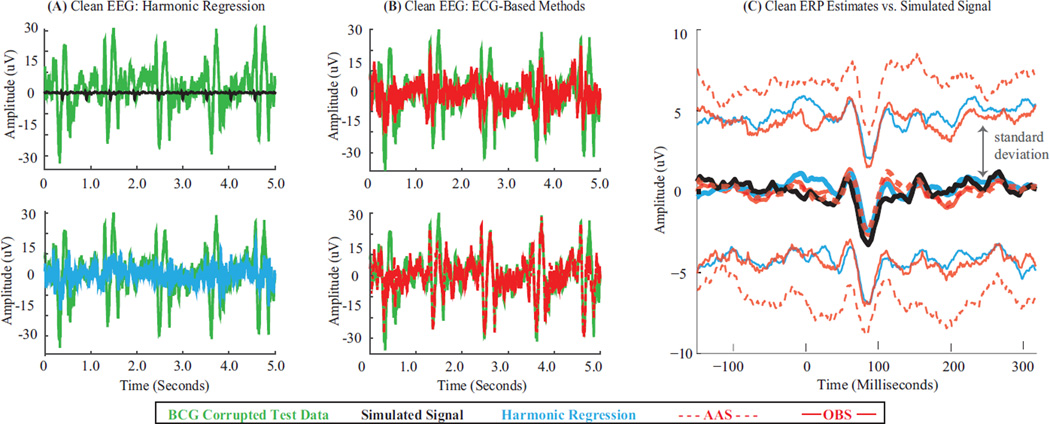
Fig. 4A–B show the BCG-corrupted test data (green) for a simulated oscillation (black) on a temporal electrode (M2 → T8). Dominant BCG artifacts obscuring simulated signals (ON periods/bands marked by black dashes) are evident in spectral and time domains. Fig. 4C–D illustrate signal recovery with harmonic regression. A large proportion of artifacts are removed (3.6% residuals). The estimated neurophysiologic signal lies within the 3 – 4 Hz simulation band, follows the simulated ON/OFF periods (7.2X improvement in SNR after BCG removal), and closely matches simulated signal amplitude and phase (cyan vs. black time courses, RMSE 5.39 µV). Fig. 4E–F illustrate signal recovery with OBS. While OBS removes a large proportion of artifacts (13.5% residuals), it also removes significant portions of the simulated signal. The recovered signal spans a broad 0–6 Hz band, does not always mimic the simulated ON/OFF periods (1.0X improvement in SNR after BCG removal), and often differs from the simulated signal in amplitude and phase (red vs. black time courses, RMSE 10.01 µV). For comparison, AAS left 18.6% residual artifacts, recovered activity in 3–5 Hz, improved SNR by 2.1X and achieved RMSE 7.69 µV. We note that ECG peak detection is poor for these data (Fig. S1). Further, OBS performance improves when the simulated oscillations have lower amplitude or less time-frequency overlap with artifacts – in those cases the principal components to be eliminated can contain less oscillatory signals mixed in with artifacts (Table S1). Together, these results show that harmonic regression recovers timing, power and phase of EEG oscillations. Further, they illustrate advantages over ECG-based approaches that assume mutual orthogonality or separability between artifact and signal - particularly in cases of substantial amplitude, time or frequency overlap.
Figure 4. Harmonic Regression Effectively Removes BCG Artifacts and Recovers Simulated Oscillations.
(A,C,E) Spectrograms of BCG-corrupted test data, and clean EEG recovered using harmonic regression and OBS respectively. Black dashes denote ON periods and frequency band for simulated 3–4 Hz oscillations. BCG artifacts dominate underlying simulated pattern in test data. Harmonic regression clearly restores the simulated pattern. Signal recovery with OBS is less apparent. (B,D,F) Time series of test data (green) and clean EEG recovered using harmonic regression (cyan) and OBS (red) – each overlaying the simulated signal (black). All data segments start at 3.14 minutes. Harmonic regression estimates preserve amplitude and phase of the simulated oscillation better than OBS.
3.3. Recovery of Simulated Evoked Responses
We generated BCG-corrupted evoked responses by adding simulated evoked response potentials (ERPs) to the resting state BCG artifact recordings (§ 2.5.1). For realistic morphology and SNR, simulated ERPs comprised identical occurrences of the average visual ERP recorded outside the scanner (§ 2.5.3) repeating every 0.5 seconds. We removed artifacts and recovered simulated signals with harmonic regression (R = 18, P = 2) and ECG-based methods. We computed the proportion of residual artifacts (while discounting harmonic power within simulated signals); average and standard deviation of the evoked responses; and RMSE between average cleaned ERP and simulated ERP.
Fig. 5A shows the BCG-corrupted test data (green) for simulated evoked potentials (black) on a central electrode (Cz → C3). Comb-like artifacts dominate the simulated signal. Fig. 5B overlays the test data series with cleaned EEG traces obtained with different artifact removal methods. Harmonic regression (cyan) removes comb-like pulsatile BCG occurrences in the test data (green) more effectively than OBS (solid red, top) and AAS (dashed red, bottom). Harmonic regression, OBS and AAS leave 8.8%, 11.7%, 33.1% residual artifacts respectively. Fig. 5C presents cleaned ERPs obtained with harmonic regression (cyan), OBS (solid red), AAS (dashed red) overlaying the simulated ERP (black). ERP traces are average (thick middle traces) +/− one standard deviation (thin traces around average) across epochs. Across methods, the average cleaned ERP matches simulated ERP morphology, peak latencies and amplitude ranges (HR, OBS and AAS RMSE values 0.37 µV, 0.36 µV, and 0.60 µV). Comparing the standard deviations, harmonic regression and OBS offer more precise estimates of the true average ERP than AAS (one-sided F-test, p < 0.025). Together, these results show that harmonic regression removes BCG combs more effectively than ECG-based methods. Averaging across epochs mitigates impact of residual artifacts and allows comparable RMSE for recovery of simulated ERPs, albeit with varying precision depending on residual artifact levels.
Figure 5. Harmonic Regression Effectively Removes BCG Artifacts and Recovers Simulated Evoked Responses.
(A) BCG-corrupted test data series (green) and underlying simulated evoked potentials (black). (B) Test data (green) overlaid by clean EEG obtained with harmonic regression (cyan) and ECG-based methods (OBS, top, solid red and AAS, bottom, dashed red). Harmonic regression leaves less residual comb-like pulsatile BCG artifact in cleaned EEG as compared to ECG-based methods. (C) Clean average ERP (thick middle traces) +/− one standard deviation (thin traces) across 200 epochs – obtained with harmonic regression (cyan), OBS (solid red) and AAS (dashed red) atop simulated ERP (black, identical across epochs). Each algorithm yields clean average ERP with morphology matching simulation – although harmonic regression and OBS estimates have lower standard deviations than AAS.
3.4. Recovery of Anesthesia-Induced Oscillations
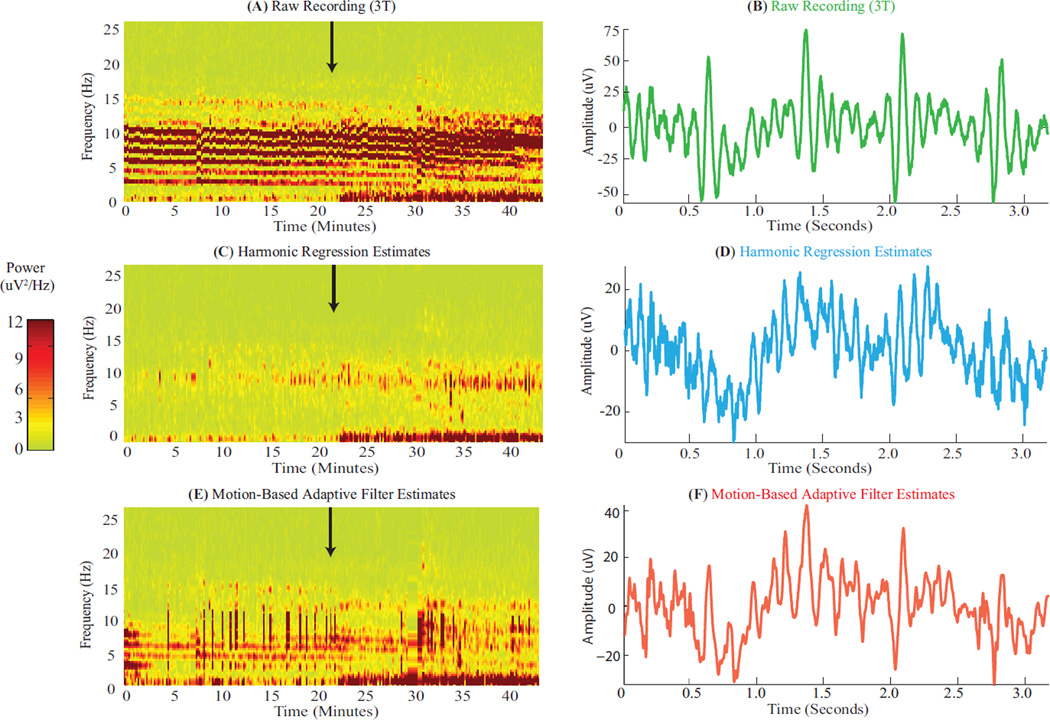
We tested performance of harmonic regression (R = 16, P = 8) and motion-based adaptive filtering on propofol anesthesia-induced EEG oscillations recorded at 3 T (§ 2.5.2). This is a challenging test because propofol induces oscillations that (a) span multiple frequencies (0.1 – 1 Hz slow and 8 – 12 Hz alpha bands), and (b) manifest in frontal electrodes with intense BCG artifacts (Allen et al., 1998; Purdon et al., 2013). We qualitatively compared neurophysiologic signals recovered after artifact removal with propofol oscillations seen outside the scanner in similar conditions (different subjects and instrumentation, (Purdon et al., 2013)). Further, we quantified residual BCG artifacts on periods preceding onset of neurophysiologic oscillations (as harmonic power in true signals is unknown).
Fig. 6A–B show the BCG-corrupted raw recording for a representative frontal electrode (F4 → Fp2). Intense BCG harmonic streaks and combs obscure neurophysiologic oscillations in the spectrogram (expected to appear at time marked by black arrow) and in the time domain. Fig. 6C–D illustrate clean EEG estimated with harmonic regression. The intense harmonic artifacts and pulsatile combs are effectively eliminated in spectral and time domains (24.0% residuals in period before black arrow). Clear oscillations in the 0 – 1 Hz slow and 8 – 12 Hz alpha bands appear in the spectrogram at the expected time (black arrow). These oscillations share qualitative trends with outside-scanner recordings under similar conditions (Fig. 1A). A slow oscillatory envelope with alpha activity atop it is evident in the time domain. Fig. 6E–F show clean EEG estimated with motion-based adaptive filtering. While the adaptive filter reduces harmonic artifacts in the spectrogram, it leaves behind significant artifacts (43.7% residuals in period before black arrow), and does not reveal the onset of 8 – 12 Hz alpha-band activity (black arrow). The time domain estimate contains residual BCG combs (time locked with raw data combs at 1.4 and 2.1 seconds) due to under-estimation of BCG artifacts (Fig. S2B vs. C). Further, motion sensor noise can derail the adaptive filter estimates (Fig. S2D–F). Together, these results demonstrate that harmonic regression recovers multi-band EEG oscillations even amidst intense, significantly overlapping artifacts. Further, they illustrate advantages in recovery of time-frequency features – conferred by not having to rely on robust reference signal recordings in the scanner.
Figure 6. Harmonic Regression Effectively Removes BCG Artifacts and Recovers Propofol-Induced Oscilations.
(A, C, E) Spectrograms of BCG-corrupted recordings in scanner, and clean EEG recovered using harmonic regression and motion-based adaptive filtering respectively. Black arrows mark time of loss of consciousness, when oscillations are expected to set in. Harmonic regression effectively removes BCG artifacts to reveal onset of 0 – 1 Hz slow and 8 – 12 Hz alpha oscillations (similar to Fig. 1A) at the expected time. Adaptive filter leaves more residual artifacts and does not restore alpha oscillations. (B, D, F) Time series of raw recording (green), and clean EEG recovered using harmonic regression (cyan) and adaptive filter (red). All data segments start at 25.6 minutes. Harmonic regression estimates contain lower residual BCG combs than adaptive filter estimates (e.g., combs at 1.4 and 2.1 seconds in B, F). Vertical axis amplitude of D ¡ F.
3.5. Recovery of Visual Evoked Responses
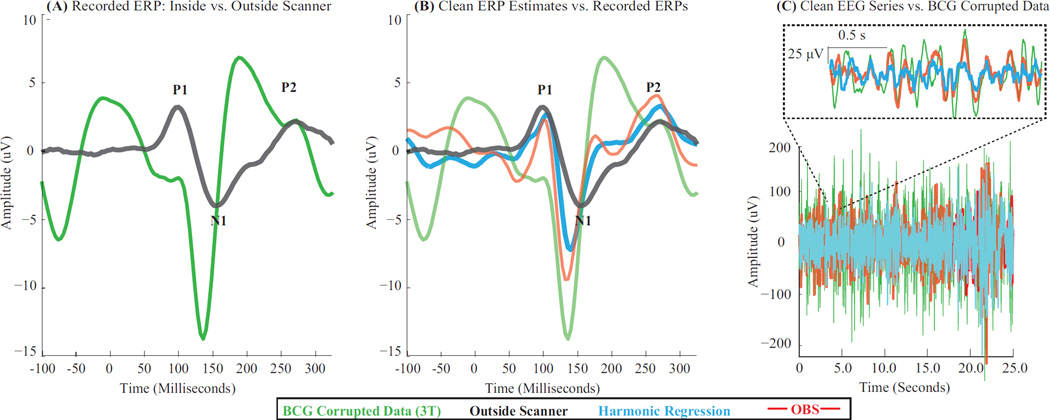
We tested performance of harmonic regression (R = 18, P = 3) and ECG-based methods (OBS and AAS) on visual evoked responses recorded at 3 T (§ 2.5.3). We qualitatively compared neurophysiologic signals recovered after artifact removal with visual evoked responses seen outside the scanner in similar conditions (different days, visual environment and subject positioning). Further, we quantified residual BCG artifacts.
Fig. 7A shows the raw average ERPs recorded inside and outside the scanner (same subject, different sessions) for a right lateral electrode displaying the maximum visual ERP in this subject (e154 location, ~ 2 cm anterior to P4). The BCG-corrupted ERP in the scanner (green) shows a large artifact in the prestimulus baseline (< 0 msec) and has ERP peaks which are clearly different from the outside scanner ERP (black). Fig. 7B shows the clean ERP estimated with harmonic regression (cyan) and OBS (red). Both clean ERPs reduce the prestimulus baseline artifact in the raw ERP (green) and recover peaks at approximately outside scanner latencies (black). Also each cleaned N1 peak inside the scanner is larger and earlier than outside. Harmonic regression (cyan) and OBS (red) estimates are qualitatively similar – with P1-N1 amplitude of 9.8 µV and 11.6 µV respectively. The harmonic regression ERP (cyan) is somewhat smoother than the OBS ERP (red) – perhaps due to a difference in residual BCG artifacts. Fig. 7C shows the clean EEG series obtained with harmonic regression (cyan) and OBS (red), in relation to the raw inside-scanner recording (green). Indeed, OBS leaves more residual comb-like pulsatile BCG artifact (25.7% residuals) than harmonic regression (20.8% residuals). AAS leaves more artifacts (54.5% residuals), but yields similar ERP shapes as OBS. ECG peak detection is satisfactory (Fig. S1). Together, these results suggest that harmonic regression effectively removes BCG artifact and restores evoked potentials with appropriate latency ranges. Further, they illustrate better artifact removal than ECG-based methods, an advantage arising from the use of an appropriate model for BCG artifacts.
Figure 7. Harmonic Regression Effectively Removes BCG Artifacts and Recovers Visual Evoked Responses.
(A) Raw average ERPs from BCG-corrupted and clean recordings obtained inside (green) and outside the scanner (black) respectively. (B) Clean average ERPs obtained using harmonic regression (cyan) and OBS (red), overlaying raw ERP from inside (green) and outside the scanner (black). Cleaned inside scanner ERPs have generally similar peak latencies as outside scanner ERP. Harmonic regerssion and OBS ERPs are qualitatively similar although cyan waveform is somewhat smoother than red one. (C) Clean EEG series obtained with harmonic regression (cyan) and OBS (red), overlaying BCG-corrupted recording inside the scanner (green). Harmonic regression leaves less residual comb-like pulsatile BCG artifact in cleaned EEG as compared to OBS. All estimates are mastoid referenced. All ERPs are averaged over 900 epochs.
In summary, harmonic regression offers substantial improvements over existing methods for recovery of oscillatory rhythms, and performs at least as well as existing methods for recovery of evoked responses. Further, harmonic regression also reduces residual artifacts in all cases (figures for typical subjects above, metrics across subjects in Table S2). Qualitative trends seen are insensitive to changes in number of principal components for OBS, Kalman filtering parameters for motion-based filtering, and number of epochs for ERP averaging.
4. Discussion
EEG-fMRI offers uniquely high spatiotemporal resolution for functional brain imaging, but its widespread utility for neurophysiologic studies is limited by ballistocardiogram (BCG) artifacts. These artifacts pose challenges because they have (a) large amplitudes, (b) significant time-frequency overlap with neurophysiologic signals, and (c) large variations in shape, timing and intensity across time and electrode location. As a result, general mathematical forms for the BCG have remained elusive. Instead, BCG artifacts have been defined using noisy reference-signal based templates (Allen et al., 1998; Bonmassar et al., 2002; Ellingson et al., 2004; Sijbers et al., 2000) and/or component analysis techniques that assume mutual orthogonality between artifact and signal (Mantini et al., 2007; Niazy et al., 2005; Srivastava et al., 2005). By contrast, we have specified a parametric mathematical representation for the BCG, and developed a statistical model-based, reference-free algorithm to estimate parameters and remove BCG artifacts.
4.1. A Model-Based Approach for BCG Artifact Removal
The key conceptual novelty of our approach is that it is based on statistical models for the BCG artifact and neurophysiologic EEG signals. To model the BCG artifacts, we reasoned that the structured nature of physiologic and physical events driving the BCG could correspond to a structured form for the BCG. Empirically, we found that BCG artifacts give rise to a clear harmonic structure in the data (Fig. 1). Theoretically, it is known that a collection of periodically repeating discrete comb-like events can be represented with a harmonic basis (Bracewell, 1986). As such, a harmonic model accounts for the natural shape, timing and dynamics of the BCG artifacts, and eliminates the need for reference-signal based templates (Allen et al., 1998; Bonmassar et al., 2002; Niazy et al., 2005). Further, to address the time-frequency overlap between artifact and signal, we include an autoregressive model that can take on the temporal structure of a variety of neurophysiologic EEG signals. The composite model reflects the empirically observed overlap in structure of artifact and signal, and thus eliminates a priori orthogonality or separability assumptions (Niazy et al., 2005; Srivastava et al., 2005). Finally, as both models have parametric forms, variations in the parameters can account for variations in the BCG artifact and neurophysiologic EEG signals. This eliminates the need to assume fixed pre-defined templates, stationary statistics or spatial homogeneity for the BCG (Allen et al., 1998; Bonmassar et al., 1999; Srivastava et al., 2005).
Given this model, we posed the BCG removal problem as a time-varying regression analysis, and developed a local likelihood algorithm to estimate and remove the artifacts (Fig. 2). Our approach allows clear statistical characterizations to explain the data (e.g., Fig. 3), and addresses the three key challenges in BCG removal. First, the algorithm exploits the high artifact-to-signal ratio nature of the problem as it fits the data to dominant harmonics. Second, the algorithm addresses the time-frequency overlap between artifact and signal by informing the harmonic fit with the AR covariance structure, and vice versa. Because the harmonic term has a discrete line spectrum and the AR term has a continuous smooth spectrum, the two terms have overlapping but separable spectral structure ((Bracewell, 1986; Kay and Cliffs, 1988)). Further, the two terms have distinct power ranges due to dominant BCG harmonics (Allen et al., 1998). Our empirical experience suggests that these characteristics together enable separation of overlapping artifact and signal. Third, the analysis paradigm tracks spatiotemporal variations in artifact and signal – in that it estimates parameters locally with moving time windows, and independently for each electrode location.
4.2. Improvements in Artifact Removal and Signal Recovery
We have demonstrated effective removal of BCG with reduced residual artifacts and improved recovery of neurophysiologic EEG signal phase, power, latencies and timing on both simulated and experimental test cases. We now analyze reasons for these performance improvements.
Reduction in Residual Artifacts
With reference-based algorithms (Allen et al., 1998; Bonmassar et al., 2002; Niazy et al., 2005), accuracy of the estimated BCG depends on quality of the reference signal, and of the model relating the reference signal to the BCG. Therefore, noise in cardiac or motion signals (e.g., Fig. S1), and inaccuracies or variations in the relation between these signals and the BCG (e.g., changes in the cardiac cycle phase when BCG occurs; or non-linearities or spatial variations in the motion-BCG relation) can cause errors in the estimated BCG and leave residual artifacts (e.g., Fig. 5, Fig. 6). With component analysis techniques (Niazy et al., 2005; Srivastava et al., 2005), the assumed artifact-signal orthogonality can cause errors in the estimated BCG and leave residual artifacts (Debener et al., 2007; Vanderperren et al., 2010; Xia et al., 2014). Further, large time variations in the BCG can cause differences between the local BCG shape and estimated principal components (e.g., Fig. 7C). Our approach addresses these challenges as (a) it is reference-free and (b) it models the BCG with the natural harmonic structure while accounting for time-frequency overlap and local variations in artifact and signal.
Improved Recovery of Neurophysiologic Signals
With reference-based algorithms, recovery of time-frequency features can depend on the implicit models assumed for the neurophysiologic EEG signal. For example, the motion-based adaptive filter (Bonmassar et al., 2002) assumes the neurophysiologic EEG is white, and thus may not fully restore oscillatory features in the clean EEG (e.g., Fig. 6). Further, ECG-based methods (Allen et al., 1998; Niazy et al., 2005) assume temporal independence of the neurophysiologic EEG components across time, and thus may not account for evolving dynamics within the EEG signal (e.g., Fig. 4). With component analysis methods, recovery of time-frequency features in the signal can depend on the degree of time-frequency overlap between signal and artifact. For example, as OBS assumes artifact-signal orthogonality, signal components overlapping artifacts may get designated as artifactual (e.g., Fig. 4) (Garreffa et al., 2004; Grouiller et al., 2007; Niazy et al., 2005). Our approach addresses these challenges by modeling the neurophysiologic EEG with a general autoregressive model that can (a) explain a variety of evolving neurophysiologic dynamics, and (b) explicitly account for the time-frequency overlap of these dynamics with harmonic BCG artifacts.
In summary, we achieve improved artifact removal and signal recovery by (a) employing an explicitly stated reference-free model that is customized to the inherent structure of the artifact, signal as well as their overlap and dynamics, and (b) developing a statistically principled algorithm to explain the data.
4.3. Practical Considerations
In addition to performance, our approach enables several practical advantages over existing methods. First, our algorithm does not require reference signals, specialized hardware or recording protocols - unlike methods that require clean reference signal recordings (Allen et al., 1998; Bonmassar et al., 2002; Niazy et al., 2005) or interactively derived reference-based templates (Fig. S1), special electrode systems with insulating reference layers (Chowdhury et al., 2014; Mullinger et al., 2013), acquisition protocols that block specific EEG channels and/or require parallel recordings inside and outside the scanner (Xia et al., 2014). Thus, it has minimal sensor and electronics requirements, and offers enhanced safety and convenience - particularly for recordings in clinical conditions, on subjects having special needs, and/or at higher field strengths. Second, our algorithm offers customizable temporal resolution to track drifts in the BCG shape or timing – as the moving window length can be reduced to as low as 1.5 – 2 seconds without compromising estimation accuracy (§ Appendix C.2). This is unlike ECG-based methods or component analysis techniques (Allen et al., 1998; Niazy et al., 2005; Srivastava et al., 2005) that require continuous EEG segments ~ 30 sec long for reliable estimation. This feature is useful when the BCG is highly time varying, and also in interleaved EEG-fMRI studies where short segments of continuous EEG data are interspersed with large gradient artifacts during fMRI acquisition. Finally, our method is computationally efficient and amenable to real-time implementation (e.g., on a graphical processing unit) for continuous monitoring and online artifact removal.
4.4. Neuroscience Applications and Future Directions
The above performance and practical advantages have implications for neuroscience studies using EEG-fMRI. Our approach significantly extends capabilities for BCG removal and signal recovery in conditions where high quality reference-based templates are hard to derive. Further, our results show improved BCG removal and signal recovery in challenging conditions having (a) intense artifacts (e.g., fronto-lateral channels), (b) complex evolving time-frequency dynamics (e.g., multiband oscillations in 0 – 15 Hz range) that overlap artifacts and cannot be averaged, and (c) significant drift in artifacts and reference signals (e.g., a long duration drug study). These advantages are particularly relevant for (a) high-field studies where reference-based templates are challenging and BCG artifacts are more severe, (b) studies of oscillations in cognitive states like attention, memory and decision-making, and (c) long duration clinical studies of sleep and anesthesia.
Future reports will develop state-space implementations of our estimation procedure to overcome the need for moving windows and enhance adaptability to beat-to-beat variations in the BCG (§ Appendix C.2). Our algorithm could be applied to reduce residual gradient artifacts that manifest as harmonics with distinct fundamental frequency from the BCG. Our work could also be expanded for (a) testing EEG time-frequency features that are better modeled with non-AR forms (e.g., evoked peaks, K-complexes and epileptic spikes), and/or (b) explicit testing of hypotheses relating to neurophysiologic EEG changes arising as a result of stimulus, drug or other intervention. Further evaluations on continuous EEG-fMRI scans with diverse stimulus paradigms and imaging conditions will enhance suitability for a variety of neuroscience studies.
Supplementary Material
Highlights.
Model EEG-fMRI ballistocardiogram (BCG) artifacts using a harmonic basis
Develop efficient maximum likelihood algorithm to estimate and remove artifacts
Demonstrate BCG removal and signal recovery in simulated and experimental tests
Show improvements over ECG and motion reference-based BCG removal methods
Practical reference-free tool to remove BCG artifact from EEG recorded with fMRI
Acknowledgments
We acknowledge clinical data collection assistance from John Walsh, Grace Harrell, Jean Kwo, Daniel Deschler, Margaret Barlow, Rebecca Merhar, Catherine Mullaly, Mary Sullivan, Sharon Maginnis, Debra Skoniecki, and Helen-Anne Higgins at the Massachusetts General Hospital. We also acknowledge helpful discussions withWasim Malik, Camilo Lamus and Demba Ba at the Massachusetts Institute of Technology. This work was funded by the National Institutes of Health: NIH Director’s Pioneer Award DP1-OD003646 and NIH Transformative Research Project TR01-GM104948 (to E.N.B.), and the NIH New Innovator Award DP2-OD006454 (to P.L.P.). Data acquisition was supported by the National Center for Research Resources Grant 1 UL1 RR025758-04, (via the Harvard Clinical and Translational Science Center), and NIH/NINDS Grant R44NS071988 (to C.P.). P.K.S., P.L.P. and E.N.B. have a patent pending on removal of artifacts from electrophysiologic recordings in the MRI scanner.
Appendix A
Prior for Harmonic Amplitude Estimation
In this appendix, we detail the implementation of steps 1 and 2 of the cyclic descent iteration described in § 2.4. The time-frequency overlap between the harmonic BCG and the autoregressive brain EEG makes it important to inform estimation of the harmonic amplitudes with the AR spectral structure. In other words, estimation of the harmonic amplitudes β must be informed by the AR covariance Q. However, at the start of the cyclic descent, the algorithm does not have an estimate of Q (we initialize with Q−1 = IT×T). Thus, the initial least squares estimate of harmonic amplitudes is:
| (A.1) |
This attributes most measurement power in the harmonic bands to the BCG artifact, although some of it may correspond to the neurophysiologic signal. As the cyclic descent proceeds and estimates Q from the data, the non-harmonic spectral structure is assigned to the AR term, and generalized least squares partitions harmonic power between artifact and signal optimally.
Hence, to guide the first few cyclic descent iterations, it is useful to have prior information to constrain the harmonic amplitude estimates. For this purpose, we incorporate a prior covariance W = E(β′ β) on the harmonic amplitudes. We assume W to be diagonal, and specify the jth diagonal term of W as the difference between measurement powers in the jth harmonic line and in a 2 Hz band centered around the jth harmonic line. As the harmonic frequencies depend on the ω under consideration, we denote the prior as W(ω).
When the measurement contains high power in the neighborhood of the harmonic streaks,W(ω) discounts β̂ and allows the AR term to retain more underlying EEG power. This is also evident in the form of the generalized least squares estimate:
| (A.2) |
If |W(ω)| >> |Q(ω)|, or W−1(ω) → 0, then nearly all measurement power in the harmonic bands is allocated to the estimated BCG. But lower values of |W(ω)| discount the harmonic fit and preserve more overlapping neurophysiologic EEG. In practice, it is efficient to pre-compute the matrices W(ω) for each possible value of ω. The prior covariance primarily affects β̂ in early cyclic descent iterations and does not significantly change ω̂.
Appendix B
Estimation of Autoregressive Structure
In this appendix, we detail the implementation of steps 4 and 5 of the cyclic descent iteration described in § 2.4. For notational convenience, we will write α̂(ω), σ̂2(ω), v̂(ω), Q̂−1(ω) without the ω dependence. The problem of estimating AR coefficients given a time series v̂T×1 is one of linear prediction which can be solved with the Levinson-Durbin Recursions (Box et al., 2008; Kay and Cliffs, 1988). A stable solution for the Levinson-Durbin Recursions in AR estimation can be found with the Burg algorithm, which minimizes the least squares forward-backward prediction error (Box et al., 2008; Kay and Cliffs, 1988). Specifically, this efficiently yields estimates of the AR coefficients and residual variances for different model orders p = 1, 2, …, P: written as α̂(1), α̂(2), …, α̂(P) and σ̂2(1),σ̂2(2), …,σ̂2(P) respectively (Malik et al., 2011). Each α̂(l) is a vector with terms for l lags.
The covariance matrix of the AR process QT×T can be written, via Cholesky decomposition, as Q = UΣU′. Then, the inverse AR covariance estimate used in our algorithm, per (Malik et al., 2011; Newton, 1988), is:
| (B.1) |
Further, as Û−1 is triangular with unit values on the diagonal:
| (B.2) |
As these forms and the necessary parameter estimates are readily available, no explicit matrix inversion or determinant computations are required. However, the multiplication in Eqn. B.1 is still the most computationally intensive part of this estimation, with complexity O(T3). Thus, we write an efficient block matrix multiplication to exploit the sparsity and repeating patterns in Û−1 and Σ̂−1. Denoting blocks within the Û−1 and Σ̂−1 matrices as F, G, H and D, we have:
| (B.3) |
| (B.4) |
| (B.5) |
Each block multiplication in Eqn. B.5 has low complexity. As T ≫ P, the F′ DF + cG′ G term has complexity O(P2T), while the cG′ H and cH′ G terms each have complexity O(PT2). The cH′ H term has complexity O(T2) as H is largely sparse with only O(T) non-zero elements. Thus, total complexity of computing Q̂−1 with our block matrix multiplication form is O(PT2). As P << T, this is significantly less than the O(T3) complexity for the naive multiplication in Eqn. B.1. An analysis of computational time shows that the multiplication in Eqn. B.5 is ~ 40X faster than that in Eqn. B.1. As the inverse AR covariance is estimated for each of ~ 2 – 6 cyclic descent iterations at each of ~ 100 ω values for each data segment, the efficiency improvement afforded by our block form is significant and necessary for computational efficiency.
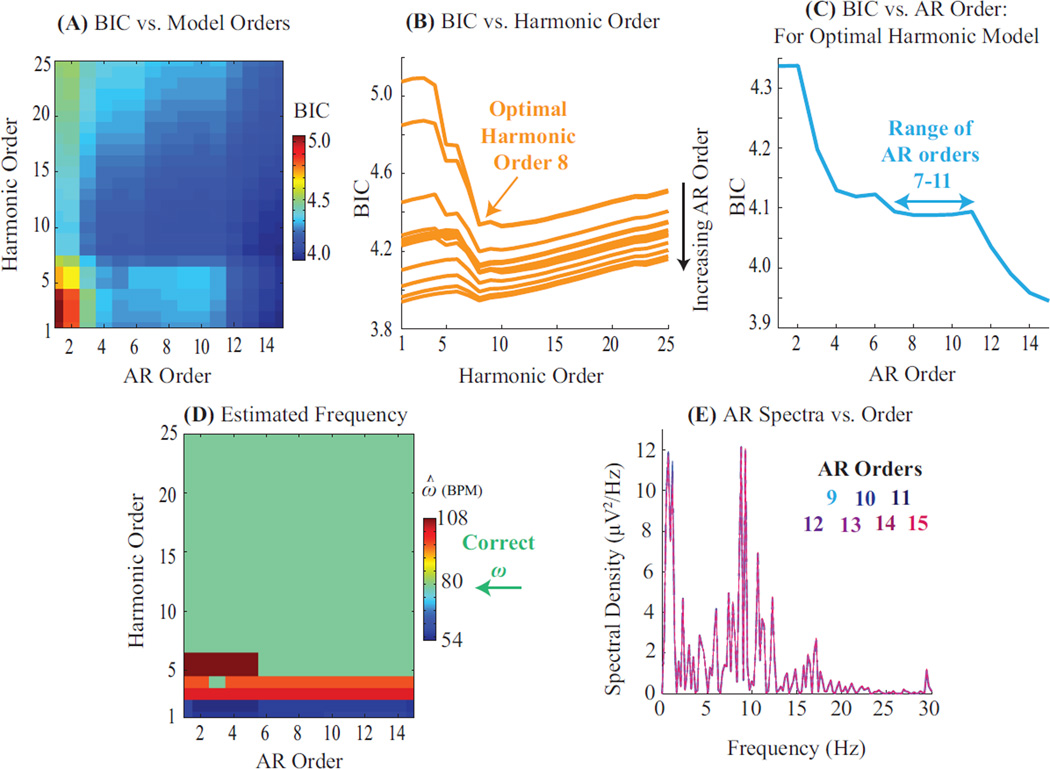
Figure B.1: Model Selection Process and Sensitivity to Model Orders. (A) Bayesian Information Criterion (BIC) as a function of harmonic and autoregressive model orders. (B) BIC from (A) plotted as a function of harmonic orders. Each trace represents a different AR order. Optimal harmonic order for this segment is 8, regardless of the AR order. (C) BIC for the optimal harmonic order from (B) plotted as a function of AR orders. BIC levels off for a range of 7 – 11 AR coefficients. Higher AR orders merely explain more background power without explaining additional oscillatory features (also Panel E). (D) Fundamental frequency estimates are identical and accurate for all models comprising over 5 harmonics and 5 AR terms. (E) Spectral structure of AR estimates is invariant for large AR orders.
Appendix C
Inputs for Analysis
Given a data recording, the inputs required for analysis are: (a) the harmonic and autoregressive model orders R, P, and (b) the moving window interval T. In this appendix, we detail procedures for setting these inputs and evaluate sensitivity to specific settings.
Appendix C.1. Model Selection
Harmonic orders R and AR orders P are jointly determined by trading off goodness of fit and model parsimony with the Bayesian Information Criterion (BIC). For data segment yT×1 and a given pair of harmonic and AR orders (r, p), the residual variance σ2 is estimated as detailed in § 2.4, and the BIC is defined as T log σ2 + (2r + p + 1) log(T). The BIC is computed for multiple (r, p) pairs (Fig. B.1a). The optimal model orders are determined as [Rbic, Pbic] = arg minr,p BIC(r, p). This is a two-step minimization. First, as the measurement is dominated by BCG harmonics, the optimal harmonic order Rbic can be determined independent of the AR orders (Fig. B.1b). In practice, Rbic is a guideline for minimum number of harmonics needed, and R is set to 2Rbic to ensure that higher harmonics are not ignored. Second, the data is fit to R harmonics, and the AR order is determined as that which best explains the remnant non-harmonic structure (Fig. B.1c). Usually, a range of AR orders Pbic can adequately explain the data and P is set as the mean of this range. The selected model order pair (R, P) is also checked to ensure that resulting residuals fulfill goodness of fit criteria (Fig. 3). This procedure is repeated across several data segments and channels to obtain one representative model order pair (R, P) for consistently analyzing a given EEG recording.
The parameter estimation is relatively insensitive to precise model orders within a suitable range. First, the BIC has largely similar values for 8 – 16 harmonics and 4 – 12 AR terms (Fig. B.1a–c). This indicates that the residual mean square error σ2 is relatively robust to selection of model order. Second, accurate and similar fundamental frequency ω estimates are obtained for models comprising a few harmonics and more than 4–5 AR terms (Fig. B.1d). This insensitivity is because the data has striking harmonic structure. Third, additional AR terms beyond Pbic do not significantly change the spectral distribution of AR power (Fig. B.1e). Finally, model order choices and sensitivity trends outlined here hold for other commonly used model selection criteria such as the Akaike Information Criterion.
Appendix C.2. Length of Moving Windows
The moving window interval T is determined by trading off the desired time and frequency resolutions. Our algorithm estimates one set of parameters for each data segment yT×1. Thus, considering shorter data segments enables greater time resolution - i.e., allows the estimated parameters to adapt faster to drifts in the BCG artifacts and the neurophysiologic EEG. However, shorter data segments correspond to lower frequency resolution for the harmonics. Thus, T is set to be the shortest interval required to sufficiently resolve the harmonics. Our algorithm provides very high frequency resolution estimates with 2 – 6 cycles of the fundamental harmonic. As the fundamental period or typical heart rate is ~ 1 second, this analysis suggests a choice of T = 2 – 6 seconds. This choice also enables sufficient resolution to adapt to time variations in the BCG (normal heart rate and blood pressure are well-maintained across 2 – 6 beats) and the neurophysiologic EEG (standard EEG spectral analysis techniques consider windows of few seconds).
The frequency estimation is generally insensitive to the precise choice of T within the ranges noted above (Fig. B.1a). The estimated harmonic amplitudes are insensitive to T when the BCG combs do not exhibit wide beat-to-beat variations in amplitude (Fig. B.1b). However, in cases where the BCG amplitude varies widely between heart beats, it is important to shorten the window length for accurate amplitude estimation and effective artifact removal (Fig. B.1c). This is because the algorithm estimates a constant set of harmonic amplitudes for a given data window. We note that future extensions of our regression procedure to state space formulations where parameter estimates evolve instantaneously with each new data-point would eliminate the need for moving windows or for setting interval T.
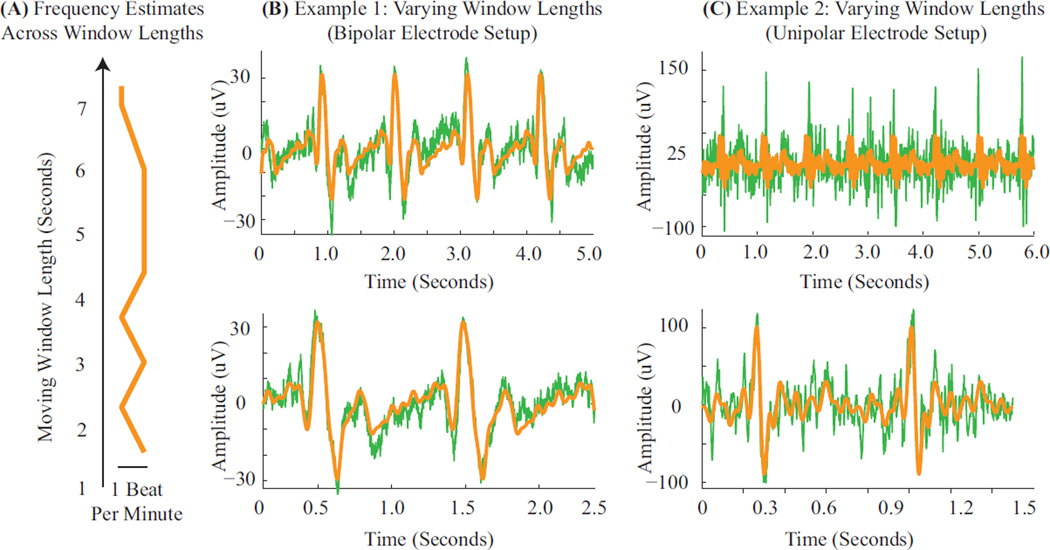
Figure C.1: Sensitivity to Moving Window Length. (A) The frequency estimates are near identical across window lengths. (B–C) Examples overlay the raw measurements (green) with the harmonic BCG estimates (orange). (B) In case the BCG comb amplitudes do not vary significantly, amplitude estimation is effective across long (top) and short (bottom) window lengths. (C) In case of extreme variations in BCG comb amplitudes across heartbeats, shorter windows are required for good performance (bottom vs. top panels). Data for Panels B and C were acquired with the bipolar and unipolar acquisition systems described in § 2.5.1 and § 2.5.1 respectively.
Appendix D
Convergence of Algorithm
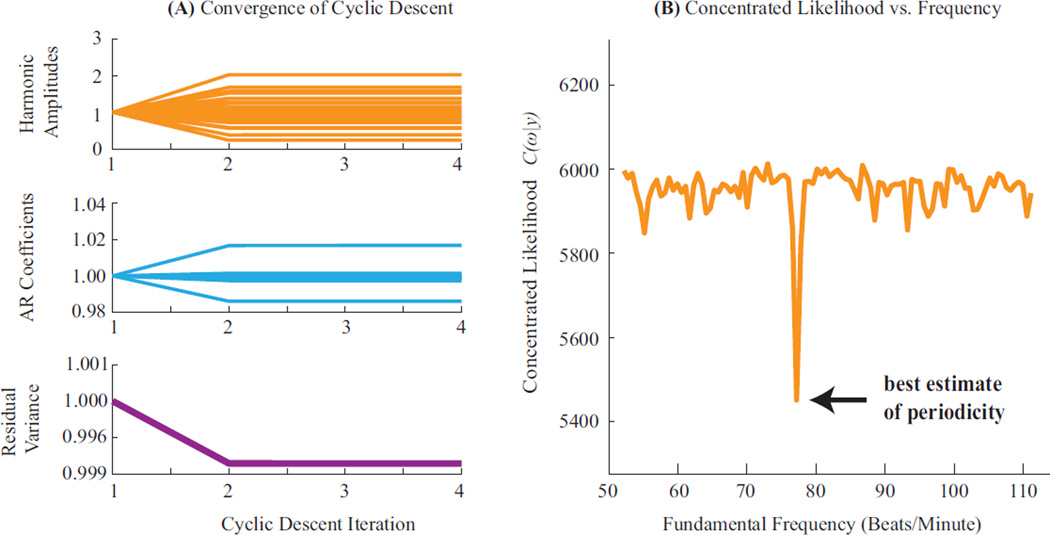
In this appendix, we show that our likelihood optimizations converge robustly. Fig. D.1 illustrates convergence characteristics of the two sequential minimization steps (Eqn. 11). First, the inner minimization uses a cyclic descent for each frequency value ω. Fig. D.1a plots estimates of β, α,σ2 through successive iterations of the cyclic descent for one ω value, showing convergence of all parameters within a few iterations. Second, the outer minimization optimizes the concentrated likelihood C(ω|y) across a range of frequencies [ωmin, ωmax]. Fig. D.1b plots C(ω|y) across the physiological range of frequencies (specified in § 2.4). Within this range, C(ω|y) consistently exhibits a unique minimum in ω. Finally, a separation theorem (Corradi, 1979) proves that given optimal fundamental frequency estimates ω̂, the associated harmonic and AR parameter estimates, û(ω̂) = [β̂ (ω̂), α̂ (ω̂), σ̂2(ω̂)], are also optimal.
Figure D.1: Convergence. (A) Parameter estimates for β̂, α̂ and σ̂2 are plotted over the course of the cyclic descent - showing fast and maintained convergence. All estimates are normalized relative to the initial estimate, for ease of comparison. (B) The concentrated likelihood is plotted across the range of plausible frequencies, binned at 0.60 beats per minute. A high resolution global minimum is seen, suggesting robust convergence of the final one-dimensional optimization.
References
- Allen PJ, Josephs O, Turner R. A method for removing imaging artifact from continuous EEG recorded during functional MRI. NeuroImage. 2000 Aug.12(2):230–239. doi: 10.1006/nimg.2000.0599. [DOI] [PubMed] [Google Scholar]
- Allen PJ, Polizzi G, Krakow K, Fish DR, Lemieux L. Identification of EEG events in the MR scanner: the problem of pulse artifact and a method for its subtraction. NeuroImage. 1998 Oct.8(3):229–239. doi: 10.1006/nimg.1998.0361. [DOI] [PubMed] [Google Scholar]
- Angelone LM, Bonmassar G. Use of resistances and resistive leads: Implications on computed electric field and SAR values. Proc.12th ISMRM. 2004:1652. [Google Scholar]
- Angelone LM, Vasios CE, Wiggins G, Purdon PL, Bonmassar G. On the effect of resistive EEG electrodes and leads during 7 T MRI: simulation and temperature measurement studies. Magnetic Resonance Imaging. 2006;24(6):801–812. doi: 10.1016/j.mri.2006.01.006. [DOI] [PubMed] [Google Scholar]
- Ansley CF, Wecker WE. The signal extraction approach to nonlinear regression and spline smoothing. Journal of the American Statistical Association. 1983 Mar;78(381):81–89. [Google Scholar]
- Bonmassar G, Anami K, Ives J, Belliveau JW. Visual evoked potential (VEP) measured by simultaneous 64-channel EEG and 3T fMRI. NeuroReport. 1999 Jun.10(9):1893–1897. doi: 10.1097/00001756-199906230-00018. [DOI] [PubMed] [Google Scholar]
- Bonmassar G, Purdon PL, Jaaskelainen IP, Chiappa K, Solo V, Brown EN, Beliveau JW. Motion and ballistocardiogram artifact removal for interleaved recording of EEG and EPs during MRI. NeuroImage. 2002 Aug.16(4):1127–1141. doi: 10.1006/nimg.2002.1125. [DOI] [PubMed] [Google Scholar]
- Bonmassar G, Schwartz DP, Liu AK, Kwong KK, Dale AM, Belliveau JW. Spatiotemporal brain imaging of visual-evoked activity using interleaved EEG and fMRI recordings. NeuroImage. 2001 Jun.13(6 Pt 1):1035–1043. doi: 10.1006/nimg.2001.0754. [DOI] [PubMed] [Google Scholar]
- Box GE, Jenkins GM, Reinsel GC. Time series analysis: forecasting and control. 4th. Hoboken, NJ: John Wiley; 2008. [Google Scholar]
- Bracewell R. The Fourier Transform and Its Applications (revised ed.) McGraw-Hill; 1986. [Google Scholar]
- Brookes MJ, Mullinger KJ, Stevenson CM, Morris PG, Bowtell R. Simultaneous EEG source localisation and artifact rejection during concurrent fMRI by means of spatial filtering. NeuroImage. 2008;40(3):1090–1104. doi: 10.1016/j.neuroimage.2007.12.030. [DOI] [PubMed] [Google Scholar]
- Brown EN, Schmid CH. Application of the Kalman filter to computational problems in statistics. Methods in Enzymology. 1994;240:171–181. doi: 10.1016/s0076-6879(94)40048-2. [DOI] [PubMed] [Google Scholar]
- Brown EN, Solo V, Choe Y, Zhang Z. Measuring period of human biological clock: infill asymptotic analysis of harmonic regression parameter estimates. Methods in Enzymology. 2004 Jan.383(1989):382–405. doi: 10.1016/S0076-6879(04)83016-7. [DOI] [PubMed] [Google Scholar]
- Chowdhury MEH, Mullinger KJ, Glover P, Bowtell R. Reference layer artefact subtraction (RLAS): a novel method of minimizing EEG artefacts during simultaneous fMRI. NeuroImage. 2014 Jan.84:307–319. doi: 10.1016/j.neuroimage.2013.08.039. [DOI] [PubMed] [Google Scholar]
- Corradi C. A note on the computation of maximum likelihood estimates in linear regression models with autocorrelated errors. Journal of Econometrics. 1979 Jan;11:303–317. [Google Scholar]
- Debener S, Mullinger KJ, Niazy RK, Bowtell RW. Properties of the ballistocardiogram artefact as revealed by EEG recordings at 1.5, 3 and 7 T static magnetic field strength. International Journal of Psychophysiology. 2008;67(3):189–199. doi: 10.1016/j.ijpsycho.2007.05.015. [DOI] [PubMed] [Google Scholar]
- Debener S, Strobel A, Sorger B, Peters J, Kranczioch C, Engel AK, Goebel R. Improved quality of auditory event-related potentials recorded simultaneously with 3T fMRI: removal of the ballistocardiogram artefact. NeuroImage. 2007 Jan.34(2):587–597. doi: 10.1016/j.neuroimage.2006.09.031. [DOI] [PubMed] [Google Scholar]
- Debener S, Ullsperger M, Siegel M, Fiehler K, von Cramon DY, Engel AK. Trial-by-trial coupling of concurrent electroencephalogram and functional magnetic resonance imaging identifies the dynamics of performance monitoring. The Journal of Neuroscience. 2005 Dec.25(50):11730–11737. doi: 10.1523/JNEUROSCI.3286-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics. Journal of Neuroscience Methods. 2004 Oct;134:9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Ellingson ML, Liebenthal E, Spanaki MV, Prieto TE, Binder JR, Ropella KM. Ballistocardiogram artifact reduction in the simultaneous acquisition of auditory ERPs and fMRI. NeuroImage. 2004 Aug.22(4):1534–1542. doi: 10.1016/j.neuroimage.2004.03.033. [DOI] [PubMed] [Google Scholar]
- Garreffa G, Bianciardi M, Hagberg GE, Macaluso E, Marciani MG, Maraviglia B, Abbafati M, Carnì M, Bruni I, Bianchi L. Simultaneous EEG-fMRI acquisition: how far is it from being a standardized technique? Magnetic Resonance Imaging. 2004 Dec.22(10):1445–1455. doi: 10.1016/j.mri.2004.10.013. [DOI] [PubMed] [Google Scholar]
- Goldman RI, Stern JM, Engel J, Cohen MS. Acquiring simultaneous EEG and functional MRI. Clinical Neurophysiology. 2000 Nov.111(11):1974–1980. doi: 10.1016/s1388-2457(00)00456-9. [DOI] [PubMed] [Google Scholar]
- Goldman RI, Stern JM, Engel J, Cohen MS. Simultaneous EEG and fMRI of the alpha rhythm. NeuroReport. 2002 Dec.13(18):2487–2492. doi: 10.1097/01.wnr.0000047685.08940.d0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gramfort A, Luessi M, Larson E, Engemann DA, Strohmeier D, Brodbeck C, Parkkonen L, Hämäläinen MS. MNE software for processing MEG and EEG data. NeuroImage. 2014 Feb.86:446–460. doi: 10.1016/j.neuroimage.2013.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grouiller F, Vercueil L, Krainik A, Segebarth C, Kahane P, David O. A comparative study of different artefact removal algorithms for EEG signals acquired during functional MRI. NeuroImage. 2007 Oct.38(1):124–137. doi: 10.1016/j.neuroimage.2007.07.025. [DOI] [PubMed] [Google Scholar]
- Huang-Hellinger F, Breiter HC, McCormack G, Cohen MS, Kwong KK, Sutton JP, Savoy RL, Weisskoff RM, Davis TL, Baker JR, Belliveau JW, Rosen BR. Simultaneous functional magnetic resonance imaging and electrophysiological recording. Human Brain Mapping. 1995 Oct.3(1):13–23. [Google Scholar]
- Iannetti GD, Di Bonaventura C, Pantano P, Giallonardo AT, Romanelli PL, Bozzao L, Manfredi M, Ricci GB. fMRI/EEG in paroxysmal activity elicited by elimination of central vision and fixation. Neurology. 2002 Mar.58(6):976–979. doi: 10.1212/wnl.58.6.976. [DOI] [PubMed] [Google Scholar]
- Iannetti GD, Niazy RK, Wise RG, Jezzard P, Brooks JCW, Zambreanu L, Vennart W, Matthews PM, Tracey I. Simultaneous recording of laser-evoked brain potentials and continuous, high-field functional magnetic resonance imaging in humans. NeuroImage. 2005 Nov.28(3):708–719. doi: 10.1016/j.neuroimage.2005.06.060. [DOI] [PubMed] [Google Scholar]
- Ives JR, Warach S, Schmitt F, Edelman R, Schomer DL. Monitoring the patient’s EEG during echo planar MRI. Electroencephalography and Clinical Neurophysiology. 1993 Aug;87:417–420. doi: 10.1016/0013-4694(93)90156-p. [DOI] [PubMed] [Google Scholar]
- Kay SM, Cliffs E. Modern spectral estimation: theory and application. Prentice Hall; 1988. [Google Scholar]
- Kim KH, Yoon HW, Park HW. Improved ballistocardiac artifact removal from the electroencephalogram recorded in fMRI. Journal of Neuroscience Methods. 2004 May;135(1–2):193–203. doi: 10.1016/j.jneumeth.2003.12.016. [DOI] [PubMed] [Google Scholar]
- Krakow K, Woermann FG, Symms MR, Allen PJ, Lemieux L, Barker GJ, Duncan JS, Fish DR. EEG-triggered functional MRI of interictal epileptiform activity in patients with partial seizures. Brain. 1999 Mar;122:1679–1688. doi: 10.1093/brain/122.9.1679. [DOI] [PubMed] [Google Scholar]
- Krishnaswamy P, Bonmassar G, Purdon PL, Brown EN. Reference-free harmonic regression technique to remove EEG-fMRI ballistocardiogram artifacts. Proceedings: Annual International Conference of the IEEE Engineering in Medicine and Biology Society. 2013 Jan.2013:5426–5429. doi: 10.1109/EMBC.2013.6610776. [DOI] [PubMed] [Google Scholar]
- Krishnaswamy P. Ph.D. thesis. Harvard-MIT Division of Health Sciences and Technology; 2014. Algorithms for enhanced spatiotemporal imaging of human brain function. [Google Scholar]
- Laufs H, Daunizeau J, Carmichael DW, Kleinschmidt a. Recent advances in recording electrophysiological data simultaneously with magnetic resonance imaging. NeuroImage. 2008 Apr.40(2):515–528. doi: 10.1016/j.neuroimage.2007.11.039. [DOI] [PubMed] [Google Scholar]
- Laufs H, Krakow K, Sterzer P, Eger E, Beyerle A, Salek-Haddadi A, Kleinschmidt A. Electroencephalographic signatures of attentional and cognitive default modes in spontaneous brain activity fluctuations at rest. Proceedings of the National Academy of Sciences. 2003 Sep.100(19):11053–11058. doi: 10.1073/pnas.1831638100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemieux L, Salek-Haddadi A, Josephs O, Allen PJ, Toms N, Scott C, Krakow K, Turner R, Fish DR. Event-related fMRI with simultaneous and continuous EEG: description of the method and initial case report. NeuroImage. 2001 Sep.14(3):780–787. doi: 10.1006/nimg.2001.0853. [DOI] [PubMed] [Google Scholar]
- Malik WQ, Schummers J, Sur M, Brown EN. Denoising two-photon calcium imaging data. PLoS One. 2011 Jan.6(6):e20490. doi: 10.1371/journal.pone.0020490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantini D, Perrucci MG, Cugini S, Ferretti A, Romani GL, Del Gratta C. Complete artifact removal for EEG recorded during continuous fMRI using independent component analysis. NeuroImage. 2007 Jan.34(2):598–607. doi: 10.1016/j.neuroimage.2006.09.037. [DOI] [PubMed] [Google Scholar]
- Mullinger KJ, Havenhand J, Bowtell R. Identifying the sources of the pulse artefact in EEG recordings made inside an MR scanner. NeuroImage. 2013 May;71:75–83. doi: 10.1016/j.neuroimage.2012.12.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musso F, Brinkmeyer J, Ecker D, London MK, Thieme G, Warbrick T, Wittsack H-J, Saleh A, Greb W, de Boer P, Winterer G. Ketamine effects on brain function - simultaneous fMRI/EEG during a visual oddball task. NeuroImage. 2011 Jun.58(2):508–525. doi: 10.1016/j.neuroimage.2011.06.045. [DOI] [PubMed] [Google Scholar]
- Nakamura W, Anami K, Mori T, Saitoh O, Cichocki A, Amari S-i. Removal of ballistocardiogram artifacts from simultaneously recorded EEG and fMRI data using independent component analysis. IEEE Transactions on Biomedical Engineering. 2006 Jul.53(7):1294–1308. doi: 10.1109/TBME.2006.875718. [DOI] [PubMed] [Google Scholar]
- Newton HJ. TIMESLAB: a time series analysis laboratory. Pacific Grove, CA: Wadsworth & Brooks/Cole Pub. Co; 1988. [Google Scholar]
- Niazy RK, Beckmann CF, Iannetti GD, Brady JM, Smith SM. Removal of fMRI environment artifacts from EEG data using optimal basis sets. NeuroImage. 2005 Nov.28(3):720–737. doi: 10.1016/j.neuroimage.2005.06.067. [DOI] [PubMed] [Google Scholar]
- Purdon PL. Ph.D. thesis, Harvard University and Massachusetts Institute of Technology. 2005. Multimodal neuroimaging with simultaneous electroencephalogram and high-field functional magnetic resonance imaging. [Google Scholar]
- Purdon PL, Millan H, Fuller PL, Bonmassar G. An open-source hardware and software system for acquisition and real-time processing of electrophysiology during high-field MRI. Journal of Neuroscience Methods. 2008;175(2):165–186. doi: 10.1016/j.jneumeth.2008.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purdon PL, Pierce ET, Bonmassar G, Walsh J, Harrell PG, Kwo J, Deschler D, Barlow M, Merhar RC, Mullaly CM, Sullivan M, Maginnis S, Skoniecki D, Higgins A, Brown EN. Simultaneous electroencephalography and functional magnetic resonance imaging of general anesthesia. Annals of the New York Academy of Sciences. 2009 Mar;1157:61–70. doi: 10.1111/j.1749-6632.2008.04119.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purdon PL, Pierce ET, Mukamel EA, Prerau MJ, Wong KF, Salazar-Gomez AF, Tavares-Stoeckel CL, Habeeb K, Merhar R, Brown EN. Electroencephalogram signatures of loss and recovery of consciousness from propofol. Proceedings of the National Academy of Sciences. 2013;110(12):E1142–E1151. doi: 10.1073/pnas.1221180110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schomer DL, Bonmassar G, Lazeyras F, Seeck M, Blum A, Anami K, Schwartz D, Belliveau JW, Ives JR. EEG-linked functional magnetic resonance imaging in epilepsy and cognitive neurophysiology. Journal of Clinical Neurophysiology. 2000 Jan;17(1):43–58. doi: 10.1097/00004691-200001000-00005. [DOI] [PubMed] [Google Scholar]
- Sijbers J, Van Audekerke J, Verhoye M, Van der Linden A, Van Dyck D. Reduction of ECG and gradient related artifacts in simultaneously recorded human EEG/MRI data. Magnetic Resonance Imaging. 2000 Sep.18(7):881–886. doi: 10.1016/s0730-725x(00)00178-8. [DOI] [PubMed] [Google Scholar]
- Srivastava G, Crottaz-Herbette S, Lau KM, Glover GH, Menon V. ICA-based procedures for removing ballistocardiogram artifacts from EEG data acquired in the MRI scanner. NeuroImage. 2005 Jan.24(1):50–60. doi: 10.1016/j.neuroimage.2004.09.041. [DOI] [PubMed] [Google Scholar]
- Tibshirani R, Hastie T. Local likelihood estimation. Journal of the American Statistical Association. 1987 Jun;82(398):559–567. [Google Scholar]
- Vanderperren K, De Vos M, Ramautar JR, Novitskiy N, Mennes M, Assecondi S, Vanrumste B, Stiers P, Van den Bergh BRH, Wagemans J, Lagae L, Sunaert S, Van Huffel S. Removal of BCG artifacts from EEG recordings inside the MR scanner: a comparison of methodological and validation-related aspects. NeuroImage. 2010 Apr.50(3):920–934. doi: 10.1016/j.neuroimage.2010.01.010. [DOI] [PubMed] [Google Scholar]
- Wan X, Iwata K, Riera J, Ozaki T, Kitamura M, Kawashima R. Artifact reduction for EEG/fMRI recording: nonlinear reduction of ballistocardiogram artifacts. Clinical Neurophysiology. 2006 Mar.117(3):668–680. doi: 10.1016/j.clinph.2005.12.015. [DOI] [PubMed] [Google Scholar]
- Xia H, Ruan D, Cohen MS. Separation and reconstruction of BCG and EEG signals during continuous EEG and fMRI recordings. Frontiers in Neuroscience. 2014 Jan.8(June):163. doi: 10.3389/fnins.2014.00163. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.