Nearest-Neighbor Interactions, Habitat Fragmentation, and the Persistence of Host-Pathogen Systems

Abstract

Spatial interactions are known to promote stability and persistence in enemy-victim interactions if instability and extinction occur in well-mixed settings. We investigate the effect of spatial interactions in the opposite case, where populations can persist in well-mixed systems. A stochastic agent-based model of host-pathogen dynamics is considered that describes nearest-neighbor interactions in an undivided habitat. Contrary to previous notions, we find that in this setting, spatial interactions in fact promote extinction. The reason is that, in contrast to the mass-action system, the outcome of the nearest-neighbor model is governed by dynamics in small “local neighborhoods.” This is an abstraction that describes interactions in a minimal grid consisting of an individual plus its nearest neighbors. The small size of this characteristic scale accounts for the higher extinction probabilities. Hence, nearest-neighbor interactions in a continuous habitat lead to outcomes reminiscent of a fragmented habitat, which is underlined further with a metapopulation model that explicitly assumes habitat fragmentation. Beyond host-pathogen dynamics, axiomatic modeling shows that our results hold for generic enemy-victim interactions under specified assumptions. These results are used to interpret a set of published experiments that provide a first step toward model testing and are discussed in the context of the literature.

Introduction

Limited movement and spatial interactions are thought to significantly affect the dynamics of ecological interaction, as, for example, nicely reviewed by Tilman and Kareiva (1997). This applies to the interactions between enemies and their victims, such as predator-prey, parasitoid-host, or host-pathogen dynamics (Crawley 1992; Hassell 2000; Briggs and Hoopes 2004). Spatial interactions and limited movement have received special attention for promoting stability and persistence of enemy-victim systems (e.g., Nicholson 1933; Murdoch and Oaten 1975; May 1978; Hassell and May 1988; Sabelis and Diekmann 1988; de Roos et al. 1991; Hassell et al. 1991; Adler 1993; Durrett and Levin 1994; Tilman and Kareiva 1997; Hassell 2000; Jansen and de Roos 2000; Keeling et al. 2000; Bonsall et al. 2002; Hagenaars et al. 2004). Under the simplest assumptions, such as in basic Lotka-Volterra or Nicholson-Bailey models, the dynamics are unstable, which can be linked to population extinction (e.g., through diverging oscillations). In a spatially structured habitat, asynchrony among a collection of coupled unstable populations can lead to persistence of the populations on a global scale. Many of these studies have been performed in the context of metapopulation models, where a collection of locally unstable patches (with perfect mixing within each patch) are coupled to each other through migration. If predator and prey populations can interact only within their immediate vicinity, persistence of otherwise unstable dynamics is associated with the emergence of specific spatial patterns (Hassell et al. 1991; Comins et al. 1992; Rohani et al. 1994; Gurney et al. 1998; Donalson and Nisbet 1999). A detailed review of the stabilizing effects of spatial predator-prey dynamics is given by Briggs and Hoopes (2004). In certain circumstances, spatial interactions can also have a destabilizing effect on predator-prey dynamics. This can be observed if the migration rate of one species is significantly higher than that of the other species (Crowley 1981; Reeve 1988; Rohani et al. 1996; Rohani and Ruxton 1999; Huang and Diekmann 2001) and can be based on Turing instability (Levin 1974).

Unstable enemy-victim dynamics can also be stabilized through mechanisms other than spatial interactions. Examples are the existence of a host carrying capacity, more realistic functional responses of the enemy, and nonrandom enemy attack (Murdoch and Oaten 1975; Hassell 1978, 2000). Such models are characterized by a stable equilibrium that describes the persistence of the enemy-victim system in mass-action settings where individuals mix perfectly.

Here, we concentrate on situations where persistence is observed in mass-action settings and investigate the effect of spatial, nearest-neighbor interactions on the outcome. This is done by comparing the dynamics in a mass-action habitat with those occurring in a corresponding spatially structured system of equivalent size. We first formulate the dynamics with a stochastic agent-based model that describes a continuous, undivided, two-dimensional habitat containing N × N individuals, where an agent can interact either only with its eight nearest neighbors or with any other agent in the system (mass action). Interestingly, we find that if persistence is observed with mass action, extinction may occur in the corresponding nearest-neighbor model. Rather than promoting persistence, spatially restricted interactions promote extinction over wide parameter regions. This effect is shown to be unrelated to the well-known Turing instability.

Furthermore, we find that the outcome of the nearest-neighbor model can be predicted by the dynamics in what we call “local neighborhoods” that can maximally contain 3 × 3 individuals. In other words, if the dynamics in such small local neighborhoods are considered in isolation, the equilibrium properties of this system predict the outcome in the full spatial habitat. Thus, although the nearest-neighbor interactions occur across an undivided habitat, they lead to properties that are reminiscent of fragmented habitats (Kareiva 1987; Bascompte and Sole 1998; Fahrig 2003; Ryall and Fahrig 2006). This is further underlined by a stochastic metapopulation model, where a large habitat is explicitly fragmented into a collection of relatively small patches, within which individuals mix perfectly and where individuals can migrate to the nearest neighboring patches. Compared to an unfragmented habitat of equivalent overall size where all individuals can interact with each other (mass action), the spatial setting again promotes extinction, and the outcome is again predicted by local dynamics, which in this case are clearly defined by the patches of the metapopulation.

Finally, the results obtained for these specific host-pathogen models are generalized to generic enemy-victim dynamics through axiomatic modeling. A set of previously published experiments is discussed that support our modeling results and that provide a first step toward testing and validating the theoretical predictions. Implications for the evolution of sessile growth in bacteria are discussed in the context of bacteriophage infections.

Results

Modeling Approaches

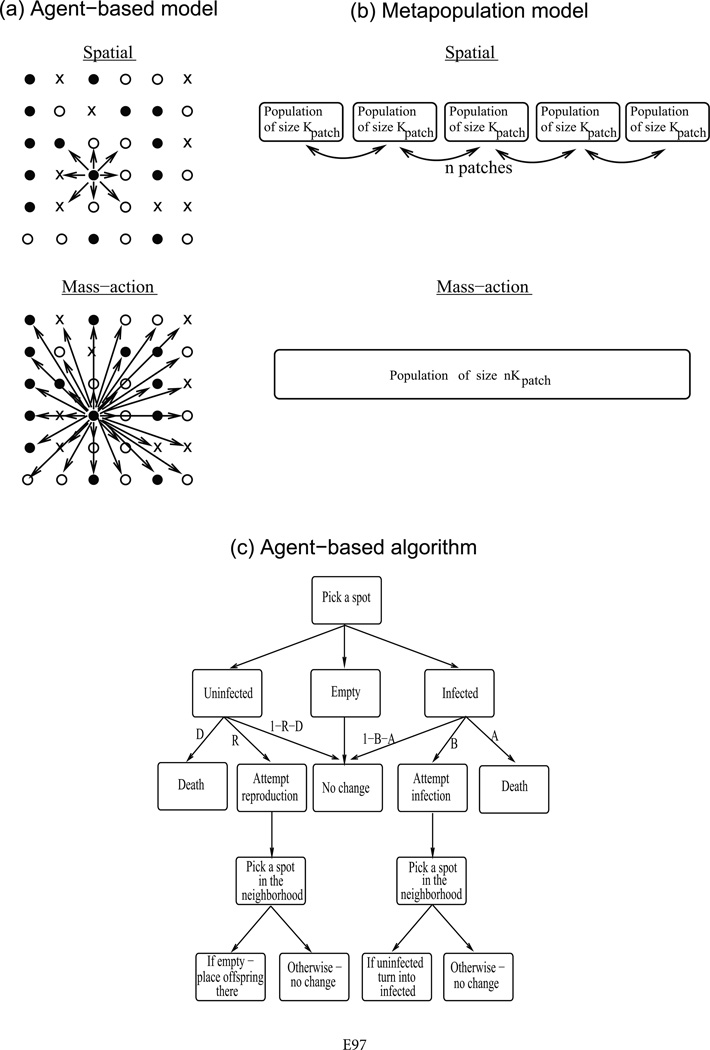
This section briefly maps out in general terms the modeling strategies that are used in this article before describing the models in detail. The basic idea is to compare host-pathogen dynamics in spatial, nearest-neighbor interactions to a corresponding mass-action scenario where individuals mix perfectly within a habitat of equivalent size. This is done in the context of two different spatial models (fig. 1a, 1b). (1) The first model is an agent-based model. In this model, we explicitly keep track of individual infected and uninfected hosts. Each spot in the grid can be occupied by an infected host or an uninfected host, or it can be empty. Specific stochastic rules determine how the system is updated at each time step. (2) The second model is the metapopulation model. Here we assume that a habitat is made up of a collection of different local patches that contain local populations. Within these patches, local dynamics occur independently of each other, with the exception that a certain degree of migration can occur between neighboring patches. The dynamics are described by Gillespie simulations of ordinary differential equations (ODEs).

Figure 1.

Schematic representation of the modeling approaches. a, An agent-based model is used to describe nearest-neighbor interactions on an undivided habitat, and the outcomes are compared to a corresponding mass-action system. Each spot can either be empty (cross), contain an uninfected host (open circle), or contain an infected host (filled circle). b, In addition, a metapopulation model is explored, where the habitat is divided into a number of relatively small local patches, in which individuals mix well. Individuals can migrate to neighboring patches. The outcomes are compared to a corresponding mass-action system of equivalent overall size. c, Update algorithm of the agent-based model, shown schematically. All these concepts are explained in detail in the text.

In both cases, we compare the spatial models to the corresponding mass-action models of equivalent size. The mass-action dynamics are formulated differently for the agent-based and the metapopulation models for ease of comparison with the respective spatial settings (fig. 1). Thus, the mass-action version of the agent-based model follows the same structure and rules as the spatial version, except that an individual in a given spot can potentially interact with one in any other spot in the system (rather than with nearest neighbors only), irrespective of spatial location. The mass-action version of the metapopulation model consists of one giant patch in which dynamics are described by the Gillespie simulation of the same ODEs but with a carrying capacity that is n times the carrying capacity of local patches, where n is the number of patches in the metapopulation.

The two mass-action models are slightly different, as the Gillespie simulation of an ODE approximating the mean dynamics is different from the underlying stochastic process. In this article we use an agent-based model and a metapopulation model as alternative approaches to study spatial interactions in pathogen-host dynamics, and we formulate corresponding mass-action systems for each type of model.

Agent-Based Model

We consider a stochastic agent-based model where each individual is tracked in time and space, occupying a certain position on a grid and interacting with other individuals according to some probabilistic rules. Both nearest-neighbor interactions and perfect mixing of individuals can be described in this framework. The rules for the nearest-neighbor interactions are as follows (see also fig. 1c). The model, based on previous work (Sato et al. 1994; Boots and Sasaki 2002), describes host-pathogen dynamics on a two-dimensional grid that contains N × N spots. Each spot is either occupied by a host (infected or uninfected) or empty. We model the development of the populations in discrete time. Given the state of the system at time t, a set of rules is applied to each spot, and this gives rise to the state of the system at time t + 1. At each time step, the grid is randomly sampled N² times. If the chosen spot is occupied by an uninfected host, it can die with a probability D, leaving the spot empty. Alternatively, the uninfected host can reproduce with a probability R, and a destination spot is randomly chosen for the offspring from the set of eight nearest neighboring spots. If the destination spot is empty, the offspring is placed there; otherwise, no reproduction occurs. If the chosen spot contains an infected host, it can die with a probability A or attempt to transmit the pathogen with a probability B. A destination spot is chosen randomly from the eight nearest neighbors, and infection proceeds only when a susceptible host is present. Infected hosts are assumed not to reproduce. We thus consider relatively virulent pathogens that induce significant morbidity in the host.

Similar rules apply to the description of the perfect mixing scenario. The difference is that instead of being placed into a spot that is randomly chosen from the set of nearest neighbors, the offspring is placed into a spot that is randomly chosen from all available spots in the system. Similarly, the target for infection is not chosen from the eight nearest neighbors but from all individuals in the system. The size of the area remains identical at K = N × N spots. In the following, we first explore the perfect-mixing scenario and subsequently the nearest-neighbor interactions.

Perfect Mixing

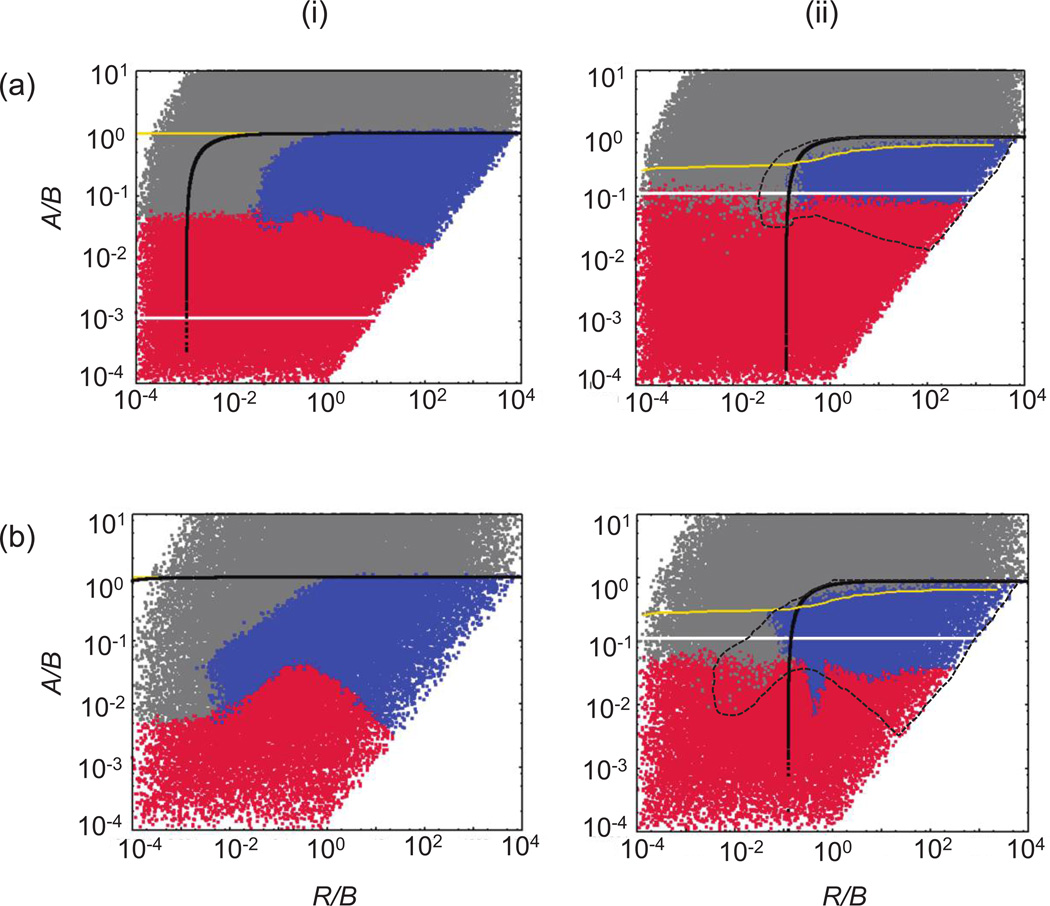
Using extensive computer simulations, we examine how the outcome of the system depends on the parameters of the model. In particular, we are interested in the conditions under which the host-pathogen system persists and when pathogen-mediated host extinction is observed. This is shown in figure 2ai, which is the result of at least 104 instances of the simulation, where the log10 of all the parameters was varied between −4 and 4. Each point represents the outcome of a single run, indicated by the color code.

Figure 2.

Parameter dependence of the outcomes in the basic agent-based model describing host-pathogen dynamics. Compared are the mass-action (i) and nearest-neighbor (ii) scenarios. Each point represents the outcome of a single run, indicated by the color code. Red indicates extinction of hosts and pathogens, blue indicates coexistence, and gray indicates persistence of the host in the absence of the pathogen. Above the white and below the black lines, the equilibrium number of hosts and pathogens, respectively, is greater than 1. This derives from corresponding ordinary differential equations with a carrying capacity K = N × N for mass-action and K_loc = 9 for nearest-neighbor interactions. Above the yellow line, the pathogen cannot invade, as determined by numerical simulations. For ease of comparison, the dashed lines in the plots of the nearest-neighbor system indicate the coexistence region for the mass-action system. The parameters A, B, and R were varied as indicated, and D = 0. The size of the grid was 30 × 30 (a) or 300 × 300 (b). Simulations were started by placing a square of 5 × 5 infected individuals within a square of 13 × 13 susceptible ones centered around the middle of the grid. The rest of the grid was empty. The cutoff time for the simulations was 3 × 10⁵ (a) or 10⁶ (b) time steps. For details, see text and Supplementary Information, section 2.1, available online.

All simulations were started with a relatively small number of infected hosts placed in a compact vicinity into a larger space filled with uninfected hosts, which was in turn embedded into an even larger “empty” space (for the exact initial conditions for particular cases, see the appropriate figure legends). The grid size for these simulations was 30 × 30. Note that while simulations were started with a relatively small number of individuals, this number was sufficiently large to avoid initial stochastic extinction and failure to establish population growth.

Because we are considering a stochastic model where for infinite times all simulations will necessarily result in extinction, it is important to establish how extinction and persistence outcomes were defined. When populations “persist,” they approach a statistical steady state, around which they fluctuate stochastically in the long term. While the populations fluctuate around this steady state, extinction can occur with a certain probability, determined by the level of the population and the extent of the stochastic variance. Figure 2ai can be viewed as a contour plot indicating whether extinction has occurred by a specific cutoff time, indicated in the legend. As the cutoff time changes, the picture will change slightly (resulting in a somewhat different “contour”), and for long enough times, all simulations will result in extinction. Here, however, we concentrate on intermediate timescales, long compared to initial colony growth and adjustment and short compared to the time it takes for an established population to become extinct by chance, because of the finiteness of this simulation. In most of the parameter space, the latter regime occurs at timescales significantly longer than that considered here, which in fact could not be observed even in the longest simulation runs performed in the course of our work. Hence, the points indicated by blue in figure 2ai are in a long-term, quasi-steady state of nonextinction. The points indicated by red in figure 2ai show simulations that have become extinct before the time cutoff, which typically tends to occur early, before the populations have reached their statistical steady state. Individual trajectories that depict typical “persistence” and “extinction” runs are discussed below. In large portions of the parameter space in figure 2ai, only one color is seen, which translates into a probability for this outcome occurring that is close to 1. In the parameter regions that are at the border between different outcomes, the relative number of dots of different colors gives an idea about the probability of the different outcomes occurring. Repeated numerical experiments produce nearly identical images, indicating that this is an informative visual tool to convey the message on the longevity of coexistence across the parameter space.

With this in mind, let us now explain the picture obtained in figure 2ai. Because perfect mixing is assumed, the average dynamics observed in this model can be approximated by ordinary differential equations that can be derived for our agent-based model (see Supplementary Information [SI], sec. 2.1; all SI is available online). This is given by

$$\frac{dS}{dt}=RS(1-\frac{S+I}{K})-\frac{BSI}{K},\frac{dI}{dt}=\frac{BSI}{K}-AI,$$ (1)

where the number of uninfected hosts is denoted by S and the number of infected hosts by I. In these equations, K = N × N has the meaning of carrying capacity. This modified Lotka-Volterra system (Anderson and May 1991; Nowak and May 2000) is characterized by two equilibria. (1) The uninfected population persists at carrying capacity, while the infected population is extinct; that is, S⁽⁰⁾ = K, I⁽⁰⁾ = 0. (2) Alternatively, the pathogen establishes a successful infection, such that S⁽¹⁾ = AK/B and I⁽¹⁾ = RK(B − A)/B(R + B). The latter equilibrium is stable if the basic reproductive ratio of the pathogen, R₀, is greater than 1, which is equivalent to the inequality A < B. The approach to the coexistence equilibrium can either be monotonic or involve damped oscillations.

In figure 2ai, information about equilibria of uninfected and infected hosts, based on equations (1), is superimposed on the graph that characterizes outcomes of the agent-based simulations across parameter ranges. The white line depicts S⁽¹⁾ = 1, while the black line depicts I⁽¹⁾ = 1. Thus, above the white line, the total equilibrium number of uninfected hosts is greater than 1, and below the black line, the equilibrium number of infected hosts is greater than 1. In the agent-based model, a necessary but not sufficient condition for host-pathogen persistence is that the equilibria predicted by model (1) are greater than 1 (shown above the white and below the black line in fig. 2ai). Because of the oscillatory nature of the dynamics, however, extinction also occurs (indicated by red in fig. 2ai) for parameters within this region. The exact areas of extinction and coexistence can depend on the initial conditions, as they influence the exact trajectory of the dynamics. If the equilibrium levels of uninfected or infected hosts are relatively low, coexistence can become impossible because of the effect of stochastic extinction. The yellow line in figure 2ai indicates R₀ = 1. Above this line, R₀ < 1 and the infection can never become established.

Nearest-Neighbor Interactions

Next we consider a system of equal size where individuals can interact only with their eight nearest neighbors. The outcomes are shown in figure 2aii, which is again the result of at least 10⁴ instances of the simulation, where the log₁₀ of all the parameters was varied between −4 and 4. Again, each point represents the outcome of a single run, indicated by the color code. Initial conditions, as well as grid size, are the same as those given above and are detailed in the figure legend. The extinction/ persistence events recorded in the figure correspond to the same cutoff time as was set for the mass-action system, indicated in the legend.

Despite the spatial structure in this habitat, the outcomes can also be explained with the help of the ODE model (1) if we give it a correct interpretation. ODEs describe situations in which a given individual can interact with all other individuals in the system. In the nearest-neighbor model, this is true in small, local subareas of the habitat, characterized by an area of 3 × 3 spots: one individual can directly interact with all of its eight nearest neighbors. Now, let us consider such an area of 3 × 3 spots in isolation and examine the equilibrium properties of this system in the context of ODE model (1). We refer to this system as the “local neighborhood,” noting that it is an abstracted entity because the spatial model is not physically subdivided into different neighborhoods but describes a spatially continuous habitat. Because in the local neighborhood, the maximum number of individuals is 9, this is referred to as the “local carrying capacity”, K_loc. We find that the population sizes at equilibrium in these local neighborhoods, as predicted by ODE model (1) with the small carrying capacity K_loc, predict the outcome of the host-pathogen system in the whole spatial model of size N × N.

This is shown in figure 2aii. The white line depicts where the equilibrium number of uninfected hosts in the local neighborhood equals 1 (S⁽¹⁾ = 1). Similarly, the black line depicts where the equilibrium number of infected hosts in local neighborhoods equals 1 (I⁽¹⁾ = 1). We can see that the coexistence region in figure 2aii corresponds to the parameters for which both local equilibrium values are greater than 1; it is enclosed by the lines S⁽¹⁾ = 1 and I⁽¹⁾ = 1, obtained directly from the host-pathogen equations (1) applied to local neighborhoods. The white line S⁽¹⁾ = 1 outlines the lower boundary of the coexistence region, while the black line I⁽¹⁾ = 1 defines the upper boundary.

The time to extinction becomes drastically different as the thresholds S⁽¹⁾ = 1 and I⁽¹⁾ = 1 are crossed. If the equilibrium values in “local neighborhoods” are greater than 1, then the populations persist for very long time spans, so long, in fact, that extinction could not be observed even during the longest simulation runs that were computationally possible in our study. This applies even if the equilibrium values are only slightly greater than 1. Spatial interactions greatly decrease stochastic fluctuations around the equilibrium, thus resulting in a low extinction probability. In contrast, if the equilibrium numbers in “local neighborhoods” is less than 1, extinction occurs with a much higher probability and thus much faster.

The values S⁽¹⁾ = 1 and I⁽¹⁾ = 1 have a special meaning in this system, for reasons somewhat different from those in the mass-action model. Although it is easy to envisage a distribution with an average number of hosts per local neighborhood less than 1, such systems can be shown to be unable to maintain an equilibrium state, despite being connected with each other. A detailed proof of this fact in one specific system is given in SI, section 4. Intuitively, for equilibrium values greater than 1, fluctuations lead to deviations from the equilibrium numbers, but those are on average compensated for by a shift in probabilities that favors a return to near-equilibrium values. For example, if the number of infected hosts is locally larger than the equilibrium, an increase in infection events will bring it down. If it is too small, then an increase in host reproduction will bring it back up. On the other hand, if the equilibrium value is less than 1, then inevitably some neighborhoods will contain no uninfected hosts, and such a fluctuation cannot be compensated for by an increased production of hosts (because reproduction cannot occur if the number of hosts is zero), but only by redistribution. On average, the total population of uninfected hosts will decay until extinction.

Comparison

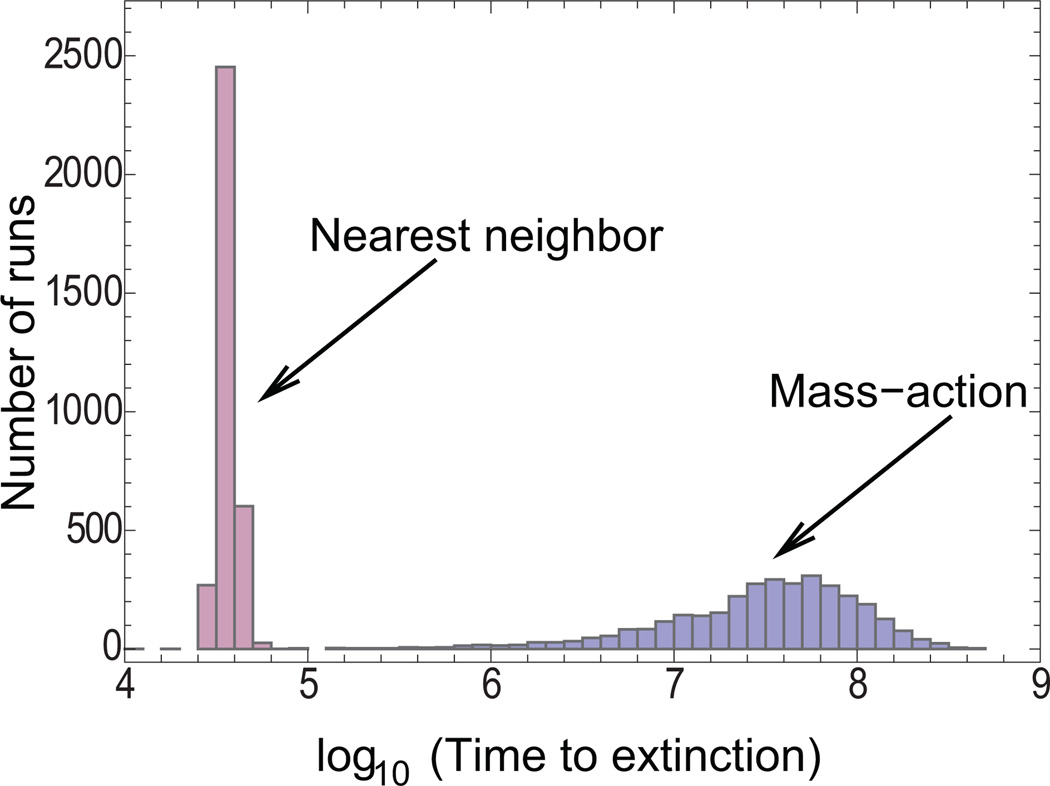
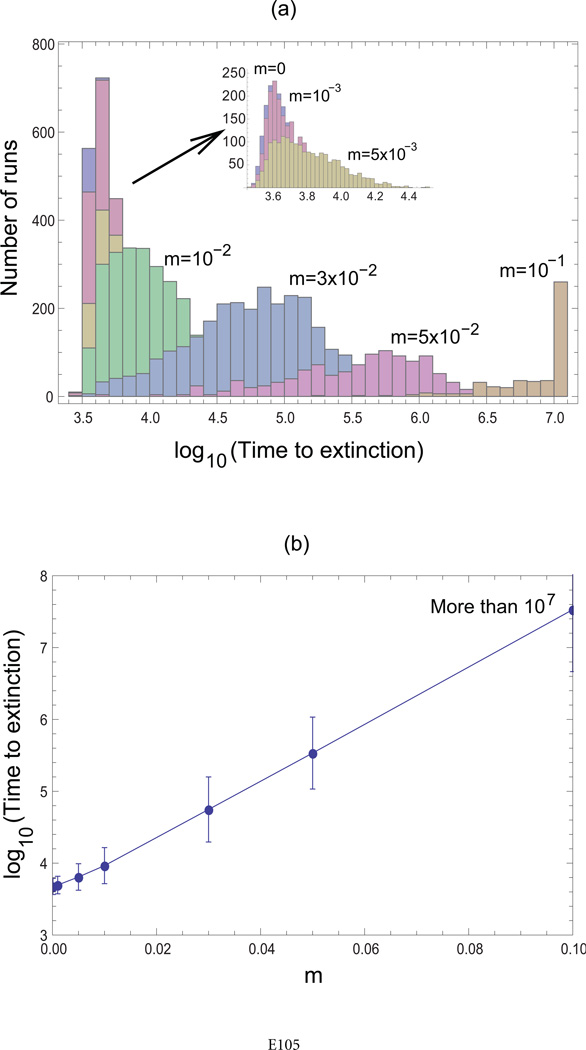
Here, we compare the conditions for persistence of the host-pathogen system in the perfect-mixing and nearest-neighbor scenarios. For reference, the coexistence regime in the mass-action setting is indicated by the dashed line in figure 2aii. This plot shows that there are large parameter regions in which extinction is observed in the nearest-neighbor scenario although persistence occurs in a mass-action setting. More precisely, in these parameter regions, the time to extinction is much shorter in the nearest-neighbor scenario than in the mass-action scenario. Because this cannot be shown in figure 2aii, which shows the outcome after a defined time threshold, we present histograms documenting the distribution of extinction times for the spatial and mass-action settings for one particular choice of parameters (fig. 3). These data clearly show that in this system, spatial nearest-neighbor interactions promote population extinction rather than persistence, as commonly thought.

Figure 3.

Histogram showing the distribution of extinction times in a nearest-neighbor and a mass-action setting for one particular parameter combination of the parameter space explored in the agent-based model, figure 2. For this parameter combination, the persistence time in the mass-action setting is about 3 orders of magnitude longer than that in the nearest-neighbor setting. Parameters were as follows: R = 0.1; B = 0.001; A = 0.000025; D = 0; N = 30 × 30. Initial conditions are the same as in figure 2a.

The reason for this effect is as follows. With mass action, long-term coexistence can occur in a significant portion of the parameter space where the equilibrium number of uninfected and infected hosts is greater than 1, as predicted by model (1). On the other hand, coexistence in the nearest-neighbor system occurs if the equilibrium numbers given by model (1) in “local neighborhoods” is greater than 1. Model (1) has the property that the equilibrium number of uninfected hosts is proportional to the carrying capacity. The carrying capacity, in turn, is much smaller for “local neighborhoods” (K_loc = 9) than for the full loc mass-action system (K = 900). Therefore, the parameter region in which coexistence occurs is smaller for the nearest-neighbor setting, compared to that in a perfectly mixed habitat.

Stated differently, nearest-neighbor interactions in our model promote extinction, because the overall outcome in the spatial setting is determined by equilibrium values characteristic of the “local 3 × 3 neighborhoods” (although these neighborhoods are not physically separated from each other in the context of this model). Even though an undivided habitat is considered, the nearest-neighbor interactions lead to outcomes that are typical of habitats that are physically fragmented into a collection of small patches, thus leading to a higher extinction probability than in a perfectly mixed system. This relationship between nearest-neighbor interactions and habitat fragmentation is further explored below.

Note that the coexistence regime in the mass-action setting depends on the initial conditions because the extent of population oscillations, which can lead to extinction, is influenced by the initial conditions. Therefore, it is possible that when the simulation is started from different initial conditions, the coexistence area in the mass-action system is smaller or larger than that indicated in figure 2. However, the result that nearest-neighbor interactions can promote extinction holds true. For a large set of initial conditions, there are significant regions in the parameter space where the host-pathogen system remains at a quasi-steady state much longer than an equivalent system with nearest-neighbor interactions.

Effect of Grid Size

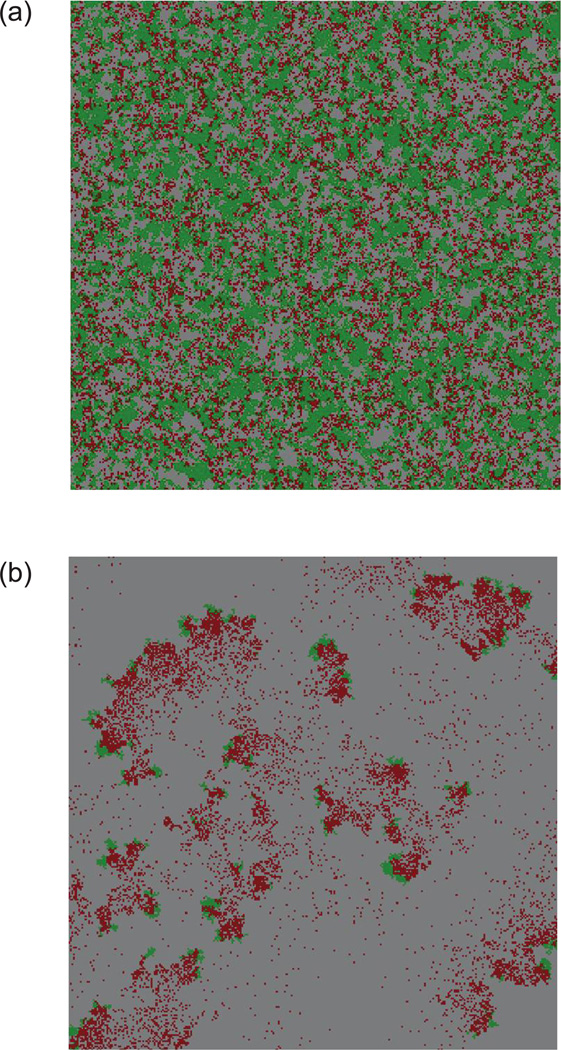
Figure 2b shows the outcomes for mass-action and nearest-neighbor interactions for a larger grid, 300 × 300 spots. The results derived from the smaller grid hold true. However, for nearest-neighbor interactions (figure 2bii), an additional area of coexistence is observed where the equilibrium number of uninfected hosts in “local neighborhoods” is somewhat less than 1. Computer simulations indicate that the area of coexistence does not grow any further for larger grid sizes. The coexistence occurring in this regime, however, is of a different nature. In the coexistence cases described above, where the local equilibrium numbers are greater than 1, the agents are evenly mixed and no macroscopic patterns exist (fig. 4a). In the additional coexistence area found in the larger grid, where the local equilibrium number of uninfected hosts is less than 1, populations become extinct in local areas but persist across the space at low levels because of temporary spatial escape of hosts from the pathogen, thus forming macroscopic structures (fig. 4b). This is a well-documented mechanism, where movement though space allows the host to temporarily escape local extinction, leading to global persistence of populations across the whole space (Hassell et al. 1991; Briggs and Hoopes 2004). In some of this parameter regime, we also observe extinction in a corresponding mass-action system because of pronounced oscillations, again confirming the established notion that spatial structure can promote persistence.

Figure 4.

Two types of coexistence in larger grids in nearest-neighbor simulations of the basic agent-based model describing host-pathogen dynamics. The spatial configuration across the grid is shown. Green indicates uninfected hosts, red infected hosts, and gray empty space. Each picture is a snapshot at a time when the system has attained its long-term behavior. a, In the parameter space where the local equilibria are greater than 1, the agents are distributed evenly across the grid and no macroscopic patterns are seen. b, If the local equilibrium number of hosts is slightly less than 1, a different type of coexistence is observed. Locally, the pathogen drives the host population to extinction, but continuous movement of the host away from the pathogen allows long-term coexistence across space. The plot shows multiple moving fronts. Parameters were as follows: R = 0.014; D = 0; B = 0.032; A = 0.008 (a). R = 0.15; D = 0; B = 0.32; A = 0.007 (b). The grid size was 300 × 300. Initial conditions are the same as in figure 2.

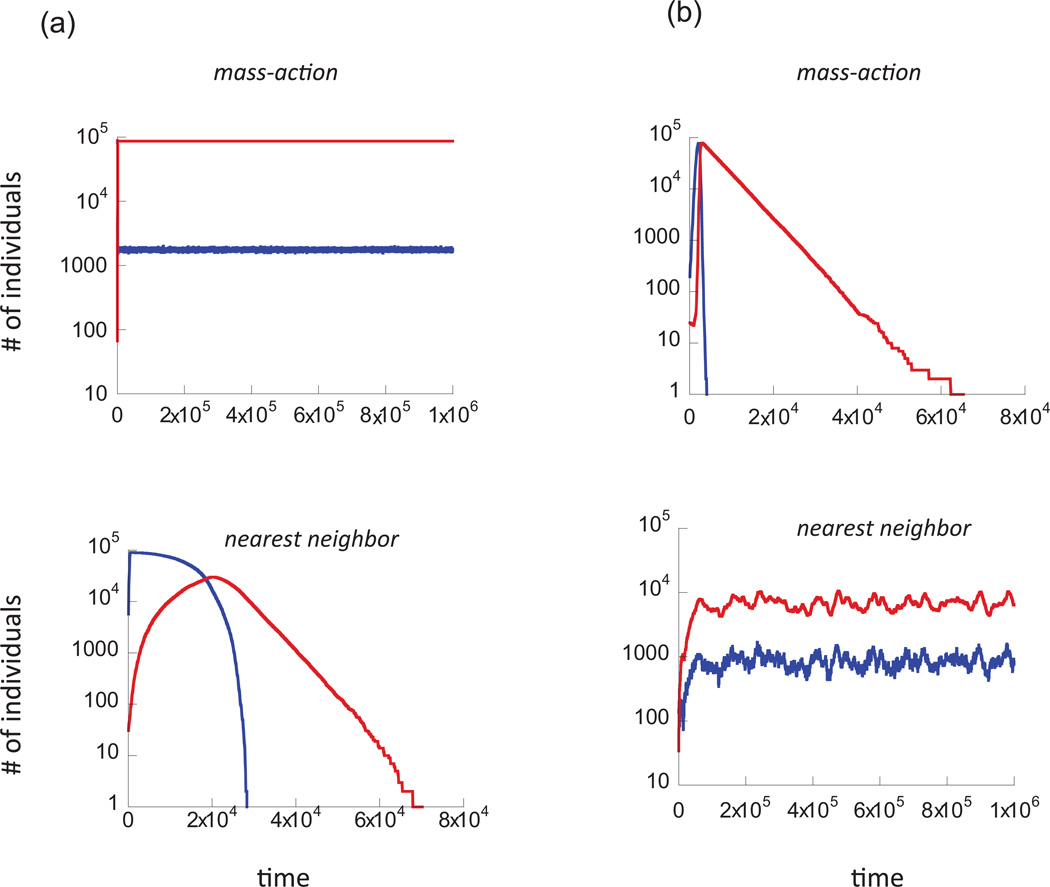
Therefore, in the context of the larger grid, we not only observe our new results but also find parameter regions in which established notions are confirmed. Hence, we can broadly state that nearest-neighbor interactions can play a dual role in determining the outcome of host-pathogen dynamics. In accordance with the literature, if extinction occurs in a mass-action setting, nearest-neighbor interactions can lead to persistence. Conversely, we have shown here that if persistence is observed in a mass-action setting, nearest-neighbor interactions can lead to extinction. These two effects are also shown in the form of individual trajectories in figure 5.

Figure 5.

Individual trajectories or time series demonstrating the dynamics that are observed in the agent-based model. Hosts are shows in blue, pathogens in red. a, These graphs demonstrate the central result of our model: if hosts and pathogens persist in a mass-action setting, then extinction can occur in a spatial, nearest-neighbor scenario. b, In certain parameter regions, the established view about the effect of space on persistence is also observed in our model: when dynamics in a mass-action setting lead to extinction, persistence can be observed in a spatial, nearest-neighbor setting. Parameters were as follows. R = 0.5; D = 0; B = 0.01; A = 0.0002 (a); R = 0.004; D = 0; B = 0.01; A = 0.0002 (b). The grid size was 300 × 300 in both cases. Initial conditions are the same as in figure 2.

Effect of Migration

The spatial model analyzed so far did not explicitly include migration. Individuals were assumed to move through the habitat via reproduction, placing the offspring in the nearest neighboring spots. Here, we show that if explicit migration is included in the spatial model, our results hold true for relatively low migration rates and that the system approaches mass-action properties for higher migration rates. A parameter regime was chosen in which extinction occurred consistently with nearest-neighbor interactions in the absence of migration and persistence was observed consistently in the mass-action system. We ran the spatial simulation with migration, using a range of migration probabilities. The distribution of the time to extinction is shown in the form of histograms in figure 6. For relatively low migration probabilities, the results were very similar to those of the simulation without migration. When the migration probability approached and exceeded the infection probability, then the time to extinction increased exponentially. For relatively large migration probabilities, the time to extinction became too long to be observed, making the behavior of the system similar to that exhibited by the mass-action system.

Figure 6.

Effect of migration on the outcome of the agent-based model. In addition to the basic processes in the agent-based model, we now also assumed that an individual (uninfected or infected) can migrate with a probability m. A parameter combination was selected in which consistent extinction was observed for nearest-neighbor interactions while consistent persistence was observed in a mass-action setting, according to the definitions described in the text and figure 2. a, The nearest-neighbor model was run for a variety of migration probabilities, and the distribution of extinction times was documented by histograms. The outcome for relatively low migration rates is the same as the outcome observed in the absence of migration, as shown in the inset. As the migration probability becomes higher than the infection probability, time to extinction increases significantly and converges to the mass-action picture for high migration probabilities (i.e., no extinction for very long periods of time). b, As the migration probability approaches and exceeds the infection probability, the time to extinction increases exponentially. Parameters were as follows: R = 0.5, B = 0.01, A = 0.0005, D = 0, N = 30 × 30. Initial conditions are the same as in figure 2a.

Metapopulation Dynamics

In the previous section, we assumed one continuous habitat and compared nearest-neighbor interaction with perfect mixing within this habitat. Here, we assume a different model structure to examine spatial dynamics. We explicitly assume that a habitat is subdivided or fragmented into a number of local patches. Within each patch, the dynamics are characterized by perfect mixing, with a carrying capacity K_patch. Migration of individuals to the nearest neighboring patches is assumed to occur. In contrast to the agent-based model, movement through space in the current patch model requires an explicit migration term, and to keep model comparison simple, it is assumed that infected and uninfected hosts have equal migration rates. This situation is described by a one-dimensional stochastic metapopulation model, which contains a collection of n local patches. Its deterministic counterpart is given by the following system of ODEs:

$$\frac{d{S}_x}{dt}=rS(1-\frac{S_x+I_x}{K_{\text{patch}}})-\frac{\beta S_x{I}_x}{K_{\text{patch}}}-{\mu }_S{S}_x+\frac{{\mu }_S}{2}(S_{x-1}+S_{x+1}),\frac{d{I}_x}{dt}=\frac{\beta S_x{I}_x}{K_{\text{patch}}}-a{I}_x-{\mu }_S{I}_x+\frac{{\mu }_I}{2}(I_{x-1}+I_{x+1}),$$ (2)

where 1 < x < n and a subscript x indicates the spatial location of the patch. With μ_S = μ_I, the migration term is equivalent to the central difference description of diffusion. The parameter r denotes the growth rate of the uninfected hosts, β the infection rate, and a the death rate of infected hosts. The boundary conditions assume no migration through the boundary patches. The stochastic dynamics in our simulations are governed by a Gillespie algorithm of model (2); see SI, section 3.1. Simulations indicate that the average behavior of the Gillespie algorithm is predicted by the ODEs.

Comparing one- and two-dimensional metapopulation models indicated that the full range of behavior observed in two dimensions is also observed in one dimension, as shown in SI, section 3.2. Because of the high computational cost of a two-dimensional model in the context of Gillespie simulations, we focused our analysis on the one-dimensional setting. The corresponding mass-action system is given by a straightforward Gillespie simulation of model (1), characterized by a carrying capacity that is n times the local carrying capacity in the metapopulation. As above, we denote the carrying capacity of the mixed system by K, and hence the local carrying capacity is given by K_patch = K/n.

In simulations, the number of local patches was set to n = 100. As the initial condition, we assume that in a subset of adjacent local patches in the middle of the space, uninfected individuals are present at their pathogen-free equilibrium levels. The rest of the patches are initially empty. A small number of infected hosts are placed into the middle patch, and the infection is allowed to spread from there (see appropriate figures for details). The initial number of pathogens was sufficiently large to ensure successful establishment of infection. In figure 7a, each point again represents the outcome of a single run, indicated by the color code. The figures show 10⁵ instances of the simulation for each scenario, where the log₁₀ of all the parameters was varied between −4 and 4. For further details of the simulations, see SI, section 3.1. The outcomes again include extinction of the host population, coexistence of uninfected and infected populations, and host persistence in the absence of the pathogen. Classification of extinction versus persistence was done according to the same principles as in the agent-based model, and the issues discussed in that context hold here.

Figure 7.

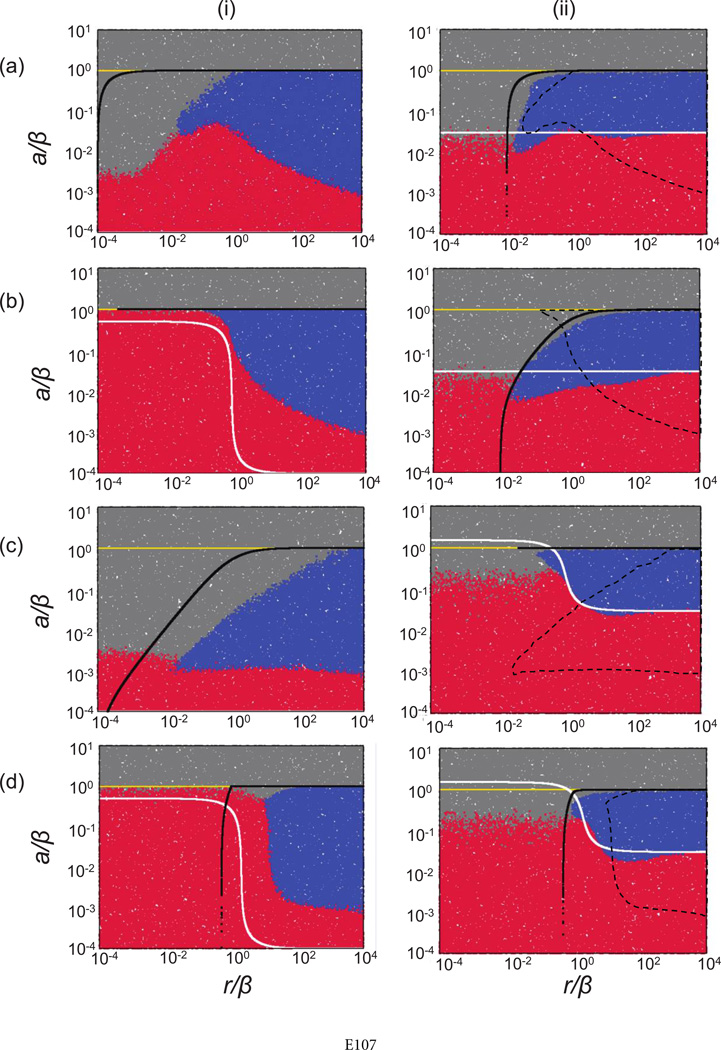
Parameter dependence of the outcomes in the nearest-neighbor metapopulation (ii) and the corresponding nonspatial models (i) in the context of four specific models describing enemy-victim dynamics. Model a corresponds to the assumptions made in the agent-based model of host-pathogen dynamics explored in figure 2. Each point represents the outcome of a single run, indicated by the color code. Red indicates extinction of victim and enemy, blue indicates coexistence, and gray indicates persistence of the victim in the absence of the enemy. Above the white and below the black lines, the equilibrium number of victims and enemies, respectively, is greater than approximately 1 (see Supplementary Information [SI], sec. 4, available online), derived from corresponding ordinary differential equation (ODE) models. In the metapopulation model, this is the local equilibrium in a patch. Above the yellow line, the enemy fails to invade and the coexistence equilibrium is unstable in the ODEs, determined analytically. For ease of comparison, the dashed lines in the plots of the metapopulation system (ii) indicate the coexistence region for the corresponding nonspatial system. The models are as follows: a, dx/dt = rx[1 − (x + y)/K] − dx − (βxy/K), dy/dt = (βxy/K) − ay; b, dx/dt = rx[1 − (x + y)/K] − dx − [β xy/(x + y + ε)], dy/dt = [βxy/(x + y + ε)] − ay; c, dx/dt = ({rx[1 − (x + y)/K]}/(x + η)) − dx − (βxy/K), dy/dt = (βxy/K) − ay; d, dx/dt = ({rx[1 − (x + y)/K]}/(x + η)) − dx − [βxy/(x + y + ε)], dy/dt = [βxy/(x + y + ε)] − ay. The parameters r, β, and a were varied. The other parameters were assigned the following constant values: d = 0; ε = 1; η = 1; μ_x = 0.1; and μ_y = 0.1. K_Ioc= 100 for the local patch in the metapoploculation, and K = 10,000 for the mass-action system. The number of patches in the metapopulation was n = 100. Equal migration rates for x and y were assumed, to facilitate comparison to the agent-based model, but results hold for unequal migration rates. For the spatial models, the simulations were started with the central patch containing K_loc individuals, including 30 infected hosts. In addition, the five adjacent patches on each side contained susceptible hosts at carrying capacity. The remaining patches were empty. The cutoff time for the simulation when determining extinction versus persistence was determined as follows: the simulation was run until populations hit the boundary of the system and was subsequently run 1,000 times longer. For details of simulations, see text and SI, section 3.1.

Perfect Mixing

For the mixed system, fig. 7ai indicates the region in which the equilibrium values of the underlying ODEs are greater than 1. This is defined by the line S⁽¹⁾ = 1 (white) and I⁽¹⁾ = 1 (black), the boundaries within which a feasible internal equilibrium occurs in the ODEs. The yellow line indicates R₀ = 1. If R₀ < 1 (above the yellow line), the pathogen cannot invade. As in the agent-based model, the stochastic dynamics converge to this equilibrium only in the subset of the parameter space where equilibria are greater than 1, while in the rest of the parameter space oscillatory dynamics will lead to population extinction for a wide range of initial conditions. The blue region in fig. 7ai indicates the coexistence regime starting from one particular set of initial conditions.

Nearest-Neighbor Interactions

The outcomes for the nearest-neighbor interactions are shown in fig. 7aii. The definition of the local equilibria is straightforward in this case, since they are defined by a local patch with a carrying capacity K_patch. As with the agent-based model, we find that the local equilibria indicate whether extinction or coexistence is observed across the whole space. The region where the local equilibria for uninfected and infected hosts are greater than 1 are again outlined by the white and black lines. In SI, section 4.1, we show that in the limit of high migration rates and with a large number of patches, the infected and uninfected individuals coexist if the local equilibria of these populations are greater than 1. For low migration rates and a small number of patches, the boundaries of the coexistence region are well approximated by S⁽¹⁾ = s and I⁽¹⁾ = s, where s is a number of the order of 1 (SI, sec. 4.2). Relatively small regions of coexistence outside those areas can arise from spatial-refuge effects, as described above.

Comparison

As with the agent-based model, we find that nearest-neighbor interactions can promote extinction (fig. 7a). This can be interpreted more clearly in the metapopulation model. It is very different from the well-known Turing instability, which requires a significant difference in diffusion/migration rates between the infected and the uninfected hosts (see SI, sec. 6). Instead, it can be a considered a consequence of habitat fragmentation. The carrying capacity is significantly smaller in the local patch of a metapopulation than in the mass-action system. Because the equilibrium number of uninfected hosts scales with the carrying capacity, extinction can occur in the nearest-neighbor metapopulation model in large parameter regions where persistence is found in the mass-action system.

To conclude, we note that the analysis of the metapopulation model performed here serves three separate goals. (1) It provides an intuitive theoretical justification for using the local dynamics to infer properties of the global dynamics, which is not at all obvious in the case of the agent-based modeling. (2) It allows for an analytical proof that the phenomenon observed here (the increased likelihood of extinction in the nearest-neighbor system, compared to that in the mass-action system) is not of the same nature as the Turing instability (Levin 1974); see SI, section 6 for the details. (3) It allows us to make the next step, which is to generalize our findings to a wider class of systems and derive conditions under which our results are expected to hold; see the next section.

Broader Application to Enemy-Victim Interactions: Axiomatic Modeling

So far, we have considered a specific host-pathogen system. We started from an agent-based model and derived an ODE that can describe these dynamics. This ODE model was subsequently used as a basis for the metapopulation model. Questions arise about the degree to which the results described here depend on the particular formulation of the model and whether they hold for enemy-victim interactions in a broader setting. This is important because the host-pathogen system makes assumptions that may not hold in the context of other enemy-victim interactions, for example, the assumption that susceptible (victim) and infected (enemy) individuals compete for available space. We examine the robustness of results using a general, axiomatic ODE model. Denoting the victim population by x and the enemy population by y, the general form of the equations is as follows:

$$\frac{dx}{dt}=xf(x,y,K)-yg(x,y,K),\frac{dy}{dt}=yF(g(x,y,K),x,y)$$ (3)

(Abrams and Ginzburg 2000).

The growth rate of the victim population is given by the function f(x, y, K), which can be described by a variety of expressions and can (but does not have to) depend on the number of victims and enemies. It is assumed that this function does not grow with the numbers of victims and enemies and that it grows with the carrying capacity, K. This is equivalent to including crowding effects in the model. The exploitation term is given by the function g(x, y, K), which corresponds to the functional response of the enemy. It is natural to assume that this function increases with the number of victims, x: the more victims, the larger the exploitation possibility. The function F(g, x, y) describes the numerical response of the enemy and is an increasing function of g. We also make an additional assumption that the numerical response contains a natural death term for the enemies. In particular, an explicit form of F could be F = g − a, where the enemy dies at a rate a in the absence of victims.

Under these assumptions, it is possible to show the following very general statement (see SI, sec. 5 for the details of the proof and the precise mathematical formulation). Spatial nearest-neighbor interactions can be more prone to extinction than corresponding mass-action systems if (∂ g/∂y)(∂ỹ/∂K) + ∂g/∂K < 0, where ∂g/∂y and ∂g/∂K are the rates of change of the exploitation function with respect to the number of enemies and the carrying capacity, respectively, and ∂ỹ/∂K is the rate of change of the steady state number of enemies with respect to the carrying capacity, which is always positive. In particular, either of the following two conditions will guarantee the presence of this effect: (1) the exploitation function, g, decreases with the number of enemies, y, and does not depend on the carrying capacity, or (2) the exploitation function decreases with the carrying capacity, K, and does not depend on y. These conditions can be interpreted biologically as follows. Condition 1 assumes the existence of a saturation effect, which is present in functional responses that assume predator interference, such as in the Beddington-De Angelis functional response (Beddington 1975), or in frequency-dependent infection terms (McCallum et al. 2001). There is extensive empirical support for such formulations in the context of both host-pathogen (McCallum et al. 2001) and predator-prey systems (Begon et al. 2006). Condition 2 corresponds to the situation where the exploitation function scales with the density of the victims, rather than with their total number, as discussed in Begon et al. (2002). Therefore, our results do not depend on particular formulations and assumptions of the host-pathogen system and hold true in the context of general enemy-victim interactions under the defined assumptions.

To confirm these theoretical findings, we used three variants of the metapopulation model that are distinct from the initial model considered and contain different growth terms for the victim populations and different exploitation terms; see figure 7. Note that in all the cases, either condition 1 or condition 2 holds. We ran the same types of simulations as in “Metapopulation Dynamics” and related the local equilibrium results to the global outcomes of the dynamics. As before, there are significant regions in the parameter space where the system with nearest-neighbor interactions is characterized by extinction while persistence is observed in the mass-action simulations. The reason is again that local equilibrium values, which are smaller than the global ones, drive the outcome of the system.

As mentioned in the context of the agent-based model, there are also parameter regions where the opposite holds: in some regions where extinction occurs in the mass-action system (because of oscillatory dynamics), coexistence occurs in the nearest-neighbor system. This corresponds to the well-known phenomenon that unstable dynamics can be stabilized in spatially structured populations (Briggs and Hoopes 2004). The exact parameter regime where this occurs depends on initial conditions, which determine the trajectories of the dynamics. This is seen in the blue region outside the area enclosed by the dashed line in the nearest-neighbor plots (fig. 7).

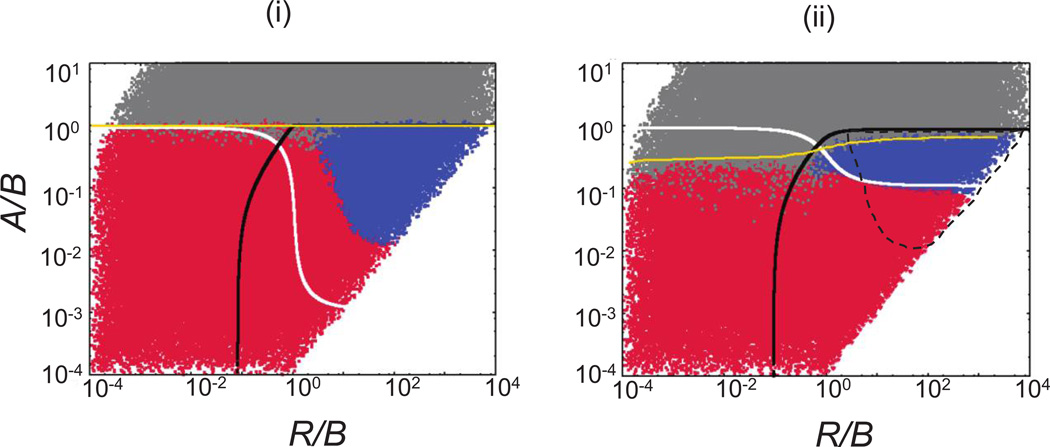
We went a step farther and set up an agent-based simulation governed by the same rules as one of the metapopulation models above (fig. 8; see SI, section 2.1 for details of implementation). We observed the same behavior, which is consistent with the theoretical predictions derived for the metapopulations. This demonstrates that spatial, nearest-neighbor interactions can have a dual effect on the persistence of enemy-victim interactions and that this result is independent of the particular form of the enemy-victim model, provided that the two above-described constraints are met. If persistence is observed in a mass-action setting, nearest-neighbor interactions lead to properties that are characteristic of a fragmented habitat, thus leading to an increased propensity for extinction. On the other hand, if well-mixed systems display unstable dynamics that lead to extinction, spatial interactions can stabilize those interactions and lead to persistence, a well-described phenomenon (Briggs and Hoopes 2004).

Figure 8.

Parameter dependence of the outcomes of the agent-based model corresponding to model d of figure 7. Compared are the mass-action (i) and nearest-neighbor (ii) scenarios. Each point represents the outcome of a single run, indicated by the color code. Red indicates extinction of victim and enemy, blue indicates coexistence, and gray indicates persistence of the victim in the absence of the enemy. Above the white and below the black lines, the equilibrium number of victims and enemies, respectively, is greater than 1. This derives from corresponding ordinary differential equations with a carrying capacity K = N × N for the mass-action and K_loc = 9 for the nearest-neighbor loc system. Above the yellow line, the enemy fails to invade, determined by numerical simulations. For ease of comparison, the dashed line in the plot of the nearest-neighbor system indicates the coexistence region for the mass-action system. The parameters A, B, and R were varied, as indicated. Other parameters were held constant: D = 0; ε = 0.09; η = 0.09. These values were chosen to adjust for the difference in carrying capacity between agent-based and metapopulation models, to facilitate comparison. The size of the grid was 30 × 30. Initial conditions and cutoff time were the same as in figure 2. For details, see text and Supplementary Information, section 2.1, available online.

Discussion

Guided by the previous theoretical literature, a variety of experiments have supported the concept that spatial habitat structure and nearest-neighbor interactions promote persistence of enemy-victim systems if they are unstable under complete mixing (Huffaker et al. 1963; van de Klashorst et al. 1992; Holyoak and Lawler 1996; Janssen et al. 1997; Holyoak 2000; Ellner et al. 2001). Other experiments, however, have confirmed the results that we present here (Burkey 1997). They were performed using a number of bacterivorous protozoa (including Colpidium striatum, Tetrahymena thermophilia, and Chilomonas paramecium) and a ciliate predator (either Euplotes aediculatus or Didinium nasutum). Predator-prey pairs were selected that were persistent in large, undivided stock cultures. Comparing undivided mircrocosms with subdivided ones of an equivalent total volume, the experiments showed a significantly higher chance of extinction across the subdivided microcosms than in the undivided habitats, supporting the theoretical findings reported here, that is, that spatially structured interactions promote extinction. While the functional responses of the predators were not determined in these studies, we hypothesize that they were characterized by the constraints assumed in our models, because the higher extinction probability observed in subdivided, linked microcosms would otherwise not be possible, according to our model. We would like to point out that although our specific models described host-pathogen interactions, our axiomatic modeling has shown that the extinction-promoting role of spatial interactions holds in generalized enemy-victim models, and thus the protozoan examples discussed here are appropriate systems to interpret in the light of our theory. The described experiments are the closest to our model setup that we could find in the literature, and they provide the first step toward testing and validating the model predictions. The agreement with our theoretical notions encourages additional work to validate the model in further detail.

As mentioned above, previous work has shown that Turing instability can destabilize dynamics in spatially structured populations under specific assumptions. The effects described here are of a different nature, as shown in SI, section 6.

An important finding concerns the conditions for extinction in the spatial, agent-based model. Although we consider a relatively large, continuous habitat in the agent-based model, interactions in a small subset of this habitat, which we call the “local neighborhood,” determine whether the populations persist or become extinct. This is interesting from a theoretical point of view. The idea of a “characteristic scale” has been proposed in the literature in the context of different predator-prey models (de Roos et al. 1991), where the system’s behavior was found most predictable on an intermediate scale defined by the individuals’ motility and interactions. Pascual et al. (2001) showed that in a class of systems exhibiting oscillatory dynamics, the functional forms governing the local predator- prey interactions at those characteristic scales are the same as the ones describing a perfectly mixed, mass-action system but contain different parameters. This allowed the authors to approximate the long-term dynamics of the spatial system at large scales with a temporal predator-prey model describing local interactions. Here, we build on this idea and show that the global outcomes of the spatially distributed system can be understood by utilizing the laws of local dynamics.

The result that local interactions can predict the outcome of the global system is of biological importance because it has implications for habitat fragmentation (Kareiva 1987; Bascompte and Sole 1998; Fahrig 2003; Ryall and Fahrig 2006). The result that interactions in small, local neighborhoods govern the outcome across the whole space in the agent-based model suggests that nearest-neighbor interactions in an undivided habitat lead to properties that are reminiscent of fragmented habitats. This was further corroborated by our metapopulation model, which was characterized by the same properties as the agent-based model. In contrast to the agent-based model, the results are more intuitive with the metapopulation model. It explicitly describes a habitat that has been fragmented into a collection of local patches in which local dynamics occur independently of each other, with the exception of migratory processes that occur at a relatively low rate. The effect of habitat fragmentation on extinction and diversity is much discussed in the context of conservation (Lindenmayer and Fischer 2006), and our model provides a link between a fragmented habitat and an undivided habitat with nearest-neighbor interactions.

Our new insights about the extinction-promoting effect of spatially restricted interactions in enemy-victim systems has wide implications in ecology and epidemiology, where spatially restricted dynamics tend to be more common than well-mixed settings (Crawley 1992). In the context of host-pathogen dynamics, the evolutionary transition of planktonic growth in bacteria to sessile growth and the formation of biofilms could be of particular interest (Jefferson 2004). To a certain extent, our agent-based model can be a good description of the most basic dynamics between bacteria in a biofilm and bacteriophages that infect them. Biofilms are characterized by pronounced spatial structures and nearest-neighbor interactions, where susceptible and infected bacteria share a defined space. While a certain degree of migration might occur, particularly with the phage population, our simulations have shown that our basic results remain robust. According to our theory, infection by phages would render the bacterial population more susceptible to extinction in the context of sessile growth than under planktonic growth, thus providing selection pressure against this transition, which is also supported by the presence of intricate defense systems in biofilms against infection. The insight that the emergence of spatial structure can lower the fitness of bacterial populations is important to take into account when considering the costs and benefits of sessile and spatially structured growth.