Charge of a quasiparticle in a superconductor

Significance

The charge of the quasiparticles in superconductors was never, to our knowledge, directly measured. Here, we used our experience and sensitive techniques in measuring the fractional excitations in the fractional quantum Hall effect via quantum shot noise, to measure the tunneling quasiparticles in a 1D superconductor–insulator–superconductor Josephson junction, and find their charge to be significantly less than that of an electron.

Abstract

Nonlinear charge transport in superconductor–insulator–superconductor (SIS) Josephson junctions has a unique signature in the shuttled charge quantum between the two superconductors. In the zero-bias limit Cooper pairs, each with twice the electron charge, carry the Josephson current. An applied bias $V_{SD}$ leads to multiple Andreev reflections (MAR), which in the limit of weak tunneling probability should lead to integer multiples of the electron charge $ne$ traversing the junction, with $n$ integer larger than $2\mathrm{\Delta }/e{V}_{SD}$ and $\mathrm{\Delta }$ the superconducting order parameter. Exceptionally, just above the gap eV_SD ≥ 2Δ, with Andreev reflections suppressed, one would expect the current to be carried by partitioned quasiparticles, each with energy-dependent charge, being a superposition of an electron and a hole. Using shot-noise measurements in an SIS junction induced in an InAs nanowire (with noise proportional to the partitioned charge), we first observed quantization of the partitioned charge q = e*$/e=n$, with n = 1–4, thus reaffirming the validity of our charge interpretation. Concentrating next on the bias region $e{V}_{SD}\sim 2\mathrm{\Delta }$, we found a reproducible and clear dip in the extracted charge to $q\hspace{0.17em}\sim 0.6$, which, after excluding other possibilities, we attribute to the partitioned quasiparticle charge. Such dip is supported by numerical simulations of our SIS structure.

Excitations in superconductors (Bogoliubov quasiparticles) can be described according to the Bardeen–Cooper–Schrieffer (BCS) theory (1) as an energy-dependent superposition of an electron with amplitude u(ε), and a hole with amplitude v(ε), where the energy ε is measured relative to the Fermi energy (2). Evidently, the expectation value of the charge operator (applied to the quasiparticle wave function), which we address as the quasiparticle charge e* = q(ε)e, is smaller than the charge of an electron, $q\left(\epsilon \right)={\left|u\left(\epsilon \right)\right|}^2-{\left|\nu \left(\epsilon \right)\right|}^2$ (3). Solving the Bogoliubov–de Gennes equations, one finds that ${\left|u\left(\epsilon \right)\right|}^2=1/2\left[1+\left(\sqrt{{\epsilon }^2-{\mathrm{\Delta }}^2}/\epsilon \right)\right]$ and ${\left|v\left(\epsilon \right)\right|}^2=1/2\left[1-\left(\sqrt{{\epsilon }^2-{\mathrm{\Delta }}^2}/\epsilon \right)\right]$, with the expected charge evolving with energy according to $q\left(\epsilon \right)=\sqrt{{\epsilon }^2-{\mathrm{\Delta }}^2}/\epsilon$––vanishing altogether at the superconductor gap edges (3). Note, however, that the quasiparticle wave function is not an eigenfunction of the charge operator (3, 4). Properties of quasiparticles, such as the excitation spectra (5), lifetime (6–10), trapping (11), and capturing by Andreev bound states (12, 13), had already been studied extensively; however, studies of their charge are lagging. In the following we present sensitive shot-noise measurements in a Josephson junction, resulting in a clear observation of the quasiparticle charge being smaller than e, q(eV_SD∼2Δ) < 1, and evolving with energy, as expected from the BCS theory.

To observe the BCS quasiparticles in transport we study a superconductor–insulator–superconductor (SIS) Josephson junction in the nonlinear regime. The overlap between the wave functions of the quasiparticles in the source and in the drain is expected to result in a tunneling current of their effective charge. This is in contrast with systems which are incoherent (14, 15) or with an isolated superconducting island, where charge conservation leads to traversal of multiples of e – Coulomb charge (16). As current transport in the nonlinear regime results from “multiple Andreev reflections” (MAR), it is prudent to make our measurements credible by first measuring the charge in this familiar regime.

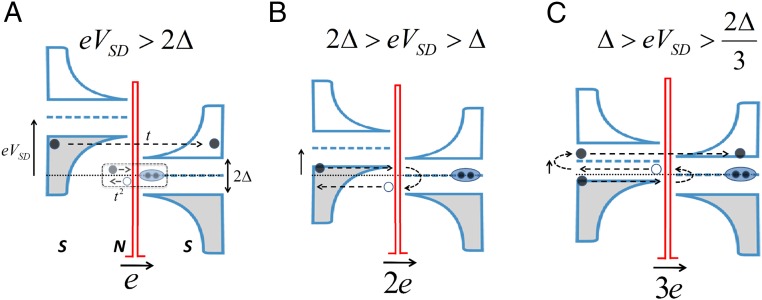
In short, the MAR process, described schematically in Fig. 1, carries a signature of the shuttled charge between the two superconductors (SCs), being a consequence of n traversals through the junction (as electron-like and hole-like quasiparticles), with n an integer larger than 2Δ/eV_SD. A low transmission probability t (via tunneling through a barrier) in the bias range $2\mathrm{\Delta }/n<e{V}_{SD}<2\mathrm{\Delta }/(n-1)$ assures dominance of the lowest order MAR process (higher orders are suppressed as tⁿ), with the charge evolving in nearly integer multiples of the electron charge. Although there is already a substantial body of theoretical (3, 17–23) and experimental (24–29) studies of the MAR process, charge determination without adjustable parameters is still missing. An important work by Cron et al. (27) indeed showed a staircase-like behavior of the charge using “metallic break junctions;” however, limited sensitivity and the presence of numerous conductance channels some of which with relatively high transmission probabilities did not allow exact charge quantization. Our shot-noise measurements, performed on a quasi-1D Josephson junction (single-mode nanowire) allowed clear observation of charge quantization without adjustable parameters. To count a few advantages: (i) the transmission of the SIS junction could be accurately controlled using a back-gate; (ii) this, along with our high sensitivity in noise measurements, enabled us to pinch the junction strongly (thus suppressing higher MAR orders); and (iii) with the Fermi level located near the 1D channel van Hove singularity, a rather monoenergetic distribution could be injected (SI Appendix, section S7).

Fig. 1.

MAR. Illustrations of the leading processes contributing to the current as function of bias. In general, for $2\mathrm{\Delta }/\left(n-1\right)>e{V}_{SD}>2\mathrm{\Delta }/n$ the leading charge contribution to the current is ne. An electron-like quasiparticle is denoted by a full circle, whereas a hole-like quasiparticle is denoted by an empty circle. (A) When the bias is larger than the energy gap, $e{V}_{SD}>2\mathrm{\Delta }$, the leading process is a single-path tunneling of single quasiparticles from the full states (Left) to the empty states (Right). This current is proportional to the transmission coefficient t. Higher-order MAR process (dashed box), being responsible for tunneling of Cooper pairs, is suppressed as t². (B) For $2\mathrm{\Delta }>e{V}_{SD}>\mathrm{\Delta }$, the main charge contributing to the current is 2e with probability t². (C) For $\mathrm{\Delta }>e{V}_{SD}>2\mathrm{\Delta }/3$, the main charge contributing to the current is 3e with probability t³.

Materials and Methods

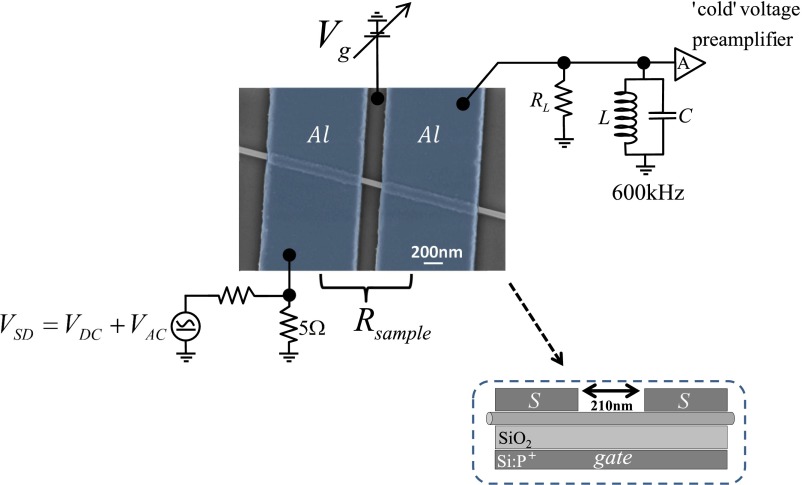
Our SIS Josephson junction was induced in a back-gate-controlled, single-channel nanowire (NW). The structure, shown in Fig. 2, was fabricated by depositing two Ti/Al (5 nm/120 nm) superconducting electrodes, 210 nm apart, onto a bare ∼50-nm-thick InAs NW, baring a pure wurtzite structure, grown by the gold assisted vapor–liquid–solid molecular beam epitaxy process. The Si:P⁺ substrate, covered by SiO₂ (150 nm thick), served as a back-gate (BG), allowing control of the number of conducting channels in the NW (SI Appendix, section S2). Whereas the central part of the NW could be fully depleted, the segments intimately covered by the Ti/Al superconducting electrodes are flooded with carriers and are barely affected by the BG voltage. The density therefore decreases smoothly toward the depleted region in the very center of the junction, so that the actual tunnel barrier is much narrower than 200 nm. On the other hand, the induced SC coherence length is expected to be much larger than 200 nm––assuring coherence of electron-hole quasiparticles along the junction (30).

Fig. 2.

Scanning electron micrograph of the device and the circuit scheme. InAs NW contacted by two superconducting Al electrodes. Conductance measurement: Sourcing by ac + dc, V_ac = 0.1 μV at ∼600 kHz, with ac output on R_L. Noise measurement: sourcing by dc and measuring voltage fluctuations on R_L at a bandwidth of 10 kHz.

Because the probability of each single-path MAR process is t, and the probability for n paths scales as t*$=t^n$, a sufficiently small t is necessary to single out the most probable (lowest n) MAR process. This evidently leads to a minute shot-noise signal, requiring sensitive electronics and weak background noise. A “cold” (∼1 K), low-noise, homemade preamplifier was used, with a sensitivity limit better than ∼10⁻³⁰ A²/Hz at ∼600 kHz. As we are interested in the current-dependent “excess noise” (with spectral density $S_{exc}^i$), the non-shot-noise components should be recognized and subtracted. The latter are composed of a thermal (Johnson–Nyquist) component, 4k_BTr (31, 32), the preamplifier’s current noise $S_{amp}^i$ (current fluctuations driven back to our device), and its voltage noise $S_{amp}^{\upsilon }$, whereas the ubiquitous 1/f noise (due to multiple sources) is negligible at our measurement frequency (SI Appendix, section S4). Altogether S^υ(0) is given by

$$S^{\upsilon }\left(0\right)=S_{exc}^i\left(0\right)r^2+4k_{B}Tr+S_{amp}^i\left(0\right)r^2+S_{amp}^{\upsilon },$$ [1]

where k_BT is the thermal energy and r is the total resistance of the SNS junction and the load resistance, namely, R_sample + 5Ω in parallel with R_L (Fig. 2). Hence, the “zero-frequency excess noise” for a stochastically partitioned single quantum channel at sufficiently low temperature (our k_BT ∼ 2 μeV while eV_SD = 50–300 μeV) (33–36) is

$$S_{exc}\left(0\right)=2e^{\ast }I\left(1-t^{\ast }\right),$$ [2]

with e* = qe, I the net dc current, and t*$=G/q{g}_Q$, where $g_Q=2e^2/h$ is the quantum conductance of a spin-degenerate channel in the normal part of the wire (SI Appendix, section S6). Hence, the charge (in units of the electron charge, e) is

$$q=\frac{S_{exc}\left(0\right)}{2eI}+\frac{G}{2e^2/h}.$$ [3]

Two comments regarding Eq. 3 are due here: (i) Using the differential conductance G for calculating the transmission probability at energies near eV_SD is justified because most of the current is carried by quasiparticles emitted in a narrow energy window, much narrower than Δ due to the van Hove singularity of the density of states in the 1D NW (see more in the discussion below); and (ii) When the transmission is small so that G/g_q ∼ 0, one resorts to the familiar Schottky (Poissonian) expression of a classical shot noise (37).

Although details of the measurement setup and the algorithm used in determining the true excess noise and the extracted charge are provided in SI Appendix, sections S3 and S4, a short description is due here. As seen in Fig. 2, conductance and noise were measured in the same configuration at an electron temperature of ∼25 mK. The differential conductance was measured by applying 1 µV at 600 kHz in addition to a variable dc bias, while noise was measured with an applied dc bias only. A load resistor of either R_L = 1 kΩ or R_L = 20 kΩ, shunted by a resonant LC circuit (with a center frequency of 60 kHz), terminated the circuit to ground. The signal was amplified by a cascade of cold and “warm” amplifiers, and measured by a spectrum analyzer with an appropriate bandwidth. The smaller R_L was used when the sample’s resistance was relatively small, thus restraining fluctuations in the background noise on the bare sample fluctuating conductance. It is important to note that the use of a “voltage source” for V_SD (rather than a “current source”) allowed access to quiescent regions of negative differential conductance, which otherwise would have been inaccessible (being within hysteretic loops in the I-V_SD characteristics).

Results and Discussion

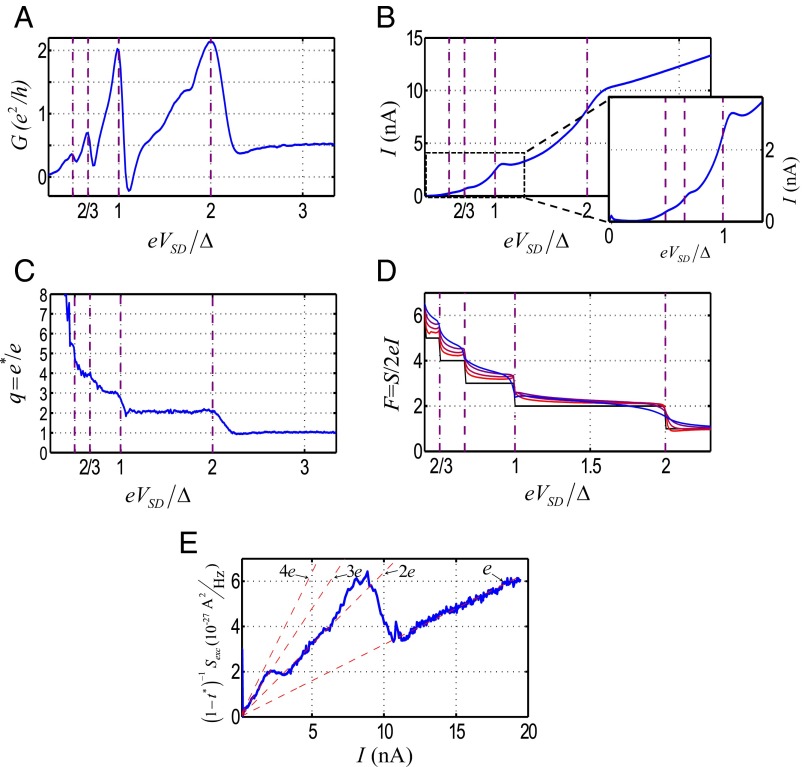
We start with R_L = 1 kΩ and junction conductance tuned by the BG to a partly transmitted single channel in the bare part of the NW. Four MAR conductance peaks were observed at V_SD = 2Δ/en = 300 μV/n (note that the induced gap in the InAs NW is nearly that of the Al SC). The static I-V_SD characteristic, required for the determination of the energy-dependent charge, was obtained by integrating the differential conductance (Fig. 3B). After a careful subtraction of the background noise (SI Appendix, section S4), we extracted the charge as shown in Fig. 3C. Clear steps are seen at values of q = n, with $1\le$ n $\le \hspace{0.17em}4$. Higher charge values (for n $>4$) are averaged out, mostly due to the successively narrowing MAR region as ∼1/n² and possibly some inelastic scattering events. It should be stressed here that whereas the conductance (and thus the deduced t*) and the total noise fluctuate violently, the extracted charge evolves smoothly between each of the quantized charge values––reassuring the process of charge extraction.

Fig. 3.

Shuttled charges in the MAR process. (A) Differential conductance (in units of $e^2/h$) as a function of applied bias, $V_{SD}$, normalized by $\mathrm{\Delta }/e$, where $\mathrm{\Delta }=150$μeV is the superconducting order parameter. The signature of the MAR processes is manifested by a series of peaks in bias corresponding to $e{V}_{SD}/\mathrm{\Delta }=2/n$. (B) The I-V characteristics as obtained by integrating the differential conductance. (Inset) A zoom of the small current range. (C) The shuttled charge q determined from Eq. 3 plotted as a function of $e{V}_{SD}/\mathrm{\Delta }$. The pronounced staircase demonstrates the quantization of charge involved in the MAR processes. (D) Numerical simulations of the Fano factor, F = S_exc/2eI, as function of $e{V}_{\text{SD}}/\mathrm{\Delta }$ for different values of the normal-region transmission t = 0.4, 0.2, 0.1, 0.05 (the transmission at $e{V}_{\text{SD}}>2\mathrm{\Delta }$), according to SI Appendix, section S1. (E) The normalized excess noise [after dividing the excess noise by (1 − t*)], as a function of the current. Note that the local slope at every MAR region equals the global slope (red dashed curves; see also text and Eq. 3), suggesting a dominant contribution of a single process to the current and the noise near the energy corresponding to the bias. This in turn also suggests that most of the current originates from a small energy range around the Fermi energy justifying the use of the differential conductance for extracting the transmission.

We performed numerical simulations of the conductance and the excess noise at various junction transmission coefficients and energies, with a Fano factor defined as F = S_exc(0)/2eI (SI Appendix, section S1). The results shown in Fig. 3D, contrary to the experimental results in Fig. 3C, predict integer charge plateaus at much lower transmission probabilities t ∼ 0.05. We attribute this difference to the sharp density of states profile resulting from the position of the Fermi level near the van Hove singularity of the 1D nanowire described to above (38) (SI Appendix, section S7), which suppresses higher-order MAR––thus allowing charge quantization at relatively high transmissions. The vicinity of the Fermi level to the bottom of the conduction band was not taken into account in the theoretical model (SI Appendix, sections S1 and S8). Consequently, the normalized excess noise S_exc*$=S_{exc}/\left(1-t*\right)$, plotted as a function of the current in Fig. 3E, reveals a straight lines with quantized slopes, all crossing the origin, confirming that in each relevant bias regime quasiparticles indeed emerge within a narrow energy window.

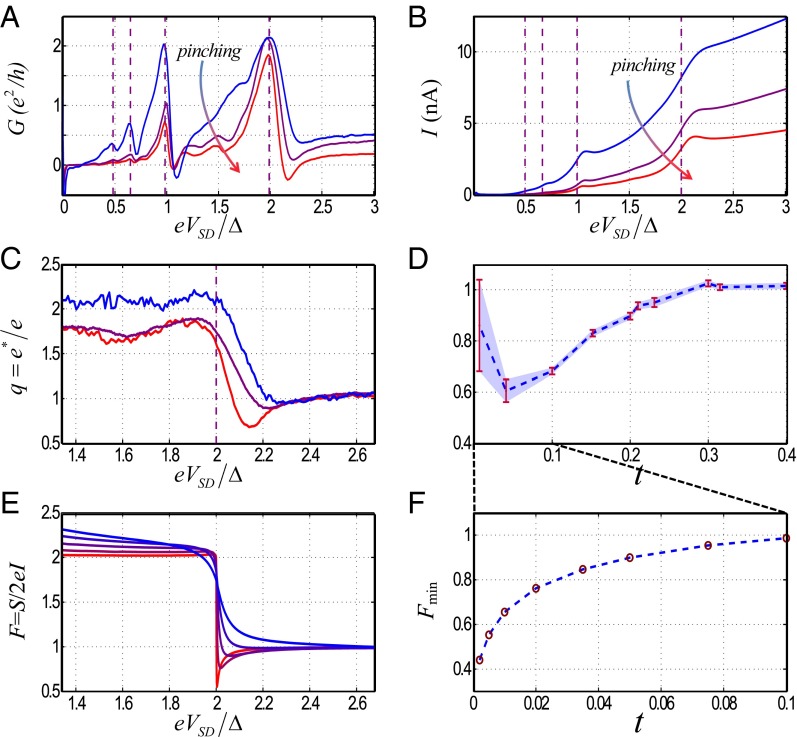
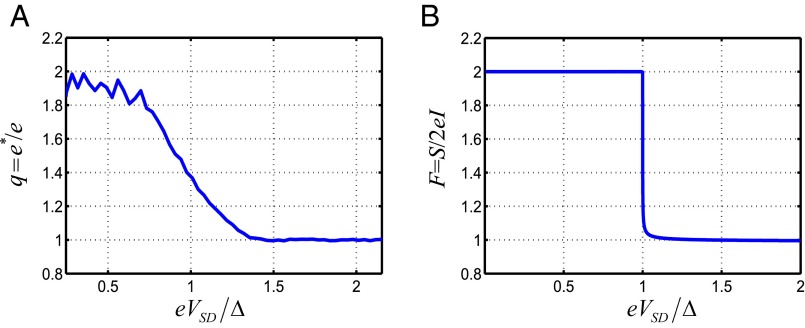
The robust quantized plateaus of the extracted charge (in two different NWs) paved the way to the determination of the traversing charge near the SC gap edge. Singling out the n = 1 process (having t* = t) very close to eV_SD = 2Δ requires strong suppression of the n = 2 process (t* = t²); thus further increasing the barrier in the bare part of the NW, as evident by the weaker MAR processes in Fig. 4A and higher junction resistances (now R_L = 20 kΩ). A few I-V_SD characteristics, obtained by integrating the differential conductance for several BG voltages, are plotted in Fig. 4B. The extracted traversing charge as a function of bias is shown in Fig. 4C for a few values of the transmission coefficient, with a clear dip in the charge appearing near eV_SD = 2Δ for lower transmissions. In Fig. 4D we plot the lowest charge measured at each transmission probability t, observing a minimum of q ∼ 0.6 at t ∼ 0.05. As the barrier is increased even further (t < 0.01), the extracted charge increases toward e.

Fig. 4.

Evolution of the quasiparticles charge near the edge of the gap. (A) Differential conductance (in units of $e^2/h$) as a function of $e{V}_{\text{SD}}/\mathrm{\Delta }$ for decreasing normal-region transmission t = 0.23, 0.15, 0.1 (red, purple, and blue, respectively). As the transmission decreases (from blue to red) the conductance due to higher-order processes diminishes with $t^n$ dependence. (B) The I-V curve obtained by integrating the differential conductance. (C) The charge determined from Eq. 3 plotted as a function of $e{V}_{\text{SD}}/\mathrm{\Delta }$. As the transmission decreases, the value of the observed minima in the charge at the transition between n = 1 and n = 2 dips. (D) The measured charge q is plotted as a function of the normal-region transmission t. (E) Results of numerical calculations showing F = S_exc/2eI as function of e$V_{SD}$/Δ for low normal-region transmissions t = 0.2, 0.1, 0.05, 0.02, 0.01. (F) Evolution of the minimum value of F (F_min) as a function of transmission.

The numerical calculation results for the Fano factor, F = S_exc(0)/2eI, around $e{V}_{SD}\sim 2\mathrm{\Delta }$ are shown in Fig. 4 E and F for various transmissions. The theoretical calculation also resulted in a dip which emerges as the transmission is lowered similarly to our experimental data. The discrepancy in the values of the transmission, in which the dip appears, can once again be attributed to the sharper profile of the density of states. Another difference from the theoretical calculation that should be noted is the decrease in the apparent charge from 2e at eV_SD < 2Δ. We relate this decrease to unavoidable processes of charge e transport which are of order t (rather than t²), such as quasiparticles excited by noise or temperature, and subgap current originating due to the soft induced gap.

To further test the validity of the dip in the extracted charge, we fabricated and tested a normal–I–S (NIS) junction. Here too, a conductance peak develops at the gap’s edge (this time at eV_SD = Δ); however, the charge evolves monotonically from e to 2e, without any sign of a dip (Fig. 5A). This result is backed by our numerical simulations shown in Fig. 5B as well as in SI Appendix, section 9 where we give a more intuitive physical picture that reflects why charge partition should not be observed in an NIS junction.

Fig. 5.

Charge measurements in an SC–normal junction. (A) The charge determined from Eq. 3 as a function of $e{V}_{\text{SD}}/\mathrm{\Delta }$ at normal-region transmission t = 0.01. The charge q increases from 1 to 2 as eV_SD crosses Δ. (B) Numerical simulations of the Fano factor, F = S_exc/2eI, as a function of $e{V}_{\text{SD}}/\mathrm{\Delta }$ at normal-region transmission t = 0.01.

Our assertion of observing the quasiparticle charge near the gap’s edge requires a discussion. One may consider three possible models of single quasiparticle transport near eV_SD = 2Δ: (i) The electric field may rip-off each quasiparticle to its electron and hole components, thus accelerating only one component (say, electrons) toward the drain, leading to current noise of partitioned charges of e and a Fano factor of 1 at t << 1. This might play a role in an SNS junction, but less likely in our SIS tunneling junction. (ii) In an SIS junction, the electric field across the insulating barrier (I) realigns full quasiparticle states in the source (S) with empty quasiparticle states in the drain (S), making tunneling events possible. One possibility is that each tunneling event collapses in the drain to an electron with probability u² or to a hole with probability v². In this case the expected charge fluctuations for t << 1 lead to a Fano factor F = (u² − v²)⁻¹ > 1 (3, 4) (SI Appendix, section S7). (iii) Alternatively, each tunneling event is that of a coherent superposition of an electron and a hole, leading to a Fano factor F = (u² − v²) < 1 at t << 1 (SI Appendix, section S7). Thus, measuring a charge which is smaller than e confirms the third scenario.

If fractionally charged quasiparticles indeed tunnel through the SIS junction, why does the extracted charge climb back to e when the tunneling probability is extremely small? Specifically, an opaque barrier is expected to allow only tunneling of electrons, as both sides of the barrier should be quantized in units of the electronic charge due to charge neutrality [recall the similar findings in the fractional quantum Hall effect (39, 40)].

Summary

In conclusion, using sensitive, low-frequency shot-noise measurements (41–43), we observed an evolution of energy-dependent tunneling of quasiparticle charge in an SIS Josephson junction induced in a one-dimensional InAs nanowire. The charge evolved as e* = ne away from the superconducting gap’s edge, with n = 1 for eV_SD > 2Δ and n = 2–4 for eV_SD < 2Δ, in agreement with our understanding of MAR. Moreover, at the gap’s edge, eV_SD ∼2Δ, with MAR processes strongly suppressed, the charge as inferred from the Fano factor was found to dip below the electron charge e* < e; agreeing with the expectation value of the Bogoliubov quasiparticles being smaller than e. Whereas such suppression of the Fano factor was observed by numerical simulations (refs. 22, 23, and here), the relation to the quasiparticle charge was so far, to our knowledge, never discussed. We suggest that this correlation between the suppressed shot noise and the quasiparticle charge in SIS junctions should be further investigated theoretically beyond the simplified theoretical picture. Moreover, similar measurements should be applied to less ubiquitous superconductors, such as topological p-wave superconductors or high-Tc superconductors, to investigate the nature of their quasiparticle excitations.