QM/MM study of Thymidylate Synthase: Enzymatic motions and the temperature dependence of the rate limiting step

Abstract

Thymidylate synthase (TS) is an enzyme that catalyzes a complex cascade of reactions. A theoretical study of the reduction of an exocyclic methylene intermediate by hydride transfer from the 6S position of 5,6,7,8-tetrahydrofolate (H₄folate), to form 2’-deoxyuridine 5’-monophosphate (dTMP) and 7,8-dihydrofolate (H₂folate), has been carried out using hybrid quantum mechanics/molecular mechanics methods. This step is of special interest since it is the rate-limiting step of the reaction catalyzed by TS. The acceptor of this hydride is an intermediate that is covalently bound to the enzyme via a thioether bond to an overall conserved active site cysteine residue (Cys146 in E. coli). Heretofore, whether the hydride transfer precedes the thiol abstraction that releases the product from the enzyme, or whether these two processes are concerted has been an open question. We have examined this step in terms of free energy surfaces obtained at the same temperatures we previously used in experimental studies of this mechanistic step (273 – 313 K). Analysis of the results reveals that substantial features of the reaction and the nature of the H-transfer seem to be temperature independent, in agreement with our experimental data. The findings also indicate that the hydride transfer and the scission of Cys146 take place in a concerted but asynchronous fashion. This 1,3-S_N2 substitution is assisted by arginine 166 and several other arginine residues in the active site that polarize the carbon-sulphur bond and stabilize the charge transferred from cofactor to substrate. Finally, the simulation elucidates the molecular details of the enzyme’s motion that brings the system to its transition state and, in accordance with the experimental data, indicates that this “tunneling ready” conformation is temperature independent.

Introduction

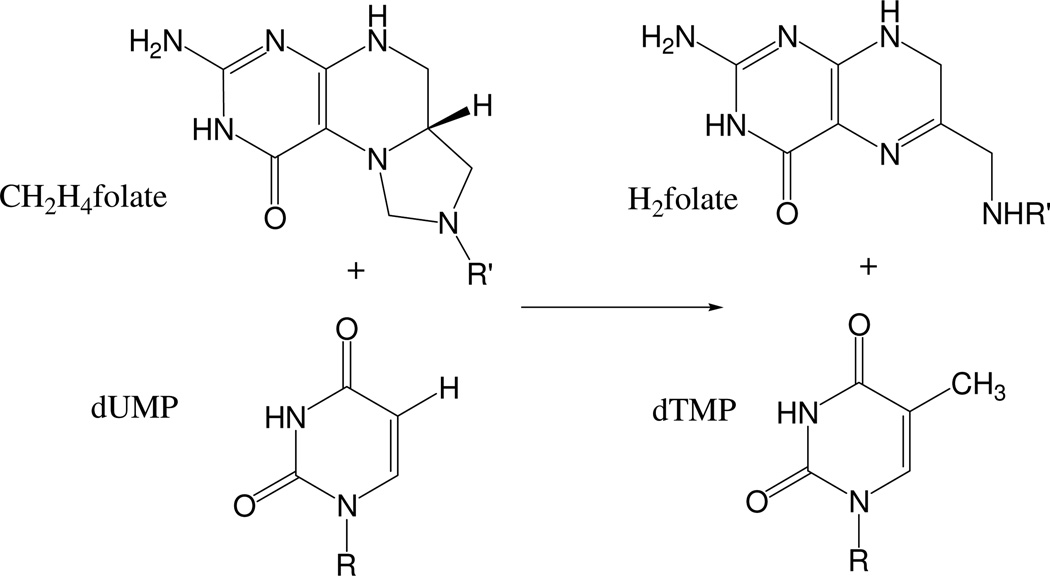
Thymidylate synthase (TS, EC 2.1.1.45) catalyzes the reductive methylation of 2’-deoxyuridine 5’-monophosphate (dUMP) to 2’-deoxythymidine 5’-monophosphate (dTMP) using the cofactor N5,N10-methylene-5,6,7,8-tetrahydrofolate (CH₂H₄folate) as a donor of both methylene and hydride, and producing 7,8-dihydrofolate (H₂folate). The overall reaction is depicted in Scheme 1.

Scheme 1.

Overall reaction catalyzed by TS. R = 2’-deoxyribose 5’-phosphate and R’ = paminobenzoyl-glutamate.

This enzyme is crucial for DNA biosynthesis, as it forms one of its building blocks (thymidine). Consequently, it is an anticancer and antibiotic drug-target, and great interest has been shown for many years in the details of its catalytic activity. A better understanding of its molecular mechanism may lead to more specific drugs that would specifically inhibit TS activity in cancerous or bacterial cells but not in normal human cells.

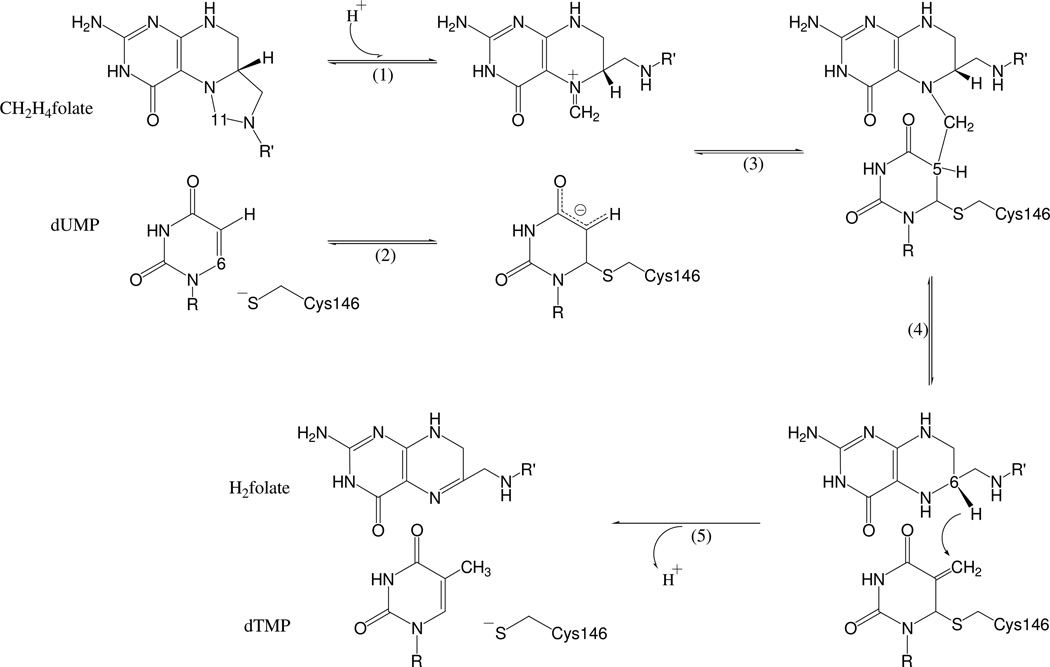
We have recently studied the entire TS multi-step mechanism Scheme 2 by means of hybrid quantum mechanics / molecular mechanics (QM/MM) potential energy surfaces exploration¹. These calculations indicated that hydride transfer from the 6S position of H₄folate, forming dTMP and H₂folate (step 5 in Scheme 2), is the rate determining step of the overall reaction. This finding was in good agreement with our experimental findings². Since the hydride transfer is rate limiting and practically not reversible, processes that are concerted with or those that follow this step are not experimentally accessible. Consequently, heretofore, the lack of such experimental information prohibited the elucidation of the relations between the H-transfer and the dissociation of the thioester bond that leads to the release of the product from the enzyme³.

Scheme 2.

The minimal reaction mechanism of TS. R= 2’-deoxyribose-5’-phosphate and R’= p-aminobenzoyl-glutamate.

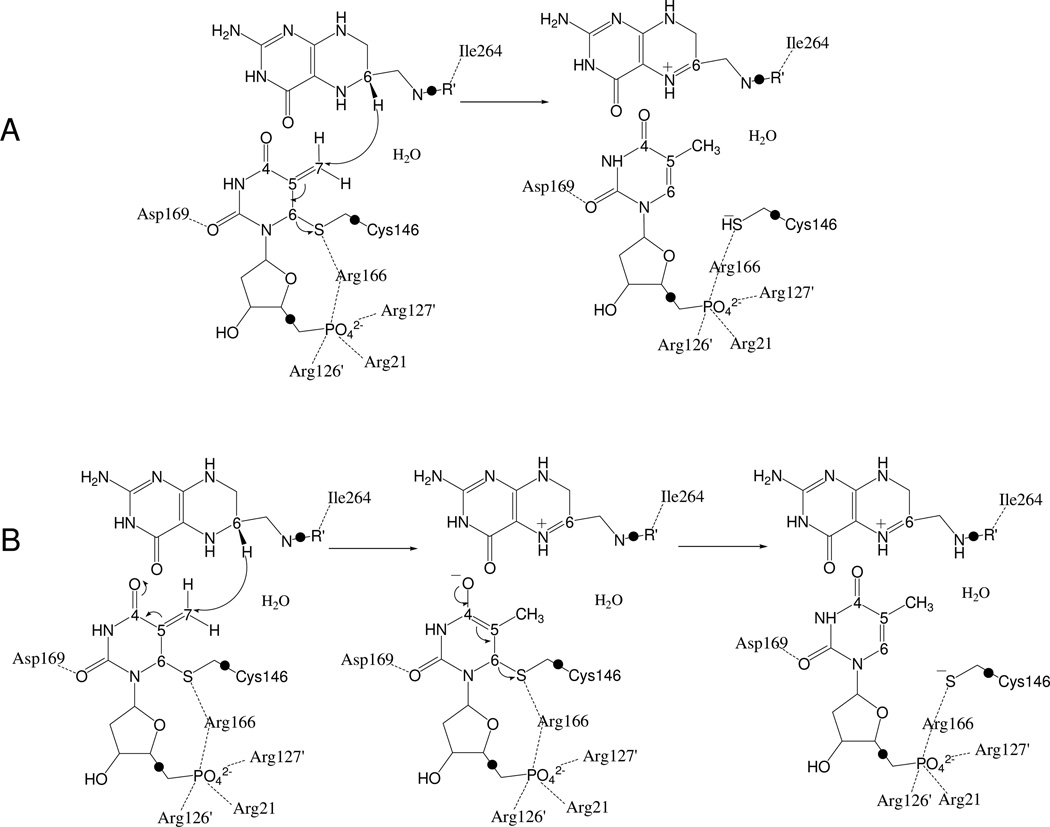
As illustrated in Scheme 3, two possible mechanisms would be consistent with the chemical transformation of this rate limiting step: (A) the hydride transfer and the thiol abstraction taking place in a concerted way, which can be viewed as a 1,3-S_N2 substitution; and (B), the hydride transfer from C6 of H₄folate to C7 of the exocyclic methylene preceding the elimination of the thioether from C6 of dUMP (i.e., the intermediate anion could be stabilized by enzymatic protonation of the C4 carbonyl, as proposed for the initial Michael addition, step 2, Scheme 2). Calculations that examine the nature of this step are not limited by the lack of reversibility and may provide the long sought insight regarding the nature of this TS-unique chemistry.

Scheme 3.

The rate limiting step of the reaction catalyzed by TS. Two possibles mechanismes are depicted; A, the concerted mechanism, and B, the stepwise mechanism. The link-atoms between the QM and the MM regions are indicated as •.

The current study examined this rate-limiting hydride transfer using two dimensional Potential of Mean Force (PMF) calculations carried out at the same four temperatures used in the experimental study². In particular, the antisymmetric combination of the distances describing the breaking and forming bonds on the hydride transfer step (d_CH-d_HC) and the distance between the C6 of the dUMP and the sulphur of the Cys146 (d_CS) have been used as distinguished reaction coordinates. The results shed light on the nature and the molecular details of the reaction, as well as on the role of the enzyme’s dynamics and active site residues in catalysis.

Computational Methods

The initial geometry for carrying out the calculations was the X-ray crystal structure of a ternary complex of E. coli TS with dUMP and an anti-folate, 10-propargyl-5,8-dideazafolate (CB3717), PDB ID 2TSC.^4–6 The inhibitor was replaced by the cofactor structure and the hydrogen atoms were incorporated into the structure using DYNAMO.⁷ After that, the “cluster method”,⁸ as implemented by Field and coworkers,⁹ was used to recalculate the standard pK_a values of the titratable amino acids of the enzyme.

The total charge of the system was not neutral, and 24 sodium counterions were placed in optimal electrostatic positions around the enzyme; farther than 10.5 Å from any atom of the system or 5 Å from another sodium, using a regular grid of 0.5 Å. The system was then placed in a prerelaxed orthorhombic box of water molecules (80Å × 80Å × 100Å). All the water molecules with an oxygen atom closer than 2.8 Å to any heavy atom were removed. The system was divided into a QM region, which includes the pteridine ring of the folate, the six-membered ring and the ribose ring of the dUMP, part of the Cys146 and a crystallization water molecule, comprising 57 atoms (Scheme 3). The MM region involves the rest of the active site, the enzyme, the crystallization and solvation water molecules and the counterions.

AM1¹⁰ semiempirical Hamiltonian was chosen to describe the QM part and OPLSAA¹¹ and TIP3P¹² force fields were chosen for the MM region. To satisfy the valence of the QM fragments when the QM-MM boundary divides a covalent bond, the link atom method was used^13,14 (marked by • in Scheme 3). The nonbonding interactions were treated by periodic boundary conditions, using a switch function with a cut-off distance in the range of 16–18Å. Then, the system was relaxed by means of hybrid QM/MM molecular dynamics (MD). A Langevin bath (293 K) was used, in a canonical thermodynamic ensemble (NVT). The MD was run for 200 ps with an integration step size of 1 fs.

Two dimensional PMF (2D-PMF) at four different temperatures (278, 293, 303 and 313 K) were obtained using the weighted histogram analysis method (WHAM) combined with the umbrella sampling approach^15,16 as implemented in DYNAMO. The distinguished reaction coordinates were the antisymmetric combination of the distances describing the breaking and forming bonds on the hydride transfer step (d_CH-d_HC) and the distance between the C6 of the dUMP and the sulphur atom of the Cys146 (d_CS). A total of 61 simulations were performed at different values of d_CH-d_HC (61 simulations in a range from −1.5 Å to 1.5 Å), with an umbrella force constant of 2500 kJ·mol⁻¹·A⁻¹ for each particular value of the distance d_CS (28 simulations with a force constant of 2500 kJ·mol⁻¹·A⁻¹, from 1.8 Å to 4.5 Å). Consequently, there are 1708 windows per PMF. The values of the variables sampled during the simulations were then pieced together to construct a full distribution function from which the 2D-PMF was obtained. On each window, 5 ps of relaxation was followed by 10 ps of production with a time step of 0.5 ps due to the nature of the chemical step involving a hydrogen transfer. The starting point for the four PMF-2Ds was the pre-equilibrated transition structure at 293K, within an averaged RMSD (root mean square deviation) of the temperature for all the windows at each temperature never higher of 2.6 K (corresponding this value to the 313 K surface). Thus, the low differences in temperature (at most 20K) have been in all cases successfully overcome with the short relaxation dynamics, confirming the enzyme was equilibrate at the new temperature. The Verlet algorithm was used to update the velocities.

A note of caution has to be introduced at this point since two dimensional free energy surfaces, as the 2D-PMF computed in this study, are associated to two coordinates, and not to only one, ξ₀, as it is defined in equation 1;

$$PMF({\xi }_0)=-\frac{1}{\beta }\text{ ln }\int \delta (\xi (r)-{\xi }_0)e^{-\beta U(r)}dr$$ (1)

As a consequence, the energy should be integrated over the additional coordinate, γ, as defined in equation 2;

$$PMF({\xi }_0)=-\frac{1}{\beta }\text{ ln }\int e^{-\beta PMF({\xi }_0,{\gamma }_0)}d\gamma$$ (2)

Nevertheless, since this error is not significant and, in any case, similar for all the four free energy surfaces computed in this study, comparison of free energy barriers can be properly estimated without integration over additional variables.

Results

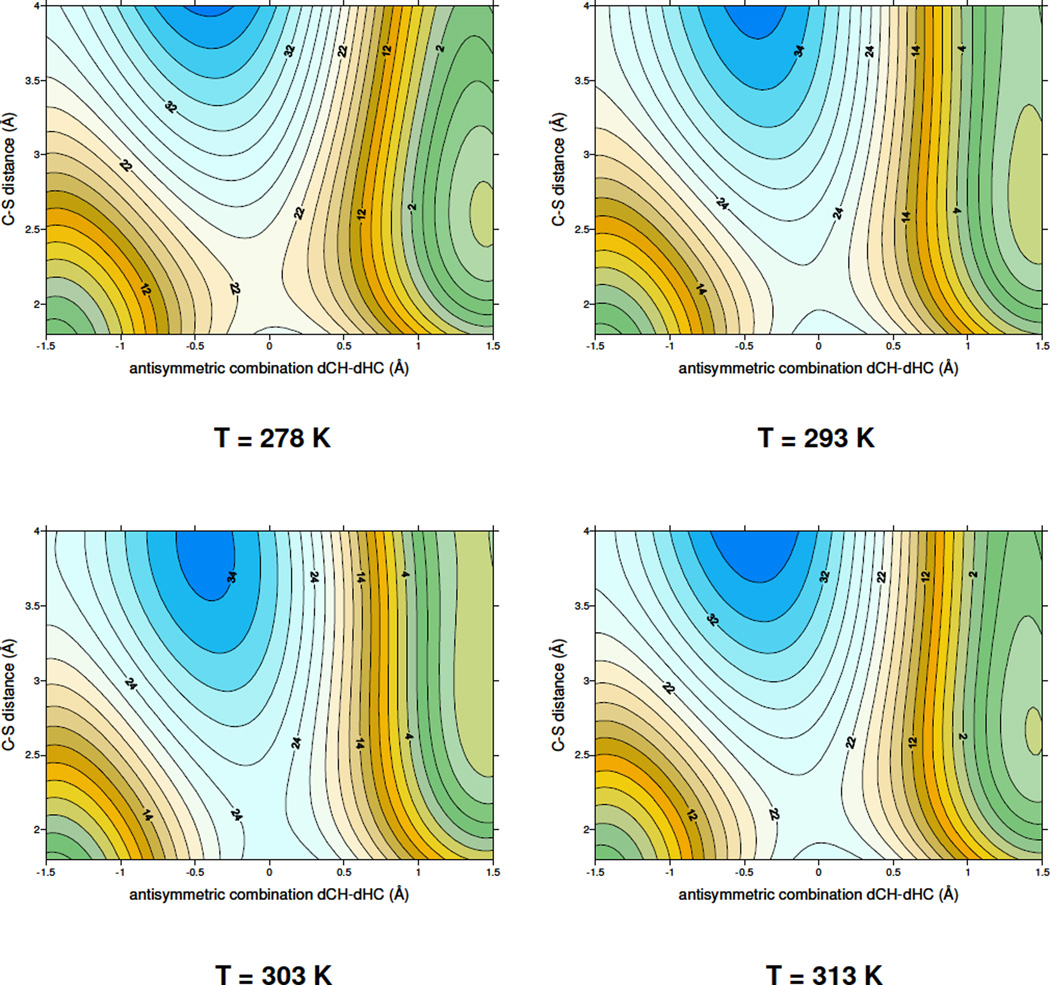
As mentioned above, four 2D-PMFs were obtained at four different temperatures (278, 293, 303 and 313 K), which are the same temperatures we examined experimentally², and the results are shown in Figure 1. The first conclusion that can be derived from Figure 1 is that the topology of the free energy surfaces is almost independent of the temperature. This would imply temperature independent kinetic isotope effects (KIEs) in accordance with the experimental findings². All free energy surfaces describe a concerted but asynchronous step, with a transition-state quadratic region located in a very early stage of the C-S breaking bond process, while hydride transfer is in between the donor and acceptor atoms. Additionally, the calculated activation free energy, ΔG^‡, is in the 22–24 kcal·mol⁻¹ range (22.2, 23.3, 24,4 and 24.1 kcal·mol⁻¹ for the four different temperatures, respectively). These values are slightly smaller than the potential energy barrier, 26 kcal·mol⁻¹, previously reported by us¹. These results are consistent with a small and positive entropy of activation. In pursuit of a molecular insight into the source of the observed temperature independent KIEs, of this hydride transfer step², averaged values of key geometrical parameters of structures selected from reactants state, transition state and products state have been obtained at the four different temperatures. The results are listed in Table 1 and Table 2.

Figure 1.

Two dimensional PMF performed at four different temperatures; 278, 293, 303 and 313 K. The distinguished reaction coodinates are C6(dUMP)-S(Cys146) and the antisymmetric combination of the breaking and forming bonds of the transferred hydrogen atom, dCH – dHC (in Å). Values on isoenergetic lines are reported in kcal·mol⁻¹.

Table 1.

Key averaged distances (Å) related to the substrate and cofactor, obtained at the reactants, transition state, and products of the rate limiting hydride transfer step of the TS catalyzed reaction, computed at AM1/MM level, at the four different temperatures; 278, 293, 303 and 313K.

T / K	interatomic distancesa	Reactants State	Transition State	Products State
278	C6(FOL)-H6(FOL)	1.14 ± 0.03	1.34 ± 0.04	4.2 ± 0.6
	H6(FOL)-C7(UMP)	2.80 ± 0.20	1.42 ± 0.04	1.12 ± 0.03
	antisymmetric combination	−1.66 ± 0.20	−0.08 ± 0.03	3.1 ± 0.6
	C6(FOL)-C7(UMP)	3.50 ± 0.18	2.74 ± 0.06	4.2 ± 0.3
	C6(UMP)-S(Cys146)	1.98 ± 0.05	2.00 ± 0.06	3.2 ± 0.3
293	C6(FOL)-H6(FOL)	1.14 ± 0.03	1.35 ± 0.04	4.3 ± 0.8
	H6(FOL)-C7 (UMP)	3.03 ± 0.21	1.41 ± 0.04	1.12 ± 0.03
	Antisymmetric combination	−1.89 ± 0.21	−0.06 ± 0.04	3.2 ± 0.8
	C6(FOL)-C7 (UMP)	3.60 ± 0.21	2.73 ± 0.07	4.0 ± 0.3
	C6(UMP)-S(Cys146)	1.97 ± 0.05	2.02 ± 0.07	3.1 ± 0.3
303	C6(FOL)-H6(FOL)	1.14 ± 0.03	1.36 ± 0.04	4.4 ± 0.9
	H6(FOL)-C7(UMP)	2.75 ± 0.21	1.40 ± 0.04	1.12 ± 0.03
	Antisymmetric combination	−1.61 ± 0.22	−0.04 ± 0.04	3.3 ± 0.9
	C6(FOL)-C7(UMP)	3.49 ± 0.21	2.74 ± 0.07	4.1 ± 0.3
	C6(UMP)-S(Cys146)	1.97 ± 0.05	2.04 ± 0.08	3.2 ± 0.3
313	C6(FOL)-H6(FOL)	1.14 ± 0.03	1.36 ± 0.04	4.3 ± 0.8
	H6(FOL)-C7(UMP)	2.92 ± 0.24	1.41 ± 0.04	1.12 ± 0.03
	Antisymmetric combination	−1.8 ± 0.3	−0.05 ± 0.04	3.17 ± 0.8
	C6(FOL)-C7(UMP)	3.43 ± 0.19	2.74 ± 0.07	4.0 ± 0.3
	C6(UMP)-S(Cys146)	1.97 ± 0.06	2.02 ± 0.07	3.1 ± 0.3

^aFOL indicates an atom on the folate derivative and UMP indicates an atom on the thymine derivative.

Table 2.

Key substrate-protein averaged distances (in Å) obtained at the reactants state, transition state, and products state of the hydride transfer step of the TS catalyzed reaction, computed at AM1/MM level, at the four different temperatures; 278, 293, 303 and 313 K. Primed residues indicate they are from subunit B of this homodimeric protein.

Reactants state					T / K
					278	293	303	313
CYS146	S	WAT	40	H2	1.93 ± 0.12	1.94 ± 0.13	1.94 ± 0.13	1.94 ± 0.13
CYS146	S	ARG	166	HH11	2.4 ± 0.3	2.5 ± 0.3	2.5 ± 0.3	2.6 ± 0.3
UMP	O2	ASP	169	H	2.00 ± 0.11	2.10 ± 0.15	2.03 ± 0.11	1.98 ± 0.11
UMP	P	ARG	166	HH22	2.32 ± 0.10	2.33 ± 0.09	2.31 ± 0.09	2.35 ± 0.10
UMP	O1P	ARG'	126	HH12	2.08 ± 0.20	2.17 ± 0.20	2.25 ± 0.19	2.10 ± 0.22
UMP	O1P	ARG	21	HE	1.59 ± 0.09	1.61 ± 0.10	1.62 ± 0.10	1.68 ± 0.13
UMP	O2P	ARG'	126	HE	1.72 ± 0.12	1.69 ± 0.12	1.70 ± 0.12	1.69 ± 0.12
UMP	O2P	ARG	166	HH22	1.63 ± 0.11	1.63 ± 0.12	1.63 ± 0.13	1.62 ± 0.12
UMP	O3P	ARG	166	HH12	1.75 ± 0.15	1.77 ± 0.17	1.78 ± 0.16	1.77 ± 0.19
UMP	O3P	ARG	166	HH22	2.37 ± 0.18	2.37 ± 0.18	2.35 ± 0.19	2.42 ± 0.19
UMP	O3P	ARG'	127	HH11	1.67 ± 0.11	1.64 ± 0.12	1.66 ± 0.12	1.67 ± 0.13
transition state					T / K
					278	293	303	313
CYS146	S	WAT	40	H2	1.93 ± 0.12	1.92 ± 0.12	1.91 ± 0.12	1.92 ± 0.13
CYS146	S	ARG	166	HH11	2.4 ± 0.3	2.4 ± 0.3	2.3 ± 0.3	2.4 ± 0.3
UMP	O2	ASP	169	H	1.97 ± 0.11	2.02 ± 0.12	2.03 ± 0.12	2.07 ± 0.13
UMP	P	ARG	166	HH22	2.30 ± 0.09	2.29 ± 0.09	2.29 ± 0.10	2.29 ± 0.10
UMP	O1P	ARG'	126	HH12	2.14 ± 0.20	2.22 ± 0.19	2.17 ± 0.20	2.18 ± 0.18
UMP	O1P	ARG	21	HE	1.58 ± 0.09	1.62 ± 0.10	1.66 ± 0.12	1.69 ± 0.13
UMP	O2P	ARG'	126	HE	1.70 ± 0.11	1.68 ± 0.11	1.69 ± 0.12	1.69 ± 0.12
UMP	O2P	ARG	166	HH22	1.62 ± 0.11	1.66 ± 0.13	1.68 ± 0.14	1.65 ± 0.13
UMP	O3P	ARG	166	HH12	1.79 ± 0.17	1.90 ± 0.22	1.9 ± 0.3	1.88 ± 0.22
UMP	O3P	ARG	166	HH22	2.36 ± 0.17	2.28 ± 0.19	2.25 ± 0.20	2.29 ± 0.19
UMP	O3P	ARG'	127	HH11	1.69 ± 0.12	1.64 ± 0.11	1.64 ± 0.11	1.73 ± 0.15
Products state					T / K
					278	293	303	313
CYS146	S	WAT	40	H2	1.76 ± 0.09	1.76 ± 0.09	1.77 ± 0.09	1.77 ± 0.09
CYS146	S	ARG	166	HH11	1.71 ± 0.08	1.71 ± 0.09	1.71 ± 0.09	1.71 ± 0.09
UMP	O2	ASP	169	H	2.00 ± 0.13	2.06 ± 0.16	2.05 ± 0.15	2.01 ± 0.14
UMP	P	ARG	166	HH22	2.33 ± 0.10	2.32 ± 0.10	2.33 ± 0.10	2.32 ± 0.10
UMP	O1P	ARG'	126	HH12	2.26 ± 0.21	2.33 ± 0.19	2.28 ± 0.19	2.04 ± 0.20
UMP	O1P	ARG	21	HE	1.58 ± 0.09	1.61 ± 0.10	1.61 ± 0.10	1.63 ± 0.12
UMP	O2P	ARG'	126	HE	1.67 ± 0.11	1.65 ± 0.11	1.65 ± 0.11	1.66 ± 0.12
UMP	O2P	ARG	166	HH22	1.62 ± 0.11	1.68 ± 0.13	1.68 ± 0.14	1.68 ± 0.13
UMP	O3P	ARG	166	HH12	2.00 ± 0.18	2.01 ± 0.20	2.02 ± 0.24	2.12 ± 0.23
UMP	O3P	ARG	166	HH22	2.37 ± 0.18	2.29 ± 0.19	2.31 ± 0.21	2.29 ± 0.21
UMP	O3P	ARG'	127	HH11	1.66 ± 0.11	1.66 ± 0.11	1.62 ± 0.11	1.62 ± 0.11

First conclusion that can be derived from the results presented in Table 1 is the invariance of the location of saddle point on the free energy surfaces. The distinguished reaction coordinates (the antisymmetric combination of distances describing the hydride transfer and the interatomic C6-S distance) are close to −0.06 and 2.02 Å, respectively, at all temperatures. This indicates that in all transition state structures, the transferring hydrogen is in between donor and acceptor atoms, while the carbon sulphur breaking bond process, defined by C6(UMP)-S(Cys146) distance, is in an early stage of the reaction. This last bond is completely broken in products at all temperatures (3.15 ± 0.03 Å). These results are in accordance with the definition of a concerted but asynchronous process. As discussed in more detail in references^17,19 the temperature independence of the KIEs on this step² suggests that the hydride is transferred from a similar conformation at all temperatures, in accordance with the data presented in Table 1.

It is also interesting to observe how folate and UMP approach each other from reactants to transition state for the hydride to be transferred from donor to acceptor atom (see C6–C7 distance). This distance is defined as the donor-acceptor distance and its evolution is coupled with relative substrate-protein residues movements (Table 2). This coupling indicates the role of the protein dynamics in enhancing the rate of H-transfer.

From data reported in Table 2, it can be observed how a water molecule and Arg166 are both interacting with sulphur atom of Cys146. Interestingly, the positively charged arginine serves as a Lewis-acid that turns the thiol into a better leaving-group. This arginine approaches the sulphur atom of Cys146 as the reaction proceeds, thus polarizing the electron density around sulphur atom and stabilizing the transition state. Also,^* Arg166, together with Arg21, Arg126’ and Arg127’, strongly interact with phosphate oxygen atoms of dUMP. This is an interesting example of dynamic effect that involves the protein, the reactants, and water in the active site, that would activate the C-H bond to a “tunneling ready” conformation².

A complementary study to this geometrical evolution analysis is carried out by averaged substrate-protein interaction energies, calculated from reactants and transition state structures. The total average interaction potential energies over the four different temperatures are −1099.5 ± 12.5 and −1141.1 ± 5.6 kcal·mol⁻¹ for reactants state and transition state, respectively. These values have no temperature dependent trend and a small standard deviation, in accordance with the observed temperature independent KIEs². Additional outcome of the simulation is that, as expected from Pauling’s postulate¹⁸, the protein interacts better with substrate in its transition state conformation than in its reactants state, which enhances confidence in the simulation procedure.

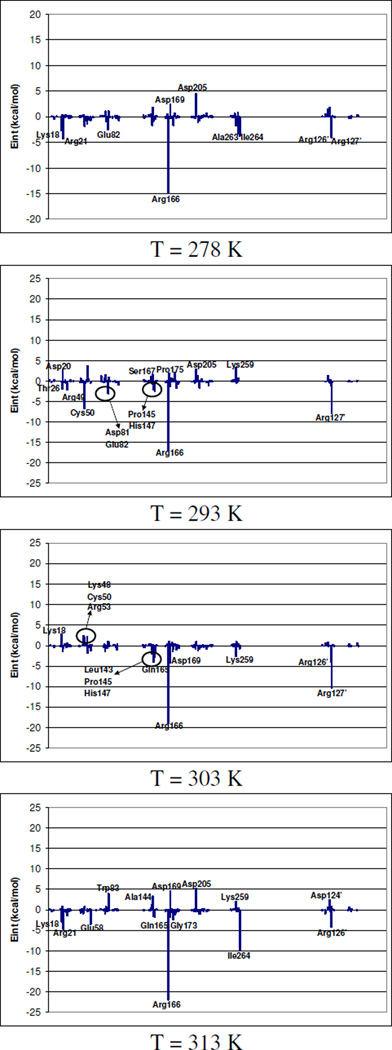
Decomposition of these substrate-protein interaction energies by residues are presented in Figure 2. In this figure; contribution of individual amino acid residues to total binding energy is presented as difference between transition state and reactants state. In this figure, negative values represent residues that interact better with substrate in the transition state than in reactants state. From Figure 2 it can be observed how the preferential stabilization of transition state is achieved, at all temperatures, by means of arginine residues located around dUMP substrate; Arg21, Arg166, Arg126’ and Arg127’. It is important to point out that the patterns of interactions established between substrate and protein, and cofactor and protein are very similar at all temperatures, both at reactants state and transition state, as revealed not only by data reported in Table 1 and 2, but by analysis of interaction energies by residue carried out at the two states (see Supplementary Material). Nevertheless, from Figure 2, where differences of interaction energies between both states are plotted, it can be observed that, Arg166 preferentially stabilizes transition state at all temperatures. This energetic contribution of Arg166 to the stabilization of the transition state reflects its role in activating the cleavage of the thioether bond (C-S) and further support the concerted nature of this cleavage and the hydride transfer form C6 of the H₄folate to the exocyclic methylene of the intermediate (step 5 in Scheme 2).

Figure 2.

Relative transition state stabilization, computed as averaged interaction energy differences between transition state and reactants state, by residues.

Conclusions

A theoretical study of the reduction of exocyclic methylene intermediate by hydride transfer from the 6S position of H₄folate, which is the rate-limiting step of the TS catalyzed reaction, has been carried out using hybrid QM/MM methods. We have examined this step in terms of free energy surfaces obtained at four different temperatures: 273, 293, 303 and 313 K. The high similarity of the PMFs in all temperatures is in good agreement with the temperature independent KIEs measured at the same temperatures.² A significant outcome of these calculations addresses a long lasting open question in the TS catalysis: is the tunneling of the hydride from H₄folate to the covalently bound intermediate, and the dissociation of the enzymatic thiol from the C6 carbon of dTMP constitutes a stepwise addition elimination reaction or a concerted 1,3-S_N2 substitution? The calculations indicate that the hydride transfer and the scission of the conserved active site cysteine residue (Cys146 in E. coli) take place in a concerted but asynchronous way, assisted by residues in the active site that polarize the carbon-sulphur bond and stabilize the charge transferred from cofactor to substrate. Between these residues, Arg166 seems to play a significant role in stabilizing the transition state.

Finally, the role of enzyme dynamics in activating a specific chemical step in its catalyzed reaction has been a matter of great interest in contemporary enzymology. In ref 2 we measured intrinsic KIEs on the same H-transfer step. These experimental KIEs were temperature independent and Marcus-like model was used to suggest that such phenomenon indicate H-tunneling form an ideal donor-acceptor distance and well tuned reorganization of the reaction coordinate throughout the experimental temperature range^17,18. The current simulation indicates that the effective transition state for this reaction is indeed temperature independent, and critically identify the atomic and molecular dynamics that constitute the reorganization term in the Marcus-like model used in ref 2. This motion of the protein toward the transition state and the electronic and geometrical details of that state are of critical importance in inhibitors and drug design²⁰. Moreover, while we did not calculated rates or KIEs, the calculated transition state geometry is relevant to small curvature tunneling (SCT) and the PMF landscape close to the transition state is relevant to large curvature tunneling (LCT).²¹ In the context of the current work, it is of critical importance that these features of our PMFs are temperature independent, since this dictates temperature independent KIEs regardless of the method used to calculate reaction rates or KIEs

Consequently, we believe that the current study may enhance rational design of potent and specific inhibitors as leads toward new antibiotic and chemotherapeutic drugs.