Modelling Risk of Cardio-Respiratory Instability as a Heterogeneous Process

Abstract

Cardio-respiratory instability (CRI) occurs frequently in acutely ill. If not identified and treated early, it leads to significant morbidity and mortality. Current practice primarily relies on vigilance of the clinical personnel for early recognition of CRI. Given limited monitoring resources available in critical care environment, it can be suboptimal. Thus, an “Early Warning Scoring” mechanism is desirable to alert medical team when a patient is approaching instability. It is widely recognized that critically ill may show subtle changes prior to the onset of CRI, but it is not well known how their risk evolves before the onset. Using large amounts of physiological data routinely gathered from continuous noninvasive monitoring of Step-Down Unit patients, we demonstrate a data-driven approach that: (1) Characterizes patient’s individual CRI risk process; (2) Identifies groups of patients that progress along similar risk evolution trajectories; (3) Utilizes grouping information to help forecast the emergence of CRI.

Introduction

Cardio-respiratory instability (CRI) is commonly observed in critically ill patients. If not caught early, CRI may escalate and require costly interventions and result in poor outcomes¹. In current practice, prompt recognition of CRI often heavily relies on the vigilance and experience of the clinical staff ², which presents a challenge especially in environments where case load is high and experienced staff is in shortage³. The study by Hravnak et al.² shows that about 25% of the patients may develop at least one episode of CRI during their Step-Down Unit(SDU)stay, however, about 83% of CRI episodes occurred without being noticed, and among those that were actually recognized, the average latency of detection may be as long as 6.3 hours.

Given that a large amount of multi-parameter continuous vital sign measurements are readily available from existing bedside monitors commonly used in critical and post-operative care, it is not only desirable, but also possible to develop “Early Warning Scoring” (EWS) systems and incorporate them into the current monitoring process that is primarily driven by human judgment. In our previous work⁴, we developed such a scoring model to predict CRI. Similarly to other EWS frameworks, it can estimate with some accuracy “if” and “when” a patient might deteriorate, however, it offers little insight into “how rapidly” it could happen. Knowing the likely rate of crisis escalation in individual patients would be tremendously valuable for clinical resource allocation and it could substantially improve medical outcomes.

We propose a data-driven approach that builds upon physiologic monitoring data to discover phenotypes of CRI risk evolution during periods before its onset. It takes a “bottom-up” approach to paint a microscopic view of each individual patient’s risk process towards CRI by explicitly modeling its dynamics as well as the heterogeneity observed between the individuals. To estimate the instantaneous risk score, it uses a popular supervised classification approach. Temporal sequences of the estimated risk scores are then used to learn a finite mixture model of risk score trajectories that are approximated as third order polynomials. The mixture model groups the individual risk trajectories into a parsimonious number of equivalence classes: the risk trajectory groups. Patients who are grouped together share similar apparent dynamics of their risk evolution in the period preceding the onset of CRI, while the risk evolution patterns differ between distinct groups.

In the first part of the paper we describe the approach we take to model risk of CRI and its evolution, and how the individual risk trajectories are grouped into phenotypic equivalence classes. We then proceed to demonstrate how the ability to identify assignment of a patient to its most likely phenotype group could help forecast the onset of CRI, especially in patients whose risk escalation is rapid and who are therefore at the highest chance of being missed under the current critical care practice until their condition substantially deteriorates. We illustrate our proposed modeling methodology with empirical evaluation on real-world bed-side monitoring data collected in a Step-Down Unit (SDU) of a hospital that includes 532 annotated monitoring episodes that escalated to a real CRI episode, combined with 370 controls.

This work has relevance to some of the EWS literature. There are basically two categories of EWS. The first type is the triage EWS. Often computed just once, at the time of admission, triage risk scores are static and designed to communicate the patient’s long-term risk in general (such as e.g. mortality) without specifying a time horizon of the possible occurrence of any particular future adverse events. Example of a triage EWS is the well-known APACHE score⁵ or its newer alternatives that use advanced machine learning models⁶. Our work however is more closely related to the second type of EWS that is designed for continuous monitoring purposes. Rothman Index⁷ is an example. This index is computed from 26 variables extracted from the electronic heath record that include vital signs, nursing assessments, laboratory test results and cardiac rhythms, and it communicates the risk of mortality within the next 24 hours, among other outcomes. Rothman Index can be updated at regular intervals (most typically hourly) or when new information about the patient’s status becomes available. Though not part of its design, if sufficiently informative data is available, scores like Rothman Index could potentially be used to model trajectories of risk evolution. In that sense, our work can be thought of as a “meta-analysis” of a particular continuous updated bed-side monitoring score.

In the setting of continuously monitored patients, our modeling framework is similar to what Guiza et al.¹⁰ developed for Neuro-ICU patients to predict the Increased Intracranial Pressure (ICP) which is a risk factor for poor outcome. They built a single model to predict the ICP events to occur in 30 minutes based on dynamic features extracted from a 4-hour period of observation in a mixed cohort of positive and control patients. In our previous work⁴, we instead built 30 independent models to predict CRI at subsequent one-minute intervals starting 30 minutes before the hypothetical onset of the event. This makes it possible to reason about the temporal trends in CRI predictions using the data available at any given point in time, which laid the basis for our current investigation.

Our approach is also related to the concept of dynamic risk process. Wiens et al.¹¹ estimated daily risk of C.diff colonization in hospitalized patients through a classifier that contrasted positive patients (who eventually tested positive) and control patients (those who never tested positive, or have never been tested) using a large number of features extracted from electronic health records as inputs. They reported a time series of Area Under the Receiver Operating Characteristic Curve (AUC) scores within days before the C.diff events to characterize the temporal pattern of the overall model performance. We have explored a similar approach to modeling temporal patterns of model performance for CRI events in our previous work.⁴ In this paper, however, we take a step further to analyze the underlying longitudinal risk process for each event for each individual patient. This allows us to have a detailed view of the risk evolution trajectories beyond what can be obtained by using the cross-sectional aggregated temporal AUC scores.

Methods

Data

Non-invasive continuous vital signals were collected from bedside monitors for patients in a 24 bed surgical/medical trauma Step-Down Units in a large urban teaching hospital during a three month period. Heart rate (HR), respiratory rate (RR) and peripheral oxygen saturation (SpO₂) were recorded at frequency of 1/20 Hz (3 readings per minute), blood pressures measurement (SysBP, DiaBP) were recorded intermittently with the minimum frequency of once every 2 hours.

Identification of CRI events

CRI events often occur in patients who show obviously abnormal vital signs for an extended period of time, the onset of CRI may signify the switch of patient’s state from being relatively “stable” to “unstable” and thus require clinical intervention. In order to identify real CRI events, and separate them from clinically irrelevant artifact often present in bed-side monitoring data, we first identify vital sign events (VSEs) which are the individual instances of any of the vital signs exceeding a predefined threshold⁸. We then apply temporal persistence criterias to filter out VSEs that last less than 3 minutes and/or the duty cycle of the observed exceedance is lower than 80%. Guided by the CRI event annotation protocol⁹, a committee of 6 clinical experts adjudicated the resultant sets of events in order to discriminate true CRI events from the artifacts. The artifact events refer to the events manifesting in data that have no relevance to patient’s physiological state, such as side effects of body movement, monitoring hardware or software malfunctions, etc. We only used the events adjudicated as true CRI in our analysis described below.

Inclusion and exclusion criteria

We have included all patients with least one CRI episode during their SDU stay in our analysis. If one patient had multiple events, all could be included, with the exception of the events that occurred within one hour of admission (for the first CRI event of a given patient) or if they occurred within one hour after the ending of a prior event (for subsequent CRI events recorded during the particular hospital stay). Since the goal of our work is to model the patient’s risk of progression towards a CRI from their currently stable state, these data filtering criteria ensure that the pre-event periods are indeed “event free” and that the patients during these time periods can be considered clinically stable.

The patients who have never experienced any CRI during their stay became our control group. For them, we identified hypothetical event onset timestamps during their first 6 hours of the SDU stay. The timestamps were spaced evenly 45 minutes apart unless there were no sufficient data available. To be more conservative about our control set, we opted to use only the data from the initial periods of SDU stay, since most patients tend to stabilize further as their stay at SDU extends.

Feature extraction

In order to analyze the dynamics of the risk processes, for each event, either positive CRI or control, we identified 30 reference timestamps, equally spaced at 1-minute intervals ending at the onset and starting up to 30 minutes before the CRI onset time. Together with the onset time (lag=0), each patient/event combination had 31 sets of observations at those subsequent timestamps, or less if no sufficient data was available. For each observation, a set of numerical features was derived from the vital signs during the time windows of 5, 10, and 15 minutes, ending at the particular timestamp. Simple statistical features of vital sign time-series were derived separately for each vital (HR, RR, SpO₂, SysBP, DiaBP), including mean, variance, min, max, range, linear slope, and fraction of valid readings, for each of the three window-width settings. This resulted in a total of 105 (3 window sizes × 5 vitals × 7 statistics) features for each observation (i.e. a patient/event/timestamp combination). Fig. 1 illustrates the feature extraction process.

Figure 1.

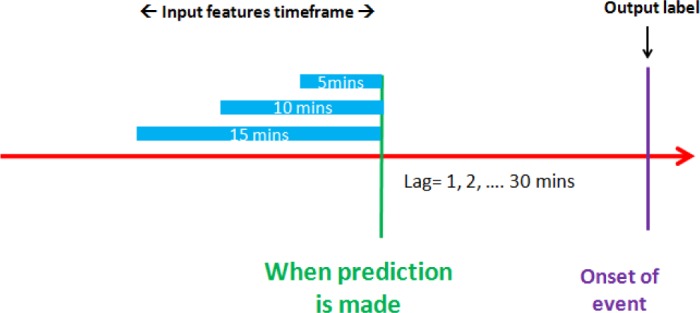
Feature extraction framework.

Modeling the risk process of as related to an individual event

We derived the risk process for each patient/event combination using a supervised machine-learning framework. We first constructed a training set of observations from positive and control data described above, with each observation represented by an array of 105 features derived from the interval of 15 minutes immediately preceding the onset of the events (i.e. lag=0), either true CRI or a control non-event, and we assigned a binary label as either positive or negative, accordingly to the output dimension of each such data point. We then trained a random forest¹² classification model from this data. We chose the random forest approach for illustrative purposes only. It is likely other popular classification models could be used in its stead with comparable success. Our choice was partially motivated by positive personal experience with this type of classifier in various application domains and due to the ability of the particular implementation used to gracefully handle missing data.

The trained random forest model was then used to score the data observed during periods preceding the onset of CRI or control non-events, separately and independently for each of the 30 reference timestamps, and for each of the patient/event combination from a held out data set that was not used to train the classifier to mitigate the risk of over-fitting.

The predictions made by the trained classifier on the held-out data served as the estimated risk scores. Their values range from 0.0 to 1.0, with the higher values reflective of a greater similarity of the currently observed vital signs features to those of patients going into an episode of CRI, and conversely, lower values suggest resemblance to the non-events obtained from control patients. Computing these scores over time at one-minute intervals, we obtained time series of scores that can be used to reflect the risk process as it is leading towards the event of interest.

We conducted our experiments using a 10-fold cross validation protocol, where the complete set of patients was split into 10 disjoint subsets. In each of 10 iterations, one of these subsets was used as a test set and the concatenation of the remaining nine subsets as the training sets. We split the data in a particular way to make sure that (1) the same patient’s data would belong to either training or a test set, but never to both in the same cross-validation iteration; (2) the proportion of positive and negative observations stayed relatively similar across all cross-validation iterations.

Group models of risk processes

We then analyzed the collection of the individual risk processes derived in the previous step, using the Group Based Modeling (GBM) approach¹³. In this approach, temporal patterns of patients’ risk processes are modeled as a mixture of polynomial functions with timestamps as the covariates. For a given risk trajectory of length T, assuming K groups, and the likelihood function of the trajectory is provided as follows:

$${\displaystyle \sum _{i=1}^K{\pi }_i}{\displaystyle \prod _{j=1}^T{P}_i}\left(Y_j|X_j\right)$$

in which π_i and P_i is the prior probability and probability function respectively for group indexed by i. Y_j is the response variable value at timestamp indexed at j, in our case it is the estimated risk score from random forest classifier; X_j is the covariate, in our case it is the timestamp value (i.e X_j = j)

Given the assumed number of distinct groups of risk trajectories (K) and the chosen order of the polynomials, the model estimates smooth trajectories for each of the groups characterized by the shape of the polynomial functions. The probability function form is determined by the response variable, in our case, since the response variable is a risk score bounded between 0 and 1, we used the truncated normal distribution. The model also estimates the prior distribution of the group membership across modeled data. The model parameters are inferred using Maximum Likelihood method through a numerical optimization procedure. We used the SAS procedure “traj” described in this paper¹⁴ and available from this website¹⁵.

After the GBM model is trained, posterior group membership for a currently observed risk process trajectory of an individual can be computed on-the-fly. Knowing the likely membership of a patient to one of the previously identified risk trajectory classes, we can inform the medical personnel of the likely near-term evolution of this patient’s status towards a possible CRI episode. The posterior membership is computed as follows:

$$P\left(\mathit{\text{group}}=i|Y,X\right)=\frac{{\widehat{\mathrm{\pi }}}_i{\displaystyle \prod _{j=1}^T{\widehat{P}}_i}\left(Y_j|X_j\right)}{{\displaystyle \sum _{i=1}^K{\widehat{\mathrm{\pi }}}_i}{\displaystyle \prod _{j=1}^T{\widehat{P}}_i}\left(Y_j|X_j\right)}$$

Prediction algorithm

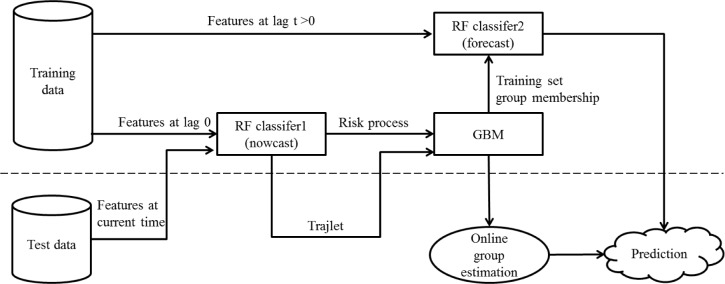
We used the trained group model above as a part of the prediction algorithm designed to estimate the expected patient’s risk status t minutes in the future from now. In order to study the utility of the risk process grouping information for forecasting CRI, we set up two alternative protocols that took the grouping information into consideration.

In the first of these protocols, the feature set of a random forest classifier included the previously described 105 statistical features of the vital signs, but also the maximum posterior group membership indicator as an additional discrete feature. In the training phase, group membership is obtained from the fully observed individual risk process (i.e. “now casting” trajectories), while in test phase it is estimated from an online prediction of the group membership based on the currently observed vital sign features and the resulting estimated risk scores. We call these current snippets of risk score time series “trajlets” since they are smallish segments of a longer risk trajectory.

The second risk-process-group aware protocol also used the current 105 statistical vital sign features, but each risk trajectory class was treated with a separate random forest risk estimation model trained using only the data of patients who have been assigned to the particular group. This was equivalent to enforcing that each decision tree in the random forest predictor used the group label as the root node feature, while the former approach allowed the grouping information to be leveraged anywhere in the decision tree hierarchies.

As a baseline, we included the third protocol that did not use estimated groupings to forecast CRI at all. It however used the 105 time series features only, consistently with what we have been doing in our previous work⁴.

In testing, the current patient’s data is processed using the trained risk score estimation models to obtain a “trajlet”: a short time-series of estimated risk scores. The trajlet is then processed by the trained GBM model to predict the risk process group category this trajlet most likely belongs to. The group information is then combined with the 105 features extracted to make a prediction. In the third, baseline protocol, the prediction is simply obtained by feeding the 105 features together with the group information into the single trained random forecast classifier. The second protocol follows that but including predicted trajectory membership information as the additional input feature. In the third protocol, since separate models are built for each group, we only make the prediction for the most likely group assignment, and to that we use the model trained for that group and the 105 statistical features.

We empirically evaluated performance of those algorithms at predicting CRI to set on in 20 minutes. We used AUC as the performance metric. Figure 2 depicts the information flow for the first and the second protocol.

Figure 2.

Information flow for the first and second protocol used to forecast CRI.

Results

Data for experiments

Subject to the inclusion/exclusion criteria described above, we included 158 positive patients and 71 control patients in our analysis, from which 532 positive events and 370 non-events were identified. The average number of events is 3.4 for each positive patient (CRI) and 5.2 for each control patient (non-events). For each event, 31 observations were generated at timestamps of 0, 1, 2,… and up to 30 minutes before the CRI onset time. This amounted to 25,983 observations. Demographic information of the positive and negative cohorts is presented in Table 1. The right hand side of the table lists the prevalence of admission diagnosis category and medical history conditions deemed to have possible relevance to CRI occurrences. As expected, control patients had significantly shorter lengths of SDU stay than the target group; however they did not reveal significant differences in any other observed characteristic.

Table 1.

Patient demographics and CRI related admission diagnosis categories and medical history conditions.

	Pos itive	Control	p-value		Positive	Control	p-value
Patients				Admission Diagnosis Categories
Total	158	71		Circulatory Digestive	28	23	0.105
% male	55%	61%	0.564	Digestive	26		0.477
age (mean,years)	60.35	55.36	0.079	Injury	96		0.754
Charlson Deyo Index(mean)	0.98	0.83	0.406	Medical History Conditions
SDU length of stay (mean,hours)	127.02	66.18	<0.001	Myocardial Infarction (MI)	17	2	0.067
Monitoring				Congestive Heart Failure (CHF)	16	6	0.811
Total monitoring hours	3,930	17,532		Chronic Pulmonary Disease (CPD)	31	8	0.132
Mean monitoring hours	111	55	<0.001	Cerebral Vascular Disease (CVD)	13	7	0.801

Estimating risk process trajectories and risk process grouping

A total of 902 individual risk evolution sequences (532 positives and 370 negatives) were generated using the supervised learning method described above. We present here the result from a 10-fold cross validation experiment in which the risk estimates are pooled from 10 disjoint test sets in the 10-fold setup. A finite mixture model of truncated normal distribution was used with the GBM approach. We chose to use K=5 groups, each modeled with a polynomial of third order.

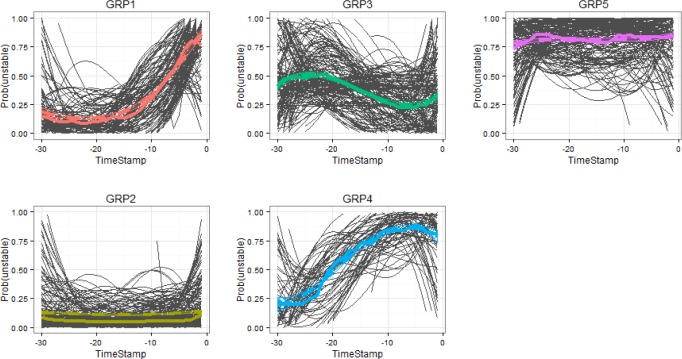
Figure 3 presents the 5 groups of risk process trajectories learned from our data. Each summarizes CRI risk progression for the cross validated set of patients during 30 minutes before the onset of their CRI event (or nonevent for the controls). Solid lines in Figure 3 show the representative risk process trajectories for each group aggregated over the individual risk trajectories underlying the particular group, where the group assignment is based on their maximum posterior probability of group membership given full length of trajectories. Dotted lines depict means and confidence intervals estimated from the trajectory group models. On the horizontal axis, timestamp 0 indicates the onset of CRI. Vertical axis scale shows the risk scores. The graph also includes group size information (with count on left and proportion in parenthesis) obtained from the GBM model. Table 2 presents the distribution of labels and types of CRI events (stratified by the type of vital sign that was first to cross the control limits) for each group. Figure 4 shows the most likely trajectories for each of the group based risk process models, overlaid with the corresponding individual risk processes, each smoothed with third order polynomials.

Figure 3.

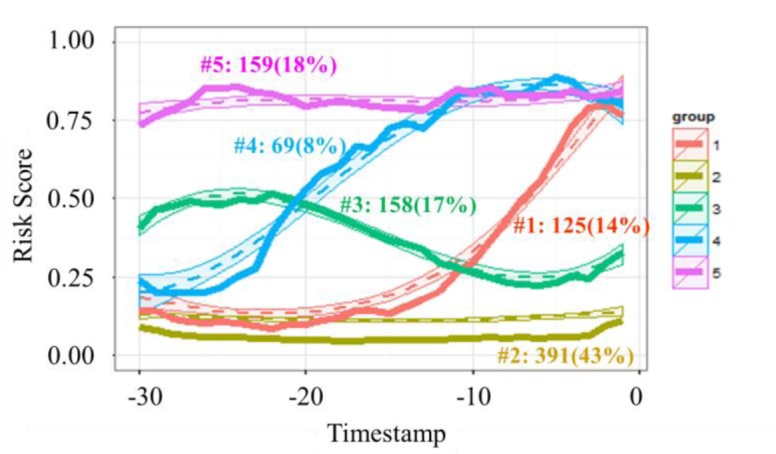
Identified groups of risk processes.

Table 2.

Profiles of the identified risk process groups.

Group ID	Type	Lead time	% of Pos	BP	HR	RR	SpO2	Pos(%)	Neg(%)	Total	TP	TN
		(A)	(B)								(C)	(D)
1	late onset	~ 10 min	19%	2	9	38	53	102(82%)	23(18%)	125	102
2	persistently low risk			30	18	18	59	125(32%)	266(68%)	391		266
3	transient			20	15	28	31	94(59%)	64(41%)	158	94
4	early onset	~25 min	12%	0	2	36	24	62(90%)	7(10%)	69	62
5	persistently high risk	>30 min	28%	4	8	104	33	149(94%)	10(6%)	159	149
Totals			59%	56	52	224	200	532	370	902	407	266

Figure 4.

Group trajectories overlaid with smoothed individual risk process trajectories participating in these groups.

As can be seen, those trajectories reveal five distinct CRI risk trends. The largest group is group 2 (trajectory plotted in yellow, “persistently low risk”), including 43% of the test cases with about 2/3 of them coming from control patients. The characteristic of this group is a flat trend of low risk over time. As can be noticed in Figure 4, individual patient trajectories that belong to this group also include some positive cases with very late (that is, rapid) onset of CRI. Most of the time these patients look stable, but then they suddenly develop CRI without leaving much lead time for the early warning system to recognize the change. With these exceptions aside, patients who could be classified as members of this group are not likely to require medical attention in the near future.

Group 5 (pink, “persistently high risk”) includes about 18% of all cases, with about 94% of them associated with positive events. This group is characterized by a persistently high risk of CRI. These patients have been in poor condition before our observation started and they remain in it throughout. Medical personnel is likely already aware of their need for close scrutiny, and early warnings are of little use in these cases.

Group 1 (red, “late onset”) and group 4 (blue, “early onset”) contain mostly positives cases (82% positives for group 1 and 90% for group 4). Different from the other groups, they exhibit gradually increasing trends of risk, though at different lead times of the onset of the patient’s status change. Group 4 picks up the risk escalation trend as early as about 25 minutes before the CRI event, while group 1’s trend looks very similar to that of group 2 (which has a negative majority) until about 10 minutes before CRI onset. These groups are very interesting from the clinical perspective. If we could establish for a patient with the apparently low risk at the moment, that their likelihood of becoming unstable would escalate in the near term, and in addition to that we could establish with some certainty how rapid will the escalation be, this would provide medical personnel with very valuable information about the outlook of all individuals under their care so that they could prepare, prioritize, and take preemptive actions if possible, to mitigate the consequences of the imminent health status deteriorations.

Lastly, group 3 (green, “transient”) is comprised of about equal number of positive and negative cases, and it is the hardest to classify apart from others. Unless a patient can be confidently assigned to the “persistently low risk” group, they will require close monitoring, so do patients belonging to this particular group.

These results show potential utility of the proposed approach to modeling evolution of risk in managing critical care resource allocation. It also has a potential to favorably impact patient outcomes by characterizing the likely rate of escalation of the imminent crisis in a particular patient, prompting medical personnel to act with a desired urgency.

In column (B) of Table 2, we show the fraction of all positive cases can be reliably identified at various lead times as members of groups 1, 4 or 5. The combined recall of patients who will eventually become unstable across these three groups is about 59% with a specificity of 92% (false positive rate of 8%). In columns (C) and (D) of Table 2, we show the true positive (TP) and true negative (TN) counts that would be produced if we were to accurately predict group membership which can be used to predict the outcome (CRI vs. non-event) using the class majority vote rule. The recall rate of such system would be 77% at a specificity of 72% (false positive rate of 28%).

Considering the distribution of data and results according to which vital sign was first exceeded during an episode of CRI, we notice a relatively small portion of BP and HR events, and when they occur they often seem to be hard to separate from negative cases. About half of RR events belong to the “persistently high risk” group, while 17% of them belong to the “late onset” group and about 16% to the “early onset” group. For SpO₂ events, 30% are mixed with negatives in the “persistently low risk” group but they are most likely the cases with the late sudden onset. Additional 27% of SpO₂ events group with “late onset” class and 12% with the “early onset” class, while 17% belong to the “persistently high risk” group.

Forecasting future occurrences of instability

In this section, we report preliminary experimental results of an attempt to use risk trajectory group estimation to support forecasting of CRI. So in this case, we only observe a portion of the full risk trajectory (a “trajlet”), from which we can make online determination of the group membership. Then, we can leverage the predicted grouping to predict expected patient’s CRI risk changes in the near time.

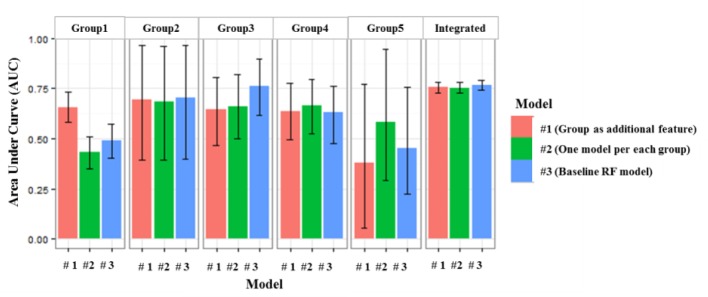
In this experiment, we set the current time to 20 minutes before the event. This leaves us with the 10 initial minutes of observations to form a “trajlet” that becomes the input for group classification algorithm. This can be done on-the-fly using the group model learned from training data. In Figure 5, AUC scores of three risk estimation models described above split by the estimated group label. Model #1 (red) is the single random forest model with an additional discrete feature encoding predicted group membership; Model #2 (green) uses five independent random forest models, one for each risk trajectory group, and Model #3 (blue) is the baseline single random forest model with no group information incorporated. In Figure 6, we present ROC curves for each of these models, separately for each CRI risk evolution trajectory group.

Figure 5.

AUC scores compared among three models for each group as well as for all 5 groups combined, showing 95% empirical bootstrap confidence intervals.

Figure 6.

ROCs for each group and each model.

We observe some divergence of performance between the baseline model and group based models, primarily in the context of group 1. This is the “late onset” group. It is interesting to see that group classification information available at 20 minutes before the onset of CRI, when the current risk score of group 1 does not differ much from the risk score of the “persistently low risk” group 2, is helping boost forecasting ability about the eventual outcome when compared to the model that does not use group assignment information. This suggests that group information carries some predictive value which is not captured effectively by the numeric features used by the baseline random forest model. This opens possibility for effective use of group information to inform clinical personnel of imminent health crises even before the moment when momentary online risk scores begin to escalate (20 minutes before the onset vs. approximately 10 minutes for group 1).

For group 2 (“persistently low risk”), all three models show very similar performance. This is not surprising since these patients often show consistency throughout the period of observation and their risk trends can be easily captured by random forest classifier even without using the group information. In case of group 4 (“early onset”), the risk trend is about to pick up around the time of making the prediction (20 minutes before the event), and it seems that the baseline model was already able to capture the information needed for forecasting, hence group information also does not help much here. It should be noted that it should be possible to repeat the interesting result discussed in the context of group 1 above, if we moved the time of observation further back. Group 5 (“persistently high risk”) is primarily composed of positive cases, with very limited representation of negatives, and the lack of class balance makes ROC characteristics look unimpressive for either of the three considered models. It is also noted that the integrated performance (five groups combined) compared across three models shows no significant difference. This is understandable since this result is driven by the differences in performance between groups and the relative group sizes. In our case, groups 2, 3 and 4 where performance variation is small, account for over 80% of the cases in data. Given the integrated performance that is similar across the three models, at the false positive rate of 30%, sensitivity is 69%, positive predictive value is 76% and specificity is 70%.

Conclusion

We described a framework designed to model evolution of risk as a heterogeneous process with the application to tracking emergence of Cardio-Respiratory Instability using continuous vital signal available from bedside monitors. We have evaluated this framework empirically using representative cohort of step-down unit patients. The presented framework is intuitive and it allows us to model explicitly the dynamics of risk changes for individual episode for individual patient. This new capability has a potentially useful clinical application in helping to understand how the patients deteriorate and not only if they will, and if so, when.

Using a group based modeling approach we discovered distinct types of risk evolution processes. Some patients exhibit persistently high-risk status, some show persistently low risk status, and some fit models that follow particular trajectories of risk escalation. The former type of patients either already receive attention of the clinical personnel, or they are not in urgent need to receive it, but patients who could be reliably identified as one of those who are on a rapid trajectory leading towards a crisis, could be flagged by the presented method for immediate attention of clinical personnel. These quickly escalating instances are particularly hard to capture by the current monitoring protocols.

Our framework establishes a linkage between the risk process and the predictive performance of the models. The distinct types of trend patterns suggest various degrees of predictability in terms of lead time and reliability. Assuming the trend patterns reflect the true underlying risk progress of the patient group, then the predictability revealed from the grouping represents an upper bound of the performance that an early warning score algorithm may achieve. It helps explaining variations of performance at various lead times and among different cohorts drawn from the population. The common practice of reporting an aggregated model performance for entire population at a fixed point of time may mask the rich underlying dynamics and heterogeneity across the individual patients and their phenotypic equivalence classes that could be informative and clinically relevant. In this aspect, our framework is general and it can be directly adapted to any other modeling scenario involving temporal escalations or de-escalations towards or away from adverse or favorable events in healthcare and beyond.

In the context of clinical care, our method reside in between of the population-level analysis where a universal model is built for the whole population of interest, and a personalized approach where individual characteristics of the individual patient are the only source of predictive information. Both these approaches have their limitations, most prominently the risk of over-generalization in the population-level modeling case, and the risk of over-specification and the perils of low data supply in the personalized modeling case. Our framework lies in between of those two extremes allowing for heterogeneity between the individuals but also providing data support to make reliable predictions possible by drawing the required evidence from the patient’s group peers.

Additional utility of our work is in providing explanatory capability by visualizing current and expected future risk trajectory and updating it dynamically at frequent intervals, in order to provide salient and timely information to the medical personnel in an intuitive and understandable fashion.