Dynamic changes of RNA-sequencing expression for precision medicine: N-of-1-pathways Mahalanobis distance within pathways of single subjects predicts breast cancer survival

Abstract

Motivation: The conventional approach to personalized medicine relies on molecular data analytics across multiple patients. The path to precision medicine lies with molecular data analytics that can discover interpretable single-subject signals (N-of-1). We developed a global framework, N-of-1-pathways, for a mechanistic-anchored approach to single-subject gene expression data analysis. We previously employed a metric that could prioritize the statistical significance of a deregulated pathway in single subjects, however, it lacked in quantitative interpretability (e.g. the equivalent to a gene expression fold-change).

Results: In this study, we extend our previous approach with the application of statistical Mahalanobis distance (MD) to quantify personal pathway-level deregulation. We demonstrate that this approach, N-of-1-pathways Paired Samples MD (N-OF-1-PATHWAYS-MD), detects deregulated pathways (empirical simulations), while not inflating false-positive rate using a study with biological replicates. Finally, we establish that N-OF-1-PATHWAYS-MD scores are, biologically significant, clinically relevant and are predictive of breast cancer survival (P < 0.05, n = 80 invasive carcinoma; TCGA RNA-sequences).

Conclusion: N-of-1-pathways MD provides a practical approach towards precision medicine. The method generates the magnitude and the biological significance of personal deregulated pathways results derived solely from the patient’s transcriptome. These pathways offer the opportunities for deriving clinically actionable decisions that have the potential to complement the clinical interpretability of personal polymorphisms obtained from DNA acquired or inherited polymorphisms and mutations. In addition, it offers an opportunity for applicability to diseases in which DNA changes may not be relevant, and thus expand the ‘interpretable ‘omics’ of single subjects (e.g. personalome).

Availability and implementation: http://www.lussierlab.net/publications/N-of-1-pathways.

Contact: yves@email.arizona.edu or piegorsch@math.arizona.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Through the incorporation of molecular data into the patient care process, personalized medicine is drastically changing the healthcare landscape; however, truly precise medicine has not been obtained. Since completion of the human genome in 2003, the inclusion of molecular data in medicine has improved our ability to make accurate diagnoses, prognoses and treatment plans. Relying on large cohorts limits the application of many of these techniques, however. While inherited or acquired DNA polymorphisms provide powerful insight in the pathogenicity of many Mendelian diseases and in cancer, a single-subject interpretation of the transcriptome may provide insight and could be deployed in diseases incurred by other insults than DNA damage or inheritable defects. Conventional transcriptome analyses rely on multiple patient data that can mask idiosyncratic signals from a single patient, and these approaches may lead to treatments only effective for the ‘average’ patient. Gene-level expression signatures found in cross patient studies do not adequately inform treatment plans for all cancer patients; therefore, there is a need for better methods to understand the biological underpinning at the single patient level.

In response to these issues, we developed a global computational framework: N-of-1-pathways. N-of-1-pathways is founded upon three principles: (1) single patient data represent the entire statistical universe, (2) significance and interpretation are derived from genesets (pathways), and (3) pathway level information is used to answer questions of clinical importance. Principle 1 allows for detection of individual signals that traditional cohort-level studies can overlook. Principle 2 anchors the results in mechanism and this affords dimension reduction and interpretation. Principle 3 provides quantitative and qualitative measures to address questions relating to patient care. The first application of the N-of-1-pathways framework, the N-of-1-pathways-Wilcoxon method (Gardeux et al., 2014a), successfully predicted lung adenocarcinoma patient outcomes using paired (normal and tumor) RNA-Seq samples from a single subject. A follow-up study established it could accurately identify experimentally deregulated pathway in ovarian and breast cancer cell lines (Gardeux et al., 2014b). While the N-of-1-pathways-Wilcoxon identified deregulated pathways with a statistical relevant, it did not quantify the magnitude of deregulation.

In this study, we extend and refine the N-of-1-pathways framework by developing a novel application of Mahalanobis Distance (MD) to create a ‘clinical relevance metric,’ (CRM) providing insight on the magnitude of the deregulation in addition to the biological significance. The design of N-of-1-pathways MD eliminates the former’s reliance on ranks (e.g. Wilcoxon test), while producing a measure of effect that is interpretable on the biological scale. We employ breast cancer gene expression data to show increased sensitivity while not increasing false positives in comparison to the Wilcoxon approach. Finally, we utilize the CRM to predict breast cancer survival.

2 Methods

2.1 Datasets and preprocessing

We used two datasets pertaining to breast cancer. Dataset I (GEO, GSE51403; (Liu et al., 2014) allow us to assess false positive and negative rate. Dataset II was used in a validation study (Table 1). RNA-Seq counts of Dataset II were adjusted for ambiguous read assignment using the RNA-Seq by Expectation Maximization (RSEM) software (Gautier et al., 2004; Li and Dewey, 2011). All measurements for both datasets were taken as base-2 logarithms (log₂) in the course of normalization. If several probes were mapped to the same HGNC gene name, the maximum expression value was retained as the gene expression value and considered for further analysis (Povey et al., 2001).

Table 1.

Datasets

Dataset Description	I Biological replicate study	II Validation Study
Aim	1. Assess false positive rate	1. Predict breast cancer survival
	2. Assess false negative rate
Authors	Liu Y, Zhou J, White KP	NA
Source	GEO, GSE51403	TCGA_BRCA
Disease	Breast Adenocarcinoma	Breast carcinoma
Data Download date	Jan 2014	Dec 2014
Data type	RNA-Seq	RNA-Seq
Genomic platform	Illumina HiSeq 2000	Illumina RNA-Seq V.2
Genes measured	22 336	20 501
Samples	MCF-7 Cell line	80 Normal/tumora
Age median (range)	NA	54 (30–90)
Disease stage I	NA	17 (21.3%)
Disease stage II	NA	40 (50.0%)
Disease stage III	NA	20 (25.0%)
Disease stage IV	NA	2 (1.25%)

^aThere were 112 original paired samples, reduced to 80 after applying the exclusion criteria (Section 2.2).

2.2 TCGA_BRCA patient exclusion criteria

Out of the 112 breast cancer patients with paired normal/tumor samples in TCGA_BRCA, 80 were considered for the validation analysis in this study. Patients were excluded from the study (i) who died of noncancer causes in the first 12 months (defined as ‘tumor-free’ or ‘unknown tumor recurrence status’), (ii) who are living tumor-free with a clinical follow-up less than 12 months (not enough time to assess recurrence risk), and (iii) if male (only 1 such occurrence).

2.3 Geneset definitions and Gene Ontology annotations of biological processes (GO-BP)

We aggregated genes into genesets (pathway) using the Gene Ontology Biological Process, GO-BP (Ashburner et al., 2000; Gene Ontology Consortium, 2010). Hierarchical GO terms were retrieved using the org.Hs.eg.db package of Bioconductor (Gentleman et al., 2004) available for R (R Development Core Team, 2011) statistical software. We used the org.Hs.egGO2ALLEGS database (downloaded on 03/15/2013), which contains a list of genes annotated to that GO term (geneset) along with all of its child nodes according the hierarchical ontology structure.

2.4 N-of-1-pathways Mahalanobis distance: producing a CRM

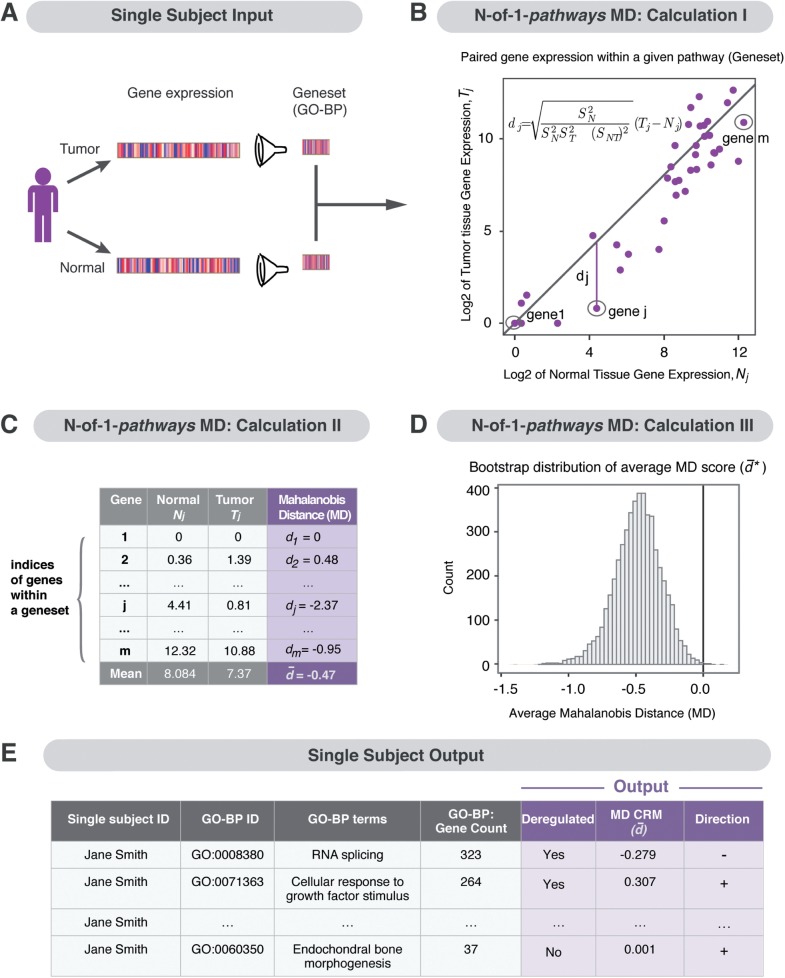
N-of-1-pathways MD method consists of three core steps from input to output that were performed. Figure 1 illustrates an overview of the method.

Fig. 1.

Method overview of N-of-1-pathways Mahalanobis Distance. (A) The input is represented by the gene expression of single patient paired samples (e.g. tumor versus normal tissue) filtered into a priori defined genesets (e.g. Gene Ontology Biological Processes: GO-BP pathways). (B) Calculation I is visualized by the bivariate relationship between normal and tumor gene expression values for a given geneset (e.g. GO-BP pathway). The vertical, signed Mahalanobis distance (MD), dj, is computed from each jth point (gene) to the diagonal line representing equal expression. (C) Calculation II: The mean MD represents the pathway-level deregulation from normal to tumor expression where a negative value indicates down-regulation and a positive value represents up-regulation. The gene indices are randomly resampled and the ‘average MD score’ is recomputed via bootstrapping (Chernick, 2008) to determine pathways with strong evidence of deregulation. (D) Calculation III: The bootstrap distribution of ‘average MD scores’. (E) The process results in pathway-level quantification of deregulation, an approach to obtain a Clinically Relevant Metric

2.4.1 Geneset (pathway) definition

For any given geneset, the paired expression values were restricted to only the genes within the pathway (Fig. 1A). To afford meaningful biological interpretation, genesets with at least 15 and no more than 500 genes were used in this study.

2.4.2 Measure of deregulation and generation of the CRM

Pathway-level deregulation measurement is illustrated in Figure 1B. All calculations involve only the expression of genes within the pathway. Genes were indexed within a given pathway by j = 1,…,m and the log₂-transformed normal and tumor expression values were denoted as N_j and T_j, respectively. For each gene, we considered no differential expression as the case where T_j = N_j. As shown in Figure 1B, the diagonal line T_j = N_j provides a reference for calculation in quantifying differential gene expression. Then, for each jth gene we computed the signed MD (Mahalanobis, 1936), d_j, from the point (N_j, Tj) to the diagonal line T_j = N_j. This is based on the distance from the point (N_j, T_j) to the point on the diagonal line of equal expression, (N_j,N_j). Let the difference between the two points be the vector $\text{Δ}x$:

$$\text{Δ}x=\left(N_j,T_j\right)-\left(N_j,N_j\right)=\left(0,T_j-N_j\right).$$ (1)

Also let the bivariate sample’s variance-covariance matrix be:

$$\widehat{\Sigma }=\left(\begin{array}{cc}{S}_N^2& S_{NT}\\ S_{TN}& S_T^2\end{array}\right),$$ (2)

where S_N is the sample standard deviation of the N_js, S_T is the sample standard deviation of the T_js, and S_TN = S_NT is their sample covariance.

Now, denote the reciprocal of the variance–covariance matrix’s determinant as:

(3)

By definition, the squared, vertical, MD for gene j is the quadratic form

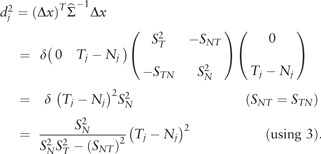(4)

Then, the signed distance is

(5)

The sign is taken to indicate the direction of deregulation: down- or up-regulated pathway. Note that when the signed distance is simple Euclidean distance it is a log₂ fold change. We opted to employ the MD, which from the derivation above is seen to be a form of adjusted distance that accounts for the variance–covariance structure of the paired samples.

Finally, after each d_j is determined, we computed the unweighted average of the distances, $\overline{d}$, to provide a geneset-level summary statistic of deregulation. This average is the CRM of pathway deregulation, the mean MD score:

$$\overline{d}={\displaystyle \sum }_{j=1}^m{d}_j/m.$$ (6) (CRM)

2.4.3 Assess certainty of the CRM via bootstrapping

To accumulate evidence that any observed difference is truly representative of differential geneset deregulation, a bootstrap distribution for $\overline{d}$ is calculated (Chernick, 2008). This is conducted by randomly sampling with replacement indices from the geneset under study and calculating a new, bootstrapped $\overline{d}*$. Figure 1C shows the measurements for a given pathway and indicates the gene indices for resampling. Figure 1D depicts a bootstrap distribution and marks the d = 0 reference line at which no deregulation occurs. Figure 1E represents an example of an MD score, $\overline{d}$, for each pathway, along with its pathway description and direction of deregulation.

Based on the bootstrap resample, we identify a pathway as deregulated if the bootstrap distribution of $\overline{d}*$ separates completely from d = 0. That is, if all its $\overline{d}*$s lie to a single side of the d = 0 reference line, either upregulated ($\hspace{0.5em}\overline{d}>0\hspace{0.5em}$) or down-regulated ($\overline{d}<0$). To set the number of bootstrap resamples, we imitated a technique often seen in multiple testing: we employed at least 1/$\propto$_J resamples, where $\propto$_J is a Sidak-adjusted $\propto$-level for comparing J pathways at a pointwise level of $\propto \hspace{0.5em}=0.01$. This is 1/$\propto$_J =1/(1– (1–$\propto$)^1/J) = 1/(1 – (0.99)^1/J). For a prototypical collection of, say, J = 5000 pathways, this gives 1/(1 – (.99)^1/J) > 497 496.3, so we operated with 500 000 bootstrap resamples. Using 500 000 bootstrap resamples, at least eight genes in the pathway are recommended as to not frequently resample the same finite possibilities (since $7^7<500\hspace{0.5em}000$).

2.5 Simulation study: assessing false-negative rate

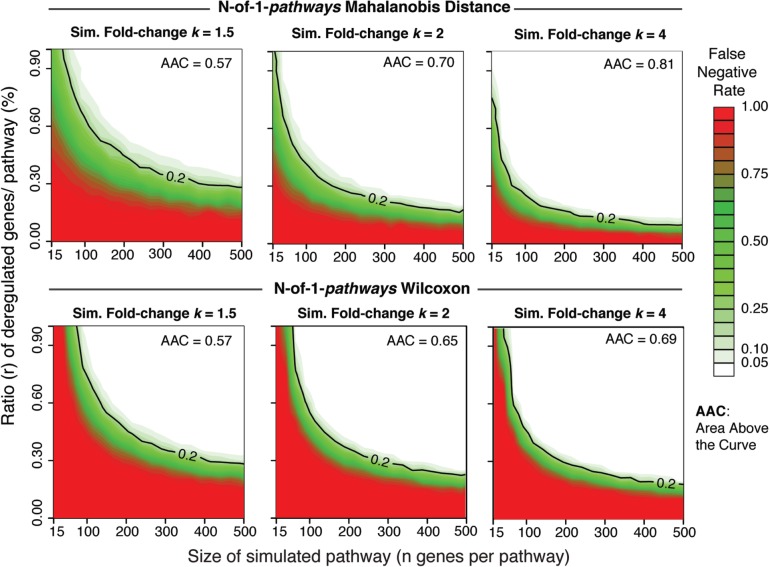
To assess false-negative rate of the N-of-1-pathways MD method, we performed a simulation study by creating synthetic genesets that contain a percentage of concordant (all up) deregulated genes using Dataset I (biological replicates of breast cancer cell lines). The intent is to simulate deregulated pathways as described in our previous work (Gardeux et al., 2014a) with some modifications. For each gene, we assumed a negative binomial distribution and estimated the mean and overdispersion parameters from the seven biological replicates via the method of moments. Under our parameterization, a negative overdispersion parameter indicates underdispersion for a gene, which is anticonservative. Thus when underdispersion occurs, we conservatively assumed that the variance equals the mean for that gene. For a fixed set of simulation settings (n = genes in pathway, r = ratio of deregulated genes in pathway, k = fold change), we produced two synthetic ‘normal’ transcriptomes (two realizations for each of the 22 336 genes measured). We then produced one artificially deregulated transcriptome by multiplying the gene mean by k. Then a geneset of size n genes was randomly selected with that genewise adjusted location parameter. We randomly indexed a subset of size r from that geneset to retrieve the artificially deregulated transcriptome. The remaining $n-r$ genes were selected from the second normal transcriptome. We combined these two genes to create a synthetic ‘tumor’ sample of size n with the correct amount of deregulation. We completed the synthetic pathway of paired gene expression by selecting the appropriate genes from the first normal transcriptome. At each combination of (n, k, r), N-of-1-pathways MD and Wilcoxon methods were executed 5000 times (implemented in R, using the University of Arizona Extremely LarGe Advanced TechnOlogy, ‘El Gato,’ computing system) (Fig. 2). For the Wilcoxon method, a pathway is found deregulated when the Bonferroni adjusted P < 0.01. The proportion of times the pathway is not detected as deregulated is the simulated false-negative error rate.

Fig. 2.

Simulation study reveals that N-of-1-pathways MD powerfully detects artificially deregulated pathways. Each point represents one size of a simulated pathway generated by randomly selecting n genes and a ratio r of the deregulated genes within the pathway (Table 1 Dataset I, Section 2.6). The ratio r is artificially increased by a k-fold change in a simulated pathway generated from biological replicates, (k = 1.5, 2, 4). We then applied separately the N-of-1-pathways-Wilcoxon (bottom) and N-of-1-pathways-MD (top) methods to identify whether the truly deregulated pathway is detected. We repeated the process 5000 times at each combination of (n, k, r) to estimate the false negative error rate (Wilcoxon P values were Bonferroni adjusted with a 1% threshold). AAC, area above the curve, quantifies the proportion of simulated pathway combinations with false negative error less than 0.20 (the black curve labeled 0.20 is the reference for this measure). Higher AAC indicates a greater number of scenarios with at least 80% power to detect deregulated pathways. N-of-1-pathways-MD outperforms N-of-1-pathways-Wilcoxon at every fold-change, requiring fewer genes in the pathway and a smaller ratio of deregulated genes. Notably, the simulated false positive rate (0.0% deregulated genes; rate along the horizontal axis) is smaller for MD than Wilcoxon, averaging 0.14 and 0.94%, respectively. This rate can also be interpreted as the simulated rate of discovery when two non-tumor samples are paired. Legend, Sim. = simulated, AAC = area above curve

2.6 Biological replication study: assessing false-positive rate

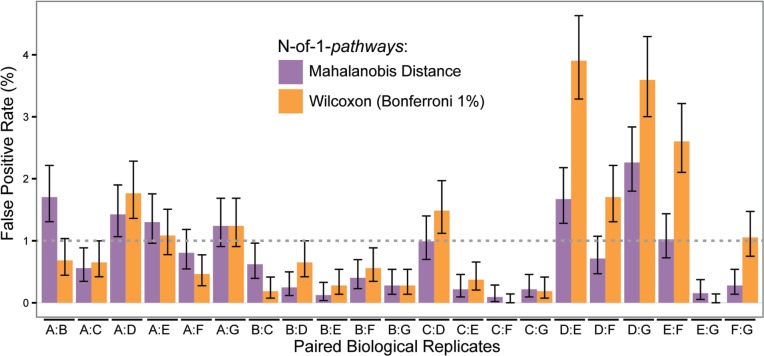
We assess the false-positive rate of the N-of-1-pathways MD method via the biological replication study. We paired biological replicates and identified GO-BP terms as deregulated using N-of-1-pathways methodology. Agresti-Coull confidence intervals (Brown et al., 2001) for the proportion of deregulated pathways found in each sample in Dataset I were computed using the binom package in R. If an interval had a lower bound less than 0, the lower bound was replaced with 0 (Fig. 3). R package ggplot2 was used for visualization (Wickham, 2009).

Fig. 3.

Evaluation of the false-positive rate of N-of-1-pathways MD compared to the Wilcoxon method. Pairs of biological replicates from breast cancer cell lines were used (Table 1 dataset III). 3228 GO-BP genesets were tested for each pair of biological replicates to find falsely deregulated pathways using both the N-of-1-pathways MD and Wilcoxon methods (Wilcoxon P values are Bonferroni adjusted and a 1% threshold is applied). Thin black lines are 95% pointwise Agresti-Coull intervals for the proportion of false positives; bar heights are the percentage of falsely identified deregulated pathways. Nof 1-pathways MD performs equally or better than Wilcoxon. Technical replicates showed similar results using GEO20194 (data not shown)

2.7 Principal component analysis of CRM

Principal component analysis (PCA) (Jolliffe, 2005) was executed on the N-of-1-pathways MD pathway scores using the prcomp function from the stats package in R. The PCA was performed using scores from GO-BP terms that were found deregulated in at least one of the 80 patients in Dataset II (validation study); 2130 GO-BP terms were selected.

2.8 Partitioning around medoids clustering of CRMs

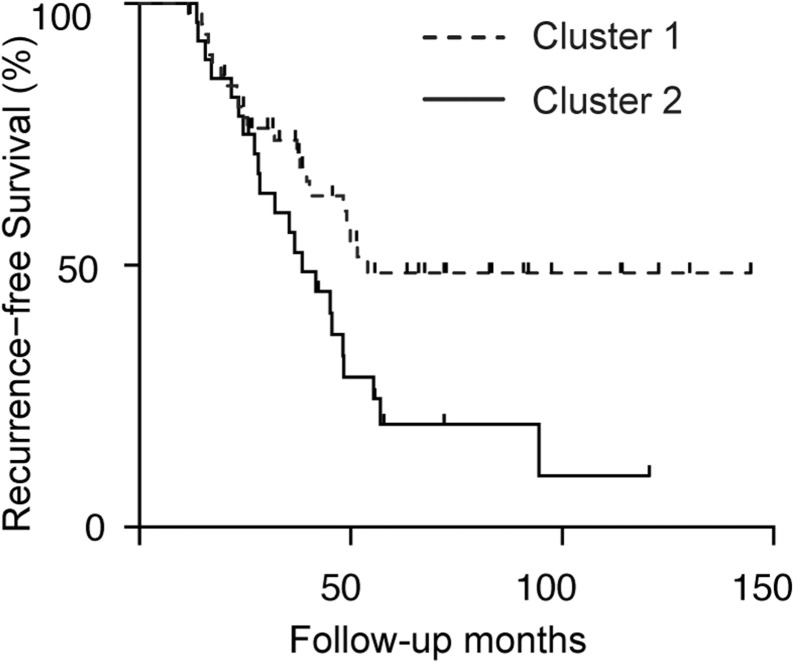
Unsupervised clustering (Witten and Frank, 2005) of pathway scores for the 2130 GO-BP terms found deregulated in at least one of the 80 breast cancer patients (Dataset II) was performed using the partitioning around medoids (PAM) method (Kaufman and Rousseeuw, 1990) (via the cluster package in R) (Fig. 4).

Fig. 4.

N-of-1-pathways MD GO-BP clinical importance metrics predict breast cancer patient survival. N-of-1-pathways MD was applied to n = 80 invasive breast carcinoma patients (TCGA_BRCA, RNA-seq, Table 1 dataset II) resulting in 3225 clinical importance metrics. Every patient has an N-of-1-pathways MD score for each of the identified deregulated pathways (2130 pathways identified in at least one patient) and we performed PCA and unsupervised clustering on these scores. As shown in the figure, unsupervised PAM clustering reveals distinct Kaplan–Meier survival curves (log-rank test P < 0.05). Additionally, the identified pathways can also be used to discover a fully specified classifier for good versus poor prognosis (Supplementary Table S5). Reducing dimensionality further, we constructed the clusters based on only the top 10 scored pathways and produced distinct survival curves (Supplementary Figure S7). When compared to gene expression, N-of-1-pathways performed similarly (Supplementary Figure S1). We found that pathway-level scores relate to pathologically determined stage (Wilcoxon P value between first principal component of MD Score = 0.02; data not shown), but did not identify receptor subtypes (ns; principal components 1–5 verified; data not shown)

2.9 Kaplan–Meier survival curve

Kaplan–Meier survival curves (Kleinbaum and Klein, 2005) were computed via GraphPad Prism V.6.02 software using the survival data associated with the breast cancer validation dataset (Dataset II); see Figure 4. PAM-derived clusters were used to distinguish the two survival curves (see Section 2.8).

2.10 Star plots of diametric extreme patients

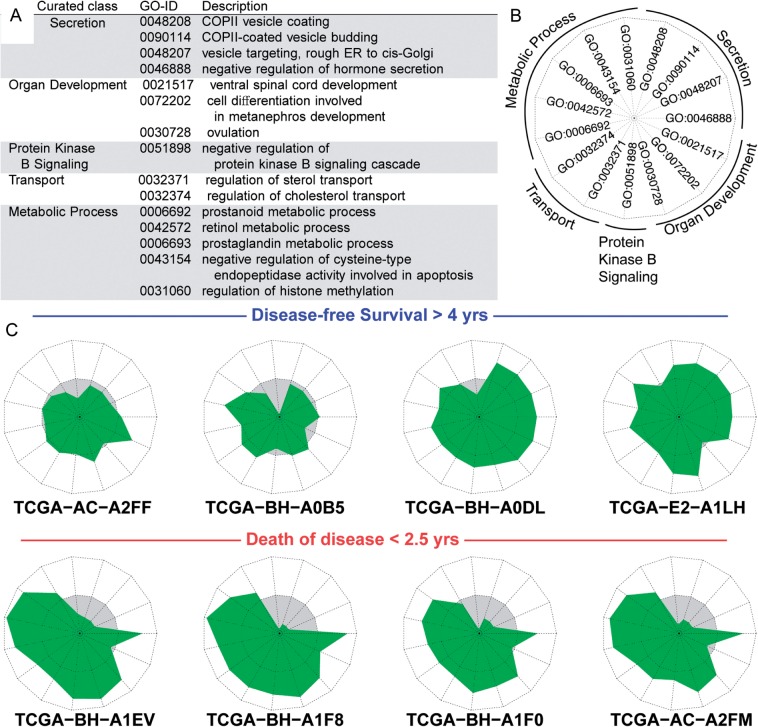
Star plots were computed in R using the stars function in the default graphics package (Fig. 5C). The stars plots display 15 pathways chosen to discriminate between the patients who are disease-free survival (DFS) longer than 4 years and the patients who suffer Death of Disease (DoD) in less than 2.5 years. The pathways were selected by retaining the top largest absolute two-sample t statistic for each GO-BP term. Once the pathways were chosen, each patient has an individual star plot where each edge represents a particular GO-BP MD CRM. In order to have a relevant representation of the star plot surface, a biologist manually curated the pathways to a representative GO-BP category as shown in Figure 5B.

Fig. 5.

N-of-1-pathways representation (star plot) of individual GO-BPs of diametric extreme patients. The top 15 most discriminating GO-BP terms were identified between the two groups of patients with diametric extreme phenotype (death of disease in less than 2.5 years, n = 5; at least 4 years of disease-free survival, n = 9; Section 2.10). (A) GO terms manually curated to interpretable categories. (B) The legend of the star plots, each edge corresponding to one GO term, each star reflects a single patient’s deregulation as measured by the MD CRM for each pathway. (C) A sample of eight patients’ star plots (four from each extreme). The white zone represents upregulated pathways (given the N-of-1-pathways direction of deregulation), while the grey zone stands for downregulation. The circle separating the gray and white areas represents nonderegulation (MD CRM = 0)

2.11 N-of-1 diametric extreme paired analysis and comparison to GSEA, DEG + Enrichment

Using the diametric extreme phenotypes (Figure 5), we produced all 45 possible combinations of DFS > 4 years patients (DFS, n = 9) with DoD < 2.5 years patients (DoD, n = 5). We applied the N-of-1-pathways MD framework to these pairs of subjects in pursuit of phenotypically deregulated pathways. To test against a conventional approach, we identified differentially expressed genes (DEGs) using the full cohort of diametric extremes via EBseq R package following the suggested protocol (Leng et al., 2013). Then we performed geneset enrichment with those DEGs using Fisher’s Exact Test (FET) to quantify the association of DEG status versus pathway inclusion. We also applied standard gene set enrichment analysis (GSEA) on the diametric extreme patients to detect deregulated GO-BP terms (Subramanian et al., 2005). To validate the results, we compared the detected pathways with an independent gold standard (GS) of 11 GO-BP terms determined through network models of 10 breast cancer survival studies (Chen et al., 2010). We summarize the overlap and functional similarity between detected pathways from the three methods and the GS in Table 2. Functional similarity between GO-BP was determine at a conservative cutoff of 0.7 using information theoretic similarity (ITS) methods we previously validated (Gardeux et al., 2014a, b; Li et al., 2012; Regan et al., 2012; Tao et al., 2007).

Table 2.

N-of-1-pathways MD identifies phenotypically deregulated pathways when conventional methods fail

GO ID	Description	Number of Detections	Patient count
			DFS	DoD
0000280	Nuclear divisiona	31	9	5
0048285	Organelle fissiona	31	9	5
0007067	Mitosisb	30	9	5
0000236	Mitotic prometaphasea	28	9	5
0051301	Cell divisionb	27	9	5
0007017	Microtubule-based processb	26	9	5
0016568	Chromatin modificationb	26	9	5

Notes: Using the diametric extreme phenotypes (Figure 5), we produced all 45 possible pairs of DFS > 4 years patients (DFS, n = 9) with DoD <2.5 years patients (DoD, n = 5). Within these pairs of diametrically opposed patients, the gene-level log₂ fold change centered around zero, indicating no systematic shift in expression. We applied the N-of-1-pathways framework to these pairs in pursuit of phenotypically deregulated pathways. Displayed are the pathways detected most often (found deregulated at least 25 times) in the 45 pairs that also share functional information similarity with an independent gold standard (GS) of 11 GO-BP terms (Section 2.11, (Chen et al., 2010). Every patient studied was deregulation in this pathway (i.e. not just a few patients causing deregulation in pairs). Note that DEG + geneset enrichment and GSEA using all 14 diametric extreme patients detected 18 and 4 pathways, respectively (FDR 25%); none of these pathways were functionally related to the GS.

^aPathway shared > 0.7 ITS with a pathway in the gold standard.

^bPathway was found in the gold standard.

3 Results

3.1 N-of-1-pathways MD identifies synthetically deregulated pathways

We aimed to assess false-negative rates by designing a simulation study using the RNA-Seq gene expression from biological replicates of breast cancer cell lines (Dataset I). We extend our previous simulation study by parametrically modeling RNA-seq counts using the negative binomial distribution. We employ this simulation to evaluate the predictive power of our N-of-1-pathways MD method (Gardeux et al., 2014a). The N-of-1-pathways MD method is consistently more powerful than Wilcoxon. Figure 2 shows that both methods perform better as the pathway size and number of deregulated genes increases. We quantify the scenarios that achieve greater than 80% power (less than 20% false-negative rate) by measuring the area above the curve (AAC). We note that N-of-1-pathways MD outperforms the Wilcoxon method at every fold-change studied.

3.2 N-of-1-pathways MD slightly outperforms Wilcoxon in false-positive rate

We evaluated the false-positive rate of the N-of-1-pathways MD compared to its Wilcoxon counterpart (Figure 3). To this end, we used Dataset I of 7 biological replicates from a breast cancer cell line. The rationale adopted was that biological replicates derived from the same breast cancer cell line should lead to similar gene expression profiles with minimal variation and, therefore, any genesets found deregulated could be labeled as a false positive.

3.3 N-of-1-pathways MD predicts breast cancer survival

While breast cancer is often effectively treated, it is known for high heterogeneity and predicting clinical outcomes remains a challenge. We sought out to predict breast cancer survival using the N-of-1-pathways MD scores from 80 women with paired RNA-Seq gene expression samples (Tumor and Normal) (Table 1; Section 2.7). We observed large variation in the number of deregulated pathways found. Using the MD CRM, the number of identified deregulated pathways per patient ranged from 19 to 970 when screening 3225 GO-BP terms (average of 278 pathways per patient). The most commonly deregulated pathways across patients were related to cell division and cell cycle, known to be associated to cancer pathology (Table 3). As a negative control, we investigated the distribution of MD CRMs from pathways not identified in any of the patients. We found that the 1095 unidentified pathway MD CRMs did not produce distinct Kaplan–Meier survival curves (log-rank P = 0.133; data not shown). Delving deeper into the N-of-1-pathways MD scores, we performed a PCA to distinguish diametric extreme patients (Supplementary Figure S4). We first identified all pathways that were found deregulated in at least one patient. This allowed for no individualized deregulation signal to be overlooked when determining cohort-level trends. There were 2130 selected GO-BP terms using this criterion; every patient has a CRM for each of these pathways. The first component of these pathway scores did not differ between the diametric extreme patients (Wilcoxon P > 0.2). We then performed unsupervised clustering of the same N-of-1-pathways MD scores to predict survival among the 80 breast cancer patients.

Table 3.

Most commonly deregulated breast cancer pathways among the 80 patients

GO-BP ID	GO-BP terms	Patient count
GO:0000236	Mitotic prometaphase	65
GO:0000216	M/G1 transition ofmitotic cell cycle	57
GO:0000280	Nuclear division	57
GO:0048285	Organelle fission	57
GO:0007059	Chromosome segregation	56
GO:0000087	M phase of mitotic cell cycle	56
GO:0003012	Muscle system process	55
GO:0007067	Mitosis	55
GO:0000075	Cell cycle checkpoint	54
GO:0006936	Muscle contraction	54

We used PAM clustering with two medoids to produce two clusters of patients. The two clusters of patients showed a statistically significant difference in survival (log-rank test P < 0.05; Figure 4). Additionally, vital status was associated with the clusters (Fisher’s exact test P < 0.01; data not shown).

Our exploration of the diametric extremes yields two key observations. The star plots display distinct, interpretable signals for DoD less than 2.5 years (Figure 5) while the pattern for DFS greater than 4 years remains ambiguous. Secondly, N-of-1-pathways finds phenotypic differences using only one subject per group. The pairing of diametric extremes resulted in 45 applications of N-of-1-pathways. The number of detected pathways ranged from 36 to 756 for the diametrically opposed pairs, averaging 161 pathways per pair. Table 2 presents the most relevant pathways.

On the other hand, traditional geneset approaches were underpowered in this setting. DEGs analysis (Leng et al., 2013) required an false discovery rate (FDR) adjusted P value less than of 20% to find 65 genes DEGs across the diametric extreme cohort (n = 14). The following geneset enrichment found only one pathway enriched at Fisher’s Exact Test FDR adjusted P < 0.1. In total, 17 pathways were found enriched at FDR 25%. None of these pathways were related to the GS. GSEA yields only 4 pathways at FDR 25%, and none of these pathways were related to our breast cancer gold standard (Subramanian et al., 2005).

4 Discussion

Rank-based, nonparametric approaches can suffer a decreased efficiency compared to appropriately implemented bootstrap, randomization, and t-test procedures (Smucker et al., 2007). Further, the Wilcoxon procedure we previously utilized assumes that the pairs are chosen randomly and independently from a population. It is presumable that gene expression values do not satisfy this assumption. We aimed to address these concerns via an evolution of our approach into the N-of-1-pathways MD method. Results from our exploration of TCGA breast cancer data show N-of-1-pathways MD improves upon our earlier N-of-1-pathways Wilcoxon approach. The success of the N-of-1-pathways framework for breast cancer builds upon the insights developed in our previous investigation of TCGA lung adenocarcinoma data (Gardeux et al., 2014b), as TCGA data share similarity in data generation, storage, and format, as well as other aspects. N-of-1-pathways MD continues to maintain the practicality of self-contained geneset testing (Goeman and Bühlmann, 2007). Additionally, the method provides a pathway-level deregulation clinically relevant metric that is predictive of clinical endpoints.

Our simulation study of the method’s ability to detect synthetically deregulated pathways indicates that N-of-1-pathways MD outperforms N-of-1-pathways Wilcoxon. Its ability to identify entire mechanistically interpretable pathways deregulated from subtly DEGs is very powerful. This feature provides a strategy to assess the notion that complex diseases may derive from multiple changes of small effect that lead to larger phenotypic outcomes. Furthermore, we note the signed nature of the N-of-1-pathways MD score that the method cannot detect deregulated pathways that are not primarily up- or downregulated. In other words, if a pathway has approximately equal numbers of genes above and below the line of equal expression, N-of-1-pathways MD would likely not identify the pathway as deregulated. It is debatable whether such a specific form of departure reflects true deregulation or simply a highly variable pathway.

Our biological replicate analysis indicates N-of-1-pathways MD produces slightly fewer false positives than Wilcoxon. There may be some concern over the somewhat inflated rate of false positives for certain samples. This might be attributed to true pathway deregulation explained by measurement variability or some aspect of the replication that led to unequal distribution of mRNA molecules. We note that this analysis is highly contingent on proper preprocessing and normalization. Normalization is particularly problematic in RNA-seq as many normalization techniques fail to compensate for library size, gene length and guanine–cytosine content (Dillies et al., 2013). Notably, N-of-1-pathways did not exhibit a bias towards longer median length of their genes (Supplementary Figure S3, A), nor higher gene intensities within the pathway (Supplementary Figure S3, B). However, there is a bias towards detecting larger pathways as deregulated (Supplementary Figure S3, C–D).

Applying N-of-1-pathways MD to breast cancer data results in the discovery of sensible deregulated pathways and produces metrics predictive of survival. This aspect validates the notion that N-of-1-pathways MD not only provides a metric interpretable at the pathway level, but also is related to important clinical endpoints. The most commonly deregulated pathways (Table 3) are associated with the hallmarks of cancer, including deregulation in DNA replication and cell cycle. We also utilized the principal components of the MD CRMs (Section 2.6) to identify clinical subtypes such as estrogen receptor (ER) + and clinical metastatic stage. The former is not significant (Wilcoxon P > 0.08; PC1, data not shown); the latter is significant (Wilcoxon P < 0.05; PC1, data not shown). Additionally, the breast cancer findings strengthen our previous indication that N-of-1-pathways was predictive of lung adenocarcinoma survival, demonstrating the robustness of our techniques for different cancer types.

Survival prediction is possible from tumor gene expression alone (Supplementary Figure S1), but the gene signatures may lack interpretability and clinically actionable targets. N-of-1-pathways is designed to first discover deregulated pathways at the individual subject level followed by learning classifiers cross-subjects. In contrast, gene expression classifiers work directly on gene expression, which may not be functionally deregulated at the individual subject level as pointed out by Simon (2005). N-of-1-pathways also allows for more power in discovering group comparisons at the pathway level that traditional differential mRNA expression followed by enrichment studies as summarized by Table 2.

N-of-1-pathways MD refines our Wilcoxon approach. We acknowledged in our previous work that independence assumptions of the N-of-1-pathways Wilcoxon signed-rank test were not met. However, the fact that a predictive and interpretable signal was captured gave credibility to the N-of-1-pathways approach. N-of-1-pathways MD improves over our previous work as it does not violate any such statistical foundations. Careful readers may note that we have avoided the notions of hypothesis testing and prefer the term ‘identified pathways’ to ‘significantly deregulated pathways.’ The MD-deregulation criterion outlined in Section 2.4.3 provides a metric to identify an up- or downregulated pathway, but does not rely on the notion of a P value. We do retain the P values and associated multiplicity corrections for the Wilcoxon approach, in order to faithfully replicate that methodology. Further study is required to create a statistically complete approach.

The introduction of N-of-1-pathways MD provides many avenues for extension. The method can be adapted to more than paired samples. Multiple samples could be obtained from within a tumor and the pathway scores would measure intratumor heterogeneity. Along the same vein, multiple samples could be obtained from a patient over time. Thus, the geneset scores would measure longitudinal change in key pathways to predict response to therapy or to make timely prescriptive decisions. Additionally, the N-of-1-pathways framework could potentially provide a basis for improved small sample normalization techniques. Or, additional ontological information could be employed to weight genes within a pathway and reflect gene importance in biochemical dynamics. It remains to be shown whether the patient-specific deregulated pathway(s) identified in the current study can be predictive and it will be addressed in future studies. N-of-1-pathways can also be applied to various scales of biology, e.g. DNA, methylation patterns, or microRNA expression.

5 Conclusion

We hypothesized that creating a biologically relevant pathway-level measure of effect will improve interpretability and detection while maintaining statistical precision. We have established a novel application of statistical MD, N-of-1-pathways MD, to quantify geneset deregulation using gene expression data from paired samples derived from a single subject. This study further validated our N-of-1-pathway framework by predicting breast cancer survival from the pathway-level metric of deregulation. We evaluated the precision and accuracy of N-of-1-pathways MD and compared it to our existing Wilcoxon approach. We found improvement in geneset deregulation detection while not suffering increased false-positive rates.

The modification of our approach is a pathway-level approach to produce a CRM in single subjects and quantifying the deregulation induced under the disease condition (e.g. tumor sample) for each pathway (Shriner et al., 2014). In addition, we are currently evaluating prospectively the method to predict future hospitalization in a clinical trial.

N-of-1-pathways MD provides a practical approach towards precision medicine. The method gives clinically actionable results derived solely from the patient. The entire transcriptome does not need to be measured, allowing for targeted experiments across multiple gene expression platforms, reducing cost and providing flexibility. The method generates the magnitude and the biological significance of personal deregulated pathways results derived solely from the patient’s transcriptome. These pathways offer an opportunity for applicability to diseases in which DNA changes may not be relevant, and thus expand the ‘interpretable omics’ of single subjects (e.g. personalome).