Abstract
Motivation
Titration experiments measuring the gene expression from two different tissues, along with total RNA mixtures of the pure samples, are frequently used for quality evaluation of microarray technologies. Such a design implies that the true mRNA expression of each gene, is either constant or follows a monotonic trend between the mixtures, applying itself to the use of order restricted inference procedures. Exploiting only the postulated monotonicity of titration designs, we propose three statistical analysis methods for the validation of high-throughput genetic data and corresponding preprocessing techniques.
Results
Our methods allow for inference of accuracy, repeatability and cross-platform agreement, with minimal required assumptions regarding the underlying data generating process. Therefore, they are readily applicable to all sorts of genetic high-throughput data independent of the degree of preprocessing. An application to the EMERALD dataset was used to demonstrate how our methods provide a rich spectrum of easily interpretable quality metrics and allow the comparison of different microarray technologies and normalization methods. The results are on par with previous work, but provide additional new insights that cast doubt on the utility of popular preprocessing techniques, specifically concerning the EMERALD projects dataset.
Availability
All datasets are available on EBI’s ArrayExpress web site (http://www.ebi.ac.uk/microarray-as/ae/) under accession numbers E-TABM-536, E-TABM-554 and E-TABM-555. Source code implemented in C and R is available at: http://statistics.msi.meduniwien.ac.at/float/cross_platform/. Methods for testing and variance decomposition have been made available in the R-package orQA, which can be downloaded and installed from CRAN http://cran.r-project.org.
1 INTRODUCTION
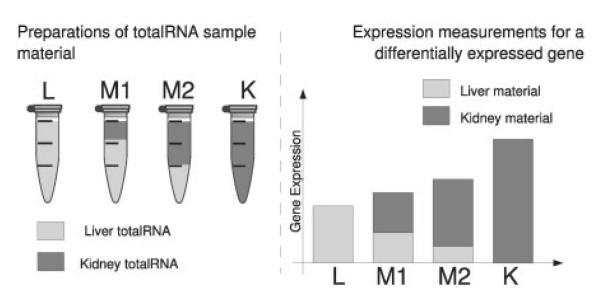
Microarrays measure the abundance of thousands of distinct mRNA fragments simultaneously. The high dimension of the acquired data pose a complex issue to quality assessment. Titration experiments that measure the gene expression in two different tissues, along with total RNA mixtures of the pure samples, have been shown to provide a valuable tool for the evaluation of quality related aspects of microarray data (Holloway et al., 2006; The MAQC Consortium, 2006). Such experiments operate on the assumption that for any fragment the abundance in the mixed samples can be determined as a function of their expression in the pure samples and the given mixture proportions (See Fig. 1 for a schematic depiction of this concept).
Fig. 1.
Schematic of the EMERALD titration series.
In contrast to spike-in studies where a set of mRNA fragments are added at predetermined concentrations to some of the samples, titration series are not based on synthetic RNA fragments [see e.g. Irizarry et al. (2006) responding to Choe et al. (2005)]. Titration series provide measurements from authentic biological samples that reflect the intricate characteristics of RNA samples. Their disadvantage is that they do not provide a gold standard (i.e. the set of true differentially expressed genes is unknown). The only knowledge available a priori in titration experiments is given by the mixture proportions and the thereby defined relationship between mRNA amounts throughout the titration series. Solely this relationship can be investigated, tested and compared on measurements acquired from several combinations of microarray platforms and preprocessing methods and is the basis for quality assessment. Holloway et al. (2006), for example, assume that the measured abundances follow a linear trend throughout the titration series. Shippy et al. (2006), however, observe ‘signal compression and expansion’, which would comprise a violation to such assumptions. Similarly, in microarray dose–response studies, Hu et al. (2005) report that linear model-based inference procedures fail to identify monotonic effects with non-linear response curves, therefore methods allowing for more general monotonic trends are more efficient.
In this article, we propose statistical analysis methods to assess the accuracy, repeatability and agreement across different platforms for high-throughput genetic data. Our methods are based solely on the postulated monotonicity of titration designs, but do not rely on assumptions about the functional form of this trend. They are able to deal with grouping factors (e.g. repeated measurements, batch factors) that induce a hierarchical variance structure. Using these methods, we compare several combinations of microarray platforms and preprocessing strategies. In Section 2, we present our methods along the lines of a large-scale titration experiment [parts of which have been previously used in (Scherer, 2009, chapter 9)] published by the EMERALD project that is described in Section 2.1. The methods, however, are applicable to titration designs in general, where one obvious candidate is the MAQC experiment presented in Shippy et al. (2006). Having a similar variance structure with one random effect ‘site’ allows the proposed methods to be directly applied.
In our analysis, we use the data structure induced by the titration design in several ways. Initially, we investigate if the postulated order structure is present in the data, estimate and test for deviations of the observed expression values from monotonicity. This part of the analysis can be considered as an assessment of accuracy, defined as the agreement between the result of a measurement and the value of the measurand (Taylor and Kuyatt, 1994). To assess to which degree the obtained measurements conform to the monotonicity requirement, we test consecutive differences between mixture groups for a significant increase or decrease in expression, separately for each gene. We construct permutation tests accounting for the specific hierarchical variance structure of the EMERALD dataset adjusting for multiple testing using a recently proposed procedure (Guo et al., 2009), which accounts for directional errors. Thereby we can identify any significant deviation from the monotonicity assumption which is in violation of the intrinsic implications of the study design. More details on the approach are given in Section 2.3 and the results are presented in Section 3.1.
Further, order restricted methods allow us to improve estimates of variance components. These can be used to quantify the repeatability [i.e. the extent to which successive measurements of the same measurand carried out under identical conditions of measuring agree (Taylor and Kuyatt, 1994)]. Decomposition of the total variance allows us to identify noise that can be attributed to either procedural variation (e.g. imperfections in the wet lab procedures) or biological variation (i.e. the variability between different biological samples). Further, being corrected for structural variance components, the residual variance provides an estimate of the technical repeatability. In Section 2.4, we propose a novel method to estimate such variance components under order restrictions. In Appendix C in Supplementary Material, we report a simulation study that demonstrates the improvement due to the new method compared with estimators not exploiting order restrictions. The application to the dataset is discussed in Section 3.2.
Finally, we raise the topic of cross-platform agreement in terms of the correspondence of differential expression analysis between the measurement technologies. Differential expression between the two different organ materials introduces (based on the monotonicity assumption) a monotonous trend throughout the titration series. We therefore derive an inference procedure to test the null hypothesis of non-differential expression for each gene from a well annotated set of common genes, found on each platform. The test was based on isotonic regression and permutation-based multiple testing methods. The corresponding methods are described in Section 2.5 with results shown in Section 3.3.
Section 4 concludes the article with a discussion of our methods and results.
2 METHODS
2.1 Microarrays and preprocessing
The probe material used in the EMERALD experiment was harvested from six rats, where total RNA was extracted from livers and kidneys. The resulting sample material was then prepared in four mixtures:
pure liver material, which we will refer to as L;
75% liver mixed with 25% kidney material, which we will call M1;
25% liver and 75% kidney, in the following simply M2; and
pure kidney material, which is denoted as K.
This yielded four times six batches of sample material. Each batch was labeled and hybridized to three arrays from each of three different commercially available microarray platforms. The microarray platforms used in the EMERALD project were as follows:
Affymetrix GeneChip Rat Genome 230 2.0;
Illumina RatRef-12 v1 Expression BeadChip; and
Agilent Whole Rat Genome Microarray 4x44K.
In summary, this amounts to:
The ArrayExpress accession page of the Illumina dataset states concerns about the quality of several arrays from this experiment. Following these suggestions and careful quality control, we removed six arrays from this dataset. Furthermore, we removed one array from the Affymetrix dataset due to quality concerns. For details, see Appendix A in Supplementary Material.
The sensitivity of the genetic material to slight aberrations in the wet lab procedure makes microarray measurements vulnerable to the introduction of systematic biases. Therefore, microarray measurements are typically subjected to extensive data preprocessing. Besides several platform-specific procedures like background correction, normalization plays an influential role during this preanalysis step. In order to see, if and how, such methods effect the quality criteria investigated in this work, the EMERALD data were subjected to two different normalization procedures [Baseline normalization (median scaling) and Quantile normalization]. This results in two additional versions of the dataset, besides the unpreprocessed data, providing insight on the effectiveness of such algorithms. For Baseline normalization, the per chip median was subtracted from the corresponding log expression values and subsequently the overall median (across all expressions measured with a particular platform) was added. Quantile normalization was performed according to the algorithm defined in Gentleman et al. (2005, chapter 1). Data were downloaded from ArrayExpress and processed using R (R Development Core Team, 2008) and Bioconductor (Gentleman et al., 2004). Recent annotation files were acquired from the respective manufacturer web sites (http://www.affymetrix.com/, http://www.agilent.com/, http://www.illumina.com/) (see Appendix B in Supplementary Material for details). In contrast to Agilent and Illumina, which provide one probe reading per reporter, Affymetrix features several probe readings per reporter. To summarize the corresponding measurements, we used the robust multiarray average (RMA) (Irizarry et al., 2003) either directly on the raw data or after normalization was applied. Normalization was performed based on the expressions of all reporters provided by each particular platform. Expression values from all platforms and normalization procedures were analyzed on the log2 scale.
To select a common set of proficiently annotated probes that were featured on each of the investigated platforms, probes were mapped to RefSeq (Pruitt et al., 2006) NM identifiers (see Appendix B in Supplementary Material). This identified a set of 5927 transcripts for which a probe was provided by all platforms. All downstream analysis after normalization and summarization (in the case of Affymetrix) were done based on this set of common reporters.
2.2 Notation and model definition
To keep notation short, we will refer to the three platforms with the shortened names Affy, Agil and Illu. Expression values are typically denoted by y using the following indices:
Note that in our terminology expression value refers to preprocessed measurement values (i.e. log-transformed, normalized). Thus, ygijk denotes a preprocessed expression value for probe g, group i, animal j and replicate k. Separate models are assumed for different platforms and normalization procedures. Corresponding indices, however, were omitted in the definition. Overlined variables indicate averages, calculated using the arithmetic mean. The relevant margins are indicated by the indices, which are replaced by dots. For example, stands for the average expression of probe g in mixture group i for all replicates and animals.
Besides the noise generated by the imprecision of the measurement technology, there is variation due to the use of animals with genetic differences. This variance structure generated by the experimental design can be directly translated into a mixed model definition, assumed for each probe separately.
| (1) |
with the assumptions:
The levels of the fixed effect αgi are comprised by the four different mixture groups. Biological variation between different rats was modeled by the random effect βgj. Since material coming from different rats was processed and mixed separately, we also included the random interaction term γgij.
To incorporate the assumption of monotonicity of the titration response, the effects αgi including the special case of constant expression are required to either follow an up- or downward trend, i.e.
| (2) |
| (3) |
2.3 Accuracy
Information on the true amounts of mRNA fragments in the sample quantifying the accuracy of the measurements is lacking. We are, therefore, limited to an investigation of the probe amount not showing a monotonous titration response. The EMERALD experiment provides three comparisons between adjacent mixture groups: L–M1, M1–M2 and K – M2. Each can be positive, zero or negative, generating 27 possibilities for the expressions to change throughout the titration series. Only 14 of these possible trends are monotonous including the special case of unchanged expression. We, therefore, employ a test for the direction of change between consecutive mixture groups describing the shape of expression changes for each gene, platform and normalization method.
For each gene g the linear contrasts (i.e. L–M1, M1 – M2, K – M2) are estimated using t-statistics. P-values of the marginal null hypotheses were computed by random permutation of samples within the animals (i.e. leaving the variance structure intact). Under the null hypothesis, we assume exchangeability of the samples within each animal regardless of titration group i. Hence, the data conditional univariate null distribution for each gene g can be computed by permuting samples of the two particular mixture groups but only within each block of the individual random effect (βj) (Pesarin, 2001). Multiplicity correction was performed as described in Guo et al. (2009). This algorithm provides control of the mixed directional false discovery rate, which is defined as the sum of the expected proportion of erroneous rejections and the expected proportion of directional errors among all rejections.
2.4 Repeatability
The model specified in (1) naturally lends itself to an analysis of repeatability as a measure of the variation observed in repeated measurements. Our primary target in this investigation was the residual error as defined by σ∊. The two random effects βgj and γgij comprise noise contributed either by actual differences in the gene expression between animals or procedural inconsistencies in the preparation of the mRNA samples. Neither of which can be solely attributed to the measurement quality provided by the used platform. It is, therefore, necessary to decompose the variance observed in the data to provide an estimate of the relevant variance term σ∊.
The order restrictions (2,3) on the levels of the fixed effect αi can be exploited to enable an improved estimate for the means of expression levels in each mixture group. Isotonic regression provides such estimates. For a given set of points and prespecified direction, it finds the set of ordered points that is closest to the original in terms of the squared distance (Brunk, 1955). The corresponding algorithm works by recursively pooling and averaging adjacent groups of points that violate the specified order restriction until a valid fit is found. We denote the isotonic estimates based on a particular set by or , where the former indicates the fit to the set of means assuming an increasing trend and the latter a decreasing trend.
Sampson et al. (2003) investigated a simplified isotonic regression scenario and suggest an improved variance estimate by incorporating information about the observed order. We extend this idea to the problem of variance decomposition. The idea is simple: specify the levels of the fixed effect according to the pooled groups given by isotonic regression and estimate the variance components using this updated model definition. As an example assume that for a particular mRNA fragment we observe but , an upward trend except for the mean in group M2 being lower than the mean in M1. Pooling groups M1 and M2, however, will generate the correct order. Therefore, we calculated the variance components using a standard method, with the levels M1 and M2 merged in the model definition. The intuition behind this approach, is that whenever the order restriction is violated for adjacent pairs, one can assume the means in either group to be equal. The corresponding means can, therefore, be estimated from a larger sample and degrees of freedom can be retained by estimating this mean only once.
The experimental design in the EMERALD dataset is balanced, however, removing arrays from the analysis, due to quality concerns, or merging levels in the fixed effect introduces imbalance to the model matrix. Classical ANOVA methods cannot be applied in such circumstances, but iterative methods like Restricted Maximum Likelihood (REML) can deal with such situations (Searle et al., 1992). We also consider Henderson’s method III (Searle et al., 1992) which is a modified ANOVA method not requiring the design to be balanced. It provides closed solutions for estimates of the variance components and hence promises improved computation times.
Our simulations (see Appendix C in Supplementary Material) show that restricted estimation of variance components using information from isotonic regression is indeed preferable to unrestricted methods. In scenarios where there is no or only a slight trend throughout the titration series, this approach yields a lower mean squared error (MSE) in estimates of the interaction term σγ, while introducing only negligible bias. Our simulations show that in terms of Bias and MSE the implementation using Henderson’s procedure is less efficient than the alternative procedure based on REML as implemented by the nlme package (Pinheiro and Bates, 2000) in GNU R (R Development Core Team, 2008). Computation times for Henderson’s procedure, however, were shorter by approximately a factor of 100. For the analysis in Section 3.2, we used the REML-based method for its improved efficiency. In situations where the number of investigated probes is even larger (e.g. next generation sequencing experiments), one might compromise some efficiency in favor for a marked speed improvement and use the procedure based on Henderson’s method.
2.5 Agreement
In this section, we investigate to which degree the different platforms and normalization methods detect the same genes as differentially expressed. Thus, we test for each gene if there is a monotone trend in the expression levels throughout the titrations. Instead of pair wise comparisons of adjacent titration levels, we use a more powerful overall test for a monotonic trend for each gene, based on a test statistic proposed by Barlow (1972), to test the null hypothesis of equal means against an order restricted alternative. Based on (1), (2) and (3), we test the null hypothesis of equal means in the fixed effects α
| (4) |
against the two ordered alternatives
| (5) |
| (6) |
with at least one strict inequality. The test statistic is given by:
| (7) |
| (8) |
| (9) |
The statistic for gene g is the ratio of the residual sum of squares of the isotonic regression fit, assuming an upward trend, against the residual sum of squares of the null model of equal means. Similarly, the is calculated accordingly using isotonic regression assuming a downward trend. The directional decision is then made by choosing the smaller of the two statistics. , therefore, gives a two-sided test statistic. Lin et al. (2007) assess a permutation version of this test in the context of genetic data and find that it is the most powerful among a selection of alternative test statistics. Approximation of the marginal null distribution of test statistics was accomplished by randomly permuting samples within each animal to account for the hierarchical structure in the data. Permutation is performed as described in Section 2.3 with the difference that samples from all four mixture groups are permuted. To adjust for multiple testing controlling the family wise error rate (FWE), we use a resampling-based approach by Westfall and Young (1993). Permuting samples in parallel for all genes, the multivariate distribution of the vector of test statistics (,…,,…,) under the global null hypothesis can be computed. We used the single-step maxT procedure, which controls the FWE in the strong sense [under the assumption of subset pivotality, see (Westfall and Young, 1993)] and also safeguards against potential errors in term of the directional decision. Alternatively, one can use the residual to total sum of squares ratio from a linear model instead of E2. This amounts to a test of the null hypothesis against a linear trend. We detail such an approach in Appendix F in Supplementary Material.
These permutation tests are applied separately to the data from each combination of platform and normalization method. For each platform and normalization, we control the FWE at a two-sided level of α = 5%. Then for each pair of platforms or normalizations we computed the specific agreement (Cicchetti and Feinstein, 1990) of the resulting lists of genes with significant upward or downward trends. This measure of overlap is defined by the number of rejected hypotheses with the same directional decision, with both platforms or normalizations, divided by the number of hypotheses rejected on average (in that direction) with these platforms or normalizations. Genes, having a significant upward trend in one analysis but a significant downward trend in another, were called discordant. For these, the shown percentages are computed as the proportion of discordant genes within all genes that show a significant trend on at least one platform or normalization.
Note that under the assumption that for all platforms the same null hypotheses are tested, specific agreement is just a function of the statistical power of the procedures. Therefore, it depends not only on the platform and pre-processing method but also on the sample size, the statistical tests and multiplicity correction used, as well as the underlying pattern of differentially expressed genes. However, lack of overlap may also be due to systematic biases of the considered platforms or analysis methods. A strong indicator for the presence of bias is the number of discordant test decisions. Since the FWE rate is controlled at level α and the test results across platforms and normalization methods can be expected to be positively correlated (since they are based on the same data or biological material), the probability to observe discordant test decisions in a specific pairwise comparison of platforms or normalization methods is lower than α2.
3 RESULTS
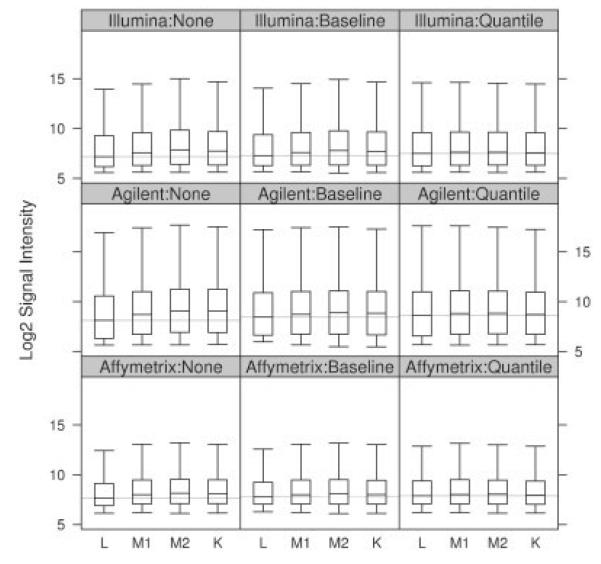
Exploratory investigation of the raw data has uncovered a distinct overall trend of expression values. Figure 2 shows that the non-normalized signals are on average larger in kidney than in liver samples. Typically, the proportion of fragments that change between conditions is expected to be small enough so that the per sample distributions of expression values are similar. This assumption is, as an example, explicitly used in several quality assessment procedures and deviations are considered as an indication for quality issues (Gentleman et al., 2005, chapter 3).
Fig. 2.
Expression value distributions for the 5971 well-annotated common probes averaged per mixture.
A likely explanation for this phenomenon is that differences in the total to messenger RNA proportions generate such an overall trend. While equal amounts of total RNA were used for each array, the observed signals reflect only the fraction constituted by messenger RNA. A higher concentration of detectable mRNA in the kidney samples would lead to overall stronger signals on arrays hybridized with this material. Since estimates (Shippy et al., 2006) of these quantities from the data are too variable to conclusively identify an imbalance in mRNA proportions as a cause of this phenomenon, further measurements would be needed. Shippy et al. (2006) describe a method for measuring these proportions. For Affymetrix, Hannah et al. (2008) propose a method to normalize such global mRNA shifts using a set of external RNA spike-ins.
We estimated that the normalization parameters based on the entirety of probes featured on a particular platform, however, restrict our analysis to the set of well-annotated probes common to all three technologies as defined in Section 2.1. Considering all measurements from a specific platform, the chip-wise medians of baseline and all chip-wise quantiles of quantile normalized data, respectively, are by definition of the respective methods, constant throughout the titration groups. Columns two and three of Figure 2 show normalized expression values from our set of well-annotated probes common to all platforms. These display remnants of the overall expression increase, from liver to kidney, observed in the raw data. This indicates that the overall trend in raw expressions is more pronounced for fragments measured by the well-annotated probes common to all platforms than in the remaining probes. Further exploration of this finding (data not shown) revealed a higher proportion of measurements with very low expressions throughout all titration groups among the set of probes not included in the analysis and suggested an increased amount of fragments that are not expressed. Such measurements, which are solely noise, would not be affected by unequal total to messenger RNA concentrations in liver and kidney material and hence not show the otherwise implied trend.
3.1 Accuracy
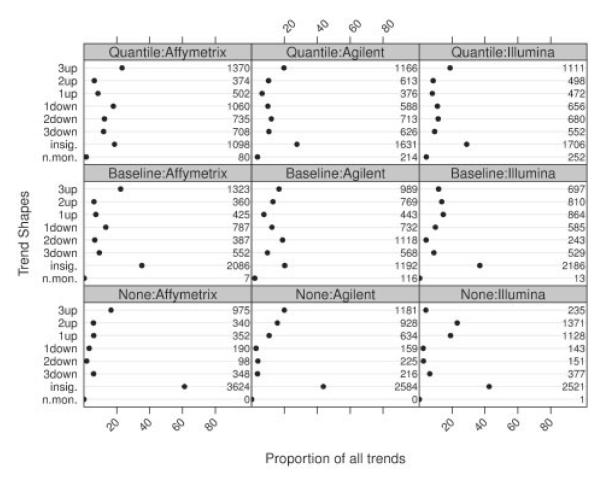
Figure 3 presents the results of the shape analysis. Each of the three consecutive differences (L–M1, M2–M1 and K–M2) were tested using the test described in Section 2.3. Multiplicity correction was applied to control the mixed directional false discovery rate at the 5% level. In Figure 3, the 27 distinct possibilities of test results for each reporter were summarized into eight categories. Significant non-monotonous trends (i.e. at least one significant increase together with at least one significant decrease), non-significant trends (i.e. for all three differences the null hypotheses of no expression change could not be rejected) and monotonous trends characterized by the number of significant expression changes. Non-monotonous trends should not be observed under the premises of a titration series and are a clear indication of data artifacts. The distribution of different trend shapes changes strongly between differently normalized data, a phenomenon that we explain in more detail in Section 3.3. Furthermore, we observe that normalization, for all platforms, leads to a larger number of rejections. With the exception of Agilent, the maximum is reached on quantile normalized data. Both normalization procedures lead to a slight increase in the number of observed non-monotonous trends, which are contrary to the implications of the titration series. Although these figures are below the error margin provisioned by the five percent mixed directional false discovery rate, such trends are not observed (with one exception in the Illumina data) on non-normalized data. This indicates that data artifacts are introduced upon normalization.
Fig. 3.
Shape profiles: distribution of detected trends for the three platforms and normalization methods. The last line (n.mon.) in each panel gives the proportion of genes with significant non-monotonous trends. The second last line (insig.) shows the proportion of genes for which none of the three linear contrasts could be rejected. The remaining lines show the proportions of genes for which one, two or three of the tested contrasts showed a significant difference in a specific direction, while the remaining comparisons showed no significant changes in expression. Numbers in the margins of each panel give the absolute numbers of genes in that category.
3.2 Repeatability
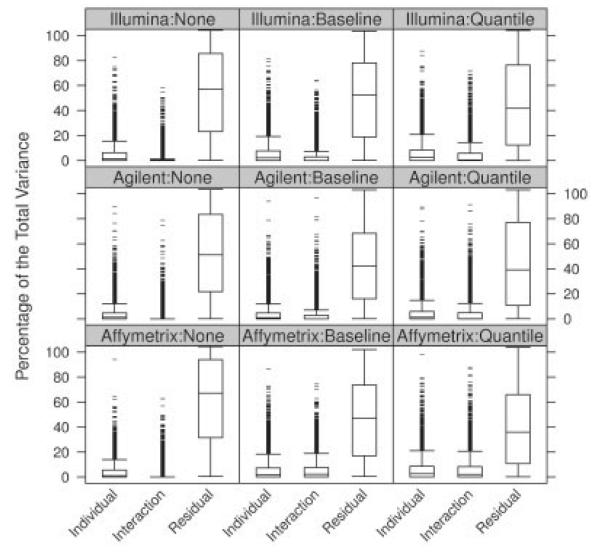
Relating to the EMERALD dataset, the variance components defined in Section 2.2 can be attributed to several sources of variation. The variation of the individual effect, σβ, represents variance introduced by differing levels of mRNA amounts between rats. The interpretation of the variation in the interaction term, σγ, is more intricate. Possible sources are inconsistencies in the mixture proportions, and also biological differences between animals in the strength of the titration response. The residual variance σ∊ is the variation introduced by unspecified factors. We use it as an estimate of the measurement error inherent to each platform, also including error introduced by any component not specified in the model (e.g. different scanners, fluidics stations, etc.). Figure 4 shows boxplots of estimates for these components computed on data preprocessed by the two normalization methods as well as on the unnormalized data. Estimates are shown as percent proportions of the total variance to provide a scale that is comparable between different normalization methods. We observe that both normalization methods manage to reduce the residual variance on all platforms. However, quantile normalization achieves slightly better results than baseline normalization. This pattern in residual error reduction corresponds well with the increased amounts of rejections achieved on normalized data presented in Figure 3.
Fig. 4.
Variance components expressed in percent of the total variance. Each panel shows boxplots of estimates based on a specific platform – normalization combination.
3.3 Trend tests and their agreement
We report for each platform and normalization method the number of genes where the null hypothesis of non-differential expression throughout titration levels is rejected, and as outlined in Section 2.5 investigate to which degree the different platforms and normalization methods detect the same genes as differentially expressed genes within the same directional decision.
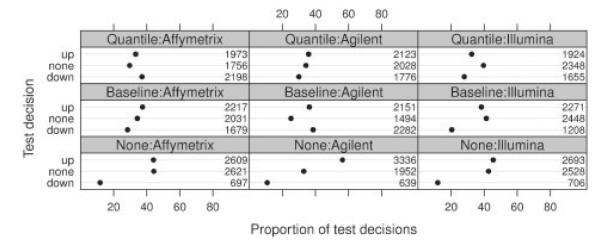
Figure 5 shows the observed proportions of significant trends. Regardless of normalization or platform, the proportion of probes for which the null of constant expression across titration levels could be rejected (at a two sided FWE level of 5%) in favor of a monotonous trend is exceptionally high and ranges from 56% to 75%. Because of the higher power of the trend test, this exceeds the number of rejections achieved by the shape test in Section 3.1. Regardless of platform, non-normalized data shows three to five times more significant upward than downward trends. This is consistent with the overall upward trend of expression values observed in Figure 2. After normalization with either method (baseline or quantile normalization), the number of significant upward and downward trends became more balanced.
Fig. 5.
Percentages and absolute numbers of probes found with a significant upward or downward trend. None, refers to probes for which the null hypothesis could not be rejected.
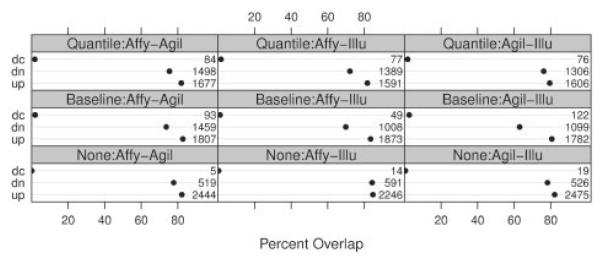
Figure 6 summarizes the absolute numbers of concordant test decisions as well as percent overlap (as defined in Section 2.5) in all pair wise comparisons of different platforms for each normalization method. We observe that the specific agreement across platforms for genes with significant upward trends ranges (depending on the platforms and normalization methods) from 79% to 85%. In contrast, the specific agreement for downward trends is in the range 63–84%. In all platfroms, normalization leads to a decrease in specific agreement for up and downward trends with the exception of Affymetrix compared with Agilent data, where non and baseline normalized data give approximately the same specific agreement for upward trends. This is surprising, since the increase in power induced by normalization (as indicated by the increased number of rejections) should lead to the contrary and suggests that normalization may introduce bias. Another indication of bias is the considerable increase of gene numbers showing significant trends of opposite directions across platforms, if the analysis is based on normalized instead of raw values. This is in clear violation of the assumption that the platform tests the same hypothesis considering the strict error control used in this analysis. This negative effect of the normalization can be alleviated to some degree by filtering out genes with overall low expression values, which improves both the agreement between platforms and decreases the proportion of contradicting directional decisions (see Appendix E in Supplementary Material). An analysis of the annotation quality of our set of 5927 common probes in Appendix B in Supplementary Material shows that further improvement of agreement (≈1% point) can be achieved by using probes that solely match the sequences of their annotated genes.
Fig. 6.
Percentage overlap (dots) and absolute numbers of concordant upwards (up), downwards (dn) and discordant (dc) test decisions for pair wise comparisons of platforms. Overlap is defined as in Section 2.5.
For all platforms and normalization methods, the specific agreement between the analysis of raw and normalized data is (in part considerably) lower for downward than for upward trends (see Appendix D in Supplementary Material ). With the exception of the Agilent platform, the number of discordant genes is relatively low. This illustrates that the increase in downward trends on normalized data is predominantly a result of genes with no significant trend in the raw data measurements, becoming significant in the downward direction after normalization. It has to be noted, however, that on raw data one tests for significant differences in absolute measurements. Normalized data lead to expression values relative to an overall amount of expression in a sample, hence possibly leading to different null hypothesis. In this light, agreement across normalization reveals more about both the distribution of expression values and amount of systematic differences between samples than of the measurement quality.
A comparison between Barlow’s E2 statistic and a statistic based on the residual sum of squares from a linear model (see Appendix F in Supplementary Material) shows that neither statistic performs uniformly better in terms of power. Whereas the former identifies more genes (up to 4%) on non-normalized and baseline normalized data (with the exception of Agilent), the latter rejects the null hypothesis of no trend for more genes (up to 4%) on quantile normalized data (see Table 4 in Appendix F in Supplementary Material). Regarding agreement, both statistics perform equally well. Barlow’s E2 statistic has power against a larger variety of trends, whereas the linear model is only advantageous against linear trends. Furthermore, and in contrast to the linear model, isotonic regression does not require knowledge of the mixture proportions.
4 DISCUSSION
The methods suggested in this article allow the inference of accuracy, repeatability and cross-platform agreement of genetic data acquired from titration experiments. Exploiting only the postulated monotonicity of this design, our framework needs little assumptions on the underlying data generating process and is therefore applicable to all sorts of genetic high-throughput data [e.g. the MAQC titration experiment (Shippy et al., 2006)]. Such data are acquired from numerable platforms each of which executes and preprocesses slightly differently. Therefore, independence from the degree of preprocessing is an essential requirement for an objective data quality evaluation. Although the focus of this article has been on microarrays, it has to be stressed that we derive our methods in the absence of microarray-specific assumptions. This makes them easily portable to upcoming technologies, as for example next-generation sequencing.
The results from the EMERALD dataset demonstrate how our methods provide easily interpretable quality metrics are on par with results from the previous work on titration experiments (Barnes et al., 2005; Hu et al., 2005; Maouche et al., 2008) as well as corresponding findings from the MAQC project (Guo et al., 2006; The MAQC Consortium, 2006). Additionally, we provide new insights regarding the investigated normalization procedures. To our knowledge, we are the first to compare non-normalized to normalized data, in the context of a microarray titration experiment, that is designed with the aim to produce authentic biological data with a proportion of differentially expressed genes larger than what can be simulated using spike-in experiments. Therefore, it poses an interesting challenge to the evaluation of such procedures. This is due to common assumptions, namely that the true differentially expressed genes are relatively few and balanced in terms of direction (Stafford, 2008, chapter 2), being violated by the measurements generated in such experiments. Under this premise, they provide an opportunity to study the robustness of such procedures against violations of their corresponding assumptions. The EMERALD dataset highlights some of the pitfalls of microarray data analysis and its subsequent interpretation. Initially, there is the issue whether the large proportion of upward trends is a biological feature or a procedural artifact. This phenomenon has been discussed in (Shippy et al., 2006) and (Stafford, 2008, chapter 6) in the context of the MAQC project titration experiment. The hypothesis of unequal total to messenger RNA concentrations would be an adequate explanation for many aspects of the data. Considering this assumption, baseline and quantile normalization would appear to be satisfactory candidate methods to remove such a trend. Our results show, however, that the performance of neither baseline or quantile normalization is convincing in the case of the EMERALD dataset. The increase in non-monotonous trends, as well as directional decisions being inconsistent across platforms, clearly indicates the introduction of bias by normalization. Non-normalized data provide preferable accuracy and agreement with the only slight disadvantage in terms of repeatability. According to our results, normalization poses a tradeoff between accuracy and agreement on the one hand and repeatability and power on the other, when dealing with a large proportion of differentially expressed genes. This tradeoff should be considered in the choice of a normalization procedure for experiments for which the assumption that the proportion of differential expressed genes is small is likely to be violated. Regarding general cross-platform gene comparisons, our results show that the agreement across platforms using the same normalization is higher than the agreement across normalizations within one platform, making it advisable to decide on a single normalization procedure. A significant limitation of the agreement measure used in this analysis is its dependency on the power of the test and the distribution of alternative hypotheses. The specific numbers are of limited generalizability with regard to other experiments, where these conditions might differ. It might be possible to construct alternative measures utilizing estimates of the power (Zehetmayer and Posch, 2010) in order to achieve better comparability between different studies.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Livio Finos, Walter Ligget, German Leparc and Terry Speed for their helpful comments.
Funding: This work was supported by the Austrian Science Fund (P23167).
Footnotes
Conflict of Interest: none declared.
Supplementary information: Supplementary data are available at Bioinformatics online.
REFERENCES
- Barlow RE. Statistical Inference Under Order Restrictions. John Wiley and Sons Ltd; New York: 1972. [Google Scholar]
- Barnes M, et al. Experimental comparison and cross-validation of the Affymetrix and Illumina gene expression analysis platforms. Nucleic Acids Res. 2005;33:5914. doi: 10.1093/nar/gki890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunk HD. Maximum likelihood estimates of monotone parameters. Ann. Stat. 1955;26:607–616. [Google Scholar]
- Choe S, et al. Preferred analysis methods for Affymetrix GeneChips revealed by a wholly defined control dataset. Genome Biol. 2005;6:R16. doi: 10.1186/gb-2005-6-2-r16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cicchetti D, Feinstein A. High agreement but low kappa: II. resolving the paradoxes. J. Clin. Epidemiol. 1990;43:551–558. doi: 10.1016/0895-4356(90)90159-m. [DOI] [PubMed] [Google Scholar]
- Gentleman R, et al. Bioconductor: open software development for computational biology and bioinformatics. Genome Biol. 2004;5:R80. doi: 10.1186/gb-2004-5-10-r80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentleman R, et al., editors. Bioinformatics and Computational Biology Solutions Using R and Bioconductor. Springer, LLC; New York: 2005. [Google Scholar]
- Guo L, et al. Rat toxicogenomic study reveals analytical consistency across microarray platforms. Nat. Biotechnol. 2006;24:1162–1169. doi: 10.1038/nbt1238. [DOI] [PubMed] [Google Scholar]
- Guo W, et al. Controlling false discoveries in multidimensional directional decisions, with applications to gene expression data on ordered categories. Biometrics. 2009;9999 doi: 10.1111/j.1541-0420.2009.01292.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannah M, et al. Global mRNA changes in microarray experiments. Nat. Biotechnol. 2008;26:741–742. doi: 10.1038/nbt0708-741. [DOI] [PubMed] [Google Scholar]
- Holloway AJ, et al. Statistical analysis of an RNA titration series evaluates microarray precision and sensitivity on a whole-array basis. BMC Bioinformatics. 2006;7:511. doi: 10.1186/1471-2105-7-511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J, et al. Analysis of dose-response effects on gene expression data with comparison of two microarray platforms. Bioinformatics. 2005;21:3524–3529. doi: 10.1093/bioinformatics/bti592. [DOI] [PubMed] [Google Scholar]
- Irizarry R, et al. Feature-level exploration of a published Affymetrix GeneChip control dataset. Genome Biol. 2006;7:404. doi: 10.1186/gb-2006-7-8-404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irizarry R, et al. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics. 2003;4:249. doi: 10.1093/biostatistics/4.2.249. [DOI] [PubMed] [Google Scholar]
- Lin D, et al. Testing for trends in dose-response microarray experiments: a comparison of several testing procedures, multiplicity and resampling-based inference. Stat. Appl. Genet. Mol. 2007;6:1. doi: 10.2202/1544-6115.1283. [DOI] [PubMed] [Google Scholar]
- Maouche S, et al. Performance comparison of two microarray platforms to assess differential gene expression in human monocyte and macrophage cells. BMC Genomics. 2008;9:302. doi: 10.1186/1471-2164-9-302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesarin F. Multivariate Permutation Tests. Wiley; New York: 2001. [Google Scholar]
- Pinheiro J, Bates D. Mixed-effects Models in S and S-PLUS. Springer; New York: 2000. [Google Scholar]
- Pruitt K, et al. NCBI reference sequences (RefSeq): a curated non-redundant sequence database of genomes, transcripts and proteins. Nucleic Acids Res. 2006;35:D61–D65. doi: 10.1093/nar/gkl842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team . R: a language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2010. ISBN 3-900051-07-0. Available at http://www.R-project.org/ [Google Scholar]
- Sampson AR, et al. Order restricted estimators: some bias results. Stat. Probab. Lett. 2003;61:299–308. [Google Scholar]
- Scherer A. Batch Effects and Noise in Microarray Experiments: Sources and Solutions. Wiley; Chichester, UK: 2009. [Google Scholar]
- Searle SR, et al. Variance Components. Wiley; New York: 1992. [Google Scholar]
- Shippy R, et al. Using RNA sample titrations to assess microarray platform performance and normalization techniques. Nat. Biotechnol. 2006;24:1123–1131. doi: 10.1038/nbt1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stafford P. Methods in Microarray Normalization. CRC; Boca Raton, US: 2008. [Google Scholar]
- Taylor B, Kuyatt C. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results. NIST; 1994. [Google Scholar]
- The MAQC Consortium The MicroArray quality control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements. Nat. Biotechnol. 2006;24:1151–1161. doi: 10.1038/nbt1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westfall P, Young S. Resampling Based Multiple Testing Procedures. Wiley; New York: 1993. [Google Scholar]
- Zehetmayer S, Posch M. Post hoc power estimation in large-scale multiple testing problems. Bioinformatics. 2010;26:1050. doi: 10.1093/bioinformatics/btq085. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.