Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Feb 29;6:22330. doi: 10.1038/srep22330

Discovery of Superconductivity in Hard Hexagonal ε-NbN

Yongtao Zou 1,2,a, Xintong Qi 3, Cheng Zhang 4, Shuailing Ma 1, Wei Zhang 5, Ying Li 2,b, Ting Chen 3, Xuebing Wang 3, Zhiqiang Chen 2, David Welch 4,6, Pinwen Zhu 1, Bingbing Liu 1, Qiang Li 4, Tian Cui 1, Baosheng Li 2
PMCID: PMC4770320  PMID: 26923318

Abstract

Since the discovery of superconductivity in boron-doped diamond with a critical temperature (TC) near 4 K, great interest has been attracted in hard superconductors such as transition-metal nitrides and carbides. Here we report the new discovery of superconductivity in polycrystalline hexagonal ε-NbN synthesized at high pressure and high temperature. Direct magnetization and electrical resistivity measurements demonstrate that the superconductivity in bulk polycrystalline hexagonal ε-NbN is below ∼11.6 K, which is significantly higher than that for boron-doped diamond. The nature of superconductivity in hexagonal ε-NbN and the physical mechanism for the relatively lower TC have been addressed by the weaker bonding in the Nb-N network, the co-planarity of Nb-N layer as well as its relatively weaker electron-phonon coupling, as compared with the cubic δ-NbN counterpart. Moreover, the newly discovered ε-NbN superconductor remains stable at pressures up to ∼20 GPa and is significantly harder than cubic δ-NbN; it is as hard as sapphire, ultra-incompressible and has a high shear rigidity of 201 GPa to rival hard/superhard material γ-B (∼227 GPa). This exploration opens a new class of highly desirable materials combining the outstanding mechanical/elastic properties with superconductivity, which may be particularly attractive for its technological and engineering applications in extreme environments.

Hard superconducting materials have attracted considerable interest in materials science, condensed matter physics and solid-state chemistry since the discovery of the superconductivity in superhard boron-doped diamond with a transition temperature of TC ∼ 4 K1,2,3,4,5. For transition-metal nitrides, some of them possess very good superconductivity (e.g. 10 K for ZrN, 8.8 K for HfN, 17.3 K for δ-NbN), as well as excellent mechanical properties such as low compressibility, high shear rigidity and high hardness6,7,8,9,10,11,12,13,14,15,16. Despite the TC for transition-metal nitrides is not very high, their remarkable mechanical properties make them good candidates of hard superconductors for specific electronic/high-field applications17 as well as potential applications in motor system, carbon-nanotube junctions and high-pressure devices18. In addition, the chemical inertness and high melting points also make these nitrides suitable for protective and wear-resistant coatings19.

It is known that rock-salt structured δ-NbN possesses the highest transition temperature among transition-metal nitrides (∼17 K), and has several polymorphs4,8,20,21,22,23 such as WC-type NbN, δ-NbN (NiAs-type) and hexagonal ε-NbN (#194, P63/mmc), but only cubic δ-NbN has been extensively investigated1,2,4,8. Recent first-principles theoretical calculations of the thermodynamic properties and structural stability in NbN polymorphs22,23 (e.g. NaCl-, NiAs- and WC-type NbN) predicted that the hexagonal-structured NbN (e.g. WC- and NiAs-type) exhibited higher hardness and lower total energy than the cubic δ-NbN. These results indicated that the hexagonal phases were more stable than the cubic counterpart which appeared to be the most energetically unfavorable structure or metastable phase with the rock-salt structure.

For hexagonal ε-NbN polymorph, despite its crystal structure was ever simply referred by Terao24 and Holec et al.25, the experimental studies on hexagonal ε-NbN are very scarce, especially for its superconductivity and mechanical/elastic properties which have never been reported. Recently, the wide and growing interest lies in searching for novel materials with comprehensive superconductivity and excellent mechanical/elastic properties, which makes ε-NbN a good candidate of hard superconductors for the possible use in extreme environments. Here, we report the discovery of superconductivity in bulk polycrystalline hexagonal ε-NbN, and the findings of its ultra-incompressibility, high shear rigidity and hardness.

Results

Synthesis and structural stability of hexagonal ε-NbN at high pressure

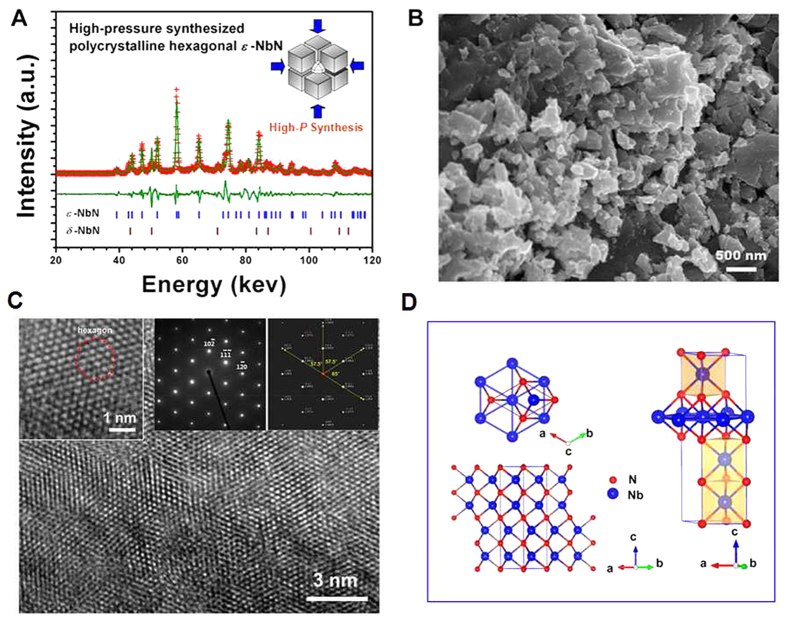
Polycrystalline hexagonal ε-NbN bulk specimens used for the current magnetization and electrical resistivity measurements were synthesized from niobium nitride starting material (Goodfellow, claimed 99% purity) at 10 GPa and 1100∼1200 °C for 1.5 hour in a high-pressure multi-anvil apparatus at Stony Brook University. Details of this experimental setup were described elsewhere26,27,28,29,30,31. As shown in Fig. 1A, the synthetic specimen is almost a pure phase of ε-NbN with the hexagonal structure (PDF: #89-4757) coexisting with a minor amount of cubic δ-NbN. The volume fraction of cubic δ-NbN was estimated to be ∼2% from the intensity of the δ-NbN peaks observed in synchrotron X-ray diffraction; and there is not any other phases observed within the resolution of the current X-ray diffraction, such as tetragonal Nb4N3, hexagonal Nb2N, and so on.

Figure 1.

Figure 1

Open in a new tab

(A) Observed (red crosses) and fitted (olivine lines) synchrotron X-ray diffraction pattern of the synthesized bulk polycrystalline niobium nitride specimen for the present magnetization and electrical resistivity measurements. The peak positions of the hexagonal ε-NbN (PDF: #89-4757) and cubic δ-NbN (PDF: #74-1218) structures are denoted by tick marks. (B) SEM image showing the microstructure of the synthesized polycrystalline hexagonal-structured ε-NbN for the current measurements. The synthetic specimen was free of visible microcracks with an average grain size of about 1 μm, exhibiting an equilibrated microstructure with homogeneous fine grains. (C) High resolution TEM (HRTEM) of the synthesized specimen; the corresponding observed and simulated SAED patterns and the enlarged portion of the HRTEM image are displayed as insets. (D) Crystal structure of the hexagonal ε-NbN (P63/mmc, No. 194). The blue large and red small spheres represent Nb and N atoms, respectively.

Further SEM observations revealed that the synthesized specimen was free of visible microcracks with an average grain size of about 1-2 μm, and exhibited an equilibrated and homogeneous microstructure, as shown in Fig. 1B. The corresponding composition analyses of the synthetic specimen yielded Nb0.98(2)N0.96(5)O0.06(4) as determined by the SEM-EDX measurements, indicating that the as-synthesized specimen was almost oxygen-free ε-NbN or stoichiometric nitride within its uncertainty. The composite has also been studied by high-resolution TEM (HRTEM), which shows that the specimen possesses perfect crystalline form (Fig. 1C). The major phase was confirmed to be hexagonal ε-NbN. The up-mid inset to the HRTEM image shows the corresponding observed selected area electron diffraction (SAED) pattern along [211] axis, which can be indexed to the relevant reported structure (space group: P63/mmc, No. 194). For further confirmation of the structure, the simulated SAED pattern projected along [211] axis is also shown in an up-right inset to Fig. 1C. The enlarged HRTEM, as an up-left inset in Fig. 1C, shows a clear hexagon formed by Nb atoms. Crystal structures of the transition-metal nitrides are generally characterized by strong intermetallic bonding with transition-metal atoms and N atoms occupying octahedral, tetrahedral or trigonal prismatic sites, giving rise to a large cohesive energy. In the hexagonal ε-NbN, each N atom is surrounded by six Nb atoms and there are six N atoms around the Nb atoms (Fig. 1D).

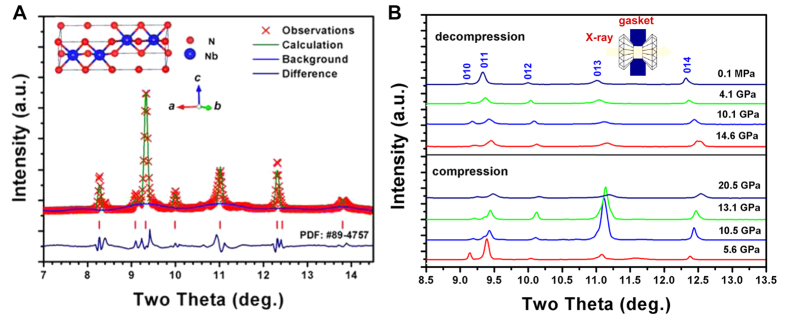
The crystal structure of ε-NbN has been further explored by the refinement of high-resolution in situ angle-dispersive X-ray diffraction pattern (Fig. 2A), yielding a = 2.9599(4) Å, c = 11.2497(22) Å and V0 = 85.352(19) Å3 (Rwp = 5.65%, Rp = 2.60%, chi^2 = 0.5977) with a space group of P63/mmc (No. 194). The lattice parameters are in good agreement with the previous experimental results (a = 2.960 Å, c = 11.270 Å) reported by Terao24, and comparable to our theoretically calculated results from GGA (a = 2.947 Å, c = 11.611 Å) and LDA (a = 2.908 Å, c = 11.464 Å), as well as the previous theoretical study (a = 2.993 Å, c = 11.415 Å)25. According to the well-known Born stability criteria32, the hexagonal ε-NbN is found to be mechanically stable, whereas the cubic δ-NbN is mechanically unstable based on our first-principles calculations of the elastic constants. Selected angle-dispersive synchrotron in situ X-ray diffraction patterns of ε-NbN upon compression in a diamond anvil cell (DAC) are shown in Fig. 2B. For comparison, the X-ray diffraction patterns of the specimen during decompression are also shown in Fig. 2B. Clearly, no phase transitions are observed throughout this experiment and the hexagonal-structured ε-NbN remains stable at pressure up to ∼20.5 GPa.

Figure 2.

Figure 2

Open in a new tab

(A) Refined synchrotron angle-dispersive X-ray diffraction pattern of NbN powder at ambient conditions, suggesting a hexagonal-structured ε-NbN: (Space group: P63/mmc, No. 194). Red crosses and olivine lines denote the observed and calculated profiles, respectively. The red tick marks correspond to the peak positions of hexagonal ε-NbN (PDF: #89-4757). The inset is the crystal structure of hexagonal ε-NbN. (B) Selected synchrotron angle-dispersive X-ray diffraction patterns of ε-NbN upon compression up to ∼20.5 GPa, in comparison with those during decompression where the peaks of the hexagonal phase were indexed (PDF: #89-4757).

Superconductivity in bulk polycrystalline hexagonal ε-NbN

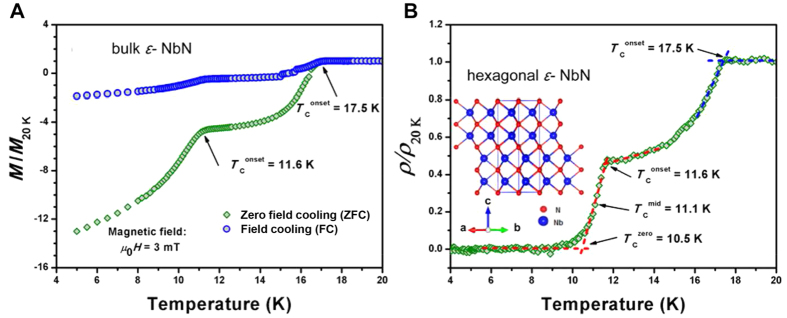
Figure 3A shows normalized magnetization for a bulk polycrystalline hexagonal ε-NbN as a function of temperature below 20 K under a magnetic field of 3 mT (or 30 Oe). Clearly, the magnetic susceptibility measurements reveal obvious diamagnetic responses at temperatures of ∼11.6 K and ∼17.5 K, respectively. The magnetic anomaly occurring at ∼17.5 K is ascribed to the superconducting transition of NaCl-structured cubic δ-NbN, while the magnetic anomaly at ∼11.6 K is related to the hexagonal ε-NbN phase. The existence of the hysteresis between the two magnetization curves for the zero-field cooling (ZFC) and field cooling (FC) modes shows that the hexagonal ε-NbN specimen is a typical type-II superconducting material.

Figure 3.

Figure 3

Open in a new tab

(A) Temperature dependence of the normalized magnetization M/M20 K of bulk polycrystalline hexagonal ε-NbN at ambient pressure. (B) Electrical resistivity of the hexagonal ε-NbN specimen as a function of temperature at ambient pressure. The data are normalized to the values at 20 K (arrows show the superconducting transition points).

The observed superconducting transition temperatures of TC = 11.6 K and 17.5 K for the hexagonal ε-NbN and cubic δ-NbN, have been further addressed/confirmed by the current energy-dispersive X-ray diffraction pattern where the two-phase coexisting specimen is identified (Fig. 1A). As shown in Fig. 1A, the as-synthesized bulk polycrystalline hexagonal ε-NbN is coexisting with a minor amount of cubic δ-NbN. Using the Voigt bound for our theoretical calculations, we know that the abundance of δ-NbN of ∼2% will result in less than 1% difference in elastic moduli as compared with those for pure hexagonal ε-NbN28. This difference is within the experimental uncertainties, indicating that the effect of the minor δ-NbN on the elasticity of the nominal hexagonal-structured ε-NbN can be negligible. In contrast, the appearance of the minor δ-NbN (∼2%) has a significant effect on its electrical/magnetic properties. On the basis of the previous studies on the superconducting transition temperature14 (TC ≈ 17.3 K) of δ-NbN and our XRD measurements, we thus conclude that the observed superconductivity at temperatures around 17.5 K should be attributed to minor phase of cubic δ-NbN, and the relatively low transition at 11.6 K is due to the hexagonal ε-NbN major phase. The nature of superconductivity in bulk hexagonal ε-NbN has further confirmed by our direct electrical resistivity measurements, exhibiting two resistive transitions at temperatures of ∼11.6 K and ∼17.5 K, respectively (Fig. 3B). These observed resistivity anomalies occur at almost the same temperatures with those obtained by magnetic susceptibility measurements (Fig. 3A). As shown in Fig. 3B, the onset transition temperature of ε-NbN is about 11.6 K, and zero resistivity is achieved at TC = 10.5 K. By using the 90/10 criterion of superconducting transition temperature, we find that the midpoint of the electrical resistivity transition (i.e. the resistivity drops to 50% of that at 11.6 K) is about 11.1 K. The transition width is as small as ∼1 K, suggesting that the bulk polycrystalline hexagonal ε-NbN (nominal) specimen owns high quality and the homogeneous nature of the crystals.

Anisotropic behavior and mechanical/elastic properties of hexagonal ε-NbN

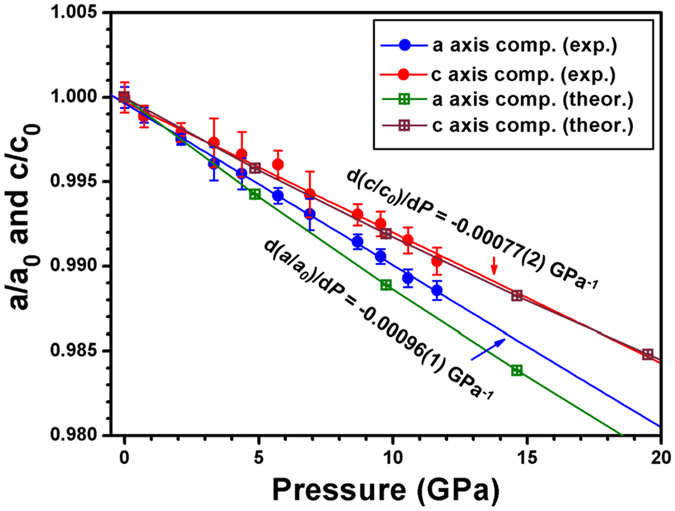
Niobium nitride polymorphs are attractive also due to their excellent mechanical/elastic properties (elastic behavior) besides their superconductivity, so understanding their hardness, elastic behavior, especially the Young’s modulus (E) and shear modulus (G), are of great importance for technological and engineering applications4. Compressibility measurements upon compression revealed a significant degree of anisotropy in the elastic behavior of hexagonal ε-NbN, where ε-NbN is more compressible along the a-axis direction, while stiffer along the c-axis. The least-squares fit of the lattice constants as a function of pressure yields d(a/a0)/dP = −0.00096(1) GPa−1 and d(c/c0)/dP = −0.00077(2) GPa−1, as shown in Fig. 4. For comparison, our theoretical first-principles calculations of the pressure-dependent lattice constants are also displayed here, agreeing well with our experimental data, especially for the compressibility of c-axis.

Figure 4. Experimental crystal-axis compression of hexagonal ε-NbN as a function of pressure, in comparison with the theoretical results by our first-principles calculations (GGA).

Figure 4

Open in a new tab

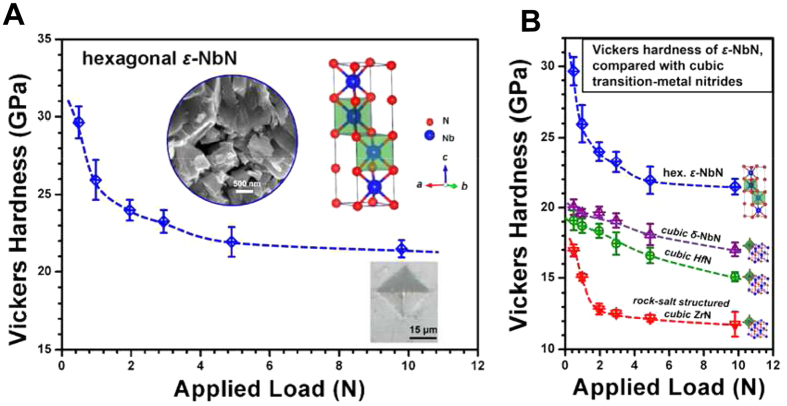
Hardness measurements were performed on the synthesized polycrystalline hexagonal ε-NbN by means of the Vickers indentation method using a pyramidal diamond indenter. The loading force of the hardness tester is adjusted from 2.94 to 9.8 N (0.49, 0.98, 1.98, 2.94, 4.9 and 9.8 N loads). The dwelling time was fixed at 15 s. At each applied load, five indentations were performed. Under a certain applied load of P, the hardness (HV) was determined by HV = 1854.4P/d2, where d is the arithmetic mean of the two diagonals of the indent in micrometers33,34. The average HV values were 29.7 ± 1.0, 26.0 ± 1.3, 24.0 ± 0.7, 21.9 ± 1.0 and 21.5 ± 0.6 GPa under a load of 0.49, 0.98, 1.98, 2.94, 4.9 and 9.8 N, respectively. The results show that the hardness appears to increase with a decrease under various loading forces. The average measured Vickers hardness HV for polycrystalline hexagonal ε-NbN under different loads are shown in Fig. 5A. Clearly, the hexagonal ε-NbN exhibits a Vickers hardness of 22∼30 GPa, which is significantly harder than the high-pressure synthesized polycrystalline ReB2 (17∼19 GPa) as reported by Qin et al.34 and is almost as hard as sapphire Al2O34. Figure 5B shows a summary of the Vickers hardness of ε-NbN as a function of applied load, compared with the previous study on rock-salt structured cubic NbN, HfN and ZrN, showing that the hexagonal-structured ε-NbN is consistently harder than cubic NbN (17∼20 GPa), HfN (15.5∼19.1 GPa) and ZrN (11.8∼16.9 GPa) under various loading forces ranging from 0 to 9.8 N, respectively4.

Figure 5.

Figure 5

Open in a new tab

(A) Average measured Vickers hardness (HV) for polycrystalline hexagonal ε-NbN under different applied loads, indicating that the tendency of hardness decreases and becomes weak with large loads; SEM image, crystal structure and a typical Vickers indentation image at a load of 9.8 N are displayed as insets. (B) Comparing the Vickers hardness of hexagonal ε-NbN with those for the rock-salt structured cubic NbN, HfN and ZrN reported by Chen et al. (ref. 4).

It is widely accepted that bulk and/or shear moduli can reflect the hardness in an indirect way27,35. To further explore the correlations between the elastic modulus (B, G, E) and other physical properties, we have performed in situ ultrasonic measurements on hexagonal ε-NbN at high pressure. The experimental procedure in details can be seen elsewhere26,27,28,29,30,31. The high-pressure elasticity and sound velocities of hexagonal ε-NbN are out of the current scope of this paper and will be published elsewhere28. The ambient-condition bulk and shear moduli derived from the acoustic measurements on ε-NbN yielded BS0 = 373(2) GPa and G0 = 201(1) GPa28. Clearly, hexagonal ε-NbN exhibits a remarkable incompressibility, which is as incompressible/stiff as superhard material cBN (∼381 GPa)36. The shear rigidity of ε-NbN (∼201(1) GPa) rivals that for superhard γ-B (∼227 GPa)37, which is well consistent with the theoretical shear modulus/rigidity of G0 = 199 GPa by our first-principles calculations. According to our experimentally obtained bulk (BS) and shear (G) moduli, the Young’s modulus (E) is derived to be 510(1) GPa by applying the equation E = 9BSG/(3BS + G), which surpasses that of superhard B6O-B4C composite (501 GPa)38, and can be comparable to that of polycrystalline cBN (587 GPa)39, indicating that the hexagonal ε-NbN will also be a good candidate for mechanical applications.

Discussion

Mechanism of superconductivity in hexagonal ε-NbN

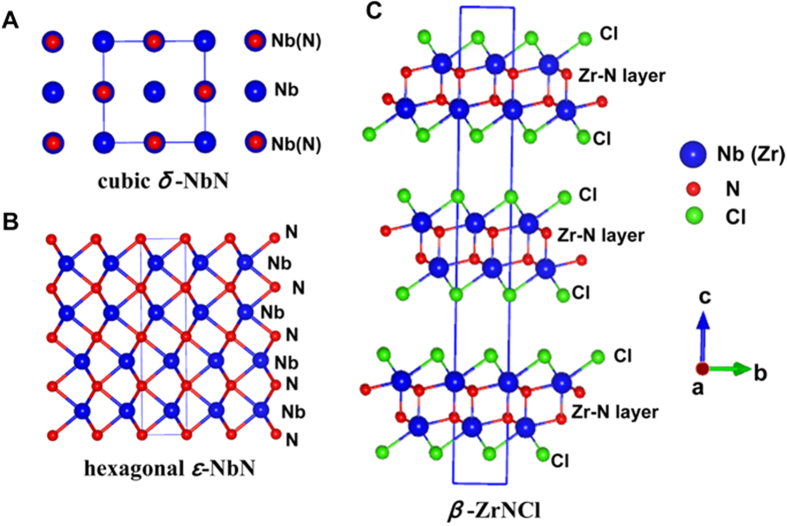
It is well known that the rock-salt structured transition-metal nitrides (e.g. ZrN, NbN, HfN) and the rhombohedral β-ZrNCl (∼13 K) and β-HfNCl (∼26 K) compounds show good superconductivity8,15,40,41. The structures of cubic δ-NbN, hexagonal ε-NbN and rhombohedral β-ZrNCl along a axis are shown in Fig. 6. In the hexagonal-structured ε-NbN, each N atom is surrounded by six Nb atoms and there are six N atoms around the Nb atoms (Fig. 6B). The rhombohedral β-ZrNCl can be considered to be composed of alternate stacking of honeycomb ZrN bilayers sliced from a ZrN crystal of the hexagonal structure and sandwiched by chloride layers, as shown in Fig. 6B,C. Therefore, the Nb-N layer in hexagonal-structured ε-NbN, as shown in Fig. 6B, is considered a critical component to stabilizing its superconductivity.

Figure 6.

Figure 6

Open in a new tab

Comparison of the atomic structures of cubic δ-NbN (A), hexagonal ε-NbN (B) and rhombohedral β-ZrNCl (C) along a axis. The corresponding single unit cell is displayed in solid line. Blue, red, and green spheres stand for Zr/Nb, N and Cl atoms, respectively.

To gain insight into the mechanism of superconductivity in hexagonal ε-NbN against those for the rock-salt structured nitrides as well as rhombohedral β-ZrNCl, their crystal structures (Fig. 6) and their structural parameters have been further investigated. The lattice constants, average bond length, bond angle and superconducting transition temperatures (TC) of niobium nitrides derived from our first-principles calculations and magnetic/electrical measurements are summarized in Table 1, in comparison with those of cubic ZrN and β-ZrNCl superconductors40,41. Our theoretical calculations show that the average bond length of Nb-N for hexagonal ε-NbN (2.2219 Å) is longer than those of the NaCl-structured NbN (2.2077 Å) and rhombohedral β-ZrNCl (2.2127 Å), but shorter than that of cubic ZrN (2.2890 Å). As shown in Fig. 6, the average bond angle (N-Nb-N) for the distorted NbN6 (trigonal prismatic coordination) of ε-NbN is ∼82.25°, and the layered hexagonal-structured ε-NbN is almost coplanar against the NaCl-structured NbN/ZrN with the bond angle of 90°. Therefore, the weaker bonding in the Nb-N network and the co-planarity may be the reason for the relatively lower TC (∼11.6 K) compared with the cubic δ-NbN counterpart (∼17.5 K). This correlation is further supported by the rock-salt structured ZrN and rhombohedral β-ZrNCl superconductors (Table 1), where a stronger bonding of Zr-N in β-ZrNCl (2.2127 Å) results in a higher TC (∼13.0 K), in comparison with the NaCl-structured ZrN (2.2890 Å, 10.7 K). On the other hand, the shorter average bond length of N-N (2.9728 Å) for ε-NbN together with the lower total energy, compared with δ-NbN (N-N: 3.2122 Å), indicated that the hexagonal ε-NbN is more stable than the cubic counterpart.

Table 1. Structural parameters and superconducting transition temperatures (T C ) of transition-metal nitrides.

Compounds hexagonal ε-NbN δ-NbN cubic ZrN β-ZrNCl
Lattice constant (Å)
 a 2.9722 4.4154 4.576 3.606
 c 11.2891 4.4154 4.576 27.67
Bond length (Å)
 M-N 2.2219 2.2077 2.2890 2.2127
 N-N 2.9728 3.2122 – –
Bond angle
 N-M-N 82.3° 90° 90° 115.9°
 TC(K) 11.6 17.5 10.7 13.0
 Ref. This study This study Ref. 40 Ref. 40,41
Open in a new tab

For phonon-mediated superconductivity, TC is given by McMillan’s formula 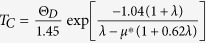Inline graphic, where ΘD is the Debye temperature, μ* is the Coulomb pseudopotential or electron-electron interaction constant and λ is the electron-phonon coupling42. Based on the obtained elastic bulk and shear moduli together with the ambient-condition density ρ = 8.30(2) g/cm3 of hexagonal ε-NbN as derived from our ultrasonic measurements28, the Debye temperature ΘDis determined to be ∼738 K from the equation28 described as 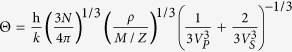Inline graphic, which is significantly larger than the theoretical result of ΘD = 629 K for cubic δ-NbN43, and is double the previously experimental value of ∼363 K (ref. 11). Using the obtained values of ΘD = 738 K, TC = 11.6 K, and a well-accepted Coulomb parameter μ* = 0.1∼0.13 for transition-metal nitrides3, we estimate the electron-phonon coupling constant λ = 0.57∼0.63. This yielded electron-phonon coupling λ = 0.57∼0.63 for ε-NbN is significantly weaker than those (λ = 0.87 and 0.906) for cubic δ-NbN counterpart 8,9.

It is clearly seen from the McMillan’s formula42 that the effects of λ (as the exponential term) on the TC is much more significant than ΘD (as the linear term), which can shed light on the relatively smaller TC = 11.6 K, compared with TC = 17 K for δ-NbN44. The relatively small value of λ for ε-NbN can be understood qualitatively from the relation of 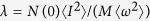Inline graphic, where N(0) is the density of electronic states at the Fermi energy, <I2> is the average square of the electron-phonon matrix element, M is the ionic mass and <ω2> is a characteristic phonon frequency averaged over the phonon spectrum having 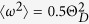Inline graphic (ref. 42). Although the ionic mass of ε-NbN is similar to that of δ-NbN, its stronger covalent bonds in ε-NbN imply a smaller N(0) and larger <ω2>, compared to those for δ-NbN. These results have been further confirmed by experimentally measured ΘD = 738 K for ε-NbN, which is larger than the ΘD = 629 K for δ-NbN43.

First-principles calculations show that the superconducting and mechanical properties for transition-metal nitrides/carbonitrides are closely related to their electronic properties45,46. For a good understanding of the mechanical/superconducting properties of ε-NbN, electronic properties of the total densities of states (TDOS) and partial densities of states (PDOS) for hexagonal ε-NbN at ambient pressure have been calculated, in comparison with those for cubic δ-NbN counterpart (see Supplementary Materials: Fig. S1). Both hexagonal ε-NbN and cubic δ-NbN show similar metallic bonding features with a finite DOS at the Fermi level (EF), originating mostly from the 4d electrons of Nb and 2p electrons of N and agree well with our electrical measurements that ε-NbN is a metallic electrical conductor at ambient conditions. Clearly, there is a strong hybridization between Nb 4d and N 2p states in ε-NbN as revealed by the appearance of “pseudogap” just below and/or above the Fermi level, indicating the covalent and/or ionic bonding between Nb and N atoms (Fig. S1(A)). When comparing with the electronic structures of hexagonal ε-NbN and cubic δ-NbN, we note that there is a small peak dominated by the Nb-d orbital at about −0.68 eV in the DOS for ε-NbN (Fig. S1(A,B)). The appearance of this peak with low energy indicates a stronger bonding arising from the metal d orbitals in ε-NbN as compared to δ-NbN, resulting in an enhancement of the elastic/mechanical strength of ε-NbN. Fig. S1(A) shows that the TDOS around the Fermi level (EF) lies in a dip for ε-NbN, whereas the density of states increases monotonically at EF for δ-NbN (Fig. S1(B)). This agrees well with the result from the total-energy calculations that the hexagonal ε-NbN is more stable than the cubic counterpart.

As reported by Oya et al.47, tetragonal phases γ-Nb4N3 and Nb4N5 with long-range-ordered arrangement of vacancies exhibited superconductivity47, whereas the hexagonal NbN and Nb5N6 didn’t show superconductivity at temperatures down to 1.77 K. For the mechanism of superconductivity in transition-metal nitrides, it is suggested that the continuous promotion of s, p electrons to the d shell in all solids under pressure is one of the factors which will induce superconductivity. As seen from Fig. S1, the contribution of the 4d-state is larger than those of the 5s and 5p states. The larger contribution of 4d state electrons clearly shows the possibility of superconductivity in hexagonal-structured NbN at ambient pressure.

In summary, we have discovered the superconductivity at ∼11.6 K in bulk polycrystalline hexagonal ε-NbN, which was synthesized at high pressure and high temperature in a high-pressure multi-anvil apparatus. The weaker bonding in the Nb-N network and the co-planarity may be the reason for the relatively lower TC (∼11.6 K) compared with the cubic δ-NbN counterpart (∼17.5 K). Our theoretical calculations reveal that the contribution of the 4d-state is larger than those of the 5s and 5p states, and the relatively larger contribution of 4d state electrons may be responsible for the superconductivity in hexagonal ε-NbN. In addition, the hexagonal ε-NbN was found to exhibit excellent mechanical properties, which is as hard as sapphire Al2O3 (21∼23 GPa)4 and possessed a remarkable incompressibility36 (as stiff as superhard cBN of ∼381 GPa). The shear rigidity of ε-NbN (∼201(1) GPa) rivals that for superhard γ-B (∼227 GPa)37, and the Young’s modulus (∼510(1) GPa) is surpassing that for B6O-B4C composite (501 GPa)38. Our theoretical calculations indicate that the hexagonal ε-NbN is more stable than the cubic δ-NbN, and the stronger bonding arising from the metal d orbitals in ε-NbN compared to δ-NbN results in an enhancement of the elastic/mechanical strength of ε-NbN. This study opens a new window for the design of desirable materials with the combination of excellent mechanical properties and superconductivity, which may be particularly attractive for its technological and engineering applications in extreme conditions.

Methods

Magnetization and electrical resistivity measurements on polycrystalline hexagonal ε-NbN

Magnetization measurements of the high-pressure synthesized bulk polycrystalline hexagonal ε-NbN were performed in a Superconducting Quantum Interference Device (SQUID) based magnetometer (MPMS, Quantum Design). Electrical resistivity measurements on hexagonal ε-NbN were conducted in a Physical Property Measurement System (PPMS, Quantum Design) using the standard four-probe method48.

In situ X-ray diffraction study of hexagonal ε-NbN at high pressure

High-pressure synchrotron X-ray experiments using diamond-anvil cell (DAC) techniques were performed at the X17C beamline of National Synchrotron Light Source, Brookhaven National Laboratory. Stainless T301 steel plates with an initial thickness of 250 μm were used as gaskets. The ε-NbN powder, a tiny ruby ball, and the methanol-ethanol pressure medium (4:1) were loaded into the hole in the gasket. The experimental cell-pressure was determined by the pressure-induced fluorescence shift of ruby49. The incident synchrotron radiation beam was monochromatized to a wavelength of 0.40722 Å. The collected two-dimensional X-ray diffraction patterns were analyzed by integrating 2D images as a function of 2θ using the program Fit2D to obtain conventional, one-dimensional profiles50.

First-principles calculations

Our first-principles calculations were performed with the CASTEP code51, based on density functional theory (DFT) using Vanderbilt-type ultrasoft pseudopotentials and a plane-wave expansion of the wave functions52. The local density approximation (LDA) and generalized gradient approximation (GGA) in the scheme of Perdew-Burke-Ernzerhof (PBE) were employed for determination of the exchange and correlation potentials for electron-electron interactions. The Broyden-Fletcher-Goldfarb-Shanno optimization method was applied to search for the ground states of ε-NbN. For the Brillouin-zone sampling, the Monkhorst-Pack scheme was adopted53. To confirm the convergence of our calculations, we have carefully analyzed the dependences of the total energy on the cutoff energy and the k-point set mesh according to the Monkhorst-Pack grid. During our first-principles calculations, the difference in total energy was minimized to below 5 × 10−7 eV/atom, the maximum ionic Hellmann-Feynman force is converged to less than 0.01 eV/Å, and the total stress tensor is reduced to the order of 0.02 GPa by using the finite basis-set corrections. The valance configuration is 4p65 s14d4 and 2s22p3 for Nb and N, respectively. Integrations in the Brillouin zone are performed using special k points generated with 10 × 10 × 2. One-electron valence states are expanded on a basis of plane waves with a cutoff energy of 600 eV in the electronic property calculations. All these parameters have been tested to be sufficient for the convergence.

Additional Information

How to cite this article: Zou, Y. et al. Discovery of Superconductivity in Hard Hexagonal ε-NbN. Sci. Rep. 6, 22330; doi: 10.1038/srep22330 (2016).

Supplementary Material

Supplementary Information
srep22330-s1.pdf (241.6KB, pdf)

Acknowledgments

This work is supported by NSF (EAR1045630) and DOE/NNSA (DENA0001815) to B. Li. Y. Z acknowledges the supports from the National Natural Science Foundation of China (No. 51032001) to T. C., as well as the Scientific Research Foundation of Jilin University for the Overseas Scholars (No. 419080500385) and Open Project of State Key Laboratory of Superhard Materials, Jilin University (No. 1G3155051460) to Y. Z. The work at Brookhaven National Lab was supported by the U.S. Department of Energy, Office of Basic Energy Science, Division of Materials Science and Engineering, under Contract No. DE-SC0012704. The current ultrasonic, magnetization and electrical resistivity measurements were performed in the U. S. when Yongtao Zou was working at the State University of New York (Stony Brook). Y. Z. very much appreciates Hiroaki Ohfuji (Ehime University, Japan) for his kind/unselfish help with the HRTEM-SAED analyses, Robert C. Liebermann for his valuable discussion and suggestions, and Qiang Tao for the assistance of the TEM measurements. The operation of X17C is supported by COMPRES, the Consortium for Materials Properties Research in Earth Sciences under NSF (EAR 10-43050). Mineral Physics Institute Publication No. 505.

Footnotes

Author Contributions Y.Z. and B.L. designed this work. Y.Z., C.Z., Q.L., D.W., P.Z., B.B.L., T.C. and B.L. analyzed the data and wrote this manuscript. Y.Z., S.M., X.Q., X.W., Y.L., W.Z., Z.C., P.Z., B.B.L., T.C. and B.L. conducted in situ ultrasonic measurements, synchrotron X-ray diffraction experiments, hardness measurements, theoretical calculations, HRTEM-SAED and SEM-EDX analyses. C.Z. and Q.L. performed superconductivity characterization by magnetization and transport measurements. All the authors contributed to discussion on the results for this manuscript.

References

  1. Yan C. S. et al. Ultrahard diamond single crystals from chemical vapor deposition. Phys. Stat. Sol. A 201, R25–27 (2004). [Google Scholar]
  2. Ekimov E. A. et al. Superconductivity in diamond. Nature 428, 542–545 (2004). [DOI] [PubMed] [Google Scholar]
  3. Occelli F., Loubeyre P. & LeToullec R. Properties of diamond under hydrostatic pressures up to 140 GPa. Nat. Mater. 2, 151–154 (2003). [DOI] [PubMed] [Google Scholar]
  4. Chen X.-J. et al. Hard superconducting nitrides . Proc. Natl. Acad. Sci. USA 102, 3198–3201 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Soignard E., Shebanova O. & McMillan P. F. Compressibility measurements and phonon spectra of hexagonal transition-metal nitrides at high pressure: ε-TaN, δ-MoN, and Cr2N. Phys. Rev. B 75, 014104 (2007). [Google Scholar]
  6. Ihara H. et al. Electronic structures of B1-MoN, fcc Mo2N, and hexagonal MoN. Phys. Rev. B 31, 3177 (1985). [DOI] [PubMed] [Google Scholar]
  7. Bull C. L., McMillan P. F., Soignard E. & Leinenweber K. Determination of the crystal structure of δ-MoN by neutron diffraction. J. Solid State Chem. 177, 1488–1492 (2004). [Google Scholar]
  8. Chen X.-J. et al. Electronic stiffness of a superconducting niobium nitride single crystal under pressure. Phys. Rev. B 72, 094514 (2005). [Google Scholar]
  9. Chen X.-J. et al. Pressure-induced phonon frequency shifts in transition-metal nitrides. Phys. Rev. B 70, 014501 (2004). [Google Scholar]
  10. Wu Z., Chen X.-J., Struzhkin V. V. & Cohen R. E. Trends in elasticity and electronic structure of transition-metal nitrides and carbides from first principles. Phys. Rev. B 71, 214103 (2005). [Google Scholar]
  11. Hulm J. K., Walker M. S. & Pessall N. High TC-experimental achievement. Physica, 55, 60 (1971). [Google Scholar]
  12. Wang S. et al. Synthesis, crystal structure, and elastic properties of novel tungsten nitrides. Chem. Mater. 24, 3023–3028 (2012). [Google Scholar]
  13. Salamat A. et al. Synthesis of tetragonal and orthorhombic polymorphs of Hf3N4 by high-pressure annealing of a prestructured nanocrystalline precursor. J. Am. Chem. Soc. 135, 9503–9511 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Williams M. W., Ralls K. M. & Pickus M. R. Superconductivity of cubic niobium carbo-nitrides. J. Phys. Chem. Solids 28, 333–341 (1967). [Google Scholar]
  15. Zerr A., Miehe G. & Riedel R. Synthesis of cubic zirconium and hafnium nitride having Th3P4 structure. Nat. Mater. 2, 185–189 (2003). [DOI] [PubMed] [Google Scholar]
  16. Zerr A. et al. High-pressure synthesis of tantalum nitride having orthorhombic U2S3 Structure. Adv. Funct. Mater. 19, 2282–2288 (2009). [Google Scholar]
  17. Deis D. W., Gavaler J. R., Hulm J. K. & Jones C. K. High field properties of pure niobium nitride thin films. J. Appl. Phys. 40, 2153 (1969). [Google Scholar]
  18. Kasumov A. Yu. et al. Supercurrents through single-walled carbon nanotubes. Science 284, 1508–1511 (1999). [DOI] [PubMed] [Google Scholar]
  19. Wen M. et al. Effects of substrate bias on the preferred orientation, phase transition and mechanical properties for NbN films grown by direct current reactive magnetron sputtering. J. Appl. Phys. 104, 023527 (2008). [Google Scholar]
  20. Isaev E. I. et al. Phonon related properties of transition metals, their carbides, and nitrides: A first-principles study. J. Appl. Phys. 101, 123519 (2007). [Google Scholar]
  21. Zhao E., Wang J., Meng J. & Wu Z. Structural, mechanical and electronic properties of 4d transition metal mononitrides by first-principles. Comp. Mater. Sci. 47, 1064–1071 (2010). [Google Scholar]
  22. Wang Z. et al. Pressure-induced structural transition and thermodynamic properties of NbN and effect of metallic bonding on its hardness. Europhys. Lett. 92, 56002 (2010). [Google Scholar]
  23. Wang C. et al. First-principles calculations on the mechanical properties of niobium nitrides. Solid State Comm. 149, 725–728 (2009). [Google Scholar]
  24. Terao N. Structure des nitrures de niobium. Japan. J. Appl. Phys. 4, 353–367 (1965). [Google Scholar]
  25. Holec D., Franz R., Mayrhofer P. H. & Mitterer C. Structure and stability of phases within the NbN-AlN system. J. Phys. D: Appl. Phys. 43, 145403 (2010). [Google Scholar]
  26. Zou Y. et al. Elasticity and sound velocities of polycrystalline Mg3Al2(SiO4)3 garnet up to 20 GPa and 1700 K. J. Appl. Phys. 112, 014910 (2012). [Google Scholar]
  27. Zou Y., Gréaux S., Irifune T., Li B. & Higo Y. Unusual pressure effect on the shear modulus in MgAl2O4 spinel. J. Phys. Chem. C 117, 24518–24526 (2013). [Google Scholar]
  28. Zou Y. et al. Hexagonal-structured ε-NbN: ultra-incompressibility, high shear rigidity, and a possible hard superconducting material. Sci. Rep. 5, 10811 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Li B. & Liebermann R. C. Study of the Earth’s interior using measurements of sound velocities in minerals by ultrasonic interferometry. Phys. Earth Plant. Inter. 233, 135–153 (2014). [Google Scholar]
  30. Li B. & Liebermann R. C. Indoor seismology by probing the Earth’s interior by using sound velocity measurements at high pressures and temperatures. Proc. Natl. Acad. Sci. USA. 104, 9145–9150 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Irifune T. et al. Sound velocities of majorite garnet and the composition of the mantle transition region. Nature 451, 814–817 (2007). [DOI] [PubMed] [Google Scholar]
  32. Hu Q. et al. First-principles studies of structural and electronic properties of hexagonal BC5. Phys. Rev. B 73, 214116 (2006). [Google Scholar]
  33. He D. et al. Boron suboxide: As hard as cubic boron nitride. Appl. Phys. Lett. 81, 643 (2002). [Google Scholar]
  34. Qin J. et al. Is rhenium diboride a superhard material? Adv. Mater. 20, 4780–4783 (2008). [Google Scholar]
  35. Chen X.-Q., Niu H., Franchini C., Li D. & Li Y. Hardness of T-carbon: Density functional theory calculations. Phys. Rev. B 84, 121405 (2011). [Google Scholar]
  36. Zhang R. F., Lin Z., Mao H.-K. & Zhao Y. Thermodynamic stability and unusual strength of ultra-incompressible rhenium nitrides. Phys. Rev. B 83, 060101(R) (2011). [Google Scholar]
  37. Qin J. et al. Polycrystalline γ-boron: As hard as polycrystalline cubic boron nitride. Scripta Mater. 67, 257–260 (2012). [Google Scholar]
  38. Chen C. et al. B6O-based composite to rival polycrystalline cubic boron nitride. Adv. Mater. 19, 4288–4291 (2007). [Google Scholar]
  39. Chou Y. K. & Evans C. J. Cubic boron nitride tool wear in interrupted hard cutting. Wear 225, 234–245 (1999). [Google Scholar]
  40. Yamanaka S., Hotehama K. & Kawaji H. Superconductivity at 25.5 K in electron-doped layered hafnium nitride. Nature 392, 580–582 (1998). [Google Scholar]
  41. Ohashi M., Yamanaka S., Sumihara M. & Hattori M. Novel synthesis of the layer structured β-ZrNCl by the direct reactions of zirconium metal or zirconium hydride with ammonium chloride. J. Solid State Chem. 75, 99–104 (1988). [Google Scholar]
  42. McMillan W. L. Transition temperature of strong-coupled superconductors. Phys. Rev. 167, 331 (1968). [Google Scholar]
  43. Ren D. H. & Cheng X. L. First-principles calculations on the elastic and thermodynamic properties of NbN. Chin. Phys. B 21, 127103 (2012). [Google Scholar]
  44. Karecki D., Pena D. E. & Perkowitz S. Far-infrared transmission of superconducting homogeneous NbN films: Scattering time effects. Phys. Rev. B 25, 1565–1571 (1982). [Google Scholar]
  45. Meenaatci A. T. A., Rajeswarapalanichamy R. & Iyakutti K. Electronic structure, structural stability, mechanical and superconducting properties of group VB nitrides: A first principles study. Solid State Sci. 19, 36–44 (2013). [Google Scholar]
  46. Jhi S. H., Ihm J., Louie S. G. & Cohen M. L. Electronic mechanism of hardness enhancement in transition-metal carbonitrides. Nature 399, 132–134 (1999). [Google Scholar]
  47. Oya G. & Onodera Y. Transition temperatures and crystal structures of single-crystal and polycrystalline NbNx films. J. Appl. Phys. 45, 1389 (1974). [Google Scholar]
  48. Si W. et al. Superconductivity in epitaxial thin films of Fe1.08Te: Ox. Phys. Rev. B 81, 092506 (2011). [Google Scholar]
  49. Mao H.-K., Bell P. M., Shaner J. W. & Steinberg D. J. Specific volume measurements of Cu, Mo, Pd, and Ag and calibration of the ruby R1 fluorescence pressure gauge from 0.06 to 1 Mbar. J. Appl. Phys. 49, 3276 (1978). [Google Scholar]
  50. Hammersley A. P. et al. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Pressure Res. 14, 235–248 (1996). [Google Scholar]
  51. Segall M. First-principles simulation: ideas, illustrations and the CASTEP code. J. Phys.: Condens. Matter 14, 2717 (2002). [Google Scholar]
  52. Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892(R) (1990). [DOI] [PubMed] [Google Scholar]
  53. Monkhorst H. J. & Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep22330-s1.pdf (241.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES