Integrating developmental theory and methodology: Using derivatives to articulate change theories, models, and inferences

Abstract

Matching theories about growth, development, and change to appropriate statistical models can present a challenge, which can result in misuse, misinterpretation, and underutilization of different analytical approaches. We discuss the use of derivatives --- the change of a construct with respect to changes in another construct. Derivatives provide a common language linking developmental theory and statistical methods. Conceptualizing change in terms of derivatives allows precise translation of theory into method and highlights commonly overlooked models of change. A wide variety of models can be understood in terms of the level, velocity and acceleration of constructs: the 0^th, 1^st, and 2^nd derivatives, respectively. We introduce the language of derivatives, and highlight the conceptually differing questions that can be addressed in developmental studies. A substantive example is presented to demonstrate how common and unfamiliar statistical methodology can be understood as addressing relations between differing pairs of derivatives.

Of great interest to developmental researchers is the association between two or more changing constructs, and whether and how they are related over time. To do so, methodological factors must be considered, such as the type of statistical model needed to investigate questions about growth, development, and change, and the time scale over which change is expected (Ferrer & McArdle, 2010; Little, 2013; Nesselroade, 1991; Sliwinski, 2011). Models exploring the longitudinal relations between constructs can take many forms (Little, 2013). For example, studies examining relations between mothers’ and children’s depressive symptoms have used correlations of observed scores, hierarchical linear models of change (e.g., Pilowsky et al., 2008), models of latent growth curves with correlated growth parameters (e.g., Garber & Cole, 2010; Gross, Shaw, & Moilanen, 2008), latent change score models (e.g., Kouros & Garber, 2010), and cross-lagged panel designs (e.g., Ge et al., 1995; Jaffee & Poulton, 2006). Each of these models is useful for describing developmental processes, but rarely are the commonalities across the models explicitly noted. This disconnect burdens researchers with the task of figuring out how each analytic approach is or is not appropriate for modeling different types of developmental processes and theories. This confusion also influences the inferences that can or cannot be drawn from specific models.

A bridge between theoretical rationale for development and the appropriate model may be achieved through a common language for statisticians and substantive researchers. In this paper we present derivative terminology, which can aid in the articulation of change and thereby better link developmental theories, models, and inferences. Derivative terminology overlaps with both developmental and statistical concepts, and could serve as a common vocabulary in modeling change. In doing so, developmental psychologists may be able to better understand a wide range of models as part of a common framework, instead of as distinct options whose overlap in commonalities and discrepancies are muddled, at best. We begin by presenting a typical developmental research question on the relation of change between mothers’ and children’s behavior, after which we introduce derivative vocabulary and apply this language to substantive examples to discuss the inferences drawn from differing statistical models.

The Dynamic Relation between Mothers and Children

Developmentalists often are interested in the mother-child dyad, and how change in one member of the dyad could affect the other. The interest in this bidirectional relation between members of a dyad is reflected in many prominent theories and developmental perspectives (dynamic systems; Thelen & Smith, 2006; family systems theory; Cox & Paley, 1997; see also Sameroff, 1975). One dynamic, bidirectional relation of this sort, the transactional association between mothers’ and children’s psychiatric symptoms, also has theoretical and empirical justification (see Gunlicks & Weissman, 2008; Elgar, McGrath, Waschbusch, Stewart, & Curtis, 2004). Theoretically, different mechanisms have been proposed to account for the effect of maternal depression on children’s psychological symptoms (e.g., impairments in parenting and quality of family environment, see Goodman & Gotlib, 1999), as well as the effect of children’s psychological symptoms on maternal depression (e.g., stress of caring for a child with psychological problems, see Elgar et al., 2004). Given strong theoretical support for bidirectional relations, research has focused on providing empirical support for this link; this has been examined with several different models. For example, Gross et al. (2008) and Garber and Cole (2010) tested parallel process models, in which the latent growth parameters representing linear change in mothers’ and children’s symptoms were correlated. Jaffee and Poulton (2006) tested an autoregressive, cross-lag model to test for time-dependent bidirectional relations. Kouros and Garber (2010) used a latent change score model to test for transactional relations. Finally, Nicholson, Deboeck, Farris, Boker, and Borkowski (2011) used differential equation modeling techniques to fit a coupled damped linear oscillator model. These studies have attempted to assess the bidirectional relation using a variety of statistical methods. Notably, some of these methods ask very similar questions about the change processes, despite using different models, whereas others make unique assumptions about how the constructs are related. These different change models may (and frequently do) yield different results and conclusions, and the similarities between models may not be readily apparent (e.g., Kouros, Quasem, & Garber, 2013).

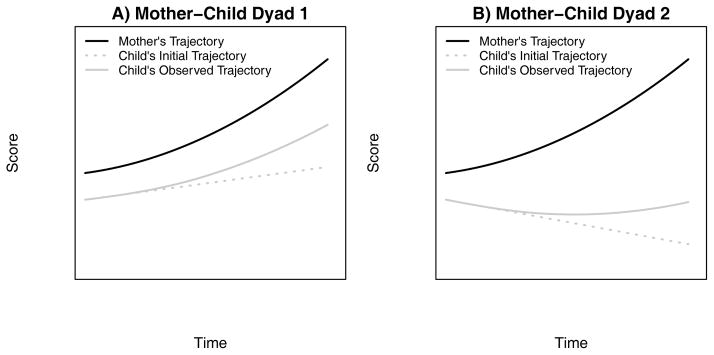
Which model should developmentalists use to test such transactional relations? The difficulty, in part, is that “transactional relation” is vaguely defined from a mathematical perspective, and could imply many different models. Figure 1 depicts hypothetical trajectories for maternal depressive symptoms and child externalizing behavior problems for two dyads. In both Figures 1A and 1B, the mother’s trajectory of depressive symptoms increases over time. Prior to the onset of maternal depression, the child could have many possible initial trajectories, corresponding to increasing or decreasing rate of externalizing behaviors. Had there not been an increase in mother’s depression, we might expect children to continue on these initial trajectories, corresponding to the dashed, gray dotted lines in Figure 1. As mother’s depressive symptoms increase, however, in both cases the children may respond by showing an increase in the number of behavioral problems relative to their expected trajectory (solid gray line).

Figure 1.

Plots of hypothetical trajectories for two mother-child dyads where mother’s depression affects the child’s externalizing behaviors. In both figures the change in child’s behavior (solid gray line) is coupled to the change in mother’s depression (solid black line). The figures differ in the initial trajectories of the children (dashed gray lines). Panel A shows a relation where the scores of the mother and child would be highly correlated. In Panel B, whereas the mother’s depression is leading to changes in the child’s trajectory from his/her initial trajectory, the scores of the mother and child would have a correlation near zero.

We expect that a child’s behaviors would change in response to mother’s depression, but the word change is mathematically vague and does not imply a specific model that can be tested. In these examples, the children in both dyads demonstrate changes in their trajectories in response to the increase in their mother’s depression, but they show very different changes over time despite their starting at baseline with similar scores on externalizing behaviors. The first child (Figure 1A) follows a pattern that would be expected, as there is a positive correlation between maternal depression and children’s externalizing scores due to both variables having positive slopes. In contrast, there would be a correlation of approximately zero between the mother and the second child (Figure 1B), as depression shows a positive slope whereas the child’s corresponding behavioral trajectory appears neutral or slightly negative. A model focused on correlating scores or correlating linear slopes would suggest that the second child’s behavior problems were not related to the mother’s depression, as the change is masked by an initially negative trajectory.

Herein are some of a few questions that can be raised related to how change is defined. In saying that the children have changed in relation to their mothers, are we expecting an increase in the observed levels of their externalizing scores or an increasing slope as with the child in the first dyad (Figure 1A), or a change in the trajectory of the child (i.e., curvature) as seen in both children? Moreover, it must be considered if the child is responding to the level of the mother’s depression, the steepness of her slope, or changes in the steepness of her slope. The imprecise vernacular of using the word change fails to articulate the forms of the relations depicted in Figure 1. Similarly, the word trajectory does not convey a specific form of change, and can be interpreted mathematically in multiple ways. Derivatives offer the potential of specifically defining what is meant by change and the ability to specify components of a trajectory.

Derivatives, being mathematically defined, also allow for translation to and from mathematical models; that is, they allow selection of models that more closely match theory and provide more precise interpretations of the inferences that can or cannot be made with a specific model. Using derivatives as a precise common denominator between theory and method would reduce misunderstandings among developmental researchers and mitigate translating theory into inappropriate statistical models. Using derivative terms to represent change easily identifies models that fit the theory and provides a framework for understanding whether different models address similar questions about change. Additionally, by identifying how current models fit in this framework, new modeling possibilities may be identified.

Derivatives: The Vocabulary of Change

In mathematics, the change in one construct with respect to change in another construct is expressed using derivatives. In this paper we will specifically consider the changes in constructs with respect to time. The value of a construct at a specified point in time is the 0^th derivative; the 0^th derivative is usually described by the name of the substantive construct to which it is referring, but despite differing names in developmental science the 0^th derivative can be generally considered the level of a construct at a specific time. In a plot of a construct (y-axis) versus time (x-axis), the 0^th derivative would be represented with a single point. Changes in the level of a construct, with respect to time, are called the 1^st derivative; the 1^st derivative is the velocity (speed in a specific direction) at which a construct is changing. In a plot of a construct versus time, the 1^st derivative would be the slope of a straight line, and can also be referred to as the rate of change, the rise over the run, and the change in a construct with respect to a change in time. The rate of change in the velocity with respect to time, that is how quickly the slope of a line changes in a single direction, is the 2^nd derivative or the acceleration. Acceleration in a construct plotted versus time would appear as a curved line. While some variation in terms occurs, the present paper utilizes level, velocity, and acceleration to refer to the 0^th, 1^st and 2^nd derivatives.

To gain familiarity with this vocabulary, consider driving a car as a metaphor for a changing construct. The 0^th derivative expresses the level of a construct at a specific time, which in a car would correspond to the position of the car at a specific time. How this position changes with respect to time, or how much of a change in position occurs divided by the elapsed amount of time, is the velocity (1^st derivative) of the car if it is assumed the car is traveling in a single direction along a straight road. The velocity of the car, however, may not be constant as there may be increases or decreases in velocity over some period of time. These changes in velocity are represented in the acceleration of the car (2^nd derivative); the term acceleration is used to represent both positive (acceleration) and negative (deceleration) changes to velocity. Using this metaphor to describe derivatives, we can articulate more clearly the property or properties of any construct of interest to inform our decision of which analysis to choose to investigate how constructs change over time.

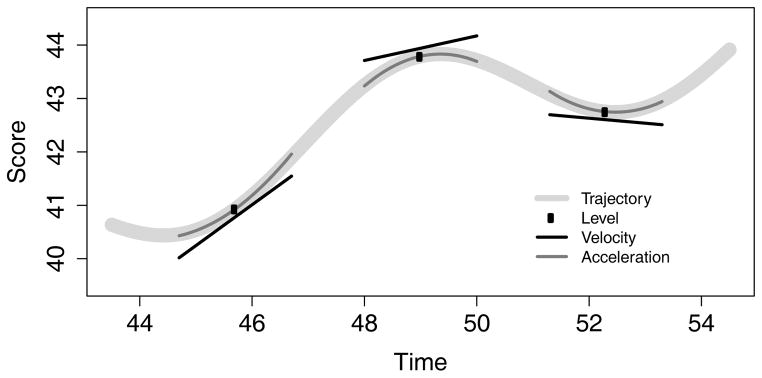
Figure 2 presents another way to visualize level (0^th derivative), velocity (1^st derivative), and acceleration (2^nd derivative). The light gray line represents a hypothetical developmental trajectory. The black circles represent the 0^th derivative, or the level of a construct at any given point in time along this trajectory. The straight black lines tangential to the trajectory represent the velocity of the construct at some particular time. If we examine the slopes just before and after a given point in time, we would see a change in velocity (i.e., acceleration, curved dark gray lines) that could be described using the 2^nd derivative. Table 1 presents a summary of several ways of expressing derivatives. Although using derivative notation may be unfamiliar, researchers who are comfortable thinking in terms of the level of a construct at a specific time (point), straight line change, and curved lines can begin to identify derivatives that correspond to these same concepts.

Figure 2.

Plot of a developmental trajectory (light gray line) with the level (black circles), instantaneous velocity (black lines), and instantaneous accelerations (dark grey lines) at three points in time. In this figure the straight black lines indicate a positive first derivative (velocity) for the first and second points at which derivatives are estimated, and a negative first derivative at the third point. The upwards curved dark gray lines indicate a positive second derivative (acceleration) at the first and last points at which derivatives are estimated; the downwards curve at the second point indicates a negative second derivative.

Table 1.

Vocabulary for Describing Change with Respect to Time

Characteristic of a construct	Name	Graphical Depiction	Derivative	Notation	Dot Notation
Value of the construct: The value of a construct at a specific point in time	Level	Single Point	0th	(x)	x
Slope of the construct: The directional speed at which the level of a person’s construct is changing (with respect to time)	Velocity	Straight Line	1st	$\left(\frac{dX}{dT}\right)$	ẋ
Curvature of the construct: The rate at which a person’s velocity is changing (with respect to time)	Acceleration	Curved Line	2nd	$\left(\frac{d^{2}X}{{dT}^2}\right)$	ẍ

Relating Constructs

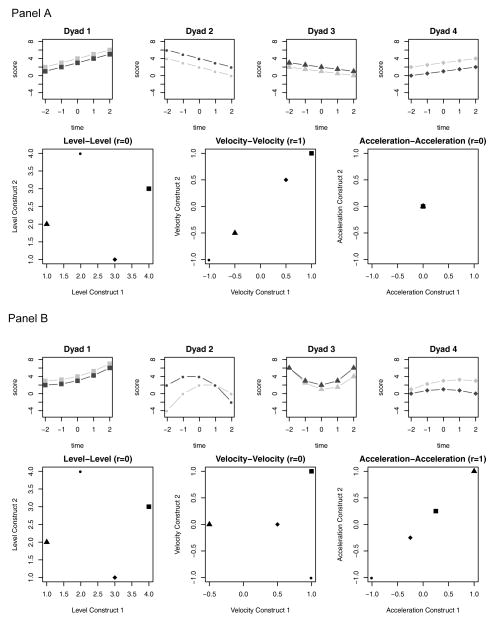
Considering levels, velocities, and accelerations on individual constructs expands the possible ways in which two or more constructs may be related. We return to our example of maternal depression and child externalizing behavior problems. In the context of related constructs, the questions about correlated levels, velocities, and accelerations would respectively address: (1) Are high levels of maternal depression scores observed with high levels of child behavioral problem scores? (2) Does the rate at which maternal depression change (i.e., velocity) correlate with the rate at which child behavioral problems are changing? (3) When the rate of change in maternal depression is increasing or decreasing (i.e., accelerating), do child behavioral problems also show increasing or decreasing rates of change? These three questions each capture a uniquely different component of change and the presence of any one relation does not imply any other relation. For example, if high maternal depression scores are correlated with high child behavior problem scores, it does not necessarily mean that the dyads’ slopes are also related. Figure 3 explores two examples (Panels A and B) of how the presence of correlated velocities or accelerations individually do not necessarily imply other related derivatives --- each relation can occur independently of the other two. The two examples each have trajectories for four participants (upper row of each panel) that are used to produce the plots of the relations between derivatives (lower row of each panel). In Panel A, there is a clear velocity-velocity relation, but level-level and acceleration-acceleration relations are equal to zero. In Panel B, there is a significant acceleration-acceleration relation, but level-level and velocity-velocity relations are equal to zero. As the significance of each relation can be independently manipulated it becomes even more necessary to explicitly express what is meant when saying that two constructs show related change.

Figure 3.

Figures demonstrating that the presence of a relation between a pair of derivatives does not necessarily imply that other derivatives will be related. The top row of each panel shows trajectories of 4 hypothetical dyads; the bottom row of each panel plots the levels, velocities, and accelerations of the dyads against each other. The symbols for the dyads in the top row correspond to the symbols plotted in the second row. Panel A demonstrates trajectories with a significant velocity-velocity relation when level-level and acceleration-acceleration relations are equal to zero. Panel B demonstrates trajectories with a significant acceleration-acceleration relation when level-level and velocity-velocity relations are equal to zero. The presence of correlated velocities (Panel A) or correlated accelerations (Panel B) does not necessarily imply the levels of constructs will be correlated. The same can be shown for correlated levels of constructs; the presence of correlated levels of constructs does not necessarily imply that correlated velocities or accelerations occur.

Thinking about level, velocity, and acceleration also offers opportunities to examine relations that may be underutilized. Table 2 presents possible relations between two constructs and examples of possible research questions regarding the relation between maternal depression and child behavioral problems. Those along the diagonal already have been discussed: level-level, velocity-velocity, and acceleration-acceleration. Relations between constructs, however, also can occur between differing derivatives; three opportunities presented in this table are level-velocity, level-acceleration, and velocity-acceleration relations. For example, a mother’s level of depression, regardless of whether her symptoms are changing or not, might be related to the rate at which a child’s behavior problems are changing (level-velocity). A mother’s level of depression may also lead to an increase or decrease in the rate at which the child’s behavioral problems are changing, such that her child’s behavior shows a curvilinear relation (level-acceleration). Finally, the absolute level of a mother’s depression could be inconsequential, whereas the rate at which a mother’s depression is changing could precipitate an increase or decrease in the rate at which the child’s behavior problems are changing (velocity-acceleration). Such different relations between derivatives can lead to important research questions that are more in line with the need for appropriate models to better explain the true nature of human behavior (Lewis, 2000; Richters, 1997; Sameroff, 2000; Sameroff & MacKenzie, 2003). Theoretical approaches, like presentations of dynamical systems by Thelen and Smith (2006), encourage a way to conceptualize, operationalize, and formalize complex patterns for how variables may differ in their change relations.

Table 2.

Possible Relations among Level, Velocity, and Acceleration of Two Constructs with Sample Questions using the Example of Mother’s Depression and Child Behavior Problems

		Construct 2
		Level	Velocity	Acceleration
	Level	Level-Level: Are high levels of maternal depression observed with high levels of child behavior problem?
Construct 1	Velocity	Velocity-Level: Is a mother’s level of depression, regardless of whether her symptoms are changing or not, related to the rate at which her child’s behavior problems increased or decreased (velocity)?	Velocity-Velocity: Does the rate at which mother’s depressive symptoms increase or decrease (velocity) predict the rate at which her child’s behavior problems increase or decrease (velocity)?
	Acceleration	Acceleration-Level: Does the mother’s level of depression predict increases or decreases in the rate of change of her child’s behavior problems (changes in velocity, acceleration)?	Acceleration-Velocity: Does the rate at which a mother’s depression improves or worsens (velocity) predict increases or decreases in the rate of change of her child’s behavior problems (changes in velocity, acceleration)?	Acceleration-Acceleration: Do increasing or decreasing rates of change in maternal depression (changes in velocity, acceleration) predict increases or decreases in the rate of change of her child’s behavior problems (changes in velocity, acceleration)?

Substantive Example

Many models are available for the description of change; models that are often presented as separate and different entities. Derivatives can provide a framework for understanding the inferences that can be drawn from particular models and understanding how they relate to concepts of change. We present here analyses to demonstrate how both familiar and unfamiliar analyses can be conceptualized as testing inferences about differing derivative relations. The first examines a Hierarchical Linear Model (HLM), a common analytic approach for developmental researchers. The second examines the same data, from the perspective of Latent Growth Curve Modeling (LGCM). We re-express both of these familiar models in terms of derivatives, and consequently discuss the inferences of parameters in terms of level, velocity, and acceleration. Finally, we introduce a more novel methodology for estimating derivatives from repeated intraindividual observations; while this method will be less familiar to most readers, the inferences that are being drawn can still be understood in terms of relations between pairs of derivatives. The present examples are provided only for pedagogical value and any specific results should be considered exploratory, if for no other reason than we have selected to focus on unidirectional relations using data where a bidirectional transactional relation is certainly plausible. Additionally, readers should use these examples to try to appreciate the differences in the derivative relations examined by differing models, and not draw conclusions about the value of any one particular method based on the significance or non-significance of the relations examined.

The examples are based on a sample of 240 youth (M age = 11.86 years, SD = .56; 54% female; 81.5% European American) and their mothers followed annually from grade 6 through grade 12. A subset of these children had a mother with a history of a mood disorder (n = 185), whereas the remaining mothers were life-time free of psychopathology (n = 55). At each annual assessment, mothers reported on their depressive symptoms on the Beck Depression Inventory (BDI; Beck, Ward, Mendelson, Mocks, & Erlbaugh, 1961; the term depression is used here for the sake of brevity) and about their child’s externalizing behavioral problems on the Child Behavior Checklist (CBCL; Achenbach, 1991). Externalizing behavioral problem t-scores were used in the subsequent analyses.

Example 1: Hierarchical Linear Modeling

A hierarchical linear model (HLM) was fit to predict changes in child behavior problems in relation to mother’s depression. We begin with a level 1 model where child behavior problems (Y_it) are predicted by time:

$${\mathrm{Y}}_{\text{it}}={\mathrm{\beta }}_{0\mathrm{i}}+{\mathrm{\beta }}_{1\mathrm{i}}\mathrm{T}+{\mathrm{\beta }}_{2\mathrm{i}}{\mathrm{T}}^2+{\text{error}}_{\text{it}}$$ (1)

where T represents time (Grade 6 = 0), and the subscripts i and t indicate observations for each individual child over several occasions of time. Although researchers are familiar with the growth parameter terms of intercept, linear slope, and quadratic slope modeled in Equation 1, the relation between variables modeled in Equation 1 also can be understood as an expression of how the change in one variable is related to another variable. Equation 1 can be re-written as:

$${\mathrm{Y}}_{\text{it}}={\mathrm{Y}}_{0\mathrm{i}}+{\left(\frac{dY}{dT}\right)}_{\mathrm{i}}(\mathrm{T})+{(0.5\frac{d^{2}Y}{{dT}^2})}_{\mathrm{i}}({\mathrm{T}}^2)+{\text{error}}_{\text{it}}$$ (2)

Notice, that the β-parameters from Equation 1 have now been replaced with their corresponding derivatives (i.e., the changes in Y with respect to time). Re-written this way, Equation 2 shows that the observed score of child behavior problems: Y_it for child i at some time t is equal to the value of the level of the child’s behavior problems when T = 0 (Y_0i), plus the velocity of the child’s behavioral problems $\left(\frac{dY}{dT}\right)$ multiplied by the elapsed time (T), plus one-half times¹ the rate at which the velocity is changing (acceleration, $\frac{d^{2}Y}{{dT}^2}$) multiplied by time squared (T²). Whereas replacing the β-parameter notation to which we are accustomed may seem unnecessarily complicated, doing so allows us to see that the β₀, β₁, and β₂ parameters respectively represent information about the level when T = 0, the velocity when T = 0, and the acceleration of a child’s behavior problems. Clearly mapping the derivative associated with these commonly tested growth parameters will ensure that the interpretation of change is accurately articulated.

For the models that follow, all models were tested using R (version 3.0.2; R Core Team, 2013), and the package lme4 (version 1.0-6; Bates, Maechler, Bolker & Walker, 2014). In any cases where more than one random effect was estimated, the models allowed for all covariances between random effects (i.e., unstructured covariance matrix). The lme4 package does not allow for specification of the variance-covariance structures for the residuals. When available, the REML=FALSE command was used, so that ML estimates were produced for the likelihood ratio tests presented.

The effect of mothers’ depression (BDI score) was considered in two ways. The first way (Model 1) tested the initial BDI score as a level 2 predictor of the β’s (intercept, linear slope, and quadratic slope) Incorporating mother’s initial depression into the model as a level 2 predictor of the β’s (Model 1) gives us the following level 2 equations:

$${\mathrm{\beta }}_{0\mathrm{i}}={\mathrm{G}}_{00}+{\mathrm{G}}_{01}(\text{BDI})+{\mathrm{U}}_0$$ (2.1)

$${\mathrm{\beta }}_{1\mathrm{i}}={\mathrm{G}}_{10}+{\mathrm{G}}_{11}(\text{BDI})+{\mathrm{U}}_1$$ (2.2)

$${\mathrm{\beta }}_{2\mathrm{i}}={\mathrm{G}}_{20}+{\mathrm{G}}_{21}(\text{BDI})+{\mathrm{U}}_2$$ (2.3)

where β_0i, β_1i, and β_2i are equivalently seen as Y_0i, ${\left(\frac{dY}{dT}\right)}_{\mathrm{i}}$, and ${(0.5\frac{d^{2}Y}{{dT}^2})}_{\mathrm{I}}$, or read as level, velocity and one-half times acceleration. Full results are provided in Table 3. A series of six models was tested, each which added an additional component to the prior model; changes in model fit, evaluated through the likelihood ratio test and AIC, were used to evaluate the contributions of additions to the model. The top-half of the table provides model comparison results testing whether including the random effect of time and the random effect of time² improved model fit (models 1a – 1c), and whether adding initial BDI scores as a Level 2 predictor of the three random effects improved model fit (models 1d – 1f).

Table 3.

Parameter Estimates and Model Fit Information for Hierarchical Linear Models Testing Mothers’ Initial Depression as a Predictor (Level 2) of Children’s Behavior Problems

Model		Model Fit Information
	Description	Deviance	df	p values	AIC
1a	Equation 1, with only random intercept	9639.52	5	--	9649.5
1b	Equation 1, with random intercept and random effect of time	9571.84	7	1a vs 1b: <.0001	9585.8
1c	Equation 1, with random intercept, random effect of time, and random effect of time2	9563.55	10	1b vs 1c: 0.040	9583.6
1d	Initial BDI as level 2 predictor of intercept	9446.35	11	1c vs 1d: <0.001	9468.4
1e	Initial BDI as level 2 predictor of intercept and time	9445.28	12	1d vs 1e: 0.301	9469.3
1f	Initial BDI as level 2 predictor of intercept, time, and time2	9440.67	13	1e vs 1f: 0.032 1d vs 1f: 0.058	9466.7

Level 1	Child Behavior Problems
	Fixed Effects
	b	SE	t
Intercept	45.31	0.86	50.83
Time	1.07	0.48	2.21
Time2	−0.15	0.07	1.97
Level 2
Initial BDI	0.25	0.08	3.04
Time * Initial BDI	−0.11	0.05	2.39
Time2 * Initial BDI	0.02	0.01	2.16
	Level 2 Random Effects
	Variance Estimate	SE
Intercept	63.72	8.00
Time	7.32	2.71
Time2	0.11	0.32

Note. Parameter estimates presented from Model 1f, which had the lowest deviance. BDI = Beck Depressive Inventory (mother self-report)

Results of the model comparisons suggested a need for incorporating both the random effects of time and time². Adding initial BDI as a predictor of differing intercepts was significant (1c vs. 1d; χ²(1) = 117.2, p<.0001), suggesting that the level of children’s behavior problems at T=0 (i.e., Grade 6) was related to their mothers’ initial level of depression. Including initial BDI scores as a predictor of the linear slope did not improve model fit (1d vs. 1e; χ²(1) = 1.07, p =.30), suggesting that the velocity (linear change) at T = 0 in behavior problem scores was not related to mother’s initial level of depression. Finally, adding initial BDI scores as a predictor of the quadratic slope improved model fit (1e vs. 1f; χ²(1) = 4.6, p = .032), suggesting that acceleration in children’s behavior problems (increases/decreases in the rate of change) was related to mother’s initial level of depression. Comparing model 1f to model 1e means that the relation between BDI and the linear slope was retained in the model, even though the comparison of models 1d and 1e suggested this was not a significant parameter. This term was retained in model 1f because when the 2-level equations are written as a single equation, this term can be seen as a lower-order regression term; such terms are typically retained in regression models when examining interactions. It should be noted that when the model with BDI as a predictor of the intercept, linear slope and quadratic slope is compared to the model with BDI as a predictor of only the intercept the criterion of α=0.05 is not met (1d vs. 1f; χ²(2) = 5.68, p=0.058); based on the closeness of the p-value to the 0.05 criterion, and support for the more complicated model by the AIC (AIC(1d)=9468.4; AIC(1f)=9466.7), we decided to interpret parameter estimates from the more complex model (model 1f). The parameter estimates appear in the bottom half of Table 3.

Interpreting the parameter estimates of model 1f, these results suggest that initial levels of mothers’ depression predict higher levels of children’s behavioral problems at T = 0 (b = 0.25). Children with higher velocities at T = 0 tend to occur for mothers with lower initial levels of depression (b = −0.11), although the comparison of models 1d and 1e suggest this relation is nonsignificant. Finally, children’s behavior problems positively accelerate for mothers with higher initial levels of depression (b = 0.02), suggesting an increasing rate at which behavioral problems are occurring when mothers have higher rates of depression. Thus, all of the level 2 questions constitute ones where the level of mother’s initial depression can alter some characteristic of the child’s behavior problem trajectory over time whether it is their level, velocity, or acceleration. What HLM, as presented, cannot draw inferences about is how changes in mother’s depression (velocity or acceleration) may predict child behavior problems.

In the second HLM model examined (Model 2), the mother’s depression at each time was tested as a level 1 predictor (i.e., a time-varying covariate) to make use of the repeated measurements of mother’s depression. The Level 1 equation for Model 2 is:

$${\mathrm{Y}}_{\text{it}}={\mathrm{\beta }}_{0\mathrm{i}}+{\mathrm{\beta }}_{1\mathrm{i}}\mathrm{T}+{\mathrm{\beta }}_{2\mathrm{i}}{\mathrm{T}}^2+{\mathrm{\beta }}_{3\mathrm{i}}(\text{depression})+{\text{error}}_{\text{it}}$$ (3)

The results of this model are presented in Table 4. Because in this model the level of depression is predicting changes in Y_it (i.e., β_3i), Equation 3 allows for conclusions on how the level of depression at different times is related to the level of child behavioral problems; this is in contrast to the prior analyses which only used an initial level of mother’s depression as a predictor. Although there are different depression scores at each time, the relation being examined is still a level-level relation. Inferences that could be drawn would be able to state whether concurrent levels of mother’s depression and child behaviors are related, controlling for time. The results in Table 4 support the suggestion that the mothers’ level of depression predicts higher concurrent levels of children’s behavior problems (b = .15, SE = .04, t = 3.80). This model does not, however, directly test whether (for example) the rate of change in depression was related to the rate of change in child behaviors (velocity-velocity). As level-level relations do not necessarily imply velocity-velocity relations, and vice versa, we cannot confidently infer one from the other.

Table 4.

Parameter Estimates from Hierarchical Linear Models Testing Mothers’ Depression as a Time-varying (Level 1) Predictor of Children’s Behavior Problems

Level 1	Child Behavior Problems
	Fixed Effects
	b	SE	t
Intercept	46.01	0.69	66.41
Time	0.19	0.37	0.50
Time2	−0.02	0.06	−0.40
BDI	0.14	0.04	3.80
	Level 2 Random Effects
	Variance Estimate	SE
Intercept	63.93	8.00
Time	8.22	2.87
Time2	0.14	0.37

Note. BDI = Beck Depressive Inventory (mother self-report). BDI treated as fixed at Level 2.

One modification to Model 2 not considered here would be to allow an interaction between depression and time at level 1. This would allow the relation between level of depression and level of child behavior problems to vary (become stronger or weaker) over time, but still would not address questions as to whether changes (i.e., velocity or acceleration) of depression were related to changes (i.e., velocity or acceleration) in child behavior problems. HLM is very useful for addressing specific questions about change. As we have seen here, several differing questions about level-level relations can be addressed, as well as level-velocity and level-acceleration questions. These models, however, do not address concordant rates of change in two constructs.

Example 2: Velocity-Velocity Relations

If one’s key question of interest is relating concordant change, it may be necessary to consider methods other than HLM. We focus on velocity-velocity relations, although the following section applies equally to acceleration-acceleration relations and velocity-acceleration relations. Equation 2 showed that the parameter associated with the effect of time could be thought of as the velocity of child behavior problems $\left(\frac{dY}{dT}\right)$. Consequently, to relate changes in mother’s depression to changes in child behavior problems, it is necessary to identify a model where a linear slope related to time (i.e., velocity) can be estimated for both constructs. In searching for a model where velocity can be related to velocity, one would come across several models. By recalling that velocity and slope are the same, one might select Latent Growth Curve Models (LGCM; Bollen & Curran, 2006), as these models allow for the slope (velocity) of two constructs to be related to each other (i.e., the Parallel Process Model; e.g., Garber & Cole, 2010). In such a model, the latent intercept (level) and slope (velocity) are estimated for each construct in structural equation modeling software, and subsequently the latent growth parameters can be correlated or regressed on each other.

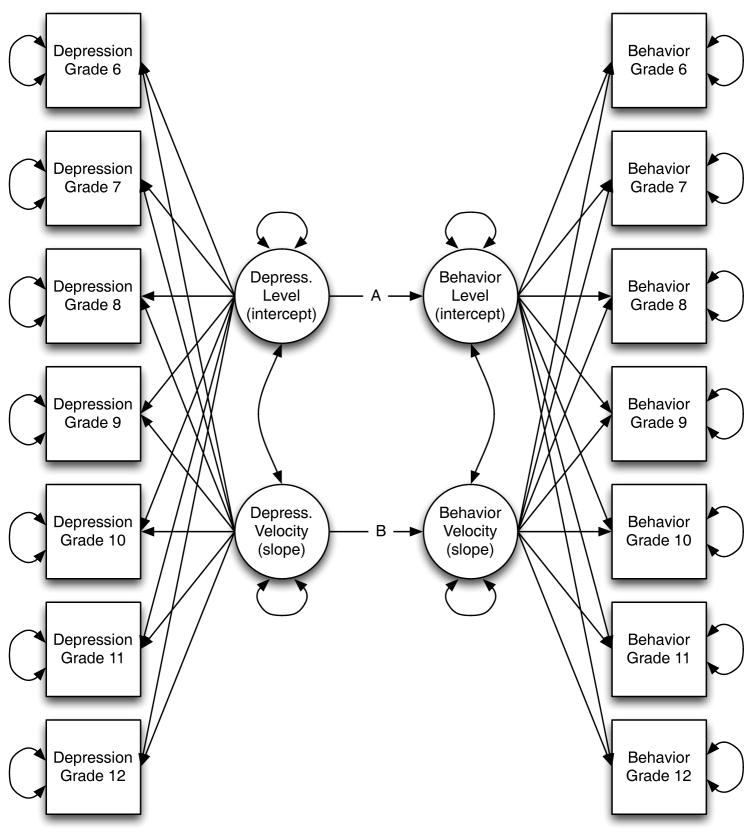
Using the maternal depression-child behavior problems data above, we explored a series of four models as shown in Figure 4: (1) no relations between levels and slopes (Model 3a), (2) depression level predicting the child behavior problems level (Model 3b), (3) depression velocity predicting the child behavior problems velocity (Model 3c), and (4) a model that included both relations from models 2 and 3 (Model 3d). All models were fit using the R (version 3.0.2; R Core Team, 2013) structural equation modeling package lavaan (version 1.5-16; Rosseel, 2012). Latent variable paths to manifest variables were constrained to 1 or a sequence from 0 to 6 (i.e., Grade 6 = 0) for the levels (intercepts) and velocities (slopes), respectively. Manifest residuals were allowed to vary across measurements, and no correlations between manifest variables were included. The latent level and velocity for each construct was allowed to correlate.

Figure 4.

SEM tested in substantive example. Four models were examined: (1) no relations between levels and slopes (no path A or B), (2) depression level predicting the child behavior problems level (inclusion of path A), (3) depression velocity predicting the child behavior problems velocity (inclusion of path B), and (4) a model that included both relations from models 2 and 3 (inclusion of both A and B).

Table 5 provides results from fitting the aforementioned models. Based on the AIC, and support from the likelihood ratio tests, the fourth model appeared to be the best fitting model. The bottom of Table 5 provides the information for specific parameters in this model. The model indicated that the relation between intercepts was significant (z = 2.83, p = .01), and that the relation between slopes was not significant (z = 1.53, p = .13). These parameters directly test level-level and velocity-velocity questions. From these results, we can draw the inference that the level of maternal depression and level of child behavior problems at T = 0 appear to be related, but we have no evidence with the current model that the velocity in depression is related to the velocity of child behavior problems. Whereas this may seem counterintuitive, Figure 1 shows that not all derivatives will necessarily be correlated; this is elaborated upon in Figure 3, which demonstrates that correlations between the levels of variables do not necessarily imply correlated velocities or accelerations in variables, nor vice-versa.

Table 5.

Results from Latent Growth Curve Model (Parallel Process Model) Correlating Level and Velocity of Mothers’ Depression and Child Behavior Problems

Model	Model Fit Information
	Description	χ2	df	p value	AIC
3a	No Child-Mother Relations	157.0	85		18308.8
3b	Child’s Intercept Predicted by Mother’s Intercept	149.9	84	3a vs. 3b: 0.008	18303.7
3c	Child’s Slope Predicted by Mother’s Slope	155.4	84	3a vs. 3c: 0.21	18309.2
3d	Child’s Intercept Predicted by Mother’s Intercept & Child’s Slope Predicted by Mother’s Slope	147.6	83	3b vs 3d: 0.13 3c vs 3d: 0.005	18303.3

Model 3d Parameter Estimates
Parameter	Estimate	SE	z	p
Child’s Intercept Predicted by Mother’s Intercept	0.23	0.09	2.83	0.01
Child Slope predicted by Mother’s Slope	0.31	0.20	1.53	0.13
Child Intercept, Slope Covariance	−4.76	1.40	−3.41	0.001
Mother Intercept, Slope Covariance	−1.65	0.72	−2.29	0.02
Child Intercept Variance	61.56	7.76
Child Slope Variance	2.12	0.38
Mother Intercept Variance	37.45	4.71
Mother Slope Variance	0.74	0.17

^*Model 3d: Observed variable intercepts and variances not reported. CFI=0.950. TLI=0.945. RMSEA=0.057.

The present example can also be used to highlight one additional consideration that using derivative terminology raises: In addition to considering the expected relations detailed in Table 2, derivatives can make one acutely aware that estimates of change can depend on the time over which the estimates are made². The LGCM example is based on slopes estimated over the entire 6 years of sampling. Although not explicitly stated, the model tested examined whether linear slopes of depression and behavior problems were related over a relatively long period of time. Alternatively, one might hypothesize that there is a velocity-velocity relation, but that it occurs over periods of time shorter than 6 years. With the present data, one could test whether the velocity of mother’s depression and child’s behavior problems are related over shorter spans (e.g., 3 years³); that is, one might need to examine differing types of change over spans of time shorter than the entire time series, as depicted in Figure 2.

This idea has led to a series of new methods in developmental psychology often titled differential equation modeling, which are literally models that include derivatives and can be understood in terms of the same derivative relations that the HLMs and LGCMs explored. One key difference in these models is that derivatives are often estimated over spans of time much shorter than the full length of time over which samples were collected, and these derivatives then can be used to build models that allow for the analysis of dynamic systems (e.g., Boker & Nesselroade, 2002; Hu, Boker, Neale, & Rausch, 2004; Montpetit, Bergeman, Deboeck, Tiberio, & Boker, 2010; Estabrook, 2013). In the examples presented, it is possible that maternal depression and child externalizing behaviors are poorly described with the derivatives used over the course of 6 years; rather these constructs may be changing at a faster rate (over the course of months or just a few years) and using estimates over the course of 6 years may serve to average over interesting variation in the constructs (Ferrer & McArdle, 2010; Nesselroade, 1991). It is also unlikely that relations between constructs are static, but rather that they take some time for a detectable relation to occur, and over longer periods of time the relation may cease to exist; the dependency of relations on time is well known in the mediation literature (Gollob & Reichardt, 1987, 1991) and is also being discussed in the developmental literature (e.g., Kouros, Cummings, & Davies, 2010). Derivatives can be estimated over differing spans of time, with the current data velocities can be estimated using anywhere from 2 to 6 years. Derivative terminology further highlights the fact that theory must also specify the time over which specific relations are expected to occur. The factors that affect a construct such as stress may differ whether one is considering changes in stress over hours, days, weeks, months, or years; that is, a construct that affects daily stress may not affect stress over the course of years (Deboeck, Montpetit, Bergeman, & Boker, 2009).

Using the previous data, we used the method of generalized orthogonal local derivative estimates (GOLD; Deboeck, 2010) to estimate the velocity of depression and the velocity of behavior problems over three year intervals using the program R (version 3.0.2; R Core Team, 2013). It should be noted that there are numerous methods for fitting differential equations to data and for estimating derivatives. We leave aside the specifics of this method as the primary purpose in presenting GOLD is to highlight how novel methodology can still be understood in terms of relations between derivatives. The inferences that can be made with this method can be discussed without the particular of its strengths and weaknesses if one uses derivative terminology.

Using GOLD, level and velocity estimates were produced for each dyad’s depression and behavior scores. Rather than using the data across all 6 years to estimate these derivatives, as in the HLM and LGCM, series of observations spanning 3 years were used (year 1–4, 2–5, 3–6, etc.). While fewer observations are used to produce each estimate, they can still be understood as conveying the level and velocity of mother’s depression and child’s behavior over the course of 3 years; just as the LGCM example estimated intercepts (levels) and slopes (velocity) over the course of 6 years, the idea is the same here that levels (intercepts) and velocities (slopes) are being estimated over 3 years. As multiple estimates are produced for each dyad, a mixed model (model with random effects, similar to an HLM with no level 2 predictors) was used to account for the nested data; the R package lme4 was used to fit this model (version 1.0-6; Bates, Maechler, Bolker & Walker, 2014). In these models, the velocity of child behaviors was predicted using a random intercept model (Model 4a), the mother’s depression velocity (Model 4b), and both mother’s depression velocity and depression level (Model 4c). Mother’s velocity was included as a predictor first, as it was expected that the rate of change in child’s externalizing behaviors is likely to be related to the rate of change in mother’s depression based on prior research introduced earlier, even though the velocity-velocity relation was not supported with the LGCM.

Table 6 provides more extensive results from fitting these models. These models indicate a significant relation between the velocity of depression and the velocity of behavior problems, estimated over three years using adjacent, annual evaluations (3a vs. 3b; χ²(1) = 6.73, p = .009). The level of depression was not predictive of the velocity of behavior problems estimated over three years, controlling for the velocity of depression (3b vs. 3c; χ²(1) = 0.71, p = .40). These results suggest a velocity-velocity relation that is not explainable by a relation between depression level on behavior problems velocity. Importantly, this relation was only apparent at shorter time scales (3 years) but not over longer periods of time (6 years).

Table 6.

Generalized Orthogonal Local Derivative Estimates of Relation between Mothers’ Depression and Child Behavior Problems, over a Shorter Time-course

Model	Model Fit Information
	Description	LL	df	p value	AIC
4a	Random Intercept Model	−1143.6	3		2293.2
4b	Random Intercept, Mother’s Velocity	−1140.2	4	4a vs 4b: 0.009	2288.4
4c	Random Intercept, Mother’s Level & Velocity	−1139.9	5	4b vs 4c: 0.40	2289.7

Model 4b Parameter Estimates
Parameter	Estimate	SE	t
Fixed Effects
Intercept	0.29	0.18	1.59
Mother’s Velocity	0.20	0.08	2.62
Random Intercept	1.31	1.14

^*LL=Log Likelihood

Conclusions

The word derivative rarely makes an appearance when learning about developmental theory or even in the presentation of many statistical methods and models. We have presented several equivalent ways to think of derivatives in Table 1. This table offers the opportunity to more specifically state development theory. If statistical models are understood in terms of derivatives and the relations being examined, as in the highlighted examples, theories expressed in terms of level, velocity, and acceleration translate more readily into mathematical models. This direct correspondence will allow developmental researchers to be both more assured that the statistical models being used lend themselves to the desired inferences, and more careful in reviewing the inferences claimed by other researchers. Derivatives provide a common language for matching theoretical relations of variables to appropriate analytical approaches, mapping new or less commonly used models onto a single existing knowledge-base, and creating a commonality between statisticians and substantive researchers.

In pursuing the question of whether change in child behavior problems is related to change in maternal depression, the substantive examples demonstrated several models using derivative terminology. In doing so, they highlighted the differences among models that test relations such as level-level, level-velocity, and velocity-velocity. The HLM example highlighted that not all theoretical questions can be addressed in every modeling framework. The LGCM example showed how one could test a velocity-velocity hypothesis, but that a level-level relation does not necessarily imply a velocity-velocity relation. The final example revealed that any conclusions about related change are dependent on the timescale that these relations are examined, and so using the common language of derivatives will highlight the need to not only formulate specific theories about change (i.e., Table 2), but also about the time-scale over which these relations exist (Ferrer & McArdle, 2010; Little, 2013; Nesselroade, 1991; Sliwinski, 2011).

While the present paper focused on highlighting differences in the relations that HLM and SEM can be used to examine, the example also allows for consideration of when models may be testing similar hypotheses. In Figure 4, aside from the Level-Level relation examined, which the HLM also examined, one could also examine a model where the latent level of mothers’ depression is used to predict the latent velocity of children’s behavior. This level-velocity relation would be similar to the earlier HLM model where differences in the linear effect of time (velocity) were predicted using depression. How close to equivalent the models are will depend, in part, on how the initial time (t=0) is defined in each of the models, as the intercepts in models with higher order terms will correspond to the level when time is equal to zero. But this relation serves to highlight that seemingly different modeling frameworks, HLM and SEM, can be used to make similar inferences under some conditions.

As the number of available models for analyzing change multiplies (Collins & Sayer, 2001), we anticipate only increased burden on developmental researchers to learn about differing models and increased confusion as to how models may or may not address similar questions. Models are often presented as unique, which makes it unlikely that researchers fully grasp the many emerging options for characterizing change relations, and how the models differ and overlap. By using the derivative framework, a scaffold is provided into which new models can be incorporated.

This framework requires that developmental researchers become much more precise in articulating theory. This challenge, however, is not without significant benefit. Our example in Figure 1 (maternal depression and child behavioral problems) allowed us to address what it is about mother’s depression that relates to her child’s behavioral problems. In this example, the children’s behavior problems were such that their level and velocity might not clearly relate to the mother’s depression, particularly for the child in Figure 1B; yet this child clearly is responding to his mother in some way because of the increase in the rate at which the child’s behavior is changing (acceleration). Because acceleration is often overlooked, considerable data may exist in file drawers because only one or a few of the relations in Table 2 were examined. Adopting the language of derivatives will highlight other change relations that could be considered.

Developmental psychology has often pushed the methodological frontier forward in psychology (Laursen, Little, & Card, 2012); in doing so, researchers who are focused on developmental theory incur a burden because speaking the languages of both developmental theory and statistical methodology fluently can be a difficult endeavor. This challenge is compounded with the continued expansion of the number and variety of statistical models available. If developmental researchers regularly use only the models with which they are familiar, and are not careful about articulating the inferences provided by such a model, a real danger presents itself. As the number of statistical models continues to expand, it may become difficult for developmental researchers to understand the inferences and limitations of related methods. If methodologists begin to describe the modeling of change in terms of derivatives, and developmental researchers precisely articulate their theories about change, these dimensions of change (level, velocity, and acceleration) can serve as the bridge between two complex languages. In this manner, the language of derivatives may serve as a common language to navigate intrapersonal and interpersonal models of change, allowing for better description and modeling of the complexity of human nature.