Visual sensory networks and effective information transfer in animal groups

Social transmission of information is vital for many group-living animals, allowing coordination of motion and effective response to complex environments. Revealing the interaction networks underlying information flow within these groups is a central challenge [1]. Previous work has modeled interactions between individuals based directly on their relative spatial positions: each individual is considered to interact with all neighbors within a fixed distance (metric range [2]), a fixed number of nearest neighbors (topological range [3]), a ‘shell’ of near neighbors (Voronoi range [4]), or some combination (Figure 1A). However, conclusive evidence to support these assumptions is lacking. Here, we employ a novel approach that considers individual movement decisions to be based explicitly on the sensory information available to the organism. In other words, we consider that while spatial relations do inform interactions between individuals, they do so indirectly, through individuals’ detection of sensory cues. We reconstruct computationally the visual field of each individual throughout experiments designed to investigate information propagation within fish schools (golden shiners, Notemigonus crysoleucas). Explicitly considering visual sensing allows us to more accurately predict the propagation of behavioral change in these groups during leadership events. Furthermore, we find that structural properties of visual interaction networks differ markedly from those of metric and topological counterparts, suggesting that previous assumptions may not appropriately reflect information flow in animal groups.

Figure 1.

The spread of information through fish schools.

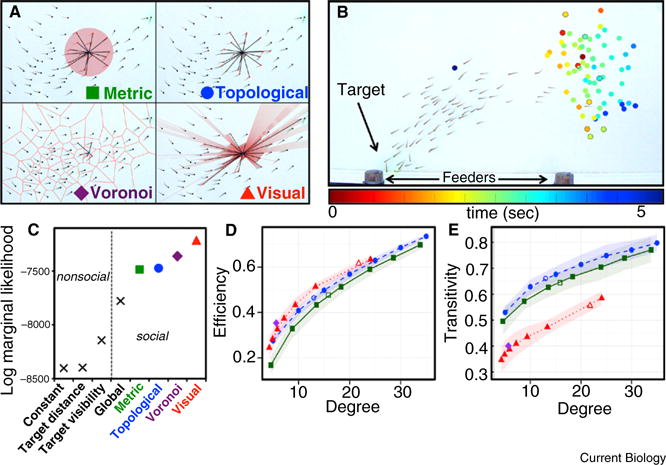
(A) Different models for the neighbors with whom a given fish interacts, shown for one example image from our dataset. Metric: all individuals within a certain distance. Topological: a fixed number of nearest neighbors. Voronoi: those individuals sharing a boundary in a Voronoi tessellation of the group. Visual: all individuals that occupy an angular area on the retina of the focal fish that is greater than a threshold value. (B) A wave of behavioral responses spreads through the group during leadership events. An image from the end of a leadership event is shown. Superimposed on this image, each filled circle marks the location of a single fish when it responded, and colors represent the time of that response. Black borders around circles denote informed (trained) fish. (C) Empirical support for different models of information transfer. Higher marginal likelihood indicates more support (note the log scale). Marginal likelihoods of each model (computed via numerical integration) represent the product of the likelihoods over all uninformed individuals and all trials. Plotted values are the mean of 10 runs, each using 10,000 random samples from parameter space. Standard deviations of these estimates are smaller than data markers. (D) Network efficiency (the speed with which information can flow through the network) vs. average degree (number of neighbors) for the different models of interaction networks. (E) Network transitivity (the extent to which individuals who share a neighbor are neighbors themselves) vs. average degree for the different interaction networks. Higher transitivity indicates a greater likelihood of one’s neighbors being mutually connected, and hence a greater level of redundant information available to each individual. Colors and marker shapes are as given in panel A. For each data point, network measurements represent mean values taken over 250 networks randomly sampled from our data (10 samples from each leadership event). Different parameterizations are generated by adjusting the interaction radius, number of nearest neighbors, or visual threshold. Because of its inherently fixed interaction range, only one data point is shown for the Voronoi model. Shaded areas show the standard deviation along the first principal component of the error distribution. Non-filled markers indicate the average degree associated with the best fit to the data. Full definitions of network measurements are given in Supplemental information.

Often, individuals with pertinent information may guide group motion, allowing all animals within a group to take advantage of information held by only a subset [5]. Such leadership may be crucial, particularly for foraging and predator detection [6]. In our experiments, we initiated leadership in fish schools by placing a known number of ‘informed’ fish (trained to move toward a stimulus) within a larger group of ‘uninformed’ (untrained) fish. By controlling when and where the stimulus was presented, we created repeatable ‘leadership events’ whereby information transfer was essential for group motion towards the target. We tracked (at 30 frames per second) the body position and posture of every fish (in groups of 70) during 25 leadership events. From this information, we reconstructed the trajectory and visual field of each fish over time (Supplemental information). We then used these sequences to test hypotheses about the nature of the interaction networks within groups. During a leadership event, fish exhibit a clear acceleration toward the target (Supplemental information), allowing us to define a discrete behavioral ‘response’ time for each individual. These responses propagate through the group in a wave (Figure 1B). Although the nature of these waves varies among trials (Supplemental information), in general they spread out spatially from the first individual to respond (LMM: p < 0.0001), suggesting a social contagion effect. Overall, informed individuals respond earlier than do uninformed (LMM: p < 0.0001), and occupy frontal positions in the group (permutation test: p < 0.001; Supplemental information, [6]).

We compare different explanatory models for the spread of behavioral responses. Models have a common structure to ensure fair comparison. Each predicts the probability that each uninformed fish will respond at each point in time:

$$P(s)=\frac{1}{1+e^{-s}},$$ (1)

where s depends on the assumptions of the model. For all social models, we assume that s depends on the fraction of an individual’s neighbors that have already responded, as supported by our analysis (Supplemental information). However, each social model specifies a different interaction range, based on metric, topological, Voronoi, or specifically visual assumptions (Figure 1A), allowing us to compare directly the support for these different interaction networks. Whereas different metric and topological ranges depend on distance, and number of neighbors, respectively, for visual ranges the structure depends on occlusion, as well as a ‘minimal visual threshold’ area subtended on the retina. We also compare these social models to nonsocial models (based on target distance or visibility) and to a null model assuming a constant response probability (see Supplemental Information for full model descriptions.)

Following the methodology of [7], we compare the validity of these different models by computing the marginal likelihood of the data conditioned on each model, with higher values indicating more empirical support (see Supplemental information). Our results (Figure 1C) confirm that behavioral responses are socially contagious, and spread locally. A comparison of different interaction ranges indicates that both Voronoi and visual models outperform metric and topological models, with the visual model best explaining the data. Visual mediation of interactions is also consistent with the lack of evidence for hydrodynamic interactions found in this, and other small freshwater, species [8].

Through network analysis, we reveal the broader consequences of different interaction ranges. From our data, we generate directed, time-varying interaction networks, as specified by each model (Figure 1A). Different parameterizations result from adjusting the interaction radius, number of nearest neighbors, or visual threshold. We compare these networks using three structural measurements relevant to information transmission: average degree (number of neighbors), network efficiency (potential speed of information transmission through the network), aurend network transitivity (how often individuals who share a neighbor are also neighbors themselves). Full definitions are given in Supplemental information. For the same average degree, visual networks show similar efficiency (Figure 1D), but substantially lower transitivity (Figure 1E) than their metric and topological counterparts. Transitivity, widely discussed in the networks literature, reflects the redundancy of information among neighbors, as neighbors connected to one another are more likely to provide the same information [9]. Based on the observed difference in transitivity, we would expect that more novel information is contributed per neighbor in the visual versus metric and topological networks. Voronoi models may more closely approximate visual ones, as their transitivity is similar (for a certain average degree; Figure 1E), and they are second only to visual models in empirical support (Figure 1C).

Our results demonstrate that metric and topological networks, commonly assumed to represent interactions in animal groups [2,3], do not reflect the visual information employed when making movement decisions, and may overestimate the local redundancy of information in groups. Explicitly considering the sensory basis of group decision-making [10] represents a new perspective that better integrates our understanding of individual and collective behavior.