Asymmetry within social groups: division of labour and intergroup competition

Abstract

Social animals vary in their ability to compete with group members over shared resources and also vary in their cooperative efforts to produce these resources. Competition among groups can promote within‐group cooperation, but many existing models of intergroup cooperation do not explicitly account for observations that group members invest differentially in cooperation and that there are often within‐group competitive or power asymmetries. We present a game theoretic model of intergroup competition that investigates how such asymmetries affect within‐group cooperation. In this model, group members adopt one of two roles, with relative competitive efficiency and the number of individuals varying between roles. Players in each role make simultaneous, coevolving decisions. The model predicts that although intergroup competition increases cooperative contributions to group resources by both roles, contributions are predominantly from individuals in the less competitively efficient role, whereas individuals in the more competitively efficient role generally gain the larger share of these resources. When asymmetry in relative competitive efficiency is greater, a group's per capita cooperation (averaged across both roles) is higher, due to increased cooperation from the competitively inferior individuals. For extreme asymmetry in relative competitive efficiency, per capita cooperation is highest in groups with a single competitively superior individual and many competitively inferior individuals, because the latter acquiesce and invest in cooperation rather than within‐group competition. These predictions are consistent with observed features of many societies, such as monogynous Hymenoptera with many workers and caste dimorphism.

Introduction

The balance between cooperation and conflict within social groups and concomitantly the equitability of resource division are major themes in evolutionary biology and behavioural ecology (Owens, 2006; West et al., 2007a; Korb & Heinze, 2008; Clutton‐Brock et al., 2009; Cant, 2012). In particular, much research has focused on explaining the origin and maintenance of eusociality in insects (e.g. Wilson, 1971; Gadagkar, 2001; Reeve, 2001; Ratnieks & Helanterä, 2009). Many insect societies exhibit such high levels of cooperation and low levels of conflict that they function as ‘superorganisms’ (Wilson & Sober, 1989; Reeve & Hölldobler, 2007; Hölldobler & Wilson, 2009) whose evolution is analogous to that of a multicellular organism (Maynard Smith & Szathmáry, 1995; Michod & Roze, 2001; Queller & Strassmann, 2009; Bourke, 2011). Insect societies vary in social complexity (Bourke, 1999) and can be viewed as part of a continuum of sociality with other cooperatively breeding taxa (Sherman et al., 1995). However, individuals across the sociality continuum face a common trade‐off: energy invested in competition or conflict (these terms are often used interchangeably) to obtain a larger share of the group's resources for personal reproduction is unavailable to invest in the cooperative production of those resources that are shared among all group members (Reeve et al., 1998).

One hypothesis to explain the observed variation in the balance between within‐group conflict and cooperation concerns the effect of competition among groups. When intergroup competition is greater, a group member benefits by investing more in within‐group cooperation and less in within‐group competition or conflict (Rabbie & Wilkens, 1971; Bornstein et al., 1990; Bornstein, 2003; Reeve & Hölldobler, 2007). This is because within‐group cooperation may allow a group to compete more effectively against other groups: intergroup competition increases the net benefit to an individual of within‐group cooperation (Reeve & Hölldobler, 2007). Thus, this hypothesis is consistent with selection at the level of the gene (due to the equivalence of inclusive fitness and multilevel selection approaches: Dugatkin & Reeve, 1994; West et al., 2011) and does not preclude the role of relatedness, but rather explains one way that within‐group cooperation can be favoured even when within‐group relatedness is low (Korb & Heinze, 2004; Reeve & Hölldobler, 2007). We note that in the case of low or zero within‐group relatedness, cooperation can yield a direct benefit to the cooperator (actor) as well as to its group‐mates (recipients) and thus may be classified as ‘mutually beneficial’ (sensu West et al., 2007b). In cases where relatedness is nonzero, the actor may pay a direct fitness cost but gain an inclusive fitness benefit through helping relatives, meaning that this behaviour is instead ‘altruistic’ (sensu West et al., 2007b).

There is wide support for the intergroup competition hypothesis, primarily from vertebrates including humans (Sherif et al., 1954; Bornstein & Ben‐Yossef, 1994; Bornstein et al., 2002; Bowles, 2009; Puurtinen & Mappes, 2009; Gneezy & Fessler, 2012), other primates (chimpanzees, Pan troglodytes: Wilson & Wrangham, 2003; Muller & Mitani, 2005) and birds (green woodhoopoes, Phoeniculus purpureus: Radford, 2008, 2011), as well as competition among groups of sperm from different males in deer mice, Peromyscus spp. (Fisher & Hoekstra, 2010), and desert ants, Cataglyphis savignyi (Pearcy et al., 2014). Intergroup competition has also been proposed as a factor selecting for superorganism‐like insect societies (Reeve & Hölldobler, 2007), although there are few tests of this hypothesis in social invertebrates (but see Rissing et al., 1989; Korb & Foster, 2010). However, it is clear that not all group members invest similarly in cooperation: insect societies, in particular, exhibit striking within‐group division of cooperative labour (Reeve & Keller, 2001; Field & Cant, 2006), for example between queens and workers.

Empirical studies on within‐group cooperation and competition suggest that it is important to take into account individual variation in cooperative behaviour (Bergmüller et al., 2010; McNamara & Leimar, 2010) and that the inclusive fitness costs and benefits of cooperation may be different for different group members. For example, group members may vary their cooperation depending on their probability of obtaining a breeding opportunity, as in the social wasps Polistes dominulus and Liostenogaster flavolineata (Cant & Field, 2001, 2005; Field et al., 2006; Leadbeater et al., 2011), or on their relatedness to the recipients, as in paper wasps, Polistes dominulus (Queller et al., 2000; but see Leadbeater et al., 2010); slime moulds, Dictyostelium discoideum (Strassmann et al., 2000); and bee‐eaters, Merops bullockoides (Emlen & Wrege, 1988). Theory indicates that within‐group inequalities in resource holdings (Frank, 1996, 2010; Gavrilets & Fortunato, 2014) and fecundity (Rodrigues & Gardner, 2013) also affect individuals’ cooperation with group members.

To better understand the effect of intergroup competition on within‐group cooperation, it is therefore crucial to explicitly consider within‐group variation. Here, we focus on the effects of variation in individuals’ ‘power’ to respond to conflict of interests (Beekman & Ratnieks, 2003; Beekman et al., 2003): that is, within‐group asymmetries in competitive efficiency, the ability to convert resources into competitive gain (Reeve et al., 1998). We present a game theoretic model in which group members adopt one of two roles, where individuals in one role may differ in competitive efficiency or power (we use these terms interchangeably) relative to individuals in the other role, and there may be different numbers of individuals in each role. We use Reeve & Hölldobler's (2007) game theoretic nested tug‐of‐war framework and allow individuals in each role to make decisions simultaneously: that is, their behaviours coevolve. We thus examine how within‐group competitive asymmetries interact with intergroup competition to affect within‐group cooperation and resource division.

Model

Overall structure

We consider a population of group‐living individuals; we do not specify the total number of groups in the entire population, but assume it is large. We also assume that individuals in one group are unrelated to individuals in other groups (i.e. intergroup relatedness is zero). Within this population, we consider a subset of groups, g, that compete over a shared resource of value v (see Table 1 for a summary of terms in the model). The contested resource can take any form, such as food or breeding opportunities, that can be converted into reproductive units. An individual's fitness, w, is determined by the total amount of resource it obtains. Using the ‘nested tug‐of‐war’ framework (Reeve & Hölldobler, 2007), an individual's fitness is determined by the fraction p of shared resource obtained by this individual's group (i.e. the group's productivity) and the fraction q of the group productivity obtained by the individual itself:

$$w=vpq$$ (1)

Table 1.

Definition of terms in the model

Variables	Definition
x i	Selfish investment in within‐group competition by the focal actor in Role i (i = 1 or 2)
$x_i^{\prime }$	Selfish investment by individual (not the focal actor) in Role i
$x_i^{\ast }$	Optimal selfish investment by individual in Role i
1 − x i	Cooperative contribution to group productivity by the focal actor in Role i
c i	Total cooperative contributions by all members of group with the focal actor in Role i
b	Fractional decrement in competitive efficiency of Role 2 players relative to Role 1
n i	Number of individuals in a group in Role i
r	Weight that one individual gives to its effect on a group member's fitness (relatedness of group members)
g	Number of competing groups (subset of the total population)
v	Value of shared resource contested by g groups
p i	Group productivity: fraction of v obtained by a group with a focal actor in Role i
q i	Individual share: fraction of p i obtained by a focal actor in Role i
w i	Inclusive fitness of individual in Role i

These fitness functions are proportional to the number of new groups founded by offspring individuals in the next generation. We assume that groups are closed to migration within a generation (e.g. due to nest‐mate recognition: Van Zweden & D'Ettore, 2010), so alleles cannot be spread except through the formation of new groups. Additionally, we assume complete dispersal of new reproductives, resulting in zero intergroup relatedness. (Note that this assumption depends on the entire population being large, while g, the number of competing groups a focal group interacts with, can be large or small.) We also follow the ‘tug‐of‐war’ approach (Reeve et al., 1998) in assuming that individuals within a group do not have the option to leave and reproduce solitarily, unlike in the original reproductive skew models (Vehrencamp, 1983; but see Shen & Reeve, 2010).

An individual invests a fraction x of its total energy budget in competing for a share of its group's resources, which translate into reproductive opportunities (we use ‘share of reproduction’ and ‘within‐group share of resources’ interchangeably). This selfish effort towards within‐group competition comes at the expense of cooperative contributions (1 − x) to the total pool resources shared by all group members (i.e. the ‘group's productivity’, or the ‘group's share’; we use these terms interchangeably). Groups’ shares are determined by competition among groups for finite resources. Each group comprises individuals in two roles: n ₁ members of Role 1 play strategy $x_1^{\prime }$ and n ₂ members of Role 2 play $x_2^{\prime }$. We assume that these strategies are encoded by simple genetic architecture (the phenotypic gambit: Grafen, 1984): in this case, that individuals are haploid.

We seek the pair of optimal selfish strategies $x_1^{\ast }$ and $x_2^{\ast }$ that simultaneously maximize a Role 1 player's and a Role 2 player's inclusive fitnesses. We do this by considering the inclusive fitness of a randomly chosen focal actor in Role 1 and that of a focal actor in Role 2, playing strategies x ₁ and x ₂, respectively, with nonfocal group‐mates playing strategies $x_1^{\prime }$ and $x_2^{\prime }$. That is, we investigate the effect of a slight change in selfish effort by a single focal actor (x ₁ or x ₂) while the selfish efforts of all other individuals ($x_1^{\prime }$ and $x_2^{\prime }$) remain constant. Each focal actor's inclusive fitness is determined by its own fitness and the fitnesses of its group‐mates in both roles. Each member of the group weights another group member's fitness by r. In the Supporting Information, we show that this weighting r in an inclusive fitness model (Hamilton, 1964) is the same as the regression of expected breeding values in a neighbour‐modulated (direct) fitness model (Taylor et al., 2007; Wenseleers et al., 2010; Gardner et al., 2011): they are equivalent definitions of relatedness. We also verify that using inclusive fitness to analyse strategies x ₁ and x ₂ gives the same results as using neighbour‐modulated fitness to find the evolutionarily stable strategies for x ₁ and x ₂ (Taylor et al., 2007).

Within‐group competition

An individual's within‐group fraction q (i.e. its share of reproduction relative to others in its group) is determined by the ratio of its own selfish effort to the total selfish effort of all group members (Reeve et al., 1998), given that there is scramble competition over the resource the group has obtained (Cant, 2012). The return on a given investment in selfish within‐group competition is asymmetric between roles: individuals in Role 2 have a reduced competitive efficiency b relative to those in Role 1 (0 < b ≤ 1; note that b = 1 is the symmetric case). For example, if b = 0.5, a given investment in competition by a Role 2 player is half as effective in determining the outcome of that competition relative to the same investment by a Role 1 player. The parameter b is the same as the relative competitive efficiency parameter in the original tug‐of‐war model (Reeve et al., 1998) and is also analogous to individuals’ power in the group (Beekman & Ratnieks, 2003; Beekman et al., 2003).

Thus, a randomly chosen focal actor in Role 1 (playing strategy x ₁ in a group of nonfocal individuals playing $x_1^{\prime }$ and $x_2^{\prime }$) acquires a fraction q ₁ of the group's resources, whereas nonfocal Role 1 and Role 2 players acquire $q_1^{\prime }$ and $q_2^{\prime }$, respectively:

$$q_1=\frac{x_1}{x_1+(n_1-1)x_1^{\prime }+b{n}_2{x}_2^{\prime }}$$ (2a)

$$q_1^{\prime }=\frac{x_1^{\prime }}{x_1+(n_1-1)x_1^{\prime }+b{n}_2{x}_2^{\prime }}$$ (2b)

$$q_2^{\prime }=\frac{b{x}_2^{\prime }}{x_1+(n_1-1)x_1^{\prime }+b{n}_2{x}_2^{\prime }}$$ (2c)

Between‐group competition

The fraction of the total resource that a group obtains in competition with other groups (i.e. group productivity p) depends on the sum of its members’ cooperative investments in resource acquisition (1 − x) relative to those of g − 1 other groups. The total cooperative effort by a group with a focal Role 1 actor is thus:

$$c_1=(1-x_1)+(n_1-1)(1-x_1^{\prime })+n_2(1-x_2^{\prime })$$ (3a)

We assume that groups are engaged in exploitative competition, with each group producing competitive resource‐acquiring units, for example foragers (‘production competition’, sensu Cant, 2012). Thus, the fraction p of the total resource that each group obtains is the ratio of its total cooperative effort c to the efforts of g − 1 other groups without the focal actor in Role 1 (Reeve & Hölldobler, 2007). Each of the latter groups without the focal actor invests a total cooperative effort c′:

$$c^{\prime }=n_1(1-x_1^{\prime })+n_2(1-x_2^{\prime })$$ (3b)

The fraction of resource obtained by a group with a focal Role 1 actor is thus:

$$p_1=\frac{c_1}{c_1+(g-1)c^{\prime }}$$ (4)

Analysing the model

We can now use equations (1), (2a), (2b), (2c), (3a), (3b), (4) and equation 19 from Taylor et al. (2007) to express the inclusive fitness effect w ₁ of a slight change in the strategy x ₁ by a randomly chosen focal actor in Role 1:

$$w_1=\frac{\mathit{\partial }v{p}_1{q}_1}{\mathit{\partial }{x}_1}+r(n_1-1)\frac{\mathit{\partial }v{p}_1{q}_1^{\prime }}{\mathit{\partial }{x}_1}+r{n}_2\frac{\mathit{\partial }v{p}_1{q}_2^{\prime }}{\mathit{\partial }{x}_1}$$ (5)

The first term represents the change in the focal Role 1 actor's direct fitness. The second two terms represent the indirect fitness effects of the focal actor on other members of its group (n ₁ − 1 other individuals in Role 1 and n ₂ individuals in Role 2, respectively). Each of the latter two terms includes the factor r, because this is the weight given by the focal to its group‐mates’ fitness increments. (We show in the Supporting Information that this is consistent with a neighbour‐modulated fitness framework and its concomitant definition of r.)

We follow the same procedure to obtain an expression for w ₂, the inclusive fitness of a randomly chosen focal actor in Role 2 playing strategy x ₂, in a group with n ₂ − 1 other Role 2 individuals playing $x_2^{\prime }$ and n ₁ Role 1 individuals playing $x_1^{\prime }$, in a population of groups whose members also play $x_1^{\prime }$ and $x_2^{\prime }$ (see Supporting Information for details).

We then find the evolutionarily stable strategies $x_1^{\ast }$ and $x_2^{\ast }$ that maximize the inclusive fitness of Role 1 and Role 2 individuals respectively. To do this, we set w ₁ and w ₂ equal to zero, $x_1=x_1^{\prime }=x_1^{\ast }$ and $x_2=x_2^{\prime }=x_2^{\ast }$. We simultaneously solved this pair of equations for the evolutionarily stable pair of solutions ($x_1^{\ast }$ and $x_2^{\ast }$) and verified that these values are fitness maxima by checking that the derivatives of the inclusive fitness effects (∂w ₁/∂x ₁ and ∂w ₂/∂x ₂) are negative. We also identified stable boundary solutions (x* = 0 or 1): we set one of $x_1^{\ast }$ and $x_2^{\ast }$ equal to one of the boundary values (0 or 1) and solved for the stable solution in the other variable, by setting the inclusive fitness effect of the nonboundary variable equal to zero. We then checked for stability by determining whether the inclusive fitness effect of the boundary solution strategy was negative (if x = 0) or positive (if x = 1) while the derivative of the other role's inclusive fitness effect with respect to the other variable was negative at the solution.

We used Wolfram Mathematica 9.0 to analyse the model (code given in the Supporting Information). Analytical solutions were prohibitively complex, so we instead solved for $x_1^{\ast }$ and $x_2^{\ast }$ under a range of representative numerical examples and examined the solutions graphically. In the results that follow, we present the solutions for two group sizes (n ₁ + n ₂ = 20 and n ₁ + n ₂ = 100), two relative frequencies of the two roles (n ₁ = n ₂ and n ₁ ≪ n ₂) and two numbers of competing groups (g = 2 and g = 10). We give additional solutions in the Supporting Information.

Results

We investigated the effects of asymmetry in within‐group competitive efficiency (b) on group members’ investments in cooperation (1 − x), when g groups are competing over a shared resource. When b = 1, there is no difference between individuals in Role 1 and Role 2, and the model yields the same results as Reeve & Hölldobler's (2007) symmetrical nested tug‐of‐war.

When b < 1, the model is asymmetrical (Role 2 individuals are less competitively efficient relative to Role 1), and the investments in cooperation by members of each role differ (Fig. 1a, b). Each Role 1 player generally invests less in cooperation (1‐x) than does each Role 2 player, and receives a larger share of reproduction (q). As asymmetry in competitive efficiency increases (Role 2's relative efficiency b decreases), each Role 2 player's cooperation increases and each Role 1 player's cooperation in many cases slightly decreases or does not change. This means that in more competitively asymmetric groups (lower b), 1) there is higher per capita cooperation (i.e. the group's total investments in cooperation divided by the number of group members; Fig. 1c, d); 2) a higher proportion of the group's total cooperative effort is invested by Role 2 individuals (Fig. 1e, f) – in fact, in many cases, Role 1 invests zero in cooperation for all but the lowest degree of asymmetry (Fig. 1a, b); and 3) Role 1 individuals gain a larger share of the group's reproductive output (Fig. 1g, h). Thus, the model yields testable predictions about the division of labour and reproductive opportunities that cannot be generated from a symmetrical model. It also demonstrates the potential for asymmetry in group members’ competitive efficiency to promote cooperation.

Figure 1.

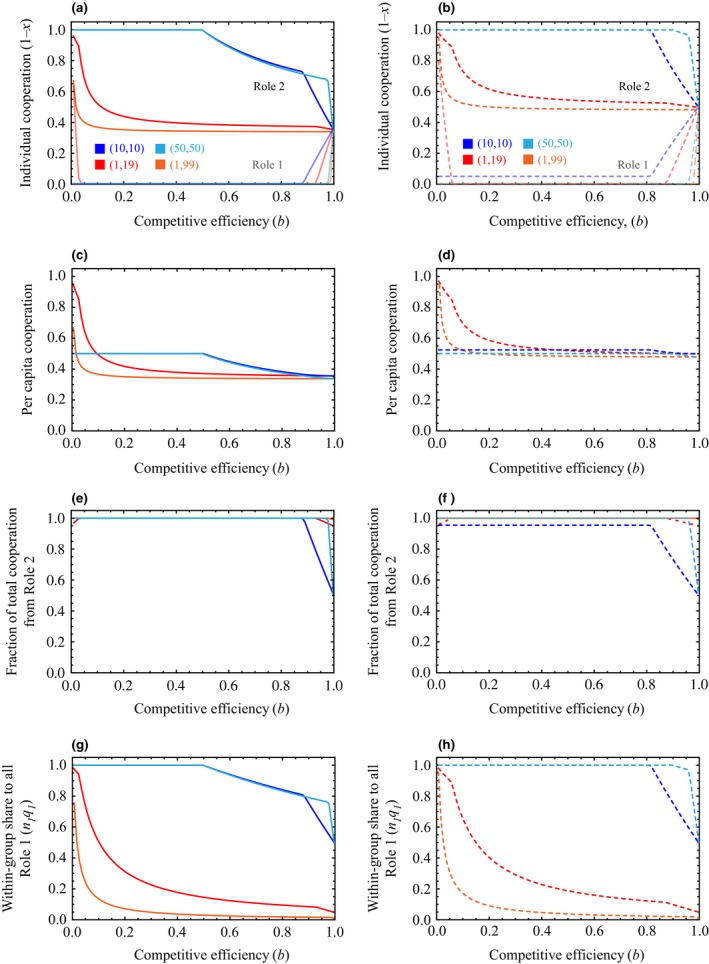
The effect of Role 2 relative competitive efficiency, b, on: (a) and (b) The individual cooperative efforts, 1 − x*, of a single individual in Role 1 (faded lines) and Role 2 (darker lines). (c) and (d) A group's per capita cooperation: $(n_1(1-x_1^{\ast })+n_2(1-x_2^{\ast }))/(n_1+n_2)$. (e) and (f) The combined cooperative efforts of all Role 2 individuals relative to the group's total cooperation: $n_2(1-x_2^{\ast })/(n_1(1-x_1^{\ast })+n_2(1-x_2^{\ast }))$. (g) and (h) The combined share of reproduction obtained by all Role 1 individuals relative to the total reproduction in the group: n ₁ q ₁ / (n ₁ q ₁ + n ₂ q ₂). Panels in the left‐hand column (a, c, e, g) show results for g = 2 competing groups, and panels in the right‐hand column (b, d, f, h) show g = 10. All panels show solutions for relatedness r = 0.5 and resource value v = 1 and use the same colour scheme. Blue and cyan lines show groups with equal numbers of Role 1 and Role 2 individuals (n ₁ = n ₂); red and orange lines show groups with a single Role 1 player and many Role 2 players (n ₁ = 1, n ₁ ≪ n ₂). Darker colours (blue and red) show groups of total size 20 (n ₁ + n ₂), and lighter colours (cyan and orange) show groups of total size 100. Note that symmetrical groups have b = 1; lower b corresponds to greater difference between the two roles’ competitive efficiency (Role 2 is less efficient relative to Role 1).

When the number of competing groups (g) increases, per capita cooperation is higher (Fig. 1c, d), as in the symmetrical case (Reeve & Hölldobler, 2007). The effect of g diminishes when g is higher (i.e. when there are more competing groups, adding even more has a small effect; see Supporting Information). The increase in cooperation with g is predominantly due to increased cooperative effort by Role 2, as in many cases Role 1 invests zero in cooperation (Fig. 1a, b). However, when g is higher, there is a larger range of Role 2 relative competitive efficiencies (b) for which Role 1 invests a nonzero amount in cooperation. Together, these results mean that an increase in g in the asymmetrical model results in slightly lower or no change in the proportion of the group's total cooperative effort collectively invested by Role 2 individuals (Fig. 1e, f), and in a slightly higher combined share of reproduction obtained by Role 1 individuals (Fig. 1g, h).

The effects of relatedness (r) and total group size (n ₁ + n ₂) also correspond to the results of the symmetrical model (Reeve & Hölldobler, 2007). Higher relatedness results in more cooperation by both roles (see Supporting Information), whereas larger group sizes lead to less cooperation by both roles (Fig. 1a, b) and thus lower cooperation per capita (Fig. 1c, d).

An additional aspect of asymmetry is the relative frequency of Role 1 and Role 2 individuals within each group (i.e. the ratio of n ₁ to n ₂). Per capita cooperation is generally higher in groups where n ₁ = n ₂ compared to groups where n ₁ ≪ n ₂, especially when b is low (Fig. 1c, d). As Role 1 players invest zero in cooperation in most cases, this effect is due to an increase in Role 2 players’ cooperation (Fig. 1a, b). This occurs because investment in within‐group competition is unprofitable for Role 2 players when many competitively superior Role 1 players are also investing in competition. Because it does not pay for Role 2 individuals to compete in these cases, they invest more in cooperation.

Because of the increase in Role 2 cooperation (relative to Role 1) in groups where n ₁ = n ₂, the total share of reproduction obtained by all Role 1 individuals is very high (because Role 2 is thus investing less in within‐group competition relative to Role 1). In many cases, Role 2 individuals invest all of their energy budgets in cooperation and thus obtain zero reproductive shares (Fig. 1g, h). The range of b for which this is the case is also larger when n ₁ = n ₂ (vs. n ₁ ≪ n ₂) and when g is higher: in groups with more equal numbers in each role experiencing more intergroup competition, Role 1 dominates the group's reproduction even when Role 2 is relatively competitively efficient (high b). This is again because the Role 1 players are competing against each other within the group, leaving Role 2 players unable to obtain reproductive shares: Role 2 players can only successfully compete for reproduction when the group is smaller or when b is higher (Role 2 is less competitively inferior).

When Role 2 players have extremely low relative competitive efficiency (b near zero), groups with highly unequal frequencies of Role 1 and Role 2 players (n ₁ ≪ n ₂) have greater per capita cooperation (Fig. 1c, d) than groups with equal composition (n ₁ = n ₂). This is because for such low b, Role 2 players all acquiesce and invest highly in cooperation (Fig. 1a, b), ceding most reproduction to the sole competing Role 1 player (Fig. 1g, h).

Discussion

In many animal societies, individuals differ in their ‘power’ to affect the outcome of conflict (Beekman et al., 2003), and thus it is important to take this parameter into account in models of competition and cooperation. We represent this parameter in our model with the factor b, the competitive efficiency of an individual in Role 2 relative to an individual in Role 1. We combine the framework of a single‐group, asymmetric two‐player tug‐of‐war model (Reeve et al., 1998) with the intergroup, symmetric multiplayer nested tug‐of‐war model (Reeve & Hölldobler, 2007). The main insight from the asymmetrical model here is that cooperative efforts (and thus also efforts in within‐group competition) are not distributed equally between the two roles, resulting in division of labour and in reproductive skew. Given that wide variation is observed among and within species in the distribution of cooperative efforts among group members (e.g. based on dominance: Cant & Field, 2005) and reproduction (‘skew’: Sherman et al., 1995; Lacey & Sherman, 2005), this model provides a more accurate picture of real social groups than does a symmetric game.

Applications to social insects and other groups

Three important points emerge from the asymmetric nested tug‐of‐war model. Firstly, more competitively efficient individuals (Role 1) cooperate less than do competitively less efficient individuals (Role 2) and in many cases do not cooperate at all (Fig. 1a, b, e, f). The more competitively efficient role also receives the larger share of the group productivity (Fig. 1g, h), which translates into reproductive output. Thus, Role 1 players may be considered ‘queens’ or ‘dominants’, with Role 2 as ‘workers’ or ‘subordinates’. This study was motivated by expanding models of intergroup competition to eusocial insects (Reeve & Hölldobler, 2007), but the results apply to any of the wide range of social groups in which members differ in power or competitive efficiency (Beekman et al., 2003).

Secondly, when there is a greater difference in competitive efficiency between the two roles (b is lower), the competitively inferior Role 2 players cooperate more relative to the competitively superior Role 1 players, because the former obtain a lower return on any investment in within‐group competition, as in a two‐player tug‐of‐war model (Reeve et al., 1998). This results in even more extreme division of cooperative labour (Fig. 1e, f) and reproductive skew (Fig. 1g, h). In addition, the increased cooperation by Role 2 leads to higher cooperation per capita (averaged over all group members; Fig. 1c, d) when the two roles differ more in competitive efficiency. In support of this prediction, paper wasp (Polistes dominulus) cofoundress associations produce more cells and workers when there is greater asymmetry in foundress size (Nonacs & Reeve, 1995).

Thirdly, the relative frequencies of individuals in each role are important. When competitively less efficient (Role 2) players greatly outnumber competitively more efficient (Role 1) players, the former cooperate less than when the frequencies of each role are more equal, because Role 2 players’ competitive investments are more profitable when there are fewer Role 1 players. However, when Role 2 is extremely competitively inefficient relative to Role 1, it is no longer profitable for Role 2 players to invest in within‐group competition, leading to the highest levels of per capita cooperation (Fig. 1c, d) when Role 2 outnumbers Role 1 and is very competitively inefficient. As many insect societies exhibit a variation in queen number (Keller, 1993; Bourke & Heinze, 1994), the model makes predictions that are both ecologically relevant and testable.

Attempts to quantify individuals’ relative competitive abilities in insect societies have had mixed success. For example, there is conflicting evidence from Polistes wasps for predictors of success in agonistic interactions, with body size, age, facial markings and order of arrival at the nest among the factors sometimes implicated in dominance (Hughes & Strassmann, 1988; Seppä et al., 2002; Tibbetts & Dale, 2004; Cervo et al., 2008; Zanette & Field, 2009; Green & Field, 2011). However, we might expect workers who are morphologically more distinct from the queen to have a lower relative competitive efficiency, because their specialization may make them less able to participate in competition over shares of group productivity (Bourke, 1999). According to the maternal manipulation hypothesis (Alexander, 1974), larval feeding can affect queen–worker morphological divergence (Wheeler, 1986), for example in sweat bees, Megalopta genalis (Kapheim et al., 2011); this could potentially be a mechanism to reduce worker competitive efficiency (Beekman & Ratnieks, 2003). Such a mechanism may be more likely to be favoured when there are more workers and when the queen mates multiply, given that in these cases workers invest less in cooperation. Indeed, more elaborate worker specialization and complex division of labour are found in larger colonies (Bourke, 1999).

Although intergroup competition has been extensively studied in social vertebrates, the effect of asymmetry in competitive efficiency is not well documented. In humans, many studies that demonstrate how intergroup competition promotes within‐group cooperation do not refer to any within‐group asymmetries (Sherif et al., 1954; Bornstein & Ben‐Yossef, 1994; Bornstein et al., 2002; Bowles, 2009; Puurtinen & Mappes, 2009; Gneezy & Fessler, 2012). Research on within‐group cooperation in the absence of intergroup competition suggests that when endowments are distributed unequally among group members, richer (‘dominant’) individuals contribute a smaller fraction of their endowment than do their poorer group‐mates (Chan et al., 1996; Barclay & Benard, 2013), and both the degree of inequality and the symmetry of its distribution (i.e. whether inequality is skewed towards rich or poor individuals) affect investments in cooperation (Anderson et al., 2008; Tavoni et al., 2011; Fung & Au, 2014). Studies of within‐group cooperation in humans typically assume that resources are equally divided among group members (Barker et al., 2012), so investigating asymmetry in competitive efficiency appears to have been overlooked. In nonhuman vertebrates, there is evidence for individual variation in investment in intergroup conflict but based on factors such as sex differences [e.g. in lions, Panthera leo (McComb et al., 1994), and chimpanzees, Pan troglodytes (Wilson & Wrangham, 2003; Muller & Mitani, 2005)], and in chimpanzees, age and the expected benefits from winning when those benefits are not shared equally (Watts & Mitani, 2001). Some empirical work suggests support for the asymmetrical model presented here: green woodhoopoe (Phoeniculus purpureus) helpers expend more effort in territorial defence than do breeders (Radford, 2003), and preening of helpers by breeders following intergroup conflict may promote helpers’ investments in future (Radford, 2008, 2011); banded mongoose (Mungos mungo) subordinate males investigated simulated intruders before dominants did, spent more time around them and were more aggressive (Cant et al., 2002).

Modelling within‐group cooperation, competition and asymmetries

Previous theory has investigated both within‐group asymmetry and between‐group competition, but the asymmetric nested tug‐of‐war model we present here brings together both components explicitly and stands out from prior models in several ways. For example, previous models of public goods provision without intergroup competition have allowed variation in the amount of resources that each group member has, and variation in the benefits and costs to each group member of contribution to the public good (Diekmann, 1993; Frank, 1996, 2010; Crowley & Baik, 2010; He et al., 2012). Gavrilets & Fortunato (2014) do explicitly investigate how intergroup competition affects cooperation via the coevolution of within‐group traits, but their model similarly considers groups with asymmetry in resource holdings, rather than the asymmetry in power that we investigate. In Gavrilets & Fortunato's (2014) model, dominants are defined as individuals who obtain a larger share of resources in intergroup competition, whereas in our model the shares are determined by the outcome of competition between the two roles. (Note that although the optimal behaviour of a Role 1 player in our model is typically associated with within‐group dominance of reproduction, and that of a Role 2 player with subordinance, these roles are not intrinsically ‘dominant’ and ‘subordinate’, especially if individuals in each role have the same competitive efficiency (b = 1); the asymmetry in reproductive shares emerged simply by assigning realistic values to the parameters in the model). Our model thus bridges the gap between models of skew (Reeve et al., 1998) and models of intergroup competition.

These previous models differ from ours in an additional key respect: with asymmetries in the amount of resources, ‘dominant’ individuals are better able to invest in both cooperation and competition, yielding the result that higher‐ranking individuals contribute more to group productivity (Frank, 1996, 2010; He et al., 2012; Gavrilets & Fortunato, 2014). This seeming contradiction with our results arises because in our model, individuals in each role are unequal in their abilities to invest in within‐group competition but equally able to invest in within‐group cooperation. Addressing asymmetry in competitive efficiency without asymmetry in cooperative ability is realistic for many groups in nature, such as primitively social wasps (e.g. Polistes spp.) and bees (e.g. halictines). In such groups, ‘dominant’ individuals may be superior at fighting or reproducing compared to their nest‐mates (Reeve, 1991), but not at cooperative tasks such as foraging or nest defence. An additional component of ‘dominance’ unrelated to cooperative ability is investigated by Rodrigues & Gardner (2013), who allow asymmetry in fecundity: low‐quality individuals (who have lower fecundity and thus lower reproductive value) invest more in ‘subordinate’‐like helping. This effect is similar to ours, although the asymmetry is in the ability to produce offspring, rather than the ability to compete with group members for resources.

Other models of intergroup competition and within‐group traits, for example altruism and parochialism (Choi & Bowles, 2007; García & van den Bergh, 2011) and competition and policing (Brandvain & Wade, 2007), do not investigate the coevolution of cooperative investments by distinct classes of individuals within a group, as we do here. Our model shows that high investment in cooperation from one class of individuals (‘workers’) can be stable in the absence of another coevolving trait such as outgroup hostility or policing. Importantly, unlike many other models of social evolution, we do not assume here that group members are coerced by policing (Frank, 2003; Wenseleers et al., 2004). Thus, our model applies well to social insect colonies where there is little enforcement of altruism, for example Melipona stingless bees (Ratnieks & Wenseleers, 2008; Ratnieks & Helanterä, 2009). We also do not assume that workers are somatic extensions of the queen (Nowak et al., 2010); that is, in this model, workers (Role 2 players) are free to make their decision only in the context of asymmetry in competitive efficiency and the number of individuals in each role, and this decision coevolves with that of the queens (Role 1 players).

Although our discussion to this point has called decreasing x ‘cooperative’ and increasing x ‘selfish’, we have not considered the effects on the actor's and recipients’ direct fitness and thus whether investing in within‐group cooperation should be classified as altruistic or mutually beneficial (sensu West et al., 2007b). Increased investment in cooperation under intergroup competition can be mutually beneficial when it allows both the cooperator (actor) and its group‐mates (recipients) to obtain more resources (the cooperator would gain a smaller fraction of resources relative to its group‐mates, but a larger absolute amount than if it did not cooperate, because its cooperative efforts increase the group's pool of resources): this is the case when r = 0 and selection is maximizing individuals’ direct fitness. However, when r > 0, increased cooperation can evolve even if the actor incurs a cost to its own direct fitness, if this cost is outweighed by inclusive fitness benefits from increasing the direct fitness of relatives: in this case, cooperation would be altruistic.

The classification of x can be revealed by examining the signs of the derivatives of the actor's and recipients’ direct fitnesses with respect to the actor's x at equilibrium. For example, if the actor's direct fitness derivative were positive, the actor would increase its direct fitness by increasing its investment in x (i.e. decreasing its investment in cooperation, 1 − x) above the equilibrium value, suggesting that it pays a direct fitness cost at equilibrium. Similarly, if a recipient's direct fitness derivative were negative, its fitness would decrease if the actor increased its investment in x (i.e. decreased its investment in cooperation, 1 − x) above the equilibrium value, suggesting that this recipient gains a direct fitness benefit. In this case, decreasing x (increasing cooperation) would be classified as altruistic (sensu West et al., 2007b); this is true for the numerical solutions we present here (results not shown). We have not identified all sections of parameter space in the current model in which increasing cooperation is altruistic vs. mutually beneficial, but in all cases both direct and indirect benefits interact to determine the optimal level of cooperative effort.

Extending the model

To simplify the analyses and focus on the effects of asymmetries in relative competitive efficiency and the number of individuals in each role, we assumed that all group members were equally related to each other by r. As many insect societies consist of mother–offspring associations (Hamilton, 1972; Bourke, 2011), the current model could be adapted to incorporate asymmetry in relatedness as well as competitive efficiency between the two roles. For example, in a hymenopteran society with queens in Role 1 and workers in Role 2, worker–worker relatedness would be lower than queen–worker relatedness, and this asymmetry would be greater when the queen's mating frequency increases. One would predict that in the latter case, Role 2 individuals would invest more in within‐group competition and less in cooperation. For simplicity, we also assumed zero intergroup relatedness. This may not be realistic if there is female philopatry (Johnstone et al., 2012), or if individuals enter and reproduce in unrelated colonies via social parasitism or drift (Sumner et al., 2007; Beekman & Oldroyd, 2008). One would predict that if individuals in competing groups are related, both roles’ investments in within‐group cooperation will decrease, all else equal, as in a symmetrical game (West et al., 2002; Reeve & Hölldobler, 2007).

An additional assumption we made is that groups compete via production competition, i.e. that intergroup competition can be modelled as the ratio of groups’ investments in within‐group cooperation. However, in many cases, groups compete with each other by fighting, meaning that the outcome of intergroup competition would be determined by the difference, rather than by the ratio, of groups’ competitive efforts (Cant, 2012). Using a difference form to model within‐group competition yields lower competitive investments than in a ratio form model, because players can still benefit even if they invest zero in within‐group competition (Cant, 2012). This suggests that if a difference form model were used for intergroup competition, stable peace among groups would be more likely. Given that investments in intergroup competition are via within‐group cooperation, if there were less selection to invest in intergroup competition in a difference form model, then intergroup competition could have less of a positive effect in promoting within‐group cooperation, compared to a ratio form model of intergroup competition. Expanding Cant's (2012) model to include multiple group members and multiple competing groups would be interesting future work.

Summary

The tug‐of‐war model presented here generates several testable predictions about the degree of within‐group cooperation in asymmetrical groups. This model provides a more realistic view of intragroup behaviour than (a) a symmetrical model, because group members frequently vary in competitive efficiency, and (b) a single‐group model, because groups rarely exist in isolation, but instead are embedded in a neighbourhood of other groups with which they compete. By incorporating asymmetry in within‐group competitive efficiency, this model is able to make predictions, for example about the equitability of within‐group resource sharing (division of reproduction, i.e. skew), that a symmetrical model is unable to make. This general asymmetric, nested tug‐of‐war framework applies not only to social insects but also to other social organisms, from bacteria (Griffin et al., 2004; Brockhurst et al., 2007) and slime moulds (Strassmann et al., 2000) to cooperatively breeding vertebrates (Solomon & French, 1997; Koenig & Dickinson, 2004; Hager & Jones, 2009). The construction of models such as this that are both more universal and more realistic paves the way for empirical tests in diverse taxa, ultimately shedding light on unifying evolutionary principles governing the balance between cooperation and competition.

Supporting information

Data S1 a) Inclusive fitness for Role 2; b) Neighbor‐modulated fitness and definitions of relatedness; c) Figures for different values of g and r.

Data S2 Mathematica code for inclusive fitness.

Data S3 Mathematica code for neighbor‐modulated fitness.