Prognostic and predictive values and statistical interactions in the era of targeted treatment

Abstract

The current era of targeted treatment has accelerated the interest in studying gene-treatment, gene-gene and gene-environment interactions using statistical models in the health sciences. Interactions are incorporated into models as product terms of risk factors. The statistical significance of interactions is traditionally examined using a likelihood ratio test (LRT). Epidemiological and clinical studies also evaluate interactions in order to understand the prognostic and predictive values of genetic factors. However, it is not clear how different types and magnitudes of interaction effects are related to prognostic and predictive values. The contribution of interaction to prognostic values can be examined via improvements in the area under the receiver operating characteristic curve due to the inclusion of interaction terms in the model (ΔAUC). We develop a resampling based approach to test the significance of this improvement and show that it is equivalent to LRT. Predictive values provide insights into whether carriers of genetic factors benefit from specific treatment or preventive interventions relative to non-carriers, under some definition of treatment benefit. However, there is no unique definition of the term treatment benefit. We show that DeltaAUC and relative excess risk due to interaction (RERI) measure predictive values under two specific definitions of treatment benefit. We investigate the properties of LRT, ΔAUC and RERI using simulations and illustrate these approaches using published data on MC1R and sun exposure in melanoma.

Introduction

During the past decade, the field of oncology has made considerable advances in the discovery of cancer-related genes [Sawyers 2008]. These successes have led to an explosion of research on preventive interventions and anticancer therapies focused on specific patient populations, and have led to the hypothesis that carriers of certain genetic variants are more likely to benefit from specialized treatments or interventions than non-carriers [Lerman et al. 2007; Amado et al. 2008; Karapetis et al. 2008]. This hypothesis has propelled investigations of targeted treatments through studies of gene-treatment, gene-environment, and gene-gene interactions using statistical models. One of the key objectives of these studies is to understand the prognostic and predictive values of a genetic factor such as a germline genetic variant or a somatic mutation [Sawyers 2008]. The objective of this paper is to examine the relationship between interaction terms in statistical models (henceforth referred to as statistical interactions or, simply, interactions) and prognostic and predictive values.

The term prognostic value refers to a genetic factor’s ability to project the natural history of disease in relation to another factor (such as treatment or environmental exposure or another genetic factor; henceforth referred to as treatment) by discriminating between good versus bad prognosis, thereby providing insights into whom to treat with novel modalities [Sawyers 2008; Italiano 2011]. The prognostic value is measured as the area under the receiver operating characteristic curve (AUC; [Pepe et al. 2013]) of a statistical model that includes the genetic factor and treatment as explanatory variables. An important issue is whether the effect of treatment on the outcome changes according to the level of the genetic factor of interest, and how this change impacts the prognostic value. Changes in treatment effects according to a genetic factor are incorporated into statistical models as gene-treatment interaction terms. The issue then is to determine whether incorporating gene-treatment interactions into a statistical model improves the prognostic value.

Often we use the likelihood ratio test (LRT) to examine the significance of interaction terms in statistical models [Agresti 2002]. When there are no interactions, we say that the model is additive. The presence of interactions depends upon the scale on which disease risk is measured [Satagopan and Elston 2013]. If interactions exist when modeling data under a clinically meaningful scale of risk, then including them in the model is anticipated to improve the prognostic value of a genetic factor. This is equivalent to the model’s ability to explain the variation in disease risk and, thus, discriminate between low-risk and high-risk individuals [for example, Khoury et al. 2004; Moore and Williams 2009; Sun et al. 2014]. This improvement is measured as the difference between the AUCs of two models: an additive model and a model including interaction terms. In this paper, we denote this difference as ΔAUC. Some studies noted that the inclusion of interactions did not lead to a considerable increase in the magnitude of ΔAUC [Aschard et al. 2012]. This raises several issues: (i) When an interaction is statistically significant, should its inclusion in a model be expected to improve ΔAUC by a considerable magnitude? (ii) Would a small ΔAUC be statistically significant when there is a statistically significant interaction? and (iii) What is the role of interaction on prognostic values? In this paper, we examine these questions by comparing the operating characteristics of LRT with those of a test for H₀ : ΔAUC = 0 against H_A : ΔAUC ≠ 0. Since an additive model is nested within a model that includes interactions, the DeLong test for H₀ [DeLong et al. 1988] is not valid [Vickers et al. 2011]. Other recent studies have proposed valid tests for ΔAUC when evaluating the incremental increase in AUC due to the inclusion of a new biomarker, without focusing on interactions in statistical models [Pepe et al. 2013; Seshan et al. 2013]. These tests are not applicable to our setting where the focus is on interactions. Therefore, we develop a novel resampling procedure for testing H₀ : ΔAUC = 0 in the interaction setting.

The term predictive value refers to a genetic factor’s ability to project the benefit of treatment under a suitable definition of the term benefit [Sawyers 2008; Italiano 2011]. When the magnitude of treatment benefit changes with the level of the genetic factor, a gene-treatment interaction can be included in a relevant statistical model to represent this change. Unlike prognostic values that are typically measured using AUC, there is no standardized way to measure treatment benefit and, hence, predictive values in the health sciences. Epidemiologists examine public health benefits of treatment using difference in the outcome (such as disease risk or response rate) between treated and untreated individuals. This difference can be calculated separately according to the levels of a genetic factor. The treatment benefit in a level of the genetic factor compared with the baseline level is referred to as the relative excess risk due to interaction (RERI; [Rothman et al. 2008]), and can be taken as a measure of predictive value. In contrast, recent clinical studies have examined predictive values of genetic factors in a two-step process: first, the statistical significance of the interaction effect in a model was examined using the LRT; next, the odds ratios for treatment were examined at each level of the genetic factor to identify the level(s) showing considerable risk reduction associated with treatment [Lerman et al. 2007; Amado et al. 2008; Karapetis et al. 2008]. Here we examine the role of interactions on the properties of these two methods for measuring predictive values.

Our paper is organized as follows. In Section 2, we first establish the notations, define interaction effect, and describe how this definition relates to AUC, ΔAUC and RERI. We describe the concepts in the main text and provide details of the hypothesis test for ΔAUC in the context of interactions in the Supplementary Material. In Section 3, we conduct simulations under a variety of parametric configurations to investigate the role of interactions on prognostic and predictive values. We illustrate these methods using published data from a study of melanoma in Section 4, and conclude the paper with a discussion in Section 5.

Methods

We consider the setting of N independent individuals having a binary disease outcome (for example, affected and unaffected) and two categorical risk factors (which we shall refer to as genetic factor and treatment). The disease outcome of a person having the j-th level of genetic factor and k-th level of treatment has a Bernoulli distribution with probability π_jk, which is modeled via logistic regression as:

$$log\left\{\frac{{\pi }_{jk}}{1-{\pi }_{jk}}\right\}=\mu +{\beta }_j+{\delta }_k+{\gamma }_{jk},$$ (1)

where μ is the baseline risk, β_j and δ_k are referred to as the main effects of the j-th level of the genetic factor and k-th level of treatment, and γ_jk are referred to as the interaction effects. Denoting 0 as the baseline level, we set β₀ = 0 = δ₀ and γ_0k = 0 = γ_j0 for all j and k. This model can be expanded easily to accommodate covariates, additional risk factors, and higher order interaction terms. When γ_jk = 0 in Equation (1), we refer to the resulting model as an additive model. The probability π_jk is also referred to as disease risk corresponding to the j-th level of the genetic factor and k-th level of treatment.

Interaction effect

Before proceeding further, it will be useful to explain interactions in relation to the scale of the outcome. Denote η_jk as the outcome summary for the j-th level of the genetic factor and the k-th level of treatment. The quantity η_jk − η_j0 measures the difference in the outcome summaries between the k-th level of treatment and its baseline level when the genetic factor is fixed at the j-th level. For each j = 0, ···, L₁ − 1 and k = 0, ···, L₂ − 1, we define the interaction effect, denoted ω_jk, as the difference in the outcome summary between the k-th and the baseline levels of treatment when the genetic factor is at the j-th level, compared to when the genetic factor is at its baseline level [Scheffe 1999]:

$${\omega }_{jk}=\{{\eta }_{jk}-{\eta }_{j0}\}-\{{\eta }_{0k}-{\eta }_{00}\}.$$ (2)

The null hypothesis of no interaction is H₀ : ω_jk = 0 for all j = 1, ···, L₁ − 1 and k = 1, ···, L₂ − 1. The choice of a summary measure for η_jk leads to different frameworks for evaluating interactions [Wang et al. 2010].

Suppose we define η_jk as the logarithm of disease odds i.e., ${\eta }_{jk}=log\left\{\frac{{\pi }_{jk}}{1-{\pi }_{jk}}\right\}$. It follows from Equation (1) that ω_jk = γ_jk, which is also referred to as multiplicative interaction. Testing the null hypothesis of no interaction is equivalent to testing H₀ : γ_jk = 0 for all j and k in Equation (1), which can be done using the LRT. Under H₀, the LRT has an asymptotic central chi squared distribution with (L₁ − 1) × (L₂ − 1) degrees of freedom.

Suppose we define η_jk as the disease odds i.e., ${\eta }_{jk}=\frac{{\pi }_{jk}}{1-{\pi }_{jk}}$. [Note that, when the disease is rare, η_jk ≈ π_jk, which is the disease risk.] Using Equations (1) and (2), the interaction effect can be written as:

$$\begin{array}{l}{\omega }_{jk}={\eta }_{00}\times \left\{\frac{{\eta }_{jk}}{{\eta }_{00}}-\frac{{\eta }_{j0}}{{\eta }_{00}}-\frac{{\eta }_{0k}}{{\eta }_{00}}+1\right\}\\ ={\eta }_{00}\times [exp\{{\beta }_j+{\delta }_k+{\gamma }_{jk}\}-exp\{{\beta }_j\}-exp\{{\delta }_k\}+1].\end{array}$$ (3)

We shall write RERI_jk = exp{β_j + δ_k + γ_jk} − exp{β_j} − exp{δ_k} + 1, which is referred to as the relative excess risk due to interaction corresponding to the j-th and k-th levels of the two factors of interest [Rothman et al. 2008]. When η₀₀ ≠ 0, testing the null hypothesis of no interaction in this setting is equivalent to testing RERI_jk = 0, which is also referred to as a test for additive interaction. When γ_jk = 0, we have RERI_jk = exp{β_j + δ_k} − exp{β_j} − exp{δ_k} + 1, and RERI_jk → 0 when β_j → 0 or δ_j → 0 Thus, under an additive logistic regression model, we will have RERI_jk ≠ 0 when the magnitudes of the effects of the genetic factor and treatment are not negligible. We can test H₀ : RERI_jk = 0 against H_A : RERI_jk ≠ 0 using a confidence interval method [Zou 2008] or a likelihood ratio test [Han et al. 2012]. Here we use the confidence interval method.

Interactions and prognostic value

Denote AUC₁ as the AUC of the model given by Equation (1). Further, denote AUC₀ as the AUC of the additive model (i.e., Equation 1 with γ_jk = 0). The contribution of interactions to the prognostic value can be measured as ΔAUC = AUC₁ − AUC₀. The theoretical value of AUC can be written by postulating a normal distribution for the logarithm of disease risk in the general population (i.e., log-normal distribution for disease risk) with some mean and variance σ². Under this approach, the theoretical value of AUC is $\mathrm{\Phi }(\sigma /\sqrt{2})$, where Φ(.) is the cumulative probability of a standard normal distribution. When the risk factors are independent and are centered and scaled to have mean 0 and variance 1, using Equation (1) we obtain ${\mathit{AUC}}_1=\mathrm{\Phi }({\sigma }_1/\sqrt{2})$ and ${\mathit{AUC}}_0=\mathrm{\Phi }({\sigma }_0/\sqrt{2})$, where ${\sigma }_0^2={\sum }_{c=1}^C{\alpha }_c^2+{\sum }_{j=1}^{L_1}{\beta }_j^2+{\sum }_{k=1}^{L_2}{\delta }_k^2$ and ${\sigma }_1^2={\sigma }_0^2+{\sum }_{j=1}^{L_1}{\sum }_{k=1}^{L_2}{\gamma }_{jk}^2$ (see Supplementary Material A). Therefore, we have:

$${\left\{\sqrt{2}{\mathrm{\Phi }}^{-1}({\mathit{AUC}}_1)\right\}}^2={\left\{\sqrt{2}{\mathrm{\Phi }}^{-1}({\mathit{AUC}}_0)\right\}}^2+\sum _{j=1}^{L_1}\sum _{k=1}^{L_2}{\gamma }_{jk}^2.$$ (4)

From Equation (4), ΔAUC = 0 if and only if γ_jk = 0 for all j and k. Since Φ(.) is a strictly monotonic function, this observation suggests that testing H₀ : ΔAUC = 0 is equivalent to testing H₀ : γ_jk = 0 for all j and k.

These observations suggest that, the properties of LRT for testing the null hypothesis of no multiplicative interaction are likely to be equivalent to those of a test for H₀ : ΔAUC = 0. Our observations also align with those of (Pepe et al.) [2013] who demonstrated the equivalence of several null hypotheses when testing the significance of the incremental improvement in AUC due to the inclusion of a new biomarker in a statistical model. Here we have shown the equivalence between two hypothesis tests in the context of interactions. The LRT for testing H₀ : γ_jk = 0 for all j and k is readily available in most statistical software packages. However, a statistic for testing H₀ : ΔAUC = 0 in the context of interactions is needed.

We develop a resampling-based approach for this test. Briefly, this is a parametric bootstrap approach and proceeds as follows. For binary outcomes, interaction measures the association between gene and treatment in the affected individuals relative to the unaffected individuals. Our approach is to first estimate this association in the observed data set by fitting a model for the genetic factors given the disease outcome and treatment. This model will provide estimates of the magnitudes of association between gene and treatment in the affected and unaffected individuals. Next, we generate data sets under the null hypothesis of no interaction via a resampling procedure using these estimated effects. Retaining the disease outcome and treatment assignment as observed, we randomly sample genetic factors for each individual such that the association between gene and treatment among affected and unaffected individuals is the same (i.e., the interaction effect is 0). We estimate ΔAUC for this data set. This is one realization from the null distribution of ΔAUC. We repeat this sampling procedure multiple times and estimate the p-value as the proportion of these ΔAUCs that are larger than that for the observed data. Detailed steps for this resampling procedure are provided in Supplementary Material B.

Interactions and predictive value

The predictive value depends upon the definition of treatment benefit. For the j-th level of genetic factor, denote B_jk as the benefit of the k-th level of treatment compared to the baseline treatment level. We consider two definitions of B_jk.

First, for the j-th level of the genetic factor, we define B_jk in terms of odds ratio: B_jk = {π_jk/(1 − π_jk)} / {π_j0/(1 − π_j0)}. From Equation (1), we have B_jk = exp {δ_k + γ_jk}. We define the predictive value of the j-th level of the genetic factor for the k-th level of treatment, denoted P_jk, as treatment benefit for the j-th level of the genetic factor relative to its baseline level: P_jk = B_jk/B_0k. It then follows from Equation (1) that P_jk = exp {γ_jk} i.e., the multiplicative interaction is a measure of predictive value in this setting. When P_jk = 1, it means that the the benefits of the k-th level of treatment is the same for the j-th and baseline levels of the genetic factor. The null hypothesis that the j-th level of the genetic factor does not predict treatment benefit is given by H₀ : P_jk = 1. The null hypothesis that no level of the genetic factor predicts treatment benefit is H₀ : P_jk = 1 for all j and k. Under the above definition of treatment benefit, this is equivalent to the null hypothesis of no multiplicative interaction: H₀ : γ_jk = 0 for all j and k i.e., H₀ΔAUC = 0.

Next, for the j-th level of the genetic factor, suppose we define B_jk as the excess disease odds for the k-th level compared to the baseline level of treatment i.e., B_jk = {π_jk/(1 − π_jk)} − {π_j0/(1 − π_j0)}. We define P_jk as the excess treatment benefit for the j-th level compared to the baseline level of the genetic factor i.e., P_jk = B_jk − B_0k. Under this definition of treatment benefit, it follows from Equation (1) that P_jk ∝ RERI_jk. The null hypothesis that the j-th level of the genetic factor does not predict treatment benefit is: H₀ : P_jk = 0 i.e., H₀ : RERI_jk = 0.

Taken together, these observations suggest the following results: (i) H₀ : γ_jk = 0 for all j and k and H₀ : ΔAUC = 0 are equivalent; (ii) this is also equivalent to the null hypothesis of no predictive value of a (genetic) risk factor when treatment benefit is defined based on odds ratios; (iii) H₀ : RERI_jk = 0 is equivalent to the null hypothesis that the j-th level of the genetic risk factor does not predict the benefits of the k-th level of treatment, when treatment benefit is defined based on differences between disease odds; and (iv) when γ_jk = 0 for some j and k in Equation (1), RERI_jk ≠ 0 only when both β_j and δ_k are not small. We performed simulation studies to assess the operating characteristics of the above tests. Table 1 lists the hypotheses being tested.

Table 1.

Hypotheses being tested

Objective	Statistic	H0	H1
Interaction Effect	Likelihood Ratio	γjk = 0a	γjk= 0b
Prognostic / Predictive	ΔAUC	AUC1− AUC0 = 0	AUC1− AUC0 ≠ 0
Predictive	RERIjk	$exp\{{\gamma }_{jk}\}=\frac{exp\{{\beta }_j\}+exp\{{\delta }_k\}-1}{exp\{{\beta }_j+{\delta }_k\}}$	$exp\{{\gamma }_{jk}\}\ne \frac{exp\{{\beta }_j\}+exp\{{\delta }_k\}-1}{exp\{{\beta }_j+{\delta }_k\}}$

^afor all j and k in Equation (1)

^bfor at least one j and k in Equation (1)

Simulation study

We simulated a genetic factor X with L₁ levels and a treatment Z with L₂ levels for N independent individuals, and generated their disease risk using the following model:

$$log\left\{\frac{\pi }{1-\pi }\right\}=\mu +\beta G+\delta T+\gamma GT,$$ (5)

where μ is the baseline risk; I(.) is an indicator variable taking value 1 when the condition in the parentheses is true and taking value 0 otherwise; $G=\frac{I(X\ge C_1)-p_x}{\sqrt{p_x(1-p_x)}};T=\frac{I(T\ge C_2)-p_z}{\sqrt{p_z(1-p_z)}}$; β and δ are the main effects of the genetic factor and treatment, respectively; γ is the interaction effect; p_x = P(X ≥ C₁); and p_z = P(Z ≥ C₂). The gene and treatment contribute to disease risk only when their levels are at least C₁ and C₂, respectively. Further, G and T denote the standardized gene and treatment variables, respectively. In our simulations we also generated data under different magnitudes of correlations (denoted ρ) between X and Z, and under two types of interactions - quantitative and qualitative (Supplementary Figure S1). When the interaction is quantitative, the magnitude of the treatment effect, but not its direction, differs according to the level of the genetic factor. In the presence of a qualitative interaction, both the magnitude and direction of the treatment effect differ according to the level of the genetic factor. In such cases where the direction of treatment effect changes, we expect that omitting the interaction term from the model may result in incorrect prognostic and predictive values, potentially leading to inappropriate decisions about treatment benefits. We chose the parameters of Equation (5) such that the theoretical AUCs were set at some desired values and ΔAUC ranged between 0.05 and 0.15. Further details of the simulation setup, model, and parametric configurations are given in the Supplementary Material C and Supplementary Table S1.

We analyzed the simulated data sets using Equation (1) and using an additive model. While the true risk model was based on Equation (5), we analyzed the data without assuming knowledge of the true model generating the disease. We estimated AUC₀, AUC₁, and ΔAUC, and tested the significance of ΔAUC using our proposed resampling procedure. We also tested the significance of interactions using a LRT. We also estimated RERI for various levels of the genetic risk factor. Under each parametric configuration, we calculated type I error and power of the LRT, and for the ΔAUC and RERI tests.

A common aim of clinical and epidemiological studies is to increase the prognostic value of models by including novel genetic factors and/or interactions of the genetic factors with other risk factors. However, few studies have reported an increase in AUC of considerable magnitude. In order to obtain insights into the properties of the estimated AUCs, we also fitted the true risk model (Equation 5) to our simulated data and calculated the AUCs, which we refer to as the attainable AUCs. Note that the estimated AUCs are obtained via non-parametric ranking procedure. The attainable AUCs are also obtained in a similar manner and, thus, serve as a benchmark in our comparison of the estimated ΔAUC against its theoretical value.

Results

Type I error

The type I errors of LRT and the test for ΔAUC were similar under all parametric configurations considered (Table 2). In general, the type I error of the test of ΔAUC was controlled around the nominal value of 0.05 for all values of N and ρ. There was a slight departure from the nominal rate of 0.05 for LRT (and ΔAUC) in some scenarios, which has also been previously reported in other simulation studies [Allison et al. 1999]. The Type I error for RERI was maintained at 0.05 when the effect of at least one of the risk factors was small (for example when δ = 0.1). The probability presented in Table 2 is the probability of rejecting the null that RERI = 0 under the assumption that γ_jk = 0. However, when both the risk factors have non-negligible main effects (e.g. β = 0.75, δ = 0.6) we are in a setting where RERI ≠ 0. As expected in this specific scenario we did not reject H₀ : RERI = 0, and hence the type I error was considerable larger than the nominal value of 0.05 (type I error of 0.70 when ρ = 0, β = 0.75, δ = 0.60, and 500 affected and 500 unaffected individuals).

Table 2.

Type I errors of ΔAUC test, LRT, and RERI test. The sample sizes are 500 and 200 affected individuals and an equal number of unaffected individuals. The correlations between the genetic factor and treatment are ρ = 0 and ρ = 0.50. The estimated type I errors are shown under various true values of the main effects β and δ (note: γ = 0). In our simulations, the genetic factor had 3 levels and treatment had 2 levels. Hence, we report two RERIs: RERI₁₁ and RERI₂₁.

Number affected	β	δ	ρ = 0				ρ = 0.50
			ΔAUC	LRT	RERI11	RERI21	ΔAUC	LRT	RERI11	RERI21
500	0.15	0.1	0.03	0.05	0.07	0.06	0.07	0.07	0.04	0.03
	0.35	0.1	0.07	0.07	0.06	0.07	0.04	0.04	0.06	0.06
	0.55	0.1	0.08	0.06	0.03	0.03	0.07	0.06	0.05	0.07
	0.75	0.1	0.02	0.03	0.05	0.03	0.04	0.09	0.06	0.08
	0.95	0.1	0.02	0.05	0.03	0.03	0.02	0.03	0.04	0.03
	0.75	0.6	0.01	0.04	0.01	0.7	0.02	0.09	0.03	0.35
200	0.15	0.1	0.03	0.04	0.04	0.03	0.06	0.08	0.01	0.02
	0.35	0.1	0.03	0.02	0.05	0.03	0.05	0.10	0.03	0.03
	0.55	0.1	0.04	0.08	0.02	0.04	0.05	0.08	0.04	0.04
	0.75	0.1	0.03	0.02	0.04	0.02	0.03	0.02	0.00	0.01
	0.95	0.1	0.05	0.07	0.01	0.01	0.05	0.05	0.01	0.02
	0.75	0.6	0.01	0.05	0.01	0.13	0.02	0.02	0.00	0.04

Power

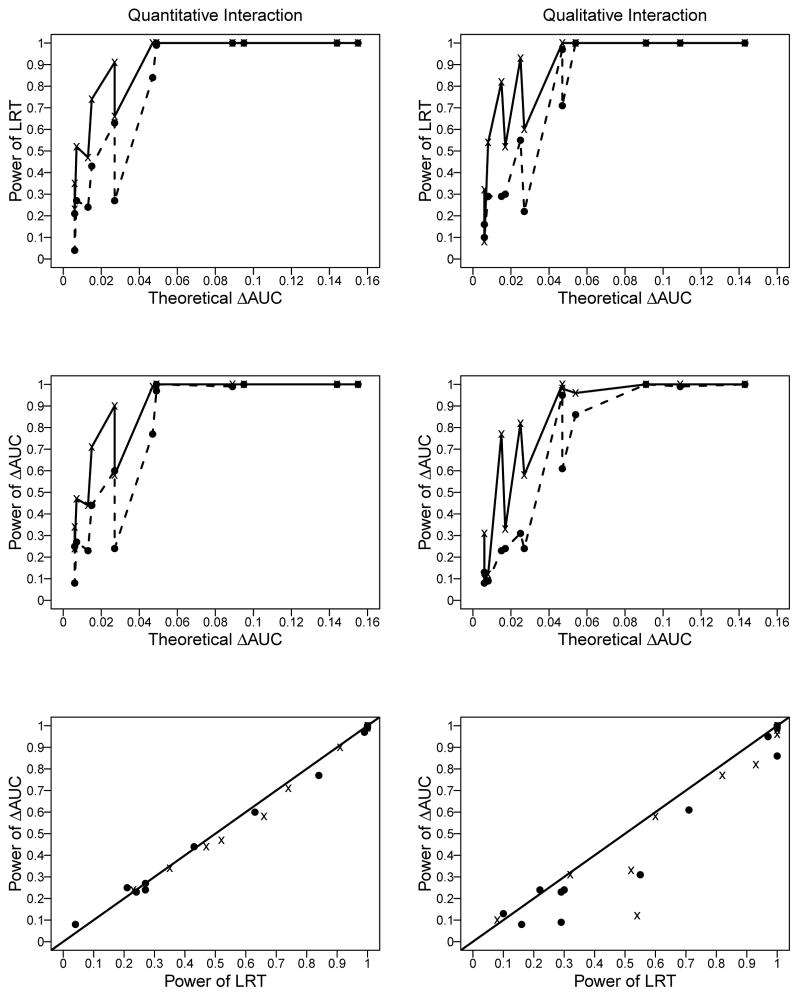
Figure 1 shows the power of LRT and the ΔAUC test for data simulated with ρ = 0. As expected, power increased with sample size. Further, power increased as the theoretical value of ΔAUC increased. The plots indicate that even with a sample size of 200, we can attain power of 1 to detect a ΔAUC of 0.05. However, whether a ΔAUC = 0.05 increase is clinically meaningful is a topic of debate (see Discussion). Note that ΔAUC = AUC₁ − AUC₀, where AUC₀ is the AUC under the null hypothesis that interactions do not contribute to the prognostic value. For a given value of ΔAUC, the power also depended upon the magnitude of AUC₀. For example, detecting ΔAUC = 0.05 when AUC₀ = 0.55 had power of 0.77 and 0.61 under quantitative and qualitative interactions respectively; whereas, the power increased to 0.97 and 0.95 under these two types of interactions when AUC₀ = 0.65. The last row of Figure 1 suggests that, in general, LRT and ΔAUC tests had similar power, although ΔAUC test had slightly lower power than LRT under a few parametric configurations. Power for simulations with ρ = 0.5 showed similar patterns (detailed results not shown).

Figure 1.

Power of the likelihood ratio test (LRT; top row) and the resampling-based ΔAUC test (middle row), and a comparison of the powers of these two tests with the 45-degree line shown as a benchmark (bottom row). The left and right columns correspond to results for data simulated based on quantitative and qualitative interactions, respectively. These results are shown for sample sizes of 500 cases and 500 controls (bold lines in the top and middle rows with points in all the panels shown as “x”) and 200 cases and 200 controls (dashed lines in the top and middle rows with points in all the panels shown as a closed circle)

Estimated and attained AUCs

The estimated and attained AUCs and ΔAUCs are shown in Table 3 for sample size of 1000 individuals (500 affected). In general, the estimated ΔAUC values were smaller than the theoretical ΔAUC values. This was particularly the case for large value of theoretical AUC₀ (for example, AUC₀ = 0.7). The attainable ΔAUCs were closer to the estimated ΔAUC than to the theoretical value. These observations suggest that the inclusion of interactions in a model may not increase ΔAUC by a considerable magnitude even when the interaction effects (and, hence, the prognostic and predictive value) are significantly different from 0. This can happen particularly when AUC of the additive model is already large (for example, theoretical AUC₀ ≈ 0.70 and ΔAUC ≈ 0.10 in our simulations). Similar results were obtained for sample size of 400 individuals (200 affected; Supplementary Table S2).

Table 3.

Theoretical, estimated and attained AUCs and ΔAUC shown for simulations with 500 affected and 500 unaffected individuals. The first column shows the true values of β, δ, and γ used for generating disease risk from Equation (5).

		ρ = 0			ρ = 0.5
(β, δ, γ)	AUC	AUC0	AUC1	ΔAUC	AUC0	AUC1	ΔAUC
Quantitative Interactions
(0.15, 0.10, 0.30)	theoretical	0.551	0.598	0.05	0.561	0.583	0.02
	attainable	0.559 (0.017)	0.596 (0.016)	0.04	0.555 (0.018)	0.572 (0.017)	0.02
	estimated	0.561 (0.018)	0.596 (0.017)	0.03	0.561 (0.014)	0.579 (0.015)	0.02
(0.15, 0.10, 0.70)	theoretical	0.551	0.695	0.14	0.561	0.663	0.10
	attainable	0.551 (0.016)	0.666 (0.013)	0.12	0.578 (0.017)	0.608 (0.015)	0.03
	estimated	0.559 (0.016)	0.669 (0.013)	0.11	0.578 (0.014)	0.607 (0.013)	0.03
(0.55, 0.10, 0.50)	theoretical	0.654	0.703	0.05	0.666	0.693	0.03
	attainable	0.657 (0.016)	0.691 (0.014)	0.03	0.638 (0.015)	0.659 (0.015)	0.02
	estimated	0.656 (0.018)	0.69 (0.017)	0.03	0.638 (0.014)	0.658 (0.013)	0.02
(0.75, 0.10, 0.90)	theoretical	0.703	0.798	0.10	0.715	0.778	0.06
	attainable	0.69 (0.02)	0.753 (0.014)	0.06	0.663 (0.015)	0.694 (0.014)	0.03
	estimated	0.689 (0.018)	0.753 (0.013)	0.06	0.663 (0.017)	0.696 (0.015)	0.03
Qualitative Interactions
(0.15, 0.10, −0.30)	theoretical	0.551	0.598	0.05	0.561	0.605	0.04
	attainable	0.537 (0.017)	0.576 (0.015)	0.04	0.559 (0.017)	0.582 (0.014)	0.02
	estimated	0.54 (0.018)	0.581 (0.016)	0.04	0.559 (0.016)	0.583 (0.016)	0.02
(0.15, 0.10, −0.70)	theoretical	0.551	0.694	0.14	0.561	0.687	0.13
	attainable	0.536 (0.022)	0.667 (0.014)	0.13	0.562 (0.031)	0.66 (0.015)	0.10
	estimated	0.54 (0.022)	0.67 (0.016)	0.13	0.562 (0.037)	0.665 (0.014)	0.10
(0.55, 0.10, −0.50)	theoretical	0.654	0.701	0.05	0.666	0.708	0.04
	attainable	0.64 (0.017)	0.668 (0.016)	0.03	0.624 (0.015)	0.652 (0.014)	0.03
	estimated	0.642 (0.019)	0.672 (0.018)	0.03	0.625 (0.015)	0.652 (0.015)	0.03
(0.75, 0.10, −0.90)	theoretical	0.703	0.794	0.09	0.715	0.793	0.08
	attainable	0.72 (0.017)	0.749 (0.015)	0.03	0.634 (0.02)	0.698 (0.015)	0.06
	estimated	0.718 (0.016)	0.748 (0.015)	0.03	0.636 (0.016)	0.698 (0.014)	0.06

Data Example

We illustrate the proposed concepts and methods using published data from an epidemiology study of melanoma [Kricker et al. 2010]. In this study, the outcome is binary, denoting the presence/absence of a second primary melanoma. Sun exposure and variants in the pigmentation gene MC1R are among the important known risk factors for melanoma. Table 4 shows the melanoma data with MC1R as a binary variable denoting the presence/absence of the R allele (i.e., red hair color variant) and sun exposure measured as a binary variable in terms of: (i) beach and water activities from age 15; (ii) average annual lifetime ambient ultraviolet (UV) exposure; and (iii) early life ambient UV exposure.

Table 4.

Application in melanoma (Kricker et al). MC1R and each of the three types of sun exposures have L₁ = L₂ = 2 levels. For the levels of MC1R, “No R” denotes that there is no variant predisposing the individuals to red hair color, and “Any R” denotes the presence of at least one such variant. The columns SPM and MPM denote the total number of individuals with single and multiple primary melanomas, respectively. The two columns on the right denote the probability of predictive value calculated via the bootstrap procedure. The notation P_RERI denote max {P (RERI > 0), P (RERI < 0)}.

MC1R	Sun Exposure	SPM	MPM	LRT (p-value)	ΔAUC (p-value)	RERI (95% CI)	Bootstrap predictive values
							P(ΔAUC > 0)	PRERI
Beach and water activities from age 15
No R	None	248	68	4.60	0.003a	−0.4038	0.29	0.89
	Any	733	380	(0.03)	(0.02)	(−1.314, 0.151)
Any R	None	236	129
	Any	644	438
Average annual lifetime ambient UV
No R	369–848 KJ/m2	573	179	0.003	0b	0.4818	0.05	0.93
	849–1500 KJ/m2	359	249	(0.95)	(0.94)	(−0.183, 1.121)
Any R	369–848 KJ/m2	495	212
	849–1500 KJ/m2	350	336
Early life ambient UV
No R	371–853 KJ/m2	563	193	0.052	0c	0.2539	0.04	0.82
	854–1520 KJ/m2	387	241	(0.82)	(0.90)	(−0.324, 0.785)
Any R	371–853 KJ/m2	483	236
	854–1520 KJ/m2	374	320

^aAUC₀ = 0.557, AUC₁ = 0.560

^bAUC₀ ≈ AUC₁ ≈ 0.619

^cAUC₀ ≈ AUC₁ ≈ 0.593

For each data set, we fitted logistic regression models to the outcome in relation to MC1R and sun exposure and tested the null hypothesis of no interaction between gene and sun exposure using a LRT, and tested H₀ : ΔAUC = 0. We also calculated RERI and tested H₀ : RERI = 0. In clinical studies, it is meaningful to refer to preditive values in terms of probability that a genetic factor projects treatment benefit [Sawyers 2008]. In our setting, this is equivalent to the probability that ΔAUC and RERI exceed certain threshold. To obtain insights into this, we calculated P(ΔAUC > 0) and max {P(RERI > 0), P(RERI < 0)} (since RERI can be positive or negative). We generated 10,000 bootstrap samples of the data, estimated ΔAUC and RERI for each sampled data set and calculated P(ΔAUC > 0) as the fraction of data sets for which the estimated ΔAUC was positive, and estimated max {P(RERI > 0), P(RERI < 0)} as the maximum of the fraction of data sets having negative and positive estimates of RERI (see Table 4 and Supplementary Figure S2).

There was a significant interaction between MC1R and sun exposure from beach and water activity (LRT = 4.60, d.f = 1, p-value = 0.03). The magnitude of the estimated ΔAUC was small (AUC₁ = 0.557, AUC₀ = 0.560, ΔAUC = 0.003). However, as expected, it was significantly different from 0 (p-value = 0.021). This suggests that interaction contributed significantly to the prognostic value. Further, when treatment benefit was defined in terms of odds ratios, this result suggests that MC1R significantly predicts the benefits of reducing sun exposure from beach and water activity. In particular, the benefit of reducing sun exposure was 1.244 (= 438 × 236/(644 × 129)) for carriers of an R variant and 1.891 (= 380 × 248/(733 × 68)) among non-carriers. These results suggest that non-carriers had significantly higher benefit in terms of reduced risk of second primary melanoma associated with reducing sun exposure than carriers (estimated predictive value is P₁₁ = 1.52 = 1.891/1.244). However deciding whether this benefit is clinically actionable will require more rigorous investigations based on further studies (see Discussion). The estimated value of RERI was −0.4038 (95% confidence interval: −1.314, 0.151), which was not significantly different from 0. This suggests that, when treatment benefit was defined in terms of excess disease odds (or excess disease risk), reduction in melanoma risk due to reducing sun exposure from beach and water activity was higher for non-carriers than carriers of an R variant, although this was not statistically significant. The bootstrap estimates of predictive values were P(ΔAUC > 0) = 0.29 and max {P(RERI > 0), P(RERI < 0)} = 0.89. Since LRT and the test for ΔAUC were significant, we would, in principle, expect the estimated P(ΔAUC > 0) to be large. The seemingly small estimated probability of 0.29 may be due to the small number of non-carrier cases without sun exposure from beach and water activities (68 multiple primary melanomas). Even though RERI was not significantly different from 0, our bootstrap approach showed that the predictive value of MC1R was approximately 89% when treatment benefit was defined in terms of differences between disease odds.

There was no significant interaction between MC1R and annual average lifetime UV (LRT = 0.0034, d.f = 1, p-value = 0.95). As expected interaction did not contribute to the prognostic value (ΔAUC ≈ 0, p-value = 0.94). When treatment benefit was defined in terms of odds ratios, the benefits of reducing annual average lifetime UV were 2.24 and 2.22 among carriers and non-carriers, respectively, of an R variant. Hence, the predictive value was P₁₁ = 1.01 = 2.24/2.22. The estimated value of RERI was 0.4818 (95% CI: −0.183, 1.121), suggesting that MC1R does not significantly predict the benefits of reducing annual average lifetime UV when benefit is defined in terms of differences between disease odds. Based on the bootstrap approach, P(ΔAUC > 0) = 0.05 and max {P(RERI > 0), P(RERI < 0)} = 0.93. Thus, even though RERI was not significantly different from 0, the bootstrap estimate of predictive probability based on RERI was greater than 90%. Similar results were obtained for the interaction between MC1R and early life ambient UV (Table 4).

Discussion

In studies of targeted treatment/intervention, often the goal is to understand how treatment benefits vary according to genetic predisposition [Lerman et al. 2007; Keedy et al. 2011]. This has accelerated the investigations of gene-treatment, gene-environment, and gene-gene interactions using statistical models in the health sciences. Interactions depend upon the scale on which the outcome is measured [Wang et al. 2010; Satagopan and Elston 2013]. In this paper we have examined the relationship between interactions (measured on two different scales) and prognostic and predictive values of (genetic) risk factors.

Specifically, we examined whether including interaction terms in the model improves the prognostic value i.e., increases ΔAUC by a significant magnitude. We showed that testing the null hypothesis that ΔAUC = 0 is equivalent to testing the null hypothesis of no multiplicative interaction, and developed a resampling approach to test the statistical significance of ΔAUC in relation to interactions. Although previous work has demonstrated the equivalence of several null hypotheses when evaluating whether a new biomarker has significant prognostic value [Pepe et al. 2013], we have shown the equivalence of two null hypotheses in the specific context of interactions. Kerr and Pepe [2011] studied the properties of receiver operating characteristic (ROC) curves in the context of interactions by evaluating ROC curves separately among carriers and non-carriers of the genetic factor of interest by fitting an additive logistic regression model. Our work is distinct from this in that it focuses specifically on how interaction terms in logistic regression models relate to ΔAUC.

It has been noted that including interactions in a model does not increase the AUC by a considerable magnitude [Aschard et al. 2012]. To obtain insights into this, we used simulation studies, which showed that, even when the true disease risk model is known, the attainable ΔAUCs are considerably smaller than the theoretical ΔAUCs. Our simulations also show that the power to reject H₀ : ΔAUC ≠ 0 of a certain magnitude in the context of interactions also depends upon the magnitude of AUC₀, which also aligns with recent work that examined model performance in the context of evaluating a new biomarker [Kerr et al. 2012]. To obtain insights into this, consider, for example, the case where AUC₀ = 0.70. The theoretical value of σ₀ is $\sqrt{2}{\mathrm{\Phi }}^{-1}(0.70)=0.74$. Then, a 10% increase in σ₀ will result in a 2% increase in AUC since $\mathrm{\Phi }(0.74\times 1.10/\sqrt{2})\approx 0.72$. We will need 55% and 100% increases in σ₀ to attain ≈ 10% and 15% increases in AUC when AUC₀ = 0.70. Whether such increases in the magnitude of σ₀ can be achieved through the inclusion of interactions in a model is an important question, but one that will require investigations in a broad range of real data sets.

While ΔAUC is a commonly used measure for evaluating prognostic values, there is no consensus on a measure of predictive values. The RERI is an important statistic in epidemiology for evaluating additive interactions, and is a measure of predictive value when treatment benefit is defined in terms of difference between disease odds or disease risk [Rothman et al. 2008]. However, recent epidemiology studies have reported predictive values of genetic factors based on the statistical significance of interactions without specifically reporting a measure of treatment benefit. For example, (Lerman et al.) [2007] used the statistical significance of a multiplicative interaction between bupropion treatment and the CYP2B6 gene in a logistic regression model to show that carriers of a variant allele may be more vulnerable to abstinance symptoms and smoking relapse. Here we have shown that multiplicative interaction (equivalently, ΔAUC) is a measure of predictive value when treatment benefit is defined based on odds ratios.

An important practical question for future study is: what values of ΔAUC and RERI would be clinically meaningful? Addressing this question is outside the scope of our work. Further investigations based on rigorous study designs with validation data sets are needed to evaluate clinically actionable magnitudes of prognostic and predictive values and compare their properties with other emerging measures in the setting of interactions in statistical models.