Abstract
Structural dynamics of nucleic acid and protein is an important physical basis of their functions. These motions are often very difficult to synchronize and too fast to be clearly resolved with the currently available single molecule methods. Here we demonstrate a novel hybrid single molecule approach combining stochastic data analysis with fluorescence correlation that enables investigations of sub-ms unsynchronized structural dynamics of macromolecules. Based on the method, we report the first direct evidence of spontaneous DNA motions at the nucleosome termini. The nucleosome, comprising DNA and a histone core, is the fundamental packing unit of eukaryotic genes that must be accessed during various genome transactions. Spontaneous DNA opening at the nucleosome termini has long been hypothesized to enable gene access in the nucleosome, but has yet to be directly observed. Our approach reveals that DNA termini in the nucleosome open and close repeatedly at 0.1–1 ms−1. The kinetics depends on salt concentration and DNA–histone interactions but not much on DNA sequence, suggesting that this dynamics is universal and imposes the kinetic limit to gene access. These results clearly demonstrate that our method provides an efficient and robust means to investigate unsynchronized structural changes of DNA at a sub-ms time resolution.
INTRODUCTION
Unsynchronized dynamics in the structures and positions of nucleic acid and protein can be efficiently monitored with single molecule fluorescence methods such as single molecule FRET (smFRET) (1) whose time-resolution can be improved by stochastic data analysis (2). One such approach is to optimize time resolved FRET dynamics according to the sequence of fluorescence photon emission intervals based on maximum likelihood estimation (MLE) (3). This type of analysis with small signal changes, however, often yields extremely large uncertainty, making the confidence in the results unacceptably low. This is because the analysis is often trapped in a local maximum likelihood and there is no practical means to resolve this issue from an analytical approach (4). In order to address this problem, we combined fluorescence correlation spectroscopy (FCS) with MLE-based data analysis. Based on this hybrid approach, here we report the first direct evidence of spontaneous nucleosomal DNA dynamics and its quantitative characteristics that will greatly help elucidate the physical mechanism of gene access at the molecular level.
The nucleosome, comprising DNA and an octameric histone protein core, is the fundamental packing unit of eukaryotic genes (5,6) that must be accessed and processed by factors and polymerases during various genome transactions such as transcription, replication and DNA repair. Spontaneous DNA opening motion at the nucleosome termini has long been hypothesized to enable gene access during these processes. However, direct observation of this motion has never been reported likely because it is too fast to be monitored with the currently available methods (7,8). Our newly developed hybrid approach enabled us to address this deficiency by providing an efficient means to directly monitor the spontaneous nucleosomal DNA motions at a sub-ms time resolution.
MATERIALS AND METHODS
Nucleosome reconstitution
Human histones and CENP-A were prepared as described elsewhere (9). For nucleosomal DNA, a 20 base single stranded DNA linker with biotin at one end was added to either a 147 bp human α-satellite sequence (10) or the 601 sequence (11). All the DNA sequences used in the experiment are shown in Supplementary Figure S1. Each of the two nucleosomal DNA constructs was prepared by ligating six fragments, two of which have a fluorophore already inserted during oligo synthesis (Integrated DNA Technology, Coraville, IA, USA). We first annealed the DNA fragments and cleaned up the annealed product with a polymerase chain reaction (PCR) purification kit (Qiagen, Valencia CA, USA). We then ligated the product (T7 ligase for 30 min at room temperature) and used a PCR purification kit (Qiagen, Valencia CA, USA) to clean up the ligated product. The ligation product was analyzed with a denaturing urea gel to verify that no significant nick is present (Supplementary Figure S2a). The major products are the 147 and 167 bp nucleosomal DNA strands as designed. The dim longer (>200 bp) and shorter strand bands (107 bp based on the lengths of the oligonucleotides) are likely due to unwanted ligation and errors in the measured amounts of the oligonucleotides for the ligation reaction. These products will not form canonical nucleosomes and are filtered out during data collection or analysis (further details are given in the next section). Consequently, they will not affect the quality of our measurements significantly. The two fluorophores form a FRET pair that reports DNA dynamics at the nucleosome termini. The FRET donor Cy3 replaces the 76th base of the forward strand (chain I in a crystal structure) which is two bases away from the dyad. ATTO647N was labeled at the 5′ end of the reverse strand (chain J). Two 40 bp ds-DNA constructs with a 20 base linker were used as DNA controls. DNA-D is labeled with Cy3 in the middle of one strand (Supplementary Figure S1). DNA-DA has an additional ATTO647N at the 5′ end of the other strand (Supplementary Figure S1). The FRET efficiency observed from DNA-DA is 0.594 similar to the values observed from the nucleosomes. The DNA-D control measurements were carried out to show that the photophysical dynamics of the fluorophores exist in both DNA-D and DNA-DA controls. Quantitative analyses were performed with the DNA-DA control only. The nucleosomes were assembled by a stepwise salt dialysis method (12,13) starting from 2M NaCl TE buffer (10 mM Tris–HCl, pH 8.00, 1 mM EDTA) followed by five successive 1 h dialyses in the same buffer at 850, 650, 500, 300 and 1 mM NaCl. The resulting nucleosomes were annealed at 54°C for 1 h. A native gel image revealing the purity of the nucleosome sample at each step of assembly is given in Supplementary Figure S2b. The final product shows a clean single nucleosome band and some aggregates in the well which are easily distinguished by abnormally high fluorescence intensity (>40 kHz Cy3 photon emission rate) and were avoided from data collection. We may still have some sample heterogeneity, which can be further filtered during data analysis based on their FRET efficiencies (discussed at the end of the next section).
Single molecule measurements
Fluorescence photons from samples were collected on a home-built scanning confocal microscope system based on an Olympus IX70 inverted microscope (Olympus, Japan) with an objective lens (x60 magnification, 1.49 numerical aperture, oil immersion, Apo from Nikon, Japan) (Figure 1a). The optics was setup as shown in Figure 1f and was aligned as following. The telescope lens pair should be selected so that the beam entering the microscope is ∼5 mm in diameter (our setup contains a pair with f = 25 and 125 mm to expand the laser beam of 0.3 mm in size to 1.5 mm). The ratio of the focal lengths of the two lenses is the magnifying power of the telescope. The distance between the two telescope lenses (Figure 1f) should be approximately the sum of the two focal lengths so that the resulting beam should be perfectly parallel. The final excitation beam (∼5 mm in size) should hit the center of the objective back focal plane. The beam should hit approximately the centers of all the optics and should not be cut by any optics or obstacles along the path. Fluorescence beam alignment to the two avalanche photodiodes (APDs) was achieved in two steps. For coarse alignment, a mercury arc lamp illuminating from the top of the microscope stage was utilized. The arc lamp was set to illuminate the center of the objective lens and the beam path was traced all the way to the capped detector areas of the two APDs. The first mirror right next to the filter turret was adjusted to make the beam steered at a 90° angle toward the second mirror. The second mirror was also adjusted to steer the beam at a 90° angle. The first laser-grade multichroic mirror (for 532 nm, zt532rdc from Chroma Technology) can be adjusted at this point so that the beam hits this surface at a 45° angle. The beam should hit the center of the long pass filter (LP, E550LP from Chroma Technology). The second dichroic mirror (cutoff 650 nm, 650DCXR from Chroma Technology) was also adjusted so that the beam hits this surface at a 45° angle. The two focusing lenses were positioned in front of the APDs so that the bifurcated beams from the dichroic mirror hit the centers of the lenses. Each APD was positioned at approximately the focal point of the lens and mounted on a single-axis translational stage for fine alignment. APD detection areas must be capped for coarse alignment to protect them from bright light. The lenses in front of the APDs are mounted on a 2-axis lens mount for fine alignment. The beams were aligned by adjusting the 2-axis lens mounts and the APD translational stages so that the beams are focused right at the centers of the APD detector caps. This was the end of coarse alignment. The laser was turned on and the laser beam may be re-aligned at this point to hit the center of the objective lens by adjusting the mirror installed right after the telescope lenses. The telescope lens positions can also be utilized to steer the beam up and down slightly. For fine alignment of the APDs, we used fluorescent beads (FluoSpheres® red fluorescent beads (580/605), Thermo Fisher Scientific) placed on a clean microscope coverslip. The beads were excited with a 532 nm laser and the fluorescence count on APD1 was monitored while adjusting the 2-axis mount of the focusing lens and the translational stage of the APD until the count is maximized. This process was repeated with APD2. This fine alignment was repeated each day with DNA or nucleosome samples before starting the measurements. Cy3 was excited with a 532 nm laser (GCL-150-L, CrystaLaser, NV, USA) at a 10μW/π(217 nm)2 power. The fluorescence photon streams from Cy3 and ATTO647N were steered to APD1 and APD2 (SPCM-AQR16 from Perkin Elmer Optoelectronics, Dumberry Canada) respectively, with a dichroic mirror and lenses (Figure 1a). The diameter of the circular active area of the APD detectors is ∼175 µm, effectively acting as a pinhole of a confocal microscope. The filters and mirrors were purchased from Chroma Technology Corp (VT, USA) and the lenses were purchased from Thorlabs Inc. (NJ, USA). The arrival times of the fluorescence photons from Cy3 and ATTO647N were determined by a general-purpose transistor–transistor logic (TTL) pulse counter at a 50 ns time resolution (NI USB-6351, National Instrument, TX, USA) and recorded separately in two files by a home-built software package. Nucleosome samples were diluted into the TE buffer with 2 mM Trolox (Sigma, MO, USA) and 2, 10, 50 or 100 mM NaCl. Trolox was used to stabilize the fluorescence emission (14). The final nucleosome concentration was adjusted to 20–50 pM for the measurements so that the nucleosome particles immobilized on a quartz cover glass surface were well separated from each other. The quartz microscope cover glass surface was thoroughly cleaned and functionalized with a silanization reagent ((3-Aminopropyl)triethoxysilane, Sigma, MO, USA) followed by a conjugation reaction to polyethyleneglycol (PEG, 5k Mw) with a succinimidyl ester group (Laysan Bio, AL, USA). Nucleosomes were immobilized on the surface via biotin-streptavidin conjugation (Figure 1b). A piezoelectrically driven microscope stage was programmed to scan across an 80 × 80 µm area and park automatically at points with Cy3 and ATTO647N signals until both of them photobleached. The APDs convert a photon detection signal to a TTL pulse that were wired to the general-purpose counter board. During a parking period, the TTL pulse counters recorded the time interval (τ) between two consecutive photons at a 50 ns time resolution for the entire set of detected photons (Figure 1d). This data collection process is automated and built within a software package written in the laboratory. This smFRET data collection can be achieved with a commercial TCSPC system with time-tagging capability which provides a high time and labor efficiency (e.g. TimeHarp 260 from PicoQuant, Berlin Germany). Data were collected for 30, 25, 20 and 15 min at 2, 10, 50 and 100 mM salt concentrations, respectively, in order to avoid disassembly of the nucleosomes during measurements. According to previous reports, histone H2A–H2B dimers are stable in the nucleosome at least for 16.7 min at 100 mM NaCl in the presence of a histone chaperone Nap1. Therefore, these data collection time windows in the absence of any histone chaperone should be short enough to ensure that the majority of the population is intact nucleosomes. There could still be some sample heterogeneity due to abnormal DNA ligation product, slight variations in the positioning and partial disassembly (tetrasomes and hexasomes). Intact nucleosomes with properly positioned histones should show an average FRET efficiency of ∼0.7, which was estimated based on a crystal structure (PDB ID: 1AOI) with a 4.9 nm Förster radius estimated from the value between ATTO550–ATTO647N (6.5 nm, provided by ATTO-TEC GmbH, Germany) and the quantum efficiency ratio between ATTO550 and Cy3 (80%/15%). The data for each FCS spectrum and MLE estimation was collected from 485–1237 nucleosomes (Supplementary Table S1). We found that 45.1–99.9% of the nucleosomes per case show an average FRET value within 0.6–0.8 (Supplementary Table S1). The variation in the sample homogeneity is likely due to the quality of the DNA oligonucleotides and variations in the quality of the ligation product. The populations deviating from the 0.6–0.8 FRET range are likely due to positioning heterogeneity and abnormally assembled nucleosomes with erroneous DNA or imperfectly ligated DNA and filtered out from data analysis. Among the population within the correct FRET range, <2% did not converge during MLE analysis. This minor population might be due to partial disassembly (tetrasomes and hexasomes) and could not be used in our analysis. Overall, 44–98% of the collected data was used for data analyses.
Figure 1.
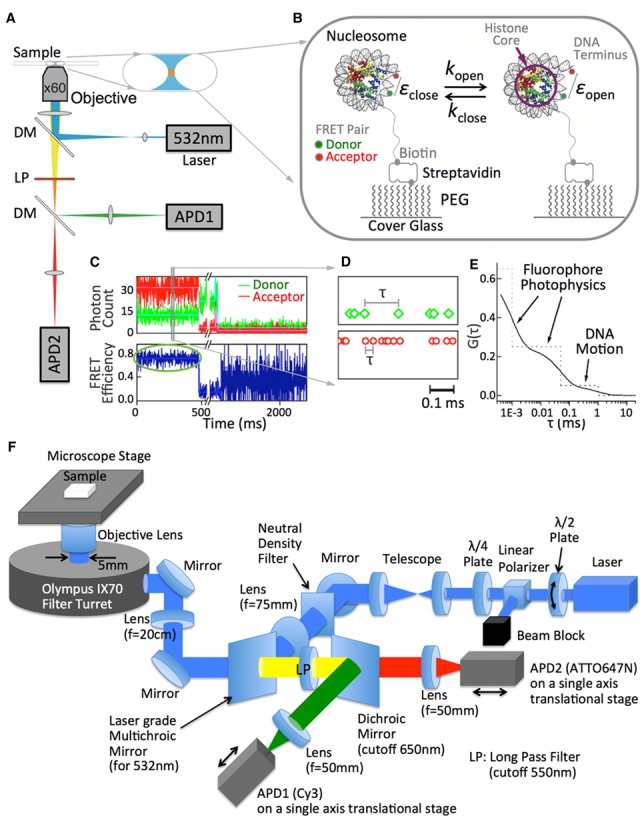
Experimental scheme to implement a hybrid single molecule approach combining smFRET-FCS with MLE to monitor fast spontaneous DNA dynamics in the nucleosome. (A) Instrumental setup. A tightly focused 532 nm laser spot was introduced to the sample on a microscope cover glass surface through an objective lens to excite the FRET donor (Cy3). Fluorescence photons from the donor and the acceptor (ATTO647N) were collected through the same objective lens, a dichroic mirror (DM, cut-off wavelength at 650 nm), a long pass filter (LP, cut-off wavelength at 650 nm) and another dichroic mirror (DM, cut-off wavelength at 650 nm) by APD1 and APD2. The arrival times of the photons at the detectors were recorded at a 50 ns resolution. (B) Experimental setup. Nucleosome core particles labeled with Cy3 near the dyad (green dot) and ATTO647N (red dot) at a terminus were attached through a biotin (gray dot)-streptavidin conjugation to a polyethyleneglycol (PEG) coated surface. Detailed information on the DNA sequence and fluorophore labeling positions are given in Supplementary Table S6. The distance between the two fluorophores is estimated to be about 4 nm according to a crystal structure (PDB ID: 1AOI), corresponding to a FRET efficiency value of ∼0.7. (C) Representative fluorescence intensity time traces of a FRET pair and the corresponding FRET efficiency time trace. The fluorescence intensity traces were obtained by binning the photon arrival times in 1 ms. The ATTO647N photobleaching event around 0.5 s is followed by Cy3 photobleaching at ∼1.5 s. (D) A section of raw data randomly selected from (c). The raw data is the arrival times of individual photons from the FRET pair. The interval between two consecutive photons (τ) is analyzed to obtain a second-order fluorescence intensity correlation spectrum G(τ) as illustrated in (E). (F) Detailed optics setup shown in (a). All the lenses and mirrors have 1-inch diameter except the dichroic mirrors which have 24 × 30 × 1 mm dimensions. The filter turret was set to a mirror to reflect both excitation and emission. λ/2 plate mounted on a rotating optic mount combined with the polarizer acts as a variable laser intensity attenuator that produces a linearly polarized light. The linearly polarized light is converted to circularly polarized light by the λ/4 plate in order to avoid any dipole orientation dependent excitation. All the dichroic/multichroic mirrors and the long pass filter (LP) were purchased from Chroma Technology Corp. (Bellows Falls, VT, part numbers can be found in the ‘Materials and Methods’ section) and all the other optics were purchased from Thorlabs Inc. (Newton, NJ, USA). All the lenses are plano-convex spherical singlet lenses with anti-reflection coating for visible wavelengths (350–700 nm coating except for the focus lens for APD2 with 650–1050 nm coating). A detailed alignment procedure can be found in the methods section.
Fluorescence correlation
The second order fluorescence intensity (I(t)) correlation G(τ) is defined by:
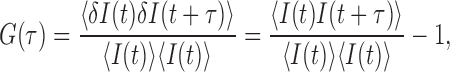 |
(1) |
where <I(t)> represents the average intensity and δI(t) is the deviation of the intensity at time t (I(t)) from <I(t)>. The fluorescence correlation spectra of the FRET donor and the acceptor were generated in a τ range of 0.4 μs–20 ms by a two stage correlation algorithm in order to reduce the computation time (15), which calculates the correlation function from photon intervals in a faster time range and from binned intensities in the rest of the τ range. We filtered out data from a nucleosome that has a fluorophore lifetime shorter than 100 ms in order to extend the FCS analysis to 20 ms to ensure errors <0.1% (16) or the average FRET efficiency lower than 0.6 in order to ensure analyses only on intact nucleosomes.
Assuming a two-state FRET dynamics for the nucleosome termini opening motion (i.e. the open and the closed states of a nucleosome terminus as shown in Figure 1b), the correlation decay of the FRET acceptor fluorescence can be expressed as following in terms of the FRET efficiencies of the two states and the kinetic rates between the two states.
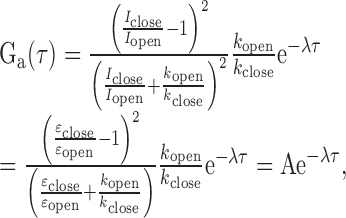 |
(2) |
where Iclose and Iopen are the fluorescence intensities of the acceptor in the closed and the open states, respectively, εclose and εopen are the FRET efficiencies of the closed and the open states respectively, kopen and kclose are the transition rates to the open and the closed states respectively, and λ = kopen+ kclose (17).
Maximum likelihood estimation (MLE)
An smFRET data analysis method based on MLE has been proposed and utilized recently (2,3). We employed this method to obtain the FRET efficiencies of the open and the closed states of the nucleosome termini. This scheme also generates the kinetic rates whose standard deviations are often too wide to be meaningful especially when the FRET change is small (demonstration follows later with simulated photon streams, Supplementary Table S2). A likelihood function that defines the likelihood of observing a photon stream obtained from a dynamic FRET pair with a given parameter set is given by
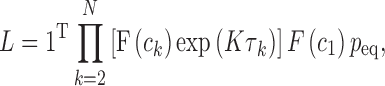 |
(3) |
where 1T is a row vector of 1, N is the number of photons in the photon stream, ck is the color (donor or acceptor) of the 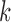 th photon and τk is the interval between (k-1)th and kth photon. F is a matrix defining the photon emission probabilities, K is a matrix of the transition rate and peq is a vector of the state population densities at equilibrium. For the nucleosome termini dynamics we investigated (close: terminal DNA closed state, open: terminal DNA open state) (Figure 1b), they are defined by
th photon and τk is the interval between (k-1)th and kth photon. F is a matrix defining the photon emission probabilities, K is a matrix of the transition rate and peq is a vector of the state population densities at equilibrium. For the nucleosome termini dynamics we investigated (close: terminal DNA closed state, open: terminal DNA open state) (Figure 1b), they are defined by
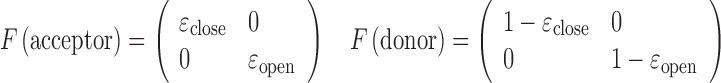 |
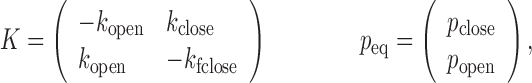 |
(4) |
where pclose and popen are the population densities of the closed and the open states at equilibrium (i.e. pclose + popen = 1). With these parameters, the likelihood function becomes
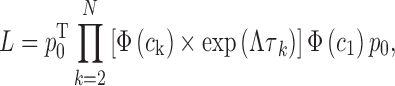 |
(5) |
where Λ is a diagonal matrix whose elements are the eigenvalues of K (Λ = U−1KU).
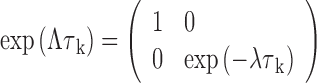 |
(6) |
Other matrices and vectors for our nucleosome systems are transformed accordingly to
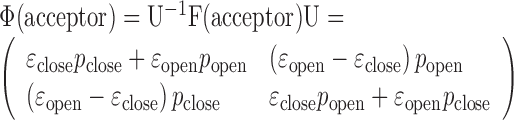 |
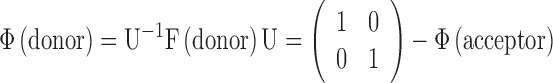 |
 |
(7) |
The values of εclose, εopen, popen (or pclose) and λ can be estimated by maximizing the likelihood function (Equation (5)) with a routine maximizing a custom function built in the IDL programming package (Exelis, McLean VA, USA). We divided a photon stream into multiple 25 ms sections for each of which the likelihood function was calculated. We maximized the sum of the log-likelihood functions from all the 25 ms sections to estimate a set of εclose, εopen, popen and λ for each nucleosome particle.
Extracting kopen and kclose from MLE and FCS combination
The εclose and εopen values obtained from MLE should contain only a small error according to our simulation study (Supplementary Table S2) while the rate constants are too widely scattered to be meaningful with a reasonable confidence level. In order to estimate the rate constants in a robust way, we utilized the εclose and εopen values obtained from MLE combined with the values of λ and A obtained from the FCS analysis to solve for kopen and kclose based on the following two equations.
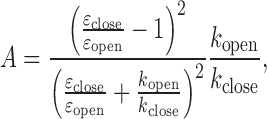 |
(8) |
and
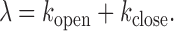 |
(9) |
For an FCS decay component that is too fast to form discrete states with well-resolved photon emission statistics at our photon emission rates (30–40 kHz or 1–2 photons per 50 μs), we used the following scheme to obtain the kinetic rates. If we assume that the dynamics is due to nucleosomal DNA motion, the closed state should be the same as the closed state found in the slower dynamics. The εclose value should be related to the average FRET value εavg and εopen as shown below (Equation (10)). The value of εavg can be obtained either from averaging FRET efficiencies or directly from MLE analysis.
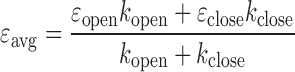 |
(10) |
Based on εavg and εopen values obtained from the measurements and MLE analysis, we can solve for the three unknowns εopen, kopen, and kclose with the three equations Equations (8)–(10).
RESULTS
Experimental setup and MLE analysis performance with simulated photon streams
We employed a time-tagged single photon counting setup which time-stamped all the detected photons from a FRET pair labeled at nucleosomal DNA (Figure 1a and b). The FRET pair emitted photons at a combined rate of 30–40 kHz (30–40 photons/ms) and the changes in the FRET efficiency reflected DNA motions at the nucleosome termini. A time-tagged fluorescence photon stream at a 50 ns resolution (Figure 1d) was binned into a fluorescence intensity time trace, which was used to generate a FRET efficiency time trace (Figure 1c). The FRET traces with 1 ms time-bins show a stable FRET state (circled in green in Figure 1c) followed by single-step photobleaching events. No obvious step-wise FRET changes in the vast majority of the nucleosomes indicate that the DNA termini motion is absent on a timescale of a few milliseconds or longer. In order to reveal the dynamics at a sub-ms time resolution, we employed a stochastic process analysis method based on an MLE algorithm (2,3). The algorithm finds the optimum values for the FRET efficiencies of the termini closed and open states (εclose and εopen in Figure 1b) and the kinetic rate constants (kopen and kclose, the rates of opening and closing transitions, respectively as shown in Figure 1b) according to the collected photon streams. We first tested the performance of the algorithm with simulated photon streams (Supplementary Table S2). The algorithm works well when the FRET change is reasonably large (2,3). Even with a photon emission rate (total 32kHz with 10% added noise) and a FRET change (ΔFRET = 0.16) similar to our experimental data, the errors in the FRET efficiencies are still as low as 3% (Supplementary Table S2).
MLE analysis of photon streams from nucleosomes
The nucleosome samples we used were made with (i) the canonical human histone core and a 147 bp human α-satellite DNA sequence (10) (H3-SAT), (ii) the canonical human histone core and the 147 bp 601 sequence (11) (H3–601) and (iii) a human histone core whose H3 was replaced with CENP-A and a 147 bp human α-satellite sequence (CA-SAT). The histone core is made of two copies of histones H2A, H2B, H3 and H4. The DNA termini in the nucleosome directly contact H3 and, therefore, chemical modifications or variations of H3 (the blue part of the histone core in Figure 1b) would affect the termini dynamics. CENP-A is an H3 variant typically assembled on α-satellite and found at the centromere (18). The α-satellite sequence is also found in the canonical nucleosome in cells. The final two turns of DNA of the CENP-A nucleosome are unprotected from nuclease digestion implying flexible termini (19), which has been correlated with biophysical approaches in solution (20,21) and a crystal structure (22).
The three nucleosomes were monitored at 2, 10, 50 and 100 mM NaCl salt concentrations and the collected photon streams were analyzed with the MLE algorithm. The values of εclose and εopen are shown in Figure 2a and b and Supplementary Table S3. For verification of the algorithm performance with experimental data on FRET efficiency estimation, table S4 reveals that the average FRET efficiencies from MLE and from the normalized acceptor intensities are in excellent agreement. The FRET efficiency difference between the closed and open states can be interpreted as 0.5 nm or 7–8 bp terminal DNA stretched out in the open state. This estimation utilized a crystal structure (PDB ID: 1AOI) and assumed a constant FRET orientation factor (κ2) in the open and closed states. This estimate may contain <20% error (4.4–5.4 nm for ±10% Förster radius variation resulted in 0.4–0.6 nm for the opening distance). The FRET efficiencies we observe for the nucleosomes in the closed and open states remain constant, regardless of salt concentration or DNA sequence. However, the FRET efficiencies measured for the CENP-A nucleosome are significantly lower in both the closed and open states (see Supplementary Table S5 for statistical analysis), suggesting that the DNA termini of the CENP-A nucleosome are more loosely wrapped when compared to the H3 nucleosomes. Overall, these results suggest that salt concentration and DNA sequence do not alter the termini structure, but histone–DNA interactions do have a significant impact.
Figure 2.
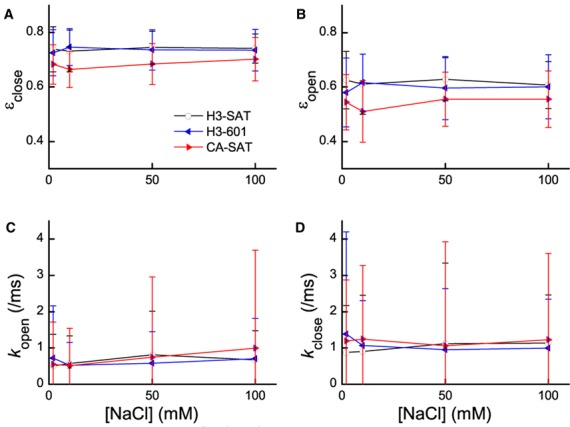
MLE analysis reveals DNA termini wrapping in the nucleosome that is histone dependent, but fails to differentiate between nucleosome termini dynamics due to the inherent pitfall of MLE (4). (A and B) FRET efficiencies of the closed (εclose, a) and open (εopen, b) states, respectively, plotted against NaCl concentrations. The CENP-A nucleosome on α-satellite DNA exhibits lower FRET efficiencies than the canonical H3 nucleosome on either 601 or α-satellite DNA (see Supplementary Table S5 for statistical analysis). (C and D) Kinetic rate constants respectively for the opening and closing motions of the DNA termini. The standard deviations are too large to accept the results at a reasonable confidence level.
Next, we turned to the dynamics of the FRET changes during termini motion. The extent of the FRET changes due to the motion (εclosed − εopen) remains constant within error (0.12–0.14) for all three nucleosomes. The kinetic rates between the open and closed states showed a reasonable range of values (0.5–1.5/ms for kopen and kclose) and no apparent salt or nucleosome dependence (Figure 2c and d). However, the rates have extremely large standard deviations (Figure 2c and d), resulting in unacceptably low confidence in the average values. This is a consequence of the inherent pitfall of MLE implementation falling often into a local maximum as was demonstrated with simulated photon streams (large standard deviations in the estimated kinetic rates in Supplementary Table S2). No practical means is currently conceivable to steer MLE iterations always to the global maximum (4). The reason why MLE performs well on the FRET efficiency estimation (Supplementary Tables S2 and S4) is because the statistics make some consecutive FRET transitions separated far enough to make the FRET levels clearly resolved.
FCS analysis for fluorophore photophysical dynamics and nucleosomal DNA dynamics
In order to obtain the kinetic rates at a reasonable confidence level, we combined fluorescence correlation spectroscopy (FCS) with the MLE analysis. We first calculated the smFRET-FCS spectra for the donor (Cy3) and the acceptor (ATTO647N) separately in a 400 ns–20 ms range to find that the ATTO647N correlation has a far lower level of noise due to the stronger fluorescence (Supplementary Figure S3). Hence, we used the ATTO647N correlation spectra for further analyses. All the correlation curves show significant amplitudes covering almost the entire spectral range (Figure 3a and Supplementary Figure S4). We identified three to four different dynamics components in each of the FCS spectra.
Figure 3.
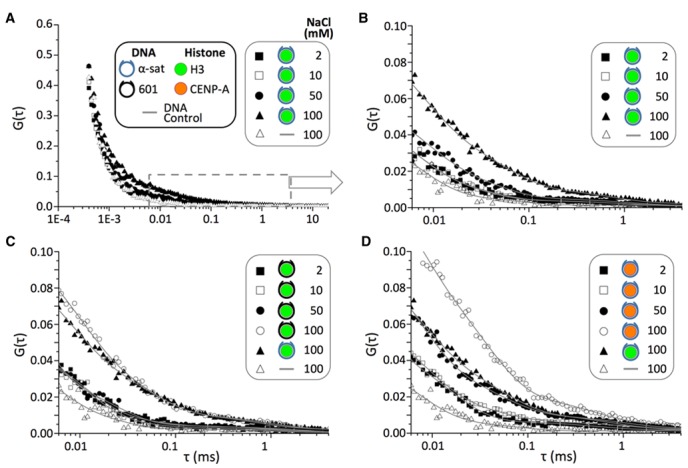
Fluorescence correlation spectra of the three nucleosomes reveal differences in DNA termini dynamics that are histone and salt-dependent. (A) FCS spectra of the ATTO647N photons from the H3-SAT nucleosome in a TE buffer at 2, 10, 50 and 100 mM NaCl. The DNA control (DNA-DA, Supplementary Figure S1 and Supplementary Table S6) spectrum at 100 mM NaCl is also added for comparison. The color-coded symbols for histones and DNA are applicable to all four panels. (B) The same spectra as shown in (a) magnified between 6 μs and 4 ms. A double exponential decay function (A1exp(−t/t1) + A2exp(−t/t2) + A0) was used to fit each FCS spectrum. (C) FCS spectra of the ATTO647N photons from the H3–601 nucleosome in a TE buffer at 2, 10, 50 and 100 mM NaCl. The H3-SAT and DNA-DA spectra at 100 mM are also shown for comparison. (D) FCS spectra of the ATTO647N photons from the CA-SAT nucleosome in a TE buffer at 2, 10, 50 and 100 mM NaCl. The H3-SAT and DNA-DA spectra at 100 mM are also added for comparison. The FCS spectra shown in (c) and (d) over the entire time range can be found in Supplementary Figure S4.
We first focused on the dynamics in the range of 400 ns–0.01 ms (Supplementary Figure S5) which are salt independent and, therefore, likely originated from the photophysical fluctuations of the fluorophores. We characterized the dynamics by fitting the FCS spectra in the range with two decay functions (Supplementary Figure S5). Both the Cy3 and ATTO647N spectra resulted in 230 ± 30 ns and 2.0 ± 0.3 μs decay components, which were also observed in all the nucleosome samples (all the identical curve shapes in Supplementary Figure S5 fit to 240 ± 60 ns and 1.8 ± 1.0 μs decays). These decays are likely due to fluorophore excitation relaxation, rotational dynamics, fluorophore triplet state relaxation, afterpulsing of the detectors and/or Cy3 cis-trans isomerization (14,23).
In order to analyze the salt dependent dynamics components in the >0.01 ms region, we divided the FCS regions into two (1–500 μs and 50 μs–20 ms) and separately fit the regions with three and two exponential decay components, respectively. The shortest components of the two regions are to protect the midrange component from errors due to the fitting boundaries. The longest component of the 1–500 μs region fitting is also inserted for the same purpose. The fit lines in Figure 3b–d are from the three decay fitting in 1–500 μs, demonstrating that even the data outside of the fitting region fit well to the equation. We set these boundaries so that their variations did not result in any significant change in the fitting results. The midrange fitting component from the 1–500 μs region and the longer component in the 50 μs–20 ms are shown in Table 1. The two decay components are on 10–30 μs and 1 ms timescales, respectively. The 10–30 μs component is also observed in the DNA control (Table 1), suggesting that this is another fluorophore dynamics. The 1 ms component is absent in the DNA control and, therefore, likely reflects the nucleosomal DNA dynamics. We characterized the kinetics of these two components by combining the MLE analysis with the FCS results.
Table 1. FCS spectra fitting results for 10–30 μs and 1 ms decay components.
| [NaCl] | Amplitude | Decay time/ms | Amplitude | Decay time/ms | |
|---|---|---|---|---|---|
| DNA-DA | 100 mM | 0.031 ± 0.006 | 0.014 ± 0.004 | N/A | N/A |
| H3-SAT | 2 mM | 0.051 ± 0.002 | 0.010 ± 0.001 | 0.0028 ± 0.0003 | 1.1 ± 0.2 |
| 10 mM | 0.048 ± 0.003 | 0.011 ± 0.001 | 0.0028 ± 0.0004 | 1.1 ± 0.3 | |
| 50 mM | 0.052 ± 0.004 | 0.016 ± 0.002 | 0.0039 ± 0.0004 | 0.9 ± 0.2 | |
| 100 mM | 0.064 ± 0.005 | 0.027 ± 0.004 | 0.0075 ± 0.0005 | 1.0 ± 0.2 | |
| H3–601 | 2 mM | 0.052 ± 0.004 | 0.012 ± 0.002 | 0.0036 ± 0.0004 | 1.2 ± 0.3 |
| 10 mM | 0.051 ± 0.005 | 0.013 ± 0.002 | 0.0026 ± 0.0004 | 0.9 ± 0.3 | |
| 50 mM | 0.03 ± 0.01 | 0.02 ± 0.01 | 0.0037 ± 0.0004 | 0.9 ± 0.2 | |
| 100 mM | 0.077 ± 0.005 | 0.025 ± 0.003 | 0.0078 ± 0.0008 | 1.0 ± 0.2 | |
| CA-SAT | 2 mM | 0.061 ± 0.004 | 0.012 ± 0.001 | 0.0038 ± 0.0004 | 0.8 ± 0.2 |
| 10 mM | 0.063 ± 0.003 | 0.011 ± 0.001 | 0.0047 ± 0.0004 | 1.0 ± 0.2 | |
| 50 mM | 0.066 ± 0.006 | 0.021 ± 0.003 | 0.0066 ± 0.0006 | 0.9 ± 0.2 | |
| 100 mM | 0.109 ± 0.005 | 0.029 ± 0.003 | 0.013 ± 0.001 | 0.6 ± 0.1 |
MLE-smFRET-FCS analysis for additional fluorophore photophysical dynamics and nucleosomal DNA dynamics
As for the FCS decay component at 10–30 μs (Table 1), we cannot obtain the FRET efficiencies directly from MLE because the time scale is beyond the limit of the analysis. MLE analysis can estimate FRET dynamics on a time scale 3–5 times longer than the average photon emission interval (i.e. 0.1–0.2 ms at 30 kHz photon emission/detection rate). If we assume that this dynamics is another type of termini breathing motion, the closed state FRET should still be the same as the one estimated from MLE (i.e. the results in Figure 2a). As the timescale of this motion is at least an order of magnitude faster than the slower motion at 1 ms, it is reasonable to assume that this motion increases the FCS amplitude independently in the relevant correlation time range. The average FRET efficiency obtained from either MLE or acceptor intensity normalization should serve as the average FRET value of the nucleosome in equilibrium (Supplementary Table S4). Therefore, by utilizing the average FRET and the closed state FRET, we can estimate the rate constants with Equations (8)–(10) (details in the ‘Materials and Methods’ section). The calculated values of kopen and kclose are plotted against salt concentrations in Supplementary Figure S6. The overall trend of salt dependence is that both the opening and closing rates decrease as the salt level increases. The closed states of the nucleosomes become more stable as the salt level increases. This trend is counterintuitive as the major interaction between the histone core and the DNA termini is electrostatic. Therefore, we concluded that this motion is due to hydrophobic interactions of the fluorophores with the nucleosome. Such dynamics of cyanine dyes labeled at DNA have been reported previously (24,25). This conclusion is further supported by that the DNA-DA control also contains a decay component at 14 μs (Table 1).
The 1 ms component points to the nucleosome termini motion because it is absent in the DNA control and is CENP-A dependent. The correlation time and amplitude obtained from the fitting (Table 1) combined with the MLE estimated εopen and εclose (Supplementary Table S3) were utilized to calculate kopen and kclose (Equations 8 and 9, details in the ‘Materials and Methods’ section) (Table 2). The calculated rate constants are plotted against salt concentrations in Figure 4a and b. The equilibrium constant between the open and the closed states and the free energy change of the opening motion are calculated based on the rate constants and plotted against salt concentrations as shown in Figure 4c and d. For the three nucleosomes investigated, the termini opening rate increases as the salt level increases (Figure 4a) while the closing rate stays more or less constant (Figure 4b). These changes result in more stable open state at a higher salt level (Figure 4c and d) as expected from the electrostatic nature of histone–DNA interactions in the nucleosome.
Table 2. Kinetic rates for the nucleosomal DNA opening/closing motion.
| [NaCl] | H3-SAT | H3–601 | CA-SAT | |
|---|---|---|---|---|
| kopen (/ms) | 2 mM | 0.12 ± 0.03 | 0.077 ± 0.024 | 0.13 ± 0.03 |
| 10 mM | 0.10 ± 0.03 | 0.094 ± 0.038 | 0.090 ± 0.015 | |
| 50 mM | 0.20 ± 0.05 | 0.12 ± 0.03 | 0.23 ± 0.05 | |
| 100 mM | 0.30 ± 0.05 | 0.28 ± 0.07 | 0.80 ± 0.19 | |
| kclose (/ms) | 2 mM | 0.78 ± 0.17 | 0.74 ± 0.20 | 1.2 ± 0.3 |
| 10 mM | 0.83 ± 0.21 | 0.97 ± 0.35 | 0.90 ± 0.13 | |
| 50 mM | 0.89 ± 0.19 | 1.0 ± 0.2 | 0.85 ± 0.18 | |
| 100 mM | 0.73 ± 0.11 | 0.67 ± 0.15 | 1.0 ± 0.2 |
Figure 4.
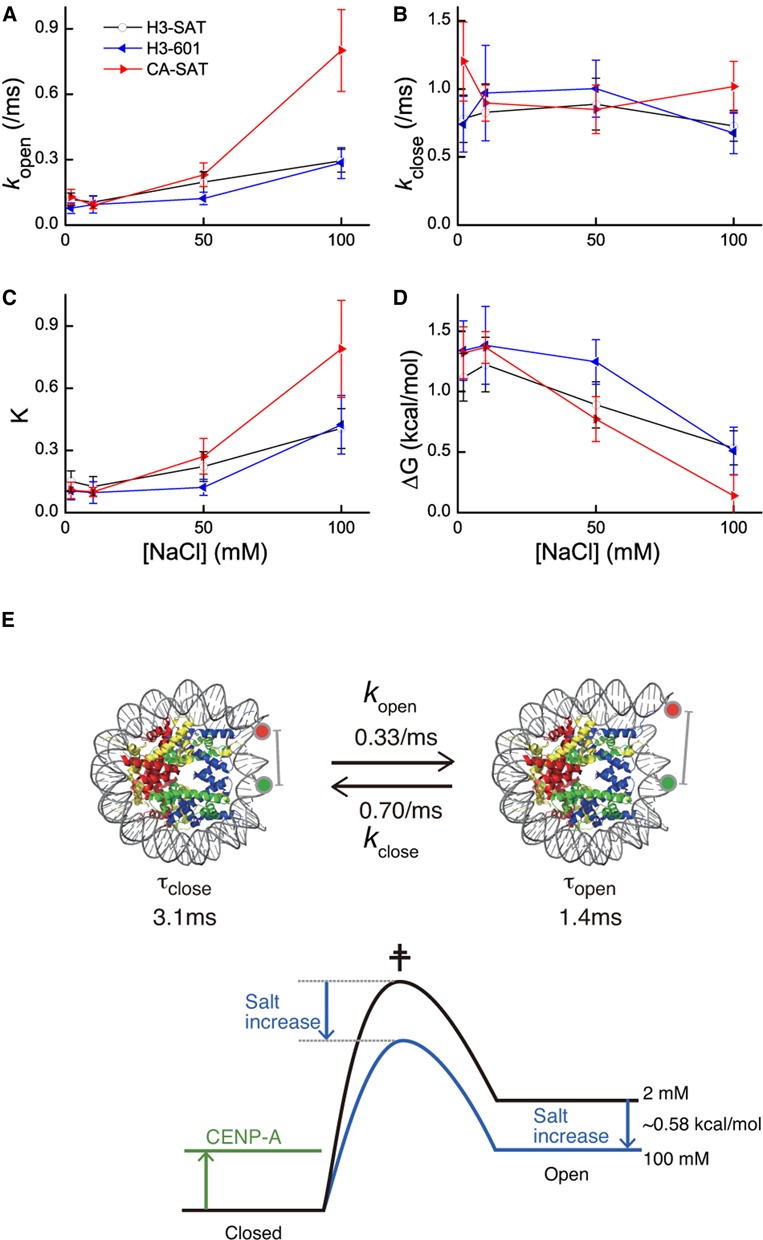
Kinetics and thermodynamics of the DNA opening motion in the nucleosome obtained from the MLE-FCS analysis. (A and B) Opening and closing rate constants, respectively, as depicted in Figure 1b. (C and D) The equilibrium constant between the open and the closed states and the free energy change of opening calculated from the rate constants. (E) H3-SAT nucleosomal termini DNA dynamics at 100 mM NaCl. Below the kinetic scheme, shifts in the relative free energies of the open, transition and closed states are illustrated.
DISCUSSION
Continuous efforts have been made in improving the time resolution of smFRET measurements since its development. A multi-parameter fluorescence data analysis approach has been employed to report evidence of structural fluctuations of an enzyme as its functional element (26,27). The method provides an efficient means to probe equilibrium population densities of conformations involved in sub-ms fluctuations. The method could also be utilized to estimate kinetic rates of fluctuations once the FRET efficiencies of the conformations are known. The FRET efficiencies can be obtained from FRET histogram fitting if the conformations are distinguishable or from independent measurements (e.g. measurements with mutants in a fixed conformation). On the contrary, our method provides both kinetics and thermodynamics of fluctuations without requiring distinguishable FRET populations or any other independent measurements. Especially when the FRET states are indistinguishable and conformational restriction is impossible, our method becomes the only method reported so far that can provide both kinetics and thermodynamics of fluctuations at a sub-ms time resolution at an acceptable confidence level.
Based on our method, we revealed the spontaneous nucleosomal DNA dynamics at the termini. We identified four different fluorescence dynamics components in the nucleosome system (Figure 1b) only one of which at 1 ms points to nucleosomal DNA dynamics (Figure 4) while the other three originate from the fluorophore photophysical dynamics. Evident in Figure 4a, the opening rate of DNA termini increases as the salt level increases in all three nucleosomes. A higher opening rate at a higher salt level is likely due to stabilization of the transition state easing the separation of DNA from H3 that are electrostatically connected to each other. The major driving force of gene compaction to nucleosomes is the electrostatic interactions between the negative charges of DNA phosphate backbone and the positive charges of the basic residues of histones (15–25% lysine/arginine contents in human histones) (28,29). Therefore, a higher salt level would facilitate the opening motion by stabilizing the transition state where DNA and histones are transiently separated. Because of the same reason, the open state should also be stabilized at a higher salt level. If both the transition state and the open state are stabilized at a higher salt level (Figure 4e), we should observe a more or less constant closing rate throughout the salt concentrations. This is indeed what we observed as shown in Figure 4b. The open state stabilization at a higher salt would be mainly due to increased conformational flexibility leading to higher entropy. There is no noticeable sequence dependence in the kinetics between the H3-SAT and H3–601 nucleosomes, suggesting that this motion is universal regardless of the DNA sequence. At 100 mM NaCl, both nucleosomes open every 3–4 ms and close within 1.4 ms (Table 2 and Figure 4e).
Ensemble FRET measurements based on stopped-flow measurements and FCS have been reported to probe the termini opening dynamics (30). The reported dynamics is at least an order of magnitude slower than our results. This discrepancy is likely because the ensemble measurements were indirect by interpreting protein (LexA) binding dynamics as nucleosome opening dynamics. Multi-step conformational changes upon enzyme binding to a substrate are common often resulting in multiple exponential growth or decay components in a stopped-flow measurement (31,32). In fact, it would be surprising to have a simple one step binding between an enzyme and a substrate as complex as a nucleosome. Therefore, what was actually measured in the ensemble study is likely the sum of the initial protein binding and subsequent conformational dynamics of the protein/nucleosome complex. Nonetheless, this ensemble study has resulted in a proposal of nucleosome structural dynamics as a functional element in gene regulation.
A significant difference is noted in the opening rate between the CENP-A nucleosome and the H3 nucleosomes at 100 mM NaCl (Figure 4a and Table 2). The CENP-A nucleosome termini open every 1.3 ms, two to three-fold more frequently than the H3 nucleosomes, validating the hypothesis of flexible CENP-A nucleosome termini. The higher opening rate is likely due to the weakened DNA–histone interactions at the termini, destabilizing the closed state and reducing the energy required to reach the transition state (Figure 4e). The closing rate, on the other hand, is not as strongly affected, suggesting that the open state stability is not altered much upon CENP-A variation. This is likely because the DNA–H3 interaction in the open state is already weak which leaves not much room for further weakening by CENP-A.
Figure 4c and d show the equilibrium constants and free energy changes of the motion calculated from the rate constants. The stability of the closed state relative to the open state decreases (K increases and ΔG decreases) as the salt concentration increases in all three nucleosomes, which reflects the main driving force of nucleosome formation being the electrostatic DNA–histone interactions (28,29). Our results revealed that the destabilization is achieved mainly by elevating the termini opening rate while maintaining a constant closing rate. At 100 mM NaCl, ΔG in the CENP-A nucleosome case becomes significantly smaller than RT at 298K ( = 0.59 kcal/mol), indicating that the threshold salt concentration to open up the CENP-A nucleosome termini at room temperature is between 50 and 100 mM.
Our hybrid single molecule approach combining MLE and smFRET-FCS resulted in the first direct evidence and invaluable quantitative aspects of fast spontaneous DNA dynamics in the nucleosome at an unprecedented time resolution. Weak sequence dependence and strong DNA–H3 interaction dependence suggest that the dynamics is universal and strongly affected by DNA–histone interactions. Therefore, this dynamics should impose the ultimate kinetic limit to gene access in the nucleosome and this limit should be affected heavily by histone variation or modification that modulates DNA–histone interactions. These results clearly demonstrate that our method provides an efficient and robust means to investigate unsynchronized structural dynamics of DNA at a sub-ms time resolution. The time resolution limit is set by the interference from fluorophore photophysical dynamics and, therefore, can be further improved by using different type of fluorophores. The method is generally applicable to an smFRET experimental system and up to our knowledge offers the only way without requiring distinguishable FRET populations or any other independent measurements to elucidate the detailed kinetics of fast and unsynchronized structural dynamics within reasonable uncertainty at a few angstroms and sub-ms spatiotemporal resolution.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
Acknowledgments
We thank Dr Ju Yeon Lee and Dr Nikolina Sekulic for their thoughtful comments on the project and the manuscript.
FUNDING
NIH [GM097286 to T.-H. L.; GM082989 to B.E.B.]. Funding for open access charge: NIH [GM097286 to T.-H. L.].
Conflict of interest statement. None declared.
REFERENCES
- 1.Ha T., Enderle T., Ogletree D.F., Chemla D.S., Selvin P.R., Weiss S. Probing the interaction between two single molecules–fluorescence resonance energy transfer between a single donor and a single acceptor. Proc. Natl. Acad. Sci. U.S.A. 1996;93:6264–6268. doi: 10.1073/pnas.93.13.6264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chung H.S., Gopich I.V., McHale K., Cellmer T., Louis J.M., Eaton W.A. Extracting rate coefficients from single-molecule photon trajectories and FRET efficiency histograms for a fast-folding protein. J. Phys. Chem. A. 2011;115:3642–3656. doi: 10.1021/jp1009669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gopich I.V., Szabo A. Decoding the pattern of photon colors in single-molecule FRET. J. Phys. Chem. B. 2009;113:10965–10973. doi: 10.1021/jp903671p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Myung I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003;47:90–100. [Google Scholar]
- 5.Kornberg R.D., Lorch Y. Twenty-five years of the nucleosome, fundamental particle of the eukaryote chromosome. Cell. 1999;98:285–294. doi: 10.1016/s0092-8674(00)81958-3. [DOI] [PubMed] [Google Scholar]
- 6.Felsenfeld G., Groudine M. Controlling the double helix. Nature. 2003;421:448–453. doi: 10.1038/nature01411. [DOI] [PubMed] [Google Scholar]
- 7.Lee J.Y., Lee T.H. Effects of DNA methylation on the structure of nucleosomes. J. Am. Chem. Soc. 2012;134:173–175. doi: 10.1021/ja210273w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee J.Y., Wei S., Lee T.H. Effects of histone acetylation by Piccolo NuA4 on the structure of a nucleosome and the interactions between two nucleosomes. J. Biol. Chem. 2011;286:11099–11109. doi: 10.1074/jbc.M110.192047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sekulic N., Bassett E.A., Rogers D.J., Black B.E. The structure of (CENP-A-H4)2 reveals physical features that mark centromeres. Nature. 2010;467:347–351. doi: 10.1038/nature09323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Harp J.M., Uberbacher E.C., Roberson A.E., Palmer E.L., Gewiess A., Bunick G.J. X-ray diffraction analysis of crystals containing twofold symmetric nucleosome core particles. Acta crystallogr. Sect. D. Biol. Crystallogr. 1996;52:283–288. doi: 10.1107/S0907444995009139. [DOI] [PubMed] [Google Scholar]
- 11.Lowary P.T., Widom J. New DNA sequence rules for high affinity binding to histone octamer and sequence-directed nucleosome positioning. J. Mol. Biol. 1998;276:19–42. doi: 10.1006/jmbi.1997.1494. [DOI] [PubMed] [Google Scholar]
- 12.Carruthers L.M., Tse C., Walker K.P. 3rd, Hansen J.C. Assembly of defined nucleosomal and chromatin arrays from pure components. Methods Enzymol. 1999;304:19–35. doi: 10.1016/s0076-6879(99)04004-5. [DOI] [PubMed] [Google Scholar]
- 13.Sinha D., Shogren-Knaak M.A. Role of direct interactions between the histone H4 tail and the H2A core in long range nucleosome contacts. J. Biol. Chem. 2010;285:16572–16581. doi: 10.1074/jbc.M109.091298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ha T., Tinnefeld P. Photophysics of fluorescent probes for single-molecule biophysics and super-resolution imaging. Annu. Rev. Phys. Chem. 2012;63:595–617. doi: 10.1146/annurev-physchem-032210-103340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schaub E. High countrate real-time FCS using F2Cor. Opt. Express. 2013;21:23543–23555. doi: 10.1364/OE.21.023543. [DOI] [PubMed] [Google Scholar]
- 16.Magatti D., Ferri F. 25 ns software correlator for photon and fluorescence correlation spectroscopy. Rev. Sci. Instrum. 2003;74:1135–1144. doi: 10.1063/1.4966983. [DOI] [PubMed] [Google Scholar]
- 17.Qian H., Elson E.L. Fluorescence correlation spectroscopy with high-order and dual-color correlation to probe nonequilibrium steady states. Proc. Natl. Acad. Sci. U.S.A. 2004;101:2828–2833. doi: 10.1073/pnas.0305962101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Black B.E., Cleveland D.W. Epigenetic centromere propagation and the nature of CENP-A nucleosomes. Cell. 2011;144:471–479. doi: 10.1016/j.cell.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hasson D., Panchenko T., Salimian K.J., Salman M.U., Sekulic N., Alonso A., Warburton P.E., Black B.E. The octamer is the major form of CENP-A nucleosomes at human centromeres. Nat. Struct. Mol. Biol. 2013;20:687–695. doi: 10.1038/nsmb.2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Conde e Silva N., Black B.E., Sivolob A., Filipski J., Cleveland D.W., Prunell A. CENP-A-containing nucleosomes: easier disassembly versus exclusive centromeric localization. J. Mol. Biol. 2007;370:555–573. doi: 10.1016/j.jmb.2007.04.064. [DOI] [PubMed] [Google Scholar]
- 21.Panchenko T., Sorensen T.C., Woodcock C.L., Kan Z.Y., Wood S., Resch M.G., Luger K., Englander S.W., Hansen J.C., Black B.E. Replacement of histone H3 with CENP-A directs global nucleosome array condensation and loosening of nucleosome superhelical termini. Proc. Natl. Acad. Sci. U.S.A. 2011;108:16588–16593. doi: 10.1073/pnas.1113621108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tachiwana H., Kagawa W., Shiga T., Osakabe A., Miya Y., Saito K., Hayashi-Takanaka Y., Oda T., Sato M., Park S.Y., et al. Crystal structure of the human centromeric nucleosome containing CENP-A. Nature. 2011;476:232–235. doi: 10.1038/nature10258. [DOI] [PubMed] [Google Scholar]
- 23.Kim H.D., Nienhaus G.U., Ha T., Orr J.W., Williamson J.R., Chu S. Mg2+-dependent conformational change of RNA studied by fluorescence correlation and FRET on immobilized single molecules. Proc. Natl. Acad. Sci. U.S.A. 2002;99:4284–4289. doi: 10.1073/pnas.032077799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Iqbal A., Wang L., Thompson K.C., Lilley D.M., Norman D.G. The structure of cyanine 5 terminally attached to double-stranded DNA: implications for FRET studies. Biochemistry. 2008;47:7857–7862. doi: 10.1021/bi800773f. [DOI] [PubMed] [Google Scholar]
- 25.Stennett E.M., Ma N., van der Vaart A., Levitus M. Photophysical and dynamical properties of doubly linked Cy3-DNA constructs. J. Phys. Chem. B. 2014;118:152–163. doi: 10.1021/jp410976p. [DOI] [PubMed] [Google Scholar]
- 26.Olofsson L., Felekyan S., Doumazane E., Scholler P., Fabre L., Zwier J.M., Rondard P., Seidel C.A.M., Pin J.-P., Margeat E. Fine tuning of sub-millisecond conformational dynamics controls metabotropic glutamate receptors agonist efficacy. Nat. Commun. 2014;5:1–12. doi: 10.1038/ncomms6206. [DOI] [PubMed] [Google Scholar]
- 27.Olofsson L., Margeat E. Pulsed interleaved excitation fluorescence spectroscopy with a supercontinuum source. Opt. Express. 2013;21:3370–3378. doi: 10.1364/OE.21.003370. [DOI] [PubMed] [Google Scholar]
- 28.Widom J. Role of DNA sequence in nucleosome stability and dynamics. Q. Rev. Biophys. 2001;34:269–324. doi: 10.1017/s0033583501003699. [DOI] [PubMed] [Google Scholar]
- 29.Luger K., Rechsteiner T.J., Richmond T.J. Preparation of nucleosome core particle from recombinant histones. Methods Enzymol. 1999;304:3–19. doi: 10.1016/s0076-6879(99)04003-3. [DOI] [PubMed] [Google Scholar]
- 30.Li G., Levitus M., Bustamante C., Widom J. Rapid spontaneous accessibility of nucleosomal DNA. Nat. Struct. Mol. Biol. 2005;12:46–53. doi: 10.1038/nsmb869. [DOI] [PubMed] [Google Scholar]
- 31.Perumal S.K., Ren W., Lee T.H., Benkovic S.J. How a holoenzyme for DNA replication is formed. Proc. Natl. Acad. Sci. U.S.A. 2013;110:99–104. doi: 10.1073/pnas.1212748110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kumar R., Nashine V.C., Mishra P.P., Benkovic S.J., Lee T.H. Stepwise loading of yeast clamp revealed by ensemble and single-molecule studies. Proc. Natl. Acad. Sci. U.S.A. 2010;107:19736–19741. doi: 10.1073/pnas.1014139107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


