Abstract
Blebs are pressure-driven protrusions that play an important role in cell migration, particularly in three-dimensional environments. A bleb is initiated when the cytoskeleton detaches from the cell membrane, resulting in the pressure-driven flow of cytosol toward the area of detachment and local expansion of the cell membrane. Recent experiments involving blebbing cells have led to conflicting hypotheses regarding the timescale of intracellular pressure propagation. The interpretation of one set of experiments supports a poroelastic model of the cytoplasm that leads to slow pressure equilibration when compared to the timescale of bleb expansion. A different study concludes that pressure equilibrates faster than the timescale of bleb expansion. To address this discrepancy, a dynamic computational model of the cell was developed that includes mechanics of and the interactions among the cytoplasm, the actin cortex, the cell membrane, and the cytoskeleton. The model results quantify the relationship among cytoplasmic rheology, pressure, and bleb expansion dynamics, and provide a more detailed picture of intracellular pressure dynamics. This study shows the elastic response of the cytoplasm relieves pressure and limits bleb size, and that both permeability and elasticity of the cytoplasm determine bleb expansion time. Our model with a poroelastic cytoplasm shows that pressure disturbances from bleb initiation propagate faster than the timescale of bleb expansion and that pressure equilibrates slower than the timescale of bleb expansion. The multiple timescales in intracellular pressure dynamics explain the apparent discrepancy in the interpretation of experimental results.
Introduction
Blebs are spherical membrane protrusions characterized by a separation of the cell membrane from the actin cytoskeleton (1), and have been observed as leading-edge protrusions during cell migration over flat surfaces (2, 3, 4), in confined channels (5), and in three-dimensional (3D) environments (6, 7). Bleb expansion is driven by intracellular pressure generated by contractile stresses acting on the cytoskeleton. Blebs differ from other types of protrusions, such as lamellipodia, in that their dynamics are primarily regulated by mechanical rather than biochemical processes. Therefore, blebs provide a good system to probe intracellular mechanics.
In animal cells, the cortex is a thin layer of the cytoskeleton directly beneath the membrane (8). It is composed of a dense meshwork of actin filaments rich in myosin molecular motors and actin-binding proteins (9). Little is known about the spatial organization of actin in the cortex, and it could have different mechanical properties from the internal cytoskeleton (10). The cortex is attached to the membrane by linker proteins such as ezrin, radixin, and moesin proteins (8). Actomyosin contractility generates tension on the cortex and leads to high intracellular pressure. Blebs are initiated by local cortical rupture or by a local disruption in the proteins that link the membrane to the cortex (6). In either scenario, pressure is locally decreased at the at the bleb nucleation site, resulting in cytoplasmic flow that locally expands the membrane. New cortex forms underneath the membrane in a bleb, and bleb retraction occurs after cortical actin and myosin are recruited to the cell membrane. The intracellular pressure dynamics during bleb expansion are determined by the rheological properties of the cytoplasm, and cytoplasmic elasticity and permeability have been hypothesized to effect blebbing dynamics (11, 12).
The interpretation of two recent experiments has led to different hypotheses regarding intracellular pressure propagation in blebbing cells. In Charras et al. (11), constitutively blebbing cells were partially treated with drugs that inhibit myosin, such as blebbistatin. Blebbing dynamics ceased in the treated part of the cell, but continued as normal in the untreated part of the cell. Based on experiments in Charras et al. (11), the authors concluded that pressure does not equilibrate throughout the cell because blebs in the untreated part of the cell were not affected. The authors proposed a poroelastic model for the cytoplasm to support their experimental data. In Tinevez et al. (12), the authors nucleated two blebs via cortical ablation with a laser. The second bleb was nucleated shortly after the first one at different locations with respect to the first bleb. The second bleb size was ∼30% smaller than the size of the first bleb regardless of its location with respect to the first bleb. The interpretation of their experiment results was that pressure equilibrated faster than the timescale of bleb expansion. These interpretations appear to contradict each other, and warrant further investigation into the pressure dynamics in blebbing cells.
Mathematical modeling is one approach to investigate intracellular pressure and blebbing dynamics. Previous mathematical models have examined various aspects of cellular blebbing. In the literature (13, 14, 15), the authors use an elastic shell model to determine how the mechanics of the membrane, cortex, and membrane/cortex adhesion influence the shape of blebbing. A particle-based model was used to show that blebs are energetically favorable when membrane area exceeds the cortex area in Spangler et al. (16). These models focused on obtaining experimentally observed blebbing cell shapes, but not on the dynamics of blebbing. An agent-based model of a blebbing cell was used to model cell motility (17, 18). Although this model took into account blebbing dynamics, the driving pressure was assumed to be uniform in space, and is not appropriate for investigating questions relating to cytoplasmic rheology. Several recent models that take into account bleb dynamics with cytoplasmic flow have been developed and used to explore cell migration in a confined channel (5, 19), circus blebbing (20), and bleb expansion (21, 22). All of these models treated the cytoplasm as a viscous fluid, and would need to be extended to model more complex cytoplasmic rheology.
In our previous model of bleb expansion, the cytoplasm was treated as a viscous fluid with a permeable cortex (22). We found the timescale of bleb inflation was dominated by intracellular drag and not fluid viscosity. In this model, the only source of intracellular drag was cytosol flowing throughout the permeable cortex. The model predicted a value of the drag coefficient that can only be achieved with a cortical gap size that is an order-of-magnitude smaller than observed experimentally. These results indicated that a viscous fluid model of the cytoplasm is inadequate to study pressure dynamics in blebbing cells, and they point to the importance of drag throughout the cytoplasm in bleb dynamics.
In Strychalski et al. (23), we extended our model from Strychalski and Guy (22) to include a poroelastic description of the cytoplasm, and we showed that poroelasticity significantly affected intracellular pressure dynamics. A poroelastic model of cytoplasm was posited in Charras et al. (11) to explain experimental observations, but the model was only used as part of scaling arguments to estimate the length scale of pressure propagation across the cell. By contrast, our model in Strychalski et al. (23) presents a computational framework to simulate dynamics of variables such as cell shape, pressure, and cytoplasmic velocity in space and time in the changing geometry of the cell. In Strychalski et al. (23) we develop the model and computational methods, but we did not thoroughly investigate the relationship between cytoplasmic rheology and blebbing dynamics.
In this article, we use our mathematical model developed in Strychalski et al. (23) to systematically investigate pressure and bleb expansion dynamics. We compare the pressure dynamics in a blebbing cell with a viscous fluid cytoplasm to the pressure dynamics in a cell with a poroelastic cytoplasm. Then we relate pressure dynamics to bleb expansion time and quantify the effects of poroelastic parameters on bleb expansion time. We simulate the two-bleb experiments similar to biological experiments from Tinevez et al. (12), and we find that pressure does not equilibrate on the timescale of bleb expansion for biologically relevant values of cytoplasmic permeability. We show that the experimental results from Tinevez et al. (12) are consistent with a poroelastic model of the cytoplasm and conclude that pressure dynamics in blebbing cells are not determined by one single long or short timescale as suggested in Charras et al. (11) and Tinevez et al. (12), but by a combination of timescales that are determined by the rheological properties of the cytoplasm.
Materials and Methods
Model formulation
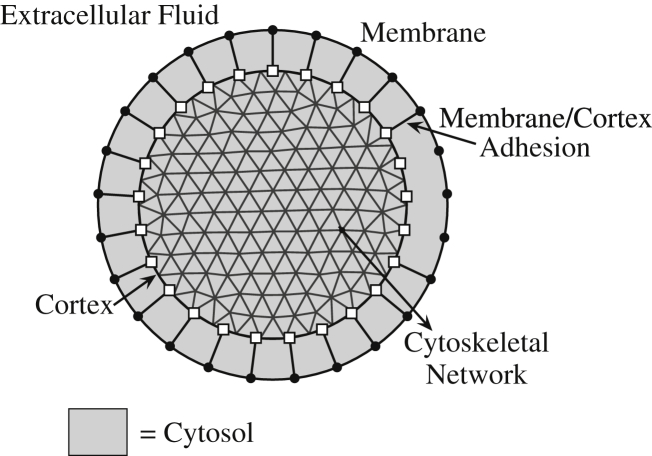
Our model of the cell is a combined fluid-structure system with a poroelastic cytoplasm, where the cytoplasm consists of a permeable, elastic cytoskeleton and liquid cytosol. Our model consists of the membrane, cortex, membrane-cortex adhesion, internal cytoskeleton, and liquid cytosol (see Fig. 1). The cell membrane is modeled as a neutrally buoyant elastic structure that moves with the fluid, and the cortex and the cytoskeleton are modeled as permeable elastic materials. The cortex is modeled as a separate structure from the internal cytoskeleton so that its mechanical properties, such as actomyosin contractility, can be altered independently from the properties of the internal cytoskeletal network. Our model of the cytoskeleton represents the mechanical contributions from the internal components of the cytoskeleton, such as the internal actin network, microtubules, and intermediate filaments. We model the cytoskeleton as a porous, isotropic elastic material that is initially in an unstressed configuration. We do not include stress relaxation due to cytoskeletal rearrangement in the model because bleb expansion occurs on a shorter timescale (5–30 s) than actin turnover (>1 min).
Figure 1.
Bleb model schematic. (Solid dots and open squares) Cell membrane and cortex, respectively. The cytoskeleton consists of points at the vertices of the triangular grid. A bleb is initiated by removing adhesive links between the membrane and the cortex.
In this article, we use a formulation of poroelasticity where the volume fraction of the network (in this case the cytoskeleton) is negligible. It was shown in Strychalski et al. (23) that the formulation used here is equivalent to the standard model of poroelastic media given by Biot (24). The structures experience internal elastic stresses and interact with each other directly through coupling forces and indirectly through the response of the cytosolic fluid to the mechanics and motion of the structures. We use the framework of the immersed boundary method to handle the coupling forces (25).
The model equations consist of force balances on the liquid cytosol, cell cortex, and cytoskeleton. Because of the small length scale (a cell radius of 10 μm), inertial terms are negligible and the equations of motion take the form of force balances. (Using a characteristic length of 10 μm, a characteristic velocity of 1 μm, and the viscosity of water, the Reynolds number is 10−5.) The membrane is a neutrally buoyant structure that moves with the fluid. In the standard formulation of the immersed boundary method, forces on such immersed structures act directly on the surrounding fluid (25). The force balance on the fluid includes internal fluid forces (viscosity, pressure), membrane forces (elasticity, membrane-cortex adhesion), and drag forces due to the relative motion of the cortex and cytoskeleton, which leads to the forced incompressible Stokes equations:
| (1) |
where represents the fluid velocity, p is the pressure, μ is the dynamic viscosity of the cytosol, and values represent forces densities arising from the structures. The drag force in the fluid equation due to the cytoskeletal drag is
| (2) |
where κ is the permeability of the cytoplasm. The drag force on the cytoskeleton is equal and opposite to the force applied to the fluid and has the form
| (3) |
Similarly, the fluid drag force on the cortex is
| (4) |
where ξ is the drag coefficient of the cortex. Here we use the convention that capital letters denote quantities located on structures (membrane, cortex, and cytoskeleton) and use lower-case letters to denote quantities relating to the fluid. We use a Lagrangian coordinate system to describe deforming elastic structure and a fixed Eulerian coordinate system for modeling fluid variables. Force densities have different scalings in the two coordinate systems (see the Supporting Material for more details).
As in our previous models (22, 23), the drag force on the cortex is balanced by elastic forces within the cortex and adhesion between the membrane and cytoskeleton. Similarly, the drag force on the cytoskeleton is balanced by elasticity and adhesion between the cytoskeleton and the cortex. The force balances are given by
| (5) |
| (6) |
The velocities of the porous cortex and cytoskeleton are determined by the above force balances and Eqs. 3 and 4:
| (7) |
| (8) |
The cell membrane moves with the velocity of the cytosol, denoted by . Constitutive laws for elasticity and other modeling details are provided in the Supporting Material and Strychalski et al. (23).
Values for model parameters and sources (when available) are located in Table 1. The cortex is modeled as an elastic object that resists stretching, and it includes a resting tension that pressurizes the cell. We attribute the resting tension to actomyosin contraction of the cortex, represented by the parameter γcortex in Table 1. We use a value of cortical tension consistent with experimental measurements from Tinevez et al. (12). The value of cortical stiffness in Table 1 is taken from Strychalski and Guy (22), where we varied cortical and membrane stiffness over several orders of magnitude and determined the effect of these parameters on bleb shape. This value is similar to the cortical elastic modulus of the cortex reported in Tinevez et al. (12). Membrane stiffness in Table 1 was chosen to be small enough so that bleb growth was limited by cytoplasmic and not membrane elasticity; we use a larger membrane stiffness value when the cytoplasm is modeled as a fluid.
Table 1.
Model Parameters
| Symbol | Quantity | Value | Source |
|---|---|---|---|
| rmem | cell radius | 10 μm | (12) |
| γmem | membrane surface tension | 40 pN/μm | (12) |
| kmem | membrane stiffness coefficient | 1 pN/μm | — |
| γcortex | cortical tension | 400 pN/μm | (12) |
| kcortex | cortical stiffness coefficient | 100 pN/μm | (22) |
| G | cytoskeletal bulk modulus | 500–1500 kPa | (26) |
| μ | cytosolic viscosity | 0.01 Pa-s | (12, 26, 27) |
| ξ | cortical drag coefficient | 10 pN-s/μm3 | (22) |
| κ | cytoskeletal permeability | (26, 28) |
We are particularly interested in quantifying the effects of cytoplasmic rheology on blebbing dynamics, and in the values of parameters that affect the poroelasticity of the cytoplasm: the bulk elastic modulus G and the permeability κ. Values for the bulk modulus of the cytoplasm vary in the literature, depending on the cytoplasmic model, experimental procedure, and cell type. Reported values range are from 300 to 2000 Pa in the literature (12, 26, 27). Permeability of the cytoplasm also varies over several orders of magnitude in the literature. For example, the range of was reported in blebbing cells in Charras et al. (11, 26). Permeability in the lamellipodium of a keratocyte was estimated to be in Keren et al. (28). Because of the variability in these parameters, we simulate over a range of values for G and κ in the Results. We related the cortical drag coefficient to pore size in Strychalski and Guy (22), and use a value consistent with experimental measurements of cortical gap size in Charras et al. (29) (details are in the Supporting Material). Other model parameters are reported and discussed in the Supporting Material.
Results
We begin with computational experiments of a cell with a single expanding bleb. To initiate a bleb, membrane-cortex adhesion is removed in a small region of length 5.6 μm on the right side of the cell. Initially the cell is pressurized due to high cortical tension. When the membrane-cortex adhesion is locally disrupted, cortical tension is no longer transmitted to the membrane, resulting in decreased intracellular pressure at the bleb nucleation site. The cytosol flows from high to low pressure, and the bleb expands. First we quantify the effects of poroelasticity on pressure dynamics and bleb expansion time. Then we simulate two-bleb experiments and measure bleb sizes over time and intracellular pressure. For the two-bleb simulations, the nucleation site of the second bleb was taken to be the same size as for the one bleb simulations. We conclude by showing that a poroelastic model of the cytoplasm is consistent with the experimental results of both Charras et al. (11) and Tinevez et al. (12).
Elastic response of cytoskeleton relieves pressure during blebbing and limits bleb size
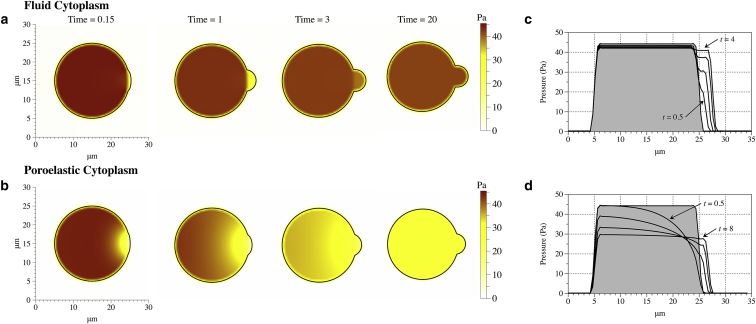
We begin by comparing the intracellular pressure dynamics during bleb expansion using two different rheological descriptions of the cytoplasm: the poroelastic model presented here and the viscous fluid model used in our previous modeling (22). Fig. 2 shows snapshots of the spatial distribution of pressure at different time points after the initiation of a single bleb on the right side of the cell for the two models of cytoplasm. Bleb nucleation size and other model parameters are identical in the two simulations (see Table 1) with the exception of fluid viscosity. In the fluid model, the fluid viscosity is 10 times larger than in the poroelastic model. The viscosity was elevated so that the bleb expansion occurs on roughly the same timescale in the two models. For both models of the cytoplasm, we increased the membrane stiffness to 100 pN/μm to limit bleb size in the fluid model.
Figure 2.
Membrane position and pressure in the bleb model at several time values for both the fluid cytoplasm (a) and poroelastic cytoplasm (b). Horizontal pressure profile across the center of the cell (when the vertical axis = 15 μm in a and b). Pressure profile at several time values for the fluid model of the cytoplasm (c) and poroelastic model (d) when permeability and G = 500 Pa. (Shaded region) Initial pressure across the cell. The intermediate time values for (c) are 1 and 2 s. The intermediate values for (d) are 2 and 4 s. To see this figure in color, go online.
There are two notable differences in the pressure dynamics in the two models. First, the pressure gradient in the poroelastic model propagates across the cell body over the timescale of bleb expansion, but in the fluid model the pressure gradient remains localized near the bleb (Fig. 2 a). In the fluid model, the only source of intracellular drag is the cortex, which leads to steplike pressure profile where the pressure is almost constant in the cell body and varies only in a small region near the bleb before approaching equilibrium (Fig. 2 c). In contrast, in the poroelastic model, there is intracellular drag throughout the cell body from the presence of the cytoskeleton. Fig. 2 d shows a pressure gradient that extends across the length of the cell and is sustained as the bleb expands. The pressure at the back of the cell remains close to its initial value for ∼1/2 s before decreasing and approaching a spatially uniform equilibrium value.
The second difference between the two models of the cytoplasm is that there is significantly more pressure relieved by the inflation of the bleb in the poroelastic model. In the fluid model of the cytoplasm, the pressure drops from an initial pressure of 45 Pa to a final pressure of 42 Pa (∼7%), while in the poroelastic model the final pressure is ∼29 Pa, which constitutes a 36% drop. The additional pressure relief in the poroelastic model results from the elastic compression of the cytoskeleton on the interior. The total volume of the cell (area in two dimensions) is conserved, and so as the bleb expands, the interior of the cell is compressed.
The deformation of the cytoskeleton results in an outward expansive force that partially balances the cortical contraction and relieves pressure. The additional pressure relief results in the smaller bleb size seen in Fig. 2 b compared to Fig. 2 a. In Fig. S2, we quantify the expansive pressure resulting from the compression of the elastic cytoskeleton for the data in Fig. 2 b. We found compression of the cytoskeleton accounts for the majority of the pressure relief during bleb expansion.
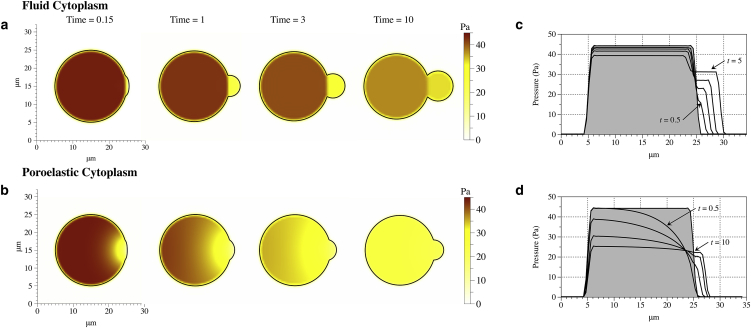
In the model of Tinevez et al. (12), it was estimated that membrane surface tension alone could not balance high intracellular pressure in blebbing cells, and the pressure relief provided by cytoplasmic elasticity was hypothesized to be the key factor limiting bleb growth. We reduced the membrane stiffness from 100 to 40 pN/μm, and we observed uncontrolled bleb growth in the pure fluid cytoplasm model (Fig. 3 a), while the bleb stops growing and reaches a steady-state size in the poroelastic model (Fig. 3 b). The horizontal pressure profiles for the fluid cytoplasm show significantly lower pressure in the bleb than in the cell body, which will continue to drive bleb expansion (Fig. 3 c). In the poroelastic model, the driving pressure decreases over time, and eventually pressure in the bleb approaches the value of pressure in the cell body (Fig. 3 d). For a purely viscous fluid cytoplasm, membrane tension and membrane elasticity can limit bleb growth if they are sufficiently strong, as illustrated previously in Fig. 2. We use the value of 1 pN/μm for the membrane stiffness in the poroelastic model for the remainder of the article to be in the regime where cytoplasmic elasticity limits bleb growth. In the poroelastic model, we found that the membrane stiffness has a mild effect on the final bleb size, but it does not affect the timescale of bleb expansion.
Figure 3.
Membrane position and pressure in the bleb model at several time values for both the fluid cytoplasm (a) and poroelastic cytoplasm (b) when the membrane stiffness was decreased to 40 pN/μm. Horizontal pressure profile at several time values for the fluid model of the cytoplasm (c) and poroelastic model (d) when permeability and G = 500 Pa. (Shaded region) Initial pressure across the cell. The intermediate time values for (c) are 1 and 5 s. The intermediate values for (d) are 2 and 5 s. To see this figure in color, go online.
Pressure equilibration and bleb expansion occur on the same timescale, but pressure propagates across the cell on a faster timescale
In Charras et al. (11), the authors relate the timescale of bleb inflation to the time it takes other parts of the cell to feel the pressure disturbance resulting from the bleb. Here we use our computational model to determine the relationship between bleb expansion dynamics and pressure propagation across the cell.
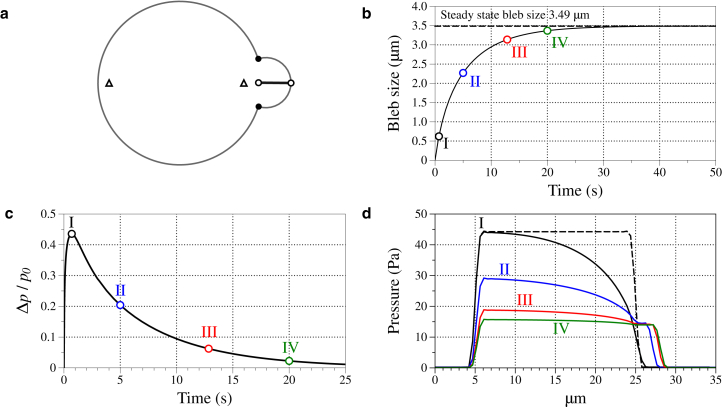
To quantify bleb expansion dynamics, we measure bleb size over time. Bleb size is measured as follows. We identify points that define the neck of the bleb (black circles in Fig. 4 a), compute the midpoint of these two points, and calculate the distance from the bleb neck midpoint to the point on the membrane that has the largest displacement. Initially, this distance is nonzero and small (∼0.4 μm), and we therefore subtract this initial distance from its value over time to obtain bleb size. Fig. 4 b shows bleb size increasing and approaching a steady-state value of 3.49 μm after ∼30 s.
Figure 4.
(a) Bleb size is measured as the distance from the midpoint of the bleb neck (defined by the solid points) to the point on the membrane with the largest horizontal coordinate, then subtracting the initial difference between these points (open circles). (Shaded representation) Membrane. (Triangles) Points where pressure is sampled to compute pressure propagation across the cell in (c). (b) Bleb size over time when G = 500 Pa and κ = 10−3μm2. (Dashed line) Steady-state bleb size. The values labeled in Roman numerals I–IV indicate time values at t = 0.63, 5, 12.85, and 20, respectively. (c) Difference between the pressure at the back of the cell minus the front of the cell (near the bleb) divided by the initial pressure over the first 25 s. (d) Horizontal pressure profiles at t = 0.63, 5, 12.85, and 20 s. To see this figure in color, go online.
To quantify intracellular pressure propagation over time, we examine the relative pressure difference across the cell, which we define as the pressure at the rear of the cell minus the pressure at the front of the cell divided by the initial pressure inside the cell (front and rear locations are the triangular points illustrated in the last panel of Fig. 4 a). Fig. 4 c shows the relative pressure difference across the cell when and G = 500 Pa. The corresponding horizontal pressure profiles for several time values enumerated by I–IV are shown in Fig. 4 d. The graph of the relative pressure difference quickly rises to a peak value at ∼1/2 s (denoted by time I in Fig. 4 c), then slowly decays. Comparing the relative pressure difference to horizontal pressure profiles at several time values, we observe that the peak pressure difference occurs right before pressure at the cell rear begins to decrease. We interpret this time to be when the rear of the cell feels the effects of pressure relief from bleb expansion at the front of the cell.
However, pressure equilibration occurs on a much longer timescale. By 20 s after bleb initiation (Fig. 4 c, IV), the relative pressure difference across the cell has dropped to ∼0.02 and slowly decays to zero beyond this time. The corresponding pressure profile in Fig. 4 d shows a shallow gradient. At the same time value, bleb size is within 4% of its steady-state value. Altogether, bleb expansion and pressure approach their equilibrium values on the same timescale (∼30 s for this parameter set).
These results point to more than one timescale in pressure dynamics in blebbing cells. On a relatively short timescale, pressure disturbances are felt by other parts of the cell. For example, before time I in Fig. 4, pressure at the back of the cell stays close to its initial value. After this time, pressure at the back of the cell slowly begins to lower as the bleb expands. We observe pressure slowly equilibrating on a longer timescale of tens of seconds, and a shallow pressure gradient on these longer timescales. Fig. 4 d show a very shallow pressure gradient 20 s after bleb nucleation.
Cytoplasmic permeability and elasticity establish the bleb expansion timescale
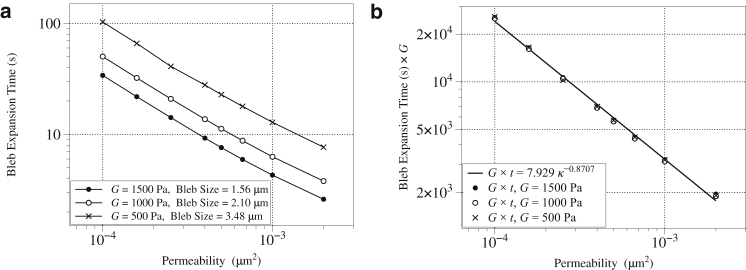
Next, we quantify the effects of varying both the permeability and stiffness of the cytoplasm on bleb expansion time. We define bleb expansion time (and pressure equilibration) to be when bleb size achieves 90% of its steady-state value. For the data in Fig. 4 b, this occurs at t = 12.85 s, enumerated by III.
Fig. 5 a shows the bleb expansion time as a function of permeability for different elastic moduli. These data show that bleb expansion can occur on biologically relevant timescales (5–30 s) for a wide range of values of cytoplasmic permeability and stiffness. Fig. 5 b shows that the product of expansion time and the elastic modulus collapses to a single curve (fit with ). Thus the bleb timescale is inversely proportional to the product of the permeability and elastic stiffness.
Figure 5.
The relationship between bleb expansion time and poroelastic properties of the cytoplasm. (a) Bleb expansion time for different values of cytoplasmic bulk modulus and permeability, and (b) bleb expansion time multiplied by the bulk modulus G as a function of permeability. The scaling relationship shows that bleb expansion time is approximately inversely proportional to the product .
In Charras et al. (11), the authors propose a poroelastic model of the cytoplasm in which intracellular pressure effectively diffuses through the cytoplasm with a diffusion coefficient proportional to both cytoplasmic permeability and stiffness, . They use scaling arguments to argue that the characteristic length of pressure propagation at time T is proportional to . Using the same scaling relationship , and noting that a diffusion coefficient has units length squared per time (L2/T) and κ has units L2, the characteristic time for bleb expansion time is . Our result that bleb timescale is inversely proportional to both cytoplasmic permeability and elasticity is consistent with the scaling arguments in Charras et al. (11). The model in Charras et al. (11) was developed to interpret experimental observations of bleb dynamics in cells with multiple blebs, which we model in the next section.
Multiple bleb simulations
Information about the spatial profile of the intracellular pressure has been inferred using experiments on cells with multiple blebs by examining the effect of one bleb on the dynamics of other blebs at different locations on the cell. Interpretations of two different experiments on cells with multiple blebs have led to conflicting hypotheses regarding intracellular pressure equilibration. Charras et al. (11) used cells that were continually blebbing all over the membrane surface. They locally treated regions of the cell with drugs that disrupted blebbing and observed that for some of these treatments, bleb dynamics proceeded relatively unchanged in the untreated regions. The authors argued that based on a poroelastic model of the cytoplasm, the length scale for pressure changes occurring on the timescale of blebbing dynamics was longer than the diameter of the cell, and therefore the spatial distribution of pressure was far from equilibrium during bleb expansion. Tinevez et al. (12) put cells in a state of high tension and initiated two different blebs one after the other at different locations of the cell by locally ablating the cortex. They observed that the second bleb was ∼30% smaller than the first bleb independent of its location with respect to the first one. Based on these experiments, they argue that the pressure is equilibrated on the timescale of blebbing. For both experiments, the relevant timescale for blebbing was estimated to be between 5 and 30 s. After this time, the cortex reforms in the bleb, and it begins to retract.
In this section, we use our model to perform a computational experiment similar to the two-bleb experiments in Tinevez et al. (12) to address these conflicting ideas about pressure propagation and equilibration. Our results show that the pressure is not equilibrated on a timescale of 5–30 s for relevant values of permeability, and this lack of equilibration is essential to explain the results from Tinevez et al. (12). Our results are in agreement with the ideas from Charras et al. (11), but unlike Charras et al. (11), we show that even when the pressure is far from equilibrium, this does not mean that the effects of blebbing are highly localized in space.
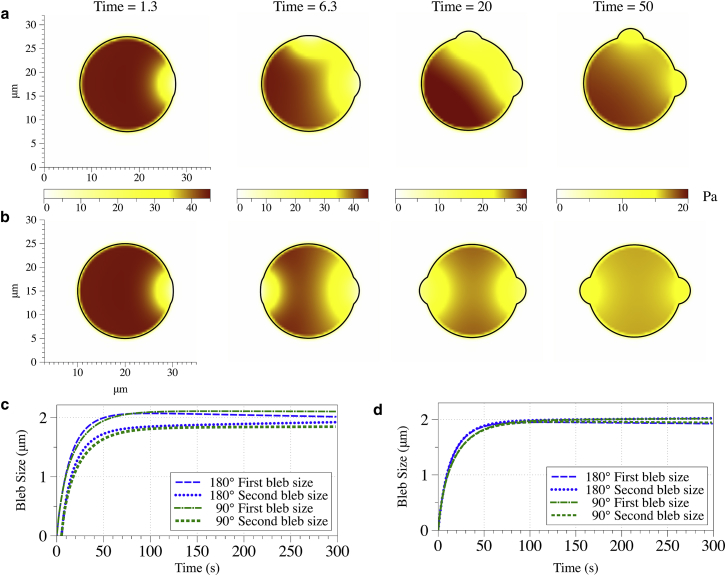
In our simulations, the first bleb was initiated at the right side of the cell. The second bleb was nucleated at two different locations: near the first bleb (at an angle of 90° with respect to the first bleb) and across the cell from the first bleb (at an angle of 180° with respect to the first bleb). The second bleb was initiated 5 s after the first. It was reported in Tinevez et al. (12) that the second bleb was initiated <30 s after the first. The typical time delay between the two bleb initiation times was ∼7 s (J. Roensch, personal communication). We use a permeability of and a bulk modulus of 500 Pa for these experiments to be consistent with the values reported in Charras et al. (11, 26). For these parameters, bleb expansion time was computed to be ∼100 s in Fig. 5. We consider other parameters in the next section.
Fig. 6, a and b, shows the spatial profile of pressure at several times for the two different placements of the second bleb. These plots show that the spatial arrangement of the blebs affects the spatiotemporal dynamics of intracellular pressure. When two blebs are relatively close, the pressure gradient across the cell is generally larger (for example, compare pressure at 20 s in Fig. 6, a and b).
Figure 6.
Pressure and membrane position at several time values when the second bleb is initiated (a) close to the first bleb (at a 90° angle), and (b) across the cell from the first bleb (at a 180° angle). Bleb size over time when the second bleb is initiated 5 s after the first one (c), and when both blebs are initiated at the same time (d). All parameters for these simulations are identical. In particular, the bulk modulus of the cytoplasm is 500 Pa and permeability is 10−4μm2. To see this figure in color, go online.
Fig. 6 c shows the bleb sizes as a function of time for these experiments from the time the first bleb is initiated at t = 0 s until 300 s. This plot shows that the size of the second bleb is always smaller than the first, independent of the placement of the second bleb, even at times well beyond the expansion timescale of 100 s. Despite the differences in the intracellular pressure gradients resulting from the arrangements of the two blebs, the time course of the expansion for the first and second blebs is insensitive to the placement of the second bleb.
After the initial inflation of both blebs, our two bleb experiments show that the second bleb is roughly 20% smaller than the first, independent of the location of the second bleb. This result is consistent with the results from Tinevez et al. (12). However, this does not mean that the pressure is equilibrated, as claimed in Tinevez et al. (12). We observe that the pressure is far from equilibrium on the bleb inflation timescale, consistent with the predictions in Charras et al. (11). One can observe in Fig. 6 c that on a long timescale (>200 s) the two blebs approach the same size as the pressure approaches the spatially uniform equilibrium.
Pressure is the driving force of bleb expansion, and thus if the blebs feel the same pressure, they will be the same size. Fig. 6 d shows that if the two blebs are nucleated at the same time, they will be the same size, independent of the spatial arrangement of the two blebs. Thus, the small delay in the initiation of the second bleb is a key to obtaining blebs of different sizes.
Two timescales are relevant for bleb expansion dynamics and affected by poroelastic parameters
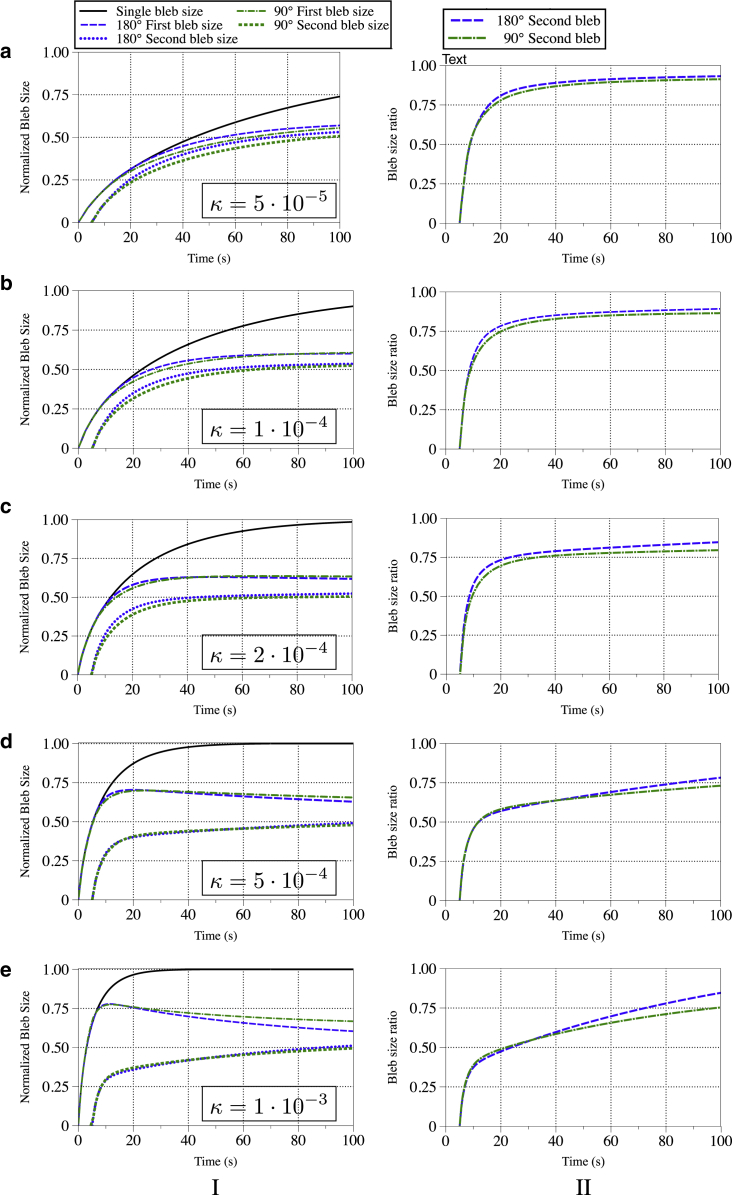
Here we repeat the two-bleb experiments for a range of permeabilities with fixed elastic stiffness to determine how the results of the previous section depend on the timescale of pressure propagation. We use a bulk modulus of 500 Pa and vary the permeability from . For these parameters the bleb expansion time for a single bleb ranges from roughly 10–100 s (see Fig. 5). The first column of Fig. 7 shows the sizes of the blebs in the two-bleb experiment as a function of time along with the size of a single bleb for the same permeability. All sizes have normalized by the maximum size of the single bleb experiment. The second column shows the ratio of the size of the second bleb to the first bleb as a function of time.
Figure 7.
(a–e) Quantifying bleb sizes as a function of cytoplasmic permeability for a second bleb initiated close to (90°) and across the cell (180°) from the first bleb. (I) Bleb size over time divided by the maximum bleb size of one single right bleb. (II) Second bleb size (left/top) divided by the first bleb size (right) over time. In all of the simulations, the bulk modulus of the cytoskeleton was G = 500 Pa, and the second bleb was initiated 5 s after the first. To see this figure in color, go online.
In the two bleb experiments, we observe two timescales, both of which are affected by the permeability. Within the first few seconds after the second bleb is initiated, the ratio of the bleb sizes changes rapidly. This period is followed by a much longer period characterized by slow change in both bleb sizes and their size ratios. As in our single bleb experiments presented in Fig. 4, the short timescale corresponds to the time for pressure changes to propagate across the cell, and the long timescale corresponds to the time of pressure equilibration.
At high permeabilities ( and ), we observe the first bleb steadily shrinks as the second bleb expands on the long timescale. As the pressure approaches the spatially uniform equilibrium, the two blebs approach the same size. For all permeabilities, we see that the size ratio is approaching one on the long timescale. This long timescale on which we see the size ratios changing slowly corresponds to the slow approach to equilibrium pressure. The timescale of the approach to equilibrium is well beyond the bleb expansion timescale for the range of permeabilities used in our experiments.
Our results on pressure equilibration are consistent with the argument presented in Charras et al. (11) that the poroelastic rheology of the cytoplasm is responsible for pressure being far from equilibrium on the bleb expansion timescale. In Charras et al. (11), the authors argue that for poroelastic cytoplasm, pressure changes resulting from a bleb’s expansion do not affect the pressure in other regions of the cell on the timescale of 5–30 s. However, we observe that the two blebs influence each other on this shorter timescale. The size of the first bleb deviates from the size of the single bleb within the first 5 s after the second bleb is initiated because the second bleb relieves some of the driving pressure expanding the first bleb. Similarly, the second bleb experiences an initial lower driving pressure because the first bleb relieves some pressure. This results in a smaller second bleb size on the long-time approach to equilibrium.
Both the short and long timescales are relevant for understanding the size difference observed in the two-bleb experiments of Tinevez et al. (12). If pressure equilibrates on the timescale of bleb expansion as stated in Tinevez et al. (12), both blebs would approach the same size on the timescale of 5–30 s. Alternatively, if pressure changes were localized to the site where the bleb is initiated, as reported in Charras et al. (11), then the second bleb expansion dynamics would be the same as those for the first bleb (and also the same as those for the single bleb). Although we find that pressure equilibrates on a timescale comparable or longer to bleb expansion time, pressure changes propagate on a timescale much shorter than bleb expansion.
Discussion
Despite the many proposed rheological descriptions, dynamic models of blebbing cells have assumed that the cytoplasm is a viscous fluid (13, 17, 19, 22). These models ignored the elastic stresses within the cytoskeleton and the friction between the fluid and the cytoskeleton. In our previous model, we modeled the cytoplasm as a viscous fluid (22). We showed that bleb growth was limited by membrane elasticity, and that drag between the cytoskeleton and the cytosol was the force that set the timescale of bleb expansion. The only component of the cytoskeleton in this model was the cortex. As a result, the cortical drag coefficient that resulted in bleb expansion times of 5–30 s corresponded to a cortical pore size that was significantly smaller than values measured from scanning electron micrographs (29). The conclusion was that drag throughout the cytoplasm contributes to blebbing dynamics, and this was the motivation to extend our model to include drag throughout the cytoplasm.
By comparing our previous model of a blebbing cell with a viscous fluid cytoplasm to the model presented here with a poroelastic model of the cytoplasm, we show that poroelasticity is important as a source of intracellular drag and for pressure relief. The values for permeability in our computational model that correspond to biological bleb expansion times agree with previously reported values of permeability, and also are consistent with experimentally measured pore sizes of the cytoplasm (26). These results support our hypothesis that intracellular drag significantly contributes to bleb dynamics. Elastic stress in the cytoskeleton is important for pressure relief. When the cytoplasm is compressed during bleb expansion, an elastic-restoring force leads to a significantly larger intracellular pressure decrease after bleb expansion. We found that the decrease in pressure can limit bleb expansion, which is in agreement with Tinevez et al. (12).
Charras and co-workers (11, 26, 27, 30) have proposed a poroelastic model of the cytoplasm, where intracellular pressure effectively diffuses through the poroelastic cytoplasm over a length proportional to , where D is a diffusion constant proportional to both cytoplasmic permeability and stiffness. We compute bleb expansion times with our model for a range of values for cytoplasmic permeability and elasticity, and found that 1) bleb expansion times over much of this range matched the experimentally observed timescale for bleb expansion of 5–30 s, and 2) bleb expansion time is inversely proportional to the product , which is in agreement with the previously reported scaling relationship.
The poroelastic model has been supported through various experiments, such as pharmacological manipulation of blebbing cells (11), rapid indentation of cells (27), and exposing cells to hyperosmotic solution to measure effective pore size (26). The results of these experiments are consistent with intracellular pressure diffusing through cytoplasm with an effective diffusion coefficient (11, 26, 27, 30, 31). The value for the diffusion coefficient was calculated from experimental data to be (27). The values of D that we compute from the data in Fig. 5 are in good agreement with these values, ranging from 5 to . The lower value corresponds to a softer cytoplasm with lower permeability (G = 500 Pa and ), while the higher value corresponds to a more stiff cytoplasm with higher permeability, G = 1500 Pa and ). Our model results are in good agreement with previous models and experiments when comparing poroelastic parameters, bleb expansion times, and diffusion coefficients.
Charras et al. (11) use a scaling argument to claim that in a poroelastic cytoplasm, pressure disturbances from blebs on opposite sides of the cell are effectively isolated from each other on the timescale of seconds. They compute a length scale for pressure diffusion of 15–30 μm, meaning that pressure can be nonequilibrated on a timescales of 10 s. This claim was called into question by Tinevez et al. (12). The authors measured bleb size dynamics in two bleb experiments when the second bleb was initiated shortly after the first bleb. After both blebs inflated, the second bleb was slightly smaller than the first bleb regardless of whether it was initiated close or across the cell from the first bleb. The interpretation of these experiments was that pressure equilibrated quickly across the cell, and in particular, faster than the timescale of bleb expansion.
We use our computational model to simulate the experiments of Tinevez et al. (12) to determine whether pressure is equilibrated in the multibleb experiments. Our results show that pressure is not equilibrated in the two bleb experiments for a range of values of cytoplasmic permeability. We find that nonequilibrated pressure and a short time delay in nucleating the second bleb are necessary to match the experimental results from Tinevez et al. (12). We measure bleb sizes and find that the second bleb is always smaller than the first bleb. Our results are in agreement with Charras et al. (11), in that the timescale of pressure equilibration is beyond the timescale of bleb inflation. However, we do not observe that pressure changes were highly localized in space, as claimed in Charras et al. (11).
We observe three regimes of bleb size dynamics in multibleb experiments that depend on poroelastic parameters. At low permeability, bleb expansion dynamics and pressure equilibrates on a longer timescale. However, even at the value of , which is small relative to other values of permeability given in Charras et al. (26), pressure relief from the second bleb causes the first bleb to be smaller in size than in the case of a single bleb. In the limit of cytoplasmic permeability approaching zero, pressure will be isolated as claimed in Charras et al. (11), but this regime corresponds to unphysical permeability values.
For larger values of cytoplasmic permeability, pressure propagates relatively quickly. Pressure relief from the second bleb causes the first bleb size to decrease on the timescale of a single bleb’s expansion. We also observe shrinking of the first bleb in two bleb experiments with a viscous fluid cytoplasm (Fig. S3), which corresponds to the case of infinite permeability. Because the decrease in the first bleb’s size as the second bleb expands has not been observed experimentally, we conclude that cytoplasmic permeability is smaller than .
For intermediate values of cytoplasmic permeability , we find that both blebs appear to be fully inflated before slowly approaching the same size on a long timescale as pressure equilibrates. The long timescale where the blebs approach the same size cannot be observed in experiments because cortical reformation and bleb retraction occur in cells after ∼30 s. In this parameter regime, pressure is not equilibrated on a timescale of 30 s, which is in agreement with Charras et al. (11), and the second bleb is smaller than the first bleb with size dynamics that are independent of its location, which agrees with Tinevez et al. (12). The results of both experiments are consistent with a poroelastic model of the cytoplasm. Additionally, these values of cytoplasmic permeability are consistent with values reported in Charras et al. (11, 26).
In single bleb experiments, we showed that a pressure disturbance from bleb initiation propagates across the cell on a relatively short timescale (<1 s) before equilibrating on a longer timescale (∼10 s). These timescales are evident in Fig. 4, c and d. The pressure disturbance propagates across the cell by time t = 0.63 s (indicated by I), which is ∼5% of bleb expansion time ( s, denoted by III). The pressure profiles at times II–IV show the pressure approaching equilibrium on the 10–20 s timescale. In our two-bleb experiments, the second bleb is initiated on the shorter of these two timescales. This means that pressure disturbances are propagated across the cell on a shorter timescale than the pressure equilibration timescale, and the nucleation of the second bleb will affect the expansion dynamics of the first bleb on this shorter timescale.
To understand the multiple timescales of pressure dynamics in a poroelastic medium, we consider a reduced model consisting of a cylinder of contractile poroelastic material held fixed at one end and open at the other end. In the Supporting Material, we show that the displacement of the network in the axial direction satisfies a diffusion equation, and the resulting diffusion coefficient has the same form previously reported by Charras and coworkers (11, 26, 27, 30). We express the solution for the displacement as an infinite series of decaying sinusoidal functions of decreasing wavelength that scale with the poroelastic diffusion coefficient. All decay rates scale with this effective diffusion coefficient. The longest wavelength solution decays most slowly, and it dominates the long-time behavior of equilibration across the whole cell. Bleb initiation creates localized, short wavelength changes in the pressure, which propagate quickly across the cell. The long timescale is identical to the timescale of pressure equilibration previously reported in Charras et al. (11). In contrast to previous work, we find that smaller wavelength terms in the solution are nonnegligible on short timescales and lead to fast propagation of local disturbances. For example, we find the pressure at one side of the cylinder drops by as much as 5% on a timescale that is an order-of-magnitude smaller than the pressure equilibration timescale. Therefore, multiple timescales contribute to the propagation of pressure disturbances, such as blebs, across a poroelastic material.
Our work constitutes a major advance toward understanding the significance of cytoplasmic rheology in protrusion dynamics because our dynamic model allows us to obtain pressure data over a range of timescales. Using our model, we identified the significance of the fast timescale of pressure propagation in blebbing cells. In the case of multibleb experiments, the short timescale of pressure propagation across the cell, the time delay in initiating the second bleb, and the long timescale for pressure equilibration can explain the difference in bleb sizes from the experiments in Tinevez et al. (12). The advantage of our model is that we are able to isolate and study intracellular pressure dynamics, which cannot be isolated in vivo. Other models of blebbing cells have ignored the poroelasticity of the cytoplasm (5, 13, 16, 20, 21, 22), which could limit our understanding of pressure-driven protrusions in migrating cells.
An in-depth knowledge of the rheology and pressure dynamics of the cytoplasm is important for understanding how cells migrate in 3D, especially for the case when cells do not use specific adhesion to the substrate. Frictional contacts may be important for pushing through gaps in interstitial tissue (6, 32). If a pressure-driven protrusion, such as a bleb, is pushed into a gap in the extracellular matrix, the rheology of the cytoplasm can be an important contributing factor for establishing traction forces exerted on the substrate. To model cell migration in this context, our blebbing model would need to include events that occur after the timescale of bleb inflation, such as cortical reformation (occurs after ∼30 s) and bleb retraction (occurs after ∼1 min). Future modeling efforts will involve incorporating these longer timescale events to understand the coordination of the mechanical processes involved in 3D cell migration.
Author Contributions
W.S. and R.D.G. designed the research, performed the research, and wrote the article; and W.S. performed computational simulations and processed the data.
Acknowledgments
The authors thank C. Copos for providing codes to generate the adaptive mesh and for computing elasticity of the cytoskeleton. They also thank J. Roensch for more detailed information regarding the initiation of the second bleb in experiments from Tinevez et al. (12), and A. Mogilner and J. Allard for helpful discussions.
This work was supported in part by National Science Foundation grants DMS-1160438 (to R.D.G.) and DMS-1226386 (to R.D.G. and W.S.).
Editor: Leah Edelstein-Keshet.
Footnotes
Supporting Materials and Methods, five figures, and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)00056-4.
Contributor Information
Wanda Strychalski, Email: wis6@case.edu.
Robert D. Guy, Email: guy@math.ucdavis.edu.
Supporting Material
References
- 1.Charras G.T. A short history of blebbing. J. Microsc. 2008;231:466–478. doi: 10.1111/j.1365-2818.2008.02059.x. [DOI] [PubMed] [Google Scholar]
- 2.Diz-Muñoz A., Krieg M., Heisenberg C.P. Control of directed cell migration in vivo by membrane-to-cortex attachment. PLoS Biol. 2010;8:e1000544. doi: 10.1371/journal.pbio.1000544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Maugis B., Brugués J., Amblard F. Dynamic instability of the intracellular pressure drives bleb-based motility. J. Cell Sci. 2010;123:3884–3892. doi: 10.1242/jcs.065672. [DOI] [PubMed] [Google Scholar]
- 4.Yoshida K., Soldati T. Dissection of amoeboid movement into two mechanically distinct modes. J. Cell Sci. 2006;119:3833–3844. doi: 10.1242/jcs.03152. [DOI] [PubMed] [Google Scholar]
- 5.Yip A.K., Chiam K.-H., Matsudaira P. Traction stress analysis and modeling reveal that amoeboid migration in confined spaces is accompanied by expansive forces and requires the structural integrity of the membrane-cortex interactions. Integr. Biol. (Camb.) 2015;7:1196–1211. doi: 10.1039/c4ib00245h. [DOI] [PubMed] [Google Scholar]
- 6.Charras G., Paluch E. Blebs lead the way: how to migrate without lamellipodia. Nat. Rev. Mol. Cell Biol. 2008;9:730–736. doi: 10.1038/nrm2453. [DOI] [PubMed] [Google Scholar]
- 7.Paluch E.K., Raz E. The role and regulation of blebs in cell migration. Curr. Opin. Cell Biol. 2013;25:582–590. doi: 10.1016/j.ceb.2013.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Alberts B., Johnson A., Walter P. 4th Ed. Garland Science; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 9.Bray D., White J.G. Cortical flow in animal cells. Science. 1988;239:883–888. doi: 10.1126/science.3277283. [DOI] [PubMed] [Google Scholar]
- 10.Clark A.G., Dierkes K., Paluch E.K. Monitoring actin cortex thickness in live cells. Biophys. J. 2013;105:570–580. doi: 10.1016/j.bpj.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Charras G.T., Yarrow J.C., Mitchison T.J. Non-equilibration of hydrostatic pressure in blebbing cells. Nature. 2005;435:365–369. doi: 10.1038/nature03550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tinevez J.Y., Schulze U., Paluch E. Role of cortical tension in bleb growth. Proc. Natl. Acad. Sci. USA. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Woolley T.E., Gaffney E.A., Goriely A. Three mechanical models for blebbing and multi-blebbing. IMA J. Appl. Math. 2014;79:636–660. [Google Scholar]
- 14.Woolley T.E., Gaffney E.A., Goriely A. Cellular blebs: pressure-driven, axisymmetric, membrane protrusions. Biomech. Model. Mechanobiol. 2014;13:463–476. doi: 10.1007/s10237-013-0509-9. [DOI] [PubMed] [Google Scholar]
- 15.Woolley T.E., Gaffney E.A., Goriely A. Global contraction or local growth, bleb shape depends on more than just cell structure. J. Theor. Biol. 2015;380:83–97. doi: 10.1016/j.jtbi.2015.04.023. [DOI] [PubMed] [Google Scholar]
- 16.Spangler E.J., Harvey C.W., Laradji M. Computer simulation of cytoskeleton-induced blebbing in lipid membranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;84:051906. doi: 10.1103/PhysRevE.84.051906. [DOI] [PubMed] [Google Scholar]
- 17.Tozluoğlu M., Tournier A.L., Sahai E. Matrix geometry determines optimal cancer cell migration strategy and modulates response to interventions. Nat. Cell Biol. 2013;15:751–762. doi: 10.1038/ncb2775. [DOI] [PubMed] [Google Scholar]
- 18.Tozluoğlu M., Mao Y., Sahai E. Cost-benefit analysis of the mechanisms that enable migrating cells to sustain motility upon changes in matrix environments. J. R. Soc. Interface. 2015;12:20141355. doi: 10.1098/rsif.2014.1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lim F.Y., Koon Y.L., Chiam K.-H. A computational model of amoeboid cell migration. Comput. Methods Biomech. Biomed. Engin. 2013;16:1085–1095. doi: 10.1080/10255842.2012.757598. [DOI] [PubMed] [Google Scholar]
- 20.Lim F.Y., Chiam K.-H., Mahadevan L. The size, shape, and dynamics of cellular blebs. Europhys. Lett. 2012;100:28004. [Google Scholar]
- 21.Young J., Mitran S. A numerical model of cellular blebbing: a volume-conserving, fluid-structure interaction model of the entire cell. J. Biomech. 2010;43:210–220. doi: 10.1016/j.jbiomech.2009.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Strychalski W., Guy R.D. A computational model of bleb formation. Math. Med. Biol. 2013;30:115–130. doi: 10.1093/imammb/dqr030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Strychalski W., Copos C.A., Guy R.D. A poroelastic immersed boundary method with applications to cell biology. J. Comput. Phys. 2015;282:77–97. [Google Scholar]
- 24.Biot M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941;12:155–164. [Google Scholar]
- 25.Peskin C.S. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977;25:220–252. [Google Scholar]
- 26.Charras G.T., Coughlin M., Mahadevan L. Life and times of a cellular bleb. Biophys. J. 2008;94:1836–1853. doi: 10.1529/biophysj.107.113605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Moeendarbary E., Valon L., Charras G.T. The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 2013;12:253–261. doi: 10.1038/nmat3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Keren K., Yam P.T., Theriot J.A. Intracellular fluid flow in rapidly moving cells. Nat. Cell Biol. 2009;11:1219–1224. doi: 10.1038/ncb1965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Charras G.T., Hu C.K., Mitchison T.J. Reassembly of contractile actin cortex in cell blebs. J. Cell Biol. 2006;175:477–490. doi: 10.1083/jcb.200602085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mitchison T.J., Charras G.T., Mahadevan L. Implications of a poroelastic cytoplasm for the dynamics of animal cell shape. Semin. Cell Dev. Biol. 2008;19:215–223. doi: 10.1016/j.semcdb.2008.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Charras G.T., Mitchison T.J., Mahadevan L. Animal cell hydraulics. J. Cell Sci. 2009;122:3233–3241. doi: 10.1242/jcs.049262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Even-Ram S., Yamada K.M. Cell migration in 3D matrix. Curr. Opin. Cell Biol. 2005;17:524–532. doi: 10.1016/j.ceb.2005.08.015. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.