Comparing Treatment Policies with Assistance from the Structural Nested Mean Model

Summary

Treatment policies, also known as dynamic treatment regimes, are sequences of decision rules that link the observed patient history with treatment recommendations. Multiple, plausible, treatment policies are frequently constructed by researchers using expert opinion, theories and reviews of the literature. Often these different policies represent competing approaches to managing an illness. Here we develop an “assisted estimator” that can be used to compare the mean outcome of competing treatment policies. The term “assisted” refers to the fact estimators from the Structural Nested Mean Model, a parametric model for the causal effect of treatment at each time point, are used in the process of estimating the mean outcome. This work is motivated by our work on comparing the mean outcome of two competing treatment policies using data from the ExTENd study in alcohol dependence.

1. Introduction

In many areas of health, treatment response is heterogeneous in which case clinicians will need to consider providing a sequence of treatments in order to obtain sufficient treatment response. Furthermore patients with chronic illnesses often require changes in treatment, that is, sequences of treatments, so as to maintain a good response. As a result clinical scientists have become increasingly interested in, and active in, the development of interventions that are composed of treatment sequences (Lavori and Dawson, 2000) in various fields including alcoholism (Oslin, 2005), substance abuse (Jones et al., 2011; McKay, 2009), leukemia (Thall et al., 2002) and autism spectrum disorder (Kasari, 2009). Ideally the treatment sequences are adapted to accommodate treatment response heterogeneity and thus result in more efficacious and less burdensome/costly treatment. Treatment policies (Lunceford et al., 2002; Wahed and Tsiatis, 2004, 2006) – also called dynamic treatment regimes (Robins, 1986; Murphy et al., 2001), adaptive treatment strategies (Lavori et al., 2000; Murphy, 2005) or adaptive interventions (Nahum-Shani et al., 2012a,b) – operationalize the dynamic adaption via a sequence of decision rules, one for each stage in the treatment process; the decision rule inputs measurements of patients’ time-varying covariates and outputs recommended treatments.

Often scientists construct treatment policies that represent competing approaches to managing an illness. For example in the treatment of ADHD, the American Psychological Association recommends starting with behavioral treatment and moving to a medication only if the behavioral treatment is not effective (Brown et al., 2008), whereas the American Academy of Child and Adolescent Psychiatry recommends starting with medication (Pliszka and AACAP Work Group on Quality Issues, 2007). Or one treatment policy might represent a least intensive or least costly version, whereas another treatment policy may represent a most intensive, most costly version. For example, the Extending Treatment Effectiveness of Naltrexone (ExTENd) trial of alcohol dependence treatments (PI: Oslin (Oslin, 2005)) involves multiple treatment policies, of which one is the most intensive and another is the least intensive.

A common approach to estimating and comparing the mean outcomes of competing treatment policies, is to use a non-parametric estimation procedure that involves inverse-probability-weights (IPW), such as those described in Murphy et al. (2001) and Zhang et al. (2013). These estimators are non-parametric in the sense that they do not require models that relate baseline or time-varying covariates with the outcome. Robins and colleagues (Robins, 1997b; Orellana et al., 2010) generalized the Murphy et al. (2001) methods by parameterizing mean outcomes with each value of the parameter representing a different policy in a class of treatment policies. In this manuscript, we develop an alternative approach for comparing treatment policies. This approach combines the non-parametric IPW estimators of the mean outcome with a model-based approach based on Robins’ Structural Nested Mean Model (SNMM; Robins (1994)). In the Structural Nested Mean Model, intermediate treatment effect functions, also called “treatment blips,” are parametrically modeled. The intermediate treatment effects isolate the causal effect of treatment at each time point, conditional on baseline and time-varying covariate history up to that time point. The resulting estimator is an “assisted” estimator in that the model-based approach assists the non-parametric estimator in estimating the mean outcomes of competing treatment policies.

Throughout this paper we focus on the comparison of two-stage treatment policies. The restriction to two-stage treatment policies allows the main ideas to be presented and in addition most sequentially randomized trials, aka Sequential Multiple Assignment Randomized Trials (SMART) (Lavori and Dawson, 2004; Murphy, 2005), concern two stages of treatment. ExTENd is a two-stage SMART. In Section 2, we formulate the estimand in a precise manner. In this section we provide a class of assisted estimators for the mean outcome based on data from a SMART; theoretical properties of the estimators are also provided. In Section 3, we briefly introduce how these estimators can be used to compare treatment policies and make inference. Simulation studies, in Section 4, are used to investigate different aspects of the methodology, including the performance of the proposed estimator under various levels of mis-specifying treatment effects. In Section 5, the methodology is illustrated by an analysis of the ExTENd data. Finally, a discussion of the paper, including ideas for future work, is presented in Section 6. Proofs of the theorems and lemmas are relegated to Web Appendix A.

2. Assisted Estimator for Policy Value

A two-stage treatment policy consists of two decision rules, d = (d₁, d₂). Each decision rule inputs available patient information at the current stage and outputs a treatment recommendation. Denote the outcome by Y (Y may be observed after the study or may be a function of the data collected during the study). The value of a policy is the expectation of Y that would result if the treatments were selected using the treatment policy d. A useful way to define the value of a policy is via the potential outcome framework (Neyman et al., 1935; Rubin et al., 1978). For each variable and each treatment sequence, we conceptualize a “potential outcome” that would have been observed under that treatment sequence. Using X_j to denote observations available prior to the j-th decision, the potential outcomes are {X₁, X₂(a₁), X₃(a₁, a₂); for all possible sequences of treatments (a₁, a₂)}. Here X₃ denotes observations after the second decision; the outcome Y(a₁, a₂) is a known function of {X₁, X₂(a₁), X₃(a₁, a₂)}. The value of the policy, d, is given by $V_d=E\left[Y(a_1,a_2){\mid }_{a_2=d_2\left(H_2\left(a_1\right)\right),a_1=d_1\left(H_1\right)}\right]$ where H₂(a₁) = (X₁, a₁, X₂(a₁)) and H₁ = X₁. V_d is the marginal mean of Y under the policy d, after integrating out H₂(a₁) and H₁.

The value of a treatment policy d, can also be written as a function of the intermediate treatment effects or “treatment blip functions,” from Robins’ Structural Nested Mean Model (Robins, 1994). We deviate briefly to define these intermediate treatment effects which we will use below; other types of treatment blip functions can be found in Murphy (2003) and Robins (2004). Corresponding to the two stages of treatment, there are two intermediate treatment effects given by ${\mu }_2(h_2,a_2)=E[Y(a_1,a_2)\mid H_2\left(a_1\right)=h_2]-E[Y(a_1,0)\mid H_2\left(a_1\right)=h_2]$ and ${\mu }_1(h_1,a_1)=E[Y(a_1,0)\mid H_1=h_1]-E[Y(0,0)\mid H_1=h_1]$, where a_t = 0 is the coding for a reference treatment. The intermediate treatment effect, μ₂, quantifies the effect of treatment a₂ relative to the reference treatment at stage two on the mean of Y, among individuals with history h₂. The intermediate treatment effect, μ₁, quantifies the effect of treatment a₁ relative to the stage one reference treatment, if always followed by the reference treatment at stage two, on the mean of Y, among individuals with history h₁ at stage one.

Consider randomized treatments in a randomized trial, denoted by capitalized letters, A₁, A₂, where the randomization distribution of A₁ given H₁ = h₁ is denoted by $p_1(\cdot \mid h_1)$ and the randomization distribution of A₂ given H₂(A₁) = h₂ is denoted by $p_2(\cdot \mid h_2)$. Throughout this paper we implicitly make all required measurability assumptions as well as existence of regular conditional densities. We have the following lemma.

Lemma 1: Assume that (i) $\max \{E\mid Y(a_1,a_2)\mid ,E\mid {\mu }_1(H_1,a_1)\mid ,E\mid {\mu }_2(H_2\left(a_1\right),a_2)\mid \}$ < ∞ for any treatment sequence (a₁, a₂) and (ii) for some δ > 0, ${\min }_{a_1}{p}_1(a_1\mid H_1)$ ≥ δ, a.s., then

$$\begin{array}{cc}\hfill V_d& =E\left[Y(A_1,A_2)-{\mu }_2(H_2\left(A_1\right),A_2)-{\mu }_1(H_1,A_1)+{\mu }_1(H_1,d_1\left(H_1\right))+{\mu }_2(H_2\left(a_1\right),d_2\left(H_2\left(a_1\right)\right)){\mid }_{a_1=d_1\left(H_1\right)}\right]\hfill \\ \hfill & =E\left[Y(A_1,A_2)-{\mu }_2(H_2\left(A_1\right),A_2)-{\mu }_1(H_1,A_1)+{\mu }_1(H_1,d_1\left(H_1\right))+\frac{I\{A_1=d_1\left(H_1\right)\}}{p_1(A_1\mid H_1)}{\mu }_2(H_2\left(A_1\right),d_2\left(H_2\left(A_1\right)\right))\right].\hfill \end{array}$$ (1)

This representation of the value, V_d, will form the basis for our method. The intuition behind this representation is that the potential outcome of Y under treatment policy d can be constructed or recovered from the potential outcome associated with the treatment sequence (A₁, A₂), by subtracting the intermediate treatment effects due to the sequence (A₁, A₂) and then adding in the intermediate treatment effects due to the policy d. The fraction involving the randomization probability in the last term (1) is used to account for the fact that the intermediate treatment effect of the second stage treatment under policy d depends on $H_2\left(a_1\right){\mid }_{a_1=d_1\left(H_1\right)}$ (the covariate history that would occur if the first stage treatment were assigned according to policy d); that is, this fraction adjusts for the fact that H₂(A₁) is not always equal to H₂(d₁(H₁)).

2.1 The Data and the Estimation Method

The observed data on each participant in a two-stage SMART is {X₁, A₁, X₂, A₂, X₃} where X_t denotes covariates observed prior to the t-th stage and A_t denotes the t-th stage randomized treatment. The primary outcome Y is a known function of {X₁, A₁, X₂, A₂, X₃}. Let H₂ = (X₁, A₁, X₂) and H₁ = X₁. The randomization probability for an individual's treatment may be a function of the individual's observed data (say $P[A_t=a\mid H_t]=p_t(a\mid H_t)$). For example, in many SMARTs, including ExTENd, participants who respond to the first stage treatment are randomized to different treatments from participants who do not respond to the first stage treatment. Thus non-responding participants have probability 0 of being assigned one of the treatments available for responders whereas responding participants have probability 0 of being assigned one of the treatments available for non-responders.

To express the intermediate effects and the value (1) in terms of the observed data, we relate the observed data to the potential outcomes. We assume (Rubin, 1986; Robins, 1997a; Robins et al., 2008), (A1) Consistency: X₂ = X₂(A₁), X₃ = X₃(A₁, A₂) and (A2) Sequential Randomization: A₁ is independent of all potential outcomes given observed X₁; A₂ is independent of all potential outcomes given observed (X₁, A₁, X₂). The consistency assumption states that the observed covariates are identical to the potential outcomes of the covariates evaluated at the observed treatment sequence. In particular this assumption implies that each subject's outcomes are uninfluenced by other subjects’ assigned treatments. This assumption may be violated if for example, treatment is provided in a group setting (group counseling). The sequential randomization assumption is valid in the setting of SMART trials because the treatment is randomized.

The intermediate treatment effects and the value, V_d, can be expressed in terms of the observed data as follows.

Lemma 2: Assume A1 and A2 and (i) $\max \{E\mid Y\mid ,E\mid {\mu }_1(H_1,a_1)\mid ,E\mid {\mu }_2(H_2,a_2)\mid \}$ < ∞ for any treatment sequence (a₁, a₂) and (ii) for some δ > 0, ${\min }_{a_1}{p}_1(a_1\mid H_1)$ ≥ δ, a.s., then

• (a)${\mu }_2(h_2,a_2)=E[Y\mid H_2=h_2,A_2=a_2]-E[Y\mid H_2=h_2,A_2=0]$,
• (b)${\mu }_1(h_1,a_1)=E[E[Y\mid H_2,A_2=0]\mid H_1=h_1,A_1=a_1]-E[E[Y\mid H_2,A_2=0]\mid H_1=h_1,A_1=0]$ and
• (c)$V_d=E[Y-{\mu }_2(H_2,A_2)-{\mu }_1(H_1,A_1)+{\mu }_1(H_1,d_1\left(H_1\right))+\frac{I\{A_1=d_1\left(H_1\right)\}}{p_1(A_1\mid H_1)}{\mu }_2(H_2,d_2\left(H_2\right))]$.

Suppose the intermediate treatment effects are known up to a finite-dimensional parameter: μ₁(h₁, a₁) = μ₁(h₁, a₁; β₁), μ₂(h₂, a₂) = μ₂(h₂, a₂; β₂). Robins (1994) provides a class of “g-estimators” for the parameters, β = (β₁, β₂). Each member in the class corresponds to a different choice of model for each of several nuisance functions; consistency of the g-estimators does not require correct models for the nuisance functions (see Robins (1994) for a detailed discussion). Furthermore this class of estimators does not require knowledge of the treatment policy, d. Thus β can be estimated and then used to form the estimators of the values of a variety of treatment policies. In Web Appendix B, we review the class of g-estimators. Each estimator in this class is consistent for the true value β₀ = (β₁₀, β₂₀) of β, and is asymptotically normally distributed (assuming a correctly specified SNMM and some finite moment conditions). Throughout the paper we implicitly assume consistency and asymptotic normality of $\widehat{\beta }$.

Then, given the results of Lemma 2 and estimators, $\widehat{\beta }$, a natural assisted estimator of the value of the policy d, V_d is:

$${\widehat{V}}_0(d;\widehat{\beta })={\mathbb{P}}_n\left[Y-{\mu }_2(H_2,A_2;{\widehat{\beta }}_2)-{\mu }_1(H_1,A_1;{\widehat{\beta }}_1)+{\mu }_1(H_1,d_1\left(H_1\right);{\widehat{\beta }}_1)+\frac{I\{A_1=d_1\left(H_1\right)\}}{p_1(A_1\mid H_1)}{\mu }_2(H_2,d_2\left(H_2\right);{\widehat{\beta }}_2)\right].$$ (2)

where ${\mathbb{P}}_{n}f(X_1,A_1,X_2,A_2,X_3)$ denotes a sample average. This estimator belongs to a class of assisted estimators, given by

$${\widehat{V}}_m(d;\widehat{\beta })={\mathbb{P}}_n\left[Y-{\mu }_2(H_2,A_2;{\widehat{\beta }}_2)-{\mu }_1(H_1,A_1;{\widehat{\beta }}_1)+{\mu }_1(H_1,d_1\left(H_1\right);{\widehat{\beta }}_1)+\frac{I\{A_1=d_1\left(H_1\right)\}}{p_1(A_1\mid H_1)}\left\{{\mu }_2(H_2,d_2\left(H_2\right);{\widehat{\beta }}_2)-m(H_1,A_1)\right\}+m(H_1,d_1\left(H_1\right))\right],$$ (3)

indexed by the function m(h₁, a₁). Note the former assisted estimator, ${\widehat{V}}_0(d;\widehat{\beta })$, corresponds to setting m(h₁, a₁) ≡ 0. We have the following lemma:

Lemma 3: Assume that the assumptions for Lemma 2 hold, then

• (a)The estimating function in (3) is unbiased for any choice of m that satisfies $E\mid m(H_1,a_1)\mid$ < ∞ for any a₁.
• (b)Assume (i) $E{\mid Y\mid }^2$ < ∞; (ii) ${\stackrel{.}{\mu }}_1(h_1,a_1;{\beta }_1)≔\frac{\partial }{\partial {\beta }_1}{\mu }_1(h_1,a_1;{\beta }_1)$ exists for all β₁, a.s., and ${\stackrel{.}{\mu }}_2(h_2,a_2;{\beta }_2)≔\frac{\partial }{\partial {\beta }_2}{\mu }_2(h_2,a_2;{\beta }_2)$ exists for all β₂, a.s.; and (iii) there exists some δ > 0 such that ${\sum }_{a_1}E{\sup }_{\Vert {\beta }_1-{\beta }_{10}\Vert \le \delta }{\mid {\mu }_1(H_1,a_1;{\beta }_1)\mid }^2+{\mid {\stackrel{.}{\mu }}_1(H_1,a_1;{\beta }_1)\mid }^2$ < ∞, and ${\sum }_{a_2}E{\sup }_{\Vert {\beta }_2-{\beta }_{20}\Vert \le \delta }{\mid {\mu }_2(H_2,a_2;{\beta }_2)\mid }^2+{\mid {\stackrel{.}{\mu }}_2(H_2,a_2;{\beta }_2)\mid }^2$ < ∞. Then if $\widehat{\beta }$ belongs to a subclass $\mathcal{B}$ of g-estimators, the choice of m resulting in the lowest variance for ${\widehat{V}}_m(d;\widehat{\beta })$ satisfies m(h₁, d₁(h₁)) = $E[{\mu }_2(H_2,d_2\left(H_2\right))\mid H_1=h_1,A_1=d_1\left(h_1\right)]$.

The subclass $\mathcal{B}$ corresponds to g-estimators for which a particular nuisance function is correctly modeled. This subclass is defined in Web Appendix B after a general review of g-estimators; in particular, in the simulation section we use an estimator $\widehat{\beta }$ based on a correctly specified model for the nuisance function, thus $\widehat{\beta }\in \mathcal{B}$. In Web Appendix C, we provide additional simulation results when using a $\widehat{\beta }$ that does not belong to $\mathcal{B}$.

The lemma above provides a guide for the choice of m; in practice m(h₁, a₁) in (3) can be replaced by a working estimator $\widehat{m}(h_1,a_1)≔m(h_1,a_1;{\widehat{\alpha }}_m)$ of $E[{\mu }_2(H_2,d_2\left(H_2\right))\mid H_1=h_1,A_1=a_1]$, resulting in ${\widehat{V}}_{\widehat{m}}(d;\widehat{\beta })$. Next we provide consistency and asymptotic normality results for the estimators of the value. We assume A1 and A2; in addition, we assume that μ₁(h₁, a₁; β₁) and μ₂(h₂, a₂; β₂) are functions that correctly specify the SNMM, with true parameter value β₀ = (β₁₀, β₂₀). In particular, Theorem 1 below implies that the assisted estimator is consistent regardless of the choice of function m (indeed one can set m ≡ 0).

Theorem 1: Assume that the assumptions for Lemma 3 hold; moreover, assume: (1) ${\widehat{\alpha }}_m$ converges in probability to some limit ${\alpha }_m^{+}$; (2) there exists some δ > 0 such that ${\sum }_{a_1}E{\sup }_{\Vert {\alpha }_m-{\alpha }_m^{+}\Vert \le \delta }\mid m(H_1,a_1,{\alpha }_m)\mid$ < ∞; and (3) $\stackrel{.}{m}(h_1,a_1;{\alpha }_m)≔\frac{\partial }{\partial {\alpha }_m}m(h_1,a_1;{\alpha }_m)$ exists for all α_m, a.s. Then ${\widehat{V}}_{\widehat{m}}(d;\widehat{\beta })$ is a consistent estimator for the policy value of d, V_d.

Theorem 2: Assume that the assumptions for Theorem 1 hold; moreover, assume: (1) there exists some δ > 0 such that ${\sum }_{a_1}E{\sup }_{\Vert {\alpha }_m-{\alpha }_m^{+}\Vert \le \delta }{\mid m(H_1,a_1;{\alpha }_m)\mid }^2+{\mid \stackrel{.}{m}(H_1,a_1;{\alpha }_m)\mid }^2$ < ∞ and (2) $\sqrt{n}({\widehat{\alpha }}_m-{\alpha }_m^{+})=O_p\left(1\right)$. Then $\sqrt{n}({\widehat{V}}_{\widehat{m}}(d;\widehat{\beta })-V_d)$ is asymptotically normal.

The asymptotic variance of the limiting normal distribution in Theorem 2 is provided in Web Appendix A. Recall that if m(h₁, a₁; α_m) is a correct model for $E[{\mu }_2(H_2,d_2\left(H_2\right))\mid H_1=h_1,A_1=a_1]$, then this asymptotic variance achieves the lowest value among all choices of m, provided that $\widehat{\beta }$ belongs to the subclass $\mathcal{B}$ of g-estimators.

3. Comparison between Treatment Policies

Suppose we are interested in comparing treatment policies d = (d₁, d₂) and $\tilde{d}=({\tilde{d}}_1,{\tilde{d}}_2)$. Then, given an estimator $\widehat{\beta }$ for the intermediate treatment effects, we obtain the following consistent estimator for the contrast between d and $\tilde{d}$, i.e., $V_{\tilde{d}}-V_d$:

$$({\widehat{V}}_{m_{\tilde{d}}}(\tilde{d};\widehat{\beta })-{\widehat{V}}_{m_d}(d;\widehat{\beta }))={\mathbb{P}}_n\left[{\mu }_1(H_1,{\tilde{d}}_1\left(H_1\right);{\widehat{\beta }}_1)-{\mu }_1(H_1,d_1\left(H_1\right);{\widehat{\beta }}_1)+\frac{I\{A_1={\tilde{d}}_1\left(H_1\right)\}}{p_1(A_1\mid H_1)}\left\{{\mu }_2(H_2,{\tilde{d}}_2\left(H_2\right);{\widehat{\beta }}_2)-m_{\tilde{d}}(H_1,A_1)\right\}-\frac{I\{A_1=d_1\left(H_1\right)\}}{p_1(A_1\mid H_1)}\left\{{\mu }_2(H_2,d_2\left(H_2\right);{\widehat{\beta }}_2)-m_d(H_1,A_1)\right\}+m_{\tilde{d}}(H_1,{\tilde{d}}_1\left(H_1\right))-m_d(H_1,d_1\left(H_1\right))\right],$$ (4)

where the function m(h₁, a₁) is now subscripted by the policy d, to reflect that a good choice of function m varies with d (see the following lemma). For ease of notation, define ${\Delta }_d(h_1,a_1)=m_d(h_1,a_1)-E[{\mu }_2(H_2,d_2\left(H_2\right))\mid H_1=h_1,A_1=a_1]$.

Lemma 4: Assume that the conditions for Lemma 3 are satisfied; in particular, assume that $\widehat{\beta }$ belongs to the subclass $\mathcal{B}$ of g-estimators. Then the choice of m_d and $m_{\tilde{d}}$ resulting in the lowest asymptotic variance for $\sqrt{n}({\widehat{V}}_{m_{\tilde{d}}}(\tilde{d};\widehat{\beta })-{\widehat{V}}_{m_d}(d;\widehat{\beta }))$, among the class of estimators in (4) with m_d and $m_{\tilde{d}}$ being arbitrary functions of (h₁, a₁), satisfy: (1) for h₁ such that $d_1\left(h_1\right)\ne {\tilde{d}}_1\left(h_1\right),{\Delta }_{\tilde{d}}(h_1,{\tilde{d}}_1\left(h_1\right))={\Delta }_d(h_1,d_1\left(h_1\right))$ = 0; (2) for h₁ such that d₁(h₁) = ${\tilde{d}}_1\left(h_1\right),{\Delta }_{\tilde{d}}(h_1,{\tilde{d}}_1\left(h_1\right))={\Delta }_d(h_1,d_1\left(h_1\right))$.

Lemma 4 implies that, for the purpose of estimating the policy contrast, it is reasonable to replace m_d(h₁, a₁) with a working estimate $m_d(h_1,a_1;{\widehat{\alpha }}_m)$ of $E[{\mu }_2(H_2,d_2\left(H_2\right))\mid H_1=h_1,A_1=a_1]$. Then we have the following lemma concerning the estimator of the contrast in (4) with m_d(h₁, a₁) replaced by $m_d(h_1,a_1;{\widehat{\alpha }}_m)$. We will also refer to this estimator as an “assisted estimator”. This lemma assumes that $m_d(h_1,a_1;{\widehat{\alpha }}_m)$ is modeled via a linear model $D_m^T{\alpha }_m$ where D_m is a function of (H₁, A₁) and α_m is estimated via least squares.

Lemma 5: Assume that the conditions for Theorem 1 and 2 are satisfied; then $\sqrt{n}(({\widehat{V}}_{{\widehat{m}}_{\tilde{d}}}(\tilde{d},\widehat{\beta })-{\widehat{V}}_{{\widehat{m}}_d}(d;\widehat{\beta }))-(V_{\tilde{d}}-V_d))$ converges in distribution to a normal distribution with mean zero and var-covariance matrix, Σ_Δ. The plug-in estimator ${\widehat{\Sigma }}_{\Delta }$ is a consistent estimator of Σ_Δ. The formulae for Σ_Δ and ${\widehat{\Sigma }}_{\Delta }$ are provided in Web Appendix A.

4. Simulation Studies

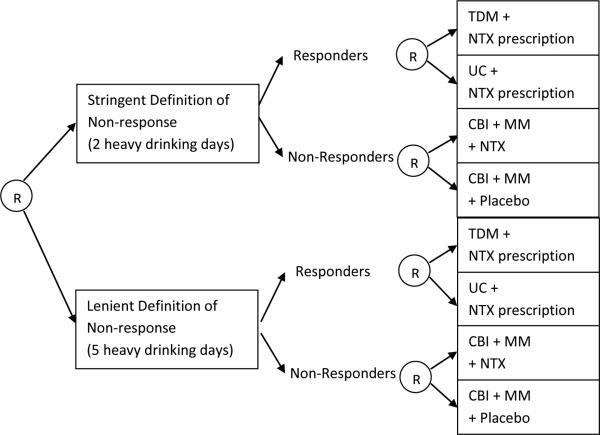
All simulation experiments are based on generative models mimicking the Extending Treatment effectiveness of Naltrexone (ExTENd) trial, a SMART trial of alcohol dependence treatment (PI: Oslin; see Figure 1). In this trial, the first-stage randomization is between two different criteria for early non-response to Naltrexone (NTX): the stringent definition (two or more heavy drinking days) or the lenient definition (five or more heavy drinking days). Participants were assessed weekly for non-response; as soon as a participant met the non-response criterion, he/she was re-randomized to either switch to combined behavioral interventions (CBI) or to a combination of CBI and Naltrexone. If the participant did not meet his/her assigned non-response criterion by the end of two months, then the participant was re-randomized to one of two relapse prevention options: usual care (UC) or telephone disease management (TDM).

Figure 1.

ExTENd SMART design for the treatment of alcohol dependence. “R” stands for (re-)randomization. TDM = Telephone Disease Management, UC = Usual Care, NTX = Naltrexone, CBI = Combined Behavioral Intervention, MM = Medical Management

The structure of the simulated data is: (X₁, A₁, X₂, R, A₂, Y). X₁ is a 3-dimension baseline covariate simulating the distribution of {baseline percent days heavy drinking, baseline craving score, baseline mental composite score}, A₁ is the binary indicator of the randomized non-response criterion, X₂ is a 2-dimension covariate simulating the distribution of {stage 1 duration, stage 1 percent days drinking}, R is the binary indicator of early response, A₂ is the re-randomized binary treatment at the second stage. Y is a primary outcome simulating the distribution of the end-of-study craving score (lower values are better). We will study various simulation scenarios that are all based on the following Y:

$$Y={\eta }_0\left(X_1\right)+A_1(1,X_1^T){\beta }_1+{\eta }_1(X_1,A_1,X_2)+A_2(1,X_2^T,A_1,R,R{X}_2^T,R{A}_1){\beta }_2+∊.$$ (5)

in which the terms involving β's are the intermediate treatment effects and ${\eta }_0(\cdot ),{\eta }_1(\cdot )$ and ε are other components in the distribution of Y that correspond to the main effect of X₁, the effect of X₂ conditional on (X₁, A₁) and the error term, respectively. We use estimates of ${\eta }_0(\cdot )$ and ${\eta }_1(\cdot )$ that are by-products of estimating an SNMM with the ExTENd data; the by-products of the estimation of SNMM also include an estimate of the variance of the error term, and we use that variance estimate to generate ε in our simulations. More details are provided in Web Appendix C.

We create nine simulation scenarios by varying β₁, β₂ in the generating model for Y. This procedure alters the magnitude of the main effects of the treatments at both stages and also the extent to which there are treatment by covariate interactions. In particular, the first coordinates in β₁ and β₂ reflect the main effects of A₁ and A₂, and the remaining coordinates reflect the interactions of A₁ and A₂ with covariates. We adopt the following definition of standardized effect size of a coordinate in β_j by slightly modifying Cohen's d measure to: $SES\left({\beta }_{jk}\right)={\beta }_{jk}∕\sqrt{Var\left({\eta }_0\left(X_1\right)\right)+Var\left({\eta }_1(X_1,A_1,X_2)\right)+Var\left(∊\right)}$. We adopt this definition of standardized effect size because η₀(X₁), η₁(X₁, A₁, X₂) and ε are uncorrelated components in the generative model of primary outcome Y, and the sum of their variances contributes to the majority of the variance in Y. Note that to ensure that this definition of standardized effect size is meaningful, we will use standardized covariates (each covariate in X₁, X₂ is standardized to come from a population with mean 0 and standard deviation equal to 1). The nine simulation scenarios correspond to combinations of no treatment effect, low treatment effect and medium treatment effect at both stages. We define no A_j treatment effect (j = 1, 2) as β_j = 0, define low A_j treatment effect as setting all coordinates in β_j to have SES equal to 0.2, and define medium A_j treatment effect as setting the first two coordinates in β_j to have SES equal to 0.5 (i.e., main effect and interaction effect with X_j1), and the other coordinates in β_j to have SES equal to 0.2. The rationale for only one medium level interaction in medium A_j treatment effect case is that it is unlikely (in real data) for the treatment to interact with many covariates at medium level. The sign of each coordinate in β_j is determined by a preliminary fit to the ExTENd data. In each simulation scenario, we generate 1000 simulated data sets.

Throughout $\widehat{\beta }$ in the assisted estimator is one of Robins’ g-estimators ($\widehat{\beta }$ is the solution to a series of least squares problems; indeed if, as discussed above a particular nuisance function is correctly modeled, then this least squares solution will belong to $\mathcal{B}$). In Web Appendix C we provide results when $\widehat{\beta }$ does not belong to $\mathcal{B}$; the simulation results are similar. Also throughout ${\widehat{m}}_d$ is estimated via least squares with (1, X₁, A₁) as predictors.

Let the triple (c₁, c₂, c₃) denote a policy in which c₁ is the assigned non-response criterion, c₂ is the assigned binary treatment for early responders at the second stage, and c₃ is the assigned binary treatment for early non-responders at the second stage. To investigate different aspects of the proposed methodology, we perform two sets of simulation experiments: The first set studies the bias and MSE of the assisted estimators of the difference in values of the most intensive policy, (1,1,1) and the least intensive policy, (0,0,0). The second set illustrates the efficiency gain of using the assisted estimator, compared with a non-parametric policy value estimator that is based on the marginal mean model (Murphy et al., 2001; Zhang et al., 2013).

Simulation 1: Here we compare bias and MSE for three types of assisted estimators for difference in value. We use the assisted estimator, ${\widehat{V}}_{{\widehat{m}}_d}(d;\widehat{\beta })$ with ${\widehat{m}}_d$, an estimator of $E[{\mu }_2(H_2,d_2\left(H_2\right))\mid H_1,A_1]$, and ${\widehat{V}}_0(d;\widehat{\beta })$, to estimate the contrast between policies (1, 1, 1) and (0, 0, 0). We also consider ${\widehat{V}}_{m_d}(d;\widehat{\beta })$ in which m_d is the unknown $E[{\mu }_2(H_2,d_2\left(H_2\right))\mid H_1,A_1]$; we call this an “oracle” assisted estimator, because in practice the optimal m_d will be unknown. The coverage of confidence intervals based on the asymptotic standard errors of each of the two non-oracle estimators is also provided in Table 1.

Table 1.

Simulation 1: Statistical properties of the assisted estimators of the contrast between values of policies (1,1,1) and (0,0,0).

N = 100
Scenario	True Value	Bias / SD			MSE			ASE Coverage
		Oracle	Assist	Assist (md = 0)	Oracle	Assist	Assist (md = 0)	Assist	Assist (md = 0)
(none,none)	0	0.04	0.04	0.04	3.51*	3.46	3.51*	95.7	95.4
(none,low)	−2.4	0.01	0.01	0.01	4.26	4.26	4.31	95.1	95.6
(none,med)	−5.2	0.03	0.03	0.01	3.94	3.93	4.3*	95.2	95.4
(low,none)	−1.4	−0.01	−0.01	−0.01	3.31	3.3	3.31	95.5	96.3
(low,low)	−3.8	0	0	0	4.08	4.14	4.12	95.5	95.9
(low,med)	−6.6	0.04	0.04	0.04	4.09	4.1	4.25*	95.6	96.3
(med,none)	−3.6	0.03	0.03	0.03	3.96	3.93	3.96	95.9	95.4
(med,low)	−6.0	−0.01	−0.01	−0.01	4.33	4.36	4.38	95.2	95.5
(med,med)	−8.8	0.01	0.01	0	4.02	4.04	4.24*	95	95.7

Oracle = contrast estimator based on ${\widehat{V}}_{m_d}(d;\widehat{\beta })$ with the true optimal m_d. Assist = contrast estimator based on ${\widehat{V}}_{{\widehat{m}}_d}(d;\widehat{\beta })$ with a working estimate of the optimal m_d. Assist (m_d = 0) = contrast estimator based on ${\widehat{V}}_0(d;\widehat{\beta })$. The displayed numbers for confidence interval coverage are the coverage proportion × 100. An Asterisk indicates that the MSE of Oracle or Assist (m_d = 0) is significantly different from MSE of Assist (at 0.05 level).

The simulation results with N = 100 are shown in Table 1 (results for N = 250 are shown in Web Appendix C). Based on the ratio of bias and standard deviation, we conclude that, as expected, the assisted estimators provide an unbiased estimate of the contrast between policies. The MSEs of all the three estimators are similar; ${\widehat{V}}_{{\widehat{m}}_d}(d;\widehat{\beta })$ tends to be slightly more efficient than ${\widehat{V}}_0(d;\widehat{\beta })$. The coverage of the confidence intervals based on the asymptotic standard errors is close to 95% in all cases.

In Web Appendix C we provide additional simulations; these simulations illustrate that ${\widehat{V}}_{{\widehat{m}}_d}(d;\widehat{\beta })$ will provide a noticeable efficiency improvement over ${\widehat{V}}_0(d;\widehat{\beta })$ in some extreme settings. However, we found that in most practical scenarios, a sophisticated chosen m_d does not substantially improve the efficiency over m_d ≡ 0; therefore for simplicity we recommend using the assisted estimator with m_d ≡ 0.

Simulation 2: Here we assess the robustness via the bias, MSE and confidence interval coverage provided by the assisted estimators to misspecification of the SNMM. As a comparison we consider estimators from the marginal mean model (Murphy et al., 2001) as these estimators do not require the SNMM. The marginal mean models are estimated via a non-parametric inverse-weighted estimator. More details about the implementation of the marginal-mean-models-based estimator in this simulation study can be found in Web Appendix B. We also present there some discussions about the equivalency between the estimators proposed in Zhang et al. (2013) and in Murphy et al. (2001). Note that when the goal is to evaluate the difference between two policies, the estimators in Orellana et al. (2010) under particular choices of nuisance functions reduce to the marginal mean model estimators.

${\widehat{V}}_{{\widehat{m}}_d}(d;\widehat{\beta })$ is estimated with two differently mis-specified SNMMs in addition to the correctly specified SNMM. The true SNMM is implied by the generative model in (5), i.e., ${\mu }_1(H_1,A_1)=A_1(1,X_1^T){\beta }_1,{\mu }_2(H_2,A_2)=A_2(1,X_2^T,A_1,R,R{X}_2^T,R{A}_2){\beta }_2$. The first mis-specification of the SNMM excludes X₁₁ from the model for μ₁(H₁, A₁) and excludes X₂₁, RX₂₁ from the model for μ₂(H₂, A₂) (denoted as Assist2 in Table 2). The second mis-specification models μ₁(H₁, A₁) as $A_1(1,X_1^{\ast T}){\beta }_1$ and models μ₂(H₂, A₂) as $A_2(1,X_2^{\ast T}){\beta }_2$, where $X_1^{\ast }$ and $X_2^{\ast }$ are 3-dimensional and 7-dimensional covariates (denoted as Assist3 in Table 2). The dimensions of $X_1^{\ast }$ and $X_2^{\ast }$ are chosen so that the model complexity is the same as in the correctly specified SNMM; $X_1^{\ast }$ and $X_2^{\ast }$ are generated independently of all the other covariates.

Table 2.

Simulation 2: Comparison between the marginal-mean-model-based estimators and the assisted estimators, with respect to the performance in estimating the policy contrasts.

N = 100
Estimation of the first contrast, (1, 1, 1) vs (0,0,0)
Scenario	True value	Bias × 100				Coverage of 95% CI × 100				Relative MSE
		MM	Assist1	Assist2	Assist3	MM	Assist1	Assist2	Assist3	Assist1	Assist2	Assist3
(none,none)	0	2.4	4.9	5.2	4.9	95.2	96.2	96	96.1	0.94	0.93	0.99
(none,low)	−2.4	5.8	4.6	4.7	6	94.5	96	95.4	95.2	0.95	0.94	1.04
(none,med)	−5.2	12	−6.8	−6.8	−2.6	93.6*	93.9	93.6*	94.6	0.95	0.95	1.01
(low,none)	−1.4	−1.9	2.5	1.7	4.8	95.6	94.6	94	95	1.01	1.01	1.09
(low,low)	−3.8	−12.5	−10.8	−11	−10.3	94.3	94.5	93.5*	94.6	0.92	0.92	0.97
(low,med)	−6.6	11	−9.9	−10.4	−5.8	93.9	94.8	94.7	95.5	0.84	0.84	0.93
(med,none)	−3.6	8.9	4.2	5.4	3.4	95.5	95.9	95.3	96.2	0.89	0.87	0.89
(med,low)	−6.0	9.7	−1.9	−2.7	−7.1	94.3	94.8	94.1	94.9	0.85	0.85	0.93
(med,med)	−8.8	28.9*	4.2	5.4	4.7	93.7	94.9	95.2	94.9	0.8	0.79	0.85

Estimation of the second contrast, the tailored policy vs (0,0,0)
Scenario	True value	Bias × 100				Coverage of 95% CI × 100				Relative MSE
		MM	Assist1	Assist2	Assist3	MM	Assist1	Assist2	Assist3	Assist1	Assist2	Assist3
(none,none)	0	6	1	2.4	2.3	96.2	97*	96.6*	96.1	0.78	0.76	0.57
(none,low)	−2.2	6.4	4.8	−2.8	16.7*	95.6	96	95.7	94.7	0.79	0.77	0.59
(none,med)	−3.9	11.5	−2.8	−22.1*	−43.9*	94.9	95.8	95.1	94.4	0.78	0.77	0.67
(low,none)	−1.1	5.3	11.2*	9.7	42.9*	95.5	95.3	94.8	93.8	0.81	0.8	0.69
(low,low)	−3.3	−7.3	−6.3	−15.1*	46.3*	93.9	95.3	93.9	95	0.77	0.74	0.59
(low,med)	−5	6.7	−1.8	−23.6*	−2.8	94	96.3	94.9	95.7	0.7	0.69	0.5
(med,none)	−2.3	9.3	8	9.1	50*	95.9	96.5*	95.8	95.4	0.76	0.74	0.57
(med,low)	−4.4	13.7*	9.4	−0.3	53.3*	93.2*	95	95.2	94.1	0.7	0.67	0.57
(med,med)	−6.2	24.7*	5.2	−15.1*	9.9*	93.1*	95.5	95.3	95.6	0.66	0.64	0.49

MM = Marginal-mean-model-based estimator. Assist1 = Assisted estimator with correctly specified SNMM. Assist2 = Assisted estimator with mis-specified SNMM that excludes X₁₁, X₂₁, RX₂₁. Assist3 = Assisted estimator with mis-specified SNMM that excludes all the covariates interacting with treatments. Bias significantly different from 0, and coverage proportion significantly different from 95%, are marked with an asterisk. Relative MSE is calculated as the ratio of MSE with that of MM.

We focus on the estimation of two contrasts: the first is the contrast between the policies (1,1,1) and (0,0,0), and the second is the contrast between a “tailored” treatment policy and the policy (0, 0, 0). This tailored treatment policy assigns a₁ = 1 if X₁₃ > 0; a₂ = 1 to all early responders and a₂ = 1 to early non-responders if X₂₁ < 0. In each of the nine simulation scenarios we compare the marginal-mean-model-based estimator with the assisted estimators for three differently specified SNMMs.

The experiment results when N = 100 are shown in Table 2 (results for N = 250 are shown in Web Appendix C). Instead of the MSE of the estimators, we present the relative MSE of the assisted estimators, with the MSE of the marginal-mean-model-based estimator (MM) as the reference. We found that, for the comparison between policies (1,1,1) and (0,0,0), the assisted estimators with correctly specified SNMM outperform MM in terms of the MSE in most cases; mis-specifying the SNMM does not seem to introduce bias, but severe mis-specification (Assist3 in the Table) can lead to lower efficiency, and sometimes can even cause the assisted estimators to have a larger MSE than MM. For the comparison between the tailored policy and policy (0,0,0), the assisted estimators with correctly specified SNMM outperform MM in terms of the MSE, and the advantage is greater than that of the first contrast. Mis-specifying the SNMM introduces bias; in particular, severe mis-specification (Assist3) leads to considerable bias. However, this bias does not seem to greatly impact the performance of the confidence interval. Interestingly, for the estimation of this contrast, mis-specifying the SNMM may even result in a smaller MSE despite of the bias, due to a smaller standard deviation in the estimate.

5. Data Analysis Example: ExTENd

The ExTENd study (see Figure 1) includes 302 participants, with 49 participants dropping out prior to experiencing two heavy drinking days. These participants are removed from our analysis as they did not experience the first randomization and both they and the clinicians were blind to this randomization. Only three participants dropped out during the first treatment stage after experiencing two heavy drinking days. The data from these participants is also removed for simplicity. Thus the data we analyze has a sample size of 250.

We use both the marginal-mean-model-based estimator and the assisted estimator to compare the most intensive versus the least intensive policies. Treatment policy (1,1,1) represents the most intensive policy in the SMART, in which the early non response is deemed to occur if and when there are 5 or more heavy drinking days in the first 8 weeks, in which early responders are provided TDM and in which early non responders are provided NTX+CBI. Treatment policy (0,0,0) represents the least intensive policy, in which early non response is deemed to occur if and when there are 2 or more heavy drinking days in the first 8 weeks, in which early responders are provided UC and in which early non responders are provided CBI only.

Besides the two treatment policies above, we will also compare a more “deeply tailored” policy versus the policy (0, 0, 0). At stage one, this tailored policy assigns the 5 or more heavy drinking days definition of non response to participants for whom the standardized pre-treatment mental score is above zero and the 2 or more heavy drinking days definition of non response to participants with a pre-treatment mental score below zero. Among early responders this policy assigns TDM if they have at least one heavy drinking day during stage one and assigns UC otherwise. Among early non responders this policy assigns NTX+CBI if their stage one duration is shorter than 49 days and otherwise assigns CBI only. The justification of this treatment policy comes from the belief that participants who were in worse mental health condition (indicated by a lower mental composite score) at baseline should proceed to stage two earlier to receive more intensive treatments. Moreover, it is considered that responders and non-responders who performed worse in stage one (i.e., responders who experienced at least one heavy drinking day and non-responders who transitioned to stage two sooner) should receive more intensive intervention in stage two.

We compare the treatment policies in terms of the Penn Alcohol Craving Scale (PACS). Here we reverse code this scale such that higher values imply less craving thus are more favorable. PACS is collected every two months during stage two. The outcome Y is the average of the measurement at two months and four months after entry into stage two. Among the 250 participants in our data set, 46 participants are missing Y. We deal with this missingness in the outcome, Y, by adopting a slightly adjusted assisted estimator that handles missingness via inverse-probability-weights (see Robins et al. (1995) for example). The adjustment requires an estimator of the conditional probability of missing the outcome. This adjustment is briefly reviewed in Web Appendix B. In particular, we make the assumption that the missing Y's are missing at random (Rubin, 1976). The marginal-mean-model-based estimator is also adjusted similarly to accommodate for missingness.

In the analysis model, we choose to include the following covariates: X₁ is a 10-dimensional baseline covariate including mean-centered versions of {gender, age, years of alcohol use, indicator of drug abuse, pre-treatment percent days heavy drinking, indicator of being married, years of alcohol intoxication, pre-treatment alcohol intoxication days within 30 days, pre-treatment percent days drinking, pre-treatment mental composite score}; X₂ is 5-dimensional covariate measured prior to re-randomization, including {duration of the first stage, number of heavy drinking days during the first stage, percent days drinking during the first stage, percent days heavy drinking during the first stage, average number of pills taken per day during the first stage}. Moreover, A₁ indicates whether (A₁ = 1) or not (A₁ = 0) a patient is randomized to the lenient definition (i.e., five or more heavy drinking days) of non-response as opposed to the stringent definition (i.e., two or more heavy drinking days); R is the indicator of being an early responder; A₂ indicates whether (A₂ = 1) or not (A₂ = 0) a responder is re-randomized to TDM as opposed to UC, or whether or not a non-responder is re-randomized to NTX+CBI as opposed to Placebo+CBI.

We run two sets of analysis with the assisted estimators, under two different SNMMs: in the first analysis we adopt a parsimonious model for SNMM by assuming ${\mu }_1(H_1,A_1)=A_1(1,{\tilde{X}}_1^T){\beta }_1$ and ${\mu }_2(H_2,A_2)=A_2(1,{\tilde{X}}_2^T,A_1,R,R{\tilde{X}}_2^T,R{A}_1){\beta }_2$, where ${\tilde{X}}_1$ is the first five dimensions in X₁ and ${\tilde{X}}_2$ is the first three dimensions in X₂; in the second analysis we adopt a more complex model for SNMM by assuming ${\mu }_1(H_1,A_1)=A_1(1,X_1^T){\beta }_1$ and ${\mu }_2(H_2,A_2)=A_2(1,X_2^T,A_1,R,R{X}_2^T,R{A}_1){\beta }_2$. Asymptotic standard errors of the policy contrast estimates are calculated and used to construct the 95% confidence intervals for the policy contrasts. Table 3 presents the analysis results.

Table 3.

Illustrative data analysis results with the ExTENd data. Evaluate the policy contrasts of both the policy (1, 1, 1) and the proposed tailored policy, in relation to the policy (0, 0, 0), with respect to PACS.

		(1,1,1) vs (0,0,0)			Tailored vs (0,0,0)
		Est (s.e.)	Lower Bound	Upper Bound	Est (s.e.)	Lower Bound	Upper Bound
PACS	MM	2.98 (1.30)	0.44	5.52	0.21 (1.05)	−1.85	2.27
	Assist1	2.83 (1.44)	0.00	5.66	0.91 (0.99)	−1.02	2.85
	Assist2	2.95 (1.48)	0.04	5.85	1.25 (1.05)	−0.80	3.31

MM = Marginal-mean-model-based estimator. Assist1 = Assisted estimator with a parsimonious SNMM. Assist2 = Assisted estimator with a complex SNMM.

The three estimators (including two assisted estimators with different SNMMs) produce similar estimates, considering the relatively large standard errors. The analyses suggest that the most intensive, (1,1,1) policy is estimated to approximately lower PACS by 3 on average compared to the least intensive, (0,0,0) policy, and this difference is significant at 0.05 level, across all three estimators. The proposed more tailored policy, on the other hand, does not significantly differ from the (0,0,0) policy. Note that the marginal-mean-model based estimator has standard error no greater than that of the assisted estimators; this might be due to either small treatment effects in the ExTENd data, or the variance due to the considerable amount of missingness in the data.

6. Discussion

Our simulations indicate that the MSE performance of the assisted estimators is robust to misspecification of the model for the intermediate treatment effects. None-the-less to reduce bias, efforts should be made to ensure good model fit in estimating the intermediate treatment effects. Data analysts should make efforts to collect all the time-varying covariates that may moderate the effect of treatment at each stage on the primary outcome and include them in the treatment effects models. Specific subject knowledge, and possibly results from past studies, may provide valuable information for choosing the models.

In this manuscript we did not derive the semi-parametrically efficient estimator for policy value and/or policy contrast. To obtain the most efficient estimator of the policy contrast, one needs to subtract from the influence function of the assisted estimator its projection on all tangent spaces that are orthogonal to the tangent space associated to the policy contrast; this appears difficult because the policy contrast is a functional of a collection of finite or infinite dimensional parameters in the data distribution and the functional is dependent on the specific policies being studied. We plan to investigate this efficiency problem in future research.

In this paper we focused on the comparison of two-stage treatment policies. When there are more than two treatment stages at which (re-)randomization may happen, similar assisted estimators can be constructed. For example, for a three-stage treatment policy d = (d₁, d₂, d₃), the assisted estimator requires additional terms characterizing the effect of d₃ when (d₁, d₂) were followed at earlier stages. This would involve inverse-probability-weights from more than one stage.

The methodology proposed in this paper is only applicable when a few candidate treatment policies have been pre-specified. When there are more than a few candidate treatment policies, usually one of the candidate treatment policies can be considered as a reference policy, and comparison can be made between any of the remaining policies and this reference policy. In future work, we will also consider a multiple comparison procedure for many treatment policies.

The assisted estimators are based upon the structural nested mean models for continuous primary outcomes. Multiplicative structural mean models (Robins, 1997a) and generalized structural mean models (Vansteelandt and Goetghebeur, 2003) have been proposed to deal with non-continuous primary outcomes and non-linear treatment effects. We expect that the assisted estimators can also be extended to deal with more complicated primary outcomes and more complicated underlying interaction between treatments and covariates, with the assistance of these more recent variations of SNMMs.