Actomyosin contraction, aggregation and traveling waves in a treadmilling actin array

Abstract

We use perturbation theory to derive a continuum model for the dynamic actomyosin bundle/ring in the regime of very strong crosslinking. Actin treadmilling is essential for contraction. Linear stability analysis and numerical solutions of the model equations reveal that when the actin treadmilling is very slow, actin and myosin aggregate into equidistantly spaced peaks. When treadmilling is significant, actin filament of one polarity are distributed evenly, while filaments of the opposite polarity develop a shock wave moving with the treadmilling velocity. Myosin aggregates into a sharp peak surfing the crest of the actin wave. Any actomyosin aggregation diminishes contractile stress. The easiest way to maintain higher contraction is to upregulate the actomyosin turnover which destabilizes nontrivial patterns and stabilizes the homogeneous actomyosin distributions. We discuss the model’s implications for the experiment.

Introduction

Dynamic polar actin filaments and myosin filaments, consisting of many molecular motors that tend to move toward the so called barbed ends of actin filaments, play multiple roles in cells. One of the most important of these roles is based on the ability of the actomyosin bundles and rings to contract. The primary examples of one-dimensional contractile bundles are stress fibers [1], and contractile cytokinetic rings [2]. Mechanics of actomyosin contraction plays a great role in biology, most notably in muscle cells [3]. In muscle, actin filaments are arranged in perfect crystalline arrays of periodically spaced sarcomeres arranged optimally for the contraction: pointed ends of actin filaments are oriented inside the sarcomere, where myosin filaments bind and move to the outward-pointing barbed ends. In the self-organized actomyosin structures of other cells, there is, however, an outstanding question: how could the disordered actomyosin array contract? Indeed, myosin would slide randomly placed actin filaments in such a way that on the average there would be an expansion, not contraction [4].

To solve this conundrum, roughly speaking, three classes of model were suggested. In the first one, multiple actin filaments are nucleated at and grow with their barbed ends focused on formin clusters, which effectively creates minisarcomeres [5]. In the second mechanism, a beautiful idea is that when there are both myosin motors and crosslinkers in the actin bundle, the actin filament pairs, which are trying to expand, buckle, while filament pairs under tension effectively develop contraction [6]. In the third mechanism, actin filament disassembly at the pointed ends together with tricky deformations of crosslinkers and myosin lead to net contraction [7]. These models emphasized the importance of passive crosslinking forces for developing contraction, which was confirmed in vitro [8]. What is crucial for understanding the contraction mechanism is not limiting the model to static actin structures, which some models do, but to examine the self-organization of the actomyosin arrays coupled with force balances. Due to its importance in cell biology and mathematical elegance of this system, there have been a surge of modeling of the coupled problem of actomyosin self-organization and contraction [9, 10, 11, 12].

In [13] we introduced an agent based model for the actomyosin constractile ring based on a large system of force balance equations for each actin and myosin filament in the ring. The model proposes to add a novel mechanism to the list of models reviewed above: actin filament treadmilling in combination with myosin processivity and cross-linking is, as shown below, sufficient to guarantee the contractility of the actomyosin ring. While the agent based model is easy to formulate and simulate, a continuum model in the form of differential equations is always desirable, as such model is much more amenable to analysis, and thus its results are easier to understand qualitatively.

In this study, we formulate a continuum version of the agent based model introduced in [13]. Then we introduce a scaling where we distinguish between two length scales, namely the characteristic length scale of the bundle and the length of actin filaments. We compute the asymptotic expansion in the limit of dense crosslinking and of actin filament length being much shorter than the length of the bundle/ring. This limit is highly relevant to cell biology, as in almost all known structures this is exactly what is observed [14]. In this limit we obtain a model for the actomyosin bundle treated as a viscous fluid. Analysis and simulations of this model provide many biologically relevant insights and estimates and predict highly nontrivial pattern formation. Note that when we write about the contractile ring or bundle, we mean idealized general actomyosin structures. Real cytokinetic rings and stress fibers are, no doubt, much more complex than the model considered here, and there is no evidence yet that the proposed treadmilling mechanism applies to the biological structures. In the Discussion we list implications of the model to cell biology.

The paper is organized as follows. In section 2 we formulate the microscopic model and in section 3 we use perturbation theory to pass to the asymptotic limit. We consider homogeneous solutions to the model in section 4, and in section 5 we use numerical simulations and linear stability analysis to investigate the pattern formation. We end with discussion of implications of the model. Most of the formal calculations have been gathered in the appendix.

2. Microscopic model formulation

We start with a continuous model for the contractile ring-like actomyosin contractile bundle, which is based on the agent based model introduced in [13], but the model description here is self-consistent. The model consists of force balance equations for all dependent variables, which are the radius of the ring as well as the angular positions of actin filaments and myosin thick filaments. While myosin filaments are represented as point-like objects, actin filaments are characterized by a specific length l and by their polarity, which is either +1 or −1 according to the directions into which their pointed ends are oriented (+1 and −1 are for pointed end in positive and negative direction, respectively). In the model derivation here, we take into account active forces generated by motor proteins and drag forces between overlapping actin filaments caused by crosslinking proteins. In addition to the force balance equations, there are transport equations for actin filaments, including a description of their treadmilling-process of simultaneous elongation of actin filaments at the barbed ends and shortening at the pointed ends. Finally, we consider movements of the myosin filaments, their random attachments to overlapping actin filaments and dissociations once they reach actin filament ends.

We initially formulate a model for an actomyosin bundle of infinite length. Only after deriving the asymptotic limit model for short filaments, we will restrict the bundle to an interval of finite length coupled to periodic boundary conditions and consider a model for a closed contractile actomyosin ring. We denote time by t > 0 and the spatial position of actin filament center points by x ∈ ℝ. We introduce the number densities ρ^± (t, x) of actin filaments pointing with their pointed ends in positive, respectively negative direction. The velocity fields υ^± = υ^± (t, x) are the material velocities of these two groups of actin filaments. In the continuum equations for their densities,

$${\partial }_t{\rho }^{\pm }(t,x)+{\partial }_x(({\upsilon }^{\pm }(t,x)\mp {\upsilon }_{\text{tr}}){\rho }^{\pm })=0,$$ (1)

we take into account the given treadmilling velocity υ_tr > 0 which additionally translocates the center points of actin filaments into the direction of their barbed ends.

The material velocities satisfy the force-balance equations:

$$0=-{\int }_{ℝ}{\vartheta }^{\pm }(t,x,y)F_s(\pm 1-\frac{{\upsilon }^{\pm }(t,x)-{\upsilon }^{\mp }(t,y)}{2V_m})dy++\eta {\rho }^{\pm }(t,x)\sum _{n=-1,+1}{\int }_{ℝ}A(x-y)({\upsilon }^{\pm }(t,x)-{\upsilon }^n(t,y)){\rho }^n(t,y)dy.$$ (2)

The first line in (2) represents the active forces exerted by myosin molecular motors, which we describe, following many previous studies of molecular motors, [15, 16] using a linear force-velocity relationship. Thus, the force is the stall force of myosin thick filaments F_s decreased by the factor in the brackets which is equal to 1 if the overlapping antiparallel actin filaments are not moving relative to each other, and which decreases linearly with the relative velocity of convergence of barbed ends. If this relative velocity is equal to twice the free myosin velocity V_m (velocity at which myosin motors move freely without generating force), the myosin filament moves with rate V_m to the barbed ends, and the active force becomes zero. Implicitly, the force balance on the myosin filaments is already satisfied in this formulation because the myosin filaments are assumed to be moving with such velocity that the total force on the myosin filament is zero. The positions of myosin filaments are described by the time dependent integration kernel ϑ = ϑ (t, x, y) representing the density of the myosin filaments with respect to the center points of connected actin filaments, as explained below. Its first spatial argument refers to the pointed end forward actin filaments while the second one refers to pointed end backward actin filaments. Therefore, in the system (2), we write this integration kernel using the specialized notation ϑ⁺ (t, x, y) = ϑ⁻ (t, y, x) = ϑ (t, x, y). Note that myosin generates force only between the antiparallel actin filaments. Myosin filaments simply glide to the barbed ends of the parallel filaments without generating force. In principle, if parallel actin filaments move with different velocities, myosin can also generate the force between them, but this is excluded by the assumption of local indistinguishability of parallel actin filaments.

The second line in equation (2) is responsible for effective drag force due to the protein friction that stems from continuous turnover, attachment, detachment and stretching of elastic cross-linking proteins. Many models and much data points out that such dynamics leads to effective viscous drag characterized by coefficient η > 0 ([17, 18, 19, 20, 21]). This coefficient is proportional to the number of the cross-linkers per unit length of actin. The viscous force is proportional to the difference of filament velocities (term in the brackets), to the length of the region where two actin filaments overlap (given by A(x − y) = max(l − |x − y|, 0) for two actin filaments with center points at positions x and y), and to the densities of the overlapping actin filaments. Note that drag forces act between actin filaments of equal and of opposite polarity which explains the summation with respect to n = {+1, −1}.

It should be noted that equation (2) determines the vector fields υ^± only up to an additive constant as the model does not include explicit anchoring with respect to the environment. Later, in the numerical treatment, we will include a minor amount of background friction which will fix that missing degree of freedom.

Finally, there is a balance between the external tension σ = σ(t) applied to the actomyosin bundle (i.e., from the cell cortex or from focal adhesions) and the contributions to tensile stress generated inside the actomyosin bundle by myosin and cross-linkers. This balance holds at any point along the bundle [13] and in the notation of this paper it reads

$$\sigma (t)={\int }_{-\infty }^z{\int }_z^{\infty }[\vartheta (t,x,y)F_s(1-\frac{{\upsilon }^{+}(t,x)-{\upsilon }^{-}(t,y)}{2V_m})--\eta \sum _{m,n=-1,+1}{\rho }^m(t,x){\rho }^n(t,y)A(x,y)({\upsilon }^m(t,x)-{\upsilon }^n(t,y))]dydx,$$ (3)

for any position z ∈ ℝ. Expression (3) sums up forces acting between actin filaments to the left and right of any position z, and it states that the contractile force σ is a global property of the bundle.

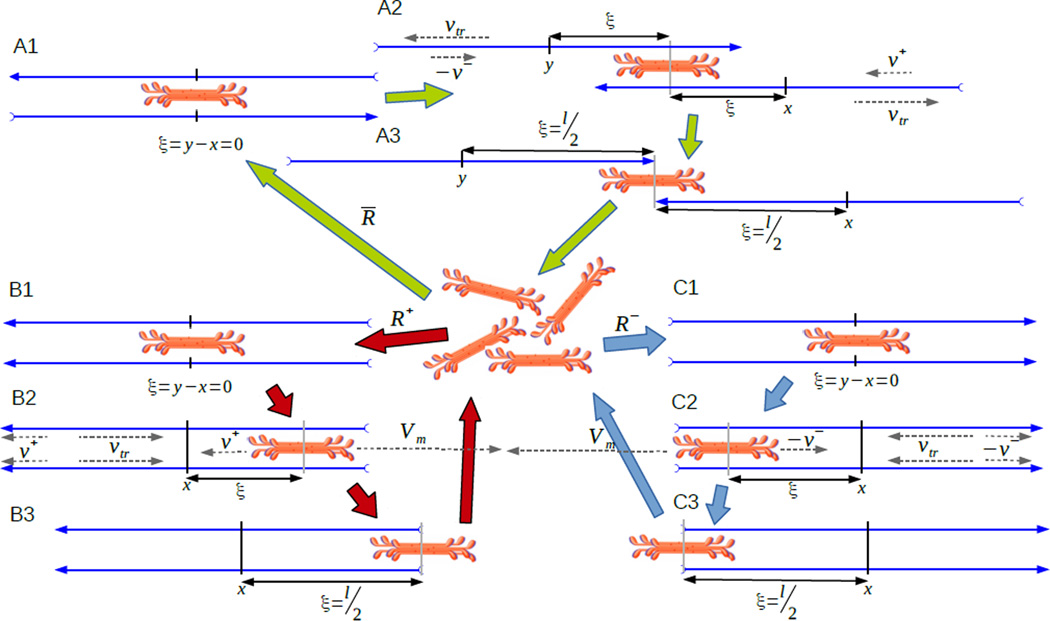
Concerning myosin filaments, we assume that they attach to at most two actin filaments and that after reaching either the barbed or the pointed ends, they slide off (in the model formulation, both ends are reached simultaneously) and reattach to other actin filaments immediately. As a consequence every myosin filament is always bound to exactly two actin filaments. For simplicity, we assume that myosin filaments always attach to two actin filaments at the same position simultaneously right at their center points. Equal length of actin filaments and indistinguishability of co-localized actin filaments of equal polarity guarantee that myosin filaments will fall off both actin filaments at the same time. We illustrate all dynamic processes for myosin and actin filaments in figure Appendix D.

We introduce structured distributions of myosin filaments, namely χ̄ = χ̄(t, x, ξ) as well as χ⁺ = χ⁺(t, x, ξ) and χ⁻ = χ⁻(t, x, ξ) respectively which represent the densities of molecular motors attached to anti-parallel actin filaments and parallel actin filaments with their pointed end pointing in positive, respectively negative direction. Here the microscopic variable ξ ∈ [0, l/2] represents the relative position of the myosin filament with respect to the center points of actin filaments (figure 1).

Figure 1.

Schematic representation of the model: Turnover of myosin thick filaments: Unbound myosin filaments bind with probability R̄ to the center points of pairs of anti-parallel actin filaments (A1), or, with probabilities R^± to the center points of parallel pointed end forward (B1), respectively backward (C1) actin filaments. Myosin forces and F-actin treadmilling have counteracting effects on the position of myosin binding sites as by itself myosin would move towards the barbed ends, while treadmilling moves binding sites towards the pointed ends. A2: Myosin filaments attached to anti-parallel actin filaments shift towards the pointed ends as treadmilling is assumed to exceed actin filament velocities through myosin action. The value ξ represents the relative position of myosin with respect to the centers of actin filaments in a way such that ξ = l/2 corresponds to the pointed ends of actin filaments. A3: Once myosin reaches the pointed ends it detaches and returns to the pool of unbound myosin. B2: Myosin attached to a pair of pointed end-forward actin filaments shifts towards the barbed ends as it can move with its free moving velocity which is faster than F-actin treadmilling. The material velocity of actin filaments moves actin and myosin simultaneously and therefore does not affect their relative position. In the case of parallel actin filaments the relative position ξ = l/2 corresponds to the barbed ends of actin filaments. B3: Once myosin reaches the barbed ends, it detaches. C2, C3: Myosin attached to a pair of pointed end-backward actin filaments moves towards the barbed ends where it detaches. Observe that the material velocity of pointed end backward actin filaments is now written as −υ⁻ as υ⁻ by convention is taken as negative.

Transport equations for myosin filaments attached to anti-parallel actin filaments have the form:

$$\{\begin{array}{c}{\partial }_t\overline{\chi }+{\partial }_x\left(\frac{{\upsilon }^{+}(t,x-\xi )+{\upsilon }^{-}(t,x+\xi )}{2}\overline{\chi }\right)++{\partial }_{\xi }\left(\frac{{\upsilon }^{-}(t,x+\xi )+{\upsilon }_{\text{tr}}-({\upsilon }^{+}(t,x-\xi )-{\upsilon }_{\text{tr}})}{2}\overline{\chi }\right)=0\hfill \\ \frac{{\upsilon }^{-}(t,x)+{\upsilon }_{\text{tr}}-({\upsilon }^{+}(t,x)-{\upsilon }_{\text{tr}})}{2}\overline{\chi }(t,x,0)=\overline{R}{M}_{\text{off}}.\hfill \end{array}$$ (4)

This transport equation accounts for drift in physical space according to a velocity field which is the average of the material velocities υ^± = υ^±(t, x) of the two anti-parallel actin filaments. As reflecting in the continuum equations above, the positions of actin filaments change according to these material velocities but taking into account a correction due to the constant treadmilling rate υ_tr > 0. The relative position ξ of myosin attached to anti-parallel actin filaments changes according to the difference of these two effective velocity fields.

The boundary condition at ξ = 0 represents reattachment of myosin molecular motors to anti-parallel actin filaments. The quantity M_off, which we will define below, represents total detachment of myosin molecular motors out of configurations with anti-parallel as well as with parallel actin filaments. This pool of detached myosin is immediately redistributed among parallel pairs of actin filaments and anti-parallel pairs according to the coefficients

$$R^{+}=\frac{{({\rho }^{+})}^2}{{({\rho }^{+}+{\rho }^{-})}^2},\hspace{1em}{R}^{-}=\frac{{({\rho }^{-})}^2}{{({\rho }^{+}+{\rho }^{-})}^2},\hspace{1em}\overline{R}=\frac{2{\rho }^{+}{\rho }^{-}}{{({\rho }^{+}+{\rho }^{-})}^2},$$ (5)

which contain the information about the polarity of the actin filament meshwork and which sum up to 1.

The integration kernel ϑ(t, x, y) introduced above can be written based on the density χ̄ as

$$\vartheta (t,x,y)=\frac{1}{2}\overline{\chi }(t,\frac{x+y}{2},\frac{y-x}{2}).$$ (6)

The distributions of myosin attached to parallel actin filaments satisfy the equations:

$$\{\begin{array}{c}{\partial }_t{\chi }^{\pm }+{\partial }_x((\mp V_m+{\upsilon }^{\pm }(t,x\pm \xi )){\chi }^{\pm })+{\partial }_{\xi }((V_m-{\upsilon }_{\text{tr}}){\chi }^{\pm })=0,\hfill \\ (V_m-{\upsilon }_{\text{tr}}){\chi }^{\pm }(t,x,0)=R^{\pm }{M}_{\text{off}},\hfill \end{array}$$ (7)

where transport in the physical space x is according to the sum of material velocity of actin filaments and the free moving velocity of myosin filaments which shifts them in the direction of the respective barbed end of actin filaments. Transport with respect to the relative position ξ, on the other hand, is with velocity V_m corrected by the effect of treadmilling which moves any fixed structure on actin filaments towards the pointed end.

Observe that the relative position ξ for myosin attached to parallel actin filaments has a slightly different meaning than in the case of the antiparallel actin filaments. While in the latter case, ξ = l/2 means that myosin is located at the pointed ends, in the case of parallel actin filaments, this means that myosin is located at the barbed ends. In both cases, ξ = l/2 is the value at which myosin slides off actin filaments’ ends, and therefore the total flux of myosin detaching from actin filaments is given by the equation:

$$M_{\text{off}}=\frac{{\upsilon }^{-}(t,x+l/2)+{\upsilon }_{\text{tr}}-({\upsilon }^{+}(t,x-l/2)-{\upsilon }_{\text{tr}})}{2}\overline{\chi }(t,x,l/2)++(V_m-{\upsilon }_{\text{tr}})({\chi }^{+}(t,x,l/2)+{\chi }^{-}(t,x,l/2)).$$

Let us note that a very important feature of the model is hidden behind math: in order to generate contraction, the treadmilling rate has to exceed a threshold, in which case overlapping antiparallel actin filaments are constantly remodeled into configurations where their pointed ends converge while barbed ends diverge from each other. Then, action of myosin that tends to bring together the barbed ends, on the average, pulls the overlapping antiparallel actin filament pairs together resulting in the net contraction.

2.1. Non-dimensionalisation

We scale the system of equations (1), (2), (3), (4), (7) as follows: x̃ = x/x₀ where x₀ is a characteristic length scale of the actomyosin bundle, for example, radius of the contractile ring. The microscopic spatial coordinate, naturally, scales as the actin filament length: ξ̃ = ξ/l. The approximations we derive below work in the limit l ≪ x₀. We use the free myosin velocity as the natural velocity scale, and so υ̃^± = υ^±/V_m, and t₀ = x₀/V_m becomes the time scale. Therefore, the rescaled time t̃ = t/t₀. The densities of actin filaments (number of filaments per unit length) are rescaled with the filament length: ρ̃^± = ρ^±l. The myosin densities (number of filaments per unit area (per physical unit length per unit length of the microscopic coordinate)) scale as follows: $\tilde{\overline{\chi }}=\overline{\chi }{x}_{0}l$, χ̃^± = χ^±x₀l. All these scales are chosen so that the dimensionless variables are of the order of unity. The contractile stress scales as: $\tilde{\eta }=\eta \frac{x_0{V}_m}{F_s}$. Our system is characterized by three dimensionless parameters: υ̃_tr = υ_tr/V_m, l̃ = l/x₀, σ̃ = σ/(F_sl̃). In what follows, in the dimensionless equations we omit the tildes; for details we refer to Appendix A.

The continuum equations for ρ^± (1) are not changed after the scaling, while (2) becomes

$$0=M^{\pm }+\eta C^{\pm },$$ (8)

where

$$M^{\pm }=-{\int }_{ℝ}\overline{\chi }(t,x\pm l\xi ,\xi )\times (\pm 1-\frac{{\upsilon }^{\pm }(t,x)-{\upsilon }^{\mp }(t,x\pm l2\xi )}{2})d\xi ,$$ (9)

$$C^{\pm }={\rho }^{\pm }(t,x)\sum _{n=-1,1}{\int }_{ℝ}A(\mathrm{\Delta }x)({\upsilon }^{\pm }(t,x)-{\upsilon }^n(t,x+l\mathrm{\Delta }x)){\rho }^n(t,x+l\mathrm{\Delta }x)d\mathrm{\Delta }x,$$ (10)

and where we applied the transformations (x − y)/2 = lξ and y − x = lΔx. Observe that after scaling we have A(Δx) = 1 − |Δx|. The equation for the contractile force (3) reads after scaling

$$\sigma =\overline{M}-\eta \overline{C},$$ (11)

where

$$\overline{M}={\int }_0^{1/2}{\int }_{-\xi }^{\xi }\overline{\chi }(t,z+l\mathrm{\Delta }z,\xi )\times \times (1-\frac{{\upsilon }^{+}(t,z+l(\mathrm{\Delta }z-\xi ))-{\upsilon }^{-}(t,z+l(\mathrm{\Delta }z+\xi ))}{2})d\mathrm{\Delta }zd\xi ,$$

$$\overline{C}={\int }_0^{\infty }A(\mathrm{\Delta }x){\int }_{-\mathrm{\Delta }x/2}^{\mathrm{\Delta }x/2}\sum _{m,n=-1,+1}{\rho }^m(t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2)){\rho }^n(t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2))\times \times ({\upsilon }^m(t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2))-{\upsilon }^n(t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2)))d\mathrm{\Delta }zd\mathrm{\Delta }x.$$

3. Perturbation approximation

It is convenient to rewrite the equations for total and differential densities and velocities of actin:

$$\upsilon =\frac{{\upsilon }^{+}+{\upsilon }^{-}}{2},\hspace{1em}\overline{\upsilon }=\frac{{\upsilon }^{+}-{\upsilon }^{-}}{2},\hspace{1em}\rho ={\rho }^{+}+{\rho }^{-},\hspace{1em}\overline{\rho }={\rho }^{+}-{\rho }^{-}.$$ (12)

Transport equations for ρ and ρ̄ have the form:

$$\{\begin{array}{c}{\partial }_t\rho +{\partial }_x(\upsilon \rho +(\overline{\upsilon }-{\upsilon }_{\text{tr}})\overline{\rho })=0,\hfill \\ {\partial }_t\overline{\rho }+{\partial }_x(\upsilon \overline{\rho }+(\overline{\upsilon }-{\upsilon }_{\text{tr}})\rho )=0.\hfill \end{array}$$ (13)

Below, we explain that we use the regime in which ῡ − υ_tr < 0. These equations are coupled to the sum and difference, respectively, of the two force balance equations (8):

$$0=(M^{+}+M^{-})+\eta (C^{+}+C^{-}),$$

$$0=(M^{+}-M^{-})+\eta (C^{+}-C^{-}).$$

We introduce the total density of myosin filaments χ = χ̄ + χ⁺ + χ⁻ and the macroscopic myosin densities

$$\mu ={\int }_0^{1/2}\chi (t,x,\xi )d\xi ,\hspace{1em}\overline{\mu }={\int }_0^{1/2}\overline{\chi }(t,x,\xi )d\xi ,\hspace{1em}{\mu }^{\pm }={\int }_0^{1/2}{\chi }^{\pm }(t,x,\xi )d\xi .$$

Furthermore, we introduce expansions of all the dependent quantities with respect to the small parameter l as l → 0 (actin filaments are much shorter than the length of the whole bundle) and use subscript 0 to denote the zeroth order approximations with respect to this small parameter, e.g. ρ = ρ₀ + O(l), ρ̄ = ρ̄₀ + O(l), υ = υ₀ + O(l), ῡ = ῡ₀ + O(l), χ̄ = χ̄₀ + O(l), μ = μ₀ + O(l), etc.

Our goal is to use perturbation theory in the limit l → 0 and to obtain a system of equations for ρ₀, ρ̄₀, υ₀, ῡ₀ and μ₀. The equations for ρ₀ and ρ̄₀ are (13) with the velocity fields υ₀ and ῡ₀. The derivation of the limit equations for μ₀, μ̄₀, ${\mu }_0^{\pm }$ can be found in Appendix A. In the limit, we obtain a transport differential equation for μ₀ and algebraic expressions which allow to obtain ${\mu }_0^{\pm }$ and μ̄₀ directly from μ₀ (see below). What we need for the derivation of the contractile stress in the limit is the fact that in this limit, χ̄₀ is a constant with respect to variable ξ, i.e. χ̄₀ (t, x, ξ) = χ̄₀ (t, x), which sets the expectation value for the myosin position relative to the actin filament coordinates:

$${\int }_0^{1/2}\xi {\overline{\chi }}_{0}d\xi ={\chi }_0\frac{1}{8}=\frac{1}{4}{\overline{\mu }}_0.$$ (14)

Here we focus on the limit equations (8) and (11). We expand (9) as follows:

$$M^{\pm }=-{\int }_{ℝ}(\overline{\chi }(t,x,\xi )\pm l\xi {\partial }_x\overline{\chi }(t,x,\xi ))\times \times (\pm 1-\frac{{\upsilon }^{\pm }(t,x)-{\upsilon }^{\mp }(t,x)\mp l2\xi {\partial }_x{\upsilon }^{\mp }(t,x)}{2})d\xi +O(l^2),=\mp {\int }_{ℝ}(\overline{\chi }(t,x,\xi )\pm l\xi {\partial }_x\overline{\chi }(t,x,\xi ))(1-\overline{\upsilon }+l\xi {\partial }_x{\upsilon }^{\mp }(t,x))d\xi +O(l^2),$$

and obtain the following asymptotic expansions,

$$M^{+}+M^{-}=-l{\int }_{ℝ}[2(-{\overline{\chi }}_0\xi {\partial }_x{\overline{\upsilon }}_0)+2\xi {\partial }_x{\overline{\chi }}_0(1-{\overline{\upsilon }}_0)]d\xi +O(l^2)=-2l\frac{d}{dx}{\int }_{ℝ}{\overline{\chi }}_0\xi (1-{\overline{\upsilon }}_0)d\xi +O(l^2)=-l\frac{1}{2}\frac{d}{dx}[{\overline{\mu }}_0(1-{\overline{\upsilon }}_0)]+O(l^2),$$

where we used (14) and

$$M^{+}-M^{-}=-2{\int }_{ℝ}{\overline{\chi }}_0(1-{\overline{\upsilon }}_0)d\xi +O(l)=-2{\overline{\mu }}_0(1-{\overline{\upsilon }}_0)+O(l).$$

We also obtain (see Appendix B):

$$C^{+}+C^{-}=-\frac{l^2}{12}{\partial }_x\left({\rho }_0^2{\partial }_x\right({\upsilon }_0+\frac{{\overline{\rho }}_0{\overline{\upsilon }}_0}{{\rho }_0}\left)\right)+O(l^4),$$

$$C^{+}-C^{-}={\overline{\upsilon }}_0({\rho }_0^2-{\overline{\rho }}_0^2)+O(l^2).$$

Together, these results imply that expanding (8), we obtain:

$$0=-\frac{l}{2}\frac{d}{dx}[{\overline{\mu }}_0(1-{\overline{\upsilon }}_0)]+O(l^2)-\eta \left[\frac{l^2}{12}{\partial }_x\right({\rho }_0^2{\partial }_x({\upsilon }_0+\frac{{\overline{\rho }}_0{\overline{\upsilon }}_0}{{\rho }_0}))+O(l^3)],$$ (15)

$$0=-2{\overline{\mu }}_0(1-{\overline{\upsilon }}_0)+O(l)+\eta [{\overline{\upsilon }}_0({\rho }_0^2-{\overline{\rho }}_0^2)+O(l^2)].$$ (16)

Note that equation (15), roughly speaking, describes the balance of myosin force with the shear force generated by crosslinking resistance to the shear-like deformations of the actin arrays. The second equation (16) is the balance of the myosin stress and viscous stress between sub-groups of actin filaments of the opposite polarity. There are two force-balance equations because of two subgroups of actin filaments. This system of equations is very involved, however, in the limit of short actin filament length and dense crosslinking, it simplifies greatly.

Namely, rather than considering constant parameter η independent of the filament length l (invariant number of crosslinkers per unit length), we consider the limit l → 0, ηl ~ 1. This limit means that we consider a constant average number of crosslinkers per filament as the filament length decreases, or, in other words, this is the limit of a very strong crosslinking. In what follows, we use the constant model parameter η̄ = ηl which has the meaning of characteristic viscous drag coefficient per filament (not per unit length). In this case, η → ∞ as l → 0, in the second equation, the second term dominates, so in the limit ${\overline{\upsilon }}_0({\rho }_0^2-{\overline{\rho }}_0^2)=0$ implies ῡ₀ = 0, since the factor $({\rho }_0^2-{\overline{\rho }}_0^2)$ can be zero only in a fully anisotropic actin filament bundle. Equality ῡ₀ = 0 means that in the limit of the dense crosslinking, relative movement of the antiparallel filaments relative to each other in the opposite direction is negligible. However, the slow shear displacement of the filaments is not negligible, because this shear originates from relative sliding of neighboring filaments overlapping only a little. Then, in the limit, (15) becomes:

$$0=-\frac{1}{2}\frac{d}{dx}{\overline{\mu }}_0-\frac{\overline{\eta }}{12}{\partial }_x({\rho }_0^2{\partial }_x{\upsilon }_0),$$

The limit of (11) in this case is (see Appendix B):

$$\sigma =\frac{1}{2}{\overline{\mu }}_0+\frac{\overline{\eta }}{12}{\rho }_0^2{\partial }_x{\upsilon }_0.$$

3.1. Asymptotic model for a closed actomyosin ring in the limit of strong crosslinking and short actin filaments

Returning to the dimensional variables, dropping subscript 0 and gathering all transport and force balance equations, we arrive at the asymptotic model:

$$\upsilon (L(t))=\upsilon (0)+\dot{L},$$ (17)

$$F_s\frac{l}{2}{\partial }_x(\overline{\alpha }\mu (t,x))+\overline{\eta }\frac{l}{12}{\partial }_x({\tilde{\rho }}^2{\partial }_x\upsilon )=0,$$ (18)

$$\sigma =F_s\frac{l}{2}\overline{\alpha }\mu +\overline{\eta }\frac{l}{12}{\tilde{\rho }}^2{\partial }_x\upsilon ,$$ (19)

$$\{\begin{array}{c}{\partial }_t\mu +{\partial }_x([\upsilon -V_m({\alpha }^{+}-{\alpha }^{-})]\mu ))=0,\hfill \\ {\partial }_t\rho +{\partial }_x(\upsilon \rho -{\upsilon }_{\text{tr}}\overline{\rho })=0,\hfill \\ {\partial }_t\overline{\rho }+{\partial }_x(\upsilon \overline{\rho }-{\upsilon }_{\text{tr}}\rho )=0,\hfill \end{array}$$

The transport equations are complemented by the periodic boundary conditions. We use the notation ρ̃ = lρ for the length density of actin filaments; this density is equivalent to what is called F-actin density in physical and biological literature. Note that (18) describes the balance of the active myosin and passive crosslinking viscous forces at each point along the actomyosin bundle. Effectively, this equation gives the resulting actin velocity in the bundle. This velocity is needed to solve three transport equations for three densities. Equation (19) gives the value of the contractile stress in the bundle, which is constant in space along the bundle, but not necessarily constant in time. Note that equations (18) and (19) are not independent: the local force is the derivative of the local stress, and so differentiation of (19) gives (18). Finally, note that our derivation results in the expression for the effective viscosity of the actin bundle equal to l(η̄/12)ρ̃², which is proportional to the square of the local actin density.

The coefficients α’s are given by formulas:

$${\alpha }^{\pm }=\frac{\frac{1}{2}{(\rho \pm \overline{\rho })}^2({\upsilon }_{\text{tr}}-{\overline{\upsilon }}_0)}{({\rho }^2+{\overline{\rho }}^2)({\upsilon }_{\text{tr}}-{\overline{\upsilon }}_0)+({\rho }^2+{\overline{\rho }}^2)(V_m-{\upsilon }_{\text{tr}})},$$ (20)

$$\overline{\alpha }=\frac{({\rho }^2-{\overline{\rho }}^2)(V_m-{\upsilon }_{\text{tr}})}{({\rho }^2+{\overline{\rho }}^2)({\upsilon }_{\text{tr}}-{\overline{\upsilon }}_0)+({\rho }^2-{\overline{\rho }}^2)(V_m-{\upsilon }_{\text{tr}})},$$ (21)

and satisfy the equality ᾱ+α⁺+α⁻ = 1. These important coefficients determine fractions of myosin associated with antiparallel actin filament pairs (ᾱ) and with parallel actin filament pairs of both orientations (α^±). These fractions are not constant but depend on actin densities, which leads to very nontrivial effects as described below.

4. General constraints on the contractile stress and rate of contraction

By integration of (19), we obtain the force-velocity relation:

$$\dot{L}=-\frac{6F_s}{\overline{\eta }}{\int }_0^L\frac{\overline{\alpha }\mu }{{\tilde{\rho }}^2}dx+\frac{12\sigma }{\overline{\eta }l}{\int }_0^L\frac{1}{{\tilde{\rho }}^2}dx.$$ (22)

Equation (22) predicts that the magnitude of the rate of contraction L̇(σ) decreases linearly with the magnitude of the contractile stress. The latter can be, for example, a certain constant given by resistance of the dividing cell cortex, and then the greater the given stress is, the slower is the rate of the contractile ring shrinking.

Two quantities are of special importance: stress developed by the actomyosin bundle under isometric conditions, and rate of contraction under zero external load, respectively:

$$\sigma =F_s\frac{l}{2}\frac{{\int }_0^L\frac{\overline{\alpha }\mu }{{\tilde{\rho }}^2}dx}{{\int }_0^L\frac{1}{{\tilde{\rho }}^2}dx},\hspace{1em}\dot{L}=-\frac{6F_s}{\overline{\eta }}{\int }_0^L\frac{\overline{\alpha }\mu }{{\tilde{\rho }}^2}dx.$$ (23)

Equation (23) has profound consequences for how much force the actomyosin bundle can generate in isometric condition, and how fast it can contract against zero load. First, the isometric stress is proportional to actin filament length. This result is easy to understand: effectively, the actomyosin bundle is a number of contractile units with the length of the order of l in series. The total stress is simply of the order of magnitude of the force developed in one such unit. The latter is proportional to the number of myosin motors working in parallel in one contractile unit, and this number, at given myosin density, is proportional to the actin filament length. Thus, if the cell needs a greater contractile stress, the filament length has to be increased. Second, the isometric stress is independent of the crosslinking density in the limit of this study. Third, the ratio of two integrals in expression for the stress in (23) can be interpreted as the probabilistic expectation for the myosin distribution in the bundle, such that the probability measure is equal to 1/ρ̃². According to this interpretation, in order to maximize the contractile stress, the cell has to concentrate myosin where the actin density is minimal. Indeed, in this case the least myosin action will be wasted on balancing effective local viscous shear of actin. The distribution of actin away from myosin does not affect the outcome. These conclusions, of course, are only valid if the actin density does not become so low that it becomes limiting for the myosin action (we do not consider such limit). As we will see below, myosin tends to aggregate together with actin, so by itself, the self-organization of the actomyosin bundle tends to decrease the contraction. The cell probably needs some special negative feedbacks to redistribute myosin into regions of the low actin density. The second of equations (23) states that the rate of zero-load contraction is independent of the actin filament length. Indeed, if the filaments are shorter, the contraction rate of each contractile unit is smaller, but the number of such units in series is greater. This rate increases proportionally to the bundle size, unlike the isometric stress: more contractile units in series add up to faster contraction, which is well-known from muscle mechanics [22]. Finally, intuitively, the denser the crosslinking and the denser the actin array is, the slower is the contraction rate.

The formulas for the contraction stress and rate become especially simple in the case of the space-homogeneous, isotropic actomyosin ring, which is especially important due to two factors. First, in many experiments the actin and myosin densities along the actomyosin bundles are, in fact, roughly constant [14] (it is much harder to measure actin polarity in dense arrays). Second, as we show below, in the absence of special additional feedbacks, such ring architecture is both the easiest to maintain, and optimal in terms of greatest possible contractile force. In this case, ρ⁺ = ρ⁻ and therefore α⁺ = α⁻ and $\overline{\alpha }=1-\frac{{\upsilon }_{\text{tr}}}{V_m}$, and by integration of (19) we obtain the force-velocity relation:

$$\sigma =\frac{F_s\mu l}{2}(1-\frac{{\upsilon }_{\text{tr}}}{V_m})+\frac{\overline{\eta }l{\tilde{\rho }}^2}{12}\frac{\dot{L}}{L}.$$

This relation results in the contractile force under isometric condition:

$$\sigma =\frac{F_s\mu l}{2}(1-\frac{{\upsilon }_{\text{tr}}}{V_m}),$$ (24)

and the differential equation for the ring length under zero external load:

$$\dot{L}=-\frac{6F_s\mu L(t)}{\overline{\eta }{\tilde{\rho }}^2}(1-\frac{{\upsilon }_{\text{tr}}}{V_m}).$$ (25)

Two nontrivial conclusions can be made from formulas (24) and (25). First, both, contraction stress and rate, are proportional to the factor (1 − υ_tr/V_m), suggesting that contraction is most efficient when the treadmilling rate is equal to zero. This seemingly contradicts the point we made above that the finite treadmilling rate is necessary for net contraction. However, when we are in the strong crosslinking limit, the relative sliding of the antiparallel actin filament pairs is very slow, and so even very slow treadmilling suffices for contraction. Clearly, there is the smallest finite treadmilling rate that has to be maintained; we estimate it in the Discussion. The reason this rate has to be as small as possible to maintain maximal contraction is that this is the condition for concentrating as much myosin as possible between the antiparallel actin filament pairs, where myosin actually contributes for contraction, instead of between the parallel actin filament pairs. Indeed, the faster the actin filaments treadmill, the longer it takes for myosin to reach the growing barbed ends of parallel actin filament pairs, slide off them and enter into the cytoplasmic pool.

Second, it was observed in many experimental systems, most notably in [23] that the rate of the ring contraction stays constant in time, and, remarkably, is proportional to the initial radius of the ring. It is also observed experimentally that the length density of actin, ρ̃, stays roughly constant during the contraction, meaning that actin is released from the ring with the rate tightly coupled to the ring radius by an as yet unidentified mechanism. In this regime, equation (25) suggests that the following two mechanisms could maintain a steady rate of contraction: One mechanism is such that actin filaments are released from the ring while the length distribution of actin filaments remains constant. Retaining all myosin filaments in the ring (as observed in one of the systems, [24]) during contraction implies that μL ~ const, and guarantees a constant rate of contraction.

The other mechanism could rely on releasing myosin from the ring keeping μ at a constant level (as observed in another system, [23]), but releasing actin from the ring by keeping their total number constant, yet by shortening actin filaments in a manner such that their length is proportional to the ring circumference, l ~ L. While both mechanisms would keep the contraction rate constant and proportional to the initial ring size, the contractile force (24) would behave differently. The contractile force would increase proportionally to the growth of myosin concentration in the first case, and it would decrease being proportional to filament length in the second case.

5. Linear stability analysis and numerical solutions

In this section we focus on the isometric case where the ring length is held constant, L̇ = 0. In addition, we add three factors that would be relatively trivial to consider in the derivation of the model, and so we did not include them until now for simplicity, but which affect model solutions significantly and in a way that makes the model much more realistic, as these factors are present in vitro and it in vivo. The first factor is effective viscous friction relative to the surface along which actin filaments slide [25]; this factor adds the term ζρυ into the force balance equation where ζ is the background friction coefficient. The second factor is the turnover of both actin and myosin due to ongoing complete disassembly of actin filaments in the ring and constant nucleation of nascent filaments, as well as the exchange of myosin between the ring and the cytoplasmic pools [26]. Respective terms are the reaction terms ~ κ(ρ₀ − ρ) where ρ is appropriate density, ρ₀ is the steady state level of this density, and κ is the respective turnover rate. Finally, we consider effective diffusion of both myosin and actin filaments. The former originates from molecular motors stepping occasionally backward [27]; the latter - from occasional disassembly events at the barbed ends and assembly at the pointer ends [28]. Respective terms in the transport equations have the form D∂_xxρ where D is the effective diffusion coefficient and ρ is the appropriate density. The modified model for the constant-length actomyosin ring reads:

$$\{\begin{array}{c}{\partial }_t\mu +{\partial }_x([\upsilon -V_m({\alpha }^{+}-{\alpha }^{-})]\mu )=D_m{\partial }_{xx}\mu +{\kappa }_m({\mu }_0-\mu ),\hfill \\ {\partial }_t\rho +{\partial }_x(\upsilon \rho -{\upsilon }_{\text{tr}}\overline{\rho })=D_a{\partial }_{xx}\rho +{\kappa }_a({\rho }_0-\rho ),\hfill \\ {\partial }_t\overline{\rho }+{\partial }_x(\upsilon \overline{\rho }-{\upsilon }_{\text{tr}}\rho )=D_a{\partial }_{xx}\overline{\rho }+{\kappa }_a({\overline{\rho }}_0-\overline{\rho }),\hfill \\ 0=\zeta \rho \upsilon -F_s\frac{l}{2}{\partial }_x(\overline{\alpha }\mu )-\overline{\eta }\frac{l}{12}{\partial }_x({\tilde{\rho }}^2{\partial }_x\upsilon ),\hfill \end{array}$$ (26)

together with initial conditions and periodic boundary conditions for the interval [0, L]. Parameters α are computed as given by (20). We compute the contractile stress using (23). Table 1 lists the model parameters. In what follows, the turnover rates κ_a and κ_m are generally assumed to be zero; only in the end of this section we discuss the effect of the turnover.

Table 1.

List of parameters and initial constant densities.

Description	Symbol	Value	Reference
length of actin filaments	l	6 µm	used in this study
density of actin filaments	ρ	2 µm−1	used in this study
density of myosin filaments	μ	2 µm−1	used in this study
Ring length	L	5 × 2π µm	used in this study
Treadmilling rate	υtr	0.1 µm s−1	[29]
Stall force for myosin filaments	Fs	5 pN	[30]
Free myosin velocity	Vm	0.5 µm s−1	[30]
Drag friction due to cross-linkers	η	~ 15 pN s µm−2	[31]
diffusion rate of F-actin	Da	~ 0.004 µm2 s−1	[32]
diffusion rate of myosin	Dm	~ 0.004 µm2 s−1	estimated in [33]
background friction	ζ	~ 10 – 100 pN s µm−1	same order of magnitude as [31]
F-actin turnover	κa	~ 0.01 – 0.1 s−1	[34]
Myosin filament turnover	κm	~ 0.01 – 0.1 s−1	estimated in [33]

5.1. Without treadmilling, actin and myosin aggregate into periodically spaced peaks

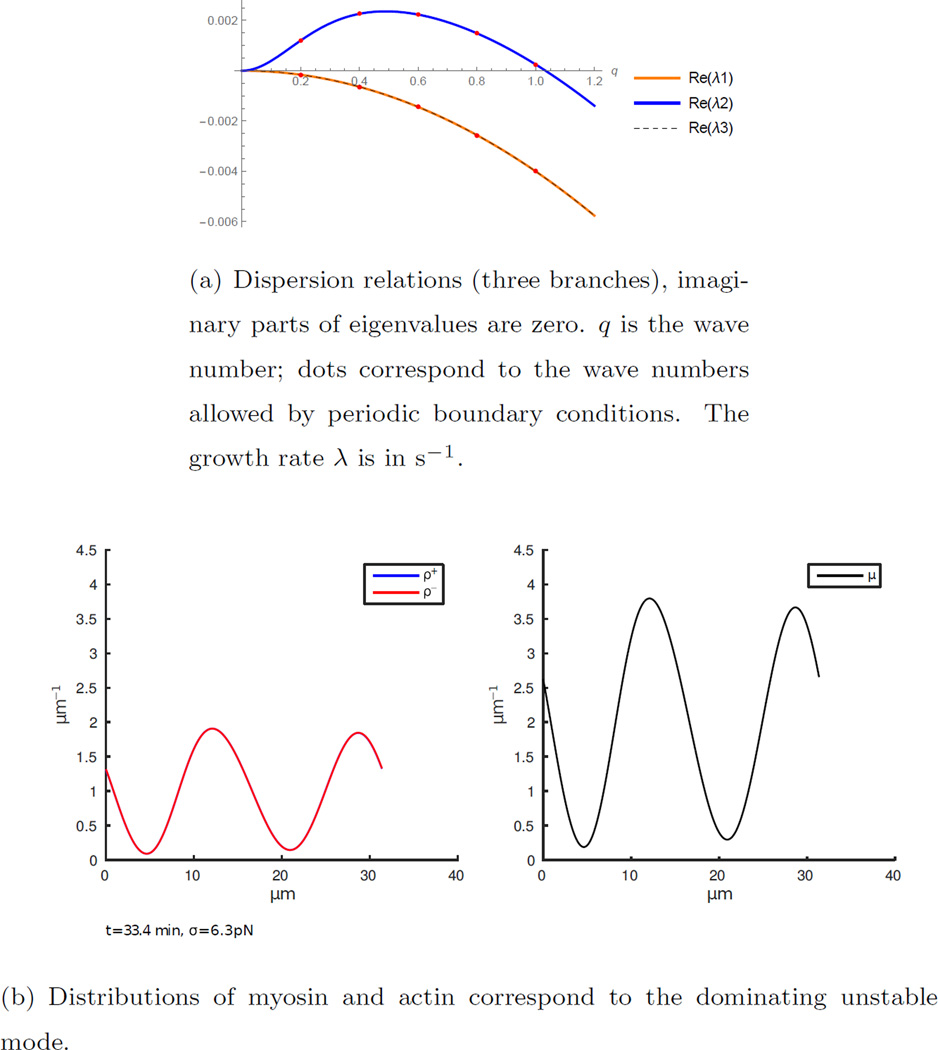
Linear stability analysis provides valuable insight into self-organization of the actomyosin bundle. It is easy to see that there is a simple steady state in which all densities are constant and velocity of actin and myosin is zero. Sine waves are the eigenfunctions of the linearized model (appendix section Appendix C). The analysis shows that myosin contraction destabilizes this state, while diffusion, friction, viscosity and turnover stabilize it. Furthermore, if average myosin density is higher than a complex expression, which is an increasing function of average actin density, diffusion and friction coefficients, crosslinking drag and turnover rate, the homogeneous state is destabilized. We start with the simplifying assumption of the negligible treadmilling rate υ_tr (it still has to be greater than the threshold, see Discussion, for contraction effect to work). Linear stability analysis (see appendix section Appendix C) in this case shows that eigenvalues of the linearized system are real and for the parameters listed in Table 1 they satisfy the dispersion relation shown in figure 2(a). Note that modes which are consistent with the length of the periodic domain are highlighted with points. The first five modes are unstable, and the second mode dominates. Numerical simulation shows that indeed this second mode evolves starting from constant densities plus small initial random perturbation (uniformly distributed random number added to the constant at every grid point). Myosin and action accumulate into two distinct, evenly spaced spots. During the simulation of the nonlinear model, accumulation at these spots continues until the numerical simulation cannot be continued due to ring disruption when the density of actin filaments approaches zero.

Figure 2.

In the absence of treadmilling (υ_tr = 0), myosin and actin accumulate at regularly spaced foci. The density profiles correspond to the dominating unstable mode.

Note that accumulation in this case is caused by myosin contracting the actin bundle against the viscous resistance of the bundle. The resulting actin flow not only concentrates actin, but also myosin itself, as both densities in the case without treadmilling satisfy the same equation and are transported exclusively by the actin flow. The characteristic spacing between the actomyosin peaks is of the order of the square root of the ratio of the effective crosslinking drag to the background friction drag, as was noted before [33, 35]. In our case, this length scale is $\sqrt{\eta \rho /10\zeta }{l}^2~10\mathrm{\mu }\mathrm{m}$. When background friction decreases, spacing between peaks increases, as is evident from figure 3.

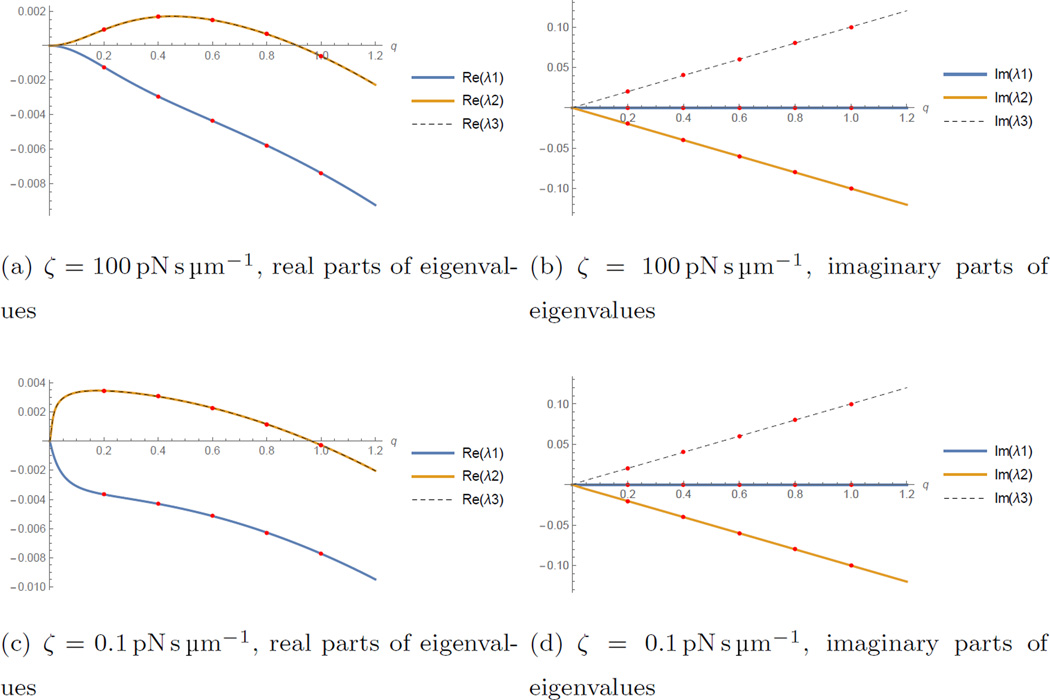
Figure 3.

Dispersion relations (three branches) show eigenvalues as functions of the wave number q in the case with stronger (ζ = 100 pN s µm⁻¹) and weaker friction (ζ = 0.1 pN s µm⁻¹). Dots mark the wavenumbers of modes which are consistent with the periodicity of the ring. The growth rate λ is in s⁻¹.

5.2. When actin treadmills, myosin peak surfs on a traveling actin peak leading to a loss of contractility

When the treadmilling rate is negligible, linear stability analysis accurately predicts solutions far from the bifurcation from the homogeneous solution. The general case with non-vanishing treadmilling rate is much more complex, as an unexpected pattern emerges far from the bifurcation.

The linear stability analysis for the parameter values shown in Table 1 shows that as in the case without treadmilling a band of lower wavenumbers is unstable while diffusion guarantees the stability of the higher wave numbers. In the (almost) absence of friction the lowest mode will be dominant (figure 3(c)). Higher modes become dominant with increased background friction (figure 3(a)).

The imaginary parts of the eigenvalues reveal directed transport of actin filaments and myosin thick filaments due to treadmilling and, depending on the polarity of the actin filament bundle, the free moving velocity of myosin motors. As both velocity fields add to the material velocity υ, damping of the imaginary parts of eigenvalues through friction is not expected.

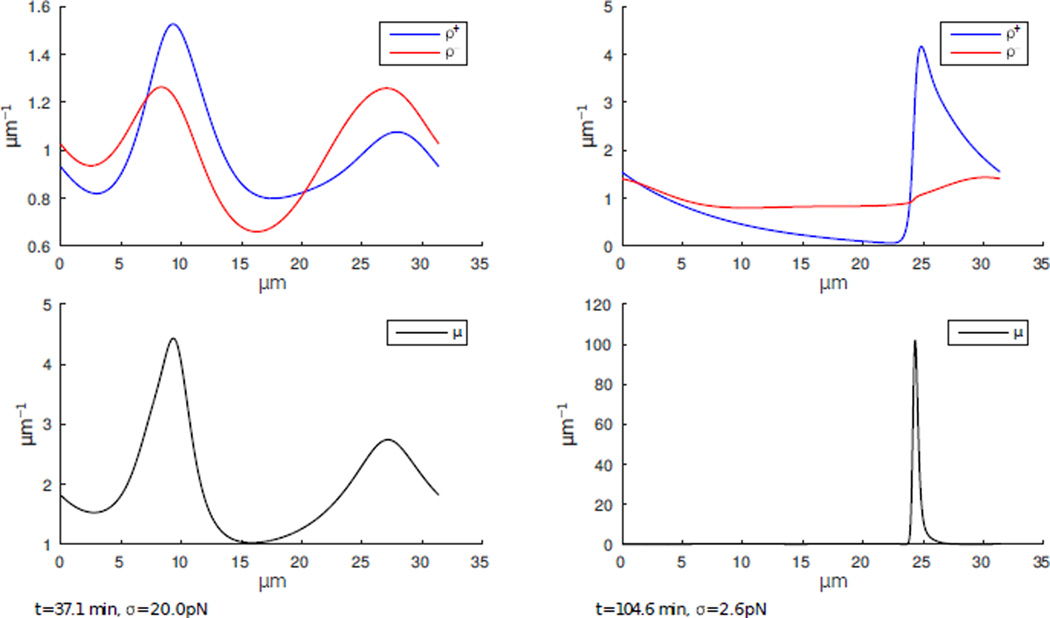
In figure 4 we show two simulation snapshots; the evolution of the densities can be gleaned from the supplemental movie. Initially, traveling sine waves evolve. Later, in the nonlinear regime, a highly nontrivial pattern emerges (figure 4(a)). Namely, the system converges to a state where only one of the two antiparallel families of actin filaments concentrates in one peak while actin filaments with the opposite polarity adopt a fairly uniform distribution (figure 4(b)). The evolved peak is a shock wave with sharp front. Simultaneously, myosin also concentrates at the actin traveling front and surfs together with the peak in actin density at a speed set by the treadmilling rate.

Figure 4.

Simulation of an actomyosin ring under isometric conditions starting from randomly perturbed initial constant distributions. Unstable sine waves develop initially. Distributions with one traveling actin peak of one polarity evolve. Myosin peak surfs together with the actin peak at treadmilling velocity. Actin filaments of the opposite polarity are distributed almost homogeneously.

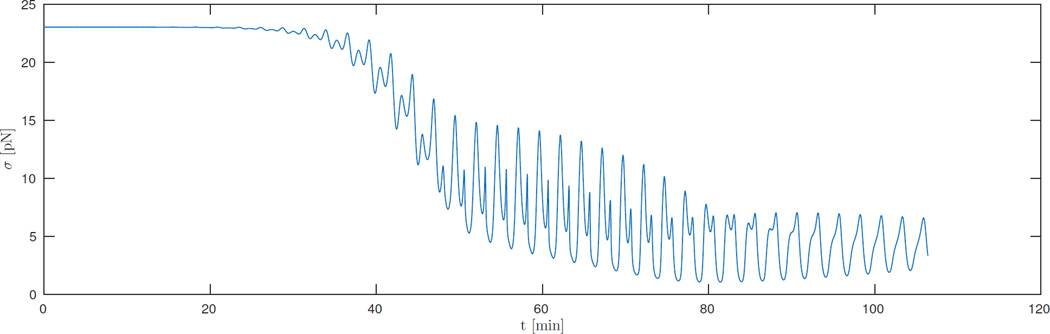
Observe that myosin co-localization with actin greatly attenuates the isometric contractile force, according to (23), leading to a massive drop in contractility (see figure 5). Higher frequency oscillations are caused by treadmilling rotations around the finite length actomyosin ring, whereas longer term decay of contractile force is caused by simultaneous myosin and F-actin accumulation.

Figure 5.

Isometric contractile force σ (according to (23)) as function of time for a simulation of an actomyosin ring under isometric conditions.

The explanation for this observed pattern is illustrated in a series of simulation snapshots in Appendix D. First, a few peaks of actin filaments of the same polarity evolve being condensed by myosin. These peaks compete for myosin; the winning peak becomes sharper and greater due to contraction, while the loosing peaks associated with less and less myosin eventually dissolve due to viscosity, diffusion and friction. Whenever two peaks in actin distributions of opposite polarity cross, similarly, the larger actin peak attracts an over-proportional fraction of myosin. This mechanism first promotes the co-localization of myosin with the highest peak in the actin distribution and finally leads to the emergence of one single peak in actin distribution. One of the main reasons for competition for myosin stems from the fact that myosin interacts with actin filament pairs, hense nonlinearities in the coefficients (20) which result in the winner-takes-all mechanism.

6. Actin and myosin turnover stabilizes the homogeneous steady state and maintains contractility

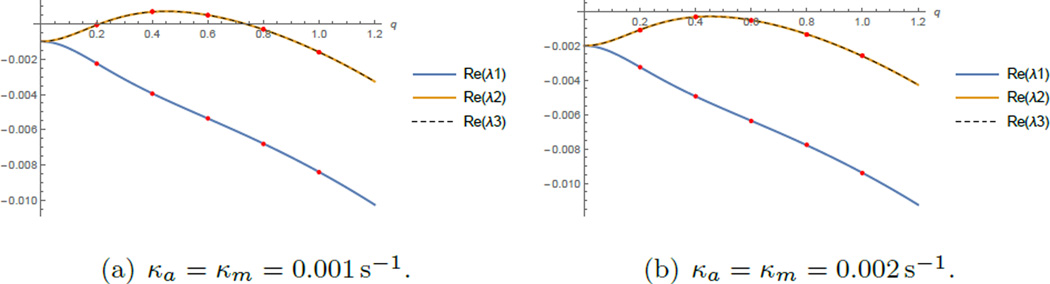
Finally, we consider the model with non-zero values of the turnover rates κ_a and κ_m. As can be seen from the linearized problem (see Appendix C) finite turnover rates κ_a = κ_m lower the dispersion relation by a constant. In figure 6(a) we show the results of the linear stability analysis at ρ ≡ ρ₀, ρ̄ = ρ̄₀ ≡ 0 and μ ≡ μ₀, where ρ₀ and μ₀ take the constant values listed in Table 1. With the turnover rates κ_a = κ_m = 0.001 s⁻¹, the first sinusoid mode becomes stable, while the 2nd and 3rd mode remain unstable. Simulations starting from randomly perturbed constant distributions, however, are governed by the same mechanism of pattern formation as without turnover, which leads to concentration of myosin in one peak surfing on a wave of F-actin.

Figure 6.

Turnover of myosin and F-actin lowers the real parts of eigenvalues. Dispersion relations (three branches) show eigenvalues as functions of the wave number q. Dots mark the wavenumbers of modes which are consistent with the periodicity of the ring. The growth rate λ is in s⁻¹. For κ_a = κ_m = 0.001 s⁻¹ some modes are still unstable, for higher turnover, κ_a = κ_m = 0.002 s⁻¹, all modes are stable.

Further increasing the turnover stabilizes the homogeneous steady state which we demonstrate in figure 6(b) with the parameters κ_a = κ_m = 0.002 s⁻¹. Simulations of the full model starting from perturbations of the homogeneous solution show perturbation’s decay and return to the homogeneous actomyosin distribution.

7. Discussion

Treadmilling rate υ_tr exceeding the velocity at which actin filaments are slid apart is crucial for contraction in the mechanism we suggest. In this regime, myosin is effectively shifted towards the pointed ends of overlapping antiparallel actin filaments, and then myosin tendency to glide towards the barbed ends keeps bringing the filament centers closer together. It is a remarkable result of the singular perturbation limit that the expectation value of myosin binding site positions along the actin filament (14) translates directly into the coefficient for the effective contractile stress, which is in agreement with conclusions in [36]. It is also striking that this coefficient for contractile stress is not affected by the actual value of the treadmilling rate in the limit of the strong crosslinking. Note that treadmilling by itself, without myosin processivity, would not lead to the contraction, because, after treadmilling, the random actin array remains random. However, processive myosin and fast enough treadmilling generate asymmetry - myosin between overlapping pointed ends but not between overlapping barbed ends -, that is the key to the contraction.

We found that in this limit, relative movement of the antiparallel filaments in the opposite direction is negligible. However, the slow shear displacement of the filaments is not negligible, because this shear originates from relative sliding of neighboring filaments overlapping only a little. In the limit, myosin works near stall, which is a very efficient way to develop a contractile stress, but which makes the rate of contraction slow.

We reached these conclusions under the assumption of myosin binding right at the center of overlapping filament pairs. This assumption, however, has been solely made to simplify the calculations. Allowing myosin to bind to actin filaments anywhere with equal probability would imply that the limiting microscopic density of myosin has the structure χ̄₀ = (ξ + 1/2)χ̄₀(t, x) which would change the expectation value in (14) to ${\int }_{-1/2}^{1/2}\xi {\overline{\chi }}_{0}d\xi /{\overline{\mu }}_0=1/6$ instead of 1/4. The contractile stress with this setup would then be F_sl/3ᾱ with additional modifications in the factor ᾱ which we did not explore. The general result, however, is still net contraction due to myosin working predominantly near the overlapping pointed ends.

One of the highly nontrivial modeling predictions is that the treadmilling has to be as slow as possible for greater contractile stress. However, the treadmilling rate cannot be zero, because the contraction does not work in this limit. Therefore, there is an optimal treadmilling rate, which can be estimated as follows. In the perturbation limit, the rate of antiparallel sliding ῡ vanishes and therefore even considering very small values of υ_tr is consistent with the basic modeling assumption. Realistically though, the contraction mechanism requires a positive treadmilling rate dominating the velocity at which anti-parallel filaments slide apart. Equation (16) suggests that this velocity is of first order in l. Note that there are no derivatives of ῡ, etc. in what would be the first order terms of the right hand side of (16) since odd moments of A vanish (see Appendix B). Therefore it holds that $\overline{\upsilon }=l2{\overline{\mu }}_0/(\overline{\eta }({\rho }_0^2-{\overline{\rho }}_0^2))+O(l^2)$. In dimensional units, the first order term reads $\overline{\upsilon }\approx 2F_s{\overline{\mu }}_0/(\eta l^2({\rho }_0^2-{\overline{\rho }}_0^2))$ which represents the lower threshold value for the rate of treadmilling at which contraction works, and which hense is the optimal rate for greater contractile stress. Note that treadmilling in vitro - simultaneous equal assembly of the barbed and disassembly of the pointed ends - is slow. However, there are many examples in the biological literature showing that in vivo accessory proteins (formins and cofilin being the most important ones) accelerate the effective treadmilling so that the barbed ends grow rapidly, while the pointed ends disassemble, likely by severing of the old parts of the filaments [37, 36, 7, 34].

The model makes a number of useful predictions. We found that isometric stress is not proportional to the length of the bundle/ring, similar to the well-known result for muscle, and that the stress is proportional to the actin filament length, as far as our limit works. The rate of contraction, on the other hand, is independent of the filament length but decreases with actin and crosslinking densities. We derive the formula for macroscopic actin bundle viscosity from microscopic considerations.

An interesting model prediction is that to develop maximal contraction stress, myosin has to be concentrated at location(s) of the lowest actin density, as far as the actin density does not become force-limiting. In the absence of special feedback that tends to anticorrelate myosin and actin, the best the cell can do is probably to keep both actin and myosin densities homogeneous, which can be achieved simply by turning actin and myosin over with a sufficient rate. In this homogeneous regime we found two ways to keep the contraction rate constant and proportional to the initial radius of the ring or length of the bundle.

It is of interest to estimate how efficient the proposed way of developing contractile stress is. The maximal contractile force with optimal sarcomeric organization is F_sMl/L where M is the number of myosin filaments ([13]). In the case of our model, the maximal contractile force of a homogeneous contractile ring is given by (24), where μ = M/L. In our calculation we have $(1-\frac{{\upsilon }_{\text{tr}}}{V_m})=4/5$, so we estimate the efficiency by (50 × 4/5)% = 40% compared to the maximal possible stress in the ideally organized sarcomeric configuration.

We found that in the limit of very slow treadmilling, myosin and actin aggregate into periodic structure (having nothing to do with sarcomeres). This aggregation dampens contraction. The number of aggregates decreases with smaller background friction. Similar aggregation was observed in the experiment [38]. We also predict that a highly nontrivial pattern evolves when treadmilling is fast enough. Due to the effective competition between actin peaks for myosin, one actin peak consisting of filaments of the same polarity wins. Myosin won by this peak maintains a highly aggregated shock-wave shape which travels with the treadmilling speed. Myosin also aggregates into the front of this actin wave and surfs on the peak of actin; meanwhile, the contractile stress drops. Recently, the traveling wave of actomyosin was experimentally observed for the first time in [39]. It remains to be investigated if the mechanism of this observed wave is the same as the one our model suggests. Another great open question for the future is how the mechanism of contraction proposed here works together with the other mechanisms discussed in the Introduction, or how the cell does choose which mechanism to use when.

Multiscale perturbation theory leads to a continuum model for the actomyosin array.

Actin treadmilling is essential for contraction.

Depending on parameters, periodic or traveling wave patterns evolve in the system.

Two regimes for contraction with constant rate are identified.

For maximal contraction, myosin has to concentrate where actin density is minimal.

Appendix A

Perturbation limit for the distribution of molecular motors

Applying the scaling introduced in section 3 the system (4), (7) reads

$$\{\begin{array}{c}{\partial }_t\overline{\chi }+{\partial }_x\left(\frac{{\upsilon }^{+}(t,x-l\xi )+{\upsilon }^{-}(t,x+l\xi )}{2}\overline{\chi }\right)++\frac{1}{l}{\partial }_{\xi }\left(\frac{{\upsilon }^{+}(t,x+l\xi )+{\upsilon }_{\text{tr}}-({\upsilon }^{+}(t,x-l\xi )-{\upsilon }_{\text{tr}})}{2}\overline{\chi }\right)=0,\hfill \\ \frac{{\upsilon }^{-}(t,x)+{\upsilon }_{\text{tr}}-({\upsilon }^{+}(t,x)-{\upsilon }_{\text{tr}})}{2}\overline{\chi }(t,x,0)=\overline{R}{M}_{\text{off}},\hfill \end{array}$$ (A.1)

$$\{\begin{array}{c}{\partial }_t{\chi }^{\pm }+{\partial }_x((\mp V_m+{\upsilon }^{\pm }(t,x\pm \xi )){\chi }^{\pm })+\frac{1}{l}{\partial }_{\xi }((V_m-{\upsilon }_{\text{tr}}){\chi }^{\pm })=0,\hfill \\ (V_m-{\upsilon }_{\text{tr}}){\chi }^{\pm }(t,x,0)=R^{\pm }{M}_{\text{off}},\hfill \end{array}$$ (A.2)

where

$$M^{\text{off}}=\frac{{\upsilon }^{-}(t,x+1/2l)+{\upsilon }_{\text{tr}}-({\upsilon }^{+}(t,x-1/2l)-{\upsilon }_{\text{tr}})}{2}\overline{\chi }(t,x,1/2)++(V_m-{\upsilon }_{\text{tr}})({\chi }^{+}(t,x,1/2)+{\chi }^{-}(t,x,1/2)).$$

We apply Taylor expansions, use the notation (12) and develop the truncated expansions, e.g. υ = υ₀ + lυ₁ + O(l²), etc., to obtain:

$$\{\begin{array}{c}{\partial }_t{\overline{\chi }}_0+{\partial }_x({\upsilon }_0{\overline{\chi }}_0)++\frac{1}{l}{\partial }_{\xi }((-{\overline{\upsilon }}_0-l{\overline{\upsilon }}_1+l\xi {\partial }_x{\upsilon }_0+{\upsilon }_{\text{tr}})({\overline{\chi }}_0+l{\overline{\chi }}_1))+O(l)=0,\hfill \\ (-{\overline{\upsilon }}_0-l{\overline{\upsilon }}_1+{\upsilon }_{\text{tr}}))({\overline{\chi }}_0(t,x,0)+l{\overline{\chi }}_1(t,x,0))=R(M_0^{\text{off}}+l{M}_1^{\text{off}})+O(l^2),\hfill \end{array}$$

$$\{\begin{array}{c}{\partial }_t{\chi }^{\pm }+{\partial }_x((\mp V_m+{\upsilon }_0\pm {\overline{\upsilon }}_0){\chi }_0^{\pm })+\frac{1}{l}{\partial }_{\xi }((V_m-{\upsilon }_{\text{tr}})({\chi }_0^{\pm }+l{\overline{\chi }}_1^{\pm }))+O(l)=0,\hfill \\ (V_m-{\upsilon }_{\text{tr}})({\chi }_0^{\pm }(t,x,0)+l{\chi }_1^{\pm }(t,x,0))=R^{\pm }(M_0^{\text{off}}+l{M}_1^{\text{off}})+O(l^2),\hfill \end{array}$$

where

$$M_0^{\text{off}}=(-{\overline{\upsilon }}_0+{\upsilon }_{\text{tr}}){\overline{\chi }}_0(t,x,1/2)+(V_m-{\upsilon }_{\text{tr}})({\chi }_0^{+}(t,x,1/2)+{\chi }_0^{-}(t,x,1/2)),$$

$$M_1^{\text{off}}=(-{\overline{\upsilon }}_1+1/2{\partial }_x{\upsilon }_0){\overline{\chi }}_0(t,x,1/2)+(-{\overline{\upsilon }}_0+{\upsilon }_{\text{tr}}){\overline{\chi }}_1(t,x,1/2)++(V_m-{\upsilon }_{\text{tr}})({\chi }_1^{+}(t,x,1/2)+{\chi }_1^{-}(t,x,1/2)).$$

The equations of order 1/l are

$$\{\begin{array}{c}{\partial }_{\xi }((-{\overline{\upsilon }}_0+{\upsilon }_{\text{tr}})){\overline{\chi }}_0)=0,\hfill \\ ({\upsilon }_{\text{tr}}-{\overline{\upsilon }}_0){\overline{\chi }}_0(t,x,0)=R{M}_0^{\text{off}},\hfill \end{array}$$

and

$$\{\begin{array}{c}{\partial }_{\xi }((V_m-{\upsilon }_{\text{tr}}){\chi }_0^{\pm })=0,\hfill \\ (V_m-{\upsilon }_{\text{tr}}){\chi }_0^{\pm }(t,x,0)=R^{\pm }{M}_0^{\text{off}}.\hfill \end{array}$$

Using equality ${\chi }_0={\overline{\chi }}_0+{\chi }_0^{+}+{\chi }_0^{-}$ and the fact that all these quantities are constant in ξ implies that χ₀ = χ₀ (t, x) and ${\mu }_0(t,x)={\int }_0^{1/2}{\chi }_{0}d\xi =\frac{1}{2}{\chi }_0$, and furthermore

$${\overline{\chi }}_0=\overline{\alpha }{\chi }_0,\hspace{1em}{\chi }_0^{\pm }={\alpha }^{\pm }{\chi }_0,$$

where

$${\alpha }^{\pm }=\frac{{({\rho }^{\pm })}^2({\upsilon }_{\text{tr}}-{\overline{\upsilon }}_0)}{({({\rho }^{+})}^2-{({\rho }^{-})}^2)({\upsilon }_{\text{tr}}-{\overline{\upsilon }}_0)+2{\rho }^{+}{\rho }^{-}(V_m-{\upsilon }_{\text{tr}})},$$

$$\overline{\alpha }=\frac{2{\rho }^{+}{\rho }^{-}(V_m-{\upsilon }_{\text{tr}})}{({({\rho }^{+})}^2+{({\rho }^{-})}^2)({\upsilon }_{\text{tr}}-{\overline{\upsilon }}_0)+2{\rho }^{+}{\rho }^{-}(V_m-{\upsilon }_{\text{tr}})},$$

and ᾱ + α⁺ + α⁻ = 1. Integrating the equations systems of order l⁰ and adding them up yields

$${\partial }_t({\mu }_0+{\mu }_0^{+}+{\mu }_0^{-})+{\partial }_x({\upsilon }_0{\mu }_0+{\upsilon }_0^{+}{\mu }_0^{+}+{\upsilon }_0^{-}{\mu }_0^{-}+V_m({\mu }_0^{-}-{\mu }_0^{+})))=0,$$

which, using the notation ${\mu }_0={\overline{\mu }}_0+{\mu }_0^{+}+{\mu }_0^{-}$, becomes

$${\partial }_t{\mu }_0+{\partial }_x([{\upsilon }_0-(V_m-{\overline{\upsilon }}_0)({\alpha }^{+}-{\alpha }^{-})]{\mu }_0)=0.$$

Appendix B

Asymptotic limits for the cross-linking related terms

We define

$$I^m=\sum _{n=-1,1}({\upsilon }^m(t,x)-{\upsilon }^n(t,y)){\rho }^m(t,x){\rho }^n(t,y),$$

and write υ^m = υ + m ῡ and ρ^m = (ρ + m ρ̄)/2 for any index m = −1, +1 and find that

$$I^{+}+I^{-}=(\upsilon (t,x)-\upsilon (t,y))\rho (t,y)\rho (t,x)--\overline{\upsilon }(t,y)\overline{\rho }(t,y)\rho (t,x)+\overline{\upsilon }(t,x)\rho (t,y)\overline{\rho }(t,x),$$ (B.1)

$$I^{+}-I^{-}=4(\upsilon (t,x)-\upsilon (t,y))\rho (t,y)\overline{\rho }(t,x)++(\overline{\upsilon }(t,x)\rho (t,y)\rho (t,x)-\overline{\upsilon }(t,y)\overline{\rho }(t,x)\overline{\rho }(t,y)).$$ (B.2)

Observe that moments of the length of the overlapping region A(Δx) (see figure B.7), where Δx is the distance between the two center points of overlapping actin filaments, are given by:

$${\int }_{-\infty }^{\infty }A(\mathrm{\Delta }x)d\mathrm{\Delta }x=l^2,$$

$${\int }_{-\infty }^{\infty }A(\mathrm{\Delta }x)\mathrm{\Delta }xd\mathrm{\Delta }x=0,$$ (B.3)

$${\int }_{-\infty }^{\infty }A(\mathrm{\Delta }x)\mathrm{\Delta }{x}^{2}d\mathrm{\Delta }x=\frac{l^4}{6},$$

$${\int }_{-\infty }^{\infty }A(\mathrm{\Delta }x)\mathrm{\Delta }{x}^{3}d\mathrm{\Delta }x=0,\text{ etc}.$$

Figure B.7.

Function A(Δx) = l − |Δx|.

Using (B.1), we obtain:

$$C^{+}+C^{-}={\int }_{ℝ}A(\mathrm{\Delta }x)(\upsilon (t,x)-\upsilon (t,x+l\mathrm{\Delta }x))\rho (t,x+l\mathrm{\Delta }x)\rho (t,x)d\mathrm{\Delta }x++{\int }_{ℝ}A(\mathrm{\Delta }x)(-\overline{\upsilon }(t,x+l\mathrm{\Delta }x))\overline{\rho }(t,x+l\mathrm{\Delta }x)\rho (t,x)d\mathrm{\Delta }x++{\int }_{ℝ}A(\mathrm{\Delta }x)(\overline{\upsilon }(t,x))\rho (t,x+l\mathrm{\Delta }x)\overline{\rho }(t,x)d\mathrm{\Delta }x.$$

Applying Taylor expansions, we conclude:

$${\int }_{ℝ}A(\mathrm{\Delta }x)(\upsilon (t,x)-\upsilon (t,x+l\mathrm{\Delta }x))\rho (t,x+l\mathrm{\Delta }x)\rho (t,x)d\mathrm{\Delta }x=={\int }_{ℝ}A(\mathrm{\Delta }x)\left[\right(-l\mathrm{\Delta }x{\partial }_x\upsilon (t,x)-\frac{{(l\mathrm{\Delta }x)}^2}{2}{\partial }_{xx}\upsilon (t,x))(\rho (t,x)+l\mathrm{\Delta }x{\partial }_x\rho (t,x))]\times \times \rho (t,x)d\mathrm{\Delta }x+O(l^4)=\frac{l^2}{6}\left[\right(-{\partial }_x\upsilon (t,x){\partial }_x\rho (t,x)-\rho (t,x)\frac{1}{2}{\partial }_{xx}\upsilon (t,x)\left)\right]\rho (t,x)+O(l^4)==-\frac{l^2}{12}{\partial }_x({\rho }_0^2{\partial }_x{\upsilon }_0)+O(l^3)$$

as l → 0, where we used (B.3). Observe that although odd moments of A vanish, we get expressions of order l³ from the expansions of υ = υ₀ +lυ₁ + …, etc. We also obtain

$${\int }_{ℝ}A(\mathrm{\Delta }x)[\overline{\upsilon }(t,x)\rho (t,x+l\mathrm{\Delta }x)\overline{\rho }(t,x)-\overline{\upsilon }(t,x+l\mathrm{\Delta }x)\overline{\rho }(t,x+l\mathrm{\Delta }x)\rho (t,x)]d\mathrm{\Delta }x==(\frac{l^2}{12}{\overline{\rho }}_0{\overline{\upsilon }}_0{\partial }_{xx}{\rho }_0-\frac{l^2}{12}{\rho }_0{\partial }_{xx}({\overline{\rho }}_0{\overline{\upsilon }}_0))+O(l^3)$$

as l → 0, which implies that

$$C^{+}+C^{-}=-\frac{l^2}{12}{\partial }_x\left({\rho }_0^2{\partial }_x\right({\upsilon }_0+\frac{{\overline{\rho }}_0{\overline{\upsilon }}_0}{{\rho }_0}\left)\right)+O(l^3).$$

Similarly, using (B.2), Taylor expansions and (B.3), we obtain

$$C^{+}-C^{-}=4{\int }_{ℝ}A(\mathrm{\Delta }x)(\upsilon (t,x)-\upsilon (t,x+l\mathrm{\Delta }x))\rho (t,x+l\mathrm{\Delta }x)\overline{\rho }(t,x)d\mathrm{\Delta }x++{\int }_{ℝ}A(\mathrm{\Delta }x)(\overline{\upsilon }(t,x)\rho (t,x+l\mathrm{\Delta }x)\rho (t,x)-\overline{\upsilon }(t,x+l\mathrm{\Delta }x)\overline{\rho }(t,x)\overline{\rho }(t,y))d\mathrm{\Delta }x=={\overline{\upsilon }}_0({\rho }_0^2-{\overline{\rho }}_0^2)+O(l^1)$$

as l → 0.

Using (B.1), we also find that

$$\overline{C}={\int }_0^{\infty }A(\mathrm{\Delta }x){\int }_{-\mathrm{\Delta }x/2}^{\mathrm{\Delta }x/2}[(\upsilon (t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2))-\upsilon (t,z+l(\mathrm{\Delta }z+\mathrm{\Delta }x/2)))\times \times \rho (t,z+l(\mathrm{\Delta }z+\mathrm{\Delta }x/2))\rho (t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2))++(-\overline{\upsilon }(t,z+l(\mathrm{\Delta }z+\mathrm{\Delta }x/2)))\overline{\rho }(t,z+l(\mathrm{\Delta }z+\mathrm{\Delta }x/2))\rho (t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2))++(\overline{\upsilon }(t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2)))\rho (t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2))\overline{\rho }(t,z+l(\mathrm{\Delta }z-\mathrm{\Delta }x/2))]d\mathrm{\Delta }zd\mathrm{\Delta }x.$$

Applying Taylor expansions at x = z and using ${\int }_{-\mathrm{\Delta }x/2}^{\mathrm{\Delta }x/2}\mathrm{\Delta }xd\mathrm{\Delta }z={(\mathrm{\Delta }x)}^2$ as well as ${\int }_{-\mathrm{\Delta }x/2}^{\mathrm{\Delta }x/2}\mathrm{\Delta }zd\mathrm{\Delta }z=0$, we obtain:

$$\overline{C}=l{\int }_0^{\infty }A(\mathrm{\Delta }x)[-{(\mathrm{\Delta }x)}^2{\partial }_x\upsilon (t,z)\rho {(t,z)}^2-{(\mathrm{\Delta }x)}^2{\partial }_x\overline{\upsilon }(t,z)\overline{\rho }(t,z)\rho (t,z)--\overline{\upsilon }(t,z){(\mathrm{\Delta }x)}^2{\partial }_x\overline{\rho }(t,z)\rho (t,z)+\overline{\upsilon }(t,z)\overline{\rho }(t,z){(\mathrm{\Delta }x)}^2{\partial }_x\rho (t,z)+O({(\mathrm{\Delta }x)}^3)]d\mathrm{\Delta }x.$$

Finally, using ${\int }_0^{\infty }A(\mathrm{\Delta }x){(\mathrm{\Delta }x)}^{2}d\mathrm{\Delta }x=1/12$, we conclude that:

$$\overline{C}=-l\frac{1}{12}\rho {(t,z)}^2{\partial }_x(\upsilon (t,z)+\frac{\overline{\upsilon }(t,z)\overline{\rho }(t,z)}{\rho (t,z)})+O(l^2).$$

Appendix C

Linear stability analysis

We apply linear stability analysis to analyze the system (26) linearized with respect to the space-homogeneous steady state, in which υ ≡ 0, ρ̄ ≡ 0, μ ≡ μ₀, ρ ≡ ρ₀. Observe that in this case α⁺ − α⁻ = 0 and $\overline{\alpha }=1-\frac{{\upsilon }_{\text{tr}}}{V_m}$. The variations of these coefficients at the homogeneous steady state are

$${\delta ({\alpha }^{+}-{\alpha }^{-})|}_{\overline{\rho }=0}=\frac{2}{\rho }\frac{{\upsilon }_{\text{tr}}}{V_m}\delta \overline{\rho }\text{ and }{\delta \overline{\alpha }|}_{\overline{\rho }=0}=0.$$

Linearization of (26) implies that

$$\{\begin{array}{c}{\partial }_t\mu +{\partial }_x\left(\right[\delta \upsilon -{\upsilon }_{\text{tr}}\frac{2}{\rho }\delta \overline{\rho }\left]\mu \right)=-{\kappa }_m\delta \mu +D_m{\partial }_{xx}\delta \mu ,\hfill \\ {\partial }_t\delta \rho +{\partial }_x(\delta \upsilon \rho -{\upsilon }_{\text{tr}}\delta \overline{\rho })=-{\kappa }_a\delta \rho +D{\partial }_{xx}\delta \rho ,\hfill \\ {\partial }_t\delta \overline{\rho }+{\partial }_x(-{\upsilon }_{\text{tr}}\delta \rho )=-{\kappa }_a\delta \overline{\rho }+D{\partial }_{xx}\delta \overline{\rho },\hfill \end{array}$$

$$\{\begin{array}{c}0=\zeta \rho \delta \upsilon -F_s\overline{\alpha }{\partial }_x\delta \mu -\hat{\eta }{\partial }_x({\rho }^2{\partial }_x\delta \upsilon ),\hfill \\ \delta \upsilon (L(t))=\delta \upsilon (0),\hfill \end{array}$$

where we used the notation η̂ = ηl³/6.

Setting δυ = V e^λte^iqx, δρ = Re^λte^iqx, δρ̄ = R̄e^λte^iqx and δμ = M e^λte^iqx, we obtain

$$\{\begin{array}{c}\lambda M+iq(V-{\upsilon }_{\text{tr}}\frac{2}{\rho }\overline{R})\overline{\mu }=-{\kappa }_{m}M-q^2{D}_{m}M,\hfill \\ \lambda R+iq(V\rho -{\upsilon }_{\text{tr}}\overline{R})=-{\kappa }_{a}R-q^{2}DR,\hfill \\ \lambda \overline{R}-iq{\upsilon }_{\text{tr}}R=-{\kappa }_a\overline{R}-q^{2}D\overline{R},\hfill \end{array}$$

and

$$0=\zeta \rho V-F_s\overline{\alpha }iqM+\hat{\eta }{q}^2{\rho }^{2}V,$$

which implies that

$$V=iq\frac{1}{\rho }\frac{F_s\overline{\alpha }}{\zeta +q^2\rho \hat{\eta }}M.$$

Thus, the linearized system reads in matrix notation:

$$\left(\begin{array}{ccc}\hfill \lambda -\frac{\overline{\mu }}{\rho }\frac{q^2{F}_s\alpha }{\zeta +q^2\rho \hat{\eta }}+{\kappa }_m+q^2{D}_m\hfill & \hfill 0\hfill & \hfill -iq{\upsilon }_{\text{tr}}\overline{\mu }\frac{2}{\rho }\hfill \\ \hfill \frac{-q^2{F}_s\overline{\alpha }}{\zeta +q^2\rho \hat{\eta }}\hfill & \hfill \lambda +{\kappa }_a+q^{2}D\hfill & \hfill -iq{\upsilon }_{\text{tr}}\hfill \\ \hfill 0\hfill & \hfill -iq{\upsilon }_{\text{tr}}\hfill & \hfill \lambda +{\kappa }_a+q^{2}D\hfill \end{array}\right)\left(\begin{array}{c}\hfill M\hfill \\ \hfill R\hfill \\ \hfill \overline{R}\hfill \end{array}\right)=0,$$

from which we obtain the dispersion relation numerically.

Appendix D

Myosin surfing on the F-actin wave

In the simulation visualized in figure D.8, we used symmetric initial conditions in which actin filaments of both polarities and also myosin densities had peaks at the center point of the simulation domain. We set the initial densities such that the height of the peak of barbed end-forward actin filaments was exactly twice the height of the peak of pointed end-forward actin filaments (widths of the peak were the same). Simulation during only a short time interval shows that as the two peaks, driven by treadmilling, move apart, the peak in myosin is split into two parts, which move together with the two actin peaks. Those peaks in myosin distribution literally surf on the actin waves. In each frame, we measure the content of myosin in its left and in its right peak and we compute the ratio. The striking observation is that this ratio, which is 2.33 in the third frame, is well above the size ratio of 2 between the size of the two actin peaks.

Figure D.8.

Numerical test to illustrate the tendency of a large F-actin peak to capture an over-proportionally large amount of myosin when colliding with and passing through a smaller F-actin peak.

This implies that at every crossing of two actin peaks, each of which is accompanied by a peak in myosin density, an exchange takes place in which a significant amount of myosin is taken over by the larger actin peak. This mechanism leads to the co-localization of myosin density with the highest peaks in the actin distribution so that finally one single myosin peak emerges. Myosin aggregates actin, so a single actin peak emerges as well. This explains the disappearance of higher modes in the early distributions of actin and myosin, and this also explains the fact that in the long time limit we always observe the concentration of myosin in one single peak accompanying one pronounced peak in actin distribution.