Dynamics inside the cancer cell attractor reveal cell heterogeneity, limits of stability, and escape

Significance

It has been proposed, based on theory of complex gene regulatory networks, that cell types, including cancer cells, represent attractor states of the network dynamics. Here, we characterize for the first time, to our knowledge, the detailed dynamics of a cancer cell attractor at single-cell resolution. The results provide quantitative knowledge on nongenetic intercellular heterogeneity and its dynamics within an isogenic cell population of cancerous cells, affording insights at a previously unidentified level of resolution between molecular pathways and macroscopic tumor behaviors. This new dimension of characterizing tumor cells might impact design of future rational cancer therapies by taking into account the dynamic robustness and high volatility of a heterogeneous cancer cell population.

Abstract

The observed intercellular heterogeneity within a clonal cell population can be mapped as dynamical states clustered around an attractor point in gene expression space, owing to a balance between homeostatic forces and stochastic fluctuations. These dynamics have led to the cancer cell attractor conceptual model, with implications for both carcinogenesis and new therapeutic concepts. Immortalized and malignant EBV-carrying B-cell lines were used to explore this model and characterize the detailed structure of cell attractors. Any subpopulation selected from a population of cells repopulated the whole original basin of attraction within days to weeks. Cells at the basin edges were unstable and prone to apoptosis. Cells continuously changed states within their own attractor, thus driving the repopulation, as shown by fluorescent dye tracing. Perturbations of key regulatory genes induced a jump to a nearby attractor. Using the Fokker–Planck equation, this cell population behavior could be described as two virtual, opposing influences on the cells: one attracting toward the center and the other promoting diffusion in state space (noise). Transcriptome analysis suggests that these forces result from high-dimensional dynamics of the gene regulatory network. We propose that they can be generalized to all cancer cell populations and represent intrinsic behaviors of tumors, offering a previously unidentified characteristic for studying cancer.

Nongenetic switching between distinct phenotypes is a pervasive fundamental property of metazoa, most prosaically epitomized by the vast diversity of cell types generated by the very same genome. The dynamical, transient nature of multiple distinct phenotype states within clonal cell populations is anticipated by theories that treat the gene regulatory network (GRN), which governs cell phenotypes, as a complex, nonlinear, dynamical system (1). A network of genes that directly or indirectly influence the expression of each other can assume a very large number of theoretical (combinatorial) gene expression configurations (states of the network). Each such gene expression combination pattern can be thought of as a position, a point, in a coordinate system with n dimensions, where n is the number of genes. Using Boolean algebra simulations, such large GRNs have been investigated as a conceptual model to represent fundamental features in the functionality of real GRNs. It can be shown that not all states of the system are equally stable (equally probable to occur) but that some network states, as dictated by the GRN, represent stable steady states, the attractor states, to which the similar (“nearby”) states that are not stable will be “attracted” (2). Thus, GRNs exhibit multistability (coexistence of multiple attractors) (3). Stochastic fluctuations caused by molecular noise in gene expression (4–6) can allow the network to “jump” from attractor to attractor—hence, the latter is actually metastable.

In this theoretical framework, the distinct cell states or substates, such as multipotent states or terminal cell types in normal tissues or the stem-like (tumor-initiating) or metastatic state in cancer, are all attractor states: they are distinct “self-stabilizing” configurations of gene activities across the genome that arise because of constraints in the collective gene expression imposed by gene–gene regulatory interactions of the GRN (1, 7). Attractor states display robustness against stochastic fluctuations, such that a clonal population of cells appears as a bounded “cloud” of cells when the gene expression pattern of each cell is displayed as a point in a high-dimensional gene expression space (7). This robustness is the reason why cells can collectively be identified as a distinct phenotype, representing what we know as “cell type,” despite the substantial cell–cell variability. The area of the cloud is designated the “basin of attraction,” corresponding to a cell type. However, cells can, in the presence of sufficiently high levels of fluctuations or in response to a deterministic regulatory signal, switch between attractors and thus, inherit their new phenotype across cell generations (8, 9). No genetic mutation is involved in these quasidiscrete phenotype transitions, although mutations can facilitate state transitions by modifying the attractor landscape (10, 11). Earlier work has shown variations and dynamics of protein levels from cell to cell. Sigal et al. (12) termed this “ergodicity” after the physics term for a system that comes close to every possible state if enough time is provided.

It has recently been shown that “edge cells” at the outer boundary of the clouds of cells, representing the noise-driven, attractor-bounded cell population heterogeneity, can represent cells primed to transition into alternative states (adjacent attractor states), thus explaining the spontaneous stochastic transition between phenotypically distinct subpopulations in a population of clonal cells (8, 13, 14). Such nongenetic but stochastic acquisition of a new phenotype is of central relevance for cancer biology. In the current climate of thought, any new malignant trait, such as stemness, drug resistance, metastatic capacity, exit from dormancy, etc., is tacitly and by default explained by a genetic mutation or an epimutation (15). This has stimulated a spate of cancer genome sequencing efforts. These (epi)genetic changes are considered irreversible and thus, thought to drive a somatic evolution process that follows the Darwinian principle of selection of the fitter (most adapted) inheritable random variants (16). However, this scheme of explanation faces the challenge of the increasing realization that nongenetic dynamics play a role in creating the variety of tumor phenotypes (i.e., tumor cells can acquire new selectable phenotype without genomic alterations but as part of their nongenetic phenotype dynamics) (11, 17, 18). As a first step, as single-cell resolution static snapshots of the tumor cell population become increasingly routine (14), it is paramount to examine quantitatively, in an experimental model of noncancerous and cancerous cells, the attractor dynamics that underlie the cell population diversity, resilience to noise, and readiness to convert to another phenotype.

In this study, we used a cell line model of closely related but distinguishable nonmalignant vs. malignant phenotypes. The phenotype of the lymphoblastoid cell line (LCL) CBM1-Ral-Sto (CBM1) is nonmalignant, although it is immortalized in vitro by EBV, and it displays an EBV latency type III pattern (19, 20). By contrast, in the cell line Rael, the Burkitt’s lymphoma (BL) phenotype represents a malignant state (tumorigenic in immunocompromised mice) and is associated with the EBV type I latency pattern (19). BL cells are expected to be CD10+ and CD54−, whereas the reverse is true for LCL cells, which result in growth in aggregates. Given that both cell states are of B-cell type origin but have distinct phenotypes makes the BL vs. LCL system well-suited to study dynamical properties of cell heterogeneity in two presumed attractor states.

Here, we explored the heterogeneity, ability of reestablishment, and dynamics of subpopulations within the cell population and the fate of the edge cells, the cell phenotype switch triggered by external force and internal force. We dissected the cell behavior into two virtual forces: one attracting the cells toward the attractor state and another, noise, that promotes diversification and diffusion in state space. We modeled the integrated behavior using the Fokker–Planck equation (FPE) for in silico simulations.

Results

Distribution of Single Cells in 3D State Space.

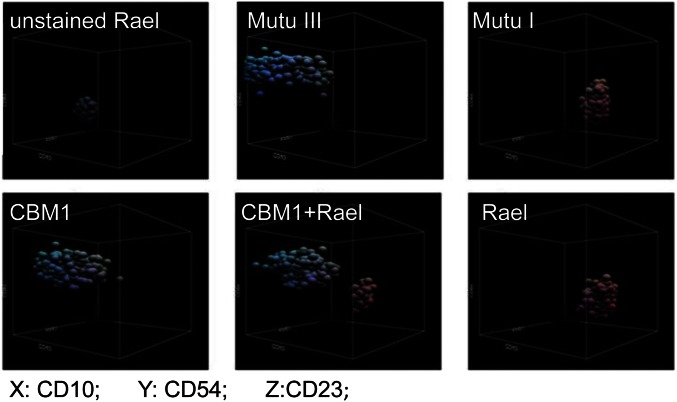
The expression level of the phenotype-defining surface proteins CD10 (cell membrane metallopeptidase), CD54 (intercellular adhesion molecule 1), and CD23 (IgE receptor) on single cells of different cell lines was mapped by flow cytometry (FCM). The three markers illustrate the distribution of the cell populations in a 3D space (Fig. 1). Each cloud of single cells together represents the phenotype of the cell line and occupies its own position separated by voids. Rael and Mutu I both represent malignant BL cells with EBV latency I type and assume similar positions in the 3D space. CBM1 represents an in vitro-transformed LCL, and Mutu III is a variant of Mutu I that has converted to EBV latency III type in vitro (21). Rael and CBM1 cocultured during 1 mo at a starting ratio of 1:1 maintained a distinct separation in 3D space (Fig. 1). This 3D cloud is a demonstration at low dimension of a virtual n-dimensional landscape created by measuring the expression level of all proteins in the cell lines.

Fig. 1.

A 3D representation of the expression of three selected surface proteins on the cell lines. The expression of CD10 (x axis), CD54 (y axis), and CD23 (z axis) on Rael, CBM1, Mutu I, Mutu III, and a coculture of Rael and CBM1. Unstained Rael is shown as the control. Each symbol corresponds to 100 cells.

Heterogeneity of Protein Expression in Apparently Clonal Cell Populations.

The expression level of CD10 in the Rael cell line showed a characteristic bell-shaped histogram with a broad basis in the log-transformed CD10 signal plot (Fig. 2A). Its variation was much broader than that of Molecules of Equivalent Soluble Fluorochrome beads (Fig. 2B), showing that the variation of surface marker expression could not be attributed to technical noise, which was also shown by others (14).

Fig. 2.

Heterogeneity between individual cells and reestablishment of the parental phenotype from edge cells. (A) CD10 [labelled with phycoerythrin (PE)] expression on Rael cells measured by FCM. (B) Five different PE Molecules of Equivalent Soluble Fluorochrome beads with a standardized number of fluorescent molecules on the surface measured by FCM. (C) CD10+ phenotype-inconsistent edge cells in CBM1 defined by unstained and isotype controls. (D) CD54+ phenotype-inconsistent edge cells in Rael defined by unstained and isotype controls. (E) Rael CD54+ edge cells (1.1%) were sorted out by FACS and cultured separately. CD54 expression checked by FCM on days 0, 2, 3, and 7 after isolation was shown in different colors. The fraction of CD54+ edge cells of the total population at each time point is shown. (F) The gene expression profiles of the Rael CD54+ cells on days 0, 3, and 56 after isolation as well as the parental Rael. The expression microarray data are presented as the GEDI self-organizing maps, which show all of the analyzed genes. Expression levels were according to the colored bar. The white markers show the location of the CD54 gene in the profile. (G) Validation of the microarray data by quantitative PCR (qPCR) for CD10 and CD54 performed on the same samples. Blue, qPCR data; gray, microarray data.

Edge Cells Dynamically Change Their Marker Protein Expression Profile.

Compared with the isotype control and unstained cells, there was a small population of CD10+ cells in CBM1, formally classified as CD10− (Fig. 2C). Similarly, there was a small fraction of CD54+ cells in the CD54− Rael (Fig. 2D). Because of the atypical protein expression status in these cells, they were designated “phenotype-inconsistent cells.”

We designate cells that are in the utmost tail of the bell-shaped distribution for any parameter as edge cells, which include the phenotype-inconsistent cells. These cells are at the edge far away from the center of the attractor. Do the edge cells represent a stable subpopulation? Are they able to revert to the entire parental state over time? What is the dynamics of such a reversion process? Such a reversion would reveal the properties of the basin of attraction.

To address these questions, CD54+ Rael edge cells, those at the right-side tail of the CD54 histogram, were isolated by FACS and cultured separately from the parental population. The expression of CD54 in these isolated edge cells was monitored over time. Initially, 1.1% of the Rael population was CD54+ (edge of the Rael CD54 distribution) (Fig. 2E). On reculturing of this sorted CD54+ subpopulation, the cells reverted to the parental phenotype (i.e., became CD54− again). The fraction of CD54+ cells in this subpopulation was reduced from 100% to 1.6% after 7 d of culturing, close to the level of the parental Rael (Fig. 2E).

The behavior of edge cells also applied to the dynamics along the CD10 axis. Rael cells isolated from the highest and lowest tails of the CD10 distribution were both capable of reestablishing the parental distribution. This behavior was independent of whether the edge cells were derived from the high or low tail of the parental population (SI Appendix, section 1.1.1 and Fig. S1).

Isolated Edge Cells Show an mRNA Expression Profile Distinctly Different from That of Parental Rael.

Because FCM measurements only present a few dimensions of the high-dimensional state space of the GRN, we next analyzed the genome-wide transcription profile using microarrays (Affymetrix) to capture the genome-wide GRN state of the inconsistent CD54+ Rael cells. The Gene Expression Dynamics Inspector (GEDI) program was applied to visualize the transcriptome. Herein, each “tile” within a “mosaic” represents a minicluster of genes that have highly similar expression pattern across all of the analyzed samples. The same genes are forced to the same mosaic position for all GEDI maps. The CD54+ Rael edge cells differed in their expression of more than 2,000 genes from the parental Rael (Fig. 2F). Thus, the selection based on one single-cell surface marker provided a population with a remarkably different gene expression profile. With time in culture, the CD54-selected cells resumed an expression profile like that of parental Rael, which is in line with the FCM analysis for the single-marker CD54. Quantitative PCR analysis of CD54 and CD10 mRNA expression validated the microarray and FCM data (Fig. 2G).

Subpopulations Representing Different Levels of Marker Expression Can Reestablish the Parental Marker Distribution on Separate Culturing.

To examine whether the capacity for repopulation is a property of states throughout the entire basin of attraction as predicted by the definition of attractor, we sorted out fractions of the Rael cell population with respect to segments in CD10 expression level representing the entire distribution of CD10 (Fig. 3A). Each segment, referred to as “subpopulation,” thus isolated, was cultured separately. CD10, CD54, forward scatter (FSC), and side scatter (SSC) were analyzed at days 1–3, 7, and 16. All subpopulations restored the original CD10 population distribution within days. Immediately after isolation (days 1 and 2), CD10 expression in the subcultures was consistent with the order of the selected population segments from lowest CD10 to highest CD10 (Fig. 3 B and C). All of the fractions reestablished the same distribution as the parental Rael cells after 3 d (Fig. 3C). CD54 expression was, as expected, inversely correlated to CD10 (Fig. 3D). In summary, observing the relaxation dynamics along these two dimensions reveals a behavior that is consistent with dynamics within an attractor basin and the presence of gene expression noise constrained by the basin.

Fig. 3.

Reestablishment of parental phenotype after selection of subfractions based on a phenotype-consistent marker (CD10). (A) Fractions of Rael with different levels of CD10 were selected by FACS from low to high expression (schematic representation of fractions 1–12) as indicated. All of the selected 12 subpopulations were cultured separately and followed by FCM analysis on days 1–3, 7, and 16. (B) CD10 expression of each of 12 subpopulations was reanalyzed at five time points. Parental Rael was used as the control (dashed line). The 1st to the 12th solid curves show the respective subpopulations. (C) An overlap view of the same FCM curves as shown in B. (D) Overlapping curves of CD54 analysis of the same selected Rael subpopulations at five time points show convergence from the initial variation. (E) Analysis of granularity (by the parameter side scatter: SSC-A) of 12 subpopulations and parental controls at five time points in the same order as shown in B. (F) Cell size analysis (by the parameter of forward scatter: FSC-A) of the subpopulations and controls at five points, with the same order as shown in B.

Reduced Proliferation and Viability of the Edge Cells.

To determine whether the position in the basin of attraction affects cell growth behavior, we monitored cell division history. Rael cells were labeled with 5- (and 6-)carboxyfluorescein diacetate succinimidyl ester (CFSE), cultured for 8 d, and then, analyzed by FCM for CD54 expression. Most CD54-high (edge) cells were found in the fraction with the highest CFSE labeling, indicating that they have not undergone cell division. By contrast, the rest of the Rael population had progressed to a second, third, and even fourth generation on the eighth day after CFSE labeling (Fig. 4F).

Fig. 4.

Redistribution of isolated cells within populations as shown by a single parameter and knockdown of Oct2 by shRNA in Rael cells. (A) Coculturing of CFSE-labeled cells with the nonlabeled population of CBM1 cells. CD54 mode cells were sorted out, labeled with CFSE, and then mixed back with the nonlabeled remaining population. CD54 mode refers to the cells at and around the peak (to the left; blue). (B) CD54 distribution of three new generations and parental CD54 mode CBM1 cells on day 8 after isolation and CFSE staining. (C) CD10 distribution of CD10-highest Rael cells on day 0 and 8 d after isolation and CFSE staining (blue) and the remaining Rael population at the same two time point (black). To visualize the small CFSE-labeled population (3% of the whole population), the scale was adjusted to percentage of maximum with Flowjo. (D) Distribution of Mutu cells in the 2D distribution 4 d after the appearance of type III Mutu cells (CD54-high CD10-low) from a culture of type I Mutu cells (CD54-low, CD10-high). CFSE+ cells were those at time 0 of type III (in the circle), and CFSE cells were type I at that time. (E) A 3D representation (x axis, CD10; y axis, CD54; z axis, CD23) of (Left) type I cells (red) appearing in the Mutu III population (blue) and (Right) their disappearance after 30 h. (F) CFSE distribution of Rael CD54-high cells 8 d after the whole Rael population was labeled with CFSE and cultured. (Left) The four peaks (analyzed by Flowjo) represents four generations by cell division. The CD54-high cells were of the CFSE level of generation 0 of the Rael cells (orange). The gating for CD54-high Rael is shown in Right. (G) Statistical analysis of apoptosis and dead cells in the isolated Rael edge cells. Data were from three independent experiments of Rael. CD10-highest or CD10-lowest cells are shown as means ± SEMs. (H) FCM of CD10 and CD54 2 d after shRNA transfection. CD10− CD54+ type III-like cells are in the circle. Empty vector-transfected cells are shown as the negative control.

Both the low (1st) and the high (12th) CD10 expression population fractions showed lower cell viability than parental Rael and the other fractions already 1–3 d after isolation (Fig. 4G and SI Appendix, Fig. S2). Apoptosis analysis in three independent experiments at different time points in Rael cell lines showed that both the CD10-highest and CD10-lowest edge cells showed significantly higher apoptosis and death rate than that of the parental Rael (Fig. 4G). This observation indicates that poor viability was associated with being at the edge of the attractor basin. The FCS parameters SSC-A and FSC-A (representing granularity and size) also showed irregularities during the reconstitution phase (Fig. 3 E and F).

Single Cells “Move Around” in the Attractor Basin over Time.

The relaxation of the edge cells is driven by the “restoring force” of attractor dynamics that act on the isolated edge cells according to our attractor model. However, isolated population fractions may behave differently from cells within a physiologically diverse population. We next examined the spontaneous, largely noise-driven shift of an individual cell’s position within the parental population (approximate position in the basin of attraction) when the restoring force of the basin of attraction is minimal and the cells are in the context of the full diversity of the entire population.

We isolated CBM1 cells from the segment of CD54 distribution that represent the mode (“peak”) of the population (Fig. 4A, Left). These “CD54 mode” cells were labeled with CFSE for tracing and mixed back into the parental population immediately. After 2 d, the CD54 mode cells had shifted away from the center. They were then distributed over a broader range of expression (Fig. 4A, Center); however, they still did not cover the whole range of CD54 expression (the edge of the basin) until day 8 (Fig. 4A, Right). The relaxation of a distribution of cells to a steady state can be modeled by an FPE as discussed below and in SI Appendix, section 2 (FPE modeling). The characteristic timescale of this process depends on the details included in the model but is generally about 3 d for the bulk of the population. We, therefore, find that cells starting from the mode of CD54 expression explore the entire basin of attraction on the similar timescale as relaxation. This redistribution could not be caused by cell division (partitioning) as shown by the tracing experiment with CFSE-labeled Rael CD54 mode cells (Fig. 4B).

The same approach was applied to the cells with the highest CD10 expression (edge of their attractor basin). Rael cells were isolated from the high CD10-expressing tail fraction, labeled with CFSE, and then, mixed back with the rest of the population. After 8 d, 54% of the CD10-high Rael cells were found below the FCM gate setting for high cells (i.e., they had moved toward the attractor point) (Fig. 4C and SI Appendix, Fig. S3). Here, the redistribution seemed slower, suggesting that the reconstituting force at the edge of the attractor basin may be weaker within the intact cell population than in isolated subpopulations.

In summary, these experiments collectively fit with the proposed model of two forces, directed out- and inward, and are consistent with stochastic changes of cell states constrained by a basin of attraction. Of interest is that the relaxation differed depending on whether the edge cells were isolated or mixed in the parental population with its intrinsic diversity of cells, suggesting that cell population context may influence the apparent restoring force (i.e., attractor basin structure).

Spontaneous Shift from One Phenotype to Another.

Multistability implies coexistence of alternative attractors and the possibility of cells transitioning between them. Thus, next, we examined the switch from one phenotype (attractor) to another. We exploit the fact that BL Mutu I cells, in contrast to Rael cells, can spontaneously shift from type I (CD10-high CD54-low) to type III (CD54-high CD10-low) in a process that takes place gradually over several months. We looked for the presence of two clusters in the 3D state space of the three surface markers detected by FCM (Fig. 1). Surprisingly, FCM followed by reculturing suggested that the transition between types I and III was not unidirectional. Early during switching from Mutu I to III, some Mutu III cells resumed their original Mutu I phenotype as revealed by CFSE labeling (Fig. 4D). After apparent completion of the switch to the Mutu III phenotype, we occasionally detected a small subpopulation of CD10-high CD54-low (type I) cells at variable time points (Fig. 4E). Thus, Mutu cells seem to oscillate spontaneously between the two attractors.

Key Regulatory Gene Can Facilitate a Switch Between Attractors.

We took advantage of our finding that knockdown of the transcription factor Oct2 by shRNA can suppress the relatively high level of Oct2 in type I cells (Rael), resulting, rarely, in a phenotype switch similar to the spontaneous transition seen in the Mutu I (22, 23) (SI Appendix, section 1.1.3 and Fig. S4). Under these conditions, a small fraction of Rael cells transiently switch from the CD10+ CD54− (type I) to CD10− CD54+ (type III) phenotype (Fig. 4H). This transition from type I to type III EBV expression pattern is inefficient, presumably because of the robustness of this molecular switch (23).

Two Virtual Forces Identified by Mathematical Modeling of the Population Reestablishment by the FPE.

The observed dynamics of relaxation of the edge cell fractions or the population segments (Fig. 3) can be explored using in silico modeling based on FPE, which describes the time evolution of a probability density function, f(X, t), under the combined influence of drift (corresponding to the deterministic force of relaxation to the attractor basin center) and diffusion (corresponding to gene expression noise). In principle, X is a high (n)-dimensional vector representing a cell state defined by a genome-wide set of key proteins; however, the observed probability density function approximation describes dynamics only in 1D, namely with respect to CD10 or CD54. A simple 1D FPE model describes the relaxation dynamics of the highest CD10 Rael cell subpopulation quite well (Fig. 5), supporting the view that the dynamics can be reduced to the two counteracting influences on cell dynamics in the cell population: deterministic attraction (homeostasis) and stochastic fluctuations (SI Appendix, section 2).

Fig. 5.

Simulation of the redistribution dynamics of CD10-high edge cells using FPE at five different time points. The dashed curves show modeling with FPE, whereas the solid curves show experimental data at the same time points. The x axis shows a logarithmic representation of CD10 intensity in arbitrary units, and the y axis shows the cell count as a relative number.

Discussion

Starting out from the cancer cell attractor concept, we analyzed cell heterogeneity of a population of cells of a nominally identical type and also, explicitly analyzed “type infidelity,” which manifests as inconsistent marker expression relative to that expected for the “average cell phenotype” of that population (1, 21). The stability of the phenotype can be visualized as a basin of attraction in a mathematical landscape, in which all cell types are represented by attractor states (24, 25). Therefore, the dissection of the intraattractor dynamics at single-cell resolution performed here represents a previously unidentified level of granularity in the analysis of cell behaviors (notably, cancer cells).

The central finding—directly predicted from the concept of the attractor basin—is that any isolated subpopulation derived from the original spectrum of the expression levels of a marker can reestablish within days to a few weeks the original parental distribution with respect to not just that marker used to define the subpopulations but the entire transcriptome. Isolated edge cells relaxed back toward the middle of the distribution, whereas cells at the center (mode) of the distribution moved away from the middle toward the edges—thus, in both cases, “diffusing” (in state space) throughout the entire population. Although we did not study cell–cell communication but assumed in the models that cells are autonomous entities, it is remarkable that the difference in relaxation rate between edge cells that were isolated vs. those that were merely marked but left in the entire heterogeneous population was apparent. This difference points to an influence of cell–cell communication (notably across diverse states within the attractor basin) on relaxation rate, which was suggested earlier (14).

The description of the cell population distribution relaxation using a simple FPE suggests that the dynamics of cell states around a cancer cell attractor are reasonably represented by a deterministic drift force and a diffusion term that captures the stochastic fluctuations caused by molecular noise that affects state markers. However, one needs to take into account that the process is not a smooth reversion to the original distribution but involves a richer structure. In our case, we observed at least two distinct temporary states (SI Appendix, section 1.1.2). This modeling effort suggests that the experimental monitoring of the temporal evolution of cell population distribution, even with respect to just 1D, can yield insights about the attractor dynamics of a cancer cell population.

One fundamental feature of the virtual cell type attractor landscape is that space between basins of attraction (“hills and ridges”) is void of cells, because cell types are quasidiscrete entities: there is no continuum of observed cell states in state space—only the attractor states are stable, whereas all others are unstable and only transiently visited (1, 11). However, because of stochastic fluctuations that disobey the regulatory interactions that push the cells to the attractor states, cells can transiently visit the border of basins of attraction—the edge cells studied here. The question is then whether they, instead of relaxing back to the basin center, can transition (escape) to neighboring attractors.

This transition would be an exceptional phenomenon, because it would violate the ordered structure of cell phenotypes and tissues in a multicellular organism. Indeed, the robustness of attractor states, as described here, suggests that such spontaneous transitions are extraordinarily rare.

In this conjunction, an important observation in our experimental cell model was the constitutive existence of cells with a nontypical marker expression at a low frequency. These cells could represent a transient shift toward another attractor or an incomplete, partial change of phenotype to a subattractor. When isolated and cultured from either Rael or CBM1, they proliferated slowly and revealed a high apoptosis rate, but ultimately, they returned to the parental status. Such cells, when isolated, showed distinct mRNA expression patterns involving a large number of genes.

Our data suggest that edge cells may represent cells transgressing the ridge between two basins. In an organized microenvironment, they might merely not survive. However, with tissue stress and disorder, such as during low-grade chronic inflammation, they might have a larger chance to survive and thus, could complete the transition to neighboring attractors. Such transitions essentially would explain the adoption of malignant, cancer stem cell-like phenotypes because of nongenetic plasticity and not mutations, as others have suggested (26–28).

The attractor model might have important implications for cancer cell biology and treatment of cancer. The current and dominant focus in designing new treatments is to target mutated oncogenes and their erroneous gene products (29). However, as much as they might represent the “original sin” in the manifest tumor in many cases, they have already made their damage when they occurred. These cells could survive at a new state space position (attractor), because the new attractor affords compensatory functions as part of the associated gene expression program, a typically stem-like phenotype that is inherent in the GRN (17, 26, 30, 31). These compensatory mechanisms are probably those that should be sought out and targeted when conventional approaches have failed (32).

Another important aspect of cancer therapy can be derived from the model. The wide distribution of single cells in a cancer cell attractor is expected to produce the constellation that some cells in the population are resistant to a given drug at a certain time point but not at another time point when they have shifted position in the state space (26, 32–36). When the selective pressure of treatment is released, the original population can be reestablished by these few temporarily resistant edge cells. If a malignant cell clone is a stochastic distribution of different gene expression states, including rare variants, it may be necessary to identify combinations of treatment that not only reduce the average viability in the population but specifically eliminate rare edge cells that may be transiently drug-resistant. This conclusion presents a challenging complementary view on drug resistance in addition to the themes of resistant cancer progenitor cells or appearance of new mutants caused by treatment selection (29). One view does not exclude the other.

Materials and Methods

Details on materials and methods are in SI Appendix, section 1.2.

Four human EBV-carrying B-cell lines were used: Rael, Mutu I, CBM1, and Mutu III were cultured, and the corresponding antibodies were labeled before FACS or FCM analysis. Molecules of Equivalent Soluble Fluorochrome kits were applied to calibrate the FCM. After the cells were sorted out, they were cultured in proper microwell tissue culture plates with the RPMI medium 1640 (Sigma-Aldrich) and then transferred to tissue culture bottles when there were enough cells. The cell apoptosis and death analysis was done with the APC Annexin V/Dead Cell Apoptosis Kit, and a paired Student t test was performed to compare the differences between groups with GraphPad Prism 6.0. The cell tracing and proliferation analysis was done by CFSE staining with the CellTrace CFSE Cell Proliferation Kit (37). Gene expression profiling was performed using HuGene-1_0-st-v1 chips, and then, the microarray data were analysis by the program GEDI. Microarray data for CD10 and CD54 were validated by quantitative PCR. Knockdown of transcription factor Oct2 was done with shRNA (anti-oct2 shRNA TI341098) by electroporation.