Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Mar 15;6:23030. doi: 10.1038/srep23030

Bacterial regulon modeling and prediction based on systematic cis regulatory motif analyses

Bingqiang Liu 1, Chuan Zhou 1, Guojun Li 1,a, Hanyuan Zhang 2, Erliang Zeng 3,4,7, Qi Liu 6, Qin Ma 5,7,b
PMCID: PMC4792141  PMID: 26975728

Abstract

Regulons are the basic units of the response system in a bacterial cell, and each consists of a set of transcriptionally co-regulated operons. Regulon elucidation is the basis for studying the bacterial global transcriptional regulation network. In this study, we designed a novel co-regulation score between a pair of operons based on accurate operon identification and cis regulatory motif analyses, which can capture their co-regulation relationship much better than other scores. Taking full advantage of this discovery, we developed a new computational framework and built a novel graph model for regulon prediction. This model integrates the motif comparison and clustering and makes the regulon prediction problem substantially more solvable and accurate. To evaluate our prediction, a regulon coverage score was designed based on the documented regulons and their overlap with our prediction; and a modified Fisher Exact test was implemented to measure how well our predictions match the co-expressed modules derived from E. coli microarray gene-expression datasets collected under 466 conditions. The results indicate that our program consistently performed better than others in terms of the prediction accuracy. This suggests that our algorithms substantially improve the state-of-the-art, leading to a computational capability to reliably predict regulons for any bacteria.

Reconstruction of global transcriptional regulatory networks is a key to understand gene function and evolution, thus it is one of the critical aspects of microbial genomics, especially in the era of high throughput genome sequencing1,2,3,4. In bacterial genome, an operon, as a basic transcriptional unit, is a group of genes (may only one gene) arranged in tandem on the same strand of a genome, which share a common promoter and terminator5. To study the mechanism of transcriptional regulation, we need to know all the operons co-regulated by each of transcription factors (TFs). The term regulon was first introduced by Maas et al. in 1964, intended to name a maximal group of co-regulated operons6, which may be scattered in a genome without apparent patterns in terms of their genomic locations. A successful elucidation of regulons will substantially improve the identification of transcriptionally co-regulated genes encoded in a bacteria genome, realistically allowing reliable prediction of global transcription regulation networks.

Experimentally, numerous regulons have been recognized in the widely–studied model organism E. coli, and were stored in the RegulonDB database7. Nevertheless, elucidating all the regulons at a genome scale using experimental approach is highly desired. Except the high cost and time-consuming8,9, one key issue is that it is difficult to know what conditions may trigger which regulons; hence unless we can exhaustively go through all possible conditions that each triggers at least one regulon, we will not be able to observe all of the regulons experimentally10. Therefore computational algorithms are urgently needed, and will play an essential role in investigating all regulons encoded in a bacterial genome.

A basis for computational regulon prediction using genomic data lies in that the operons regulated by one TF should have conserved cis regulatory motifs (motifs for short) around their promoter regions. So the problem can be defined as to find all maximal sets of operons in a genome, with each set sharing conserved motifs. Typically, computational regulon prediction has two categories: (i) prediction of new operon members of a known regulon11, and (ii) ab initio inference of novel regulons using de novo motif finding strategy3. In early stage, most of the studies on regulon identification focused on some specific TFs, falling in the first category. For example, Tan et al. predicted the CRP and FNR regulons in E. coli, through searching for new binding sites based on the known motif profiles in RegulonDB, and then in H. influenza by the comparative genomics strategy12. The TyrR and RpoS regulons were analyzed in similar ways in E. coli and Pseudomonas aeruginosa13. Su et al. developed a program for prediction of specific regulons such as the ntcA14, phoB15, cbbR16 and σ38 regulons in cyanobacteria. Latterly, computational algorithms for general regulon prediction were developed to facilitate the systematic studies in gene regulation17,18. In the second category, for regulon prediction without known motifs, phylogenetic footprinting plays an important role through identifying conserved motifs from other relevant species (so-called reference genomes)19,20. An ab initio regulon inference should at least contain three steps: operon identification, motif prediction and clustering21,22, where a cluster corresponds to a regulon. Although the problem seems to be simple conceptually and there are numerous computational tools published3,23,24,25, it is still in its early stage with a variety of computational challenges, especially at a genome scale: (i) de novo motif prediction still performances poorly in terms of its accuracy, e.g. the high false positive rate. And the phylogenetic footprinting technology is still not well defined in the selection of reference genomes and measuring the evolutionary distance between any pair of genomes, limiting the usage efficacy on motif finding23,24; (ii) there is a lack of a reliable measurement for motif similarity, and current motif comparison using aligned motif profiles usually produces too many false positives26; (iii) better operon prediction algorithms are missing, especially utilizing the high-throughput RNA-sequencing data24,27; and (iv) current regulon prediction methods usually cluster the motif signals directly, thus leads to unreliable predictions due to randomly matching between motifs23. Apparently, a more ingenious design is required in the step of clustering.

In this paper, we developed an ab initio computational framework for elucidation of all regulons encoded in a bacterial genome (see Fig. 1). There are several unique features in our framework: (i) we derived high-quality operon predictions from the DOOR2.0 database that contains complete and reliable operons of 2,072 bacteria genomes, and we also fully considered operon structures in both motif finding and their clustering; (ii) for an operon in a target genome, we designed a new strategy to define and select its orthologous operons from the reference genomes in the same phylum but different genus with the target genome, and then refine the promoter set by eliminating redundancies. This strategy followed by our motif finding tool, BOBRO, can increase the quality of predicted regulatory motifs; and (iii) instead of calculating pair-wise similarity score for predicted motifs and then identifying regulons through motif clusters as the previous methods did, we designed a new method to build similarity relationship on operon level and then perform clustering through a heuristic graph model. Specifically, we defined a novel co-regulation score (CRS) among operons to evaluate the co-regulation property of them, which is much better than other similar scores that are defined through various functional and evolutionary relationships28,29,30. Based on the CRS, we then proposed a novel graph model for regulon identification, making the operon-clustering problem easier to solve. We evaluated and refined our methods based on the 177 documented E. coli regulons from RegulonDB and its genome-scale microarray gene expression data collected under 466 conditions7. The results suggest that, with this new implementation, the regulon prediction problem becomes substantially more solvable and our program has consistently better performance than others, especially for the 12 largest regulons each of which contains at least 20 known component operons. All the programs used in this paper, are implemented by the C computer language and are publicly released under the GPL agreement license and can be freely downloaded at http://csbl.bmb.uga.edu/DMINDA/download.php and are also implemented on a web server: http://csbl.bmb.uga.edu/DMINDA/.

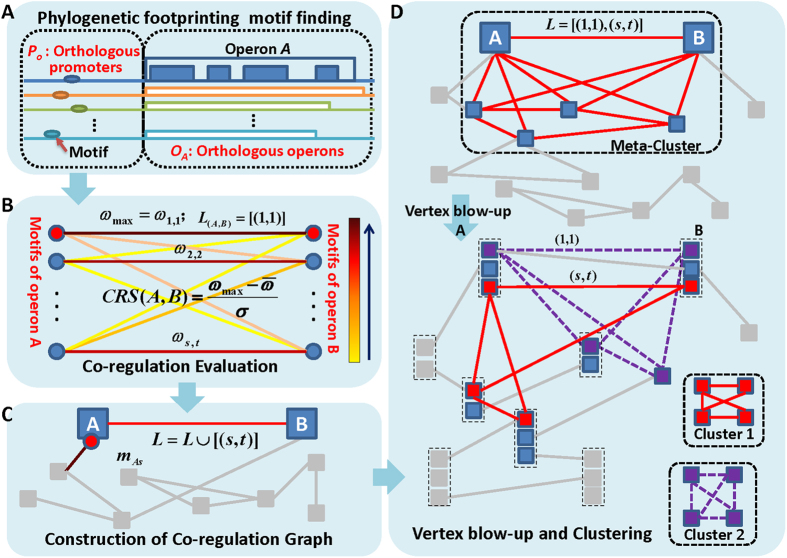
Figure 1. An outline of the regulon prediction framework.

Figure 1

Open in a new tab

The blue arrows indicate data flows within this framework; and the blue rectangles represent different steps across the whole analysis. (A) Identification of motifs by a phylogenetic footprinting framework; (B) calculation of co-regulation score between a pair of operons by a highly sensitive motif similarity score. The higher the similarity score is, the darker of the corresponding edge’s color will be; (C) construction of graph G reflecting the co-regulation relationship among operons based on the similarity of their predicted motifs; and (D) vertex blow-up in graph G by re-involving motif information and clustering operons to construct accurate regulons.

Results

Framework Overview

The flowchart of our regulon prediction can be found in Fig. 1, and more details of the relevant algorithms are showcased in the MATERIALS AND METHODS section. All the programs mentioned in the following were implemented using the default parameters, unless otherwise indicated. We applied the proposed regulon prediction framework on E. coli K12, during which the co-regulation scores between any operon pairs were generated and computational significant regulons were identified. The prediction performance was assessed comparing with documented regulons from the RegulonDB database. It is noteworthy that we have implemented the framework on our in-house motif analysis web server, DMINDA31. Hence, the users can easily apply this proposed framework on any of 2,072 sequenced bacterial genomes included in this server.

The orthologous operons can benefit motif finding in a phylogenetic footprinting framework

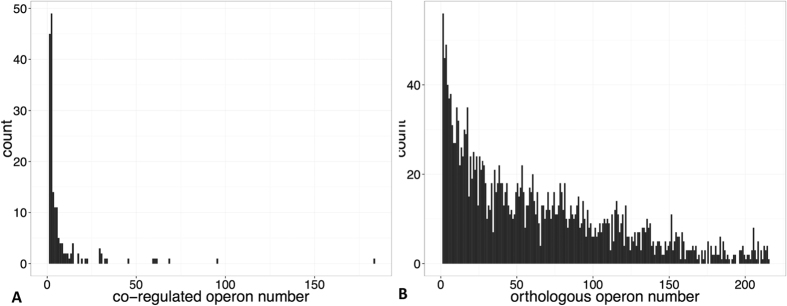
The effective regulon identification relies on a collection of promoters containing corresponding motifs. However, such promoters are not easy to be accessed for a regulon containing only a few operons according to current regulon databases in the public domain. Specifically, only 40.4% of the 2,462 operons in E. coli have more than 10 co-regulated operons according to the RegulonDB database7 and the average number of co-regulated operons is only eight, meaning an overall non-sufficient up-streaming regulatory promoters for motif identification using the host genome solely. Intuitively, we can fix this bottleneck, expanding to 216 selected non-redundant reference genomes, through a well-designed phylogenetic footprinting framework. And the identified orthologous operons for any query operon can provide more informative promoters (see details in the MATERIALS AND METHODS section). Specifically, the average number of orthologous operons for all the 2,462 operons in E. coli is 84, and the percentage having over 10 orthologous operons increases to 84.3% (see details in Supplementary file 1 and corresponding orthologous promoters can be found in Supplementary file 2). The distribution comparison between co-regulated operon and orthologous operon is shown in Fig. 2. Therefore, we can claim that such a phylogenetic footprinting strategy can provide more informative promoters in motif finding for those operons involved in local regulons, without or with low number of co-regulated operons in their host genome. As described in MATERIALS AND METHODS, we applied BOBRO on these promoter sets to predict conserved motifs, which will be used to generate co-regulation relationship between operons in E. coli.

Figure 2.

Figure 2

Open in a new tab

(A) the distribution of co-regulated operons for each operon in E. coli according to RegulonDB database; and (B) the distribution of orthologous operons for each operon in E. coli using 216 reference genomes.

CRS can represent co-regulation relationship between a pair of operons

For each pair of operons, we calculated the CRS based on a well-designed similarity comparison of their predicted motifs (Fig. 1). It elucidates the co-regulation relationship, which is the foundation of regulon identification. Here we firstly verified that the performance of CRS, in terms of representing known co-regulation relationship, is much better than the following two widely-used scores: partial correlation score (PCS) and gene functional relatedness score (GFR). The PCS and GFR are defined based on co-evolution, co-expression, and co-functional analysis among operons. Specifically, the GFR between a pair of genes is calculated from three different perspectives: phylogenetic profile analysis, gene ontology analysis, and gene neighborhood property along the genome28. Here we applied the concept in GFR to operon level by averaging all the involved GFRs in a pair of operons. And the PCS between a pair of operons was calculated as follows. For an operon A in the genome of E. coli K12, we constructed an evolutional 0–1 vector across the 216 reference genomes, where 1 means there is an orthologous operon of A in a specific genome and 0 means the opposite. The PCS between a pair of operons in E. coli K12 is measured based on the two corresponding 0–1 vectors using the similar strategy in literatures29,30, which can elucidate their evolution similarity by removing indirect relationship in a large network.

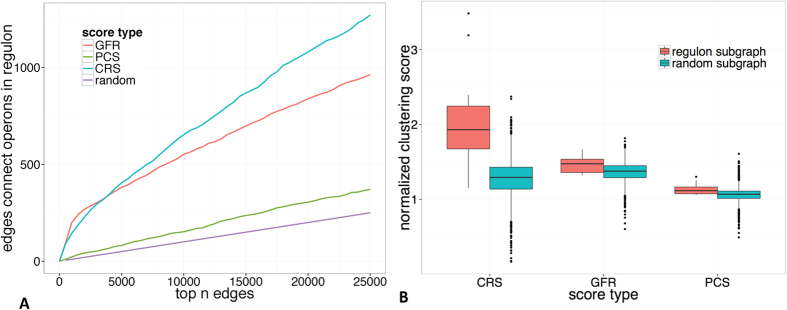
Let G be the graph with operons as vertices and edges connecting each pair of vertices. The weight of an edge could be one of the three kinds of scores (CRS, PCS and GFR) between the corresponding two operons. Firstly, the efficiency of a score is defined as the numbers of operon pairs, being in known regulons, in top n operon pairs (n is from 0 to 25,000 by 500 intervals) out of totally 3,247,426 operon pairs ranked according to this score. As shown in Fig. 3A, the efficiency of CRS is obviously better than PCS, GFR, and a randomly selection; and the efficiency of CRS has the fastest increasing rate among all the scores as n increases from 0 to 25,000. GFR shows better performance in limited scale (≤4,000), because it takes more information into consideration, in support of the identification of the most significant co-regulatory relationships. This phenomenon indicates that the CRS has the best signal-noise ratio in to-be-selected operon pairs and will perform better in the following regulon prediction compared to the others, especially in genome scale application. See details in Supplementary Table S1.

Figure 3. Performance comparison of CRS, PCS, and GFR.

Figure 3

Open in a new tab

(A) The efficiencies of these scores along with a randomly selection, where edges correspond to operons pairs as defined in graph G. (B) Comparison of the normalized clustering coefficient (nCC) regardning known regulons in G keeping the top 25,000 operons pairs. For each score out of the three, the normalized CCs of a group of randomly selected vertex sets with similar sizes are listed as background. For CRS, the nCCs of known regulons are much higher than randomly selected operon sets, with the the P-value of the Wilcoxon test as 1.7e-09. And the corresponding P-vaules for PCS and GFR are 0.0009 and 0.0018, respectively.

On the other hand, we compared above three scores in terms of the normalized Clustering Coefficient (nCC) of 17 known regulons (containing more than 20 operons). The normalized clustering coefficient can be used to infer the potential capability of a specific set of vertices to be identified as a cluster in a graph. Intuitively, a regulon corresponds to a sub-graph H in the graph G, with operons as vertices and 25,000 selected edges. E(H) and V(H) represent the edge set and vertex set in H and |X| means the number of elements in a set X. The Clustering Coefficient (CC) is a measure of the degree to which vertices in a graph tend to be clustered together based on triplets of vertices32. Specifically, a triplet consisting of three vertices is called close if the three vertices are connected by three edges; and CC(H) is calculated as the number of closed triplets over the total number of connected triplets in H. Then CC(H) is normalized by

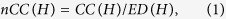graphic file with name srep23030-m1.jpg

where ED(H) represents the edge density of H, and can be calculated as

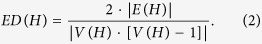graphic file with name srep23030-m2.jpg

Intuitively, a set of vertices with higher nCC tend to be identified as a cluster much easier. From the comparison analysis in Fig. 3B, we found that (i) a regulon has the largest superiority compared to same-size and randomly selected operons using CRS (with the P-value as 1.7e-9) than using the other two scores; and (ii) the nCCs of 17 regulons based on CRS are significantly higher than those based on PCS and GFR (see Supplementary Table S2 for details), indicating CRS will have better performance in the following regulon predictions.

The performance of our regulon prediction

Based on the CRS, our framework built a co-regulated graph and generated operon clusters for regulon prediction. In this step, instead of directly clustering on operons, we involved the predicted motifs to construct a new vertex-blowup graph model (Fig. 1C), and then took the compact cliques to generate primary operon clusters, represented by CRS-c in Fig. 4. It is noteworthy that the cliques are too strict for regulon prediction as the operons in one regulon may share weakly conserved motif patterns. Hence, we took the corresponding motifs to scan the whole genome, and optimize the corresponding operon clusters by making the operons with significant motif hits involved, otherwise excluded. The final optimized operon clusters were recognized as predicted regulons in our study (represented by CRS in Fig. 4).

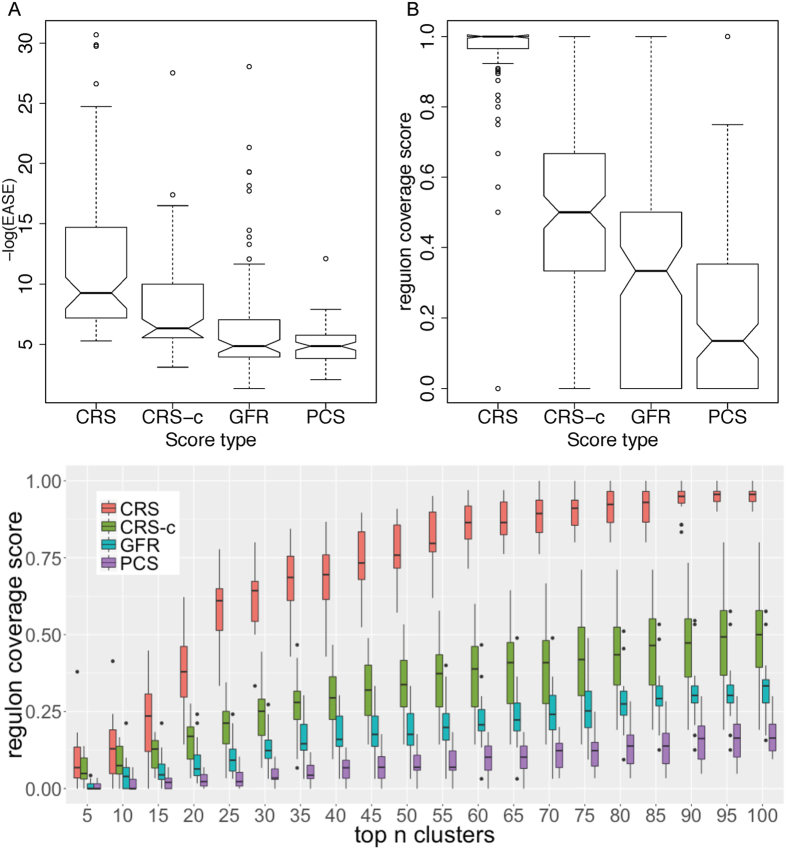
Figure 4. Performance of regulon prediction.

Figure 4

Open in a new tab

(A) Comparison of EASE distribution among CRS, CRS-c, GFR and PCS clusters. For each cluster, only the smallest EASE score with a regulon is kept. Note that the EASE score in y-axis is in −log() scale. (B) Comparison of the regulon coverage scores (RCSs) among CRS, CRS-c, GFR and PCS clusters. Each box represents the RCSs of the 177 documented regulons. (C) Comparison of the regulon coverage scores of CRS, CRS-c, GFR and PCS regarding the largest 12 known regulons. Each box represents the regulon coverage scores of these 12 regulons covered by the union of top n clusters (n = 10, 20, …, 100).

To further access the regulon identification power of our new framework, we compared its predicted regulons with the operon clusters identified based on GFR and PCS (represented by GFR, and PCS in Fig. 4). These clusters are generated by widely-used clustering tool MCL33,34. Here, we used 177 documented regulons in the RegulonDB database as benchmark data to evaluate the performance of predictions. We took the top 100 clusters for each of the three scores into consideration (see Supplementary Table S3). For an individual cluster, we assess the statistical significance of the coincidence level between it and a specific regulon using a modified Fisher Exact test, EASE35. Specifically, for the whole genome M and a known regulon R, if a predicted regulon P is random, then the probability of P and R sharing exactly n (>1) operons is:

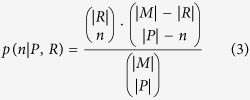graphic file with name srep23030-m3.jpg

where |X| means number of operons in set X. The EASE score is computed as:

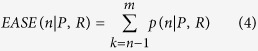graphic file with name srep23030-m4.jpg

where m = min{|P|, |R|}. Intuitively, the smaller an EASE score is, the more significant matching between a predicted operon cluster and a known regulon has. Since a predicted regulon could overlap with many known regulons, only the smallest EASE score was kept. As shown in Fig. 4A, the primary operon clusters, CRS-c, using the score designed by us have much lower EASE scores than those of the other two scores, where the EASE scores are transferred to the −log() scale. And the optimized clusters can reach even better performance (More details can be found in Supplementary Table S4).

On the other hand, we defined the regulon coverage score for a known regulon as Ma et al. did26 to measure the coverage of individual operons of a regulon by certain predicted operon clusters, which provides another way to evaluate the consistency between predicted clusters and known regulons. Note that the larger the score is, the more component operons of the corresponding regulon this predicted clusters could correctly cover. Here, we used the top n (n = 10, 20, …, 100) clusters to calculate these scores for all the known 177 regulons, and the comparison among these four sets of clusters (CRS, CRS-c, GFR and PCS) are shown in Fig. 4B. It is very clear that the regulon coverage scores corresponding to CRS are remarkably higher than those for the other two scores, especially for optimized ones. More details can be found in Supplementary Table S5. Furthermore, Fig. 4C showcases a comparison among the clusters generated by the three functional relatedness scores in terms of the 12 largest regulons each of which contains at least 20 component operons: CRP, Fur, FNR, IHF, Fis, Lrp, CpxR, LexA, NsrR, NarL, Cra and ArcA. We can see that CRS based clusters still keep the significant performance advantages. Further analysis showed the coverage scores of the small regulons tend to have large variance between 0 and 1, especially for those having less than five operons. See Figure S2 in Supplementary materials for more details.

Validation of developed methods based on available microarray gene expression data

Since the 177 regulons documented in the RegulonDB probably only represent a portion of all the regulons encode in E. coli K12, we also validated our predicted regulons against the co-expression gene sets identified by applying our in-house bi-clustering program, QUBIC36,37 on the genome-scale microarray gene expression data. Because co-expression indicates co-regulation, these co-expressed gene sets could be used for validation. For each of our predicted regulons, we compute an EASE score in the same way as did in above section, using the co-expressed gene sets inferred from microarray data instead of documented ones. If the corresponding EASE score of a predicted regulon is under a certain cutoff (1e-3), its member genes tend to be co-expressed under specific conditions and it is determined as a supported one by the transcriptomic data. It is also worth noting that, three different parameters of QUBIC were used to generate co-expressed gene sets with various scales for our regulon validation, as the scale of co-expressed gene sets does have impacts on the EASE score calculation and different scales may lead to different conclusion based on the same predicted regulons. The details of QUBIC’s parameters and matching identified bi-clusters can be found in Table 1. As shown in Fig. 5, over 65% of our predicted regulons are supported by all three types of bi-clusters, which are consistently higher than those results using the other two scores. Please see details in Supplementary Table S6. The performance of the GFR is slightly worse than our CRS score and much better than the PCS. It is not surprised because GFR score already integrated the co-expression information when it is calculated. This also demonstrates that our CRS score, based on genomic sequences alone, and has a very competitive prediction power.

Table 1. Three types of bi-clusters (default, loose and strict) correspond to the different parameters of c (conservedness of the bi-clusters), 0.95, 0.90 and 1.00, respectively.

Bi-cluster type #bi-cluster Largest size Smallest size Average size
default 500 526 32 105.9
loose 500 588 32 122.7
strict 500 250 41 66.8
Open in a new tab

Figure 5. Percentage of predicted regulons supported by the co-expression gene sets.

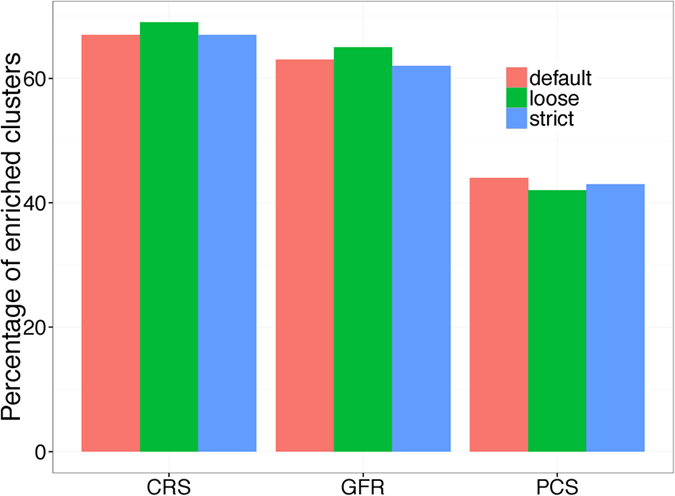
Figure 5

Open in a new tab

Each of CRS, GFR and PCS identified regulons combined with a clustering method. Three kinds of co-expression gene sets correspond to different parameters of QUBIC (Table 1).

Implementation on DIMINDA web server

To facilitate the usage and application of our new framework, we have implemented and integrated it into DMINDA31. It is an integrated user-friendly web server for DNA motif prediction and analyses based on motif finding programs BOBRO38, motif analysis package BOBRO2.039, and the DOOR2.0 database containing operons for more than 2,000 prokaryotic genomes40. We listed all 2,072 prokaryotic genomes on the web server, and the users can perform our new computational framework on any of them to calculate CRS and predict regulons easily. An illustration of how to use the new framework in DMINDA can be found in the Supplementary Appendix 1.

Discussion

While numerous regulons have been experimentally identified in a few model organisms including E. coli K12, the full elucidation of all the regulons encoded in this or any bacterial genome may have to rely heavily on computational approaches. The reason is that experimental detection of a regulon depends on the ability to design the conditions that can activate the regulon to be experimentally observable. However, there is no information that can guide the experimental design to have every regulon in a bacterium be activated. In this paper, we have designed a computational tool for regulon identification in bacterial genomes, by integrating genome-scale motif analyses and accurate operon identification into a phylogenetic footprinting framework. The key intellectual contributions of this framework include (i) the discovery of a new co-regulation score (CRS) between any pair of operons, which complements the known linkages among operons in the same regulon, and has made it possible, in conjunction with the conserved motif information, to solve the regulon problem at a genome scale; (ii) a suite of programs for solving a number of important and currently not well solved bacterial genome analysis problems, namely mapping of orthologous genes between two genomes, prediction of motifs with high efficacy and prediction of regulons; and (iii) a collection of new regulons in E. coli K12. With the new framework, people can identify all encoded regulons for any newly sequenced complete genome systematically, which could be applied to elucidate global transcriptional regulatory network and associated metabolic pathways. In addition, people can identify regulons responsive to particular stimuli, whose operon members have their expression values changed, i.e. up- or down-regulated, in the corresponding high-throughput transcriptomic data. Upon getting genome-scale regulons identified in substantial organisms, it is a good opportunity for researchers to understand how the regulatory systems have evolved in bacteria through comparative genomics studies. It is noteworthy that our whole framework can be easily extended to regulon identification in eukaryotic genomes by withdrawing the operon concept in the orthology mapping step. As there are more and more Chip-seq data accumulated in human and mouse, we expect that it should have similar performance as in bacterial genomes.

However, there is still a big room to improve in computational prediction of regulons. The key issue is that our understanding about regulons is not much beyond its basic definition, i.e., operons sharing conserved motifs; and this information by itself is too weak to allow the current motif-finding methods to reliably identify all the co-regulated operons encoded in a genome. It is not hard to imagine that by chance, some sequence segments across some promoters may look alike among over 2,000 E. coli promoters, while at the same time, some regulons have only a few component operons, i.e., having conserved motifs among just a few promoters. Hence it is very challenging to distinguish the true motifs of local regulons from the accidental ones. Some global regulators’ binding sites show several branch of conservation thus may be divided into several local clusters25. Also for some regulons, their motifs tend to be less conserved41 and are hard to be identified, which makes the motif prediction suffers the high false positive rate in their prediction. We believe that a key to overcome above issues is through identification of new and more specific characteristics of regulons, based on which more reliable predictions could be made. For example, documented motifs tend to cluster together with other motifs in their genomic neighborhoods42. In future, we plan to explore various scoring schemes to include such information, among other relevant information that we will explore. Meanwhile, with the advent of large-scale ChIP-seq data in the prediction of TF binding sites43,44, people can reliably assess the possibility for each nucleotide in a given promoter to be occupied by specific TF. Such information can help to decrease the false positive rate in motif prediction and make the computational prediction of regulons more reliable.

Materials and Methods

Data Preparation

All the data included in this paper is publicly available. We used E. coli K12 as the target genome for assessing our algorithms and other selected 216 bacterial genomes as its reference genomes, which were downloaded from the NCBI (released as of November 2011). These reference genomes belong to the same phylum and different genus of E. coli, which were used to identify orthologous genes as in literatures45,46. To evaluate predicted regulons, we downloaded gene expression data of E. coli collected under 466 conditions from the M3D database47. In addition, we retrieved 2,462 operons of the target genome E. coli K12 and 454,181 operons for those 216 reference genomes from the operon database DOOR2.040,48. This database contains predicted operons for 2,072 organisms with 2,205 chromosomes and 1,645 plasmids, consisting of a total of 3,902,851 operons.

Identification of cis regulatory motifs by a phylogenetic footprinting framework

The basic assumption of the phylogenetic footprinting technique is that orthologous genes across related organisms tend to use orthologous transcription regulators, and their binding sites are more conserved at the DNA sequence level than surrounding non-functional sequences24,49. It usually has three steps: orthology identification, promoter collection, and motif finding (Fig. 1A).

Orthology identification for genes in target genome

Identification of orthologous genes between two genomes is a foundation for phylogenetic footprinting. Here we used our in-house program GOST50, which takes the operon information into consideration as a functional guidance to perform orthology identification. Specifically, GOST first assigns the genes as working partners of each other if they belong to the same uber-operon51, and then performs orthology mapping between two bacterial genomes using a constrained maximum matching algorithm on a bipartite graph. Finally, the genes are considered as orthologous genes if they have working partners that are homologous across the two genomes.

Collection of orthologous promoters based on orthology and the operon structure

For an operon A in E. coli, the new framework first constructed an orthologous graph GA. The vertices in GA represent the operon A and the other operons across all the reference genomes that share at least one orthologous gene with A. For any pair of vertices in GA, we added an non-weighted edge if the two corresponding operons share at least one orthologous gene; and then identified the largest operon group containing A using MCL34, denoted as OA. All the other operons in OA are called orthologous operons of A. Finally, we extracted the upstream sequence set PA, according to the operon group OA, as the orthologous promoters. Specifically, we used upstream 300 bps or the whole intergenic region (if less than 300 bps) as promoters starting from translation start site of each of these operons (the transcription start sites are typically not easy to be collected). In addition, we eliminated redundant promoters by CD-HIT52, as the reference genomes cannot be too close to target genome, otherwise the motifs in promoters are not sufficiently better conserved than surrounding nonfunctional sequence.

Application of motif finding on orthologous promoter set

We ran our in-house motif-finding tool, BOBRO26,31, on the orthologous promoter set to find motifs. BOBRO had been tested on phylogenetic footprinting data and showed consistently better performance than other existing tools38. The identified motifs are used in calculating co-regulation scores between any pair of operons in the next sub-section.

Calculation of the Co-Regulation Score (CRS) between a pair of operons

Our regulon prediction algorithm is based on the observation that any two conserved motifs (a motif presents as a set of gapless aligned motif instances in algorithm design) without functional relationship are statistically hard to be similar to each other. First of all, we used BOBRO to identify all statistically significant motifs in regulatory promoters PA for each operon A in target genome as described in previous section. Then the motif similarity score can be calculated based on their corresponding position weight matrix (PWM)26. For any pair of operons, A and B, in the target genome, the two sets of identified motifs in their regulatory promoters are denoted as MA = {mA1, mA2, …, mAs} and MB = {mB1, mB2, …, mBt}, respectively (Fig. 1B). We calculated the similarity scores for each pair mAi and mBj (i = 1, …, s and j = 1, …, t), which are denoted as ωi,j. Now we can define a Co-Regulation Score (CRS) between A and B along as following,

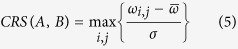graphic file with name srep23030-m5.jpg

where 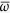Inline graphic and σ represent the average and variance of similarity scores between any pair of motifs from MA and MB respectively (Fig. 1B). Intuitively, the larger the CRS is, the higher probability of co-regulatory relationship these two operons have. In order to eliminate the effect of insignificant motif pairs, we set CRS to zero if the maximum ω between two operons is not higher than a given threshold (we use 0.5 in this analysis according to our previous study39). Besides, we assigned a label set L for each operon pairs to record the labels of motif pairs, which represent the potential co-regulation relationship of two operons. Initially, the L for each two operons contains the indexes of motif pairs with maximum CRS (>0). For example, L = [(1, 1)] for operon A and B because ωmax = ω1,1 (Fig. 1B). It is worth noting that, two operons can be co-regulated by different TFs, thus some other significant motif pairs, besides the one reaching CRS, should also be included. The label set L will be expanded in the following graph construction section, aiming to retrieve these significant motif pairs and get rid of randomly generated noises.

Construct of co-regulated graph G

Based on the CRSs in the previous sub-section, we can construct a completed graph G in which each vertex represents an operon and the weight of each edge is the CRS (along with its label set) between the two corresponding operons. This graph represents the co-regulated relationship between any two operons and the normalized CRS scores will facilitate the following regulon construction. It is well known that one operon can be regulated by various TFs; hence, for an operon A, different motifs in MAmay reach CRS with different operons. This point will be used to improve the graph G by extending the label set L between any two operons. First, the motifs showing in at least one label set of G are denoted as effective motifs. Next, the labels of a motif pair (mAi, mBj) will be added to L, if (i) 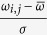Inline graphic is higher than a specific threshold (we used 2 in this paper), and (ii) at least one of the two motifs is the effective motif. Taking operons A and B as an example (Fig. 1C), suppose that the motif pairs (mA2, mB2) and (mAs, mBt) have the second and third largest similarity scores with 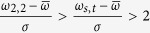Inline graphic; and only mAs is annotated as an effective motif in above graph G. In this situation, the labels (s, t) will be added to L, while (2, 2) is excluded (Fig. 1B,C). The above strategy is standing on following view that the real co-regulated motif pairs could only be defeated by another co-regulated motif pairs or noise with higher scores by chance, between a pair of its regulating operons. And the updated label sets in G will benefit the regulon identification showcased in the next sub-section.

Regulon identification through clustering operons on a novel graph model

Intuitively, the operons belonging to the same regulon will compose a heavier cluster in G (that is, a sub-graph with higher weight edges). However, a heavy cluster has not necessary to be a regulon, since one operon may belong to several regulons thus the heavy edges in the heavy cluster may be derived from different motifs, which are called meta-clusters in this study (Fig. 1D). In fact, the regulons encoded in a genome could be overlapped or even inclusive. Therefore, the clustering for regulon prediction should first allow overlapped clusters, and also be capable of decomposing meta-clusters. It brings great challenges in algorithm design. Besides, identifying all heavy sub-graphs in a weighted graph itself is NP-hard. Hence, in this paper, we designed a heuristic clustering algorithm to identify regulons.

We attempted to address the above issues by building a new graph from G. Firstly, we blew up each vertex in G into several new vertices corresponding to a set of motifs of this particular operon and their related label set L; then set the edge weight and modified it based on the neighborhood similarity of the motif pairs, with the biological insight that two vertices belonging to a same regulon should more likely to have similar neighbors. Finally, we identified heavy sub-graphs in the new graph to infer regulons.

Step 1: Construction of new graph G′

We reconstructed a new graph G′, by splitting each vertex in G into a set of new vertices, which correspond to the motifs included in all its related label sets. And the motif pairs in the label sets of G are connected as the edges of G′ (Fig. 1D). The weight of the edge between vertices Ai and Bj corresponding to motifs mAi and mBj will be assigned as

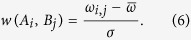graphic file with name srep23030-m9.jpg

Obviously, the construction of G eliminated most of edges derived from randomly matching between motifs, thus will greatly reduce false positives in regulon prediction. More importantly, in the new graph G′, the meta-clusters have been decomposed and each heavy cluster in G′ will correspond to a regulon, without any overlap with other regulons. Hence, we can solve a much easier clustering problem for identifying heavy sub-graphs in G′ than in G, without introducing too much false positives.

Step 2: Modification of graph G′

For any edge (Ai, Bj) in G′, its weight is modified as following:

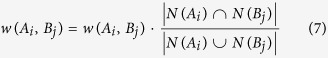graphic file with name srep23030-m10.jpg

where N(x) represents all the vertices adjacent with vertex x and |X| represents the number of elements in X. Then we only kept the top α% edges in G′ according to their weights. For each vertex, we retrieved top β adjacent edges if less than β adjacent edges left after deletion. The default values for α and β are 20 and 10 in this study, respectively. The modification should make the graph model represent the biological reality more accurately. Actually the strategy for defining similarity in networks used here has been proved to be effective in previous study26. In the next two steps, we will identify cliques in the modified graph and then expand them to heavy sub-graphs.

Note that the idea of finding regulons through finding cliques or near cliques has been widely used in the existing regulon-finding programs (22–23). However, there are two technical issues: (i) the constructed graphs are generally quite noisy, leading to high false positive predictions, and (ii) the cliques alone are not adequate to capture the majority of the regulons, hence leading high false negative predictions. We have addressed the issue (i) by the well-designed CRS and newly constructed graph G′ with a high signal-to-noise ratio; and we have addressed (ii) by decomposing the regulon identification problem into two steps: finding cliques in the representing graph G′ and using them as the seeds of regulons to find the other regulon members through refining and expanding the cliques.

Step 3: Clique finding in G′

We identified all disjoint maximal cliques in G′ using the following greedy approach:

  1. set C to be empty;

  2. choose an edge (u, v) in G′ with the largest N(u) ∩ N(v);

  3. add u and v to the current clique C;

  4. repeat the above procedure on the sub-graph induced by N(u) ∩ N(v) until the sub-graph is empty;

  5. remove the current clique from G′, and repeat this step on the remaining graph for M times (the default is M = 300 according to the approximate number of known TFs in bacterial genomes).

Step 4: Refinement and optimization of identified cliques

For each clique C identified in Step 3, its corresponding operons are denoted as R and its most statistical significant motif as mc according to the P-value derived by BOBRO. Then motif mc is scanned against the orthologous promoter sets of all the operons using BBS, which also provides P-value for the scanning results. For operon A belongs to R, if corresponding P-value of scanning results is larger than 0.05, then R = R\A. For any operon A not in R, if its corresponding P-value of scanning results is less than 0.05, then add A to R. Finally, the cliques will be expanded to heavy sub-graphs, from which the candidate regulons will be generated.

Additional Information

How to cite this article: Liu, B. et al. Bacterial regulon modeling and prediction based on systematic cis regulatory motif analyses. Sci. Rep. 6, 23030; doi: 10.1038/srep23030 (2016).

Supplementary Material

Supplementary Information
srep23030-s1.pdf (4.7MB, pdf)
Supplementary Dataset 1
srep23030-s2.xls (7.7MB, xls)
Supplementary Dataset 2
srep23030-s3.xls (12.7MB, xls)

Acknowledgments

This work was supported by the State of South Dakota Research Innovation Center and the Agriculture Experiment Station of South Dakota State University. This work was also supported by the National Nature Science Foundation of China (NSFC) [61303084 to B. Liu, 31571354, 61272016 and 61432010 to G. Li.]; B. Liu’s work also be supported by Young Scholars Program of Shandong University (YSPSDU, 2015WLJH19).

Footnotes

Author Contributions G.L. and Q.M. conceived the basic idea. Q.M. planned the project. B.L. and C.Z. designed the algorithms, developed the programs, and carried out the experiments. H.Z. and C.Z. implemented the web server of the programs. E.Z. and Q.L. helped polish the paper. All authors edited the manuscript and approved the final manuscript.

References

  1. Ishihama A. Prokaryotic genome regulation: a revolutionary paradigm. Proc Jpn Acad Ser B Phys Biol Sci 88, 485–508 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ishihama A. Prokaryotic genome regulation: multifactor promoters, multitarget regulators and hierarchic networks. FEMS Microbiol Rev 34, 628–645 (2010). [DOI] [PubMed] [Google Scholar]
  3. Novichkov P. S. et al. RegPredict: an integrated system for regulon inference in prokaryotes by comparative genomics approach. Nucleic Acids Res 38, W299–307 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ma S. et al. Integrated Modeling of Gene Regulatory and Metabolic Networks in Mycobacterium tuberculosis. PLoS Comput Biol 11, e1004543 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Jacob F., Perrin D., Sanchez C. & Monod J. Operon: a group of genes with the expression coordinated by an operator. C R Hebd Seances Acad Sci 250, 1727–1729 (1960). [PubMed] [Google Scholar]
  6. Manson McGuire A. & Church G. M. Predicting regulons and their cis-regulatory motifs by comparative genomics. Nucleic Acids Res 28, 4523–4530 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gama-Castro S. et al. RegulonDB (version 6.0): gene regulation model of Escherichia coli K-12 beyond transcription, active (experimental) annotated promoters and Textpresso navigation. Nucleic Acids Res 36, D120–124 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Lobo D. & Levin M. Inferring regulatory networks from experimental morphological phenotypes: a computational method reverse-engineers planarian regeneration. PLoS Comput Biol 11, e1004295 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Wang P. et al. ChIP-Array 2: integrating multiple omics data to construct gene regulatory networks. Nucleic Acids Res 43, W264–269 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chen Y. H., Yang C. D., Tseng C. P., Huang H. D. & Ho S. Y. GeNOSA: inferring and experimentally supporting quantitative gene regulatory networks in prokaryotes. Bioinformatics 31, 2151–2158 (2015). [DOI] [PubMed] [Google Scholar]
  11. Kumka J. E. & Bauer C. E. Analysis of the FnrL regulon in Rhodobacter capsulatus reveals limited regulon overlap with orthologues from Rhodobacter sphaeroides and Escherichia coli. BMC Genomics 16, 895 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Tan K., Moreno-Hagelsieb G., Collado-Vides J. & Stormo G. D. A comparative genomics approach to prediction of new members of regulons. Genome Res 11, 566–584 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Pittard J., Camakaris H. & Yang J. The TyrR regulon. Mol Microbiol 55, 16–26 (2005). [DOI] [PubMed] [Google Scholar]
  14. Su Z. et al. Computational inference and experimental validation of the nitrogen assimilation regulatory network in cyanobacterium Synechococcus sp. WH 8102. Nucleic Acids Res 34, 1050–1065 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dam P., Olman V., Harris K., Su Z. & Xu Y. Operon prediction using both genome-specific and general genomic information. Nucleic Acids Res 35, 288–298 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dam P., Su Z., Olman V. & Xu Y. In silico construction of the carbon fixation pathway in Synechococcus sp. WH8102. J Biol. Syst. 12, 97–125 (2004). [Google Scholar]
  17. Yellaboina S., Seshadri J., Kumar M. S. & Ranjan A. PredictRegulon: a web server for the prediction of the regulatory protein binding sites and operons in prokaryote genomes. Nucleic Acids Res 32, W318–320 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. De Jong A., Pietersma H., Cordes M., Kuipers O. P. & Kok J. PePPER: a webserver for prediction of prokaryote promoter elements and regulons. BMC Genomics 13, 299 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Katara P., Grover A. & Sharma V. Phylogenetic footprinting: a boost for microbial regulatory genomics. Protoplasma 249, 901–907 (2012). [DOI] [PubMed] [Google Scholar]
  20. Newberg L. A. et al. A phylogenetic Gibbs sampler that yields centroid solutions for cis-regulatory site prediction. Bioinformatics 23, 1718–1727 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gupta S., Stamatoyannopoulos J. A., Bailey T. L. & Noble W. S. Quantifying similarity between motifs. Genome Biol 8, R24 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Qin Z. S. et al. Identification of co-regulated genes through Bayesian clustering of predicted regulatory binding sites. Nat Biotechnol 21, 435–439 (2003). [DOI] [PubMed] [Google Scholar]
  23. Jensen S. T., Shen L. & Liu J. S. Combining phylogenetic motif discovery and motif clustering to predict co-regulated genes. Bioinformatics 21, 3832–3839 (2005). [DOI] [PubMed] [Google Scholar]
  24. Alkema W. B., Lenhard B. & Wasserman W. W. Regulog analysis: detection of conserved regulatory networks across bacteria: application to Staphylococcus aureus. Genome Res 14, 1362–1373 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Brohee S. et al. Unraveling networks of co-regulated genes on the sole basis of genome sequences. Nucleic Acids Res 39, 6340–6358 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Fuxman Bass J. I. et al. Using networks to measure similarity between genes: association index selection. Nat Med 10, 1169–1176 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Chou W. et al. Analysis of strand-specific RNA-seq data using machine learning reveals the structures of transcription units in Clostridium thermocellum. Nucleic Acids Res 43, e67 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wu H., Su Z., Mao F., Olman V. & Xu Y. Prediction of functional modules based on comparative genome analysis and Gene Ontology application. Nucleic Acids Res 33, 2822–2837 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Schafer J. & Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat Appl Genet Mol Biol 4, Article32 (2005). [DOI] [PubMed] [Google Scholar]
  30. Kim P. J. & Price N. D. Genetic co-occurrence network across sequenced microbes. PLoS Comput Biol 7, e1002340 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ma Q. et al. DMINDA: an integrated web server for DNA motif identification and analyses. Nucleic Acids Res, 42 (W1), W12–W19 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). [DOI] [PubMed] [Google Scholar]
  33. Enright A. J., Van Dongen S. & Ouzounis C. A. An efficient algorithm for large-scale detection of protein families. Nucleic Acids Res 30, 1575–1584 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Van Dongen S. Graph clustering by flow simulation PhD thesis, University of Utrecht (2000).
  35. Huang da W., Sherman B. T. & Lempicki R. A. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat Protoc 4, 44–57 (2009). [DOI] [PubMed] [Google Scholar]
  36. Li G., Ma Q., Tang H., Paterson A. H. & Xu Y. QUBIC: a qualitative biclustering algorithm for analyses of gene expression data. Nucleic Acids Res 37, e101 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Zhou F., Ma Q., Li G. & Xu Y. QServer: a biclustering server for prediction and assessment of co-expressed gene clusters. PLoS One 7, e32660 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Li G., Liu B., Ma Q. & Xu Y. A new framework for identifying cis-regulatory motifs in prokaryotes. Nucleic Acids Res 39, e42 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ma Q. et al. An integrated toolkit for accurate prediction and analysis of cis-regulatory motifs at a genome scale. Bioinformatics 29, 2261–2268 (2013). [DOI] [PubMed] [Google Scholar]
  40. Mao X. et al. DOOR 2.0: presenting operons and their functions through dynamic and integrated views. Nucleic Acids Res 42, D654–659 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang S., Xu M., Li S. & Su Z. Genome-wide de novo prediction of cis-regulatory binding sites in prokaryotes. Nucleic Acids Res 37, e72 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Hobert O. Gene regulation by transcription factors and microRNAs. Science 319, 1785–1786 (2008). [DOI] [PubMed] [Google Scholar]
  43. Pepke S., Wold B. & Mortazavi A. Computation for ChIP-seq and RNA-seq studies. Nat Met 6, S22–32 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Guo Y., Mahony S. & Gifford D. K. High resolution genome wide binding event finding and motif discovery reveals transcription factor spatial binding constraints. PLoS Comput Biol 8, e1002638 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhou C. et al. New Insights into Clostridia Through Comparative Analyses of Their 40 Genomes. Bioenergy Research 7, 1481–1492 (2014). [Google Scholar]
  46. Ma Q. et al. Understanding the commonalities and differences in genomic organizations across closely related bacteria from an energy perspective. Sci China Life Sci 57, 1121–1130 (2014). [DOI] [PubMed] [Google Scholar]
  47. Faith J. J. et al. Many Microbe Microarrays Database: uniformly normalized Affymetrix compendia with structured experimental metadata. Nucleic Acids Res 36, D866–870 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Mao F., Dam P., Chou J., Olman V. & Xu Y. DOOR: a database for prokaryotic operons. Nucleic Acids Res 37, D459–463 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Snel B., van Noort V. & Huynen M. A. Gene co-regulation is highly conserved in the evolution of eukaryotes and prokaryotes. Nucleic Acids Res 32, 4725–4731 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Li G. et al. Integration of sequence-similarity and functional association information can overcome intrinsic problems in orthology mapping across bacterial genomes. Nucleic Acids Res 39, e150 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Che D., Li G., Mao F., Wu H. & Xu Y. Detecting uber-operons in prokaryotic genomes. Nucleic Acids Res 34, 2418–2427 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Huang Y., Niu B., Gao Y., Fu L. & Li W. CD-HIT Suite: a web server for clustering and comparing biological sequences. Bioinformatics 26, 680–682 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep23030-s1.pdf (4.7MB, pdf)
Supplementary Dataset 1
srep23030-s2.xls (7.7MB, xls)
Supplementary Dataset 2
srep23030-s3.xls (12.7MB, xls)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES