Mesoscopic Fluorescence Molecular Tomography for Evaluating Engineered Tissues

Abstract

Optimization of regenerative medicine strategies includes the design of biomaterials, development of cell-seeding methods, and control of cell-biomaterial interactions within the engineered tissues. Among these steps, one paramount challenge is to non-destructively image the engineered tissues in their entirety to assess structure, function, and molecular expression. It is especially important to be able to enable cell phenotyping and monitor the distribution and migration of cells throughout the bulk scaffold. Advanced fluorescence microscopic techniques are commonly employed to perform such tasks; however, they are limited to superficial examination of tissue constructs. Therefore, the field of tissue engineering and regenerative medicine would greatly benefit from the development of molecular imaging techniques which are capable of non-destructive imaging of three-dimensional cellular distribution and maturation within a tissue-engineered scaffold beyond the limited depth of current microscopic techniques. In this review, we focus on an emerging depth-resolved optical mesoscopic imaging technique, termed Laminar Optical Tomography (LOT) or Mesoscopic Fluorescence Molecular Tomography (MFMT), which enables longitudinal imaging of cellular distribution in thick tissue engineering constructs at depths of a few millimeters and with relatively high resolution. The physical principle, image formation, and instrumentation of LOT/MFMT systems are introduced. Representative applications in tissue engineering include imaging the distribution of human mesenchymal stem cells (hMSCs) embedded in hydrogels, imaging of bio-printed tissues, and in vivo applications.

1. Introduction

Regenerative medicine has emerged as an important discipline which aims at introducing living cells or functioning tissues for repair or replacement of damaged tissues and organs [1-3]. One major challenge in regenerative medicine is spatial and temporal assessment of functional and molecular cellular states throughout a biodegradable scaffold. The current state-of-the-art method for quantifying 3D cell distribution in scaffolds several millimeters thick involves fluorescent confocal microscopy imaging of cryo-sectioned samples and then digital 3D image recompiling [4]. Although robust, this approach is destructive and time-consuming, and therefore is not appropriate for longitudinal inspection of a large set of samples and/or for assessment of tissue maturation prior to implantation. Thus, there is a critical need for the development of methods that can image and analyze the structure and function of engineered tissue in a non-destructive manner and with high resolution.

In addition, constructing a 3D tissue and maintaining its vitality often requires preservation of a tissue construct in vitro, which places considerable challenges on tissue characterization methodologies such as imaging techniques. Characterization of the engineered tissue may be performed at the morphological or molecular level, where the former delivers structural information and the latter helps to extract functional information. Delicacy of live cells and the extracellular matrix requires the imaging technique to be non-contact and in reflectance configuration for minimal interference and ease of operation. Moreover, as the microenvironment is typically precisely controlled and should not be perturbed, the imaging technique should be able to directly capture information while the tissue is embedded in a closed bio-chamber.

Optical imaging enables the non-destructive quantification of both scaffold architecture and cell distribution at high resolution. Tissue engineering scaffolds are typically constructed from laden hydrogels, electron spun fibers, porous scaffolds, or 3D printed scaffolds [5-8]. These materials can exhibit significant scattering such that light penetration into the samples is limited. Available optical modalities include conventional microscopy, non-linear optical techniques as well as tomographic techniques [9]. The most popular technique, fluorescence confocal microscopy (FCM), can visualize cells and molecules via a wide variety of fluorescent probes at sub-cellular resolution. However, FCM has a limited imaging depth of 100-200 μm [10]. For deeper investigation of engineered tissues, two-photon microscopy (TPM) is preferred [10], but typically still limited to ~500 μm [11-13]. Note that by leveraging the lower scattering in longer wavelengths (>1200 nm), TPM may enable imaging up to 1.5 mm, but this approach is still not widely available [14, 15]. Hence, although these microscopic methods offer high resolution, they typically provide only a partial picture of the tissue construct (small field of view and limited penetration depth) and require long imaging times [9, 15]. Thus, methods other than optical microscopy need to be employed in order to image at depths of a few millimeters.

For instance, optical coherence tomography (OCT) can perform high resolution, cross-sectional subsurface tomographic imaging of the microstructure of engineered tissues. OCT has been used for imaging cell formation within a tissue construct with high resolution [16, 17] and is able to deliver fast 3D structural information of tissues up to 1-2 mm thick. However, OCT image formation relies on back-scattered photons and provides mainly morphological information. Only recently, spectroscopic OCT (SOCT) [18, 19] has enabled imaging of molecular signatures [20], and has been successfully applied to imaging of engineered scaffolds to discern cellular phenotypes [21]. However, this approach does not rely on the wide libraries of fluorophores available. For many applications, fluorescence techniques based on gene reporters or established immunostains are required.

Laminar optical tomography (LOT)/Mesoscopic Fluorescence Molecular Tomography (MFMT) is an emerging optical tomographic imaging modality that relies on fluorescence signals similar to FCM but with the unique combination of millimeter-depth imaging and relatively high tomographic resolution [22]. Similar to diffuse optical tomography (DOT) [23, 24], LOT/MFMT is based on multiple detectors with millimeter-range separation from the illumination source and image formation via an optical inverse problem [25, 26]. The combination of dense spatial data sets with an accurate forward model enables 3D reconstructions of fluorophore distributions with a resolution of 100-200 μm at imaging depths of ~3 mm [27]. Initially, LOT/MFMT had been developed to image absorption contrast for hemodynamic imaging [28, 29] and cancer detection [30]. Then it was rapidly adapted to molecular imaging (fluorescent LOT or FLOT) using fluorescent contrast agents [31-34]. The technique has since been employed for diverse in vivo applications as well as tissue engineering applications and with different names such as mesoscopic epifluorescence tomography (MEFT) [35-37] or mesoscopic fluorescence molecular tomography (MFMT) [27, 38, 39].

In this review, we will first cover the physical principle of the technique that enables depth-resolved imaging. Then, we will introduce the formulation of the optical inverse problem and summarize current algorithmic implementations. We will then recapitulate the overall designs and sub-system components of typical instrumentation. Lastly, we will provide representative applications in tissue engineering to highlight the potential of LOT/MFMT to non-destructively evaluate structure and function of engineered tissues and tissue constructs.

2. Materials and Methods

2.1 Principle of LOT/MFMT

The working principle of LOT/MFMT is based on diffuse optics, in which light is shined on a turbid sample and scattered light exiting the sample at a distant location is collected [25, 40]. As light propagates, it may experience three main physical processes: scattering, absorption, and fluorescence [41]. The relative probability of occurrence for each of these processes is dependent on the type of sample imaged [42]; for in vivo and tissue engineering applications, scattering is the prevailing phenomenon. As deeper tissues are imaged (millimeter-scale), the path-length of photons is increased and the light propagation is then akin to a random-walk process in which multiple scattering events are becoming predominant [43]. In this regime, direct imaging methods that rely on non-scattered photons, such as FCM, cannot operate due to limitations in the illumination power that can be employed safely.

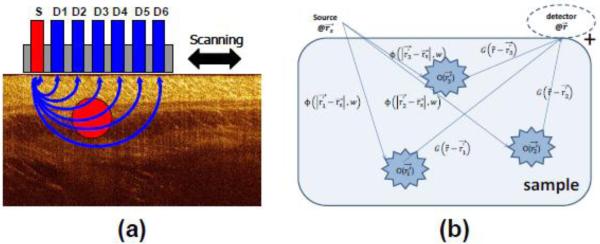
On the other hand, LOT/MFMT is designed to collect scattered photons. However, performing imaging solely based on collection of these diffuse photons yields low resolution images without depth-resolving power. To perform tomographic imaging with depth discrimination and relatively high resolution, scattered photons are collected at different locations on the surface of the sample to yield multiple projections. In the case of LOT/MFMT an epi-configuration is employed, leading to a proportional relationship between the source-detector separation and the average investigation depth [32]. Fig. 1a shows the cross-sectional diagram of a typical LOT/MFMT source-detector configuration, with the average photon path depicted by the blue lines. Typically, LOT/MFMT utilizes small source-detector separation (from a couple of hundred microns to a few millimeters) so that the detectors collect information from a relatively shallow depth (mesoscopic regime). This range of source-detector separations imparts depth sensitivity and, when associated with a light propagation model that accounts for excitation and emission light, allows for tomographic imaging with high resolution compared to DOT.

FIGURE 1.

(a) Schematic of LOT/MFMT source (S) and detector (D1...D6) configuration. (b) Graphical illustration of photon propagation in LOT/MFMT.

Mathematically, the fluorescence signals collected by a detector positioned at r_d after illumination from a source positioned at r_s can be expressed as [44]

$$F(\overrightarrow{r_s},\overrightarrow{r_d})=\frac{{\sigma }_{ex}.\gamma }{4\pi }\int \Phi (\overrightarrow{r}-\overrightarrow{r_s}).O\left(\overrightarrow{r}\right).G(\overrightarrow{r_d}-\overrightarrow{r})d^3\overrightarrow{r}$$ (1)

where σ_ex is the absorption cross-section of the fluorophores at the excitation wavelength, γ is the fluorescence quantum yield, Φ(r) is the excitation fluence distribution calculated from the excitation photon radiance, O(r) is the fluorophore concentration at position r, and G(r) the probability that a photon emitted by a source at position r will be detected at r_d. Fig. 1b shows a graphical illustration of this process. Eq. 1 is the basis of the optical inverse problem in LOT/MFMT. We can form a linear system of equations that link the acquired measurements with the unknown distribution of the fluorescent probe. The image space is discretized in elements of unit volumes (voxel) and then the linear system can be expressed as:

$$F\equiv \left[\begin{array}{c}\hfill F(\overrightarrow{r_{s1}},\overrightarrow{r_{d1}})\hfill \\ \hfill F(\overrightarrow{r_{s2}},\overrightarrow{r_{d2}})\hfill \\ \hfill ⋮\hfill \\ \hfill F(\overrightarrow{r_{sM}},\overrightarrow{r_{dM}})\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill W_{11}\hfill & \hfill \cdots \hfill & \hfill W_{1N}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill W_{M1}\hfill & \hfill \cdots \hfill & \hfill W_{MN}\hfill \end{array}\right]\left[\begin{array}{c}\hfill O\left(\overrightarrow{r_1^{\prime }}\right)\hfill \\ \hfill O\left(\overrightarrow{r_2^{\prime }}\right)\hfill \\ \hfill ⋮\hfill \\ \hfill O\left(\overrightarrow{r_N^{\prime }}\right)\hfill \end{array}\right]\equiv WO$$ (2)

where M different measurements are acquired to solve $O\left(\overrightarrow{r}\right)$, which is represented by N discrete voxels. W = [W]_M×N is referred to the weight matrix or sensitivity (Jacobian) matrix. The optical inverse problem aims to solve this set of linear equations to retrieve $O\left(\overrightarrow{r^{\prime }}\right)$. This is done by first constructing the Jacobian matrix using a light-propagation model and a-priori knowledge of the sample geometry, optical endogenous properties (absorption and scattering coefficients), and fluorophore characteristics (extinction coefficient and quantum yield) as well as the relative positions of the source-detector pairs. Then, since the linear system cannot be directly inverted, an appropriate solver is employed to form the tomographic reconstructions.

2.2 Forward Model

There are a variety of methods to model photon propagation in scattering samples [45]. Although the diffusion equation, which is an approximation to the radiative transport equation (RTE), has been the preferred forward model in DOT due to its computational efficiency and ease of implementation, it cannot be employed for LOT/MFMT due to limited volume interrogation and thus, anisotropic light propagation [46]. In such cases, the RTE is the appropriate model but it is difficult to implement analytically and is notoriously unstable for the optical properties encountered in tissue engineering applications. Hence, the vast majority of LOT/MFMT work employs the Monte Carlo method to compute the optical forward problem [47, 48].

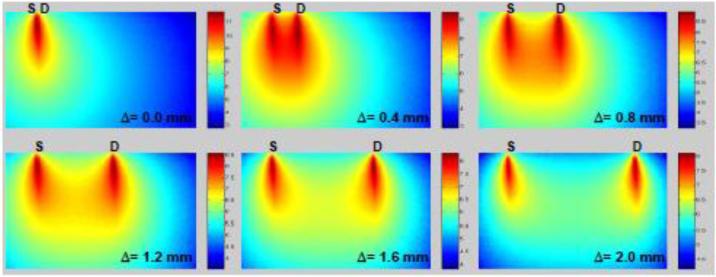
The Monte Carlo method is a stochastic forward model that tracks the interaction of photons through biological tissues. It is considered to be the gold standard for modeling light propagation in bio-photonics [49]. To obtain simulations with stochastic accuracy in a scattering medium, large packets of photons need to be simulated (10⁵ to 10⁹). In turn, this leads to lengthy computational time, especially for optical tomography in which thousands of source-detector pairs must be simulated. However, thanks to efficient formulations [50-52] as well as massively parallel computing (GPU or multi-core/CPU), Monte Carlo methods have recently become computationally attractive [53, 54]. Then the Jacobian can be computed efficiently via the perturbative Monte Carlo method or by the adjoint Monte Carlo method [47], with the latter mainly employed in LOT/MFMT. For instance, in the case of planar boundary conditions and symmetrical imaging arrangement, the computation of the Jacobian can be performed in less than 5 minutes on a personal computer using GPU-based MC code [38, 39, 46]. Fig. 2 depicts typical Jacobian profiles as computed by an adjoint Monte Carlo method for continuous-wave illumination and different detector offsets. The sensitivity profile varies as the source-detector separation (Δ) changes, with increased sensitivity to deep tissues when the detector is set farther away from the illumination.

FIGURE 2.

Monte-Carlo simulated measurement sensitivity distribution of FLOT measurements (log scale). Tissue geometry is 3 mm (lateral) by 2 mm (depth) with scattering coefficient μ_s = 8 mm⁻¹ for excitation and 7 mm⁻¹ for emission (g = 0.9). Adapted from Ref. 34 with permission.

2.3 Image Reconstruction for LOT/MFMT

After forming the forward problem, the 3D distribution of the fluorophore can be estimated using an inverse solver [55]. The diffuse optical inverse problem is well-known as one of the most difficult one to solve. It is typically ill-posed (less measurements than unknowns) and always ill-conditioned due to the diffuse nature of the light propagation. Moreover, reflectance geometry provides a more challenging inverse problem than transmittance geometry due to limited angular sampling [56].

The standard approach to solving inverse problems is to minimize ǁAx – bǁ using an iterative solver where is A stands for the Jacobian, x the unknown fluorophore distribution, and b the LOT/MFMT measurements. With such solvers, the estimate (image space) is updated iteratively to minimize the norm between the experimental measurements and the estimated measurements as obtained by the product of the Jacobian and the image space. Typically the iterative process is terminated either when a preset number of iterations is reached and/or when the residual of the norm is below a set value (tolerance). The maximum number of iterations and tolerance are chosen ad hoc and may vary based on the solver used. The most common iterative solvers employed in the field are the conjugate gradient (CG) method [27, 38, 39, 46], the least squares (LSQR) method [36, 57], and algebraic techniques [33, 58].

However, solving the linear system using these iterative solvers is still difficult since the system is ill-conditioned and thus very sensitive to noise propagation [59]. Hence, a regularization term is typically introduced to reach a balance between the accuracy and the high-frequency noise mitigation in the estimate. This regularization parameter is used to effectively control the influence of the model mismatch, noise, and systemic error during reconstruction [22]. Even in the case of over-determined systems such as LOT/MFMT systems in the de-scanned configuration [29, 38], regularization is still required. A typical formulation of the inverse problem in LOT/MFMT is:

$$x^{\prime }={({\mathrm{A}}^{\mathrm{T}}\mathrm{A}+\lambda \mathrm{D})}^{-1}{\mathrm{A}}^{\mathrm{T}}\mathrm{b}$$ (3)

where b is the measurement vector, x′ is the estimated fluorophore distribution, A is the Jacobian matrix, and λD is a regularization parameter. If D is the identity matrix, then it forms the Tikhonov regularization that has been used successfully in LOT/MFMT [22, 60]. However, for optimal performances in reflectance geometry, λD should be a depth-dependent regularization term [61]. In this case, D is a diagonal matrix whose elements are the square-root of the corresponding diagonal elements of A^TA [38, 62], and λ is a scaling factor selected via L-curve analysis [63].

One caveat of these approaches is that the classical L₂-norm employed in conjunction with regularization “smooths” out the reconstructions, degrading the resolution. To enhance the resolution, a hybrid scheme of L₂-norm Tikhonov regularization and simultaneous iterative reconstruction technique (SIRT) was proposed [33, 34]. Theoretically, if the iterative process in SIRT leads to a regularized solution, it is a semi-convergent technique that produces better resolution than the Tikhonov regularization in the case of sparse solutions. Better resolution is obtained for high iteration numbers at which the SIRT is over-reconstructing the results.

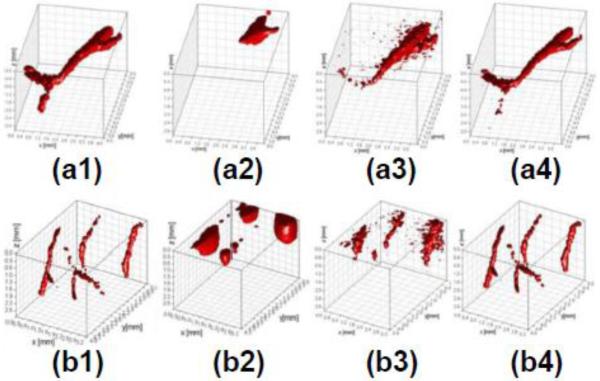
Alternatively, there has been considerable development in the retrieval of sparse signals in the last decade, leading to the blossoming field of compressive sensing [64]. Among all the different approaches, sparsity constraints implemented as regularization terms have been successfully applied to DOT to improve resolution [65, 66]. These techniques are extremely well-suited for LOT/MFMT due to their inherently sparse fluorescence signals (by design) [46]. An example of improvement in LOT/MFMT performances when using sparsity constraints (L₁-norm) over CG/LSQR is demonstrated in Fig. 3 [67]. This example focuses on retrieving labeled vasculature in murine brain tissue. Compared to CG and LSQR methods, the L₁-norm approach retrieves the vascular beds at all depths with high accuracy. Note that these continuous structures are the most difficult to image and even better results are expected for sparse cell imaging such as that mentioned in section 3.1. Ultimately, the combination of dense spatial data sets with compressive sensing-based methods should push LOT/MFMT resolution close to 100 μm or beyond even at depths of several millimeters.

FIGURE 3.

LOT/MFMT reconstruction of synthetic brain vasculature: (a1) and (b1) are the ground truth; (a2), (a3), and (a4) are the reconstruction of (a1) with Conjugate Gradient, Least Square, and L₁-norm iteration method, respectively. (b2), (b3), and (b4) are the reconstruction of (b1) with Conjugate Gradient, Least Square, and L₁-norm iteration method, respectively. Adapted from Ref. 67 with permission.

2.4 Instrumentation for LOT/MFMT

A typical LOT/MFMT system has three main components: source, detector, and scanning device. In this section, we will focus on reviewing different source types, detector configurations/types, and scanning methods/devices used in LOT/MFMT systems.

2.4.1 Excitation Sources

LOT/MFMT operates in the multiple-scattering regime so the back-scattered light collected by the detector loses all its original properties such as directionality, coherence, intensity, and polarization. In fluorescence imaging, color filtering plays an important role in separating the excitation light from the emission signals, thus enabling higher sensitivity for capturing the molecular/functional signals from the sample. LOT/MFMT systems typically use either laser diodes or solid-state lasers as the light source. The bleed-through effect in fluorescence imaging is a limiting factor for sensitivity. Depending on the Stokes shift between the excitation and emission peaks, the user needs to select a color filter on the detection side with sufficient spectral separation (typically >30 nm) from the illumination wavelength. LOT/MFMT can operate in either single wavelength [34] or multi-wavelength mode [29, 38].

2.4.2 Detector Types

In LOT/MFMT systems, detectors act not only as photo-sensors but also as pseudo-pinholes analogous to those in confocal microscopy. Each detector collects the back-scattered photons from a specific average depth/region and within a limited numerical aperture (NA), and rejects the ones that come from regions outside this range. Two main characteristics govern the performance of the detector: quantum efficiency (QE) and noise level (NL). LOT/MFMT systems are built with three detector types: avalanche photodiode (APD), photomultiplier tube (PMT), and charge-coupled device (CCD) or electron multiplying CCD (EMCCD). Each of the detectors has its own strengths and weaknesses. The back-illuminated EMCCD has the highest QE (~95%), followed by APD (~80%) and PMT (~40%). A more accurate performance comparison can be made when QE is incorporated with NL, since signal to noise ratio (SNR) is characterized by both of these parameters.

$$\mathit{SNR}=\mathit{QE}\ast n_p∕\sqrt{\mathit{QE}\ast n_p+{n_n}^2}$$

where n_p is the number of electrons generated from the incident photons, and n_n is the number of electrons generated by detector noise. If the number of electrons converted from photons is high enough, the system performance is governed by QE. Otherwise the performance is limited by the system noise. When the number of electrons is higher than 25, the CCD outperforms PMTs and APDs. However, for low-light situations, PMT or EMCCD becomes advantageous. Especially, EMCCDs with high QE becomes more effective at low-light conditions QE[68]. Detection speed is another important parameter to consider for LOT/MFMT imaging. Among all mentioned detectors, the APD has the fastest response time (0.2 ns), which leads to 10⁶ pixel/sec acquisition speed, followed by the PMT (15 ns). Although the CCD has the slowest response time (5-10 μs), due to high sampling density, it yields the highest acquisition speed (6×10⁶ pixel/sec) [68]. For studies of fast hemodynamic response, the APD is the preferred detector [29]. For imaging of static or slowly-varying samples such as those in tissue engineering, the CCD typically offers a suitable performance with the advantage of dense spatial sampling.

2.4.3 Detector Configurations

Detector configuration is a critical aspect of LOT/MFMT and impacts tomographic imaging. 2D-array detectors (CCD, EMCCD, or 2D-PMT) offer more flexibility than 1D-array detectors (APD or PMT arrays). LOT/MFMT relies on detection of signals from multiple source-detector separations; therefore aligning detectors with respect to the source has an impact on both projection depth and data quality. Yuan et al. [32] established the relationship between source-detector separation and the shadow-effect that arises from selection of different depths. The impact of detector configuration on image reconstruction was shown by Björn et al. [35]. Chen et al. investigated the effect of detector number and density on yielding useful data for reconstruction [60]. These studies suggest that, for applications which do not demand high-speed data acquisition (>50 fps) 2D array detectors, especially EMCCD, should be preferred due to high sensitivity and speed.

2.4.4 Scanning Modes

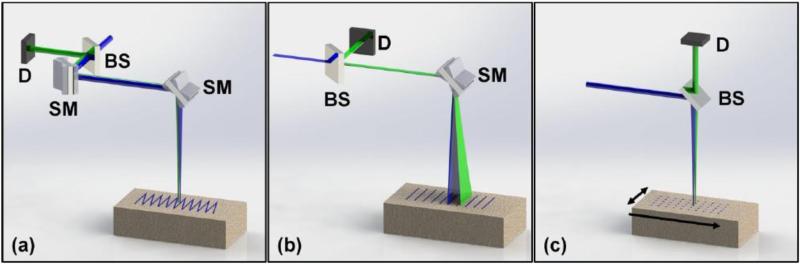
Scanning configuration is also a major component that defines the speed of data collection of LOT/MFMT systems. Scanning can be performed in raster scan, point scan, or line scan modes as shown in Fig. 4. Each scanning mode requires selection of devices such as resonant-galvanometer mirrors, galvanometer mirror pairs, and micro-stage controlled scanner. One main difference in the scanning modes is that galvanometer mirror scanning (raster or line scanning) uses de-scanning to focus the image onto the detector, whereas stage scanning (point or line scanning) does not de-scan the emission light from the sample.

FIGURE 4.

Different scanning configurations in LOT/MFMT. (a) Raster scanning mode accepts an excitation light (blue color) through a beam splitter (BS). The light is scanned in two dimensions with two scanning mirrors (SM). The emission light (green) follows the similar path of excitation, is de-scanned by the SMs, and then captured by a detector (D). (b) Line scanning mode utilizes line sheet illumination thus one scanning mirror (SM) is sufficient to cover the entire field of view. (c) Point scanning hosts stationary optical elements. In order to cover a field of view, while sample itself is translated with a micro stage.

Among these modes, raster scanning with resonant-galvanometer mirrors shows similar performance to raster scanning with galvanometer mirror pairs. Resonant mirrors have a fixed scanning speed so the dwell time on each pixel (exposure) is fixed. However, it precludes the capability of adjusting the exposure time based on the signal level. On the other hand, although it is slower than resonant mirrors, using galvanometer mirrors gives the flexibility to change the frequency of the operation. As a result, galvanometer mirrors offer the users more flexibility for adjustment of the exposure time.

Ouakli et al. [29] utilized resonant mirrors and attained data collection times of ~8 μs per acquisition point. This scanning mode requires a fast data acquisition system that can retain synchronization with the speed of data collection. With a data acquisition board (250 kS/s), they were able to reach 7.5 fps. Burgess et al. used a galvanometer mirror pair and a faster acquisition board (2.5 MS/s/ch) to achieve 23 fps [69]. This comparison shows the preeminent role of the data acquisition board in improving acquisition speeds. Indeed, even though resonant mirrors are inherently faster, Burgess et al. [69] and Yuan et al. [32] achieved threefold acquisition speed compared to the speed of the setup used by Ouakli et al. [29].

The speed of the line scanning mode is limited by the speed of the scanning mirror or scanning stage [33]. Since it reduces the scanning into one dimension, there is a proportional gain on acquisition time. However, similar to confocal microscopy, the line scanning mode potentially decreases the axial resolution [70].

Point scanning is the slowest mode, but it gives the flexibility to scan according to the exposure time (1-4000 ms). Therefore it can mitigate drastically-changing signal intensity [36]. Bjorn et al. used this mode for patterning the source positions [36]. They compared different source positions in terms of reconstruction quality and concluded that sources surrounding the detector area would yield better results. As a demonstration, they reconstructed 200 nM DiO dye in a capillary inserted in an euthanized mouse [35].

3. Representative applications in tissue engineering

3.1 Longitudinal Imaging of hMSCs in Alginate Bead Scaffolds

One present challenge in tissue engineering is the inability to successfully culture a large, clinically relevant 3D construct in vitro due to a decrease in oxygen and nutrient supply at the center of the graft. Often, a scaffold is constructed in its final shape and then seeded with cells. However, the large size of the scaffold limits homogeneous cell proliferation and deposition in the matrix. Alternatively, alginate bead scaffolds have been used as small-scale building blocks, and each can be cultured individually before being assembled into the larger final construct [71]. This strategy allows for in vitro development of tissue engineering constructs on scales not easily possible with the aforementioned methods. Alginate is a natural biomaterial derived from algae that is frequently used in bone tissue engineering [72, 73]. A model system like an alginate bead scaffold is suitable for FLOT/MFMT imaging, as the size of cell clusters is relevant to the resolution of FLOT/MFMT (100-200 μm) and the size of the bead is relevant to the penetration depth of FLOT/MFMT (2-4 mm). The ability of FLOT/MFMT to monitor cell proliferation in the construct provides a powerful tool for optimizing tissue engineering strategies.

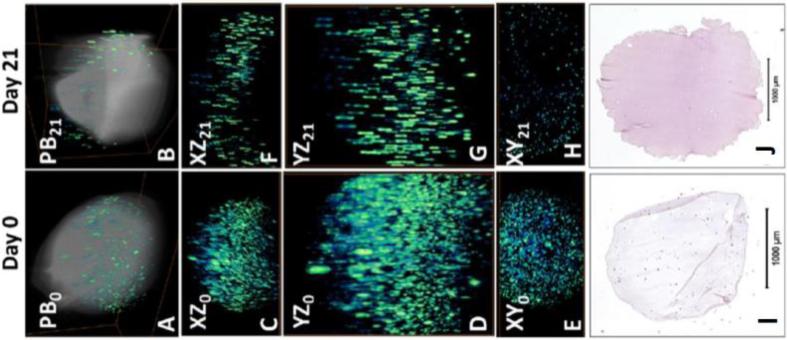
LOT/MFMT has been used for a time-lapsed study over 21 days to determine cell viability within the scaffold. Human stem cells (hMSCs) were mixed into 2% w/v alginate solution and used to construct spherical alginate scaffolds (10⁶ cells/scaffold) by adding the mixture dropwise into a suspension of 0.1M calcium chloride and then stirring for 10 minutes. To increase the supply of oxygen and nutrients, the scaffolds were cultured in the tubular perfusion system (TPS) bioreactor described previously [74]. To visualize the cells using FLOT, the scaffolds were removed from the TPS bioreactor and labeled with green-fluorescent Live Assay (calcein-AM, Ex/Em = 494/517 nm) following standard protocols. Fig. 5a-b shows the FLOT/MFMT tomograms of the hMSC distributions before and after 21 days of dynamic culturing, overlaid on the LOT/MFMT reflectance tomograms showing the shape of the scaffold. This imaging technique allowed for 3D reconstruction of an entire construct without disruption of the scaffold. During fabrication, hMSCs were evenly mixed in the alginate solution before cross-linking with CaCl₂. Therefore, a homogeneous cell distribution can be expected. At day 0, hMSCs were homogeneously distributed (Fig. 5c-e). After 21 days of dynamic culture in the TPS bioreactor, the constantly circulating medium kept cells within the periphery of the bead scaffold viable. In contrast, cells in the center of the bead were exposed to modestly hypoxic conditions. As expected, greater cell distribution can be seen on the periphery compared to the core of the scaffold (Fig. 5f-h). H&E staining confirmed uniform cell distribution on day 0 (cells labeled in dark blue, alginate scaffold in pink/purple) with decreased cell numbers by day 21, signifying a loss of cells due to cell death (Fig. 5i-j).

FIGURE 5.

(a-b) 3D FLOT tomograms of fluorescent-labeled hMSCs (green-blue color scale) in alginate scaffolds (grey color scale) at day 0 and 21, respectively. (c-h) Projection view of FLOT. XZ, YZ, and XY are the tomographic projections of an alginate sample on day 0 and 21. FOV: 4.6 × 1.6 × 2.56 mm³ (day 0) and 4.6 × 2.3 × 3.7 mm³ (day 21). (i-j) H&E staining of histology sections. Cells are stained dark pink and the alginate is stained purple/pink.

3.2 Imaging of Bioprinted Tissues

One of the fastest areas of growth in tissue engineering is the field of bio-printing, in which 3D tissues are constructed using a layer-by-layer approach. The main appeal of bio-printing techniques is the ability to simultaneously deposit live cells and growth factors along with biomaterial scaffolds with spatial accuracy to mimic native tissues [75]. It is expected that bio-printing will revolutionize regenerative medicine and drug development by creating on-demand fully functional organs [3, 76]. However, 3D bio-printed tissues often incorporate thick opaque scaffolds and dense populations of cells, leading to large samples (1-100 mm) that are difficult to image with conventional techniques. Moreover, as the printed tissues would ideally be implanted in patients or used in longitudinal studies in drug development, non-destructive assessment is required.

Preliminary studies have demonstrated the potential of LOT/MFMT as an imaging tool to assess bio-printed tissues within a bioreactor. It was first successfully integrated with inkjet printing [38] and then also used to image samples created using Laser Direct Writing (LDW). In these applications, cells labeled with gene reporters (GFP and mCherry) or exogenous fluorophores (Far red bead) were printed in collagen (Inkjet Printed) or gelatin/alginate (LDW). The samples were imaged in less than one minute and the optical reconstructions were performed in less than 10 minutes. The imaging field of view was typically ~8×6 mm². An example of LOT/MFMT imaging applied to multiple cell lines printed in thick scaffolds is provided in Fig. 6. The main application sought here is the development of perfused tissue constructs with functional vascular channels to support the growth and maturation of bio-fabricated tissue constructs. This study demonstrated the ability to image different vascular channels based on cellular phenotype as well as to visualize structure based on perfusion using far-red cell tracker. The technique is currently applied to monitor vascular tree formation and maturation and as a tool to assist bio-printing at the multiscale.

FIGURE 6.

(a) Example of cell printing with phenotype encoded vie gene reporters as seen with wide-field fluorescence (before toping with scaffold layers) and (b) LOT/MFMT reconstruction; (c1) Inkjet bioprinting methodology can also create perfused vasculature in thick constructs, which resides in bioreactor/perfused chamber (c2). (d) LOT/MFMT reconstructions of two cellular phenotypes and fluid flow in a vascular constructs. The imaging field of view is 7×3 mm². Adapted from Ref. 27 with permission.

3.3 In vivo imaging

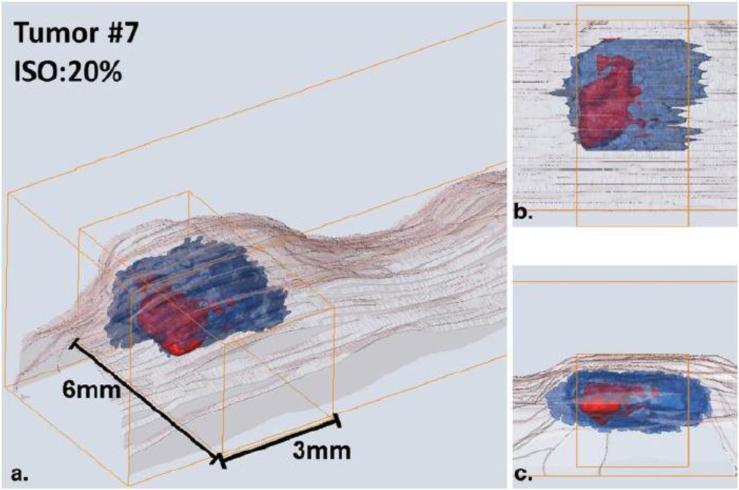
LOT/MFMT is an attractive imaging modality for tissue engineering applications beyond in vitro applications. Indeed, as LOT/MFMT enables imaging up to 3 mm in intact tissue [39] and up to 10mm in silico studies [36], it can image beyond the depth of the epithelium in vivo. To date, the reported in vivo applications of LOT/MFMT mainly focus on oncological applications. For instance, the technique has been applied in clinical settings to image skin cancers based on endogenous markers to describe the depth and thickness of pigmented skin lesions, providing additional information compared to that attained using simple white light examination [30]. It was also employed to image in vivo the bio-distribution of a photodynamic therapeutic agent in skin cancer models prior to therapy [39]. All lesions exhibited strong fluorescence that allowed for mesoscopic optical reconstructions at depths up to 4 mm. This study highlights the potential of LOT/MFMT to retrieve bio-distribution of the 3D photosensitizer (HPPH, Ex/Em: 660nm/690nm) in vivo within a few minutes. Examples of in vivo LOT/MFMT imaging of a tumor model with ultrasound (US) co-registration is provided in Fig. 7.

FIGURE 7.

A 3D image of a skin tumor model (basal cell carcinoma). (a) Ultrasound (US, blue) and MFMT (red) reconstructions delineate the tumor area and agent bio-distribution area. US data also gave tail structure (pink). MFMT data was acquired using the photodynamic therapy agent (HPPH)'s fluorescent signals. (b) Top view and (c) depth view of the co-registered tumor images. The results indicate a strong heterogeneity between the tumor margin and agent bio-distribution. Adapted from Ref. 39 with permission.

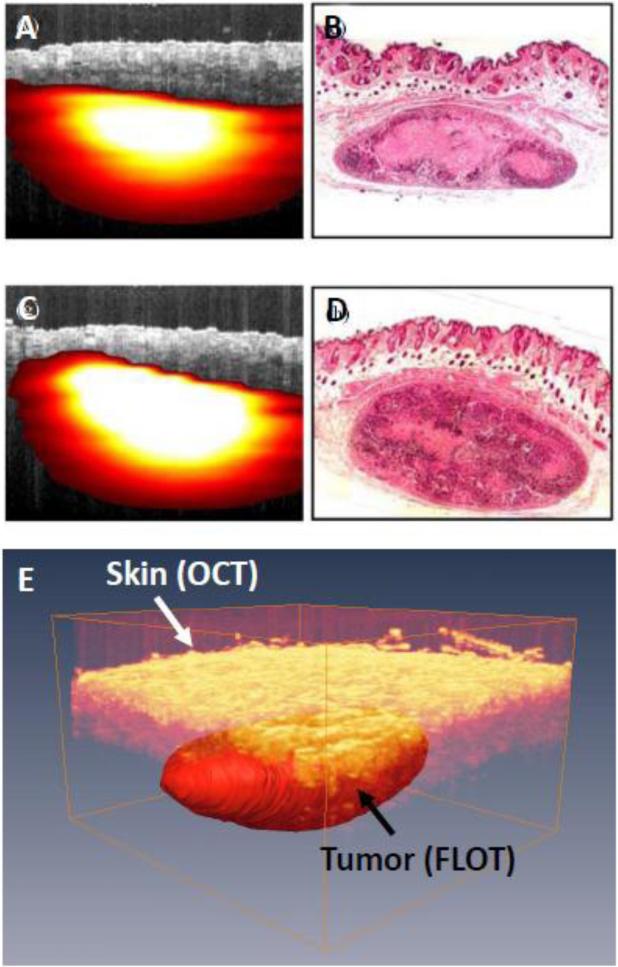
LOT/MFMT has also been employed to image tumors models labeled with gene reporters in living small animals. For instance, LOT/MFMT was employed to estimate the size and volume of tumor models labeled with GPF and RFP [37]. LOT/MFMT results were compared to planar reflectance imaging and benchmarked against cryo-sectioning, micro-US, and micro-CT results. While planar reflectance imaging led to estimation errors beyond 50%, LOT/MFMT provided accurate estimates within <5%. Similarly, Chen et al. [34] reported the imaging of a subcutaneous tumor model labeled with tdTomato (Ex/Em: 554/581 nm) in live animals. Good congruence between LOT/MFMT and histology was observed. Moreover, the LOT/MFMT data were fused with OCT to provide both structural and molecular imaging. An example of in vivo LOT/MFMT images of this tumor model with co-registered OCT is provided in Fig. 8.

FIGURE 8.

(a) Fused OCT-FLOT image of subcutaneous human breast tumor xenograft in a mouse model in vivo (breast cancer cells MDA-MB-231 labeled with tdTomato red fluorescence protein) and (b) Corresponding histology. (c) and (d) are OCT-FLOT image and corresponding histology of another cross-section of the same tumor. Image size: 2.2 mm (depth) × 2.8 mm (lateral). (e) 3D co-registered OCT and FLOT image. (a-d) are adapted from Ref. 34 with permission.

These results indicate that LOT/MFMT provides the ability to image tissue-engineered constructs after implantation, either in preclinical models or in humans. Hence, LOT/MFMT offers the unique capability of using the same image-driven assessment criteria during the construction phase, maturation, and after implantation of tissue construct in vivo for regenerative medicine applications.

4. Conclusion

The development of engineered tissue products has been limited by the lack of laboratory imaging techniques that are capable of non-destructive evaluation of the three-dimensional morphology and cellular response in a tissue-engineered scaffold. LOT/MFMT is a unique functional and molecular imaging modality that enables assessment of thick tissues based on diffuse optical signals. It operates well beyond the depth limitations of current optical microscopic techniques (~3-5 mm range) but still provide relatively high-resolution (≤200 μm), multiplexing capabilities, large field of view, and fast acquisition times. Therefore, LOT/MFMT is a promising new imaging technique for non-destructive evaluation of the structure and function of engineered tissues and tissue constructs, with the advantage of capability of imaging tissues within the confinement of bio-chambers and potential translation to in vivo applications. In this review, we provided a comprehensive review of the different aspects of LOT/MFMT, including instrument design and reconstruction strategies. We also reported on representative applications in tissue engineering.