An efficient Bayesian inference framework for coalescent-based nonparametric phylodynamics

Abstract

Motivation: The field of phylodynamics focuses on the problem of reconstructing population size dynamics over time using current genetic samples taken from the population of interest. This technique has been extensively used in many areas of biology but is particularly useful for studying the spread of quickly evolving infectious diseases agents, e.g. influenza virus. Phylodynamic inference uses a coalescent model that defines a probability density for the genealogy of randomly sampled individuals from the population. When we assume that such a genealogy is known, the coalescent model, equipped with a Gaussian process prior on population size trajectory, allows for nonparametric Bayesian estimation of population size dynamics. Although this approach is quite powerful, large datasets collected during infectious disease surveillance challenge the state-of-the-art of Bayesian phylodynamics and demand inferential methods with relatively low computational cost.

Results: To satisfy this demand, we provide a computationally efficient Bayesian inference framework based on Hamiltonian Monte Carlo for coalescent process models. Moreover, we show that by splitting the Hamiltonian function, we can further improve the efficiency of this approach. Using several simulated and real datasets, we show that our method provides accurate estimates of population size dynamics and is substantially faster than alternative methods based on elliptical slice sampler and Metropolis-adjusted Langevin algorithm.

Availability and implementation: The R code for all simulation studies and real data analysis conducted in this article are publicly available at http://www.ics.uci.edu/∼slan/lanzi/CODES.html and in the R package phylodyn available at https://github.com/mdkarcher/phylodyn.

Contact: S.Lan@warwick.ac.uk or babaks@uci.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Population genetics theory states that changes in population size affect genetic diversity, leaving a trace of these changes in individuals’ genomes. The field of phylodynamics relies on this theory to reconstruct past population size dynamics from current genetic data. In recent years, phylodynamic inference has become an essential tool in areas like ecology and epidemiology. For example, a study of human influenza A virus from sequences sampled in both hemispheres pointed to a source-sink dynamics of the influenza evolution (Rambaut et al., 2008).

Phylodynamic models connect population dynamics and genetic data using coalescent-based methods (Griffiths and Tavare, 1994; Kuhner et al., 1998; Strimmer and Pybus, 2001; Drummond et al., 2002; Drummond et al., 2005; Opgen-Rhein et al., 2005; Heled and Drummond, 2008; Minin et al., 2008; Palacios and Minin, 2013). Typically, such methods rely on Kingman’s coalescent model, which is a probability model that describes formation of genealogical relationships of a random sample of molecular sequences. The coalescent model is parameterized in terms of the effective population size, an indicator of genetic diversity (Kingman, 1982).

While recent studies have shown promising results in alleviating computational difficulties of phylodynamic inference (Palacios and Minin, 2012, 2013), existing methods still lack the level of computational efficiency required to realize the potential of phylodynamics: developing surveillance programs that can operate similarly to weather monitoring stations allowing public health workers to predict disease dynamics to optimally allocate limited resources in time and space. To achieve this goal, we present an accurate and computationally efficient inference method for modeling population dynamics given a genealogy. More specifically, we concentrate on a class of Bayesian nonparametric methods based on Gaussian processes (Minin et al., 2008; Gill et al., 2013; Palacios and Minin, 2013). Following Palacios and Minin (2012) and Gill et al. (2013), we assume a log-Gaussian process prior on the effective population size. As a result, the estimation of effective population size trajectory becomes similar to the estimation of intensity of a log-Gaussian Cox process (LGCP; Møller et al., 1998), which is extremely challenging since the likelihood evaluation becomes intractable: it involves integration over an infinite-dimensional random function. We resolve the intractability in likelihood evaluation by discretizing the integration interval with a regular grid to approximate the likelihood and the corresponding score function.

For phylodynamic inference, we propose a computationally efficient Markov chain Monte Carlo (MCMC) algorithm using Hamiltonian Monte Carlo (HMC; Duane et al., 1987; Neal, 2010) and one of its variants, called Split HMC (Leimkuhler and Reich, 2004; Neal, 2010; Shahbaba et al., 2013), which speeds up standard HMC’s convergence. Our proposed algorithm has several advantages. First, it updates all model parameters jointly to avoid poor MCMC convergence and slow mixing rates when there are strong dependencies among model parameters (Knorr-Held and Rue, 2002). Second, unlike a recently proposed Integrated Nested Laplace Approximation method (INLA, Rue et al., 2009; Palacios and Minin, 2012), which approximates the posterior distribution of model parameters given a fixed genealogy, our approach can be extended to more general settings where we observe genetic data (as opposed to the genealogy of sampled individuals) that provide information on genealogical relationships. Third, we show that our method is up to an order of magnitude more efficient than alternative MCMC algorithms, such as Metropolis-adjusted Langevin algorithm (MALA; Roberts and Tweedie, 1996), adaptive MALA (aMALA; Knorr-Held and Rue, 2002) and Elliptical Slice Sampler (ES²; Murray et al., 2010) that are commonly used in the field of phylodynamics. Finally, although in this article we focus on phylodynamic studies, our proposed methodology can be easily applied to more general point process models.

The remainder of the article is organized as follows. In Section 2, we provide a brief overview of coalescent models and HMC algorithms. Section 3 presents the details of our proposed sampling methods. Experimental results based on simulated and real data are provided in Section 4. Section 5 is devoted to discussion and future directions.

2 Preliminaries

2.1 Coalescent

Assume that a genealogy with time measured in units of generations is available. The coalescent model allows us to trace the ancestry of a random sample of n genomic sequences: two sequences or lineages merge into a common ancestor as we go back in time until the common ancestor of all samples is reached. Those ‘merging’ times are called coalescent times. The coalescent with variable population size is an inhomogeneous Markov death process that starts with n lineages at present time, t_n = 0, and decreases by one at each of the consequent coalescent times, $t_{n-1}<\cdots <t_1$, until reaching their most recent common ancestor (Kingman, 1982; Griffiths and Tavare, 1994).

Suppose we observe a genealogy of n individuals sampled at time 0. Under the standard (isochronous) coalescent model, given the effective population size trajectory, $N_{\text{e}}(t)$, the joint density of coalescent times $t_n=0<t_{n-1}<\cdots <t_1$ is

$$\begin{array}{l}P[t_1,\dots ,t_n|N_{\text{e}}\left(t\right)]={\displaystyle \prod _{k=2}^{n}P}[t_{k-1}|t_k,N_{\text{e}}(t\left)\right]\\ ={\displaystyle \prod _{k=2}^n\frac{A_k}{N_{\text{e}}\left(t_{k-1}\right)}}\text{exp}\left\{-{\displaystyle {\int }_{I_k}}\frac{A_k}{N_{\text{e}}\left(t\right)}dt\right\},\end{array}$$ (1)

where A_k = $\left(\underset{2}{\overset{k}{}}\right)$ and $I_k=(t_k,t_{k-1}]$. Note that the larger the population size, the longer it takes for two lineages to coalesce. Further, the larger the number of lineages, the faster two of them meet their common ancestor.

For rapidly evolving organisms, we may have different sampling times. When this is the case, the standard coalescent model can be generalized to account for such heterochronous sampling (Rodrigo and Felsenstein, 1999). Under the heterochronous coalescent, the number of lineages changes at both coalescent times and sampling times. Let ${\left\{t_k\right\}}_{k=1}^n$ denote the coalescent times as before, but now let $s_m=0<s_{m-1}<\cdots <s_1$ denote sampling times of $n_m,\dots ,n_1$ sequences respectively, where ${\sum }_{j=1}^m{n}_j=n$. Further, let s and n denote the vectors of sampling times ${\left\{s_j\right\}}_{j=1}^m$ and numbers of sequences ${\left\{n_j\right\}}_{j=1}^m$ sampled at these times, respectively. Then we can modify density (1) as

$$\begin{array}{l}P[t_1,\dots ,t_n|s,n,N_{\text{e}}(t)]=\\ {\displaystyle \prod _{k=2}^n\frac{A_{0,k}\exp \left\{-{\displaystyle {\int }_{I_{0,k}}\frac{A_{0,k}}{N_{\text{e}}(t)}}dt-{\displaystyle \sum _{i\ge 1}}{\displaystyle {\int }_{I_{i,k}}\frac{A_{i,k}}{N_{\text{e}}(t)}}dt\right\}}{N_{\text{e}}(t_{k-1})}},\end{array}$$ (2)

where the coalescent factor $A_{i,k}=(\begin{array}{c}{l}_{i,k}\\ 2\end{array})$ depends on the number of lineages $l_{i,k}$ in the interval $I_{i,k}$ defined by coalescent times and sampling times. For $k=2,\dots ,n$, we denote half-open intervals that end with a coalescent event by

$$I_{0,k}=(\max \{t_k,s_j\},t_{k-1}],$$ (3)

for $s_j<t_{k-1}$ and half-open intervals that end with a sampling event by (i > 0)

$$I_{i,k}=(\max \{t_k,s_{j+i}\},s_{j+i-1}],$$ (4)

for $t_k<s_{j+i-1}\le s_j<t_{k-1}$. In density (2), there are n – 1 intervals ${\left\{I_{i,k}\right\}}_{i=0}$ and m – 1 intervals ${\left\{I_{i,k}\right\}}_{i>0}$ for all (i, k). Note that only those intervals satisfying $I_{i,k}\subset (t_k,t_{k-1}]$ are non-empty. See Figure 1 for more details.

Fig. 1.

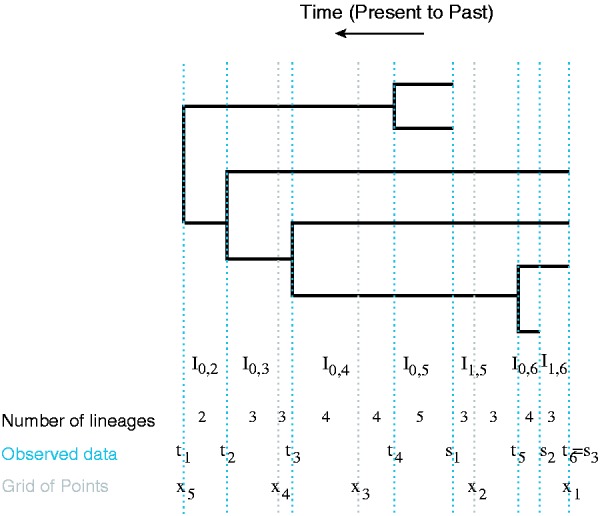
A genealogy with coalescent times and sampling times. Blue dashed lines indicate the observed times: coalescent times $\{t_1,\cdots ,t_6\}$ and sampling times $\{s_1,s_2,s_3\}$. The intervals where the number of lineages change are denoted by $I_{i,k}$. The superimposed grid $\{x_1,\cdots ,x_5\}$ is marked by gray dashed lines. We count the number of lineages in each interval defined by grid points, coalescent times and sampling times

We can think of isochronous coalescence as a special case of heterochronous coalescence when $m=1,A_{0,k}=A_k,I_{0,k}=I_k,I_{i,k}=\varnothing$ for i > 0. Therefore, in what follows, we refer to density (2) as the general case.

We assume the following log-Gaussian Process prior on the effective population size, $N_{\text{e}}(t)$:

$$N_{\text{e}}(t)=\exp [f(t)],\hspace{1em}f(t)\sim \mathcal{GP}(0,\mathbf{C}(\mathit{\theta })),$$ (5)

where $\mathcal{GP}(0,\mathbf{C}(\mathit{\theta }))$ denotes a Gaussian process with mean function $0$ and covariance function $\mathbf{C}(\mathit{\theta })$. A priori, $N_{\text{e}}(t)$ is a log-Gaussian process.

For computational convenience, we use a Gaussian process with inverse covariance function ${\mathbf{C}}_{\text{in}}^{-1}(\kappa )=\kappa {\mathbf{C}}_{\text{in}}^{-1}$, where ${\mathbf{C}}_{\text{in}}^{-1}$ corresponds to a modified inverse covariance matrix of Brownian motion (${\mathbf{C}}_{\text{BM}}^{-1}$) that starts with an initial Gaussian distribution with mean 0 and large variance. This corresponds to an intrinsic autoregression model (Besag and Kooperberg, 1995; Knorr-Held and Rue, 2002). The computational complexity of computing the density of this prior is $\mathcal{O}(D)$ since the inverse covariance matrix is tri-diagonal (Kalman, 1960; Rue and Held, 2005; Palacios and Minin, 2013). The precision parameter κ is assumed to have a $\text{Gamma}(\alpha ,\beta )$ prior.

2.2 HMC

Bayesian inference typically involves intractable models that rely on MCMC algorithms for sampling from the corresponding posterior distribution, $\pi (\mathit{\theta })$. HMC (Duane et al., 1987; Neal, 2010) is a state-of-the-art MCMC algorithm that suppresses the random walk behavior of standard Metropolis-based sampling methods by proposing states that are distant from the current state but nevertheless have a high probability of being accepted. These distant proposals are found by numerically simulating Hamilton dynamics, whose state space consists of position, denoted by the vector $\mathit{\theta }$, and momentum, denoted by the vector p. It is common to assume $p\sim \mathcal{N}(0,\mathbf{M})$, where M is a symmetric, positive-definite matrix known as the mass matrix, often set to the identity matrix I for convenience.

For Hamiltonian dynamics, the potential energy, $U(\mathit{\theta })$, is defined as the negative log density of $\mathit{\theta }$ (plus any constant); the kinetic energy, $K(p)$ for momentum variable p, is set to be the negative log density of p (plus any constant). Then the total energy of the system, the Hamiltonian function, is defined as their sum: $H(\mathit{\theta },p)=U(\mathit{\theta })+K(p)$. The system of $(\mathit{\theta },p)$ evolves according to the following set of Hamilton’s equations:

$$\begin{array}{l}\dot{\mathit{\theta }}={\nabla }_{p}H(\mathit{\theta },p)={\mathbf{M}}^{-1}p,\\ \dot{p}=-{\nabla }_{\mathit{\theta }}H(\mathit{\theta },p)=-{\nabla }_{\mathit{\theta }}U(\mathit{\theta }).\end{array}$$ (6)

In practice, we use a numerical method called leapfrog to approximate the Hamilton’s equations (Neal, 2010) when the analytical solution is not available. We numerically solve the system for L steps, with some step size, ε, to propose a new state in the Metropolis algorithm and accept or reject it according to the Metropolis acceptance probability (see Neal, 2010, for more discussions).

3 Method

3.1 Discretization

As discussed above, the likelihood function (2) is intractable in general. We can, however, approximate it using discretization. To this end, we use a fine regular grid, $x={\left\{x_d\right\}}_{d=1}^D$, over the observation window and approximate $N_{\text{e}}(t)$ by a piecewise constant function as follows:

$$N_{\text{e}}(t)\approx {\displaystyle \sum _{d=1}^{D-1}\exp }[f(x_d^{*})]1_{t\in (x_d,x_{d+1}]},\hspace{1em}{x}_d^{*}=\frac{x_d+x_{d+1}}{2}.$$ (7)

Note that the regular grid x does not coincide with the sampling coalescent times, except for the first sampling time $s_m=x_1$ and the last coalescent time $t_1=x_D$. To rewrite (2) using the approximation (7), we sort all the time points $\{t,s,x\}$ to create new $D+m+n-4$ half-open intervals $\left\{I_{\alpha }^{*}\right\}$ with either coalescent time points, sampling time points or grid time points as the end points (Fig. 1).

For each $\alpha \in \{1,\cdots ,D+m+n-4\}$, there exists some i, k and d such that $I_{\alpha }^{*}=I_{i,k}\cap (x_d,x_{d+1}]$. Each integral in density (2) can be approximated as a sum:

$${\displaystyle {\int }_{I_{i,k}}\frac{A_{i,k}}{N_{\text{e}}(t)}}dt\approx {\displaystyle \sum _{I_{\alpha }^{*}\subset I_{i,k}}{A}_{i,k}}\exp [-f(x_d^{*})]{\Delta }_{\alpha },$$

where ${\Delta }_{\alpha }$ is the length of the interval $I_{\alpha }^{*}$. This way, the joint density of coalescent times (2) can be rewritten as a product of the following terms:

$${\left\{\frac{A_{i,k}}{\exp [f(x_d^{*})]}\right\}}^{y_{\alpha }}\exp \left\{-\frac{A_{i,k}{\Delta }_{\alpha }}{\exp [f(x_d^{*})]}\right\},$$ (8)

where $y_{\alpha }$ is an auxiliary variable set to 1 if $I_{\alpha }^{*}$ ends with a coalescent time and to 0 otherwise. Then, density (2) can be approximated as follows:

$$\begin{array}{l}P[t_1,\dots ,t_n|s,n,N_{\text{e}}(t)]\approx {\displaystyle \prod _{\alpha =1}^{D+m+n-4}P}[y_{\alpha }|s,n,N_{\text{e}}(t)]\\ ={\displaystyle \prod _{d=1}^{D-1}{\displaystyle \coprod _{I_{\alpha }^{*}\subset (x_d,x_{d+1}]}^{}{\left\{\frac{A_{i,k}}{\exp [f(x_d^{*})]}\right\}}^{y_{\alpha }}\exp \left\{-\frac{A_{i,k}{\Delta }_{\alpha }}{\exp [f(x_d^{*})]}\right\},}}\end{array}$$ (9)

where the coalescent factor $A_{i,k}$ on each interval $I_{\alpha }^{*}$ is determined by the number of lineages $l_{i,k}$ in $I_{\alpha }^{*}$. We denote the expression on the right-hand side of Equation (9) by $\text{Coalescent}(f)$, where $f:={\{f(x_d^{*})\}}_{d=1}^{D-1}$.

3.2 Sampling methods

Our model can be summarized as

$$\begin{array}{r}{\left\{y_{\alpha }\right\}}_{\alpha =1}^{D+m+n-4}|s,n,f\sim \text{Coalescent}(f),\\ f|\kappa \sim \mathcal{N}\left(0,\frac{1}{\kappa }{\mathbf{C}}_{in}\right),\\ \kappa \sim \text{Gamma}(\alpha ,\beta ).\end{array}$$ (10)

After transforming the coalescent times, sampling times and grid points into $\{y_{\alpha },A_{i,k},{\Delta }_{\alpha }\}$, we condition on these data to generate posterior samples for $f=\log N_e(x^{*})$ and κ, where $x^{*}=\left\{x_d^{*}\right\}$ is the set of the middle points in (7). We use these posterior samples to make inference about $N_{\text{e}}(t)$.

For sampling f using HMC, we first compute the discretized log-likelihood

$$l=-{\displaystyle \sum _{d=1}^{D-1}{\displaystyle \sum _{I_{\alpha }^{*}\subset (x_d,x_{d+1}]}\left\{y_{\alpha }f(x_d^{*})+A_{i,k}{\Delta }_{\alpha }\exp [-f(x_d^{*})]\right\}}}$$

and the corresponding gradient (score function)

$$s_d=-{\displaystyle \sum _{I_{\alpha }^{*}\subset (x_d,x_{d+1}]}\left\{y_{\alpha }-A_{i,k}{\Delta }_{\alpha }\exp [-f(x_d^{*})]\right\}}.$$

based on (9).

Because the prior on κ is conditionally conjugate, we could directly sample from its full conditional posterior distribution,

$$\kappa |y,s,n,f\sim \text{Gamma}(\alpha +(D-1)/2,\beta +f^{\text{T}}{\mathbf{C}}_{in}^{-1}f/2).$$ (11)

However, updating f and κ separately is not recommended in general because of their strong interdependency (Knorr-Held and Rue, 2002): large value of precision κ strictly confines the variation of f, rendering slow movement in the space occupied by f. Therefore, we update $(f,\kappa )$ jointly in our sampling method. In practice, of course, it is better to sample $\mathit{\theta }:=(f,\tau )$, where $\tau =\log (\kappa )$ is in the same scale as $f=\log N_e(x^{*})$. Note that the log-likelihood of $\mathit{\theta }$ is the same as that of f because density (2) does not involve τ. The log-density prior on $\mathit{\theta }$ is defined as follows:

$$\log P(\mathit{\theta })\propto ((D-1)/2+\alpha )\tau -(f^{\text{T}}{\mathbf{C}}_{\text{in}}^{-1}f/2+\beta ){\text{e}}^{\tau }.$$ (12)

3.3 Speed up by splitting Hamiltonian

The speed of HMC could be increased by splitting the Hamiltonian into several terms such that the dynamics associated with some of these terms can be solved analytically (Leimkuhler and Reich, 2004; Neal, 2010; Shahbaba et al., 2013). For these analytically solvable parts (typically in quadratic forms), simulation of the dynamics does not introduce a discretization error, allowing for faster movements in the parameter space.

For our model, we split the Hamiltonian $H(\mathit{\theta },p)=U(\mathit{\theta })+K(p)$ as follows:

$$\begin{array}{l}H(\mathit{\theta },p)=\frac{-l-[(D-1)/2+\alpha ]\tau +\beta {\text{e}}^{\tau }}{2}+\\ \frac{f^{\text{T}}{\mathbf{C}}_{\text{in}}^{-1}f{\text{e}}^{\tau }+p^{\text{T}}p}{2}+\frac{-l-[(D-1)/2+\alpha ]\tau +\beta {\text{e}}^{\tau }}{2}.\end{array}$$ (13)

We further split the middle part into two dynamics involving $f|\tau$ and $\tau |f$, respectively,

$$\{\begin{array}{ll}\dot{f}|\tau & =p_{-D},\\ {\dot{p}}_{-D}& =-{\mathbf{C}}_{\text{in}}^{-1}f{\text{e}}^{\tau }.\end{array}$$ (14a)

$$\{\begin{array}{ll}\dot{\tau }|f& =p_D,\\ {\dot{p}}_D& =-f^{\text{T}}{\mathbf{C}}_{\text{in}}^{-1}f{\text{e}}^{\tau }/2,\end{array}$$ (14b)

where the subindex ‘– D’ means all but the Dth element. Using the spectral decomposition ${\mathbf{C}}_{\text{in}}^{-1}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{-1}$ and denoting $f^{*}:=\sqrt{\mathbf{\Lambda }}{\text{e}}^{\tau /2}{\mathbf{U}}^{-1}f$ and $p_{-D}^{*}:={\mathbf{U}}^{-1}{p}_{-D}$, we can analytically solve the dynamics (14a) as follows (Lan, 2013) (more details are provided in the Supplementary Material):

$$\left[\begin{array}{c}{f}^{*}(t)\\ p_{-D}^{*}(t)\end{array}\right]=\left[\begin{array}{cc}\cos (\sqrt{\mathbf{\Lambda }}{\text{e}}^{\tau /2}t)& \sin (\sqrt{\mathbf{\Lambda }}{\text{e}}^{\tau /2}t)\\ -\sin (\sqrt{\mathbf{\Lambda }}{\text{e}}^{\tau /2}t)& \cos (\sqrt{\mathbf{\Lambda }}{\text{e}}^{\tau /2}t)\end{array}\right]\left[\begin{array}{c}{f}^{*}(0)\\ p_{-D}^{*}(0)\end{array}\right]$$ (15)

where diagonal matrix $\sqrt{\mathbf{\Lambda }}$ scales different dimensions. We then use the standard leapfrog method to solve the dynamics (14b) and the residual dynamics in (13). Note that we only need to diagonalize ${\mathbf{C}}_{\text{in}}^{-1}$ once prior to sampling and then calculate $f^{\text{T}}{\mathbf{C}}_{in}^{-1}f{\text{e}}^{\tau }=f^{*}{}^{\text{T}}{f}^{*}$; therefore, the overall computational complexity of the integrator is $\mathcal{O}(D^2)$. Algorithm 1 shows the steps for this approach, which we refer to as splitHMC.

Algorithm 1. splitHMC for the coalescent model
Initialize ${\mathit{\theta }}^{(1)}$ at current $\mathit{\theta }=(f,\tau )$
Sample a new momentum value $p^{(1)}\sim \mathcal{N}(0,\mathbf{I})$
Calculate $H({\mathit{\theta }}^{(1)},p^{(1)})=U({\mathit{\theta }}^{(1)})+K(p^{(1)})$ according to (13)
for $\ell =1$ to L do  $$\begin{array}{l}{p}^{(\ell +\frac{1}{2})}=p^{\left(\ell \right)}+\epsilon /2\left[\begin{array}{c}{s}^{\left(\ell \right)}\\ \left(\right(D-1)/2+\alpha )-\beta \exp \left({\tau }^{\left(\ell \right)}\right)\end{array}\right]\\ p_D^{(\ell +\frac{1}{2})}=p_D^{\left(\ell \right)}-\epsilon /2f^{*\left(\ell \right)}{}^{\text{T}}{f}^{*\left(\ell \right)/2}\\ {\tau }^{(\ell +\frac{1}{2})}={\tau }^{\left(\ell \right)}+\epsilon /2p_D^{(\ell +\frac{1}{2})}\\ \left[\begin{array}{c}{f}^{*(\ell +1)}\\ p_{-D}^{*(\ell +\frac{1}{2})}\end{array}\right]\leftarrow \left[\begin{array}{cc}\cos \left(\sqrt{\mathbf{\Lambda }}{\text{e}}^{\frac{1}{2}{\tau }^{(\ell +\frac{1}{2})}}\epsilon \right)& \sin \left(\sqrt{\mathbf{\Lambda }}{\text{e}}^{\frac{1}{2}{\tau }^{(\ell +\frac{1}{2})}}\epsilon \right)\\ -\sin \left(\sqrt{\mathbf{\Lambda }}{\text{e}}^{\frac{1}{2}{\tau }^{(\ell +\frac{1}{2})}}\epsilon \right)& \cos \left(\sqrt{\mathbf{\Lambda }}{\text{e}}^{\frac{1}{2}{\tau }^{(\ell +\frac{1}{2})}}\epsilon \right)\end{array}\right]\left[\begin{array}{c}{f}^{*\left(\ell \right)}\\ p_{-D}^{*(\ell +\frac{1}{2})}\end{array}\right]\\ {\tau }^{(\ell +1)}={\tau }^{(\ell +\frac{1}{2})}+\epsilon /2p_D^{(\ell +\frac{1}{2})}\\ p_D^{(\ell +1)}=p_D^{(\ell +\frac{1}{2})}-\epsilon /2f^{*(\ell +1)}{}^{\text{T}}{f}^{*(\ell +1)/2}\\ p^{(\ell +1)}=p^{(\ell +\frac{1}{2})}+\epsilon /2\left[\begin{array}{c}{s}^{(\ell +1)}\\ \left(\right(D-1)/2+\alpha )-\beta \exp \left({\tau }^{(\ell +1)}\right)\end{array}\right]\end{array}$$
end for
Calculate $H({\mathit{\theta }}^{(+1)},p^{(L+1)})=U({\mathit{\theta }}^{(L+1)})+K(p^{(L+1)})$ according to (13)
Calculate the acceptance probability $\alpha =\min \{1,\exp [-H({\mathit{\theta }}^{(+1)},p^{(L+1)})+H({\mathit{\theta }}^{(1)},p^{(1)})]\}$
Accept or reject the proposal according to α for the next state $\mathit{\theta }\prime$

4 Experiments

We illustrate the advantages of our HMC-based methods using four simulation studies. We also apply our methods to analysis of a real dataset. We evaluate our methods by comparing them to INLA in terms of accuracy and to several sampling algorithms, MALA, aMALA and ES², in terms of sampling efficiency. We measure sampling efficiency with time-normalized effective sample size (ESS). Given B MCMC samples for each parameter, we define the corresponding ESS = $B[1+2{\sum }_{k=1}^K\gamma (k){]}^{-1}$ and calculate it using the ‘effectiveSize’ function in R Coda. Here, ${\sum }_{k=1}^K\gamma (k)$ is the sum of K monotone sample autocorrelations (Geyer, 1992). We use the minimum ESS over all parameters normalized by the CPU time, s (in seconds), as the overall measure of efficiency: $\min (\text{ESS})/\text{s}$.

We tune the stepsize and number of leapfrog steps for our HMC-based algorithm, such that their overall acceptance probabilities are in a reasonable range (close to 0.70). In all experiments, we use Gamma hyper prior parameters $\alpha =\beta =0.1$.

Since MALA (Roberts and Tweedie, 1996) and aMALA (Knorr-Held and Rue, 2002) can be viewed as variants of HMC with one leapfrog step for numerically solving Hamiltonian dynamics, we implement MALA and aMALA proposals using our HMC framework. MALA, aMALA and HMC-based methods update f and τ jointly. aMALA uses a joint block-update method designed for Gaussian Markov Random Field (GMRF) models: it first generates a proposal ${\kappa }^{*}|\kappa$ from some symmetric distribution independently of f and then updates $f^{*}|f,{\kappa }^{*}$ based on a local Laplace approximation. Then, $(f^{*},{\kappa }^{*})$ is either accepted or rejected. It can be shown that aMALA is equivalent to Riemannian MALA (Roberts and Stramer, 2002; Girolami and Calderhead, 2011, also see Supplementary Material). In addition, aMALA closely resembles the most frequently used MCMC algorithm in Gaussian process-based phylodynamics (Minin et al., 2008; Gill et al., 2013).

ES² (Murray et al., 2010) is another commonly used sampling algorithm designed for models with Gaussian process priors. Palacios and Minin (2013) used ES² for phylodynamic inference. ES² implementation relies on the assumption that the target distribution is approximately normal. This, of course, is not a suitable assumption for the joint distribution of $(f,\tau )$. Therefore, we alternate the updates $f|\kappa$ and $\kappa |f$ when using ES². Note that we are sampling κ in ES² to take advantage of its conjugacy.

4.1 Simulations

We simulate four genealogies for n = 50 individuals with the following true trajectories:

• 1. logistic trajectory:

  $$N_{\text{e}}(t)=\{\begin{array}{ll}10+\frac{90}{1+\exp (2(3-(t \mathrm{mod} 12)))},& t \mathrm{mod} 12\le 6,\\ 10+\frac{90}{1+\exp (2(-9+(t \mathrm{mod} 12)))},& t \mathrm{mod} 12>6;\end{array}$$

• 2. exponential growth: $N_{\text{e}}(t)=1000\exp (-t)$;

• 3. boombust:

  $$N_{\text{e}}(t)= \{\begin{array}{ll}1000\exp (t-2),& t\le 2,\\ 1000\exp (-t+2),& t>2;\end{array}$$
• 4. bottleneck:

  $$N_{\text{e}}(t)= \{\begin{array}{ll}1,& t\le 0.5,\\ 0.1,& t\in (0.5,1.0),\\ 1,& t\ge \mathrm{1.0.}\end{array}$$

To simulate data under heterochronous sampling, we selected 10 of our samples to have sampling time 0. The sampling times for the remaining 40 individuals were selected uniformly at random. Our four simulated genealogies were generated using the thinning algorithm detailed in Palacios and Minin (2013) and implemented in R. Simulated genealogies are displayed in the Supplementary File.

We use D = 100 equally spaced grid points in the approximation of likelihood when applying INLA and MCMC algorithms (HMC, splitHMC, MALA, aMALA and ES²). Figure 2 compares the estimates of $N_{\text{e}}(t)$ using INLA and MCMC algorithms for the four simulations. In general, the results of MCMC algorithms match closely with those of INLA. It is worth noting that MALA and ES² are occasionally slow to converge. Also, INLA fails when the number of grid points is large, e.g. 10 000, while MCMC algorithms can still perform reliably.

Fig. 2.

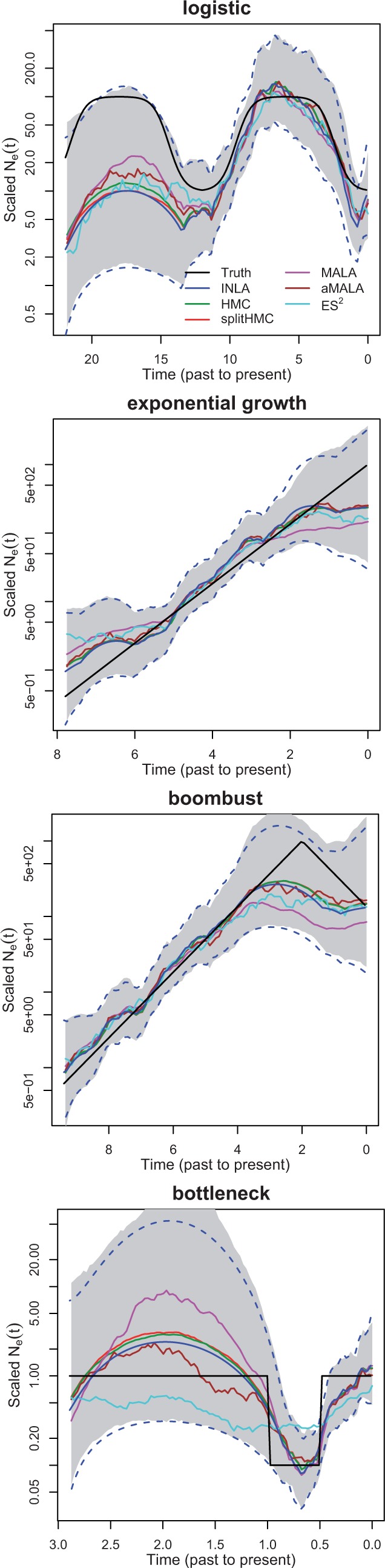
INLA versus MCMC: simulated data under logistic (top 1), exponential growth (top 2), boombust (top 3) and bottleneck (bottom) population size trajectories. Dotted blue lines show 95% credible intervals given by INLA and shaded regions show 95% credible interval estimated with MCMC samples given by splitHMC

For each experiment, we run 15 000 MCMC iterations with the first 5000 samples discarded. We repeat each experiment 10 times. The results provided in Table 1 are averaged over 10 repetitions. As we can see, our methods substantially improve over MALA, aMALA and ES². Note that due to high computational cost of Fisher information, aMALA is much worse than MALA in terms of time-normalized ESS.

Table 1.

Sampling efficiency in modeling simulated population trajectories

	Method	AP	s/iter	minESS(f)/s	spdup(f)	ESS(τ)/s	spdup(τ)
	ES2	1.00	1.62E-03	0.19	1.00	0.27	1.00
	MALA	0.77	1.06E-03	0.70	3.76	2.13	7.86
I	aMALA	0.64	7.73E-03	0.14	0.73	0.10	0.37
	HMC	0.75	9.39E-03	1.88	10.08	1.77	6.52
	splitHMC	0.72	6.71E-03	2.64	14.17	2.71	10.02
	ES2	1.00	1.68E-03	0.22	1.00	0.28	1.00
	MALA	0.76	1.05E-03	0.55	2.53	2.11	7.40
II	aMALA	0.66	8.00E-03	0.06	0.29	0.12	0.41
	HMC	0.73	1.23E-02	2.94	13.47	1.34	4.69
	splitHMC	0.75	7.12E-03	5.22	23.93	2.73	9.58
	ES2	1.00	1.67E-03	0.21	1.00	0.33	1.00
	MALA	0.75	1.12E-03	0.55	2.66	1.91	5.81
III	aMALA	0.65	8.11E-03	0.07	0.34	0.10	0.31
	HMC	0.75	1.27E-02	2.23	10.68	1.05	3.20
	splitHMC	0.75	7.66E-03	3.78	18.09	2.04	6.23
	ES2	1.00	1.66E-03	0.25	1.00	0.14	1.00
	MALA	0.83	1.11E-03	0.51	2.05	1.69	12.18
IV	aMALA	0.65	8.18E-03	0.07	0.30	0.08	0.60
	HMC	0.81	1.17E-02	0.58	2.30	0.87	6.25
	splitHMC	0.76	7.78E-03	0.80	3.21	1.38	9.96

The true population trajectories are (I) logistic, (II) exponential growth, (III) boombust and (IV) bottleneck. AP, acceptance probability; s/iter, seconds per sampling iteration; ‘spdup’, speedup of efficiency measurement minESS/s using ES² as baseline.

Figure 3 compares different sampling methods in terms of their convergence to the stationary distribution when we increase the size of grid points to D = 1000. As we can see in this more challenging setting, Split HMC has the fastest convergence rate. HMC, ES² and MALA take longer time (around 500 s, 1000 s and 2000 s, respectively) to converge, while aMALA does not reach the stationary distribution within the given time-frame.

Fig. 3.

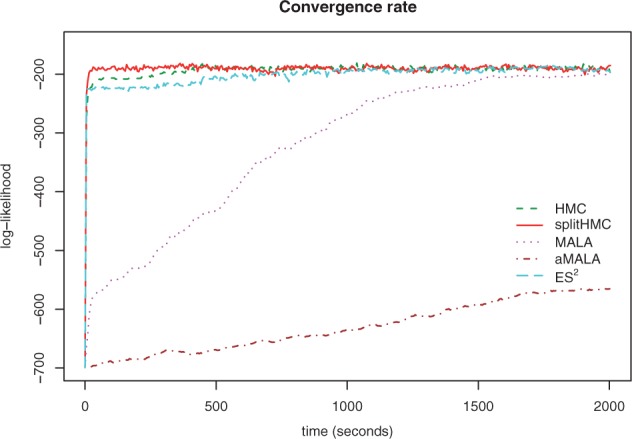
Trace plots of log-likelihoods for different sampling algorithms based on a simulated coalescent model with logistic population trajectory. splitHMC converges the fastest

In Figure 4, we show the estimated population size trajectory for the four simulations using our splitHMC, Bayesian Skyline Plot (Drummond et al., 2005) and Bayesian Skyride (Minin et al., 2008). Comparison of recovered estimates from these three methods show that our Gaussian-process-based method (using splitHMC algorithm) performs better than the other two: our point estimates are closer to the truth and our credible intervals cover the truth almost everywhere. Bayesian Skyride and splitHMC perform very similar; however, the BCIs recovered with splitHMC cover entirely the two peaks in the logistic simulation, the peak in the boombust simulation and the entire bottleneck phase in the bootleneck simulation. A direct comparison of efficiency of these three methods is not possible since Bayesian Skyline Plot and Bayesian Skyride assume different prior distributions over $N_{\text{e}}(t)$. Additionally, Bayesian Skyline Plot and Bayesian Skyride are implemented in BEAST (Drummond et al., 2012) using a different language (Java). Supplementary Figure S2 in the Supplementary File shows the trace plots of the posterior distributions of the results displayed in Figure 4 to assess convergence of the posterior estimates.

Fig. 4.

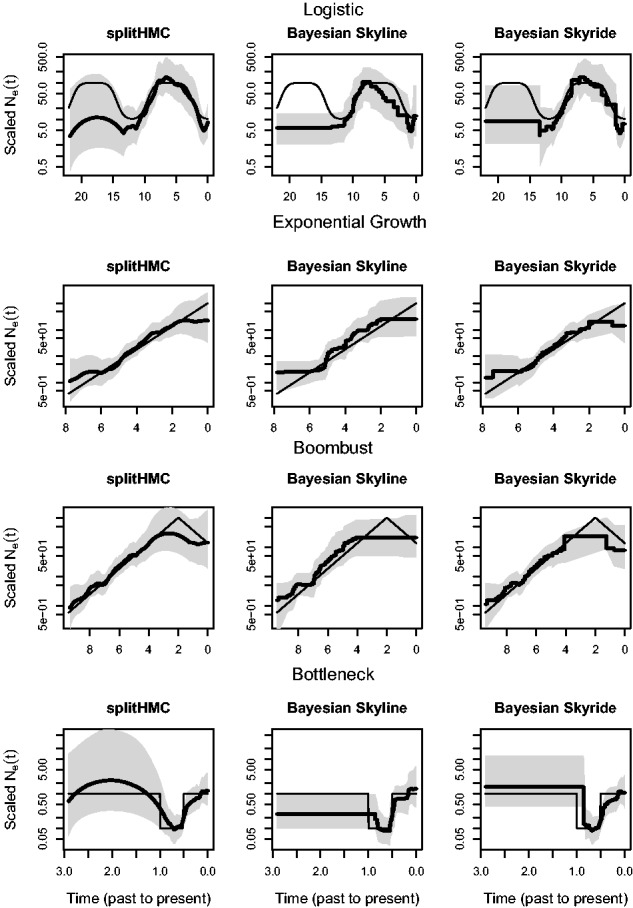
Comparison of recovered population size trajectories for the four simulations using our splitHMC, Bayesian Skyline and Bayesian Skyride. Posterior medians are displayed as bold black curves and shaded areas represent 95% BCIs. The truth is displayed as black thin line

4.2 Human influenza A in New York

Next, we analyze a real dataset previously used to estimate influenza seasonal dynamics (Palacios and Minin, 2012, 2013). The data consist of a genealogy estimated from 288 human influenza H3N2 sequences sampled in New York state from January 2001 to March 2005. The key feature of the influenza A virus epidemic in temperate regions like New York is the epidemic peaks during winters followed by strong bottlenecks at the end of the winter season. We use 120 grid points in the likelihood approximation. The results depicted in Figure 5 based on intrinsic precision matrix, ${\mathbf{C}}_{\text{in}}^{-1}$, are quite comparable to that of INLA. However, estimates using splitHMC with different covariances show that using ${\mathbf{C}}_{\text{in}}^{-1}$ is more conservative than ${\mathbf{C}}_{\text{BM}}^{-1}$ in estimating the variation of population size trajectory. In Table 2, we can see that the speedup by HMC and splitHMC over other MCMC methods is substantial.

Fig. 5.

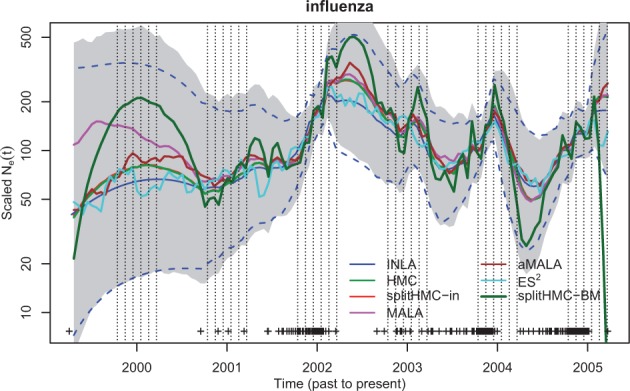
Population dynamics of influenza A in New York (2001–2005): shaded region is the 95% credible interval calculated with samples given by splitHMC with ${\mathbf{C}}_{\text{in}}^{-1}$. SplitHMC with ${\mathbf{C}}_{\text{in}}^{-1}$ (red) is more conservative than splitHMC with ${\mathbf{C}}_{\text{BM}}^{-1}$ (dark green) in estimating the variation of population size trajectory

Table 2.

Sampling efficiency of MCMC algorithms in influenza data

Method	AP	s/Iter	minESS(f)/s	spdup(f)	ESS(τ)/s	spdup(τ)
ES2	1.00	1.88E-03	0.15	1.00	0.57	1.00
MALA	0.79	1.28E-03	0.60	3.89	2.20	3.85
aMALA	0.79	8.61E-03	0.09	0.60	0.14	0.25
HMC	0.72	1.31E-02	2.06	13.34	1.72	3.03
splitHMC	0.79	1.05E-02	2.88	18.69	3.01	5.29

5 Discussion

Phylodynamic inference has become crucial in conservation biology, epidemiology and other areas. Bayesian nonparametric methods coupled with coalescent models provide a powerful framework to infer changes in effective population sizes with many advantages. One of the main advantages of Bayesian nonparametric methods over traditional parametric methods that assume fixed functional form of $N_{\text{e}}(t)$, such as exponential growth (Kuhner et al., 1998), is the ability of Bayesian nonparametric methods to recover any functional form without any prior knowledge about $N_{\text{e}}(t)$. With the technological advance of powerful tools for genotyping individuals, it is crucial to develop efficient methodologies that can be applied to large number of samples and multiple genes.

In this article, we have proposed new HMC-based sampling algorithms for phylodynamic inference. We have compared our methods to several alternative MCMC algorithms and showed that they substantially improve computational efficiency of GP-based Bayesian phylodynamics. (More results are provided in the Supplementary Document.) Further, our analysis shows that our results are not sensitive to the prior specification for the precision parameter κ. This is inline with previously published results for similar models (see Supplementary Material of Palacios and Minin, 2013).

To obtain the analytical solution of (14a) in splitHMC, we Eigen-decompose the precision matrix ${\mathbf{C}}_{\text{in}}^{-1}$, sacrificing sparsity. One can, however, use the Cholesky decomposition instead ${\mathbf{C}}_{\text{in}}^{-1}={\mathbf{R}}^{\text{T}}\mathbf{R}$ and transform $f^{*}=Rf$. This way, the dynamics (14a) would be much simpler with the solution as a rotation (Pakman and Paninski, 2014). Because R is also tridiagonal similar to ${\mathbf{C}}_{in}^{-1}$, in theory the computational cost of splitHMC could be reduced to $\mathcal{O}(D)$. In practice, however, we found that this approach would work well when the Hamiltonian (13) is mainly dominated by the middle term. This condition does not hold for the examples discussed in this article. Nevertheless, we have provided the corresponding splitHMC method with Cholesky decomposition in the Supplementary File, since it can still be used for situations where the middle term does in fact dominate the overall Hamiltonian.

There are several possible future directions. One possibility is to use ES² as a proposal generating mechanism in updating f as opposed to using it for sampling from the posterior distribution. Finding a good proposal for κ (or τ), however, remains challenging. Another possible direction it to allow κ to be time dependent. When there is rapid fluctuation in the population, one single precision parameter κ may not well capture the corresponding change in the latent vector f. Our future work will include time-varying precision $\kappa (t)$ or more informative covariance structure in modeling Gaussian prior. Also, we can extend our existing work by allowing irregular grids, which may be more suitable for rapidly changing population dynamics.

Another important extension of the methods presented here is to allow for multiple genes and genealogical uncertainty. The MCMC methods proposed here can be incorporated into a hierarchical framework to infer population size trajectories from sequence data directly. In contrast, INLA cannot be adapted easily to perform inference from sequence data. This greatly limits its generality.

Funding

J.A.P. acknowledges scholarship from CONACyT Mexico to pursue her research work. This work was supported by NIH grant R01 AI107034 (to S.L., M.K., V.N.M. and B.S.), the NSF grant IIS-1216045 (to B.S.) and the NIH grant U54 GM111274 (to V.N.M.).

Conflict of Interest: none declared.