Categorical spectral analysis of periodicity in nucleosomal DNA

Abstract

DNA helical twist imposes geometric constraints on the location of histone–DNA interaction sites along nucleosomal DNA. Certain 10.5-bp periodic nucleotides in phase with these geometric constraints have been suggested to facilitate nucleosome positioning. However, the extent of nucleotide periodicity in nucleosomal DNA and its significance in directing nucleosome positioning still remain unclear. We clarify these issues by applying categorical spectral analysis to high-resolution nucleosome maps in two yeast species. We find that only a small fraction of nucleosomal sequences contain significant 10.5-bp periodicity. We further develop a spectral decomposition method to show that the previously observed periodicity in aligned nucleosomal sequences mainly results from proper phasing among nucleosomal sequences, and not from a preponderant occurrence of periodicity within individual sequences. Importantly, we show that this phasing may arise from the histones’ proclivity for putting preferred nucleotides at some of the evenly spaced histone–DNA contact points with respect to the dyad axis. We demonstrate that 10.5-bp periodicity, when present, significantly facilitates rotational, but not translational, nucleosome positioning. Finally, although periodicity only moderately affects nucleosome occupancy genome wide, reduced periodicity is an evolutionarily conserved signature of nucleosome-depleted regions around transcription start/termination sites.

INTRODUCTION

Helical twist of the DNA polymer imposes important geometric constraints on its interaction with DNA-binding proteins, as well as on the interactions between DNA-binding proteins themselves. For example, cooperative binding of transcription factors can be highly dependent on their relative phase with respect to the DNA helix (1), and transcription levels can be also sinusoidally modulated by the distance between transcription factor binding sites and transcription start sites (TSS) (2). The geometric constraint imposed by the DNA helix may further put selective pressure toward having functional sites separated by full helical turns (i.e. multiples of 10.5 bp) in the genome (3). One of the most well-known and intriguing cases of this geometric constraint lies in the fundamental repeating subunits of chromatin in eukaryotes, namely the nucleosomes consisting of 147 basepairs (bp) of DNA wrapping around histone octamers, where regularly spaced nucleotides in phase with the relative orientation between DNA helix and histone octamer can facilitate DNA bending and thus nucleosome formation (4,5). Nucleosomal sequences aligned at the dyad were first shown to possess 10.5-bp nucleotide periodicity three decades ago (4,6,7), and recent high-throughput sequencing experiments have detected similar patterns in various organisms (8–13). However, the notion of periodicity in nucleosomal DNA has been subjected to much debate for the past three decades and continues to pose outstanding problems that require clarification using rigorous analysis methods.

In eukaryotes, the precise location of nucleosomes regulates protein–DNA interactions by controlling the local DNA accessibility. Elucidating the mechanism of nucleosome positioning is thus a major step toward understanding diverse regulatory processes taking place on chromatin template. Despite extensive studies, the significance of nucleotide periodicity in directing nucleosome positioning remains an ongoing and heated debate (14–18). One the one hand, statistical models based on nucleotide periodicity are able to provide decent predictions of genome-wide nucleosome landscape (8,19,20), suggesting that periodic genomic features provide a nucleosome positioning signal. One the other hand, it has been shown that in vitro and in vivo nucleosome positioning patterns correlate only poorly, indicating that other forces play a major role in positioning nucleosomes in vivo (16,21). Furthermore, it has been noted (22) that, while computational models accounting for nucleotide periodicity have the highest accuracy in predicting single nucleosome positioning (23), models based on simple sequence features such as the G/C content are sufficient to reproduce nucleosome occupancy (24), which refers to the probability of a given base pair in the genome being occupied by a nucleosome in cell population (25). These findings indicate that nucleotide periodicity may play different roles in influencing single nucleosome positioning versus population-level nucleosome occupancy.

Several key questions regarding the role of periodicity in nucleosomal DNA thus remain. First, is nucleosomal DNA enriched for 10.5-bp periodic sequence features? If it is, what is the genome-wide level of 10.5-bp periodicity statistically? Second, how does periodicity affect single nucleosome positioning in vivo? More precisely, what is the role of periodicity in translational positioning, referring to the location of the 147-bp DNA contacting the histone octamer, and in rotational positioning, referring to the rotational orientation of DNA helix relative to the histone surface (25), respectively? Furthermore, how does periodicity affect nucleosome occupancy? Lastly, what can one learn about histone–DNA interactions from the analysis of nucleotide periodicity? Specifically, does the observed periodicity in dyad-aligned nucleosomal sequences reflect a sequence preference of histone–DNA interaction?

We address these questions by developing a computational framework based on categorical spectral analysis and applying it to high-resolution nucleosome maps in yeast (‘Materials and Methods’ section) (12,13). The computational framework developed here can be easily adapted and applied to analyzing genome-wide nucleosome maps generated by various experimental techniques.

MATERIALS AND METHODS

Datasets

We downloaded the genome-wide nucleosome maps in Saccharomyces cerevisiae and Schizosaccharomyces pombe generated by the chemical cleavage method from the supplementary materials of (12) and (13), respectively. For each yeast species, there is a redundant map representing all possible nucleosome positions in the population, as well as a unique map representing consensus nucleosome positions. We used the UCSC SAC2 version of the S. cerevisiae genome as in (12) and the Ensembl release 16 version of the S. pombe genome, which is the same as the genome (PomBase 10 March 2012 version) used in (13).

The TSS and transcription termination site (TTS) coordinates of S. cerevisiae genome were obtained from (26). We downloaded the original annotations of TSS and TTS coordinates in Saccharomyces Genome Database (SGD) 7 August 2005 version of the S. cerevisiae genome from Supplementary Table S3 of (26), retaining only those genes that were indicated with complete 5′ UTRs and 3′ UTRs (in total 3017). We then used BLAT to map the genes to the UCSC SAC2 version of the S. cerevisiae genome. After removing genes mapping to multiple genomic locations or to disjoint blocks (blockCount > 1), we were left with 3005 genes with correctly annotated TSS and TTS coordinates.

The TSS and TTS coordinates of S. pombe genome were obtained from (27). We downloaded the original annotations of TSS and TTS coordinates in PomBase 16 July 2008 version of the S. pombe genome from Supplementary Table S2 of (27), retaining only those genes with both annotated TSS and TTS coordinates and not marked in red in the original Excel file (See Supplementary Table S2 of (27) for details) (in total 3692). The PomBase 16 July 2008 version of the S. pombe genome is the same as the Ensembl release 16 version. We thus used the TSS and TTS coordinates of these 3692 genes directly.

We used the genome version K12 MG1655 (U00096) for Escherichia coli.

Spectral envelope

We follow the notation used in (28,29). Consider a DNA sequence s_t of length L, where t = 0, 1, …, L − 1 and s_t ∈ {A, C, G, T}. To perform spectral analysis, we convert the categorical DNA sequence s_t into a numerical sequence by using a scaling function 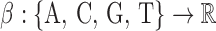that maps nucleotides to real numbers. We denote the resulting real-valued sequence as x_t = β(s_t). The spectral envelope of the DNA sequence s_t at a specific frequency is defined as the maximum spectral density among all possible non-trivial (i.e., 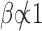) scaling functions at that frequency; i.e.,

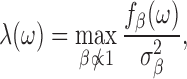(1)

where f_β(ω) is the power spectral density of x_t at angular frequency ω, and 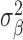is the variance of x_t. A peak at ω in the spectral envelope spectrum indicates a dominant periodic component of angular frequency ω, or period 2π/ω. To calculate the sample spectral envelope, the power spectral density and variance in Equation 1 should be replaced by the periodogram (Supplementary Methods section 1.1) and sample variance, respectively (30). The sample spectral envelope can be efficiently calculated by converting the maximization to an eigenvalue problem (30). We used a modified version of the R code included in (30) to compute the sample spectral envelope.

The spectral envelope defined in Equation 1 quantifies the periodic component in mono-nucleotide patterns of the DNA sequence. To generalize the definition for quantifying periodic components in k-mer patterns of any fixed integer k, we simply need to generalize our alphabet {A, C, G, T} to a set of all k-mers and let the scaling function β map all k-mers to real numbers. For example, di-nucleotide spectral envelope is defined in the same way as in Equation 1, except that the scaling function is now 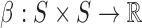, where S = {A, C, G, T}, and the numerical representation of s_t is given by x_t = β(s_t, s_{t + 1}), for t = 0, 1,…, L − 2.

Computational details

A detailed description of the computational analysis performed in this paper is provided in Supplementary Methods, including derivation of the spectral decomposition, definitions of circular-linear and circular-circular correlations, and definitions of translational and rotational fuzziness scores.

RESULTS

Periodicity in aligned sequences does not imply periodicity in individual sequences

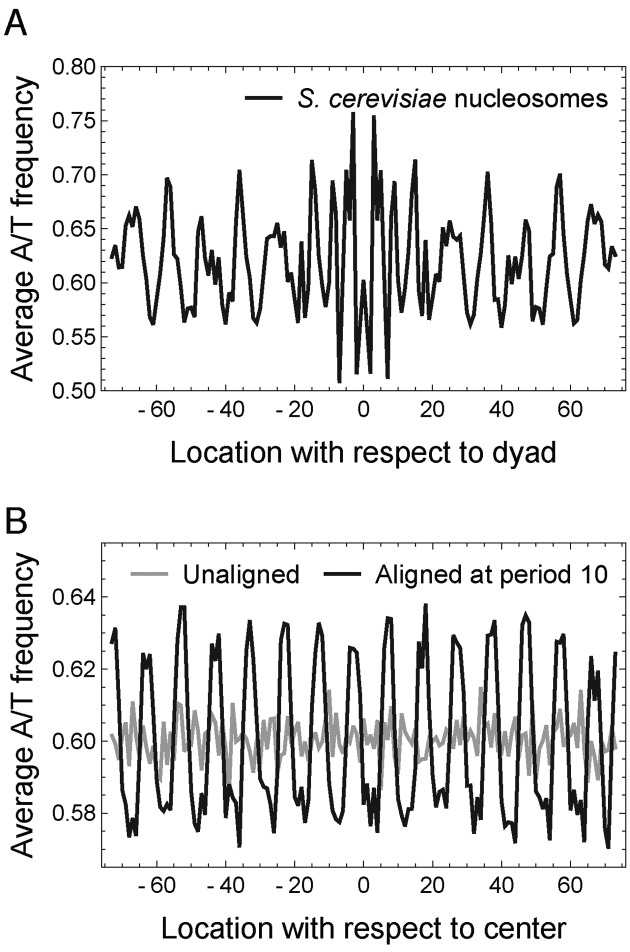
The idea of periodic nucleosome positioning signals has been mainly based on observing 10.5-bp periodic patterns in the average nucleotide frequencies of nucleosomal sequences aligned at the dyad (Figure 1A) (8). It is important to note that both the periodicity of individual sequences and the proper phasing of multiple sequences can contribute to the observed periodicity in the average nucleotide frequencies. In the extreme case where DNA sequences are randomly generated, a periodic pattern of any desired period can be easily created by a systematic manipulation of alignment (Figure 1B, Supplementary Methods section 1.2) (31). Therefore, the observed periodicity in average nucleotide frequency does not a priori imply periodicity in each individual nucleosomal sequence.

Figure 1.

Periodicity in dyad-aligned nucleosomal sequences and systematically shifted random sequences. (A) A/T frequency averaged across dyad-aligned nucleosomal sequences in Saccharomyces cerevisiae. (B) A 10-bp periodicity (black curve) can be created from 10 000 random sequences (gray curve) by systematically shifting the sequences by at most 5 bp (Supplementary Methods section 1.2).

In mathematical terms, two problems often confound the discussion of periodicity in the literature: (i) a mathematically rigorous way of studying periodic patterns in a DNA sequence is to Fourier decompose the sequence into its harmonic components, computing the magnitude of oscillations at each frequency. However, averaging the Fourier spectra of individual sequences is not equivalent to computing the Fourier spectrum of averaged sequences; (ii) Detecting periodicity with Fourier analysis critically depends on the representation of categorical nucleotide contents into real numbers. Several studies to date have employed particular choices of representing nucleotides as numbers and reported different nucleotide patterns to be significant at 10.5-bp periodicity, such as AA/TT/TA (8), AA/TT (32) and AA/TT/AT/TA (12,13). As these particular representations were designed to capture the presumed dinucleotide patterns, it is plausible that the previous studies were biased and missed other intrinsic periodic patterns; thus, a spectral method that simultaneously explores all possible representations of DNA as real numbers is needed. We here present a rigorous mathematical formalism for addressing these two problems and perform genome-wide quantification of periodicity in individual nucleosomal sequences in yeast species.

Only a small fraction of nucleosomal sequences contain significant 10.5-bp periodicity

We applied the method of spectral envelope (28,29) (‘Materials and Methods’ section, Supplementary Methods section 1.1) to quantify the strength of periodicity in individual nucleosomal sequences. Briefly, the algorithm automatically explores all possible representations of a DNA sequence as real numbers and computes the maximum spectral density among all possible representations at each period. A significant peak in mono-/di-nucleotide spectral envelope thus indicates a dominant periodic component in mono-/di-nucleotides of the corresponding DNA sequence.

We calculated the mono-nucleotide spectral envelope of 67 531 and 75 818 consensus nucleosomal sequences of length 147 bp in S. cerevisiae (12) and S. pombe (13), respectively. The average spectral envelope of nucleosomal sequences in both S. cerevisiae (Figure 2A) and S. pombe (Supplementary Figure S1A) shows a distinct peak at period 10.5 bp, indicating enriched 10.5-bp periodicity compared to randomly permuted sequences, although the enrichment was only of order 10%, indicating that only a small fraction of nucleosomal sequences contain significant 10.5-bp periodicity. To assess the statistical significance of the 10.5-bp periodicity, we calculated empirical p-values by permuting each sequence 100 times (Supplementary Methods section 1.1), as previously done (28,33). The p-value distributions are skewed toward small values (Figure 2B for S. cerevisiae, Supplementary Figure S1B for S. pombe), providing evidence for 10.5-bp periodicity in a subset of individual nucleosomal sequences. To estimate the fraction of nucleosomal sequences that contained some degree of 10.5-bp periodicity—i.e. the fraction in excess of what might be expected from randomly permuted sequences (Figure 2B, dashed gray curve)—we fitted the distribution of empirical p-values (for example, Figure 2B, solid black curve) using a beta-uniform mixture model (Supplementary Methods section 1.1, Supplementary Figure S1C and D). The obtained mixing coefficients showed that an excess amount of only about 15–20% of nucleosomal sequences contained some degree of 10.5-bp periodicity in mono-nucleotides (Supplementary Table S1). However, it is important to note that not all of these 15–20% of nucleosomal sequences contained statistically significant 10.5-bp periodicity. In fact, after correcting for multiple hypothesis testing (Supplementary Methods section 1.1) (34), the fraction of nucleosomal sequences containing statistically significant 10.5-bp periodicity in mono-nucleotides was at most 4–5% at 5% false discovery rate (Supplementary Table S2). The calculation of di-nucleotide spectral envelope shows similar results (Supplementary Figure S2, Tables S1 and S2). These results show that the majority of nucleosomes do not possess any statistically significant 10.5-bp periodicity, which further suggests that periodic sequence features play only a minor role in positioning nucleosomes genome wide in vivo.

Figure 2.

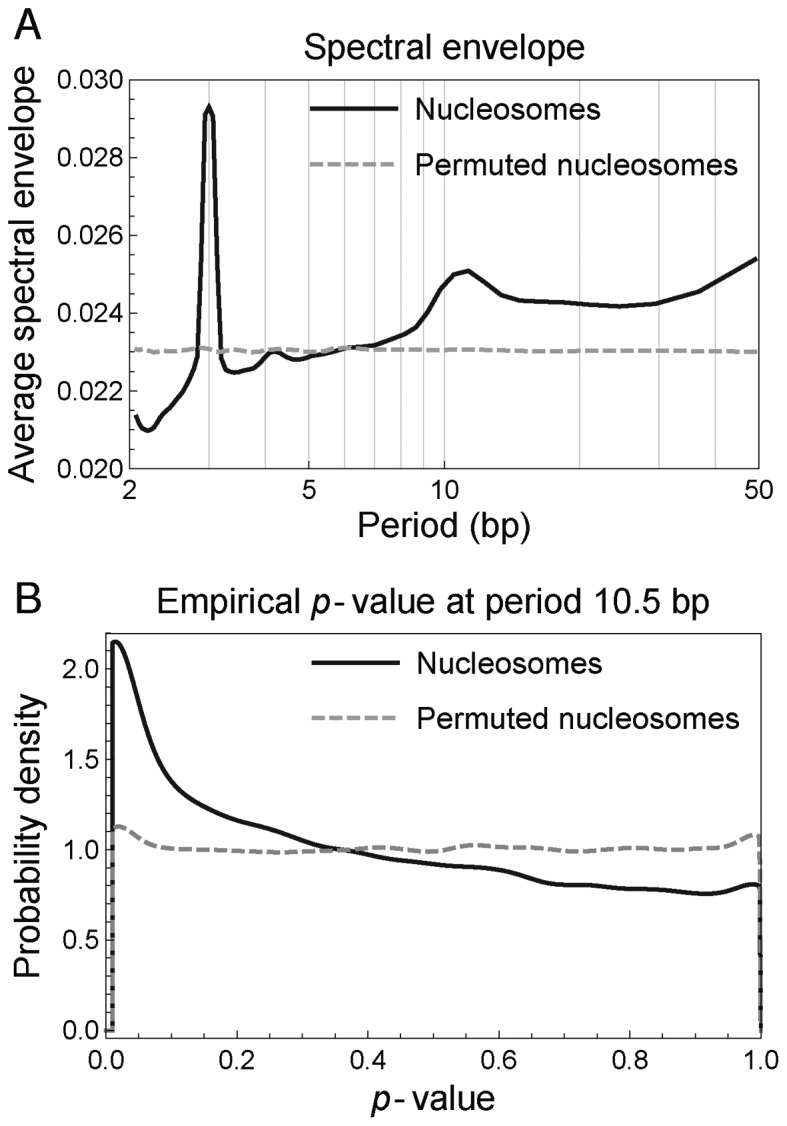
Nucleosomal sequences in Saccharomyces cerevisiae have enriched 10.5-bp periodicity in mono-nucleotides compared to randomly permuted sequences. (A) Average mono-nucleotide spectral envelope of nucleosomal sequences (solid black curve) and randomly permuted sequences (dashed gray curve). (B) Distribution of p-values assessing the statistical significance of 10.5-bp periodicity in mono-nucleotides of nucleosomal sequences (solid black curve) and randomly permuted sequences (dashed gray curve).

In vitro, it has been shown that nucleosomes preferentially form on S. cerevisiae DNA compared to E. coli DNA (16). Since E. coli does not have histones, its genome must have evolved neutrally with respect to its potential to form nucleosomes. Thus, one may expect to observe fewer occurrences of putative nucleosome-preferred sequence features, such as the 10.5-bp periodicity, in the E. coli genome compared to eukaryotic genomes. To test this hypothesis, we calculated the spectral envelope and empirical p-values of randomly selected 147-bp genomic regions from E. coli as well as S. cerevisiae and S. pombe. Surprisingly, the strength of 10.5-bp periodicity was comparable among the three genomes (Supplementary Figure S3, Tables S1 and S2), showing that factors other than the level of 10.5-bp periodicity in the genome may contribute to the preferential in vitro reconstitution of nucleosomes on S. cerevisiae DNA. Furthermore, these results suggest that the enrichment of 10.5-bp periodicity in yeast nucleosomal DNA compared to permuted sequences may not be a consequence of co-evolution between histones and genomic DNA (35), casting doubt on the belief that a 10.5-bp periodic genomic code associated with nucleosomes (8) has evolved. Nevertheless, the 10.5-bp periodicity, when present, may still be utilized by some nucleosomes to guide their positioning.

The observed 10.5-bp periodicity in average nucleotide frequencies mainly stems from phasing among nucleosomal sequences

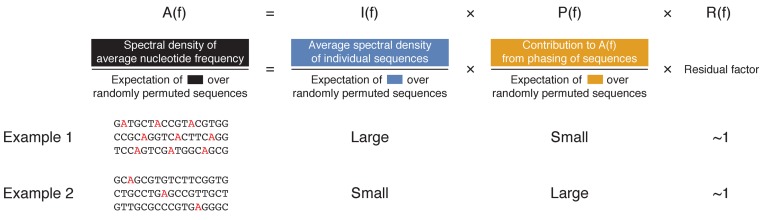
We have so far shown that only a small fraction of nucleosomal sequences contain statistically significant 10.5-bp periodicity, even when the spectrum for each individual nucleosome is maximized over all possible representations of nucleotides as real numbers. As previously mentioned, both periodicity in individual sequences and proper phasing among sequences may contribute to the observed 10.5-bp periodic average nucleotide frequencies in dyad-aligned nucleosomal sequences (Figure 1A). This section develops a novel spectral decomposition method for quantifying the origin of the observed periodicity in average nucleotide frequency (Supplementary Methods section 1.3, Figure 3).

Figure 3.

Illustration of the spectral decomposition (Supplementary Methods section 1.3). The last three rows provide an intuitive definition and graphical illustrations of the corresponding factors in the decomposition equation (top row). To save space, the decomposition is illustrated for the 5-bp periodicity (instead of 10.5-bp periodicity) of A nucleotides in three DNA sequences. The aligned enrichment A(f) characterizes the enrichment of periodicity in the average frequency of A obtained from aligning the three sequences. Two distinct factors contribute to the 5-bp periodicity observed in average frequency: (i) 5-bp periodicity of the A nucleotides within individual sequences (illustrated by the red A's in Example 1); and, (ii) phasing of A nucleotides at 5-bp intervals across sequences, even when individual contributing sequences do not contain 5-bp periodicity (illustrated by the red A's in Example 2). The individual enrichment I(f) and the phasing enrichment P(f) characterize the contributions to A(f) from these two factors, respectively. Thus, the dominant contribution to A(f) at 5-bp in Example 1 is from the 5-bp periodicity in individual sequences (i.e. large I(f)), while that in Example 2 is from the phasing of sequences (i.e. large P(f)).

Consider N nucleosomal sequences s_k(t) of length L (typically L = 147), where k = 1, 2, …, N indexes the nucleosomes and t = 0, 1, …, L − 1 indexes the nucleotides. Choosing a specific representation of nucleotides maps the nucleosomal sequences into corresponding numerical sequences x_k(t). A common example is to convert A and T to 1 and C and G to 0. The degree of periodicity in average nucleotide frequency 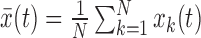is then captured by the spectral density of 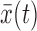, and it is this density that is commonly used in the literature to describe 10.5-bp periodicity in nucleosomal sequences (12).

To quantify the strength of periodicity in observed average nucleotide frequency compared to randomly permuted sequences, we defined a quantity A(f), termed ‘aligned enrichment’ at fundamental frequency f, as the spectral density of average nucleotide frequency normalized by its expectation value taken over separate and independent permutations of the N nucleosomal sequences s_k(t) (Supplementary Methods section 1.3, Figure 3). A peak in A(f) at fundamental frequency f thus indicates an enriched periodic component in the average nucleotide frequency of dyad-aligned nucleosomal sequences compared to randomly permuted sequences.

To separate the effect of alignment from individual nucleosome's periodicity, we decomposed A(f) as (Supplementary Methods section 1.3, Figure 3)

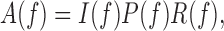(2)

where I(f), P(f) and R(f) are defined as follows: I(f), termed the ‘individual enrichment’, characterizes the spectral density enrichment of individual nucleosomal sequences compared to randomly permuted sequences. More precisely, I(f) is the average spectral density of individual sequences x_k(t) normalized by its expectation over randomly permuted sequences (Supplementary Methods section 1.3, Figure 3). Thus, a peak in A(f) that coincides with a peak in I(f) is likely to arise from the periodicity in individual nucleosomal sequences.

Likewise, P(f), termed the ‘phasing enrichment’, characterizes the contributions to A(f) arising from the phasing of nucleosomal sequences. More precisely, P(f) depends only on the phases of the Fourier-transformed sequences and reaches its maximum value when all sequences are completely in phase with each other (Supplementary Methods section 1.3, Figure 3). Thus, a peak in A(f) that coincides with a peak in P(f) is likely to arise from the phasing of nucleosomal sequences. Finally, R(f) is a residual factor in the decomposition (Supplementary Methods section 1.3).

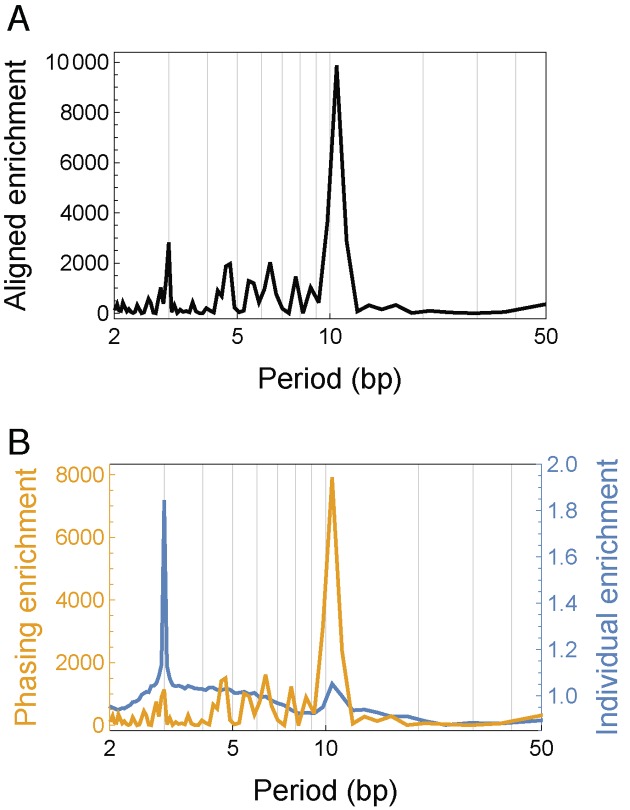
We applied the spectral decomposition method in both S. cerevisiae and S. pombe, representing A and T as 1 and C and G as 0 in order to disentangle the effect of phasing in the findings commonly reported in the literature. The overall aligned enrichment spectrum A(f) showed a predominant peak at period 10.5 bp (Figure 4A for S. cerevisiae, Supplementary Figure S4A for S. pombe), confirming the previously reported 10.5-bp periodicity in the average nucleotide frequency (Figure 1A). The secondary peak at period 3 bp corresponded to codons (28). The individual enrichment spectrum I(f) still showed a predominant peak at period 3 bp, but the peak at period 10.5 bp was not nearly as prominent as that in the overall aligned enrichment A(f) (blue curves in Figure 4B and Supplementary Figure S4B, for S. cerevisiae and S. pombe, respectively), consistent with our result that only a small fraction of individual nucleosomal sequences possess significant 10.5-bp periodicity. By contrast, the phasing enrichment P(f) showed a distinct peak only at period 10.5 bp (yellow curves in Figure 4B and Supplementary Figure S4B, for S. cerevisiae and S. pombe, respectively), and the local maximum at period 3 bp dropped to the level seen at periods around 4–9 bp. The residual factor R(f) showed no reproducible features (Supplementary Figure S5), as subsampling nucleosomal sequences yielded unstable residual factors, whereas the aligned, individual and phasing enrichments remained stable (compare Figure 4 and Supplementary Figure S5A with Figure S6). The residual factor was thus sensitive to noise and did not contain useful information in practice.

Figure 4.

Spectral decomposition of periodicity in average nucleotide frequency of dyad-aligned nucleosomal sequences in Saccharomyces cerevisiae, where A and T were set to 1 and C and G to 0. (A) The spectrum of aligned enrichment (see main text) for nucleosomal sequences in S. cerevisiae. (B) The spectrum of individual enrichment (blue curve) and phasing enrichment (yellow curve) (see main text) in S. cerevisiae.

We further focused on the 3 and 10.5 bp periods, considering the fluctuations at other periods as background. To determine the background average of each factor, we calculated the geometric mean across all periods after masking out the three periods centered at 3 bp and the three periods centered at 10.5 bp, respectively. We then calculated the fold-increase of each factor at 3 and 10.5 bp, respectively, relative to the corresponding background average (Table 1 for S. cerevisiae, Supplementary Table S3 for S. pombe). Note that taking geometric mean preserves the decomposition relation (Equation 2) in the signal-to-background ratio. We found that at period 10.5 bp, the fold-increase for the phasing enrichment was almost equal to that for the aligned enrichment, but the individual enrichment was only slightly greater than the background average. The 10.5-bp periodicity in individual nucleosomal sequences thus contributed only a small multiplicative correction to the observed overall spectrum A(f), while the phasing term was the dominant contribution, similar to the phenomenon seen in Figure 1B. By contrast, at period 3 bp, both individual periodicity and phasing contributed to the overall spectrum A(f). This analysis indicates that there indeed exist preferred evenly spaced locations for putting specific nucleotides, but the constraints at most of these locations are generally not satisfied in a single nucleosome. We investigate this idea further in the subsequent section.

Table 1. Ratio of the value of each factor at 3 and 10.5 bp, respectively, to the corresponding background average.

1/f	A(f)	I(f)	P(f)	R(f)
3 bp	22.9	1.88	11.5	1.06
10.5 bp	80.2	1.07	80.1	0.936

Phasing among nucleosomal sequences arises from a preference in nucleotide content at evenly spaced histone–DNA helical contact points

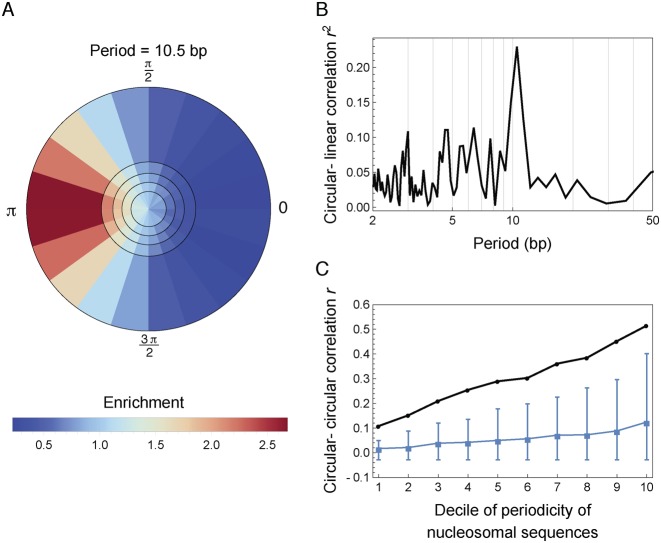
The pronounced peak at period 10.5 bp in the phasing enrichment P(f) (Figure 4B) suggested strong phasing of A/T nucleotide locations across nucleosomal sequences. One hypothesis is that this phasing might arise from a preference in nucleotide content at evenly spaced histone–DNA helical contact points facilitating DNA bending. Under this hypothesis, the 10.5-bp periodic nucleotide pattern in nucleosomal DNA sequences should have a definite phase relative to the evenly spaced preference points. Since these preference points are fixed with respect to the dyad axis in each nucleosome, one can test the hypothesis by studying whether the Fourier transform of individual nucleosomal sequences at 10.5-bp has a fixed phase relative to the dyad axis. In addition, nucleosomal sequences with stronger 10.5-bp periodicity are likely to better satisfy these preferential geometric constraints and thus should have a more definite phase relative to the dyad compared to sequences with weaker periodicity. To check these two implications of the hypothesis, we ranked the nucleosomal sequences according to the strength of 10.5-bp periodicity, and plotted the distribution of their phases with respect to the dyad in each quintile as a density map in the complex plane (Supplementary Methods section 1.4) (Figure 5A for S. cerevisiae and Figure S7A for S. pombe). We found that the phases of 10.5-bp periodicity in nucleosomal sequences were indeed enriched at one definite value with respect to the dyad, as indicated by the concentrated red color along one direction; and, the enrichment became more definite as the strength of periodicity increased (i.e. increasing radial coordinate in Figure 5A and Supplementary Figure S7A), as indicated by the blue-to-red gradient from inner rings to outer rings. Importantly, the phase of A/T nucleotides at period 10.5 bp was enriched toward π with respect to the dyad axis, in accordance with the phase (∼3.12) of primary bound-phosphate group contact points determined by the crystal structure of nucleosome (36) (Supplementary Methods section 1.4). To further quantify the association between the phase and strength of 10.5-bp periodicity in nucleosomal sequences, we calculated the circular-linear correlation between the phase and strength of Fourier transformed sequences, where A and T were set to 1 and C and G to 0 (Supplementary Methods section 1.4). The correlation coefficient showed a prominent peak at period 10.5-bp in both yeast species (Figure 5B for S. cerevisiae and Supplementary Figure S7B for S. pombe). Lastly, the periodic nucleotide patterns in nucleosomal sequences had a definite phase relative to the dyad axis only at period 10.5 bp but not any other periods (Supplementary Figure S8). These results supported the hypothesis that the phasing among nucleosomal sequences arose from a preference in nucleotide content at evenly spaced histone–DNA helical contact points.

Figure 5.

The effects of phasing of nucleosomal sequences in Saccharomyces cerevisiae. For this analysis, A and T were set to 1, and C and G to 0. (A) Phasing of sequences is evident in the Fourier space at period 10.5 bp. Nucleosomes were ranked according to the strength of 10.5-bp periodicity and divided into five quintiles (the five circular rings separated by black circles). The phases (with respect to the dyad) of their discrete Fourier transform at period 10.5 bp were then binned into 20 equal intervals (the 20 bins within each ring). Colors indicate the fraction of nucleosomes lying in each bin divided by the expectation under a uniform null distribution (Supplementary Methods section 1.4). (B) Circular-linear correlation between the phase and strength of 10.5-bp periodicity (Supplementary Methods section 1.4). (C) Circular–circular correlation between the phase of nucleotide Fourier transform and the phase of nucleosome location Fourier transform at period 10.5 bp (black curve, Supplementary Methods section 1.4). Consensus nucleosomes were first ranked according to the strength of their 10.5-bp nucleotide periodicity and then divided into 10 groups of equal size. The x-axis represents the group index, with group 1 having the smallest strength of 10.5-bp periodicity. Blue curve shows the median correlation coefficient among all fundamental frequencies excluding 1/10.5, with whiskers showing the range from the 5th percentile to the 95th percentile.

One consequence of a periodic sequence preference is that if one nucleosome configuration is stabilized by a highly periodic sequence, then configurations shifted by full periods along the genome should have similar stability, since the preference and sequence would remain aligned. To test this hypothesis, we analyzed previously published nucleosome maps that utilized chemical cleavages near the dyad to measure nucleosome positions at high resolution in S. cerevisiae and S. pombe (12,13). These studies reported both ‘consensus’ maps characterizing the most common position of each nucleosome and ‘redundant’ maps capturing alternate positions across cell population. An implication of the preference in nucleotide content at evenly spaced histone–DNA helical contact points is that when the underlying DNA sequence possesses 10.5-bp periodicity, a nucleosome will try to align itself with respect to the periodic signal. Our hypothesis thus suggested that in regions where the sequence periodicity is sufficiently strong, a consensus nucleosome should have periodically spaced redundant nucleosomes in phase with sequence periodicity. We thus sought to directly study the phasing between redundant nucleosome positions and nucleotide periodicity in the underlying sequence. We created a 147-component indicator vector for each consensus nucleosome, taking a value of 1 at all possible dyad locations of redundant nucleosomes and 0 at all other locations, where the center of the vector corresponds to the dyad location of the consensus nucleosome. We then calculated the circular–circular correlation between the phase of this indicator vector and the phase of consensus nucleosomal sequence at period 10.5-bp (Supplementary Methods section 1.4) (Figure 5C for S. cerevisiae and Supplementary Figure S9 for S. pombe). In support of our hypothesis, we found that as the strength of the 10.5-bp periodicity in nucleosomal sequence increased, its phasing relative to redundant nucleosome positions became stronger, indicated by the increasing circular-circular correlation as a function of spectral density (Figure 5C, Supplementary Figure S9).

10.5-bp periodicity facilitates rotational but not translational positioning

In the following sections, we will provide a detailed study of how 10.5-bp periodicity contributes to different aspects of nucleosome positioning. To characterize the degree to which the translational location and the rotational orientation of a nucleosome vary across cells, we defined fuzziness scores for translational and rotational positioning respectively. Briefly, for each consensus nucleosome, we collected redundant nucleosomes located within ±60 bp of its dyad position. We considered these redundant nucleosomes as possible locations that the consensus nucleosome may occupy in different cells. We thus defined translational fuzziness of the consensus nucleosome as the variance of genomic coordinates of these redundant nucleosomes, weighted by the nucleosome center positioning (NCP) score that measures the relative abundance of nucleosomes at a specific genomic location (12,37). Rotational fuzziness was defined as the circular variance (38) of the genomic coordinates of redundant nucleosomes modulo the DNA helical repeat length, also weighted by the NCP score (Supplementary Methods section 1.5).

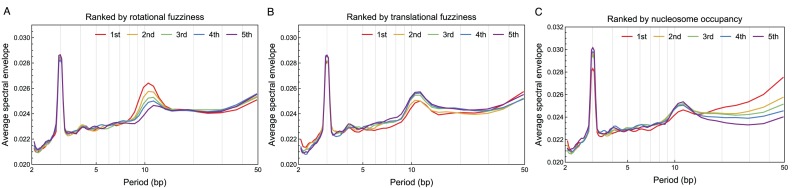
We calculated the translational and rotational fuzziness of 30 628 consensus nucleosomes (out of 67 531) in S. cerevisiae and 40 384 consensus nucleosomes (out of 75 818) in S. pombe that have at least five redundant nucleosomes lying within ±60 bp from the dyad position. We then ranked the nucleosomes in increasing order of translational and rotational fuzziness respectively, and plotted the average mono-nucleotide spectral envelope within each quintile. In both species, the smaller the rotational fuzziness of a nucleosome, the stronger was the 10.5-bp periodicity in its sequence (Figure 6A for S. cerevisiae, Supplementary Figure S10A for S. pombe). Specifically, in S. cerevisiae, the increase in spectral envelope (at period 10.5 bp) of the first quintile (Figure 6A, red curve) compared to randomly permuted sequences (Figure 2A, dashed gray curve) was about 0.0265 − 0.0230 = 0.0035, while that of the fifth quintile (Figure 6A, purple curve) was about 0.0245 − 0.0230 = 0.0015. Thus, the first quintile, which had the smallest rotational fuzziness, contained about 0.0035/0.0015 ≈ 2.3-fold higher 10.5-bp periodicity compared to the fifth quintile, indicating a strong effect of 10.5-bp periodicity on rotational positioning of nucleosomes (similarly, 2.4-fold higher in S. pombe, Supplementary Figure S10A). In contrast, translational fuzziness did not correlate with 10.5-bp periodicity in S. pombe (Supplementary Figure S10B). In S. cerevisiae, we observed a slight correlation between translational fuzziness and 10.5-bp periodicity (Figure 6B); but this correlation was a mere consequence of the anti-correlation between translational and rotational fuzziness (Supplementary Figure S11). Alternatively, ranking the nucleosomes by their mono-nucleotide spectral envelope at period 10.5 bp and plotting the distribution of translational and rotational fuzziness within each of the five equally binned intervals of spectral envelope yielded similar results (Supplementary Figure S12). Furthermore, analysis of the di-nucleotide spectral envelope is consistent with the mono-nucleotide results (Supplementary Figure S13). Our genome-wide analysis of individual nucleosomes thus demonstrates that 10.5-bp periodicity facilitates the rotational positioning of nucleosomes, so that nucleosomes in genomic regions with stronger 10.5-bp periodicity are more well positioned rotationally (i.e. redundant nucleosomes take the same orientation with respect to DNA helix); however, 10.5-bp periodicity does not affect whether a nucleosome is well positioned translationally.

Figure 6.

Spectral envelope of nucleosomes in Saccharomyces cerevisiae grouped by the level of nucleosome positioning and occupancy: (A) rotational positioning, (B) translational positioning and (C) nucleosome occupancy. Nucleosomes in S. cerevisiae were ranked from small to large values by rotational fuzziness, translational fuzziness and nucleosome occupancy, respectively. The average mono-nucleotide spectral envelope of nucleosomal sequences within each quintile was then plotted, where the first quintile contains nucleosomes with the smallest rotational fuzziness, translational fuzziness and nucleosome occupancy, respectively.

10.5-bp periodicity only moderately affects nucleosome occupancy genome wide

To study how 10.5-bp periodicity affects nucleosome occupancy (Supplementary Methods section 1.6) (13), we ranked the nucleosomes according to their occupancy level and plotted the average mono-nucleotide spectral envelope of nucleosomes within each quintile (Figure 6C for S. cerevisiae, Supplementary Figure S14 for S. pombe). Overall, the 10.5-bp periodicity only moderately affected nucleosome occupancy. However, the first quintile, consisting of nucleosomes with the lowest occupancy level, contained notably weaker 10.5-bp periodicity than the other four quintiles, indicating that nucleosomes may disfavor, but by no means exclude, genomic regions with low 10.5-bp periodicity. To confirm this observation on a finer scale, we divided the nucleosomes into 50 groups of equal size according to their occupancy levels and plotted the average mono-nucleotide spectral envelope at period 10.5 bp against average nucleosome occupancy within each group (Supplementary Figure S15). As nucleosome occupancy increases, the strength of 10.5-bp periodicity increases only at low occupancy level and then quickly plateaus. Analysis of di-nucleotide spectral envelope showed similar results (Supplementary Figure S16).

In addition, we compared the periodicity content in nucleosomal sequences with those in randomly selected 147-bp genomic regions and nucleosome depleted regions (NDRs), defined as linker regions of length >147 bp (Supplementary Figure S17). We found that randomly selected regions had 10.5-bp periodicity abundance similar to nucleosomal sequences, while NDRs contained much less pronounced 10.5-bp periodicity (Supplementary Tables S1 and S2). Taken together, our analysis shows that although the level of 10.5-bp periodicity only moderately affects nucleosome occupancy genome wide, very low periodicity might play a role locally in establishing genomic regions that disfavor nucleosome occupancy. Since NDRs are rare compared to the prevailing occupancy of nucleosomes in the genome, this effect is hardly discernible in a genome-wide study, but may be revealed if the analysis is focused on extreme low-occupancy regions, which motivated us to further perform a detailed analysis focused on NDR.

Reduced 10.5-bp periodicity is an evolutionarily conserved signature of nucleosome-depleted regions around transcription start/termination sites

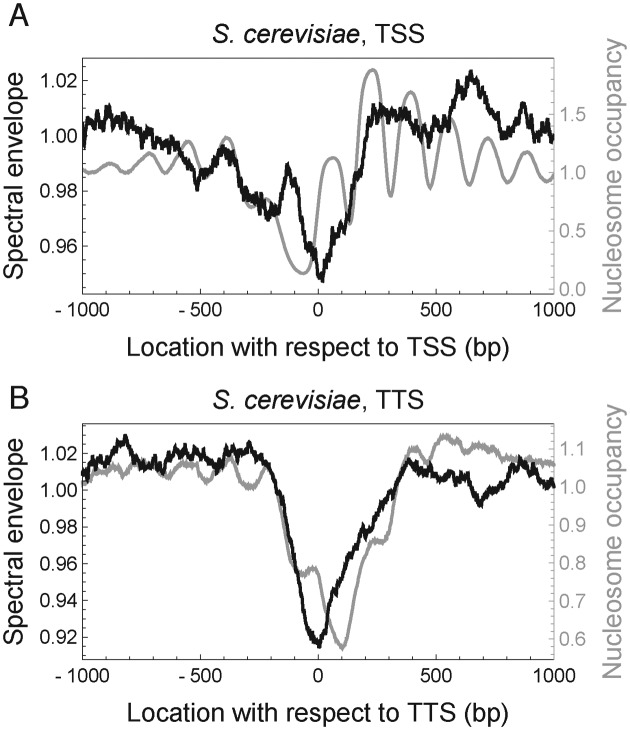
Given that genomic regions with low nucleosome occupancy contained reduced 10.5-bp periodicity, we further hypothesized that NDRs upstream of TSS and around TTS may be depleted of 10.5-bp periodicity. To test this hypothesis, we calculated spectral envelope at period 10.5 bp for each 147-bp sequence in the genome, and assigned it to the center location of the 147-bp sequence as a score characterizing the extent of local 10.5-bp periodicity. Consistent with our hypothesis, the NDRs at TSS and TTS in both S. cerevisiae (Figure 7 and Supplementary Figure S18 for mono- and di-nucleotides, respectively) and S. pombe (Supplementary Figure S19) contained reduced 10.5-bp periodicity. Our analysis thus suggests that reduced 10.5-bp periodicity is a conserved signature of NDR at both TSS and TTS, indicating a potentially conserved function of sequence periodicity in creating NDR, although the effect of sequence periodicity might be small, as indicated by the small reduction of periodicity (at most of order 10%; Figure 7 and Supplementary Figures S18 and S19) at NDR compared to the genome-wide average.

Figure 7.

Nucleosome-depleted regions in Saccharomyces cerevisiae contain reduced 10.5-bp periodicity. (A) Nucleosome occupancy (gray) and spectral envelope at 10.5 bp aligned at the TSS of 3005 genes. Black curve shows the average mono-nucleotide spectral envelope of running 147-bp windows centered at each location, normalized to the genome-wide mean. (B) Same as in (A), but aligned at TTS.

It is important to note that trans-factors such as chromatin remodelers, transcription factors and RNA polymerases also play a role in establishing NDR (14). In addition, rigid poly(dA:dT) tracts have been suggested as the main intrinsic signal in DNA sequences for creating NDR (39,40) and are enriched in S. cerevisiae NDR (41) (Supplementary Figure S20A and B) (Supplementary Methods section 1.7). However, NDR upstream of TSS in S. pombe is depleted of poly(dA:dT) tracts (27) (Supplementary Figure S20C), even though an enrichment is seen in NDR near TTS (Supplementary Figure S20D), indicating that poly(dA:dT) tracts are not universally conserved features in NDR. It is possible that different factors synergize in evicting nucleosomes at NDR, with reduced 10.5-bp periodicity and enriched poly(dA:dT) tracts affecting intrinsic histone–DNA interactions and trans-factors acting as active modifiers (42). For example, reduced 10.5-bp periodicity and enriched poly(dA:dT) tracts might destabilize nucleosomes and increase histone turnover at NDR (43) to facilitate the competitive binding of transcription factors against histones (44).

DISCUSSION

We have developed a computational framework based on categorical spectral analysis and applied it to high-resolution nucleosome maps in yeast, thereby obtaining quantitative results regarding the extent and origin of 10.5-bp nucleotide periodicity in nucleosomal sequences. Our results can be systematically explained by a simple model of histone–DNA interaction where the geometric constraints imposed by DNA helix induce a preference in nucleotide content at evenly spaced histone–DNA helical contact points. We have shown that only a small fraction of individual nucleosomes in yeast actually contain a detectable 10.5-bp periodic pattern in nucleotide content and that the previously observed periodicity in dyad-aligned nucleotide frequencies arises mostly from the phasing of multiple nucleosomal sequences where preferred nucleotides are located at a few, but by no means most, regularly spaced histone–DNA contact points. In other words, even though the histone–DNA contact points are periodic, the distribution of preferred nucleotides at these sites is not periodic in most nucleosomes. These results help resolve the counterpoints that have been the source of much debate in the chromatin field.

It is instructive to view nucleosome positioning using the following physical model: when the histone octamer reads a DNA sequence through the evenly spaced contact points, it sees a potential landscape with local minima located at positions where the number of preferred nucleotides at the contact points are locally maximized. At genomic locations where the 10.5-bp periodicity of preferred nucleotides is strong, these local minima are deep and evenly spaced by 10.5 bp. In this case, the resulting nucleosome positions are constrained at these local minima with small fluctuations around them, leading to rotationally well-positioned nucleosomes. However, these nucleosomes are not necessarily well positioned translationally, because the evenly spaced local minima may be similar in level, resulting in an equiprobable distribution of nucleosomes to these minima and thus large translational fuzziness cross cell population. By contrast, at genomic locations where the 10.5-bp periodic signal is weak, the local minima of the potential landscape are not deep enough to trap nucleosomes and also not necessarily evenly spaced by 10.5 bp. In this case, the resulting nucleosome positions are not well confined around each minima, and both rotational and translational fuzziness may be large. Nevertheless, given a sufficiently large number of nucleosomal DNA sequences, the locations of preferred nucleotides will be phased on average with the locations of histone–DNA contact points, and it is this phasing effect that has been reported in previous studies, as simulated in Figure 1B and demonstrated in Figure 5.

One might expect that genomic locations with strong 10.5-bp periodicity might have high probability of being occupied by a nucleosome, since the periodic pattern might help satisfy the nucleotide preference at evenly spaced histone–DNA helical contact points. However, we found that the effect of periodicity on nucleosome occupancy is hardly detectable on a genome-wide scale. By contrast, reduction in 10.5-bp periodicity was found to be an evolutionarily conserved signal of NDR around TSS and TTS, potentially contributing to destabilizing nucleosomes at important regulatory sites.

It is important to note that factors other than nucleotide periodicity also modulate nucleosome positioning in vivo. For example, steric exclusion between neighboring nucleosomes shapes the regularly-spaced nucleosome arrays downstream of TSS (45,46). Furthermore, trans-factors such as chromatin remodelers, transcription factors and RNA polymerase can actively regulate nucleosome positions (14,42). All of these factors act on the potential landscape determined by DNA sequence preference in histone–DNA interaction. Genomic sequence thus synergizes with other factors to direct nucleosome positioning in vivo (47–49). Interestingly, recent studies show that when trans-factors are massively malfunctioning—e.g. in early stages of cancer progression (50), upon viral infection (51) or upon drug treatments (52)—DNA sequence plays a more prominent role in determining nucleosome redistribution, highlighting the need for a computational model that can account for the dynamic interplay between trans-acting proteins and intrinsic DNA sequence to explain the regulation of local chromatin structure. This paper takes a stride toward this goal and provides a general computational framework for quantifying the presence of hidden periodic sequence features and relating these features to distinct characteristics of nucleosome positioning. The presented framework may also find its application in studying geometric constraints imposed by DNA helical twist on other DNA-binding proteins (1).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

NSF [1442504]. Funding for open access charge: NSF [DBI-1442504].

Conflict of interest statement. None declared.