An Atlas of Genetic Correlations across Human Diseases and Traits

Abstract

Identifying genetic correlations between complex traits and diseases can provide useful etiological insights and help prioritize likely causal relationships. The major challenges preventing estimation of genetic correlation from genome-wide association study (GWAS) data with current methods are the lack of availability of individual genotype data and widespread sample overlap among meta-analyses. We circumvent these difficulties by introducing a technique – cross-trait LD Score regression – for estimating genetic correlation that requires only GWAS summary statistics and is not biased by sample overlap. We use this method to estimate 276 genetic correlations among 24 traits. The results include genetic correlations between anorexia nervosa and schizophrenia, anorexia and obesity and associations between educational attainment and several diseases. These results highlight the power of genome-wide analyses, since there currently are no significantly associated SNPs for anorexia nervosa and only three for educational attainment.

Introduction

Understanding the complex relationships among human traits and diseases is a fundamental goal of epidemiology. Randomized controlled trials and longitudinal studies are time-consuming and expensive, so many potential risk factors are studied using cross-sectional correlations studies at a single time point. Obtaining causal inferences from such studies can be challenging due to issues such as confounding and reverse causation, which can lead to spurious associations and mask the effects of real risk factors [1, 2]. Genetics can help elucidate cause and effect, since inherited genetic risks cannot be subject to reverse causation and are correlated with a smaller list of confounders.

The first methods for testing for genetic overlap were family studies [3, 4, 5, 6, 7]. In order to estimate genetic overlaps among many pairs of phenotypes, family designs require measuring multiple traits on the same individuals. Consequently, it is challenging to scale family designs to a large number of traits, especially traits that difficult or costly to measure (e.g., low-prevalence diseases). More recently, genome-wide association studies (GWAS) have allowed us to obtain effect-size estimates for specific genetic variants, so it is possible to test for shared genetics by looking for correlations in effect-sizes across traits, which does not require measuring multiple traits per individual.

There exists a large class of methods for interrogating genetic overlap via GWAS that focus only on genome-wide significant SNPs. One of the most influential methods in this class is Mendelian randomization, which uses significantly associated SNPs as instrumental variables to attempt quantify causal relationships between risk factors and disease[1, 2]. Methods that focus on significant SNPs are effective for traits where there are many significant associations that account for a substantial fraction of heritability [8, 9]. For many complex traits, heritability is distributed over thousands of variants with small effects, and the proportion of heritability accounted for by significantly associated variants at current sample sizes is small [10]. In such situations, one can often obtain more accurate results by using genome-wide data, rather than just significantly associated variants [11].

A complementary approach is to estimate genetic correlation, which includes the effects of all SNPs, including those that do not reach genome-wide significance (Methods). The two main existing techniques for estimating genetic correlation from GWAS data are restricted maximum likelihood (REML) [11, 12, 13, 14, 15, 16] and polygenic scores [17, 18]. These methods have only been applied to a few traits, because they require individual genotype data, which are difficult to obtain due to informed consent limitations.

In order to overcome these limitations, we have developed a technique for estimating genetic correlation using only GWAS summary statistics that is not biased by sample overlap. Our method, cross-trait LD Score regression, is a simple extension of single-trait LD Score regression [19] and is computationally very fast. We apply this method to data from 24 GWAS and report genetic correlations for 276 pairs of phenotypes, demonstrating shared genetic bases for many complex diseases and traits.

Results

Overview of Methods

The method presented here for estimating genetic correlation from summary statistics relies on the fact that the GWAS effect-size estimate for a given SNP incorporates the effects of all SNPs in linkage disequilibrium (LD) with that SNP [19, 20]. For a polygenic trait, SNPs with high LD will have higher χ² statistics on average than SNPs with low LD [19]. A similar relationship holds if we replace χ² statistics for a single study with the product of z-scores from two studies of traits with non-zero genetic correlation.

More precisely, under a polygenic model [11, 13], the expected value of z_1jz_2j is

$$E[z_{1j}{z}_{2j}]=\frac{\sqrt{N_1{N}_2}{\rho }_g}{M}{\ell }_j+\frac{\rho N_s}{\sqrt{N_1{N}_2}},$$ (1)

where N_i is the sample size for study i, ρ_g is genetic covariance (defined in Methods), ℓ_j is LD Score [19], N_s is the number of individuals included in both studies, and ρ is the phenotypic correlation among the N_s overlapping samples. We derive this equation in the Supplementary Note. If study 1 and study 2 are the same study, then Equation 1 reduces to the single-trait result from [19], because genetic covariance between a trait and itself is heritability, and χ²=z². As a consequence of equation 1, we can estimate genetic covariance using the slope from the regression of z_1jz_2j on LD Score, which is computationally very fast (Methods).

Sample overlap creates spurious correlation between z_1j and z_2j, which inflates z_1jz_2j. The expected magnitude of this inflation is uniform across all markers, and in particular does not depend on LD Score. As a result, sample overlap only affects the intercept from this regression (the term $\rho N_s/\sqrt{N_1{N}_2}$) and not the slope, so the estimates of genetic correlation will not be biased by sample overlap. Similarly, shared population stratification will alter the intercept but have minimal impact on the slope, because the correlation between LD Score and the rate of genetic drift is minimal [19]. If we are willing to assume no shared population stratification, and we know the amount of sample overlap and phenotypic correlation in advance (i.e., the true value of $\rho N_s/\sqrt{N_1{N}_2}$), we can constrain the intercept to this value. We refer to this approach as constrained intercept LD Score regression. Constrained intercept LD Score regression has lower standard error – often by as much as 30% – than LD Score regression with unconstrained intercept, but will yield biased and misleading estimates if the intercept is misspecified, e.g., if we specify the wrong value of N_sρ or do not completely control for population stratification.

Normalizing genetic covariance by the SNP-heritabilities yields genetic correlation: $r_g:={\rho }_g/\sqrt{h_1^2{h}_2^2}$, where $h_i^2$ denotes the SNP-heritability [11] from study i. Genetic correlation ranges between −1 and 1. Results similar to Equation 1 hold if one or both studies is a case/control study, in which case genetic covariance is on the observed scale. Details are provided in the Supplementary Note. There is no distinction between observed and liability scale genetic correlation for case/control traits, so we can define and estimate genetic correlation between a case/control trait and a quantitative trait and genetic correlation between pairs of case/control traits without the need to specify a scale (Supplementary Note).

Simulations

We performed a series of simulations to evaluate the robustness of the model to potential confounders such as sample overlap and model misspecification, and to verify the accuracy of the standard error estimates (Methods).

Table 1 shows cross-trait LD Score regression estimates and standard errors from 1,000 simulations of quantitative traits. For each simulation replicate, we generated two phenotypes for each of 2,062 individuals in our sample by drawing effect sizes approximately 600,000 SNPs on chromosome 2 from a bivariate normal distribution. We then computed summary statistics for both phenotypes and estimated heritability and genetic correlation with cross-trait LD Score regression. The summary statistics were generated from completely overlapping samples. Results are shown in Table 1. These simulations confirm that cross-trait LD Score regression yields accurate estimates of the true genetic correlation and that the standard errors match the standard deviation across simulations. Thus, cross-trait LD Score regression is not biased by sample overlap, in contrast to estimation of genetic correlation via polygenic risk scores, which is biased in the presence of sample overlap [18]. We also evaluated simulations with one quantitative trait and one case/control study and show that cross-trait LD Score regression can be applied to binary traits and is not biased by oversampling of cases (Supplementary Table 1).

Table 1.

Simulations with complete sample overlap. Truth shows the true parameter values. Estimate shows the average cross-trait LD Score regression estimate across 1000 simulations. SD shows the standard deviation of the estimates across 1000 simulations, and SE shows the mean cross-trait LD Score regression SE across 1000 simulations. Further details of the simulation setup are given in the Methods.

Parameter	Truth	Estimate	SD	SE
h2	0.58	0.58	0.072	0.075
ρg	0.29	0.29	0.057	0.058
rg	0.50	0.49	0.079	0.073

Estimates of heritability and genetic covariance can be biased if the underlying model of genetic architecture is misspecified, e.g., if variance explained is correlated with LD Score or MAF [19, 21]. Because genetic correlation is estimated as a ratio, it is more robust; biases that affect the numerator and the denominator in the same direction tend to cancel. We obtain approximately correct estimates of genetic correlation even in simulations with models of genetic architecture where our estimates of heritability and genetic covariance are biased (Supplementary Table 2).

Replication of Pyschiatric Cross-Disorder Results

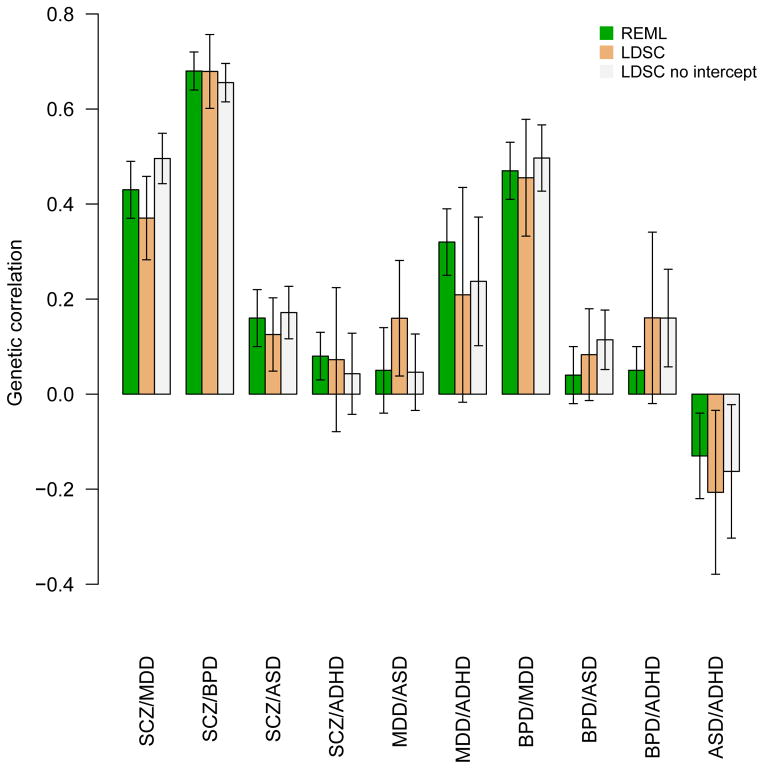
As technical validation, we replicated the estimates of genetic correlations among psychiatric disorders obtained with individual genotypes and REML in [14], by applying cross-trait LD Score regression to summary statistics from the same data [22]. These summary statistics were generated from non-overlapping samples, so we applied cross-trait LD Score regression using both unconstrained and constrained intercepts (Methods). Results from these analyses are shown in Figure 1. The results from cross-trait LD Score regression were similar to the results from REML. Cross-trait LD Score regression with constrained intercept gave standard errors that were only slightly larger than those from REML, while the standard errors from cross-trait LD Score regression with intercept were substantially larger, especially for traits with small sample sizes (e.g., ADHD, ASD).

Figure 1.

Application to Summary Statistics From 25 Phenotypes

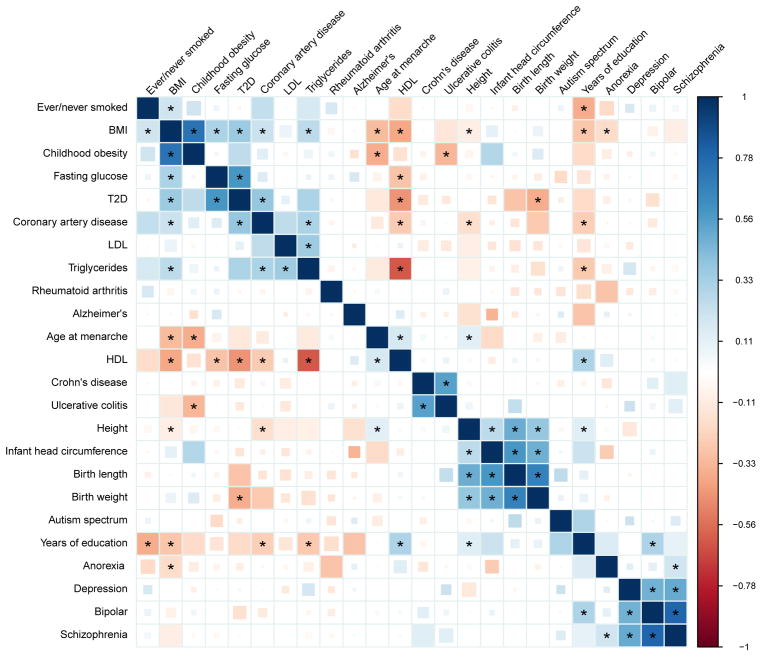
We used cross-trait LD Score regression to estimate genetic correlations among 24 phenotypes (URLs, Methods). Genetic correlation estimates for all 276 pairwise combinations of the 24 traits are shown in Figure 2. For clarity of presentation, the 24 phenotypes were restricted to contain only one phenotype from each cluster of closely related phenotypes (Methods). Genetic correlations among the educational, anthropometric, smoking, and insulin-related phenotypes that were excluded from Figure 2 are shown Supplementary Figures 1, 2, 3 and 4, respectively. A full table of 1176 genetic correlations among 49 traits is provided in Supplementary Table 4. References and sample sizes are shown in Supplementary Table 3.

Figure 2.

The first section of Table 2 lists genetic correlation results that are consistent with epidemiological associations, but, as far as we are aware, have not previously been reported using genetic data. The estimates of the genetic correlation between age at menarche and adult height [29], triglycerides [30] and type 2 diabetes [30, 31] are consistent with the epidemiological associations. The estimate of a negative genetic correlation between anorexia nervosa and obesity suggests that the same genetic factors influence normal variation in BMI as well as dysregulated BMI in psychiatric illness. This result is consistent with the observation that BMI GWAS findings implicate neuronal, rather than metabolic, cell-types and epigenetic marks [32, 33]. The negative genetic correlation between adult height and coronary artery disease agrees with a replicated epidemiological association [34, 35, 36]. We observe several significant associations with the educational attainment phenotypes from Rietveld et al. [37]: we estimate a statistically significant negative genetic correlation between college and Alzheimer’s disease, which agrees with epidemiological results [38, 39]. The positive genetic correlation between college and bipolar disorder is consistent with previous epidemiological reports [40, 41]. The estimate of a negative genetic correlation between smoking and college is consistent with the observed differences in smoking rates as a function of educational attainment [42].

Table 2.

Genetic correlation estimates, standard errors and p-values for selected pairs of traits. Results are grouped into genetic correlations that are new genetic results, but are consistent with established epidemiological associations (“Epidemiological”), genetic correlations that are new both to genetics and epidemiology (“New/Nonzero”) and interesting null results (“New/Low”). The p-values are uncorrected p-values. Results that pass multiple testing correctionw for the 300 tests in Figure 2 at 1% FDR have a single asterisk; results that pass Bonferroni correction have two asterisks. We present some genetic correlations that agree with epidemiological associations but that do not pass multiple testing correction in these data.

	Phenotype 1	Phenotype 2	rg(se)	p-value
Epidemiological	Age at menarche	Adult height	0.13 (0.03)	2×10−6**
	Age at menarche	Type 2 diabetes	−0.13 (0.04)	2×10−3*
	Age at menarche	Triglycerides	−0.12 (0.04)	1×10−3*
	Coronary artery disease	Age at menarche	−0.12 (0.05)	3×10−2
	Coronary artery disease	Years of education	−0.25 (0.06)	1×10−4**
	Coronary artery disease	Adult height	−0.17 (0.04)	1×10−5**
	Alzheimer’s	Years of education	−0.29 (0.1)	5×10−3*
	Bipolar disorder	Years of education	0.30 (0.06)	9×10−7**
	BMI	Years of education	−0.28 (0.03)	6×10−16**
	Triglycerides	Years of education	−0.26 (0.06)	2×10−8**
	Anorexia nervosa	BMI	−0.18 (0.04)	3×10−7**
	Ever/never smoker	Years of education	−0.36 (0.06)	2×10−8**
	Ever/never smoker	BMI	0.20 (0.04)	8×10−7**
New/Nonzero	Autism spectrum disorder	Years of education	0.30 (0.08)	2×10−4*
	Ulcerative colitis	Childhood obesity	−0.34 (0.08)	3.1 × 10−5**
	Anorexia nervosa	Schizophrenia	0.19 (0.04)	2×10−5**
New/Low	Schizophrenia	Alzheimer’s	0.04 (0.06)	>0.1
	Schizophrenia	Ever/never smoker	0.04 (0.06)	>0.1
	Schizophrenia	Triglycerides	−0.04 (0.04)	>0.1
	Schizophrenia	LDL cholesterol	−0.04 (0.04)	>0.1
	Schizophrenia	HDL cholesterol	0.03 (0.04)	>0.1
	Schizophrenia	Rheumatoid arthritis	−0.04 (0.05)	>0.1
	Crohn’s disease	Rheumatoid arthritis	−0.03 (0.08)	>0.1
	Ulcerative colitis	Rheumatoid arthritis	0.09 (0.08)	>0.1

The second section of Table 2 lists three results that are, to the best of our knowledge, new both to genetics and epidemiology. One, we find a positive genetic correlation between anorexia nervosa and schizophrenia. Comorbidity between eating and psychotic disorders has not been thoroughly investigated in the psychiatric literature [43, 44], and this result raises the possibility of similarity between these classes of disease. Two, we estimate a negative genetic correlation between ulcerative colitis (UC) and childhood obesity. The relationship between premorbid BMI and ulcerative colitis is not well-understood; exploring this relationship may be a fruitful direction for further investigation. Three, we estimate a positive genetic correlation between autism spectrum disorder (ASD) and educational attainment (which has very high genetic correlation with IQ [37, 45, 46]). The ASD summary statistics were generated using a case-pseudocontrol study design, so this result cannot be explained by oversampling of ASD cases from the more highly educated parents, which is observed epidemiologically [47]. The distribution of IQ among individuals with ASD has lower mean than the general population, but with heavy tails [48] (i.e., an excess of individuals with low and high IQ). There is also emerging evidence that the genetic architecture of ASD varies across the IQ distribution [49].

The third section of Table 2 lists interesting examples where the genetic correlation is close to zero with small standard error. The low genetic correlation between schizophrenia and rheumatoid arthritis is interesting because schizophrenia has been observed to be protective for rheumatoid arthritis [50], though the epidemiological effect is weak, so it is possible that there is a real genetic correlation, but it is too small for us to detect. The low genetic correlation between schizophrenia and smoking is notable because of the increased tobacco use (both prevalence and number of cigarettes per day) among individuals with schizophrenia [51]. The low genetic correlation between schizophrenia and plasma lipid levels contrasts with a previous report of pleiotropy between schizophrenia and triglycerides [52]. Pleiotropy (unsigned) is different from genetic correlation (signed; see Methods); however, the pleiotropy reported by Andreassen, et al. [52] could be explained by the sensitivity of the method used to the properties of a small number of regions with strong LD, rather than trait biology (Supplementary Figure 5). We estimate near-zero genetic correlation between Alzheimer’s disease and schizophrenia. The genetic correlations between Alzheimers disease and the other psychiatric traits (anorexia nervosa, bipolar, major depression, ASD) are also close to zero, but with larger standard errors, due to smaller sample sizes. This suggests that the genetic basis of Alzheimer’s disease is distinct from psychiatric conditions. Last, we estimate near zero genetic correlation between rheumatoid arthritis (RA) and both Crohn’s disease (CD) and UC. Although these diseases share many associated loci [53, 54], there appears to be no directional trend: some RA risk alleles are also risk alleles for UC and CD, but many RA risk alleles are protective for UC and CD [53], yielding near-zero genetic correlation. This example highlights the distinction between pleiotropy and genetic correlation (Methods).

Finally, the estimates of genetic correlations among metabolic traits are consistent with the estimates obtained using REML in Vattikuti et al. [15] (Supplementary Table 6), and are directionally consistent with the recent Mendelian randomization results from Wuertz et al. [55]. The estimate of 0.54 (0.07) for the genetic correlation between CD and UC is consistent with the estimate of 0.62 (0.04) from Chen et al. [16].

Discussion

We have described a new method for estimating genetic correlation from GWAS summary statistics, which we applied to a dataset of GWAS summary statistics consisting of 24 traits and more than 1.5 million unique phenotype measurements. We reported several new findings that would have been difficult to obtain with existing methods, including a positive genetic correlation between anorexia nervosa and schizophrenia. Our method replicated many previously-reported GWAS-based genetic correlations, and confirmed observations of overlap among genome-wide significant SNPs, MR results and epidemiological associations.

This method is an advance for several reasons: it does not require individual genotypes, genome-wide significant SNPs or LD-pruning (which loses information if causal SNPs are in LD). Our method is not biased by sample overlap and is computationally fast. Furthermore, our approach does not require measuring multiple traits on the same individuals, so it scales easily to studies of thousands of pairs of traits. These advantages allow us to estimate genetic correlation for many more pairs of phenotypes than was possible with existing methods.

The challenges in interpreting genetic correlation are similar to the challenges in MR. We highlight two difficulties. First, genetic correlation is immune to environmental confounding, but is subject to genetic confounding, analogous to confounding by pleiotropy in MR. For example, the genetic correlation between HDL and CAD in Figure 2 could result from a causal effect HDL→CAD, but could also be mediated by triglycerides (TG) [9, 56], represented graphically [57] as HDL←G→TG→CAD, where G is the set of genetic variants with effects on both HDL and TG. Extending genetic correlation to multiple genetically correlated phenotypes is an important direction for future work [58]. Second, although genetic correlation estimates are not biased by oversampling of cases, they are affected by other forms of biased sampling, such as misclassification [14] and case/control/covariate sampling (e.g., a BMI-matched study of T2D).

We note several limitations of cross-trait LD Score regression as an estimator of genetic correlation. First, cross-trait LD Score regression requires larger sample sizes than methods that use individual genotypes in order to achieve equivalent standard error. Second, cross-trait LD Score regression is not currently applicable to samples from recently-admixed populations. Third, we have not investigated the potential impact of assortative mating on estimates of genetic correlation, which remains as a future direction. Fourth, methods built from polygenic models, such as cross-trait LD Score regression and REML, are most effective when applied to traits with polygenic genetic architectures. For traits where significant SNPs account for a sizable proportion of heritability, analyzing only these SNPs can be more powerful. Developing methods that make optimal use of both large-effect SNPs and diffuse polygenic signal is a direction for future research.

Despite these limitations, we believe that the cross-trait LD Score regression estimator of genetic correlation will be a useful addition to the epidemiological toolbox, because it allows for rapid screening for correlations among a diverse set of traits, without the need for measuring multiple traits on the same individuals or genome-wide significant SNPs.

Methods

Definition of Genetic Covariance and Correlation

All definitions refer to narrow-sense heritabilities and genetic covariances. Let S denote a set of M SNPs, let X denote a vector of additively (0-1-2) coded genotypes for the SNPs in S, and let y₁ and y₂ denote phenotypes. Define β:=argmax_α∈R^MCor[y₁,Xα], where the maximization is performed in the population (i.e., in the infinite data limit). Let γ denote the corresponding vector for y₂. This is a projection, so β is unique modulo SNPs in perfect LD. Define $h_S^2$, the heritability explained by SNPs in S, as $h_S^2(y_1):={\displaystyle \sum _j}{\beta }_j^2$ and ρ_S(y₁,y₂), the genetic covariance among SNPs in S, as ${\rho }_S(y_1,y_2):={\displaystyle \sum _{j\in S}}{\beta }_j{\gamma }_j$. The genetic correlation among SNPs in S is $r_S(y_1,y_2):={\rho }_S(y_1,y_2)/\sqrt{h_S^2(y_1)h_S^2(y_2)}$, which lies in [−1,1]. Following [11], we use subscript g (as in $h_g^2$, ρ_g,r_g) when the set of SNPs is genotyped and imputed SNPs in GWAS.

SNP genetic correlation (r_g) is different from family study genetic correlation. In a family study, the relationship matrix captures information about all genetic variation, not just common SNPs. As a result, family studies estimate the total genetic correlation (S equals all variants). Unlike the relationship between SNP-heritability [11] and total heritability, for which $h_g^2\le h^2$, no similar relationship holds between SNP genetic correlation and total genetic correlation. If β and γ are more strongly correlated among common variants than rare variants, then the total genetic correlation will be less than the SNP genetic correlation.

Genetic correlation is (asymptotically) proportional to Mendelian randomization estimates. If we use a genetic instrument $g_i:={\displaystyle \sum _{j\in S}}{X}_{ij}{\beta }_j$ to estimate the effect b₁₂ of y₁ on y₂, the 2SLS estimate is b̂_2SLS:= g^Ty₂/g^Ty₁ [59]. The expectations of the numerator and denominator are E[g^Ty₂]=ρ_S(y₁, y₂) and $E[g^T{y}_1]=h_S^2(y_1)$. Thus, $\mathit{pli}{m}_{N\to \infty }{\widehat{b}}_{2\mathit{SLS}}=r_S(y_2,y_1)\sqrt{h_S^2(y_1)/h_S^2(y_2)}$. If we use the same set S of SNPs to estimate b₁₂ and b₂₁ (e.g., if S is the set of all common SNPs, as in the genetic correlation analyses in this paper), then this procedure is symmetric in y₁ and y₂.

Genetic correlation is different from pleiotropy. Two traits have a pleiotropic relationship if many variants affect both. Genetic correlation is a stronger condition than pleiotropy: to exhibit genetic correlation, the directions of effect must also be consistently aligned.

Cross-Trait LD Score Regression

Recall from the Overview of Methods that the cross-trait LD Score regression equation is

$$E[z_{1j}{z}_{2j}]=\frac{\sqrt{N_1{N}_2}{\rho }_g}{M}{\ell }_j+\frac{\rho N_s}{\sqrt{N_1{N}_2}},$$ (2)

where z_ij denotes the z-score for study i and SNPj, N_i is the sample size for study i, ρ_g is genetic covariance, ℓ_j is LD Score [19], N_s is the number of individuals included in both studies, and ρ is the phenotypic correlation among the N_s overlapping samples. We derive this equation in the Supplementary Note. We estimate genetic covariance by regressing z_1jz_2j against ${\ell }_j\sqrt{N_{1j}{N}_{2j}}$, (where N_ij is the sample size for SNP j in study i) then multiplying the resulting slope by M, the number of SNPs in the reference panel with MAF between 5% and 50% (technically, this is an estimate of the genetic covariance among SNPs with 5–50% MAF; Supplementary Note).

If we know the correct value of the intercept term $\rho N_s\sqrt{N_1{N}_2}$ ahead of time, we can reduce the standard error by constraining the intercept to this value using the -constrain-intercept flag in ldsc (for pairs of binary traits, we give a corresponding expression in terms of the number of overlapping cases and controls in the Supplementary Note). Note that this works even when there is known nonzero sample overlap

We recommend using the in-sample estimate of ρ (denoted ρ̂), rather than the population value of ρ. Under unbiased sampling ρ̂ is consistent for ρ with O(1/N) variance, so in this case, the distinction between ρ and ρ̂ is not of great importance. Under biased sampling (as discussed in the previous section), the expected LD Score regression intercept depends on the expected sample correlation E[y_i1y_i2|s=1] (which is estimated consistently by ρ̂), not population ρ. Thus, we advise to use ρ̂ rather than ρ when constraining the intercept.

Regression Weights

For heritability estimation, we use the regression weights from [19]. If effect sizes for both phenotypes are drawn from a bivariate normal distribution, then the optimal regression weights for genetic covariance estimation are

$$\mathit{Var}[z_{1j}{z}_{2j}\mid {\ell }_j]=\left(\frac{N_1{\ell }_j}{M}+1\right)\left(\frac{N_2{\ell }_j}{M}+1\right)+{\left(\frac{\sqrt{N_1{N}_2}{\rho }_g}{M}{\ell }_j+\frac{\rho N_s}{\sqrt{N_1{N}_2}}\right)}^2$$ (3)

(Supplementary Note). This quantity depends on several parameters ( $h_1^2,h_2^2$, ρ_g, ρ,N_s) which are not known a priori, so it is necessary to estimate them from the data. We compute the weights in two steps:

1. The first regression is weighted using heritabilities from the single-trait LD Score regressions, ρN_s=0, and ρ_g estimated as ${\widehat{\rho }}_g:={(\sqrt{N_1{N}_2})}^{-1}{\displaystyle \sum _j}{z}_{1j}{z}_{2j}$.

2. The second regression is weighted using the estimates of ρN_s and ρ_g from step 1. The genetic covariance estimate that we report is the estimate from the second regression.

Linear regression with weights estimated from the data is called feasible generalized least squares (FGLS). FGLS has the same limiting distribution as WLS with optimal weights, so WLS p-values are valid for FGLS [59]. We multiply the heteroskedasticity weights by 1/ℓ_j (where ℓ_j is LD Score with sum over regression SNPs) in order to downweight SNPs that are overcounted. This is a heuristic: the optimal approach is to rotate the data so that it is de-correlated, but this rotation matrix is difficult to compute.

Two-Step Estimator

As noted in [19], SNPs with very large effect sizes can result in large LD Score regression standard errors for single-trait LD Score regression with unconstrained intercept; cross-trait LD Score regression with unconstrained intercept behaves similarly. This is due to the well-known fact that linear regression deals poorly with outliers in the response variable (LD Score regression with constrained intercept is not nearly as adversely affected by large-effect SNPs). The solution proposed in [19] was to remove SNPs with χ²>80 from the LD Score regression. This is a satisfactory solution when the goal is to estimate the LD Score regression intercept. If the goal is to distinguish polygenicity from population stratification, and we are willing to assume that the population stratification is subtle, such that SNPs with χ²>80 are much more likely to be real causal SNPs rather than artifacts, then we can make the task much easier by removing those SNPs. However, this is unsatisfactory if the goal is to estimate h²: ignoring large-effect SNPs with χ²>80 would bias estimates of h² and ρ_g towards zero. Therefore, for estimating h² or ρ_g, we take a two step approach. The first step is to estimate the LD Score regression intercept with all SNPs with χ²>30 removed (i.e., all genome-wide significant SNPs; the threshold can be adjusted with the -two-step flag in ldsc). The second step is to estimate h² or ρ_g using all SNPs and constrained intercept LD Score regression with the intercept constrained to the value from the first step (note that we account for uncertainty in the intercept when computing a standard error; see the next section).

Assessment of Statistical Significance via Block Jackknife

Summary statistics for SNPs in LD are correlated, so the OLS standard error will be biased downwards. We estimate a heteroskedasticity-and-correlation-robust standard error with a block jackknife over blocks of adjacent SNPs. This is the same procedure used in [19], and gives accurate standard errors in simulations (Table 1). We obtain a standard error for the genetic correlation by using a ratio block jackknife over SNPs. The default setting in ldsc is 200 blocks per genome, which can be adjusted with the -num-blocks flag.

For the two-step estimator, if we were to estimate the intercept in the first step, then obtain a jackknife standard error for the second step treating the intercept as fixed, the standard error would be biased downwards, because it would not take into account the uncertainty in the intercept. Instead, we jackknife both steps of the procedure, which appropriately accounts for uncertainty in the intercept and yields a valid standard error.

Reverse Causation

Consider a scenario where a risk factor E₁ causes a disease D, but incidence of disease D changes postmorbid levels of E₁ (this could occur e.g., incidence of disease persuades affected individuals to change their behavior in ways that lower E₁). If D is sufficiently common in our GWAS sample, then the genetic correlation may be affected by reverse causation. LD Score regression (or any genetic correlation estimator) will yield a consistent estimate of the cross-sectional genetic correlation between E₁ and D at the given timepoint; however, the cross-sectional genetic correlation between E₁ and D will be attenuated relative to the genetic correlation between disease and pre-morbid levels of E₁. The genetic correlation between disease and pre-morbid levels of the risk factor will typically be the more interesting quantity to estimate, because it is more closely related to the causal effect of E₁ on D. We can estimate this quantity by excluding all post-morbid measurements of the risk factor from the risk factor GWAS. This allows us to circumvent reverse causation, at the cost of a small decrease in sample size. If D is uncommon, then modification of behavior after onset of D will account for only a small fraction of the population variance in E₁, so the effect of reverse causation on the genetic correlation will be small. Thus, reverse causation is primarily a concern for high-prevalence diseases.

Non-Random Ascertainment

We show in the Supplementary Note that LD Score regression is robust to oversampling of cases in case/control studies, modulo transformation observed and liability scale heritability and genetic covariance. Oversampling of cases is the most common form of biased sampling, but there are many other forms of biased sampling. For example, consider case/control/covariate ascertainment, where the sampling of cases and controls takes into account a covariate. As as concrete example, we know that high BMI is a major risk factor for T2D. If we wish to discover genetic variants that influence risk for T2D via mechanisms other than BMI, we may wish to perform a case/control study for T2D where we compare BMI-matched cases and controls. If we were to use such a T2D study and a random population study of BMI to compute the genetic correlation between BMI and T2D, the result would be substantially attenuated relative to the population genetic correlation between T2D and BMI. (Note that this example holds irrespective of whether there is sample overlap and applies to all genetic correlation estimators, not just LD Score).

More generally, let s_i=1 denote the event that individual i is selected into our study, and let C_i denote a vector of covariates describing individual i (which may include the phenotype of individual i). Then we can represent an arbitrary biased sampling scheme by specifying the selection probabilities f(C_i):=P[s_i=1|C_i] (note that case/control ascertainment is the special case where C_i=y_i). Suppose that phenotypes are generated following the model from Section 1.1 of the Supplementary Note, but that our sample is selected following the biased sampling scheme f. Let a_ij denote the additive genetic component for phenotype j in inidividual i. If there is no direct ascertainment on genotype (i.e., if C_i does not include genotypes), then the proof of Proposition 1 in the Supplementary Note goes through, except that ρ is replaced with E[y_i1y_i2|s_i=1] and ρ_g is replaced with E[a_i1a_i2|s_i=1].

This has two practical implications: first, in studies with biased sampling schemes and sample overlap, if one wishes to constrain the intercept, one should use the sample correlation between phenotypes ρ̂ rather than the population correlation ρ. Under biased sampling, plim_N→∞ρ̂=E[y_i1y_i2|s_i=1], which is typically not equal to ρ. Second, even if there is no sample verlap, biased sampling can affect the genetic correlation estimate. If the biased sampling mechanism (i.e., the function f(C_i):=P[s_i=1|C_i]) is known, then it may be possible to explicitly model the biased sampling and derive a function for converting genetic correlation estimates from the biased sample to population genetic correlations (similar to the derivations in sections 1.3 and 1.4 of the Supplementary Note). If the biased sampling mechanism can only be described qualitatively, then it should at least be possible to guess the magnitude and direction of the bias by reasoning about E[y_i1y_i2|s_i=1] and E[a_i1a_i2|s_i=1].

Computational Complexity

Let N denote sample size and M the number of SNPs. The computational complexity of the steps involved in LD Score regression are as follows:

1. Computing summary statistics takes O(MN) time.

2. Computing LD Scores takes O(MN) time, though the N for computing LD Scores need not be large. We use the N=378 Europeans from 1000 Genomes.

3. LD Score regression takes O(M) time and space.

For a user who has already computed summary statistics and downloads LD Scores from our website (URLs), the computational cost of LD Score regression is O(M) time and space. For comparison, REML takes time O(MN²) for computing the GRM and O(N³) time for maximizing the likelihood.

Practically, estimating LD Scores takes roughly an hour parallelized over chromosomes, and LD Score regression takes about 15 seconds per pair of phenotypes on a 2014 MacBook Air with 1.7 GhZ Intel Core i7 processor.

Simulations

We simulated quantitative traits under an infinitesimal model in 2062 controls from a Swedish study. To simulate the standard scenario where many causal SNPs are not genotyped, we simulated phenotypes by drawing causal SNPs from 622,146 best-guess imputed 1000 Genomes SNPs on chromosome 2, then retained only the 90,980 HM3 SNPs with MAF above 5% for LD Score regression.

We note that the simulations in [19] show that single-trait LD Score regression is only minimally biased by uncorrected population stratification and moderate ancestry mismatch between the reference panel used for estimating LD Scores and the population sampled in GWAS. In particular, LD Scores estimated from the 1000 Genomes reference panel are suitable for use with European-ancestry meta-analyses. Put another way, LD Score is only minimally correlated with F_ST, and the differences in LD Score among European populations are not so large as to bias LD Score regression. Since we use the same LD Scores for cross-trait LD Score regression as for single-trait LD Score regression, these results extend to cross-trait LD Score regression.

Summary Statistic Datasets

We selected traits for inclusion in the main text via the following procedure:

1. Begin with all publicly available non-sex-stratified European-only summary statistics.

2. Remove studies that do not provide signed summary statistics.

3. Remove studies not imputed to at least HapMap 2.

4. Remove studies that adjust for heritable covariates [60].

5. Remove all traits with heritability z-score below 4. Genetic correlation estimates for traits with heritability z-score below 4 are generally too noisy to report.

6. Prune clusters of correlated phenotypes (e.g., obesity classes 1–3) by picking the trait from each cluster with the highest heritability heritability z-score.

We then applied the following filters (implemented in the script munge_sumstats.py included with ldsc):

1. For studies that provide a measure of imputation quality, filter to INFO above 0.9.

2. For studies that provide sample MAF, filter to sample MAF above 1%.

3. In order to restrict to well-imputed SNPs in studies that do not provide a measure of imputation quality, filter to HapMap3 [61] SNPs with 1000 Genomes EUR MAF above 5%, which tend to be well-imputed in most studies. This step should be skipped if INFO scores are available for all studies.

4. If sample size varies from SNP to SNP, remove SNPs with effective sample size less than 0.67 times the 90th percentile of sample size.

5. For specialty chip (e.g., metabochip) meta-analyses, remove SNPs with N above the maximum GWAS N.

6. Remove indels and structural variants.

7. Remove strand-ambiguous SNPs.

8. Remove SNPs whose alleles do not match the alleles in 1000 Genomes.

Genomic control (GC) correction at any stage biases the heritability and genetic covariance estimates downwards (see the Supplementary Note of [19]. The biases in the numerator and denominator of genetic correlation cancel exactly, so genetic correlation is not biased by GC correction. A majority of the studies analyzed in this paper used GC correction, so we do not report genetic covariance and heritability.

Data on Alzheimer’s disease were obtained from the following source:

International Genomics of Alzheimer’s Project (IGAP) is a large two-stage study based upon genome-wide association studies (GWAS) on individuals of European ancestry. In stage 1, IGAP used genotyped and imputed data on 7,055,881 single nucleotide polymorphisms (SNPs) to meta-analyze four previously-published GWAS datasets consisting of 17,008 Alzheimer’s disease cases and 37,154 controls (The European Alzheimer’s Disease Initiative, EADI; the Alzheimer Disease Genetics Consortium, ADGC; The Cohorts for Heart and Aging Research in Genomic Epidemiology consortium, CHARGE; The Genetic and Environmental Risk in AD consortium, GERAD). In stage 2, 11,632 SNPs were genotyped and tested for association in an independent set of 8,572 Alzheimer’s disease cases and 11,312 controls. Finally, a meta-analysis was performed combining results from stages 1 and 2.

We only used stage 1 data for LD Score regression.

URLs

1. ldsc software:

   github.com/bulik/ldsc

2. This paper:

   github.com/bulik/gencor_tex

3. PGC (psychiatric) summary statistics:

   www.med.unc.edu/pgc/downloads

4. GIANT (anthopometric) summary statistics:

   www.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files

5. EGG (Early Growth Genetics) summary statistics:

   www.egg-consortium.org

6. MAGIC (insulin, glucose) summary statistics:

   www.magicinvestigators.org/downloads/

7. CARDIoGRAM (coronary artery disease) summary statistics:

   www.cardiogramplusc4d.org

8. DIAGRAM (T2D) summary statistics:

   www.diagram-consortium.org

9. Rheumatoid arthritis summary statistics:

   www.broadinstitute.org/ftp/pub/rheumatoid_arthritis/Stahl_etal_2010NG/

10. IGAP (Alzheimers) summary statistics:

    www.pasteur-lille.fr/en/recherche/u744/igap/igap_download.php

11. IIBDGC (inflammatory bowel disease) summary statistics:

    www.ibdgenetics.org/downloads.html

    We used a newer version of these data with 1000 Genomes imputation.

12. Plasma lipid summary statistics:

    www.broadinstitute.org/mpg/pubs/lipids2010/

13. SSGAC (educational attainment) summary statistics:

    www.ssgac.org/

14. Beans:

    www.barismo.com

    www.bluebottlecoffee.com

Author Contributions

MJD provided reagents. BMN and ALP provided reagents. CL, ER, VA, JP and FD aided in the interpretation of results. JP and FD provided data on age at menarche. The caffeine molecule is responsible for all that is good about this manuscript. BBS and HKF are responsible for the rest. All authors revised and approved the final manuscript.

Competing Financial Interests

The authors declare no competing financial interests.