The filament forming reactions of vimentin tetramers studied in a serial-inlet microflow device by small angle x-ray scattering

Abstract

The structural organization of metazoan cells and their shape are established through the coordinated interaction of a composite network consisting of three individual filament systems, collectively termed the cytoskeleton. Specifically, microtubules and actin filaments, which assemble from monomeric globular proteins, provide polar structures that serve motor proteins as tracks. In contrast, intermediate filaments (IFs) assemble from highly charged, extended coiled coils in a hierarchical assembly mechanism of lateral and longitudinal interaction steps into non-polar structures. IF proteins are expressed in a distinctly tissue-specific way and thereby serve to generate the precise plasticity of the respective cells and tissues. Accordingly, in the cell, numerous parameters such as pH and salt concentration are adjusted such that the generation of functional networks is ensured. Here, we transfer the problem for the mesenchymal IF protein vimentin to an in vitro setting and combine small angle x-ray scattering with microfluidics and finite element method simulations. Our approach is adapted to resolve the early assembly steps, which take place in the sub-second to second range. In particular, we reveal the influence of ion species and concentrations on the assembly. By tuning the flow rates and thus concentration profiles, we find a minimal critical salt concentration for the initiation of the assembly. Furthermore, our analysis of the surface sensitive Porod regime in the x-ray data reveals that the formation of first assembly intermediates, so-called unit length filaments, is not a one-step reaction but consists of distinct consecutive lateral association steps followed by radial compaction as well as smoothening of the surface of the full-width filament.

I. INTRODUCTION

Eukaryotic cells possess very distinct mechanical properties which support their biological function. To a great part, these mechanical properties are governed by the cytoskeleton, a sophisticated, hierarchical composite network of actin filaments, microtubules, and intermediate filaments (IFs) as well as corresponding cross linking and motor proteins.^1–4 Among these filamentous proteins, IFs display a specific hierarchical assembly mechanism leading to intriguing mechanical properties, i.e., high flexibility and resistance to mechanical stress.^5–7 IF proteins are cell type- and organism-specific⁸ and form 10 nm diameter, several μm long filaments with a persistence length on the order of a few μm.^9–16 Vimentin belongs to this multigene family of IF proteins and is found in cells of mesenchymal origin.^3,17 The rod-shaped vimentin monomer shares the tripartite structure of all IF proteins with an α-helical rod domain flanked by intrinsically disordered head and tail domains (Fig. 3(d)).

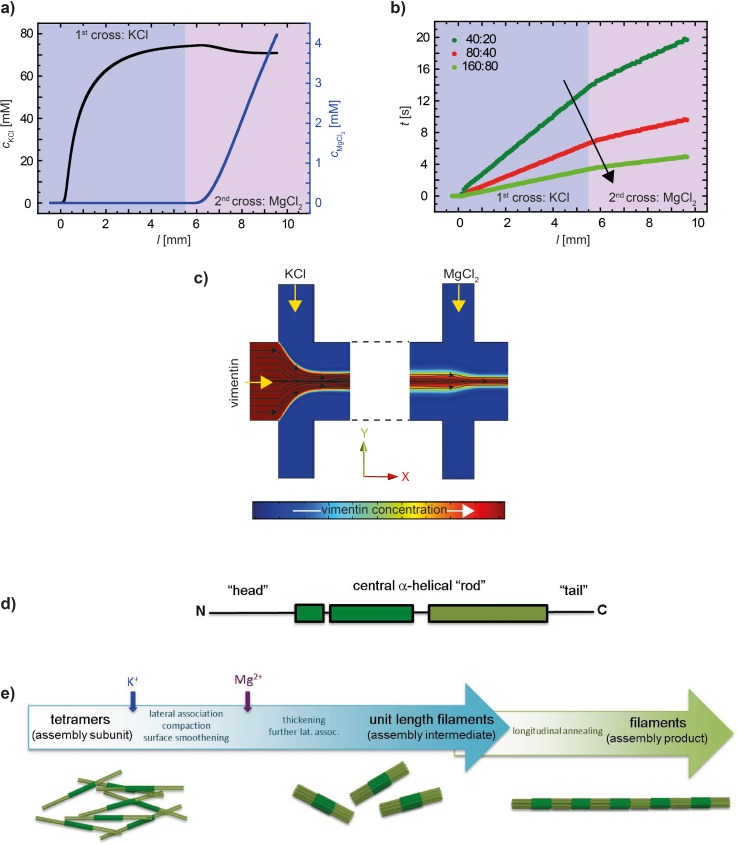
FIG. 3.

Results derived from the FEM simulations shown in Fig. 2 for the central flow line (y = z = 0). (a) Concentrations of KCl and MgCl₂. (b) Time evolution along the channel for different flow rates. The black arrow indicates increasing flow rates. The legend shows the respective flow speed: first number—lateral buffer inlets, and second number—central vimentin inlet. (c) Streamlines (black lines) for the hydrodynamically focused central jet. (d) Sketch of the monomer structure of vimentin with the α-helical rod domain and the intrinsically disordered head and tail domains. (e) Scheme of the different steps during the assembly of vimentin proteins into filaments, including sketches of the respective assembly steps (from left to right: tetramers, ULFs, and filaments).

IFs are notoriously insoluble under physiological conditions and in order to obtain monomers, as needed in the course of purification, they have to be solubilized in chaotropic reagents such as 8 M urea. In order to renature the proteins, they are dialyzed with stepwise reduction of the urea concentration into low ionic strength buffers such as 2 mM sodium phosphate. At 6 M urea, the IF proteins spontaneously form 45 nm long, coiled coil dimers. At 5 M urea, two dimers associate into anti-parallel, half-staggered complexes of 60 nm length and 5 nm diameter. These tetramers are stable upon further removal of urea and persist as a homogenous tetrameric complex in 2 mM sodium phosphate (pH 7.0) as determined by analytical ultracentrifugation.¹⁸ By the addition of monovalent ions, tetramers are “kick-started” into an assembly-competent state: (i) eight tetramers instantaneously associate laterally into typically 17 nm wide “unit-length” filaments (ULFs); (ii) ULFs longitudinally anneal to short IFs by end-on association; and (iii) short filaments together with leftover ULFs elongate further into extended micrometer-long filaments.^5,18 This process is sketched in Fig. 3(e). During the latter phase, filaments radially compact to 11 nm diameter after about 10 min under standard assembly conditions.

According to the amino acid sequence of vimentin protein monomers, the emerging filaments are highly negatively charged polyelectrolytes which interact strongly with counter ions. Such charge interaction could also play a role in physiological settings and in order to gain a better principle understanding of the processes involved, a number of different experimental techniques have been employed. Macro- and microrheology measurements show that already low concentrations, on the order of a few mM, of divalent Mg²⁺ cross link filaments in vimentin networks^19–21 and higher ion concentrations even lead to a strong aggregation effect visible directly by fluorescence microscopy, where the individual filaments “zip” together within minutes.^22–24 By contrast, nanoscale methods like atomic force microscopy (AFM), electron microscopy (EM), small angle x-ray scattering (SAXS), and transient electric birefringence (TEB) have been used to investigate the influence of different ion species and concentrations on the individual filaments, or even subunits thereof. The studies show that the results depend on a variety of parameters like buffer conditions and origin of the protein (tissue or recombinant).^25,26 SAXS is sensitive to the internal structure of the assemblies²⁷ and showed that the ion species, valence, and the ion concentration influence the resulting filaments. Importantly, the addition of magnesium chloride alone (0.5 to 4 mM) leads to the formation of filaments as well, but the assembly process is considerably slower than for monovalent salt at 50 mM.²⁸

It has been known for 20 years already that the addition of salt, such as KCl, “unblocks” the formerly unproductive head domains of the molecules and thus initiates assembly.^18,29 Once unblocked, however, the assembly starts immediately. It is an important and so far not fully answered question, at which KCl concentration exactly assembly starts. Most previous experiments looked at the static end point of the assembly results and did not address the temporal evolution of the process. Exceptions are the direct imaging of filaments at different “snap shot” time points by EM or AFM with a time resolution of 30 s and mathematical modeling of the processes.³⁰ In bulk experiments, typically all components (namely, protein and all ions) are mixed at once, and therefore subsequent controlled mixing-in of additional ions is difficult. Both these challenges, however, can be overcome by combining the chosen observation technique with microfluidics as shown for time-resolved SAXS³¹ and for a fluorescence microscopy study of MgCl₂ addition to preassembled vimentin filaments.^22,23 The absence of a lag phase in the beginning of the assembly process makes these proteins an ideal candidate for microfluidic studies.

Here, we use a SAXS-compatible microfluidic device with serial inlets for the addition of first KCl and then, subsequently, MgCl₂. The combination of SAXS and continuous flow microfluidics enables us to investigate the structures on the nanometer scale with second temporal resolution, and thus match the processes during vimentin assembly very well. We choose a q-range which is sensitive to the compaction and surface structure properties of the scattering material. We find that while KCl initiates assembly within seconds, it simultaneously smoothens the surfaces. By contrast, the further addition of MgCl₂ has no influence on surface properties. Instead, MgCl₂ leads to an enlargement of the emerging assemblies, and the data are in agreement with an accumulation of ions on the filaments.

II. MATERIALS AND METHODS

A. Microfluidic devices

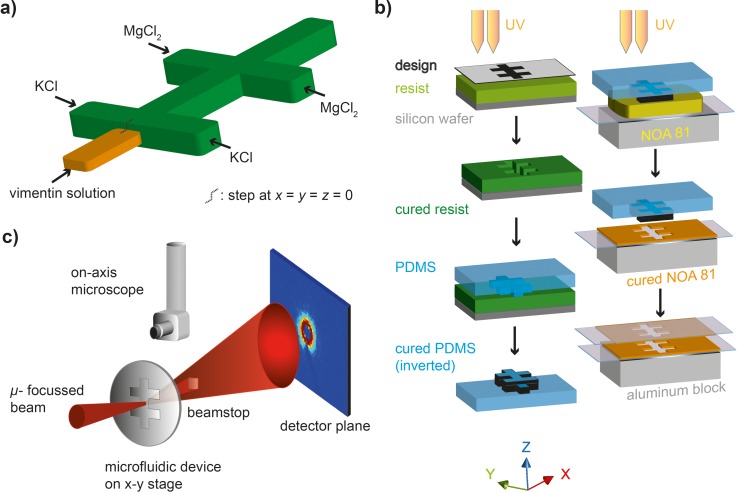
The device geometry we used in our experiments is shown in the schematic in Fig. 1(a), and the device fabrication is described in detail elsewhere³¹ and shown in the schematic in Fig. 1(b). Briefly, double-layer photolithography was performed to structure the channel geometry, including a “step” at the central inlet channel using SU-8 3050 negative photo resist (MicroChem, Newton, MA, USA). The structure was molded into polydimethylsiloxane (PDMS) stamps (Silgard 184, Dow Corning GmbH, Wiesbaden, Germany). The PDMS stamps were used to transfer the structure to thin films of UV-curable glue NOA 81 (Norland Optical Adhesive, Norland, Cranberry, NJ, USA). Two of these films were aligned to form closed channels, and tubing was connected for injection of the liquids. The resulting channels were designed such that the height of the central inlet for the protein inflow was less high than the other channels. Thus, the assembled protein remained enclosed by buffer flow, and clogging of the channels was avoided. The final channel height for the buffer inlets and for the outlet was about 240 μm; the height of the central inlet was 110 μm. The total sample thickness was about 500 μm. Thus, the NOA layer on each side of the device was about 130 μm thick. All channels were 300 μm wide. For the analysis shown here, the main flow direction is the x-direction, z is the height, and y is the width of the channel. The origin x = y = z = 0 is located at the center of the main channel where the “step” is positioned. The devices were connected to gastight glass syringes (Hamilton, Reno, NV, USA) via polyethylene tubing (Intramedic™ PE20, BD, Sparks, MD, USA). The syringes were controlled by precise syringe pumps through a remotely accessible software (neMESYS, cetoni GmbH, Korbußen, Germany). Vimentin tetramers at a concentration of 4 mg ml⁻¹ in 2 mM phosphate buffer (PB), pH 7.5, were injected into the central inlet at 20, 40, or 80 μl h⁻¹, respectively, and salt containing buffers were injected into the subsequent lateral inlets: 100 mM KCl into the first set of inlets and 10 mM MgCl₂ with 80 mM KCl into the second set of inlets (all in 2 mM PB pH 7.5), at 40, 80, or 160 μl h⁻¹, respectively.

FIG. 1.

Device geometry and fabrication. (a) Sketch of the device geometry with one central inlet (orange, reduced height) and two sets of lateral inlets (for KCl and MgCl₂, respectively). (b) Step-by-step schematic of the device fabrication. Silicon wafers are structured by standard photolithography. These wafers are utilized for fabricating PDMS stamps. Finally, the stamps are pressed into UV-curable glue (Norland Optical Adhesive, NOA 81). Two identical copies of structured NOA 81 are produced, aligned, and bonded. (c) Schematic of the experimental setup; the microfluidic device is scanned through a microfocused x-ray beam, and the SAXS signal in each position is recorded in the detector plane. Additionally, an optical microscope is available at the beamline and can be moved down to facilitate the positioning of the device with respect to the beam.

B. Protein purification and assembly

Human vimentin protein was expressed in Escherichia coli bacteria and then purified from inclusion bodies.³² Vimentin was stored at −80 °C in 8 M urea, 5 mM Tris-HCl (pH 7.5), 1 mM EDTA, 0.1 mM EGTA (ethylene glycol tetraacetic acid), 1 mM DTT (dithiothreitol), and 10 mM methyl ammonium chloride (MAC). The purity of the protein was verified by SDS-PAGE (sodium dodecyl sulfate polyacrylamide gel electrophoresis). All solutions were prepared using 2 mM PB, pH 7.5. Before use in the experiments, the protein was dialyzed against 8 M urea for 30 min and then in a stepwise manner at 4, 2, and 1 M urea for 30 min each at room temperature. Finally, an overnight dialysis into 2 mM PB was performed at 4 °C. All dialysis steps were performed using membranes of 50 kDa cut-off. The protein concentration was determined by measuring the absorption at 280 nm (Nanodrop ND-1000, ThermoScientific Technologies, Inc., Wilmington, USA). Assembly was initiated in the microfluidic devices by diffusive addition of 100 mM KCl to the vimentin solution and, subsequently, additional 25 mM MgCl₂ to the preassembled vimentin (concentrations refer to solutions in the syringes).

C. Finite element method (FEM) simulations of the micro-flow

COMSOL multiphysics 4.4 and 5.0 (COMSOL GmbH, Göttingen, Germany) was used to perform FEM simulations of the flow conditions. To reduce the computational effort and for symmetry reasons, only a quarter of the entire geometry was modeled (cut in the x-z plane and the y-z plane). The lengths of the inlet channels were reduced in the model but were long enough to ensure the correct flow and mixing profiles. Simulations were performed in the laminar flow regime, and no-slip boundary conditions were used at channel walls. While running the simulation, the inflow velocity had a fixed constant value with the inlets long enough for the parabolic flow profile to develop. We used the following diffusion coefficients: for vimentin,³³ D_vim = 2.4 × 10⁻¹¹ m² s⁻¹; for KCl,³⁴ $D_{K^{+}}=1.84\times {10}^{-9}{\mathrm{m}}^2\hspace{0.17em}{\mathrm{s}}^{-1}$; and for MgCl₂,³⁵ $D_{M{g}^{2+}}=7.5\times {10}^{-10}{\mathrm{m}}^2\hspace{0.17em}{\mathrm{s}}^{-1}$. Note that the diffusion coefficient for vimentin is an estimate of the upper bound, since it decreases as the protein assembles. Lateral assembly, which is mostly occurring on the time scales investigated here, does not change the diffusion coefficient much and elongation occurs at longer time scales. A maximum mesh size of 11.1 μm and minimum mesh size of 0.724 μm were used to define the tetrahedral mesh in the simulations. The simulations were performed considering the Stokes equation, thereby neglecting the inertial terms. We did not include the change in viscosity upon assembly in our simulation, since viscometry measurements show that the viscosity increases only very little during the first seconds of the assembly process.^18,25

For determining the time evolution of the involved kinetics, we employed LiveLink for MATLAB provided by COMSOL to first identify the streamlines, which are crucial for a region of interest and then integrate over a particular streamline to obtain the relevant time scales.³⁷

D. SAXS measurements and analysis

A schematic of the setup is shown in Fig. 1(c). The SAXS measurements were performed at the beamline ID13 of ESRF (European Synchrotron Radiation Facility, Grenoble, France). The beam size was 5 × 5 μm², the photon energy was 12.4 keV, and the sample to detector distance was 0.52 m. The beam was pre-focused with refractive beryllium lenses and defined by secondary slits to the order of 80 μm. The focusing of the micron-sized beam onto the sample was further performed by Kirkpatrick-Baez (KB) mirrors. Consequently, the q_r-range was 0.24 nm⁻¹–9.21 nm⁻¹. However, the q_r range for plotting the data in Fig. 5(a) is adapted to exclude the beamstop region at lower q_r and noise at higher q_r. The data were collected with a FReLoN 4 M camera (2048 × 2048 pixels; 50 × 50 μm² pixel size; developed by the ESRF detector group), and the exposure time for each measurement position was 5 s. All experiments were performed at room temperature. The resulting scattering profiles were radially integrated and corrected for background arising from the device material and the buffer. For determining the sample-to-detector distance, we used silver behenate powder as a standard sample and the software Fit2D.³⁶ Further data analysis was performed using MATLAB (R2009b).

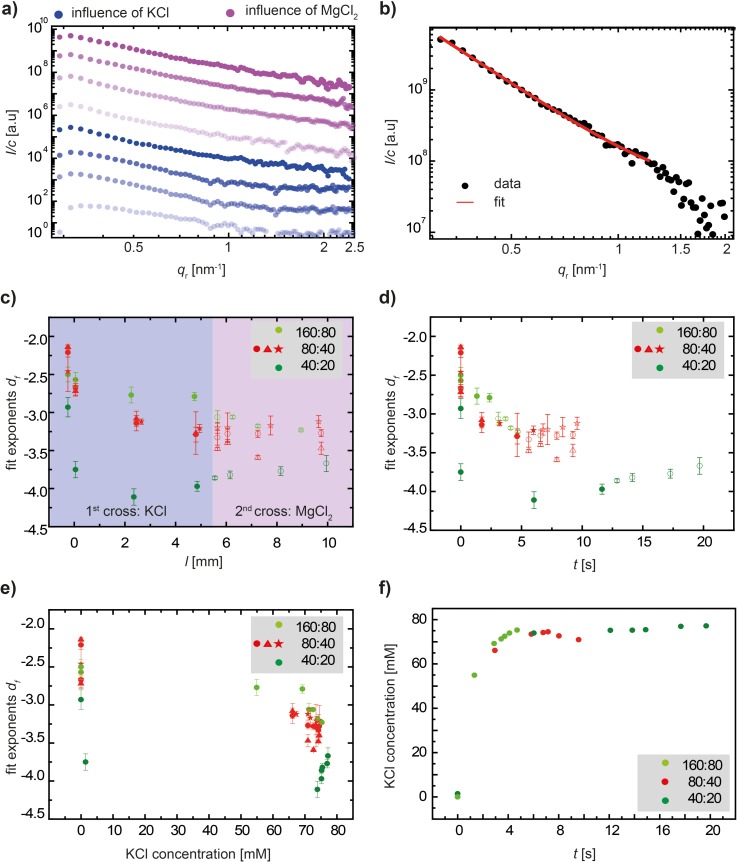
FIG. 5.

Experimental results of SAXS measurements. (a) Double-logarithmic plot of typical scattering curves. The blue data curves refer to vimentin in the presence of only KCl, and the purple curves refer to vimentin in the presence of both KCl and MgCl₂. The same color code is used throughout the figure and the text. (b) Representative data curve with the fit to determine power law exponents. (c) Power law exponents d_f derived from fitting Porod's equation for the intensity decay to the data plotted versus the measurement position in the channel. The legend shows the respective flow speed: first number—lateral buffer inlets, and second number—central vimentin inlet. The closed symbols represent the influence of KCl, and the open symbols represent the influence of MgCl₂. In the case of intermediate flow rates (80:40), we show three independent experiments indicated by red circles, triangles, and stars. (d) Fit exponents d_f plotted versus the time evolved since the “step” position in the device. (e) Fit exponents d_f plotted versus the KCl concentration, which rapidly jumps from 0 to about 70 mM, as shown in (f).

III. RESULTS

A. FEM simulations for tracing species in micro-flow

In order to understand the assembly kinetics for vimentin in flow, exact knowledge of the flow conditions, such as concentration distributions of salt and protein and velocities in each position of the device, is essential. Therefore, we perform FEM simulations of the laminar flow for the chosen device geometry.³⁷ As explained in Sec. II, the central inlet channel for the vimentin inflow is reduced in height in comparison to the salt buffer inlets and the outlet to avoid assembled vimentin to get in contact with the walls, which might lead to adhesion and eventually clog the channels.^31,38–40

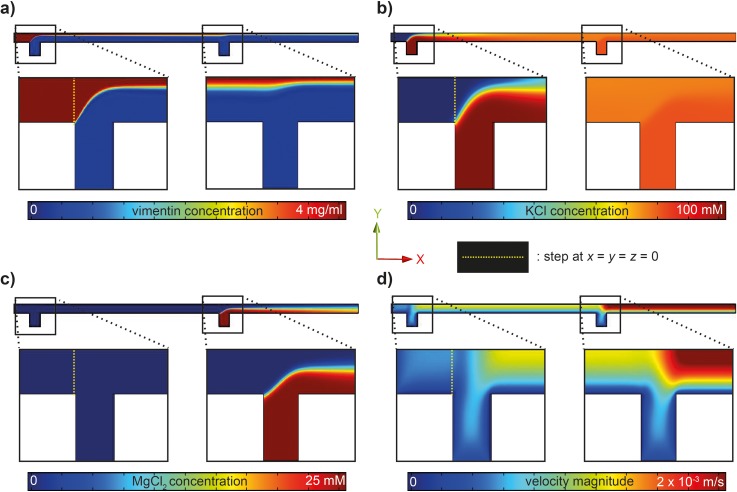
We here primarily discuss the results for the intermediate set of flow rates chosen in this study. Further below, we compare the different flow rates. The vimentin tetramers are injected into the central inlet, and the stream is hydrodynamically focused by the first lateral inlets (KCl inflow). In the experiment, we choose a vimentin concentration of 4 mg ml⁻¹ to achieve sufficient signal to noise for the weakly scattering biomaterial. In cells,⁴¹ the concentration of vimentin is on the order of 0.2 mg ml⁻¹, a concentration at which we routinely perform assembly experiments. However, we have determined assembly to occur reliably at higher concentrations when compared to what is revealed at the above stated lower concentration.^14,28 At 5.5 mm downstream, the protein stream is focused again by the second set of lateral inlets (MgCl₂ inflow; see the cut in the x–y plane in Fig. 2). The diffusion coefficient of the rod-shaped tetramers is small and decreases even more when they start to further assemble. Thus, the concentration of vimentin decreases merely by a factor of 2 from 4 mg ml⁻¹ at the inlet to 2 mg ml⁻¹ 10 mm downstream at the last measurement position, and the protein remains mostly in the center of the laminar flow, as shown in Fig. 2(a). This is an estimate of the maximum decrease, since for the simulations we did not take into account the change in diffusion coefficient upon assembly. By contrast, the much smaller and therefore faster diffusing ions move into the central stream more readily, and the final concentration of 70 mM KCl becomes distributed evenly across the channel width at about 4 mm downstream from the step at the central inlet. From here onwards, the KCl concentration remains constant throughout the channel length (Figs. 2(b) and 3(a)). The concentration of MgCl₂ increases approximately linearly from zero to about 4 mM (Figs. 2(c) and 3(a)) starting from the second set of lateral inlets.

FIG. 2.

FEM simulations of the flow conditions and local concentrations in the microfluidic devices. Simulations shown here are for a vimentin flow speed (central inlet) of 335 μm s⁻¹ (40 μl h⁻¹) and salt buffer flow speeds for each lateral inlet of 310 μm s⁻¹ (80 μl h⁻¹). The mid-plane (x–y) is shown. (a) Vimentin concentration in the device. Enlarged are parts of the inflow of KCl (first cross) and MgCl₂ (second cross). The vimentin concentration remains high in the central part, since the large proteins diffuse slowly; the concentration drops from 4 mg ml⁻¹ to about 2 mg ml⁻¹ during the entire length of 10 mm. (b) Change in KCl concentration. KCl is injected at the first cross, diffuses into the central protein stream, and remains at a constant concentration when MgCl₂ is injected. (c) Change in MgCl₂ concentration. (d) Velocity magnitude.

There is an overall increase in the velocity magnitude over the length of the channel (Fig. 2(d)) due to the additional inflows. Estimating the shear rates ${\dot{\gamma }}_{\mathit{x}\mathit{y}}=(\partial v_x/\partial x_y+\partial v_y/\partial x_x)$, we arrive at ∼3.2 s⁻¹ between the first and second set of lateral inlets and ∼5.5 s⁻¹ from the second set of lateral inlets onwards. In order to derive the shear stress from these shear rates, the viscosity of the fluids needs to be taken into account. Since we consider only the first few seconds of assembly, and in agreement with viscosity measurements from the literature,⁴² we assume water viscosity and thus derive shear stresses on the order of 5 mPa.

One great advantage in microfluidic mixing is the controlled diffusion of the ions and the absence of unpredictable turbulences. Therefore, as presented above, the concentrations for each position of the device are known. The short diffusion lengths in a microchannel lead to fast mixing and short dead times. However, we do not mix instantaneously and cannot easily define a zero time point for the start of the assembly reaction. By contrast, we are faced with a convolution of mixing and reaction kinetics in flow. Therefore, in order to investigate the time scales on which the assembly reaction takes place, the streamlines in the flow are calculated starting at x = −0.35 mm with a spacing Δy = 1 μm between the streamlines at the position of the inlet, but for better visibility only a few streamlines are shown in Fig. 3(c). However, volume elements of protein solution are tracked only along the central streamline starting at z = y = 0. The involved time scales are derived by integrating over the inverse of the flow velocity along a streamline

$$t\left(s\right)={\int }_0^s\frac{\mathrm{d}s\prime }{v(s\prime )}.$$ (1)

The results for the different sets of flow rates used in the experiments are displayed in Fig. 3(b). For the example of the simulation shown in Fig. 2 (40 μl h⁻¹ in the central inlet and 80 μl h⁻¹ in the lateral inlets), the flow time from the step to the second set of lateral inlets is 7 s, and the total flow time is 9.5 s (red curve). For reduced flow rates (dark green curve), the total time is 19.8 s, and for faster flow rates (light green curve) it is 4.8 s.

B. Structural information of vimentin from SAXS measurements

We employ SAXS with a micro-focused beam to study the structural changes in vimentin during assembly in the presence of ions. Since SAXS is an inherently “slow” technique due to the required exposure times for weakly scattering biological molecules (5 s in this specific case), we combine the x-ray method with continuous flow microfluidics. The laminar flow conditions (the maximum Reynolds number is $\mathcal{R}{e}_{\mathit{m}\mathit{a}\mathit{x}}=0.4$) in the small channels ensure that by exposing a specific position, we ensemble-average identical states of the assembly process. Therefore, the temporal resolution is given by the distance between the measurement positions along the outlet channel rather than the exposure time. An additional advantage of the continuous flow is the reduced radiation damage affecting the protein, since it is continuously passing by the x-ray beam. The microfocused x-ray beam (5 μm × 5 μm) has dimensions smaller than the channel width (300 μm), leading to high spatial resolution in real space.

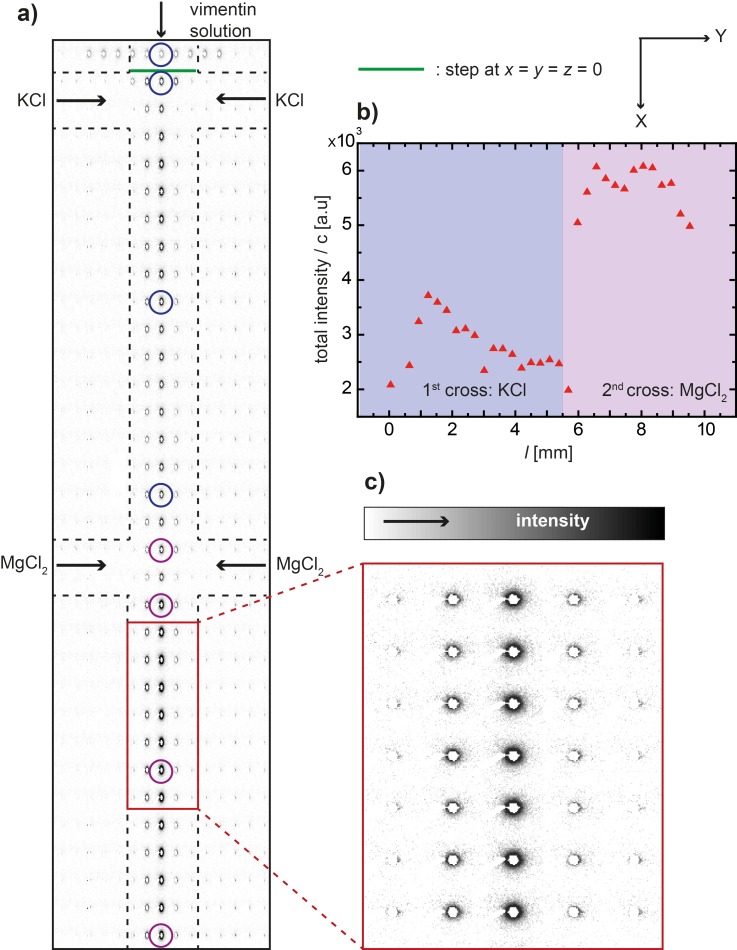
The device is scanned through the beam in a rectangular lattice (step size Δx × Δy is 100 μm × 30 μm) to localize the protein stream in the center of the channel. This experimental strategy is shown in a composite image of the individual SAXS patterns (Fig. 4). In Fig. 4(a), the aspect ratio x/y of the SAXS patterns is shown in a distorted way in order to match the anisotropic step sizes used in the scanning. In Fig. 4(c), the SAXS patterns are shown with their real aspect ratio. The total intensity of each pattern along the main flow axis of the device is integrated, normalized by the respective protein concentration derived from the simulations, and plotted against the position l in Fig. 4(b). The representative measurement positions which we refer to in the analysis further down are circled in Fig. 4(a). As color code, we use blue for vimentin in the presence of only KCl and purple for vimentin in the presence of both KCl and MgCl₂.

FIG. 4.

Measurement strategy. (a) Composite image of individual SAXS patterns taken at different positions in the channel; inverted gray scale, i.e., the darker regions refer to increased intensity; the colored circles refer to the measurement positions depicted in Fig. 5(a). (b) The total scattered intensity along the main flow direction normalized by the protein concentration. (c) Zoom-in of a detail from (a). Note that whereas in (a) the aspect ratio of the individual SAXS patterns has been distorted in order to match the aspect ratio of the channel (line and column spacing in the scan are different), in (b) the SAXS patterns are displayed as recorded.

The composite representation of the individual SAXS patterns presented in Fig. 4(a) shows that the channel can be precisely mapped by employing the 5-μm-beam. The intensity (inverted gray scale) is increased in the central stream where the protein is located (see also detail in Fig. 4(c)). Furthermore, when moving along the x-direction downstream the flow, the intensity increases upon addition of KCl (first set of lateral inlets) and again upon the addition of MgCl₂ (second set of lateral inlets). Fig. 4(b) shows an initial increase in the total intensity when KCl is added. This increase is followed by a decrease, which could be due to hydrodynamic shaping of the protein stream. At the second lateral inlet, where MgCl₂ is added, we observe a large jump in intensity.

We choose SAXS patterns, as indicated by the circles in Fig. 4(a), for further analysis. The data are integrated azimuthally and plotted against the scattering vector q_r, as shown in Fig. 5(a). The individual I(q) curves are shifted with respect to each other by a factor of 10 for better visibility. In the past,³¹ we have analyzed scattering from vimentin assembled in microflow at small q_r values up to about 0.5 nm⁻¹ before reaching the noise level and performed a Guinier analysis of the data. Here, with a complementary setup at different beamlines, we access higher q_r values before reaching the noise level. We therefore analyze the data according to Porod's law of asymptotic decay⁴³

$$I(q)\propto q^{d_f}.$$ (2)

By plotting the intensities in a double-logarithmic representation, the slope is directly associated with the power law exponent d_f. Interpretation of these values will be discussed further below. The correct range applicable for Porod's law can be determined by plotting I(q) × q⁴ versus q⁴ and choosing a smooth linear region limited by noise in the higher q_r. An example is shown in the supplementary material.⁴⁴ The data are fitted in the q_r-range between 0.32 nm⁻¹ and 1.2 nm⁻¹ for all the datasets, as shown for a representative curve in Fig. 5(c). These fits yield exponents from −2.2 to −3.2 for the influence of KCl and from −3.2 to −3.3 for the influence of MgCl₂ for datasets with flow-rates of 80 μl h⁻¹ in the lateral inlets and 40 μl h⁻¹ in the central inlet. We find (see Fig. 5(c), red circles, triangles, and stars for three individual measurements) a steep decay in d_f upon addition of KCl, whereas upon the addition of MgCl₂, the exponents remain constant. In comparison, for decreased flow-rates (40 μl h⁻¹ in the lateral inlets and 20 μl h⁻¹ in the central inlet), the exponents decrease in a more pronounced way when KCl is added (dark green circles). For increased flow-rates (160 μl h⁻¹ in the lateral inlets and 80 μl h⁻¹ in the central inlet), the exponents trace a less steep decay (light green circles).

The streamline tracking presented in Sec. III A allows us to translate positions in the channels into flow times, as shown in Fig. 3(b). When plotting the exponents versus time, as shown in Fig. 5(d), we find that the data for the different sets of flow velocities do move closer together and for the two faster velocities (160:80 and 80:40, light green and red) they even collapse, but not for the slowest velocity (40:20, dark green). Note that in Fig. 5(c) the position l = 0 deviates slightly (by about 150 μm) from the position where the protein first encounters a threshold concentration of 10 mM KCl. By contrast, when plotting the exponents against the concentration of KCl in Fig. 5(e), the data collapse into two groups, one with larger values at 0 and one with smaller values at about 70 mM. A plot of the concentration of KCl against time (Fig. 5(f)) reveals a fast “jump” from 0 to 70 mM salt after about 3 s and thus explains this observation. We therefore conclude that while fast, the assembly reaction is not instantaneous, and the temporal evolution is resolved in Fig. 5(d).

IV. DISCUSSION AND CONCLUSION

By combining experimental microfluidics and numerical FEM simulations, we obtain precise knowledge of the flow conditions in the microfluidic device. The continuous flow approach offers high control of the mixing conditions which are completely governed by diffusion in the laminar flow. It is well known that addition of KCl initiates the assembly of tetrameric complexes into bona fide IFs in vitro. We and others have shown that MgCl₂ influences the nanostructure of assembled filaments as well.^25,26,28 However, in previous SAXS studies, we mixed the ions either each separately with the vimentin or at once, but not in sequence.

Using microfluidics, we are able to mix in ions successively in a precise and controlled manner, as previously shown in a microscopy study.^22–24 Here, we take this approach to the nanometer scale by employing SAXS and mixing in monovalent KCl first and thereafter divalent MgCl₂. The length scales probed by our SAXS setup (approximately 3 to 60 nm) and the time scales defined by the microfluidics parameters (up to 20 s) are adapted to the lateral assembly of vimentin tetramers to ULFs. We observe an intensity increase along the center stream upon addition of KCl, which is indicative of vimentin assembly and thus stronger overall scattering. Mixing in MgCl₂ leads to an even stronger intensity increase, which can be attributed to thickening of the ULFs or to the formation of larger aggregates. Moreover, we have observed in the past for vimentin, that MgCl₂ accumulates in the unstructured tail regions of the filaments, which are presented at the surface of the filament core and thus leads to higher relative scattering;²⁸ the present data are in agreement with these results.

In order to understand the structural-molecular changes, we analyze the Porod exponents derived from the scattering curves. The standard Porod-Debye law^43,45 for the interpretation of the exponents requires a compact domain with a smooth surface and sharp interface and leads to information of the shape of the scatterers: d_f = −4 for spheres, −2 for discs, and −1 for rods. However, biomolecules do not have such a smooth surface, and the theory has been generalized to non-integer values for fractal geometry as mass fractal dimensions.^46,47 The predictions of this generalized theory are valid for (i) a monodisperse particles and (ii) if the self-similarity conditions prevail over at least one full order of magnitude.^46,48 Values between −1 and −3 for the exponents d_f correspond to the transition of loosely packed, Gaussian-chain mass fractals to densely packed mass fractals. Values between −3 and −4, by contrast, correspond to ever-smoother surfaces. We are aware that for biological and technical reasons our data do not completely fulfill the two conditions (i) and (ii) above, but still use the theory as a first approximation of the observed molecular processes.

Plotting the exponents d_f against the channel position (Fig. 5(c)), we show the results for three different sets of flow rates and three individual data sets were analyzed in the case of the intermediate flow rates (red circles, triangles, and stars). Their strong agreement underlines the reproducibility of the microfluidics measurements. From the results of the simulations (see Figs. 2 and 3 and compare to Figs. 2–4 in the supplementary material⁴⁴), we know that as the flow rates decrease, the channel length needed for the ions to diffuse into the central stream is shorter, and the maximum ion concentration is reached at smaller values for the channel position l. Thus, we observe an assembly and smoothening in the presence of KCl for smaller values of l at the slowest flow rate (dark green data points in Fig. 5), represented by a rapid drop in the d_f values. The d_f values for higher flow rates show a drop as well, albeit not as rapid and not as pronounced. Upon the diffusive addition of MgCl₂ up to a concentration of 2.5 mM, 4 mM, or 7 mM for the different sets of flow rates, respectively, the exponents remain constant indicating no further compaction of the assemblies. We also observe here that the differing maximum ion concentrations reached for the different flow rates do not significantly influence the results.

From these data, we conclude that a critical concentration of KCl is necessary to unblock the formerly unproductive head domains and thus initiate assembly. Assuming a critical concentration of 10 mM,²⁸ it is reached at l ≈ 0.17 mm for the slowest flow rate and only at l ≈ 0.5 mm for the highest flow rate. This corresponds very well with the positions where we measure a value for the Porod exponent of d_f ≈ 2.7 for both data sets, which we thus assign to the onset of lateral association of tetramers. Note that a critical protein concentration has not been found so far,¹⁸ and ULF formation was observed even for protein concentrations as low as 5 μg ml⁻¹.

By contrast, when plotting the same data against the time axis (Fig. 5(d)), we see the development of the nanostructure during a certain time period since first contact with the ions. Interestingly, when plotting the data against time, the curves for the faster flow rates (light green and red data points) collapse, but not the data for the slowest flow rates (dark green data points). At this point, we can only speculate, what the reason for this observed behavior may be. Partly this different behavior could be due to the more rapid addition of KCl and thus initiation of assembly. Another possible explanation could be found in an influence of the flow velocities and associated shear stresses. We do not observe anisotropy in the scattering patterns and thus no orientation effect of the flow on the vimentin assemblies. However, it is possible that the involved shear stresses change the behavior of the protein during assembly, and in particular, the tails of the monomers, which stick out of the filament body forming a “bottle brush” structure,²⁸ could be influenced. A “slight” alignment of the tetramers by the flow could also influence the assembly speed, since it would bring the tetramers already into the right rotational orientations and thus decreases the number of degrees of freedom.

One of the major advantages of the microfluidic geometry used in the present work is the possibility to mix the ions subsequently. In corresponding bulk SAXS experiments, by contrast, all the ions have to be mixed with the tetrameric proteins at once, and the end state of the assembly process is measured in glass capillaries.²⁸ Nevertheless, our present observation of a strong overall intensity increase upon the addition of MgCl₂, which is less pronounced for the addition of KCl, supports the idea of a direct, strong interaction of the divalent, but not monovalent ions with the unstructured tail regions of the vimentin filaments.

In a different microfluidic setting, employing picoliter drops imaged by fluorescence microscopy, we have previously exposed preassembled vimentin filaments to different concentrations of MgCl₂^22–24 and observed dynamics of the network formation. In that study, we found that a concentration of 10 mM MgCl₂ represents a sharp threshold, above which vimentin filaments bundle into very dense aggregates on a microscopic scale. Changes on the nanometer scale were not observable by fluorescence microscopy. Here, we focus on lower MgCl₂ concentrations, which are closer to physiological conditions, and observe that the surface character of the filaments is not influenced. Transmission electron microscopy (TEM), which is a complementary, nanometer resolution technique, leads to consistent results, where no change in filament morphology could be observed for MgCl₂ concentrations up to 4 mM.²⁰ Macro- and microrheology studies show a cross linking of vimentin filament networks in the presence of a few mM MgCl₂,^19,20 consistent with the increase of overall scattering intensity observed in our present SAXS experiments.

To summarize and conclude, we present a microfluidic technique that enables us to functionally activate an assembly-competent protein complex of the IF protein vimentin by addition of ions to non-filamentous vimentin, namely, tetramers, and observe the effect in a time resolved manner. The combination of SAXS and microfluidics provides exactly the sub-second time scales and nanometer length scales needed to study the association process of these proteins. Accessing the Porod regime of q-resolution enables us to probe the surface structure of the emerging assemblies. We demonstrate the effect of monovalent and divalent ions in two subsequent steps: The addition of KCl at a critical minimal concentration initiates the lateral association of average eight vimentin tetramers and in parallel smoothens the surface of the protein assemblies. The addition of MgCl₂ up to 7 mM does not significantly influence the surface but leads to a further lateral addition of tetramers to the ULFs and to an accumulation of the ions in the side chains which are present on the surface of the filaments. The observed smoothening of the vimentin filaments in statu nascendi, which takes place on the times scale of a few seconds, indicates that this is the time needed by the tetramers from first encounter to the formation of an ordered structure, i.e., a full-width filament unit, which is then ready for further longitudinal association with other ULFs, i.e., for filament elongation. Thus, our combined microfluidics-SAXS experiments reveal the time scale for assembly, which is not a one-step reaction but a process that apparently takes several seconds. Our data for vimentin may have impact on other IF proteins such as desmin or neurofilaments as well.