MEGSA: A Powerful and Flexible Framework for Analyzing Mutual Exclusivity of Tumor Mutations

Abstract

The central challenges in tumor sequencing studies is to identify driver genes and pathways, investigate their functional relationships, and nominate drug targets. The efficiency of these analyses, particularly for infrequently mutated genes, is compromised when subjects carry different combinations of driver mutations. Mutual exclusivity analysis helps address these challenges. To identify mutually exclusive gene sets (MEGS), we developed a powerful and flexible analytic framework based on a likelihood ratio test and a model selection procedure. Extensive simulations demonstrated that our method outperformed existing methods for both statistical power and the capability of identifying the exact MEGS, particularly for highly imbalanced MEGS. Our method can be used for de novo discovery, for pathway-guided searches, or for expanding established small MEGS. We applied our method to the whole-exome sequencing data for 13 cancer types from The Cancer Genome Atlas (TCGA). We identified multiple previously unreported non-pairwise MEGS in multiple cancer types. For acute myeloid leukemia, we identified a MEGS with five genes (FLT3, IDH2, NRAS, KIT, and TP53) and a MEGS (NPM1, TP53, and RUNX1) whose mutation status was strongly associated with survival (p = 6.7 × 10⁻⁴). For breast cancer, we identified a significant MEGS consisting of TP53 and four infrequently mutated genes (ARID1A, AKT1, MED23, and TBL1XR1), providing support for their role as cancer drivers.

Introduction

Cancers, driven by somatic mutations, cause more than eight million deaths worldwide each year. Recent technical advances in next-generation sequencing and bioinformatic analyses have greatly advanced the characterization of tumor genomes. Large-scale cancer genomics projects, e.g., the Therapeutically Applicable Research to Generate Effective Treatments (TARGET) for childhood cancers, The Cancer Genome Atlas (TCGA), and the International Cancer Genome Consortium (ICGC) for adult cancers, have accumulated a large amount of multi-dimensional genomic data for dozens of cancers. The primary aim in analyzing these unprecedented “big” genomic data is to identify “driver” mutation events related with tumor initiation and progression. Typically, driver genes are nominated by examining whether the non-synonymous mutation rate exceeds the background silent mutation rate.^{1, 2} However, identifying infrequently mutated driver genes requires a very large sample size to achieve statistical significance. A closely related challenge is to investigate relationships among mutated genes and to identify oncogenic pathways. Mutual exclusivity (ME) analysis is an effective computational approach that helps address both problems.

ME analysis was initially proposed for pairs of genes and has produced important findings that have been consistently replicated, e.g., ME between EGFR (MIM: 131550) and KRAS (MIM: 190070) in lung adenocarcinoma.^{3, 4, 5} Because cancer pathways typically involve multiple genes, recent methods^{6, 7, 8, 9, 10, 11} have tried to extend pairwise analyses to search for mutually exclusive gene sets (MEGS), which also has much better power than pairwise analyses. In brief, given a somatic mutation matrix for N subjects and M genes, we aim to identify “optimal” gene subsets that are mutually exclusively mutated.

Multiple methods have been proposed for ME analysis. Dendrix⁷ and two other methods^{9, 10} use a “weight” statistic as the criterion to search for MEGS. However, this statistic is inappropriate to compare gene sets and tends to identify large MEGS with many false-positive genes, as we will show in simulations. MEMo⁶ uses external biological data to form “cliques” (fully connected gene networks) and searches for MEGS within each clique to increase power by reducing multiple testing. As we will demonstrate, MEMo results in incorrect false-positive rates for each clique and tends to select MEGS with false-positive genes. Szczurek and Beerenwinkel⁸ proposed a non-standard likelihood ratio test but ended up with a severely misspecified null distribution. Mutex¹¹ has improved existing methods and used permutations to control false-positive rates, but its overly simple statistic warrants further improvement. In summary, most of the existing methods fail to correctly control for false-positive rates and lack a criterion for selecting “optimal” MEGS. Because some of these MEGS methods have been widely used in tumor sequencing projects, previous results might need to be interpreted with caution.

Ideally, an analytic framework for identifying MEGS would have the following components. First, given a subset of m (m ≤ M) genes, a statistically powerful test is required to examine whether mutations in these m genes show ME. Second, it is crucial to determine whether any subset of the M genes is statistically significant after adjusting for multiple testing. Third, a model selection criterion is required to compare nested gene sets to select the “optimal” MEGS. An inappropriate criterion can falsely include genes into MEGS or exclude true genes from MEGS.

We developed a framework that fits all above requirements. We developed a likelihood ratio test (LRT) for testing ME and performed a multiple-path linear search together with permutations to test the global null hypothesis, i.e., the set of M genes does not contain MEGS of any size. When global null hypothesis was rejected, we proposed a model selection procedure based on permutations to identify “optimal” MEGS. All algorithms have been implemented in an R package called MEGSA (mutually exclusive gene set analysis). Extensive simulations demonstrated that MEGSA outperformed existing methods for de novo discovery and dramatically improved the accuracy of recovering exact MEGS, particularly for imbalanced MEGS. MEGSA can be used either for de novo discovery or by incorporating existing biological datasets (e.g., KEGG pathways and protein-protein interactions) to improve statistical power by reducing multiple testing, in spirit similar to MEMo⁶ and Mutex.¹¹ We can also use MEGSA to expand well-established small MEGS with further improved power.

We applied MEGSA to analyze the whole-exome sequencing data of 13 cancer types from TCGA. We identified multiple significant non-pairwise MEGS for breast cancer, low-grade glioma, uterine corpus endometrial carcinoma, skin cutaneous melanoma, head and neck squamous cell carcinoma, and acute myeloid leukemia with important biological implications. Incorporating KEGG pathway data further identified eight MEGS for breast cancer and ten for low-grade glioma. Although de novo discovery has lower power due to the high multiple testing burden, it has the potential to identify a more complete MEGS. Incorporating external information might identify significant but probably incomplete oncogenic pathways. Thus, MEGSA should be applied using these complimentary search strategies. We expect MEGSA to be useful for identifying oncogenic pathways and driver genes that would have been missed by frequency-based methods.

Material and Methods

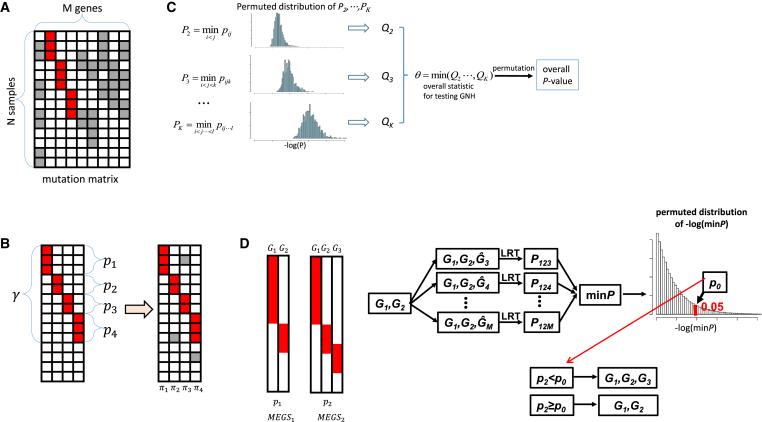
We consider a binary mutation matrix A with N rows (subjects with cancer) and M columns (genes), where each row represents the mutational status for one subject and each column for one gene (Figure 1A). Let a_ik denote the mutation status with a_ik = 1 if gene k is somatically mutated for subject i and a_ik = 0 otherwise. Here, a somatic mutation could be copy-number alternations, non-synonymous point mutations, or point mutations predicted to be deleterious. We consider non-synonymous point mutations in this manuscript. MEGSA has three components: (1) an efficient likelihood ratio test (LRT) for examining mutual exclusivity for a subset of genes, (2) a multiple-path linear search algorithm and a permutation framework to evaluate the global null hypothesis (GNH), and (3) a model selection procedure to identify the “optimal” MEGS.

Figure 1.

Overview of the Algorithms Implemented in MEGSA for Searching Mutually Exclusive Gene Sets

(A) Observed somatic mutation matrix. Each row is for one sample and each column for one gene. Red entries represent MEGS mutations and gray entries represent background mutations.

(B) A data generative model for MEGS. The left panel shows a MEGS with four genes showing complete mutual exclusivity. The right panel shows MEGS mutations and background mutations. γ is the coverage of the MEGS, defined as the proportion of samples covered by the MEGS. (p₁,..., p_m) are the relative mutation frequencies normalized to have p₁ +...+ p_m = 1. (π₁,..., π_m) are the background mutation frequencies.

(C) Overall statistic for testing global null hypothesis and its significance. p_ij is the p value of our LRT for a gene pair (i, j). p_ijk is the p value for a gene triplet (i, j, k). For each k, let P_k as the minimum p value of all sets of k genes and evaluate its significance (denoted as Q_k) using permutations preserving mutational frequencies. The overall statistic is defined as θ = min(Q₂,⋯, Q_K) and its significance is assessed by permutations.

(D) Model selection based on permutations. Two nested putative MEGS—(G₁,G₂) and (G₁,G₂,G₃)—have nominal p value p₁ and p₂ based on LRT. We permute mutations in (G₃, ⋯, G_M) by keeping the mutual exclusivity of (G₁, G₂) unchanged. Ĝ_k represents permuted mutations for gene k. For each permutation, we calculate the minimum p value for all M-2 triplets (G₁,G₂, Ĝ_k). Threshold p₀ is chosen at level 5%.

A Likelihood Ratio Statistic for Testing Mutual Exclusivity

Given a subset of m (m ≤ M) genes and the binary mutation matrix (denoted as A₀, a sub matrix of A), we describe a data generative model for MEGS. We assume that the m genes in the MEGS are completely mutually exclusive with coverage denoted as γ, defined as the proportion of samples covered by the MEGS. Within the MEGS, we assume (p₁,..., p_m) as the relative mutation frequencies with p₁ + ... + p_m = 1. We assume that the observed mutation matrix A₀ is generated in three steps (Figure 1B):

• (1)Given N subjects and coverage γ, we randomly sample n subjects coved by the MEGS according to the distribution Bionomial(N, γ).
• (2)For each sampled subject covered by the MEGS, we randomly choose a “mutated” gene according to (p₁,..., p_m).
• (3)Independent of the MEGS, we randomly simulate background mutations to each entry of matrix A₀ with gene-specific background mutation rates Π = (π₁,..., π_m). Here, background mutations refer to the mutations that do not belong to the MEGS.

Based on this data generative model and further assuming ${\mathit{p}}_{\mathit{k}}\propto {\pi }_{\mathit{k}}$, the log likelihood is given as

$$\log \mathit{L}\mathrm{(}\gamma \mathrm{,}\Pi \mathrm{;}{\mathit{A}}_0\mathrm{)}=\sum _{\mathit{i}=1}^N\log \left(\left(1-\gamma \right)\prod _{\mathit{k}=1}^{\mathit{m}}{\pi }_{\mathit{k}}^{{\mathit{a}}_{\mathit{ik}}}{\left(1-{\pi }_{\mathit{k}}\right)}^{1-{\mathit{a}}_{\mathit{ik}}}+\gamma \frac{1}{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\pi }_{\mathit{j}}}\sum _{\mathit{k}=1}^{\mathit{m}}{\pi }_{\mathit{k}}{\mathit{I}}_{\left\{{\mathit{a}}_{ik}=1\right\}}\prod _{\mathit{j}\ne \mathit{k}}{\pi }_{\mathit{j}}^{{\mathit{a}}_{\mathit{ij}}}{\left(1-{\pi }_{\mathit{j}}\right)}^{1-{\mathit{a}}_{\mathit{ij}}}\right)\mathrm{.}$$

Here, γ = 0 corresponds to the null hypothesis that the m genes are randomly mutated. Π = (π₁,..., π_m) are nuisance parameters. LRT can be derived to test H₀: γ = 0 versus H₁: γ > 0. Asymptotically, LRT has a null distribution $0.5{\chi }_0^2+0.5{\chi }_1^2$, a mixture distribution with 0.5 probability at point mass zero and 0.5 probability as ${\chi }_1^2$. See Appendix A for details.

Testing the Global Null Hypothesis

Given a mutation matrix A with all M genes, it is crucial to test GNH that all genes are mutated independently. Suppose that we are interested in MEGS with no more than K genes. We have ${\sum }_{\mathit{k}=2}^{\mathit{K}}\left(\begin{array}{c}\mathit{M}\\ \mathit{k}\end{array}\right)$ combinations of genes to be tested, which equals to 2.0 × 10¹¹ if M = 100 and K = 8. The multiple testing burden increases with size exponentially when K < M/2. Importantly, the total multiple testing burden is dominated by the largest MEGS with K genes. When M = 100 and K = 8, the number of tests for MEGS with 8 genes account for 91.5% of total 2.0 × 10¹¹ tests while such proportion is only 8.0 × 10⁻⁵% for MEGS of 3 genes. Intuitively, for the same nominal p value of 10⁻⁶, a MEGS with 3 genes should be much more significant than the one with 8 genes. Thus, putative MEGS of different sizes must be differentially treated. Moreover, the statistical tests can be highly correlated; thus the Bonferroni correction is too conservative. We propose a permutation-based procedure to address these problems (Figure 1C). Note that permutations were performed by preserving the mutation frequency for each gene.^{7, 11}

In brief, we first perform multiple test correction separately for MEGS of each size. For a given k (k ≤ K), we search all gene sets of size k to test for ME using our LRT and denote the minimum p value as P_k. The significance of P_k, (denoted as Q_k) is estimated by permutations. Because we search for MEGS of different sizes, the overall statistic for testing GNH is θ = min(Q₂,⋯, Q_K), with significance evaluated by permutations. Finding the minimum p value P_k by exhaustive search is computationally challenging even for a moderate k. Thus, we implemented a multiple-path linear search algorithm to approximate P_k (Appendix A).

Identifying Optimal Mutually Exclusive Gene Sets by Model Selection

When GNH is rejected, we can use the multiple-path linear search algorithm to identify all significant putative MEGS. These putative MEGS can be nested. Consider two significant putative MEGS: MEGS1 has two genes (G₁, G₂) with nominal p value p₁ and MEGS2 has three genes (G₁, G₂, G₃) with nominal p value p₂ based on LRT. Intuitively, if p₂<<p₁, we choose MEGS2 with three genes. However, a simple criterion p₂ < p₁ is too liberal and tends to include G₃ into MEGS even if G₃ is independent of (G₁, G₂). This is because G₃ is chosen from the M-2 genes (G₃, ⋯, G_M) to form the strongest MEGS with G₁ and G₂.

We addressed the problem in a statistical testing framework (Figure 1D). The null hypothesis is that none of the M-2 genes (G₃, ⋯, G_M) is mutually exclusive of (G₁, G₂). We reject the null hypothesis (and thus choose MEGS2) if p₂ < p₀ with p₀ chosen to control false-positive rate < 5% based on permutations. Note that we keep the relationship between G₁ and G₂ unchanged and permute mutations only in (G₃, ⋯, G_M). If (G₃, ⋯, G_M) are independent of (G₁, G₂), using p₀ as threshold will correctly choose MEGS1 with probability 95%.

Identifying Mutually Exclusive Gene Sets by Three Search Strategies

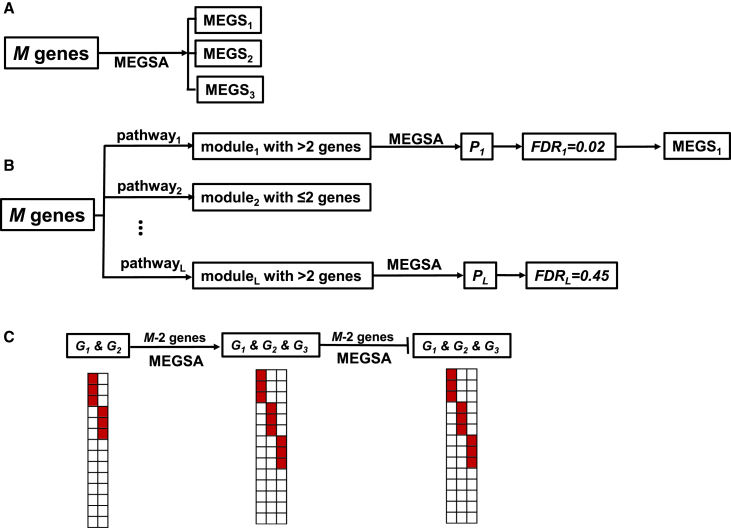
We propose three complimentary strategies for searching MEGS via MEGSA, as illustrated in Figure 2. The first strategy is de novo discovery by directly applying MEGSA to all M genes (Figure 2A). The advantage of de novo discovery is that it does not rely on any prior information and has the potential to identify a complete MEGS. However, de novo analyses might have low power because of heavy multiple testing burden.

Figure 2.

Three Strategies for Searching Mutually Exclusive Gene Sets via MEGSA

(A) De novo analyses for all M genes.

(B) Search MEGS by incorporating KEGG pathways. For each pathway, we derive the subset (called a module) of M genes (with mutation data) in the pathway. We eliminate duplicate modules or modules with fewer than three genes and analyze each module via MEGSA to derive module-wise p values. We control FDR < 0.05 using these module-wise p values to choose significant modules and identify optimal MEGS.

(C) Expanding established small MEGS (G₁, G2) by the model selection procedure described in Figure 1D.

MEGSA can also be applied by incorporating existing biological data, in spirit similar to MEMo⁶ and Mutex.¹¹ MEMo searches for fully connected sub graphs (called “cliques”) using existing pathway and functional information (e.g., protein-protein interaction and gene coexpressoin) and analyzes each clique. Mutex restricts search space so that genes in MEGS have a common downstream signaling target. Although MEGSA can be modified to perform similar search, we exemplify this approach by using the KEGG pathway database (Figure 2B). In brief, we compare M genes with KEGG pathways and identify subsets (called modules) with more than two genes. We analyze each module using MEGSA and produce an overall p value. We choose significant modules by controlling FDR at 5%.

The third strategy is to search MEGS starting with a well-established small MEGS (e.g., EGFR and KRAS in lung cancer). We use our model selection procedure (Figure 1D) to “grow” the MEGS until no gene can be included (Figure 2C).

Results

Type I Error Rate and Power Behavior of LRT

Because the LRT is the foundation for our algorithm, we first evaluated its type I error rate and the power behavior for a fixed set of m genes. Under H₀, LRT ∼ $0.5{\chi }_0^2+0.5{\chi }_1^2$ asymptotically. Results based on 100,000 simulations verified that the p values calculated based on the asymptotic distribution agreed well with the simulation-based p values (Table S1) for different combinations of parameters, including background mutation rate, sample size, and the size of gene sets. The power of LRT increases with sample size and coverage and reduces with background mutation rates (Figure S1).

Comparison with Other Methods that Detect Mutually Exclusive Gene Mutations via Simulations

We compared the performance of MEGSA with the performances of existing methods including RME,¹² MEMo,⁶ Dendrix,⁷ LRT-SB,⁸ and Mutex.¹¹ MDPFinder⁹ uses the same “weight” statistic as Dendrix but a more efficient computational method for searching MEGS; thus the comparative study does not include MDPFinder. A systematic comparison is very difficult for following reasons. Dendrix, RME, and LRT-SB perform de novo analyses; MEMo uses existing biological data to reduce the search space; and MEGSA and Mutex can perform both analyses. In addition, for RME, Dendrix, and LRT-SB, it is unclear how multiple testing was corrected. Mutex¹¹ compared the performances using receiver operating characteristic (ROC) analysis, but it is unclear how false positives and false negatives were calculated. A more detailed summary and critique of these methods can be found in the Supplemental Note.

We empirically evaluated the null distribution of LRT-SB.⁸ Simulation results show that the empirical distribution of LRT-SB deviates dramatically from the claimed null distribution N(0,1) (Figure S2; see also the theoretical explanation in Supplemental Note). MEMo derives a p value for each “clique” and selects significant cliques by controlling FDR using these p values. Controlling FDR requires p values for null statistics to follow a uniform distribution U[0,1].¹³ However, our simulation results (under H₀) show that the p values dramatically deviate from the uniform distribution U[0,1] (Figure S3), suggesting that MEMo has incorrect false-positive rates. In addition, MEMo does not select “optimal” MEGS sets appropriately and typically includes many false positives (Figure S4 and Supplemental Note). Therefore, we excluded LRT-SB and MEMo from the comparison.

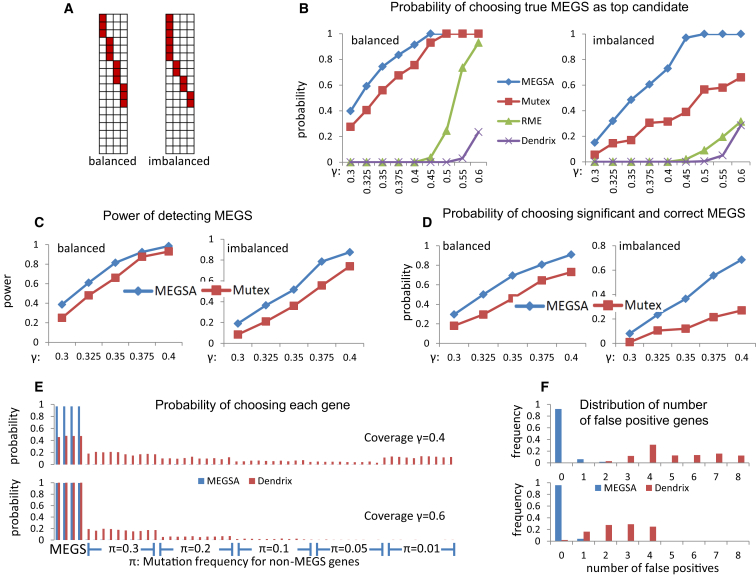
In the first set of simulations, we simulated a mutation matrix for 54 genes in 500 samples. Among the 54 genes, mutations in 50 genes were randomly distributed. The 50 genes were classified into five groups; each group had 10 genes with mutation frequencies 1%, 5%, 10%, 20%, or 30%. The simulated MEGS had four genes. The background mutation rates for these four genes were set as 1%. We simulated two types of MEGS (Figure 3A). One had balanced mutation frequencies, i.e., all four genes in MEGS were mutated with the same frequency. The other had imbalanced mutation frequencies with ratio 3:1:1:1. Comparison was based on de novo analyses. The maximum size of MEGS was set as eight. The simulation results for MEGS with three genes are reported in Figure S5.

Figure 3.

Performance Comparison of Methods for Detecting Mutually Exclusive Gene Sets on Simulated Datasets

In all simulations, we have 54 genes with 50 being randomly simulated with specific mutation frequencies and 4 genes as MEGS.

(A) Balanced and imbalanced MEGS with four genes. In imbalanced MEGS, the mutational frequencies have a ratio 3:1:1:1.

(B) Probability of ranking the exact MEGS as the top candidate. The X-coordinate is the coverage (γ) of simulated MEGS.

(C) Power of detecting MEGS via MEGSA and Mutex.

(D) Probability that the identified top MEGS is statistically significant and identical to the true MEGS. Coverage (γ) of MEGS ranges from 0.3 to 0.4.

(E) Probability of choosing each gene in the identified top MEGS by MEGSA and Dendrix. The top figure is based on a MEGS with coverage γ = 0.4 and the bottom figure based on coverage γ = 0.6. π is the mutation frequencies for the 50 non-MEGS genes. The first four are MEGS genes and the rest are non-MEGS genes.

(F) The distribution of the number of falsely detected genes for the top MEGS identified by in MEGSA and Dendrix. MEGSA had few false-positive genes whereas Dendrix detected many false-positive genes.

We first compared the performance of these methods as a “scoring” method without considering the statistical significance. Therefore, we calculated the probability of choosing the true MEGS identified as the top candidate for each method. Simulation results show that MEGSA performs the best for all simulations and greatly improves existing methods particularly for imbalanced MEGS (Figure 3B). Of note, the performances are heavily impacted by the coverage of the MEGS for all methods. Dendrix has the worst performance and cannot identify the true MEGS even when the coverage is high. RME performs poorly for low-coverage MEGS but reasonably well when coverage increases to 60% for balanced MEGS. Mutex outperforms RME and Dendrix.

Among Dendrix, RME, Mutex, and MEGSA, only Mutex and MEGSA performed permutations to accurately evaluate overall significance (either family-wise error rate or FDR). Therefore, we compared the performance of these two methods for statistically significant findings. For MEGSA, a significant finding was identified if its multiple testing corrected p value < 0.05. For Mutex, a significant finding was identified if FDR < 0.05. A simulation was considered successful if the detected top MEGS involved any pair of the four genes in the simulated MEGS. The power is calculated as the proportion of “successful” simulations (Figure 3C). A much more rigorous criterion required that the top MEGS was statistically significant and identical to the simulated MEGS (Figure 3D). We also calculated the average number of correctly identified genes (out of four) and number of falsely identified genes (Figure S6). MEGSA outperforms Mutex in all comparisons. Importantly, the performance of MEGSA is superior to that of Mutex for imbalanced MEGS, which are much more frequent than balanced MEGS in real data.

Although the three methods (RME, Mutex, and MEGSA) have different performances, the probability of choosing the exact MEGS increases to one when sample sizes increase to infinity, an important statistical property called “consistency.” However, the widely used Dendrix algorithm does not have this property and tends to include many false-positive genes (see Supplemental Note for explanation). Here, we report more detailed simulation results for Dendrix, investigating the false positives in the selected top candidate. Figure 3E reports the probability of choosing each gene based on 1,000 simulations assuming coverage γ = 40% (top) and γ = 60% (bottom). Figure 3F reports the distribution of the number of selected false-positive genes. For example, when coverage γ = 40%, in about 30% of simulations, Dendrix’s top candidate includes four false-positive genes. For low-coverage MEGS with γ = 40%, Dendrix chooses too many false positives, mostly in highly mutated genes (frequency π = 30%) and lowly mutated genes (frequency π = 1%). When coverage increases to 60%, Dendrix identified almost all genes in MEGS but still included many false-positive genes. These simulation results suggest that a high-coverage MEGS identified by Dendrix might include multiple false-positive genes. Thus, MEGS identified by Dendrix might need to be interpreted with caution. Encouragingly, MEGSA has consistently high sensitivity and low false-positive rates.

In the second set of simulations, we performed simulations using the breast cancer tumor sequencing data with 989 samples from The Cancer Genome Atlas (TCGA). Our simulations were based on 39 driver genes reported in the TumorPortal website. As we will show in next section, TP53, CDH1, GATA3, and MAP3K1 were detected as a highly significant MEGS for breast cancer with estimated coverage $\hat{\gamma }=0.547$, $\left({\hat{\mathrm{\pi }}}_1\mathrm{,}{\hat{\mathrm{\pi }}}_2\mathrm{,}{\hat{\mathrm{\pi }}}_3\mathrm{,}{\hat{\mathrm{\pi }}}_4\right)=\left(0.071\mathrm{,}0.024\mathrm{,}0.023\mathrm{,}0.015\right)$ and $\left({\hat{\mathrm{p}}}_1\mathrm{,}{\hat{\mathrm{p}}}_2\mathrm{,}{\hat{\mathrm{p}}}_3\mathrm{,}{\hat{\mathrm{p}}}_4\right)=\left(0.534\mathrm{,}0.180\mathrm{,}0.173\mathrm{,}0.113\right)$. In each simulation, we simulated MEGS mutation data with four genes (TP53, CDH1, GATA3, MAP3K1) according to the estimated parameters and randomly permuted the mutations across subjects for the remaining 35 genes to generate background mutations for these genes. We performed 1,000 simulations to evaluate the performance. RME could not converge to produce results possibly because of multiple genes with low mutation frequencies. Thus, we compared the performance for Dendrix, Mutex, and MEGSA. Dendrix included many false-positive genes (mean of 2.8 false-positive genes per simulations) and chose the true MEGS as the top candidate in only 2% of simulations. Both Mutex and MEGSA had low false-positive rates, including mean of 0.06 and 0 false-positive genes in each simulation, respectively. MEGSA correctly chose the true MEGS as the top candidate in 93.4% simulations, and Mutex chose the true MEGS as the top candidate in 33.2% simulations. Further investigation showed that Mutex missed one gene in 44.1% simulations and two genes in 22.7% simulations. This set of simulations based on realistic settings confirmed previous simulation results that MEGSA had a better performance for detecting the exact MEGS.

In the third set of simulations, we investigated the power performance of MEGSA when input genes can be partitioned into L modules of equal sizes by incorporating pathway information. MEGSA was applied separately to each module to generate a module-wise p value. A module was statistically significant if its p value < 0.05/L based on the Bonferroni correction. Under the assumption that the true MEGS is completely contained in one of the modules, the power of detecting MEGS can be substantially improved compared to de novo analysis that simultaneously analyzes all genes (Figure S7).

Analysis of TCGA Mutation Data

We analyzed non-synonymous point somatic mutations identified by whole-exome sequencing for 13 cancers in TCGA with data downloaded from the data portal. For cancer types included in the TumorPortal website, we included candidate driver genes reported by the website¹⁴ using MutSigCV.¹ Brain low-grade glioma (LGG) is not reported in the TumorPortal website. Therefore we identified candidate driver genes using MutSigCV¹ and included these genes into analysis. Sample sizes, numbers of selected genes, and mutational frequencies are summarized in Tables S2 and S3. For each cancer type, we performed de novo analysis followed by the secondary analysis incorporating KEGG pathways. For de novo analysis, gene sets were considered statistically significant if p < 0.05 after multiple testing based on 10,000 permutations. For KEGG-guided analysis, we derived a module-wise p value for each module and declared significance by controlling FDR < 0.05. Note that MEGS from pathway-guided analyses were discarded if they were a subset of any MEGS identified in de novo analyses.

De novo analyses identified non-pairwise MEGS for acute myeloid leukemia (LAML), LGG, breast invasive carcinoma (BRCA), skin cutaneous melanoma (SKCM), head and neck squamous cell carcinoma (HNSC), and uterine corpus endometrial carcinoma (UCEC). For other cancer types, de novo analysis identified only pairwise MEGS. Here, we report detailed results for BRCA and LAML. The complete results are summarized in Table S4.

We also performed de novo analysis using RME, Dendrix, and Mutex with results summarized in Table S5 and Figure S8. Because we lack the gold standard for accurate comparison, we here briefly describe the putative similarities and differences in the results produced from these algorithms. When there existed strong MEGS with high coverage, e.g., AKT1 (MIM: 164730), PTEN (MIM: 601728), and TP53 (MIM: 191170) with coverage 91.9% in UCEC and BRAF (MIM: 164757), KIT (MIM: 164920), and NRAS (MIM: 164790) with coverage 83.7% in SKCM, Dendrix detected these MEGS with results consistent with Mutex and MEGSA. However, when there were no strong MEGS with high coverage, Dendrix selected a large gene set as the top candidate, e.g., it chose a set of eight genes (the maximum number of genes we allowed in analysis) as the top candidate for BRCA, GBM, KIRC, and LAML. According to simulations, some of the genes from these large putative MEGS might be false positives. RME detected 25 MEGS; however, only two MEGS (pairwise) were identical to those identified by Mutex or MEGSA and the majority of them did not overlap with those by Mutex or MEGSA. The mutation data did not seem to support the large MEGS identified by RME. MEGSA and Mutex produced the most similar results among the four algorithms and detected 42 and 34 significant MEGS in total, respectively. Among the 34 significant MEGS detected by Mutex, 14 were identical to those identified by MEGSA, 11 were subsets of those in MEGSA, and 7 overlapped with those in MEGSA for at least two genes. Mutex frequently identified multiple subsets of one MEGS identified by MEGSA. For example, MEGSA detected EGFR, IDH1 (MIM: 147700), IDH2 (MIM: 147650), and NF1 (MIM: 162200) whereas Mutex detected two subsets: EGFR, IDH1, and IDH2 and IDH1, IDH2, and NF1. These results together with the simulation results suggest that MEGSA might have a better performance for identifying a more complete oncogenic pathway. Mutex tends to select smaller MEGS, consistent with its algorithm that considers the weakest mutual exclusivity when scoring a putative MEGS.

Analysis Results for BRCA

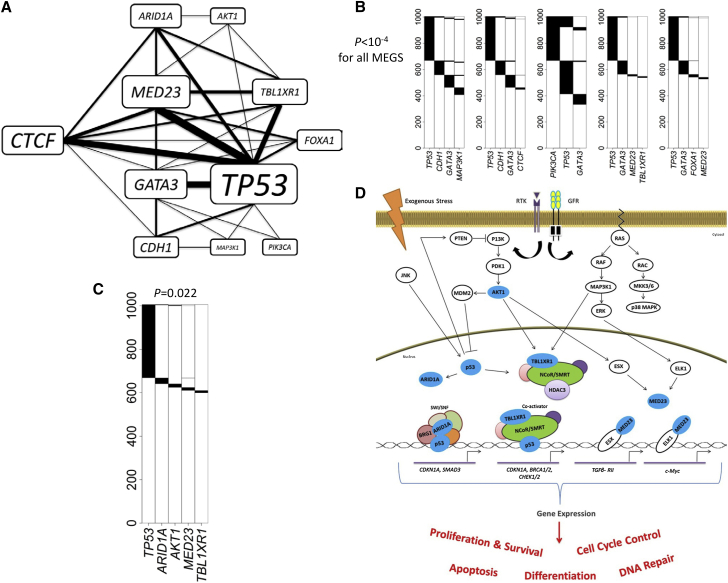
De novo analyses identified 10 significant but overlapping MEGS for BRCA with 989 subjects. These MEGS involved 11 genes with TP53 involved in all MEGS (Figure 4A). We identified five MEGS with p < 10⁻⁴ (Figure 4B). These MEGS were not reported by the TCGA breast cancer article¹⁵ using MEMo⁶ that relies on functional data, emphasizing the necessity of de novo search.

Figure 4.

Analysis Results for TCGA Breast Cancer Whole-Exome Sequencing Data

p values were adjusted for multiple testing for all reported MEGS.

(A) A network constructed based on the ten significant MEGS. Thickness of the edges and sizes of the gene labels are proportional to the times in the detected MEGS.

(B) Five significant MEGS with p < 10⁻⁴.

(C) A significant MEGS with five genes.

(D) Illustration showing MEGS pattern including protein products (colored blue) of AKT1, TP53, ARID1A, MED23, and TBL1XR1 in their relevant biological pathways. Connections including activation and interaction as well as effects on gene expression and biological processes are indicated. Components in the NCoR/SMRT and SWI/SNF complexes and the potential interaction of MED23 with p53 via the overall mediator complex are not illustrated. Connections including activation (lines with arrow) and inhibition (bar-headed lines) as well as end biological effects between the gene products are illustrated. Abbreviations are as follows: RTK, receptor tyrosine kinases; GFR, growth factor receptor.

The most significant MEGS has four genes—TP53, CDH1 (MIM: 192090), GATA3 (MIM: 131320), and MAP3K1 (MIM: 600982)—and covers 59.6% of subjects. E-cadherin, encoded by CDH1, is important in epithelial-mesenchymal transition (EMT). Moreover, GATA3, p53, and MAP3K1 are related to the expression of CDH1. Loss of p53 represses E-cadherin expression in vitro as a result of CDH1 promoter methylation;¹⁶ GATA3 expression is correlated with E-cadherin levels in breast cancer cells;¹⁷ and E-cadherin expression can be repressed by Snail/Slug after activation by the MAPK/ERK pathway.¹⁷

The largest MEGS (p = 0.022) has five genes—TP53, AKT1, ARID1A (MIM: 603024), MED23 (MIM: 605042), and TBL1XR1 (MIM: 608628)—covering 40.4% of subjects (Figures 4C and 4D). Of note, this MEGS is extremely imbalanced: all genes except TP53 are infrequently mutated with frequency 1%–2% and could not be identified by other methods, consistent with the results of simulations. TBL1XR1 belongs to and regulates the core transcription repressor complexes NCoR/SMRT,¹⁸ and p53 gene targets might be regulated by the SMRT in vitro in response to DNA damage.¹⁹ ARID1A encodes BAF250a, a component of the SWI/SNF chromatin-remodeling complex that directly interacts with p53.^{20, 21, 22, 23} Therefore, loss of ARID1A might have a similar effect as p53 deficiency. The mutual exclusivity between MED23 and other genes have not been reported previously. MED23 is a subunit of the mediator complex, a key regulator of gene expression, and is required for Sp1 and ELK1-dependent transcriptional activation in response to activated Ras signaling.^{24, 25, 26, 27} MED1 and MED17 directly interact with p53,²⁷ suggesting a possible connection between p53 and MED23 via the mediator complex. Also, MED23 interacts directly with the transcription factor ESX/ELF3,²⁷ which is downstream of AKT1 in the PI3K pathway. ESX-dependent transcription after activation by AKT is key for cell proliferation and survival. In summary, these genes have key roles in chromatin remodeling (TBL1XR1 and ARID1A), gene expression regulation (MED23 and TP53), and signaling (AKT1), and probably regulate a common set of gene targets downstream of the p53, PI3K, and MAPK/ERK signaling pathways that are important for cell cycle control, survival, and proliferation.

Importantly, these infrequently mutated genes are unlikely to achieve high statistical significance via frequency-based driver gene test, e.g., MutSigCV.¹ In fact, in the TCGA breast cancer article,¹⁵ MED23 and ARID1A were not reported as significantly mutated whereas FOXA1 (MIM: 602294) and CTCF (MIM: 604167) were reported only as “near significance.” Because MutSigCV is highly sensitive to the choice of “Bagle” gene set for estimating the silent mutation rate, a very large sample size is required to replicate these findings. Given that TP53 is a well-established driver gene, the observed mutual exclusivity provides strong and independent evidence for establishing these genes’ role as drivers.

Pathway-guided analysis identified eight MEGS that were not detected by de novo analyses. Interestingly, we found that CBFB (MIM: 121360) was mutually exclusive of ARID1A, MED23, and TP53. As described above, p53 can interact with ARID1A in the SWI/SNF chromatin remodeling complex via BRG1 (see Figure 4D for SWI/SNF complex). The transcriptional coactivator CBFB is known to interact with the tumor-suppressor RUNX1, the predominant RUNX family member in breast epithelial cells.²⁸ RUNX1 interacts with SWI/SNF via BRG1²⁹ and can act as transcriptional coactivator for p53 in response to DNA damage.³⁰ Thus, we propose that the loss of either one of these genes would be sufficient to lead to abnormal SWI/SNF complexes and dysregulation of chromatin-related epigenetics and gene expression, leading to inhibition of apoptosis.

Breast cancer is highly heterogeneous with only two genes—TP53 and PIK3CA (MIM: 171834)—with mutation frequencies greater than 15% (Table S3). The majority of genes have mutation frequencies around 1%–2%, making it difficult to identify MEGS. We successfully identified ten significant MEGS based on de novo analyses and additional eight guided by KEGG pathways. Other biological databases, e.g., functional data and Human Reference Network in MEMo⁶ or the common downstream target database in Mutex,¹¹ could be used in the future to guide the search of MEGS.

Analysis Results for LAML

Compared with other cancer types, AML genomes have the lowest somatic mutation rates,¹ with only 13 mutations in coding regions in average. Such a low overall (and also background) mutation rate suggests a good statistical power even with a small sample size according to our simulations (Figure S1). In fact, de novo analyses identified five distinct but overlapping significant MEGS. These significant MEGS involve nine genes with TP53 and FLT3 (MIM: 136351) shared by four MEGS (Figure 5A). The pathway-guided search did not detect additional MEGS.

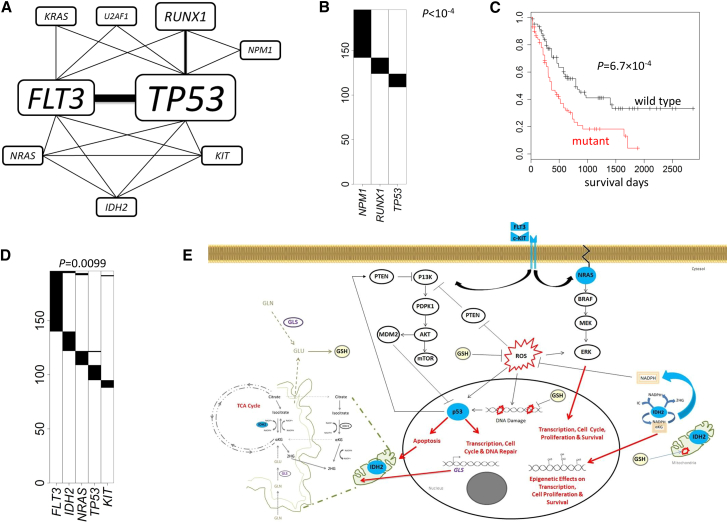
Figure 5.

Analysis Results for TCGA Acute Myeloid Leukemia Whole-Exome Sequencing Data

p values were adjusted for multiple testing for all reported MEGS.

(A) A network constructed based on the five significant MEGS. Thickness of the edges and sizes of the gene labels are proportional to the times in the detected MEGS.

(B) The most significant MEGS with three genes: NPM1, RUNX1, and TP53.

(C) The mutation status of the triplet (NPM1, RUNX1, and TP53) is strongly associated with survival.

(D) A significant MEGS with five genes.

(E) Illustration showing MEGS pattern including protein products (colored blue) of FLT3, IDH2, KIT, NRAS, and TP53 in their relevant biological pathways. Connections including activation (lines with arrow) and inhibition (bar-headed lines) as well as end biological effects between the gene products are indicated. IDH2, which locates to the mitochondria, is shown outside (or in-part) of the illustrated organelle for clarity and only the relevant components of glutamine (GLN) and glutathione (GSH) metabolism and TCA cycle are indicated. PI3K pathway (receptor tyrosine kinases [RTK], FLIT3, and KIT), MAPK/ERK pathway (NRAS). Abbreviations are as follows: ROS, reactive oxygen species, αKG, alpha-ketoglutarate; 2HG, 2-hydroxyglutarate; TCA, tricarboxylic acid cycle; GLN, glutamine; GLU, glutamate; and GLS, glutaminase 2; GSH (glutathione).

The most significant MEGS (Figure 5B) has three genes—NPM1 (MIM: 164040), RUNX1 (MIM: 151385), and TP53 (p < 10⁻⁴)—which is a subset of the top MEGS (four genes and four fusions) reported by the TCGA LAML article.³¹ We further tested the association of the mutations in these three genes and their combinations with survival, adjusting for age, stage, and gender. Strikingly, the strongest association was detected for the MEGS (p = 6.7 × 10⁻⁴; Figure 5C) but not any subset (P_TP53 = 0.002, P_NPM1 = 0.13, P_RUNX1 = 0.24, P_TP53/NPM1 = 0.0034, P_TP53/RUNX1 = 0.0032, and P_RUNX1/NPM1 = 0.042), suggesting the usefulness of the MEGS for predicting clinical outcomes. Note that in the LAML article, the top MEGS included CEBPA (MIM: 116897), which had 3 (out of 13) mutations co-occurring with the triplet. In fact, including CEBPA into the triplet lowered the LRT statistic from 25.1 to 22.7. Thus, our model selection procedure excluded CEBPA. Moreover, including CEBPA did not significantly improve the prediction of survival (p = 5.9 × 10⁻⁴ with CEBPA versus p = 6.7 × 10⁻⁴ without CEBPA). These results suggest that the mutual exclusivity between CEBPA and other genes is at least suspicious and requires independent replication.

The largest MEGS (Figure 5D) has five genes—FLT3, IDH2, KIT, NRAS, and TP53 (p = 0.0099)—covering 55.1% of subjects. This MEGS was not reported by the TCGA LAML article³¹ and was not detected by other algorithms. Figure 5E describes important connections between function/pathways for the five gene products, suggesting biological plausibility. FLT3 and KIT encode receptor tyrosine kinases upstream of the PI3K and MAPK/ERK signaling pathways, and NRAS is also part of MAPK/ERK. Mutations activating these pathways or inactivating TP53 are common mechanisms that cancer cells use to proliferate and escape apoptosis.³²

Interestingly, we discovered that IDH2 belongs to this MEGS. IDH2 encodes a mitochondrial enzyme that converts isocitrate to α-ketoglutarate (αKG) in the tricarboxylic acid cycle and in this process produces the antioxidant nicotinamide adenine dinucleotide phosphate (NADPH), which is necessary to combat oxidative damage/stress.^{33, 34} Mutant IDH2 is predicted to result in depletion of α-KG, a decrease in NADPH, and production of 2-hydroxyglutarate (2-HG) and might elevate cytosolic reactive oxygen species (ROS).³⁵ Mutant IDH2 can result in epigenetic effects on gene transcription (including DNA hypermethylation and histone demethylation), whereas loss of p53 function can result in increased expression of DNA methyltransferase 1 (DNMT1).^{16, 36} Thus, a reasonable explanation for the observed mutual exclusivity between TP53 and IDH2 is that the loss of either protein activity can result in similar aberrant gene methylation patterns across the genome and dysregulated gene expression. We also suggest a further novel hypothesis. Depleted α-KG levels in IDH2 mutant cells might be replenished by the conversion of glutamate to α-KG in the mitochondria.³⁷ The provision of glutamate in the mitochrondria is regulated by p53 via expression of the enzyme glutaminase (GLS), which also regulates antioxidant defense function in cells by increasing reduced glutathione (GSH) levels.³⁸ Thus, IDH2 and TP53 mutations are mutually exclusive because loss of both genes (or gene activity) would not be conducive to tumorgenesis or survival as a result of further depletion of αKG levels in the mitochondria and DNA damage caused by high levels of ROS. The mutual exclusivity between IDH2 mutation and FLT3, KIT, and NRAS is also biologically plausible. Mutant IDH2 might also be linked to the activation of RAS/ERK and the PI3K pathways via ROSs, which can act as potent mitogens when apoptosis is inhibited.³⁹ Elevated ROS levels can activate ERKs, JNKs, or p38 and reversibly inactivated PTEN.^{40, 41} Thus, IDH2 mutation might be sufficient to exclusively deregulate cell proliferation and survival processes important for AML development.

Discussion

We developed a powerful and flexible framework, MEGSA, for identifying mutually exclusive gene sets (MEGS). MEGSA outperforms existing methods for de novo analyses and greatly improves the capability of recovering the exact MEGS, particularly for highly imbalanced MEGS. The key components of MEGSA are a likelihood ratio test and a model selection procedure. Because likelihood ratio test is asymptotically most powerful, MEGSA is expected to be nearly optimal for de novo search. Our algorithms can be easily adapted to other methods that integrate with external information, e.g., MEMo and Mutex, to improve performance. As an important contribution, we carefully examined the performance of existing methods. We concluded that many methods had incorrect false-positive rates and poor performance for selecting optimal MEGS. Importantly, mutual exclusivity analysis might help identify infrequently mutated driver genes, as we demonstrated in the TCGA BRCA data. CoMEt⁴² was recently published for identifying MEGS using the approximate p value of an exact test as the scoring criterion. CoMEt has to specify the size of MGES and it is not clear how CoMEt compares nested putative MEGS models to select the optimal one.

MEGSA can be further improved in several ways. First, MEGSA does not consider the extremely variable somatic mutation rates across subjects. Including subjects with very high mutation rate might increase the background mutation rate and thus decrease the statistical power. We are currently extending MEGSA by modeling subject-specific background mutation rates. Second, MEGSA uses a multiple-path search algorithm for computational consideration and might miss findings. The Markov Chain Monte Carlo (MCMC) or the genetic algorithm might address the issue.

In the current manuscript, we analyzed TCGA non-synonymous point mutations for the purpose of testing the MEGSA algorithm. We plan to extend the analysis to include somatic copy-number aberrations (SCNAs), recurrent gene fusions,³¹ and epigenetic alternations. Moreover, it would be extremely interesting to restrict analysis to clonal point mutations that are carried by all cancer cells. Clonal mutations happen before the most recent common ancestor and are located early in the evolution tree of the tumor;⁴³ thus, clonal mutations are probably relevant for tumorigenesis. Focusing the analysis on clonal mutations, although technically challenging,^{44, 45, 46} can substantially reduce the background mutation rates and consequently improve statistical power. More importantly, this refined analysis might better reveal oncogenic pathways related with tumorigenesis.

Published: February 18, 2016

Appendix A

A Likelihood Ratio Statistic for Testing Mutual Exclusivity

Suppose that a MEGS has m genes with mutation matrix denoted as A₀. We assume that the m genes are completely mutually exclusive. A MEGS is characterized by two parameters: the coverage γ, defined as the proportion of samples covered by the MEGS, and the relative mutation frequencies P = (p₁,..., p_m). Background mutations are mutually independent and also independent of the MEGS mutations. We allow different background mutation rates Π = (π₁,..., π_m) for different genes. See Figure 1B.

For subject i, let (a_i1,..., a_im) be the observed binary mutation vector for m genes. Let C_i be a discrete binary variable. If the subject is not covered by the MEGS, C_i = 0. If the subject has a mutation in gene k in the MEGS, then C_i = k. The likelihood of observing (a_i1,..., a_im) is given by

$$\begin{array}{l}\mathit{P}\left({\mathit{a}}_{\mathit{i}1}\mathrm{,}\cdots \mathrm{,}{\mathit{a}}_{\mathit{im}}\right)=\sum _{\mathit{k}=0}^{\mathit{m}}\mathit{P}\left({\mathit{a}}_{\mathit{i}1}\mathrm{,}\cdots \mathrm{,}{\mathit{a}}_{\mathit{im}}|{\mathit{C}}_{\mathit{i}}=\mathit{k}\right)\mathit{P}\left({\mathit{C}}_{\mathit{i}}=\mathit{k}\right)\\ =\mathit{P}\left({\mathit{a}}_{\mathit{i}1}\mathrm{,}\cdots \mathrm{,}{\mathit{a}}_{\mathit{im}}|{\mathit{C}}_{\mathit{i}}=0\right)\mathit{P}\left({\mathit{C}}_{\mathit{i}}=0\right)+\mathit{P}\left({\mathit{C}}_{\mathit{i}}>0\right)\sum _{k=1}^m\mathit{P}\left({\mathit{a}}_{\mathit{i}1}\mathrm{,}\cdots \mathrm{,}{\mathit{a}}_{\mathit{im}}|{\mathit{C}}_{\mathit{i}}=\mathit{k}\right)\mathit{P}\left({\mathit{C}}_{\mathit{i}}=\mathit{k}|{\mathit{C}}_{\mathit{i}}>0\right)\\ =\mathit{P}\left({\mathit{C}}_{\mathit{i}}=0\right)\prod _{\mathit{j}=1}^{\mathit{m}}\mathit{P}\left({\mathit{a}}_{\mathit{ij}}|{\mathit{C}}_{\mathit{i}}=0\right)+\mathit{P}\left({\mathit{C}}_{\mathit{i}}>0\right)\sum _{\mathit{k}=1}^{\mathit{m}}\mathit{P}\left({\mathit{C}}_{\mathit{i}}=\mathit{k}|{\mathit{C}}_{\mathit{i}}>0\right)\prod _{\mathit{j}=1}^{\mathit{m}}\mathit{P}\left({\mathit{a}}_{\mathit{ij}}|{\mathit{C}}_{\mathit{i}}=\mathit{k}\right)\mathrm{.}\end{array}$$ (Equation A1)

The last equation holds because mutations are independent across genes. By the definition of coverage,

$$\mathit{P}\left({\mathit{C}}_{\mathit{i}}>0\right)=\gamma \mathrm{and}\mathit{P}\left({\mathit{C}}_{\mathit{i}}=0\right)=1-\gamma \mathrm{.}$$ (Equation A2)

Also,

$$\mathit{P}\left({\mathit{C}}_{\mathit{i}}=\mathit{k}|{\mathit{C}}_{\mathit{i}}>0\right)={\mathit{p}}_{\mathit{k}}\mathrm{.}$$ (Equation A3)

If the subject is not covered by the MEGS,

$$\mathit{P}\left({\mathit{a}}_{\mathit{ik}}=1|{\mathit{C}}_{\mathit{i}}=0\right)={\pi }_{\mathit{k}}\mathrm{.}$$ (Equation A4)

Furthermore,

$$\mathit{P}\left({\mathit{a}}_{\mathit{ij}}=1|{\mathit{C}}_{\mathit{i}}=\mathit{k}\right)=\{\begin{array}{l}1\mathrm{if}\mathit{j}=\mathit{k}\\ {\pi }_{\mathit{j}}\mathrm{if}\mathit{j}\ne \mathit{k}\end{array}\mathrm{.}$$ (Equation A5)

Combining Equations A1, A2, A3, A4, and A5, we have

$$\mathit{P}\left({\mathit{a}}_{\mathit{i}1}\mathrm{,}\cdots \mathrm{,}{\mathit{a}}_{\mathit{im}}\right)=\left(1-\gamma \right)\prod _{\mathit{k}=1}^{\mathit{m}}{\pi }_{\mathit{k}}^{{\mathit{a}}_{\mathit{ik}}}{\left(1-{\pi }_{\mathit{k}}\right)}^{1-{\mathit{a}}_{\mathit{ik}}}+\gamma \sum _{\mathit{k}=1}^{\mathit{m}}{\mathit{p}}_{\mathit{k}}{\mathit{I}}_{\left\{{\mathit{a}}_{\mathit{ik}}=1\right\}}\prod _{\mathit{j}\ne \mathit{k}}{\pi }_{\mathit{j}}^{{\mathit{a}}_{\mathit{ij}}}{\left(1-{\pi }_{\mathit{j}}\right)}^{1-{\mathit{a}}_{\mathit{ij}}}\mathrm{.}$$

The total likelihood across N subjects is

$$\log \mathit{L}\left(\gamma \mathrm{,}\Pi \mathrm{,}\mathit{P}\mathrm{;}{\mathit{A}}^0\right)=\sum _{\mathit{i}=1}^{\mathit{N}}\log \left(\left(1-\gamma \right)\prod _{\mathit{k}=1}^{\mathit{m}}{\pi }_{\mathit{k}}^{{\mathit{a}}_{\mathit{ik}}}{\left(1-{\pi }_{\mathit{k}}\right)}^{1-{\mathit{a}}_{\mathit{ik}}}+\gamma \sum _{\mathit{k}=1}^{\mathit{m}}{\mathit{p}}_{\mathit{k}}{\mathit{I}}_{\left\{{\mathit{a}}_{\mathit{ik}}=1\right\}}\prod _{\mathit{j}\ne \mathit{k}}{\pi }_{\mathit{j}}^{{\mathit{a}}_{\mathit{ij}}}{\left(1-{\pi }_{\mathit{j}}\right)}^{1-{\mathit{a}}_{\mathit{ij}}}\right)\mathrm{.}$$ (Equation A6)

We test H₀: γ = 0 versus H₁: γ > 0. P = (p₁,..., p_m) and Π = (π₁,..., π_m) are nuisance parameters. Although both parameters can be estimated under H₁, P = (p₁,..., p_m) is not involved in the likelihood under H₀, which causes problems in deriving the asymptotic null distribution for the likelihood ratio test (LRT). To overcome this problem, we further assume that the MEGS mutation frequencies are proportional to the background mutation frequencies, i.e., ${\mathit{p}}_{\mathit{k}}\propto {\pi }_{\mathit{k}}$. Under this assumption, Equation A6 reduces to

$$\log \mathit{L}\left(\gamma \mathrm{,}\Pi \mathrm{;}{\mathit{A}}^0\right)=\sum _{\mathit{i}=1}^{\mathit{N}}\log \left(\left(1-\gamma \right)\prod _{\mathit{k}=1}^{\mathit{m}}{\pi }_{\mathit{k}}^{{\mathit{a}}_{\mathit{ik}}}{\left(1-{\pi }_{\mathit{k}}\right)}^{1-{\mathit{a}}_{\mathit{ik}}}+\gamma \frac{1}{{\sum }_{\mathit{j}=1}^{\mathit{m}}{\pi }_{\mathit{j}}}\sum _{\mathit{k}=1}^{\mathit{m}}{\pi }_{\mathit{k}}{\mathit{I}}_{\left\{{\mathit{a}}_{\mathit{ik}}=1\right\}}\prod _{\mathit{j}\ne \mathit{k}}{\pi }_{\mathit{j}}^{{\mathit{a}}_{\mathit{ij}}}{\left(1-{\pi }_{\mathit{j}}\right)}^{1-{\mathit{a}}_{\mathit{ij}}}\right)\mathrm{.}$$ (Equation A7)

Let ${\hat{\Pi }}_1$ and ${\hat{\gamma }}_1$ be the estimate under H₁ and ${\hat{\Pi }}_0$ be the estimate under H₀. The LRT is calculated as $\mathit{S}=2\left(\log \mathit{L}\left({\hat{\gamma }}_1\mathrm{,}{\hat{\Pi }}_1\mathrm{;}{\mathit{A}}^0\right)-\log \mathit{L}\left(0\mathrm{,}{\hat{\Pi }}_0\mathrm{;}{\mathit{A}}^0\right)\right)$. Asymptotically, LRT has a null distribution $0.5{\chi }_0^2+0.5{\chi }_1^2$, a mixture distribution with 0.5 probability at point mass zero and 0.5 probability as ${\chi }_1^2$.

We have two comments. First, the assumption ${\mathit{p}}_{\mathit{k}}\propto {\pi }_{\mathit{k}}$ does not affect the null distribution of LRT because p_k is not involved in the data generation process under H₀. However, violation of this assumption might cause power loss, which warrants further investigation. Second, the LRT in the LRT-SB method was derived based on a different data generative model, which incorrectly and unnecessarily assumed that background mutations could happen only for subjects covered by the MEGS. Under this model, their likelihood function degraded as the coverage γ→0, preventing them from using the standard statistical theory to derive the null distribution. To overcome this problem, they used Vuong’s⁴⁷ method (but incorrectly) to derive an incorrect asymptotic null distribution. More details are in the Supplemental Note.

Testing the Global Null Hypothesis

Our algorithm for testing the global null hypothesis (GNH) has the following steps. (1) For k ≤ K k, we search all gene sets of size k from M genes to test for ME using LRT and denote the minimum p value as P_k. (2) We run T permutations, calculate the minimum LRT p value P_k(t) for permutation t, and estimate the significance (denoted as Q_k) of the observed P_k as the proportion of simulations with P_k(t) smaller than the observed P_k. Intuitively, Q_k measures the significance when searching only for MEGS of size k. (3) Because we search for MEGS of different sizes, the overall statistic for testing GNH is defined as θ = min(Q₂,⋯, Q_K), with overall significance evaluated by permutations again.

Although conceptually straightforward, it is computationally infeasible. Finding the minimum p value P_k even for a moderate k (e.g., k = 6) is computationally very challenging and not feasible for thousands of permutations. We propose a multiple-path search algorithm to address the problem. In brief, we calculate the p values for all M(M-1)/2 pairs of genes and choose the top L (e.g., L = 10) pairs to start linear search. For the l^th pair (assuming G₁ and G₂), let q₂(l) be the LRT p value. Next, we calculate the LRT p values for M-2 triplets (G1,G₂,G₃), ⋯, (G1,G₂,G_M) and choose the gene (assuming G₃) with the smallest p value, denoted as q₃(l). We repeat until q_K(l). For each k, we approximate P_k by $\mathrm{mi}{\mathrm{n}}_{\mathit{l}\le \mathit{L}}{\mathit{q}}_{\mathit{k}}\left(\mathit{l}\right)$, instead of exhaustive search.

Identify Statistically Significant MEGS

Remember that we use θ = min(Q₂,⋯,Q_K) as the overall statistic for testing GNH. Once GNH is rejected at level α = 0.05, we need to identify all combinations of genes that reach significance. First of all, based on permutations, we can identify a cut-off θ_1-α. In the multiple-path search algorithm described above, for each combination of k genes, we transform its nominal LRT p value to Q based on permutations and declare this gene set as significant if Q<θ_1-α. This procedure can identify significant but nested putative MEGS. We designed a model selection procedure described in Figure 1D to make a choice between nested models.

Web Resources

The URLs for data presented herein are as follows:

• Dendrix, http://compbio.cs.brown.edu/software/

• HPC @ NIH, http://hpc.nih.gov

• MEGSA, http://dceg.cancer.gov/tools/analysis/MEGSA

• Mutex, http://code.google.com/p/mutex

• MutSigCV, http://www.broadinstitute.org/cancer/software/genepattern/modules/docs/MutSigCV

• OMIM, http://www.omim.org/

• RME, https://github.com/chrisamiller/RMEmod

• The Cancer Genome Atlas, http://cancergenome.nih.gov/

• TumorPortal, http://www.tumorportal.org/