Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Mar 18;7:10983. doi: 10.1038/ncomms10983

Spin–orbit coupling of light in asymmetric microcavities

L B Ma 1,a, S L Li 1, V M Fomin 1, M Hentschel 2, J B Götte 3, Y Yin 1, M R Jorgensen 1, O G Schmidt 1,4
PMCID: PMC4802038  PMID: 26987401

Abstract

When spinning particles, such as electrons and photons, undergo spin–orbit coupling, they can acquire an extra phase in addition to the well-known dynamical phase. This extra phase is called the geometric phase (also known as the Berry phase), which plays an important role in a startling variety of physical contexts such as in photonics, condensed matter, high-energy and space physics. The geometric phase was originally discussed for a cyclically evolving physical system with an Abelian evolution, and was later generalized to non-cyclic and non-Abelian cases, which are the most interesting fundamental subjects in this area and indicate promising applications in various fields. Here, we enable optical spin–orbit coupling in asymmetric microcavities and experimentally observe a non-cyclic optical geometric phase acquired in a non-Abelian evolution. Our work is relevant to fundamental studies and implies promising applications by manipulating photons in on-chip quantum devices.

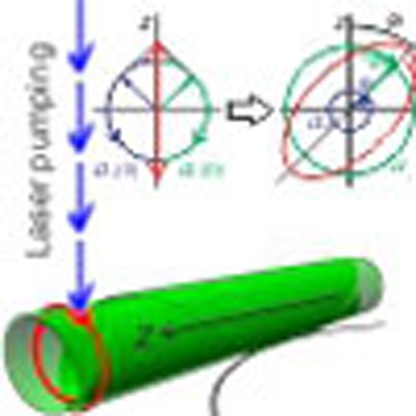Inline graphicOptical spin–orbit coupling is known to occur in open systems such as helical waveguides. Here, the authors enable spin–orbit coupling of light confined to a closed path within an asymmetric optical microcavity and demonstrate a non-cyclic Berry phase acquired in a non-Abelian evolution.

In optics, spin–orbit coupling leads to two important observable effects, the geometric phase1,2,3,4,5,6 and the spin Hall effect3,6,7,8, which play an important role in a surprisingly large number of physical contexts7,9,10,11,12. The geometric phase has been generalized from a cyclic and Abelian context to non-cyclic and non-Abelian cases13,14,15, which have been realized in many physical systems, such as spinning neutrons16 and superconducting artificial atoms17. In optics, it is of fundamental interest to realize a non-cyclic geometric phase acquired in a non-Abelian evolution by enabling optical spin–orbit coupling in a weakly anisotropic medium3,18. Optical spin–orbit coupling has been observed in open systems by the refraction across an interface7 or in the propagation along helical waveguides3,19.

Here we report on the spin–orbit coupling of light confined to a closed path within an asymmetric optical microcavity. The polarization state of light is found to change in both orientation and eccentricity due to the occurrence of a geometric phase together with a mode conversion, generating a non-cyclic geometric phase in a non-Abelian evolution.

Results

Theory of light evolution applied to optical microcavities

Optical microcavities, which confine light to small volumes by resonant circulation in a dielectric medium, play an indispensable role in a wide range of applications and fundamental studies20. In a general theory describing the evolution of light in a dielectric medium, a quantum mechanical diagonalization procedure was applied to the Maxwell equations and Berry's phase theory18, where the effective Hamiltonian takes the form:

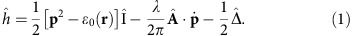graphic file with name ncomms10983-m1.jpg

Here p is the momentum operator, ɛ0(r) represents the scalar isotropic component of the propagation medium, 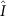Inline graphic stands for a unit matrix, the matrix 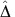Inline graphic denotes the anisotropic component of the dielectric permittivity, λ is the wavelength, 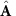Inline graphic represents the gauge potential, and 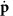Inline graphic is the derivative of p. The Hamiltonian can be divided into three parts 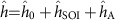Inline graphic. The first part 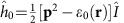Inline graphic characterizes the ordinary light propagation and interference. The second part 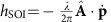Inline graphic denotes the spin–orbit coupling of photons, and the third part 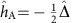Inline graphic describes the medium anisotropy18.

In conventional optical whispering-gallery-mode (WGM) microcavities, such as a cylindrical ring resonator (see Fig. 1a), the electric field vector does not change with respect to the wave vector k. In addition, the resonant light propagates along a closed-loop trajectory, which is distinct from the open helical trajectories that have been widely used to enable the optical spin–orbit interactions2,3,19,21. Unlike the propagation via helical trajectories, the wave vector k experiences a trivial evolution when propagating along a closed loop. As such, the optical spin–orbit interaction is irrelevant and the corresponding Hamiltonian contains only the 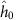Inline graphic part, which results in ordinary discrete eigenmodes in optical WGM resonators. Experimentally, the eigenmodes manifest themselves by discrete peaks in the resonant spectra. Each peak in the resonant spectrum is formed by self-interference with an integer number of waves along the closed-loop trajectory20,22. In these systems the optical polarization states are conserved at each resonance.

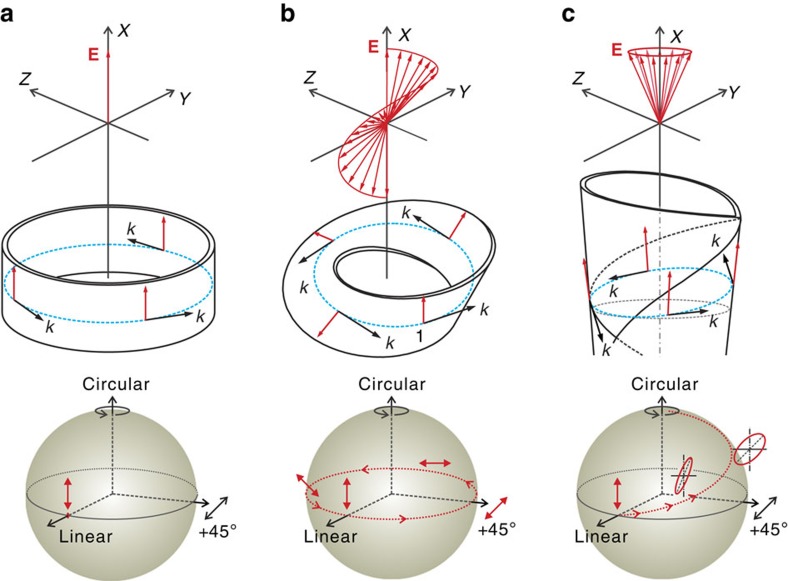
Figure 1. Optical spin–orbit coupling in WGM microcavities (top panel) and the corresponding polarization evolution on the Poincaré sphere (bottom panel).

Figure 1

Open in a new tab

(a) In-plane polarized light does not provide orbital angular momentum in a symmetric ring resonator due to the unchanged electric field (E) vector with respect to the wave vector k, which results in a stationary point on the Poincaré sphere. (b) In a Möbius-ring resonator, the twisted electric field E along the Möbius strip causes a varying orbital angular momentum for spin–orbit coupling, which results in a cyclic evolution on the Poincaré sphere. (c) An effective orbital angular momentum along X is generated due to the rotation of the major axis of the electric field E regulated by the cone-shaped tube wall of an anisotropic medium, allowing for an interaction with the spin angular momentum, which results in a non-cyclic evolution on the Poincaré sphere. The variations of the major polarization axis of the field E (red arrows) are shown with respect to the laboratory coordinate frame (XYZ). The blue dashed lines represent light trajectories, while the red dotted lines represent the polarization evolution trace on Poincaré sphere.

However, optical spin–orbit coupling can be induced in specially designed cavity structures. For example, one can introduce topology into a WGM cavity by employing a Möbius strip23 as an optical micro-ring cavity. Although the wave vector k experiences a trivial evolution in this geometry, the transverse electric field twists around during the propagation in the strip (see Fig. 1b). In this way, an effective orbital angular momentum (OAM), similar to that of an optical vortex24,25,26 or transformed light beam27, is generated for the spin–orbit coupling. Thus, the effective Hamiltonian takes the form 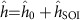Inline graphic, where the spin–orbit coupling leads to the occurrence of a geometric phase. This extra phase leads to a non-integer number of waves for constructive interferences along a closed-loop trajectory, which has been revealed in classical Möbius-ring resonators28. Similar to the previously reported helical waveguides3,29, this behavior represents an Abelian evolution, where the polarization orientation varies, while the polarization eccentricity does not.

Here, we experimentally realize light evolution in the presence of both the spin–orbit interaction and the medium anisotropy in an on-chip cone-shaped microtube resonator. The cone-shaped resonator (see Supplementary Figs 1 and 2) is an asymmetric tube made of a rolled-up SiOx thin film30 as schematically shown in Fig. 1c. The tube is around 7 μm in diameter with a wall thickness of ∼100 nm. In the microtube cavity, optical WGM-type resonances are established via optical self-interferences along a closed-loop trajectory guided by the cylindrical tube wall. To pump the resonances, a linearly polarized laser (at 532 nm) is focused on the larger diameter tube end, where resonant modes of higher quality (Q) factor exist (see Supplementary Fig. 2). The laser excites luminescent defects31 in the amorphous silicon oxide microtube, which emit light in the visible spectral range at room temperature. Due to the subwavelength-thin tube wall, photons linearly polarized along the tube wall are allowed to circulate around a closed trajectory within the microtubes22, which ensures that the initial state of the resonant light is linearly polarized with the polarization orientated around the tube axis. The photons circulating along the closed trajectory eventually escape from the microtube cavity and can then be measured and analyzed.

When the light propagates in the thin-walled microtube, the electric field vector rotates around the tube axis due to the cone-shape of the microtube (see Fig. 1c). This rotation generates an effective OAM along the tube axis15. In conventional WGM cylindrical cavities, the wave vector k (indicating the direction of the spin angular momentum ) of the resonant light is orthogonal to the tube axis; thus, there is no possibility to generate the spin–orbit interactions even if there is an OAM along the axis. However, at the larger-diameter-end part of a cone-shaped tube, the average refractive index is made to vary along the tube axis owing to the variation in the number of windings30. In this particular geometry, the resonant trajectory slightly tilts out of plane (see Fig. 1c) to reduce the optical path according to Fermat's principle (see Supplementary Note 3). It is this tilted trajectory which causes the spin angular momentum to be not orthogonal to the OAM and which, in turn, enables the coupling between spin and orbital degree of freedom 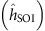Inline graphic. In addition, the resonant light experiences an anisotropic refractive index (see Supplementary Fig. 5) in the asymmetric tube when it propagates along a tilted trajectory, which contributes to the 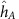Inline graphic term.

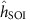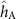The terms Inline graphic and Inline graphic determine the polarization evolution of the optical wave. By expanding the two terms in equation (1) in the basis of Pauli matrices 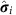Inline graphic (i=1,2,3), the expression 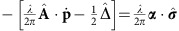Inline graphic exhibits a similar form to that of electrons under the interaction between spin and orbital magnetic moments, where the vector α plays the role of an ‘effective magnetic field'18 and 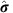Inline graphic is a vector formed of the Pauli matrices. Based on the Schrödinger equation, the polarization evolution equation reads13,18

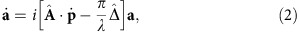graphic file with name ncomms10983-m18.jpg

where the polarization state 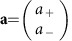Inline graphic is comprised of right 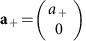Inline graphic and left 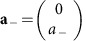Inline graphic components in the circular polarization basis. A well-known solution of equation (2) takes the form13,18

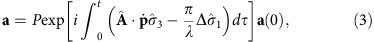graphic file with name ncomms10983-m22.jpg

where P represents the path-ordering operator and 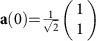Inline graphic is the linear polarization state parallel to the tube axis, which is the initial state in this work. The first term in the integral accounts for the Berry phase1,18

graphic file with name ncomms10983-m24.jpg

The second term in the integral in equation (3) results in a factor CA that originates from the anisotropy of the system. CA enables the interplay between the two polarization states that gives rise to the mutual conversion of the right and left circular polarization components a+ and a−. One should note that the tensor 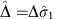Inline graphic is non-diagonal due to the anisotropy of the medium. In our work the Berry phase is non-cyclic; in general it takes the form15

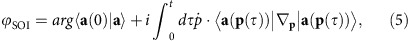graphic file with name ncomms10983-m26.jpg

where a (a≡a(t)) is the final state after an evolution on an open path in the parameter space. Unlike for the cyclic case, a non-cyclic geometric phase usually cannot easily be derived from equation (5), and practical measurements could be more complicated32,33,34. In the present work, we show a different convenient strategy to measure this noncyclic geometric phase.

Starting from equation (3), one can present the final polarization state in terms of the Jones vector3 (see Supplementary Note 6), where the time variable is omitted as we have only access to the measured polarization state at the end of its evolution,

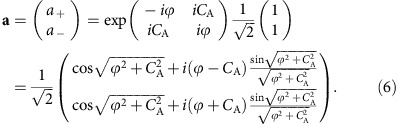graphic file with name ncomms10983-m27.jpg

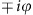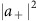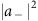The Inline graphic terms denote the geometric phase acquired for each circular basis state. Inline graphic and Inline graphic represent the redistributed circular components after the mode conversion, where (see Supplementary Note 6)

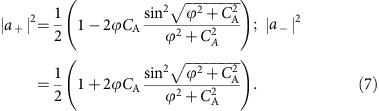graphic file with name ncomms10983-m31.jpg

It is the non-diagonal element iCA in the matrix in equation (6) that leads to the coupling and, consequently, to a mutual conversion between the two circular polarization components a+ and a−.

Characterizations of optical polarization evolution

For optical characterizations, a 50 × objective lens was used to focus the excitation laser beam on the tube wall, while the emitted photons were collected by the same objective and sent to the spectrometer. The polarization states of the resonant light were examined by a fixed polarizer in front of the detector of the spectrometer and a rotatable λ/2 plate. By rotating the λ/2 plate, the polarization orientation of the measured light can be rotated step-by-step and subsequently filtered by the polarizer and recorded by the detector. In this way, both the polarization orientation (with respect to the tube axis) and the polarization eccentricity can be resolved.

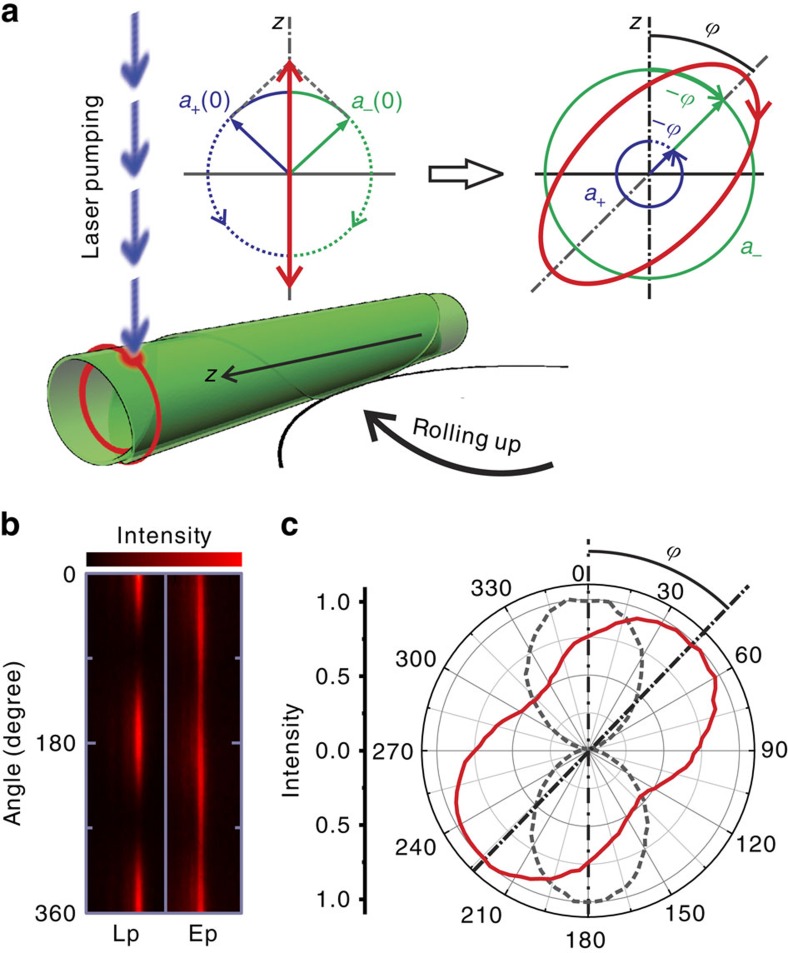
It is well known that the resonant light in WGM microcavities is either transverse magnetic or transverse electric linearly polarized22. For symmetric microtubes, the measured electric field of the light is linearly polarized and oriented parallel to the tube axis for the transverse magnetic modes22. However, in cone-shaped microtube cavities the resonant light is no longer linearly polarized. Figure 2b shows the intensity maps for the linearly (Lp) and elliptically polarized (Ep) modes as a function of the orientation angle (0–360°), which were respectively measured from a symmetric and an asymmetric tube. In the intensity map measured from the symmetric tube, the polarization state is clearly shown to be linearly polarized along the tube axis. In the asymmetric tube case, the varying but unbroken polarization trace is characteristic for elliptical polarization. Moreover, the major axis of the ellipse, or in other words the polarization orientation, is found to tilt away from the tube axis. The polar plots in Fig. 2c clearly reveal the eccentricity and the tilt angle (ϕ∼44.5°) of one of the measured polarization states after evolution in the asymmetric microtube cavity. These unusual phenomena go beyond the conventional knowledge of optical WGM resonances in microcavities and can be attributed to the occurrence of a geometric phase in a non-Abelian evolution of light.

Figure 2. Elliptical polarization state of light in a cone-shaped microtube cavity.

Figure 2

Open in a new tab

(a) In a rolled-up asymmetric microtube being pumped by a laser beam (532 nm), the linearly polarized light evolves into elliptically polarized one with the major axis tilted out of (with an angle ϕ) the tube axis. (b) Resonant mode intensity maps of a linear polarization (Lp) state measured from a symmetric tube where spin–orbit interaction is absent and an elliptical polarization (Ep) state measured in the presence of spin–orbit coupling of light in an asymmetric tube. In the corresponding polar diagrams shown in (c) the linear polarization (dashed line) is oriented parallel to tube axis while the elliptical polarization exhibits a tilt angle ϕ with respect to the tube axis.

As mentioned above, the initial state of the resonant light in the microtube cavity is linearly polarized. A linear polarization state is comprised of the in-phase components of the right and left circular polarization components as a(0)=a+(0)+a−(0), with the same probability amplitude 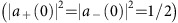Inline graphic, as schematically shown in Fig. 2a. 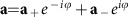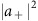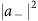Due to the spin–orbit coupling, the right and left circular components acquire a geometric phase with opposite signs: Inline graphic, where ϕ is a geometric phase3, Inline graphic and Inline graphic are redistributed vector amplitudes for each component due to the mode conversion, as described in equation (7). As shown in Fig. 2a, the conversion of amplitudes between the two circular components leads to a change from a linear to an elliptical polarization, while the geometric phase causes the orientation of the major axis of the polarization to tilt by an angle (equal to ϕ) with respect to the initial orientation. Since the final output state differs from the initial one, the evolution generates a non-cyclic geometric phase. Here we show that the non-cyclic geometric phase can be readily measured by simply recording the tilt angle of the light polarization ellipse. The change of the circular bases is evidence for the lack of independent modes, which is a consequence of the intricate non-Abelian evolution as described above. Since the photons are guided in the tube wall and their polarization states vary smoothly, the evolution can be described by an adiabatic process2,3.

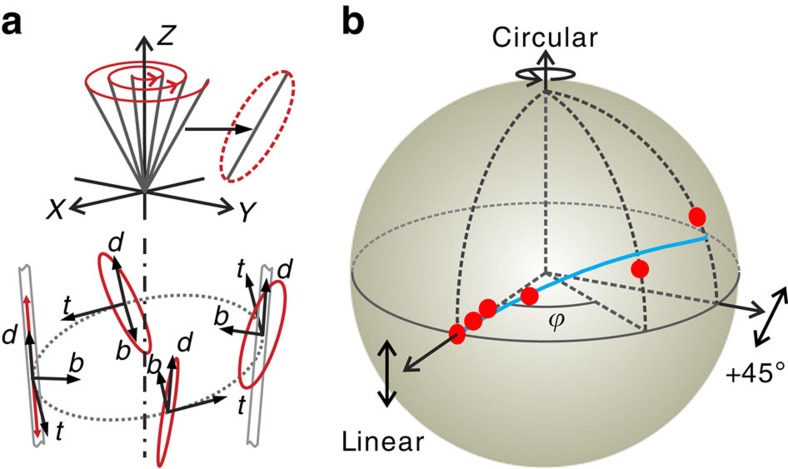
The resonant light experiences the spin–orbit coupling in an anisotropic medium when resonating in an asymmetric microtube cavity, hence the polarization state (described by the eccentricity and the tilt angle) continuously changes as the light resonates in the microtube, as schematically shown in Fig. 3a. However, the polarization state can only be measured when the light escapes from the microtube cavity, at which point the final state of the evolution has been reached. In order to depict the evolution trace, a series of final polarization states were measured from different asymmetric tubes, in which the resonant light experiences different extents of the polarization evolution. Figure 3b shows these series of polarization states plotted on a Poincaré sphere. In our measurements, tilt angles (Berry phase) up to ∼44.5° and an eccentricity of 0.7 have been recorded. It is found that a larger eccentricity is accompanied by a larger tilt angle (ϕ) due to their coupled evolution in equation (3). The corresponding evolution trace can be well reproduced by equation (6), indicating a good agreement between the theoretical model and measurements (see Supplementary Note 6). In addition, we have performed polarization measurements for different mode frequencies in the same tube cavity and found that the tilt angle as well as the eccentricity is independent of the wavelength. This is a clear evidence that the effect is of purely geometric, rather than dynamical origin.

Figure 3. Non-cyclic evolution of degenerate photon systems in asymmetric microcavities.

Figure 3

Open in a new tab

(a) The polarization state of light circulating in an asymmetric tube changes from linear to elliptical, which is visualized by defining a wave-accompanying coordinate (t, d, b) frame (bottom panel). In this process, the major axes of the evolving polarization state assumes a spiral around the tube axis which is shown with respect to the laboratory coordinate frame (top panel). (b) A series of measured polarization states (red dots) in the asymmetric tubes are plotted on a Poincaré sphere, which are fitted (blue curve) based on equation (6).

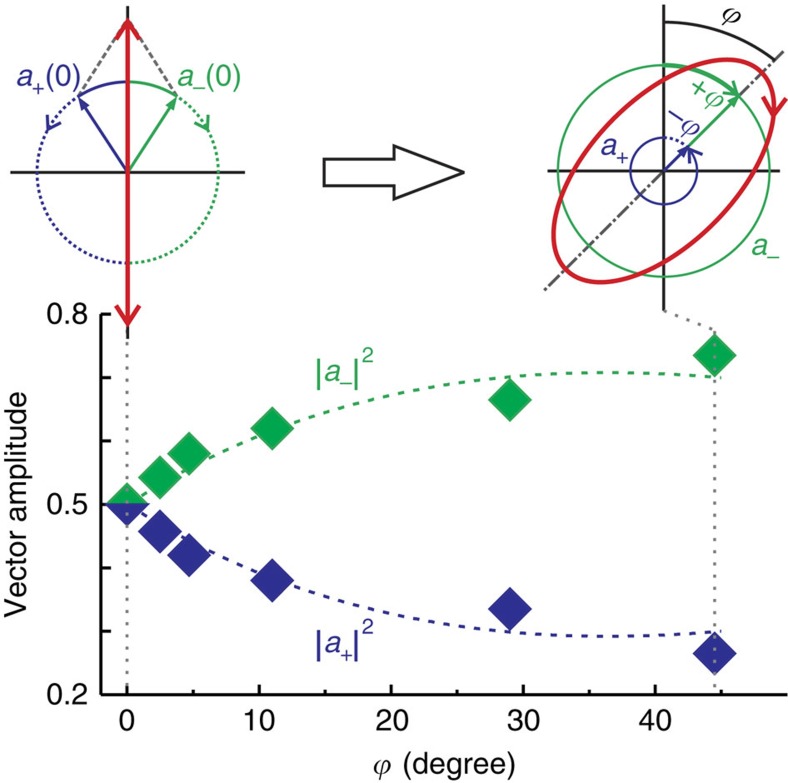
In contrast to previous reports on optical spin–orbit coupling3,7,8, where the right and left handed circular polarization bases are often spatially separated, here we do not observe such a spatial separation of the spin components, but rather an amplitude conversion between basis vectors during the evolution, as discussed above. This process is systematically shown in Fig. 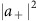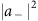4 by comparing the variation of the squared moduli of the coefficients Inline graphic and Inline graphic accompanied by the tilt angle ϕ. In the measured elliptical polarization curves, the maximum intensity represents the sum of the two moduli squared 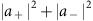Inline graphic, while the minimum represents the difference 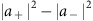Inline graphic. Based on the measured results, the respective squared amplitudes for the right 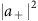Inline graphic and left 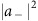Inline graphic circular components are extracted. The two squared vector amplitudes vary in an opposite way and therefore result in the vector splitting of the spinning photons in a Hilbert space. The evolution traces of the two vector amplitudes agree well with the theoretical model of equation (7), as shown in Fig. 4.

Figure 4. Change in the magnitude of the polarization components.

Figure 4

Open in a new tab

Measured vector amplitudes of the right (a+) and left (a−) components with the concurrent geometric phase ϕ. The evolution traces agree well with the theoretical model in equation (7) (dashed curves). Top panel shows (left) a linear polarization comprised of in-phase rotating right and left circular polarization components, and (right) geometric phase +ϕ (shown with bold green arc) acquired for a− and −ϕ (shown with dotted blue arc) acquired for a−.

Discussion

In a previous report, light propagating around a dielectric microsphere cavity was used to mimic the effect of gravitational lensing35. Furthermore, the analogy between a static gravitational field and an anisotropic medium has been utilized to realize a spin–Hall effect triggered by gravitational field36. In this sense, our asymmetric microtube cavity could provide an effective analogue for the laboratory study of the light evolution in a gravitational field. Moreover, in WGM microcavities light is confined in a small volume. This avoids a large space required in the previously reported open light-path systems3,29, and is therefore attractive for integrating photonic applications on a chip. This finding may motivate the search for many novel applications, such as those for on-chip quantum information technologies, or exploiting interactions of light with chiral molecules37.

Our work shows that the non-cyclic geometric phase and the mode conversion for degenerate photon systems, in a non-Abelian evolution, can be readily demonstrated in a compact optical microtube cavity. The cone-like asymmetric optical microcavities establish an ideal platform to realize spin–orbit coupling for the examination of non-trivial topological effects in the context of a non-Abelian evolution. In our microtube structures, the geometric phase can be directly measured by simply monitoring the polarization tilt angles, while the eccentricities indicate the mode conversion between the right and left circular bases. Geometric phase and amplitude variations of components in the circular polarization basis reveal essential physical processes in a non-Abelian evolution, which is of interest for both fundamental and applied physics.

Methods

Microtube preparation

In our experiment, tubular microcavities were prepared by rolling-up pre-strained nanomembranes30,38,39. The cone-like microtubes were self-assembled by curling up a circularly patterned SiOx/SiO2 bilayer nanomembrane on a silicon substrate30, forming an asymmetric microtube. After roll-up, a 30-nm-thick hafnium oxide film was grown on the microtube surface using atomic-layer-deposition. The tube is around 7 μm in diameter with a wall thickness of about 100 nm. The tube length is 45 μm and the polarization states were measured at the larger-diameter-end, where high-Q resonant modes exist30. All high-Q resonant modes in an asymmetric tube exhibit the same output polarization state.

Optical measurements

The optical polarization analyzer consists of a fixed polarization beam splitter in front of a spectrometer detector and an assisted rotatable half wave plate. The microtubular cavities are measured using a laser confocal microscope (50 × ), by which the excitation laser beam (at 532 nm) is focused at an area of 1 μm2 on the tube wall. The emission signal is collected through the same objective and then sent to the polarization analyzer. The initial orientation of the polarization beam splitter and half wave plate is calibrated by a predefined linearly polarized light, where the polarization orientation is set parallel to the tube axis. In the measurements, the eccentricities as well as the major axis orientation of the emission light polarizations are revealed by rotating the half wave plate (in a step of 2°).

Additional information

How to cite this article: Ma, L. B. et al. Spin–orbit coupling of light in asymmetric microcavities. Nat. Commun. 7:10983 doi: 10.1038/ncomms10983 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-8, Supplementary Notes 1-6 Supplementary References.

ncomms10983-s1.pdf (962.1KB, pdf)

Acknowledgments

The authors gratefully acknowledge V. Bolaños and S. Kumar for experimental assistance and M. Daghofer for fruitful discussions. This work was supported by the Volkswagen Foundation (I/84072), the U.S. Air Force Office of Scientific Research MURI program under grant FA9550-09-1-0550 and the DFG priority program FOR 1713. S.L.L. thanks the financial support from China Scholarship Council (CSC, file no. 2008617109). Y.Y. thanks the financial support from China Scholarship Council (CSC, file no. 201206090008). M.R.J thanks the Alexander von Humboldt Foundation for financial support. L.B.M. thanks the support from National Science Foundation of China (NSFC) with the grant no. 11104343.

Footnotes

Author contributions L.B.M. and O.G.S. had the idea for this experiment; L.B.M. prepared the samples; L.B.M. and S.L.L. performed the measurements and analyzed the data; M.H. and J.B.G. provided theoretical support on optical spin–orbit coupling, which culminated in the model to explain the observed phenomenon formulated by L.B.M., S.L.L. Y.Y. and V.M.F.; L.B.M. drafted the manuscript with the assistance of O.G.S., M.H., J.B.G., M.R.J. and V.M.F.

References

  1. Berry M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. London Ser. A 392, 45–57 (1984). [Google Scholar]
  2. Berry M. V. Interpreting the anholonomy of coiled light. Nature 326, 277–278 (1987). [Google Scholar]
  3. Bliokh K. Y., Niv A., Kleiner V. & Hasman E. Geometrodynamics of spinning light. Nat. Photon 2, 748–753 (2008). [Google Scholar]
  4. van Enk S. J. Geometric phase, transformations of gaussian light beams and angular momentum transfer. Opt. Commun. 102, 59–64 (1993). [Google Scholar]
  5. Souza C. E. R., Huguenin J. A. O., Milman P. & Khoury A. Z. Topological phase for spin-orbit transformations on a laser beam. Phys. Rev. Lett. 99, 160401 (2007). [DOI] [PubMed] [Google Scholar]
  6. Bliokh K. Y., Rodriguez-Fortuno F. J., Nori F. & Zayats A. V. Spin-orbit interactions of light. Nat. Photon 9, 796–808 (2015). [Google Scholar]
  7. Hosten O. & Kwiat P. Observation of the spin Hall effect of light via weak measurements. Science 319, 787–790 (2008). [DOI] [PubMed] [Google Scholar]
  8. Yin X., Ye Z., Rho J., Wang Y. & Zhang X. Photonic spin Hall effect at metasurfaces. Science 339, 1405–1407 (2013). [DOI] [PubMed] [Google Scholar]
  9. Shapere A. & Wilczek F. Geometric Phase in Physics Vol. 5, , pp 45–104 (World Scientific (1989). [Google Scholar]
  10. Hsieh D. et al. Observation of Unconventional Quantum Spin Textures in Topological Insulators. Science 323, 919–922 (2009). [DOI] [PubMed] [Google Scholar]
  11. Milman P. & Mosseri R. Topological phase for entangled two-qubit states. Phys. Rev. Lett. 90, 230403 (2003). [DOI] [PubMed] [Google Scholar]
  12. Du J., Zhu J., Shi M., Peng X. & Suter D. Experimental observation of a topological phase in the maximally entangled state of a pair of qubits. Phys. Rev. A 76, 042121 (2007). [Google Scholar]
  13. Wilczek F. & Zee A. Appearance of gauge structure in simple dynamical systems. Phys. Rev. Lett. 52, 2111–2114 (1984). [Google Scholar]
  14. Zak J. Berry's geometrical phase for noncyclic hamiltonians. Europhys. Lett. 9, 615 (1989). [Google Scholar]
  15. Garcia de Polavieja G. Noncyclic geometric phase shift for quantal revivals. Phys. Rev. Lett. 81, 1–5 (1998). [Google Scholar]
  16. Wagh A. G., Rakhecha V. C., Fischer P. & Ioffe A. Neutron interferometric observation of noncyclic phase. Phys. Rev. Lett. 81, 1992–1995 (1998). [Google Scholar]
  17. Abdumalikov A. A. Jr et al. Experimental realization of non-Abelian non-adiabatic geometric gates. Nature 496, 482–485 (2013). [DOI] [PubMed] [Google Scholar]
  18. Bliokh K. Y., Frolov D. Y. & Kravtsov Y. A. Non-Abelian evolution of electromagnetic waves in a weakly anisotropic inhomogeneous medium. Phys. Rev. A 75, 053821 (2007). [Google Scholar]
  19. Tomita A. & Chiao R. Y. Observation of Berry's topological phase by use of an optical fiber. Phys. Rev. Lett. 57, 937–940 (1986). [DOI] [PubMed] [Google Scholar]
  20. Vahala K. J. Optical microcavities. Nature 424, 839 (2003). [DOI] [PubMed] [Google Scholar]
  21. Chiao R. Y. & Wu Y.-S. Manifestations of Berry's topological phase for the photon. Phys. Rev. Lett. 57, 933–936 (1986). [DOI] [PubMed] [Google Scholar]
  22. Bolaños Quiñones V. A. et al. Optical resonance tuning and polarization of thin-walled tubular microcavities. Opt. Lett. 34, 2345–2347 (2009). [DOI] [PubMed] [Google Scholar]
  23. Tanda S. et al. Crystal topology: A Mobius strip of single crystals. Nature 417, 397–398 (2002). [DOI] [PubMed] [Google Scholar]
  24. Marrucci L., Manzo C. & Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006). [DOI] [PubMed] [Google Scholar]
  25. Nye J. F. & Berry M. V. Dislocations in wave trains. Proc. R. Soc. Lond. A 336, 165–190 (1974). [Google Scholar]
  26. Souza C. E. R., Huguenin J. A. O. & Khoury A. Z. Topological phase structure of vector vortex beams. J. Opt. Soc. Am. A 31, 1007–1012 (2014). [DOI] [PubMed] [Google Scholar]
  27. Galvez E. J. et al. Geometric phase associated with mode transformations of optical beams bearing orbital angular momentum. Phys. Rev. Lett. 90, 203901 (2003). [DOI] [PubMed] [Google Scholar]
  28. Ballon D. J. & Voss H. U. Classical möbius-ring resonators exhibit Fermion-Boson rotational symmetry. Phys. Rev. Lett. 101, 247701 (2008). [DOI] [PubMed] [Google Scholar]
  29. Chiao R. Y. et al. Observation of a topological phase by means of a nonplanar Mach-Zehnder interferometer. Phys. Rev. Lett. 60, 1214–1217 (1988). [DOI] [PubMed] [Google Scholar]
  30. Bolaños Quiñones V. A., Ma L., Li S., Jorgensen M., Kiravittaya S. & Schmidt O. G. Enhanced optical axial confinement in asymmetric microtube cavities rolled up from circular-shaped nanomembranes. Opt. Lett. 37, 4284–4286 (2012). [DOI] [PubMed] [Google Scholar]
  31. Ma L. B., Schmidt T., Jäger C. & Huisken F. Evolution of multiple-peak photoluminescence of Ge-doped silicon oxide nanoparticles upon thermal annealing. Phys. Rev. B 82, 165411 (2010). [Google Scholar]
  32. Sjöqvist E. et al. Geometric phases for mixed states in interferometry. Phys. Rev. Lett. 85, 2845–2849 (2000). [DOI] [PubMed] [Google Scholar]
  33. Weinfurter H. & Badurek G. Measurement of Berry's phase for noncyclic evolution. Phys. Rev. Lett. 64, 1318–1321 (1990). [DOI] [PubMed] [Google Scholar]
  34. Filipp S., Hasegawa Y., Loidl R. & Rauch H. Noncyclic geometric phase due to spatial evolution in a neutron interferometer. Phys. Rev. A 72, 021602 (2005). [Google Scholar]
  35. Sheng C., Liu H., Wang Y., Zhu S. N. & Genov D. A. Trapping light by mimicking gravitational lensing. Nat. Photon 7, 902–906 (2013). [Google Scholar]
  36. Gosselin P., Bérard A. & Mohrbach H. Spin Hall effect of photons in a static gravitational field. Phys. Rev. D 75, 084035 (2007). [Google Scholar]
  37. Tang Y. & Cohen A. E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 332, 333–336 (2011). [DOI] [PubMed] [Google Scholar]
  38. Schmidt O. G. & Eberl K. Nanotechnology: Thin solid films roll up into nanotubes. Nature 410, 168–168 (2001). [DOI] [PubMed] [Google Scholar]
  39. Prinz V. Y. et al. Free-standing and overgrown InGaAs/GaAs nanotubes, nanohelices and their arrays. Physica E 6, 828–831 (2000). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-8, Supplementary Notes 1-6 Supplementary References.

ncomms10983-s1.pdf (962.1KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES