TIPR: transcription initiation pattern recognition on a genome scale

Abstract

Motivation: The computational identification of gene transcription start sites (TSSs) can provide insights into the regulation and function of genes without performing expensive experiments, particularly in organisms with incomplete annotations. High-resolution general-purpose TSS prediction remains a challenging problem, with little recent progress on the identification and differentiation of TSSs which are arranged in different spatial patterns along the chromosome.

Results: In this work, we present the Transcription Initiation Pattern Recognizer (TIPR), a sequence-based machine learning model that identifies TSSs with high accuracy and resolution for multiple spatial distribution patterns along the genome, including broadly distributed TSS patterns that have previously been difficult to characterize. TIPR predicts not only the locations of TSSs but also the expected spatial initiation pattern each TSS will form along the chromosome—a novel capability for TSS prediction algorithms. As spatial initiation patterns are associated with spatiotemporal expression patterns and gene function, this capability has the potential to improve gene annotations and our understanding of the regulation of transcription initiation. The high nucleotide resolution of this model locates TSSs within 10 nucleotides or less on average.

Availability and implementation: Model source code is made available online at http://megraw.cgrb.oregonstate.edu/software/TIPR/.

Contact: megrawm@science.oregonstate.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Transcription start sites (TSSs) and their associated promoter regions play a critical role in the transcription of genes by RNA Polymerase II. However, the mechanisms by which transcription is initiated at specific genomic locations is still not fully understood, including how the spatial distribution of TSSs is defined, how promoter architecture influences this spatial pattern, and how genes lacking canonical elements within the core promoter are transcribed. The advent of high-throughput TSS sequencing (TSS-Seq) protocols such as Cap Analysis of Gene Expression (CAGE) and Paired End Analysis of Transcription start sites (PEAT) have transformed the field of promoter analysis, providing genome-wide nucleotide-resolution information on TSS usage (Carninci et al., 2005; Ni et al., 2010). One important goal in this field is the identification of TSS locations when TSS-Seq data is unavailable. While start codons are easily identified, the length of the 5′ untranslated region (5′ UTR) upstream of the first exon varies from gene to gene and even between transcripts of the same gene, yielding different mRNA products. Several studies have taken computational approaches to TSS identification, building machine learning models that predict the location of TSSs from the surrounding sequence content with varying degrees of success and resolution, ranging from the prediction at the level of individual nucleotides to regions up to 500 nt wide (Abeel et al., 2009; de Boer et al., 2014; Knudsen, 1999; Megraw et al., 2009; Morton et al., 2014; Ohler et al., 2000; Sonnenburg et al., 2006; Zhao et al., 2007).

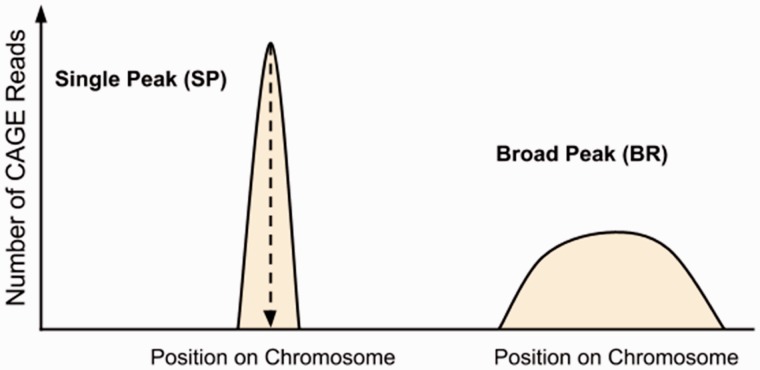
The mRNA products produced during the transcription of genes typically do not all initiate at a single genomic location. Instead, transcription initiates upstream of the gene’s start codon in a region that can range from very narrow (2—3 nt) to wide (upwards of 50 nt or more), forming a collection of individual TSSs known as a TSS cluster or transcription start region (TSR) (Carninci et al., 2006; Ni et al., 2010; Rach et al., 2009). TSS clusters can be grouped by the shape of their positional distribution—that is, the transcription initiation pattern—of individual TSSs that defines the cluster (Fig. 1). In this study, we focus on the single peak (or narrow peak) and broad peak (or weak peak) patterns defined in previous TSS-Seq studies (Carninci et al., 2006; Ni et al., 2010). Previous studies have shown that different initiation patterns are associated with different types of genes, tissues and regulatory mechanisms such as transcription factors (TFs) and CpG islands (Ohler and Wassarman, 2010; Sandelin et al., 2007; Morton et al., 2014). While there has been success in the identification of single peak initiation patterns (Megraw et al., 2009), it has remained unclear whether other initiation patterns can be predicted from sequence content alone at the same nucleotide-level resolution. Models incorporating additional data types such as histone modifications have had success in the prediction of these less well-defined patterns (Rach et al., 2011), though prediction of broadly distributed patterns is still clearly a greater challenge. An analysis of 17 TSS prediction models found that these broad patterns could be predicted with low resolution (500 nt) from sequence content alone but did not explore nucleotide-resolution models (Abeel et al., 2009).

Fig 1.

Transcription initiation patterns recognized by TIPR. The TSR initiation patterns predicted by TIPR, and introduced by Carninci et al. (2006), as identified in genome-wide mouse and human CAGE studies

In this work, we present a machine learning model capable of predicting TSSs of multiple initiation patterns with high performance and positional resolution, while also suggesting the probable initiation pattern that the TSS cluster would form along the chromosome. The transcription initiation pattern recognition (TIPR) model utilizes features derived from sequence content and TF binding affinity to predict the probability of transcription initiation at an individual nucleotide. Because this model provides both nucleotide resolution and initiation pattern prediction, the model can be used to address a wide variety of topics, including a better understanding of promoter architecture, improved gene finding and annotations, identification of TFs which could be involved in the regulation of genes and positional information guiding wet-laboratory experiments. We evaluate the TIPR model using a publicly available high-throughput TSS-Seq dataset from mouse (Carninci et al., 2006), where it performs well, achieving area under the receiver operating characteristic curve (AUROC) of 0.99 and area under the precision-recall curve (AUPRC) of 0.82. TIPR uses only sequence information in predicting the location and type of TSS initiation patterns and is therefore applicable in cases where TSS-Seq data are not yet available.

2 Methods

2.1 Overview of TIPR pipeline

Our TSS prediction pipeline begins with the creation of a dataset containing the genomic locations of TSSs identified by high-throughput TSS-Seq protocols. We have focused on TSS-Seq based data, as a previous study showed that, even in the well-annotated Arabidopsis genome, gene annotations alone were insufficient to construct a highly accurate TSS prediction model (Morton et al., 2014). In this analysis, we have restricted our model to the prediction in protein coding genes, due to the limited knowledge regarding differences in the promoter structures of other gene products (Alam et al., 2014). We restrict our analysis to TSSs that are located no further than 500 nt upstream of a protein-coding gene’s annotated 5′ UTR. TSS tag clusters (spatially grouped TSS-Seq reads) are next filtered by read count, ensuring that only commonly transcribed TSSs are used to build the model. After filtering, TSS tag clusters are grouped by initiation pattern (single peak and broad peak, Fig. 1) into individual datasets. Finally, the mode of each tag cluster (the nucleotide where transcription most frequently initiates within the cluster) is determined and used as a single representative genomic location for the tag cluster. Additional specifics on the filtering, clustering and initiation pattern annotation process are provided in Carninci et al. (2006), where the dataset was originally published.

After the set of TSS tag clusters are created, 5 kb of genomic sequence is extracted upstream and downstream of each tag cluster mode. The sequences are converted into numerical features representing the presence of DNA regulatory sequences—including TF binding sites (TFBSs) and TATA-binding protein associated sites—in regions where they are likely to be functional and involved in recruitment of transcription machinery. In this work, we use TFBSs as a general term for all vertebrate binding sequences described by the TRANScription FACtor (TRANSFAC) database (Wingender, 2008). These include both TFBSs and TATA-binding protein associated (TAF) site sequences. In addition to positive examples (locations where transcription initiates), negative examples (locations with no evidence of transcription initiation) are selected by randomly choosing locations from genic, intergenic and promoter-proximal regions.

Multiple logistic regression classifiers are constructed during the training and evaluation of TIPR (Table 1). We train three classifiers to construct the TIPR model capable of predicting TSS locations and initiation patterns simultaneously, along with an additional independent model as part of the model evaluation and comparison process, which is described in detail in Section 2.4. Models are constructed using a modified version of the l1_logreg package, an implementation of the interior-point method for L1-regularized logistic regression (Koh et al., 2007). The l1_logreg package has been modified to support a more compact file format, and modifications are provided in the Supplementary Data. Cross-validation is used to select the TIPR model parameters. The optimal L1 penalty parameter λ is chosen by finding the λ value that yields the highest AUROC for each validation partition, and computing the average of this set of partition-specific values. This averaged λ value is used to train a final model using all training examples. A second parameter d is selected for each model on a secondary held-out validation partition by F1 score. This parameter is the probability threshold used to determine the class label prediction of a model. After parameter selection, final models of each type are constructed using the entire training dataset with the optimal λ parameter.

Table 1.

List of binary classification models trained and tested in this study

Model name	Class 1	Class 2
SP versus NO	Single peak TSSs	Negative (non-TSS) genomic locations
BR versus NO	Broad peak TSSs	Negative (non-TSS) genomic locations
SP versus BR	Single peak TSSs	broad peak TSSs
SP+BR (All)a	SP and BR TSSs	Negative (non-TSS) genomic locations

^aUnused by MSC classifier but used for baseline comparison.

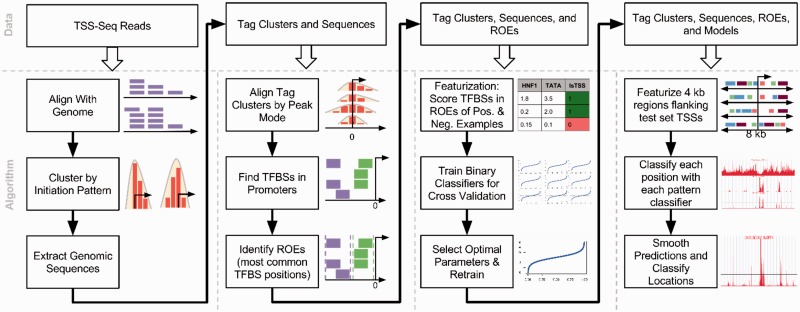
Finally, each model is evaluated by classifying examples from a held-out test set, composed of 20% of all examples in each dataset (including negative examples described above) and an additional 100 000 negative examples drawn randomly from the entire genome. After the models in Table 1 have been trained and used to predict all test set TSSs (Section 2.4), we arrive at the multi-stage classifier (MSC), capable of predicting TSS locations and initiation patterns. In the final MSC model (evaluated in Section 2.5), the SP versus BR classifier is used to predict the expected initiation pattern of a site that has been predicted as transcribed. This process can be applied on a genomic scale by repeating this prediction process at every nucleotide in the region of interest, producing a signal along the chromosome representing the probability of transcription initiation at each nucleotide. Figure 2 shows a flow chart summarizing our TSS prediction data preparation pipeline and classification process.

Fig 2.

Flowchart of TIPR training procedure

2.2 Identification of regions of enrichment

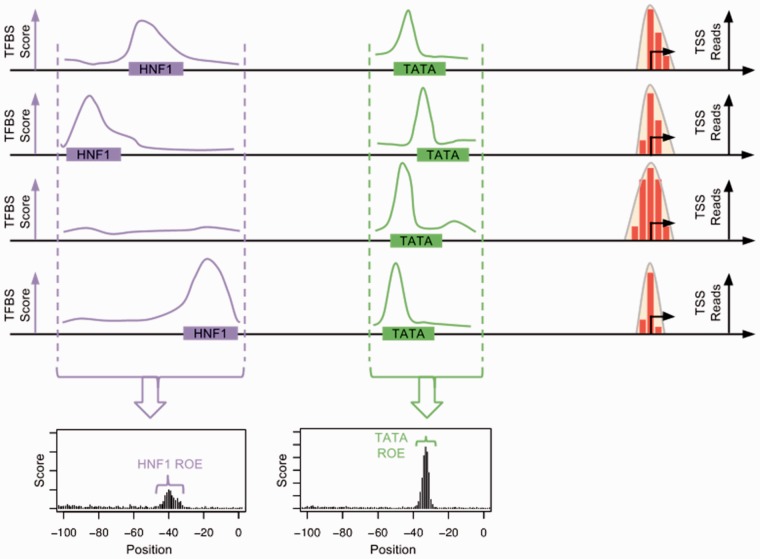
In this study, TFBSs are characterized by experimentally supported positional weight matrices (PWMs) curated by the TRANSFAC project (Wingender, 2008). A PWM approximates the affinity of each TF binding domain for potential DNA binding sequences. Because TFBSs are often short, degenerate sequences, they occur frequently throughout the genome for many TFs. Even if we assume that TF binding does occur at every TFBS location in the genome, a majority of this binding almost certainly does not lead to transcription. For example, the TATA box site is typically located in a window 25–35 bp upstream of the TSS, where it binds to the TFIID protein, forming a multi-protein complex which binds to the Pol-II complex and initiates transcription. If a TATA box binding site is observed hundreds of base pairs upstream from a TSS, it is unlikely that this TATA site is involved in the transcription of this TSS. Therefore, as part of our training process, we computationally identify regions of the promoter in which each TFBS in our dataset is likely to be functional. This procedure specifically focuses our model on TFBSs located in regions of the promoter where they are likely to be involved in transcription, as opposed to including every TFBS in the surrounding sequence regardless of location. We call these locations ‘regions of enrichment’ (ROEs), as an ROE is defined by our model to be a region positioned relative to training-set TSSs in which a particular TFBS is significantly enriched in a majority of training set TSSs when compared with the promoter background sequence distribution (Fig. 3). Our machine learning analysis is restricted to TFBSs which fall within these regions. This technique has two major advantages. First, it serves as a feature reduction technique, enabling faster model training and testing. Second, it allows the model to identify features which are more likely to be biologically relevant.

Fig. 3.

Diagram of how ROEs are identified from raw TSS-Seq reads

To identify the ROE associated with each PWM and determine if enrichment of a particular TFBS is present, we consider all TSS tag clusters grouped by TSS initiation pattern. TFBS PWMs are scanned along regions 2 kb upstream and downstream of the TSS, and the likelihood score of the TFBS at every nucleotide is computed and compared to the promoter background distribution. The dinucleotide background distribution is computed with a local first-order Markov model, computed over the sequence 250 nt upstream and downstream of the TSS. Scores are computed using a modified version of the log-likelihood scanner published and described in Morton et al. (2014). The software has been modified to use a more efficient binary storage format for performance and is provided in supplementary materials. All positive log-likelihood scores are combined and averaged into a single score at each nucleotide. Starting from the highest scoring nucleotide within 100 nt of the TSS, the ROE is expanded left and right until the average log-likelihood score falls below the average log-likelihood score of the promoter (within 2 kb of the TSS) for at least 5 nt. This region represents the most common positions in which the TFBS of a particular TF occurs relative to the TSS. During feature extraction and prediction, only TFBSs that fall within the ROE are considered by the TIPR model. Figure 3 shows a diagram of this process. Additional details of this procedure are provided in supplementary methods: ROE Identification.

2.3 Model feature extraction

After TSS tag clusters have been identified from the TSS-Seq data and ROE have been defined, we convert the DNA sequence surrounding TSSs into numerical features for the purpose of model training and evaluation (Supplementary Fig. S1). These numerical features characterize the presence of TFBSs within ROEs. Within the defined ROE of a given TFBS, the log-likelihood score of the TFBS PWM (with respect to the promoter dinucleotide background distribution) is calculated at every nucleotide within the ROE and summed together to produce a single numerical score. This score is therefore large when the ROE contains sequences which closely match the TFBS of the given TF, and small otherwise. In order to increase the resolution of the features and allow the model to select the most informative locations, each ROE is split into 7 sub-regions of equal length, 5 central overlapping windows and 2 flanking windows (Megraw et al., 2009, Fig. 3). In addition, sequence enrichments for GC, GA and CA dinucleotides surrounding the TSS are included as features. Sequence enrichment features are computed as the frequency of the given nucleotides as a proportion of region 250 nt upstream and downstream of the TSS.

The ROEs used to construct the ALL model were computed by combining the SP and BR TSS datasets together before performing ROE selection. The specialized SP and BR models listed in Table 2 are constructed using ROEs selected only from TSSs of a single initiation pattern. For the sub-models of the TIPR model used to predict initiation pattern, ROE selection was performed on individual initiation pattern datasets, and the resulting ROEs from each dataset were combined together. This was done because initiation patterns appear to have differing preferred locations for TFBSs relative to the TSS. On average, these ROEs are fairly narrow—the median width of the ROEs used by the ALL model was 56 nt with a standard deviation of 36 nt (Supplementary Table S1). A previous study suggested that in Arabidopsis, wider, more general ROEs were less effective TSS predictors than peak-type specific ROEs calculated from accurate TSS-Seq data (Morton et al., 2014).

Table 2.

CAGE datasets used to train and test TIPR model

Initiation pattern	Total Tag clusters	Training tag clusters	Testing tag clusters
Single peak	1247 (33%)	998	249
Broad peak	2497 (66%)	1998	499
All	3744 (100%)	2996	748

Negative training and testing datasets are created as mentioned earlier, but rather than using TSS-proximal sequences, they are composed of randomly selected genomic locations at which there is no evidence of transcription initiation. In order to create a model that performs with high sensitivity and specificity at any nucleotide in the genome, the model must differentiate between true TSSs and nearby sequences that are not transcribed but which have similar sequence content. To ensure the model training and testing sets support this goal, we select 20 negative examples for every positive TSS example; these are drawn from genomic locations located 200–2000 nt upstream of the TSS. In addition, we also draw one negative example from exonic and intergenic regions for every positive example in the training set. This yields a proportion of 21 negative training examples for every positive training example. Finally, an additional 100 000 negative examples are drawn randomly from the entire genome and used for testing.

2.4 Model construction

After feature extraction, the TIPR model is constructed by training the four models listed in Table 1 independently, using 80% of the dataset. Eighty percent of each cross-validation fold is used for model training, 10% for regularization parameter (λ) selection and the remaining 10% for the classification threshold parameter (d) selection. The regularization parameter λ is selected using the same procedure as the S-Peaker model (Megraw et al., 2009), by choosing the value which provides the highest AUROC on the validation partition of each fold. The average of these selected λ values is the penalty parameter used to construct the final model using all training data. The cutoff parameter d is selected by choosing the probability value which optimizes the classifier’s F1 score over the partition held out for selection of the parameter. The optimal λ of each fold is used when selecting d, ensuring that no example used to select d was used to choose λ. The optimal λ (and associated AUROC) of each cross-validation fold is provided in Supplementary Table S2.

After all parameters are selected and models have been built using the full 80% of the training data, the held-out testing data is classified by each model independently. After classification by the TSS models (SP versus No and BR versus No), a two-stage classification procedure is used to produce the final class label. If either of the TSS models predict that the site is likely to be transcribed (with a probability greater than the model’s parameter d), the SP versus BR model is used to predict the initiation pattern (SP or BR). We call this classifier the MSC model, as it applies a hierarchical procedure for determining the appropriate classification models. This allows for more flexibility in the selection of probability cutoff thresholds by choosing a separate threshold for each model, compared with other multi-class prediction techniques such as All-versus-All models. Additional details on model construction, cross-validation, and parameter selection are provided in the supplementary data: Model Training and Selection of Model Parameters. During the development of TIPR, we tested several alternative multi-class prediction techniques, with the purpose of understanding which order and combination of the SP versus NO, BR versus NO, SP versus BR and ALL classifiers resulted in the best classifier performance. These techniques and their results are reported in the supplementary materials: Multi-class Prediction Models and Supplementary Results: Multi-class Prediction Models. In Section 3.1, we discuss the implications of these comparisons, their significance and when the ALL and MSC models should be applied.

2.5 Model evaluation and testing

We evaluate the TIPR model using a variety of metrics. For each binary classifier, the AUROC and AUPRC are calculated. We include auPRC because auROC does not account for precision (i.e. positive predictive value), which determines how many of the sites that were predicted to be a TSS were actually TSSs. The multi-class MSC classifier is evaluated on sensitivity, specificity and micro/macro F1 scores, reported in Section 3. In addition to standard numerical metrics, we evaluate the model in a more practical setting by predicting TSSs on a larger scale, using entire regions of the genome.

Although the model can be successfully applied to predict the probability that an individual nucleotide is a TSS, more commonly we wish to know of regions where transcription initiation is likely to occur. To evaluate the TIPR model on a practical scale, we tested the model on 4 kb regions upstream and downstream of TSSs in the held-out set. First, for each nucleotide in the surrounding 8 kb region features are generated as mentioned earlier. Next, nucleotides are classified as TSSs or non-TSSs using the general-purpose “All” model. After this signal is produced, it is smoothed using a moving average with a 2 nt window. After smoothing, predicted TSS regions are defined from this signal by locating regions where the probability value rises above a threshold. A TSS region begins when the signal rises above the probability threshold and ends after the signal has fallen below the threshold for 10 consecutive nucleotides.

The earlier procedure was repeated using a range of probability threshold values between 0.05—0.95. The distance between the center of the predicted TSS region and CAGE-supported TSS tag cluster mode were calculated, along with the number of correctly predicted TSSs (true positives) and additional positive predictions (false positives). A region was considered to be a true positive if the predicted region contained a CAGE-supported TSS tag cluster mode.

3 Results

3.1 TIPR successfully predicts broad initiation patterns

Previous high-resolution TSS prediction models focused primarily on the prediction of single peak TSS initiation patterns (Megraw et al., 2009), reasoning that these promoters are likely more tightly regulated by specific TFs, as opposed to non-sequence mechanisms such as histone markers and chromatin structure (Rach et al., 2011). We trained and tested the TIPR model on multiple initiation patterns, using the CAGE mouse dataset (Carninci et al., 2006), filtered as described in Section 2. The training and testing sets used are shown in Table 2.

Our results show that our model can predict initiation patterns beyond the single peak class with high accuracy (both high AUROC and AUPRC) from sequence content alone (Table 3, Supplementary Figs S2 and S3). The models trained on a dataset containing TSSs of a single initiation pattern perform well in classifying TSSs of their respective types, meaning that the model describes a set of TFBS enrichments which well characterize the initiation pattern used to build and test the model. Because L1-regularized logistic regression models weight features by their predictive power, these weights can be used to infer the TFs that may regulate different initiation patterns and families of genes. Feature weights from all four models are provided in Supplementary Table S3.

Table 3.

Performance of TIPR’s three binary TSS classifiers and S-Peaker in mouse, tested using classes listed in Table 1

Dataset	TIPR AUROC	TIPR AUPRC	S-Peaker AUROC	S-Peaker AUPRC
Single peak versus NO	0.99	0.72	0.99	0.66
Broad peak versus NO	0.99	0.81	0.99	0.76
SP + BR (ALL) versus NO	0.99	0.82	0.99	0.70

While the individual initiation pattern classifiers perform well on their respective datasets, a general purpose classifier is required for the prediction of TSSs without prior knowledge of the initiation pattern. When the SP versus No TSS model is used to classify the BR versus No TSS testing set, the AUPRC drops to 0.51, compared with 0.72 when tested on the SP versus No set. Similarly, the BR versus No TSS model achieves an AUPRC of 0.59, compared with 0.81 when predicting Broad initiation patterns (Supplementary Figs S4–S7). Both the general classifiers constructed in this study (ALL and MSC) performed well at the task of general TSS identification. The ALL model, trained on the combination of both single peak and broad initiation patterns, forms a general-purpose TSS prediction model. Due to this model’s simplicity, it is useful for the task of predicting TSSs when the spatial initiation pattern is of little interest to the user. The more complex MSC classifier functions as a general-purpose TSS prediction model, it also provides specific spatial initiation pattern predictions with the same predictive accuracy as the ALL classifier.

As a comparison, an S-Peaker model (Megraw et al., 2009) was trained and tested on the same dataset used to build the TIPR models (with the same individual TSSs used to train and test both models). Both models achieve approximately the same AUROC, but TIPR outperforms S-Peaker by 5–12% on AUPRC depending on the dataset. This increase in AUPRC means that the TIPR model is capable of achieving higher precision (positive predictive value) while also maintaining high sensitivity compared with S-Peaker (Supplementary Figs S2, S3 and S8–S17).

Next, we applied the TIPR model to the prediction of human TSSs as a comparison to the epigenetic model described in Rach et al. (2011). Rach et al. (2011) used sequence features (like TIPR) along with chromatin features to predict TSSs in human and was constructed using TSSs identified from CAGE data provided by the FANTOM4 consortium (Kawaji et al., 2009). We trained the TIPR model using the same dataset that was used in Rach et al. (2011) to construct the epigenetic chromatin-based model. The results of this comparison are provided in Table 4 and Supplementary Figures S18–S21. Additional details on the construction of this model are provided in the supplementary materials. These results show that TIPR is able to predict both single peak and broad peak promoters in human with the same (or better) performance without the use of chromatin-based features.

Table 4.

Comparison of TIPR and Rach et al. (2011) in human

Initiation pattern	TIPR		Rach et al.
	AUROC	AUPRC	AUROC	AUPRC
Single peak	0.95	0.30	0.80	0.01
Broad peak	0.99	0.82	0.99	0.79

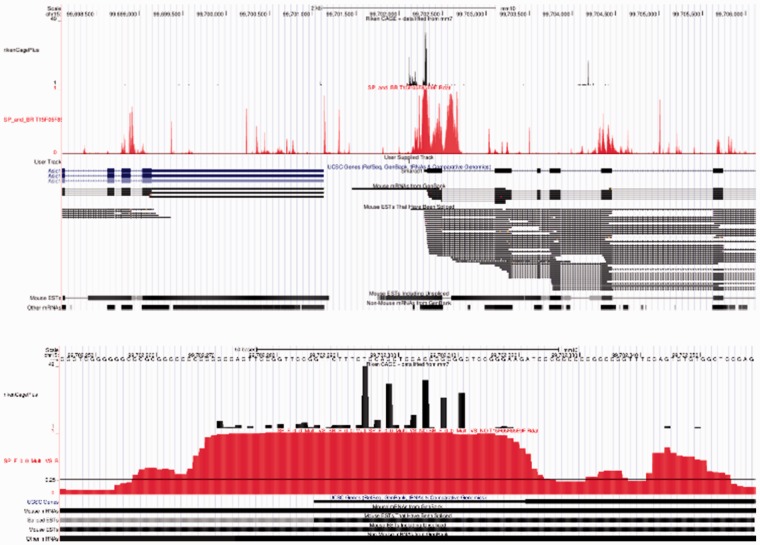
As transcription of a gene typically initiates at many locations within a genomic region—as opposed to one single location at a specific nucleotide—a successful model must predict these regions with high resolution and precision. To evaluate the performance of our model in this context, we performed a scanning procedure where the model was used to predict the probability of a TSS at each nucleotide within an 8 kb region containing an experimentally observed TSS tag cluster. A representative example of this scanning procedure is shown in Figure 4.

Fig 4.

Example of TIPR gene scan on 8 kb region of sequence. This figure shows the TIPR ALL model used to predict TSSs in the 8 kb region (top) and 100 nt region (bottom) surrounding the gene Smarcd1. The top track (black) displays the alignment of TSS-Seq (CAGE) reads along chromosome 15 of the M. musculus genome (CAGE tag cluster T15F05F85E9F). The second track (in red) is the probability output from the TIPR ALL model. The expanded track below the TIPR shows that Mouse ESTs align well with TIPR’s predictions. Some additional TIPR predictions are located near other CAGE tag clusters or ESTs

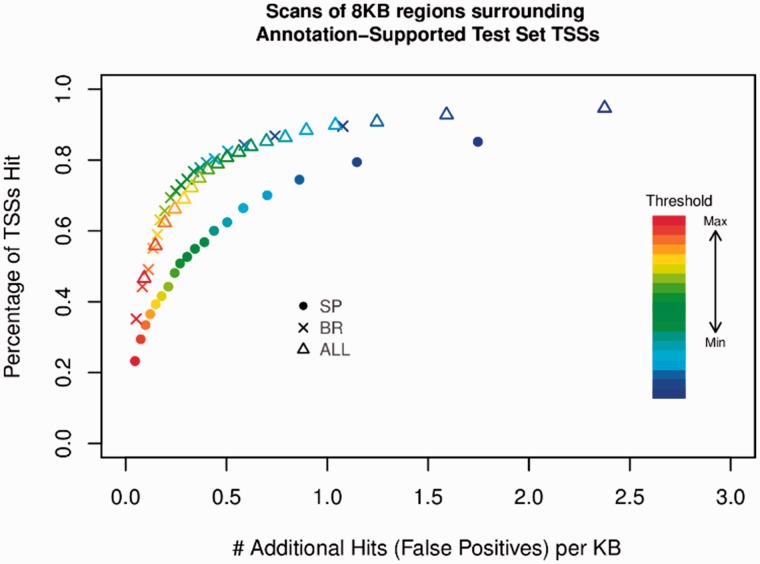
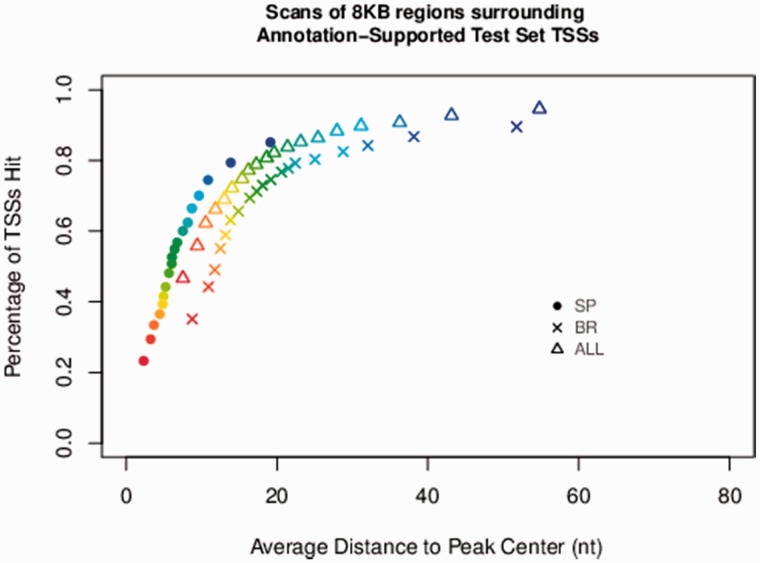
After smoothing of the probability signal output by the model, we evaluated performance on two metrics: the number of TSSs predicted at a given probability threshold compared with the number of false positives (Fig. 5) and the distance between the predicted and ground-truth TSS locations (Fig. 6). These results show that the generic ALL models can identify TSS clusters with high accuracy regardless of initiation pattern. This also demonstrates the performance of the SP versus NO and BR versus NO classifiers, and how the ALL classifier performs better overall than either of these specialized classifiers. The SP classifier curve (diamond, Fig. 5) falls below all other models, meaning that this model identifies fewer true positives. SP initiation patterns are less common overall, as expected, because the SP classifier is trained to identify only single peak patterns, whereas a majority of the dataset is composed of BR TSS tag clusters. On the other hand, Figure 6 shows that the SP classifier is more accurate in terms of locating the position of TSSs. The broad initiation pattern classifier identifies TSSs with roughly the same accuracy as the ALL model, but the locational accuracy of the BR model is slightly reduced. Particularly important to the scanning performance of all classifiers is the achievement of a strong AUPRC, because genomic sequence is overwhelmingly composed of true negatives (locations that are not TSSs). Models with outstanding AUROC can still yield a relatively noisy scanning signal outcome on the genome that doesn’t ‘narrowly capture’ true TSS regions if AUPRC is poor; this is because true negatives are strongly reflected in precision score (where false positives sit in the denominator). TIPR’s scanning performance achievement is due in large part to its ability to effectively identify true negative examples, as reflected in its strong AUPRC scores.

Fig 5.

Performance of all classifiers during gene scanning. The accuracy of all classifiers when applied on a large scale to the entire testing dataset. The vertical axis shows the percentage of TSSs in the test set which are correctly predicted (TSSs). The horizontal axis measures the number of additional TSSs which are predicted (false positives). The color scale shows the probability cutoff threshold, the value the model prediction must be above to be considered a TSS

Fig 6.

Locational accuracy of all classifiers during gene scanning. The location accuracy of all TSS classifiers, as quantified by the distance between the TSS tag cluster mode (experimentally supported ground truth data) and the center of the predicted tag cluster

3.2 TIPR predicts initiation pattern type

In addition to predicting the locations of TSSs from sequence content, our model predicts which initiation pattern the surrounding TSS cluster is likely to form. This is a more complex type of prediction, because the classifier must incorporate information that effectively considers an entire genomic region of nucleotides as possible TSSs. On a held-out test set composed of TSSs of both initiation patterns, the binary SP versus BR model achieves an average AUROC of 0.88 with an AUPRC of 0.84 when differentiating between the two patterns (Supplementary Figs S22–S23). We remind the reader that this model is combined with the TSS classifiers built on individual initiation patterns to produce the final multi-class MSC model. After applying the individual initiation pattern models to predict which genomic locations are transcribed, the SP versus BR model is used to predict the initiation patterns of the sites in question. The performance of the MSC model in the multi-class prediction context is summarized in the confusion matrix provided in Table 5, with additional performance metrics provided in Supplementary Table S4. Evaluated using the macro-F1 statistic to adjust for the prevalence of negatives in this classification problem, the MSC classifier achieves a score of 0.74. The ROC and Precision-Recall Curve (PRC) plots of the individual binary classifiers which build the MSC model are provided in Supplementary Figures S8–S11. Complete confusion matrices and other statistics for each model are provided in Supplementary Table S5.

Table 5.

Confusion matrix of MSC model predictions

Prediction	Reference
	No TSS	Single peak	Broad peak
No TSS	115 145 (99.72%)	45 (18%)	72 (14%)
Single peak	145 (0.12%)	160 (64%)	55 (11%)
Broad peak	169 (0.14%)	44 (18%)	372 (75%)

While the MSC model performs no better than the simple ALL classifier on the single-nucleotide classification dataset, it does provide important additional information—the predicted spatial initiation pattern of the TSS. This extra information is highly relevant from a biological perspective, as initiation patterns have been shown to associate with different biological interpretations. Genes associated with single peak initiation patterns are often tissue-specific developmental genes, while genes with broad patterns are more commonly involved in general and housekeeping processes. The initiation pattern of a gene has been demonstrated to be related to the promoter structure of the gene, including the presence of TFBS elements, sequence enrichments including CpG islands in mammals and gene function (Carninci et al., 2006; Megraw et al., 2009; Morton et al., 2014; Rach et al., 2009).

3.3 Transcription initiation pattern classes yield insight into gene function

As previously reported in Megraw et al. (2009), single peak initiation patterns have many well-defined ROEs for TFs, as opposed to general sequence enrichments. These TF enrichments are much less pronounced in the broad initiation pattern, where only 312/843 TFBSs were detected as containing an ROE on the forward strand, compared with 511/843 in SP. The feature weights of the SP versus BR model can also provide insight into the TFs associated with each initiation pattern. The model’s highly weighted features are in agreement with factors previously associated with these initiation patterns, including TATA binding protein (TBP) for SP patterns and higher GC content for BR patterns (Sandelin et al., 2007). The model also suggests other associations, such as a predominance of binding sites for caudal type homeobox CDXA and cap signal (CAP) TFs in proximity to SP patterns and sites from the E2F family of TFs in proximity to BR patterns (Supplementary Table S3).

Previous studies have examined the classes of genes associated with each initiation pattern as well as the differences between these classes, including gene function, spatiotemporal expression and transcriptional regulation (Carninci et al., 2006; Haberle et al., 2014; Morton et al., 2014; Rach et al., 2009). Using a model that provides the most likely transcription initiation pattern in a region of interest is therefore particularly informative in cases where a gene’s functional annotation is incomplete. By making predictions of initiation patterns, the model can provide data-informed suggestions of a gene’s function in the absence of extensive experimentally supported information. By using the ROEs and TIPR model feature weights, one can additionally gain direct insight into the specific regulatory elements that are likely to control expression of transcripts produced at the site of interest.

4 Discussion

TSS prediction has many practical applications, including a potential for use in organisms with poorly annotated genomes. TIPR requires only DNA sequence as input in order to make predictions and does not require any a-priori knowledge of gene annotation. The training of TIPR does require TSS-Seq data and through the training process TIPR identifies TF binding profiles that are enriched at position-specific locations with respect to the TSS—TF-based features are then generated, and the model learns which of these features are most useful in determining TSS location for each peak type. Thus, it is important that the species in which predictions are made is expected to share many orthologous TFs with the training species. The earlier S-Peaker model showed that a model trained exclusively from mouse TSSs could identify the TSSs of human miRNAs (Megraw et al., 2009). This ability provides a strong potential for informative cross-species application in sequenced genomes of agronomic interest—these species may not yet have extensive high-throughput genomic data or even gene annotations available, but are often anticipated to share substantial TF binding domain orthology with a model species in which TSS-Seq information is available. For example, models trained in the dicot Arabidopsis could be useful guides for further experiments on genes in crop species such as tomato.

Predictions can be used to assist in the identification of the regulatory networks controlling genes by identifying which TFBSs are positioned in biologically relevant locations relative to the predicted TSS. These models can also be used to identify potential alternative start sites and the regulators which may control them, leading to the transcription of genes in different conditions, or the transcription of different mRNA products altogether. Many genes have been shown to have tissue-specific TSSs (Fürbass et al., 1997; Shemer et al., 1992; Toffolo et al., 2007; White et al., 1998), and different regulatory networks of TFs have been implicated in at least some of these genes (Toffolo et al., 2007; White et al., 1998). Another recent study showed a change in TSS selection, initiation pattern and TF usage during the transition from maternal to zygotic transcription in zebra fish (Haberle et al., 2014). TSS prediction tools can be used to identify potential alternative TSSs, which can help guide wet-lab experiments to validate sites and regulatory networks. The prediction of spatial TSS initiation pattern along the genome can also provide insights into the nature of transcripts produced from the site. For example, it may suggest spatiotemporal expression that is more consistent with housekeeping functions, or more consistent with tissue or time-related functions.

The TIPR model provides a large boost in performance (12% increase in AUPRC) over previous sequence-based models (Megraw et al., 2009). This is likely to be due in part to the use of a negative set filtering algorithm that selects locations with appropriately similar sequence backgrounds to TSSs while excluding false negatives. Another primary contributor to performance is an increased number of TFBS PWMs (the complete TRANSFAC dataset in vertebrates) and the inclusion of new sequence enrichment features. For example, the model feature measuring the sequence enrichment of the CA di-nucleotide (not included in the S-Peaker model) was highly negatively weighted, implying that promoter regions may be significantly depleted of CA. In humans, CA is known to be the most common simple-sequence repeat motif, with 19.4 repeats occurring per Mb (Hui et al., 2005). Several studies have shown that intronic CA repeats play a role in the regulation of alternative splicing in some genes (Hui et al., 2005; Yang et al., 2013). Sawaya et al. (2013) report that the AC motif is significantly depleted directly downstream of human TSSs, but the same depletion is not seen in the entire promoter region.

5 Final remarks

In this work, we have proposed a new machine-learning based TSS prediction model, capable of identifying TSSs with high accuracy and resolution, along with the spatial initiation patterns that TSSs will form along the genome—a feature that previous models have not provided. We have also shown for the first time that it is possible to predict TSSs with a broad peak initiation pattern from sequence content alone. Accurate TSS predictions can be used to guide wet-lab experiments, improve gene annotations in poorly studied genomes, identify genes with multiple or alternate TSSs and to infer information about the biological mechanisms regulating the transcription of genes.

Funding

This work was supported by the National Institutes of Health [GM097188 to M.M]; and by startup funds from Oregon State University.

Conflict of Interest: none declared.