Refinement of Generalized Born Implicit Solvation Parameters for Nucleic Acids and their Complexes with Proteins

Abstract

The Generalized Born (GB) implicit solvent model has undergone significant improvements in accuracy for modeling of proteins and small molecules. However, GB still remains a less widely explored option for nucleic acid simulations, in part because fast GB models are often unable to maintain stable nucleic acid structures, or they introduce structural bias in proteins, leading to difficulty in application of GB models in simulations of protein-nucleic acid complexes. Recently, GB-neck2 was developed to improve the behavior of protein simulations. In an effort to create a more accurate model for nucleic acids, a similar procedure to the development of GB-neck2 is described here for nucleic acids. The resulting parameter set significantly reduces absolute and relative energy error relative to Poisson Boltzmann for both nucleic acids and nucleic acid-protein complexes, when compared to its predecessor GB-neck model. This improvement in solvation energy calculation translates to increased structural stability for simulations of DNA and RNA duplexes, quadruplexes, and protein-nucleic acid complexes. The GB-neck2 model also enables successful folding of small DNA and RNA hairpins to near native structures as determined from comparison with experiment. The functional form and all required parameters are provided here and also implemented in the AMBER software.

Introduction

Experimental structural and functional studies of nucleic acids are being supplemented by genomic and epigenomic projects, which provide vast information at the sequence level, as well as computer simulations, which can give models with high resolution in both time and space, and insight into the couple of structure and energy. A remaining challenge is that nucleic acids (NA) have traditionally been difficult to accurately model in simulations due to their highly charged backbones and the importance of bound ions.¹ The incorporation of Particle Mesh Ewald² and the introduction of second generation force fields³ has allowed for stable simulations of nucleic acids in explicit solvent. ⁴ Therefore nucleic acid simulations in explicit solvent are the norm, pushing to longer simulation times,⁵ increasing force field accuracy, ⁶ and aiming to understand the sequence dependent structure and dynamics of nucleic acids.^{1, 7}

Although explicit solvent simulations are the state of the art in protein and nucleic acid simulations, there are multiple reasons why more approximate implicit solvent models, such as Generalized Born (GB), at times can be a useful option: (i.) lower number of particles can result in faster simulation times, (ii.) greater energy overlap⁸ in replica exchange molecular dynamics⁹ (REMD) can reduce the number of replicas required to span a temperature range, (iii.) more efficient conformational sampling when used with artificially low solvent viscosity,¹⁰ (iv.) better scaling with number of CPUs¹¹, and (v.) much higher performance on standard GPU-based computer architectures¹² especially for pairwise GB models, breaching the microsecond/day barrier¹³.

Implicit solvent simulations are already standard for proteins, and rapid simulation of folding for diverse protein topologies has become possible.¹⁴ In nucleic acids, however, the volume of a periodic box required to enclose the solute is higher than in globular proteins with the same number of atoms (linear vs globular geometry), making simulations of long nucleic acids in explicit water very expensive unless overall tumbling is prohibited through artificial restraints. As a result, typical simulation systems are shorter than 20 base pairs, even though some interesting features like DNA persistence length happens near the 150 base pair regime, and MD simulations have been used to study distortions in larger DNA structures such as minicircles¹⁵. Implicit solvent simulations of nucleic acids appear to be one possible way to study those properties at reduced cost.¹

Despite these potential benefits, to the best of our knowledge there are only few GB models that can maintain stable nucleic acid structures.¹⁶ Three are widely used in the CHARMM program¹⁷ (GBMV,¹⁸ GBMV2¹⁹ and GBSW²⁰) while two others (GB-HCT²¹ and GB-OBC²²) are widely used in the AMBER program.²³ These models have been applied to simulations of RNA and DNA.^{1, 11, 24} The challenge in implicit solvent models is to reproduce high theory level solvation free energies (typically using the Poison Boltzmann method²⁵ as reference data) and the computational expense in doing so comes from accurately determining the molecular surface defining the boundary between solute and solvent.²⁶ CHARMM and AMBER implicit solvents initially had very different philosophies: CHARMM focused on reproducing solvation energies and AMBER focused on speed. GBMV and GBMV2 are arguably among the most accurate GB models, ^25-26 but the use of a sharp molecular surface boundary between solute and solvent can in some cases introduce unstable force calculations in long time scale simulations when using the standard 2fs timestep.²⁷ This diminishes the practical application of GBMV and GBMV2 models for MD simulation, especially now that methods for improving stability of simulations using 4fs timesteps have been reported.^{13, 28} GBSW²⁰ is an analytical version of GBMV and GBMV2 that sacrifices some accuracy for speed.²⁶ It uses the van der Waals (VDW) surface to define the solute/solvent boundary.²⁶ AMBER's GB-HCT²¹ and GB-OBC²² are both based on a pairwise approximation approach introduced by Hawkins et al.²¹, which is computationally much faster than other GB solvent models. The latter model (GB-OBC) introduced correction parameters to reduce the overestimation of solvation energy of the former model (GB-HCT).

A comparison among several GB models available at the time (not including the GB Neck variants) concluded that GBMV models and GB-OBC were the most accurate for protein solvation energy calculations when using the higher level Poisson-Boltzmann calculation as a benchmark.²⁶ In practice, GB-OBC is better suited for long MD simulations because of its fast speed and its suitability for parallel or GPU calculations.^{11, 12b} Ultimately, implicit solvent simulations should reproduce experimental structural properties and not just Poisson-Boltzmann energies. In a recent report comparing different GB models for NA, Gaillard et al.^24a concluded that GBMV2 and GB-HCT models were better in reproducing DNA parameters (such as major and minor groove width) from experimental data than the GB-OBC model. However, GB-HCT (and even GB-OBC) introduce strong helical structural bias in protein simulations,²⁹ preventing its application to simulations of proteins in complex with DNA or RNA, Furthermore, their performance on more complex NA structure and dynamics has not been well studied.

Recently, the GB-neck model was developed by introducing an additional physically motivated correction to the GB-OBC model, to better mimic the molecular surface while maintaining speed in calculating solvation forces.³⁰ Theoretically GB-neck should be a promising approach, achieving both reasonably good accuracy and fast speed. However GB-neck was shown to lead to unstable structures for proteins and nucleic acids.^{24a, 30-31} Overall, it is clear that there remains a need for a fast and numerically stable GB model that works with proteins and nucleic acids at the same time. We address this issue in the current work.

We recently improved GB-neck by allowing the parameters for the calculation of effective Born radii to vary for different elements (GB-neck2³²). The physical motivation behind this approach is that these corrections for interstitial spaces likely depend on the size of the atoms involved. Parameters were fit to optimize agreement with Poisson-Boltzmann calculations for a large data set of peptide and protein conformations.³² GB-neck2 has better agreement for proteins in solvation free energy calculations, and reproduces explicit solvent secondary structure and salt bridge strength profiles better than previous AMBER GB models. Quantitative reproduction of experimental structures and thermodynamic stability profiles for small peptide motifs such as hairpins or mixtures of alpha helix, 3-10 helix or PP2, are also improved.³² Ultimately, these improvements are reflected in the successful folding of a series of proteins up to 100 amino acids in the μs to ms experimental folding time scale¹⁴, a challenging problem in the field³³.

In this work, we extend the training and testing of new parameters in GB-neck2 to nucleic acids. We describe the development of the new GB-neck2 parameters and show results for several systems representative of likely applications: stable simulation of DNA and RNA duplexes, DNA quadruplexes, protein-NA complexes, and folding of DNA and RNA hairpins. This sets the stage for more accurate simulations of protein-nucleic acid complexes with implicit solvent, a major deficiency in current models. In particular, faster implicit solvent simulations of protein-NA complexes could enable the study of long-time dynamics of larger systems like the nucleosome core particle, ribosomes, and DNA replication or repair assemblies; these currently remain largely intractable in explicit solvent.

Methods

Generalized Born theory

In implicit solvent models, solvation free energy is normally decomposed into two terms, polar and nonpolar: ΔG_solvation = ΔG_polar + ΔG_np. The nonpolar term can be roughly approximated by ΔG_np = σ*A (where σ is surface tension coefficient and the A term is solute surface area) although more sophisticated approaches are available.³⁴ Since the solvation energy in water is dominated by the polar part (particularly for high charge density nucleic acids),³⁵ most efforts have focused on developing more accurate polar models.^{19-20, 22, 30, 32}

Polar solvation energy can be calculated from the very accurate, but computationally expensive, Poisson Boltzmann (PB) method²⁵ or from the much faster Generalized Born (GB) model. GB models approximate the polar solvation energy by summing energies of pairwise atomic interactions (solvent screening) as well as self-interactions (charge solvation). The GB approach was first introduced by Still et al.³⁶ (Equation 1)

$$\Delta {\mathrm{G}}_{\mathrm{GB}}=-\frac{1}{2}\left(\frac{1}{{ϵ}_{\mathrm{in}}}-\frac{1}{{ϵ}_{\mathrm{out}}}\right){\sum }_{\mathrm{i},\mathrm{j}}\frac{{\mathrm{q}}_{\mathrm{i}}{\mathrm{q}}_{\mathrm{j}}}{{\mathrm{f}}_{\mathrm{ij}}^{\mathrm{GB}}\left({\mathrm{r}}_{\mathrm{ij}}\right)}$$ (1)

where q_i and q_j are the partial charges of atoms i and j with interatomic distance of r_ij. The function f_ij^GB is defined by Equation 2

$${\mathrm{f}}_{\mathrm{ij}}^{\mathrm{GB}}\left({\mathrm{r}}_{\mathrm{ij}}\right)=\sqrt{{\mathrm{r}}_{\mathrm{ij}}^2+{\mathrm{R}}_{\mathrm{i}}{\mathrm{R}}_{\mathrm{j}}\exp \left(\frac{-{\mathrm{r}}_{\mathrm{ij}}^2}{4{\mathrm{R}}_{\mathrm{i}}{\mathrm{R}}_{\mathrm{j}}}\right)}$$ (2)

where R_i and R_j are the effective Born radii of atoms i and j, representing their degree of burial inside the solute.

In GB models, effective Born radii can be calculated using either the Coulomb Field Approximation (CFA) or a non-CFA approach.³⁷ Although the former is notorious for overestimating effective radii,^37-38 it is still widely implemented in MD simulation due to its simple approximation that makes it easy to derive the analytical form for calculating effective radii. More accurate non-CFA-based GB models, such as GBMV, GBMV2^19-20 or the recently developed R6 model,³⁷ show excellent agreement of energies and effective radii with PB calculations.³⁷ However, they are computationally more expensive, limiting their use in extensive MD simulations. Moreover, the development of the analytical form of the R6 model has thus far focused on small molecules, and it has not yet been extensively tested in biopolymer simulations.³⁹

Although not useful in practice for MD simulation with GB, the effective Born radius for a given atom in a particular conformation can be calculated exactly by first calculating PB energy with all other charges turned off and then applying Equation 3.

$${\mathrm{R}}_{\mathrm{i}}=-\frac{1}{2}\left(\frac{1}{{ϵ}_{\mathrm{in}}}-\frac{1}{{ϵ}_{\mathrm{out}}}\right)\frac{{\mathrm{q}}_{\mathrm{i}}^2}{\Delta {\mathrm{G}}_{\mathrm{self}\left(\mathrm{i}\right)}}$$ (3)

These so-called “perfect” radii were shown to yield the best agreement⁴⁰ between GB and PB energies if they were applied in the GB equation (Equation 1), suggesting that improving the calculation of the effective radii is an important step toward better GB models. The perfect radii thus provide a useful benchmark^40-41 for testing the quality of radii calculated from various GB models.

Our previous work focused on improving the accuracy of the effective Born radii in the CFA-based GB-neck model³⁰ by introducing rigorous parameter training and testing using large sets of peptide and protein conformations.³² Based on CFA, effective radii can be approximated by Equation 4³⁶

$${\mathrm{R}}_{\mathrm{i}}^{-1}={\rho }_{\mathrm{i}}^{-1}-\mathrm{I}$$ (4)

where I is the 3D integral defined by Equation 5

$$\mathrm{I}=\frac{1}{4\pi }{\int }_{\mathrm{r}>{\rho }_{\mathrm{i}}}{\mid \mathrm{r}\mid }^{-4}\mathrm{dV}$$ (5)

and r is a vector centered at atom I, ρ_i is intrinsic radius of i^th atom and the integral region is inside the molecule but outside the atom i. Depending on the definition of the boundary between solute and solvent, the integral region could be molecular volume (I_MS) or van der Waals volume (I_vdw). The van der Waals (VDW) volume approach is more computationally approachable than the molecular volume.²⁶ Hawkins et al. followed the VDW approach and introduced pairwise approximations to analytically calculate the effective radii (GB-HCT model)²¹ using Equation 6

$${\mathrm{R}}_{\mathrm{i}}^{-1}={\rho }_{\mathrm{i}}^{-1}-\mathrm{I}\approx {\rho }_{\mathrm{i}}^{-1}-{\mathrm{I}}_{\mathrm{vdw}}\approx {\rho }_{\mathrm{i}}^{-1}-\frac{1}{4\pi }{\sum }_{\mathrm{j}}{\int }_{\mid {\mathrm{r}}_{\mathrm{ij}}-\mathrm{r}\mid <{\rho }_{\mathrm{i}}}{\mid \mathrm{r}\mid }^{-4}{\mathrm{d}}^3\mathrm{r}$$ (6)

where I_vdw is approximated by summing all individual integrals contributed by atoms j ≠ i. To avoid the overestimation of I_vdw, a set of scaling factors S_x (x = H, C, N, O, P, S ...) was introduced (ρ _i → S_i * ρ _i). However this approach neglects the interstitial region between atoms, which leads to underestimation of the effective radii for deeply buried atoms. Onufriev et al. attempted to alleviate this problem by introducing an additional set of parameters (α, ß, γ) to empirically scale up the effective radii of buried atoms (GB-OBC model)²² using Equation 7

$${\mathrm{R}}_{\mathrm{i}}^{-1}={\tilde{\rho }}_{\mathrm{i}}^{-1}-{\rho }_{\mathrm{i}}^{-1}\tanh (\alpha \omega -\beta {\omega }^2+\gamma {\omega }^3)$$ (7)

where ${\tilde{\rho }}_{\mathrm{i}}={\rho }_{\mathrm{i}}-\text{offset}$, $\omega ={\tilde{\rho }}_{\mathrm{i}}$ * I_vdw.

The offset parameter was introduced by Still et al. as a free parameter to minimize the error between GB and experimental solvation energy.³⁶ Mongan et al. later added an I_neck correction to I_vdw to approximate the molecular surface boundary I_“MS” ≅ I_vdw + I_neck (GB-neck model).³⁰ I_neck is easily approximated following the Mongan et al. approach.³⁰ The ω term in Equation 7 can be re-calculated with the updated boundary using $\omega ={\tilde{\rho }}_{\mathrm{i}}$ * I_“MS”. To minimize the overlap of the “neck” regions of pairs of atoms, a scaling factor S_neck was introduced.³⁰

The GB-neck model is theoretically better than the GB-OBC and GB-HCT models, but it was shown to quickly unfold protein and nucleic acid native structures in MD simulations.^{24a, 30-31} We hypothesized that this was due to weakness in the parameters rather than the functional form, and we reported³² more rigorous refitting of GB-neck parameters for proteins that showed improvement in reproducing PB solvation energy and reproducing explicit solvent MD data such as secondary structure content. Following the success of the resulting GB-neck2 model for protein simulations, we therefore adopt the same strategy for nucleic acids and make their [α, ß, γ] parameters element-dependent.

There are 20 parameters to fit, which are 5 scaling factors S_x (introduced by Hawkins et al.)²¹ (with x=H, C, N, O, P) and 5 sets of [α, ß, γ]_x (x=H, C, N, O, P). The offset (introduced by Still et al.³⁶) and S_neck parameter³⁰ are fixed at the values in the GB-neck2 protein model so that both nucleic acid and protein parameters can be combined in protein/nucleic acid complex MD simulations.

Fitting procedure

Objective function

Twenty parameters [S, α, ß, γ]_x (x=H, C, N, O, P) were treated as variables in the objective function (Equation 8). The objective function was the sum of weighted normalized root-mean-square-deviation (RMSD) between GB and PB absolute energy, relative energy and the inverse of effective radii for different structure sets. The weighting factors were chosen as done previously³² to avoid any specific structure set bias.

$$\mathrm{obj}\_\mathrm{funct}={\mathrm{w}}_{\mathrm{abs}}{\sum }_{\mathrm{i}}\mathrm{abs}\_{\mathrm{rmsd}}_{\mathrm{i}}∕{\mathrm{natom}}_{\mathrm{i}}+{\mathrm{w}}_{\mathrm{rel}}{\sum }_{\mathrm{i}}\mathrm{rel}\_{\mathrm{rmsd}}_{\mathrm{i}}∕{\mathrm{natom}}_{\mathrm{i}}+{\mathrm{w}}_{\mathrm{r}}\ast \mathrm{rad}\_\mathrm{rmsd}$$ (8)

Here abs_rmsd and rel_rmsd are absolute and relative energy RMSD, respectively, between GB and PB calculations, rad_rmsd is the RMSD between the inverse of GB and PB effective radii and w_abs, w_rel and w_r are weighting factors for abs_rmsd, rel_rmsd and rad_rmsd respectively. To account for the dependence of error magnitude on system size, the abs_rmsd and rel_rmsd for each training system were normalized by dividing by the number of atoms (natom_i).

Due to the large number of variables and expensive objective function, we sought the best local minimized function values rather than the global value, the same choice we made for the protein parameter optimization. The local optimization method NEWUOA⁴² was chosen for objective function minimization because of its quick convergence compared to other local optimization methods.⁴³ Additionally, NEWUOA is an improved version of UOBYQA⁴⁴ which we successfully used for refitting protein parameters in our previous work. A total of ~2400 optimization runs were carried out for each round of fitting; each optimization run started from a random guess given the following boundaries: S_x ∈ [0.0, 2.0], [α_x, β_x, γ_x] ∈ [0.0, 5.0] where x = H, C, N, O, P. Weighting factors for radii and for relative energies, relative to absolute energies, were varied to see how they affected the fitting (using w_rel = 5.0; w_abs = 1.0 combined with w_r = 1.5, 2.5, or 5.0). In the final round, w_r=2.5 was also tested with w_rel=10.0 (four weight combinations total. Five rounds of fitting were carried out, in which later rounds had more structures in the training set, as described below.

Phosphate is the only element not present in the protein data set we previously derived³². We tested multiple scenarios for optimizing additional parameters beyond those developed in our protein model (see Supporting Information for more details). We decided to keep GB parameters for proteins and NA independent of each other, retaining our previously published protein parameters and optimizing new parameters for application to NA. This approach is described below.

Training set

To avoid over fitting due to the large number of parameters, we included as many structure variations as possible in the training. We tested several different training sets of varying diversity (see Supporting Information for details). In the work described below, we included only DNA and RNA duplex conformations in the training set, anticipating that the resulting parameters may also work reasonably well for conformations not included in training. This hypothesis was explored during the testing phase.

Due to the computational expense of the many optimization runs, we chose a small size 10-base pair DNA duplex (CCAACGTTGG)₂ and its complementary RNA duplex (CCAACGUUGG)₂ for training the energy (see Table S1). These training sets are designated dnadup and rnadup, respectively. The same sequences were used in the past for extensive study of GB models.^{11, 24b, 24c, 45} All bases (A, T/U, C, G) are present in each system, and each is long enough to form a complete, stable duplex. Canonical A and B-form structures of the DNA duplex (CCAACGTTGG)₂ were used for training effective radii (this set is named dnadupRad). The range of RMSD values for the training set structures as compared to canonical A and B-form is provided in the supplementary information (see Figures S1, S2).

Procedure for parameter fitting

We adopted the following iterative procedure: (i) We first trained parameters by using only DNA duplex structures from MD using older GB models (GB-HCT,²¹ GB-neck³⁰) and MD using TIP3P⁴⁶ explicit water. The initial training set had 200 structures, which were equally extracted from 10 ns MD simulations at 300 K in explicit water and GB-HCT, starting from both canonical A and B-forms, and 1 ns MD simulation using GB-neck starting from A-form. This initial training set was designed to have both ‘good’ (associated DNA dimer strands from explicit water and GB-HCT MDs) and ‘bad’ (dissociated DNA dimer strands from GB-neck MD) to train for duplex stability. However, simulations of A-form DNA using the optimized parameters from this training set favored compact, non-canonical structures not seen in the training set. Analysis of these new structures showed that the GB model introduced bias, with more negative solvation energies than values obtained from PB calculations and with differences larger than seen for the training set structures. This indicates the conformational space covered by this training set is too narrow. We had observed similar trends while optimizing our protein solvation model³²; this was alleviated here by (1) introducing RNA to the training set and (2) iteratively increasing the training set size.

Each fitting round was carried out testing all combinations of weighting factors (see above). A single best solution was selected by comparing results for the ten parameter sets with the best objective function. Solutions with negative scaling factors were discarded, and when objective functions were similar (within 5%) preference was given to solutions with lower relative energy error. After each round of fitting, the parameters from the best solution were used to carry out 0.5 to 1.0 μs MD simulations for the DNA and RNA duplexes in the training set. We then uniformly extracted 50 to 100 structures from these MD runs and used them to expand the training set and then re-optimize the parameters (see Figures S1 and S2), again testing all combinations of weight factors. Initial parameters were reset to random values, with the exception that the best previous solution was also carried over to the next round. This procedure was repeated five times until the relative rmsd (rel_rmsd) difference between two consecutive fitting rounds was small (<2% change in the rel_rmsd from the former fitting round). The final training set had ~600 structures from explicit water, GB-HCT, GB-neck and GB intermediate model MD simulations.

In summary, each round of optimization included: (i) calculating PB energies for structures added to the training set, (ii) refitting the GB parameters by performing ~300-600 independent optimization runs for each weighting factor combination, (iii) running long MD simulation (0.5 to 1 μs) using the best solution, and (iv) adding resulting structures from the new simulations to the training set. The top scoring parameters from the final round are provided in Table S2.

Test sets for comparing solvation energy between GB and PB

Following our previous work on proteins, we also designed two types of structure sets to test the transferability of the new GB parameters to calculating solvation energies for structures beyond those in the training set (see Tables S1 and S3). Type I test set uses the same DNA and RNA sequences as the training set, but combines all the structures in training and the structures from MD simulations using the final GB parameters (Figures S3, S4). This test set was designed to check if the energy error for any newly sampled conformations was similar to that seen in the training set. Type I has dnadup_plus150 (adding 150 structures that were uniformly extracted from 0.75 μs MD simulation of DNA duplex (CCAACGTTGG)₂ using the final GB parameter set) and rnadup_plus200 (adding 200 structures that were uniformly extracted from 1.0 μs MD simulation of RNA duplex (CCAACGUUGG)₂ using the final GB parameter set).

Type II test sets (Tables S1, S3) have structures for sequences and systems different from those in the training set, including the Dickerson-Drew dodecamer DNA duplex (CGCGAATTCGCG)₂⁴⁷ (DNA DD) and its analog RNA duplex (CGCGAAUUCGCG)₂ which are two popular DNA and RNA models for experimental and computational studies.^{5a, 6a} We also used structures from the GCC-box binding domain protein in complex with DNA (PDB ID: 1GCC⁴⁸) for testing the combination of GB-neck2 parameters for NA (this work) with GB-neck2 parameters for proteins.³² Each test set for nucleic acid duplexes had structures extracted from MD simulations at 300K using explicit water as well as intermediate GB models. The 1GCC test set included structures from 300 K and 500 K explicit water simulations. High temperature was used to increase structure variety, particularly important since we wanted to include partially dissociated structures to train for desolvation of the interface. We characterized the training sets and test sets by their RMSD to canonical (DNA and RNA duplexes) or experimental (1GCC) structures; details are provided in supplementary information.

Test set for MD simulations

Evaluating the agreement between GB and PB calculations is only the initial step to justify the performance of a GB model. We also tested the behavior in MD simulations, checking if GB-neck2 is able to maintain stable DNA/RNA duplexes and a DNA/protein complex, since previous studies showed that duplexes were unstable with GB-neck.^{24a, 30} We carried out simulations in explicit solvent for use as a reference in order to minimize influence of potential inaccuracies in the underlying MM energy function. The testing structures include DNA duplex (CCAACGTTGG)₂ and RNA duplex (CCAACGUUGG)₂ which were used in training parameters. It also includes the popular Dickerson-Drew dodecamer (DD) DNA duplex (CGCGAATTCGCG)₂ and RNA duplex (CGCGAAUUCGCG)_2. We also tested the longer DNA sequence corresponding to “seq2” in Pérez et al.⁴⁹ (CTAGGTGGATGACTCATT)₂. We additionally tested the stability of non-duplex systems using DNA quadruplexes. Since stability could simply indicate an overly rigid model, we also tested structural conversion, such as A to B-form DNA, and B to A-form RNA, and folding of single-stranded DNA and RNA hairpins. The DNA hairpin was GCGCAGC with a GCA loop; the NMR structure of a homologue has been solved (PDB ID 1ZHU)⁵⁰. This system is small enough to enable the μs timescale simulations needed to characterize the structural ensembles. The same DNA hairpin was also successfully folded in the past⁵¹ using simulation in TIP3P explicit water. We also tested the folding of an RNA UUCG hairpin loop with 5 base pairs in the stem (PDB ID: 2KOC,⁵² sequence GGCACUUCGGUGCC). This hairpin system was shown to be stable in explicit solvent simulation.^6b Folding this system is extremely challenging in explicit water simulations. For instance, to observe 19 folding events in TIP3P explicit water, Sorin et al. utilized more than 10,000 CPU cores with an aggregated simulation time of 168.1 μs.⁵³ A REMD study by Otyepka et al. ⁵⁴ in TIP3P explicit solvent and the same RNA force field used here (bsc0χ_OL3) required 48 replicas. In our study, only 6 replicas were used for a GB-neck2 REMD simulation (producing ~0.5 μs/day/replica on a single GPU per replica). We also performed MD for the 1GCC protein-DNA complex described above. The summary of test systems is given in Table S3.

We generated two runs for all DNA and RNA duplexes, starting from both canonical A and B-forms. The lengths of MD simulations in GB-neck2 are between 50 ns (protein/DNA complex) to 1 μs. Since DNA and RNA duplexes were previously reported to be stable in the μs timescale in TIP3P explicit water MD simulation with the bsc0 force field^{5a, 6a} (DNA) and bsc0χ_OL3^{6b, 55} (RNA), we only performed relatively short MD simulations (100 ns) for explicit water, while 50ns in explicit water were used to sample fluctuations of the stable protein/DNA complex.

PB calculations

We used a similar approach from our previous parameterization of proteins for calculation of PB solvation energies and ‘perfect’ radii:³² Delphi II software,²⁵ non-linear PB model with solvent probe radius of 1.4 Å, very fine grid spacing (0.25 Å); interior dielectric constant was set to 1.0 while exterior value was set to 78.5 and 1000.0 for solvation and effective radii calculation respectively.⁵⁶ The different value of exterior dielectric constant used for the perfect radii calculation followed published suggestions.^{37, 56} The mbondi3 radii set was used to define the boundary between solute/solvent for all PB calculations. Mbondi3 is a small adjustment to mbondi2²² that improves the agreement of Arg/Lys and Glu/Asp salt bridge pairs PMFs between GB-neck2 and TIP3P explicit water.³² For the NA simulations reported here, mbondi2 and mbondi3 are equivalent; the distinction was only important for simulations of the protein-DNA complex.

Simulation protocol

Basic setup

The selected force fields were the widely used models for each polymer: ff99SB⁵⁷ was used for proteins, the bsc0^6a modification to parm99 was used for DNA and the bsc0_χOL3^{6b, 55} modification was used for RNA. Canonical A and B-forms of DNA and RNA duplexes were built with the NAB program from Ambertools 12.^23b Topologies and coordinates for MD simulations were generated by LEaP.^23b All MD simulations were carried out by using either the sander or pmemd program in AMBER version 12 or 14.^{23b, 23c} Long (μs) MD runs were performed with the GPU version of pmemd.^12b The AMBER code was modified to support the new GB parameters; as with the protein model, it is available in AMBER 15. Production MD simulations were performed at 300 K with a time step of 2 fs. SHAKE⁵⁸ was used to constrain bonds involving hydrogen. GB simulations used the Langevin thermostat with no cutoff and collision rate of 1 ps⁻¹, while simulations in explicit water used the TIP3P water model and the Berendsen thermostat⁵⁹ with the Particle Mesh Ewald (PME) method² for long range interactions with a direct space cutoff of 8 Å. Systems in explicit solvent were solvated by an explicit water truncated octahedron box with a minimum buffer size of 10 Å. Explicit ions were not used in these GB simulations, we also did not include them in the explicit water simulations to facilitate more direct comparison, although PME neutralizes the net charge on the system in the periodic calculation. Debye-Hückel salt screening of 0.1 was included in the GB model to roughly approximate the PME net charge neutralization; more detailed analysis of salt effects in the GB model were not tested here, since differences between the water models could be obscured by differences between implicit and explicit ion effects.⁶⁰ mbondi3 intrinsic Born radii³² were used with GB-neck variants (see discussion above). GB-HCT MD used the mbondi radii set with an offset = 0.13; these are the suggested values for use with this GB model and nucleic acids. ¹¹

We performed standard MD simulations for all systems except the RNA hairpin UUCG loop. This structure has 5 base pairs in the stem and is very stable in MD simulations (data not shown). We therefore used replica exchange molecular dynamics (REMD)⁹ simulation to accelerate the sampling. Each run had 6 replicas (4.5-6 μs/replica) with temperatures of [300.0, 317.0, 334.9, 353.9, 373.9, 395.1] to give an acceptance ratio of ~0.25. Exchanges were attempted every picosecond. Two simulations were performed, starting from the NMR⁵² (hairpin) and from canonical A-form (single stranded) conformations.

Equilibration

In GB equilibration, the starting structures were first minimized for 500 steps and then were heated from 100 K to 300 K with 10.0 kcal/mol/Ų atomic positional restraints on heavy atoms. In the next 3 steps (250 ps each), the temperature was kept at 300 K and the restraint force constant was reduced from 10.0, 1.0 to 0.1 kcal/mol/Ų. In explicit water equilibration, the solvated structure was minimized for 10000 steps, then was heated from 100 to 300 K in the NVT ensemble, then was equilibrated in the NPT ensemble with 100.0, 10.0, 1.0 and 0.1 kcal/mol/Ų positional restraints for heavy atoms in next four 250ps stages. Production runs were performed in the NVT ensemble.

Data analysis

Backbone RMSD (BB-RMSD) and cluster analysis (k-means algorithm) were carried out by the ptraj and cpptraj⁶¹ programs in Ambertools version 12 and 14.^{23b, 23c} The trajectory for each simulation was grouped into 50 clusters. Clustering was performed using RMSD for heavy atoms in the phosphate groups and sugars. All residues were used for RMSD calculation and clustering, except the case of 1GCC protein/DNA complex. For this complex, we excluded the flexible protein termini, used only residue 1-22 (DNA) and 27-74 (protein). DNA and RNA helical parameter analysis were performed by the CURVES+ program (version 1.31).⁶² The major and minor groove width in the outputs from CURVES+ were incremented by 5.8 Å to account for the P diameter, as suggested.⁶² The H-bond fraction was defined as the ratio between the number of H-bonds in each trajectory frame and the starting structure. The average H-bond fraction was calculated over the whole trajectory. The number of H-bonds for each base pair was calculated using the “nastruct” command in cpptraj.⁶¹

Results and Discussion

Parameter fitting

Our goal was to extend and re-optimize the nucleic acid parameters for the GB-neck model following our previous work optimizing protein parameters. As before, we used PB solvation energy (absolute energy and relative energy between structure pairs) and ‘perfect’ radii as benchmarks and designed the objective function as the sum of weighted contributions from the energy and effective radii RMSD between GB and PB calculations.³² A total of ~2400 optimization runs were performed for minimizing the objective function (Eqn. 8), testing several combinations of weighting factor at each round of fitting (see Methods). Each optimization started from a random guess within the boundaries given in Methods. We stopped minimization runs after 5 rounds when the energies errors did not change when new structures were added to the training set (Figure S3, S4).

Among the weighting factor combinations tested, we chose the optimized parameters from (w_r = 2.5, w_rel = 5.0, w_abs = 1.0) as our final candidate since this combination gave the best compromise between having low error for both energy and effective radii (Table S4). These optimal weighting factors are different from the ones we used in protein training,³² perhaps reflecting differences in training set size or molecular charge density between proteins and nucleic acids. The results for the top 10 optimization runs for (w_r = 2.5, w_rel = 5.0, w_abs = 1.0) are given in Table S2, with the final parameter set for GB-neck2 provided in Table 1.

Table 1.

Optimized parameters for GB-neck2.

Parameter	Value	Parameter	Value
SH	1.697	α N	0.686
SC	1.269	β N	0.463
SN	1.426	γ N	0.139
SO	0.184	α O	0.606
Sp	1.545	β O	0.463
α H	0.537	γ O	0.142
β H	0.363	α P	0.418
γ H	0.117	β P	0.290
α C	0.332	γ p	0.106
β C	0.197
γ C	0.093

Table 2 shows the abs_rmsd, rel_rmsd and rad_rmsd for the individual training sets. The data show a marked improvement over GB-neck, with GB-neck2 reducing the error about 80% for absolute energy, and 65% and 15% for relative energy of dnadup and rnadup, respectively. Figure S1 shows the energy comparison for all structures in dnadup training between GB (GB-neck, GB-neck2) and PB. GB-neck2 has better agreement to PB for the entire range of structures, while GB-neck underestimates the magnitude of the energies for most of the structures and has close energy to PB calculation only for structures having large RMSD to both A and B-form DNA. The same trend is also observed for the rnadup training set (Figure S2).

Table 2.

abs_rmsd, rel_rmsd and rad_rmsd for individual training sets.

	Solvation energy rmsd (kcal/mol)				Inverse of effective radii rmsd (1/Å) (DNA, natom = 632)		obj_funct
	dnadup natom = 632		rnadup natom = 640		A-form	B-form
	abs_rmsd w = 1.0	rel_rmsd w = 5.0	abs_rmsd w = 1.0	rel_rmsd w = 5.0	rad_rmsd w = 2.5	rad_rmsd w = 2.5
GB-neck	68.3	29.5	144.6	13.8	0.068	0.075	0.850
GB-neck2	14.0	10.3	25.4	11.7	0.045	0.038	0.338
%reduced_error	80%	65%	82%	15%	34%	49%	60%

%reduced_error shows degree of improvement of GB-neck2 compared to GB-neck, defined by %reduced_error = 100*(X_GB-neck-X_GB-neck2)/X_GB-neck where “X” is either abs_rmsd, rel_rmsd, rad_rmsd or obj_funct. “natom” is the number of atoms for each structure in the training set. Weighting factors “w” are also shown for each set.

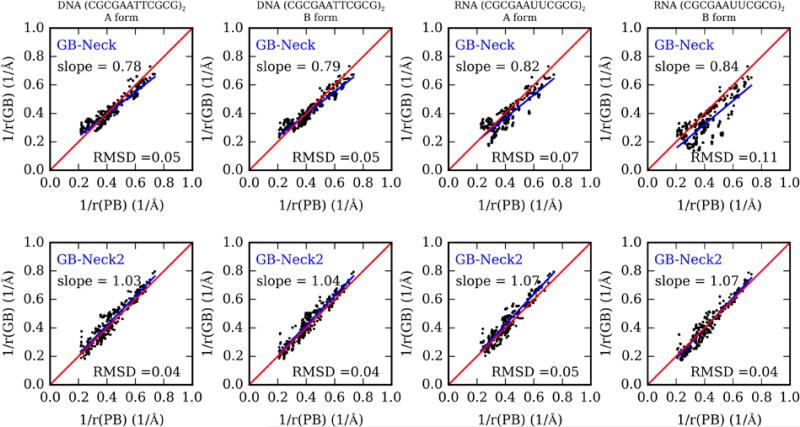
The effective radii errors are also reduced by 34% and 49% (compared to the original GB-neck model) for A and B-forms of the dnadupRad training set. Figure S5 shows better correlation to PB ‘perfect’ radii for GB-neck2 effective radii those from the GB-neck model. Consistent with the trends seen in the energy, GB-neck tends to overestimate effective radii for most atoms; a similar trend was also observed when using the GB-neck model in protein simulations.³² Additionally, slopes near 0.8 with GB-neck indicate that the effective radii for buried atoms in the GB-neck model tend to be too large. This is significantly improved in GB-neck2, where the slopes of the best-fit lines are near 1.06.

Effective radii for test set structures

We trained effective radii for only A and B-forms of the DNA duplex (CCAACGUUGG)_2. It is of interest to evaluate if the improvement obtained for those structures will transfer to other nucleic acid structures, such as protein/nucleic acid complexes, or other DNA and RNA duplexes and non-duplexes. We chose 8 systems to investigate this (Table 3); two are A and B-form DNA duplexes, and four are two RNA sequences, each in A and B-form duplex structures (see Methods). We also used a DNA quadruplex (PDB ID: 1L1H⁶³) and a protein/DNA complex (PDB ID: 1GCC⁴⁸).

Table 3.

RMSD between the inverse of GB effective radii and the inverse of PB ‘perfect’ radii (1/Å) for test sets

	GB-neck	GB-neck2	%reduced_error
A-form DNA (CGCGAATTCGCG)2	0.046	0.045	2%
B-form DNA (CGCGAATTCGCG)2	0.047	0.042	11%
A-form RNA (CCAACGUUGG)2	0.069	0.051	26%
B-form RNA (CCAACGUUGG)2	0.112	0.040	64%
A-form RNA (CGCGAAUUCGCG)2	0.069	0.050	28%
B-form RNA (CGCGAAUUCGCG)2	0.114	0.040	65%
DNA G-quadruplex (PDB ID: 1L1H)	0.067	0.062	7%
DNA-protein complex (PDB ID: 1GCC)	0.070	0.062	11%

Table 3 shows the RMSD between the inverse of effective radii (GB) and the inverse of ‘perfect’ radii (PB) for these test systems. Overall, GB-neck2 modestly improved the radii. For example, the scatter in the data is reduced; the rad_rmsd of A-form RNA (CCAACGUUGG)₂ is 0.051 for GB-neck2 but 0.069 for GB-neck model. In the case of B-form RNA, GB-neck2 shows substantial improvement over GB-neck. GB-neck strongly overestimates the effective radii of B-form RNA, while GB-neck2 has better agreement to ‘perfect’ radii. In this case, GB-neck2 reduced 65% of the error in the GB-neck model. Manually inspecting the effective radii calculated from GB-neck reveals that this model overestimates the effective radii for atoms nearby HO2’ atoms (Figure S6, Table S5). This issue is not seen for these atoms in A, B-form DNA and A-form RNA since those structures are less compact than B-form RNA. This improved accuracy may arise from the training of GB-neck2 on a diverse set of nucleic acid structures, while nucleic acids were not part of the GB-neck training sets. Although RNA duplexes prefer A-form over B-form, this improved accuracy for B-form may be important for modeling the more complex range of functional structures adopted by RNA. As was seen for the training data in Figure S5, the overall trend in the data is also significantly better reproduced with GB-neck2 for all systems, with slopes of 1.03-1.07 as compared to 0.78 to 0.84 with GB-neck (Figure 1). Beyond these duplexes, the agreement between GB-neck2 effective radii and the PB radii is better than in the GB-neck model for quadruplexes and the protein-DNA complex (Figure S7). MD simulations for these systems are discussed below.

Figure 1.

Comparison of inverse of PB “perfect” radii with inverse of effective radii between GB-neck (top), GB-neck2 (bottom) for the test sets: A and B-forms of DNA duplex (CGCGAATTCGCG)₂, and A and B-forms of RNA duplex (CGCGAAUUCGCG)₂. The red line in each subplot indicates the ideal agreement between GB and PB effective radii. The blue line indicates the best fit line.

Solvation energies for test set structures

We tested the transferability of GB-neck2 parameters for solvation energy calculations from our training set to two different test sets. For test set type I, we compared abs_rmsd and rel_rmsd in longer simulations (0.75-1 μs MD simulation using the final parameters) of our test set structures, named dnadup_plus150 and rnadup_plus200. For type II we tested different sequences that were not used in training. The test set type II includes structures of a DNA duplex (CGCGAATTCGCT)₂, an RNA duplex (CGCGAAUUCGCG)₂ and a protein/DNA complex (1GCC). Table 4 shows the abs_rmsd and rel_rmsd for the different test sets. For test set type I, the abs_rmsd and rel_rmsd for dnadup_plus150 and rnadup_plus200 are similar to the training set dnadup and rnadup (for example, abs_rmsd of dnadup and dnadup_plus150 are 68.3 and 70.8 kcal/mol respectively). This indicates that any new structures sampled in the MD simulation using the final parameters were modeled at a similar level of accuracy to the training data.

Table 4.

abs_rmsd, rel_rmsd for type I and II test sets. In the case of the protein/DNA complex with the original GB-neck parameters, we show two cases: 1) the original GB-neck parameters were applied to both protein and DNA. 2) The original GB-neck parameters applied to DNA while GB-neck2 parameters were applied to protein (results shown in parentheses).

	Test set name	GB-neck		GB-neck2		%reduced_error
		abs_rmsd	rel_rmsd	abs_rmsd	rel_rmsd	abs_rmsd	rel_rmsd
Type I	dnadup_plus150	70.8	26.2	16.4	10.7	77%	59%
	rnadup_plus200	144.3	11.1	21.5	10.4	85%	6%
Type II	DNA duplex (CGCGAATTCGCG)2	104.2	17.8	15.3	13.6	85%	24%
	RNA duplex (CGCGAAUUCGCG)2	177.4	13.3	29.9	9.9	83%	26%
	Protein/DNA complex 1GCC	126.0 (63.7)	23.3 (46.9)	39.2	19.1	69% (38%)	18% (59%)

For test set type II, both absolute and relative energy RMSD are significantly reduced in GB-neck2 as compared to GB-neck. Specifically, the abs_rmsd is about 69-85 % reduced and the rel_rmsd is about 18-26% reduced. The abs_rmsd and rel_rmsd are also 69% and 18% reduced for the protein/DNA complex, even though training was only performed for solvated duplexes. The comparison between GB and PB energies for individual structures in the 3 type II test sets are shown in Figures S8-S11.

Performance in MD simulations of stable structures

We have shown that GB-neck2 reduces the error in reproduction of PB solvation energies and effective radii as compared to the original GB-neck model. A key motivation for this work was the observation that MD simulations using the original GB-neck resulted in loss of all H-bonds in DNA duplexes.^24a We therefore tested the hypothesis that better performance of GB-neck2 in reproducing PB solvation energy calculation would result in better structural stability in MD simulations. Six systems were tested; two were used for training GB-neck2 (DNA duplex (CCAACGTTGG)₂, RNA duplex (CCAACGUUGG)₂) and three were used for comparing GB and PB energies (DNA duplex (CGCGAATTCGCG)₂, RNA duplex (CGCGAAUUCGCG)₂ and protein/DNA complex 1GCC). We also tested a longer DNA duplex (18 base pairs) corresponding to “seq2” from Pérez et al.⁴⁹, as well as a DNA quadruplex (discussed below).

We performed μs timescale MD simulations using GB-neck2 for the quadruplex and duplexes as well as shorter simulations (50ns) for the protein/DNA complex. Reference simulations were performed for each system in explicit water (0.05-0.1 μs). The GB simulations were much longer to allow the system time to reveal any pathological behavior of the new model on long timescales, as compared to the behavior in explicit water which has been studied extensively in the past. We calculated the average BB-RMSD over time for GB-neck2 and explicit water MD simulations relative to the canonical (duplexes) or experimental (quadruplex and protein complex) structures.

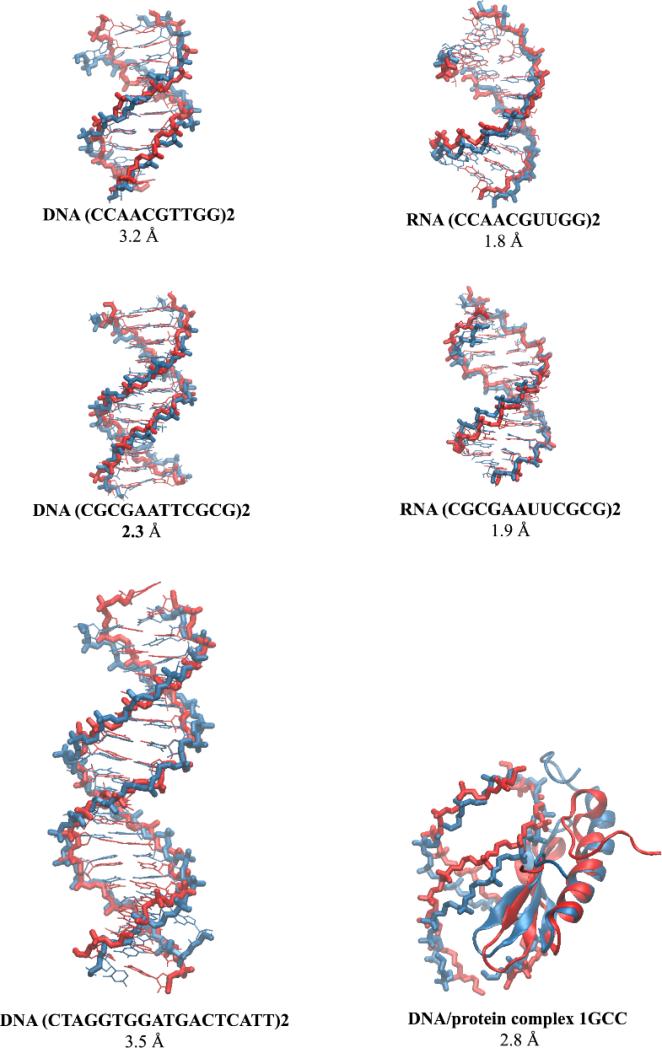
For the DNA and RNA duplexes and the DNA/protein complex, plateau values are reached and no further trend was seen in the time dependence of the RMSD values (Figures S12, S13). Both solvent models perform similarly at this level; in all cases, the difference in average BB-RMSD between GB-neck2 and explicit water is within 1.5 Å (Table 5). It is interesting to note, however, that explicit water provides lower RMSD values to canonical B-form than does GB in each of the DNA simulations, while the GB-neck2 simulations are slightly better at reproducing canonical A-form RNA in each of the RNA simulations. Representative structures of the most populated cluster in GB-neck2 and explicit water MD simulations are compared in Figure 2, which shows a good agreement between structures preferred in the GB model and in explicit water.

Table 5.

Summary of testing structural stability and structural conversion in MD simulations.

System		Length (ns)		Average BB RMSD (Å)		Notes on GB results
	starting structure	GB-neck2	explicit water	GB-neck2	explicit water
DNA (CCAACGTTGG)2	A-form	1000	100	4.3 (A); 4.3 (B)	4.2 (A); 3.1 (B)	A → B, stable
	B-form	1000	100	4.2(A); 4.3(B)	4.0(A); 3.1(B)	Stable
DNA (CGCGAATTCGCG)2	A-form	1000	100	5.2 (A); 4.2 (B)	5.3 (A); 3.0 (B)	A → B, stable
	B-form	1000	100	5.2 (A); 4.2 (B)	5.4 (A); 2.9 (B)	Stable
RNA (CCAACGUUGG)2	A-form	1000	100	2.1 (A); 6.1 (B)	2.8 (A); 5.6 (B)	Stable
	B-form	1000	100	2.2 (A); 6.4 (B)	2.8 (A); 5.5 (B)	B → A, stable
RNA (CGCGAAUUCGCG)2	A-form	1000	100	2.3 (A); 6.7 (B)	3.6 (A); 6.3 (B)	Stable
	B-form	1000	100	2.7 (A); 6.7 (B)	3.7(A); 5.8(B)	B → A, stable
DNA seq2 (CTAGGTGGATGACTCATT)2	A-form	~1000	100	6.2 (A) 6.9 (B)	6.1 (A) 5.1 (B)
	B-form	1000	100	5.7 (A) 6.5 (B)	6.0 (A) 5.0 (B)	Stable
DNA quadruplex (GGGG)4		1000	200	1.6 (NMR)	4.4 (NMR)	Stable
DNA quadruplex (GGGGTTTTGGGG)2 (PDB ID: 1L1H)		1000	300	1.7 (X-ray)	4.4 (X-ray)	Stable
DNA-protein complex (PDB ID: 1GCC)		50	50	2.7 (NMR)	2.4 (NMR)	Stable

For duplex simulations, the canonical structure used as reference (A or B) is given in parentheses after the RMSD value. “A → B” or “B → A” indicates the conversion of A to B-form in DNA simulation (starting from A-form) or B to A for in RNA simulation (starting from B-form), respectively.

Figure 2.

Structural overlap and BB-RMSD between representative structures of the most populated clusters from GB-neck2 (blue) and explicit water (red) MD simulations. Only backbones of DNA are shown in the DNA/protein 1GCC complex for clarity.

Table 6 shows the average percent of H-bonds (see Methods) in GB-neck2 and explicit water MD simulations. Over the 1 μs simulation time, GB-neck2 maintained 83 to 97% of H-bonds for the DNA (RNA) duplex and DNA/protein complex system if all base pairs were included in calculation. In explicit water, 95 to 98 % of H-bonds were maintained on the 50-100 ns timescale. Since fraying of terminal base pairs was seen in both explicit water and GB simulations, we also compared H-bond fractions by excluding each terminal base pair. In this case, explicit water and GB-neck2 maintained ~100% and 91-98% of H-bonds, respectively. Among these, GB-neck2 maintained 97 to 98 % of H-bonds in the 4 DNA and RNA sequences with C-G terminal base pairs. As expected, terminal A-T pairs were somewhat weaker, and DNA sequences with a terminal A-T pair (DNA seq2 and DNA/protein complex 1GCC) showed somewhat lower H-bond fractions of 90 to 91%. In explicit water, the difference between terminal G-C and A-T pairs was less pronounced, and a fraction of 99% was still obtained for these systems. End fraying was primarily responsible for the reduced H-bond fractions; neglecting the outer 3 base pairs in DNA seq2 and outer 2 base pairs in the shorter protein-bound DNA, H-bond fractions were almost 100% (Table 6). Although A-T pairs are known to be weaker than G-C pairs, with terminal A-T pairs showing significant fraying in NMR experiments⁶⁴, poly-AT duplexes were not stable when tested in this GB model (data not shown). More quantitative benchmarks for base pair fraying, such as comparing H-bond PMFs between GB and explicit water MD, will be the focus of future efforts. Discrepancies in the PMFs could be improved by adjusting the hydrogen intrinsic radii, following previous work on both nucleic acids^24c and proteins.^{22, 32, 65}

Table 6.

Average H-bond fraction in GB-neck2 and explicit water simulation for DNA (RNA) duplexes and DNA/protein complex.

System	explicit water		GB-neck2
	All base pairs	Skip terminal base pairs	All base pairs	Skip terminal base pairs
DNA (CCAACGTTGG)2	94±5	100±1	93±1	98±1
DNA (CGCGAATTCGCG)2	95±1	100±1	88±1	98±1
RNA (CCAACGUUGG)2	96±2	98±1	97±1	98±1
RNA (CGCGAAUUCGCG)2	98±1	98±1	92±1	97±1
DNA seq2 (CTAGGTGGATGACTCATT)2	94±1	99±1 100±1a	81±1	90±1 99±1a
DNA-protein complex (PDB ID: 1GCC) DNA sequence: (TAGCCGCCAGC)2	94±1	99±1 99±1a	88±1	91±1 99±1a

For DNA and RNA duplexes, uncertainties were calculated from independent runs initiated from A and B-forms. For DNA/protein complex (1GCC), the uncertainties were calculated from independent runs with different starting velocities.

^aFor DNA systems having A-T base pairs in the terminal (shown in bold), we also report the H-bond fraction excluding the outer 2 or 3 base pairs (shown in italics, see text for details).

Besides testing the stability of canonical duplexes, we also extended our analysis to quadruplex systems, which were not included in parameter training and therefore may not be expected to perform well with this GB model. We chose a small antiparallel strand (aps) DNA G-quadruplex (GGGG)₄^6a that is a truncated version of dimeric quadruplex (PDB ID: 156D) from Oxytricha telomeric oligonucleotide, along with a larger four-stranded Oxytricha telomeric DNA (PDB ID: 1L1H). The truncated version was used for testing the bsc0 force field.^6a In GB-neck2, both structures are stable on the microsecond timescale with very low average BB-RMSD (1.6-1.7 Å, Table 5) In contrast, the structures of the two quadruplex systems were not maintained in explicit water MD simulation (200-300 ns). The average BB-RMSD was 4.2 to 4.4 Å for both systems, and most of the native H-bonds were lost. Instead, simulations in explicit water tend to favor non-native H-bond patterns (Figure S14). As discussed above, simulations in explicit water reported here were carried out in the absence of explicit ions to facilitate comparison with the GB results. However, prior simulation studies of quadruplexes in TIP3P explicit water have suggested that inclusion of explicit ions may be necessary for stabilizing the structure.⁶⁶ For example, average BB-RMSD values of ~1.2 Å were reported for the aps system in TIP3P explicit water with neutralizing Na⁺ ions, maintaining ~100% of H-bonds during 10 ns MD.^6a Another study by Rueda et al.^66b with much longer simulation time (up to 1 μs) showed that simulations of quadruplexes in water without ions made the native structure collapse quickly while with ions, the native structure was still stable even in vacuum simulation. It is unclear why the quadruplexes are stable in GB without explicit ions, although it likely represents a fortuitous cancellation of error. Although overestimation of base stacking or hydrogen bonding energies could be responsible for the increased quadruplex stability in GB, these effects seem to be inconsistent with the increased fraying of terminal base pairs in GB-neck2 vs. explicit water discussed above, which suggest stacking or H-bonding may be too weak in the model.

We also tested the stability of the protein/DNA complex in MD simulation. 50 ns of GB-neck2 MD of GCC-box binding domain in complex with DNA (PDB ID: 1GCC⁴⁸) was compared with the same length of explicit water MD simulation. The average backbone RMSD to the NMR structure for GB-neck2 is comparable to that from explicit water (2.7 and 2.4 Å respectively). GB-neck2 was able to maintain 88±1 % of H-bonds (vs. 94±1 % in explicit water). If the terminal TA base pairs were excluded from H-bond fraction calculations, both GB-neck2 and explicit water maintained 99±1 % H-bonds. Further testing of the details of the performance of the model for protein complexes with nucleic acids will be carried out in the future.

Modeling structural interconversions

The results described above have tested the ability of the GB model to maintain a reasonably accurate initial structure for a variety of conformations. Ideally, simulations would also be able to locate an accurate conformation despite being initiated in a non-ideal conformation. To further characterize the performance of the GB-neck2 model, we thus tested if GB-neck2 is able to reproduce the structural conversion from A to B-form for DNA and B to A-form for RNA, as seen in explicit solvent simulations⁶⁷. These are traditional tests when developing new force fields^{6a, 55} or testing solvent models.¹¹ We carried out simulations of DNA duplexes initiated in both A and B-form, as well as RNA duplexes in both A and B-form. It is expected that accurate simulations initiated from A-form DNA and B-form RNA converge to B-form DNA and A-form RNA, respectively.

As shown in Table 5, for the DNA and RNA duplexes, the final average structure does not depend on whether the simulation was initiated in A-form or B-form; all DNA duplexes adopted a B-form, while all RNA simulations adopted an A-form. The major and minor groove widths of DNA in GB-neck2 are in excellent agreement with those obtained from simulations in explicit water (Tables 7, S6 and S7). The RNA minor groove widths from GB-neck2 MD are also similar to those from explicit water. The RNA major groove widths in GB-neck2 MD simulations are smaller by about 4 Å as compared to explicit water MD simulation (~15 Å for GB-neck2 and ~19 Å for explicit water). These explicit water results are comparable to those previously reported, where it was noted that this combination of TIP3P explicit water and force field (bsc0χOL3) overestimates RNA major groove widths by 2.5-3.2 Å relative to X-ray and NMR data.⁵⁵ Interestingly, using GB-neck2 and bsc0χOL3 provides a better match to experimental major groove width for RNA; as we noted for the quadruplex, this suggests the presence of fortuitous error cancellation between bsc0χOL3 force field and GB-neck2 solvent model, or possibly weakness in the TIP3P explicit water model.

Table 7.

Groove width (Å) of DNA duplex (CGCGAATTCGCG)₂ and RNA duplex (CGCGAAUUCGCG)₂ from GB-neck2 and explicit water MD simulations.

Groove width (Å)	DNA (CGCGAATTCGCG)2			RNA (CGCGAAUUCGCG)2
	GB-neck2	explicit water	Experiment (NMR/ X-ray)6a	GB-neck2	explicit water	Experiment (X-ray)
Major	18.7±0.1	18.8±0.1	18.0 ± 3.0/18.0 ± 0.3	15.1±0.5	19.2±0.1	16.2+/−3.0
Minor	12.8±0.1	12.1±0.1	12.0 ± 1.0 /10.0 ± 0.2	15.9±0.1	15.1±0.1	17.4 +/− 1.4

Two runs were performed for each solvent model, starting from A and B-forms. Uncertainties in MD data were calculated from two simulations. RNA experimental values reflect average and standard deviation from a survey of 50 crystal structures. DNA experimental values are from a published survey of crystal structures.^6a

Folding DNA and RNA hairpins

We have shown above that GB-neck2 is able to maintain stable DNA and RNA duplexes and is able to reproduce the structural conversion from A to B-form for DNA and B to A-form for RNA. However, these conversions involve relatively small rearrangements. A major potential advantage to implicit solvent is the ability to use artificially low friction and rapidly model global dynamics that are typically hindered by viscosity in explicit solvent. Diffusion-limited processes, such as RNA folding or formation of complexes, may be inaccessible to more accurate explicit solvent simulations, thus a GB model that provides even a qualitative view of these rare events may be valuable. Furthermore, the large number of explicit water molecules required to fill the periodic cells that fully enclose these systems suggests that GB would provide even greater benefit than for canonical duplexes, potentially enabling atomistic simulation of systems that remain wholly intractable in explicit water, such as simulations that were reported for nucleosomal DNA.^24d These advantages are analogous to those that enabled our recent study of folding of a variety of proteins¹⁴ using the protein version³² of the GB-neck2 model.

As a representative application, we tested the folding of single stranded DNA and RNA hairpins. Besides performing simulations using GB-neck2, we performed additional runs using the GB-HCT model.²¹ This model was developed 20 years ago and is the foundation of later pairwise models. GB-HCT has been shown to strongly bias overly compact structures in protein MD simulations.²⁹ However, it is still being used for simulating DNA duplexes, RNA duplexes, and hairpin structures.^{24a, 24b, 24h, 45, 68} We hypothesized that this older GB model would bias misfolded structures (compared to native ones) in long time scale simulations of nucleic acids, and the reported stability of duplexes in GB-HCT simulations may reflect kinetic trapping on the timescales of the simulations that have been reported, or perhaps accuracy limited to canonical duplexes. We tested the hypothesis with DNA and RNA hairpin systems small enough to enable simulations on the μs timescale that would enable observation of large-scale structural changes.

We tested if these two GB solvent models could correctly reproduce known experimental structures of short hairpins. For DNA, we simulated the GCA hairpin loop system (sequence GCGCAGC). Successful folding of this hairpin (to 1.5 Å heavy atom RMSD for the corresponding region of the NMR structure of a longer homologue, PDB ID 1ZHU⁵⁰) has been reported⁵¹ using TIP3P explicit water. We also tested the folding of an RNA hairpin UUCG loop (PDB ID: 2KOC,⁵² sequence GGCACUUCGGUGCC) with 5 base pairs in the stem. This hairpin system was shown to be stable in explicit solvent simulation.^6b A shorter and modified sequence of this hairpin loop was also reported to fold to experimental structure from unfolded state in explicit water REMD simulation.⁵⁴

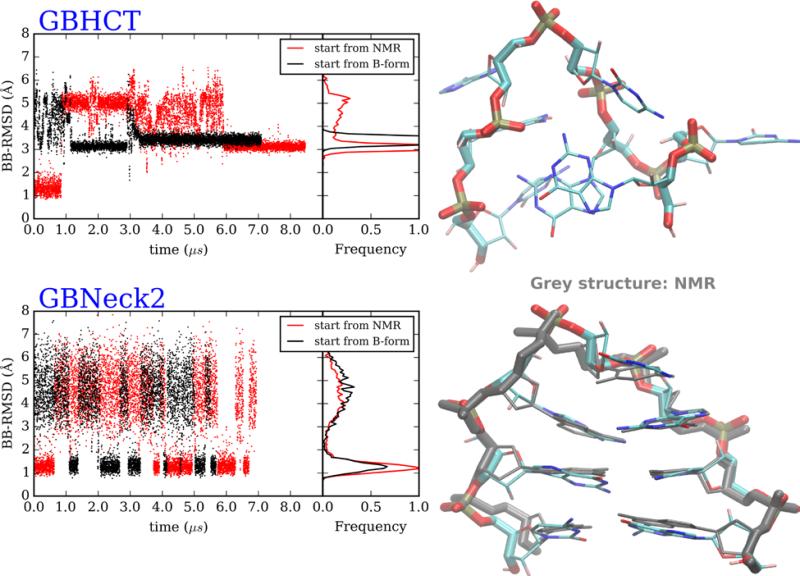
For the DNA GCA hairpin, GB MD simulations were carried out from the hairpin (NMR of homologue) and single stranded canonical B-form conformations (Table S3). In the GB-HCT simulation starting from the hairpin structure, the native conformation was maintained for the first ~1 μs, but it subsequently unfolded to > 3 Å BB RMSD, and the hairpin did not refold in the remainder of the >8 μs simulation (Figure 3). GB-HCT simulations starting from the B-form did not fold, and converged to a structure similar to that adopted at the end of the hairpin simulation. The results are consistent with previous observations in protein folding simulations, in which GB-HCT favors misfolded structures.^{29, 69} In contrast, both simulations in GB-neck2 showed reversible folding to a structure in agreement with experiment, with multiple folding/unfolding events occurring over the course of each MD simulations (Figure 3). The folded structure from this simulation has remarkably low BB-RMSD (1.2 Å for cluster representative) to the corresponding NMR structure. Unlike the GB-HCT simulations in which a significant population of specific misfolded structures was sampled, folding with GB-neck2 was 2-state in character with sampling of a well-defined folded structure and a flexible unfolded ensemble (Figure 3).

Figure 3.

DNA GCA hairpin loop MD simulations, starting from B-form and NMR structures. (Top left) Backbone RMSD versus time and RMSD histograms, from GB-HCT simulations starting from 2 conformations. (Bottom left) Backbone RMSD versus time and RMSD histograms, from GB-neck2 simulations starting from 2 conformations. Right: representative structures of most populated clusters from simulations starting from hairpin structures. (Top right) GB-HCT (misfolded). (Bottom right) GB-neck2 (folded, with NMR reference shown in grey). 2^nd half of data was used for cluster analysis and histogram calculations.

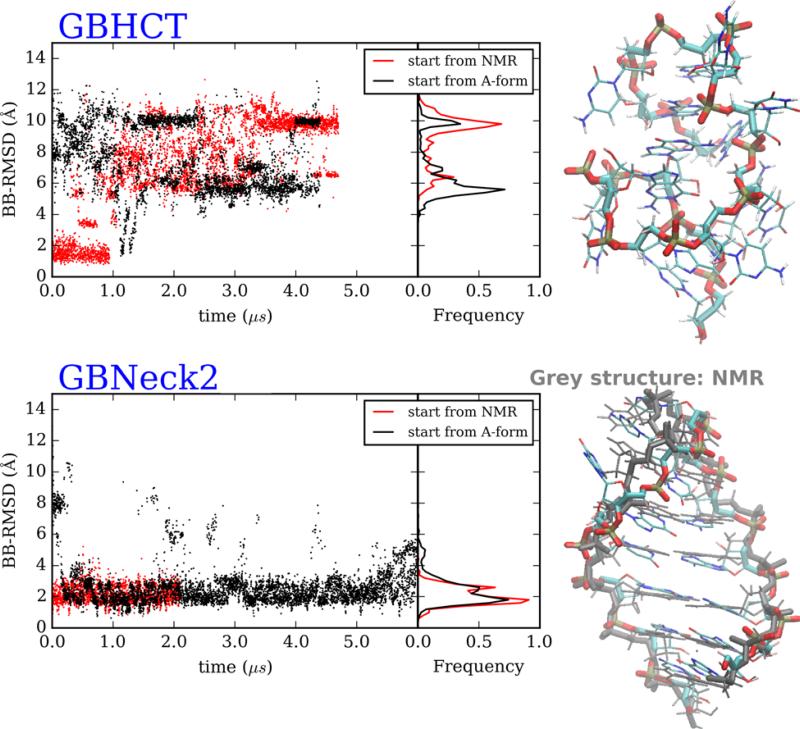
We next tested the folding of the RNA UUCG hairpin loop. Since this hairpin has 5 base pairs in the stem, the hairpin structure was very stable in standard MD simulations and reversible folding was not seen (data not shown). We used REMD to accelerate the folding/unfolding, again testing each GB model (GB-HCT and GB-neck2), starting from both NMR and single stranded A-form conformations. GB-HCT again favors an incorrect structure (BB-RMSD to NMR structure: 8.6 Å) while GB-neck2 is able to fold to a structure similar to the NMR structure (BB-RMSD of 1.9 Å and stem BB-RMSD of 1.1 Å) (Figure 4). While the structure of the stem region sampled in GB-neck2 is very accurate, the loop is not accurately folded; however, this may reflect inaccuracies in the RNA force field rather than the GB model since the same discrepancy was reported for simulations using explicit solvent.⁵⁴

Figure 4.

RNA UUCG hairpin loop REMD simulations starting from A-form and NMR structures. Structures correspond to those sampled at 300K. (Top left) Backbone RMSD versus time and RMSD histogram from GB-HCT simulations starting from 2 conformations. (Bottom left) Backbone RMSD versus time and RMSD histogram from GB-neck2 simulations starting from 2 conformations. Right: representative structures of most populated clusters from simulations starting from hairpin structures. (Top right) GB-HCT (misfolded). (Bottom right) GB-neck2 (folded, with NMR reference shown in grey). 2^nd half of data was used for cluster analysis and histogram calculation.

Conclusions

In this study, we have extended and refit the GB-neck model for MD simulations of nucleic acids and their complexes with proteins. The fitting reduces the error by 70%-80% for absolute energy and 15%-65% for relative energy calculations from GB-neck, using PB calculations as a benchmark. The quality of the effective Born radii is also modestly improved. The improvement in energy and effective radii calculations translate to better structural stability for duplex, quadruplex and duplex/protein complex simulations. The model is also able to fold hairpin loop conformations for both DNA and RNA; such calculations remain very expensive in explicit water.

We also show that the A-T base pair H-bonds may be too weak in the GB-neck2 model. Future efforts will focus on quantitative comparison to data from explicit solvent, and possible tuning of stability by adjusting intrinsic Born radii as done previously for GB models of nucleic acids^24c and proteins.^{22, 32, 65}