Folding cooperativity in a 3-stranded β-sheet model

Summary

The thermodynamic behavior of a previously designed three-stranded β-sheet was studied via several µs of standard and replica exchange molecular dynamics simulations. The system is shown to populate at least four thermodynamic minima, including 2 partially folded states in which only a single hairpin is formed. Simulated melting curves show different profiles for the C and N-terminal hairpins, consistent with differences in secondary structure content in published NMR and CD/FTIR measurements, which probed different regions of the chain. Individual β-hairpins that comprise the 3-stranded β-sheet are observed to form cooperatively. Partial folding cooperativity between the component hairpins is observed, and good agreement between calculated and experimental values quantifying this cooperativity is obtained when similar analysis techniques are used. However, the structural detail in the ensemble of conformations sampled in the simulations permits a more direct analysis of this cooperatively than has been performed based on experimental data. The results indicate the actual folding cooperativity perpendicular to strand direction is significantly larger than the lower bound obtained previously.

Introduction

How a protein folds into its final three-dimensional structure based on the information contained in a linear chain of amino acids is one of the most important problems in molecular biology. At the basic level of this process is the formation of units of protein secondary structure, α-helices and β-sheets. β-sheet formation is more complex than α-helix formation; β-sheets are made up of two distinct structural elements, strands and turns. Interactions between strands can occur between residues that are quite distant from each other in the protein chain, and whether these residues are in hydrogen-bonded sites or not can change the stability of their interaction¹. The type of turn linking strands together can also have a profound effect on stability²; a strongly turn-promoting sequence reduces the entropy cost of bringing two β-strands together.

The folding process of many proteins is thought to be cooperative and consisting of two-states³: the native or folded state, and the unfolded state. Cooperativity can also be seen at the level of secondary structure. The formation of isolated α-helix structure has been shown to be cooperative^{4; 5; 6}. Unlike α-helices however, β-sheets have the ability to exhibit cooperativity in two dimensions: parallel to strand direction and perpendicular to strand direction⁷.

Cooperativity in β-sheet formation along the direction of the strand can be thought of in terms of native backbone hydrogen bond formation between two adjacent strands (essentially β-hairpin formation). If the process is cooperative, the formation of each hydrogen bond between strands has a lower free energy cost than the formation of the preceding hydrogen bond. Stanger et al. observed that the stability of several designed β-hairpins was increased when the strand length was increased from 5 to 7 residues⁸. In a model study of backbone hydrogen bond formation in β-sheets, Guo et al. found there was a sequence-independent cooperativity parallel to strand direction inherent in β-sheet structure hydrogen bond formation⁹.

Cooperativity perpendicular to strand direction can be thought of in terms of multiple hairpin formation: the formation of one hairpin will reduce the free energy cost of forming another hairpin. In studies of a designed three-stranded β-sheet, Beta3s, de Alba et al. found little cooperativity if any between strands, i.e. perpendicular to strand direction¹⁰. However, the reference peptides used to calculate cooperativity in Beta3s contained charged termini while Beta3s did not, and the overall population values were quite low (13–31%), so a cooperative effect (if present) may not have been seen. In another study, Sharman & Searle found that a designed three-stranded β-sheet was more stable than its isolated C-terminal hairpin in aqueous methanol¹¹, indicating some cooperativity. Griffiths-Jones & Searle obtained similar results for 3β, another designed three-stranded β-sheet, and calculated that adding the N-terminal strand stabilized 3β by 0.26 kcal mol⁻¹¹².

Syud et al. observed a larger effect in studies of yet another designed three-stranded β-sheet, DPDP, and calculated that the formation of the N-terminal hairpin stabilized the C-terminal hairpin by as much as 0.42 kcal mol⁻¹¹³. DPDP was originally designed by Schenck & Gellman⁷ specifically to study the cooperativity of β-sheets perpendicular to strand direction. DPDP takes its name from the D-Pro residues in its two hairpin turns. D-Pro residues are strong promoters of type I’ and II′ turns¹⁴ which strongly favor β-hairpin formation¹⁵. For example, significant stabilization of Beta3s occurred when its turn sequences were replaced with D-Pro-Gly turns¹⁶. DPDP was observed to fold into the expected three-stranded β-sheet structure by NMR spectroscopy¹³. The β-sheet population of DPDP ranges from 75–83% at 277 K as estimated from NMR data by Hα chemical shift deviations, to 42–59% at 278 K as estimated by CD and FTIR¹⁷. We note that the NMR experiment probed the amount of secondary structure present only in the C-terminal hairpin, while the CD/FTIR data reflects overall secondary structure content for the entire peptide. Melting curves calculated for DPDP via these methods lacked the sigmoidal characteristic expected for two-state folding. The varying β-sheet populations given by the two different probes are also consistent with a non-two-state process. Syud et al. have suggested that a four-state model is more reasonable for DPDP¹³.

In order to study cooperativity perpendicular to strand direction in DPDP, Schenck et al. created LPDP, an analogue of DPDP in which the turn D-Proline in the N-terminal hairpin was replaced with L-Proline, effectively abolishing N-terminal hairpin formation. A subsequent analysis by Syud et al. compared the free energy of formation of the C-terminal hairpin in DPDP (with the N-terminal hairpin at least partially present) to the free energy of formation of the C-terminal hairpin in LPDP (N-terminal hairpin absent)¹³. The resulting data established that having the N-terminal hairpin present in DPDP stabilized the formation of the C-terminal hairpin by about 0.4 kcal mol⁻¹. Syud et al. also found cooperativity in similar experiments with a designed four-stranded β-sheet¹³.

In this study, the thermodynamic behavior of DPDP was studied via more than 2.4 µs of standard molecular dynamics (MD) and replica exchange molecular dynamics^{18; 19} (REMD) simulations. REMD (also known as parallel tempering MD) is a simulation technique that is able to cross high energy barriers in a shorter amount of time and provide improved sampling at lower temperatures than standard MD. REMD works by simulating N non-interacting replicas at N different temperatures, where N is chosen so that there is sufficient energy overlap between replicas. A replica at low temperature is given a greater chance to cross energy barriers by being exchanged with a replica at a higher temperature. This exchange is accepted or rejected based on a Metropolis criterion. Further details of the method have been presented elsewhere^{18; 19}.

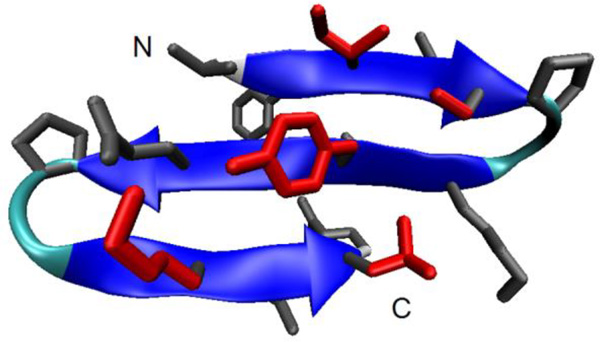
Unlike standard MD, REMD simulations were able to provide reproducible free energy surfaces, illustrating the improved convergence of REMD over normal MD. The global free energy minimum obtained with REMD (Figure 1) is shown to adopt the expected 3-stranded β-sheet conformation (an atomic-detail structure for the 3-stranded sheet form of DPDP has not been published). The simulation data shows that the C-terminal hairpin is significantly more stable than the N-terminal hairpin, consistent with the higher β-sheet population observed via NMR experiments (which focused on the C-terminal hairpin) as compared CD/FTIR measurements, which probed the entire peptide.

Figure 1.

Three stranded β-sheet model of DPDP as determined through simulation. Backbone is shown as a cartoon, sidechains are shown in a ‘licorice’ representation. Residues that form the hydrophobic cluster (I3, S5, Y10, K17, L19) are shown in red. Picture generated with VMD 1.8.3.

Previous experiments have only provided a lower bound for the cooperativity between the component hairpins of DPDP due to the uncertainty of the state of the N-terminal hairpin in fully folded DPDP. When we analyze our full ensemble of structures, we are able to reasonably reproduce this lower limit to folding cooperativity. However, due to the atomic-level resolution provided by the computational data, the state of each hairpin is known for every structure in the ensemble. The cooperativity can therefore be calculated directly by comparing the free energy of formation of a hairpin among subsets of the ensemble in which the state of the other hairpin is well-defined (either present or absent). The results of this work indicate that the actual cooperativity perpendicular to strand direction is about 2 kcal/mol larger than previously estimated lower limit. Similar values of cooperativity are obtained for both hairpins, suggesting this may be a general effect in β-sheets.

An alternate approach to quantifying the extent of cooperativity could be investigated through comparing hairpin stabilities in full-length DPDP to those in peptides containing only the region corresponding to each hairpin. This type of fragment analysis has been employed to study the unfolded state of proteins under conditions in which is it poorly populated²⁰. We chose not to investigate that route in the present case since the truncation of the sequence could lead to end effects such as fraying, resulting in an additional level of uncertainty that we believe can be avoided through detailed structural analysis of for the full-length peptide. Our approach of examining only the full sequence is also consistent with published DPDP cooperativity analysis based on experimental data¹³, thus permitting a direct validation of our results.

Results

Since no atomic-resolution structure has yet been published for DPDP, several different conformations were generated as starting points for simulations: a model of the fully folded 3-stranded β-sheet, a completely extended structure generated by the Leap module of AMBER using only the amino acid sequence (referred to hereafter as linear), and a compact structure (referred to hereafter as collapsed). The collapsed structure was chosen at random from an ensemble of structures generated with standard MD simulations starting from the linear system at 350K (see Methods for details, total simulation time ∼161 ns), with the sole criteria that no β-sheet backbone hydrogen bonding be present. A structure candidate for the fully formed sheet was selected from the same simulations as a structure that exhibited the backbone hydrogen bonding scheme expected based on analysis of NMR data for DPDP¹³ (Figure 1). Although this structure was chosen based on backbone hydrogen bonding atom distances and not energy, further MD and REMD simulations verify that this structure falls within the global free energy minimum at 279K (average RMSD <1.0 ÅǺ), and is therefore representative of the 3-stranded β-sheet state in the simulation model in addition to possessing the secondary structure indicated by experimental measurements.

A list of 28 “native” contacts were defined, as listed in Table 1 (see Methods). Q_Total is defined as the fraction of 3-stranded sheet contacts formed, Q_H1 is the fraction of N-terminal hairpin contacts formed, and Q_H2 is the fraction of C-terminal hairpin contacts formed. Hereafter we refer to the N-terminal hairpin (residues 1–13) as hairpin 1 and the C-terminal hairpin (residues 8–20) as hairpin 2. For each of these contact parameters 1.0 means all contacts were present and 0.0 means no contacts were present. Hairpin 1 was considered folded if Q_H1 > 0.5, hairpin 2 was considered folded if Q_H2 > 0.5, and DPDP was considered folded only if both cutoffs were satisfied. In addition to contacts, the radius of gyration (R_G) for the side-chains of residues I3, S5, Y10, K17, and L19 was used as an alternate order parameter. A clustering of these residues on one face of DPDP was inferred from NOE data¹³.

Table 1.

Native contact list for DPDP. Contacts obtained from 10 ns of standard MD simulation at 277K.

Hairpin	Contact	Type	Hairpin	Contact	Type
1	V1-I3	Sidechain	2	T9-Q20	Sidechain
1	V1-E12	Sidechain	2	Y10-K17	Sidechain
1	F2-T11	Sidechain	2	Y10-L19	Sidechain
1	I3-S5	Sidechain	2	T11-V13	Sidechain
1	I3-E12	Sidechain	2	T11-I18	Sidechain
1	T4-G7	Sidechain	2	T11-Q20	Sidechain
1	T4-T9	Sidechain	2	E12-dP14	Sidechain
1	S5-Y10	Sidechain	2	E12-G15	Sidechain
1	V1H–E12O	Hbond	2	E12-K17	Sidechain
1	V1O–E12H	Hbond	2	V13-I18	Sidechain
1	I3H–Y10O	Hbond	2	T9O–Q20H	Hbond
1	I3O–Y10H	Hbond	2	T11H–I18O	Hbond
2	K8-Y10	Sidechain	2	T11O–I18H	Hbond
2	K8-Q20	Sidechain	2	V13H–K16O	Hbond

Molecular Dynamics Simulations

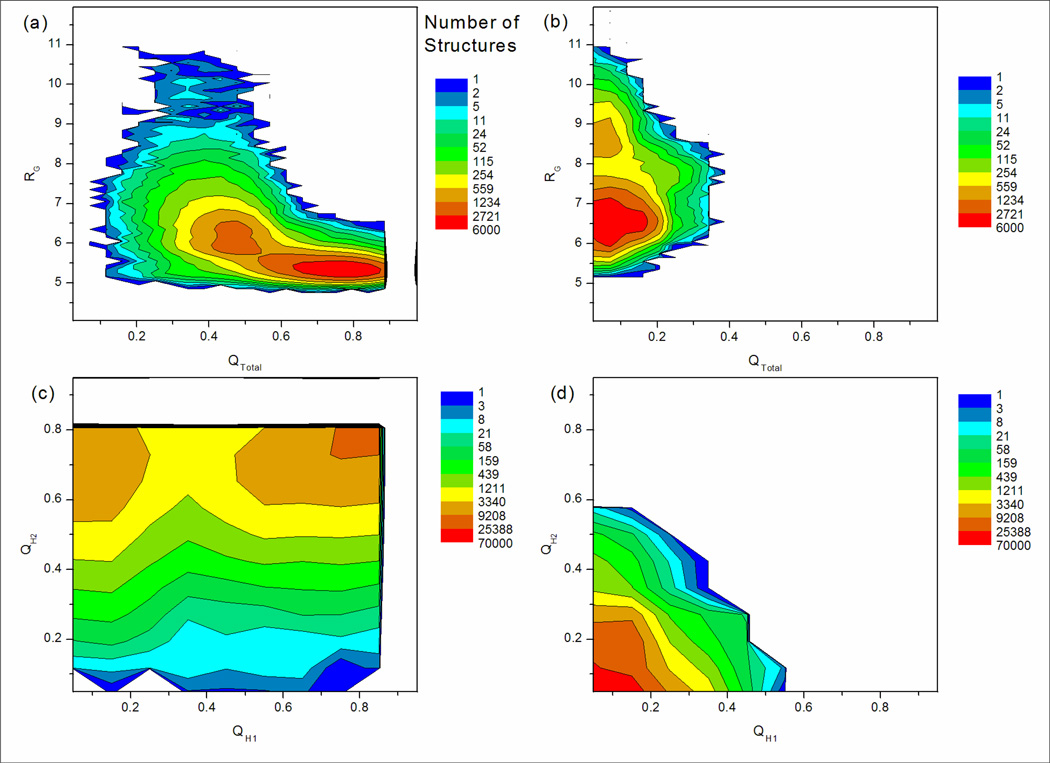
It is important to validate the extent of sampling convergence before performing thermodynamic analysis of simulation data. A reasonable measure of convergence is obtained by comparing data obtained from simulations initiated from different conformations to look for evidence of kinetic trapping²¹ on the timescale that is simulated. Any differences in the resulting data provide a lower bound for true uncertainty. Two normal MD simulations of DPDP were performed at 350K starting from both the 3-stranded sheet structure and the linear structure (referred to hereafter as the β-sheet and linear MD simulations) for 235 and 218 ns respectively. Two-dimensional population histograms of these simulations calculated from various coordinates are shown in Figure 2.

Figure 2.

Two-dimensional population histograms of DPDP from standard MD simulations at 350K representing about 230,000 structures. A logarithmic contour scale is used. (a) and (b) show Q_Total vs. R_G for simulations starting from the 3-stranded sheet model and linear structures respectively. The linear simulation (b) is trapped and never forms the three-stranded sheet. The β-sheet model simulation (a) explores some conformational space but never fully unfolds. (c) and (d) show Q_H1 vs. Q_H2 for simulations starting from β-sheet model and linear structures respectively. Again, the linear simulation (d) is trapped. While hairpin 1 shows a tendency to unfold in the simulation starting from the model three stranded sheet (c), hairpin 2 never unfolds. Overall, data is poorly converged.

Figure 2a and 2b show population as a function of the Q_Total and R_G order parameters. In the β-sheet MD simulation (Figure 2a) DPDP mainly stays in a wide (Q_Total) and narrow (R_G) peak centered on a Q_Total of about 0.80, which corresponds to the fully formed sheet. In this state the core tends to be compact, with R_G around 5.5 Ǻ. A second peak located around Q_Total=0.45 and R_G=6.0 Ǻ corresponds to partially unfolded structures. A fully unfolded state is never reached. In contrast, DPDP in the linear simulation remains in a peak located below Q_Total=0.20, indicating that few β-sheet contacts form and the folded state is never reached. In this unfolded state, R_G fluctuates between 6.5 Ǻ and 8.5 Ǻ, indicating the hydrophobic core is much less compact than when the sheet is fully formed.

Next, the fractional structure sampled by each of the component hairpins was examined. Two-dimensional population histograms for order parameters Q_H1 vs.Q_H2 are shown in Figures 2c and 2d. The β-sheet simulation (Figure 2c) contains two major peaks: the fully formed sheet (top right) and hairpin 1 unfolded (top left). This suggests that hairpin 1 is less stable than hairpin 2. In contrast, structures in the linear simulation (Figure 2d) never form a significant fraction of either hairpin; Q_H1 and Q_H2 mainly stay at about 0.0 with no other peaks present.

It should be noted that calculation of free energies from population data requires sampling of a proper Boltzmann weighted ensemble, and the large differences between the landscapes in Figure 2 indicate that the simulations are kinetically trapped on this timescale (∼200ns). Thus, any free energies obtained from these simulations would have extremely large uncertainties and convey little insight into the thermodynamic properties of DPDP, therefore they were not calculated. In addition, the complete lack of correspondence between the overall topology of the landscapes shown in Figure 2 suggests that they may not even provide a reliable indication of the positions or characteristics of important local minima that may be traversed during the folding process. However, the relatively high stability of the β-sheet structure during the 235 ns simulation suggests that our initial structure model is at least reasonable. In order to further probe the conformational space of DPDP, verify that the 3-stranded β-sheet model is indeed the “native” conformation under these simulation conditions, and to calculate free energy landscapes employing various order parameters, more extensive sampling was obtained using REMD.

Replica Exchange Molecular Dynamics

Two sets of REMD simulations were run, with all 12 replicas in one simulation starting from the extended linear structure and all 12 replicas in the other simulation starting from the collapsed conformation (see Methods for details). The alternate starting structures were used in order to obtain convergence estimates, as described above. Neither simulation included any of the β-sheet model structure, nor did any initial structure have any β-hairpin hydrogen bonds. Each simulation was carried out for ∼130,000 exchange attempts, for a total simulation length of ∼1.5 µsec for each initial structure.

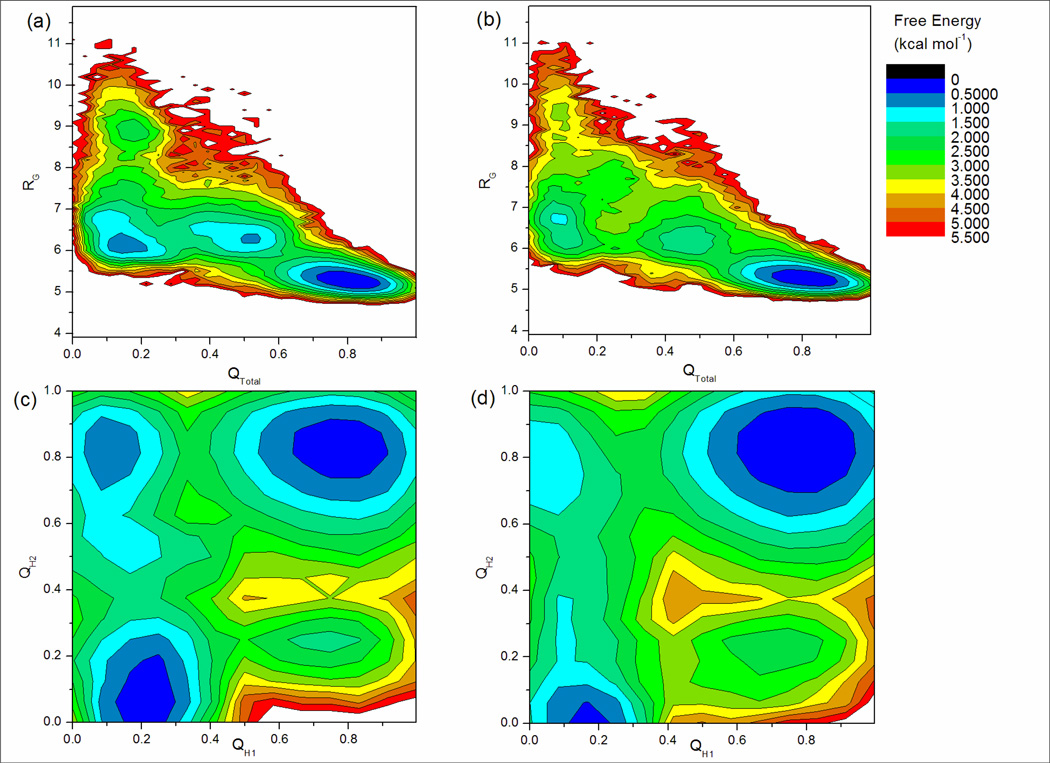
Figure 3 shows the free energy landscapes for Q_Total vs. R_G and Q_H1 vs. Q_H2 at 346K. This temperature was chosen to enable comparison to the standard MD results at 350K shown in Figure 2. In addition, since this temperature is above the melting point (T_m) of the 3-stranded sheet conformation (see below), minima corresponding to non-native conformations are reasonably well populated. This facilitates visual interpretation of the folding landscape. The qualitative features of the landscape are consistent with other temperatures, and the temperature-dependent populations of the various minima will be discussed in more detail below. In order to permit direct comparison to experimental data obtained at 277K, quantitative folding cooperativity analyses are performed using the ensemble sampled at 279K.

Figure 3.

Free energy landscapes of DPDP from REMD simulations at 346K representing about 130,000 structures. Data is much better converged than that obtained from standard MD, as seen from the similarity of the landscapes from simulations starting from different structures. (a) and (b) show Q_Total vs. R_G for simulations starting from collapsed and linear structures respectively. There are at least three major minima in these landscapes, showing that DPDP is a non-two-state system. (c) and (d) show Q_H1 vs. Q_H2 for simulations starting from collapsed and linear structures respectively. These landscapes indicate DPDP behaves more like a four-state system, with minima corresponding to (clockwise from top-right) fully formed β-sheet, only hairpin 1 folded, unfolded, and only hairpin 2 folded. Both (c) and (d) show that hairpin 2 alone is about 1.0 kcal mol⁻¹ more stable than hairpin 1 alone.

Despite some quantitative differences in relative depth of the minima, it appears that the major features of the free energy landscape of DPDP are qualitatively consistent between both REMD simulations. This is a dramatic difference from the poorly converged data obtained using standard MD.

It is apparent from the Q_Total vs. R_G landscapes shown in Figures 3a and 3b that DPDP is not a two-state system,. Both landscapes contain at least three well-populated free energy minima (with depths ranging from 0–2 kcal mol⁻¹) centered at Q_Total=0.80, 0.45, and 0.15. The global free energy minimum, located at Q_Total=0.80 in both REMD data sets, corresponds to the fully formed β-sheet under the simulation conditions, with high similarity (average RMSD <1.0) to the 3-stranded model structure we selected from our MD simulation (see Methods). This is particularly encouraging because no β-sheet hydrogen bonds were present in any of the initial structures for these REMD simulations, yet both predict the 3-stranded sheet as the global free energy minimum. The minimum is centered slightly lower than Q_Total=1.00, reflecting some fraying at the ends of each hairpin due to thermal fluctuations; this is expected as contacts were defined at the lower temperature of 277 K. The broad oval shape of the minimum with respect to Q_Total is also consistent with a moderate degree of conformational flexibility in the fully formed sheet, though the narrow range of R_G values sampled in this basin indicates that the hydrophobic core remains substantially intact during these fluctuations. The next of the three minima, centered at Q_Total=0.45, corresponds to an ensemble of partially folded structures, the nature of which will be discussed below.

The minimum at Q_Total=0.15 corresponds to the unfolded state. The core is much less compact in this state, as seen from the R_G coordinate which ranges from about 6.5 to 9.0 Ǻ. The non-zero Q_Total indicates that this ensemble retains at least some structure elements of the β-sheet, although this data does not reveal whether the residual contacts are consistent among all structures in this state. Analysis of the fraction of each of the contacts sampled in this fairly well-defined minimum reveals that the residual contacts arise predominantly from turn formation, which is not surprising considering the strong propensity of D-proline to form type I′ and II′ β-turns^{14; 15}. It is this drive toward turn formation that provides DPDP with significant stability as compared to peptides of similar length without D-proline residues^{7; 13; 16}, as a strong turn is related to greater hairpin stability^{2; 22; 23}.

Next, the stability of hairpin 1 compared to hairpin 2 was examined. Figure 3c and 3d show free energy landscapes calculated from the Q_H1 and Q_H2 order parameters. These landscapes suggest that DPDP populates at least 4 states, with the four basins corresponding to formation of (clockwise from top right) both hairpins (3-stranded sheet), only hairpin 1, neither hairpin (unfolded), and only hairpin 2. This 4-state model is consistent with that proposed by Syud et al.¹³ and Griffiths-Jones & Searle¹² for three-stranded anti-parallel β-sheet folding. It is apparent from these figures that the basin with hairpin 2 present and hairpin 1 absent is lower in free energy than that with hairpin 1 present and hairpin 2 absent, i.e. hairpin 2 is thermodynamically more stable than hairpin 1. Based on relative free energies of these basins, it is estimated that formation of hairpin 2 alone is ∼1.0 kcal mol⁻¹ more stable than hairpin 1 alone in both simulations. Difference in hairpin stability has been observed for other 3-stranded β-sheets^{24; 25}.

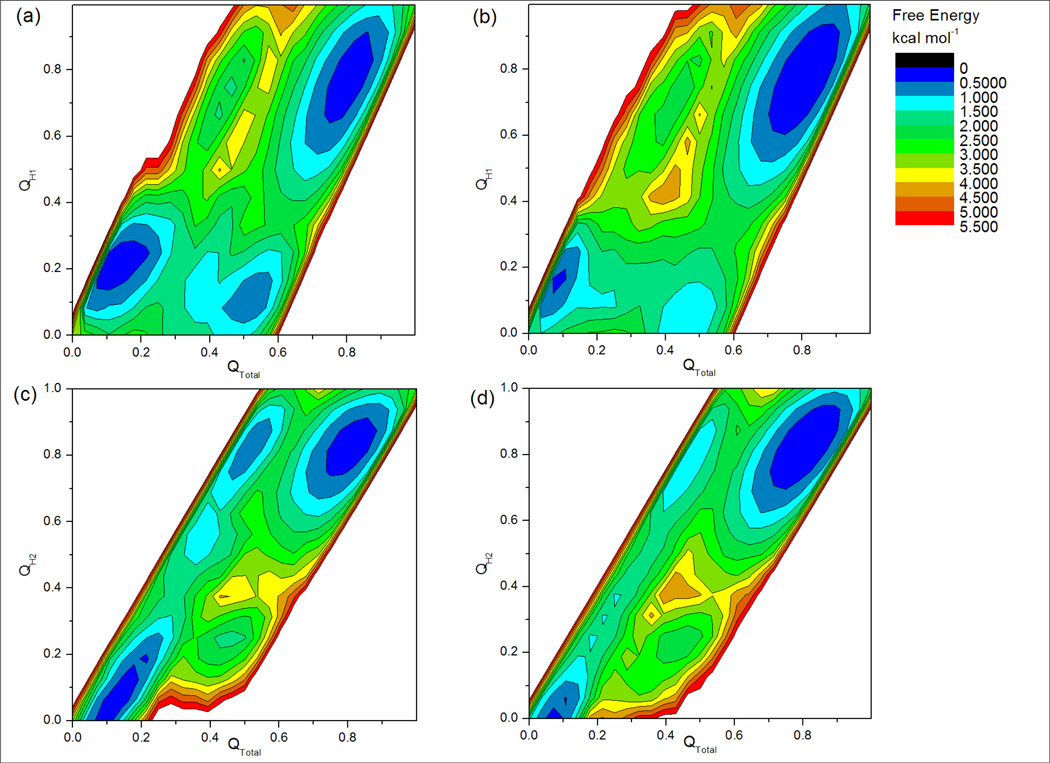
In order to further examine the nature of the structures in the partially unfolded ensemble (Q_Total=0.45), free energy landscapes were plotted as a function of Q_Total and either Q_H1 or Q_H2 (Figure 4). These landscapes show that the minima in the previous Q_Total vs. R_G landscapes (Figures 3a and 3b) centered at Q_Total=0.45 are themselves made up of two separate minima corresponding to having either hairpin 1 or hairpin 2 folded. This data matches the Q_H1 vs. Q_H2 landscapes shown in Figures 3c and 3d, showing that four states are indeed present under these conditions. Also, it is seen that at Q_Total =0.45 it is more favorable (again ∼1.0 kcal mol⁻¹ in both simulations) to have hairpin 2 folded than hairpin 1. Since partially formed hairpins are not well-populated, each of the two hairpins shows significant cooperativity parallel to the strand direction. This is consistent with NMR data¹³ that indicates similar populations of hairpin 2 when measured using different residues in the C-terminal strand.

Figure 4.

Free energy landscapes from REMD simulations at 346K representing approximately 130,000 structures. (a) and (b) show Q_Total vs Q_H1 for simulations starting from collapsed and linear structures respectively. (c) and (d) show Q_Total vs Q_H2 for simulations starting from collapsed and linear structures respectively. The minima at Q_Total=0.45 previously seen in Figures 3a and 3b are seen here to be made up of partially folded hairpin 1 and hairpin 2 structures. Again, hairpin 1 is less stable than hairpin 2; at Q_Total=0.45 structures with high Q_H1 are about 1.0 kcal mol⁻¹ higher in free energy than structures with high Q_H2.

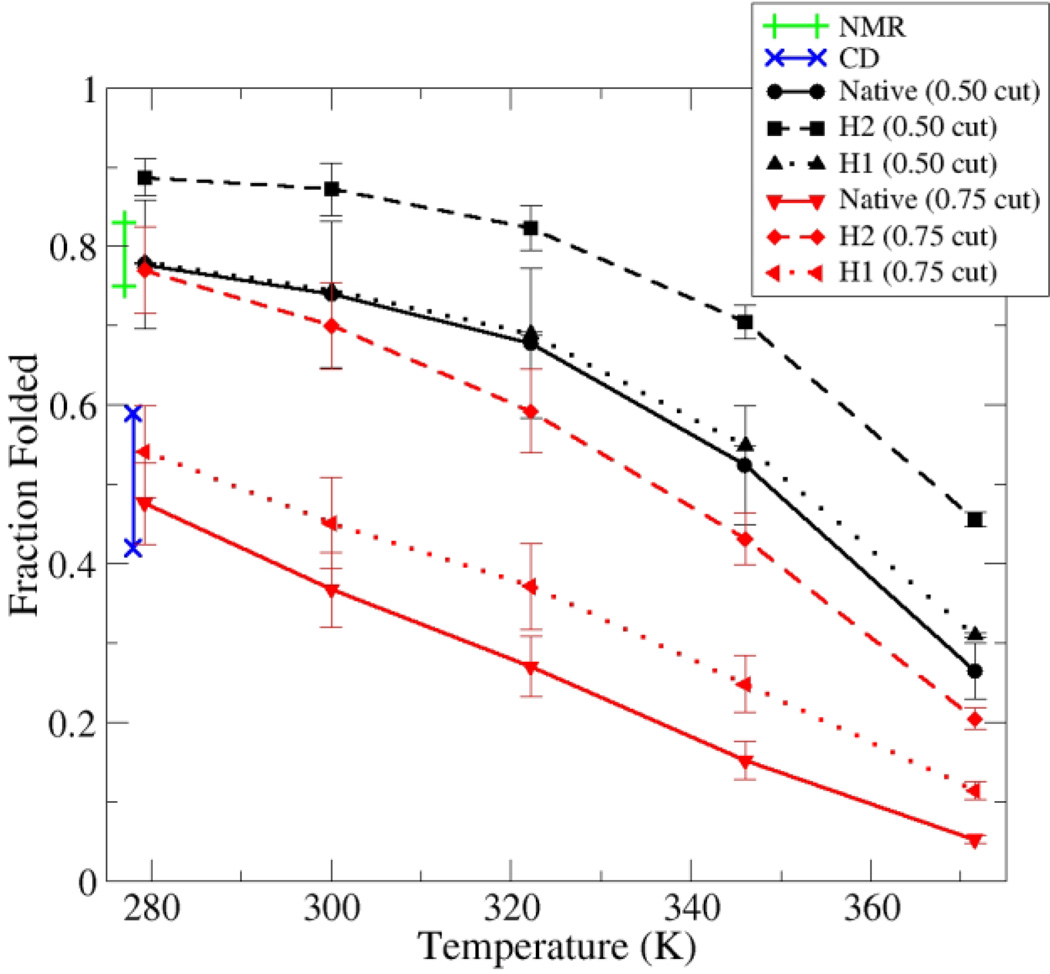
Melting curves for DPDP and its component hairpins are shown in Figure 5. However, it should be noted that these curves are not intended to quantitatively reproduce experimental values since the order parameter used to calculate fraction folded in this case (Q) may be quite different from the data obtained from various experimental probes, particularly since folding is not two-state; such behavior has been reported previously²⁶. As described above, we use a contact fraction cutoff of 0.5 since it reasonably matches the boundaries of the free energy basins observed in Figures 3 and 4. However, melting curves obtained with this cutoff slightly overestimate the hairpin and sheet stability as compared to NMR and CD measurements. This may indicate that our simulation model overestimates the stability of β-sheet formation, although the differences correspond to only a few tenths of kcal/mol in free energy, well below our expectation of error for an additive molecular mechanics force field with a continuum solvent model. The difference may also reflect the challenge in comparing fractional population based on atomic coordinates to those based on experimental observables, particularly for systems that do not fold cooperatively. If a more restrictive cutoff value of 0.75 is used, the agreement with both sets of experimental data is significantly improved, with the melting curve for hairpin 2 falling within the range based on NMR data and the melting curve for the 3-stranded sheet falling within the range indicated by the CD data. In any case, one must always exercise caution when interpreting data obtained using a strict cutoff based on structural properties.

Figure 5.

Average melting curves for DPDP hairpin 1, hairpin 2, and overall ensemble from linear and collapsed REMD simulations. The data is quite sensitive to choice of cutoff. The black lines represent a less restrictive cutoff of 0.50, while the red lines represent a more restrictive cutoff of 0.75. Hairpin 1 structures were considered folded when Q_H1 was greater than the cutoff, hairpin 2 structures were considered folded when Q_H2 was greater than the cutoff, and fully formed β-sheet structures were considered formed when both cutoffs were satisfied. Using a more restrictive cutoff (0.75), the hairpin 2 melting curve intersects with NMR data (green line) and overall melting behavior intersects with CD data (blue line). Regardless of cutoff, hairpin 2 is more stable than hairpin 1 in each case. Error bars reflect differences between the linear and collapsed REMD data sets.

The calculated curves are also quite useful in comparing the stability of the individual hairpins to that of the full β-sheet. It is clear from Figure 5 that the relative temperature-dependent stabilities do not strongly depend on the choice of cutoff; for both values tested, hairpin 2 is much more stable as compared to hairpin 1.

Cooperativity perpendicular to strand direction in our simulations was measured in two ways using the ensemble of structures at 279 K from the REMD simulations. Since our cooperativity calculations are based solely on simulation data for DPDP, there is the additional advantage that the effect of the L-Pro substitution (LPDP) need not be considered.

The first calculation was intended to generate data comparable to that which had been obtained through experiment¹³, in which hairpin 2 population was compared between DPDP and LPDP (in which hairpin 1 is expected to be absent). For this case, we calculated the free energy for formation (ΔG) of hairpin 2 in two sets of DPDP structures: our entire ensemble (to match DPDP in experiments) and only the subset of structures which lacked hairpin 1 (Q_H1<0.5, analogous to LPDP in experiments). Differences in the free energy of formation of hairpin 2 (ΔΔG) between these sets of structures are presumably attributable to the influence of the conformation of hairpin 1. Since hairpin 1 is only partially folded in DPDP, the effect on hairpin 2 will depend on the extent of hairpin 1 folding (which was not determined in the experiments and is therefore not evaluated for the purpose of this particular calculation). It is for this reason that Syud et al. acknowledged that their values for cooperativity represent only a lower limit.

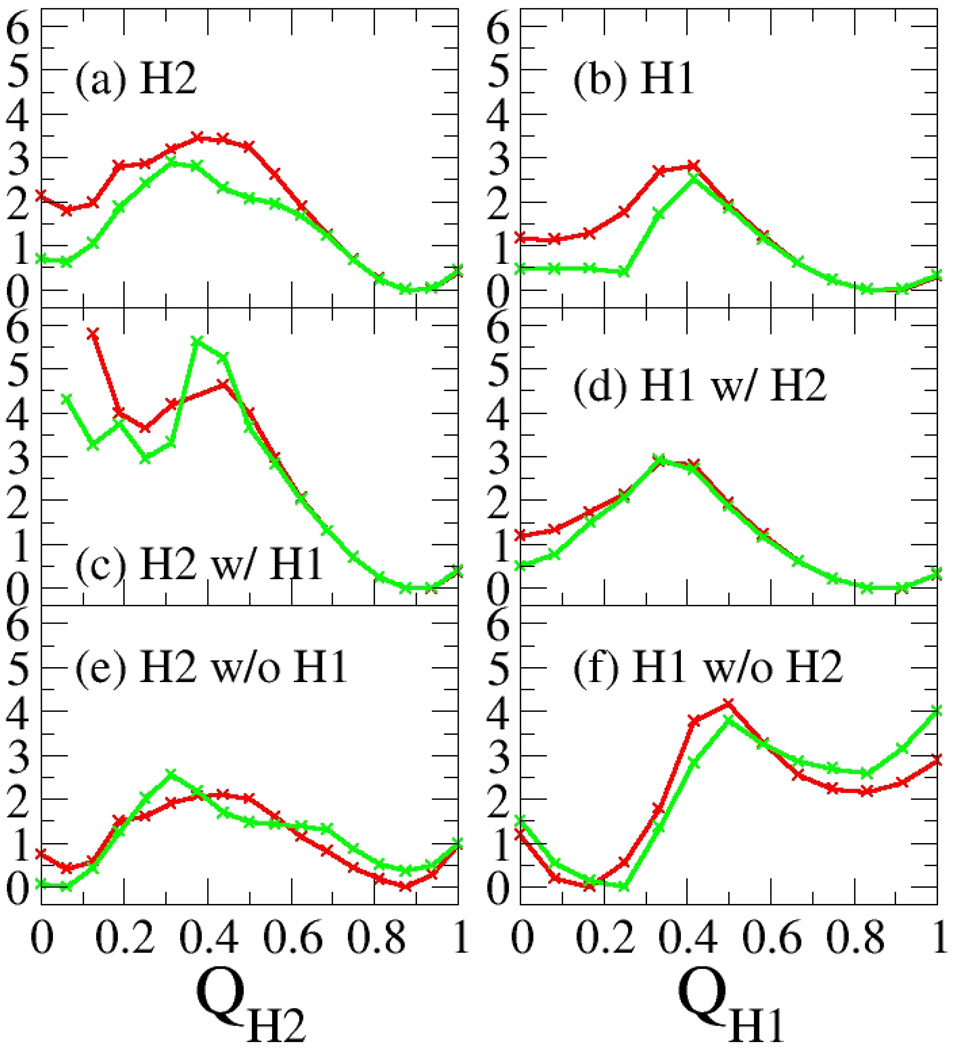
The resulting free energy profiles for the sub-ensembles are shown in Figure 6, and the free energies of hairpin formation and cooperativity are listed in Table 2 (obtained from the ensembles at 279K as described in Methods). It is immediately apparent that the free energy profile of formation for a given hairpin is strongly influenced by the presence or absence of the neighbor, indicating at least partial cooperativity. The formation of hairpin 2 in the overall ensemble (Figure 6a, comparable to DPDP in experiments) becomes 1.1 ± 0.7 kcal mol⁻¹ less favorable when hairpin 1 is known to be absent (Figure 6e, comparable to LPDP in experiments). This is in reasonable agreement with the values of 0.38 to 0.42 kcal mol⁻¹ obtained by Syud et al.¹³. Although only hairpin 2 was used as an experimental probe of cooperativity, we also calculated the effect of (partial) hairpin 2 formation on the stability of hairpin 1. This effect is much greater than was calculated for hairpin 2; the formation of hairpin 1 becomes 3.0 ± 0.5 kcal mol⁻¹ less favorable when hairpin 2 is absent. It is apparent that without hairpin 2, the formation of hairpin 1 is very unfavorable. It is important to note that this approach resulted in a β-sheet cooperativity value that depends significantly on which hairpin is considered in the analysis (−1.1 vs. −3.0 kcal mol⁻¹).

Figure 6.

Free energy of individual hairpin formation in DPDP at 279 K for varying states of the other hairpin. The red curves were calculated from the REMD simulation starting from the linear structure, and the green curves were calculated from the REMD simulation starting from the collapsed structure. Hairpin 2 formation is shown as a function of Q_H2 (a) with the state of hairpin 1 undetermined (equivalent to DPDP in experiments), (c) with hairpin 1 present, and (e) with hairpin 1 absent (equivalent to LPDP in experiments). Hairpin 1 formation is shown as a function of Q_H1 (b) with the state of hairpin 2 undetermined, (d) with hairpin 2 present, and (f) with hairpin 2 absent. Hairpin X was considered present if Q_HX>0.50 and absent if Q_HX≤0.50. The noise at low values of Q_H2 in (a) reflects the fact that there is a low population of structures with only hairpin 1 folded.

Table 2.

Average cooperativity values calculated from both REMD simulations in kcal mol⁻¹ at 279 K for various hairpin states of DPDP. ΔΔG_exp refers to cooperativity values obtained using ensembles corresponding to those studied experimentally, while ΔΔG_sim uses ensembles that correct for partial formation of the neighbor hairpin in ensemble (a). A detailed discussion of this difference is presented in the text, and uncertainty calculations are described in Methods.

a) ΔG H2	−1.3 ± 0.6	d) ΔG H1	−0.8 ± 0.4
b) ΔG H2 w/ H1	−3.4 ± 0.4	e) ΔG H1 w/ H2	−1.1 ± 0.3
c) ΔG H2 w/o H1	−0.2 ± 0.3	f) ΔG H1 w/o H2	2.2 ± 0.2
ΔΔG H2exp (a–c)	−1.1 ± 0.7	ΔΔG H1exp (d–f)	−3.0 ± 0.5
ΔΔG H2sim (b–c)	−3.2 ± 0.5	ΔΔG H1sim (e–f)	−3.3 ± 0.4

Our next measure of cooperativity was intended to be more direct than was possible by comparing DPDP and LPDP. In this case, the free energy of formation of a given hairpin in the ensemble of structures lacking the other hairpin (Figures 6e and 6f) was compared to the free energy of formation of that hairpin when the other hairpin is known to be present (Figure 6c and 6d). For hairpin 2, this ΔΔG was calculated by comparing the free energy of formation of hairpin 2 in two sets of structures; those with hairpin 1 absent (Q_H1 less than 0.50) (Figure 6e) and those with hairpin 1 present (Q_H1 greater than 0.50) (Figure 6c). This corrects the cooperativity value for the partial hairpin folding within DPDP. In this case the formation of hairpin 2 when hairpin 1 is present becomes 3.2 ± 0.5 kcal mol⁻¹ more favorable than the formation of hairpin 2 when hairpin 1 is absent. This ΔΔG value is nearly three times that obtained when the state of hairpin 1 was not taken into account (−1.1 ± 0.7 kcal mol⁻¹).

In contrast, the values obtained for hairpin 1 formation when hairpin 2 is known to be present are quite similar to those obtained when the state of hairpin 2 is not taken into consideration (−3.3 ± 0.4 kcal mol⁻¹). This is because no significant fraction of structures having hairpin 1 without hairpin 2 is sampled, as stated above. In each case, the end result is that having one hairpin present stabilizes the formation of the other hairpin by ∼3 kcal/mol, indicating significant cooperativity perpendicular to strand direction.

We noted that the cooperativity values obtained for the two hairpins differed significantly when the partial folding of the partner hairpin is not considered. In contrast, when the data is corrected for partial folding of the neighboring hairpin the values become quite similar (−3.2 ± 0.5 vs. −3.3 ± 0.4 kcal mol⁻¹). This sequence independence of the resulting cooperativity measure indicates that including the partial folding correction results in a more robust analysis method, and also suggests that the value may reflect general properties of β-sheets; further study on other sequences should be carried out to confirm this hypothesis.

Discussion

Both REMD simulations were started from unfolded structures, yet both found the fully formed β-sheet within a reasonable amount of simulation time (<15 ns, data not shown). This is quite good compared with our standard MD simulation starting from an unfolded state, which showed no β-sheet-like structure even after 200 ns of simulation time. The simulations were able to reproducibly find three-stranded β-sheet structures that were consistent with experimental observations of DPDP as a fully formed sheet. These structures were the global free energy minimum at low temperatures under our simulation conditions and should be good representatives of the 3-stranded sheet state of DPDP, for which an atomic-resolution structure has not yet been published. The agreement between free energy landscapes calculated from REMD simulations is also much better than that obtained from normal MD and illustrates the superior convergence of the REMD method as has been observed by others²⁵.

The overall ensemble of structures consists of four states: folded, unfolded, and a partially folded state that is composed of structures with either one of the two hairpins formed, in agreement with the non-two-state folding behavior of DPDP observed by Syud et al.¹³. There exists some population of structures with only hairpin 1 or only hairpin 2 folded, resulting in a four-state folding model as has been proposed for 3-stranded β-sheets by Griffiths-Jones & Searle¹².

Our simulations indicate that hairpin 2 is more stable than hairpin 1. The melting curve in Figure 5 shows the β-sheet population ranges obtained from NMR¹³ and CD/FTIR¹⁷ experiments. The difference between these ranges agrees well with the observed difference between our simulated melting curves for hairpin 2 and the fully formed β-sheet. Syuid et al. measured the change in Hα chemical shifts of residues in hairpin 2, using a cyclic peptide that corresponded to a DPDP hairpin 2 as the fully folded reference state and LPLP as the random coil reference state (replacing D-proline with L-proline abolishes the hairpin turn⁷). They noted that, since folding is not 2-state, their NMR measurements only provided the population of hairpin 2, which were used to estimate cooperativity values. In contrast, the CD/FTIR measurements of Kuznetsov et al.¹⁷ probe the entire peptide and thus the average β-sheet content for all states.

A previous computational study of DPDP by Wang & Sung²⁷ indicated that hairpin 1 was more stable than hairpin 2. However, their result was based on 100 ns of standard MD data at 297K; our standard MD simulations were very poorly converged on this timescale even though they were run at a higher temperature of 350K. In addition, this observation does not appear to be consistent with the results from NMR and CD experiments; if hairpin 1 were more stable, then the NMR experiment should report a lower population than CD, which was not observed.

Why is hairpin 2 so much more stable than hairpin 1? Our computational observation appears to be consistent with experimental studies of DPDP. Syud et al. found that replacing the second D-Pro in DPDP with Asn did not alter the folding pattern or cooperativity values of that hairpin significantly¹³ (although overall stability was reduced). Chen et al. reported that mutating D-Pro in hairpin 1 to Asp resulted in formation of a β-bulge instead of a β-turn, while the same mutation in hairpin 2 retained the β-hairpin shape²². The fact that hairpin 2 appears less sensitive to mutations may indicate that it is intrinsically more stable than hairpin 1, though this is by no means a comprehensive analysis. It is also possible that having Ser5 in the i position of hairpin 1 β-turn detracts from the stability of hairpin 1. Amino acid propensities²⁸ indicate that Ser is strongly turn-promoting, which may lead it to compete for turn geometry with D-Pro and Gly in hairpin 1, reducing the population of the native hairpin. In contrast, the i position in hairpin 2 is occupied by Val, which is considered turn-breaking. This suggests that mutating Ser5 to Val may confer additional stability to hairpin 1, and perhaps also to the 3-stranded sheet state due to the cooperativity between the hairpins. Furthermore, analysis of contact melting profiles (data not shown) reveals that hairpin 2 in DPDP contains two strong non-turn contacts: a salt-bridge between Glu13 and Lys18 and a hydrophobic cross-strand interaction between Tyr11 and Leu20. Cross-strand salt-bridging is known to have a stabilizing effect in β-hairpins^{29; 30}. Rao & Caflisch suggested that the C-terminal hairpin of another designed 3-stranded β-sheet was more stable than the N-terminal hairpin due to strong hydrophobic interactions, particularly a contact between aromatic Trp and Tyr²⁵. In contrast, hairpin 1 has no salt bridge and weaker hydrophobic interactions overall.

The experimentally observed cooperativity between the individual hairpins is reproduced in our simulations, although our data is more amenable to direct calculation of the actual magnitude of the effect. Schenck & Gellman studied the population of hairpin 2 in two sequences: DPDP and LPDP, in which the D-Pro in hairpin 1 was replaced by L-Pro, effectively “turning off” formation of hairpin 1. DPDP demonstrated increased population of hairpin 2 as a result of partial hairpin 1 formation. Subsequent NMR experiments by Syud et al.¹³ estimated that the additional stability conferred upon DPDP by “turning on” hairpin 1 to be from −0.42±0.22 kcal/mol to −0.38±0.13 kcal/mol at 277K, depending on the Hα resonance chosen. Importantly, they noted that this value is a lower limit on the true cooperativity since hairpin 1 is not always in the hairpin state in DPDP, thus limiting the effect on hairpin 2. In other words, hairpin 1 in DPDP is not fully “turned on”.

Experimental cooperativity values are not available for hairpin 1, but our calculations show a similar effect; the free energy difference between a) having hairpin 1 irrespective of the state of hairpin 2 and b) having hairpin 1 without hairpin 2 is −2.9 ± 0.5 kcal mol⁻¹ at 279K. Interestingly and unlike hairpin 2, this value is relatively insensitive to whether we consider the state of hairpin 2; the ΔΔG value for formation of hairpin 1 in ensembles of structures with hairpin 2 fully present or fully absent is −3.3 ± 0.4 kcal mol⁻¹. This insensitivity most likely reflects the relative instability of hairpin 1 with respect to hairpin 2 and the relatively low population of hairpin 1 in the absence of the full 3-stranded β-sheet.

It is interesting to note that all of our calculations place the value for hairpin cooperativity at about −3.3 ± 0.5 kcal mol⁻¹ at 279K. Further investigation is needed to determine whether this value reflects general properties of β-sheet systems.

Methods

A model system was created from the sequence of DPDP (V₁FITSdPGKTY₁₀TEVdPGOKILQ₂₀, dP=D-proline, O=ornithine) except that a Lysine was substituted for the Ornithine. Replacing Ornithine with a Lysine in a related peptide analogous to the C-terminal hairpin of DPDP caused no detectable effect on the structure³¹. The termini were amidated and acetylated in accordance with experiments. DPDP was designed with a net charge of +2 to prevent aggregation⁷, and our model retains this net charge.

Simulations were carried out using Amber version 8.0³². All hydrogen atom bond lengths were constrained using the SHAKE algorithm³³. All nonbonded interactions (ie. without cutoff) were calculated at each time step. All systems were modeled with the AMBER ff99 force-field with modified backbone parameters to reduce α-helical bias³⁴. Steepest descent energy minimization was performed on all structures for 500 steps prior to simulation. All simulations were carried out using Amber’s implementation^{35; 36} of the Generalized Born (GB) implicit solvent model³⁷. Explicit counterions were not included, consistent with most studies that employ continuum solvation models. Some studies have questioned the validity of implicit solvent models^{38; 39} for protein folding studies, however, implicit solvent models have been used successfully in studies of both β-hairpin and β-sheet systems^{25; 40; 41; 42; 43; 44}. Also, previous studies of β-sheets in explicit solvent have not shown that water plays a specific structural role in the folding/unfolding process^{45; 46}. Obtaining well-converged thermodynamic data in explicit solvent remains a significant challenge even for systems of the size of DPDP; therefore we employed an implicit solvent model with the understanding that careful validation against available experimental data must be obtained.

Simulations were performed using REMD as implemented in Amber version 8. A total of 12 replicas were used for REMD simulations of DPDP at the following temperatures: 260.1, 279.3, 300.0, 322.2, 346.0, 371.6, 399.1, 428.7, 460.4, 494.5, 531.0, and 570.3 K. The number of replicas was chosen so that sufficient energy overlap would be achieved between replicas. The temperature for each replica was generated based on an exponential distribution and chosen so that an exchange acceptance ratio of 0.15 would be achieved. Exchanges between replicas at neighboring temperatures were attempted at an interval of 1 ps. Temperatures were maintained between exchanges by coupling to an external bath using Berendsen’s scheme⁴⁷.

A list of contacts in the β-sheet state (Table 1) were defined from analysis of a low temperature (277 K) 10 ns normal MD run starting from the model 3-stranded sheet structure. Hydrogen bond contacts were included if they existed for more than 70% of the simulation, and side-chain contacts were considered extant if the center of mass of the side-chain (Cα for the glycines) was less than 6.5 Å from another non-neighboring side-chain more than 60% of the time. This procedure is similar to that followed in a study of a different three-stranded β-sheet⁴⁵. Based on these criteria 28 contacts were defined, as listed in Table 1. Cutoffs for Q_H1 and Q_H2 were chosen based on the boundaries of the free energy basins obtained for these order parameters in DPDP (Figure 3). Hydrogen bonds were defined as a distance between hydrogen donor and acceptor of less than 2.5Å. No angle cutoff was used.

Free energy landscapes were calculated from multidimensional histograms according to ΔG_i = -RTln(N_i/N₀), where N_i is the population of a particular histogram bin along the desired coordinates (e.g. fraction of contacts and radius of gyration), and N₀ is the most populated bin, making 0 kcal/mol the lowest free energy state. The free energy curves in Figure 6 were calculated in a similar manner using 1-dimensional histograms. Hairpin X was considered ‘present’ when Q_HX was greater than 0.5.

ΔG values for each hairpin state in table 2 were calculated at 279K using ΔG = -RTln(X/N-X). For the data corresponding to the experiments in which the state of the neighboring hairpin was not determined, X is the number of structures with the hairpin of interest present and N is the total number of structures. This corresponds to the net ΔG for formation of the hairpin in the entire ensemble. For the data in which the state of the neighboring hairpin is considered, X is the number of structures with the hairpin of interest present and also with the neighboring hairpin in the specified state (either present or absent). N is the total number of structures with the neighboring hairpin in the specified state. For example, in the case of ΔG for formation of hairpin 2 with hairpin 1 present, X is the number of structures with both Q_H2>0.5 and Q_H1>0.5, while N is the number of structures with Q_H1>0.5.

Uncertainties in these ΔG values were calculated as half the difference between the values obtained from the linear and collapsed simulations. Uncertainties in ΔΔG values were obtained from the square root of the sum of squares of the individual ΔG uncertainties.