Abstract
Rotating frame spin-lattice relaxation, with characteristic time constant T1ρ, provides a means to access motion-restricted (slow) spin dynamics in MRI. Due to their restricted motion, these spins are sometimes characterized by a short transverse relaxation time constant T2 and thus can be difficult to detect directly with conventional image acquisition techniques. Here we introduce an approach for three-dimensional adiabatic T1ρ mapping based on a magnetization prepared Sweep Imaging with Fourier Transformation (MP-SWIFT) sequence which captures signal from almost all water spin populations including the extremely fast relaxing pool. A semi-analytical procedure for T1ρ mapping is described. Experiments on phantoms and musculoskeletal tissue specimens (tendon, articular and epiphyseal cartilages) were performed at 9.4 Tesla for both the MP-SWIFT and fast spin echo (FSE) read outs. In the phantom with liquids having fast molecular tumbling and single-valued T1ρ time constant, the measured T1ρ values obtained with MP-SWIFT and FSE are similar. Conversely, in normal musculoskeletal tissues, T1ρ values measured with MP-SWIFT are much shorter relative to values obtained with FSE. Studies of biological tissue specimens demonstrated that T1ρ-weighted SWIFT provides higher contrast between normal and diseased tissues as compared to conventional acquisitions. Adiabatic T1ρ mapping with SWIFT readout captures contributions from the otherwise undetected fast relaxing spins allowing more informative T1ρ measurements of normal and diseased states.
Keywords: rotating frame relaxation, bound water, ultrashort T2, SWIFT, relaxometry, Musculeskeletal
Introduction
The time constant T1ρ characterizes spin-lattice relaxation in the rotating frame (1).T1ρ is sensitive to the interactions between motion-restricted water molecules and the corresponding local macromolecular environment (2,3). With T1ρ, the slow motional regime can be accessed at high magnetic field (2,3). Previous studies have shown that T1ρ is sensitive to structural alterations in musculoskeletal tissues, often providing more information than might be obtained from analysis of conventional longitudinal or transverse relaxations (2,4-7). Specifically, T1ρ relaxation has been shown to be sensitive to the proteoglycan (PG) loss in the early stage of articular cartilage degeneration (8-14) and in cases of vertebral disc degeneration (15), and has been found utility in the study of epiphyseal cartilage of the developing skeleton (16).
T1ρ is traditionally measured by applying a continuous wave (CW) pulse which “locks” the magnetization to the effective field direction (17). The CW spin-lock (CW-SL) pulse creating an effective field (in the kHz range) in the ‘y’ direction (in the first rotating frame) is usually embedded between 90°x and 90°-x rotations that are accomplished with short hard pulses or adiabatic half passage pulses (18). Alternatively, relaxation in the rotating frame can be studied using a time-dependent spin-locking field, for example, created by a train of frequency-modulated adiabatic full-passage (AFP) pulses (19-22). This technique, entitled “adiabatic T1ρ”, was recently shown to provide sensitive detection of structural changes in articular cartilage (13,14,23). Adiabatic T1ρ characterizes relaxation during RF irradiation when the magnetization vector is aligned with the direction of the time-dependent effective field (Beff(t)) (Fig.1). As compared with the conventional CW-SL method, the adiabatic T1ρ method is less affected by inhomogeneity of B1 and static field B0 due to the offset independent adiabaticity property of the AFP pulses (24). The adiabatic relaxation methods are inherently sensitive to a broader range of molecular motions as compared to the CW method (19). Further, it has been recently demonstrated that adiabatic T1ρ reduces magic angle dependence in relaxation mapping (25). All these features are critical for tissue characterization and especially during in vivo study when homogeneity of the B1 and B0 fields could be altered by patient motion (23).
Fig.1.
(a) Illustration of adiabatic T1ρ relaxation in the Larmor rotating frame. During the adiabatic rotation the magnetization follows the effective field Beff. (b) Schematic of the magnetization prepared SWIFT sequence. MP blocks are embedded after each m number of SWIFT readout periods (mTR periods). Each MP block is composed of four AFP pulses, with consecutive phases prescribed according to the MLEV4 scheme.
In real tissues, multiple spin populations which are characterized by short and long relaxation time constants have been shown to exist. Different T2 or T1ρ relaxation times were found in tendon or cartilage tissues by using rapid imaging sequence or spectroscopy methods (26-28). Water bound tight or closely associated to macromolecules tends to have short T2 and T1ρ values, thus has conventionally been undetected due to very short transverse relaxation time (26,27). Characterization of these pools and the correlation of MR properties with tissue microstructure are critically important (29). On the other hand, conventionally, T1ρ relaxation measurements are performed by interleaving the readout of an imaging sequence with magnetization preparation (MP) blocks used for generating T1ρ weighting. In tissues having fast relaxing components in sub-millisecond range, e.g. in highly ordered tissues or highly mineralized tissues, the measurement of T1ρ using conventional sequences as read out is problematic due to considerable signal decay during the echo time (TE) before the detection (30).
In this paper, we introduce a three-dimensional (3D) adiabatic T1ρ relaxation time mapping utilizing an ultrashort T2-sensitive sequence for readout, in addition to the existing 3D T1ρ relaxation time mapping techniques (31-34). Multiple MRI pulse sequences capable of preserving signal from fast relaxing spins have been developed in recent decades (35-40). In general all these developed techniques are applicable to use as readout for the proposed T1ρ relaxation mapping with preserved short T2 components. In this paper, the Sweep Imaging with Fourier Transformation (SWIFT) sequence was used as the readout sequence (39,41). SWIFT is an emerging technique that allows imaging of almost all biological tissues including tissues with ultra-short T2 relaxation times in the microsecond time scale (39,41,42). With appropriate parameters, SWIFT provides nearly pure proton density weighted imaging, and by utilizing magnetization preparation embedded within this sequence, different types of contrasts (T1, T2, T1ρ, T2ρ etc.) can be generated (42-45). Here, we describe the experimental setup and semi-analytical procedure to generate and quantify the T1ρ relaxation with SWIFT readout, and demonstrate application of T1ρ for quantification of osteochondral and tendon specimens.
Methods
Pulse sequence
The pulse sequence diagram is shown in Fig.1b. MP blocks are embedded after each m number of SWIFT readout periods (m TR periods). Each MP block is composed of four AFP pulses of the hyperbolic secant HSn family (here n is the stretching factor) (46), each having a duration of t180 with phases prescribed according to the MLEV4 phase cycling scheme (47). The minimal duration for one MP block is defined as ΔTmp = 4t180. The variable duration of the MP train is equal then to Tmp = ΔTmp · Nmp, with Nmp as the number of MP blocks.
Steady state signal equation
In regular SWIFT without any magnetization preparation, the repeated excitation drives the spin system to the steady state with equilibrium magnetization:
| [1] |
where and θ is the excitation flip angle (39,48) With the preparation block, the steady-state magnetization generated during MP-SWIFT is different and depends on Tmp. Simulations based on Bloch equations show the evolutions of Mz to different steady states for different Tmp settings (Fig. 2). Of relevance, as shown in Fig. 2, two competitive processes, i.e., signal decay with time constant T1ρ and signal recovery with T1, cause the steady-state signal to oscillate about an average value. This oscillating steady state is used for the reconstruction of 3D images. The average steady-state signal intensity in this case is given by (see Appendix A):
Fig.2.
Bloch simulations showing evolution of the signal to the steady-state during MP-SWIFT pulse sequence with different Tmp values. The observed signal oscillation is the result of two processes: T1ρ decay during each Tmp (black portion) and T1 recovery during m SWIFT readouts (color-coded points). The parameters used for simulations were: T1 = 500 ms, T1ρ = 40 ms, TR = 2.6 ms, m = 16, t180 = 1.5 ms and SWIFT flip angle = 2°.
| [2] |
where and . After normalization by , the Eq. 2 becomes
| [3] |
By separating out the exponential decay Eρ and taking the logarithm:
| [4] |
Se is the modified signal, which is a mono-exponential function in this case. On the logarithmic scale, Se is represented by a straight line with slope equal to . In practice, T1ρ can be estimated from the set of data measured with different Tmp. Obviously, the signal also depends on T1 relaxation, and thus an independent acquisition for measuring T1 is required. Here, the variable flip angle method with SWIFT readout was used to acquire T1 maps (49).
Two water pools: the fitting strategy
In the previous section the description of the single pool spin system was presented. In the case of real tissues, multiple pools of water populations should be considered (27,50). The most practical model is a two pool system, characterized by two different proton populations: free water and bound water (27), having “slow relaxation” with long and “fast relaxation” with short , respectively. The signal having contributions from both slow and fast relaxing components can be described as:
| [5] |
where and , and Cs and Cf are normalized populations of the two components separately (Cs + Cf = 1). The average relaxation time constant is the slope of ln(Se) at Tmp → 0:
| [6] |
In principle, the relaxation parameters can be estimated by fitting the experimental data using Eq. 5. The quality of fitting, however, critically depends on the relative difference between intrinsic relaxation parameters of the two pools and also on the sufficiency of sampling points of the relaxation decay curves. Note that the relaxation time constants of the two components should be sufficiently different in order to be separable with a given noise level (51). Even if these two components are very different, an adequate sampling of the short component could be problematic because of the limited duration of the AFP pulses which require sufficient peak power to satisfy adiabaticity. Thus, the reliability of experimental mapping of the exact , or even values is questionable. Therefore, we propose to use two values, and , representing the asymptotic average relaxation time and the slow relaxation time, respectively. The value can be determined from the slope of the line connecting the first two data points on the logarithmic scale (red solid line in Fig. 3a). The value of approaches (empty circles in Fig. 3b) when ΔTmp → 0, as shown in Fig. 3b. With increasing Tmp, the contribution of the fast relaxing component vanishes, which allows the long T1ρ component to be estimated from the tail of the relaxation decay curve (see Appendix B for details). A representative example of the fitting is shown in Fig. 3a.
Fig.3.
(a) Fitting example of the simulated decay S(Tmp) (red circles). The parameters used for simulations are: and . T1 was assumed to be the same for both fast and slow relaxing components, T1 = 1000 ms. The red solid line shows the fitting using just the first two data points ( ) to provide an estimation approaching . The grey dash-dot line shows the resulting and Cs obtained from the intermediate fitting (black dash line) (see Appendix B for details). (b) Examples of the asymptotic approaching at different conditions. The empty circles are the values of .
Experimental details
Phantoms
Test experiments were performed on three separate phantoms containing 0.1, 0.1, and 0.4 mM MnCl2 in DI water, agar, and DI water, respectively. These solutions were poured in glass tubes immersed in a bigger tube containing saline solution. The T2 values of these three phantoms were all above 20 ms.
Tissue specimens
Two specimens were studied: a piece of mature bovine Achilles tendon (size = 1×1×1 cm3), and a juvenile femoral condyle from a 12 week-old pig (size = 3×3×3 cm3) including both articular and epiphyseal cartilage layers. The animal specimens were placed in tubes and immersed in Fluorinert (3M, Minnesota, USA) to match the magnetic susceptibility.
All images were acquired on a 9.4 T-31 cm bore horizontal animal MRI scanner (Agilent Technologies, Santa Clara, CA USA), using a volume transmit/receive coil (Agilent Technologies) or a homemade coil with three parallel loops of a 22 mm diameter. All simulations and data processing were performed using MATLAB (R2012b, The Mathworks). For T1ρ measurement, variable numbers of MP blocks were added after every 16 SWIFT readout periods (m = 16 in Eq. 2) to obtain images with different Tmp. The experimental parameters are summarized in Table 1. Different durations of the AFP pulses (t180) were utilized in order to test the effect of different weighting of fast and slow relaxing components. The peak RF power was matched to ensure adiabatic condition of the AFP pulses, and the time-bandwidth product of the pulse (R) was adjusted to keep excitation bandwidth of the pulse (BWmp) the same for different pulse durations (24). Thus, the Beff(t) functions were the same for the different t180 values (20). The specific values of the maximal effective frequency and the averaged effective frequency are shown in Table 1. The time to acquire 128,000 radial spokes with each setting of Tmp varied from 5 to 11 minutes, depending on Tmp. The spokes in k-space were isotropically distributed on a sphere using the pseudo-random Halton approach to minimize signal oscillation effects on the steady state (52). All MP-SWIFT and maps were generated using linear least squares fitting on a pixel-by-pixel basis in the logarithmic coordinate of the transformed signal (Se) according to the developed algorithm. For T1 measurement, images with flip angles of 1, 3, 5, 7, 10 degrees were acquired, then fitted to the Ernst equation using a non-linear least square algorithm to generate the corresponding T1 map (49). BW = 125 kHz and TR = 2.6 ms were used for all SWIFT acquisitions.
Table 1. Parameters Used In FSE and SWIFT T1ρ Measurements.
| Sample | t180 (ms) | Nmp | BWmp (kHz) | (kHz) | (kHz) | θ (°) | Resolution (μm2) |
|---|---|---|---|---|---|---|---|
| Phantom 1 | 1.5 | SWIFT: 0, 2, 4 FSE: 0, 4, 8 |
10 | 5 | 5 | 2 | 130 × 130 |
| Phantom 2 | 3 | SWIFT: 0, 1, 2 FSE: 0, 2, 4 |
10 | 5 | 5 | 2 | 130 × 130 |
| Phantom 3 | 3 | SWIFT: 0, 1, 2 FSE: 0, 2, 4 |
4.8 | 5 | 2.7 | 2 | 130 × 130 |
| Tendon | 0.3 | SWIFT: 0, 1, 2, 3, 4, 6, 8, 12, 16 | 18 | 10 | 8.5 | 4 | 78 × 78 |
| 1.2 | SWIFT: 0, 1, 2, 3, 4, 5 | 18 | 10 | 8.5 | 4 | 78 × 78 | |
| Femoral condyle | 2 | SWIFT: 0, 1, 2, 3, 4 FSE: 0, 1, 2, 3, 4, 6 |
10 | 5 | 5 | 3 | 130 × 130 |
For comparison, the T1ρ relaxation time constants were also measured with a single-slice 2D fast spin echo (FSE) sequence used as readout following a number of MP blocks. The preparation pulse parameters were matched to the MP-SWIFT (i.e., the same AFP pulses, duration and RF power). With FSE, TR = 5000 ms, effective TE = 5.5 ms, ETL = 4, thickness = 1 mm, matrix size = 256 × 256 and bandwidth = 130 kHz were used. The choice of 2D FSE which was used here for comparison with MP-SWIFT is justified because it is a commonly used as readout for T1ρ measurements and has sufficient SNR to guarantee good accuracy. The long TR in FSE destroys the steady-state condition and therefore signal decays exponentially during the length of Tmp, and thus, T1ρ maps were generated using linear least squares fitting on a pixel-by-pixel basis to the exponential function:
| [7] |
For comparison with FSE, SWIFT images were averaged to the same thickness (= 1 mm) as the FSE images.
To assess the reproducibility of the proposed technique, a distal humeral trochlea of a 10-week old pig (size = 3×3×3 cm3) was scanned 3 times during the same day utilizing the same parameter set as was used for the porcine femoral condyle (Table 1).
Results
The signal-to-noise ratio (SNR) of the SWIFT image in all experiments with Nmp = 0 was higher than 60. The SNR decreases as Tmp increases, but was greater than 20 for all Tmp. SNR was calculated by taking the ratio of the mean of the signal intensities in a given ROI and the standard deviation of the signal of a ROI from the background.
In Fig.4 the T1ρ relaxation time constants of the MnCl2 phantoms (with T2>20ms) measured by FSE and SWIFT sequences are shown. The T1ρ of the 0.1 mM of MnCl2 solution was approximately 320 ms. The addition of agar to the 0.1 mM MnCl2 solution changed the T1ρ time constant to approximately 200 ms as measured by either sequence. The T1ρ values of the phantom with higher concentration of MnCl2 at 0.4 mM were around 85 ms in both FSE and SWIFT measurements (Fig. 4). The T1ρ of saline was around 2.6 s with both SWIFT and FSE measurements, as expected for the fast tumbling spins. This also further verified that the signal equation for the single component is accurately described by Eq. 2.
Fig.4.
(a) Representative T1ρ time constant maps of MnCl2 doped agar (smaller tube) merged in the bigger tube containing saline. (b) Example plots of the signal evolution for both saline and MnCl2 doped agar. Both FSE and SWIFT plots are indicating single component decay. (c) Comparison of the adiabatic T1ρ values of three different phantoms measured with FSE and SWIFT sequences. 400 data points were plotted for each phantom. The solid line is the line of identity, representing perfect correspondence. The dash line is the linear fit of the averaged T1ρ values from the three data sets, with r = 0.999 and p < 0.01. Each data point corresponds to one voxel in the T1ρ maps.
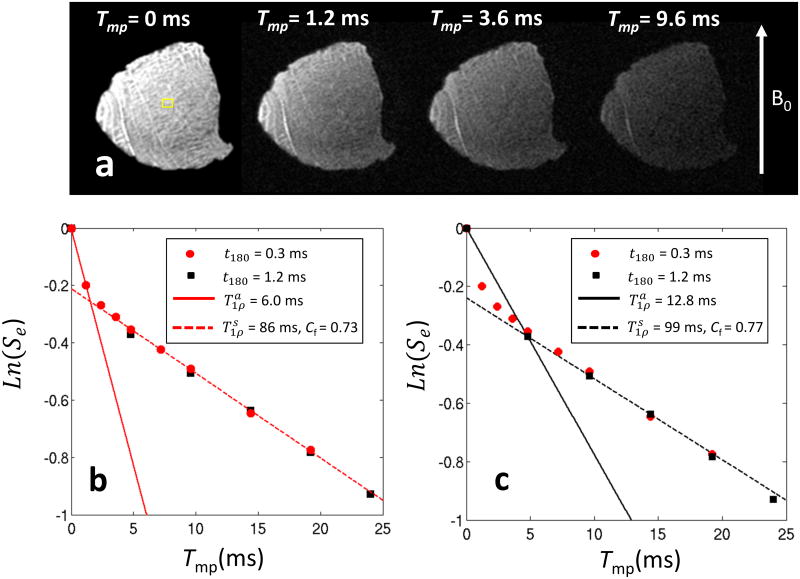
The T1ρ decay curves of a bovine tendon specimen obtained with the MP-SWIFT sequence at different t180 values are shown in Fig. 5. Because tendon is a highly ordered tissue and characterized by short T2, it is practically undetectable with conventional MRI sequences. Therefore, only measurements with SWIFT are presented. From the data points shown in Fig. 5, it is apparent that the Se decay has multiple components with different decay rates. Since the effective fields produced with t180 = 0.3 and 1.2 ms were kept the same, some data points are overlapped as expected. In the case of t180 = 2.0 ms, the fitted is equal to 16.8 ms, whereas for t180 equal to 0.3 ms, decreases to 6.0 ms. These results suggest that reducing t180 increases weights of fast relaxing spins. Fittings of with Tmp > 5 ms demonstrate the method of extraction of information about slowly relaxing spins. In both t180 = 0.3 and 1. 2 ms cases, the fitted value and the population are similar.
Fig.5.
MP-SWIFT images of the bovine tendon specimen acquired with different Tmp (a) and graphs (b,c) representing Se signal measured in ROI (shown in the image by yellow square) with two different t180 durations. The data points did not fall on the same line indicate multiple decay rates. Since the effective field for pulses with durations of t180 = 0.3 and 1.2 ms were kept the same, some data points were overlapped as expected. (b,c) The solid lines are drawn by connecting first two data points, the slopes of which determines in experiments with different t180. The asymptotic decreases with decreasing t180 demonstrating increased weighting from the fast relaxing spins. The dash lines are the fittings of data points with Tmp > 5 ms from which the contribution from slowly relaxing spins can be retrieved.
T1ρ maps and decay plots of a juvenile porcine femoral condyle are shown in Fig.6. The juvenile femoral condyle reveals the homogenous appearing epiphyseal cartilage (z2 in Fig.6a), in addition to the articular cartilage in the most superficial layer of the tissue (z1 in Fig.6a). Longer T1ρ in the articular cartilage compared to the epiphyseal cartilage is observed. The zonal organization is similar in both SWIFT (Fig.6a) and FSE T1ρ maps (Fig.6b), however with different absolute values. A focal lesion due to vascular failure within the epiphyseal cartilage is easily identifiable (black arrows, Fig.6a). The focal lesion near the interface of cartilage and bone reveals higher T1ρ values in all T1ρ maps. The corresponding hematoxylin and eosin (H&E) stain histology shows the necrotic cartilage matching the focal lesion (Fig.6c). The T1ρdecays on the logarithmic scale of the 2D FSE and 3D SWIFT T1ρ measurements are shown in Fig.6d and Fig.6e, respectively. For normal tissues, the signal obtained with FSE readout (blue line in Fig.6d) is apparently single component decay, while the signal from SWIFT readout (blue line in Fig.6e) reveals multiple decay rates. Interestingly, the lesion shows multiple components even in the FSE measurement (red data points in Fig.6d). The fitted and values from the ROI in the lesion are very similar in both SWIFT (Fig.6e) and FSE (Fig.6d) measurements (red points and lines). This implies the absence of fast relaxing components within the lesion. SWIFT maps obtained using the strategy described above are shown in Fig.6f. Notably, the SWIFT map is very similar to the FSE T1ρ map in Fig.6b. The apparent population map of the fast relaxing spins, which was generated from Cs in the SWIFT measurement, is shown in Fig.6g. The overall fraction of the fast relaxing component is around 50% in epiphyseal cartilage and 30% in articular cartilage. The fraction of the fast relaxing component in the area of the lesion is close to 2%. The T1 value measured in the lesion area was ∼1600 ms, which is longer than the T1 of normal surrounding tissues (1100 ms). The contrast between normal tissue and the lesion is shown in Fig.6h. The maximal relative relaxation time's difference (RRTD) between normal and lesion tissues RRTD = [T1ρ(lesion) - T1ρ (normal)]/ T1ρ (normal) from SWIFT map is about 6 times higher than that obtained with FSE readout.
Fig.6.
T1ρ maps and example of the fitting strategies of the juvenile porcine femoral condyle specimen. The maps in (a) are the same map presented with different color scale. A gradient of the T1ρ values along the direction of the cartilage depth is observed in all maps. Below the articular cartilage (labeled as z1 in (a) is the epiphyseal cartilage (labeled as z2 in a). SWIFT values of the normal epiphyseal growth and articular cartilage are much shorter than T1ρ measured by FSE (b), while the SWIFT (f) values are close to FSE T1ρ (b). (c) H&E stain of the same specimen revealing the focal area of chondronecrosis matching the lesion detected in MR images. The signal from a ROI in normal tissues (blue line in d) from FSE experiment is apparently single component decay, while the signal from SWIFT experiment (blue line in e) exhibits multi-component decay. The signal from the ROI in the lesion region shows multi-exponential decay even in the FSE measurement (red data points in d). Of note, the T1ρ values within the lesion region is comparatively similar for SWIFT and FSE measurements, which implies the absence of fast relaxing components within the lesion. This conclusion is also supported by population map of the short component shown in (g). (h) The average values of T1ρ from ROI over the normal epiphyseal cartilage and the focal lesion areas. The relative contrast between normal and lesion tissues in the SWIFT map is much higher than in the FSE T1ρ map.
Since an independent acquisition aiming at measuring T1 is needed for determination of T1ρ values, the dependence of the deviation in T1ρ estimation (defined a ) on the deviation of T1 ( ) is analyzed and shown in Fig.7a. As can be seen, DT1ρ does not have an apparent dependency on the T1ρ values, and is roughly linear with the DT1. From the theory section and Appendix B, the obtained and Cf will deviate from the true values if the approximation is not fully satisfied. Figure 7b-d shows examples of the estimated deviation of , Cs and Cf originating from the fitting procedure. Within the range of ratio from 10 to 30, the error from the fitting model is less than 15% in most cases. The fitting error source from SNR were also analyzed by Monte-Carlo simulation and showed in Fig. 7e & f.
Fig.7.
(a) The dependence of the deviation of T1ρ, , on the deviation of T1, . (b), (c) & (d) show the relative deviations , with v representing, , Cs or Cf respectively. The deviations originated from the approximations used in the fitting procedure. was fixed to 10 ms. For the ratio in the range from 10 to 30, the intrinsic error from the fitting model was less than 15%. (e) & (f) Dependence of the fitting error on SNR by using Monte-Carlo simulation. and was used with equal population. For each data point in (e) & (f), the fitting process was repeated 1000 times with noise chosen from the corresponding normal distribution randomly.
For the reproducibility experiment, the measured relaxation time constants and population from the three separate scans with SWIFT readout on the same specimen in the epiphyseal cartilage layer from the same ROI were [average ± standard deviation (coefficient of variation) over the three scans]: , , Cf = 0.59 ± 0.03 (5.08%).
Discussion
In this work measurement of adiabatic T1ρ in 3D using the SWIFT sequence was proposed and analyzed. Sensitivity of the sequence to different spin populations, including both fast and slow relaxing spins, was shown and the application to the musculoskeletal system was exemplified.
In biological tissues, several types of motional processes contribute to the relaxation mechanisms. Depending on the tissue, more than one relaxation mechanism may be operative simultaneously, but with different relative contributions. Generally, the more rapidly relaxing component is assigned to water that is more tightly bound to macromolecules (such as proteoglycans and collagens in cartilage), and the slow relaxing component is assigned to bulk water.
In the phantom study of single component relaxation with comparatively long T2, FSE-T1ρ matches well with the SWIFT-T1ρ in phantoms with different T1ρ values (Fig.4). For the juvenile porcine femoral condyle (Fig. 6), the measured FSE-T1ρ in the articular and epiphyseal cartilage is around 300 and 200 ms, respectively. This is similar to the values previously reported by Toth etc. on juvenile goat specimens using FSE readout (16), but higher than the adiabatic T1ρ values measured in mature specimens with FSE readout, which fall in 100-200 ms range (13,14,23). Note besides specimens, the specific parameters used in these studies were also not the same. While only one relaxing component was found in these previous studies with FSE readout, here by using SWIFT, apparent multi-component decay rates are observed in biological specimens (Fig.5 & 6). The measured values using SWIFT were all much shorter than the T1ρ measured with FSE (Fig.6). In Fig.6, the T1ρ values of a focal lesion in a juvenile porcine femoral condyle specimen are much longer than those in the normal surrounding tissues in both FSE and SWIFT measurements. T1ρ within the lesion is much closer in SWIFT and FSE mapping comparing to normal tissues, which implies the lack of fast relaxing spins within the area of concern. It is consistent with the histological finding of chondronecrosis, a disease process characterized by the degradation of the normal, tightly bound collagen and proteoglycan structures. This is also in agreement with the population map of the short component shown in Fig.6g, where in the lesion region, the lowest population of fast relaxing component is close to 2%.
From the apparent population map of the fast relaxing spins shown in Fig.6g, the overall fraction of the fast relaxing component was around 30% in the articular cartilage. The fast relaxing component originated from water with highly restricted motion, which is more tightly bound to proteoglycan and collagen in cartilage. Prior reports estimated the population of water pool bound to proteoglycan in cartilage at about 15-30% (26,27,50,53), and at 3-6% for the pool of water bound to collagen (50). Thus the total population of fast relaxing spins is measured in same range as our result. In contrast, the populations of the fast relaxing component in epiphyseal cartilage in the developing skeleton from our experiments are around 50% which is a considerably higher value relative to that obtained in articular cartilage. This is expected due to difference in matrix composition between epiphyseal and articular cartilage, for example, the greater concentration of glycosaminoglycan in epiphyseal cartilage (54). A full explanation will require a separate analysis which is beyond the scope of the present work.
The fact that the abnormal tissue within the lesion is dominated by slowly relaxing spins, while the surrounding tissue remains normal with multiple pools of water, reveals the different range of sensitivity of T1ρ values obtained with SWIFT and FSE readouts. The fitting for of the slow relaxing components showed in Appendix B was mainly for the purpose of providing proof of principle. In practice, the map of would be more informative and useful. As illustrated in the theory section, is a parameter approaching to which is the weighted harmonic mean of the long and short T1ρ values. The slope for first two data points was calculated as the asymptotic value. contains weighting from , , Cs, Cl and. From Fig.6, the SWIFT map not only showed the similar multilayer features as the FSE T1ρ map, but also provided much higher relative contrast between normal and lesion tissues as compared to the T1ρ maps obtained with FSE readout. Therefore, with the capability of measuring the full dynamic range of the entire spin population in biological tissues, SWIFT map can maximize contrast for detecting pathology.
The fitting of only uses the first two data points. The first points are crucial since they include contribution from fast relaxing spins. In the adiabatic T1ρ, the first point is obtained without any preparation pulse which can preserve maximal fast relaxing signal. In the case of the CW-SL T1ρ mapping, the first point is measured in presence of two 90° pulses with zero spin-lock time to keep the condition the same for measurements of all points in the relaxation decay. During these pulses the signal from spins having relaxing times comparable to the pulse durations could decay significantly. The latter is why the adiabatic version of T1ρ was preferred for the present study.
There are several limitations of the developed method and analytical formalism, which need to be elaborated further. Firstly, since the approximation was used during the fitting, the fitted , Cs and Cf have intrinsic deviation from the fitting model in addition to experimental errors. Therefore, if separation of the multiple components is desirable, a more extended fitting strategy will be needed to better separate different relaxing components. Secondly, four AFP pulses were used in one MP block which may lead to SAR limitation for in vivo applications, particularly at high field. To reduce SAR and increase efficiency, the AFP preparation was applied every m TR (m = 16 in this paper) instead of every single TR. The SAR of adiabatic pulses could be compared with that of CW-T1ρ by calculating the root-mean-square RF power; however, due to the differences in pulse modulations, the relaxation phenomena probed by the two methods would be different (20). The benefit of adiabatic pulses is that they offer additional flexibility for alleviating SAR issues (24). Finally, an independent T1 measurement is required for the quantification of T1ρ, which leads to a longer total acquisition time. In future work, a view-sharing method might be utilized to reduce the total measurement time (55). Furthermore, the assumption of a single T1 component, which was applied in both the T1 and T1ρ measurements, was based on our earlier work in which multiple T1 components were not observed in the cartilage system (49). To be more precise, for the systems with multiple T1 components, further extension of the analytical procedure will be needed. Despite these limitations, many MRI applications may benefit from the improved contrast provided by approaches similar to those introduced here.
Conclusion
In conclusion, a method called MP-SWIFT has been described for measuring T1ρ in tissues containing fast relaxing spins. The signal equation of the proposed method and a semi-analytical procedure for the T1ρ mapping were derived. SWIFT-T1ρ and FSE-T1ρ values matched well with each other in the case of spins having long T2 values. However, in normal biological tissues, multiple T1ρ relaxing components were observed in SWIFT measurements. Besides information about slowly relaxing spins, both simulations and experimental results suggest that SWIFT , a parameter approaching the weighted harmonic mean of the T1ρ of all decaying components, contains extra contributions from fast relaxing spins which are undetected with FSE readout. The relative contrast ratio between normal and lesion tissues in SWIFT map was also much higher than in the FSE T1ρ map. The potential application for detecting degeneration in the musculoskeletal system has been demonstrated, but the extent to which this method can be used remains to be shown. Furthermore, T1ρ is not only applicable in musculoskeletal tissues, but has also been associated with neurological disorders such as Parkinson's and Alzheimer's diseases (56,57), and has been proposed recently for applications in cardiac (58) and abdominal (59) MRI. The developed 3D SWIFT T1ρ relaxation mapping technique in this paper also has high potential for studying these diseases.
Supplementary Material
Acknowledgments
We thank Dr. Ferenc Toth for providing the animal specimens and histology.
Grant sponsor: NIH P41 EB015894, WM KECK foundation, Academy of Finland #260321 and #285909.
Abbreviations
- T1ρ
spin-lattice relaxation time in rotating frame
- SWIFT
sweep imaging with Fourier transformation
- MP-SWIFT
magnetization prepared-SWIFT
- FSE
fast spin echo
References
- 1.Redfield AG. Nuclear spin thermodynamics in the rotating frame. Science. 1969;164(3883):1015–1023. doi: 10.1126/science.164.3883.1015. [DOI] [PubMed] [Google Scholar]
- 2.Sepponen RE, Pohjonen JA, Sipponen JT, Tanttu JI. A method for T1 rho imaging. J Comput Assist Tomo. 1985;9(6):1007–1011. doi: 10.1097/00004728-198511000-00002. [DOI] [PubMed] [Google Scholar]
- 3.Rommel E, Kimmich R. Volume-selective determination of the spin-lattice relaxation time in the rotating frame T1 rho, and T1 rho imaging. Magn Reson Med. 1989;12(2):209–218. doi: 10.1002/mrm.1910120207. [DOI] [PubMed] [Google Scholar]
- 4.Duvvuri U, Charagundla SR, Kudchodkar SB, Kaufman JH, Kneeland JB, Rizi R, Leigh JS, Reddy R. Human knee: In vivo T1(p)-weighted MR imaging at 1.5 T - Preliminary experience. Radiology. 2001;220(3):822–826. doi: 10.1148/radiol.2203001662. [DOI] [PubMed] [Google Scholar]
- 5.Duvvuri U, Goldberg AD, Kranz JK, Hoang L, Reddy R, Wehrli FW, Wand AJ, Englander SW, Leigh JS. Water magnetic relaxation dispersion in biological systems: the contribution of proton exchange and implications for the noninvasive detection of cartilage degradation. Proc Natl Acad Sci U S A. 2001;98(22):12479–12484. doi: 10.1073/pnas.221471898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Borthakur A, Mellon E, Niyogi S, Witschey W, Kneeland JB, Reddy R. Sodium and T1rho MRI for molecular and diagnostic imaging of articular cartilage. NMR in biomed. 2006;19(7):781–821. doi: 10.1002/nbm.1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Keenan KE, Besier TF, Pauly JM, Han E, Rosenberg J, Smith RL, Delp SL, Beaupre GS, Gold GE. Prediction of glycosaminoglycan content in human cartilage by age, T1rho and T2 MRI. Osteoarthr Cartil. 2011;19(2):171–179. doi: 10.1016/j.joca.2010.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Duvvuri U, Reddy R, Patel SD, Kaufman JH, Kneeland JB, Leigh JS. T1rho-relaxation in articular cartilage: effects of enzymatic degradation. Magn Reson Med. 1997;38(6):863–867. doi: 10.1002/mrm.1910380602. [DOI] [PubMed] [Google Scholar]
- 9.Duvvuri U, Kudchodkar S, Reddy R, Leigh JS. T-1 rho relaxation can assess longitudinal proteoglycan loss from articular cartilage in vitro. Osteoarthr Cartil. 2002;10(11):838–844. doi: 10.1053/joca.2002.0826. [DOI] [PubMed] [Google Scholar]
- 10.Regatte RR, Akella SV, Borthakur A, Kneeland JB, Reddy R. Proteoglycan depletion-induced changes in transverse relaxation maps of cartilage: comparison of T2 and T1rho. Acad Radiol. 2002;9(12):1388–1394. doi: 10.1016/s1076-6332(03)80666-9. [DOI] [PubMed] [Google Scholar]
- 11.Jordan CD, McWalter EJ, Monu UD, Watkins RD, Chen W, Bangerter NK, Hargreaves BA, Gold GE. Variability of CubeQuant T1rho, quantitative DESS T2, and cones sodium MRI in knee cartilage. Osteoarthr Cartil. 2014;22(10):1559–1567. doi: 10.1016/j.joca.2014.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kumar D, Souza RB, Singh J, Calixto NE, Nardo L, Link TM, Li X, Majumdar S. Physical activity and spatial differences in medial knee t1rho and t2 relaxation times in knee osteoarthritis. J Orthop Sports Phys Ther. 2014;44(12):964–972. doi: 10.2519/jospt.2014.5523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rautiainen J, Nissi MJ, Liimatainen T, Herzog W, Korhonen RK, Nieminen MT. Adiabatic rotating frame relaxation of MRI reveals early cartilage degeneration in a rabbit model of anterior cruciate ligament transection. Cartil Osteoarthr. 2014;22(10):1444–1452. doi: 10.1016/j.joca.2014.04.023. [DOI] [PubMed] [Google Scholar]
- 14.Rautiainen J, Nissi MJ, Salo EN, Tiitu V, Finnila MA, Aho OM, Saarakkala S, Lehenkari P, Ellermann J, Nieminen MT. Multiparametric MRI assessment of human articular cartilage degeneration: Correlation with quantitative histology and mechanical properties. Magn Reson Med. 2015;74:249–259. doi: 10.1002/mrm.25401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang YX, Zhao F, Griffith JF, Mok GS, Leung JC, Ahuja AT, Yuan J. T1rho and T2 relaxation times for lumbar disc degeneration: an in vivo comparative study at 3.0-Tesla MRI. Eur Radiol. 2013;23(1):228–234. doi: 10.1007/s00330-012-2591-2. [DOI] [PubMed] [Google Scholar]
- 16.Toth F, Nissi MJ, Wang L, Ellermann JM, Carlson CS. Surgical induction, histological evaluation, and MRI identification of cartilage necrosis in the distal femur in goats to model early lesions of osteochondrosis. Osteoarthr Cartil. 2014 doi: 10.1016/j.joca.2014.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Santyr GE, Fairbanks EJ, Kelcz F, Sorenson JA. Off-resonance spin locking for MR imaging. Magn Reson Med. 1994;32(1):43–51. doi: 10.1002/mrm.1910320107. [DOI] [PubMed] [Google Scholar]
- 18.Grohn HI, Michaeli S, Garwood M, Kauppinen RA, Grohn OHJ. Quantitative T-1p and adiabatic Carr-Purcell T-2 magnetic resonance imaging of human occipital lobe at 4.T. Magn Reson Med. 2005;54(1):14–19. doi: 10.1002/mrm.20536. [DOI] [PubMed] [Google Scholar]
- 19.Michaeli S, Sorce DJ, Springer CS, Jr, Ugurbil K, Garwood M. T1rho MRI contrast in the human brain: modulation of the longitudinal rotating frame relaxation shutter-speed during an adiabatic RF pulse. J Magn Reson. 2006;181(1):135–147. doi: 10.1016/j.jmr.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 20.Mangia S, Liimatainen T, Garwood M, Michaeli S. Rotating frame relaxation during adiabatic pulses vs. conventional spin lock: simulations and experimental results at 4 T. Magn Reson Imaging. 2009;27(8):1074–1087. doi: 10.1016/j.mri.2009.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Taheri S, Sood R. Spin-lock MRI with amplitude- and phase-modulated adiabatic waveforms: an MR simulation study. Magn Reson Imaging. 2006;24(1):51–59. doi: 10.1016/j.mri.2005.10.020. [DOI] [PubMed] [Google Scholar]
- 22.Blicharski J. Nuclear magnetic relaxation in rotating frame. Acta Phys Pol A. 1972;41:223. [Google Scholar]
- 23.Ellermann J, Ling W, Nissi MJ, Arendt E, Carlson CS, Garwood M, Michaeli S, Mangia S. MRI rotating frame relaxation measurements for articular cartilage assessment. Magn Reson Imaging. 2013;31(9):1537–1543. doi: 10.1016/j.mri.2013.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tannus A, Garwood M. Adiabatic Pulses. NMR in biomed. 1997:10. doi: 10.1002/(sici)1099-1492(199712)10:8<423::aid-nbm488>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 25.Nissi MJ. Orientation anisotropy of rotating frame and T2 relaxation parameters in articular cartilage. Proc Natl Acad Sci U S A. 2013;3552 [Google Scholar]
- 26.Wang N, Xia Y. Dependencies of multi-component T2 and T1rho relaxation on the anisotropy of collagen fibrils in bovine nasal cartilage. J Magn Reson. 2011;212(1):124–132. doi: 10.1016/j.jmr.2011.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Du J, Diaz E, Carl M, Bae W, Chung CB, Bydder GM. Ultrashort echo time imaging with bicomponent analysis. Magn Reson Med. 2012;67(3):645–649. doi: 10.1002/mrm.23047. [DOI] [PubMed] [Google Scholar]
- 28.Liu F, Choi KW, Samsonov A, Spencer RG, Wilson JJ, Block WF, Kijowski R. Articular Cartilage of the Human Knee Joint: In Vivo Multicomponent T2 Analysis at 3.0 T. Radiology. 2015;277(2):11. doi: 10.1148/radiol.2015142201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pauli C, Bae WC, Lee M, Lotz M, Bydder GM, D'Lima DL, Chung CB, Du J. Ultrashort-echo time MR imaging of the patella with bicomponent analysis: correlation with histopathologic and polarized light microscopic findings. Radiology. 2012;264(2):484–493. doi: 10.1148/radiol.12111883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Du J, Carl M, Diaz E, Takahashi A, Han E, Szeverenyi NM, Chung CB, Bydder GM. Ultrashort TE T1rho (UTE T1rho) imaging of the Achilles tendon and meniscus. Magn Reson Med. 2010;64(3):834–842. doi: 10.1002/mrm.22474. [DOI] [PubMed] [Google Scholar]
- 31.Aronen HJ, Ramadan UA, Peltonen TK, Markkola AT, Tanttu JI, Jaaskelainen J, Hakkinen AM, Sepponen R. 3D spin-lock imaging of human gliomas. Magn Reson Imaging. 1999;17(7):1001–1010. doi: 10.1016/s0730-725x(99)00041-7. [DOI] [PubMed] [Google Scholar]
- 32.Borthakur A, Wheaton A, Charagundla SR, Shapiro EM, Regatte RR, Akella SVS, Kneeland JB, Reddy R. Three-dimensional T1 rho-weighted MRI at 1.5 Tesla. J Magn Reson Imaging. 2003;17(6):730–736. doi: 10.1002/jmri.10296. [DOI] [PubMed] [Google Scholar]
- 33.Regatte RR, Akella SV, Wheaton AJ, Lech G, Borthakur A, Kneeland JB, Reddy R. 3D-T1rho-relaxation mapping of articular cartilage: in vivo assessment of early degenerative changes in symptomatic osteoarthritic subjects. Acad Radiol. 2004;11(7):741–749. doi: 10.1016/j.acra.2004.03.051. [DOI] [PubMed] [Google Scholar]
- 34.Li X, Han ET, Busse RF, Majumdar S. In vivo T(1rho) mapping in cartilage using 3D magnetization-prepared angle-modulated partitioned k-space spoiled gradient echo snapshots (3D MAPSS) Magn Reson Med. 2008;59(2):298–307. doi: 10.1002/mrm.21414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hafner S. Fast imaging in liquids and solids with the Back-projection Low Angle ShoT (BLAST) technique. Magn Reson Imaging. 1994;12(7):1047–1051. doi: 10.1016/0730-725x(94)91236-p. [DOI] [PubMed] [Google Scholar]
- 36.Madio DP, Lowe IJ. Ultra-Fast Imaging Using Low Flip Angles and Fids. Magn Reson Med. 1995;34(4):525–529. doi: 10.1002/mrm.1910340407. [DOI] [PubMed] [Google Scholar]
- 37.Robson MD, Gatehouse PD, Bydder M, Bydder GM. Magnetic resonance: an introduction to ultrashort TE (UTE) imaging. J Comput Assist Tomo. 2003;27(6):825–846. doi: 10.1097/00004728-200311000-00001. [DOI] [PubMed] [Google Scholar]
- 38.Weiger M, Brunner DO, Dietrich BE, Muller CF, Pruessmann KP. ZTE imaging in humans. Magn Reson Med. 2013;70(2):328–332. doi: 10.1002/mrm.24816. [DOI] [PubMed] [Google Scholar]
- 39.Idiyatullin D, Corum C, Park JY, Garwood M. Fast and quiet MRI using a swept radiofrequency. J Magn Reson. 2006;181(2):342–349. doi: 10.1016/j.jmr.2006.05.014. [DOI] [PubMed] [Google Scholar]
- 40.Wu Y, Ackerman JL, Chesler DA, Graham L, Wang Y, Glimcher MJ. Density of organic matrix of native mineralized bone measured by water- and fat-suppressed proton projection MRI. Magn Reson Med. 2003;50(1):59–68. doi: 10.1002/mrm.10512. [DOI] [PubMed] [Google Scholar]
- 41.Zhang J, Idiyatullin D, Corum CA, Kobayashi N, Garwood M. Gradient-modulated SWIFT. Magn Reson Med. 2015 doi: 10.1002/mrm.25595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Garwood M, Idiyatullin D, Corum C, Chamberlain R, Moeller S, Kobayashi N, Lehto L, Zhang J, O'Connell R, Tesch M, Nissi M, Ellermann J, Nixdorf D. SWIFT Encycloepedia of Magnetic Resonance. John Wiley & Sons; 2012. Capturing Signals from Fast-relaxing Spins with Frequency-Swept MRI: SWIFT. [Google Scholar]
- 43.Kendi AT, Khariwala SS, Zhang J, Idiyatullin DS, Corum CA, Michaeli S, Pambuccian SE, Garwood M, Yueh B. Transformation in mandibular imaging with sweep imaging with fourier transform magnetic resonance imaging. Arch Otolaryngol Head Neck Surg. 2011;137(9):916–919. doi: 10.1001/archoto.2011.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zhang J, Chamberlain R, Etheridge M, Idiyatullin D, Corum C, Bischof J, Garwood M. Quantifying iron-oxide nanoparticles at high concentration based on longitudinal relaxation using a three-dimensional SWIFT look-locker sequence. Magn Reson Med. 2014;71(6):1982–1988. doi: 10.1002/mrm.25181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ellermann J, Idiyatullin D, Corum C, Moeller S, Ling W, Garwood M. The ultrastructure of bone using selective saturation in SWIFT at 9.4 T. Proc Natl Acad Sci U S A. 2009;849 [Google Scholar]
- 46.Garwood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153(2):155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 47.Levitt MH, Freeman R, Frenkiel T. Supercycles for Broad-Band Heteronuclear Decoupling. J Magn Reson. 1982;50(1):157–160. [Google Scholar]
- 48.Ernst RR, Anderson WA. Application of Fourier transform to magnetic resonance spectroscopy. Rev Sci Instrum. 1966;37:93. [Google Scholar]
- 49.Nissi MJ, Lehto LJ, corum CA, Idiyatullin D, Ellermann JM, Grohn OHJ, Nieminen MT. Measurement of T1 Relaxation Time of Osteochondral Specimens Using VFA-SWIFT. Magn Reson Med. 2015 doi: 10.1002/mrm.25398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Reiter DA, Lin PC, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magn Reson Med. 2009;61(4):803–809. doi: 10.1002/mrm.21926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Degroen P, Demoor B. The Fit of a Sum of Exponentials to Noisy Data. J Comput Appl Math. 1987;20:175–187. [Google Scholar]
- 52.Wong TT, Luk WS, Heng PA. Sampling with Hammersley and Halton Points. J Graph Tools. 1997;2(2):9–24. [Google Scholar]
- 53.Reiter DA, Roque RA, Lin PC, Irrechukwu O, Doty S, Longo DL, Pleshko N, Spencer RG. Mapping proteoglycan-bound water in cartilage: Improved specificity of matrix assessment using multiexponential transverse relaxation analysis. Magn Reson Med. 2011;65(2):377–384. doi: 10.1002/mrm.22673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cobb JG, Kan JH, Gore JC. T1rho mapping of pediatric epiphyseal and articular cartilage in the knee. Journal of magnetic resonance imaging : JMRI. 2013;38(2):299–305. doi: 10.1002/jmri.23963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Altbach MI, Outwater EK, Trouard TP, Krupinski EA, Theilmann RJ, Stopeck AT, Kono M, Gmitro AF. Radial fast spin-echo method for T2-weighted imaging and T2 mapping of the liver. J Magn Reson Imaging. 2002;16(2):179–189. doi: 10.1002/jmri.10142. [DOI] [PubMed] [Google Scholar]
- 56.Michaeli S, Oz G, Sorce DJ, Garwood M, Ugurbil K, Majestic S, Tuite P. Assessment of brain iron and neuronal integrity in patients with Parkinson's disease using novel MRI contrasts. Mov Disord. 2007;22(3):334–340. doi: 10.1002/mds.21227. [DOI] [PubMed] [Google Scholar]
- 57.Borthakur A, Sochor M, Davatzikos C, Trojanowski JQ, Clark CM. T1rho MRI of Alzheimer's disease. NeuroImage. 2008;41(4):1199–1205. doi: 10.1016/j.neuroimage.2008.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Muthupillai R, Flamm SD, Wilson JM, Pettigrew RI, Dixon WT. Acute myocardial infarction: tissue characterization with T1rho-weighted MR imaging--initial experience. Radiology. 2004;232(2):606–610. doi: 10.1148/radiol.2322030334. [DOI] [PubMed] [Google Scholar]
- 59.Wang YX, Yuan J, Chu ES, Go MY, Huang H, Ahuja AT, Sung JJ, Yu J. T1rho MR imaging is sensitive to evaluate liver fibrosis: an experimental study in a rat biliary duct ligation model. Radiology. 2011;259(3):712–719. doi: 10.1148/radiol.11101638. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.