High codimensional bifurcation analysis to a six-neuron BAM neural network

Abstract

In this article, the high codimension bifurcations of a six-neuron BAM neural network system with multiple delays are addressed. We first deduce the existence conditions under which the origin of the system is a Bogdanov–Takens singularity with multiplicities two or three. By choosing the connection coefficients as bifurcation parameters and using the formula derived from the normal form theory and the center manifold, the normal forms of Bogdanov–Takens and triple zero bifurcations are presented. Some numerical examples are shown to support our main results.

Introduction

It is believed that the successful applications of neural network in many fields such as optimization solvers, pattern recognition, automatic control and encryption of image (Cochoki and Unbehauen 1993; Ripley 1996; He et al. 2013; Kadone and Nakamutra 2005; Hoppensteadt and Izhikevich 1997) heavily depend on the theoretical studies about the neuron systems, especially the investigation of the dynamical behaviors of neural network models has became focus over the past decade years.

Following currently available literatures, the interest in studying the dynamics of the neural network has focused on two main aspects. One topic is aimed at the study of the local and global stability of the equilibrium, the existence and stability of periodic solutions yielded from Hopf bifurcation, as reported in (Xu and Li 2012; Yang and Ye 2009; Xu et al. 2011; Cao 2003; Sun et al. 2007; Zheng et al. 2008; Liu and Cao 2011; Yang et al. 2014), and another topic is aimed at the study of more complex dynamics mainly involving some degenerate bifurcations existing in the neighborhood of the codimensional singularity. Such issues have been addressed by several articles (Ding et al. 2012; He et al. 2012a, b, 2013, 2014; Li and Wei 2005; Dong and Liao 2013; Song and Xu 2012; Campbell and Yuan 2008; Guo et al. 2008; Yang 2008; Liu 2014; Garliauskas 1998; Kepler et al. 1990). For instance, Ding et al. (2012) have considered the zero–Hopf bifurcation of a generalized Gopalsamy neural network model, the normal forms of near a zero–Hopf critical point were deduced by using multiple time scales and center manifold reduction methods respectively. The similar work has been carried out by He et al. (2014), but contraposing a different neural network. The authors in (Dong and Liao 2013; He et al. 2012a; Li and Wei 2005; Song and Xu 2012, 2013; Campbell and Yuan 2008; Guo et al. 2008; Yang 2008) have devoted to the analysis of the Bogdanov–Takens (B–T) bifurcation with codimension two. Guo et al. have deduced the existence of the double Hopf (Guo et al. 2008). Campbell and Yuan (2008) and Liu (2014) have investigated triple zero bifurcation induced by the delays and the connection topologies existing among the neurons. For the cases of Hopf–Pitchfork bifurcation and chaos see (Yang 2008; Garliauskas 1998; Kepler et al. 1990).

In application of neural networks, some dynamical phenomena of neural networks have been explained and shown by simulations and applied to memory systems and algorithmic designs (Kadone and Nakamutra 2005; Hoppensteadt and Izhikevich 1997; He et al. 2013; Chen and Aihara 1999; Wang and Shi 2006). For example, attractors, homoclinic and heteroclinic orbits can be interpreted as a single storage or memory pattern, or an optimal object, and various complex patterns in the application and design of neural networks. Chaotic behavior of neural networks also has been confirmed to be benefit to design the efficient searching algorithm for solving optimization problems due to its bidirectional structure (Chen and Aihara 1999; Wang and Shi 2006). Undoubtedly, the deeper investigations to dynamic of neural networks facilitates the extensive applications and optimum design of some searching algorithms. This also motivate us to study the more complicated bifurcation behaviors of delayed multi-neuron memory systems, especially, the codimension-2 and codimension-3 bifurcations.

Due to the complexity of the problem, more attentions on the investigations of multiple-delay neural network focus on small sized networks or on some special architecture (Sun et al. 2007; Zheng et al. 2008; Dong and Liao 2013; He et al. 2012a). Although, it is convinced that the dynamics investigation to neural networks with a few neurons contributes to understanding large-scale networks, there are inevitably some complicated and pivotal problems that may be neglected if large-scale networks is simplified. On the other hand, from the practical point of the view, improving the designs of the neural networks and extending its application in more fields also need consider the more complex and larger-scale associative models because the real neural networks are complex and large-scale nonlinear dynamical systems, and commonly involve interactions among multiple neurons. For example, the exact control to the roughness of categorization by the proportion between excitatory signal and inhibitory signal depends on the complex layered design (Carpenter and Grossberg 1987). Meanwhile it also is an important mathematical subject to investigate the dynamics of the larger scale neuron systems (Xu and Li 2012; Xu et al. 2011; Yang and Ye 2009; Cao 2003; Liu 2014). As Xu and Li (2012) have studied a bidirectional associative memory (BAM) six-neuron networks, which is described by

$$\left\{\begin{array}{c}\dot{x_1}(t)=-{\mathit{\mu }}_1{x}_1(t)+\sum _{j=2}^6{c}_{j1}{f}_1(x_j(t-{\mathit{\tau }}_2)),\hfill \\ \dot{x_2}(t)=-{\mathit{\mu }}_2{x}_2(t)+c_{12}{f}_2(x_1(t-{\mathit{\tau }}_1)),\hfill \\ ⋮\hfill \\ \dot{x_6}(t)=-{\mathit{\mu }}_6{x}_6(t)+c_{16}{f}_6(x_1(t-{\mathit{\tau }}_1)),\hfill \end{array}\right.$$ 1

where $x_i(t)(i=1,2,\dots ,6)$ denotes the state of the neuron at time t; ${\mathit{\mu }}_i$ characterizes the attenuation rate of internal neurons processing on the I-layer and the J-layer and ${\mathit{\mu }}_i>0$; the real constants $c_{j1}(j=2,3,\dots ,6)$ and $c_{1j}$ show the connected weights between the neurons in two layers: the I-layer and the J-layer.

Xu and Li (2012) have considered the stability of the nondegenerate origin and the existence of Hopf bifurcation of (1) induced by the delays. Compared with (Xu and Li 2012), the contributions of this work are to address Bogdanov–Takens and triple zero bifurcation computations of the BAM six-neuron network, and show the curves of different bifurcation occurrences.

The Hopf bifurcation is corresponding the characteristic equation has a pair of purely imaginary roots. While the B–T or triple zero bifurcation is corresponding the characteristic equation has a double-zero or triple zero root. We choose two or three parameters as the bifurcation parameters, by using the center manifold reduction and the normal form method, one can compute the normal form which is equivalent to (1). Finally, different kinds of bifurcation curves used to explain the dynamical behaviors of (1) can be drawn.

Note that the authors in (Xiao et al. 2013; Liu and Yang 2014) have considered the stability and Hopf bifurcation of some delayed neural network models with $n+1$ or n neurons, especially model (1) as a special case of the model in (Xiao et al. 2013) has been studied detailedly by Xu and Li (2012), nevertheless, the degenerated dynamics of system (1) at the neighborhood of the origin has never been addressed. Thus, in this article, we devote to investigate the high codimension properties of model (1). The study to the high codimension properties of the model in (Xiao et al. 2013) will be left as our future work.

The organization of this paper is: in “Existence of B–T bifurcation” section, the existence conditions under which the origin is B–T singularity are given. In “B–T bifurcation” section, by applying the center manifold reduction and normal form computation, we obtain the normal form and bifurcation curves near the origin of the neural network. In “Triple zero bifurcation” section, triple zero bifurcation is also investigated. In “Numerical examples and simulations” section, some numerical examples and simulations are shown to verify our main results. Finally, a conclusion is given to sum up our works.

Existence of B–T bifurcation

Let $u_1(t)=x_1(t-{\mathit{\tau }}_1),u_j(t)=x_j(t)(j=2,\dots ,6)$ and $\mathit{\tau }={\mathit{\tau }}_1+{\mathit{\tau }}_2$, then system (1) is equivalent to the following system

$$\left\{\begin{array}{c}\dot{u_1}(t)=-{\mathit{\mu }}_1{u}_1(t)+\sum _{j=2}^6{c}_{j1}{f}_1(u_j(t-\mathit{\tau })),\hfill \\ \dot{u_2}(t)=-{\mathit{\mu }}_2{u}_2(t)+c_{12}{f}_2(u_1(t)),\hfill \\ ⋮\hfill \\ \dot{u_6}(t)=-{\mathit{\mu }}_6{u}_6(t)+c_{16}{f}_6(u_1(t)).\hfill \end{array}\right.$$ 2

To obtain our main results, we make the following assumptions

(H1)

$f_i(0)=0,f_i^{\prime }(0)=1,i=1,2,\dots ,6$.

From (H1), we know that the origin is always the equilibrium of system (2).

Linearizing system (2) at the zero equilibrium, then it becomes

$$\left\{\begin{array}{c}\dot{u_1}(t)=-{\mathit{\mu }}_1{u}_1(t)+\sum _{j=2}^6{c}_{j1}{u}_j(t-\mathit{\tau }),\hfill \\ \dot{u_2}(t)=-{\mathit{\mu }}_2{u}_2(t)+c_{12}{u}_1(t),\hfill \\ ⋮\hfill \\ \dot{u_6}(t)=-{\mathit{\mu }}_6{u}_6(t)+c_{16}{u}_1(t).\hfill \end{array}\right.$$ 3

The characteristic equation of system (3) is

$$\begin{array}{cc}\hfill F(\mathit{\lambda })& =-e^{-\mathit{\lambda }\mathit{\tau }}(b_1{\mathit{\lambda }}^4+b_2{\mathit{\lambda }}^3+b_3{\mathit{\lambda }}^2+b_4\mathit{\lambda }+b_5)\hfill \\ \hfill & +{\mathit{\lambda }}^6+a_1{\mathit{\lambda }}^5+a_2{\mathit{\lambda }}^4+a_3{\mathit{\lambda }}^3+a_4{\mathit{\lambda }}^2\hfill \\ \hfill & +a_5\mathit{\lambda }+a_6=0,\hfill \end{array}$$ 4

where

$$\begin{array}{cc}\hfill a_k& =\sum _{1\le i_1<i_2<i_3<\cdots <i_k\le 6}{\mathit{\mu }}_{i_1}{\mathit{\mu }}_{i_2}{\mathit{\mu }}_{i_3}\dots {\mathit{\mu }}_{i_k},k=1,\dots 6,\hfill \\ \hfill b_1& =c_{13}{c}_{31}+c_{14}{c}_{41}+c_{15}{c}_{51}+c_{16}{c}_{61}+c_{12}{c}_{21},\hfill \\ \hfill b_2& =\sum _{j=2}^6\left[c_{1j}{c}_{j1}\sum _{i_1=2,i_1\ne j}^6{\mathit{\mu }}_{i_1}\right],\hfill \\ \hfill b_3& =\sum _{j=2}^6\left[c_{1j}{c}_{j1}\sum _{2\le i_1<i_2\le 6,i_1,i_2\ne j}{\mathit{\mu }}_{i_1}{\mathit{\mu }}_{i_2}\right],\hfill \\ \hfill b_4& =\sum _{j=2}^6\left[c_{1j}{c}_{j1}\sum _{2\le i_1<i_2<i_3\le 6,i_1,i_2,i_3\ne j}{\mathit{\mu }}_{i_1}{\mathit{\mu }}_{i_2}{\mathit{\mu }}_{i_3}\right],\hfill \\ \hfill b_5& =\sum _{j=2}^6\left[c_{1j}{c}_{j1}\sum _{2\le i_1<i_2<i_3<i_4\le 6,i_1,i_2,i_3,i_4\ne j}{\mathit{\mu }}_{i_1}{\mathit{\mu }}_{i_2}{\mathit{\mu }}_{i_3}{\mathit{\mu }}_{i_4}\right].\hfill \end{array}$$

Let

$$\begin{array}{cc}\hfill c_{21}^0& =-\frac{{\mathit{\mu }}_2^2}{{\mathit{\mu }}_6^2{\mathit{\mu }}_5^2{\mathit{\mu }}_4^2\left({\mathit{\mu }}_3-{\mathit{\mu }}_2\right)c_{12}}\left[+c_{14}{c}_{41}{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_3-{\mathit{\mu }}_4\right)\right.\hfill \\ \hfill & +{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_1+{\mathit{\mu }}_3+{\mathit{\mu }}_3\mathit{\tau }{\mathit{\mu }}_1\right)\hfill \\ \hfill & +c_{15}{c}_{51}{\mathit{\mu }}_4^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)+c_{16}{c}_{61}{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)],\hfill \end{array}$$ 5

$$\begin{array}{cc}\hfill c_{31}^0& =\frac{{\mathit{\mu }}_3^2}{c_{13}{\mathit{\mu }}_6^2{\mathit{\mu }}_5^2{\mathit{\mu }}_4^2\left({\mathit{\mu }}_3-{\mathit{\mu }}_2\right)}\left[{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_1+{\mathit{\mu }}_2+\mathit{\tau }{\mathit{\mu }}_1{\mathit{\mu }}_2\right)\right.\hfill \\ \hfill & +c_{14}{c}_{41}{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_2-{\mathit{\mu }}_4\right)\hfill \\ \hfill & \left.+c_{15}{c}_{51}{\mathit{\mu }}_4^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)+c_{16}{c}_{61}{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right)\right],\hfill \end{array}$$ 6

$$\begin{array}{cc}\hfill c_{41}^0& =\frac{{\mathit{\mu }}_4^3}{2{\mathit{\mu }}_6^3{\mathit{\mu }}_5^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_4\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_4\right)c_{14}}\left[{\mathit{\mu }}_2{\mathit{\tau }}^2{\mathit{\mu }}_3{\mathit{\mu }}_5^3{\mathit{\mu }}_6^3{\mathit{\mu }}_1\right.\hfill \\ \hfill & +2{\mathit{\mu }}_5^3{\mathit{\mu }}_6^3\left({\mathit{\mu }}_2{\mathit{\mu }}_1+{\mathit{\mu }}_2{\mathit{\mu }}_3+{\mathit{\mu }}_3{\mathit{\mu }}_1\right)\mathit{\tau }\hfill \\ \hfill & -2c_{15}{c}_{51}{\mathit{\mu }}_6^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\hfill \\ \hfill & \left.-2c_{16}{c}_{61}{\mathit{\mu }}_5^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right)+2{\mathit{\mu }}_5^3{\mathit{\mu }}_6^3\left({\mathit{\mu }}_2+{\mathit{\mu }}_3+{\mathit{\mu }}_1\right)\right],\hfill \end{array}$$ 7

$$\begin{array}{cc}\hfill c_{51}^0& =-\frac{{\mathit{\mu }}_5^4}{6{\mathit{\mu }}_6^4{c}_{15}\left({\mathit{\mu }}_4-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)}\hfill \\ \hfill & \times \left[{\mathit{\tau }}^3{\mathit{\mu }}_2{\mathit{\mu }}_4{\mathit{\mu }}_3{\mathit{\mu }}_1{\mathit{\mu }}_6^4+3{\mathit{\mu }}_6^4({\mathit{\mu }}_2{\mathit{\mu }}_3{\mathit{\mu }}_4+{\mathit{\mu }}_1{\mathit{\mu }}_2{\mathit{\mu }}_3\right.\hfill \\ \hfill & +{\mathit{\mu }}_1{\mathit{\mu }}_2{\mathit{\mu }}_4+{\mathit{\mu }}_1{\mathit{\mu }}_3{\mathit{\mu }}_4){\mathit{\tau }}^2+6c_{16}{c}_{61}\left({\mathit{\mu }}_4-{\mathit{\mu }}_6\right)\hfill \\ \hfill & \times \left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right)+6{\mathit{\mu }}_6^4\left({\mathit{\mu }}_1+{\mathit{\mu }}_4+{\mathit{\mu }}_2\right.\hfill \\ \hfill & \left.\left.+{\mathit{\mu }}_3\right)+6{\mathit{\mu }}_6^4\left({\mathit{\mu }}_3{\mathit{\mu }}_4+{\mathit{\mu }}_1{\mathit{\mu }}_4+{\mathit{\mu }}_2{\mathit{\mu }}_4+{\mathit{\mu }}_1{\mathit{\mu }}_2+{\mathit{\mu }}_1{\mathit{\mu }}_3+{\mathit{\mu }}_2{\mathit{\mu }}_3\right)\mathit{\tau }\right].\hfill \end{array}$$ 8

(H2)

$c_{21}=c_{21}^0,c_{31}=c_{31}^0,c_{41}\ne c_{41}^0,{\mathit{\mu }}_2\ne {\mathit{\mu }}_3\ne {\mathit{\mu }}_4$,

(H3)

$c_{21}=c_{21}^0,c_{31}=c_{31}^0,c_{41}=c_{41}^0,c_{51}\ne c_{51}^0,{\mathit{\mu }}_2\ne {\mathit{\mu }}_3\ne {\mathit{\mu }}_4\ne {\mathit{\mu }}_5$.

Then we can get the following result.

Lemma 1

The characteristic Eq. (4) has the double zero eigenvalues if (H1) and (H2) hold, and has the triple zero eigenvalues if (H1) and (H3) hold.

Proof

By (4), we have

$$\begin{array}{cc}\hfill F(0)& =a_6-b_5,\hfill \\ \hfill F^{\prime }(0)& =a_5+\mathit{\tau }{b}_5-b_4,\hfill \\ \hfill F^{\prime \prime }(0)& =2a_4-{\mathit{\tau }}^2{b}_5+2\mathit{\tau }{b}_4-2b_3,\hfill \\ \hfill F^{\prime \prime \prime }(0)& =6a_3+{\mathit{\tau }}^3{b}_5-3{\mathit{\tau }}^2{b}_4+6\mathit{\tau }{b}_3-6b_2.\hfill \end{array}$$ 9

It follows from (H1) and (H2) that $F(0)=F^{\prime }(0)=0$ and

$$\begin{array}{cc}\hfill F^{\prime \prime }(0)& ={\mathit{\mu }}_4{\mathit{\mu }}_5{\mathit{\mu }}_6\left[{\mathit{\tau }}^2{\mathit{\mu }}_2{\mathit{\mu }}_3{\mathit{\mu }}_1+2({\mathit{\mu }}_2+{\mathit{\mu }}_1+{\mathit{\mu }}_3)\right.\hfill \\ \hfill & \left.+2\left({\mathit{\mu }}_2{\mathit{\mu }}_1+{\mathit{\mu }}_2{\mathit{\mu }}_3+{\mathit{\mu }}_3{\mathit{\mu }}_1\right)\mathit{\tau }\right]\hfill \\ \hfill & -\frac{2}{{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2}\left[{\mathit{\mu }}_6^3{\mathit{\mu }}_5^3{c}_{14}{c}_{41}({\mathit{\mu }}_3-{\mathit{\mu }}_4)({\mathit{\mu }}_2-{\mathit{\mu }}_4)\right.\hfill \\ \hfill & +{\mathit{\mu }}_6^3{\mathit{\mu }}_4^3{c}_{15}{c}_{51}\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\hfill \\ \hfill & \left.+{\mathit{\mu }}_5^3{\mathit{\mu }}_4^3{c}_{16}{c}_{61}\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right)\right]\ne 0.\hfill \end{array}$$ 10

Thus, $\mathit{\lambda }=0$ is a double root of Eq. (4).

Similarly, that (H1) and (H3) hold can lead to $F(0)=F^{\prime }(0)=F^{\prime \prime }(0)=0$ and

$$\begin{array}{cc}\hfill F^{\prime \prime \prime }(0)& ={\mathit{\mu }}_5{\mathit{\mu }}_6\left[{\mathit{\mu }}_1{\mathit{\mu }}_2{\mathit{\mu }}_3{\mathit{\mu }}_4{\mathit{\tau }}^3+3\sum _{1\le i_1<i_2<i_3\le 4}{\mathit{\mu }}_{i_1}{\mathit{\mu }}_{i_2}{\mathit{\mu }}_{i_3}{\mathit{\tau }}^2\right.\hfill \\ \hfill & \left.+6\sum _{1\le i_1<i_2\le 4}{\mathit{\mu }}_{i_1}{\mathit{\mu }}_{i_2}\mathit{\tau }+6\sum _{i=1}^4{\mathit{\mu }}_i\right]\hfill \\ \hfill & +\frac{6}{{\mathit{\mu }}_5^3{\mathit{\mu }}_6^3}\left[{\mathit{\mu }}_6^4{c}_{15}{c}_{51}\left({\mathit{\mu }}_4-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\right.\hfill \\ \hfill & \left.+{\mathit{\mu }}_5^4{c}_{16}{c}_{61}\left({\mathit{\mu }}_4-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)\left(-{\mathit{\mu }}_6+{\mathit{\mu }}_2\right)\right]\ne 0.\hfill \end{array}$$

This completes the proof.

Next, under the conditions (H1)–(H2) or (H1)–(H3), we will find the conditions under which the other eigenvalues of Eq. (4) have negative real parts except for zero roots.

Let $\mathit{\lambda }=\mathrm{i}w$ be a root of Eq. (4) and substitute it into Eq. (4), then separating the real and imaginary parts, we have

$$\begin{array}{cc}& w^6-a_2{w}^4+a_4{w}^2-a_6=(-b_1{w}^4+b_3{w}^2-b_5)cos\left(w\mathit{\tau }\right)\hfill \\ \hfill & +(b_2{w}^3-b_{4}w)sin\left(w\mathit{\tau }\right),\hfill \\ \hfill & a_3{w}^3-a_1{w}^5-a_{5}w=+(b_1{w}^4-b_3{w}^2+b_5)sin\left(w\mathit{\tau }\right)\hfill \\ \hfill & +(b_2{w}^3-b_{4}w)cos\left(w\mathit{\tau }\right).\hfill \end{array}$$ 11

Let (H1) and (H2) hold, then one can obtain

$$\begin{array}{cc}& w^2\left[w^{10}+\left(a_1^2-2a_2\right)w^8+\left(2a_4-2a_1{a}_3-b_1^2+a_2^2\right)w^6\right.\hfill \\ \hfill & +\left(2b_1{b}_3-2b_5+2a_5{a}_1-b_2^2-2a_2{a}_4+a_3^2\right)w^4\hfill \\ \hfill & +\left(b_3^2-2b_1{b}_5+2a_2{b}_5+2b_2{a}_5+2b_2\mathit{\tau }{b}_5+a_4^2-2a_3{a}_5\right)w^2\hfill \\ \hfill & \left.+\left(2b_3{b}_5-2a_4{b}_5-2a_5\mathit{\tau }{b}_5-{\mathit{\tau }}^2{b}_5^2\right)\right]=0.\hfill \end{array}$$ 12

Without loss of generality, we assume that Eq. (12) has at most five positive roots, denoting them as $w_i$$(i=1,2,3,4,5)$. By (11) we have

$${\mathit{\tau }}_i=\frac{1}{w_i}arccos\frac{-D}{{(b_1{w}_i^4-b_3{w}_i^2+b_5)}^2+{(b_2{w}_i^3-b_4{w}_i)}^2},$$ 13

where

$$D=\left(w_i^6-a_2{w}_i^4+a_4{w}_i^2-b_5\right)\left(b_1{w}_i^4-b_3{w}^2+b_5\right)-w_i^2\left(b_2{w}_i^2-b_4\right)\left(a_3{w}_i^2-a_1{w}_i^4-a_5\right),$$

define ${\mathit{\tau }}_0={min}_{i\in \{1,2,\dots ,5\}}\{{\mathit{\tau }}_i\}$. If Eq. (12) has no positive root, we take ${\mathit{\tau }}_0=+\infty .$

Let (H1) and (H3) hold, it follows from (11) that

$$\begin{array}{cc}& w^4\left[w^8+\left(a_1^2-2a_2\right)w^6+\left(-b_1^2-2a_1{a}_3-{\mathit{\tau }}^2{b}_5-2\mathit{\tau }{a}_5+2b_3+a_2^2\right)w^4\right.\hfill \\ \hfill & +\left(a_2{\mathit{\tau }}^2{b}_5+2a_2\mathit{\tau }{a}_5+2b_1{b}_3-b_2^2-2a_2{b}_3-2b_5+2a_1{a}_5+a_3^2\right)w^2\hfill \\ \hfill & +\left({\mathit{\tau }}^3{b}_5{a}_5-2\mathit{\tau }{a}_5{b}_3-{\mathit{\tau }}^2{b}_5{b}_3+2a_2{b}_5-2a_3{a}_5+2b_2\mathit{\tau }{b}_5+2a_5{b}_2\right.\hfill \\ \hfill & \left.\left.+{\mathit{\tau }}^2{a}_5^2-2b_1{b}_5+\frac{{\mathit{\tau }}^4{b}_5^2}{4}\right)\right]=0.\hfill \end{array}$$ 14

Similarly, if Eq. (14) has no positive root, we take ${\overline{\mathit{\tau }}}_0=+\infty$, or else, Eq. (14) has at most four positive roots, denote them by ${\overline{w}}_i$$(i=1,2,3,4)$. Following (11) we have

$${\overline{\mathit{\tau }}}_i=\frac{1}{{\overline{w}}_i}arccos\frac{-\overline{D}}{{(b_1{\overline{w}}_i^4-b_3{w}^2+b_5)}^2+{(b_2{w}^3-b_{4}w)}^2},$$ 15

where

$$\overline{D}=({\overline{w}}_i^6-a_2{\overline{w}}_i^4+a_4{\overline{w}}_i^2-b_5)(b_1{\overline{w}}_i^4-b_3{w}^2+b_5)-{\overline{w}}_i^2(b_2{\overline{w}}_i^2-b_4)(a_3{\overline{w}}_i^2-a_1{\overline{w}}_i^4-a_5),$$

define ${\overline{\mathit{\tau }}}_0=\underset{i\in \{1,2,\dots ,4\}}{min}\{{\overline{\mathit{\tau }}}_i\}$.

Lemma 2

[See Ruan and Wei (2003)] Consider the exponential polynomial$P(\mathit{\lambda },e^{-\mathit{\lambda }{\mathit{\tau }}_0}\dots ,e^{-\mathit{\lambda }{\mathit{\tau }}_m})={\mathit{\lambda }}^n+P_1^{(0)}{\mathit{\lambda }}^{n-1}+\cdots +P_{n-1}^{(0)}\mathit{\lambda }+P_n^{(0)}+[P_1^{(1)}{\mathit{\lambda }}^{n-1}+\cdots +P_{n-1}^{(1)}\mathit{\lambda }+P_n^{(1)}]e^{-\mathit{\lambda }{\mathit{\tau }}_0}+\cdots +[P_1^{(m)}{\mathit{\lambda }}^{n-1}+\cdots +P_{n-1}^{(m)}\mathit{\lambda }+P_n^{(m)}]e^{-\mathit{\lambda }{\mathit{\tau }}_m},$where${\mathit{\tau }}_i\ge 0$$(i=1,2,\dots ,m)$and$P_j^{(i)}(j=1,2,\dots ,m)$are constants. As$({\mathit{\tau }}_1,{\mathit{\tau }}_2,\dots ,{\mathit{\tau }}_m)$vary, the sum of the order of the zeros of$P(\mathit{\lambda },e^{-\mathit{\lambda }{\mathit{\tau }}_0}\dots ,e^{-\mathit{\lambda }{\mathit{\tau }}_m})$on the open right half plane can change only if a zero appears on or crosses the imaginary axis.

Lemma 3

Let$(\mathrm{H}1)$and$(\mathrm{H}3)$hold. All the roots of Eq. (4), except for the double zero or triple zero roots, have negative real parts if one set of the following conditions holds

(H4)

$0<\mathit{\tau }<{\mathit{\tau }}_0,A_1{A}_2-A_3>0,A_1(A_2{A}_3-A_1{A}_4)-A_3^2>0,A_4>0$;

(H5)

$0<\mathit{\tau }<{\overline{\mathit{\tau }}}_0,A_1>0,A_1{A}_2-A_3>0,A_3>0$,

with$A_1=a_1$, $A_2=a_2-b_1$, $A_3=a_3-b_2$, $A_4=a_4-b_3$.

Proof

Let $(\mathrm{H}1)$–$(\mathrm{H}2)$. For $\mathit{\tau }=0$, Eq. (4) becomes

$${\mathit{\lambda }}^2[{\mathit{\lambda }}^4+A_1{\mathit{\lambda }}^3+A_2{\mathit{\lambda }}^2+A_3\mathit{\lambda }+A_4]=0,$$ 16

By Routh-Hurwiz criterion, we have if

$$A_1{A}_2-A_3>0,A_1(A_2{A}_3-A_1{A}_4)-A_3^2>0,A_4>0,$$ 17

then the rest of roots of Eq. (16) have negative real parts except ${\mathit{\lambda }}_{1,2}=0$.

Let $(\mathrm{H}1)$–$(\mathrm{H}2)$. For $\mathit{\tau }=0$, Eq. (4) becomes

$${\mathit{\lambda }}^3[{\mathit{\lambda }}^3+A_1{\mathit{\lambda }}^2+A_2\mathit{\lambda }+A_3]=0,$$ 18

By Routh–Hurwize criterion, we know if

$$A_1>0,A_1{A}_2-A_3>0,A_3>0,$$ 19

then the rest roots of Eq. (18) have negative real parts except the triple zero root. We complete the proof.

From Lemmas 1–3 we have the following Theorem.

Theorem 1

Assume$(\mathrm{H}1)$holds. Then system (2) at the origin undergoes B–T or triple zero bifurcation if$(\mathrm{H}2)$and$(\mathrm{H}4)$or$(\mathrm{H}3)$and$(\mathrm{H}5)$hold.

B–T bifurcation

In this section, we will give the normal form of B–T bifurcation by using the methods introduced in Hale and Verduyn (1993), Xu and Huang (2006). Rescaling the time by $t\to \frac{t}{\mathit{\tau }}$ to normalize the delay, and rewriting $c_{21}$ and $c_{31}$ as $c_{21}=c_{21}^0+{\mathit{\alpha }}_1$ and $c_{31}=c_{31}^0+{\mathit{\alpha }}_2$ where $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ near (0, 0), then system (2) is translated to

$$\left\{\begin{array}{cc}& \dot{u_1}(t)=\mathit{\tau }[-{\mathit{\mu }}_1{u}_1(t)+\left(c_{21}^0+{\mathit{\alpha }}_1\right)f_1(u_2(t-1))\hfill \\ \hfill & +\left(c_{31}^0+{\mathit{\alpha }}_2\right)f_1(u_3(t-1))+\sum _{j=4}^6{c}_{j1}{f}_1(u_j(t-1))],\hfill \\ \hfill & \dot{u_2}(t)=\mathit{\tau }[-{\mathit{\mu }}_2{u}_2(t)+c_{12}{f}_2(u_1(t))],\hfill \\ \hfill & ⋮\hfill \\ \hfill & \dot{u_6}(t)=\mathit{\tau }[-{\mathit{\mu }}_6{u}_6(t)+c_{16}{f}_6(u_1(t))].\hfill \end{array}\right.$$ 20

Taking the Taylor expansion of $f_i(x)$, $i=1,2,\dots ,6$, then system (20) takes the form

$$\left\{\begin{array}{cc}& \dot{u_1}(t)=\mathit{\tau }[-{\mathit{\mu }}_1{u}_1(t)+\left(c_{21}^0+{\mathit{\alpha }}_1\right)u_2(t-1)+\left(c_{31}^0+{\mathit{\alpha }}_2\right)u_3(t-1)\hfill \\ \hfill & +c_{41}{u}_4(t-1)+c_{51}{u}_5(t-1)+c_{61}{u}_6(t-1)+H_1+h.o.t.],\hfill \\ \hfill & \dot{u_2}(t)=\mathit{\tau }[-{\mathit{\mu }}_2{u}_2(t)+c_{12}{u}_1(t)+H_2+h.o.t.],\hfill \\ \hfill & ⋮\hfill \\ \hfill & \dot{u_6}(t)=\mathit{\tau }[-{\mathit{\mu }}_6{u}_6(t)+c_{16}{u}_1(t)+H_6+h.o.t.],\hfill \end{array}\right.$$ 21

where

$$\begin{array}{cc}\hfill H_1& =\frac{c_{21}^0+{\mathit{\alpha }}_1}{6}\left(3f_1^{\prime \prime }(0)u_2^2(t-1)+f_1^{\prime \prime \prime }(0)u_2^3(t-1)\right)\hfill \\ \hfill & +\frac{c_{31}^0+{\mathit{\alpha }}_2}{6}\left(3f_1^{\prime \prime }(0)u_3^2(t-1)+f_1^{\prime \prime \prime }(0)u_3^3(t-1)\right)\hfill \\ \hfill & +\frac{c_{41}}{6}\left(3f_1^{\prime \prime }(0)u_4^2(t-1)+f_1^{\prime \prime \prime }(0)u_4^3(t-1)\right)\hfill \\ \hfill & +\frac{c_{51}}{6}\left(3f_1^{\prime \prime }(0)u_5^2(t-1)+f_1^{\prime \prime \prime }(0)u_5^3(t-1)\right)\hfill \\ \hfill & +\frac{c_{61}}{6}\left(3f_1^{\prime \prime }(0)u_6^2(t-1)+f_1^{\prime \prime \prime }(0)u_6^3(t-1)\right),\hfill \\ \hfill H_j& =\frac{1}{6}{c}_{1j}\left(3f_j^{\prime \prime }(0)u_1^2(t)+f_j^{\prime \prime \prime }(0)u_1^3(t)\right).\hfill \end{array}$$

Then following (Xu and Huang 2006), the second term of the Taylor expansion of system (21) also can be expressed in the form

$$\begin{array}{cc}\hfill \frac{1}{2}{\widehat{F}}_2(x_t,\mathit{\alpha })& =A_{1}u(t){\mathit{\alpha }}_1+A_{2}u(t){\mathit{\alpha }}_2+B_{1}u(t-1){\mathit{\alpha }}_1\hfill \\ \hfill & +B_{2}u(t-1){\mathit{\alpha }}_2+\sum _{i=1}^6{E}_i{u}_i(t)u(t-1)\hfill \\ \hfill & +\sum _{i=1}^6{F}_i{u}_i(t)u(t)+\sum _{i=1}^6{G}_i{u}_i(t-1)u(t-1),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill A_1& =A_2=O_{6\times 6},E_i=O_{6\times 6},i=1,2,\dots ,6,\hfill \\ \hfill G_1& =F_2=F_3=F_4=F_5=F_6=O_{6\times 6},\hfill \\ \hfill B_1& =\mathit{\tau }{\left(\begin{array}{cccccc}0& 1& 0& 0& ⋮& 0\\ 0& 0& 0& 0& ⋮& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0\end{array}\right)}_{6\times 6},\hfill \\ \hfill B_2& =\mathit{\tau }{\left(\begin{array}{cccccc}0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0\end{array}\right)}_{6\times 6},\hfill \\ \hfill F_1& =\mathit{\tau }{\left(\begin{array}{cccc}0& 0& \cdots & 0\\ \frac{1}{2}{f}_2^{\prime \prime }(0)c_{12}& 0& \cdots & 0\\ \frac{1}{2}{f}_3^{\prime \prime }(0)c_{13}& 0& \cdots & 0\\ \frac{1}{2}{f}_4^{\prime \prime }(0)c_{14}& 0& \cdots & 0\\ \frac{1}{2}{f}_5^{\prime \prime }(0)c_{15}& 0& \cdots & 0\\ \frac{1}{2}{f}_6^{\prime \prime }(0)c_{16}& 0& \cdots & 0\end{array}\right)}_{6\times 6},\hfill \\ \hfill G_2& =\mathit{\tau }{\left(\begin{array}{ccccc}0& \frac{f_1^{\prime \prime }(0)}{2}{c}_{21}^0& 0& \cdots & 0\\ 0& 0& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & 0\end{array}\right)}_{6\times 6},\hfill \\ \hfill G_3& =\mathit{\tau }{\left(\begin{array}{cccccc}0& 0& \frac{f_1^{\prime \prime }(0)c_{31}^0}{2}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& 0& 0& 0\end{array}\right)}_{6\times 6},\hfill \\ \hfill G_4& =\mathit{\tau }{\left(\begin{array}{cccccc}0& 0& 0& \frac{f_1^{\prime \prime }(0)c_{41}}{2}& 0& 0\\ 0& 0& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0\end{array}\right)}_{6\times 6},\hfill \\ \hfill G_5& =\mathit{\tau }{\left(\begin{array}{ccccc}0& \cdots & 0& \frac{f_1^{\prime \prime }(0)}{2}{c}_{51}& 0\\ 0& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& \cdots & 0& 0& 0\end{array}\right)}_{6\times 6},\hfill \\ \hfill G_6& =\mathit{\tau }{\left(\begin{array}{cccc}0& \cdots & 0& \frac{f_1^{\prime \prime }(0)}{2}{c}_{61}\\ 0& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& \cdots & 0& 0\end{array}\right)}_{6\times 6}.\hfill \end{array}$$

To obtain the normal form of system (21) on its center manifold, we need the following lemma.

Lemma 4

[See Xu and Huang (2006)] The bases ofPand its dual space$P^{\ast }$have the following representations

• $P=span\mathit{\Phi }$, $\mathit{\Phi }(\mathit{\theta })=({\mathit{\phi }}_1(\mathit{\theta }),{\mathit{\phi }}_2(\mathit{\theta }))$, $-1\le \mathit{\theta }\le 0$,

• $P^{\ast }=span\mathit{\Psi }$, $\mathit{\Psi }(s)=col({\mathit{\psi }}_1(s),{\mathit{\psi }}_2(s))$, $0\le s\le 1$,

where${\mathit{\phi }}_1(\mathit{\theta })={\mathit{\phi }}_1^0\in R^n\backslash \{0\}$, ${\mathit{\phi }}_2(\mathit{\theta })={\mathit{\phi }}_2^0+{\mathit{\phi }}_1^0\mathit{\theta }$, ${\mathit{\phi }}_2^0\in R^n$ and ${\mathit{\psi }}_2(s)={\mathit{\psi }}_2^0\in R^{n\ast }\backslash \{0\}$, ${\mathit{\psi }}_1(s)={\mathit{\psi }}_1^0-s{\mathit{\psi }}_2^0,{\mathit{\psi }}_1^0\in R^{n\ast }$,which satisfy

$$\begin{array}{cc}& (1)(A+B){\mathit{\phi }}_1^0=0,(2)(A+B){\mathit{\phi }}_2^0=(B+I){\mathit{\phi }}_1^0,(3){\mathit{\psi }}_2^0(A+B)=0,\hfill \\ \hfill & (4){\mathit{\psi }}_1^0(A+B)={\mathit{\psi }}_2^0(B+I),(5){\mathit{\psi }}_2^0{\mathit{\phi }}_2^0-\frac{1}{2}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_1^0+{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_2^0=1,\hfill \\ \hfill & (6){\mathit{\psi }}_1^0{\mathit{\phi }}_2^0-\frac{1}{2}{\mathit{\psi }}_1^{0}B{\mathit{\phi }}_1^0+{\mathit{\psi }}_1^{0}B{\mathit{\phi }}_2^0+\frac{1}{6}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_1^0-\frac{1}{2}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_2^0=0.\hfill \end{array}$$

For system (21), we have

$$A=\mathit{\tau }\left(\begin{array}{cccccc}-{\mathit{\mu }}_1& 0& 0& 0& 0& 0\\ c_{12}& -{\mathit{\mu }}_2& 0& 0& 0& 0\\ c_{13}& 0& -{\mathit{\mu }}_3& 0& 0& 0\\ c_{14}& 0& 0& -{\mathit{\mu }}_4& 0& 0\\ c_{15}& 0& 0& 0& -{\mathit{\mu }}_5& 0\\ c_{16}& 0& 0& 0& 0& -{\mathit{\mu }}_6\end{array}\right),B=\mathit{\tau }{\left(\begin{array}{cccccc}0& c_{21}^0& c_{31}^0& c_{41}& c_{51}& c_{61}\\ 0& 0& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0\end{array}\right)}_{6\times 6}.$$

By Lemma 4, we have

$$\begin{array}{cc}\hfill \mathit{\Phi }(\mathit{\theta })& =\left(\begin{array}{cc}1& \mathit{\theta }\\ \frac{c_{12}}{{\mathit{\mu }}_2}& \frac{c_{12}}{{\mathit{\mu }}_2}\left(\mathit{\theta }-\frac{1}{\mathit{\tau }{\mathit{\mu }}_2}\right)\\ ⋮& ⋮\\ \frac{c_{16}}{{\mathit{\mu }}_6}& \frac{c_{16}}{{\mathit{\mu }}_6}\left(\mathit{\theta }-\frac{1}{\mathit{\tau }{\mathit{\mu }}_6}\right)\end{array}\right),\hfill \\ \hfill \mathit{\Psi }(0)& =\left(\begin{array}{cccccc}{n}_1& n_2& n_3& n_4& n_5& n_6\\ \frac{{\mathit{\mu }}_3}{c_{31}^0}{n}_0& \frac{c_{21}^0{\mathit{\mu }}_3}{c_{31}^0{\mathit{\mu }}_2}{n}_0& n_0& \frac{{\mathit{\mu }}_3{c}_{41}}{c_{31}^0{\mathit{\mu }}_4}{n}_0& \frac{{\mathit{\mu }}_3{c}_{51}}{c_{31}^0{\mathit{\mu }}_5}{n}_0& \frac{{\mathit{\mu }}_3{c}_{61}}{c_{31}^0{\mathit{\mu }}_6}{n}_0\end{array}\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill n_0& =\frac{-2\mathit{\tau }{\mathit{\mu }}_2{\mathit{\mu }}_3^2{\mathit{\mu }}_4{\mathit{\mu }}_5{\mathit{\mu }}_6}{c_{13}\left({\mathit{\mu }}_2-{\mathit{\mu }}_3\right)\overline{n}}[{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2({\mathit{\mu }}_1+{\mathit{\mu }}_2+\mathit{\tau }{\mathit{\mu }}_1{\mathit{\mu }}_2)+c_{14}{c}_{41}{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2({\mathit{\mu }}_2-{\mathit{\mu }}_4)\hfill \\ \hfill & +c_{15}{c}_{51}{\mathit{\mu }}_4^2{\mathit{\mu }}_6^2({\mathit{\mu }}_2-{\mathit{\mu }}_5)+c_{16}{c}_{61}{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2({\mathit{\mu }}_2-{\mathit{\mu }}_6)],\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill \overline{n}& ={\mathit{\mu }}_6^3{\mathit{\mu }}_5^3{\mathit{\mu }}_4^3[{\mathit{\mu }}_2{\mathit{\mu }}_3{\mathit{\tau }}^2{\mathit{\mu }}_1+2\left({\mathit{\mu }}_2{\mathit{\mu }}_1+{\mathit{\mu }}_3{\mathit{\mu }}_1+{\mathit{\mu }}_2{\mathit{\mu }}_3\right)\mathit{\tau }+2({\mathit{\mu }}_1+{\mathit{\mu }}_2+{\mathit{\mu }}_3)]\hfill \\ \hfill & -2c_{14}{c}_{41}{\mathit{\mu }}_5^3{\mathit{\mu }}_6^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_4\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_4\right)-2c_{15}{c}_{51}{\mathit{\mu }}_4^3{\mathit{\mu }}_6^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\hfill \\ \hfill & -2c_{16}{c}_{61}{\mathit{\mu }}_4^3{\mathit{\mu }}_5^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill n_1& =\frac{n_3\mathit{\tau }{\mathit{\mu }}_3+(1+\mathit{\tau }{\mathit{\mu }}_3)n_0}{\mathit{\tau }{c}_{31}^0},\hfill \\ \hfill n_2& =\frac{c_{21}^0\left({\mathit{\mu }}_2{n}_3\mathit{\tau }{\mathit{\mu }}_3+({\mathit{\mu }}_2-{\mathit{\mu }}_3)n_0\right)}{\mathit{\tau }{\mathit{\mu }}_2^2{c}_{31}^0},\hfill \\ \hfill n_3& =\frac{2{\mathit{\mu }}_3^2{m}_1{m}_2}{3c_{13}{m}_3^2},n_j=\frac{c_{j1}\left({\mathit{\mu }}_j{n}_3\mathit{\tau }{\mathit{\mu }}_3+({\mathit{\mu }}_j-{\mathit{\mu }}_3)n_0\right)}{\mathit{\tau }{\mathit{\mu }}_j^2{c}_{31}^0},j=4,5,6,\hfill \\ \hfill m_1& ={\mathit{\mu }}_4^2{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_1+{\mathit{\mu }}_2+\mathit{\tau }{\mathit{\mu }}_1{\mathit{\mu }}_2\right)+c_{14}{c}_{41}{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_2-{\mathit{\mu }}_4\right)\hfill \\ \hfill & +c_{15}{c}_{51}{\mathit{\mu }}_4^2{\mathit{\mu }}_6^2\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)+c_{16}{c}_{61}{\mathit{\mu }}_4^2{\mathit{\mu }}_5^2\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right),\hfill \\ \hfill m_2& ={\mathit{\mu }}_4^4{\mathit{\mu }}_5^4{\mathit{\mu }}_6^4\left[{\mathit{\mu }}_2^2{\mathit{\mu }}_3{\mathit{\tau }}^3{\mathit{\mu }}_1+3{\mathit{\mu }}_2^2\left({\mathit{\mu }}_1+{\mathit{\mu }}_3\right){\mathit{\tau }}^2+6\left({\mathit{\mu }}_2^2-{\mathit{\mu }}_3{\mathit{\mu }}_1\right)\mathit{\tau }-6({\mathit{\mu }}_1+{\mathit{\mu }}_3)\right]\hfill \\ \hfill & +6c_{14}{c}_{41}{\mathit{\mu }}_5^4{\mathit{\mu }}_6^4\left({\mathit{\mu }}_2-{\mathit{\mu }}_4\right)\left({\mathit{\mu }}_2+{\mathit{\mu }}_4\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_4\right)\hfill \\ \hfill & +6c_{15}{c}_{51}{\mathit{\mu }}_4^4{\mathit{\mu }}_6^4\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2+{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\hfill \\ \hfill & +6c_{16}{c}_{61}{\mathit{\mu }}_4^4{\mathit{\mu }}_5^4\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_2+{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right),\hfill \\ \hfill m_3& ={\mathit{\mu }}_4^3{\mathit{\mu }}_5^3{\mathit{\mu }}_6^3\left[{\mathit{\mu }}_2{\mathit{\mu }}_3{\mathit{\tau }}^2{\mathit{\mu }}_1+2\left({\mathit{\mu }}_2{\mathit{\mu }}_1+{\mathit{\mu }}_3{\mathit{\mu }}_1+{\mathit{\mu }}_2{\mathit{\mu }}_3\right)\mathit{\tau }+2({\mathit{\mu }}_1+{\mathit{\mu }}_2+{\mathit{\mu }}_3)\right]\hfill \\ \hfill & -2c_{14}{c}_{41}{\mathit{\mu }}_5^3{\mathit{\mu }}_6^3({\mathit{\mu }}_3-{\mathit{\mu }}_4)\left({\mathit{\mu }}_2-{\mathit{\mu }}_4\right)-2c_{15}{c}_{51}{\mathit{\mu }}_4^3{\mathit{\mu }}_6^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\hfill \\ \hfill & -2c_{16}{c}_{61}{\mathit{\mu }}_4^3{\mathit{\mu }}_5^3\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right).\hfill \end{array}$$

Following the formulas in (Xu and Huang 2006), we have the following Lemma.

Lemma 5

Let$(\mathrm{H}1)$$(\mathrm{H}2)$and$(\mathrm{H}4)$hold.Then the system (21) can be reduced to the following system on the center manifold at$(u_t,\mathit{\alpha })=(0,0)$

$$\left\{\begin{array}{c}{\dot{z}}_1=z_2,\hfill \\ {\dot{z}}_2={\mathit{\gamma }}_1{z}_1+{\mathit{\gamma }}_2{z}_2+{\mathit{\eta }}_1{z}_1^2+{\mathit{\eta }}_2{z}_1{z}_2+h.o.t.,\hfill \end{array}\right.$$ 22

where

$$\begin{array}{cc}\hfill {\mathit{\gamma }}_1& =\frac{n_0\mathit{\tau }{\mathit{\mu }}_3{c}_{12}}{c_{31}^0{\mathit{\mu }}_2}{\mathit{\alpha }}_1+\frac{n_0\mathit{\tau }{c}_{13}}{c_{31}^0}{\mathit{\alpha }}_2,\hfill \\ \hfill {\mathit{\gamma }}_2& =\frac{c_{12}\left({\mathit{\mu }}_2{n}_3\mathit{\tau }{\mathit{\mu }}_3+{\mathit{\mu }}_2{n}_0-{\mathit{\mu }}_3{n}_0\right)}{{\mathit{\mu }}_2^2{c}_{31}^0}{\mathit{\alpha }}_1+\frac{c_{13}{n}_3\mathit{\tau }}{c_{31}^0}{\mathit{\alpha }}_2,\hfill \\ \hfill {\mathit{\eta }}_1& =\frac{{\mathit{\mu }}_3{n}_0\mathit{\tau }{f}_1^{\prime \prime }(0)}{2c_{31}^0}\left(\frac{c_{12}^2{c}_{21}^0}{{\mathit{\mu }}_2^2}+\frac{c_{13}^2{c}_{31}^0}{{\mathit{\mu }}_3^2}+\frac{c_{14}^2{c}_{41}}{{\mathit{\mu }}_4^2}+\frac{c_{15}^2{c}_{51}}{{\mathit{\mu }}_5^2}+\frac{c_{16}^2{c}_{61}}{{\mathit{\mu }}_6^2}\right)\hfill \\ \hfill & +\frac{n_0{\mathit{\mu }}_3\mathit{\tau }}{2c_{31}^0}\left(\frac{c_{21}^0{f}_2^{\prime \prime }(0)c_{12}}{{\mathit{\mu }}_2}+\frac{f_3^{\prime \prime }(0)c_{13}{c}_{31}^0}{{\mathit{\mu }}_3}+\frac{c_{41}{f}_4^{\prime \prime }(0)c_{14}}{{\mathit{\mu }}_4}\right.\hfill \\ \hfill & \left.+\frac{c_{51}{f}_5^{\prime \prime }(0)c_{15}}{{\mathit{\mu }}_5}+\frac{c_{61}{f}_6^{\prime \prime }(0)c_{16}}{{\mathit{\mu }}_6}\right),\hfill \\ \hfill {\mathit{\eta }}_2& =\frac{f_1^{\prime \prime }(0)}{c_{31}^0}\left(\frac{c_{12}^2{c}_{21}^0\left({\mathit{\mu }}_3{\mathit{\mu }}_2{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_2{n}_0\right)}{{\mathit{\mu }}_2^3}+\frac{c_{14}^2{c}_{41}\left({\mathit{\mu }}_3{\mathit{\mu }}_4{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_4{n}_0\right)}{{\mathit{\mu }}_4^3}\right.\hfill \\ \hfill & \left.+\frac{c_{15}^2{c}_{51}\left({\mathit{\mu }}_3{\mathit{\mu }}_5{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_5{n}_0\right)}{{\mathit{\mu }}_5^3}+\frac{c_{16}^2{c}_{61}\left({\mathit{\mu }}_3{\mathit{\mu }}_2{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_2{n}_0\right)}{{\mathit{\mu }}_6^3}\right)\hfill \\ \hfill & +\frac{c_{21}^0\left({\mathit{\mu }}_3{\mathit{\mu }}_2{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_2{n}_0\right)f_2^{\prime \prime }(0)c_{12}}{{\mathit{\mu }}_2^2{c}_{31}^0}+n_3\mathit{\tau }{f}_3^{\prime \prime }(0)c_{13}\hfill \\ \hfill & +\frac{c_{41}\left({\mathit{\mu }}_3{\mathit{\mu }}_4{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_4{n}_0\right)f_4^{\prime \prime }(0)c_{14}}{{\mathit{\mu }}_4^2{c}_{31}^0}+\frac{n_3\mathit{\tau }{c}_{13}^2{c}_{31}^0}{{\mathit{\mu }}_3}\hfill \\ \hfill & +\frac{c_{51}\left({\mathit{\mu }}_3{\mathit{\mu }}_5{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_5{n}_0\right)f_5^{\prime \prime }(0)c_{15}}{{\mathit{\mu }}_5^2{c}_{31}^0}\hfill \\ \hfill & +\frac{c_{61}\left({\mathit{\mu }}_3{\mathit{\mu }}_6{n}_3\mathit{\tau }-{\mathit{\mu }}_3{n}_0+{\mathit{\mu }}_6{n}_0\right)f_6^{\prime \prime }(0)c_{16}}{{\mathit{\mu }}_6^2{c}_{31}^0}.\hfill \end{array}$$

Since

$$\left|\frac{\mathit{\partial }({\mathit{\gamma }}_1,{\mathit{\gamma }}_2)}{\mathit{\partial }({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)}\right|=-\frac{n_0^2\mathit{\tau }{c}_{12}{c}_{13}\left({\mathit{\mu }}_2-{\mathit{\mu }}_3\right)}{{(c_{31}^0)}^2{\mathit{\mu }}_2^2}\ne 0,$$

then the map$({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)\to ({\mathit{\gamma }}_1,{\mathit{\gamma }}_2)$is regular. Hence we can get the following theorem.

Theorem 2

Let$(\mathrm{H}1)$$(\mathrm{H}2)$and$(\mathrm{H}4)$hold.If$f_i^{\prime \prime }(0)\ne 0$, $i=1,\dots ,6$, on the center manifold, system (20) is equivalent to system (22).

Referring Dong and Liao (2013), system (22) has two equilibrium $E_1=(0,0)$ and $E_2=(-\frac{{\mathit{\gamma }}_1}{{\mathit{\eta }}_1},0)$, the bifurcation curves near (0, 0) in the ${\mathit{\alpha }}_1$ and ${\mathit{\alpha }}_2$ parameter space are the following

1. system (22) undergoes a transcritical bifurcation on the curve

   $S=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):{\mathit{\gamma }}_1=0,{\mathit{\gamma }}_2\in R\}$,

2. at $E_1$ system (22) undergoes an unstable Hopf bifurcation in the half line

   $H=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):{\mathit{\gamma }}_2=0,{\mathit{\gamma }}_1<0\}$,

3. at $E_2$, system (22) undergoes a stable Hopf bifurcation in the half line

   $T=\left\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):{\mathit{\gamma }}_2=\frac{{\mathit{\eta }}_2}{{\mathit{\eta }}_1}{\mathit{\gamma }}_1,{\mathit{\gamma }}_1>0\right\}$.

In “Numerical examples and simulations” section, a numerical example is given.

Remark

From the point of the view of application, the results of Theorem 2 under the conditions (H1), (H2), (H4) and $f_i^{\prime \prime }(0)\ne 0,(i=1,\dots ,6)$ can be explained as the exchanges of various stored patterns or memory patterns occurring in perturbed system (20) when the parameters ${\mathit{\alpha }}_1$ and ${\mathit{\alpha }}_2$ vary in the small neighborhood of the $(0,0)$. Notice that a stable equilibrium is corresponding to a single storage pattern, thus, when parameters $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ pass the transcritical bifurcation curve determined by ${\mathit{\gamma }}_1({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=0$, system (20) transforms its stored patten from one to other. Similarly, system (20) can exhibit more complex memory pattern (a periodic pattern) when ${\mathit{\alpha }}_1,{\mathit{\alpha }}_2$ approach the Hopf bifurcation curve defined by ${\mathit{\gamma }}_2-{\mathit{\eta }}_2{\mathit{\gamma }}_1/{\mathit{\eta }}_1=0$, $({\mathit{\gamma }}_1({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)>0)$.

Furthermore, if $f_i^{\prime \prime }(0)=0$, $i=1,\dots ,6$, to discuss the properties of the origin of system (21), we need to compute the third order normal form of the B–T bifurcation.

Let $u_t=\mathit{\Phi }(\mathit{\theta })z(t)+y$, then (21) can be decomposed as

$$\left\{\begin{array}{c}\dot{z}=Bz+\mathit{\Psi }(0)F(\mathit{\Phi }z+y,\mathit{\alpha }),\hfill \\ \dot{y}=A_{Q^1}y+(I-\mathit{\pi })X_{0}F(\mathit{\Phi }z+y,\mathit{\alpha }),\hfill \end{array}\right.$$ 23

where $z={(z_1,z_2)}^T$, $y={(y_1,y_2)}^T$ and

$${\mathit{\phi }}_1(\mathit{\theta })=z_1+\mathit{\theta }{z}_2,{\mathit{\phi }}_j(\mathit{\theta })=\frac{c_{1j}}{{\mathit{\mu }}_j}{z}_1+\frac{c_{1j}}{{\mathit{\mu }}_j}\left(\mathit{\theta }-\frac{1}{\mathit{\tau }{\mathit{\mu }}_j}\right)z_2,j=2,3,\dots ,6.$$ 24

It follows from (Faria and Magalhaes 1995; Jiang and Yuan 2007) that

$$g_3^1(z,0,\mathit{\alpha })=\left(I-P_{I,3}^1\right){\tilde{f}}_3^1(z,0,\mathit{\alpha })={\mathrm{Proj}}_{Im{(M_3^1)}^c}{\tilde{f}}_3^1(z,0,\mathit{\alpha }),$$ 25

where

$$\begin{array}{cc}\hfill {\tilde{f}}_3^1(z,0,\mathit{\alpha })& =f_3^1(z,0,\mathit{\alpha })+\frac{3}{2}\left[\left(D_z{f}_2^1\right)(z,0,\mathit{\alpha })U_2^1(z,\mathit{\alpha })+\left(D_y{f}_2^1\right)(z,0,\mathit{\alpha })U_2^2(z,\mathit{\alpha })\right.\hfill \\ \hfill & \left.-\left(D_z{U}_2^1\right)(z,\mathit{\alpha })g_2^1(z,0,\mathit{\alpha })\right].\hfill \end{array}$$

By (21) and (24), one can get

$$\begin{array}{cc}& f_3^1(z,0,\mathit{\alpha })\hfill \\ \hfill & =\left(\begin{array}{c}\left[n_1{h}_1\left(c_{21}^0{\mathit{\phi }}_2^3(-1)+c_{31}^0{\mathit{\phi }}_3^3(-1)+\sum _{j=4}^6{c}_{j1}{\mathit{\phi }}_j^3(-1)\right)+\sum _{j=2}^6{n}_j{h}_j{c}_{1j}{\mathit{\phi }}_1^3(0)\right]\hfill \\ \frac{n_0{\mathit{\mu }}_3}{c_{31}^0}\left[h_1\left(c_{21}^0{\mathit{\phi }}_2^3(-1)+c_{31}^0{\mathit{\phi }}_3^3(-1)+\sum _{j=4}^6{c}_{j1}{\mathit{\phi }}_j^3(-1)\right)+d_0\right]\hfill \end{array}\right),\hfill \end{array}$$ 26

where

$$h_j=f_j^{{}^{\prime \prime \prime }}(0),d_0={\mathit{\phi }}_1^3(0)\left(\frac{c_{21}^0{h}_2{c}_{12}}{{\mathit{\mu }}_2}+\frac{c_{31}^0{h}_3{c}_{13}}{{\mathit{\mu }}_3}+\sum _{j=4}^6\frac{c_{j1}{c}_{1j}{h}_j}{{\mathit{\mu }}_j}\right).$$

To obtain the third-order normal form, it needs the decomposition

$$V_3^4(R^2)=I_m\left(M_3^1\right)\oplus I_m{(M_3^1)}^c.$$

Then the canonical basis in $V_3^4(R^2)$ has forty elements: ${({(z,\mathit{\alpha })}^3,0)}^T$, ${(0,{(z,\mathit{\alpha })}^3)}^T$, the bases of $I_m(M_3^1)$ and $I_m{(M_3^1)}^c$ one can see in (Jiang and Yuan 2007).

Together with the definition of $M_3^1$, one can obtain that the space of $I_m(M_3^1)$ can be spanned by the following elements

$$\begin{array}{cc}& \left(\begin{array}{c}{z}_1^2{z}_2\\ 0\end{array}\right),\left(\begin{array}{c}{z}_1{z}_2^2\\ 0\end{array}\right),\left(\begin{array}{c}{z}_2^3\\ 0\end{array}\right),\left(\begin{array}{c}{z}_1{z}_2{\mathit{\mu }}_i\\ 0\end{array}\right),\left(\begin{array}{c}{z}_2{\mathit{\mu }}_i^2\\ 0\end{array}\right),\hfill \\ \hfill & \left(\begin{array}{c}{z}_2^2{\mathit{\mu }}_i\\ 0\end{array}\right),\left(\begin{array}{c}{z}_2{\mathit{\mu }}_1{\mathit{\mu }}_2\\ 0\end{array}\right),\left(\begin{array}{c}-z_1^3\\ 3z_1^2{z}_2\end{array}\right),\left(\begin{array}{c}-z_1^2{z}_2\\ 2z_1{z}_2^2\end{array}\right),\left(\begin{array}{c}-z_1{z}_2^2\\ z_2^3\end{array}\right),\hfill \\ \hfill & \left(\begin{array}{c}-z_1^2{\mathit{\mu }}_i\\ 2z_1{z}_2{\mathit{\mu }}_i\end{array}\right),\left(\begin{array}{c}-z_1{\mathit{\mu }}_i^2\\ z_2{\mathit{\mu }}_i^2\end{array}\right),\left(\begin{array}{c}-z_1{z}_2{\mathit{\mu }}_i\\ z_2^2{\mathit{\mu }}_i\end{array}\right),\hfill \\ \hfill & \left(\begin{array}{c}-z_1{\mathit{\mu }}_1{\mathit{\mu }}_2\\ z_2{\mathit{\mu }}_1{\mathit{\mu }}_2\end{array}\right),\left(\begin{array}{c}{\mathit{\mu }}_i^3\\ 0\end{array}\right),\left(\begin{array}{c}-{\mathit{\mu }}_1^2{\mathit{\mu }}_2\\ 0\end{array}\right),\left(\begin{array}{c}{\mathit{\mu }}_1{\mathit{\mu }}_2^2\\ 0\end{array}\right),i=1,2,\hfill \end{array}$$

and the complementary space $I_m{(M_3^1)}^c$ can be spanned by the elements

$$\begin{array}{cc}& \left(\begin{array}{c}0\\ z_1^3\end{array}\right),\left(\begin{array}{c}0\\ z_1^2{z}_2\end{array}\right),\left(\begin{array}{c}0\\ z_1^2{\mathit{\mu }}_i\end{array}\right),\left(\begin{array}{c}0\\ z_1{z}_2{\mathit{\mu }}_i\end{array}\right),\left(\begin{array}{c}0\\ z_1{\mathit{\mu }}_i^2\end{array}\right),\hfill \\ \hfill & \left(\begin{array}{c}0\\ z_2{\mathit{\mu }}_i^2\end{array}\right),\left(\begin{array}{c}0\\ z_i{\mathit{\mu }}_1{\mathit{\mu }}_2\end{array}\right),\left(\begin{array}{c}0\\ {\mathit{\mu }}_i^3\end{array}\right),\left(\begin{array}{c}0\\ {\mathit{\mu }}_1^2{\mathit{\mu }}_2\end{array}\right),\left(\begin{array}{c}0\\ {\mathit{\mu }}_1{\mathit{\mu }}_2^2\end{array}\right),i=1,2.\hfill \end{array}$$

From (25), (27) and

$$\begin{array}{cc}& {\mathrm{Proj}}_{Im{(M_3^1)}^c}p=\left\{\begin{array}{cc}p,\hfill & p\in Im{(M_3^1)}^c,\hfill \\ 0,\hfill & p\in Im(M_3^1),\hfill \end{array}\right.{\mathrm{Proj}}_{Im{(M_3^1)}^c}\left(\begin{array}{c}{z}_1^3\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 3z_1^2{z}_2\end{array}\right),\hfill \\ \hfill & {\mathrm{Proj}}_{Im{(M_3^1)}^c}\left(\begin{array}{c}{z}_1{\mathit{\alpha }}_i^2\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ z_2{\mathit{\alpha }}_i^2\end{array}\right),{\mathrm{Proj}}_{Im{(M_3^1)}^c}\left(\begin{array}{c}{z}_1{\mathit{\alpha }}_1{\mathit{\alpha }}_2\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ {\mathit{\alpha }}_1{\mathit{\alpha }}_2{z}_2\end{array}\right),\hfill \\ \hfill & {\mathrm{Proj}}_{Im{(M_3^1)}^c}\left(\begin{array}{c}{z}_1^2{\mathit{\alpha }}_i\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 2z_1{z}_2{\mathit{\alpha }}_i\end{array}\right),\hfill \end{array}$$

we obtain the third order normal form of system (21) as follows

$$\left\{\begin{array}{c}{\dot{z}}_1=z_2,\hfill \\ {\dot{z}}_2={\mathit{\gamma }}_1{z}_1+{\mathit{\gamma }}_2{z}_2+a_3{z}_1^3+b_3{z}_1^2{z}_2+h.o.t.,\hfill \end{array}\right.$$ 27

where the higher terms of $\mathit{\alpha }$ are omitted and

$$\begin{array}{cc}\hfill a_3& =\frac{1}{6}{f}_{30}^2,b_3=\frac{1}{6}(f_{21}^2+3f_{30}^1),\hfill \\ \hfill f_{30}^1& =\left(n_1{h}_1\sum _{j=2}^6\frac{c_{j1}{c}_{1j}^3}{{\mathit{\mu }}_j^3}+\sum _{j=2}^6{n}_j{h}_j{c}_{1j}\right),\hfill \\ \hfill f_{30}^2& =\frac{n_0{\mathit{\mu }}_3}{c_{31}^0}\left(h_1\sum _{j=2}^6\frac{c_{j1}{c}_{1j}^3}{{\mathit{\mu }}_j^3}+\frac{c_{21}^0{h}_2{c}_{12}}{{\mathit{\mu }}_2}+\frac{c_{31}^0{h}_3{c}_{13}}{{\mathit{\mu }}_3}+\frac{c_{41}{c}_{14}}{{\mathit{\mu }}_4}+\frac{c_{51}{c}_{15}}{{\mathit{\mu }}_5}+\frac{c_{61}{c}_{16}}{{\mathit{\mu }}_6}\right),\hfill \\ \hfill f_{21}^2& =-\frac{3h_1{\mathit{\mu }}_3{n}_0}{c_{31}^0}\sum _{j=2}^6\frac{c_{j1}{c}_{1j}^3\left(1+\frac{1}{\mathit{\tau }{\mathit{\mu }}_j}\right)}{{\mathit{\mu }}_j^3}.\hfill \end{array}$$

After time rescaling and coordinate transformation given by $\overline{t}=-\frac{|a_3|}{b_3}t$, $w_1=\frac{a_4}{\sqrt{|a_3|}}{z}_1$, $w_2=-\frac{a_4^2}{|a_3|\sqrt{|a_3|}}{z}_2$, system (27) is equivalent to the following system

$$\left\{\begin{array}{c}{\dot{w}}_1=w_2,\hfill \\ {\dot{w}}_2=v_1{w}_1+v_2{w}_2+s{w}_1^3-w_1^2{w}_2+h.o.t.,\hfill \end{array}\right.$$ 28

where $v_1={\left(\frac{b_3}{a_3}\right)}^2{\mathit{\gamma }}_1$, $v_2=-\frac{b_3}{|a_3|}{\mathit{\gamma }}_2$, $s=\mathrm{sgn}(a_3)$. From (He et al. 2012a; Dong and Liao 2013) we know the bifurcations of system (28) is related to the sign of s. If $s=1$, we have

1. system (28) undergoes a Pitchfork bifurcation on the curve

   $$S=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_1=0,v_2\in R\},$$
2. system (28) undergoes a Hopf bifurcation H at the trivial equilibrium on the curve

   $$H=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_2=0,v_1<0\},$$
3. system (28) undergoes a heteroclinic bifurcation on the curve

   $$T=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_2=-\frac{1}{5}{v}_1+O(v_1^2),v_1<0\},$$

If $s=-1$, we have

1. system (28) undergoes a Pitchfork bifurcation on the curve

   $$S=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_1=0,v_2\in R\},$$
2. system (28) undergoes a Hopf bifurcation at the trivial equilibrium on the curve

   $$H_0=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_2=0,v_1<0\},$$
3. system (28) undergoes a Hopf bifurcation at the nontrivial equilibrium on the curve

   $$H_1=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_1=v_2,v_1>0\},$$
4. system (28) undergoes a homoclinic bifurcation on the curve

   $$T=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_2=\frac{4}{5}{v}_1+O(v_1^2),v_1>0\},$$
5. system (28) undergoes a double cycle bifurcation on the curve

   $$H_d=\{({\mathit{\alpha }}_1,{\mathit{\alpha }}_2):v_2=d{v}_1+O(v_1^2),v_1>0,d\approx 0.752\}.$$

To verify above results, two numerical examples and some simulations are shown in “Numerical examples and simulations” section.

Remark

One can see if the condition $f^{\prime \prime }(0)\ne 0$, $(i=1,\dots ,6)$ in the Theorem (2) does not holds, then with $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ varying in the small neighborhood of $(0,0)$, system (20) can exhibit the more complicated stored patterns or memory patterns, including the transition of stored pattern from one to two through a Pitchfork bifurcation. The two stored patterns also may lead to three kinds periodic memory patterns. In fact, a stable limit cycle (a periodic memory pattern) is yielded when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ cross the Hopf bifurcation curve $H_0$. With $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ moving continuously and passing the Pitchfork bifurcation curve $S^{+}$ to the side of ($v_1>0$), two unstable nontrivial equilibria are bifurcated from the trivial equilibrium. Further, the two unstable nontrivial equilibria become locally stable stored pattern when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ cross the Hopf bifurcation curve $H_1$ which also gives rise to two unstable small limit cycles located inside the surrounding big limit cycle.

Triple zero bifurcation

To discuss the triple zero bifurcation of system (20), we rewrite $c_{21}$, $c_{31}$ and $c_{41}$ as $c_{21}=c_{21}^0+{\mathit{\beta }}_1$, $c_{31}=c_{31}^0+{\mathit{\beta }}_2$ and $c_{41}=c_{41}^0+{\mathit{\beta }}_3$, where $({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3)$ vary near (0, 0, 0), taking the Taylor expansion then system (20) becomes

$$\left\{\begin{array}{c}\dot{u_1}(t)=\mathit{\tau }[-{\mathit{\mu }}_1{u}_1(t)+\left(c_{21}^0+{\mathit{\beta }}_1\right)u_2(t-1)+\left(c_{31}^0+{\mathit{\beta }}_2\right)u_3(t-1)+\left(c_{41}^0+{\mathit{\beta }}_3\right)u_4(t-1)+c_{51}{u}_5(t-1)+c_{61}{u}_6(t-1)+T_1+h.o.t.],\hfill \\ \dot{u_2}(t)=\mathit{\tau }[-{\mathit{\mu }}_2{u}_2(t)+c_{12}{u}_1(t)+H_2+h.o.t.],\hfill \\ ⋮\hfill \\ \dot{u_6}(t)=\mathit{\tau }[-{\mathit{\mu }}_6{u}_6(t)+c_{16}{u}_1(t)+H_6+h.o.t.],\hfill \end{array}\right.$$ 29

where

$$\begin{array}{cc}\hfill T_1& =\frac{c_{21}^0+{\mathit{\beta }}_1}{6}\left(3f_1^{\prime \prime }(0)u_2^2(t-1)+f_1^{\prime \prime \prime }(0)u_2^3(t-1)\right)+\frac{c_{31}^0+{\mathit{\beta }}_2}{6}\left(3f_1^{\prime \prime }(0)u_3^2(t-1)\right.\hfill \\ \hfill & \left.+f_1^{\prime \prime \prime }(0)u_3^3(t-1)\right)+\frac{c_{41}^0+{\mathit{\beta }}_3}{6}\left(3f_1^{\prime \prime }(0)u_4^2(t-1)+f_1^{\prime \prime \prime }(0)u_4^3(t-1)\right)\hfill \\ \hfill & +\frac{c_{51}}{6}\left(3f_1^{\prime \prime }(0)u_5^2(t-1)+f_1^{\prime \prime \prime }(0)u_5^3(t-1)\right)\hfill \\ \hfill & +\frac{c_{61}}{6}\left(3f_1^{\prime \prime }(0)u_6^2(t-1)+f_1^{\prime \prime \prime }(0)u_6^3(t-1)\right),\hfill \\ \hfill H_j& =\frac{1}{6}{c}_{1j}\left(3f_j^{\prime \prime }(0)u_1^2(t)+f_j^{\prime \prime \prime }(0)u_1^3(t)\right).\hfill \end{array}$$

Then following Qiao et al. (2010), the second term of the Taylor expansion of system (29) also can be expressed in the form

$$\begin{array}{cc}\hfill \frac{1}{2}{\widehat{F}}_2(x_t,\mathit{\beta })& =A_{1}u(t){\mathit{\beta }}_1+A_{2}u(t){\mathit{\beta }}_2+A_{3}u(t){\mathit{\beta }}_3+B_{1}u(t-1){\mathit{\beta }}_1+B_{2}u(t-1){\mathit{\beta }}_2\hfill \\ \hfill & +B_{3}u(t-1){\mathit{\beta }}_3+\sum _{i=1}^6{E}_i{u}_i(t)u(t-1)\hfill \\ \hfill & +\sum _{i=1}^6{F}_i{u}_i(t)u(t)+\sum _{i=1}^6{G}_i{u}_i(t-1)u(t-1),\hfill \end{array}$$

where,

$$A_3={(0)}_{6\times 6},B_3=\mathit{\tau }{\left(\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& 0& 0& 0\end{array}\right)}_{6\times 6},$$ 30

the other coefficient matrices are the same as them in (22).

To obtain the normal form it also needs to compute the corresponding expressions of $\mathit{\Phi }(\mathit{\theta })$ and $\mathit{\Psi }(s)$ of system (29) by using the following Lemma.

Lemma 6

[See (Qiao et al. 2010)] The bases ofPand its dual space$P^{\ast }$have the following representations

$$\begin{array}{cc}\hfill P& =span\mathit{\Phi },\mathit{\Phi }(\mathit{\theta })=({\mathit{\phi }}_1(\mathit{\theta }),{\mathit{\phi }}_2(\mathit{\theta }),{\mathit{\phi }}_3(\mathit{\theta })),-1\le \mathit{\theta }\le 0,\hfill \\ \hfill P^{\ast }& =span\mathit{\Psi },\mathit{\Psi }(s)=col({\mathit{\psi }}_1(s),{\mathit{\psi }}_2(s),{\mathit{\psi }}_3(s)),0\le s\le 1\hfill \end{array}$$

where${\mathit{\phi }}_1(\mathit{\theta })={\mathit{\phi }}_1^0\in R^n\backslash \{0\},$${\mathit{\phi }}_2(\mathit{\theta })={\mathit{\phi }}_2^0+{\mathit{\phi }}_1^0\mathit{\theta },$${\mathit{\phi }}_3(\mathit{\theta })={\mathit{\phi }}_3^0+{\mathit{\phi }}_2^0\mathit{\theta }+\frac{1}{2}{\mathit{\phi }}_1^0{\mathit{\theta }}^2,$${\mathit{\phi }}_2^0$, ${\mathit{\phi }}_3^0\in R^n$and${\mathit{\psi }}_3(s)={\mathit{\psi }}_3^0\in R^{n\ast }\backslash \{0\}$, ${\mathit{\psi }}_2(s)={\mathit{\psi }}_2^0-s{\mathit{\psi }}_3^0$, ${\mathit{\psi }}_1(s)={\mathit{\psi }}_1^0-s{\mathit{\psi }}_2^0+\frac{1}{2}{s}^2{\mathit{\psi }}_3^0$, ${\mathit{\psi }}_1^0,{\mathit{\psi }}_2^0\in R^{n\ast }$, which satisfy

$$\begin{array}{cc}& (1)(A+B){\mathit{\phi }}_1^0=0,(2)(A+B){\mathit{\phi }}_2^0=(B+I){\mathit{\phi }}_1^0,\hfill \\ \hfill & (3)(A+B){\mathit{\phi }}_3^0=(B+I){\mathit{\phi }}_2^0-\frac{1}{2}B{\mathit{\phi }}_1^0,\hfill \\ \hfill & (4){\mathit{\psi }}_3^0(A+B)=0,(5){\mathit{\psi }}_2^0(A+B)={\mathit{\psi }}_3^0(B+I),\hfill \\ \hfill & (6){\mathit{\psi }}_1^0(A+B)={\mathit{\psi }}_2^0(B+I)-\frac{1}{2}{\mathit{\psi }}_3^{0}B,\hfill \\ \hfill & (7){\mathit{\psi }}_3^0(B+I){\mathit{\phi }}_3^0-\frac{1}{2}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_2^0+\frac{1}{6}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_1^0=1,\hfill \\ \hfill & (8){\mathit{\psi }}_2^0(B+I){\mathit{\phi }}_3^0-\frac{1}{2}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_2^0+\frac{1}{6}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_1^0-\frac{1}{2}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_3^0+\frac{1}{6}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_2^0\hfill \\ \hfill & -\frac{1}{24}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_1^0=0,\hfill \\ \hfill & (9){\mathit{\psi }}_1^0(B+I){\mathit{\phi }}_3^0-\frac{1}{2}{\mathit{\psi }}_1^{0}B{\mathit{\phi }}_2^0+\frac{1}{6}{\mathit{\psi }}_1^{0}B{\mathit{\phi }}_1^0-\frac{1}{2}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_3^0+\frac{1}{6}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_2^0-\frac{1}{24}{\mathit{\psi }}_2^{0}B{\mathit{\phi }}_1^0\hfill \\ \hfill & +\frac{1}{6}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_3^0-\frac{1}{24}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_2^0+\frac{1}{120}{\mathit{\psi }}_3^{0}B{\mathit{\phi }}_1^0=0.\hfill \end{array}$$

The expressions of coefficient matrices A and B see (30), but it needs change $c_{41}$ as $c_{41}^0$, then together with Lemma 6, we can obtain the expressions of $\mathit{\Phi }(\mathit{\theta })$ and $\mathit{\Psi }(0)$ as follows:

$$\begin{array}{cc}\hfill \mathit{\Phi }(\mathit{\theta })& =\left(\begin{array}{ccc}1& \mathit{\theta }& \frac{1}{2}{\mathit{\theta }}^2\\ \frac{c_{12}}{{\mathit{\mu }}_2}& \frac{c_{12}}{{\mathit{\mu }}_2}\left(\mathit{\theta }-\frac{1}{\mathit{\tau }{\mathit{\mu }}_2}\right)& \frac{c_{12}}{{\mathit{\mu }}_2}\left(\frac{1}{{\mathit{\tau }}^2{\mathit{\mu }}_2^2}-\frac{\mathit{\theta }}{\mathit{\tau }{\mathit{\mu }}_2}+\frac{1}{2}{\mathit{\theta }}^2\right)\\ ⋮& ⋮& ⋮\\ \frac{c_{16}}{{\mathit{\mu }}_6}& \frac{c_{16}}{{\mathit{\mu }}_6}\left(\mathit{\theta }-\frac{1}{\mathit{\tau }{\mathit{\mu }}_6}\right)& \frac{c_{16}}{{\mathit{\mu }}_6}\left(\frac{1}{{\mathit{\tau }}^2{\mathit{\mu }}_6^2}-\frac{\mathit{\theta }}{\mathit{\tau }{\mathit{\mu }}_6}+\frac{1}{2}{\mathit{\theta }}^2\right)\end{array}\right),\hfill \\ \hfill \mathit{\Psi }(0)& =\left(\begin{array}{cccccc}{e}_1& e_2& e_3& e_4& e_5& e_6\\ r_1& r_2& r_3& r_4& r_5& r_6\\ l_1& l_2& l_3& l_4& l_5& l_6\end{array}\right),\hfill \end{array}$$

where

$$l_1=\frac{6{\mathit{\mu }}_4{\mathit{\mu }}_3{\mathit{\tau }}^2{\mathit{\mu }}_2{\mathit{\mu }}_6^4{\mathit{\mu }}_5^4}{{\mathit{\mu }}_5^4{\mathit{\mu }}_6^4\left({\mathit{\mu }}_2{\mathit{\tau }}^3{\mathit{\mu }}_1{\mathit{\mu }}_3{\mathit{\mu }}_4+{\mathit{\delta }}_1{\mathit{\tau }}^2+{\mathit{\delta }}_2\mathit{\tau }+{\mathit{\delta }}_3\right)+{\mathit{\delta }}_4},$$

with

$$\begin{array}{cc}\hfill {\mathit{\delta }}_1& =3({\mathit{\mu }}_2{\mathit{\mu }}_1{\mathit{\mu }}_4+{\mathit{\mu }}_3{\mathit{\mu }}_1{\mathit{\mu }}_4+{\mathit{\mu }}_2{\mathit{\mu }}_1{\mathit{\mu }}_3+{\mathit{\mu }}_4{\mathit{\mu }}_3{\mathit{\mu }}_2),\hfill \\ \hfill {\mathit{\delta }}_2& =6({\mathit{\mu }}_3{\mathit{\mu }}_1+{\mathit{\mu }}_1{\mathit{\mu }}_4+{\mathit{\mu }}_2{\mathit{\mu }}_4+{\mathit{\mu }}_2{\mathit{\mu }}_3+6{\mathit{\mu }}_2{\mathit{\mu }}_1+6{\mathit{\mu }}_4{\mathit{\mu }}_3),\hfill \\ \hfill {\mathit{\delta }}_3& =6({\mathit{\mu }}_2+6{\mathit{\mu }}_3+6{\mathit{\mu }}_1+6{\mathit{\mu }}_4),\hfill \\ \hfill {\mathit{\delta }}_4& =6c_{15}{c}_{51}{\mathit{\mu }}_6^4\left({\mathit{\mu }}_4-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\hfill \\ \hfill & +6c_{16}{c}_{61}{\mathit{\mu }}_5^4\left({\mathit{\mu }}_4-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)({\mathit{\mu }}_2-{\mathit{\mu }}_6),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill l_2& =\frac{c_{21}^0{l}_1}{{\mathit{\mu }}_2},l_3=\frac{c_{31}^0{l}_1}{{\mathit{\mu }}_3},l_4=\frac{c_{41}^0{l}_1}{{\mathit{\mu }}_4},l_5=\frac{c_{51}{l}_1}{{\mathit{\mu }}_5},l_6=\frac{c_{61}{l}_1}{{\mathit{\mu }}_6},\hfill \\ \hfill r_1& =\frac{l_1{\sum }_{j=2}^6\left[c_{1j}{c}_{j1}{\sum }_{2\le i_1<i_2<i_3<i_4\le 6}^{i_1,i_2,i_3,i_4\ne j}{\mathit{\mu }}_{i_1}^5{\mathit{\mu }}_{i_2}^5{\mathit{\mu }}_{i_3}^5{\mathit{\mu }}_{i_4}^5{D}_1\right]}{4\mathit{\tau }{\mathit{\mu }}_5{\mathit{\mu }}_2{\mathit{\mu }}_3{\mathit{\mu }}_4{\mathit{\mu }}_6{\sum }_{j=2}^6\left[c_{1j}{c}_{j1}{\sum }_{2\le i_1<i_2<i_3<i_4\le 6}^{i_1,i_2,i_3,i_4\ne j}{\mathit{\mu }}_{i_1}^4{\mathit{\mu }}_{i_2}^4{\mathit{\mu }}_{i_3}^4{\mathit{\mu }}_{i_4}^4{D}_2\right]},\hfill \\ \hfill r_j& =\left\{\begin{array}{cc}\frac{c_{j1}^0\left(r_1\mathit{\tau }{\mathit{\mu }}_j-l_1\mathit{\tau }{\mathit{\mu }}_j-l_1\right)}{\mathit{\tau }{\mathit{\mu }}_j^2},\hfill & j=2,3,4,\hfill \\ \frac{c_{j1}\left(r_1\mathit{\tau }{\mathit{\mu }}_j-l_1\mathit{\tau }{\mathit{\mu }}_j-l_1\right)}{\mathit{\tau }{\mathit{\mu }}_j^2},\hfill & j=5,6,\hfill \end{array}\right.\hfill \\ \hfill e_1& =\frac{-{\sum }_{j=2}^6\left[c_{1j}{c}_{j1}{\sum }_{2\le i_1<i_2<i_3<i_4\le 6}^{i_1,i_2,i_3,i_4\ne j}{\mathit{\mu }}_{i_1}^6{\mathit{\mu }}_{i_2}^6{\mathit{\mu }}_{i_3}^6{\mathit{\mu }}_{i_4}^6{\mathit{\epsilon }}_j\right]}{20{\mathit{\mu }}_5^2{\mathit{\mu }}_6^2{\mathit{\mu }}_2^2{\mathit{\mu }}_3^2{\mathit{\mu }}_4^2{\mathit{\tau }}^2{\sum }_{j=2}^6\left[c_{1j}{c}_{j1}{\sum }_{2\le i_1<i_2<i_3<i_4\le 6}^{i_1,i_2,i_3,i_4\ne j}{\mathit{\mu }}_{i_1}^4{\mathit{\mu }}_{i_2}^4{\mathit{\mu }}_{i_3}^4{\mathit{\mu }}_{i_4}^4{D}_2\right]},\hfill \\ \hfill e_j& =\left\{\begin{array}{cc}-\frac{c_{j1}^0\left(-2e_1{\mathit{\tau }}^2{\mathit{\mu }}_j^2-2l_1+2r_1{\mathit{\tau }}^2{\mathit{\mu }}_j^2+2r_1\mathit{\tau }{\mathit{\mu }}_j-2l_1\mathit{\tau }{\mathit{\mu }}_j-l_1{\mathit{\tau }}^2{\mathit{\mu }}_j^2\right)}{2{\mathit{\tau }}^2{\mathit{\mu }}_j^3},\hfill & j=2,3,4,\hfill \\ -\frac{c_{j1}\left(-2e_1{\mathit{\tau }}^2{\mathit{\mu }}_j^2-2l_1+2r_1{\mathit{\tau }}^2{\mathit{\mu }}_j^2+2r_1\mathit{\tau }{\mathit{\mu }}_j-2l_1\mathit{\tau }{\mathit{\mu }}_j-l_1{\mathit{\tau }}^2{\mathit{\mu }}_j^2\right)}{2{\mathit{\tau }}^2{\mathit{\mu }}_j^3},\hfill & j=5,6,\hfill \end{array}\right.\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill D_1& ={\mathit{\tau }}^4{\mathit{\mu }}_j^4+4{\mathit{\tau }}^2{\mathit{\mu }}_j^2(\mathit{\tau }{\mathit{\mu }}_j+3)+24(1+\mathit{\tau }{\mathit{\mu }}_j),\hfill \\ \hfill D_2& ={\mathit{\tau }}^2{\mathit{\mu }}_j^2(\mathit{\tau }{\mathit{\mu }}_j+3)+6(1+\mathit{\tau }{\mathit{\mu }}_j),\hfill \\ \hfill {\mathit{\epsilon }}_j& ={\mathit{\mu }}_j^5\left(l_1-5r_1\right){\mathit{\tau }}^5+5{\mathit{\mu }}_j^4\left(l_1-4r_1\right){\mathit{\tau }}^4+20{\mathit{\mu }}_j^3\left(l_1-3r_1\right){\mathit{\tau }}^3\hfill \\ \hfill & +60{\mathit{\mu }}_j^2\left(l_1-2r_1\right){\mathit{\tau }}^2+120{\mathit{\mu }}_j\left(l_1-r_1\right)\mathit{\tau }+120l_1,\hfill \end{array}$$

such that $<\mathit{\Psi },\mathit{\Phi }>=I$, $\dot{\mathit{\Phi }}=\mathit{\Phi }J$, $\dot{\mathit{\Psi }}=-J\mathit{\Psi }$, where

$$J=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right)$$

The normal form of system (29) on its center takes the form

$$\left\{\begin{array}{c}\dot{z_1}=z_2,\hfill \\ \dot{z_2}=z_3,\hfill \\ \dot{z_3}=g_1{z}_1+g_2{z}_2+g_3{z}_3+{\mathit{\Omega }}_1{z}_1^2+{\mathit{\Omega }}_2{z}_2^2+{\mathit{\Omega }}_3{z}_1{z}_2+{\mathit{\Omega }}_4{z}_1{z}_3+h.o.t.,\hfill \end{array}\right.$$ 31

where

$$\begin{array}{cc}\hfill g_1& =\frac{c_{12}{l}_1\mathit{\tau }{c}_1}{{\mathit{\mu }}_2}+\frac{c_{13}{l}_1\mathit{\tau }{\mathit{\beta }}_2}{{\mathit{\mu }}_3}+\frac{c_{14}{l}_1\mathit{\tau }{\mathit{\beta }}_3}{{\mathit{\mu }}_4},\hfill \\ \hfill g_2& =\frac{c_{12}(\mathit{\tau }{\mathit{\mu }}_2(r_1-l_1)-l_1)}{{\mathit{\mu }}_2^2}{\mathit{\beta }}_1+\frac{c_{13}(\mathit{\tau }{\mathit{\mu }}_3(r_1-l_1)-l_1)}{{\mathit{\mu }}_3^2}{\mathit{\beta }}_2\hfill \\ \hfill & +\frac{c_{14}(\mathit{\tau }{\mathit{\mu }}_4(r_1-l_1)-l_1)}{{\mathit{\mu }}_4^2}{\mathit{\beta }}_3,\hfill \\ \hfill g_3& =\sum _{j=2}^4\frac{c_{1j}[{\mathit{\mu }}_j^2(l_1+2e_1-2r_1){\mathit{\tau }}^2+2{\mathit{\mu }}_j(l_1-r_1)\mathit{\tau }+2l_1]}{2\mathit{\tau }{\mathit{\mu }}_j^3}{\mathit{\beta }}_{j-1},\hfill \\ \hfill {\mathit{\Omega }}_1& =\sum _{j=2}^6\frac{\mathit{\tau }{c}_{1j}{c}_{j1}{l}_1}{2{\mathit{\mu }}_j}\left(\frac{c_{1j}{f}_1^{\prime \prime }(0)}{{\mathit{\mu }}_j}+f_j^{\prime \prime }(0)\right),\hfill \\ \hfill {\mathit{\Omega }}_2& =\sum _{j=2}^6\left(\frac{c_{1j}^2{c}_{j1}\mathit{\tau }{f}_1^{\prime \prime }(0)}{{\mathit{\mu }}_j^2}{e}_1+\frac{f_j^{\prime \prime }(0)c_{1j}{c}_{j1}}{2\mathit{\tau }{\mathit{\mu }}_j^3}[{\mathit{\mu }}_j^2(l_1+2e_1-2r_1){\mathit{\tau }}^2\right.\hfill \\ \hfill & \left.+2{\mathit{\mu }}_j(l_1-r_1)\mathit{\tau }+2l_1]\right)\hfill \\ \hfill & +\sum _{j=2}^6\frac{c_{1j}^2{c}_{j1}{f}_1^{\prime \prime }(0)}{2}\frac{(1+\mathit{\tau }{\mathit{\mu }}_j)(l_1-2\mathit{\tau }{\mathit{\mu }}_j{r}_1)}{\mathit{\tau }{\mathit{\mu }}_j^4},\hfill \\ \hfill {\mathit{\Omega }}_3& =\sum _{j=2}^6\frac{c_{1j}{c}_{j1}[\mathit{\tau }{\mathit{\mu }}_j(r_1-l_1)-l_1]}{{\mathit{\mu }}_j^3}(f_1^{\prime \prime }(0)c_{1j}+f_j^{\prime \prime }(0){\mathit{\mu }}_j),\hfill \\ \hfill {\mathit{\Omega }}_4& =\sum _{j=2}^6\left(\frac{c_{1j}^2{c}_{j1}\mathit{\tau }{f}_1^{\prime \prime }(0)}{{\mathit{\mu }}_j^2}{e}_1+\frac{f_j^{\prime \prime }(0)c_{1j}{c}_{j1}}{2\mathit{\tau }{\mathit{\mu }}_j^3}[{\mathit{\mu }}_j^2(l_1+2e_1-2r_1){\mathit{\tau }}^2\right.\hfill \\ \hfill & \left.+2{\mathit{\mu }}_j(l_1-r_1)\mathit{\tau }+2l_1]\right)\hfill \\ \hfill & +\sum _{j=2}^6\frac{f_1^{\prime \prime }(0)c_{1j}^2{c}_{j1}}{2\mathit{\tau }{\mathit{\mu }}_j^4}[{\mathit{\mu }}_j^2(l_1-2r_1){\mathit{\tau }}^2+2{\mathit{\mu }}_j(l_1-r_1)\mathit{\tau }+2l_1].\hfill \end{array}$$

One can see that

$$\frac{\mathit{\partial }(g_1,g_2,g_3)}{\mathit{\partial }({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3)}{|}_{\mathit{\beta }=0}=\frac{216c_{12}{\mathit{\tau }}^6{\mathit{\mu }}_6^{12}{\mathit{\mu }}_5^{12}{c}_{13}{c}_{14}\left({\mathit{\mu }}_3-{\mathit{\mu }}_4\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_4\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_3\right)}{{\mathit{\delta }}^3}\ne 0,$$

where

$$\begin{array}{cc}\hfill \mathit{\delta }& ={\mathit{\mu }}_5^4{\mathit{\mu }}_6^4[{\mathit{\mu }}_2{\mathit{\tau }}^3{\mathit{\mu }}_1{\mathit{\mu }}_3{\mathit{\mu }}_4+3\left({\mathit{\mu }}_2{\mathit{\mu }}_1{\mathit{\mu }}_3+3{\mathit{\mu }}_2{\mathit{\mu }}_1{\mathit{\mu }}_4+{\mathit{\mu }}_3{\mathit{\mu }}_1{\mathit{\mu }}_4+{\mathit{\mu }}_2{\mathit{\mu }}_3{\mathit{\mu }}_4\right){\mathit{\tau }}^2\hfill \\ \hfill & +6\left({\mathit{\mu }}_1{\mathit{\mu }}_3+{\mathit{\mu }}_1{\mathit{\mu }}_2+{\mathit{\mu }}_2{\mathit{\mu }}_4+6{\mathit{\mu }}_1{\mathit{\mu }}_4+{\mathit{\mu }}_2{\mathit{\mu }}_3+6{\mathit{\mu }}_3{\mathit{\mu }}_4\right)\mathit{\tau }\hfill \\ \hfill & +6({\mathit{\mu }}_3+6{\mathit{\mu }}_2+6{\mathit{\mu }}_1+6{\mathit{\mu }}_4)]+6c_{51}{c}_{15}{\mathit{\mu }}_6^4\left({\mathit{\mu }}_4-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_5\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_5\right)\hfill \\ \hfill & +6c_{61}{c}_{16}{\mathit{\mu }}_5^4\left({\mathit{\mu }}_4-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_3-{\mathit{\mu }}_6\right)\left({\mathit{\mu }}_2-{\mathit{\mu }}_6\right).\hfill \end{array}$$

Theorem 3

Let$(\mathrm{H}1)$, $(\mathrm{H}3)$and$(\mathrm{H}5)$hold. If$f_i^{\prime \prime }(0)\ne 0$, $i=1,\dots ,6$, then on the center manifold, system (29) is equivalent to the normal form (31).

Following Campbell and Yuan (2008) the bifurcation diagrams of system (31) at the origin are as follows:

1. system (31) undergoes a transcritical bifurcation when

   $$T=\{({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3):g_1=0\},$$
2. system (31) undergoes a Hopf bifurcation when

   $${\tilde{H}}_1=\left\{({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3):g_3=-\frac{g_1}{g_2},g_2<0\right\},$$
3. system (31) undergoes a Hopf bifurcation at the non-trivial equilibrium point $(-\frac{g_1}{h_1},0,0)$ when

   $${\tilde{H}}_2=\left\{({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3):g_3=\left(\frac{{\mathit{\Omega }}_4}{{\mathit{\Omega }}_1}-\frac{{\mathit{\Omega }}_1}{{\mathit{\Omega }}_3{g}_1-{\mathit{\Omega }}_1{g}_2}\right)g_1,\frac{{\mathit{\Omega }}_1}{{\mathit{\Omega }}_3{g}_1-{\mathit{\Omega }}_1{g}_2}>0\right\},$$
4. system (31) undergoes a B–T bifurcation when

   $$\tilde{B}=\{({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3):g_1=0,g_2=0\},$$
5. system (31) undergoes a zero–Hopf bifurcation when

   $${\tilde{H}}_3=\{({\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3):g_1=0,g_3=0,g_2<0\}.$$

Numerical examples and simulations

In this section, first several numerical examples and bifurcation curves corresponding to our results are given. Second, some numerical simulations of an example is given to verify our results.

Example 1

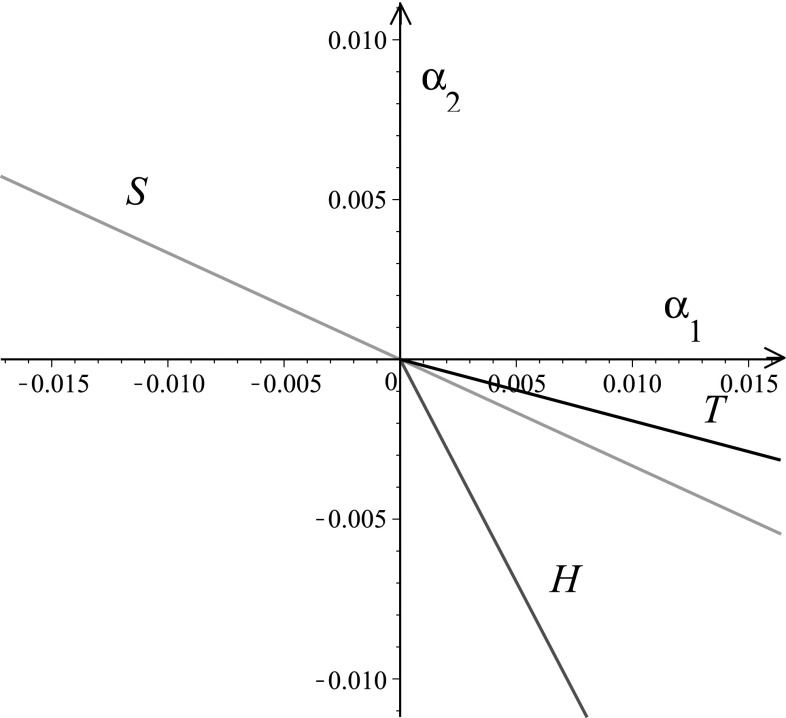
Take ${\mathit{\mu }}_1=0.2$, ${\mathit{\mu }}_2=0.6$, ${\mathit{\mu }}_3=0.2$, ${\mathit{\mu }}_4=0.4$, ${\mathit{\mu }}_5=0.5$, ${\mathit{\mu }}_6=0.8$, $c_{41}=0.5$, $c_{51}=0.6$, $c_{61}=0.8$, $c_{12}=c_{13}=c_{15}=1$, $c_{14}=3$, $c_{16}=2$, $f_i(x)=tanh(x)+0.2x^2(i=1,2,\dots ,6)$, $\mathit{\tau }=2$, then $f_i^{\prime }(0)=1$, $f_i^{\prime \prime }(0)=0.4$, by (5)-(8), we can obtain $c_{21}^0=-3.2535$, $c_{31}^0=-0.2655$$c_{41}\ne c_{41}^0=-0.7344$. Eq. (13) has only one positive root $w_1\approx 0.2957156781$, then ${\mathit{\tau }}_0\approx 5.341141624$ which implies $0<\mathit{\tau }<{\mathit{\tau }}_0$, one can obtain that (17) is satisfied. Hence, the conditions Theorem 2 are all satisfied. The bifurcation curves of Theorem 2 were shown in Fig. 1.

Fig. 1.

The bifurcation curves of Theorem 2 corresponding to the Example 1

Example 2

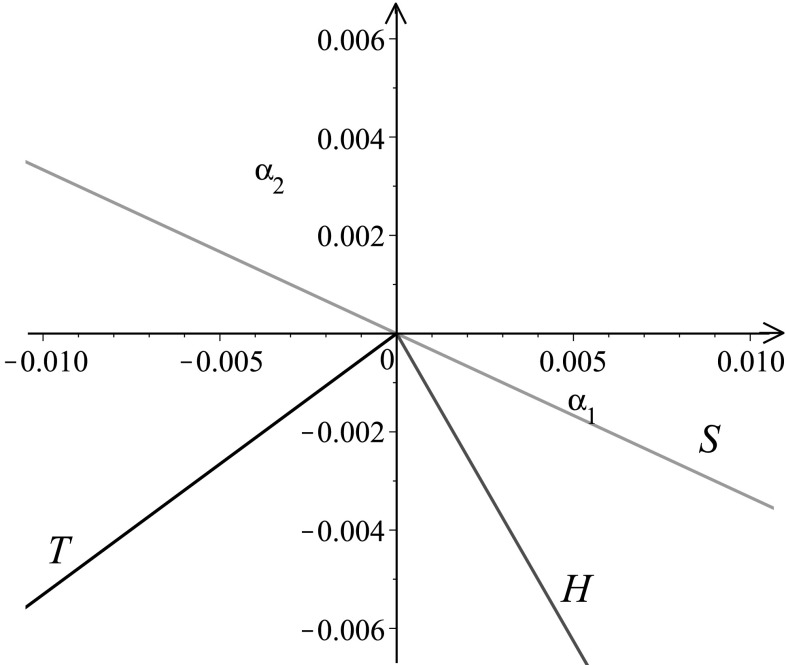
For the case of $f_i^{\prime \prime }(0)=0$, $i=1,\dots ,6$, we take $f_i(x)=tanh(x)+2x^3/3$, $i=1,\dots ,6$. Other parameters share the same values as in Example 1. It is easy to verify that $f_i^{\prime }(0)=1,$$f_i^{\prime \prime }(0)=0,$$f_i^{\prime \prime \prime }(0)=2$, $a_3\approx 6.228127027,$$b_3\approx 37.84176265$, thus $s=1$. The corresponding bifurcation curves are shown in Fig. 2.

Fig. 2.

The bifurcation curves for $s=1$ when $f(0)=0$, $f_i^{\prime }(0)=1$, $f_i^{\prime \prime }(0)=0$ and $f_i^{\prime \prime \prime }(0)\ne 0$

Example 3

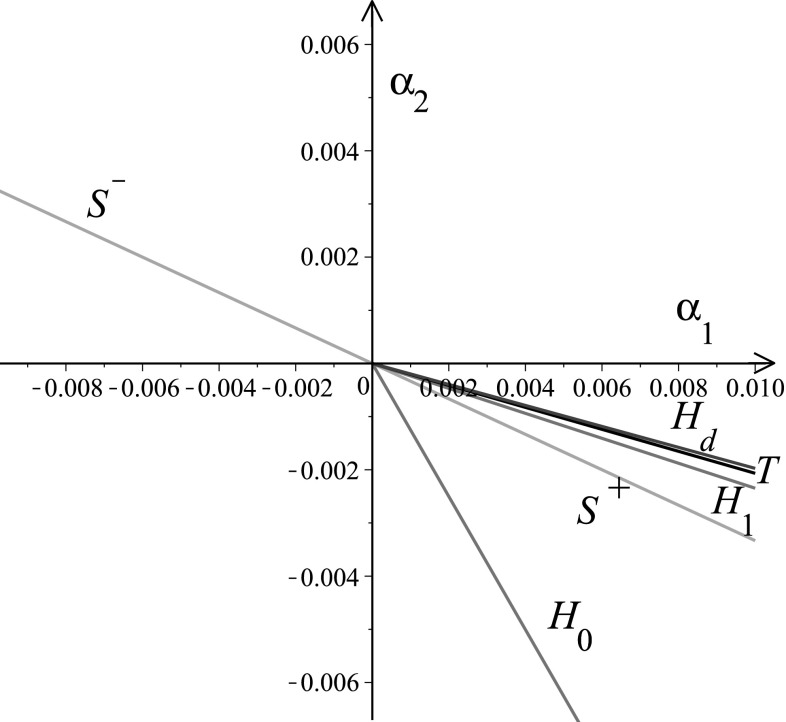
To get the case of $s=-1$ when $f_i(0)=0$, $f_i^{\prime }(0)=1$, $f_i^{\prime \prime }(0)=0$ and $f_i^{\prime \prime \prime }(0)\ne 0$, we choose $f_i(x)=tanh(x)$, $(i=1,2,\dots ,6)$, ${\mathit{\mu }}_1=0.2$, ${\mathit{\mu }}_2=0.6$, ${\mathit{\mu }}_3=0.2$, ${\mathit{\mu }}_4=0.4$, ${\mathit{\mu }}_5=0.5$, ${\mathit{\mu }}_6=0.8$, $c_{41}=0.5$, $c_{51}=0.6$, $c_{61}=0.8$, $c_{12}=1$, $c_{13}=1$, $c_{14}=3$, $c_{15}=0.1$, $c_{16}=2$ and $\mathit{\tau }=1.5$. To satisfy the conditions (H1) and (H2), we take $c_{21}^0=-2.6883$ and $c_{31}^0=-0.2379$. Some simple computations show $s=-1$, $f_i(0)=0$, $f_i^{\prime }(0)=1$, $f_i^{\prime \prime }(0)=0$ and $f_i^{\prime \prime \prime }(0)=-2$, ($i=1,\dots ,6$), thus, by using the results obtained in “B–T bifurcation” section, we get a full picture of bifurcation diagram of system (20) in the parameter space $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ which is shown in Fig. 3.

Fig. 3.

The bifurcation curves for $s=-1$ when $f(0)=0$, $f_i^{\prime }(0)=1$, $f_i^{\prime \prime }(0)=0$ and $f_i^{\prime \prime \prime }(0)=-2$

Example 4

Take ${\mathit{\mu }}_1=0.2,$${\mathit{\mu }}_2=0.6,$${\mathit{\mu }}_3=0.2,$${\mathit{\mu }}_4=0.4,$${\mathit{\mu }}_5=0.5,$${\mathit{\mu }}_6=0.8,$$c_{51}=0.6,$$c_{61}=0.8,$$c_{12}=c_{13}=c_{15}=1,$$c_{14}=3,$$c_{16}=2,$$f_i(x)=tanh(x)+0.2x^2(i=1,2,\dots ,6)$, $\mathit{\tau }=2,$ then $f_i^{\prime }(0)=1,f_i^{\prime \prime }(0)=0.4.$ By (5)–(8), one can obtain $c_{21}^0=0.9126,$$c_{31}^0=0.1974,$$c_{41}^0=-0.7344,$$c_{51}\ne c_{51}^0\approx -59.52708333$. Eq. (13) has only one positive root ${\overline{w}}_1\approx 0.8509803928$, then ${\mathit{\tau }}_0\approx 2.040926698$ which implies $0<\mathit{\tau }<{\overline{\mathit{\tau }}}_0$, one can obtain that (17) is satisfied. Hence, the conditions of Theorem 3 are all satisfied.

Next, for the Example 3 we carry out some numerical simulations to demonstrate the corresponding dynamical behaviors when parameters $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ are chosen in appropriate regions in Fig. 3.

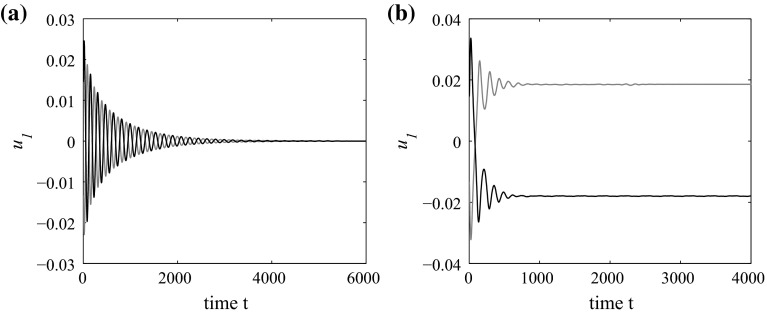
First we take parameters $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$=$(-0.003,-0.003)$, then under initial conditions (0.02, 0.000004, 0.0002, 0.0004, 0.0002, 0.0004) and (−0.02, −0.000004, −0.0002, −0.0004, −0.0002, 0.0004), a time evolutions of system (20) is shown in Fig. 4a. As expected, two trajectories asymptotically reach the trivial equilibrium which, however, loses its stability, and bifurcates two asymptotically stable nontrivial equilibrium when the parameters $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ cross the Pitchfork bifurcation curve $S^{-}$ to the side of $v_1>0$ (see Fig. 4b).

Fig. 4.

System (20) undergoes a Pitchfork bifurcation when parameters $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ pass the curve $S$ in Fig. 2. a The origin is locally asymptotically stable when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(-0.003,-0.003)$ under initial conditions $(0.02,0.000004,0.0002,0.0004,0.0002,0.0004)$ (the black curve) and $(-0.02,-0.000004,-0.0002,-0.0004,-0.0002,0.0004)$ (the blue curve). b System (20) has two locally asymptotically stable nontrivial equilibria when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ = $(-0.003,0.003)$ with the same initial conditions as a. (Color figure online)

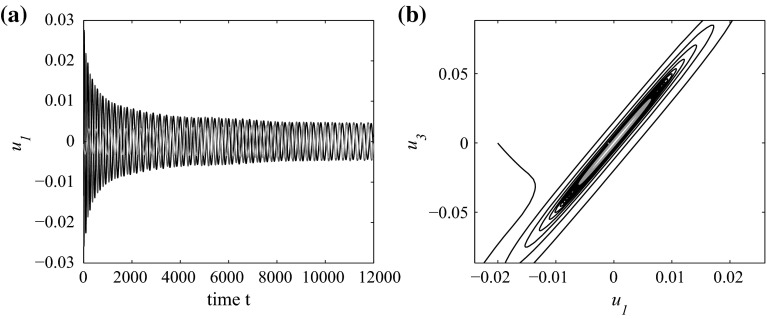
Within the region surrounded by the curves $S^{-}$ and $H_0$, system (20) has a stable trivial equilibrium which may undergo a nondegenerate Hopf bifurcation on the curve $H_0$ as shown in Fig. 5. One can see that a stable limit cycle is bifurcated when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.002,-0.002)$.

Fig. 5.

System (20) undergoes a Hopf bifurcation at the trivial equilibrium when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.002,-0.002)$ with initial conditions $(-0.02,-0.000004,-0.0002,-0.0004,-0.0002,0.0004)$ (the blue curve), $(0.02,0.000004,0.0002,0.0004,0.0002,0.0004)$ (the black curve) and $(-0.001,0.0,0.0,0.0,0.0,0.0)$ (the red curve), respectively. a The time series in the plane $(t,u_1)$. b The phase portrait in plane $(u_1,u_3)$. (Color figure online)

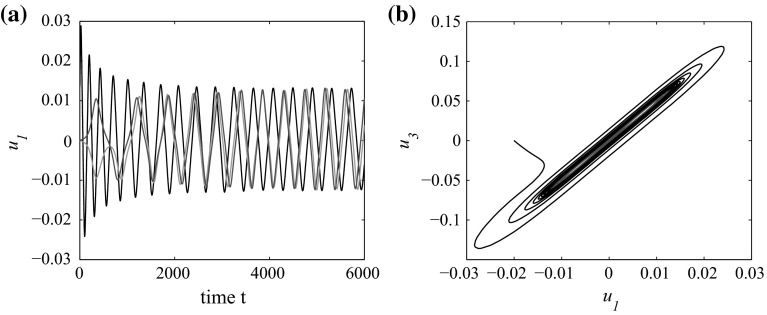
When parameters $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ cross the Pitchfork bifurcation curve $S^{+}$ from the bottom up, two unstable nontrivial equilibria are branched from the trivial equilibrium. If choose $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.006,-0.0014)$, then with different initial conditions, all trajectories approach the stable periodic solution (see Fig. 6).

Fig. 6.

System (20) has two unstable nodes when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.006,-0.0014)$ with initial conditions $(0.00006,0.0,0.0,0.0,0.0,0.0)$ (the blue curve), $(-0.00006,0.0,0.0,0.0,0.0,0.0)$ (the red curve) and $(-0.02,0.0,0.0,0.0,0.0,0.0)$ (the black curve), respectively. a The time series in the plane $(t,u_1)$. b The phase portrait in plane $(u_1,u_3)$. (Color figure online)

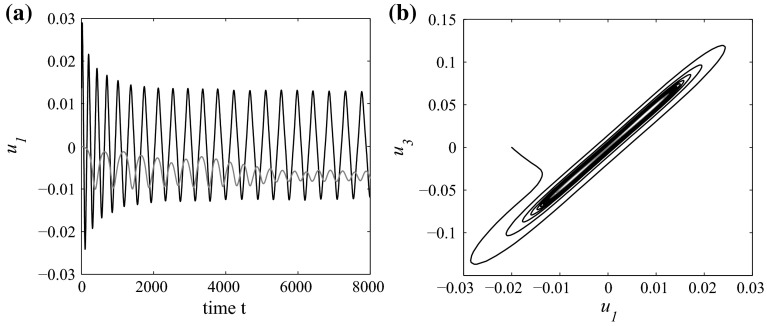
Moving parameters toward the Hopf bifurcation curve $H_1$, the big stable limit cycle is still present. Two nontrivial eqilibria become stable, and two unstable small limit cycles surrounding two nontrivial equilibria are yielded when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ pass $H_1$. Moreover, the two cycles are located inside the big limit cycle. From Fig. 7, we can see that if the initial condition is chosen close the outer of one of small cycle, then the solution asymptotically approaches the small limit cycle. However, if the initial condition is far away from two nontrivial equilibria, then the solution reach the big cycle.

Fig. 7.

The dynamics of system (20) when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ are located between the lines $H_1$ and $H_d$. a System (20) has a unstable limit cycle bifurcated from a nontrivial equilibrium when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.006,-0.00134)$ with initial conditions $(-0.00003,0.0,0.0,0.0,0.0,0.0)$ (the red curve) and $(-0.02,0.0,0.0,0.0,0.0,0.0)$ (the black curve), respectively. b The phase portrait in plane $(u_1,u_3)$ when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.006,-0.00124)$ with initial conditions $(0.00004,0.0,0.0,0.0,0.0,0.0)$ (the red curve) and $(-0.02,0.0,0.0,0.0,0.0,0.0)$ (the black curve). (Color figure online)

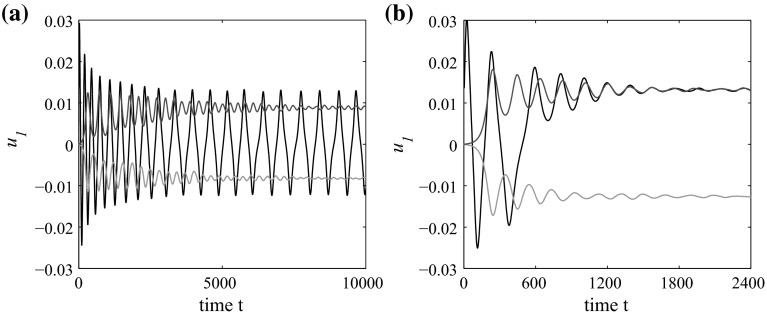
As parameters sequentially cross the homoclinic curve $T$, two small limit cycles disappear via a homoclinic loop bifurcation as shown in Fig. 8a where two nontrivial equilibria are still asymptotically stable and surrounded by the limit cycle. Finally, we choose $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ in the interior made up by the cures $H_d$ and $S^{-}$ where the big limit cycle also disappears, only the nontrivial equilibria are stable. Thus, in the region, all trajectories are attracted to one of the nontrivial equilibria (see Fig. 8b).

Fig. 8.

The dynamics of system (20) when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ across the lines $H_d$ from the bottom up. a System (20) has two locally asymptotically stable nontrivial equilibria and a stable limit cycle when $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.006,-0.00112)$ with initial conditions $(-0.00005,0.0,0.0,0.0,0.0,0.0)$ (the red curve), $(0.00005,0.0,0.0,0.0,0.0,0.0)$ (the blue curve) and $(-0.02,0.0,0.0,0.0,0.0,0.0)$ (the black curve), respectively. b The case of $({\mathit{\alpha }}_1,{\mathit{\alpha }}_2)=(0.006,0)$ where initial conditions are same as a. (Color figure online)

Discussion

In this work, we have devoted to derive the sufficient conditions for the existence of B–T and triple zero bifurcations, and the normal forms in a delayed BAM network with six neurons. Moreover, the bifurcation analysis near the B–T and triple zero critical points are given respectively, showing that the system may exhibit Pithfork bifurcation, heteroclinic bifurcation, transcritical bifurcation, Hopf bifurcation, zero–Hopf bifurcation in the neighborhood of the degenerate equilibrium. These give an important guiding significance in improving the design of BAM and extending associated application in the more fields. However, for (1), it is believed that there are still interesting and complex dynamical behaviors to be completely exploited. In the future, we will focus on the B–T and triple zero bifurcations analysis for neural networks with multiple neurons and multiple delays.