Optical Pushing: A Tool for Parallelized Biomolecule Manipulation

Abstract

The ability to measure and manipulate single molecules has greatly advanced the field of biophysics. Yet, the addition of more single-molecule tools that enable one to measure in a parallel fashion is important to diversify the questions that can be addressed. Here we present optical pushing (OP), a single-molecule technique that is used to exert forces on many individual biomolecules tethered to microspheres using a single collimated laser beam. Forces ranging from a few femtoNewtons to several picoNewtons can be applied with a submillisecond response time. To determine forces exerted on the tethered particles by the laser, we analyzed their measured Brownian motion using, to our knowledge, a newly derived analytical model and numerical simulations. In the model, Brownian rotation of the microspheres is taken into account, which proved to be a critical component to correctly determine the applied forces. We used our OP technique to map the energy landscape of the protein-induced looping dynamics of DNA. OP can be used to apply loading rates in the range of 10⁻⁴–10⁶ pN/s to many molecules at the same time, which makes it a tool suitable for dynamic force spectroscopy.

Introduction

Single-molecule techniques such as tethered-particle motion (TPM) (1), magnetic tweezers (MTs) (2), optical tweezers (OTs) (3), biomembrane-force probe (4), centrifuge force microscopy (CFM) (5), and atomic force microscopy (6) have greatly advanced our ability to quantify the mechanical properties, dynamics, and interactions of biological macromolecules (7, 8, 9). Dynamic force spectroscopy, an approach in which molecular interactions are subjected to various loading rates to quantify their energy landscapes, is a particularly popular approach in biophysics (4). Many single-molecule methods that probe one molecule at a time are limited by low experimental throughput, which makes obtaining statistical information over many molecules and identifying rare events challenging. Techniques such as TPM, MTs, and CFM tackle this problem by measuring multiple single molecules in parallel. All these techniques, however, have their limitations: in TPM, no forces are applied, and in CFM and MTs, constant forces are applied that can only be varied on a timescale of seconds. Here we present a bionano-sensing method that combines high throughput with rapid force application: optical pushing (OP). OP uses the momentum of laser-generated photons to apply tensions from a few femtoNewtons of up to several picoNewtons to multiple DNA molecules tethered between a surface and microspheres.

Materials and Methods

For the implementation of OP, we used a single, collimated laser beam, coupled to an inverted microscope to apply controlled forces to multiple microsphere-tethered biomolecules distributed over a field of view with a size of hundreds of micrometers squared. The setup (Fig. 1) contained three sets of components: the optical pathway of the laser, the flow cell with sample, and the imaging pathway.

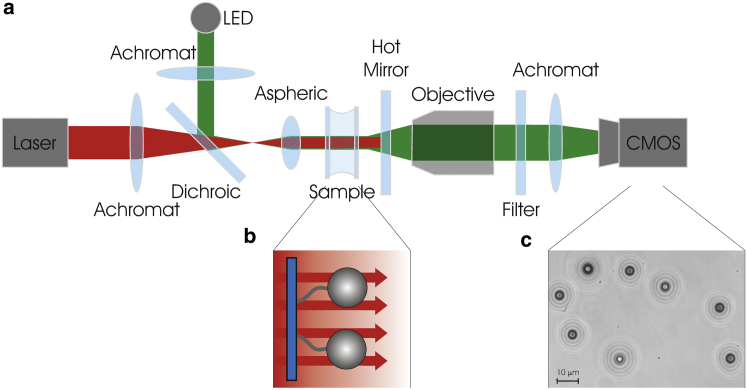
Figure 1.

(a) Schematic drawing of the setup: a 1070 nm laser that is directed through two lenses is used to apply an optical pushing force to microspheres in the sample. Behind the sample, the beam is reflected back using a hot mirror, to prevent heating of the imaging objective. For imaging of the microspheres, the sample is illuminated with a LED. The LED light is transmitted through the hot mirror and imaged on a CMOS camera. (b) Biomolecules are tethered to the surface and attached to microspheres. (c) Example image of the CMOS camera (25 Hz, 40 ms integration time). The radial ring patterns around the microsphere images are used to determine their distance relative to the surface.

As a source of radiation pressure, a collimated laser (YLP-20-LP-IPG; IPG Photonics, Oxford, MA) beam was used with a wavelength of 1070 nm, maximum power of 20 W (power regulation was achieved by a combination of a half-wave plate and a polarizing beam splitter), and a beam diameter of ∼70 μm (full width at half-maximum) generated using a telescope consisting of an achromatic lens (focal length = 150 mm) and an aspherical lens (focal length = 4 mm).

The flow cell with sample chamber consisted of a quartz microscope slide and a quartz coverslip separated by parafilm spacers. Quartz was used to minimize sample heating by the laser. Functionalized molecules were attached to both the surface and the microspheres (Fig. 1 b) (9).

For imaging, a 455-nm-light-emitting diode (M455L3; IMM Photonics, Unterschleissheim, Germany) was used, coupled into the aspherical lens using a dichroic mirror. The light transmitted by the sample was collected with a long-working-distance air microscope objective (50× NA0.42, No. 58-237; Edmund Optics, York, UK) and imaged, using the tube lens of the microscope, on a complementary metal-oxide semiconductor (CMOS) camera (DCC1545M; Thorlabs, Newton, NJ) (Fig. 1 c), which allowed taking images with a frame rate of 25 Hz (full frame). An infrared neutral density filer was placed in front of the camera, to remove remaining laser light. The particles in the images were tracked in three dimensions using a cross-correlation algorithm (x, y), and by comparing the measured radial profile against a database of calibrated radial profiles, made at known heights (z) using a piezo stage (P-517.3CL; Physik Instrumente, Auburn, MA). This resulted in a three-dimensional subpixel precision for the particle tracking of <2 nm in x, y and <5 nm in the z (see Fig. S1 in the Supporting Material). For stable use of OP it was essential to avoid heating of the objective by the laser, which induced drifting aberrations in the acquired images. The heating was minimized by redirecting the laser light after interacting with the sample, before entering the imaging objective, using a hot mirror back into the sample. Because of the divergence of the Gaussian laser beam, the radiation pressure due to the reflected laser light was >1 order-of-magnitude weaker than that due to the direct light.

Results

Validation of the technique

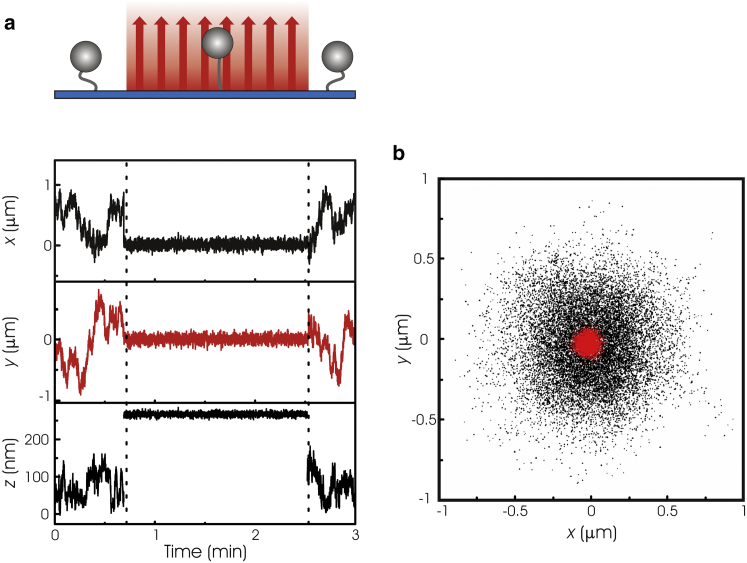
To demonstrate that OP is suitable for the manipulation of tethered molecules, we investigated the restriction of three-dimensional Brownian motion of a single, DNA-tethered (1.1 kbps) microsphere (Ø 2.10 μm polystyrene), with root-mean-square (RMS) displacement detection (Fig. 2). When a laser power of 1.6 W was applied to the sample, the random motion of the microsphere in all three dimensions was restricted. In addition, the distance of the microsphere with respect to the surface (z) increased. Both observations indicate that the radiation pressure of the laser beam actively pushed the microsphere away from the surface. Note that the microsphere found its new equilibrium position, within one camera frame, demonstrating that OP allows switching on and off forces faster than 40 ms (acquisition time of a single camera frame).

Figure 2.

Proof of principle of optical pushing. (a) Raw motion trace of a DNA (1.1 kbp) tethered microsphere (ϕ 4.26 μm) when there is no laser pushing force and when the laser is set to 2 W (between dashed lines). The motion of the microsphere is quenched in all three dimensions when the laser is on. Distances are relative to the DNA-surface anchor point. (b) An x,y-scatter plot of the beads position when the laser is off (black data) and set to 2 W (red data).

The performance of OP on the forces exerted on the biomolecules was determined by measuring and analyzing the Brownian motion of the microspheres. Apart from translational Brownian motion, the microspheres also underwent rotational Brownian motion, which caused them to swivel around their attachment points (see Fig. S2). Because of this swiveling motion, force-calibration methods for tethered microspheres, as used for, e.g., MTs, are not directly applicable to our system (10). In MTs, the paramagnetic microspheres have a fixed alignment with respect to the external magnetic field, which allows neglecting Brownian rotation (11). In the absence of this fixed alignment, the swiveling of the microsphere increases its motion, leading to an underestimation of the force with up to 10% if the swiveling is not taken into account (with DNA tethers that are short compared to the microsphere radius; see Fig. S3). Solving the linearized system of Langevin equations for translation and rotation (Eqs. 1 and 2) (12, 13), under the assumption that the exerted force is substantially larger than the thermal fluctuations, yielded an analytical expression for the double-sided power spectrum of the microsphere’s motion in the x- and y directions (Eq. 3) (see the Supporting Material for derivation):

$$m\frac{d\overrightarrow{v}}{dt}={\overrightarrow{F}}_{\text{brown}}\left(t\right)-\overrightarrow{\gamma }\overrightarrow{v}\left(t\right)+{\overrightarrow{F}}_{\text{ext}}\left(t\right),$$ (1)

$$I\frac{d\overrightarrow{\omega }}{dt}={\overrightarrow{T}}_{\text{brown}}\left(t\right)-\overrightarrow{\beta }\overrightarrow{\omega }\left(t\right)+{\overrightarrow{T}}_{\text{ext}}\left(t\right),$$ (2)

$$P\left(f\right)=2k_{\text{B}}T\frac{\left(\beta +\gamma {\langle z\rangle }^2\right)R^2{F}_{\text{laser}}^2+{\left(\langle z\rangle -R\right)}^2{\beta }^2\gamma {\left(2\pi f\right)}^2}{{\left(\left(R-\langle z\rangle \right)\beta \gamma {\left(2\pi f\right)}^2+R{F}_{\text{laser}}^2\right)}^2+{\left(2\pi f\left(R\gamma \langle z\rangle -\beta \right)F_{\text{laser}}\right)}^2}.$$ (3)

In Eqs. 1–3, m is the mass of the microsphere, $\overrightarrow{v}$ is its velocity, ${\overrightarrow{F}}_{\text{brown}}$ is the random Brownian force, $\overrightarrow{\gamma }$ is the effective translational drag coefficient, ${\overrightarrow{F}}_{\text{ext}}$ is the external forces acting on the microsphere, I is the microsphere’s moment of inertia, $\overrightarrow{\omega }$ is its angular velocity, ${\overrightarrow{T}}_{\text{brown}}$ is the random Brownian torque, $\overrightarrow{\beta }$ is the effective rotational drag coefficient, ${\overrightarrow{T}}_{\text{ext}}$ is the external torques acting on the particle, k_B is the Boltzmann’s constant, T is the temperature, 〈z〉 is the average microsphere height, R is the microsphere radius, F_laser is the exerted laser force, and f is the frequency. Recently, Daldrop et al. (14) derived a similar analytical expression (Eq. 15 in their article) for the single-sided power spectrum of a sphere undergoing rotation about its tether point. Their expression corresponds closely to our analytical expression (Eq. 3, and see Fig. S3). To confirm the validity of our analytical solution, we compared it to simulations. Simulated data was obtained by implementing an initial microsphere position and rotation, and recursively solving Eqs. 1 and 2 (for full derivation, see the Supporting Material) using randomly varying instantaneous Brownian forces and torques. The difference between the simulated data and the analytically obtained restoring force and torque data (red) lies within a few percent (see Fig. S2 c). Moreover, the analytical solution of the power spectrum (Eq. 3) agrees with the power spectra of simulated data traces (see Fig. S2 d), for forces F_laser >> F_brown, confirming that our rotational model is a suitable calibration method for the optical force acting on the biomolecules.

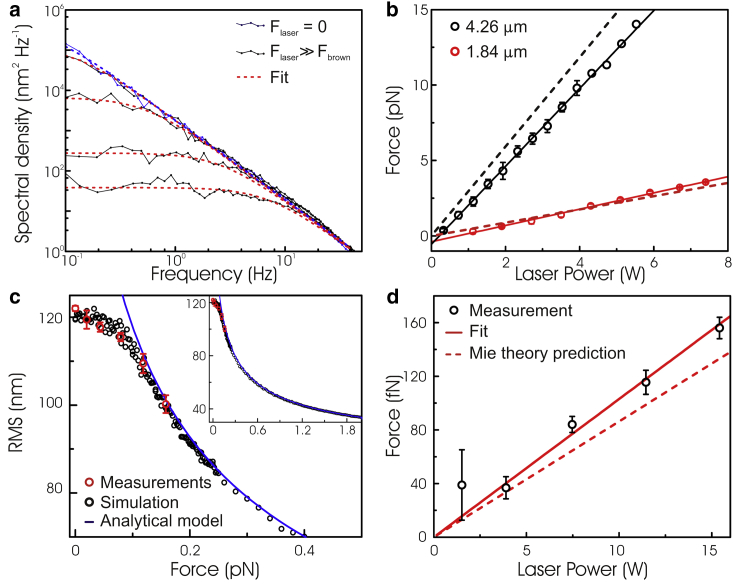
With a calibration method in place, we validated OP and determined what forces could be obtained. Power spectra of DNA tethers attached to microspheres of two different sizes were obtained as a function of laser power and fitted using Eq. 3 (Fig. 3). For both microsphere sizes a linear dependency of force on total laser power was obtained, as expected from the linear dependence of radiation pressure on light intensity (Fig. 3 b, open symbols and solid lines). Moreover, the measured forces match theoretical predictions based on Mie scattering theory (16) (Fig. 3 b, dashed curves). These measurements demonstrate that our OP instrument is capable of applying forces up to 2.6 pN/W to 4.26-μm microspheres. Due to the Gaussian profile of the laser intensity, the force acting on the tethered microspheres is not constant over the field of view, but follows the illumination profile (see Fig. S4). To account for this, we calibrate the force on each microsphere individually. It is important to note that the maximum measured pushing force ∼15 pN is limited by the strength of the dig-antiDIG interaction used to attach the DNA to the surface, not by a physical constraint of our approach. These forces are not as high as forces obtained using OTs on similar microspheres (typically of ∼100 pN/Watt (8)). In OP, the maximum force can be readily increased by using different microsphere sizes or composition. Mie scattering theory predicts that the force is approximately fourfold higher when gold-coated (instead of bare) polystyrene microspheres are used (see Fig. S5). Our setup also allows sampling of smaller microspheres and lower forces. Our linearized model, however, does not allow correct determination of forces that lie in the entropic regime (<0.1 pN) (Fig. 3 c, black points and blue line). At these low forces, the force can be calibrated accurately by determining the RMS displacement of the microspheres (see the Supporting Material) and comparing that with simulated data using the full kinetic model based on Eqs. 1 and 2 (Fig. 3 c, red dots). Note that RMS displacement determination is the key detection method in TPM experiments (15). Using this approach, OP forces were determined accurately for 440-nm-diameter microspheres to be 10.6 fN/W at the sample (Fig. 3 d), again in agreement with Mie theory.

Figure 3.

(a) Fitted power spectra of the measured x,y motion of 4.26-μm tethered microspheres. A power spectrum obtained in the absence of force is shown for reference. The other spectra from top to bottom are obtained using laser powers of 0.2 W (0.3 ± 0.1 pN), 0.7 W (1.0 ± 0.2 pN), 2.7 W (5.2 ± 0.3 pN), and 6.2 W (12.7 ± 0.8 pN). (b) Exerted optical pushing force as a function of total laser intensity at the sample. Forces are determined by fitting the power spectra of measured polystyrene tethers with the analytical theory (error bars, mean ± SE). (Solid lines) Linear fits yielding slopes of 2.6 ± 0.1 pN W⁻¹ and 0.5 ± 0.1 pN W⁻¹. (c) RMS motion of small (ϕ 440 nm) microspheres for measured, simulated, and calculated data using our analytical model (Eq. 3). (d) The derived force, using the RMS fitted data sets, as a function of laser power applied. The linear fit yielded a slope of 10.6 fN/W (see the Supporting Material).

Manipulating protein looped DNA

To demonstrate the power of OP in bionano-technological applications, we performed a force-spectroscopy study of protein-induced DNA looping. Looping is often studied with TPM setups because of their ability to detect looping at very low forces. DNA loops occur whenever proteins interact with multiple sites on the same DNA molecule (17). Loops have both organizing and regulatory functions in processes such as DNA replication, repair, transcription, and cleavage (18, 19). We chose Type-II restriction endonuclease FokI as our model system, because FokI has been well studied by biochemical and biophysical (TPM) means (20, 21, 22). Two FokI monomers each bind to distinct recognition sites on the DNA (5-GGATG-3); subsequently, they associate in dimers while both monomers remain attached to the DNA, forming a DNA loop (20). When only Ca²⁺ (and not Mg²⁺) is present in solution as a cofactor, the restriction enzymes specifically bind to the DNA, forming loops, but they cannot cut the DNA (23, 24). Looping of multiple DNA molecules with a contour length of 184 nm containing two FokI recognition sites (spaced 65 nm apart) was monitored in real-time using our OP microscope. Excursions of DNA-tethered microspheres depend on the length of the DNA and, as a consequence, loop formation can be observed as a decrease in the microspheres’ RMS motion. In this study we only analyzed the transition from looped to unlooped state, which occurs in a single kinetic step. The opposite transition, from unlooped to looped state, consists of two distinct, subsequent kinetic steps, one of which depends on protein concentration and tether activity, and is therefore far more complex to interpret (see Fig. 4 a) (21).

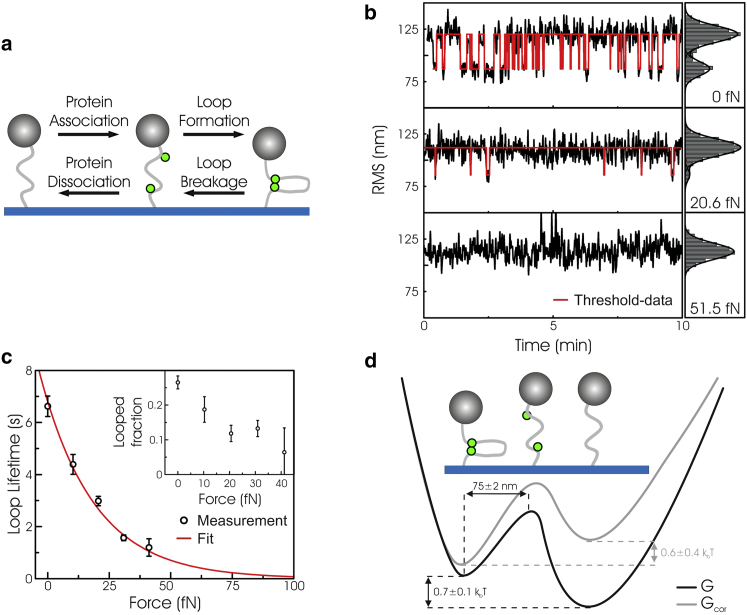
Figure 4.

(a) Kinetic scheme of protein-induced DNA looping. (b) Time traces of the RMS motion of a single DNA tether (left panel, black line) calculated over a 2 s time-window, and the corresponding histograms (right panel), with increasing optical pushing force. The histograms show two distinct states corresponding to the unlooped (large RMS) and looped state (small RMS). From the histograms a threshold value is obtained, which is used to determine the dwell times (red lines, left panels). (c) Average loop lifetime plotted as a function of optical pushing force. (Black circles) Experimental data points (error bars, mean ± SE); (red line) fit using Arrhenius’ law; (inset) looped fraction as a function of the optical pushing force (error bars, mean ± SE). (d) Energy landscape obtained from the force spectroscopy measurements. The corrected free energy G_cor takes the volume exclusion force into account due to the close proximity of the surface.

Example OP time traces of the RMS displacement in the presence of FokI are shown in Fig. 4 b. The RMS motion of each microsphere was calculated as described by Laurens et al. (21). When the laser is off, the system stochastically switched between the unlooped and looped state. With increasing laser intensity, and thus increased force applied to the DNA tether, loop formation was less frequent (Fig. 4 b) and loops lasted for shorter times (Fig. 4 c). Measurements on multiple microspheres simultaneously enhanced experimental throughput (see Fig. S6) and allowed obtaining the force dependence of the average loop lifetime t_loop (Fig. 4 c). This lifetime decayed exponentially with force, as expected from Arrhenius’ law t_loop = 1/k₀ exp(−F_laser × Δx/k_BT) (with k₀ being the unlooping rate at zero force, and Δx as the distance to the barrier along the direction at which the force F_laser is applied). The expected heating near the sample is <3 K for the used laser power, hence the temperature change should hardly affect the kinetics of the reaction (see the Supporting Material). The single-exponential decay indicates that the transition from looped to unlooped state involves a single kinetic step. From the fit, a zero-force unlooping rate (k₀) of 0.15 ± 0.01 s⁻¹ was obtained, in agreement with earlier measurements (21). In addition, a length change from looped state to transition state (Δx) of 75 ± 2 nm was obtained. This length change is relatively large because it exceeds the size of the protein by at least one order of magnitude, which demonstrates that only very small forces, in the femtoNewton range, are required to disrupt the DNA looping. At these low forces, the DNA is in a coiled conformation and therefore the elasticity of the DNA contributes significantly to Δx, because force is applied to the protein complex via two elastic DNA linkers. Because the volume-exclusion effect is of the same order of magnitude as the protein-protein bond strength, it is important to correct the unlooping rate at zero force for this volume-exclusion effect, which, in turn, is dependent on the size of the microspheres and the interactions with the surface. In our setup, the volume-exclusion effect generates an effective force on the DNA of ∼52 fN in the looped state (25). Under the assumption that the volume-exclusion force acts as a constant force offset (see Fig. S7), correction reduces the unlooping rate by a factor of 10, k_0,cor = 0.015 ± 0.003 s⁻¹. Apart from the looping rate, the looped fraction was also obtained from the data, which allowed calculation of the force dependence of the free energy change from the unlooped to the looped state (see Fig. S8). This approach yielded a standard free energy change ΔG⁰ of 0.7 ± 0.1 k_BT (with the unlooped state having a lower free energy). However, this ΔG⁰ needs to be corrected because the volume-exclusion effect introduces an energy penalty for looping to occur. When we correct for this, it yields a ΔG⁰_corr of −0.6 ± 0.4 k_BT (G⁰_loop,cor – G⁰_unloop,cor), i.e., leading to the expected situation in which the looped state has a lower free energy. The low forces that are needed to disrupt the protein-induced DNA loops indicate that thermal fluctuations are sufficient to cross the energy barrier from looped to unlooped state and vice versa, which from a biological point of view makes sense because restriction enzyme function is to recognize and cut specific sequences within a few seconds and not to mechanically stabilize DNA loops for longer time periods (21). This determination of energetics and kinetics of the FokI restriction enzyme demonstrates the great level of control OP provides in the femtoNewton force regime, allowing the extraction of subtleties in the energy landscapes of molecular interactions as well as the characterization of the impact of surfaces on bond formation (see Fig. 4 d).

Discussion

We have characterized the performance of our novel, to our knowledge, OP method and shown its potential by unraveling the energy landscape of the DNA-looping FokI restriction enzyme by the use of constant force measurements. Apart from applying a constant force, OP is capable of rapidly switching and changing forces, by shuttering or strobing the incoming light, or varying the intensity using, for example, an acousto-optical modulator. This allows OP to apply a wide dynamic range of loading rates, as is required for dynamic force spectroscopy (4). Radiation pressure travels at the speed of light, the theoretical response time of a typical DNA-tethered microsphere is, however, limited by viscous drag (slowing down the motion of the microsphere and thus the extension of the loading of the tether) to typically ∼100 μs (see the Supporting Material). From this, we estimate that OP can be used to apply linear force ramps in the range of 10⁻⁴ to 10⁶ pN/s to DNA (see Fig. S9). Today’s MT systems allow access to a more limited range of loading rates from 10⁻⁴ to 10² pN/s (26).

It should be noted that one does need to take care of sample and instrument heating caused by the high laser powers used. We were able to reduce heating effects by using quartz microscope slides and coverslips. We estimate that the heating in the center of the flow cell is ∼0.7 K/W (see calculations in the Supporting Material). Note that the coverslip acts as an effective heat sink, which substantially reduces the effect of heating near the glass surface (27) where our assay is mostly located, and thus the 0.7 K/W heating represents an upper limit. Although the laser power used in OP is typically an order-of-magnitude higher than in optical tweezers, the laser intensity is approximately three orders-of-magnitude lower, because the laser beam is not focused. The heating of the instrument is mostly due to light absorption in the objective. The subsequent warming of the objective causes slow but considerable drift in the instrument. Currently, it limits the force range that can be reliably be sampled to several picoNewtons.

To calibrate the forces in OP, we derived an analytical description of the power spectrum, taking into account Brownian rotation of the tethered microspheres (Eq. 3). We note that our equation can be used more generally for tethered systems (including MTs) as long as the externally applied force on the microsphere dominates the Brownian force, i.e., F_ext >> F_brown. Fig. S3 shows how the analytical power spectrum derived here compares to the MT power spectrum used by te Velthuis et al. (11) for the dimension perpendicular to the direction of the field lines as

$$P\left(f\right)=\frac{2\gamma k_{\text{B}}T}{{\gamma }^2{\left(2\pi f\right)}^2+{\left(F_{\text{ext}}/\left(L_{\text{ext}}+R\right)\right)}^2},$$ (4)

with L_ext as the DNA extension. The MT model only holds for microspheres with diameters smaller than the contour length of the DNA (Fig. S10 c); for larger microspheres, the MT model underestimates the Brownian motion of the microsphere (Figs. S10 a and S9 b). In contrast, our model was able to describe the Brownian motion for the larger microspheres; it fails, however, for external forces lower than the Brownian force (<0.1 pN). We have shown that the Brownian motion can be predicted accurately in this low-force regime (down to ∼30 fNs) with numerical simulations. By making use of the analytical solution (Eq. 3) for the enthalpic regime (>0.1 pN) and the numerical simulations in the entropic regime (<0.1 pN), we were able to predict microsphere motion subjected to forces that are biophysically relevant. Due to its generality, applicability of our model is not constrained to OP alone—it is also applicable to microsphere-tether systems such as MTs and TPM.

We have shown that a collimated laser beam can be used to apply a force to multiple biomolecules in parallel (Fig. S6). We have demonstrated the feasibility of OP as a flexible (dynamic) force spectroscopy technique. In future implementations, improvements can be made, inspired by other force-spectroscopy approaches. For example, spatial light modulators (21, 28) could be used to flatten the light intensity; the number of usable tethers could be increased by printing antibodies in a periodic pattern on a coverslip (29); (sub)millisecond dynamics of weak DNA-enzyme interactions could be imaged using integrated fluorescence microscopy (29, 30); or the polarization of the laser light could be employed to control the torque acting on the biomolecules (31, 32). Finally, OP instruments can be readily implemented in any existing OTs instrument: placing a single lens, by converting a collimated beam in one focused in the back-focal plane of the microscope objective, will convert an OTs into an OP apparatus.

Author Contributions

The article was written with the contributions of all authors. All authors gave their approval to the final version of the article.

Editor: Jennifer Curtis.