Anisotropic Membrane Curvature Sensing by Amphipathic Peptides

Abstract

Many proteins and peptides have an intrinsic capacity to sense and induce membrane curvature, and play crucial roles for organizing and remodeling cell membranes. However, the molecular driving forces behind these processes are not well understood. Here, we describe an approach to study curvature sensing by simulating the interactions of single molecules with a buckled lipid bilayer. We analyze three amphipathic antimicrobial peptides, a class of membrane-associated molecules that specifically target and destabilize bacterial membranes, and find qualitatively different sensing characteristics that would be difficult to resolve with other methods. Our findings provide evidence for direction-dependent curvature sensing mechanisms in amphipathic peptides and challenge existing theories of hydrophobic insertion. The buckling approach is generally applicable to a wide range of curvature-sensing molecules, and our results provide strong motivation to develop new experimental methods to track position and orientation of membrane proteins.

Introduction

Curvature sensing and generation by membrane proteins and lipids is ubiquitous in cell biology, for example to maintain highly curved shapes of organelles, or drive membrane remodeling processes (1). Membrane curvature sensing occurs if a molecule’s binding energy depends on the local curvature (2). For proteins, the presence of multiple conformations with different curvature preferences can couple protein function to membrane curvature (3), with interesting but largely unexplored biological implications.

Curvature sensing by lipids is often rationalized by a lipid shape factor, classifying lipids as cylindrical or conical when they prefer flat or curved membranes, respectively (1, 2). Membrane proteins offer a wider range of sizes, shapes, and anchoring mechanisms (4), and thus potentially more diverse sensing mechanisms. In particular, shape asymmetry implies that the binding energy depends on the protein orientation in the membrane plane (5), and thus cannot be a function of only mean and Gaussian curvature, which are rotationally invariant. This calls for more complex descriptions, and one natural extension is to model the binding energy in terms of the local curvature tensor C_ij in a frame rotating with the protein (5, 6, 7, 8, 9, 10, 11), which allows different curvature preferences in different directions. For example, a preference for longitudinal curvature is generally associated with proteins that are curved in this direction, such as BAR domains (12, 13), whereas amphipathic helices (14) are expected to sense transverse curvature, because their insertion into the membrane-water interface is energetically favored if the membrane curves away in the transverse direction (15, 16, 17).

Anisotropic curvature sensing is potentially complex, and theoretical investigations have demonstrated a wide range of qualitative behavior in local curvature models (5, 6, 7, 8, 9, 10, 11), but the models have not been rigorously tested. In principle, the curvature-dependent binding energy landscape E(C_ij) could be determined by measuring the Boltzmann distribution of protein configurations on curved membranes of known shape. However, current experimental techniques track only protein positions (18, 19, 20, 21, 22, 23, 24), and hence orientational information is averaged out. Here, we track both position and orientation of single molecules, using a computational approach based on simulated membrane buckling.

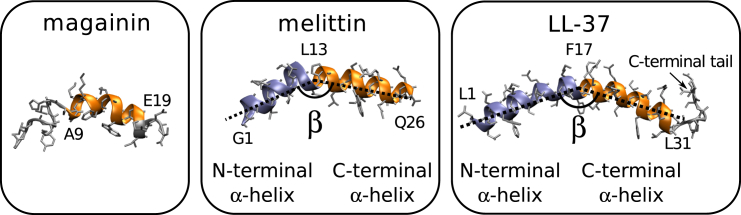
The method is applied to three amphipathic antimicrobial model peptides: magainin, which is found in the skin of the African clawed frog (25); melittin, an active component in bee venom (26); and LL-37, a peptide derived from the human protein cathelicidin, which is involved in the innate immune defense system (27). As shown in Fig. 1, the peptides vary in length and shape, and can thus be expected to display different sensing characteristics. Many antimicrobial peptides are believed to work by mediating membrane disruption (28). The peptides studied here are thought to mediate the formation of toroidal membrane pores with a highly curved inner surface partly lined with lipids (29, 30, 31, 32, 33, 34), although the evidence appears less clear for LL-37 (35). The ability to stabilize highly curved membrane structures suggests an intrinsic preference for curved membranes, as is generally expected for amphipathic peptides.

Figure 1.

Structures of magainin (52), melittin (53), and LL-37 (64). The melittin and LL-37 structures contain two α-helices that form an angle β (not the same for both structures). The α-helices used in the analysis are N-terminal (blue) and C-terminal (orange), with the limiting amino acids labeled on the structure. (Gray) Side-chain and nonhelical residues. To see this figure in color, go online.

Our method uses simulated membrane buckling to sample the unconstrained interaction of single biomolecules with a range of membrane curvatures, and extends previous simulation studies of buckling mechanics (36, 37), curvature-dependent folding and binding of amphipathic helices (38), and lipid partitioning (39). We obtain joint distributions of peptide positions and orientations that yield detailed information about curvature sensing mechanisms. The three model peptides display similar rotation-averaged curvature preferences but differ in orientational preferences, demonstrating the value of directional information. The asymmetry of the position-orientational distributions challenges continuum models of amphipathic helices as cylindrical membrane inclusions (15, 16). We speculate that such asymmetry is important for certain modes of antibacterial activity, and argue that it might be common also for larger curvature-sensing proteins. Finally, we discuss the limitations of characterizing curvature-sensing mechanisms from assays with zero Gaussian curvature, and conclude that this uncertainty affects the overall binding energy, but not the orientational preferences. These results motivate efforts to track positions and orientations of membrane proteins experimentally, and to develop assays with a broader range of local curvatures.

Materials and Methods

To study curvature sensing by single peptides, we simulate their interactions with a buckled membrane using the coarse-grained Martini model (40), and track their position and orientation, as shown in Fig. 2. On a microscopic level, curvature sensing by amphipathic helices is associated with the density and size of bilayer surface defects (38, 41), which are well described by the Martini model (42).

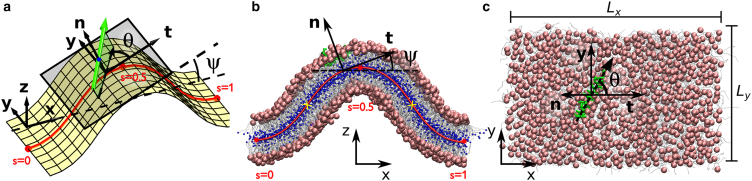
Figure 2.

Buckled simulation and analysis. (a) The position s of a peptide is defined by the projection of the center-of-mass (blue dot) onto the midplane surface (yellow). The in-plane orientation θ is defined by projecting the peptide backbone direction (green arrow, pointing toward the C-terminal end) onto the local tangent plane (gray) at s. The local tangent and normal vectors are indicated by t and n, respectively. (b) Side and (c) top view of a simulation snapshot with peptide position and orientation indicated using the notation and local coordinate system in (a). The system size is L_x = 20.88 nm and L_y = 13.05 nm. (Green) Peptide (LL-37 in this case); (gray) lipid tails; (light red) lipid phosphate groups; (blue) lipids’ innermost tail beads. The side view (b) also shows the Euler buckling profile (red line) fitted to the bilayer midplane, and the inflection points at s = 0.5 ± 0.25 (yellow crosses) used to align the buckled configurations. Molecular graphics generated with VMD (65). To see this figure in color, go online.

Simulation parameters

We performed molecular dynamics simulations using GROMACS 4.6.1 (43), the coarse-grained Martini force-field with polarizable water model (40, 44, 45), and a relative dielectric constant of 2.5 (as recommended in Yesylevskyy et al. (45)). We used standard lipid parameters for POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) (46), POPG (1-palmitoyl-2-oleoyl phosphatidylglycerol) (47), and peptides (48). The peptide structures for magainin (PDB: 1DUM), melittin (PDB: 2MLT), and LL-37 (PDB: 2K6O) were obtained from the Protein Data Bank, and coarse-grained with the Martinize script provided by the MARTINI developers. Constant temperature was maintained with the velocity rescaling thermostat (49) with a 1.0-ps time constant, and pressure was controlled with the Berendsen barostat (50) using a time constant of 12 ps and a compressibility of 3 × 10⁻⁴ bar⁻¹. Peptide (when present), lipids, and solvent were coupled separately to the temperature bath. Coulomb interactions were modeled with the particle-mesh Ewald method (51) setting the real-space cutoff to 1.4 nm and the Fourier grid spacing to 0.12 nm. Lennard-Jones interactions were shifted to zero between 0.9 and 1.2 nm. A time step of 25 fs was used in all simulations.

System assembly and membrane buckling

We assembled and equilibrated three rectangular (L_x = 2L_y) bilayer patches of 1024 lipids each, with 80% POPC and 20% POPG, solvated with ∼21,000 coarse-grained water beads and neutralized with sodium ion beads. POPG is negatively charged, which promotes peptide binding. These patches were equilibrated for 25 ns in an NPT ensemble at 300 K and 1 bar, with pressure coupling applied semiisotropically.

After equilibration, all systems were laterally compressed in the x direction by a factor γ = (L − L_x)/L = 0.2, where L is the linear size of the flat system, and L_x is the size of the compressed simulation box, in the x direction. This was done by scaling all x coordinates, and the box size L_x, by a factor 1 − γ = 0.8 at the end of the equilibration run, yielding L_x = 20.88, 20.81, and 20.89 nm for the three patches, respectively. After rescaling, the compressibilities were set to 0 in the x and y directions to keep the system size constant in those directions for subsequent simulations. Pressure coupling was then applied anisotropically in the z direction only. We then performed an energy minimization and a short equilibration run (25 ns) to let the bilayer buckle.

Next, we added one peptide to each system, using the three independent patches to create three independent replicas for each peptide. The peptide was initially placed ∼3 nm above the membrane surface, but quickly attached to the bilayer. After the binding event, we equilibrated the system for another 5 μs before starting a production run of 15 μs, where we collected data every 5 ns. All peptides remained essentially parallel to the membrane surface, in agreement with experimental results for low peptide concentrations (35, 52, 53, 54).

Membrane alignment and peptide tracking

The buckled membrane profile diffuses as a traveling wave during the simulation (see Movie S1 in the Supporting Material), but curvature sensing by a peptide is reflected in its distribution relative to the buckled shape. Hence, the buckled configurations must be aligned to extract useful information. To do this, we fit the xz profile of the membrane by the ground state of the Helfrich model with periodic boundary conditions, which is one of the Euler buckling profiles of an elastic beam (36, 37). This shape depends only on the dimensionless buckling parameter γ (γ = 0 is the flat state). Hence, if we compute the shape for some reference system, the general case can be obtained by shifting and scaling. We chose L_x = 1 as reference, and write the buckling profile as a parametric curve x = s + ξ(s,γ), z = ζ(s,γ), parameterized by a normalized arclength coordinate 0 < s < 1 (the absolute arclength is given by sL = sL_x(1 – γ)⁻¹).

For fast evaluation, we expanded ξ(s,γ) and ζ(s,γ) in truncated Fourier series in s, and created lookup tables for Fourier coefficients versus γ. We defined s to give the curve z(x) a maximum at s = 0.5, minima at s = 0, 1, and inflection points at s = 0.5 ± 0.25, and aligned the buckled shapes by fitting the bilayer in each frame to the buckling profile and aligning the inflection points (Fig. 2; Movies S2 and S3). Specifically, we fit the rescaled buckling profile to the innermost tail beads of all lipids in each frame using least-squares in the x and z directions, i.e., minimizing

$$\sum _i{\left(x_0+L_x\left(s_i+\xi \left(s_i,\gamma \right)\right)-x_i\right)}^2+{\left(z_0+L_x\zeta \left(s_i,\gamma \right)-z_i\right)}^2,$$ (1)

with respect to γ, the translations x₀, z₀, and the normalized arclength coordinates s_i of each bead (x_i, z_i are bead positions). The time-averaged bilayer shape, after alignment, agrees well with the theoretical buckled shape (Fig. 3 a).

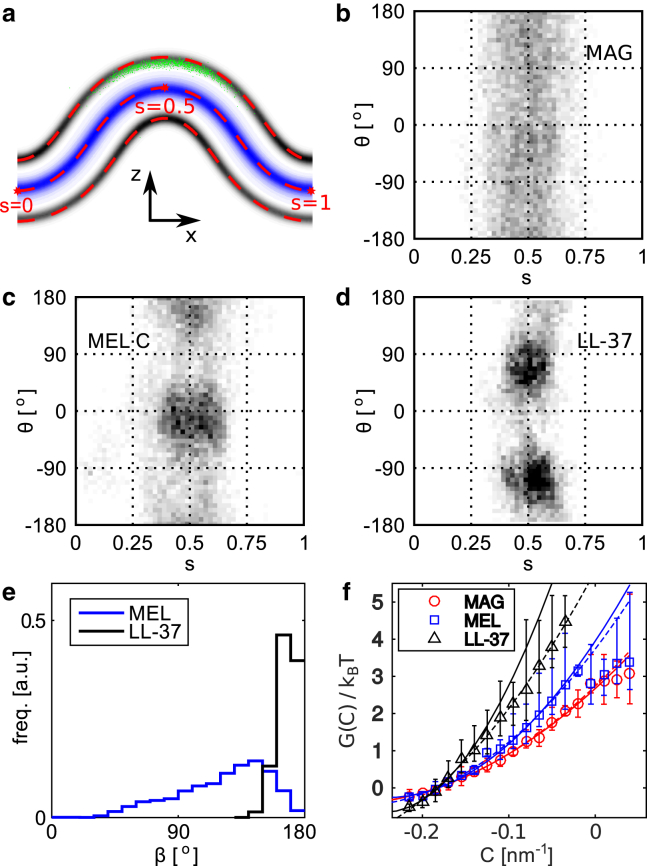
Figure 3.

Distributions of peptide positions and orientations in the buckled bilayer. (a) Average buckled shape in terms of densities of inner lipid tail beads (blue) and phosphate groups (gray) after alignment, for one production run with LL-37. (Green dots) Representative peptide center-of-mass positions. (Dashed red lines) Average fitted midplane ± 2.15 nm offsets in the normal direction. (b–d) Aggregated (s,θ)-histograms for (b) magainin, (c) melittin (using the orientation of the C-terminal helix), and (d) LL-37. (e) Distributions of internal angle β (see Fig. 1) for melittin and LL-37. (f) Orientation-averaged binding free energy versus curvature at the peptide center-of-mass (Eq. 4) for the three peptides. Error bars show maximum and minimum values from three independent simulations. (Dashed lines) Guides to the eye (fits to quadratic curves); (solid lines) results for the E_C model (Eq. 8) using the fit parameters in Fig. 4. To see this figure in color, go online.

The normalized arclength coordinate s of the peptide was computed by projecting the peptide center of mass onto the buckled profile fitted to the membrane midplane. The in-plane orientation θ was then computed by fitting a line through the backbone particles of the α-helical part of the peptide, projecting it onto the tangent plane at s, and computing the in-plane angle to the tangent vector t (see Fig. 2 a). The local curvature at s, in the tangent direction of the buckled shape, is given by

$$C\left(s\right)=\frac{1-\gamma }{L_x}\frac{d\psi }{ds},$$ (2)

where ψ is the bilayer midplane tangent angle of Fig. 2, a and b (55). (Note that the opposite sign convention is also common (1).) In the theoretical analysis, we neglect small shape and area fluctuations (SD(γ) ≈ 0.005) and use the nominal value γ = 0.2.

Fitting

We used least-squares routines in MATLAB (MathWorks, Natick, MA) to fit the Boltzmann distributions $e^{-E\left(s,\theta \right)}/Z$ of the E_C (Eq. 8) and E₂ (Table S1) models to (s,θ)-histograms built from the aggregated data with 50 bins for each coordinate. Both data and model histograms were normalized numerically. Error bars in Fig. 4 d are bootstrap SDs from 1000 bootstrap realizations, using blocks of length 100 (500 ns) as the elementary data unit for resampling (56).

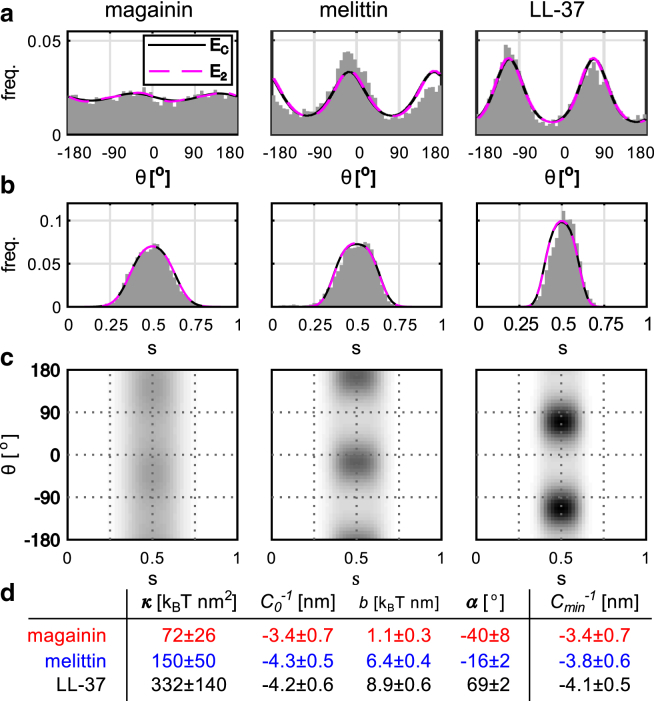
Figure 4.

Fitting quadratic models to data. (a and b) Marginal position and angle distributions, showing data (gray) and nearly identical curves from the E_C and general quadratic model (E₂, see Table S1). (c) (s,θ)-distributions for the E_C model. (d) E_C fit-parameters ± boostrap SD (see Materials and Methods) due to finite sampling (see Section S1 in the Supporting Material), with α indicating the preferred orientation. C_min is the preferred curvature, from minimizing Eq. 12. To see this figure in color, go online.

Results

Preferred curvature and orientations

We simulated single peptides interacting with a buckled bilayer, using three independent production runs of 15 μs for each peptide, and tracked their normalized arclength coordinate s ∈ [0,1] and in-plane orientation θ (Fig. 2 a). Aggregated (s,θ)-histograms are shown in Fig. 3, b–d, and convergence is discussed in Section S1 in the Supporting Material.

All three peptides prefer the concave high-curvature regions with a maximum at s = 0.5, as expected for hydrophobic insertion mechanisms (15, 16, 17, 38, 41, 42). Regarding the angle distributions, the three peptides behave differently. Magainin displays a rather uniform angle distribution, probably because its short α-helical segment creates a fairly symmetric insertion footprint. For melittin, the joint between the N- and C-terminal helices appears very flexible, resulting in a broad distribution of the internal angle β (Fig. 3 e). Both helices prefer directions nearly parallel to the x axis, the direction of maximum curvature, but the preference is stronger and slightly offset (θ_max ≈ −15°, 165°) for the C-terminal helix shown in Fig. 3 c, while the N-terminal helix is more symmetrically oriented (Fig. S2).

LL-37 maintains a linear structure, and its θ-distribution displays two sharp maxima near θ = 70° and θ = −110° (Fig. 3 d). This is remarkable because, by reflection symmetry around s = 0.5, the curvatures in those directions are the same as along −70° and 110°, orientations that are clearly not preferred. As we will argue below, this can be understood as curvature sensing along directions different from that of the peptide itself. These sensing directions adopt θ = 0,90°, and thus map onto themselves under reflection. Notably, none of the peptides orient directly along the flat direction θ = 90° as commonly assumed in mechanical models (15, 16).

Orientation-averaged binding free energy

Next, we look at the orientation-averaged binding free energy, corresponding to the curvature-dependent enrichment measured in many in vitro assays (18, 19, 20, 21, 22, 23, 24). To extract the curvature dependence of the binding energy, we analyze center-of-mass positions along the buckled shape. These should follow a Boltzmann distribution, proportional to e^−G(s), where G(s) is the orientation-averaged binding free energy in units of k_BT. We model this as depending on the local curvature only, and hence set G(s) = G(C(s)), and extract G(C) from curvature histograms, weighted according to the change-of-variable transformation that relates the density of curvatures, ρ(C), to the density of positions ρ(s). Indeed, dropping normalization constants, we have

$${\rho }_s\left(s\right)ds\propto e^{-G\left(C\left(s\right)\right)}ds\propto e^{-G\left(C\right)}|dC/ds{|}^{-1}dC\propto {\rho }_C\left(C\right)dC,$$ (3)

from which it follows that

$$G\left(C\right)=-\text{ln}\left({\rho }_C\left(C\right)|dC/ds|\right)+\text{const}.$$ (4)

The weights |dC/ds| can be understood as compensating for the fact that not all curvatures have equal arclength footprints along the buckled profile. To estimate G(C), we estimated ρ(C) using a simple histogram, and the weights as the mean of |dC/ds| for all contributions to each bin.

Fig. 3 f shows the binding free energy profiles G(C) for the different peptides, which are more similar than the (θ,s)-distributions, and well fit by quadratic curves. Note that Eq. 4 does not yield absolute binding energies of the peptides, and the G(C) curves are instead offset vertically for easy visualization. Experimental binding free energies of these peptides to flat membranes with anionic lipids range from −15 to −10 k_BT (57).

Quantitative models

We now turn to quantitative models of the peptides’ curvature sensing. As described in the Introduction, we model the binding energy of a peptide as a function of the local curvature tensor in a frame rotating with the peptide, and treat the bilayer itself as having fixed shape and thus a fixed deformation energy, which we neglect. Generally, if the principal curvatures and directions are c_1,2 and ${\overrightarrow{e}}_{\mathrm{1,2}}$, the curvature tensor, or second fundamental form, in a frame rotated by an in-plane angle θ relative to ${\overrightarrow{e}}_1$, is given by

$$C_{ij}=\left[\begin{array}{cc}H+D\text{cos}2\theta & D\text{sin}2\theta \\ D\text{sin}2\theta & H-D\text{cos}2\theta \end{array}\right]=\left[\begin{array}{cc}{C}_{\parallel }& C_X\\ C_X& C_{\perp }\end{array}\right],$$ (5)

where H = (c₁ + c₂)/2 and D = (c₁ − c₂)/2 are the mean and deviatoric curvatures, and the Gaussian curvature is given by K = c₁c₂ = C_||C_⊥ − C_X². Note the symmetry under rotations by 180°, because the curvature of a line is the same in both directions. For the buckled surface, c₁ = C(s), c₂ = 0 (and hence K = 0, H = D = C(s)/2), ${\overrightarrow{e}}_1=\mathbf{t}$, and ${\overrightarrow{e}}_2=\mathbf{y}$. As shown in Fig. 2, we define the rotating frame using the peptide’s center of mass and the direction of the α-helical parts, and thus θ is the peptide in-plane orientation, and ||,⊥ denote the longitudinal (θ) and transverse (θ + 90°) directions.

The simplest models are linear in C_ij, but can be ruled out because they cannot reproduce the convex binding free energies in Fig. 3 f. To see this, we write a general linear model in the form E₁ = aH + bDcos(2(θ − α)) (5), and integrate out the angular dependence to get

$$G_1=-\text{ln}{\int }_0^{2\pi }{e}^{-E_1}d\theta =aH-\text{ln}{I}_0\left(bD\right)+\text{const}.$$ (6)

Because H = D = C(s)/2 on the buckled surface, and the modified Bessel function I₀ is convex, G₁ will be either downward-convex (if b ≠ 0) or linear- and direction-insensitive (when b → 0), in disagreement with Fig. 3.

Moving on to quadratic terms, Akabori and Santangelo (10) explored a model of the form

$$E_X=\frac{k_{\parallel }}{2}{\left(C_{\parallel }-C_{\parallel 0}\right)}^2+k_X{\left(C_X-C_{X0}\right)}^2+\frac{k_{\perp }}{2}{\left(C_{\perp }-C_{\perp 0}\right)}^2,$$ (7)

where C_||0, C_X0, and C_⊥0 are preferred curvatures. Further simplifications k_X = 0 and k_X = k_⊥ = 0 have also been studied (6, 7, 8, 9). While these models can all display nontrivial behavior, E_X is not the most general quadratic model, which would include all nine linear and quadratic combinations of the three independent curvature tensor components. In particular, E_X does not contain a simple preferred mean curvature as a special case, because H = (C_|| + C_⊥)/2, and hence (H – H₀)² contains a term C_||C_⊥, which is absent in Eq. 7.

However, the general quadratic model is not identifiable on surfaces with only one nonzero principal curvature. This is because the Gaussian curvature K is zero, and hence the model can only be specified up to a term proportional to K. Also, E_X can then be made to behave as a mean curvature sensor, because all angular dependence cancels if k_|| = k_⊥ = k_X, C_||0 = C_⊥0, and C_X0 = 0. These limitations apply to our buckled surface, as well as to tubular and plane-wave geometries used experimentally (18, 19, 22, 23, 24). A curvature-sensing mechanism therefore cannot be completely characterized using such surfaces, but some conclusions can be drawn.

In particular, setting k_X = 0 in Eq. 7 yields an intuitive model with curvature sensing only along the longitudinal and transverse directions (6, 7, 8, 9). From Eq. 5, this means angular dependence only in the form cos2θ, which is symmetric around θ = 0, $\pm \left(\pi /2\right)$, and ±π. However, the orientational distributions in Fig. 4 a do not display this symmetry, although the statistics is not quite clear in the case of melittin (see Fig. S2). Apparently, the curvature-sensing directions are not generally aligned with the actual helices. This resembles results for α-synuclein, where peptides and induced membrane deformations appear similarly misaligned (58). A simple quadratic model incorporating these observations is

$$E_C=\frac{\kappa }{2}{\left(2H-C_0\right)}^2+bD\text{cos}\left(2\left(\theta -\alpha \right)\right)+{\kappa }_{G}K,$$ (8)

where the Gaussian curvature coefficient κ_G is unidentifiable because K = 0 in our data. As shown in Fig. 4, E_C describes all peptides reasonably well, and using the full quadratic model does not significantly improve the fit.

To better understand the physical meaning of this model, we explore some alternative formulations. First, using Eq. 5 to trade H,D for the C_ij, and rearranging the terms, we find an equivalent formulation that resembles the E_X model,

$$E_C^{\prime }=\frac{\kappa }{2}{\left(C_{\parallel }-C_0+\frac{b}{2\kappa }\text{cos}2\alpha \right)}^2+\kappa {\left(C_X+\frac{b}{2\kappa }\text{sin}2\alpha \right)}^2+\frac{\kappa }{2}{\left(C_{\perp }-C_0-\frac{b}{2\kappa }\text{cos}2\alpha \right)}^2+\left(\kappa +{\kappa }_G\right)K.$$ (9)

Continuing, we can rotate the basis attached to the peptide by α, and thus generate a transformed curvature tensor with elements $C_{ij}^{\left(\alpha \right)}\left(\theta \right)=C_{ij}\left(\theta +\alpha \right)$, satisfying

$$\begin{array}{c}{C}_{\parallel }^{\left(\alpha \right)}+C_{\perp }^{\left(\alpha \right)}=2H,\\ C_{\parallel }^{\left(\alpha \right)}-C_{\perp }^{\left(\alpha \right)}=2D\text{cos}\left(2\left(\theta -\alpha \right)\right).\end{array}$$ (10)

In this rotated basis, there is an E_X-like equivalent model that lacks off-diagonal elements,

$$E_C^{″}=\frac{\kappa }{2}{\left(C_{\parallel }^{\left(\alpha \right)}-C_0+\frac{b}{2\kappa }\right)}^2+\frac{\kappa }{2}{\left(C_{\perp }^{\left(\alpha \right)}-C_0-\frac{b}{2\kappa }\right)}^2+\left(\kappa +{\kappa }_G\right)K,$$ (11)

i.e., sensing curvature along two orthogonal directions that are rotated by an angle α with respect to the peptide backbone. Note that because Gaussian curvature is rotationally invariant, the unidentifiable Gaussian curvature term only affects the overall affinity to membranes with Gaussian curvature, and not the orientational preferences of the peptides.

As a consistency check, we integrated out θ from E_C. Proceeding as for G₁ in Eq. 6 and setting H = D = C(s)/2, K = 0, we get

$$G_C=-\text{ln}{\int }_0^{2\pi }d\theta e^{-E_C}=\frac{\kappa }{2}{\left(C-C_0\right)}^2-\text{ln}{I}_0\left(bC/2\right),$$ (12)

which we compare with G(C) in Fig. 3 f using the parameters of Fig. 4 d. Magainin and melittin show good agreement, but not LL-37, whose (s,θ)-distribution (Fig. 3 d) is also less symmetric around s = 0.5 than expected from the symmetry of the buckled shape. A simple explanation is that the effective sensing site does not coincide with the center of mass used to define s. This is illustrated in Fig. 5 by a hypothetical peptide that is fixed at s = 0.5 but free to rotate. As a result, the N-terminal end shows (s,θ)-correlations resembling those seen for the LL-37 center of mass, indicating that its sensing site is located in the C-terminal part. Numerical experiments in Section S2 agree qualitatively with this geometric argument, and both symmetry and consistency improve when tracking the LL-37 C-terminal helix instead (but the fit parameters do not change significantly).

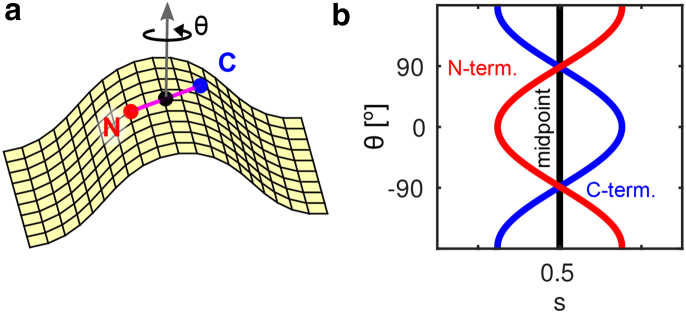
Figure 5.

Curvature-sensing site and (s,θ)-correlations. (a) A freely rotating peptide whose midpoint (black) is fixed at s = 0. (b) Resulting correlations s_C,N ∝ cosθ for the N- and C-terminal ends (red, blue). To see this figure in color, go online.

Discussion

We describe a simulation approach to study membrane curvature sensing by tracking positions and orientations of single molecules interacting with a buckled lipid bilayer. This approach is widely applicable, and the utility of angular information is obvious from the observation that the three peptides show distinct orientational distributions, but very similar orientation-averaged binding energy curves (Fig. 3).

Our data is well described by modeling the binding energy in terms of local curvatures, yielding more complex models than commonly used to fit orientation-averaged data (18, 19, 20, 21), and also less symmetric than some theoretical suggestions (6, 7, 8, 9). The observed asymmetry also seems difficult to reconcile with continuum elasticity models of hydrophobic insertion in terms of cylindrical membrane inclusions (15, 16). Recently, continuum elasticity models were found to underpredict the induced curvature of a hydrophobic insertion compared to atomistic simulations (17). Our data shows an additional qualitative effect of molecular detail, which we believe reflects the fact that the mirror symmetry of cylinder-shaped inclusions is absent from the peptide structures. Instead, our data can be described in terms of curvature-sensing directions that are not aligned with the inserted α-helices. Because amphipathic helices are common curvature-sensing motifs (14) and mirror symmetry is generally absent also in multimeric proteins (59), such asymmetric sensing might be common.

These results should motivate efforts to track the position and orientation of membrane proteins experimentally, for example using polarization-based optical techniques (60) or electron microscopy (61). It would also be valuable to vary mean and Gaussian curvatures independently to probe Gaussian curvature sensing, for example by extending supported bilayer assays with plane-wave surfaces (22) to shapes with nonzero Gaussian curvature. Another possibility might be to combine assays with cylindrical geometries (K = 0), such as plane waves (22) or membrane tethers (18, 19, 20, 21, 23) with spherical geometries (K = H²) such as vesicles (3, 41) or deposited nanoparticles (24).

An interesting aspect of the E_C model is that it predicts a free energy minimum, i.e., a preferred curvature, at least when K = 0 (Eq. 12). The preferred curvature radii $C_{\text{min}}^{-1}$ of our peptides, listed in Fig. 4 c, are well above the monolayer thickness of ∼2.2 nm (Fig. 3 a) where the bilayer folds back on itself, but below the lowest radius in our simulations (∼4.5 nm), meaning that this prediction is somewhat speculative, because higher-order terms might become important at very high curvatures. On a molecular level, curvature sensing by amphipathic peptides is thought to reflect an affinity for packing defects in the membrane-water interface (38, 41, 42). It is not clear that this mechanism predicts a preferred curvature at all. Testing this seems like an interesting question for future work.

Our results also have biophysical implications. At high concentrations, the three peptides are thought to mediate the formation of membrane pores with highly curved inner surfaces (29, 30, 31, 32, 33, 34). The orientational preferences we see in single peptides are consistent with atomistic (31) and coarse-grained (34) simulations of multipeptide pores. In particular, the asymmetric curvature preference of LL-37 should help select for a single-handedness of the resulting tilted pore structure (34), which might facilitate pore formation by reducing frustration. This mechanism may represent a general way for membrane proteins to induce a particular orientation or handedness in patterns on curved surfaces (62).

Author Contributions

J.G.-L. and M.L. designed research; J.G.-L. and F.E.-W. performed research; J.G.-L. and M.L. analyzed data; and J.G.-L., F.E.-W., and M.L. wrote the article.

Editor: Markus Deserno.

Supporting Citations

Ref. (63) appears in the Supporting Material.