Abstract
Purpose
To develop a CEST saturation scheme sensitive to hydroxyl protons at 3 T. Clinical imaging of hydroxyl moieties can have an impact on osteoarthritis, neuropsychiatric disorders, cancer.
Theory
By varying saturation amplitude linearly with frequency offset, the direct water saturation component of the Z-spectrum is flattened and can be subtracted to produce a difference spectrum (MTRdiff) that isolates solute resonances. Variable saturation power allows for near optimization of hydroxyl and amine/amide moieties in one Z-spectrum.
Methods
Phantom studies were used to test vCEST performance in 2 environments: (1) aqueous single-solute (glycogen, glucose); (2) aqueous multiple solute (glycogen with BSA). In vivo vCEST imaging of glycosaminoglycan content (GAG) in patellar-femoral cartilage was performed in a subject with history of cartilage transplant.
Results
In solutions with overlapping resonances, vCEST resolves separate hydroxyl and amine/amide peaks. CEST hydroxyl signal in cartilage is negligible, but with vCEST, hydroxyl signal ranged from 2 – 5%·ppm and showed distinct contrast between lesions and normal appearing cartilage.
Conclusion
Introduced a variable saturation amplitude CEST (vCEST) scheme to improve sensitivity to exchangeable hydroxyl moieties at 3 T resulting in detection of hydroxyl in the presence of multiple solutes with overlapping resonances.
Keywords: Chemical exchange, cartilage, glycosaminoglycan, glycogen, glucose, endogenous contrast
Introduction
Chemical exchange saturation transfer (CEST) techniques probe the direct transfer of spins from one molecule to another. The CEST effect and its impact on NMR spectra have been understood for many decades, but only recently has CEST been applied as a mechanism for creating contrast in MRI [1]. In a typical CEST imaging experiment, contrast is obtained by applying a radiofrequency (RF) saturation pulse at the resonant frequency of mobile protons associated with labile exchange groups. This saturation is then transferred to the surrounding free water, resulting in an observed signal attenuation that is proportional to the concentration and exchange rate of the protons of interest. To date, CEST MRI has been applied to detect mobile proteins [2–4], glycogen [5], glucose [5–9], glycosaminoglycans (GAG) [10–13], and mobile macromolecules [14, 15] as well as metabolites such as creatine [16–19], glutamate [20, 21], and myoinositol [22, 23]. Recent applications in stroke imaging [24–28], cancer [29–34], osteoarthritis [10–12, 35], and neurological disease [21, 36] have also shown promise.
In a typical CEST experiment, the resonant frequency of a narrow-bandwidth RF saturation pulse is swept over numerous offset frequencies to generate a so-called CEST z-spectrum [37]. In addition to contrast from labile protons on functional groups (e.g. amides, amines, hydroxyls), the resultant z-spectrum is composed of three competing signals. First, magnetization transfer (MT)[38] between semi-solid protons and surrounding water via dipole-dipole and chemical exchange mechanisms yield a broad background in the z-spectrum. Second, the finite bandwidth of the saturation pulse and rotation effects result in direct water saturation (DWS) when the offset frequency is close to the water resonance. Third is the exchange-mediated nuclear Overhauser effect (NOE) [39] which influences the symmetry of the z-spectrum.
In general, sensitivity in a CEST experiment is driven by: (1) the abundance of the exchange moiety, (2) the requirement that the exchange rate be less than the chemical shift (slow-intermediate exchange [40]), and (3) the chemical shift being sufficiently far from the water resonance to minimize the effect of DWS. Because of these limitations, many CEST studies have focused on detection of amide protons on protein/peptide backbones, referred to as amide proton transfer (APT) MRI. Amide protons are an ideal CEST target because of their large chemical shift with respect to water (3.5 ppm = 448 Hz at 3 T) and slow exchange (50 Hz). Other exchangeable moieties, such as amine and hydroxyl protons, are critical to assess due to their intimate relationship with clinically relevant metabolites such as glutamate and carbohydrates, respectively. However, these proton moieties are not as well suited to produce CEST contrast because all have rapid exchange rates (> 500 Hz), and chemical shifts nearer to the water resonance. While these challenges have been overcome to some degree by transitioning to ultra-high field strength (> 7 T), it is important to develop tools to assess these protons at lower, clinical field strengths if a clinical implementation is to be realized.
Therefore, in this study we propose a novel CEST saturation scheme to improve the sensitivity to rapidly exchanging hydroxyl protons with chemical shift less than 1.5 ppm at clinical field strength. The approach employs a variable power saturation scheme (vCEST) designed to minimize DWS contributions to the z-spectrum. We show that minimizing the DWS contribution increases the sensitivity to solutes in fast exchange and/or those resonating close to water relative to traditional CEST.
Theory
Direct water saturation
The z-spectrum is a convolution of DWS, MT, NOE, and CEST contributions. The goal in CEST MRI is to maximize CEST contributions while minimizing the non-CEST components. An approximation of the CEST spectrum is often calculated directly from the z-spectrum through asymmetry analysis. If both DWS and MT are symmetric about the water resonance, the difference in the z-spectrum between ± offsets will offer a signal that is sensitive to the CEST effect. However, in practice at clinical field strengths, though DWS is by definition symmetric, the spillover effect and MT are not [41, 42]. Additionally, tissue in vivo has many different exchanging moieties, some of them up-field (e.g. NOE contributions), which are inherently asymmetric about the water resonance.
Therefore, modeling the DWS and MT spectra may be necessary in many cases. In general, the shapes of DWS and MT spectra in tissue can be modeled as Lorentzian and super-Lorentzian, respectively [43, 44]. The CEST spectrum of a single exchanging proton moiety can also be modeled by a Lorentzian function [45, 46]. Based upon this, Lorentzian line-fitting has been used to extract CEST information [14, 19, 46, 47], but is still challenged when protons are in the fast exchange regime where the Lorentzian curves from CEST and DWS significantly overlap. Therefore, we attempt to minimize the DWS component to improve isolation of CEST resonances close to water. Starting from Zaiss et al. [46], the DWS Lorentzian shape can be written as
| (1) |
| (2a) |
| (2b) |
where ω1 is the irradiation amplitude (in rad/s), Δω is the offset frequency with respect to water, R and k are the relaxation and exchanges rates of both water and solute protons. The subscripts w and s denote water and solute pools, respectively. Equation 1 is derived from the Bloch equations assuming a weak saturation pulse (WSP) [48] and steady-state. The WSP approximation assumes the RF field is only applied to the solute pool without perturbing the water pool (i.e. Δωs = 0 and Δωw → ∞).
From this, it can be seen that the DWS curve is dependent not only on the relaxation rates of the free water pool, but also on the T1 and T2 of solutes present and the exchange rates [46]. However, if we tailor the irradiation amplitude as a linear function of the frequency offset, we can model the DWS curve as a constant with the assumption that Δω2 ≫ QP (see online supporting information for value estimates)
| (3) |
| (4) |
By using a pulse sequence where the saturation irradiation is a linear function of the frequency offset, the rotational effects on water magnetization due to off-resonance saturation are equal for all frequency offsets. As long as the weak saturation pulse approximation applies, this scheme results in a flat DWS curve. The z-spectrum is still a convolution of DWS, MT, and CEST, but, the DWS contribution is trivialized.
However, this assumes no B0 inhomogeneity (Δω0 = 0 Hz), or a perfectly homogeneous medium, which cannot be assumed for in vivo applications. If a ΔB0 shift is present due to field inhomogeneities, the irradiation function becomes,
| (5) |
and the DWS is no longer constant:
| (6) |
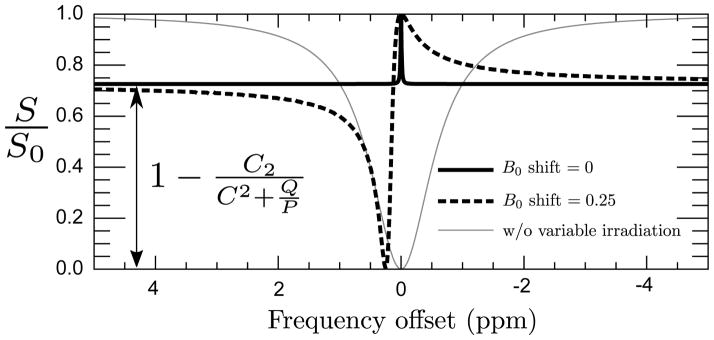
Figure 1 illustrates this effect: for large offset frequencies, and irrespective of Δω0 inhomogeneities, the DWS curve is flat. However, when Δω = B0 inhomogeneity/shift, the DWS curve is significantly altered.
Figure 1.
Analytic solution to DWS using values from simulation 3 (C = 0.33, Q = 0.52 s−1, P = 1.67 s−1) for vCEST without B0 shift (solid), vCEST withΔB0 = 0.25 ppm (dashed), and CEST (gray–thin).
In the case where there is a negligible B0 shift, or the CEST solute of interest is far from the water resonance, the DWS spectrum is flat and can be removed from the z-spectrum by subtraction rather than complicated deconvolution. In the presence of moderate B0 shift, and thus significant modulation of the DWS curve, removal of the DWS component is non-trivial. For the purposes of this study we will assume the B0 shifts encountered are small enough that simple subtraction will suffice.
Z-spectrum analysis modification
As described above, in a standard CEST experiment, the CEST signal of interest is extracted through asymmetry analysis and usually denoted as MTRasym (Eq. 8). In this type of analysis it is imperative that an accurate B0 map is obtained in order to center the z-spectrum on the water resonance for every voxel and the assumption that the contributions to the CEST spectra are symmetric.
In the variable power CEST experiment (vCEST), the CEST signal of the resonance of interest is extracted through subtracting a constant contribution from the DWS, which is obtained through simulation after acquiring T1, T2, B0, and B1 maps. The algebraic equation for the vCEST DWS (Eq. 6) assumes a long, continuous-wave saturation. However, in a pulsed-CEST experiment, the saturation pulses have shape and finite duration, causing some broadening of the water peak. Therefore, numerical approximation is a more accurate representation of the DWS than simply applying the algebraic form of Equation 6. In the vCEST paradigm, we represent the difference between the calculated DWS curve and the vCEST z-spectrum as MTRdiff (Eq. 7). It is important that good shimming of the volume of interest is performed during data acquisition. The resulting MTRdiff still includes the MT contribution, but will not be confounded by the presence of up-field proton moieties in the tissue nor spillover or DWS contributions. In fact, the contribution from any up-field solutes will be observed in the MTRdiff spectrum. If we assume a small MT effect, the removal of the DWS contributions results in a CEST observation of the proton moieties of interest even near the water resonance.
Methods
Simulation
To assess the theoretical performance of the vCEST scheme versus the standard CEST experiment, the Bloch-McConnell equations [49] were numerically solved as described in refs. [50, 51] for pulsed RF irradiation, using software written in IDL 8.2 (Exelis VIS, Boulder, CO USA). CEST saturation duration was set to 75 ms, long enough to avoid peaks near 1 ppm due to the power spectrum of a short pulse-train [52]. The pulse shape was modeled as a single-lobed sinc function with Gaussian apodization. To adapt to RF amplifier constraints of clinical MRI systems, the minimum TR allowed was set to twice the total irradiation duration; therefore, the TR was set to 155 ms. Lastly, the z-magnetization was calculated after 65 repetitions, which corresponds to approximately 5 seconds of pulsed irradiation over 10 seconds of the pulse sequence (50% duty cycle) to ensure steady state is reached.
To generate the MTRdiff spectra, the z-magnetization (Mz) derived from a 2-pool model (CEST + DWS) were subtracted from the modeled z-magnetization (Mz,DWS) of a single pool DWS.
| (7) |
For all simulations, we allowed the pulse peak B1 amplitudes to be varied according to the scheme described in equation 3, with the exception that the peak amplitude was not allowed to go to zero at Δω = 0, but instead repeats its previous value such that there is still an appreciable saturation near the water resonance for visual reference. Additionally, we simulated standard, single-power CEST sequences and report the MTRasym by taking the difference in the z-component magnetization between contralateral offsets (Mz(±Δω)) and then normalizing by the z-magnetization without saturation (M0),
| (8) |
Simulation 1
The first simulation seeks to understand the impact of sequence parameters on the CEST and vCEST signals for cartilage under ideal conditions (e.g. no MT signal). To simulate the cartilage environment with exchangeable hydroxyls, model physical parameters were as follows: T1w = 1200 ms, T2w = 30 ms, T1s = 1000 ms, T2s = 29 ms, and pool ratio = 2% —which is roughly equivalent to 200 mM GAG— and Δωs = 1 ppm. As described in Stikov et al. [53] and extrapolating for relaxation rate changes between 1.5 and 3 T, the relaxation constraints of the water pool were chosen such that R1T2 = 0.024. Additionally, the hydroxyl proton relaxation rates were chosen from studies of glycogen by Zang et al. [54]. To observe the effect of solute exchange rate on the CEST and vCEST signals, we varied the exchange rate from 0 to 5000 Hz in steps of 25 Hz. Optimization of irradiation power was performed by varying the peak B1 from 0 to 5 μT in the CEST simulations and 0 to 5 μT/ppm for vCEST in steps of 0.25 Hz. Once CEST (MTRasym(Δω)) and vCEST (MTRdiff (Δω)) curves were generated for each combination of exchange rate and peak B1 amplitude, the value of each curve at Δω= 1 ppm was studied.
Simulation 2
The goal of the second simulation was to model the impact of field inhomogeneities on both the CEST and vCEST schemes at 3 T. We modeled the effect of B0 field inhomogeneity on the vCEST spectrum by allowing B0 shifts of ±0.2 ppm. Physical parameters are the same as above with exchange rate (ksw) = 1500 Hz. The peak B1 amplitude for vCEST was 1 μT/ppm, and two CEST spectra are modeled at peak amplitudes of 1 and 3.5 μT.
Simulation 3
The final simulation was performed to model glucose/glycogen exchange moieties that will be explored with phantom studies. In each case, the solute pool is the same as above, with T1w = 2000 ms, T2w = 1000 ms. B1 amplitudes of vCEST and CEST are the same as above.
Phantoms
Four 15ml Falcon tubes were filled with solutions of phosphate-buffered solution (PBS) and glycogen (type IX bovine liver CAS 9005-79-2, Sigma-Aldrich) and four with solutions of PBS and glucose at concentrations of 20 and 50 mM (glycogen similar to exercised mammalian skeletal muscle [55, 56]), 100 mM (skeletal muscle at rest), and 200 mM (liver of fed mammal [57]). Powdered NaOH was added to adjust pH to 7.4. Additionally, five tubes were filled with solutions of PBS and 10% albumin (BSA fraction V CAS 9048-46-8, Chem-Impex) with glycogen at concentrations of 0, 20, 50, 100, 200 mM.
Human subjects
After IRB approval, one subject was imaged to test the feasibility of the vCEST scheme in vivo. This subject had a history of microfracture surgery and autologous cartilage transplant.
Imaging
Phantom imaging
Phantom scans were performed on a 3 T Achieva (Philips, Cleveland, Ohio) with a 2-channel transmit body coil and an 8-channel receive head coil. T1, T2, B1, and B0 mapping were performed by multi-inversion recovery, multi-echo, dual TR, and WASSR [58], respectively (sequence details can be found in the online supporting information). CEST and vCEST sequence details were as follows: CEST [3D SPGR with 75 ms 1μT and 3.5μT sinc-gauss pulses, TR=152 ms, 49 offsets from −5 to 5 ppm and one S0 image at −100kHz]; vCEST [3D SPGR with 75 ms sinc-gauss pulses, peak amplitude varying by 1μT/1ppm with 0.21μT at 0ppm, TR=152 ms, 49 offsets from −5 to 5 ppm and one S0 image at −100kHz]. These sequences were rapid 3D steady-state (similar to pulsed MT [59] and pulsed CEST [14]) reading one k-space line per saturation pulse. CEST at 1μT and 3.5μT were studied to match the amplitude of the vCEST (1μT) and to demonstrate more optimal saturation amplitudes for hydroxyl protons. The FOVs for all phantom studies were 190×190×9 mm and voxel size 1.5×1.5×3 mm, except the B1 map voxel size 3×3×3 mm. T1 and T2 were calculated by fitting the inversion recovery and spin echo signal equations for each voxel.
Human imaging
Human imaging was performed on a 3 T Ingenia (Philips, Cleveland, Ohio) with a 16-channel transmit/receive dSTREAM knee coil. T1, T2, B1, and B0 mapping were performed by multi-flip angle, multi-echo, dual TR, and WASSR [58], respectively (see online supporting information). CEST and vCEST sequence details were as follows: CEST [water-selective (ProSet) 3D SPGR with 75 ms, 1μT single-lobe sinc-gauss pulses, TR=155 ms, 33 offsets from −2 to 2 ppm and one S0 image at −100kHz]; vCEST [water-selective (ProSet) 3D SPGR with 75 ms single-lobe sinc-gauss pulses, TR=155 ms, peak amplitude varying by 1μT/1ppm with 0.125μT at 0ppm, 33 offsets from −3 to 3 ppm and one S0 image at −100kHz]. These were steady-state sequences using EPI to readout 9 k-space lines per saturation pulse. All scans acquired in the axial plane with FOV 170×170×45 mm and voxel size 1×1×3 mm, with the exception of the B1 voxel size 2.2×2.2×3 mm. Total scan duration 27 minutes for parameter mapping sequences.
Data analysis
All parameter maps were generated using in-house software written in IDL 8.2 (Exelis VIS, Boulder, CO USA).
Phantoms
CEST MTRasym were generated by asymmetry analysis (Eq. 8) with WASSR B0 correction [58]. Each 49 point CEST z-spectrum of range −5 to +5 ppm was Fourier transformed to the time domain where 1 Hz line-broadening was applied for sensitivity enhancement and removal of high frequency information. Additionally, the z-spectra were zero padded to 2048 points before being transformed back to the frequency domain. The vCEST MTRdiff curves were generated by subtraction of the measured z-spectrum from a simulated DWS curve (Eq. 7). For every 49 point vCEST z-spectrum of range −5 to +5 ppm a corresponding 49 point DWS curve was generated by the methods described above using a single-pool water system with measured B0, B1, T1, and T2 values. Both curves were line-broadened by 1 Hz and zero-padded to 2048 points, similar to the CEST data. Given the shape of the vCEST z-spectrum, the maximum signal up-field from water will be where MT, solute CEST, and NOE contribute least and therefore the contribution is assumed to be only DWS. This serves as a reference point from which to locate the simulated DWS in relation to the measured z-spectrum. MTRdiff is then generated by subtraction of the vCEST data from the simulated DWS curve on a voxel by voxel basis.
To produce parameter maps that are reflective of hydroxyl signals, MTRasym and MTRdiff curves were integrated over a range of 0.5 to 1.5 ppm for each voxel. This step is performed to account for variations in the exact chemical shift of exchanging hydroxyls. Likewise, for the BSA phantoms the MTR curves were also integrated over a range from 2.0 to 3.0 ppm to map amide proton signals. These area-under-curve (AUC) measurements will be written as AUC [MTRdiff,asym(0.5–1.5)] in units of %·ppm.
In vivo
CEST MTRdiff and vCEST MTRasym curves were generated from the measured z-spectra in the same manner as described above using the offset range −2 to 2 ppm to focus on hydroxyl exchange, which reduced the z-spectrum to 33 points. To generate the DWS curve for the in vivo vCEST analysis, an estimate of T2 of free water (T2f) was calculated using the relationship R1T2 = 0.024 as described above (see simulation 1). Two slices were chosen; one through a transplant tissue on the trochlear ridge of the femor, the other through a patellar lesion. Three regions-of-interest (ROIs) were drawn in each slice (lesion, femoral, and patellar cartilage) and mean values were calculated for comparison
Results
Simulations
Simulation 1
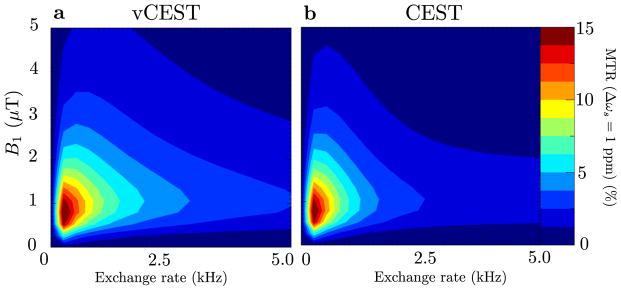
Given the chosen model parameters to simulate cartilage, surface plots of the hydroxyl MTR signals suggest that the optimal peak amplitude is approximately 1μT for CEST and 1μT/ppm for vCEST (Fig. 2). Note that for slow exchange, it is not apparent that vCEST has a sensitivity advantage over CEST, but for hydroxyls in the intermediate to fast exchange range (kex > 1000Hz), vCEST MTRdiff is greater than CEST MTRasym by roughly a factor of 2 and for kex = 1000Hz, vCEST MTRdiff is greater than 1μT CEST MTRasym by 29% and 3.5μT CEST MTRasym by 380%.
Figure 2.
MTR(Δωs = 1ppm) for vCEST (a) and CEST (b) sequences by numerically solving the Bloch equations from simulation 1.
Simulation 2
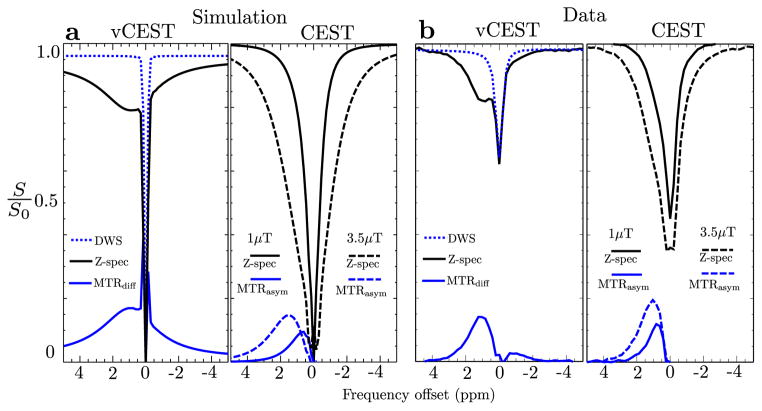
Figure 3a,b,c show simulated vCEST z-spectra, DWS, and MTRdiff curves with and without ΔB0 shifts of ±0.2 ppm, and the corresponding CEST (Fig. 3d) spectra. The vCEST simulation without ΔB0 shift (Fig. 3a) shows the flat shape of the DWS for Δω > ±0.5 ppm, while the MTRdiff curve is broad and centered at 1 ppm. When a ΔB0 shift is present, the DWS flattens at larger offset frequencies. Importantly, though the DWS curve is not flat at 1 ppm for ±ΔB0 shifts both towards and away from 1 ppm, subtraction of the z-spectrum still produces an MTRdiff curve similar to the curve produced with ΔB0 = 0.
Figure 3.
Z-spectra, DWS, and MTR curves by numerically solving the Bloch equations from simulation 2 for vCEST without B0 shift (a), with negative shift (b), with positive shift (c)and CEST at 1 and 3.5μT (d). Simulation parameters assumed cartilage tissue relaxivity and a 200 mM glycogen solute concentration.
Since B0 correction in CEST does not modulate the z-spectrum shape, correction results in identical z-spectra. At 1 ppm MTRdiff = 6.2% for vCEST and MTRasym = 4.2% and 1.4% for 1μT and 3.5μT CEST, respectively. Peak values for the vCEST and 1μT CEST curves both occur at 1 ppm, which is the chemical shift set by the simulation. However, the 3.5μT CEST MTRasym curve peaks at 2.1 ppm with a value of 4.2%.
Simulation 3
Figure 4a shows a simulation of 200mM glycogen. In the simulation of the aqueous environment, the vCEST curve peaks at 1 ppm at a value MTRdiff = 26%; the low-amplitude CEST peak is shifted up-field at 0.75 ppm with a value MTRasym = 13%; and the high-amplitude CEST peak is positioned down-field at 1.7 ppm with a value MTRasym = 18%. At 1 ppm, MTRasym = 12% and 13%, for low-amplitude and high-amplitude CEST, respectively.
Figure 4.
(a) Z-spectra, DWS, and MTR curves from simulation 3 for vCEST and CEST. Simulation parameters assumed relaxivity found in aqueous solution and 200 mM glycogen concentration. (b) Measured curves for 200 mM glycogen aqueous phantom.
Phantoms
Aqueous glycogen and glucose
Figure 4b shows representative curves for both CEST and vCEST for a single voxel in the 200 mM glycogen phantom. The vCEST z-spectrum is markedly different than the CEST spectra and clearly shows the glycogen resonance at 1ppm. Its shape is comparable to the vCEST simulation in Figure 4a suggesting that the DWS was indeed minimized by the saturation scheme. The vCEST MTRdiff curve is centered between 1.0 and 1.25 ppm, has a width that overlaps the water peak and AUC [MTRdiff (0.5–1.5)] = 11.6 %·ppm. Low-amplitude CEST MTRasym is centered between 0.65 – 0.85 ppm (slightly up-field from where the hydroxyl resonance is expected at 1 ppm) and AUC [MTRasym] = 8.9 %·ppm. High-amplitude CEST MTRasym is centered between 0.8 – 1.2 ppm and AUC [MTRasym] = 18 %·ppm.
A colormap of AUC [MTRdiff,asym] values for all phantoms is shown in Figure 5. Mean and standard deviations are shown in table 1 as well as the Pearson correlation coefficient for linear relationship with concentration. The magnitude of the glucose signal is highest for the high-amplitude CEST, but a linear relationship is lost at high concentrations. For example, though the correlation coefficient is large for the glucose phantom using high-amplitude CEST (R = 0.959), a doubling of concentration from 100 mM to 200 mM does not lead to a proportional increase in AUC [MTRasym] (21.2 to 32.1 %·ppm). Conversely, for both low-amplitude CEST and vCEST, doubling the concentration leads to a proportional increase in signal within measurement errors.
Figure 5.
Parameter maps of AUC[MTRdiff,asym(0.5–1.5ppm)] for glycogen, glucose, and BSA phantoms. For each set starting in the top-right and going clockwise, concentrations are 200 mM, 100 mM, 50 mM, 20 mM with 0 mM in the center.
Table 1.
AUC MTRdiff,asym(0.5–1.5 ppm) measurements for all phantoms
| AUC MTRdiff,asym(0.5–1.5 ppm)(%·ppm) ± SD | ||||
|---|---|---|---|---|
| Solute | Concentration (mM) | vCEST | Low-amp CEST | High-amp CEST |
| Glycogen | 0 | −1.6 ± 1.2 | −1.1 ± 0.4 | −2.8 ± 0.8 |
| 20 | 0.5 ± 1.0 | 0.15 ± 0.4 | 1.7 ± 0.9 | |
| 50 | 2.2 ± 1.0 | 2.3 ± 0.5 | 4.9 ± 0.8 | |
| 100 | 6.4 ± 0.8 | 5.0 ± 0.5 | 10.6 ± 1.0 | |
| 200 | 11.6 ± 0.8 | 8.9 ± 0.7 | 18.0 ± 1.3 | |
| Correlation | 0.994 | 0.991 | 0.985 | |
|
| ||||
| Glucose | 0 | −1.6 ± 1.2 | −1.1 ± 0.4 | −2.9 ± 0.8 |
| 20 | 1.4 ± 1.5 | 1.93 ± 0.5 | 6.3 ± 0.8 | |
| 50 | 5.0 ± 2.1 | 5.3 ± 1.1 | 14.4 ± 1.7 | |
| 100 | 13.4 ± 1.0 | 8.9 ± 0.8 | 21.2 ± 1.6 | |
| 200 | 30.5 ± 1.8 | 21.3 ± 1.4 | 32.1 ± 2.0 | |
| Correlation | 0.999 | 0.996 | 0.959 | |
|
| ||||
| Glycogen BSA | 0 | 2.7 ± 0.8 | 0.4 ± 0.3 | 8.6 ± 0.5 |
| 20 | 3.8 ± 1.1 | 0.5 ± 0.7 | 9.8 ± 1.1 | |
| 50 | 3.6 ± 0.6 | 1.0 ± 0.3 | 9.9 ± 0.4 | |
| 100 | 6.6 ± 1.2 | 1.7 ± 0.3 | 10.6 ± 0.5 | |
| 200 | 10.1 ± 1.2 | 6.0 ± 1.0 | 14.9 ± 1.0 | |
| Correlation | 0.986 | 0.965 | 0.969 | |
Aqueous glycogen with BSA
Average AUC [MTRdiff,asym(0.5–1.5)] is shown in Table 1. Notice that when glycogen concentration is zero, all AUC [MTRdiff,asym] values are positive. For CEST asymmetry, this is an artifact of the analysis technique (though there may be some amide signal contribution), but for vCEST, the non-zero value suggests the amine/amide curve overlaps the location of a hydroxyl curve. The AUC [MTRdiff,asym(2.0–3.0)] values for each phantom (not shown) are equal within measurement error, suggesting that the hydroxyl signal is not encroaching on the amine/amide signal.
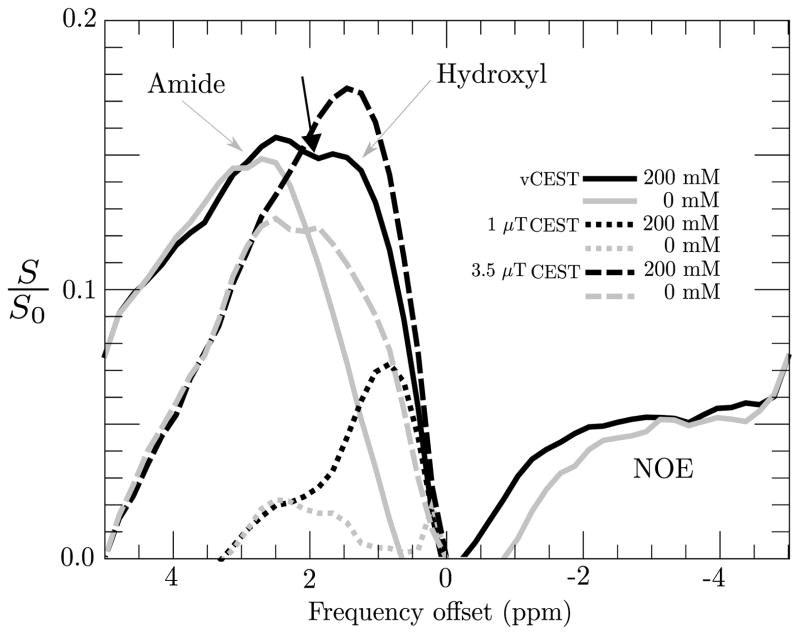
Figure 6 shows plots of vCEST MTRdiff and CEST MTRasym curves for aqueous phantoms of glycogen with 10% BSA. In the phantom without glycogen, a clear amine/amide signal is observed peaking at 2.5 ppm for vCEST (gray, solid), CEST at 1uT (gray, small dashes), and CEST at 3uT (gray, large dashes). For glycogen at the highest concentration of 200 mM (black curves), the hydroxyl peak occurs at 0.8 ppm for low-amplitude CEST (black, small dashes) and 1.5 ppm for high-amplitude CEST (black, large dashes) and vCEST (black, solid). There is a dip in the vCEST MTRdiff curve (black arrow) at 2 ppm, highlighting the fact that the MTRdiff curves consist of multiple CEST solute components, hydroxyls, amines, and amides. High-amplitude CEST shows one broad peak without hydroxyl/amide differentiation, whereas low-amplitude CEST and vCEST show two distinct resonances. The concentration of glycogen has no effect on the measured amide signal for any of the sequences.
Figure 6.
MTRdiff,asym curves for glycogen/BSA phantoms. vCEST (solid), Low-amplitude CEST (dotted), high-amplitude CEST (dashed). Glycogen concentrations: 200 mM (black), 0 mM (gray).
Also observed in figure 6 is a broad component of the spectrum that is up-field from water. In the absence of semi-solid macromolecules and bound water, it is presumed that this signal is due to NOE.
In vivo
Two axial slices with CEST-derived MTRasym, vCEST-derived MTRdiff, T1, T2, B1, and B0 maps are shown in Figure 7 along with anatomical images for positional reference. The cartilage transplant located in the trochlear ridge is in the inferior slice (Fig. 7a) denoted by the white arrowheads. A lesion located in the patellar cartilage is denoted by the yellow arrowheads in the superior slice (Fig. 7b). ROIs are drawn on the anatomical images. Mean and standard deviations for vCEST, CEST, T1 and T2 mapping are listed in Table 2.
Figure 7.
Parameter maps of patellar-femoral cartilage in a patient with a a patellar cartilage lesion (a) femoral cartilage transplant (b). ROIs are shown with green outline in the axial anatomic images. White arrowheads: location of the cartilage transplant. Yellow arrowheads: patellar lesion. White arrows: region of large negative B0 shift.
Table 2.
AUC MTRdiff,asym(0.5–1.5 ppm) measurements for ROIs in the knee cartilage
| AUC MTRdiff,asym(0.5–1.5 ppm)(%·ppm) ± SD
| |||||
|---|---|---|---|---|---|
| Slice | ROI | vCEST | CEST | T1 (ms) | T2 (ms) |
| Fig. 7a | Transplant | 1.78 ± 3.2 | −1.4 ± 2.7 | 1015 ± 249 | 82 ± 26 |
| Femoral | 2.6 ± 1.5 | −1.1 ± 0.8 | 1308 ± 161 | 57 ± 24 | |
| Patellar | 5.2 ± 2.5 | −2.3 ± 1.3 | 591 ± 94 | 50 ± 7 | |
|
| |||||
| Fig. 7b | Lesion | 4.6 ± 2.3 | 1.1 ± 2.0 | 1013 ± 93 | 54 ± 7 |
| Femoral | 2.7 ± 1.8 | −1.1 ± 1.3 | 1068 ± 132 | 44 ± 9 | |
| Patellar | 1.6 ± 1.1 | −0.4 ± 0.8 | 1042 ± 183 | 44 ± 10 | |
Mean CEST AUC[MTRasym]in all ROIs is zero or below within measurement error. Mean vCEST AUC[MTRdiff] is positive for all regions, though the transplant is heterogenous with a standard deviation (3.2 %·ppm) larger than the mean (1.8 %·ppm). In the superior slice (Fig. 7b) there is a prominent negative B0 shift at the lateral edges of the patellar cartilage (white arrows). As expected, this shift does not have much of an effect on the CEST MTRasym, but is large enough to artificially reduce the vCEST MTRdiff signal.
Discussion
Detecting exchangeable hydroxyl protons in vivo at clinical field strengths is difficult. When considering simpler systems with one or two solutes in aqueous solution, saturation transfer based CEST MRI is able to detect and quantify the effects arising from these spin systems. However, in real systems, which include numerous solutes, multiple moieties of exchangeable protons, a bound water pool, and NOE, CEST MRI does not often provide a mechanism to isolate hydroxyl moieties. In addition, since hydroxyl exchange is fast (>1 kHz), and close to the water resonance (1 ppm) (the fast-exchange regime), resolving a separation between hydroxyl and water peaks pose further challenges to conventional CEST MRI. Rather than using higher field strengths to better isolate CEST effects from hydroxyl protons, we focused on developing a novel saturation scheme that can be operated at clinical field strengths to more clearly resolve CEST effects from fast exchanging species by minimizing the contribution from the direct water saturation. That is, we developed a new tool, termed vCEST (variable power CEST) which can remove the water peak from the z-spectrum by utilizing a saturation scheme that flattens the DWS across a range of offsets.
Simulated and acquired z-spectra in Figures 3 and 4 show that subtracting a known DWS curve from the vCEST z-spectrum can produce a sensitive measure of faster exchanging protons found on carbohydrates. However, this relies on two important assumptions: (1) the DWS function is known (or can be calculated) and (2) it is flat, meaning a complicated deconvolution reduces to a simple subtraction. In the vCEST scheme, both requirements were met by generating a flattened DWS spectrum by varying the irradiation power proportionally with offset frequency and measuring (or assuming) T1 and T2 values. In addition, B0 maps were used to correct deviations from flatness brought about by inhomogeneities and imperfect shimming.
The newly developed vCEST method utilizes a saturation power variation as a function of offset frequency. Though optimized for a single frequency of interest (in this case hydroxyl), a benefit of vCEST is that additional solutes at higher offsets (such as amine or amide) may be saturated near to their optimal power. In terms of detecting hydroxyl moieties in various environments (aqueous, presence of prominent amide signal), the vCEST scheme can offer information that is unique to a single power CEST scan thereby providing a reduced scan time. In the aqueous environment with a single solute (Figures 4 and 5) we see that high-amplitude CEST is superior to low-amplitude CEST for detecting hydroxyls. In this case, there is no MT and thus utilizing the CEST acquisition at higher irradiation power outweighs the broadening of the DWS. When compared to the vCEST scheme, the MTRdiff provides information on hydroxyl exchange similar to that of a high-amplitude CEST acquisition. In the more complicated, but still aqueous, environment with confounding/competing solutes (additional BSA solute), Figure 6 shows that low-amplitude CEST is better to resolve the signals produced by the two solute proton pools. High-amplitude CEST leads to higher AUC[MTRasym] (Table 1) for each solute, but the broadened spectral lineshape makes independent detection of two solutes less straightforward. In contrast, the vCEST scheme shows AUC[MTRdiff] values on par with high-amplitude CEST (Table 1), but at high glycogen concentrations, an appreciable inflection is seen at 2ppm indicating the potential to resolve both contributions to exchange.
Exchangeable hydroxyl protons are found on many biological molecules and metabolites of interest such as glycogen, glucose, GAG, and myoinositol. Detecting these molecules has applications in cartilage injury, osteoarthritis, metabolic disease, liver disease, cancer, and neuro-psychiatric disorders. In this study we chose to use knee cartilage imaging as a demonstration of vCEST feasibility in vivo. In normal articular cartilage, GAG content is assumed to be 50 – 70 mg/L of tissue water [10, 60] or approximately 100 – 150 mM concentration. GAG is a chain of linked saccharides with three –OH per unit, similar to glycogen which consists of a glucose chain with four –OH per unit. Given the similarity in structure, it was hypothesized that endogenous GAG can be a measurable CEST agent in cartilage. The first study of CEST imaging in cartilage at 3 T [10] defined the CEST ratio as CESTR = [S(−1ppm) −S(+1ppm)]/S(−1ppm) and reported values of CESTR = 35% in femoral cartilage and 20% in patellar. However, without B0 correction and normalization using an unsaturated image, it is difficult to compare these numbers with other experiments. A later study at both 3 T and 7 T found that with B0 correction, MTRasym at 1ppm was negligible at 3 T and 6% at 7 T [12]. However, a recent study of lumbar intervertebral discs shows MTRasym of 2 – 5% at 3 T in various regions of the disc suggesting that GAG-CEST imaging is feasible on clinical scanners. As in the Singh et al. study [12], our CEST scheme produced negligible MTRasym in the cartilage tissue. However, using vCEST MTRdiff, we measured values from approximately 2 – 5 % in cartilage, comparable to the results in the 7 T study. The mean vCEST measurement in the transplant tissue (1.8 %·ppm) was less than the femoral and patellar regions in the same slice (2.6 and 5.2 %·ppm), however the mean value in the patellar lesion on the superior slice (Fig. 7b) (4.6 %·ppm) was larger than adjacent femoral and patellar cartilage, challenging the expectation that it should be lower due to decreased GAG in unhealthy cartilage, which is considered a precursor to gross changes in osteoarthritis [61]. From the T2-weighted image in fig. 7b, the hypointense signal suggests this is a full-thickness defect. The higher vCEST signal may be due to the presence of CEST solutes in the fluid filling the space. However, the calculation of vCEST MTR was not optimal for fluid analysis because of the chosen T2 estimation, therefore this conclusion is purely speculative.
Figure 6 illustrates the CEST and vCEST MTR curves for the glycogen-BSA aqueous phantoms. As shown in Jones et al. [14], a CEST spectrum of 10% BSA has a NOE contribution up-field at 7 T of similar magnitude as the down-field amide and amine signals, resulting in MTRasym curves that are a composite of NOE and CEST effects. Jones et al. [14] used a 1μT pulsed CEST EPI sequence, and observed spectral separation between the CEST peaks and DWS. The DWS was fit to a Lorentzian and an MTRdiff spectrum was calculated, similar to what was performed here. This analysis was aided by greater spectral separation at 7 T compared to 3 T and may not provide adequate detection of multiple solutes at 3 T.
Varying saturation pulses within sequences is not entirely new. Variable delay [14, 62], and variable angle [4, 63, 64] schemes are being used to minimize or cancel the effects of DWS and MT on the z-spectrum. These techniques are useful for quantifying physical characteristics of amide and NOE exchange and probing the exact physical mechanisms by which they occur. However, the existing literature does not highlight the ability of these techniques to study protons in the intermediate/fast exchange regimes or at lower field strengths.
The vCEST scheme as described above assumes minimal MT contribution near the offset range of hydroxyl solutes. For in vivo cartilage imaging, this may not be a good assumption. In the presence of MT the DWS spectrum may not be flat and therefore any modeled curve used as a baseline must include an MT pool (see supporting online material for an additional experiment with glucose and agar phantoms that shows the behavior of vCEST in the presence of MT). One possible solution is to perform quantitative MT imaging (qMT) [65–68] to derive parameters specific to the MT component. These parameters can then be used to create a combined DWS/MT baseline curve from which the vCEST z-spectrum can be subtracted. An analysis methodology similar to this has been proposed by Zaiss et al. [69] by utilizing T1ρ imaging to remove the MT component, however, this method has not been tested extensively in vivo, and warrants further investigation. Additonally, adapting the vCEST scheme to amide, amine, or NOE detection in tissue will require analysis methods where MT is non-negligible.
Simulation of vCEST z-spectra indicate that the technique should be extremely sensitive to B0 inhomogeneities (Fig. 3). This sensitivity is partly corrected by modeling the DWS including B0 shift. However, in the same manner that the variable power modulates the water peak, it will also modulate any other proton resonances in the system. Therefore, applying B0 shifts to correct the modeled DWS is insufficient to completely cancel the effect of field inhomogeneity. An example is in Figure 7b where a region with extreme negative B0 shift, results in a loss of signal artifact in the vCEST measurement (white arrows).
B1 inhomogeneity was input into the DWS model, but the effect on saturation efficiency of the CEST solutes was not corrected. Any B1 inefficiency is not applied equally across the z-spectrum but is actually magnified at high and minimized at low offsets, leading to modulation of peak shapes. Additionally, the non-constant B1 amplitude will cause the vCEST signal to be offset-dependent. This may make using an AUC metric problematic. It may be prudent to explore a model that corrects for both B1 inhomogeneity and offset-dependent modulation prior to MTRdiff calculation.
Another limitation of the vCEST scheme is the reliance on multiple quantitative MRI datasets. Four parameters must be input to model the DWS: T1, T2, B0, and B1. More exactly, T1 and T2 should be relaxation times for an isolated free water pool (i.e. T1f and T2f) that can be different from the averaged multi-component relaxation measured by standard multi-flip angle and multi- echo time imaging. An assumption is made for cartilage imaging that R1f · T2f = 0.024 and T1f = T1 [53], reducing the required parameter maps to three. The quantitative MRI protocol for the knee added 30 minutes to a clinical imaging exam already more than 30 minutes in duration. It is possible to explore the use of higher EPI or turbo factors as well as k-space sharing techniques such as Keyhole [70] to reduce scan time, but regardless, the dependence on multiple quantitative maps may prohibit the use of vCEST for some applications.
The vCEST scheme can characterize down-field solute and up-field NOE contributions simultaneously, which is a result of subtracting the DWS instead of using asymmetry. But if T1, T2, B0, and B1, are measured, why not just generate a modeled DWS and subtract from it a typical CEST spectrum? An advantage vCEST has over a typical CEST experiment is the ability to use optimized or nearly-optimized B1 saturation amplitude for multiple solutes of interest in a single z-spectrum. Low-amplitude is favorable for hydroxyls with low chemical shift and fast exchange, while amide protons with larger chemical shift and slow exchange require more saturation power in order to produce significant water signal attenuation. Future work includes analyzing the sensitivity of our model to T1/T2 parameters and perhaps identifying a subtraction scheme that does not require relaxation or at least can use valid assumptions without paying a penalty in accuracy.
Conclusion
In this study we introduced a new variation of the CEST technique that has the potential to detect hydroxyl solutes at clinical field strengths in tissue. By applying a saturation amplitude scheme that varies as a linear function of frequency offset, we showed that the DWS component of the z-spectrum can be flattened and then subtracted, resulting in increased sensitivity to hydroxyl moieties when compared to asymmetry analysis. This results in robust detection of hydroxyl moieties in the presence of multiple solutes with overlapping resonances. We showed that in vivo imaging can be performed in a clinically feasible scan time and results in contrast between normal appearing cartilage and transplant tissue that is not detected in CEST.
S1 Z-spectra and MTRdiff,asym plots for glucose/agar phantoms.
Supplementary Material
Acknowledgments
The authors thank Dr. David Flanigan for his assistance with in vivo imaging. This research was funded by NIH/NIBIB and DOD research grants.
Contributor Information
Daniel James Clark, Department of Radiology, The Ohio State University, Columbus, OH, USA. Wright Center of Innovation, The Ohio State University, Columbus, OH, USA. Department of Biomedical Engineering, The Ohio State University, Columbus, OH, USA
Alex K. Smith, Institute of Imaging Science, Vanderbilt University, Nashville, TN, USA. Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, USA
Richard D. Dortch, Department of Radiology and Radiological Sciences, Vanderbilt University, Nashville, TN, USA. Institute of Imaging Science, Vanderbilt University, Nashville, TN, USA. Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, USA
Michael V. Knopp, Department of Radiology, The Ohio State University, Columbus, OH, USA. Wright Center of Innovation, The Ohio State University, Columbus, OH, USA
Seth A. Smith, Department of Radiology and Radiological Sciences, Vanderbilt University, Nashville, TN, USA. Institute of Imaging Science, Vanderbilt University, Nashville, TN, USA. Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, USA
References
- 1.Ward KM, Aletras AH, Balaban RS. A New Class of Contrast Agents for MRI Based on Proton Chemical Exchange Dependent Saturation Transfer (CEST) Journal of Magnetic Resonance. 2000;143(1):79–87. doi: 10.1006/jmre.1999.1956. [DOI] [PubMed] [Google Scholar]
- 2.van Zijl PC, Zhou J, Mori N, Payen JF, Wilson D, Mori S. Mechanism of magnetization transfer during on-resonance water saturation. A new approach to detect mobile proteins, peptides, and lipids. Magn Reson Med. 2003;49(3):440–449. doi: 10.1002/mrm.10398. [DOI] [PubMed] [Google Scholar]
- 3.Zhou J, Wilson DA, Sun PZ, Klaus JA, van Zijl PC. Quantitative description of proton exchange processes between water and endogenous and exogenous agents for WEX, CEST, and APT experiments. Magn Reson Med. 2004;51(5):945–952. doi: 10.1002/mrm.20048. [DOI] [PubMed] [Google Scholar]
- 4.Zu Z, Janve VA, Li K, Does MD, Gore JC, Gochberg DF. Multi-angle ratiometric approach to measure chemical exchange in amide proton transfer imaging. Magn Reson Med. 2012;68(3):711–719. doi: 10.1002/mrm.23276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zijl PCMv, Jones CK, Ren J, Malloy CR, Sherry AD. MRI detection of glycogen in vivo by using chemical exchange saturation transfer imaging (glycoCEST) PNAS. 2007;104(11):4359–4364. doi: 10.1073/pnas.0700281104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ren J, Trokowski R, Zhang S, Malloy CR, Sherry AD. Imaging the tissue distribution of glucose in livers using a PARACEST sensor. Magn Reson Med. 2008;60(5):1047–1055. doi: 10.1002/mrm.21722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jin T, Autio J, Obata T, Kim SG. Spin-locking versus chemical exchange saturation transfer MRI for investigating chemical exchange process between water and labile metabolite protons. Magn Reson Med. 2011;65(5):1448–1460. doi: 10.1002/mrm.22721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jin T, Mehrens H, Hendrich KS, Kim SG. Mapping brain glucose uptake with chemical exchange-sensitive spin-lock magnetic resonance imaging. J Cereb Blood Flow Metab. 2014 doi: 10.1038/jcbfm.2014.97.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rivlin M, Tsarfaty I, Navon G. Functional molecular imaging of tumors by chemical exchange saturation transfer MRI of 3-O-Methyl-D-glucose. Magn Reson Med. 2014;72(5):1375–1380. doi: 10.1002/mrm.25467. [DOI] [PubMed] [Google Scholar]
- 10.Ling W, Regatte RR, Navon G, Jerschow A. Assessment of glycosaminoglycan concentration in vivo by chemical exchange-dependent saturation transfer (gagCEST) PNAS. 2008;105(7):2266–2270. doi: 10.1073/pnas.0707666105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schmitt B, Zbyn S, Stelzeneder D, Jellus V, Paul D, Lauer L, Bachert P, Trattnig S. Cartilage Quality Assessment by Using Glycosaminoglycan Chemical Exchange Saturation Transfer and 23na MR Imaging at 7 T. Radiology. 2011;260(1):257–264. doi: 10.1148/radiol.11101841. [DOI] [PubMed] [Google Scholar]
- 12.Singh A, Haris M, Cai K, Kassey VB, Kogan F, Reddy D, Hariharan H, Reddy R. Chemical exchange saturation transfer magnetic resonance imaging of human knee cartilage at 3 T and 7 T. Magn Reson Med. 2012;68(2):588–594. doi: 10.1002/mrm.23250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kogan F, Singh A, Cai K, Haris M, Hariharan H, Reddy R. Investigation of chemical exchange at intermediate exchange rates using a combination of chemical exchange saturation transfer (CEST) and spin-locking methods (CESTrho) Magn Reson Med. 2012;68(1):107–119. doi: 10.1002/mrm.23213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jones CK, Huang A, Xu J, et al. Nuclear Overhauser enhancement (NOE) imaging in the human brain at 7T. NeuroImage. 2013;77:114–124. doi: 10.1016/j.neuroimage.2013.03.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xu J, Yadav NN, Bar-Shir A, Jones CK, Chan KWY, Zhang J, Walczak P, McMahon MT, van Zijl PCM. Variable delay multi-pulse train for fast chemical exchange saturation transfer and relayed-nuclear overhauser enhancement MRI. Magn Reson Med. 2014;71(5):1798–1812. doi: 10.1002/mrm.24850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Haris M, Nanga RPR, Singh A, Cai K, Kogan F, Hariharan H, Reddy R. Exchange rates of creatine kinase metabolites: feasibility of imaging creatine by chemical exchange saturation transfer MRI. NMR Biomed. 2012;25(11):1305–1309. doi: 10.1002/nbm.2792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kogan F, Haris M, Singh A, Cai K, Debrosse C, Nanga RPR, Hariharan H, Reddy R. Method for high-resolution imaging of creatine in vivo using chemical exchange saturation transfer. Magn Reson Med. 2014;71(1):164–172. doi: 10.1002/mrm.24641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kogan F, Haris M, Debrosse C, Singh A, Nanga RP, Cai K, Hariharan H, Reddy R. In vivo chemical exchange saturation transfer imaging of creatine (CrCEST) in skeletal muscle at 3t. J Magn Reson Imaging. 2014;40(3):596–602. doi: 10.1002/jmri.24412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cai K, Singh A, Poptani H, Li W, Yang S, Lu Y, Hariharan H, Zhou XJ, Reddy R. CEST signal at 2ppm (CEST@2ppm) from Z-spectral fitting correlates with creatine distribution in brain tumor. NMR Biomed. 2015;28(1):1–8. doi: 10.1002/nbm.3216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cai K, Singh A, Roalf DR, Nanga RPR, Haris M, Hariharan H, Gur R, Reddy R. Mapping glutamate in subcortical brain structures using high-resolution GluCEST MRI. NMR Biomed. 2013;26(10):1278–1284. doi: 10.1002/nbm.2949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kogan F, Singh A, Debrosse C, Haris M, Cai K, Nanga RP, Elliott M, Hariharan H, Reddy R. Imaging of glutamate in the spinal cord using GluCEST. Neuroimage. 2013;77:262–267. doi: 10.1016/j.neuroimage.2013.03.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Haris M, Singh A, Cai K, Nath K, Crescenzi R, Kogan F, Hariharan H, Reddy R. MICEST: a potential tool for non-invasive detection of molecular changes in Alzheimer’s disease. J Neurosci Methods. 2013;212(1):87–93. doi: 10.1016/j.jneumeth.2012.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Haris M, Cai K, Singh A, Hariharan H, Reddy R. In vivo mapping of brain myo-inositol. Neuroimage. 2011;54(3):2079–2085. doi: 10.1016/j.neuroimage.2010.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sun PZ, Murata Y, Lu J, Wang X, Lo EH, Sorensen AG. Relaxation-compensated fast multislice amide proton transfer (APT) imaging of acute ischemic stroke. Magn Reson Med. 2008;59(5):1175–1182. doi: 10.1002/mrm.21591. [DOI] [PubMed] [Google Scholar]
- 25.Tietze A, Blicher J, Mikkelsen IK, stergaard L, Strother MK, Smith SA, Donahue MJ. Assessment of ischemic penumbra in patients with hyperacute stroke using amide proton transfer (APT) chemical exchange saturation transfer (CEST) MRI. NMR Biomed. 2014;27(2):163–174. doi: 10.1002/nbm.3048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zaiss M, Xu J, Goerke S, Khan IS, Singer RJ, Gore JC, Gochberg DF, Bachert P. Inverse Z-spectrum analysis for spillover-, MT-, and T1 -corrected steady-state pulsed CEST-MRI–application to pH-weighted MRI of acute stroke. NMR Biomed. 2014;27(3):240–252. doi: 10.1002/nbm.3054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tee YK, Harston GWJ, Blockley N, et al. Comparing different analysis methods for quantifying the MRI amide proton transfer (APT) effect in hyperacute stroke patients. NMR Biomed. 2014;27(9):1019–1029. doi: 10.1002/nbm.3147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li H, Zu Z, Zaiss M, Khan IS, Singer RJ, Gochberg DF, Bachert P, Gore JC, Xu J. Imaging of amide proton transfer and nuclear Overhauser enhancement in ischemic stroke with corrections for competing effects. NMR Biomed. 2015;28(2):200–209. doi: 10.1002/nbm.3243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhou J, Lal B, Wilson DA, Laterra J, van Zijl PCM. Amide proton transfer (APT) contrast for imaging of brain tumors. Magn Reson Med. 2003;50(6):1120–1126. doi: 10.1002/mrm.10651. [DOI] [PubMed] [Google Scholar]
- 30.Zhou J, Blakeley JO, Hua J, Kim M, Laterra J, Pomper MG, van Zijl PC. Practical data acquisition method for human brain tumor amide proton transfer (APT) imaging. Magn Reson Med. 2008;60(4):842–849. doi: 10.1002/mrm.21712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jones CK, Schlosser MJ, van Zijl PC, Pomper MG, Golay X, Zhou J. Amide proton transfer imaging of human brain tumors at 3t. Magn Reson Med. 2006;56(3):585–592. doi: 10.1002/mrm.20989. [DOI] [PubMed] [Google Scholar]
- 32.Jia G, Abaza R, Williams JD, et al. Amide proton transfer MR imaging of prostate cancer: a preliminary study. J Magn Reson Imaging. 2011;33(3):647–654. doi: 10.1002/jmri.22480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dula AN, Arlinghaus LR, Dortch RD, Dewey BE, Whisenant JG, Ayers GD, Yankeelov TE, Smith SA. Amide proton transfer imaging of the breast at 3 T: Establishing reproducibility and possible feasibility assessing chemotherapy response. Magn Reson Med. 2013;70(1):216–224. doi: 10.1002/mrm.24450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Xu J, Zaiss M, Zu Z, Li H, Xie J, Gochberg DF, Bachert P, Gore JC. On the origins of chemical exchange saturation transfer (CEST) contrast in tumors at 9.4T. NMR Biomed. 2014;27(4):406–416. doi: 10.1002/nbm.3075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jia G, Takayama Y, Flanigan DC, et al. Quantitative assessment of mobile protein levels in human knee synovial fluid: feasibility of chemical exchange saturation transfer (proteinCEST) MRI of osteoarthritis. Magnetic Resonance Imaging. 2011;29(3):335–341. doi: 10.1016/j.mri.2010.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dula AN, Asche EM, Landman BA, Welch EB, Pawate S, Sriram S, Gore JC, Smith SA. Development of chemical exchange saturation transfer at 7 T. Magn Reson Med. 2011;66(3):831–838. doi: 10.1002/mrm.22862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Danek AN, Bryant RG. Magnetic relaxation contrast agents in magnetization transfer imaging. Invest Radiol. 1998;33(11):773–778. doi: 10.1097/00004424-199811000-00001. [DOI] [PubMed] [Google Scholar]
- 38.Wolff SD, Balaban RS. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn Reson Med. 1989;10(1):135–144. doi: 10.1002/mrm.1910100113. [DOI] [PubMed] [Google Scholar]
- 39.Anderson WA, Freeman R. Influence of a Second Radiofrequency Field on HighResolution Nuclear Magnetic Resonance Spectra. The Journal of Chemical Physics. 1962;37(1):85–103. doi: 10.1063/1.1732980. [DOI] [Google Scholar]
- 40.McConnell HM. Reaction Rates by Nuclear Magnetic Resonance. The Journal of Chemical Physics. 1958;28(3):430–431. doi: 10.1063/1.1744152. [DOI] [Google Scholar]
- 41.Baguet E, Roby C. Off-Resonance Irradiation Effect in Steady-State NMR Saturation Transfer. Journal of Magnetic Resonance. 1997;128(2):149–160. doi: 10.1006/jmre.1997.1230. [DOI] [PubMed] [Google Scholar]
- 42.Hua J, Jones CK, Blakeley J, Smith SA, van Zijl PC, Zhou J. Quantitative description of the asymmetry in magnetization transfer effects around the water resonance in the human brain. Magn Reson Med. 2007;58(4):786–793. doi: 10.1002/mrm.21387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29(6):759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- 44.Morrison C, Stanisz G, Henkelman RM. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-Lorentzian lineshape and dipolar reservoir. J Magn Reson B. 1995;108(2):103–113. doi: 10.1006/jmrb.1995.1111. [DOI] [PubMed] [Google Scholar]
- 45.Sun PZ, Farrar CT, Sorensen AG. Correction for artifacts induced by B0 and B1 field inhomogeneities in pH-sensitive chemical exchange saturation transfer (CEST) imaging. Magnetic Resonance in Medicine. 2007;58(6):1207–1215. doi: 10.1002/mrm.21398. [DOI] [PubMed] [Google Scholar]
- 46.Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J Magn Reson. 2011;211(2):149–155. doi: 10.1016/j.jmr.2011.05.001. [DOI] [PubMed] [Google Scholar]
- 47.Desmond KL, Moosvi F, Stanisz GJ. Mapping of amide, amine, and aliphatic peaks in the CEST spectra of murine xenografts at 7 T. Magn Reson Med. 2014;71(5):1841–1853. doi: 10.1002/mrm.24822. [DOI] [PubMed] [Google Scholar]
- 48.Zhou J, Zijl PCv. Chemical exchange saturation transfer imaging and spectroscopy. Progress in Nuclear Magnetic Resonance Spectroscopy. 2006;48(2–3):109–136. doi: 10.1016/j.pnmrs.2006.01.001. [DOI] [PubMed] [Google Scholar]
- 49.McConnell HM, Thompson DD. Molecular Transfer of Nonequilibrium Nuclear Spin Magnetization. The Journal of Chemical Physics. 1959;31(1):85–88. doi: 10.1063/1.1730341. [DOI] [Google Scholar]
- 50.Portnoy S, Stanisz GJ. Modeling pulsed magnetization transfer. Magn Reson Med. 2007;58(1):144–155. doi: 10.1002/mrm.21244. [DOI] [PubMed] [Google Scholar]
- 51.Desmond KL, Stanisz GJ. Understanding quantitative pulsed CEST in the presence of MT. Magn Reson Med. 2012;67(4):979–990. doi: 10.1002/mrm.23074. [DOI] [PubMed] [Google Scholar]
- 52.Schmitt B, Zai M, Zhou J, Bachert P. Optimization of pulse train presaturation for CEST imaging in clinical scanners. Magn Reson Med. 2011;65(6):1620–1629. doi: 10.1002/mrm.22750. [DOI] [PubMed] [Google Scholar]
- 53.Stikov N, Keenan KE, Pauly JM, Smith RL, Dougherty RF, Gold GE. Cross-relaxation imaging of human articular cartilage. Magn Reson Med. 2011;66(3):725–734. doi: 10.1002/mrm.22865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zang LH, Rothman DL, Shulman RG. 1h NMR visibility of mammalian glycogen in solution. PNAS. 1990;87(5):1678–1680. doi: 10.1073/pnas.87.5.1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.McKenzie EC, Hinchcliff KW, Valberg SJ, Williamson KK, Payton ME, Davis MS. Assessment of alterations in triglyceride and glycogen concentrations in muscle tissue of Alaskan sled dogs during repetitive prolonged exercise. American Journal of Veterinary Research. 2008;69(8):1097–1103. doi: 10.2460/ajvr.69.8.1097. [DOI] [PubMed] [Google Scholar]
- 56.Rajanayagam V, Fabry ME, Gore JC. In vivo quantitation of water content in muscle tissues by NMR imaging. Magnetic Resonance Imaging. 1991;9(4):621–625. doi: 10.1016/0730-725X(91)90050-V. [DOI] [PubMed] [Google Scholar]
- 57.Bergmeyer HU. Methods of Enzymatic analysis. Elsevier; 2012. [Google Scholar]
- 58.Kim M, Gillen J, Landman BA, Zhou J, van Zijl PC. Water saturation shift referencing (WASSR) for chemical exchange saturation transfer (CEST) experiments. Magn Reson Med. 2009;61(6):1441–1450. doi: 10.1002/mrm.21873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sled JG, Pike GB. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn Reson Med. 2001;46(5):923–931. doi: 10.1002/mrm.1278. [DOI] [PubMed] [Google Scholar]
- 60.Gray ML, Burstein D, Kim YJ, Maroudas A. Magnetic resonance imaging of cartilage glycosaminoglycan: Basic principles, imaging technique, and clinical applications. J Orthop Res. 2008;26(3):281–291. doi: 10.1002/jor.20482. [DOI] [PubMed] [Google Scholar]
- 61.Malemud CJ. Changes in proteoglycans in osteoarthritis: biochemistry, ultrastructure and biosynthetic processing. J Rheumatol Suppl. 1991;27:60–62. [PubMed] [Google Scholar]
- 62.Yadav NN, Jones CK, Xu J, Bar-Shir A, Gilad AA, McMahon MT, van Zijl PCM. Detection of rapidly exchanging compounds using on-resonance frequency-labeled exchange (FLEX) transfer. Magn Reson Med. 2012;68(4):1048–1055. doi: 10.1002/mrm.24420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zu Z, Li K, Janve VA, Does MD, Gochberg DF. Optimizing pulsed-chemical exchange saturation transfer imaging sequences. Magn Reson Med. 2011;66(4):1100–1108. doi: 10.1002/mrm.22884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zu Z, Xu J, Li H, Chekmenev EY, Quarles CC, Does MD, Gore JC, Gochberg DF. Imaging amide proton transfer and nuclear overhauser enhancement using chemical exchange rotation transfer (CERT) Magn Reson Med. 2014;72(2):471–476. doi: 10.1002/mrm.24953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Smith AK, Dortch RD, Dethrage LM, Smith SA. Rapid, high-resolution quantitative magnetization transfer MRI of the human spinal cord. NeuroImage. 2014;95:106–116. doi: 10.1016/j.neuroimage.2014.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Yarnykh VL, Yuan C. Cross-relaxation imaging reveals detailed anatomy of white matter fiber tracts in the human brain. NeuroImage. 2004;23(1):409–424. doi: 10.1016/j.neuroimage.2004.04.029. [DOI] [PubMed] [Google Scholar]
- 67.Yarnykh VL. Pulsed Z-spectroscopic imaging of cross-relaxation parameters in tissues for human MRI: Theory and clinical applications. Magn Reson Med. 2002;47(5):929–939. doi: 10.1002/mrm.10120. [DOI] [PubMed] [Google Scholar]
- 68.Underhill HR, Yuan C, Yarnykh VL. Direct quantitative comparison between cross-relaxation imaging and diffusion tensor imaging of the human brain at 3.0T. NeuroImage. 2009;47(4):1568–1578. doi: 10.1016/j.neuroimage.2009.05.075. [DOI] [PubMed] [Google Scholar]
- 69.Zaiss M, Zu Z, Xu J, Schuenke P, Gochberg DF, Gore JC, Ladd ME, Bachert P. A combined analytical solution for chemical exchange saturation transfer and semi-solid magnetization transfer. NMR Biomed. 2015;28(2):217–230. doi: 10.1002/nbm.3237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Varma G, Lenkinski RE, Vinogradov E. Keyhole chemical exchange saturation transfer. Magn Reson Med. 2012;68(4):1228–1233. doi: 10.1002/mrm.23310. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.