Abstract
A flexible linker region between three fragments allows antibodies to adjust their binding sites to an antigen or receptor. Using Neutron Spin Echo Spectroscopy we observed fragment motion on a timescale of 7 ns with motional amplitudes of about 1 nm relative to each other. The mechanistic complexity of the linker region can be described by a spring model with Brownian motion of the fragments in a harmonic potential. Displacements, timescale, friction and force constant of the underlying dynamics are accessed. The force constant exhibits a similar strength to an entropic spring, with friction of the fragment matching the unbound state. The observed fast motions are fluctuations in pre-existing equilibrium configurations. The Brownian motion of domains in a harmonic potential is the appropriate model to examine functional hinge motions dependent on the structural topology and highlights the role of internal forces and friction to function.
Antibodies are large Y-shaped glycoproteins produced by the humoral immune system and are generically called immunoglobulins (Ig). They consist of three equal-sized fragments (see IgG1 in Fig. 1) connected by a flexible linker region: two antigen-binding fragments (Fab) and one constant fragment (Fc). Each Fab fragment has a constant region (C) attached to the linker region and a variable antigen-binding region (V) that accounts for the specificity of an Ig molecule to a target1. The Fc fragment imparts signalling and effector functions. The flexibility and fragment motion seem to be crucial to understand the functionality of antibodies. Therefore, over the years, an extensive amount of research has been performed in order to understand the structure and flexibility2,3,4,5,6,7. Specificity and constancy make antibodies attractive for use in immunotherapy. They have been used to develop new drugs targeting specific cells for inhibition/activation of cell processes, as antibody-dependent cellular cytotoxicity or phagocytosis1, and to deploy specific drugs by immunoliposomes8 or radiation therapy9.
Figure 1. Immunoglobulin G1 with Fc and two Fab fragments with the van der Waals surface in grey.
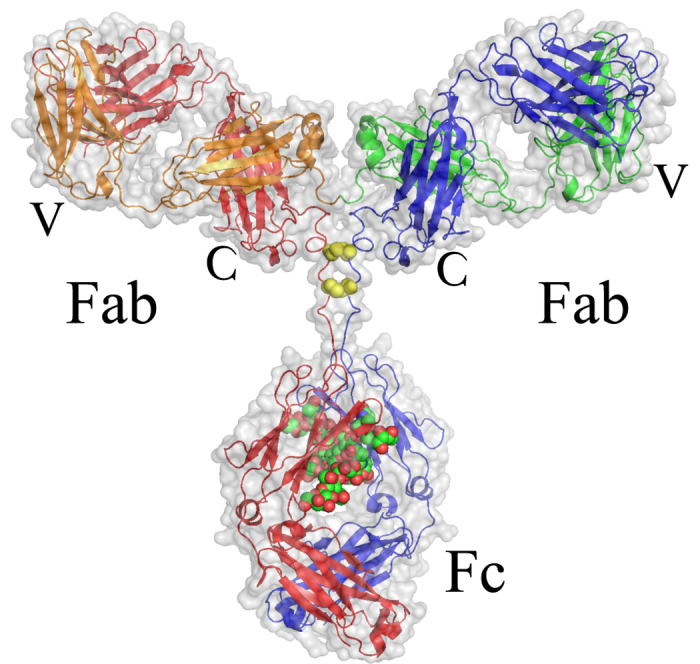
The Fc fragment is build from parts of the heavy chains (red and blue cartoon) and the glycans (red and green spheres) between the two heavy chains. Fab fragments are built from heavy and light chains (orange and green cartoon) with a hinge between the variable region (V) and the constant region (C) of the Fab fragment. The heavy chains are connected in the linker region by two disulfide bonds (yellow spheres). The structure displayed is based on the human IgG1 structure IgG-ALL.pdb of Padlan37. IgG-ALL is a composite model with the Fc fragment from 1FC2.pdb and the Fab fragment of 2IG2.pdb49,60. Details, as the flexible linker region, are modeled to display a complete structure including the linker region. Figures created with PyMOL (www.pymol.org).
Antibody fragments are built from four peptide chains joined together by disulphide bonds. Two heavy chains (Mw ~ 50 kDa), joined by disulphide bonds, form the Fc fragment from about half of their length. Two shorter light chains (Mw ~ 25 kDa) complement the other half of the heavy chains to build up the Fab fragments. The linker region is responsible for the high flexibility between the 3 fragments and allows Fab to bind to antigens of various shapes while the Fc fragment simultaneously can bind to a receptor or complement. The linker region has three components10. The core segment contains a CPPC amino acid motif connecting the heavy chains with several disulfide bonds between the cysteines (C) and proline pairs (PP) that make this motif rigid (IgG4 has sequence CPSC with serine (S)). The flexible upper and lower linker regions connect the Fab and the Fc fragments to the core, respectively. While the upper linker regions influence the Fab-Fab flexibility, the lower linker regions influence the Fab-Fc flexibility.
Variations in the Fc fragment distinguish the five major classes of immunoglobulins. Among those, IgG is the most abundant in serum, with four subclasses numbered according to their abundance. The subclasses differ in the length of the linker region and how many disulfide bonds link the chains11. IgG1, IgG2 and IgG4 with about 60%, 32% and 4% abundance, respectively, have a similar short linker region with two or four disulfide bonds. IgG3, with about 4% abundance, has a longer linker region with eleven disulfide bonds. IgG preparations from serum may contain monomeric and dimeric populations in dynamic equilibrium, where dimers may also have higher activity, e.g. for intracellular antigens12. IgG may be considered as a good general model for studying immunoglobulins, as it is also a model for the majority of immune drug developments.
Small-angle X-ray and neutron scattering (SAXS/SANS) are used to examine the global conformation of different species of antibodies in solution. Conformations depend on species, type and buffer solvent observed, with a high degree of variability2,3,4,13.
The dynamics of IgG antibodies are difficult to explore since most experimental methods are limited to conformationally averaged structures, like SAXS/SANS or with artificially frozen configurations for electron microscopy or crystallography. Fluorescence anisotropy can be used to examine the rotational diffusion of an attached chromophore. Ref.14 showed correlation times of 168 ns attributed to the global motion of the entire rabbit IgG molecule together with shorter correlation times of about 33 ns attributed to faster motion of Fab arms over an restricted angle. This reinforced the model of an IgG molecule with flexible joints at the junction of the Fab segments15. Ref.16 and17 found similar rotational correlation times of hundreds of nanoseconds that were attributed to global motions of IgG molecules. Several years later, similar antibodies from rabbit were re-examined using fluorescence spectroscopy and the new data indicated that the observed long correlation times were not from tumbling of the whole IgG molecule but rather from large domain motions, e.g. the Fab arms wobbling over the hinge region18. This led to a new dynamic model of the IgG in which large protein domains like Fab arms are not restricted to movements over small angles but are very flexible.
Given such a large molecule, it is a challenge to determine what types of intramolecular motions can be observed and to relate these motions to overall functionality. Neutron Spin Echo (NSE) is a high-resolution space-time resolving spectroscopy that reveals information on time scales from about 10 ps to 500 ns and covers length scales from fractions of a nm to the size of the molecule and beyond, with the advantage that native proteins without special markers are used19,20. NSE has already been successfully applied to investigate the internal dynamics of phosphoglycerate kinase, alcohol dehydrogenase21,22 and intrinsically disordered proteins23. A first NSE study on IgG24 measured the effective diffusion coefficient of pig IgG in solution and showed that some domain motions were present. From a structural perspective, new research involving SAXS shows a strong conformational diversity of IgG molecules in solution with both compact and more “open” conformations and reports angular ranges between the Fab-domains of 100–166°25. A recent combined fluorescence anisotropy and molecular dynamics simulation study finds highly flexible IgG molecules. Simulations suggest strongly correlated inter-domain motions such that antibody molecules can form different contacts for different inter-domain motions26.
We report a detailed study of human IgG domain motions using NSE spectroscopy on a protein solution in order to resolve the motional pattern in space and time. At long Fourier times (t > 15 ns) we observe translational and rotational diffusion with a clear signature of internal dynamics at shorter times. The internal dynamics are related to the fragment motions held together by the linker region and show characteristics of Brownian motion in a harmonic potential. We access information about fragment relaxation time, the force constant related to the flexible linker region, motional amplitudes and the friction exerted on the fragments. NSE is a unique technique that is able to deliver this detailed information, which cannot be accessed by other methods. The results may help to develop new or improved strategies for drug design with the ability to include specific details on the domain dynamics within this complex and unique protein class.
Results
Conformation of IgG in solutions
We used X-ray scattering to investigate the configurations of IgG in solution in a concentration range between 3 and 26.4 mg/ml. Lyophilized IgG powder from human serum was reconstituted in a D2O buffer, thus containing all subclasses of IgG. The measured background corrected and concentration (N/V) normalized intensities are shown in Fig. 2a. The scattering intensity I(Q) of N identical particles is proportional to I(Q) ~ NP(Q)S(Q,c) with the orientation averaged, concentration-independent form factor P(Q) containing information about the shape of the protein and the concentration-dependent structure factor S(Q,c) containing information about the protein-protein interaction as
Figure 2. IgG SAXS scattering profiles.
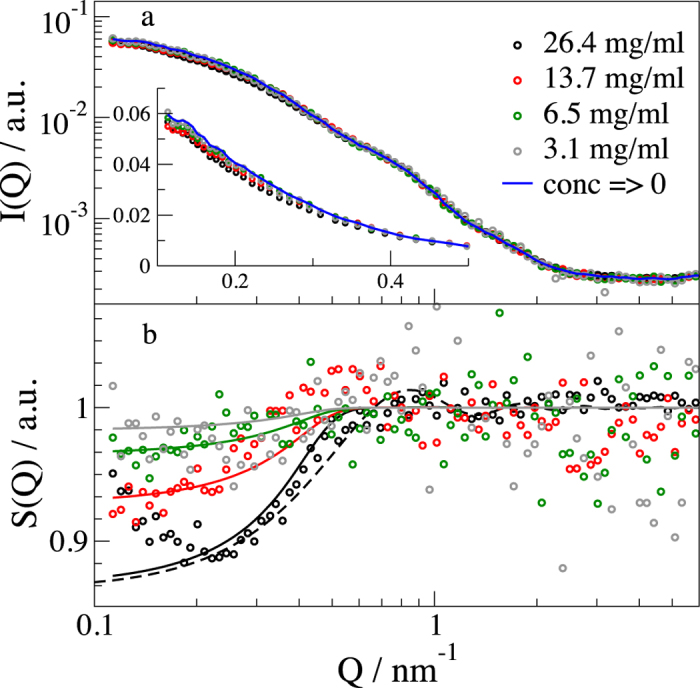
(a) Background corrected and concentration scaled SAXS scattering profiles of IgG. The solid line represents the zero concentration as the form factor. The inset shows the low Q data in linear scale to increase visibility of the structure factor effect. (b) The structure factor extracted by dividing with the form factor. Solid lines represent a fit corresponding to the MSA structure factor including the asymmetry. The dashed black line shows the effect of the asymmetry factor β. For the highest concentration, a small effect of aggregates leads to an increase in the structure factor, which is not observed for lower concentration.
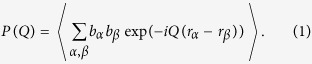 |
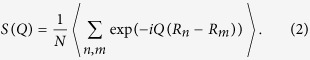 |
Here bα are the scattering amplitude of atom α at position rα and centre of mass positions Rn within the ensemble average indicated by <> and Q represents the solid scattering angle. The scattering length bα is the coherent scattering length for neutron scattering or a Q dependent scattering amplitude27 with bα(0) = Zre for SAXS, where re is the classical radius of the electron and Z is the electron number of the atom. The form factor of a protein can be calculated from the atomic coordinates, if a structure is known e.g. from the PDB databank28. For hard sphere interactions, the structure factor can be calculated in terms of the Percus-Yevick approach29,30. For additional screened coulomb repulsion a MSA structure factor31,32 is expected as observed for many compact proteins in buffers with high salinity33,34. An attractive component is observed if trivalent salts are added to the buffer35. For non-compact and asymmetric particles an apparent structure factor S´(Q) has to be used dependent on the scattering amplitude 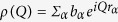 and the asymmetry factor β(Q)36
and the asymmetry factor β(Q)36
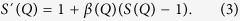 |
with
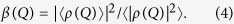 |
From a measurement of several concentrations the form factor and structure factor can be separated (see Methods). In order to obtain a description of the form factor in terms of an atomic model we modified the human IgG monomer structure taken from IgG-ALL.pdb37 (see Fig. 1) to account for the major subclasses IgG1 and IgG2. We allowed for bending and stretching of the linker region with rigid Fab and Fc fragments (see Methods for details). It was not possible to model the scattering data by the monomer alone. However, the dynamic light scattering (DLS) data showed a narrow peak (about 30% width) so only an additional dimer could be present in our sample, which cannot be discriminated within DLS. Modelling with an additional Beaucage function results in a second species with a radius of gyration Rg = 7.4 nm. This is slightly larger than the IgG-ALL.pdb Rg of 5.7 nm but significantly smaller than a dimer with a connection at the variable region of the Fc fragment with Rg of 10.4 nm. Ref.38 proposes head-to-head double Fab arm bound dimers or single arm bound dimers. Using the monomer as a template, we modelled the double arm bound dimer with interlocked Fab fragments with arbitrary touching points resulting in Rg = 7.4 nm as a prototype. Accordingly, the measured form factor is a weighted sum of the form factors of dimer and monomer, and the structure factor is an apparent structure factor including contributions between monomers only, dimers only and between monomers and dimers. In a least squares fit procedure of the mixed form factor, we allow the Fc fragments of the dimer to move around the linker regions. For the monomer, we allow bending and stretching of all fragments around the linker region. Fig. 3 shows the result of the fitting procedure with the individual contributions of monomer, dimer and a residual background together with the corresponding resulting structures. We find a 48% fraction of monomers incorporated into dimers. Dimers show a small bending of the Fc fragments, resulting in Rg = 6.4 nm. The monomer mainly presents a bending of the Fc fragment to one of the arms, resulting in a more compact structure with Rg = 4.8 nm compared to the starting structure. This value is very close to 4.9 nm for IgG1 and 4.7 nm for IgG2 of ref.39. Although we typically obtain a single conformation describing the SAXS data reasonably well, this conformation has to be considered as a representative for the ensemble present in solution. Ensemble fitting, as in the work of ref.39, can result in similar quality fits but may be biased by the choice of flexible connections or by the fact that we also observe dimers. The static picture of a small angle scattering measurement interpreted by a single conformation or a minimal ensemble cannot show directly any dynamics or conformational change. In our single conformation analysis the fit errors of individual bending angles (see Materials and Methods) are large for the monomer α236 = 26° ± 23°, α241 = −44° ± 23°, α247 = −50° ± 28° showing a high degree of flexibility within an acceptable quality of the fit. We might interpret this as a sign of flexibility within the conformation. Nevertheless, the monomer and dimer structures can be used as models to determine the diffusion constants of IgGs.
Figure 3. The SAXS form factor with the fit result.
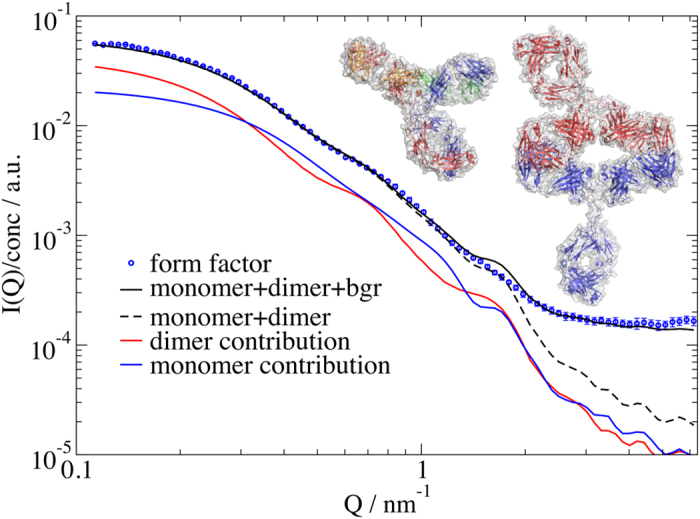
The form factor fit includes 52 ± 4% monomer as monomer and 48 ± 4% monomer in dimers and a background contribution (bgr). The dashed line shows the combined monomer-dimer scattering, the red line shows the contribution of the dimer, while the blue line shows the monomer, all without the residual background. The remaining peak at 1.65 nm−1 might be due to bending inside of the Fab fragments. The graphics show the resulting structure of the monomer with colouring of the chains as in Fig. 1 while the two chains of the dimer are coloured red and blue, both with a grey surface. Figures created with PyMOL (www.pymol.org).
Fig. 2b shows the resulting structure factor for all concentrations. The structure factor is Percus-Yevick like with a hard sphere radius of 3.5 nm, not too far from the results of Scherer et al. with 4.4 nm by light scattering40. As seen for the highest concentration, the asymmetry of IgG described by the asymmetry factor β(Q) has a small influence at low Q but already suppresses the first structure factor peak around 0.9 nm−1 and the following peaks completely. At high Q we observe a plateau in the form factor as residual background, which is about two orders of magnitude below the measured buffer background.
NSE results
Figure 4 displays the intermediate scattering function I(Q,t)/I(Q,t = 0) as measured by NSE. Already by simple inspection, a clear deviation from a simple diffusion process is observed on short times. Fitting the data by the corresponding single exponential decay I(Q,t)/I(Q,t = 0) = exp(−Deff Q2t) one can see a proper fit for long times t with an effective diffusion coefficient Deff. Also, on a ten nanosecond scale, clear indications for a faster relaxation can be observed, which we attribute to motions within the molecule.
Figure 4. Intermediate scattering functions I(Q,t)/I(Q.

,0) of IgG. The Q values are 0.5 nm−1, 0.8 nm−1, 1.1 nm−1, 1.4 nm−1, 1.7 nm−1and 2.0 nm−1 as indicated. Spectra were shifted for clarity upwards by a consecutive factor of 1.3, with the highest Q not shifted. Solid lines in the same color represent the fit by equation (5) with contributions from translational and rotational diffusion from equation (6) & (7) and internal dynamics described by equation 10 with 9 degrees of freedom as described in the text. Dashed lines correspond to the contribution of translational and rotational diffusion and are close to a single exponential for times t > 15 ns. The amplitude of internal dynamics is the difference between the contribution of diffusion and the observed signal, respectively the solid line of the fit curve.
Separation of global and internal dynamics
The coherent intermediate scattering intensity I(Q,t)/I(Q,0) measured by NSE on a protein in solution has contributions from overall translational and rotational diffusion and from motions within the molecule that we call internal dynamics. In the general case, all motions might be coupled. In a simplifying assumption, known as a decoupling approximation, we assume that the internal dynamics (int) do not alter the overall diffusion and that translational (trans) and rotational (rot) diffusion are decoupled too. For the single particle pair correlation function or coherent scattering function we assume
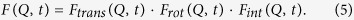 |
Global diffusion
The diffusional terms for a single rigid protein can be described by
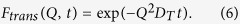 |
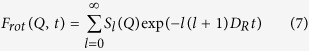 |
with
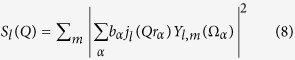 |
where Sl(Q) are the coefficients of a multipole expansion of the asymmetric form factor with scattering length bα of the atom α at position rα and orientation Ωα, jl(Qr) are the spherical Bessel functions and Yl,m(Ωα) the spherical harmonics20,41. The internal dynamics will be discussed later. The measured NSE signal is independent of direct concentration effects as I(Q,t)/I(Q,0) is normalized by I(Q,t = 0). For larger concentrations the protein scalar translational diffusion coefficient DT is influenced by direct interactions subsumed in the structure factor S(Q) and hydrodynamic interaction described by the hydrodynamic function HT(Q). This leads to the correction DT(Q) = DT0HT(Q,c)/S(Q,c)42,43. The hydrodynamic function HT(Q) is found to be constant for flexible proteins20,21,22 and reduces the translational diffusion coefficient with HT(Q) = HT(Q = ∞) = η0/η < 144,45,46. η0/η is measured as the ratio between solvent viscosity η0 and protein solution viscosity at the measured concentration η. Hydrodynamic effects also influence the rotational diffusion coefficient subsumed in the hydrodynamic factor HR for rotational diffusion. According to ref.47 for spherical particles, this effect can be estimated as 1−HR = (1−HT(Q = ∞))/3. For the strongly asymmetric IgG this may be different. From the 6 × 6 diffusion tensor D the effective single rigid protein diffusion coefficient D0(Q) comprising rotational and translational diffusion together can be calculated by19
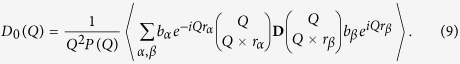 |
The 6 × 6 diffusion tensor D was calculated by HYDROPRO on basis of a valid PDB conformation48. As result we get the scalar diffusion coefficients DT0 = 3.48 × 10−2 nm49/ns and DR0 = 6.96 × 10−4 ns−1 for the monomer and DT0 = 2.71 × 10−2 nm49/ns and DR0 = 3.53 × 10−4 ns−1 for the dimer. The rotational correlation times τr=1/6DR0 for the monomer and dimer are on a scale of 260 ns−1 respectively 500 ns−1 and are longer than the translational diffusion times (e.g. 29 ns at Q = 1 nm−1). Therefore, we can extract the effective diffusion Deff(Q) comprising translational and rotational contributions of the overall protein by applying a single exponential fit for times t > 15 ns. The result is shown in Fig. 5 together with the DLS result for the same concentration as used for NSE measurement. We use equation (9) and the 6 × 6 diffusion tensor D together with the monomer and dimer structure to calculate D0(Q) of the rigid structures (see inset in Fig. 5). The increase from low Q to the higher Q values results from the stronger visibility of the rotational diffusion, if the observation length scale (2π/Q) reaches the size of the protein. At low Q we see only the translational diffusion as measured by DLS. The expected diffusion Deff(Q) of the monomer/dimer mixture can be calculated as the average of monomer and dimer diffusion weighted by the scattering contribution to the form factor as shown in Fig. 3. To include the hydrodynamic effects, the translational contribution Deff(Q = 0) is corrected by HT(Q = ∞) = 0.66 as calculated from viscosity and correspondingly the rotational diffusion contribution Deff(Q)–Deff(Q = 0) as described above by HR. At higher Q we observe a coincidence with the experimental data including only the hydrodynamic correction (see Fig. 5). The additional correction by the structure factor (1/S(Q)) leads to an upturn at low Q and results in an excellent agreement with the DLS measured diffusion coefficient. We note that the excellent agreement of the model and the diffusion coefficients determined from NSE is achieved without fitting of any parameter and proves that the long-time dynamics is attributed to an overall translational and rotational diffusion.
Figure 5. Effective diffusion coefficient Deff.
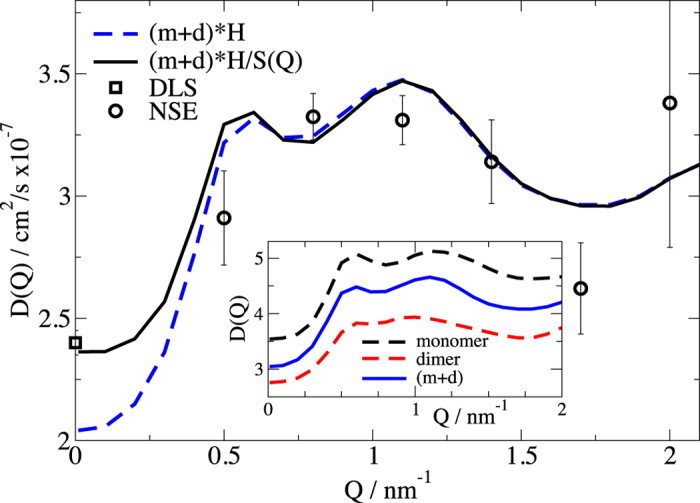
for long Fourier times. Deff (black circles) is the result of fitting I(Q,t)/I(Q,0) = exp(−Q2Defft) for t > 15 ns to the concentration of 29 mg/ml. Black square shows the effective diffusion for low Q as measured by dynamic light scattering at the same concentration. The dashed blue line shows the result for Deff(Q) as a mixture between monomer and dimer including the effect of hydrodynamic interactions. The black solid line additionally includes the structure factor correction. The inset shows the diffusion coefficients for monomer and dimer with the intensity averaged Deff(Q).
Internal dynamics
The specific structure of IgG with three nearly equal sized fragments connected by flexible linkers suggests a simple model of three fragments within a harmonic potential. The flexible linkers may act as springs fixing the relative equilibrium position of the fragments but allowing fluctuations around the equilibrium position. The model is not restricted to IgG but may be used for any protein structure that can be described by relatively rigid domains connected by flexible linkers taking into account the specific three-dimensional arrangement of the fragments and can include additional internal motions in the connected domains (for details see Methods).
We consider Brownian motion of the fragments in a harmonic potential around the equilibrium position 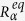 , a problem described by the Ornstein-Uhlenbeck process50,51. The coherent intermediate scattering function
, a problem described by the Ornstein-Uhlenbeck process50,51. The coherent intermediate scattering function 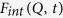 is (for details see Methods)
is (for details see Methods)
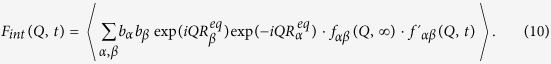 |
Here fαβ(Q,∞) is a time independent Debye–Waller like factor. The time dependent part is
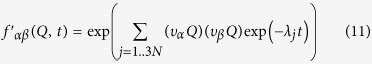 |
with displacements 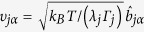 in Brownian normal mode j with relaxation time 1/λj and friction Γj. The contribution of internal dynamics to the NSE signal is
in Brownian normal mode j with relaxation time 1/λj and friction Γj. The contribution of internal dynamics to the NSE signal is 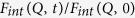 . The dynamics of single independent particles or subunits can be described by the much simpler function (see Methods)
. The dynamics of single independent particles or subunits can be described by the much simpler function (see Methods)
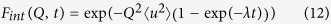 |
with the mean square displacement <u2> in the harmonic potential52. Nevertheless, in this simplification, the specific arrangement of the conformation is lost.
Instead of normal modes that are based on an elastic network model53 with a simplified force field, we chose a reduced set of obvious displacements patterns. In the first model, we consider three perpendicular vectors of unit length for each of the three fragments. One is aligned parallel to the linker from the IgG centre of mass to a fragment centre of mass, the second is aligned perpendicular to the plane spanned by the fragments centre of masses and the third is perpendicular to both, laying inside the plane. The nine displacement vectors were used as vibrational and Brownian modes with equal amplitude and represent nine degrees of freedom (dof 9). The diagonal elements of the friction matrix are equal for all subunits and we use one friction parameter for all. In a second model, we consider a less flexible linker region assuming a length restriction of the linker with forbidden movements along the linker (dof 6). The simplest model, according to equation (12), assumes independent movements of the fragments but results only in the mean square displacement (msd). Fig. 4 shows NSE data and the fit according to equation (5) with contributions from translational and rotational diffusion from equation (6) & (7) and internal dynamics described by equation (10). For all models the translational diffusion DT is fixed to the corrected HYDROPRO result. HR can only be estimated for spherical particles. Here we allow it to be fitted together with the relaxation time and the friction coefficient determining the displacements  . We find an excellent description of the data independent of the model used, with parameters shown in Table 1.
. We find an excellent description of the data independent of the model used, with parameters shown in Table 1.
Table 1. Resulting fit parameters according to different models.
| model | dof 9 | dof 6 | msd |
|---|---|---|---|
| relaxation time [ps] | 6300 ± 1100 | 6600 ± 1100 | 7500 ± 1700 |
| rmsd per mode [nm] | 0.39 ± 0.04 | 0.48 ± 0.04 | 0.44 ± 0.03 |
| friction per atom [g/ps/mol] | 5.7 ± 0.4 | 3.9 ± 0.3 | |
| friction per fragment (Fc/Fab) [g/ps/mol] | 41100 ± 2900/37100 ± 2600 | 28300 ± 2200/25500 ± 2000 | |
| force constant of fragment (Fc/Fab [g/ps2/mol] | 6.5 ± 1.2/5.9 ± 1.1 | 4.2 ± 0.8/3.8 ± 0.7 | 12.8 |
| force constant of fragment (Fc/Fab)[pN/nm] | 10.9 ± 2.0/9.8 ± 1.8 | 7.1 ± 1.3/6.4 ± 1.2 | 21.2 |
| HR | 0.82 ± 0.05 | 0.77 ± 0.06 | 0.77 ± 0.07 |
dof 9 is fitted with 9 degrees of freedom, dof 6 is fitted with 6 degrees of freedom due to restricted motion along the linker, msd is the simplified model according to equation (12). Conversion to pN/nm = 1.66 g/ps2/mol is given for easier comparison with other work
HR is smaller than calculated for hard spheres with 1−(1–0.66)/3 = 0.88, but in reasonable agreement considering the strong asymmetry of IgG reflecting a stronger hydrodynamic interaction. The relaxation time 1/λ is, within the error bars, equal. The displacements 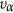 for the models dof 9 and dof 6 have a comparable root mean square displacement (rmsd) as found in the simpler msd model.
for the models dof 9 and dof 6 have a comparable root mean square displacement (rmsd) as found in the simpler msd model.
The friction of the dof 6 model is reduced compared to the dof 9 model to allow larger amplitudes and compensate the smaller number of degrees of freedom with about equal rmsd. The friction of a fragment is the sum over all atoms and differs between Fc and Fab fragments due to the different size. The friction of a non-linked fragment in solvent can be determined by γ = kBT/DT with the Boltzmann constant kB for diffusion at temperature T. DT of the single fragments calculated by HYDROPRO are on the order of 0.06 nm2/ns, leading to a friction of 42500 g/ps/mol and 39200 g/ps/mol for the unbound Fc and Fab fragments, which are very close to the total friction of the bound fragments within the dof 9 model.
We can calculate a force constant for the linker as kj = λjΓj for the dof models and may estimate a corresponding force constant from equipartition for the msd model as k = kBT/rmsd2. We can compare the values given in Table 1 to the force constant of an entropic spring ke = 3kBT/N/b2. With a monomer length b of 0.38 nm per amino acid corresponding to the average distance between Calpha atoms and a length N = 8 residues from the disulfide bonds to the fragment, the entropic force constant is 6.4 g/ps2/mol. Eight segments seem too short to build an entropic spring but even accounting for a twice larger effective length (N = 16) does not change the entropic spring force constant significantly. From the above we can summarize that the linker region acts like a spring. Considering that the friction for the dof 9 model is close to the unbound fragment friction and the force constant is close to an entropic spring, the dof 9 model needs to be favoured.
Estimating the influence of the dimers present, we may assume an extreme case: Within the msd model the average mean square displacement is proportional to the number of fragments contributing to the amplitude. As the dimer is still active38, we can assume that the fragments are partially mobile with the only restriction that the adhered fragments are less mobile or stiff and cannot contribute to the mean square displacement. In this case, 4 bound fragments in a dimer are stiff and 2 are movable. Consequently, 68% of the fragments are mobile and 32% are not flexible and cannot contribute to the observed dynamics. This can be compensated by a 21% increase of the displacement amplitude in the rmsd.
On the other hand, we may compare the expected force at 1 nm displacement (10.7 pN) to the unfolding force of some proteins’ secondary structure. The myomesin domain My6 unfolds at about 200 pN, titin unfolds between 150–300 pN, while spectrin unfolds at about 30 pN54. The observed force is able to unfold loosely bound secondary structure but seems to stay below the ability to unfold even weaker bound secondary structure.
Amplitude of internal motions
The amplitude of the internal dynamics within the NSE signal can be evaluated from the ratio of the internal contribution Fint(Q,t) at infinite time and t = 0. Amplitudes are shown in Fig. 6. In general, we observe an increasing amplitude that follows basically an exp(Q2<u2>) dispersion as expected according to the simple model of a free particle of equation (12). Using dof 9 we find similar, but slightly smaller, amplitude due to interference between the fragments. Restricting to dof 6, we find a smaller contribution at larger Q with a larger contribution at lower Q. Inspecting the individual contributions with respect to the displacement direction, we observe that the displacement along the linker has a stronger contribution at Q > 1.3 nm−1, which is missing for larger Q in the restricted model. Accordingly, the fitting procedure increases the amplitudes to result in an overall good fit.
Figure 6. Amplitude of internal motion as 1−Fint(Q,∞)/(Fint(Q,0).
The result of various models describing the internal dynamics by nine degrees of freedom (dof 9, red squares), as independent particles (msd, black circles) and by six degrees of freedom with the displacements along the spring fixed (dof 6, green triangle). The dispersion of 9 (black solid line) is composed of the individual contributions of displacements perpendicular (dashed, grey) and in the plane (dashed, red) and along the linker (dashed, green). Restricting the movements along the linker to six dof shows smaller amplitudes at larger Q corresponding to the stronger contribution of the movements along the linker above 1.3 nm−1. Adding hinge bending within the Fab fragments to the dof 9 model (dash-double-dotted, blue) shows stronger amplitude around 1.3 nm−1 in correspondence to the single contribution (dash-dotted, blue). A fit with this model reduces the hinge contribution to small amplitudes.
To test whether we can observe an additional contribution from hinge bending in the Fab fragment we allow for bending of the variable region (V) against the constant region (C) of the Fab fragments. With this movement included into the model, the fit leads to negligible amplitude for this bending intra Fab displacement. In order to show how such a displacement would reveal itself in the experimental results, we assume a bending contribution of ±30°. In Fig. 6 this additional contribution gives rise to peaks contributing between 1 and 1.5 nm−1, which is not seen in the NSE measurements. We therefore conclude that such bending amplitudes are quite small, or possible conformational changes are much slower than the observed timescale.
The angle between fragments can be defined as the angle between the fragment centers of mass with the disulfide bonds in the linker as the origin, which are in fact close to the center of mass of the IgG-ALL.pdb. For the IgG-ALL.pdb structure the angle between the Fab fragments is 103° and from Fab to Fc fragments it is 128°. The angular amplitude for the dof 9 model is about 5° for each fragment and around 6° for the restricted dof 6 model. The “in plane” angle provides the main contribution to the angular displacement between the fragments. Symmetric and asymmetric deformations lead to an angular range ±10° between two fragments. Consequently, the full width in angular range is about 20° for displacements within an average energy of kBT in the harmonic potential. If we allow 3 kBT to include 31/2 times the width of the Gaussian distribution in the harmonic potential (about 95% of the allowed deformations), then we obtain about 35°. Ref. 25 reports within an ensemble optimized fitting (EOM) analysis of SAXS experiments an angular range from 100°–166° between the Fab fragments and 56°–124° between Fab-Fc fragments. Ref.55 reports 115°–172° between the Fab and 66°–123° to the Fc fragment from crystallographic analysis. Ref.39 classifies less accurately between more T-shaped and Y-shaped conformations. Both of the first analyses try to define sets, which reflect a minimal to maximal allowed range that are about 2–3 times larger compared to our results. Ref.25 finds a bimodal distribution of sizes interpreted as “open” or “closed” configuration in structural equilibrium25. These “open” or “closed” structures are interpreted within the pre-existing equilibrium model initially formulated by Pauling. Different coexisting configurations are assumed to exist in equilibrium exhibiting different binding sites and binding specifity56. The pre-existing equilibrium model was shown to be valid for antibodies in ref.57 for different IgG1 monoclonal antibodies and in ref.58 for SPE7. EOM seems to capture an average picture of all equilibrium configurations and might give a picture of different pre-existing configurations. However, in contrast to the EOM method, our measurement is a direct determination of displacements and force constant in an equilibrium configuration that is also independent of the actual mean configuration. The relaxation time of about 6.3 ns seems quite fast but is comparable to the necessary time for the free fragment to diffuse over a length of the rmsd we found.
Conclusion
This study focused on the fragment motion of IgG. In the experiment, aside from strong diffusion contributions, a clear signature of the internal dynamics on a timescale of 6–7 ns was observed. The combination of translational and rotational diffusion of the rigid protein describes the observed long time dynamics on an absolute scale, despite the fact that we have a mixed population of monomers and dimers, as found in serum.
The fragment motion shows itself in terms of a strong decay of S(Q,t) at short times, well separated from the overall diffusional relaxation. The data were analysed in terms of an Ornstein-Uhlenbeck like relaxation within a harmonic potential. Such an approach neglects the details of the complex linker region interaction on the residue level. Nevertheless, the dynamics is described in an excellent way. Even for a short flexible linker the ensemble average seems to be sufficient to produce the characteristics of a harmonic spring. The obtained spring constant appears to be realistic compared to an entropic spring of similar length. The resulting forces stay below the limits that would be necessary to unfold the secondary structure of the attached fragments. The observed effective friction appears to be close to the friction of a free unbound fragment. None of the directions seems to be suppressed.
The pre-existing equilibrium hypothesis56, with multiple local minima in the configurational energy landscape, will have long transition times between the minima but is compatible with fast 6–7 ns motions in the local minima. Consequently, NSE observes the fast dynamics in pre-existing equilibrium states. The conformational flexibility in a pre-existing equilibrium configuration might be needed to adapt faster to a specific antigen when the antigen approaches the binding site of a fragment.
NSE delivers unique, direct information about the internal dynamics of IgG, which cannot be resolved by any other technique. The Ornstein-Uhlenbeck model is able to give information about amplitude, friction, and force constant of domains bound by flexible linkers or for domain motions with more complex joint topology. Therefore, different hinge types dependent on the protein structure can be directly compared within the same model. For IgG the key questions for the future will be how the buffer environment or mutations to IgG influence the dynamics. Also, the dynamics of the various types of immunoglobulins can be examined. This information may be relevant to understand how monoclonal antibodies can be used as drugs and how to improve biocompatibility and bioavailability.
Methods
Sample preparation and characterization
IgG from human serum was purchased from Sigma-Aldrich as lyophilized powder (Prod. Code 56834) and reconstituted in a 50 mM sodium phosphate D2O buffer with 0.1 M sodium chloride at pH 6.6. All measurements were done at 25 °C. Samples were centrifuged overnight to remove any larger aggregates. Samples with 3.1, 6.5, 13.7 and 26.4 mg/ml concentration were prepared for SAXS measurements. For the NSE experiment, one sample was prepared with a concentration of 29 mg/ml. Protein concentration was determined by absorbance at 280 nm with E1% = 14. Protein solutions for NSE were dialyzed for 24 h of equilibration within the D2O buffer. As a background sample, we used the dialysate after equilibration to account for exchanged hydrogen atoms. Dynamic Light Scattering (DLS) measurements (Zetasizer Nano, Malvern) on a concentration series from 0.8 to 29 mg/ml were performed to observe the size distribution, detect possible aggregation and to obtain the diffusion coefficient of IgG for infinite dilution by extrapolation to zero concentration (see supplementary information). Larger aggregates were only observed in negligible amount during DLS measurements. The width of the observed peak was about 30% typical for monomeric solutions. The experimental DLS diffusion coefficients as a function of protein concentration are shown in supplementary Fig. S1a. Viscosity measurements (rolling ball viscometer, Lovis 2000, Anton Paar) also were performed for the same concentration series to determine the intrinsic viscosity. Viscosity experimental data are shown in supplementary Fig. S1b.
Small-Angle X-ray scattering
SAXS was measured on a Kratky type SAXS instrument (SAXSpace, Anton Paar) at FZ-Jülich with X-ray wavelength of 0.154 nm. Samples were loaded in quartz capillaries of 1 mm diameter and measured for 1 h counting time per sample. The measured intensities were corrected for dark current, empty cell and solvent scattering following standard procedures and desmeared according to the built-in Lake algorithm within the SAXQuant software (Anton Paar). Data were averaged over Q to achieve a smaller noise at larger Q.
Form factor and structure factor are separated by a self-consistent optimization procedure. The measured intensities I(Q,c) are background corrected and scaled by concentration c followed by division with a structure factor S´(Q,c) to result in a form factor P(Q,c) = (I(Q,c)-bgr)/c/S´(Q,c). Form factors P(Q,c) for all concentrations yield the averaged form factor 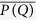 . Structure factor parameters as size or charge, concentration and background contribution are iteratively optimized to minimize the squared relative deviation of the form factors from the average form factor χ2 = Σc(P(Q,c)/
. Structure factor parameters as size or charge, concentration and background contribution are iteratively optimized to minimize the squared relative deviation of the form factors from the average form factor χ2 = Σc(P(Q,c)/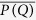 −1) to result in a self-consistent pair of averaged form factor
−1) to result in a self-consistent pair of averaged form factor 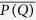 and structure factor parameters. Compared to the usual procedure of extrapolating the data to zero concentration to yield the form factor and subsequently the structure factor, this procedure results in lower errors for the form factor and the structure factor.
and structure factor parameters. Compared to the usual procedure of extrapolating the data to zero concentration to yield the form factor and subsequently the structure factor, this procedure results in lower errors for the form factor and the structure factor.
Neutron Spin Echo Spectroscopy experimental setup
The NSE experiment was performed at J-NSE instrument, JCNS outstation at the MLZ Garching, Germany, at incident wavelengths of 8 Å, 10 Å and 12 Å accessing a dynamical range of 0.1 ≤ tmax ≤ 130 ns for several momentum transfers, Q, between 0.05 Å−1 and 0.2 Å−1. The entire detector area was summed up to reduce errors. The sample was loaded in a top loader quartz container of 40 × 30 × 4 mm and NSE spectra were taken at 25 °C. As a reference measurement, we used a Graphite powder sample loaded in an identical container and measured with the same instrument setup. Solvent buffer measurement was done under the same conditions with the dialysate for proper data reduction. Data analysis to yield the intermediate scattering function was performed with the ECHODET software package of the NSE instrument.
Modelling and calculations
For atomic modelling we use MMTK from ref.59 to handle pdb structure files, access atomic coordinates and perform rotations and translations of subparts of the protein structure. SAXS scattering is calculated with a coarse graining on the amino acid level by assuming Q dependent scattering amplitudes for each amino acid including the contrast to the solvent buffer similar to ref.57. The NSE intermediate scattering function is calculated by coarse graining to 199 individual grains. Individual scattering amplitudes for each grain are calculated as the root of the grain form factors in sufficient accuracy compared to atomic resolution, similar to ref.57 for amino acids.
As a starting configuration, we use IgG-ALL.pdb of Padlan37 as shown in Fig. 1. Fragment bending flexibility in the linker is realized by two rotations around the axis through both Pro236-Ca atoms respectively Pro241-Ca of the heavy chains (α236, α241). These axes are approximately perpendicular to each other and located close to two disulfide bonds of IgG1 in the linker region. Additionally, the Fc fragment can move around the axis between both Pro247-Ca of the heavy chains to allow asymmetric deformation (α247). Stretching of the linker region is implemented by stretching all atom positions of both heavy chains with a stretching factor between Pro236-Ca and Pro246-Ca and each chain individually between Pro231-Ca atoms respectively Pro236-Ca. Bending in the Fab fragments could be achieved by rotation around the axis defined by Ser228-Ca of the light and heavy chains. Specific positions for bending are arbitrarily chosen but represent positions where a good description of an overall flexibility can be expected. Coarse Graining is applied after application of bending and stretching.
Brownian motion of the fragments in a harmonic potential
In the following, we consider Brownian motion in a harmonic potential around the equilibrium position 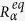 , a problem described by the Ornstein-Uhlenbeck process50,51 and follow refs.55,60 in the derivation of the corresponding correlation function for coherent neutron scattering Fcoh(Q,t). Restricting the analysis to the internal coordinates of the protein, the translational and rotational degrees of freedom are separated. The rotational and translational degrees of freedom are described by rotational and translational diffusion, which can be treated within the decoupling approximation according to equation (5) and equation (6). The coherent intermediate scattering function Fcoh(Q,t) of atoms or subunits α with coherent scattering length bα at positions Rα describing our internal dynamics can be written as
, a problem described by the Ornstein-Uhlenbeck process50,51 and follow refs.55,60 in the derivation of the corresponding correlation function for coherent neutron scattering Fcoh(Q,t). Restricting the analysis to the internal coordinates of the protein, the translational and rotational degrees of freedom are separated. The rotational and translational degrees of freedom are described by rotational and translational diffusion, which can be treated within the decoupling approximation according to equation (5) and equation (6). The coherent intermediate scattering function Fcoh(Q,t) of atoms or subunits α with coherent scattering length bα at positions Rα describing our internal dynamics can be written as
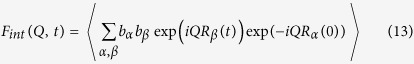 |
For larger subunits or coarse graining the scattering amplitude can be substituted by Q dependent scattering amplitude. With displacements 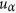 from the time independent equilibrium position
from the time independent equilibrium position 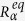 we can use
we can use 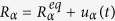 and
and  resulting in
resulting in
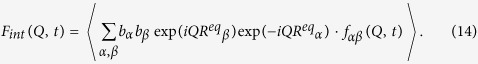 |
We describe the internal dynamics by a Langevin type equation as 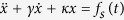 with position vector x, friction matrix γ, force constant matrix κ and random acceleration fs(t) in mass weighted coordinates and mass weighted friction and force constants52. In the case of vanishing friction (γ = 0), normal mode analysis with the eigenequation
with position vector x, friction matrix γ, force constant matrix κ and random acceleration fs(t) in mass weighted coordinates and mass weighted friction and force constants52. In the case of vanishing friction (γ = 0), normal mode analysis with the eigenequation 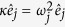 of eigenvalues
of eigenvalues 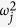 and eigenvectors
and eigenvectors 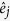 results in oscillating solutions describing vibrational motion. Here, we restrict ourselves to the highly over-damped case of high friction with a negligible acceleration term
results in oscillating solutions describing vibrational motion. Here, we restrict ourselves to the highly over-damped case of high friction with a negligible acceleration term  . The high friction solution of Smoluchowski dynamics is solved by the eigenequation
. The high friction solution of Smoluchowski dynamics is solved by the eigenequation 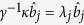 of eigenvalues λj and eigenvectors
of eigenvalues λj and eigenvectors 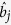 with characteristic exponentially decaying solutions. For details about the derivation of low and high friction limits see refs.55,60. According to the nature of the modes, the
with characteristic exponentially decaying solutions. For details about the derivation of low and high friction limits see refs.55,60. According to the nature of the modes, the 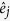 are called elastic or vibrational normal modes, while the
are called elastic or vibrational normal modes, while the 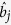 are called brownian normal modes indicating that the Brownian motion characterizes the modes and eigenvalues.
are called brownian normal modes indicating that the Brownian motion characterizes the modes and eigenvalues.
Using the normal modes we may decompose the last term fαβ(Q,t) in equation (14) in a constant term and a term describing the time dependence
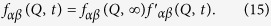 |
The constant term is related to the vibrational modes and only dependent on the harmonic potential as
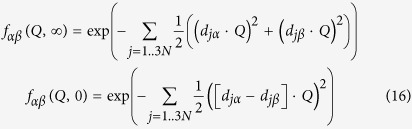 |
with vibrational displacement 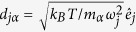 of subunit α in normal mode j. djα is the displacement vector that corresponds to the width in a Gaussian distribution around equilibrium configuration
of subunit α in normal mode j. djα is the displacement vector that corresponds to the width in a Gaussian distribution around equilibrium configuration 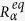 in the harmonic potential with force constant
in the harmonic potential with force constant 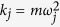 along normal mode j.
along normal mode j.
In the high friction limit the time dependent part within Smoluchowski dynamics is described by
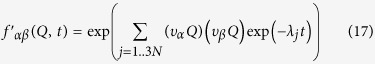 |
with displacements 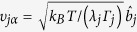 of subunit α in Brownian normal mode j and friction
of subunit α in Brownian normal mode j and friction 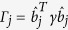 .
. 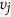 is the displacement vector within relaxation time 1/λj. A force constant can be estimated by
is the displacement vector within relaxation time 1/λj. A force constant can be estimated by 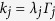 . We assume the friction matrix γ to be diagonal and zero off diagonal terms61. For equal valued diagonal friction matrix, the vibrational and Brownian modes are equal and mode displacements can be used to calculate the displacement between the fragments. Friction with the solvent may be attributed to surface subunits, but can also be equally distributed for rigid domains for simplicity. For independent relaxing modes the mean square displacement is
. We assume the friction matrix γ to be diagonal and zero off diagonal terms61. For equal valued diagonal friction matrix, the vibrational and Brownian modes are equal and mode displacements can be used to calculate the displacement between the fragments. Friction with the solvent may be attributed to surface subunits, but can also be equally distributed for rigid domains for simplicity. For independent relaxing modes the mean square displacement is 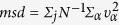 .
.
The coherent intermediate scattering function describing the internal dynamics is finally
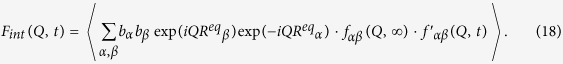 |
The contribution of internal dynamics to the NSE signal can be calculated accordingly by
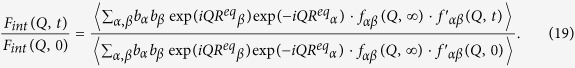 |
The close similarity of numerator and denominator let us perceive that the dominating term describing the time evolution is of the form exp(−~exp(−t)). In fact, for the case of a single independent particle in a harmonic trap, the dynamics can be described by the much simpler function shown in equ. (12).
Additional Information
How to cite this article: Stingaciu, L. R. et al. Fast antibody fragment motion: flexible linkers act as entropic spring. Sci. Rep. 6, 22148; doi: 10.1038/srep22148 (2016).
Supplementary Material
Acknowledgments
Neutron beam time for this research was allocated by Jülich Center for Neutron Sciences, JCNS1, outstation at MLZ, 85747 Garching, Germany. The authors acknowledge Dr. Christopher B. Stanley from Oak Ridge National Laboratory for proofreading the manuscript.
Footnotes
Author Contributions L.S. and R.B. designed and performed the experiments, analyzed the data, discussed results and wrote the paper; R.B. developed the model, wrote the code and supervised; D.R. supervised, discussed the results and wrote the paper; O.I. was the local contact for the NSE experiment and contributed to editing; M.O. discussed data and contributed to editing.
References
- Weiner L. M. & Carter P. The rollercoaster ride to anti-cancer antibodies. Nat. Biotechnol. 21, 510–1 (2003). [DOI] [PubMed] [Google Scholar]
- Tian X., Langkilde A. E., Thorolfsson M., Rasmussen H. B. & Vestergaard B. Small-angle x-ray scattering screening complements conventional biophysical analysis: comparative structural and biophysical analysis of monoclonal antibodies IgG1, IgG2 and IgG4. J. Pharm. Sci. 103, 1701–10 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cser L. et al. Neutron small-angle scattering studies of the general structure of the immunoglobulin G molecule. FEBS Lett. 68, 283–287 (1976). [DOI] [PubMed] [Google Scholar]
- Rayner L. E. et al. The solution structure of rabbit IgG accounts for its interactions with the Fc receptor and complement C1q and its conformational stability. J. Mol. Biol. 425, 506–23 (2013). [DOI] [PubMed] [Google Scholar]
- Gregory L et al. The solution conformations of the subclasses of human IgG deduced from sedimentation and small angle X-ray scattering studies. Mol. Immunol. 24, 821–829 (1987). [DOI] [PubMed] [Google Scholar]
- Sandin S., Ofverstedt L.-G., Wikström A.-C., Wrange O. & Skoglund U. Structure and flexibility of individual immunoglobulin G molecules in solution. Structure 12, 409–15 (2004). [DOI] [PubMed] [Google Scholar]
- Kamerzell T. J., Ramsey J. D. & Middaugh C. R. Immunoglobulin dynamics, conformational fluctuations and nonlinear elasticity and their effects on stability. J. Phys. Chem. B 112, 3240–50 (2008). [DOI] [PubMed] [Google Scholar]
- Krauss W. C., Park J. W., Kirpotin D. B., Hong K. & Benz C. C. Emerging antibody-based HER2 (ErbB-2/neu) therapeutics. Breast Dis. 11, 113–24 (2000). [DOI] [PubMed] [Google Scholar]
- Milenic D. E., Brady E. D. & Brechbiel M. W. Antibody-targeted radiation cancer therapy. Nat. Rev. Drug Discov. 3, 488–99 (2004). [DOI] [PubMed] [Google Scholar]
- Correia I. R. Stability of IgG isotypes in serum . MAbs 2, 221–232 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidarsson G., Dekkers G. & Rispens T. IgG Subclasses and Allotypes: From Structure to Effector Functions. Front. Immunol. 5, 520 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wymann S. et al. Monomerization of dimeric IgG of intravenous immunoglobulin (IVIg) increases the antibody reactivity against intracellular antigens. Mol. Immunol. 45, 2621–8 (2008). [DOI] [PubMed] [Google Scholar]
- Boehm M. K., Woof J. M., Kerr M. A. & Perkins S. J. The Fab and Fc fragments of IgA1 exhibit a different arrangement from that in IgG: a study by X-ray and neutron solution scattering and homology modelling. J. Mol. Biol. 286, 1421–47 (1999). [DOI] [PubMed] [Google Scholar]
- Yguerabide J., Epstein H. F. & Stryer L. Segmental flexibility in an antibody molecule. J. Mol. Biol. 51, 573–590 (1970). [DOI] [PubMed] [Google Scholar]
- Valentine R. C. & Green N. M. Electron microscopy of an antibody-hapten complex. J. Mol. Biol. 27, 615–617 (1967). [DOI] [PubMed] [Google Scholar]
- Chan L. M. & Cathou R. E. The role of the inter-heavy chain disulfide bond in modulating the flexibility of immunoglobulin G antibody. J. Mol. Biol. 112, 653–656 (1977). [DOI] [PubMed] [Google Scholar]
- Lovejoy C., Holowka D. A. & Cathou R. E. Nanosecond fluorescence spectroscopy of pyrenebutyrate-anti-pyrene antibody complexes. Biochemistry 16, 3668–3672 (1977). [DOI] [PubMed] [Google Scholar]
- Hanson D. C., Yguerabide J. & Schumaker V. N. Segmental flexibility of immunoglobulin G antibody molecules in solution: a new interpretation. Biochemistry 20, 6842–6852 (1981). [DOI] [PubMed] [Google Scholar]
- Biehl R., Monkenbusch M. & Richter D. Exploring internal protein dynamics by neutron spin echo spectroscopy. Soft Matter 7, 1299 (2011). [Google Scholar]
- Biehl R. & Richter D. Slow internal protein dynamics in solution. J. Phys. Condens. Matter 26, 503103 (2014). [DOI] [PubMed] [Google Scholar]
- Inoue R. et al. Large Domain Fluctuations on 50-ns Timescale Enable Catalytic Activity in Phosphoglycerate Kinase. Biophys J 99, 2309–2317 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biehl R. et al. Direct Observation of Correlated Interdomain Motion in Alcohol Dehydrogenase. Phys. Rev. Lett. 101, 138102 (2008). [DOI] [PubMed] [Google Scholar]
- Stadler A. M. et al. Internal nanosecond dynamics in the intrinsically disordered myelin basic protein. J. Am. Chem. Soc. 136, 6987–94 (2014). [DOI] [PubMed] [Google Scholar]
- Alpert Y. et al. Segmental flexibility in pig immunoglobulin G studied by neutron spin-echo technique. Biopolymers 24, 1769–1784 (1985). [DOI] [PubMed] [Google Scholar]
- Lilyestrom W. G., Shire S. J. & Scherer T. M. Influence of the cosolute environment on IgG solution structure analyzed by small-angle X-ray scattering. J. Phys. Chem. B 116, 9611–8 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kortkhonjia E. et al. Probing antibody internal dynamics with fluorescence anisotropy and molecular dynamics simulations. MAbs 5, 306–322 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rez D., Rez P. & Grant I. Dirac–Fock calculations of X-ray scattering factors and contributions to the mean inner potential for electron scattering. Acta Crystallogr. Sect. A Found. Crystallogr. 50, 481–497 (1994). [Google Scholar]
- Berman H. M. The Protein Data Bank. Nucleic Acids Res. 28, 235–242 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Percus J. K. & Yevick G. J. Analysis of Classical Statistical Mechanics by Means of Collective Coordinates. Phys. Rev. 110, 1–13 (1958). [Google Scholar]
- Wertheim M. S. Exact Solution of the Percus-Yevick Integral Equation for Hard Spheres. Phys. Rev. Lett. 10, 321–323 (1963). [Google Scholar]
- Hayter J. B. & Penfold J. An analytic structure factor for macroion solutions. Mol. Phys. 42, 109–118 (1981). [Google Scholar]
- Longeville S., Doster W. & Kali G. Myoglobin in crowded solutions: structure and diffusion. Chem. Phys. 292, 413–424 (2003). [Google Scholar]
- Doster W. & Longeville S. Microscopic Diffusion and Hydrodynamic Interactions of Hemoglobin in Red Blood Cells. Biophys J. 93, 1360–1368 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svergun D. I., Koch M. H. J., Timmins P. A. & May R. P. Small Angle X-Ray and Neutron Scattering from Solutions of Biological Macromolecules. (OUP Oxford, 2013). [Google Scholar]
- Zhang F. et al. Reentrant Condensation of Proteins in Solution Induced by Multivalent Counterions. Phys. Rev. Lett. 101, 148101 (2008). [DOI] [PubMed] [Google Scholar]
- Kotlarchyk M. & Chen S.-H. Analysis of small angle neutron scattering spectra from polydisperse interacting colloids. J. Chem. Phys. 79, 2461 (1983). [Google Scholar]
- Padlan E. A. Anatomy of the antibody molecule. Mol. Immunol. 31, 169–217 (1994). [DOI] [PubMed] [Google Scholar]
- Deperalta G. et al. Structural analysis of a therapeutic monoclonal antibody dimer by hydroxyl radical footprinting. MAbs 5, 86–101 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian X. et al. In-depth analysis of subclass-specific conformational preferences of IgG antibodies. IUCrJ 2, 9–18 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherer T. M., Liu J., Shire S. J. & Minton A. P. Intermolecular interactions of IgG1 monoclonal antibodies at high concentrations characterized by light scattering. J. Phys. Chem. B 114, 12948–57 (2010). [DOI] [PubMed] [Google Scholar]
- Lindsay H., Klein R., Weitz D., Lin M. & Meakin P. Effect of rotational diffusion on quasielastic light scattering from fractal colloid aggregates. Phys. Rev. A 38, 2614–2626 (1988). [DOI] [PubMed] [Google Scholar]
- Pusey P. N. The dynamics of interacting Brownian particles. J. Phys. A. Math. Gen. 8, 1433–1440 (1975). [Google Scholar]
- Ackerson B. J. Correlations for interacting Brownian particles. J. Chem. Phys. (1976). doi: 10.1063/1.431957 [DOI] [Google Scholar]
- Mazur P. & Saarloos W. Van. Many-sphere hydrodynamic interactions and mobilities in a suspension. Phys. A Stat. Mech. its Appl. 115, 21–57 (1982). [Google Scholar]
- Beenakker C. W. J. & Mazur P. Self-diffusion of spheres in a concentrated suspension. Phys. A Stat. Mech. its Appl. 120, 388–410 (1983). [Google Scholar]
- Beenakker C. W. J. & Mazur P. Diffusion of spheres in a concentrated suspension II. Phys. A Stat. Mech. its Appl. 126, 349–370 (1984). [Google Scholar]
- Degiorgio V., Piazza R. & Jones R. B. Rotational diffusion in concentrated colloidal dispersions of hard spheres. Phys. Rev. E 52, 2707–2717 (1995). [DOI] [PubMed] [Google Scholar]
- Ortega A., Amorós D., Torre J. de la & de la Torre J. G. Prediction of Hydrodynamic and Other Solution Properties of Rigid Proteins from Atomic- and Residue-Level Models. Biophys. J. 101, 892–898 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquart M., Deisenhofer J., Huber R. & Palm W. Crystallographic refinement and atomic models of the intact immunoglobulin molecule Kol and its antigen-binding fragment at 3.0 Å and 1.9 Å resolution. J. Mol. Biol. 141, 369–391 (1980). [DOI] [PubMed] [Google Scholar]
- Uhlenbeck G. & Ornstein L. On the Theory of the Brownian Motion. Phys. Rev. 36, 823–841 (1930). [Google Scholar]
- Wang M. & Uhlenbeck G. On the Theory of the Brownian Motion II. Rev. Mod. Phys. 17, 323–342 (1945). [Google Scholar]
- Kneller G. R. Quasielastic neutron scattering and relaxation processes in proteins: analytical and simulation-based models. Phys. Chem. Chem. Phys. 7, 2641–55 (2005). [DOI] [PubMed] [Google Scholar]
- Tirion & Tirion M. M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys Rev Lett 77, 1905–1908 (1996). [DOI] [PubMed] [Google Scholar]
- Fisher T. E., Oberhauser A. F., Carrion-Vazquez M., Marszalek P. E. & Fernandez J. M. The study of protein mechanics with the atomic force microscope. Trends Biochem. Sci. 24, 379–84 (1999). [DOI] [PubMed] [Google Scholar]
- Saphire E. O. et al. Contrasting IgG structures reveal extreme asymmetry and flexibility. J. Mol. Biol. 319, 9–18 (2002). [DOI] [PubMed] [Google Scholar]
- Pauling L. A Theory of the Structure and Process of Formation of Antibodies *. J. Am. Chem. Soc. 62, 2643–2657 (1940). [Google Scholar]
- Yang S., Park S., Makowski L. & Roux B. A rapid coarse residue-based computational method for x-ray solution scattering characterization of protein folds and multiple conformational states of large protein complexes. Biophys. J. 96, 4449–63 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kneller G. R. Inelastic neutron scattering from damped collective vibrations of macromolecules. Chem. Phys. 261, 1–24 (2000). [Google Scholar]
- Hinsen K. The molecular modeling toolkit: A new approach to molecular simulations. J. Comput. Chem. 21, 79–85 (2000). [Google Scholar]
- Deisenhofer J. Crystallographic refinement and atomic models of a human Fc fragment and its complex with fragment B of protein A from Staphylococcus aureus at 2.9- and 2.8-A resolution. Biochemistry 20, 2361–70 (1981). [PubMed] [Google Scholar]
- Hinsen K., Petrescu A.-J., Dellerue S., Bellissent-Funel M.-C. & Kneller G. R. Harmonicity in slow protein dynamics. Chem. Phys. 261, 25–37 (2000). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


